Research on Dynamic Modeling Method and Flying Gait Characteristics of Quadruped Robots with Flexible Spines
Abstract
1. Introduction
2. Quadruped Robot Model
2.1. Dynamic Models of Varying Degrees of Simplification
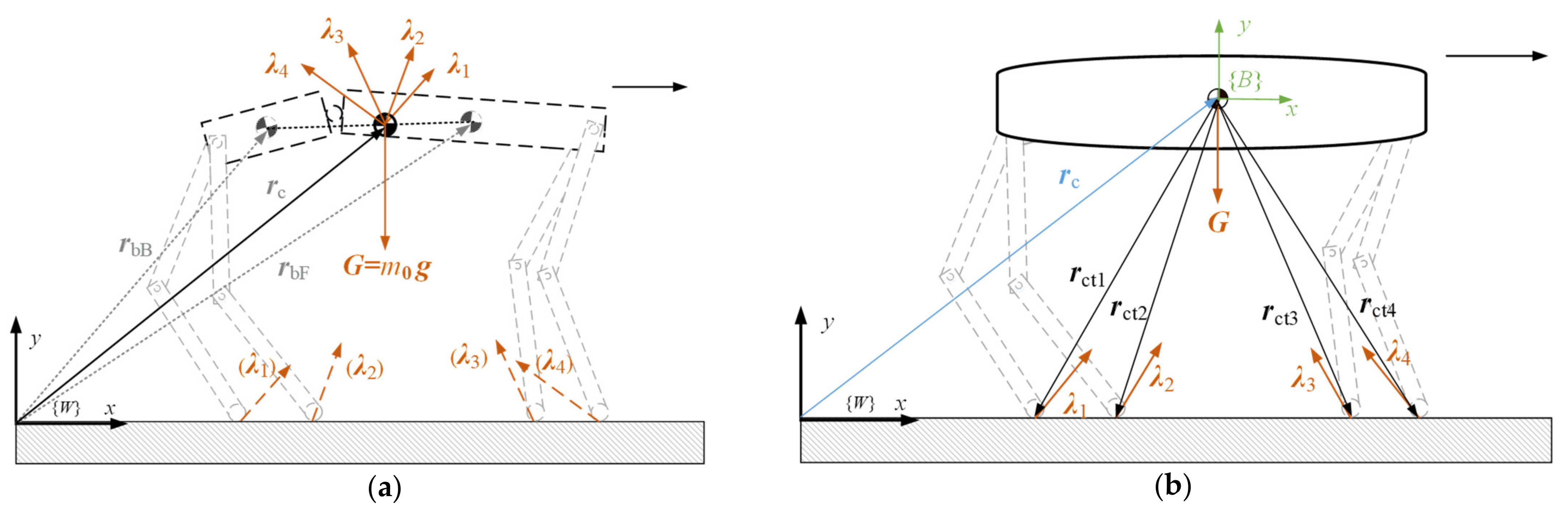
2.1.1. Point Mass Model
2.1.2. Single-Rigid-Body Model
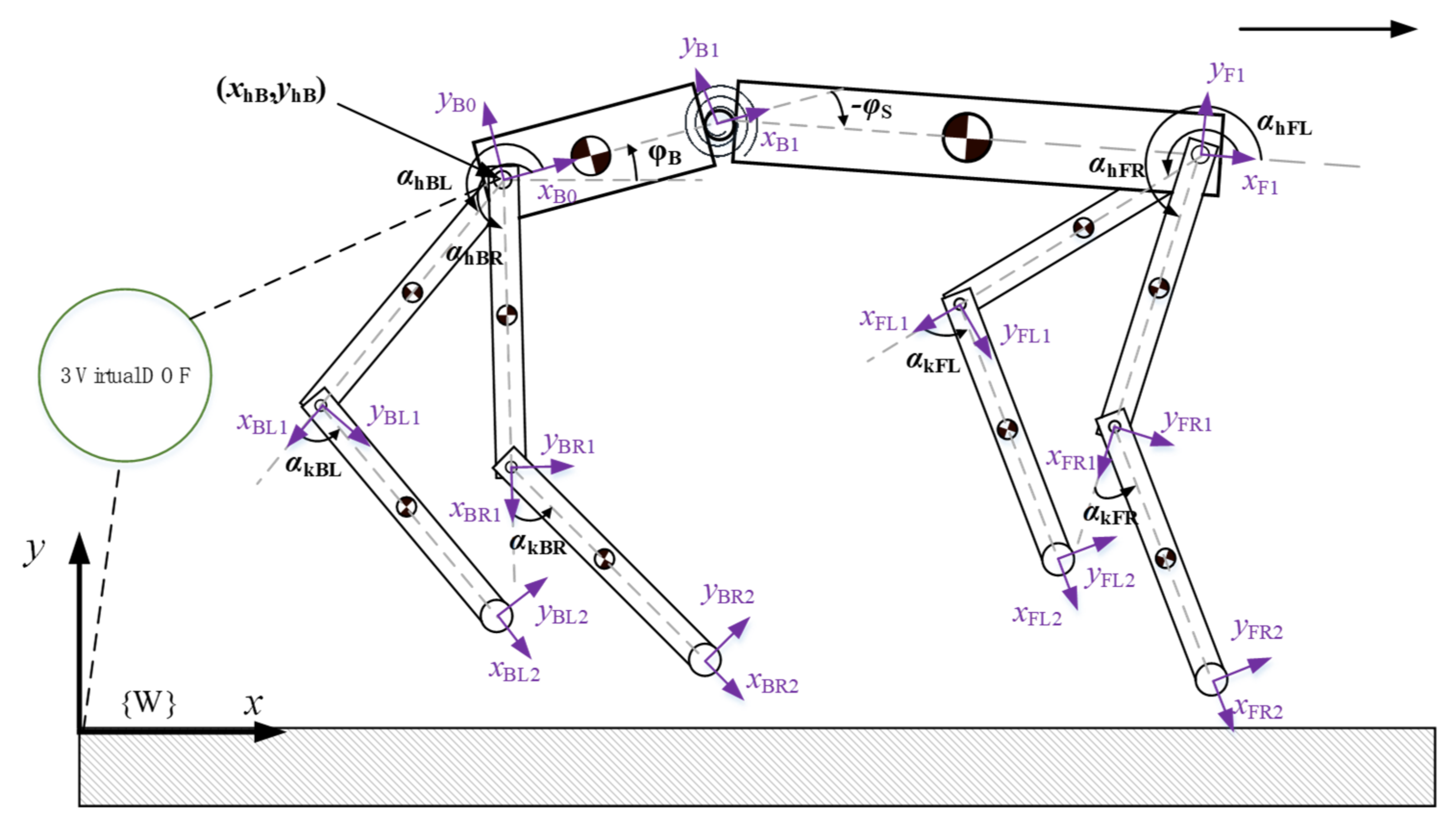
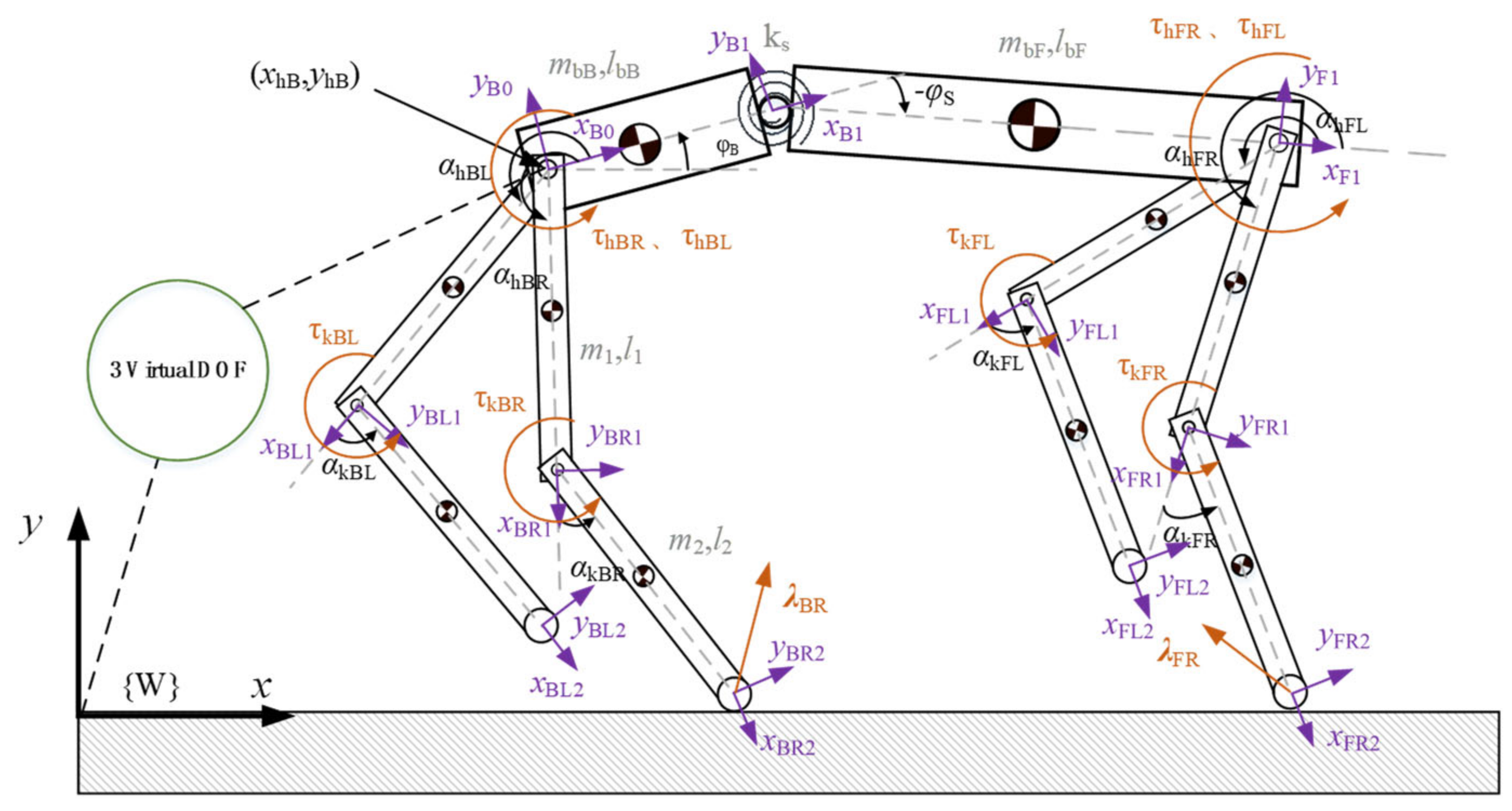
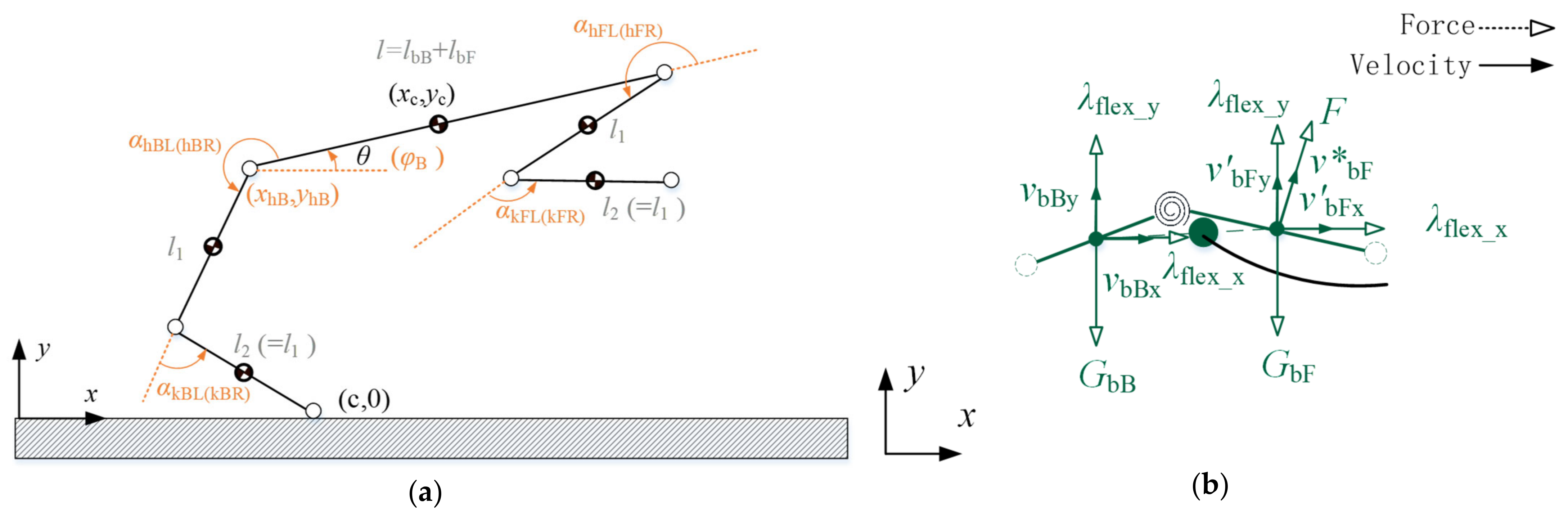
2.1.3. Planar Multiple-Rigid-Body Model
3. Quadruped Robot Flight Phase Motion Parameterization
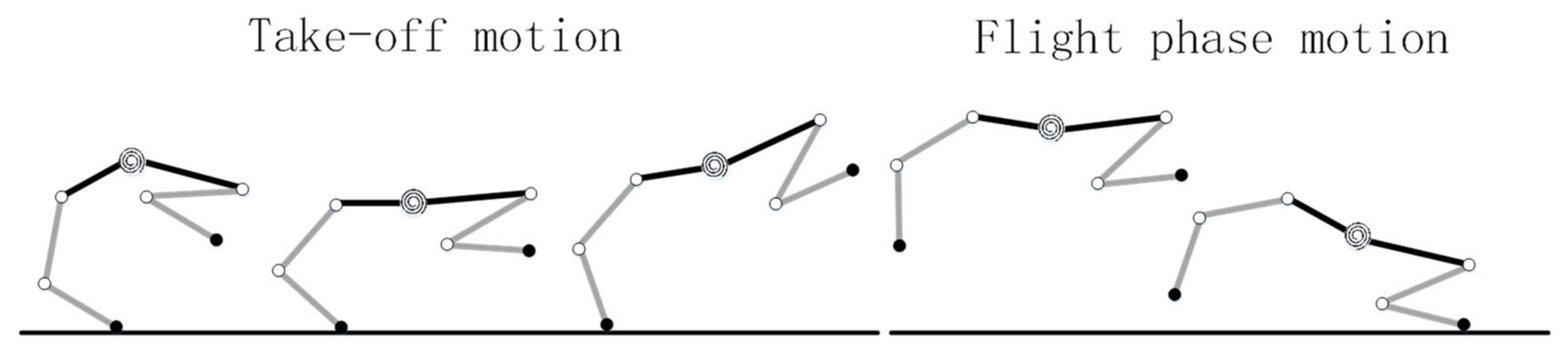
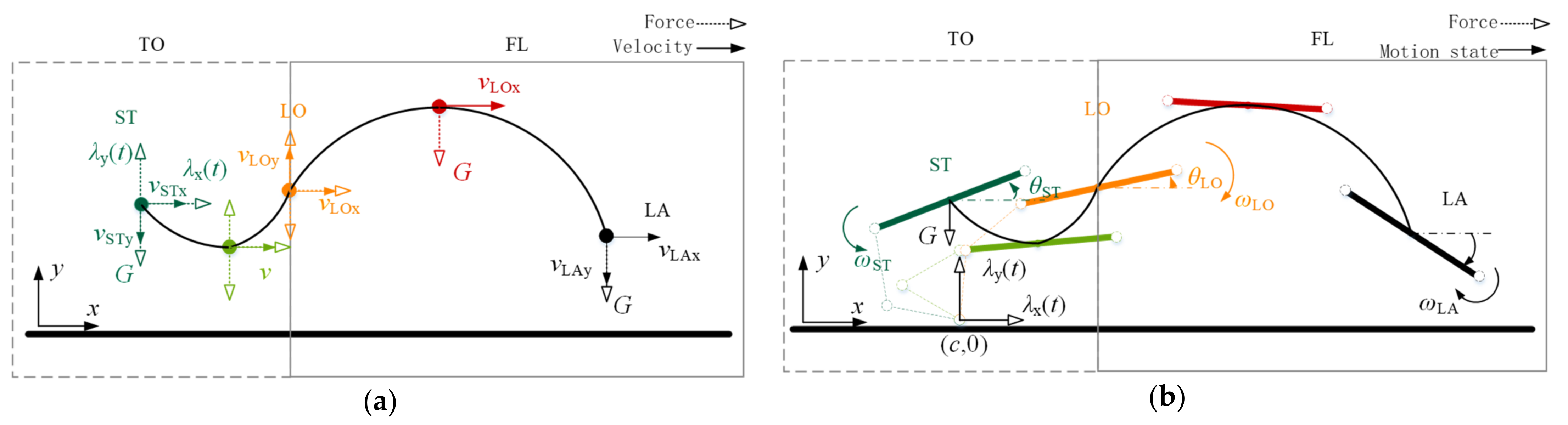
3.1. Flight Phase Motion Simplification
3.2. Rigid-Torso Quadruped Robot Flight Phase Motion Parameterization
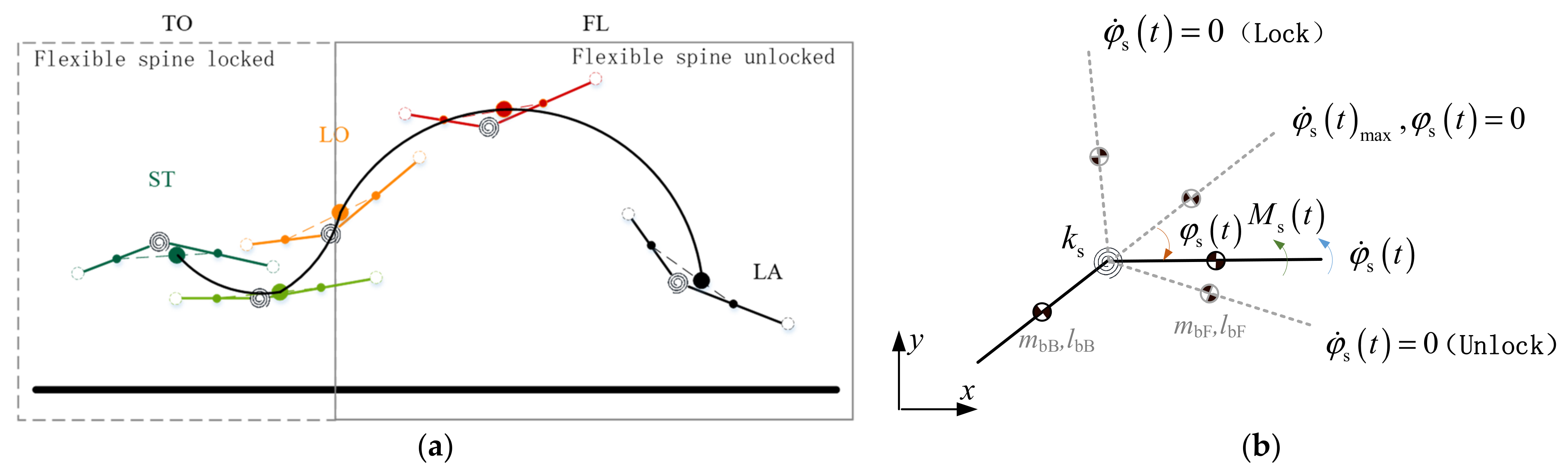
3.3. Flexible-Spine Quadruped Robot Flight Phase Motion Parameterization
3.3.1. Spinal Joint Trajectory Planning
3.3.2. Ground Reaction Force
3.3.3. Flight Phase Motion Parameterization
4. Flight Phase Motion Experiment
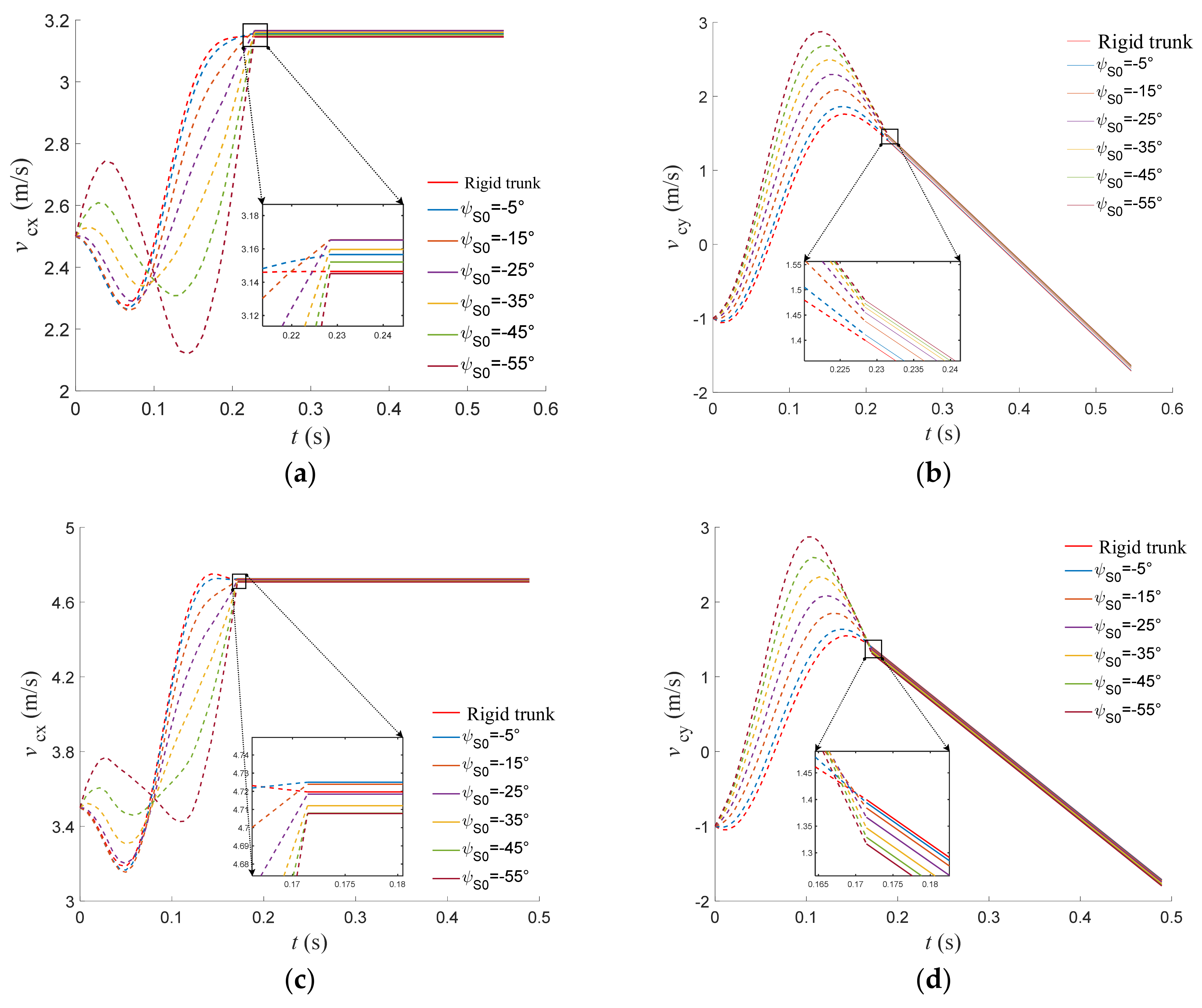
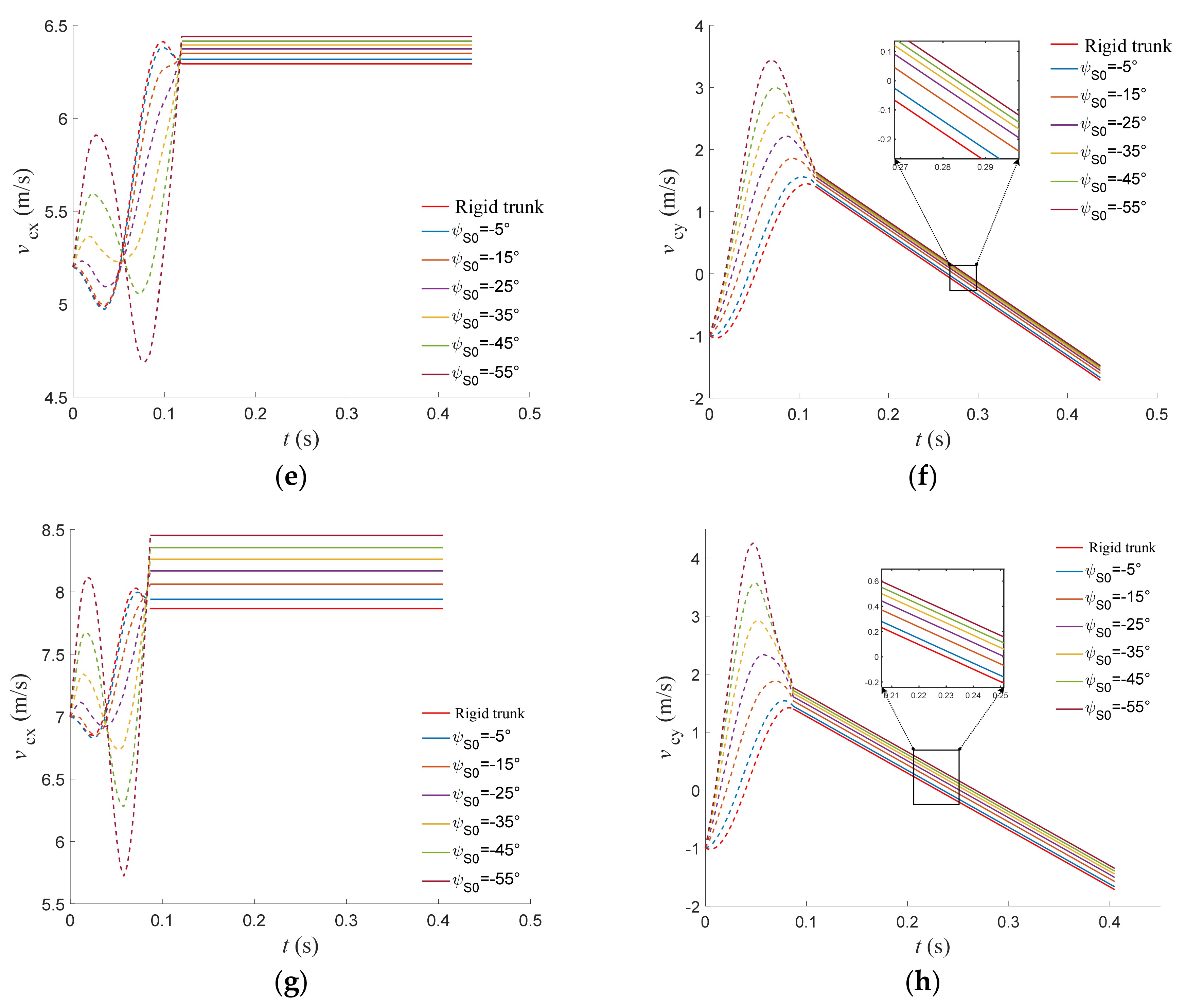
4.1. Trunk Center of Mass Trajectory
4.2. Trunk Center of Mass Velocity
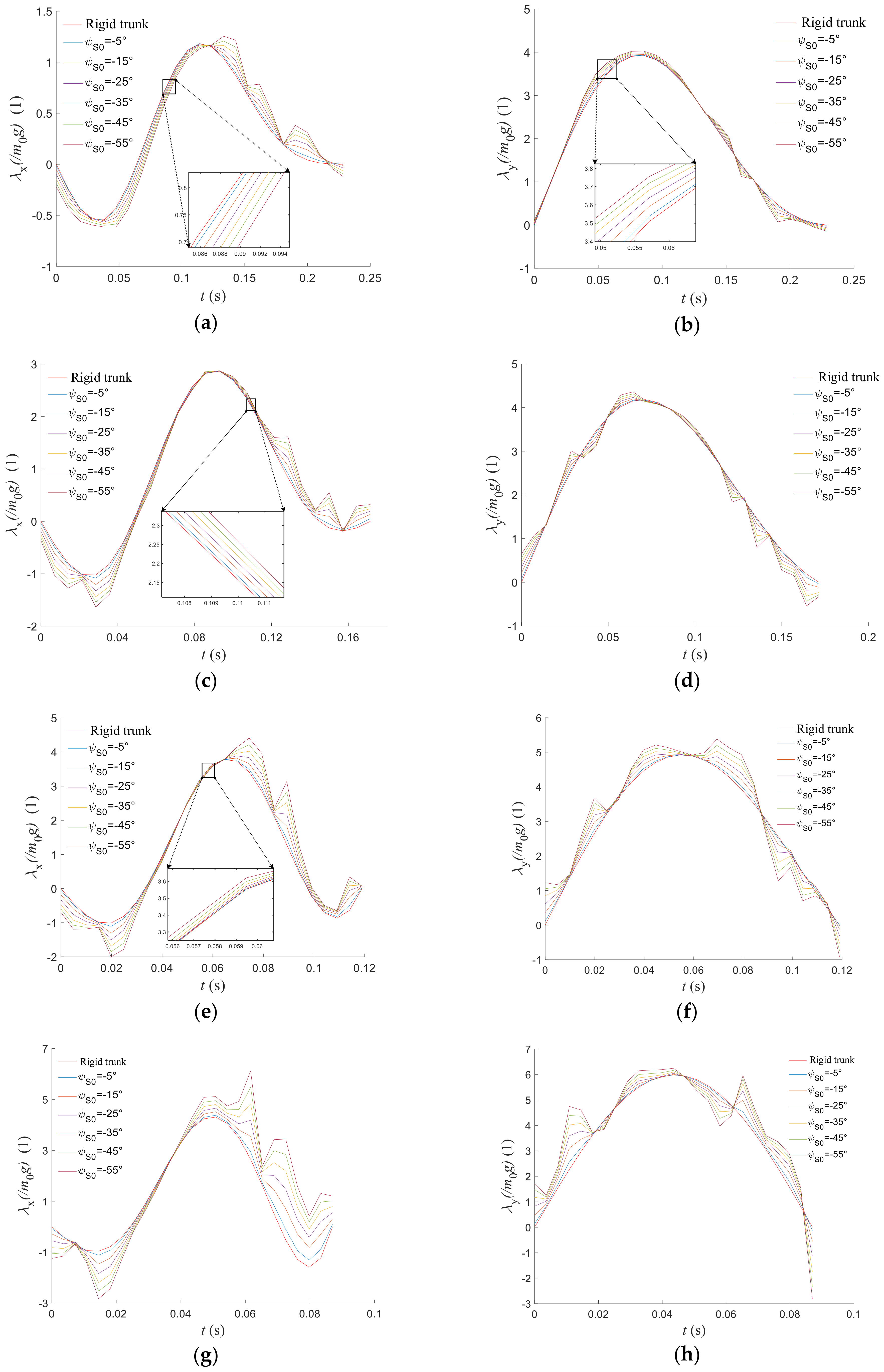
4.3. Ground Reaction Force
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Details of Planar Multiple-Rigid-Body Model
References
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, eaau5872. [Google Scholar] [CrossRef] [PubMed]
- Katz, B.; Di Carlo, J.; Kim, S. Mini Cheetah: A Platform for Pushing the Limits of Dynamic Quadruped Control. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 6295–6301. [Google Scholar]
- Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning quadrupedal locomotion over challenging terrain. Sci. Robot. 2020, 5, eabc5986. [Google Scholar] [CrossRef] [PubMed]
- Miki, T.; Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning robust perceptive locomotion for quadrupedal robots in the wild. Sci. Robot. 2022, 7, eabk2822. [Google Scholar] [CrossRef] [PubMed]
- Rudin, N.; Hoeller, D.; Reist, P.; Hutter, M. Learning to Walk in Minutes Using Massively Parallel Deep Reinforcement Learning. In Proceedings of the 5th Conference on Robot Learning, London, UK, 8–11 November 2021; Volume 164, pp. 91–100. [Google Scholar]
- Bhattacharya, S.; Singla, A.; Abhimanyu; Dholakiya, D.; Bhatnagar, S.; Amrutur, B.; Ghosal, A.; Kolathaya, S. Learning Active Spine Behaviors for Dynamic and Efficient Locomotion in Quadruped Robots. In Proceedings of the 2019 28th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), New Delhi, India, 14–18 October 2019. [Google Scholar]
- Li, W.; Zhou, Z.; Cheng, H. In Dynamic Locomotion of a Quadruped Robot with Active Spine via Model Predictive Control. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 1185–1191. [Google Scholar]
- Kawasaki, R.; Sato, R.; Kazama, E.; Ming, A.G.; Shimojo, M. Development of A Flexible Coupled Spine Mechanism For A Small Quadruped Robot. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (Robio), Qingdao, China, 3–7 December 2016; pp. 71–76. [Google Scholar]
- Park, H.W.; Kim, S. Quadrupedal galloping control for a wide range of speed via vertical impulse scaling. Bioinspir. Biomim. 2015, 10, 025003. [Google Scholar] [CrossRef] [PubMed]
- Seok, S.; Wang, A.; Chuah, M.Y.; Otten, D.; Lang, J.; Kim, S. Design Principles for Highly Efficient Quadrupeds and Implementation on the MIT Cheetah Robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 3307–3312. [Google Scholar]
- Zhao, Q.; Nakajima, K.; Sumioka, H.; Yu, X.X.; Pfeifer, R. Embodiment Enables the Spinal Engine in Quadruped Robot Locomotion. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2449–2456. [Google Scholar]
- Pusey, J.L.; Duperret, J.M.; Haynes, G.C.; Knopf, R.; Koditschek, D.E. Free-Standing Leaping Experiments with a Power-Autonomous, Elastic-Spined Quadruped. In Unmanned Systems Technology XV; SPIE: Bellingham, WA, USA, 2013; Volume 8741. [Google Scholar]
- Duperret, J.; Koditschek, D.E. Empirical Validation of a Spined Sagittal-Plane Quadrupedal Model. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1058–1064. [Google Scholar]
- Kani, M.H.H.; Derafshian, M.; Bidgoly, H.J.; Ahmadabadi, M.N. Effect of Flexible Spine on Stability of a Passive Quadruped Robot: Experimental Results. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; pp. 2793–2798. [Google Scholar]
- Deng, Q.; Wang, S.G.; Xu, W.; Mo, J.Q.; Liang, Q.H. Quasi passive bounding of a quadruped model with articulated spine. Mech. Mach. Theory 2012, 52, 232–242. [Google Scholar] [CrossRef]
- Maleki, S.; Parsa, A.; Ahmadabadi, M.N. Modeling, Control and Gait Design of a Quadruped Robot with Active Spine Towards Energy Efficiency. In Proceedings of the 2015 3RD RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; pp. 271–276. [Google Scholar]
- Phan, L.T.; Lee, Y.H.; Kim, D.Y.; Lee, H.; Choi, H.R. Hybrid Quadruped Bounding with a Passive Compliant Spine and Asymmetric Segmented Body. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2016), Daejeon, Republic of Korea, 9–14 October 2016; pp. 3387–3392. [Google Scholar]
- Phan, L.T.; Lee, Y.H.; Lee, Y.H.; Lee, H.; Kang, H.; Choi, H.R. Study on effects of spinal joint for running quadruped robots. Intell. Serv. Robot. 2020, 13, 29–46. [Google Scholar] [CrossRef]
- Wei, X.H.; Long, Y.J.; Wang, C.L.; Wang, S.G. Rotary galloping with a lock-unlock elastic spinal joint. J. Mech. Eng. Sci. 2015, 229, 1088–1102. [Google Scholar] [CrossRef]
- Wang, C.L.; Zhang, T.; Wei, X.H.; Long, Y.J.; Wang, S.G. Dynamic characteristics and stability criterion of rotary galloping gait with an articulated passive spine joint. Adv. Robot. 2017, 31, 168–183. [Google Scholar] [CrossRef]
- Yesilevskiy, Y.; Yang, W.; Remy, C.D. Spine morphology and energetics: How principles from nature apply to robotics. Bioinspir. Biomim. 2018, 13, 036002. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.; Tan, Y.G.; Li, Z.; Wu, P.; Li, T.L.; Li, J.F.; Yin, H.B. Effect of Mass-Center Position of Spinal Segment on Dynamic Performances of Quadruped Bounding with a Flexible-Articulated Spine. Appl. Sci. 2020, 10, 1491. [Google Scholar] [CrossRef]
- Bertram, J.E.A.; Gutmann, A. Motions of the running horse and cheetah revisited: Fundamental mechanics of the transverse and rotary gallop. J. R. Soc. Interface 2009, 6, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Maes, L.D.; Herbin, M.; Hackert, R.; Bels, V.L.; Abourachid, A. Steady locomotion in dogs: Temporal and associated spatial coordination patterns and the effect of speed. J. Exp. Biol. 2008, 211, 138–149. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.E.; Corr, S.A.; Wilson, A.M. High speed galloping in the cheetah (Acinonyx jubatus) and the racing greyhound (Canis familiaris): Spatio-temporal and kinetic characteristics. J. Exp. Biol. 2012, 215, 2425–2434. [Google Scholar] [CrossRef] [PubMed]
- Walter, R.M.; Carrier, D.R. Ground forces applied by galloping dogs. J. Exp. Biol. 2007, 210, 208–216. [Google Scholar] [CrossRef] [PubMed]




| Parameter | Measure | Definition |
|---|---|---|
| m | Back hip joint position | |
| rad | Hindquarters pitch | |
| rad | Trunk angles | |
| rad | Joint angles |
| Parameter | Measure | Definition |
|---|---|---|
| m | Altitude of flight phase | |
| m | Landing point position | |
| m | Starting point velocity | |
| m | Starting point position | |
| m | Foot position | |
| rad/s | Starting point angular velocity | |
| rad | Landing point attitude angle |
| Parameter | Measure | Definition |
|---|---|---|
| rad | Angle of the spinal joints | |
| m | Starting point position | |
| m/s | Starting point velocity |
| Parameter | Value | Definition |
|---|---|---|
| 10.72 kg | Posterior trunk mass | |
| 16.08 kg | Anterolateral trunk mass | |
| 2.6 kg | Femur link mass | |
| 0.81 kg | Tibia link mass | |
| 0.24 m | Posterior trunk length | |
| 0.36 m | Anterolateral trunk length | |
| 0.42 m | Femur link length | |
| 0.42 m | Tibia link length |
| Parameter | Value | Definition |
|---|---|---|
| 0.1 m | Flight phase trajectory height | |
| (1, −0.05), (1.5, −0.05) (2, −0.05), (2.5, −0.05) | Landing point position | |
| (2.5, −1), (3.5, −1) (5.2, −1), (7, −1) | Starting point velocity | |
| (0, 0.45) | Starting point position | |
| 0.155, 0.132, 0.161,0.182 | Touching point position | |
| 0 | Starting point angular velocity | |
| −15° | Landing point attitude angle | |
| −5°, −15°, −25°,−35°, −45°, −55° | Angle of the spinal joints |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Xu, Z.; Zheng, T.; Zhang, X.; Yang, J. Research on Dynamic Modeling Method and Flying Gait Characteristics of Quadruped Robots with Flexible Spines. Biomimetics 2024, 9, 132. https://doi.org/10.3390/biomimetics9030132
Jiang L, Xu Z, Zheng T, Zhang X, Yang J. Research on Dynamic Modeling Method and Flying Gait Characteristics of Quadruped Robots with Flexible Spines. Biomimetics. 2024; 9(3):132. https://doi.org/10.3390/biomimetics9030132
Chicago/Turabian StyleJiang, Lei, Zhongqi Xu, Tinglong Zheng, Xiuli Zhang, and Jianhua Yang. 2024. "Research on Dynamic Modeling Method and Flying Gait Characteristics of Quadruped Robots with Flexible Spines" Biomimetics 9, no. 3: 132. https://doi.org/10.3390/biomimetics9030132
APA StyleJiang, L., Xu, Z., Zheng, T., Zhang, X., & Yang, J. (2024). Research on Dynamic Modeling Method and Flying Gait Characteristics of Quadruped Robots with Flexible Spines. Biomimetics, 9(3), 132. https://doi.org/10.3390/biomimetics9030132





