Interacting with Obstacles Using a Bio-Inspired, Flexible, Underactuated Multilink Manipulator
Abstract
1. Introduction
2. Related Work
3. Methodology
4. Simulations
4.1. Fixed Obstacles
4.2. Model Verification in MSC Adams
4.3. Movable Obstacles
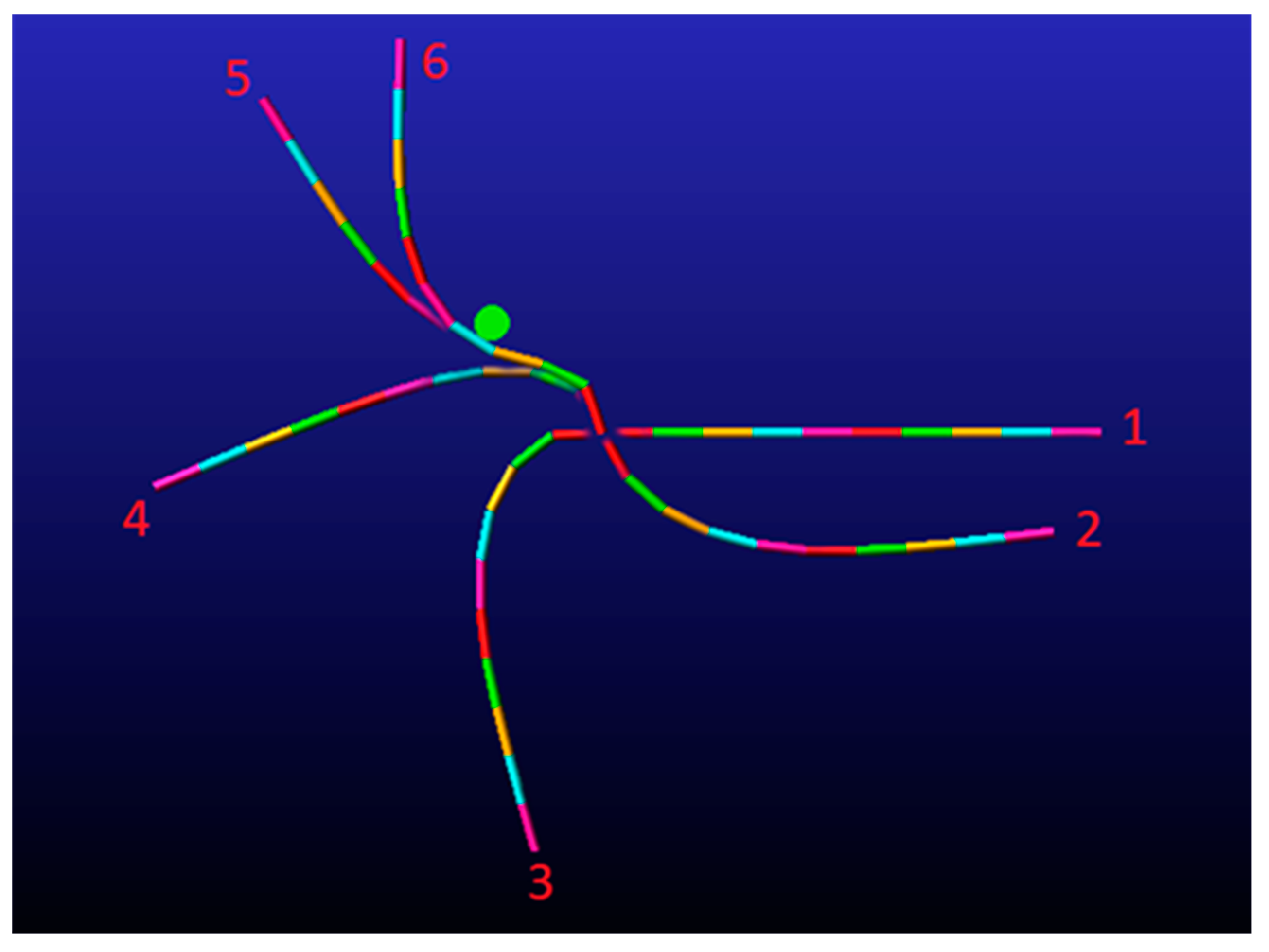
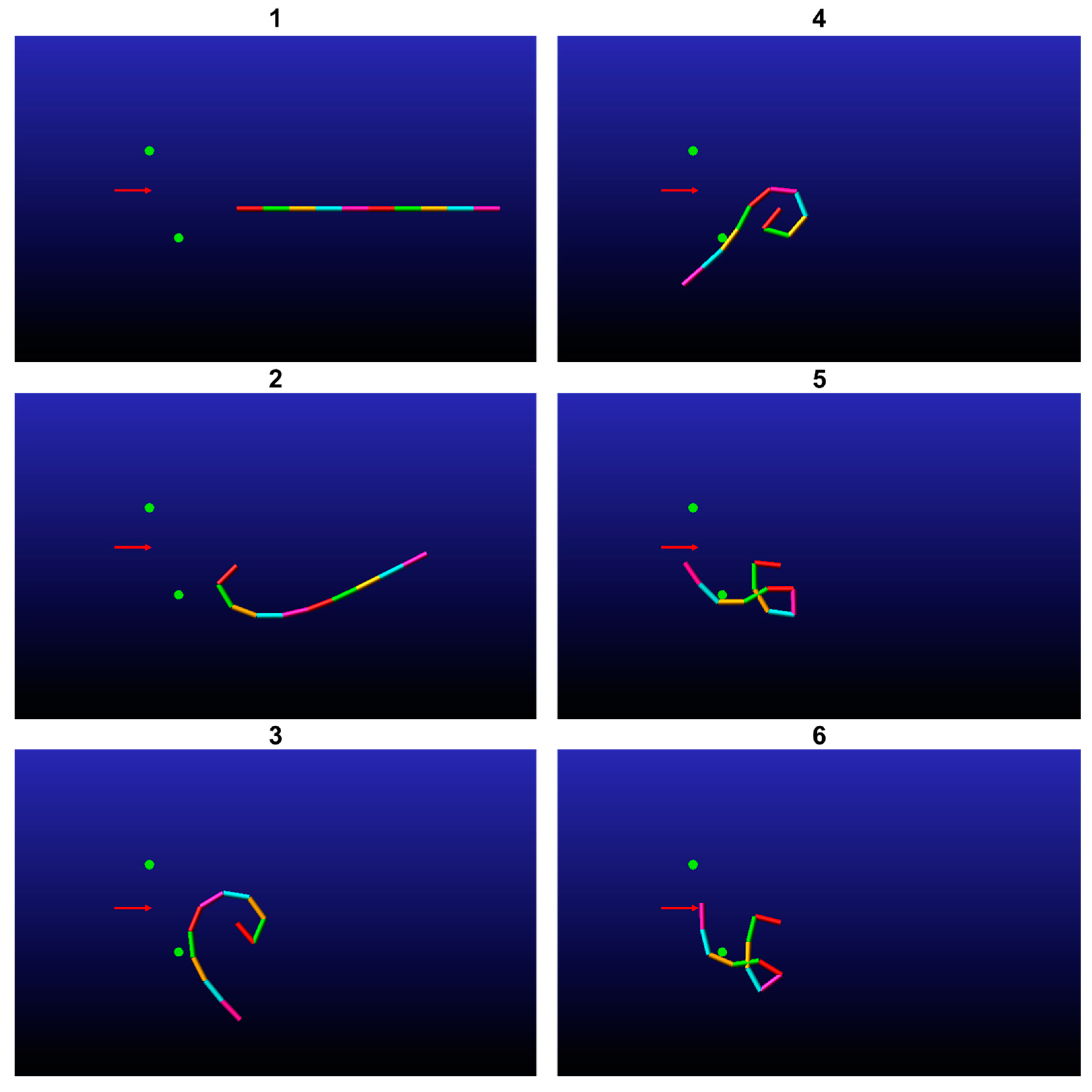
5. Experiments
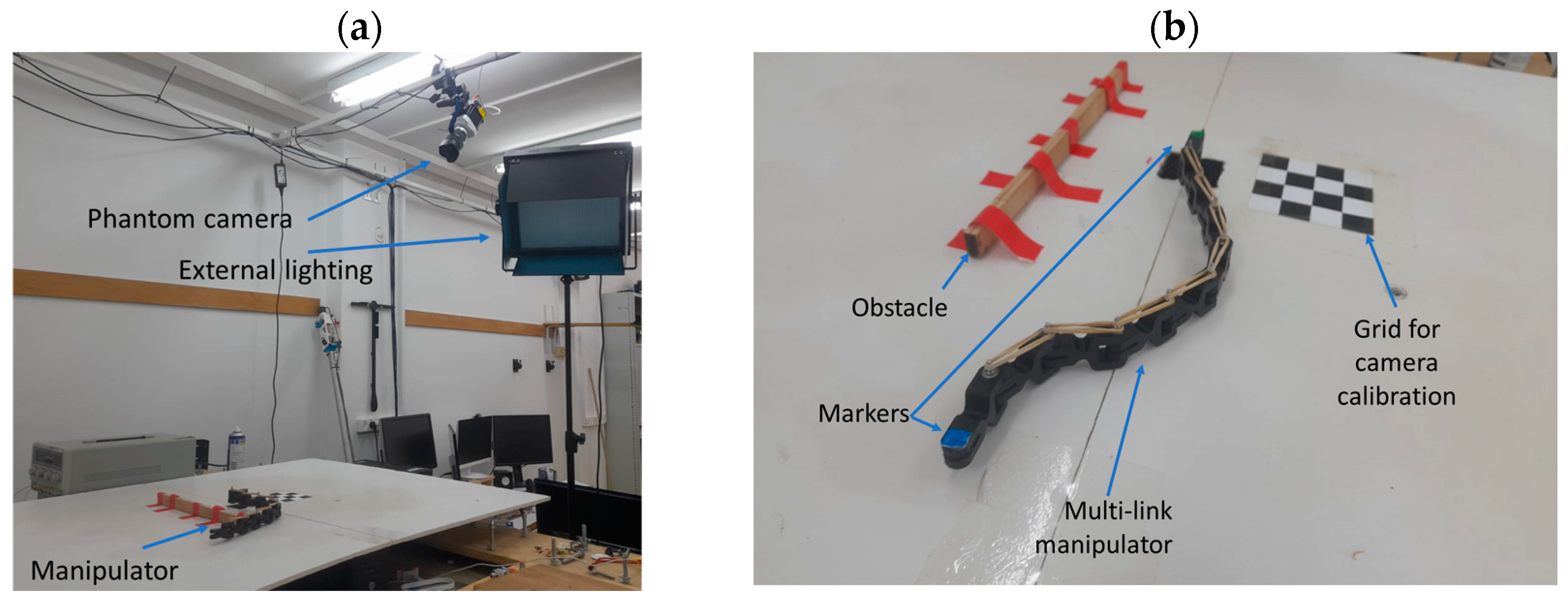
5.1. Experimental Setup
5.2. Experiments with Fixed Obstacles
5.3. Experiments with Movable Obstacles
6. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hooper, S.L. Motor control: Elephant trunks ignore the many and choose a few. Curr. Biol. 2021, 31, R1430–R1432. [Google Scholar] [CrossRef] [PubMed]
- Dagenais, P.; Hensman, S.; Haechler, V.; Milinkovitch, M.C. Elephants evolved strategies reducing the biomechanical complexity of their trunk. Curr. Biol. 2021, 31, 4727–4737.e4. [Google Scholar] [CrossRef] [PubMed]
- Prigozin, A.; Degani, A. A Minimalistic Hyper-Flexible Manipulator: Modeling and Control. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021. [Google Scholar]
- Wilson, J.F.; Mahajan, U.; Wainwright, S.A.; Croner, L.J. A continuum model of elephant trunks. J. Biomech. Eng. 1991, 113, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.K.; Samantaray, A.K.; Chakraborty, G.; Jain, A.; Pathak, P.M.; Merzouki, R. Dynamic modelling of an elephant trunk like flexible bionic manipulator. In Proceedings of the ASME 2019 International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019; Volume 4. [Google Scholar] [CrossRef]
- Kang, M.; Han, Y.-J.; Han, M.-W. A Shape Memory Alloy-Based Soft Actuator Mimicking an Elephant’s Trunk. Polymers 2023, 15, 1126. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Wang, P.; Wang, Y.; Xia, X.; Li, S. Kinematic Analysis of Bionic Elephant Trunk Robot Based on Flexible Series-Parallel Structure. Biomimetics 2022, 7, 228. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.P.; Dhyan, S.B.; Mai, V.; Han, B.S.; Chow, W.T. Bioinspiration and Biomimetic Art in Robotic Grippers. Micromachines 2023, 14, 1772. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Chang, P.; Luh, J. Formulation and Optimization of Cubic Polynomial Joint Trajectories for Industrial Robots. IEEE Trans. Autom. Control. 1983, 28, 1066–1074. [Google Scholar] [CrossRef]
- Kyriakopoulos, K.J.; Saridis, G.N. Minimum Jerk Path Generation. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 364–369. [Google Scholar] [CrossRef]
- Zavlangas, P.G.; Tzafestas, S.G. Industrial robot navigation and obstacle avoidance employing fuzzy logic. J. Intell. Robot. Syst. 2000, 27, 85–97. [Google Scholar] [CrossRef]
- Rubio, F.; Llopis-Albert, C.; Valero, F.; Suñer, J.L. Industrial robot efficient trajectory generation without collision through the evolution of the optimal trajectory. Robot. Auton. Syst. 2016, 86, 106–112. [Google Scholar] [CrossRef]
- Suzuki, T.; Ebihara, Y.; Ando, Y.; Mizukawa, M. Casting and winding manipulation with hyper-flexible manipulator. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 1674–1679. [Google Scholar] [CrossRef]
- Yamakawa, Y.; Namiki, A.; Ishikawa, M. Dexterous manipulation of a rhythmic gymnastics ribbon with constant, high-speed motion of a high-speed manipulator. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 1896–1901. [Google Scholar] [CrossRef]
- Yamakawa, Y.; Namiki, A.; Ishikawa, M. Motion planning for dynamic folding of a cloth with two high-speed robot hands and two high-speed sliders. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5486–5491. [Google Scholar] [CrossRef]
- Yamakawa, Y.; Namiki, A.; Ishikawa, M. Motion planning for dynamic knotting of a flexible rope with a high-speed robot arm. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 49–54. [Google Scholar] [CrossRef]
- Mochiyama, H.; Nakajima, H.; Hatakeyama, T. Chameleon-like shooting manipulator for accurate 10-meter reaching. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Fagiolini, A.; Belo, F.A.W.; Catalano, M.G.; Bonomo, F.; Alicino, S.; Bicchi, A. Design and control of a novel 3D casting manipulator. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4169–4174. [Google Scholar] [CrossRef]
- Hill, L.; Woodward, T.; Arisumi, H.; Hatton, R.L. Wrapping a target with a tethered projectile. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1442–1447. [Google Scholar] [CrossRef]
- Ito, K.; Yamakawa, Y.; Ishikawa, M. Winding manipulator based on high-speed visual feedback control. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017; pp. 474–480. [Google Scholar] [CrossRef]
- Li, X.; Yue, H.; Yang, D.; Sun, K.; Liu, H. A Large-Scale Inflatable Robotic Arm Toward Inspecting Sensitive Environments: Design and Performance Evaluation. IEEE Trans. Ind. Electron. 2023, 70, 12486–12499. [Google Scholar] [CrossRef]
- Li, X.; Sun, K.; Guo, C.; Liu, H. Hybrid adaptive disturbance rejection control for inflatable robotic arms. ISA Trans. 2022, 126, 617–628. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, Y.; Wolf, A.; Gabor, K. Bi-bellows: Pneumatic bending actuator. Sens. Actuators A Phys. 2011, 167, 484–494. [Google Scholar] [CrossRef]
- Hertz, H. Über die berührung fester elastischer körper. J. Für Die Reine Und Angew. Math. 1881, 171, 156–171. [Google Scholar]
- Goodman, L.E. Contact stress analysis of normally loaded rough spheres. J. Appl. Mech. Trans. ASME 1960, 29, 515–522. [Google Scholar] [CrossRef]
- Mossakovskii, V. Compression of elastic bodies under conditions of adhesion (Axisymmetric case). J. Appl. Math. Mech. 1963, 27, 630–643. [Google Scholar] [CrossRef]
- Spence, D.A. Self similar solutions to adhesive contact problems with incremental loading. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1968, 305, 55–80. [Google Scholar] [CrossRef]
- Spence, D.A. The hertz contact problem with finite friction. J. Elast. 1975, 5, 297–319. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Lingle, R. Alleles, loci, and the traveling salesman problem. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications, Pittsburg, PA, USA, 24–26 July 1985; Volume 154, pp. 154–159. [Google Scholar]

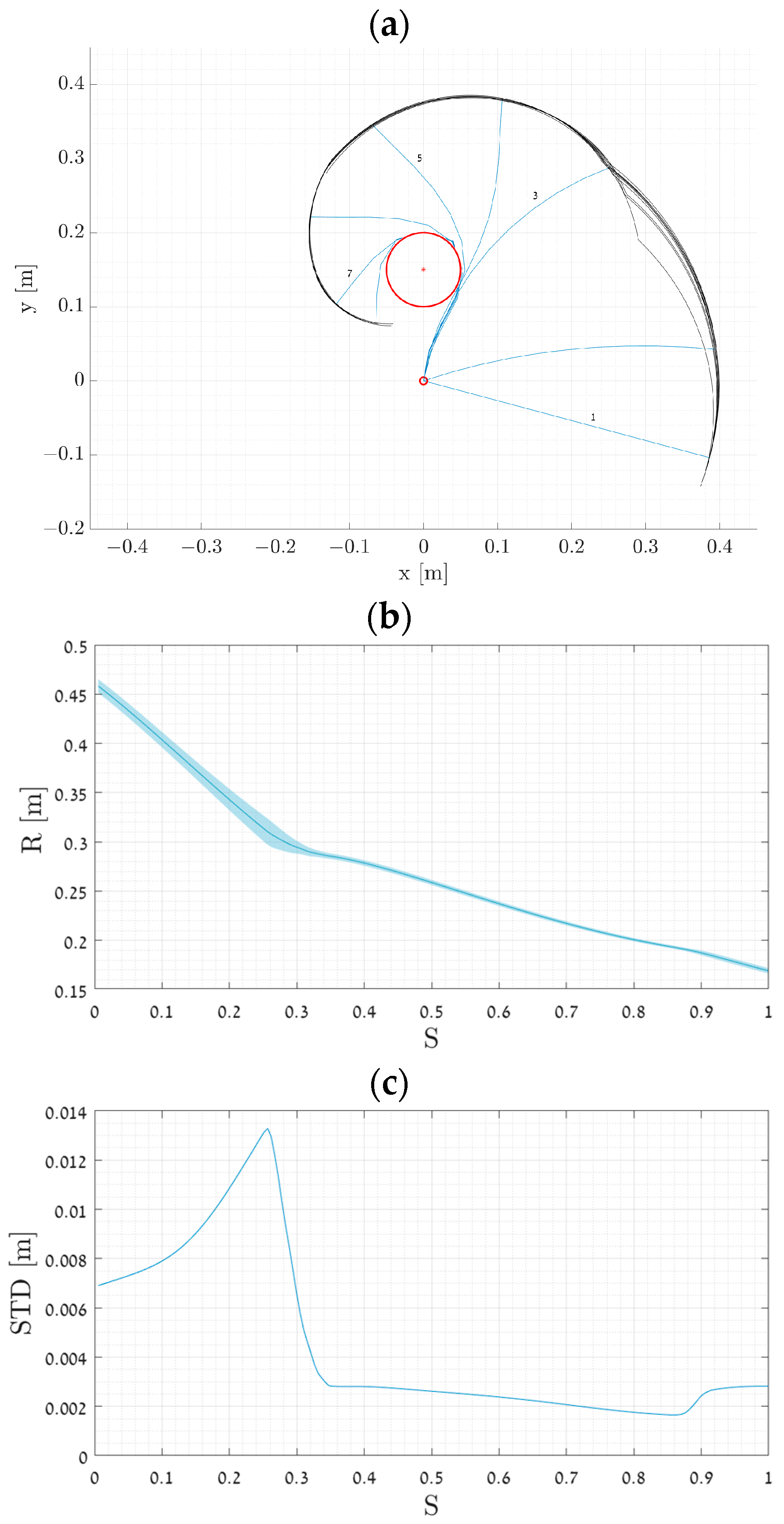
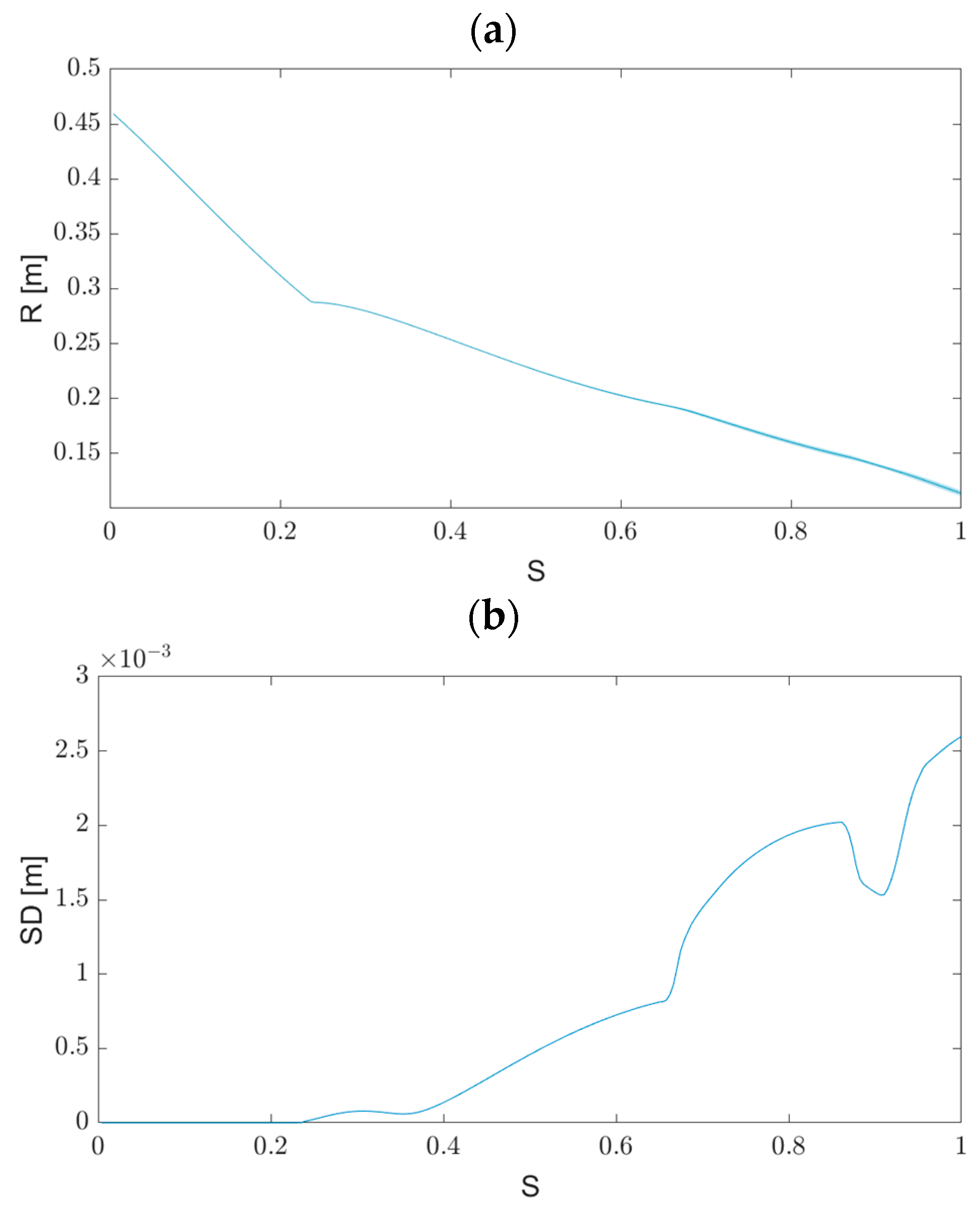

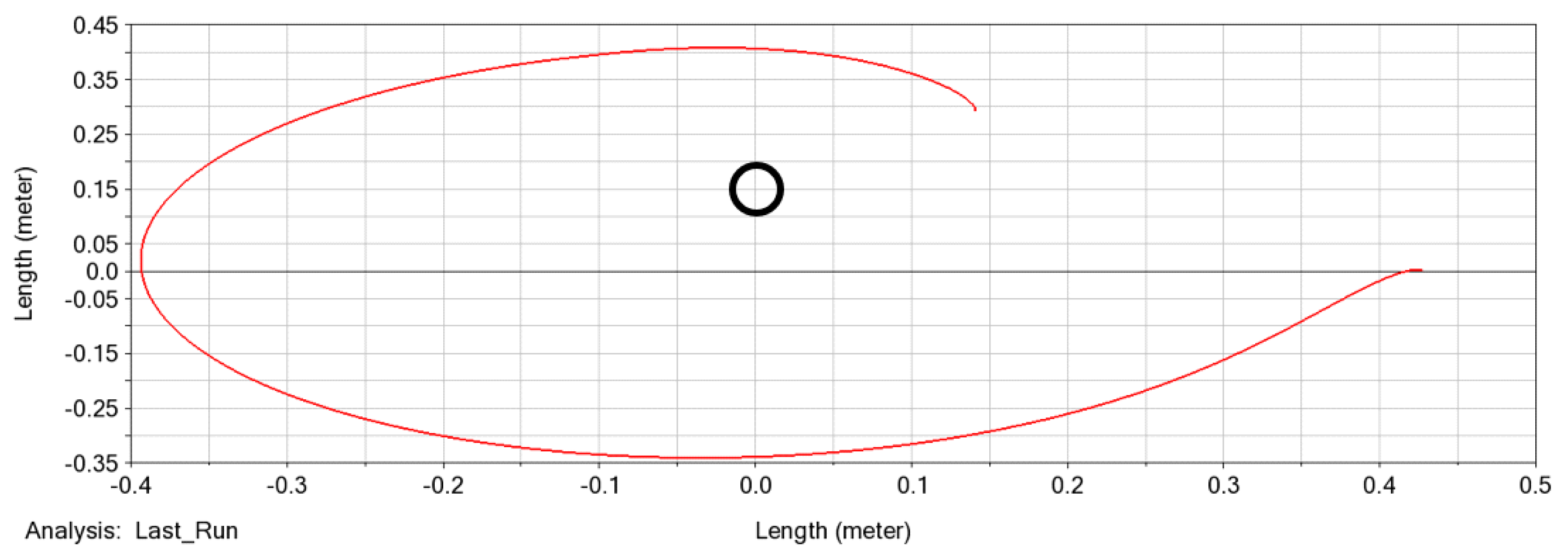
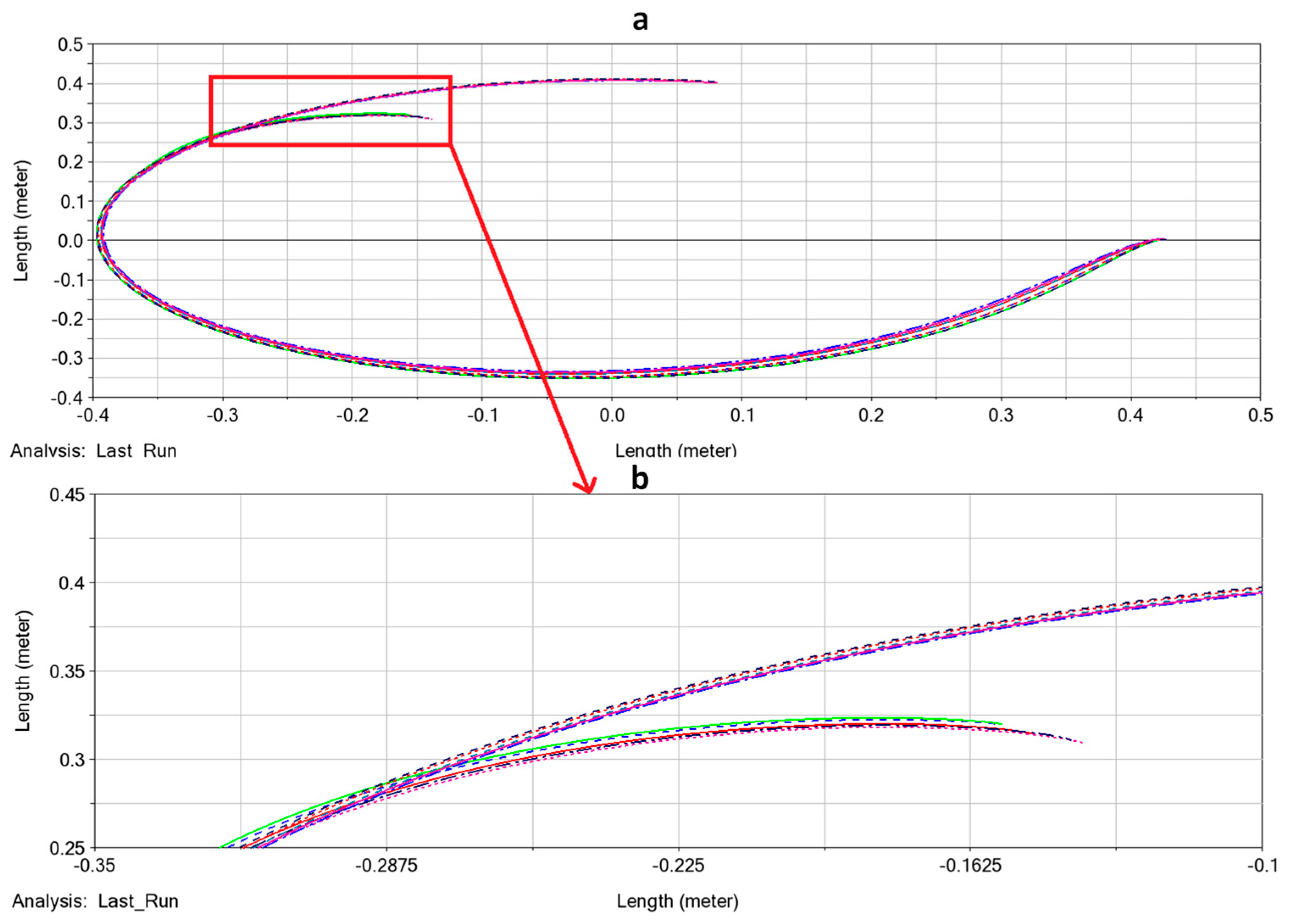





| Noise Amplitude | SD Max | SD Difference |
|---|---|---|
| 10% | 0.01 | 0.005 |
| 25% | 0.015 | 0.003 |
| 33% | 0.018 | 0.004 |
| 50% | 0.02 | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prigozin, A.; Degani, A. Interacting with Obstacles Using a Bio-Inspired, Flexible, Underactuated Multilink Manipulator. Biomimetics 2024, 9, 86. https://doi.org/10.3390/biomimetics9020086
Prigozin A, Degani A. Interacting with Obstacles Using a Bio-Inspired, Flexible, Underactuated Multilink Manipulator. Biomimetics. 2024; 9(2):86. https://doi.org/10.3390/biomimetics9020086
Chicago/Turabian StylePrigozin, Amit, and Amir Degani. 2024. "Interacting with Obstacles Using a Bio-Inspired, Flexible, Underactuated Multilink Manipulator" Biomimetics 9, no. 2: 86. https://doi.org/10.3390/biomimetics9020086
APA StylePrigozin, A., & Degani, A. (2024). Interacting with Obstacles Using a Bio-Inspired, Flexible, Underactuated Multilink Manipulator. Biomimetics, 9(2), 86. https://doi.org/10.3390/biomimetics9020086







