A Novel Hybrid Deep Learning Method for Predicting the Flow Fields of Biomimetic Flapping Wings
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations and CFD Solver Setup
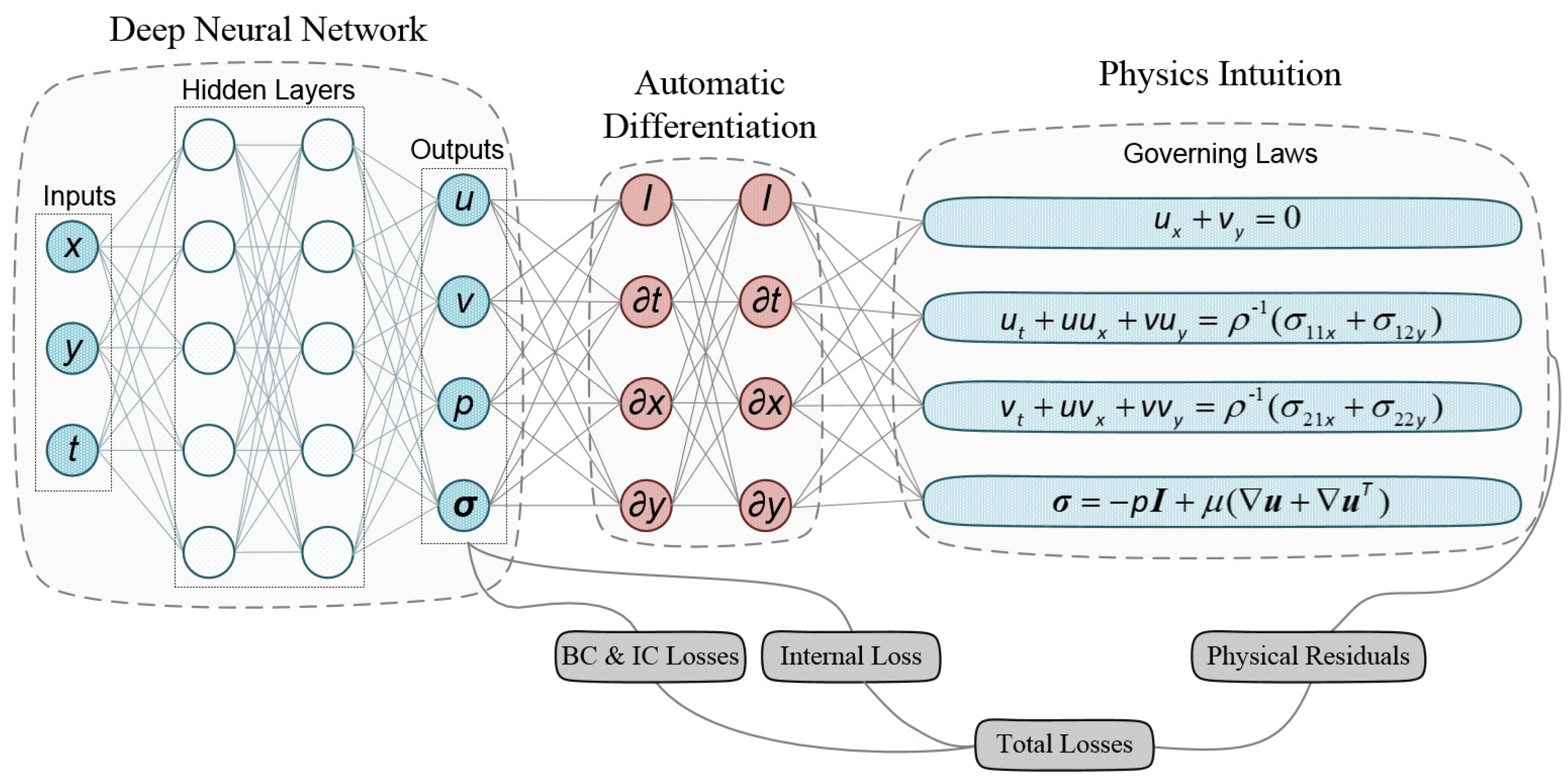
2.2. Hybrid Coarse Data-Driven with Physics-Informed Neural Network (HCDD-PINN)
- Step1: establish the physical model of flapping wing, including the governing equations, and boundary conditions, and prepare the training data for the coarser CFD results, including the initial condition and coarse internal data;
- Step2: design the suitable deep neural network, including the NN structure, function, learning rate, iteration, and so on; and create the corresponding loss function according to the physical model;
- Step3: train the DNN using the coarser internal data, and establish the map relationship between the input and output layers; use Adam and L-BFGS-B optimizers to update the weight and bias of DNN and reduce the error of the loss function; end training when the converged conditions are satisfied;
- Step4: save the trained model, residual histories, and predicted flow field information.
3. Problem Setup and Numerical Results
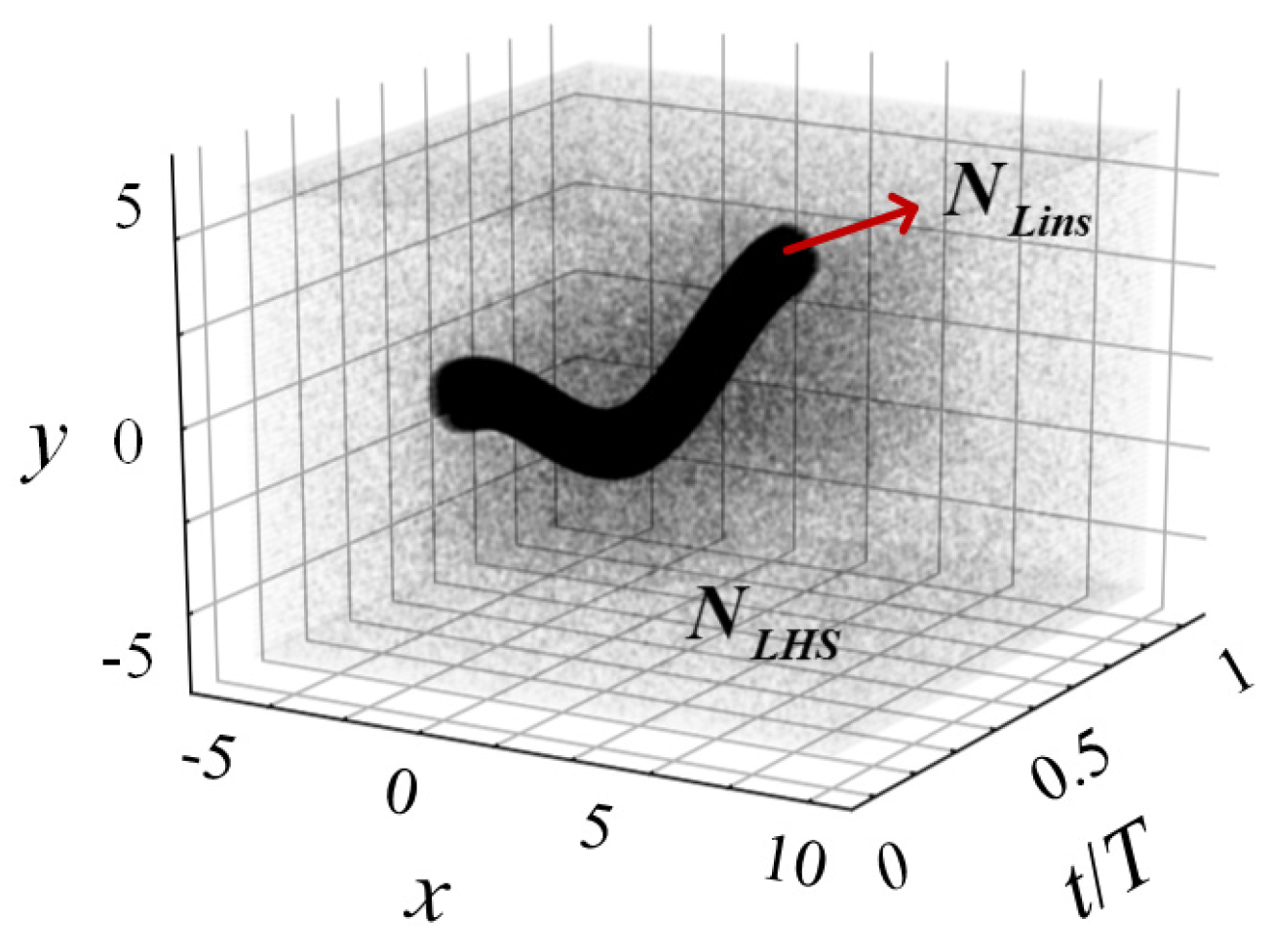
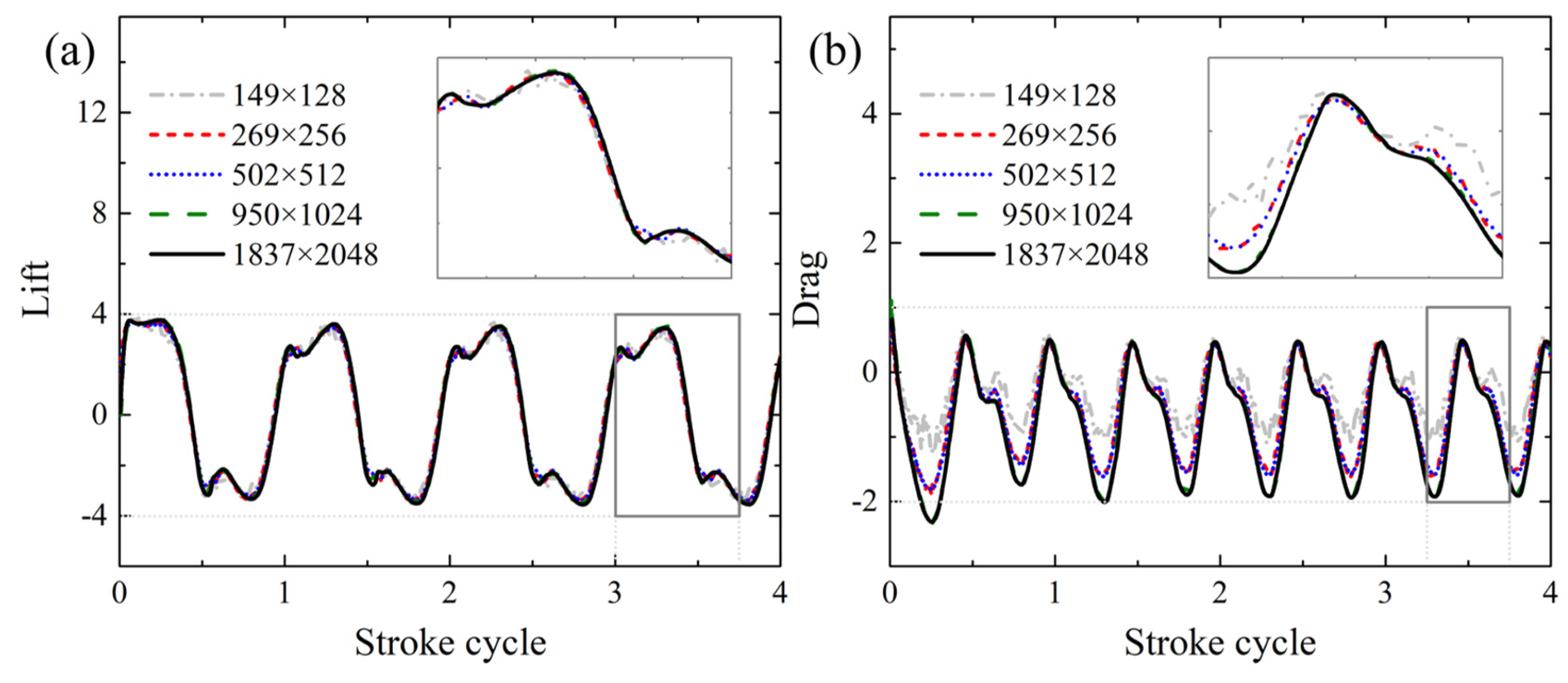
3.1. Problem Description
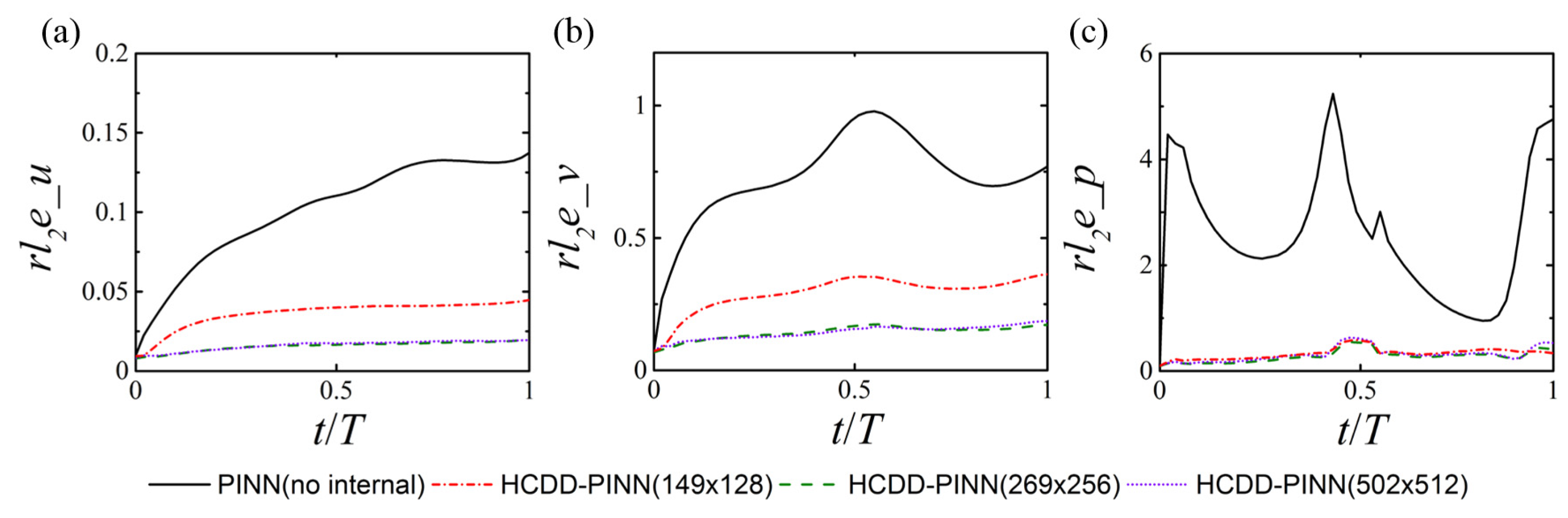
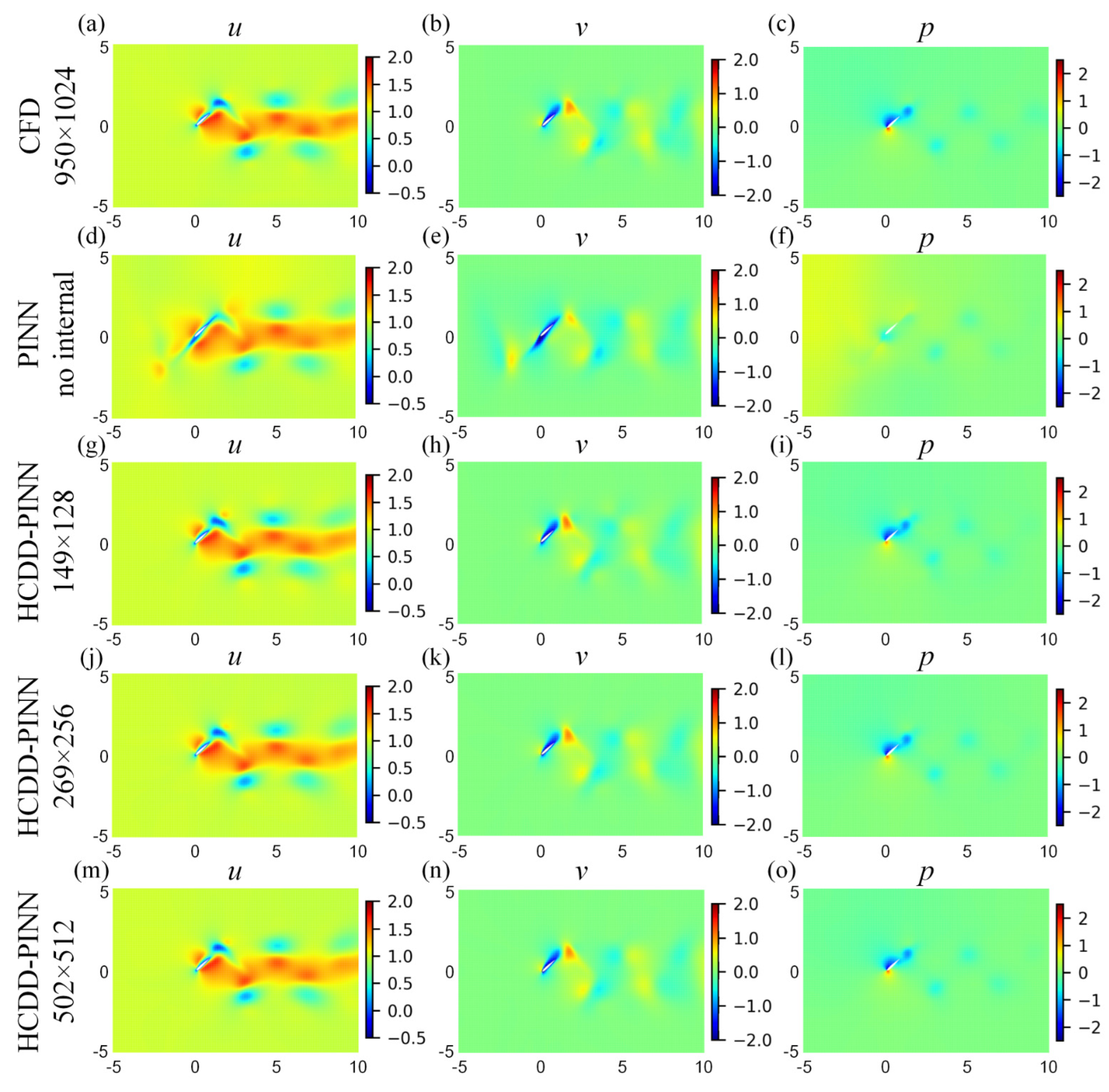
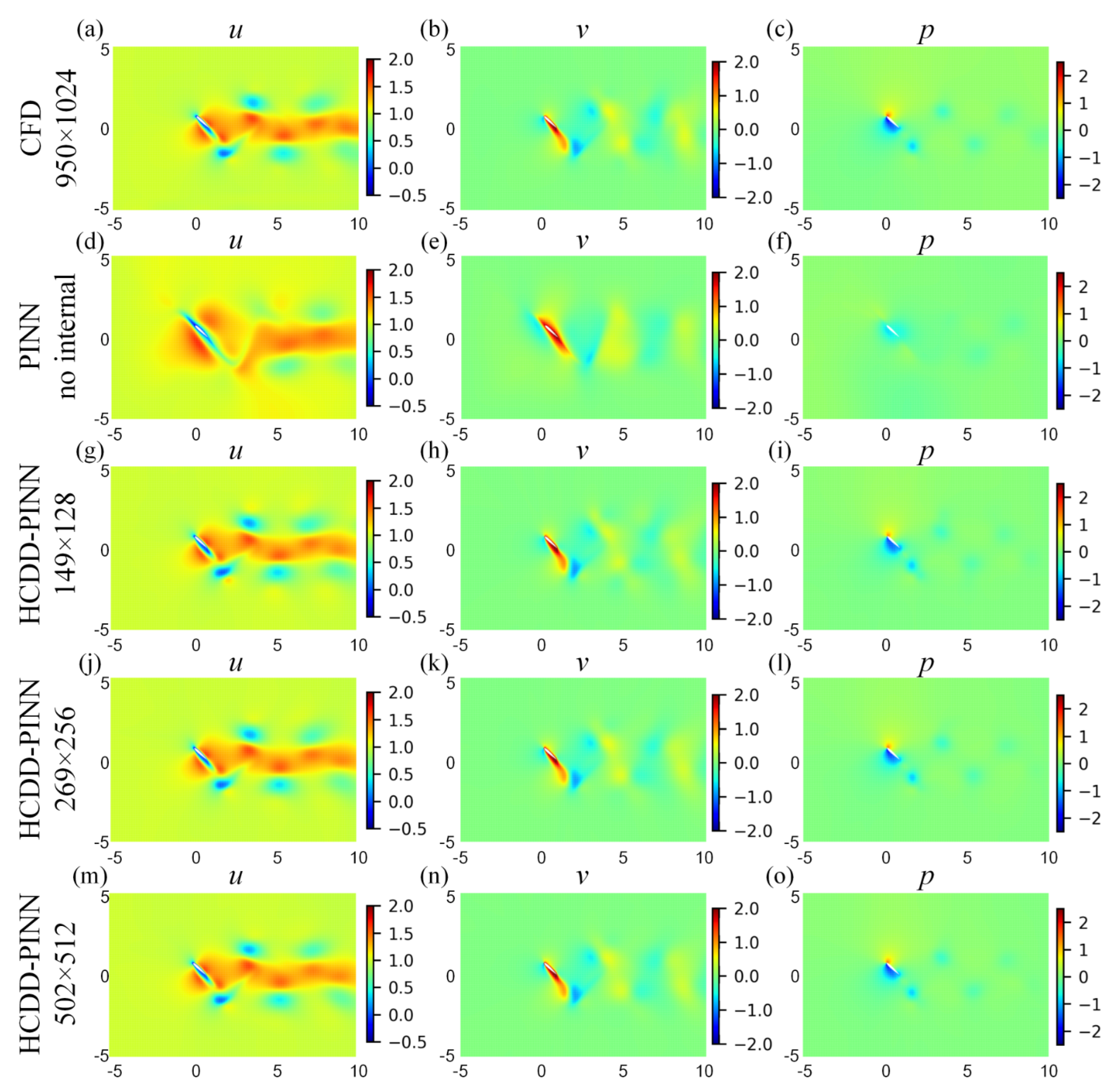
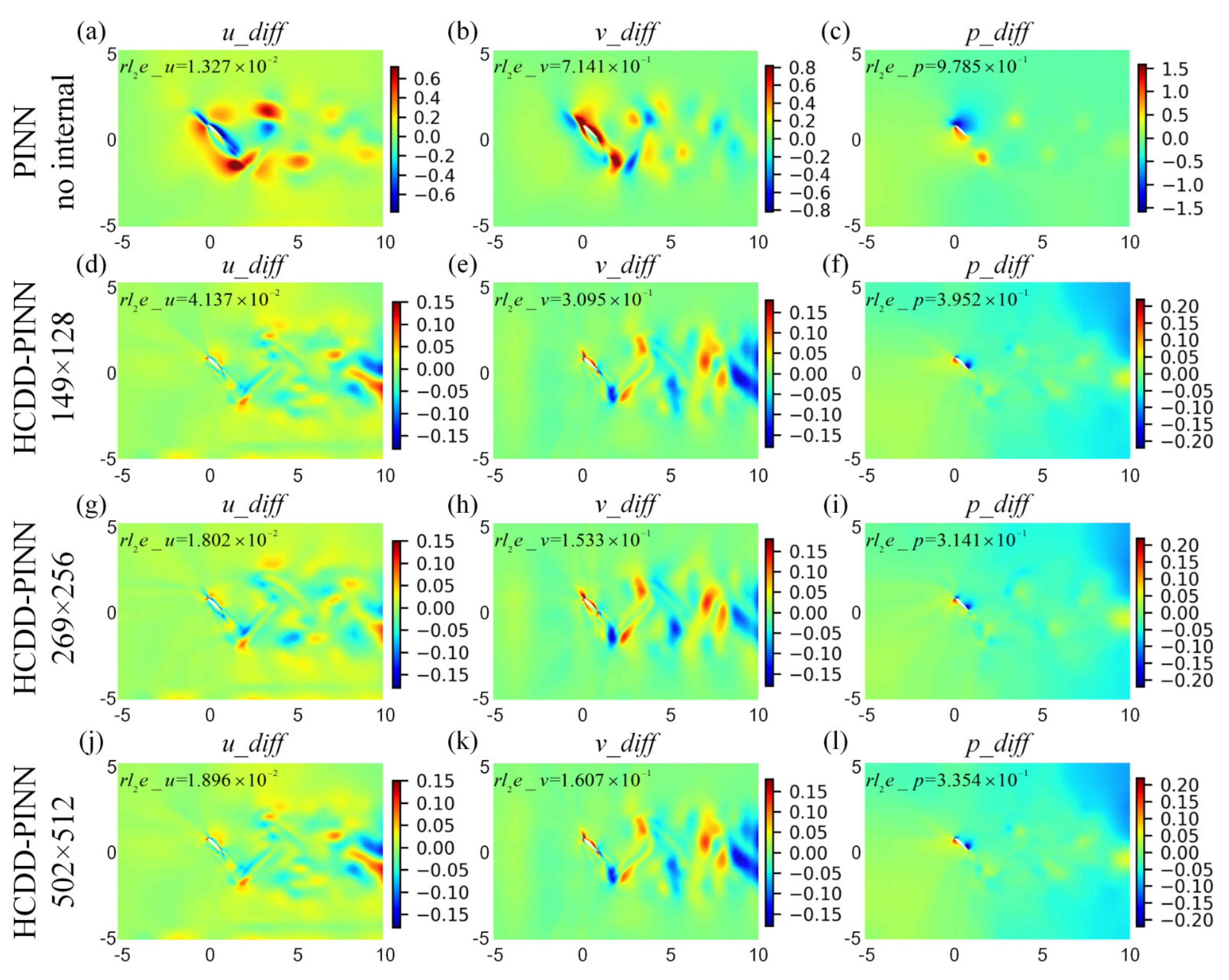
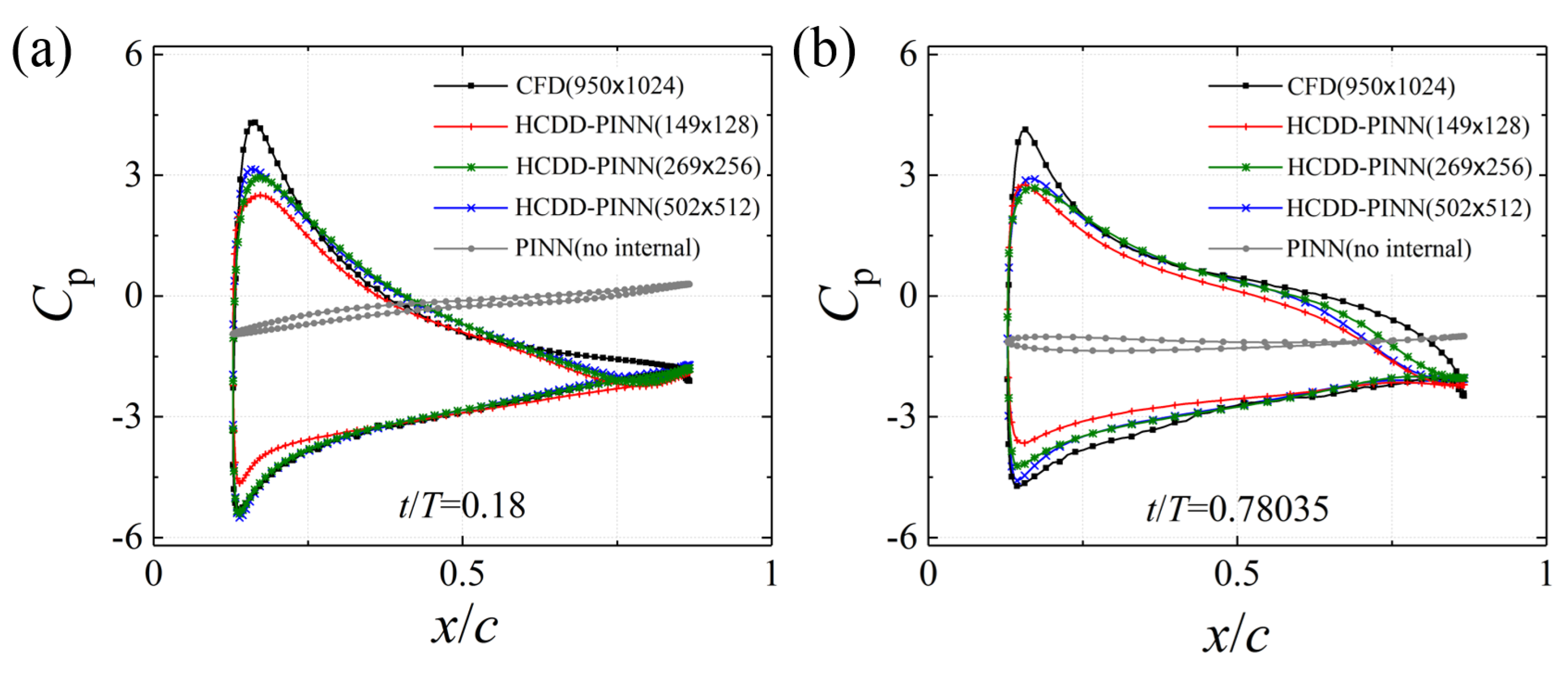
3.2. Prediction Results
4. Discussions
4.1. Optimal Parameters Search
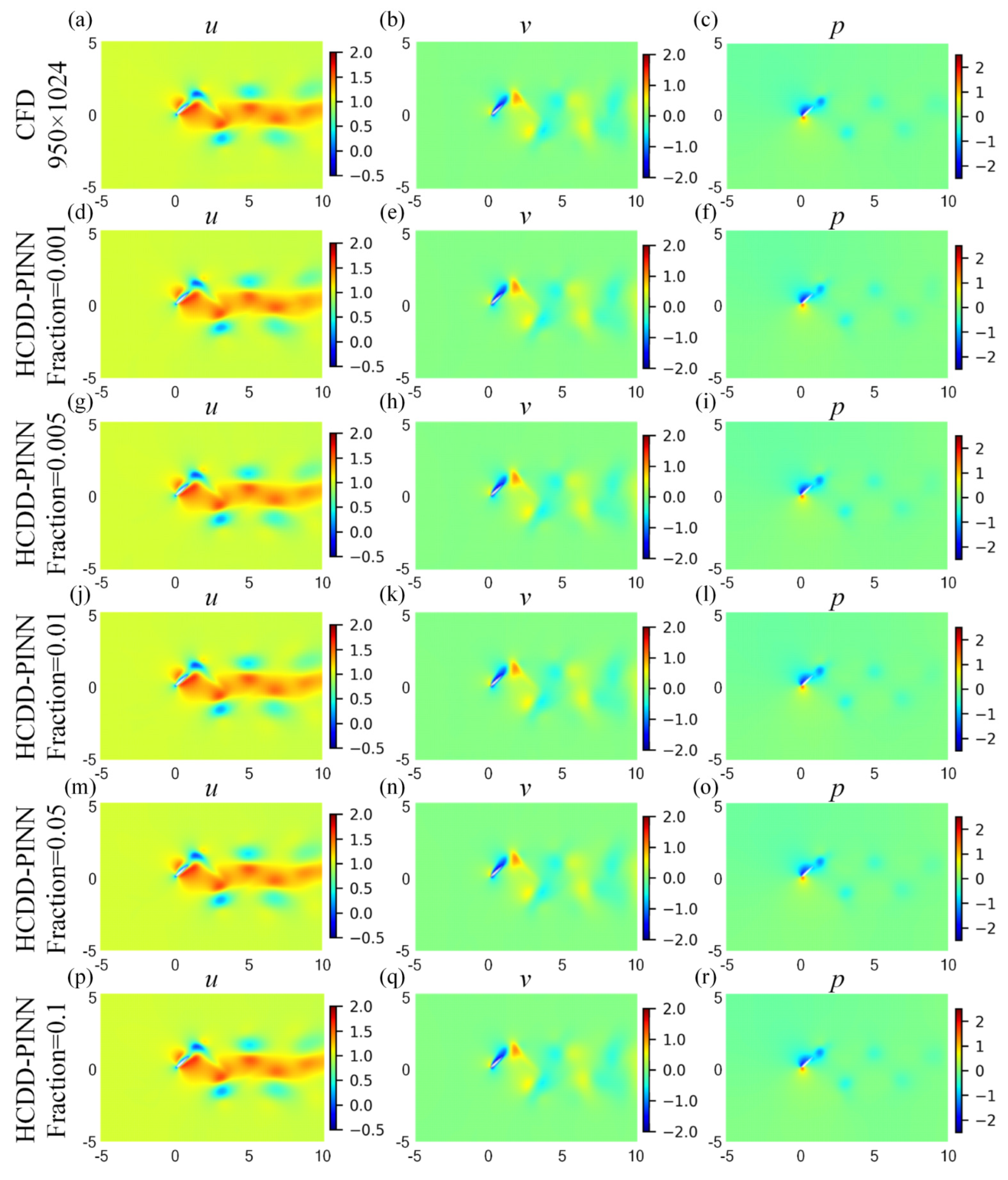
4.2. Effect of the Fraction of Coarse Internal Data
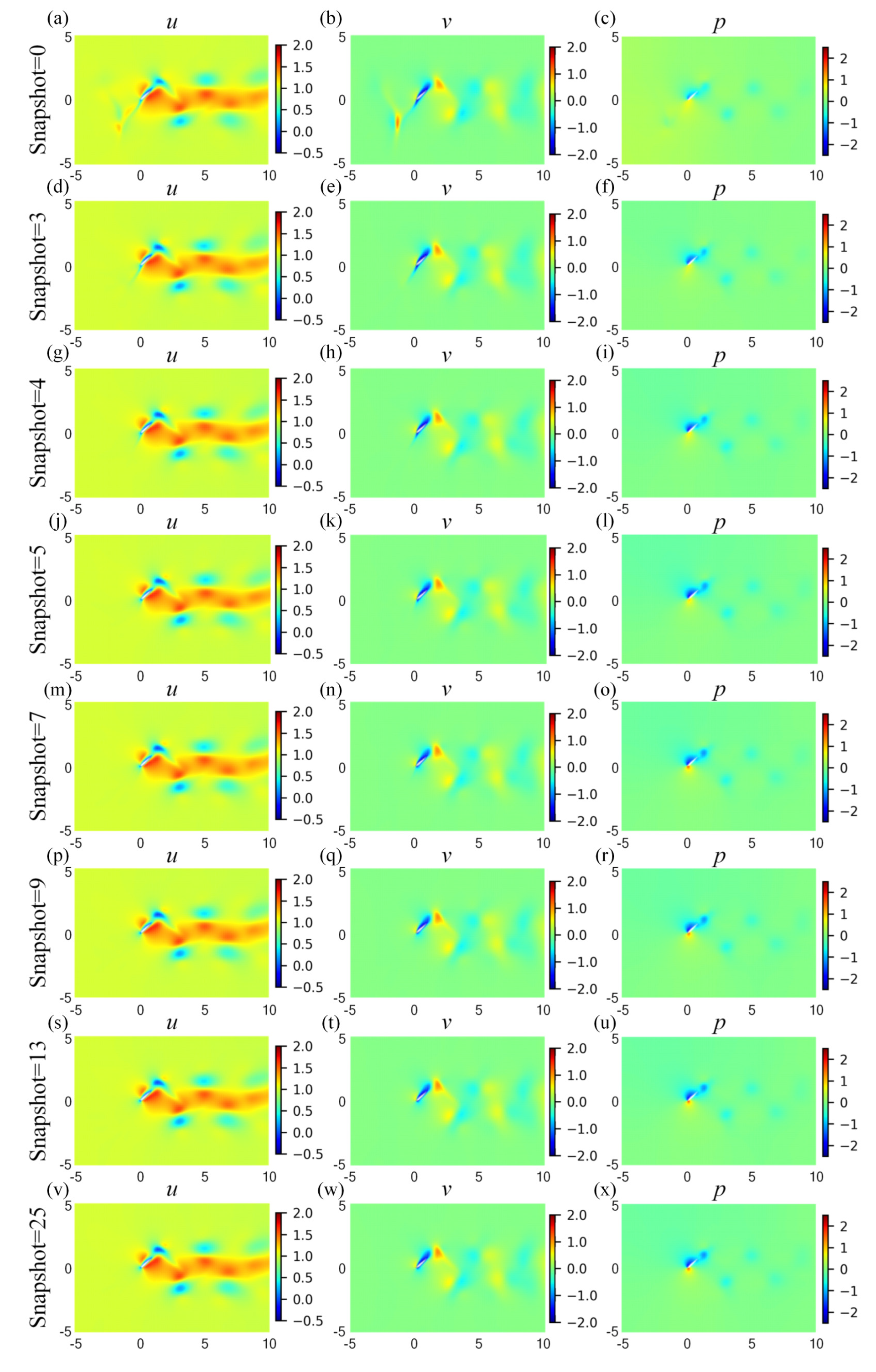
4.3. Effect of the Snapshot Number of Coarse Internal Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| c | chord length, m |
| pressure coefficient | |
| f | stroke frequency, s−1 |
| hm | plunge amplitude, m |
| mean square error of u | |
| mean square error of v | |
| mean square error of p | |
| cycle-averaged mean square error of u | |
| cycle-averaged mean square error of v | |
| cycle-averaged mean square error of p | |
| total collocation points | |
| collocation points for the entire spatial-temporal space | |
| instant collocation points around the flapping wing | |
| Re | Reynolds number |
| T | stroke period, s |
| αm | pitch amplitude, ° |
| boundary condition loss | |
| governing equations loss | |
| coarse internal data loss | |
| initial condition loss | |
| governing equations loss | |
| weighting coefficient for initial and boundary condition losses | |
| weighting coefficient for coarse internal data loss | |
| σ | Cauchy stress tensor |
References
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Xiong, H.Y.; Alipanahi, B.; Lee, L.J.; Bretschneider, H.; Merico, D.; Yuen, R.K.C.; Hua, Y.; Gueroussov, S.; Najafabadi, H.S.; Hughes, T.R.; et al. The human splicing code reveals new insights into the genetic determinants of disease. Science 2015, 347, 1254806. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid. Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Miyanawala, T.P.; Jaiman, R.K. An efficient deep learning technique for the Navier-Stokes equations: Application to unsteady wake flow dynamics. arXiv 2017, arXiv:1710.09099. [Google Scholar]
- Jin, X.; Cheng, P.; Chen, W.L.; Li, H. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys. Fluids 2018, 30, 047105. [Google Scholar] [CrossRef]
- Sekar, V.; Jiang, Q.; Shu, C.; Khoo, B.C. Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 2019, 31, 057103. [Google Scholar] [CrossRef]
- Han, R.; Wang, Y.; Zhang, Y.; Chen, G. A novel spatial-temporal prediction method for unsteady wake flows based on hybrid deep neural network. Phys. Fluids 2019, 31, 127101. [Google Scholar] [CrossRef]
- Dissanayake, M.; Phan-Thien, N. Neural-network-based approximations for solving partial differential equations. Commun. Numer. Methods Eng. 1994, 10, 195–201. [Google Scholar] [CrossRef]
- van Milligen, B.P.; Tribaldos, V.; Jiménez, J.A. Neural Network Diff erential Equation and Plasma Equilibrium Solver. Phys. Rev. Lett. 1995, 75, 3594–3597. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid. Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Leung, W.T.; Lin, G.; Zhang, Z. NH-PINN: Neural homogenization-based physics-informed neural network for multiscale problems. J. Comput. Phys. 2022, 470, 111529. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Mao, Z.; Adams, N.; Karniadakis, G.E. Physics-informed neural networks for inverse problems in supersonic flows. J. Comput. Phys. 2022, 466, 111402. [Google Scholar] [CrossRef]
- Rao, C.; Sun, H.; Liu, Y. Physics-informed deep learning for incompressible laminar flows. Theor. Appl. Mech. Lett. 2020, 10, 207–212. [Google Scholar] [CrossRef]
- Choi, S.; Jung, I.; Kim, H.; Na, J.; Lee, J.M. Physics-informed deep learning for data-driven solutions of computational fluid dynamics. Korean J. Chem. Eng. 2022, 39, 515–528. [Google Scholar] [CrossRef]
- Wu, P.; Pan, K.; Ji, L.; Gong, S.; Feng, W.; Yuan, W.; Pain, C. Navier–stokes generative adversarial network: A physics-informed deep learning model for fluid flow generation. Neural Comput. Appl. 2022, 34, 11522–11539. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, G.T. Deep learning method based on physics informed neural network with Resnet block for solving fluid flow problems. Water 2021, 13, 423. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Wang, J.X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Fuks, O.; Tchelepi, H.A. Limitations of physics informed machine learning for nonlinear two-phase transport in porous media. J. Mach. Learn. Model. Comput. 2020, 1, 19–37. [Google Scholar] [CrossRef]
- Raissi, M. Deep hidden physics models: Deep learning of nonlinear partial differential equations. J. Mach. Learn. Res. 2018, 19, 932–955. [Google Scholar]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning–accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef] [PubMed]
- Wootton, R. From insects to microvehicles. Nature 2000, 403, 144–145. [Google Scholar] [CrossRef]
- Thomas, A.L.R.; Taylor, G.K.; Srygley, R.B.; Nudds, R.L.; Bomphrey, R.J. Dragonfly flight: Free-flight and tethered flow visualizations reveal a diverse array of unsteady lift-generating mechanisms, controlled primarily via angle of attack. J. Exp. Biol. 2004, 207, 4299–4323. [Google Scholar] [CrossRef]
- Srygley, R.B.; Thomas, A.L.R. Unconventional lift-generating mechanisms in free-flying butterflies. Nature 2002, 420, 660–664. [Google Scholar] [CrossRef]
- Birch, J.M.; Dickinson, M.H. Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 2001, 412, 729–733. [Google Scholar] [CrossRef]
- Mujtaba, A.; Latif, U.; Uddin, E.; Younis, M.Y.; Sajid, M.; Ali, Z.; Abdelkefi, A. Hydrodynamic energy harvesting analysis of two piezoelectric tandem flags under influence of upstream body’s wakes. Appl. Energy 2021, 282, 116173. [Google Scholar] [CrossRef]
- Min, Y.; Zhao, G.; Pan, D.; Shao, X. Aspect ratio effects on the aerodynamic performance of a biomimetic hummingbird wing in flapping. Biomimetics 2023, 8, 216. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.J.; Liu, X.M. Effects of stroke deviation on hovering aerodynamic performance of flapping wings. Phys. Fluids 2019, 31, 111901. [Google Scholar] [CrossRef]
- Tay, W.B.; Deng, S.; van Oudheusden, B.W.; Bijl, H. Validation of immersed boundary method for the numerical simulation of flapping wing flight. Comput. Fluids 2015, 115, 226–242. [Google Scholar] [CrossRef]
- Noda, R.; Nakata, T.; Liu, H. Effect of hindwings on the aerodynamics and passive dynamic stability of a hovering hawkmoth. Biomimetics 2023, 8, 578. [Google Scholar] [CrossRef]
- Ellington, C.P.; Coen, V.D.B.; Willmott, A.P.; Thomas, A.L.R. Leading-edge vortices in insect flight. Nature 1996, 384, 626–630. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, F.O.; Pick, S. The aerodynamic benefit of wing-wing interaction depends on stroke trajectory in flapping insect wings. J. Exp. Biol. 2007, 210, 1362–1377. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Wang, Y.; Li, D.; Liu, X. Effects of asymmetric stroke deviation on the aerodynamic performance of flapping wing. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 237, 480–499. [Google Scholar] [CrossRef]
- Lim, K.B.; Tay, W.B. Numerical analysis of the s1020 airfoils in tandem under different flapping configurations. Acta Mech. Sin. 2010, 26, 191–207. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]




| No Internal | Coarse Internal Data Obtained from Different Resolution | |||
|---|---|---|---|---|
| 149 × 128 | 269 × 256 | 502 × 512 | ||
| Training cost | 11,412 s | 30,643 s | 18,465 s | 13,427 s |
| Prediction cost | 298 s | 314 s | 345 s | 311 s |
| Training loss | 2.64 × 10−3 | 5.08 × 10−3 | 4.59 × 10−3 | 4.90 × 10−3 |
| Predicting error | 1.01 × 10−1 | 3.63 × 10−2 | 1.56 × 10−2 | 1.61 × 10−2 |
| Predicting error | 7.25 × 10−1 | 2.92 × 10−1 | 1.43 × 10−1 | 1.44 × 10−1 |
| Predicting error | 2.59 | 3.32 × 10−1 | 2.75 × 10−1 | 3.12 × 10−1 |
| Collocation points | |||||||||||||||||||||||||||||||||||||||||||||
| () | 1.6 | 2.4 | 3.2 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | ||||||||||||||||||||||||||||||||||||
| 1500 | 1500 | 0 | 500 | 2500 | 1500 | 1500 | 1500 | ||||||||||||||||||||||||||||||||||||||
| timestep | 100 | 100 | 100 | 100 | 100 | 100 | 50 | 150 | 200 | ||||||||||||||||||||||||||||||||||||
| Training cost ( s) | 1.847 | 2.651 | 3.186 | 1.798 | 1.896 | 2.805 | 1.018 | 2.794 | 3.070 | ||||||||||||||||||||||||||||||||||||
| Training loss | 4.592 | 3.649 | 3.356 | 80.24 | 3.155 | 4.114 | 4.077 | 4.464 | 5.068 | ||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.564 | 1.540 | 1.532 | 3.256 | 1.528 | 1.544 | 1.507 | 1.581 | 1.607 | ||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.433 | 1.411 | 1.390 | 6.326 | 1.411 | 1.407 | 1.412 | 1.441 | 1.450 | ||||||||||||||||||||||||||||||||||||
| Predicting error () | 2.753 | 2.520 | 2.468 | 4.821 | 2.596 | 2.557 | 2.657 | 2.614 | 2.757 | ||||||||||||||||||||||||||||||||||||
| Architecture of DNN | |||||||||||||||||||||||||||||||||||||||||||||
| Layer | 6 | 8 | 10 | ||||||||||||||||||||||||||||||||||||||||||
| Neurons (per layer) | 50 | 100 | 150 | 50 | 100 | 150 | 50 | 100 | 150 | ||||||||||||||||||||||||||||||||||||
| Training cost ( s) | 2.273 | 2.944 | 2.944 | 1.847 | 2.235 | 3.403 | 1.640 | 2.835 | 5.082 | ||||||||||||||||||||||||||||||||||||
| Training loss | 6.136 | 2.686 | 2.720 | 4.592 | 3.344 | 2.997 | 4.773 | 3.544 | 2.677 | ||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.630 | 1.537 | 1.511 | 1.564 | 1.551 | 1.546 | 1.567 | 1.562 | 1.551 | ||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.461 | 1.383 | 1.385 | 1.433 | 1.438 | 1.437 | 1.474 | 1.436 | 1.415 | ||||||||||||||||||||||||||||||||||||
| Predicting error () | 2.794 | 2.333 | 2.377 | 2.753 | 2.558 | 2.511 | 2.743 | 2.698 | 2.571 | ||||||||||||||||||||||||||||||||||||
| Loss weighting coefficients | |||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 1 | 1 | |||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 1 | 2 | 3 | |||||||||||||||||||||||||||||||||||||||||
| Training cost ( s) | 1.847 | 1.715 | 1.747 | 1.430 | 1.620 | ||||||||||||||||||||||||||||||||||||||||
| Training loss | 4.592 | 4.820 | 4.815 | 5.600 | 6.269 | ||||||||||||||||||||||||||||||||||||||||
| () | 2.585 | 2.781 | 2.813 | 3.037 | 3.228 | ||||||||||||||||||||||||||||||||||||||||
| ) | 4.466 | 1.990 | 1.206 | 5.602 | 6.476 | ||||||||||||||||||||||||||||||||||||||||
| () | 2.075 | 1.115 | 0.827 | 2.197 | 2.837 | ||||||||||||||||||||||||||||||||||||||||
| () | 1.353 | 1.418 | 1.392 | 0.891 | 0.703 | ||||||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.564 | 1.606 | 1.539 | 1.568 | 1.592 | ||||||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.433 | 1.419 | 1.427 | 1.412 | 1.430 | ||||||||||||||||||||||||||||||||||||||||
| Predicting error () | 2.753 | 2.774 | 2.659 | 2.420 | 2.283 | ||||||||||||||||||||||||||||||||||||||||
| Adam optimizer | |||||||||||||||||||||||||||||||||||||||||||||
| Learning rate () | 5 | 1 | 0.5 | 5 | 5 | ||||||||||||||||||||||||||||||||||||||||
| Iteration () | 5 | 5 | 5 | 10 | 15 | ||||||||||||||||||||||||||||||||||||||||
| Training cost ( s) | 1.847 | 1.585 | 1.693 | 1.934 | 2.185 | ||||||||||||||||||||||||||||||||||||||||
| Training loss | 4.592 | 4.801 | 4.500 | 4.167 | 4.392 | ||||||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.564 | 1.562 | 1.543 | 1.544 | 1.590 | ||||||||||||||||||||||||||||||||||||||||
| Predicting error () | 1.433 | 1.432 | 1.424 | 1.424 | 1.421 | ||||||||||||||||||||||||||||||||||||||||
| Predicting error () | 2.753 | 2.711 | 2.620 | 2.610 | 2.633 | ||||||||||||||||||||||||||||||||||||||||
| Coarse internal data (269 × 256) | ||||||||||||||||||||||||||||||||||||||||
| Snapshot (fraction = 0.005) | ||||||||||||||||||||||||||||||||||||||||
| 0 | 3 | 4 | 5 | 7 | 9 | 13 | 25 | |||||||||||||||||||||||||||||||||
| Training cost (s) | 35,694 | 30,926 | 28,742 | 28,495 | 28,010 | 27,624 | 23,496 | 22,712 | ||||||||||||||||||||||||||||||||
| Training loss | 0.806 | 1.405 | 1.512 | 1.599 | 1.658 | 1.683 | 1.902 | 2.079 | ||||||||||||||||||||||||||||||||
| Predicting error () | 5.311 | 2.064 | 1.751 | 1.682 | 1.584 | 1.569 | 1.554 | 1.537 | ||||||||||||||||||||||||||||||||
| Predicting error () | 4.193 | 1.770 | 1.568 | 1.464 | 1.415 | 1.396 | 1.380 | 1.363 | ||||||||||||||||||||||||||||||||
| Predicting error () | 1.435 | 4.857 | 4.108 | 2.879 | 2.749 | 2.597 | 2.375 | 2.325 | ||||||||||||||||||||||||||||||||
| Fraction (snapshot = 25) | ||||||||||||||||||||||||||||||||||||||||
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | ||||||||||||||||||||||||||||||||||||
| Training cost (s) | 26,267 | 22,712 | 24,717 | 24,629 | 33,146 | |||||||||||||||||||||||||||||||||||
| Training loss | 1.676 | 2.079 | 2.447 | 2.406 | 2.017 | |||||||||||||||||||||||||||||||||||
| Predicting error () | 1.631 | 1.537 | 1.532 | 1.540 | 1.534 | |||||||||||||||||||||||||||||||||||
| Predicting error () | 1.385 | 1.363 | 1.354 | 1.385 | 1.384 | |||||||||||||||||||||||||||||||||||
| Predicting error () | 2.852 | 2.325 | 2.206 | 2.103 | 2.068 | |||||||||||||||||||||||||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, F.; Tay, W.; Zhou, Y.; Khoo, B. A Novel Hybrid Deep Learning Method for Predicting the Flow Fields of Biomimetic Flapping Wings. Biomimetics 2024, 9, 72. https://doi.org/10.3390/biomimetics9020072
Hu F, Tay W, Zhou Y, Khoo B. A Novel Hybrid Deep Learning Method for Predicting the Flow Fields of Biomimetic Flapping Wings. Biomimetics. 2024; 9(2):72. https://doi.org/10.3390/biomimetics9020072
Chicago/Turabian StyleHu, Fujia, Weebeng Tay, Yilun Zhou, and Boocheong Khoo. 2024. "A Novel Hybrid Deep Learning Method for Predicting the Flow Fields of Biomimetic Flapping Wings" Biomimetics 9, no. 2: 72. https://doi.org/10.3390/biomimetics9020072
APA StyleHu, F., Tay, W., Zhou, Y., & Khoo, B. (2024). A Novel Hybrid Deep Learning Method for Predicting the Flow Fields of Biomimetic Flapping Wings. Biomimetics, 9(2), 72. https://doi.org/10.3390/biomimetics9020072




