Capillary Wicking on Heliamphora minor-Mimicking Mesoscopic Trichomes Array
Abstract
1. Introduction
2. Materials and Methods
2.1. Biological Characterization and the Fabrication of Biomimetic Samples
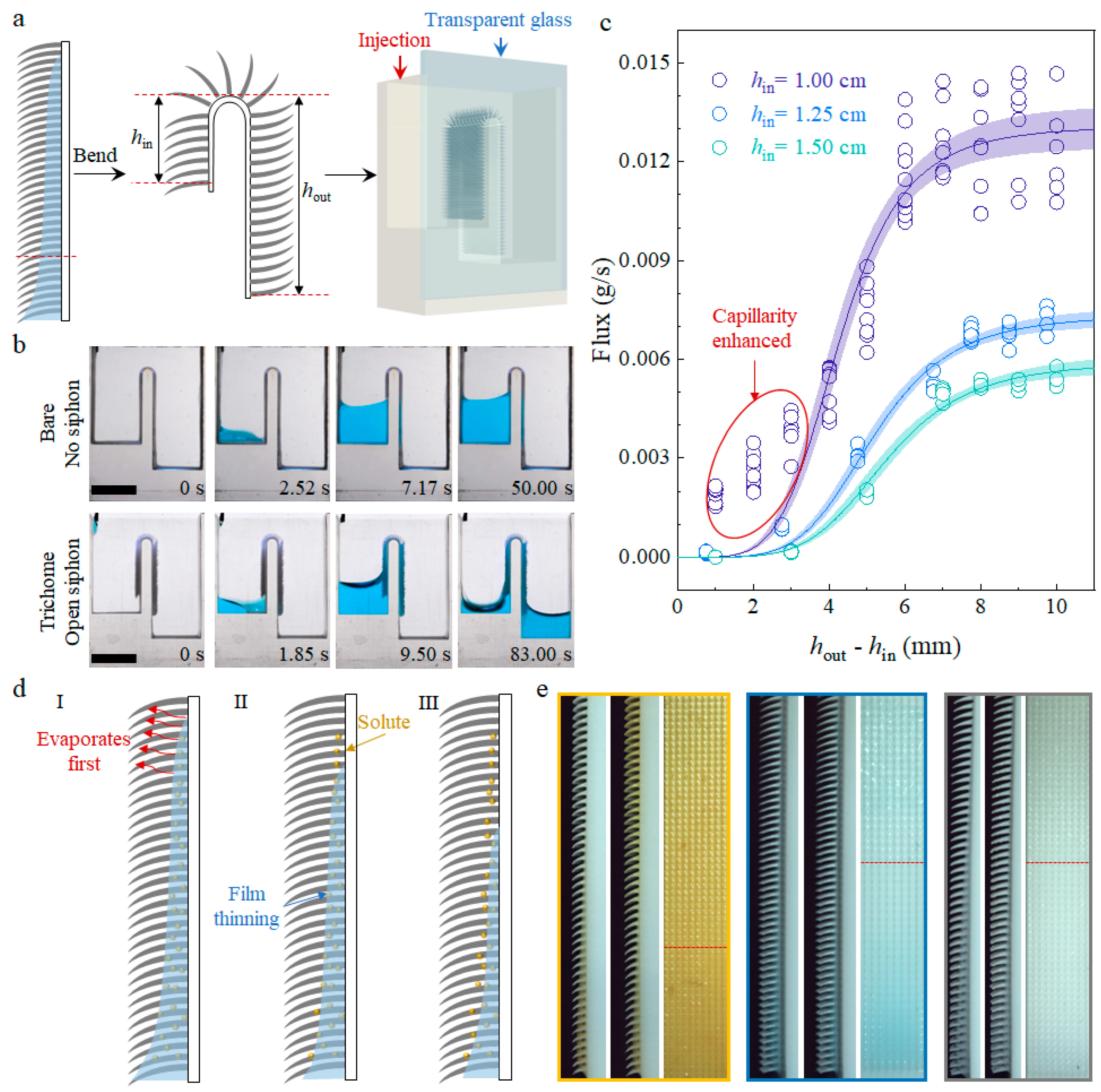
2.2. Capillary Wicking, High-Flux Siphon Application, and Mass Transportation
3. Results and Discussion
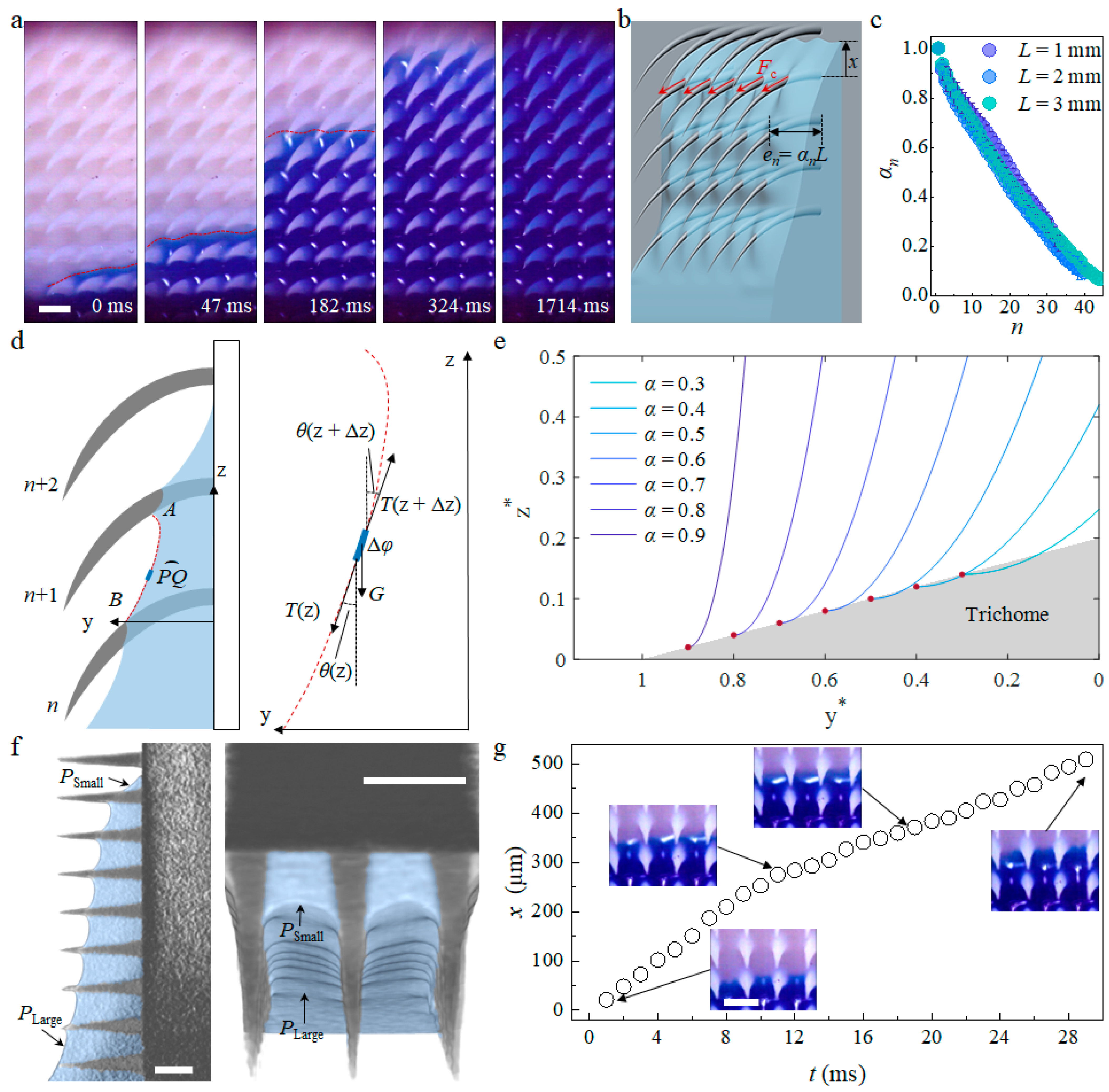
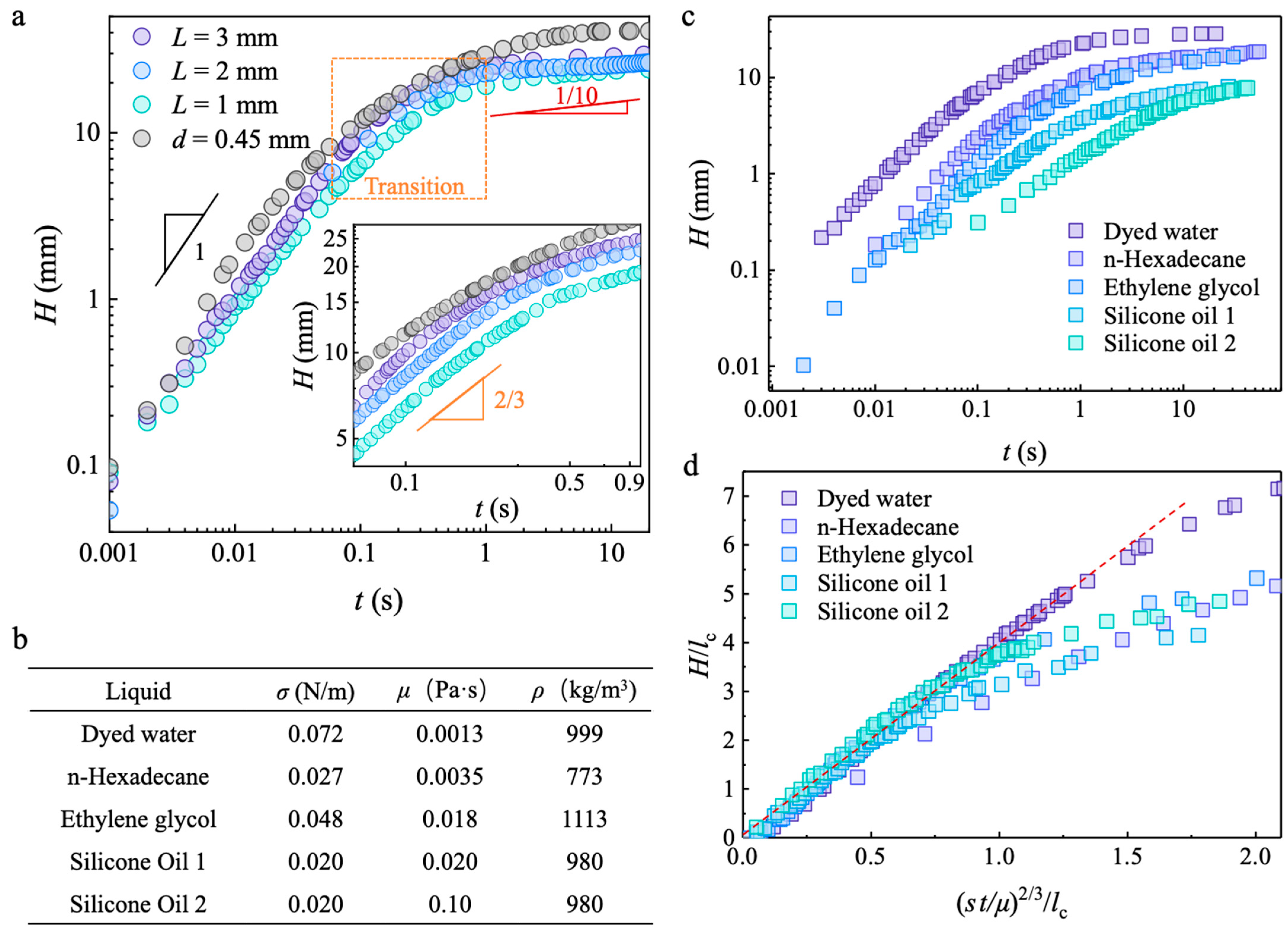
3.1. Capillary Wicking Height and Film Thickness
3.2. Microscopic Capillary Wicking Dynamics
3.3. Macroscopic Capillary Wicking Dynamics
3.4. High-Flux Open Siphon Applications and Mass Transportation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Let w(z) = f′(z), and the equation transforms intoThe direct integration of Equation (A1) giveswhere C is an integral constant determined by the boundary condition. And w can be expressed by v = Knz + c as
- The solution of w from Equation (A3) can be obtained by substituting w(z) = f′(z) = Knf′(v):and f expressed by v isand C′ is determined by the boundary conditions. The expressing of v in terms of z can generate a profile f represented by z.
- From Equation (A5), the curvature of meniscus κ, which is defined ascan be obtained as κ = −Kn/(Knz + C)2.
- Take m = k′ρH2p and u = H′ into consideration; eliminating p obtainsH2H″ + 2H(H′)2 = σ*/pk′
- Let Φ(H) = H′; Equation (A7) can be transformed intowhich can be solved directly asH2ΦΦ′ + 2HΦ2 = σ*/pk′where C1 is an integral constant.Φ2 = 2σ*/3pHk′ + C1/H4
- Replace Φ with H′, and the solution to Equation (A9) can be acquired asand the boundary condition of the initial stage is that H = 0 for t = 0 s, which implies C1 = C22. If the initial velocity is considered infinitely small or zero, the simplest form of the scaling law is Equation (9), that is C1 = C2 = 0.2H3σ*/3pk′ + C1 = (tσ*/pk′ + C2)2
Appendix B
| Symbols | Definition | Unit |
|---|---|---|
| σ | Surface tension | N/m |
| ρ | Density of liquids | kg/m3 |
| μ | Viscosity of liquids | Pa·s |
| g | Gravitational acceleration constant | kg·m/s2 |
| lc | Capillary length | m |
| L | Length of trichomes | m |
| p | Center-to-center pitch of trichome’s base | m |
| d | Diameter of trichome’s base | m |
| H | Capillary wicking height | m |
| u | Capillary wicking velocity | m/s |
| T | Tension force on meniscus profile | N |
| θ | Deflection angle of profile tangent with respect to the z direction | ° |
| F | Constant lateral force representing Tsinθ | N |
| f | Function describing the meniscus profile | \ |
| φ | Path length from point B to P | m |
| en | Thickness in the nth interval | m |
| αn | Ratio of thickness to trichome length | \ |
| Sn | Area of cross-section perpendicular to z axis | m2 |
| Kn | Coefficient equals ρgSn/F | m−1 |
| κ | Curvature of meniscus | m−1 |
References
- Bico, J.; Tordeux, C.; Quéré, D. Rough wetting. Europhys. Lett. 2001, 55, 214–220. [Google Scholar] [CrossRef]
- Bico, J.; Thiele, U.; Quéré, D. Wetting of textured surfaces. Colloids Surf. A Physicochem. Eng. Asp. 2002, 206, 41–46. [Google Scholar] [CrossRef]
- Ishino, C.; Reyssat, M.; Reyssat, E.; Okumura, K.; Quéré, D. Wicking within forests of micropillars. Europhys. Lett. 2007, 79, 56005. [Google Scholar] [CrossRef]
- Kim, J.; Moon, M.-W.; Kim, H.-Y. Dynamics of hemiwicking. J. Fluid Mech. 2016, 800, 57–71. [Google Scholar] [CrossRef]
- Chen, X.; Chen, J.; Ouyang, X.; Song, Y.; Xu, R.; Jiang, P. Water Droplet Spreading and Wicking on Nanostructured Surfaces. Langmuir 2017, 33, 6701–6707. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Suh, Y.; Dubey, P.P.; Barako, M.T.; Won, Y. Capillary Wicking in Hierarchically Textured Copper Nanowire Arrays. ACS Appl. Mater. Interfaces 2019, 11, 1546–1554. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Jung, B.; Park, G.-S.; Kim, H.-Y. Condensation and wicking of water on solid nanopatterns. Phys. Rev. Fluid 2022, 7, 024202. [Google Scholar] [CrossRef]
- Courbin, L.; Denieul, E.; Dressaire, E.; Roper, M.; Ajdari, A.; Stone, H.A. Imbibition by polygonal spreading on microdecorated surfaces. Nat. Mater. 2007, 6, 661–664. [Google Scholar] [CrossRef] [PubMed]
- McHale, G. Surface wetting: Liquids shape up nicely. Nat. Mater. 2007, 6, 627–628. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Song, Y.; Zheng, H.; Feng, S.; Xu, W.; Wang, Z. Designing biomimetic liquid diodes. Soft Matter 2019, 15, 1902–1915. [Google Scholar] [CrossRef]
- Gelebart, A.H.; Mc Bride, M.; Schenning, A.P.H.J.; Bowman, C.N.; Broer, D.J. Photoresponsive Fiber Array: Toward Mimicking the Collective Motion of Cilia for Transport Applications. Adv. Funct. Mater. 2016, 26, 5322–5327. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, J.; Chen, Z.; Yang, S.; Lai, Y. Liquid mobility on superwettable surfaces for applications in energy and the environment. J. Mater. Chem. A 2019, 7, 38–63. [Google Scholar] [CrossRef]
- Dittrich, P.S.; Manz, A. Lab-on-a-chip: Microfluidics in drug discovery. Nat. Rev. Drug Discov. 2006, 5, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Si, Y.; Wang, T.; Li, C.; Yu, C.; Li, N.; Gao, C.; Dong, Z.; Jiang, L. Liquids Unidirectional Transport on Dual-Scale Arrays. ACS Nano 2018, 12, 9214–9222. [Google Scholar] [CrossRef] [PubMed]
- van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Quéré, D. Wetting and Roughness. Annu. Rev. Mater. Res. 2008, 38, 71–99. [Google Scholar] [CrossRef]
- Kim, S.J.; Moon, M.-W.; Lee, K.-R.; Lee, D.-Y.; Chang, Y.S.; Kim, H.-Y. Liquid spreading on superhydrophilic micropillar arrays. J. Fluid Mech. 2011, 680, 477–487. [Google Scholar] [CrossRef]
- Hancock, M.J.; Sekeroglu, K.; Demirel, M.C. Bioinspired Directional Surfaces for Adhesion, Wetting and Transport. Adv. Funct. Mater. 2012, 22, 2223–2234. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, P.; Zhang, L.; Liu, H.; Jiang, Y.; Zhang, D.; Han, Z.; Jiang, L. Continuous directional water transport on the peristome surface of Nepenthes alata. Nature 2016, 532, 85–89. [Google Scholar] [CrossRef]
- Krishnan, S.R.; Bal, J.; Putnam, S.A. A simple analytic model for predicting the wicking velocity in micropillar arrays. Sci. Rep. 2019, 9, 20074. [Google Scholar] [CrossRef]
- Feng, S.; Zhu, P.; Zheng, H.; Zhan, H.; Chen, C.; Li, J.; Wang, L.; Yao, X.; Liu, Y.; Wang, Z. Three-dimensional capillary ratchet-induced liquid directional steering. Science 2021, 373, 1344–1348. [Google Scholar] [CrossRef]
- Lecointre, P.; Laney, S.; Michalska, M.; Li, T.; Tanguy, A.; Papakonstantinou, I.; Quéré, D. Unique and universal dew-repellency of nanocones. Nat. Commun. 2021, 12, 3458. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Li, B.; Li, S.; Luo, G.; Zheng, B.; Zhang, J. Superamphiphobic Cu/CuO Micropillar Arrays with High Repellency towards Liquids of Extremely High Viscosity and Low Surface Tension. Sci. Rep. 2019, 9, 702. [Google Scholar] [CrossRef] [PubMed]
- de Gennes, P.-G.; Brochard-Wyart, F.; Quéré, D.; Reisinger, A.; Widom, B. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer: New York, NY, USA, 2004. [Google Scholar]
- Delannoy, J.; Lafon, S.; Koga, Y.; Reyssat, É.; Quéré, D. The dual role of viscosity in capillary rise. Soft Matter 2019, 15, 2757–2761. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Zhao, Y.-P. Multiscale dynamic wetting of a droplet on a lyophilic pillar-arrayed surface. J. Fluid Mech. 2013, 716, 171–188. [Google Scholar] [CrossRef]
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Quéré, D. Inertial capillarity. Europhys. Lett. 1997, 39, 533. [Google Scholar] [CrossRef]
- Kim, J.; Moon, M.-W.; Kim, H.-Y. Capillary rise in superhydrophilic rough channels. Phys. Fluids 2020, 32, 032105. [Google Scholar] [CrossRef]
- Jaffe, K.; Michelangeli, F.; Gonzalez, J.M.; Miras, B.; Christine Ruiz, M. Carnivory in pitcher plants of the genus Heliamphora (Sarraceniaceae). New Phytol. 1992, 122, 733–744. [Google Scholar] [CrossRef]
- Bauer, U.; Scharmann, M.; Skepper, J.; Federle, W. ‘Insect aquaplaning’ on a superhydrophilic hairy surface: How Heliamphora nutans Benth. pitcher plants capture prey. Proc. R. Soc. Lond. B Biol. Sci. 2013, 280, 20122569. [Google Scholar] [CrossRef]
- Wang, X.; Shen, C.; Meng, P.; Tan, G.; Lv, L. Analysis and review of trichomes in plants. BMC Plant Biol. 2021, 21, 70. [Google Scholar] [CrossRef]
- Vogler, E.A. Structure and reactivity of water at biomaterial surfaces. Adv. Colloid Interface Sci. 1998, 74, 69–117. [Google Scholar] [CrossRef]
- Jurin, J., II. An account of some experiments shown before the Royal Society; with an enquiry into the cause of the ascent and suspension of water in capillary tubes. Philos. Trans. R. Soc. Lond. 1718, 30, 739–747. [Google Scholar] [CrossRef]
- Weislogel, M.M. Compound capillary rise. J. Fluid Mech. 2012, 709, 622–647. [Google Scholar] [CrossRef]
- Das, S.; Mitra, S.K. Different regimes in vertical capillary filling. Phys. Rev. E 2013, 87, 063005. [Google Scholar] [CrossRef]
- Tanner, L.H. The spreading of silicone oil drops on horizontal surfaces. J. Phys. D Appl. Phys. 1979, 12, 1473. [Google Scholar] [CrossRef]
- de Gennes, P.G. Wetting: Statics and dynamics. Rev. Mod. Phys. 1985, 57, 827–863. [Google Scholar] [CrossRef]
- Delgadino, M.G.; Mellet, A. On the Relationship between the Thin Film Equation and Tanner’s Law. Commun. Pure Appl. Math. 2021, 74, 507–543. [Google Scholar] [CrossRef]
- Ganci, S.; Yegorenkov, V. Historical and pedagogical aspects of a humble instrument. Eur. J. Phys. 2008, 29, 421–430. [Google Scholar] [CrossRef]
- Boatwright, A.; Hughes, S.; Barry, J. The height limit of a siphon. Sci. Rep. 2015, 5, 16790. [Google Scholar] [CrossRef]
- Wang, K.; Sanaei, P.; Zhang, J.; Ristroph, L. Open capillary siphons. J. Fluid Mech. 2022, 932, R1. [Google Scholar] [CrossRef]
- Yu, K.; Cheng, Y.-G.; Zhang, X.-X. Hydraulic characteristics of a siphon-shaped overflow tower in a long water conveyance system: CFD simulation and analysis. J. Hydrodyn. Ser. B 2016, 28, 564–575. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Cheng, Z.; Jiang, L.; Dong, Z. Capillary Wicking on Heliamphora minor-Mimicking Mesoscopic Trichomes Array. Biomimetics 2024, 9, 102. https://doi.org/10.3390/biomimetics9020102
Chen F, Cheng Z, Jiang L, Dong Z. Capillary Wicking on Heliamphora minor-Mimicking Mesoscopic Trichomes Array. Biomimetics. 2024; 9(2):102. https://doi.org/10.3390/biomimetics9020102
Chicago/Turabian StyleChen, Fenglin, Ziyang Cheng, Lei Jiang, and Zhichao Dong. 2024. "Capillary Wicking on Heliamphora minor-Mimicking Mesoscopic Trichomes Array" Biomimetics 9, no. 2: 102. https://doi.org/10.3390/biomimetics9020102
APA StyleChen, F., Cheng, Z., Jiang, L., & Dong, Z. (2024). Capillary Wicking on Heliamphora minor-Mimicking Mesoscopic Trichomes Array. Biomimetics, 9(2), 102. https://doi.org/10.3390/biomimetics9020102










