A New Single-Parameter Bees Algorithm
Abstract
1. Introduction
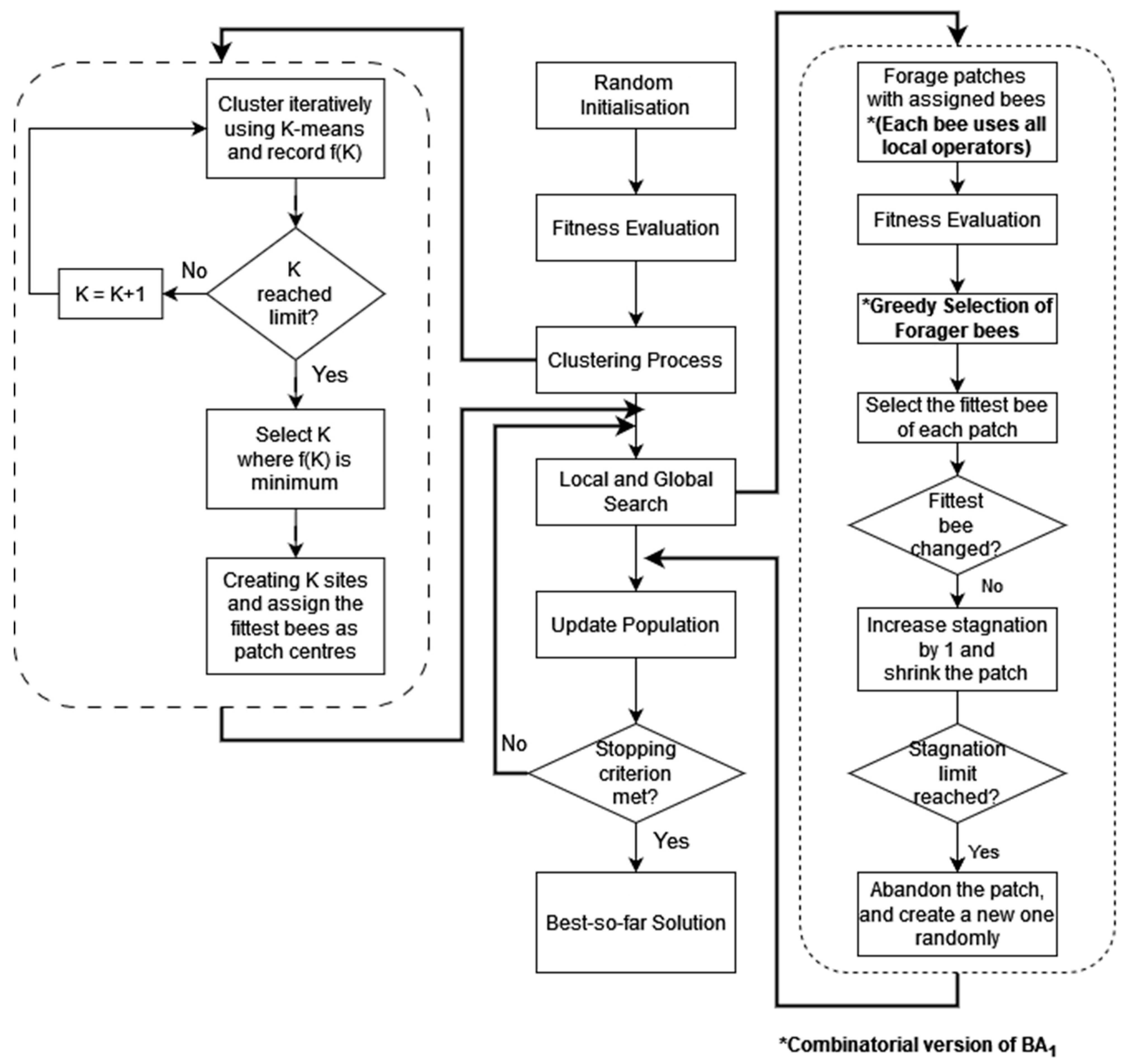
2. The Bees Algorithm
| Algorithm 1: Original Bees Algorithm | ||||
| 1 | Start | |||
| 2 | Input the required parameters n, e, m, nep, nsp, ngh, MaxIt | |||
| 3 | Generate n initial solutions | |||
| 4 | Evaluate the fitness of the n initial solutions | |||
| 5 | Select the best m solution for neighbourhood search | |||
| 6 | while iteration < MaxIt do | |||
| 7 | for each site i, (i = 1, …, e) do | |||
| 8 | Exploit site within ngh of the site with nep forager bees (Equation (3)) and Evaluate fitness | |||
| 9 | if better solution found replace site | |||
| 10 | end for | |||
| 11 | for each site j, (j = e + 1, …, m) do | |||
| 12 | Exploit site within ngh of the site with nsp forager bees (Equation (3)) and Evaluate fitness | |||
| 13 | if better solution found replace site | |||
| 14 | end for | |||
| 15 | for each site k, (k = m + 1, …, n) do | |||
| 16 | Explore site n-m scout bees (Equation (2)) and Evaluate fitness | |||
| 17 | end for | |||
| 18 | end while | |||
| 19 | Return the best-so-far solution | |||
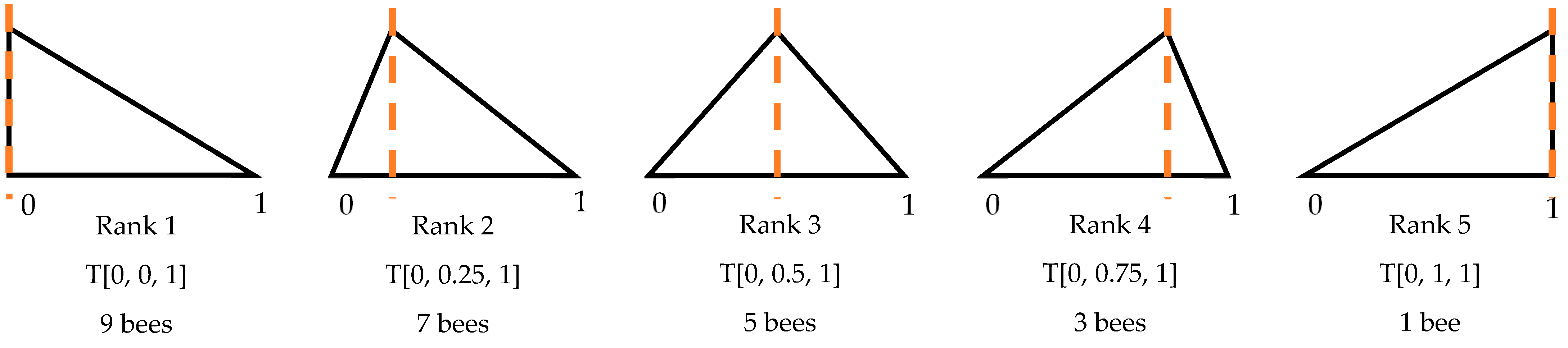
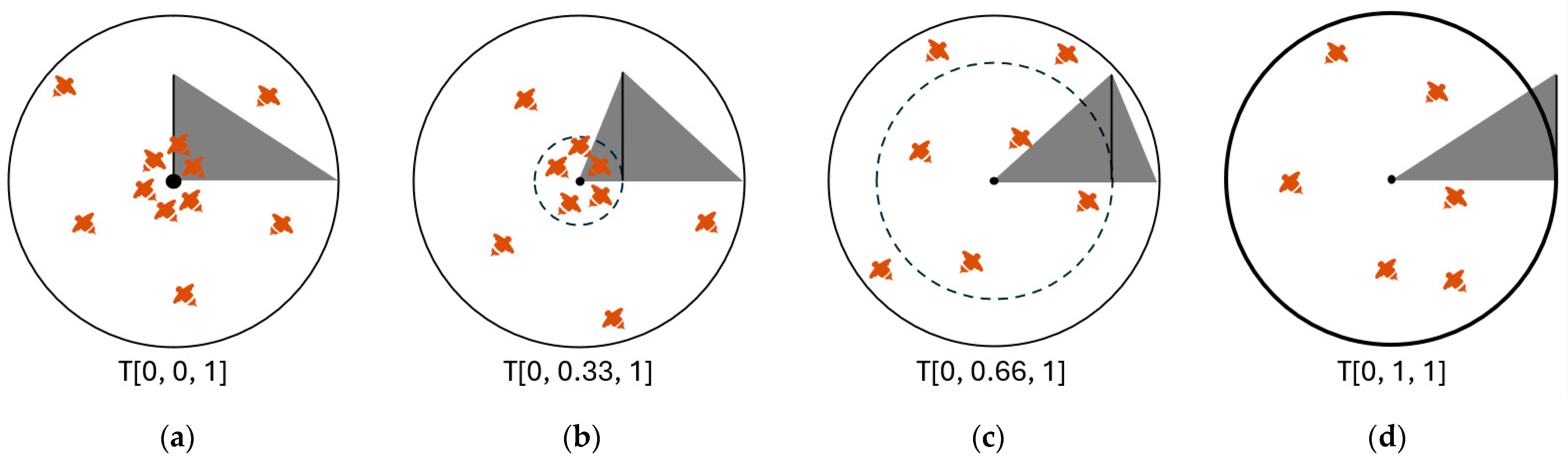
3. Details of BA1
4. Experiments and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ezugwu, A.E.; Adeleke, O.J.; Akinyelu, A.A.; Viriri, S. A conceptual comparison of several metaheuristic algorithms on continuous optimisation problems. Neural Comput. Appl. 2020, 32, 6207–6251. [Google Scholar] [CrossRef]
- Malarczyk, M.; Katsura, S.; Kaminski, M.; Szabat, K. A Novel Meta-Heuristic Algorithm Based on Birch Succession in the Optimization of an Electric Drive with a Flexible Shaft. Energies 2024, 17, 4104. [Google Scholar] [CrossRef]
- Çaşka, S. The Performance of Symbolic Limited Optimal Discrete Controller Synthesis in the Control and Path Planning of the Quadcopter. Appl. Sci. 2024, 14, 7168. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, R.; Zhong, X.; Yao, Y.; Shan, W.; Yuan, J.; Xiao, J.; Ma, Y.; Zhang, K.; Wang, Z. Multi-Strategy Enhanced Crested Porcupine Optimizer: CAPCPO. Mathematics 2024, 12, 3080. [Google Scholar] [CrossRef]
- Ismail, W.N.; Alsalamah, H.A. Efficient Harris Hawk Optimization (HHO)-Based Framework for Accurate Skin Cancer Prediction. Mathematics 2023, 11, 3601. [Google Scholar] [CrossRef]
- Ang, M.C.; Ng, K.W. Minimising printed circuit board assembly time using the bees algorithm with TRIZ-inspired operators. In Intelligent Production and Manufacturing Optimisation—The Bees Algorithm Approach; Springer International Publishing: Cham, Switzerland, 2022; pp. 25–41. [Google Scholar]
- Liu, C.; Zhang, D.; Li, W. Crown Growth Optimizer: An Efficient Bionic Meta-Heuristic Optimizer and Engineering Applications. Mathematics 2024, 12, 2343. [Google Scholar] [CrossRef]
- Mayouf, C.; Salhi, A.; Haidara, F.; Aroua, F.Z.; El-Sehiemy, R.A.; Naimi, D.; Aya, C.; Kane, C.S.E. Solving Optimal Power Flow Using New Efficient Hybrid Jellyfish Search and Moth Flame Optimization Algorithms. Algorithms 2024, 17, 438. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Yue, Y. Heuristic Optimization Algorithm of Black-Winged Kite Fused with Osprey and Its Engineering Application. Biomimetics 2024, 9, 595. [Google Scholar] [CrossRef]
- Riff, M.-C.; Montero, E. A new algorithm for reducing metaheuristic design effort. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 3283–3290. [Google Scholar]
- Barragan-Vite, I.; Medina-Marin, J.; Hernandez-Romero, N.; Anaya-Fuentes, G.E. A Petri Net-Based Algorithm for Solving the One-Dimensional Cutting Stock Problem. Appl. Sci. 2024, 14, 8172. [Google Scholar] [CrossRef]
- Castellani, M.; Pham, D.T. The bees algorithm—A gentle introduction. In Intelligent Production and Manufacturing Optimisation—The Bees Algorithm Approach; Springer International Publishing: Cham, Switzerland, 2022; pp. 3–21. [Google Scholar]
- Aljarah, I.; Faris, H.; Mirjalili, S. (Eds.) Evolutionary Data Clustering: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Shi, N.; Liu, X.; Guan, Y. Research on k-means clustering algorithm: An improved k-means clustering algorithm. In Proceedings of the Third International Symposium on Intelligent Information Technology and Security Informatics, Jian, China, 2–4 April 2010; pp. 63–67. [Google Scholar]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. An incremental K-means algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 783–795. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. Selection of K in K-means clustering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 103–119. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Suluova, H.F.; Hartono, N.; Pham, D.T. The Fibonacci Bees Algorithm for Continuous Optimisation Problems—Some Engineering Applications. In Proceedings of the International Workshop of the Bees Algorithm and Its Applications (BAA) 2023, Online, 15 November 2023. Paper 13. [Google Scholar]
- Pham, D.T.; Castellani, M. The bees algorithm: Modelling foraging behaviour to solve continuous optimization problems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 2919–2938. [Google Scholar] [CrossRef]
- Pham, D.T.; Ghanbarzadeh, A.; Koc, E.; Otri, S.; Rahim, S.; Zaidi, M. The Bees Algorithm. Technical Note; Manufacturing Engineering Centre, Cardiff University: Cardiff, UK, 2005. [Google Scholar]
- Pham, D.T.; Koc, E.; Lee, J.Y.; Phrueksanant, J. Using the bees algorithm to schedule jobs for a machine. In Proceedings of the Eighth International Conference on Laser Metrology, CMM and Machine Tool Performance, LAMDAMAP, Euspen, Cardiff, UK, 25–28 June 2007; pp. 430–439. [Google Scholar]
- Pham, D.T.; Otri, S.; Darwish, A.H. Application of the Bees Algorithm to PCB assembly optimisation. In Proceedings of the 3rd Virtual International Conference on Intelligent Production Machines and Systems (IPROMS 2007), Online, 2–13 July 2007; pp. 511–516. [Google Scholar]
- Pham, D.T.; Ghanbarzadeh, A. Multi-objective optimisation using the bees algorithm. In Proceedings of the 3rd International Virtual Conference on Intelligent Production Machines and Systems, Online, 2–13 July 2007; Volume 6. [Google Scholar]
- Pham, D.T.; Darwish, A.H. Fuzzy selection of local search sites in the Bees Algorithm. In Proceedings of the 4th International Virtual Conference on Intelligent Production Machines and Systems (IPROMS 2008), Cardiff, UK, 1–14 July 2008; pp. 1–14. [Google Scholar]
- Ismail, A.H.; Ruslan, W.; Pham, D.T. A user-friendly Bees Algorithm for continuous and combinatorial optimisation. Cogent Eng. 2023, 10, 2278257. [Google Scholar] [CrossRef]
- Ismail, A.H. Enhancing the Bees Algorithm Using the Traplining Metaphor. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2021. [Google Scholar]
- Hartono, N.; Pham, D.T. A novel Fibonacci-inspired enhancement of the Bees Algorithm: Application to robotic disassembly sequence planning. Cogent Eng. 2024, 11, 2298764. [Google Scholar] [CrossRef]
- Lin, S. Computer solutions of the traveling salesman problem. Bell Syst. Technol. J. 1965, 44, 2245–2269. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, G.; Suganthan, P.N.; Song, A.; Luo, Q. Performance assessment and exhaustive listing of 500+ nature-inspired metaheuristic algorithms. Swarm Evol. Comput. 2023, 77, 101248. [Google Scholar] [CrossRef]
- Yang, X.S.; Slowik, A. Bat algorithm. In Swarm Intelligence Algorithms; CRC Press: Boca Raton, FL, USA, 2020; pp. 43–53. [Google Scholar]
- Zhang, J.; Hong, L.; Liu, Q. An improved whale optimization algorithm for the traveling salesman problem. Symmetry 2020, 13, 48. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
| Functions | Dim | Bounds | Global Optimum |
|---|---|---|---|
| 30 | [−100, 100] | ||
| 30 | [−100, 100] | ||
| 30 | [−100, 100] | ||
| 30 | [−100, 100] | ||
| 30 | [−30, 30] | ||
| 30 | [−100, 100] | ||
| 30 | [−1.28, 1.28] | ||
| 30 | [−500, 500] | ||
| 30 | [−5.12, 5.12] | ||
| 30 | [−32, 32] | ||
| 30 | [−600, 600] | ||
| 30 | [−50, 50] | ||
| 30 | [−50, 50] | ||
| 2 | [−65, 65] | ||
| 4 | [−5, 5] | ||
| 2 | [−5, 5] | ||
| 2 | [−5, 5] | ||
| 2 | [−2, 2] | ||
| 3 | [1, 3] | ||
| 6 | [0, 1] | ||
| 4 | [0, 10] | ||
| 4 | [0, 10] | ||
| 4 | [0, 10] | ||
| - | - | - |
| BA1 | BAT | GWO | WOA | |
|---|---|---|---|---|
| Total Population | 100 | 100 | 100 | 100 |
| Loudness | NA | 1 | NA | NA |
| Pulse Rate | NA | 1 | NA | NA |
| Alpha | NA | 0.97 | NA | NA |
| Gamma | NA | 0.1 | NA | NA |
| Minimum Frequency | NA | 0 | NA | NA |
| Maximum Frequency | NA | 2 | NA | NA |
| Functions | BA1 | BAT | GWO | WOA | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std Dev | Mean | Std Dev | Mean | Std Dev | Mean | Std Dev | |
| F1 | 0.00 | 0.00 | 1.43 × 104 | 3.07 × 103 | 0.00 | 0.00 | 0.00 | 0.00 |
| F2 | 0.00 | 0.00 | 1.15 × 103 | 1.02 × 102 | 0.00 | 0.00 | 0.00 | 0.00 |
| F3 | 1.57 × 10−2 | 1.72 × 10−2 | 1.94 × 104 | 5.39 × 103 | 0.00 | 0.00 | 6.75 | 9.04 |
| F4 | 3.91 | 3.54 | 6.06 × 101 | 4.65 | 0.00 | 0.00 | 1.62 | 5.43 |
| F5 | 2.71 | 4.38 | 1.61 × 102 | 2.63 × 102 | 2.82 × 101 | 1.03 | 2.37 × 101 | 2.06 × 10−1 |
| F6 | 0.00 | 0.00 | 1.47 × 104 | 2.71 × 103 | 3.50 | 6.21 × 10−1 | 7.90 × 10−7 | 3.12 × 10−7 |
| F7 | 4.87 × 10−2 | 1.99 × 10−2 | 2.97 × 10−2 | 1.24 × 10−2 | 4.16 × 10−4 | 1.01 × 10−4 | 9.59 × 10−5 | 1.07 × 10−4 |
| F8 | −1.14 × 104 | 1.79 × 102 | −6.03 × 103 | 5.84 × 102 | −5.93 × 103 | 7.84 × 102 | −1.24 × 104 | 4.37 × 102 |
| F9 | 1.99 × 10−2 | 1.39 × 10−1 | 1.78 × 102 | 2.69 × 101 | 2.44 × 101 | 4.03 | 0.00 | 0.00 |
| F10 | 0.00 | 0.00 | 1.90 × 101 | 2.23 × 10−1 | 2.05 | 1.37 | 0.00 | 0.00 |
| F11 | 1.48 × 10−4 | 1.04 × 10−3 | 4.68 × 102 | 4.27 × 101 | 6.14 × 10−3 | 4.12 × 10−3 | 4.03 × 10−4 | 2.03 × 10−3 |
| F12 | 0.00 | 0.00 | 3.44 × 101 | 9.20 | 1.06 | 6.42 × 10−1 | 1.44 × 10−7 | 6.22 × 10−8 |
| F13 | 0.00 | 0.00 | 1.03 × 102 | 9.52 | 2.09 | 4.98 × 10−1 | 2.68 × 10−6 | 2.58 × 10−6 |
| F14 | 9.98 × 10−1 | 3.33 × 10−16 | 9.53 | 7.53 | 7.16 | 4.89 | 9.98 × 10−1 | 4.66 × 10−15 |
| F15 | 6.68 × 10−4 | 2.10 × 10−3 | 1.34 × 10−3 | 1.66 × 10−3 | 4.04 × 10−3 | 7.71 × 10−3 | 4.19 × 10−4 | 2.97 × 10−4 |
| F16 | −1.03 | 0.00 | −9.99 × 10−1 | 1.60 × 10−1 | −1.03 | 1.42 × 10−11 | −1.03 | 1.96 × 10−15 |
| F17 | 3.98 × 10−1 | 1.67 × 10−16 | 3.98 × 10−1 | 1.67 × 10−16 | 3.98 × 10−1 | 2.10 × 10−9 | 3.98 × 10−1 | 1.83 × 10−11 |
| F18 | 3.00 | 2.66 × 10−15 | 7.32 | 9.90 | 3.00 | 7.34 × 10−8 | 3.00 | 9.98 × 10−10 |
| F19 | −3.00 × 10−1 | 2.78 × 10−16 | −3.86 | 0.00 | −3.00 × 10−1 | 2.78 × 10−16 | −3.00 × 10−1 | 2.78 × 10−16 |
| F20 | −3.32 | 3.11 × 10−15 | −3.26 | 5.94 × 10−2 | −3.27 | 5.87 × 10−2 | −3.25 | 6.49 × 10−2 |
| F21 | −1.02 × 101 | 7.11 × 10−15 | −5.48 | 3.08 | −8.45 | 2.94 | −1.02 × 101 | 1.72 × 10−7 |
| F22 | −1.04 × 101 | 0.00 | −5.41 | 3.37 | −9.68 | 2.01 | −1.04 × 101 | 9.04 × 10−8 |
| F23 | −1.05 × 101 | 1.74 × 10−14 | −5.78 | 3.53 | −9.79 | 2.27 | −1.05 × 101 | 8.16 × 10−8 |
| Problem (BKS) | BA1 | BAT | DWOA | GWO | MFO | PSO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | ER (%) | Mean | ER (%) | Mean | ER (%) | Mean | ER (%) | Mean | ER (%) | Mean | ER (%) | |
| Berlin52 (7542) | 7930 | 5.14 | 7694 | 2.02 | 7727 | 2.45 | 7898 | 4.72 | 8184 | 8.51 | 7862 | 4.24 |
| Ch150 (6528) | 6928 | 6.13 | 7440 | 13.97 | 7329 | 12.27 | 7384 | 13.11 | 7329 | 12.27 | 7833 | 19.99 |
| D198 (15,780) | 16,240 | 2.92 | 16,849 | 6.77 | 16,603 | 5.22 | 17,109 | 8.42 | 16,911 | 7.17 | 18,130 | 14.89 |
| Eil51 (426) | 437 | 2.58 | 439 | 3.05 | 445 | 4.46 | 441 | 3.52 | 449 | 5.4 | 445 | 4.46 |
| Eil76 (538) | 562 | 4.46 | 561 | 4.28 | 579 | 7.62 | 565 | 5.02 | 577 | 7.25 | 595 | 10.59 |
| Fl417 (11,861) | 13,099 | 10.44 | 15,532 | 30.95 | 13,886 | 17.07 | 15,492 | 30.61 | 14,087 | 18.77 | 18,688 | 57.56 |
| KroA100 (21,282) | 22,018 | 3.46 | 23,424 | 10.06 | 22,471 | 5.59 | 22,963 | 7.9 | 23,456 | 10.22 | 23,480 | 10.33 |
| Oliver30 (420) | 424 | 0.95 | 420 | 0 | 420 | 0 | 422 | 0.48 | 423 | 0.71 | 424 | 0.95 |
| Pr76 (108,159) | 111,410 | 3.01 | 111,989 | 3.54 | 111,511 | 3.1 | 114,261 | 5.64 | 114,377 | 5.75 | 115,265 | 6.57 |
| Pr107 (44,303) | 50,514 | 14.02 | 46,419 | 4.78 | 45,780 | 3.33 | 46,083 | 4.02 | 47,437 | 7.07 | 46,919 | 5.9 |
| St70 (675) | 696 | 3.11 | 718 | 6.37 | 712 | 5.48 | 726 | 7.56 | 710 | 5.19 | 732 | 8.44 |
| Tsp225 (3916) | 4192 | 7.05 | 4427 | 13.05 | 4399 | 12.33 | 4620 | 17.98 | 4469 | 14.12 | 5049 | 28.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suluova, H.F.; Pham, D.T. A New Single-Parameter Bees Algorithm. Biomimetics 2024, 9, 634. https://doi.org/10.3390/biomimetics9100634
Suluova HF, Pham DT. A New Single-Parameter Bees Algorithm. Biomimetics. 2024; 9(10):634. https://doi.org/10.3390/biomimetics9100634
Chicago/Turabian StyleSuluova, Hamid Furkan, and Duc Truong Pham. 2024. "A New Single-Parameter Bees Algorithm" Biomimetics 9, no. 10: 634. https://doi.org/10.3390/biomimetics9100634
APA StyleSuluova, H. F., & Pham, D. T. (2024). A New Single-Parameter Bees Algorithm. Biomimetics, 9(10), 634. https://doi.org/10.3390/biomimetics9100634








