An Improved Dung Beetle Optimizer for the Twin Stacker Cranes’ Scheduling Problem
Abstract
1. Introduction
- For sequential allocation: .
- For reverse allocation: .
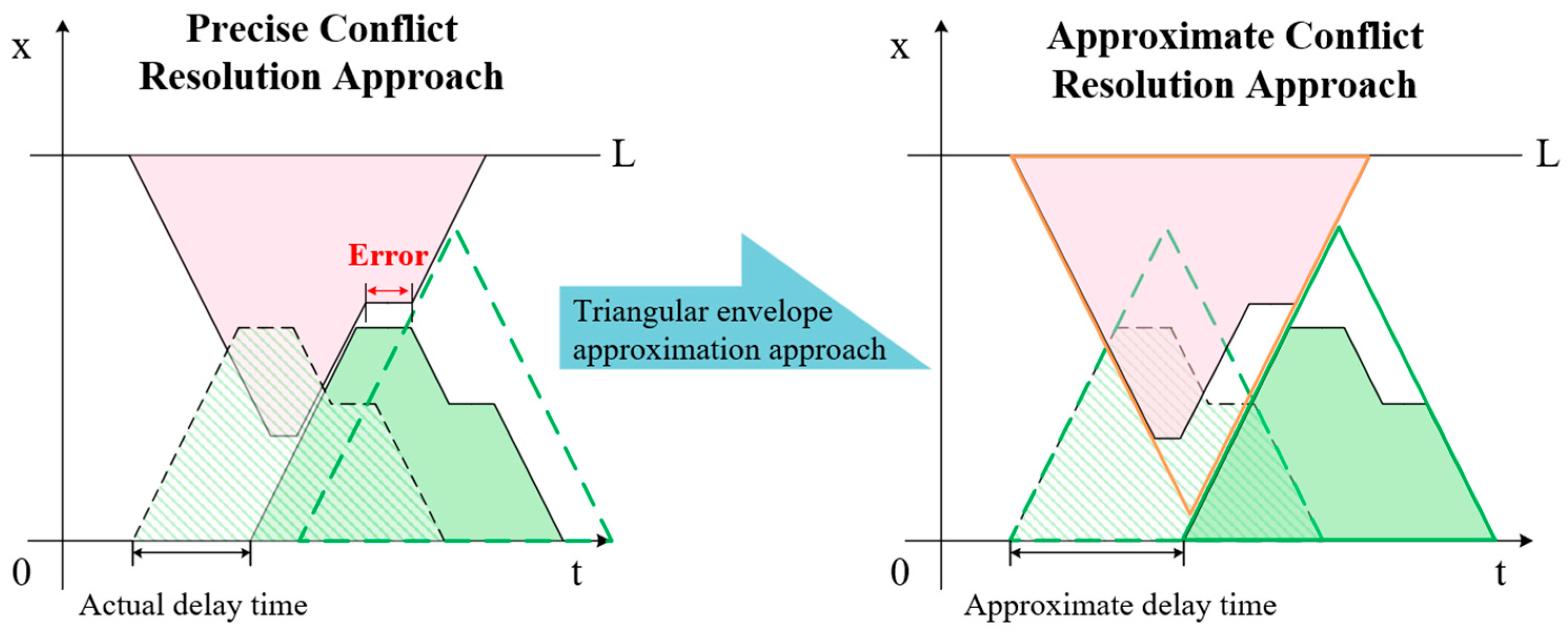
- This paper proposes a new idea to solve the TSSP, and according to this idea, a relaxation collision resolution approach by adding the trip start waiting time is proposed.
- This paper proposes an improved dung beetle optimizer (IDBO) for large-scale TSSPs. We design a key component called a double-layer code mechanism, as well as other improvement strategies, to enhance the performance of the metaheuristic dung beetle optimizer (DBO).
- The feasibility and applicability of the IDBO are verified through numerical experiments and enterprise case verification with the most powerful and classical metaheuristic algorithms.
2. Related Work
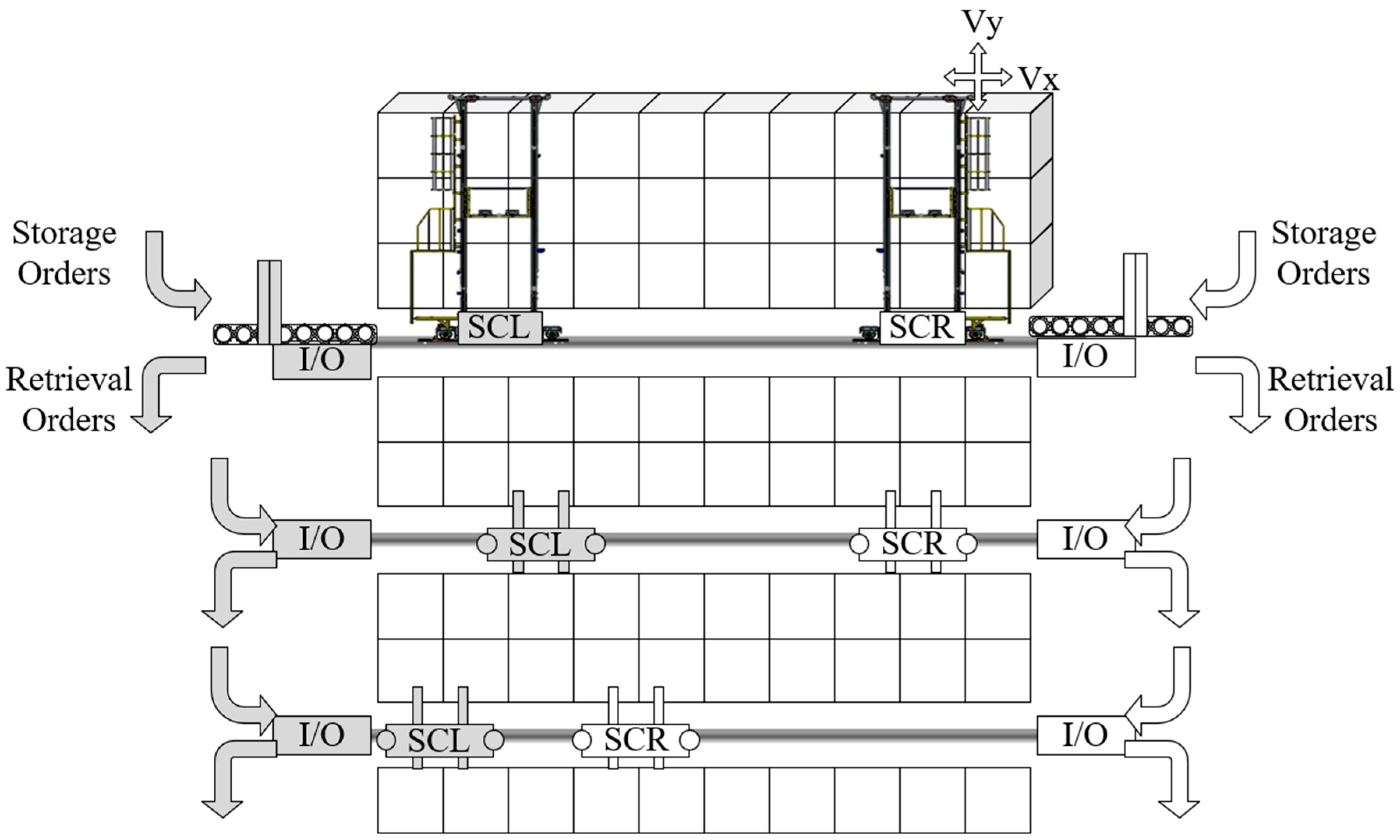
3. Problem Description and Modeling
3.1. Problem Description
- Only single-sided shelves are considered.
- Storage orders can be received from any I/O point without considering the differences in I/O point allocation.
- The horizontal and vertical movement speeds of the stacker crane are considered uniform without considering the acceleration and deceleration processes.
- The stacker crane has the same operation time for loading and unloading each time, including interaction with the shelves and interaction with I/O points.
- For the convenience of calculation, we normalize the horizontal and vertical distances in the model formulation section, that is, we use the horizontal/vertical movement distance of the stacker crane per unit time as the unit distance in the horizontal/vertical direction.
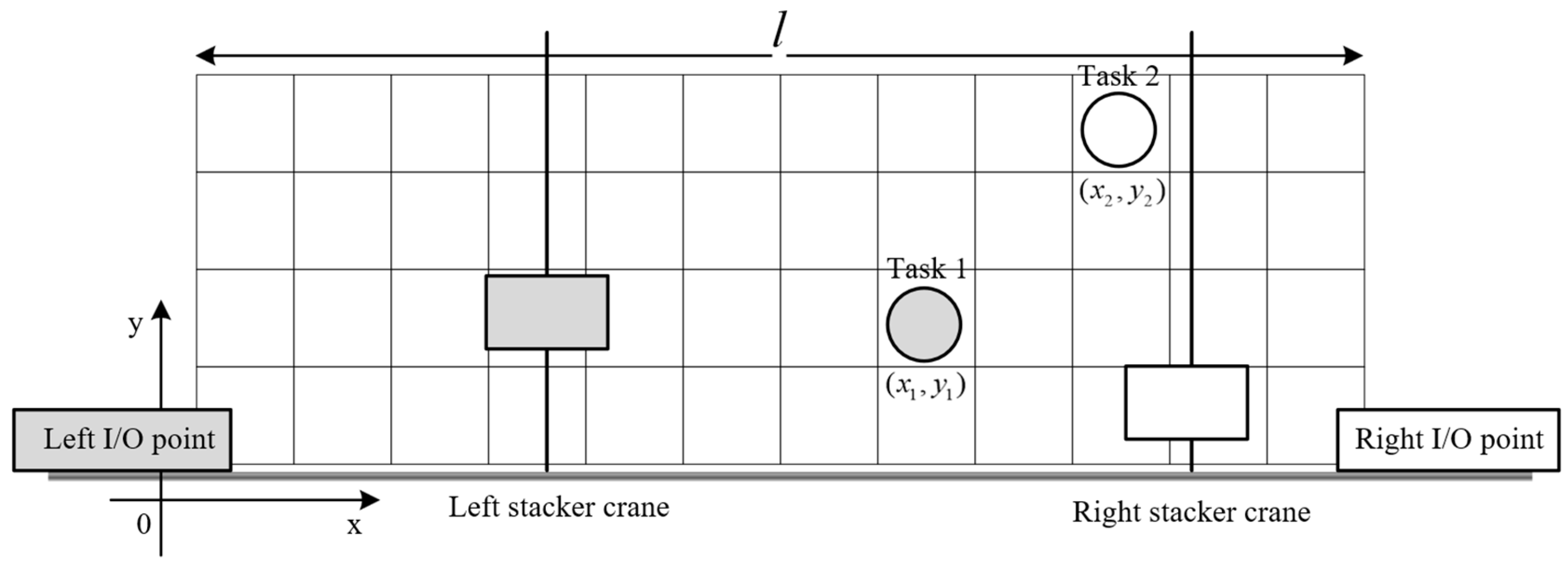
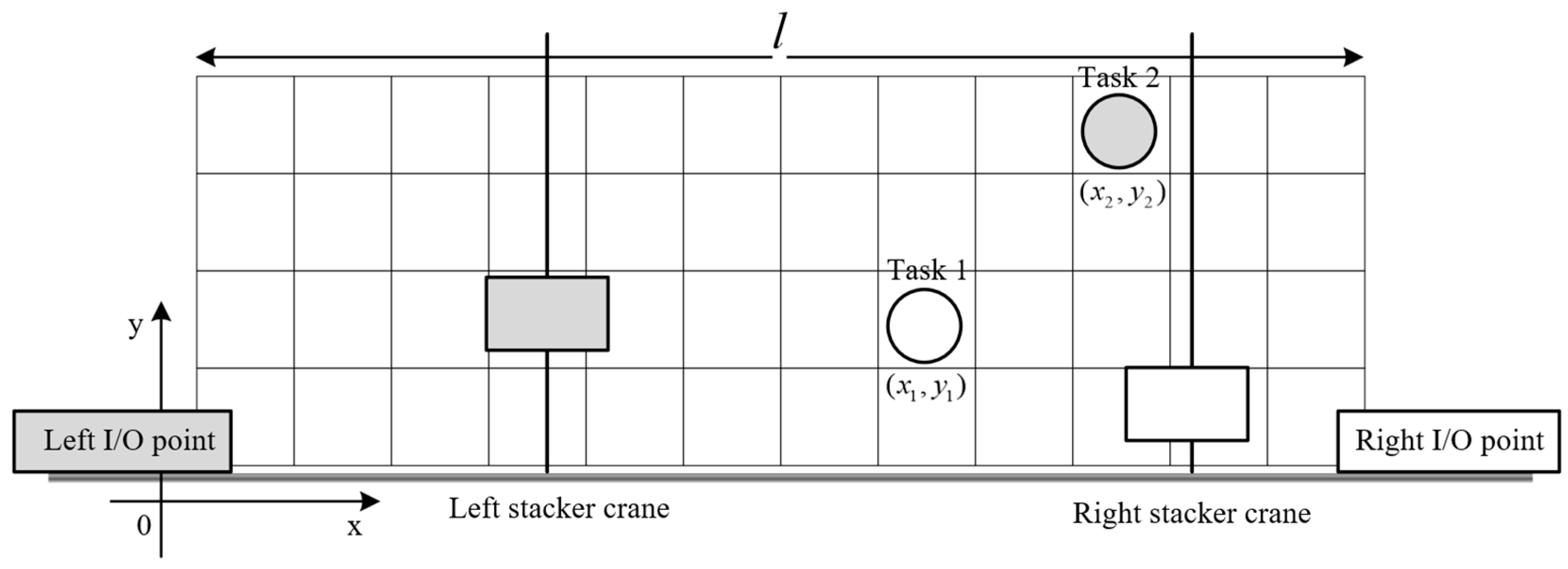
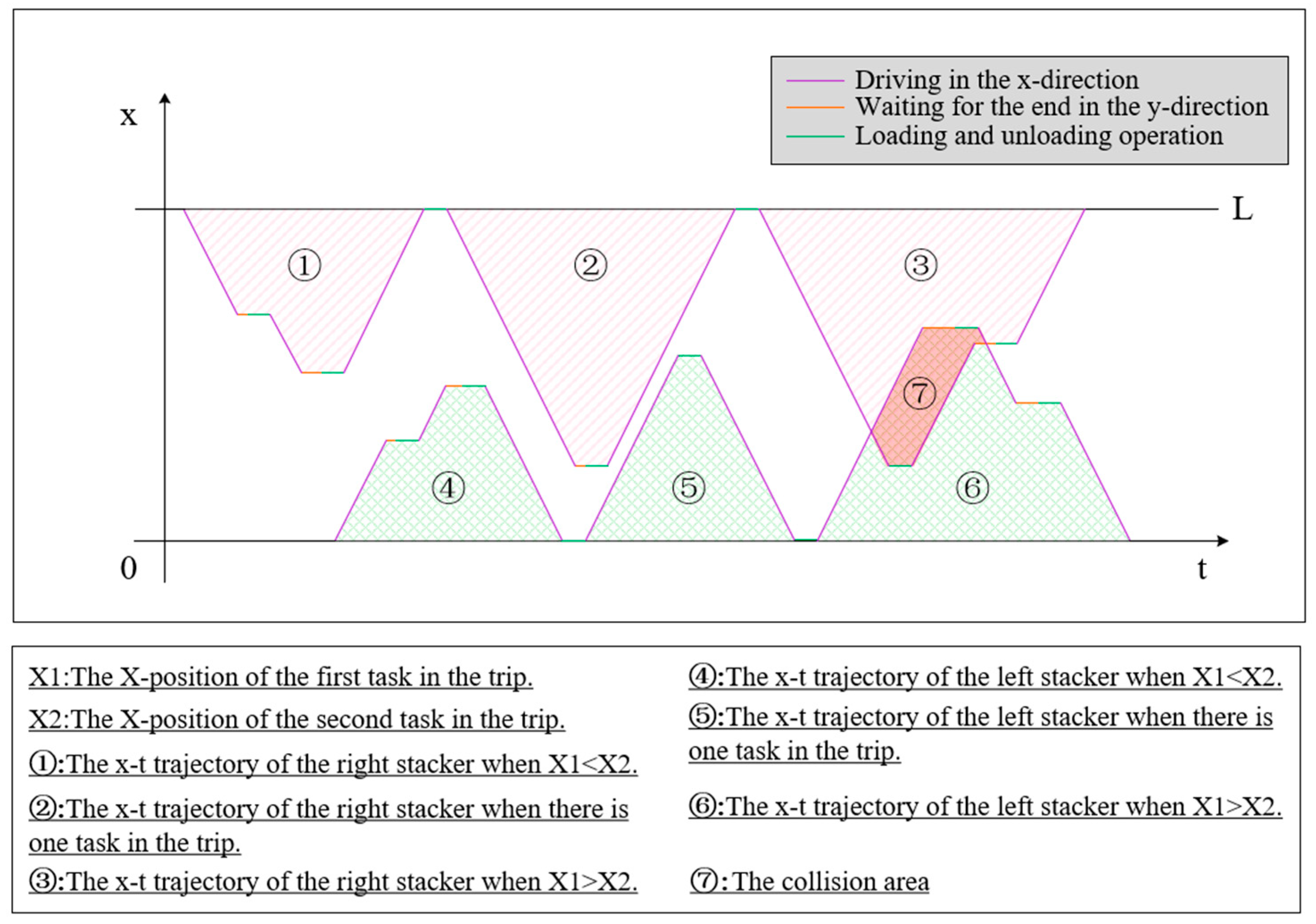
3.2. Collision Avoidance Approach
3.3. Mathematical Formulation
3.3.1. Basic Notations
3.3.2. Objective Function
3.3.3. Constraints
- Constraint 1: Each task is executed only once, which can be guaranteed by Equations (7) and (8).
- Constraint 2: The stacker must leave after completing a task point, which can be guaranteed by Equation (9).
- Constraint 3: Each trip starts from the I/O point, which can be guaranteed by Equation (10).
- Constraint 4: Each trip ends at the I/O point, which can be guaranteed by Equation (11).
- Constraint 5: The time to leave a task point cannot be earlier than the completion time of this task point, and there should not be any sub-loops in the task sequence, which can be guaranteed by Equation (12).
- Constraint 6: The start time of each trip cannot be earlier than the end time of the same stacker’s previous trip, which can be guaranteed by Equation (14).
- Constraint 7: The storage and retrieval tasks within a single trip need to meet the stacker’s capacity constraint, which can be guaranteed by Equation (15).
- Constraint 8: Two stackers shall not collide during operation. According to the collision avoidance method proposed above, we can express the constraint in Equation (16).
- Constraint 9: take the start time of this order pool as the time origin, which can be guaranteed by Equation (17).
4. Improved Dung Beetle Optimizer Design for TSSP
4.1. Structure of Basic Dung Beetle Optimizer
- (1)
- Ball-rolling dung beetles
- (2)
- Breeding dung beetles
- (3)
- Small dung beetles
- (4)
- Stealing dung beetles
4.2. Improved Dung Beetle Optimizer Design
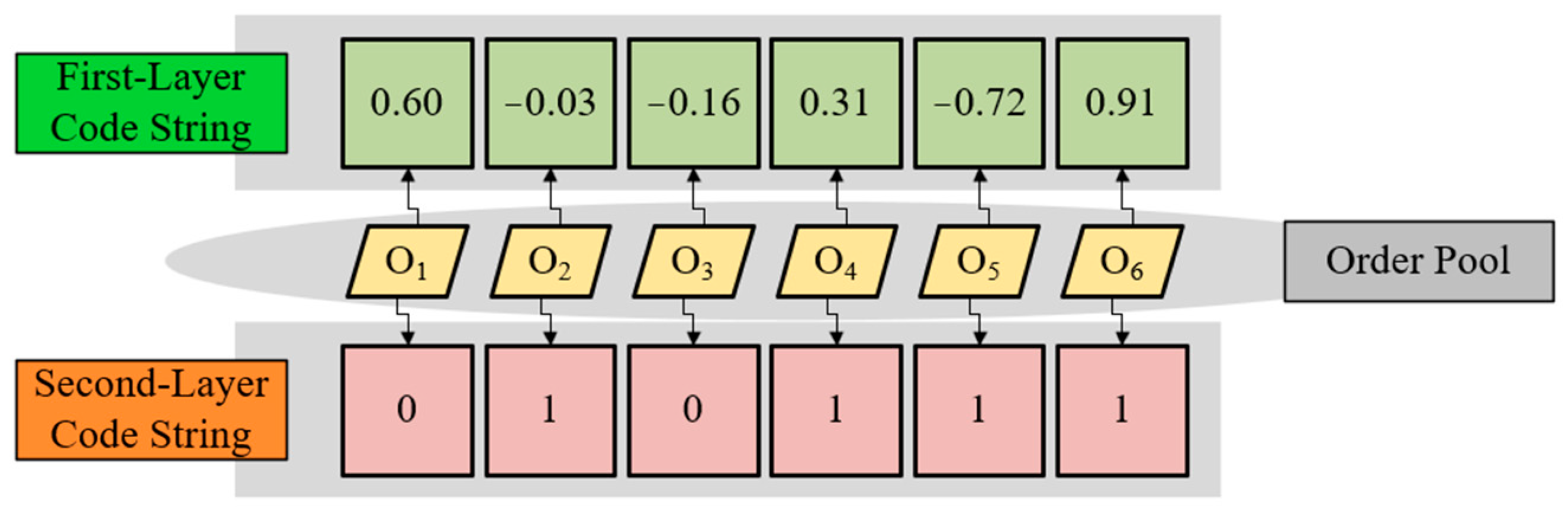
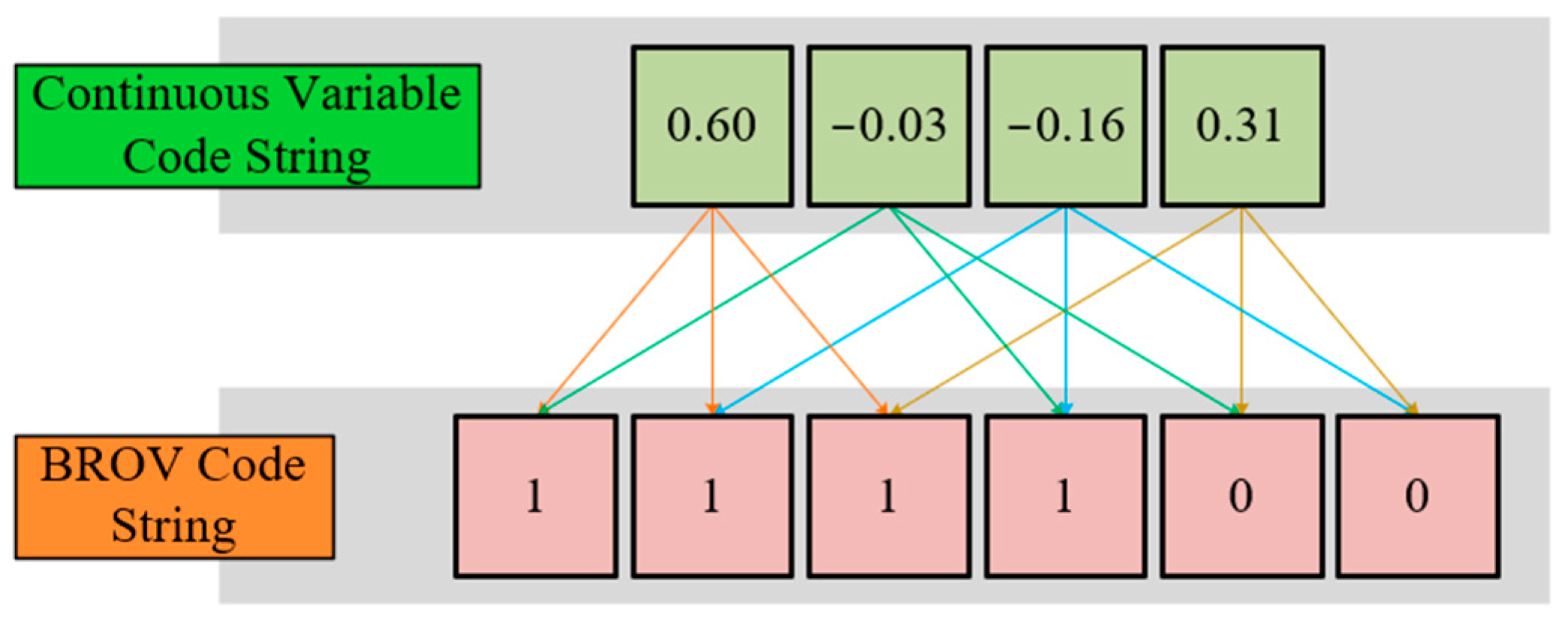
4.2.1. Double-Layer Code Mechanism
Encoding Mechanism
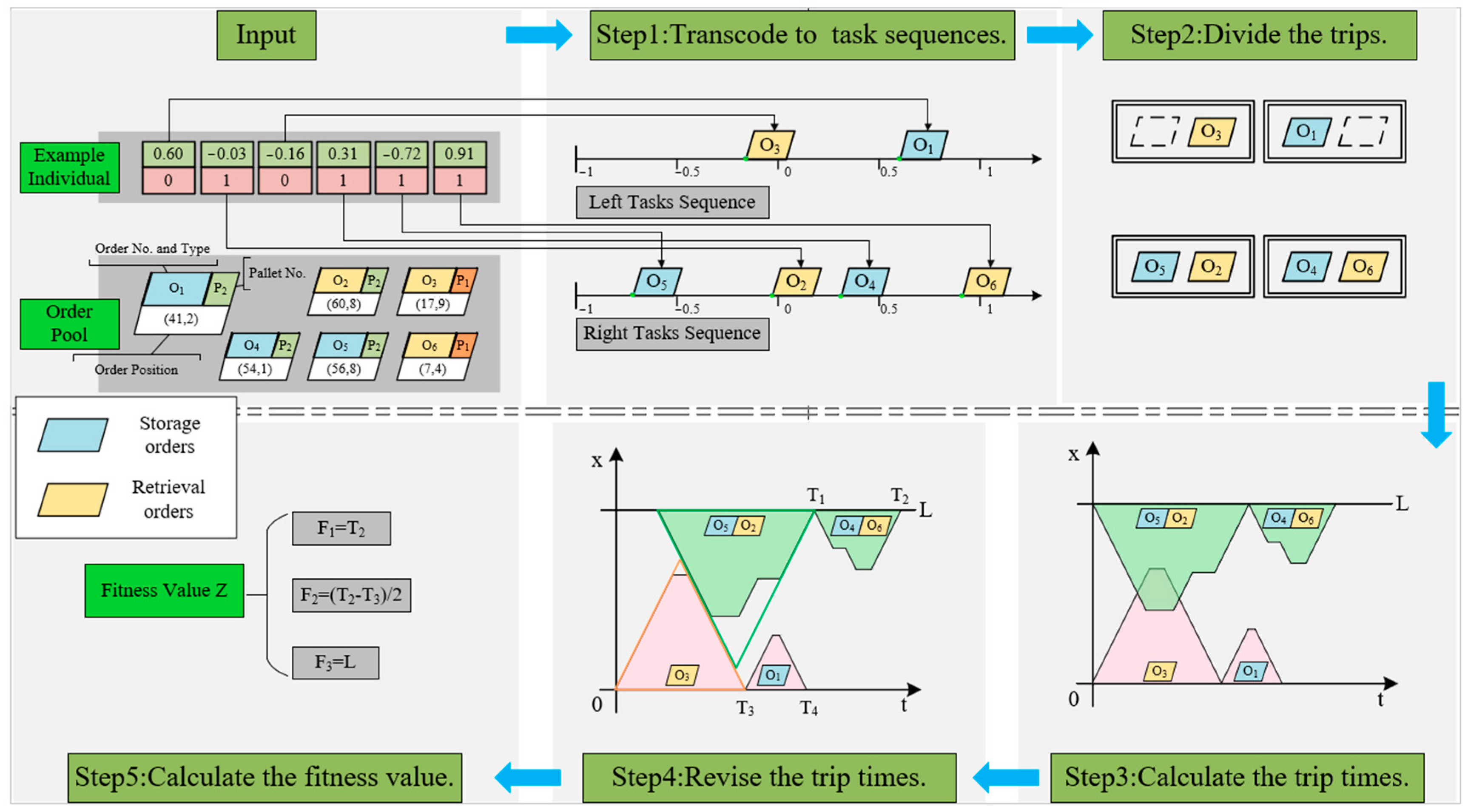
Decoding Mechanism
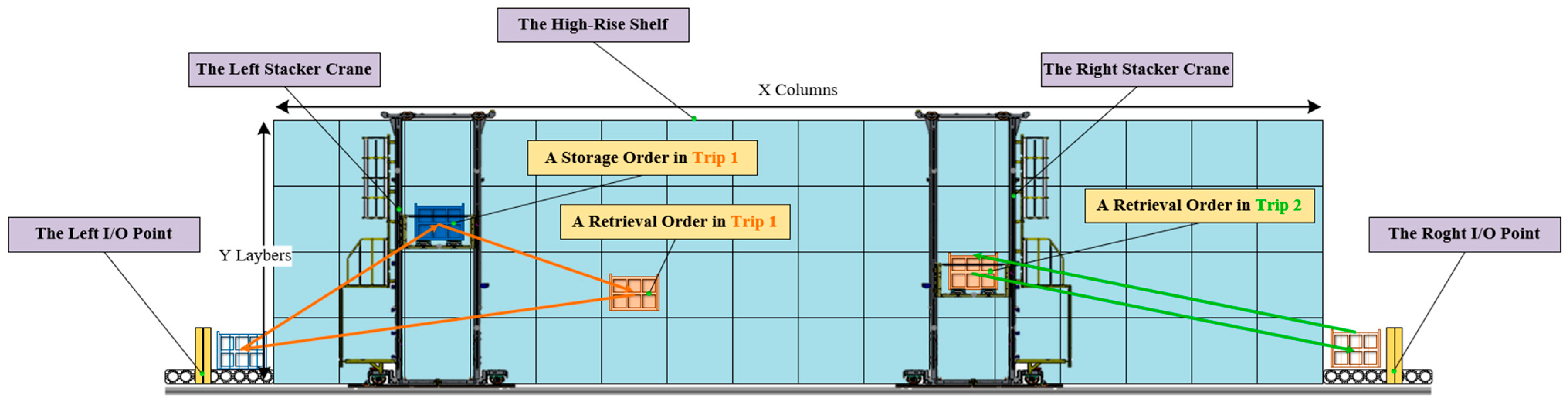
- Step 1: Transcode to stackers’ task sequences. By reading the information in the double-layer code string and tracing each task point on the time axis, the stacker task sequence can be easily obtained in chronological order.
- Step 2: Divide the trips. According to the task category of each order, find all the “storage-retrieval” combinations in the task sequences and divide them into the same trips, and then treat each remaining task as a separate trip. It is obvious that the optimal trip partition result for an individual is unique.
- Step 3: Calculate the trips’ start and end times. Starting from the first trip, the start and end times of each trip without considering collisions can be obtained by accumulating the Chebyshev travel times between task points in the trip and the operation time of each task point.
- Step 4: Revise the trips’ start and end times. Add the start delay time for each trip according to Equations (1) and (2).
- Step 5: Calculate the fitness value. Inspect the two stackers’ revised trip start and end schedules and take the maximum completion time of the stackers as F1. Then, check the ready time of retrieval orders in each pallet (take the time when the order is sent to the I/O point as the order ready time) and calculate the open time of the pallet with the earliest and latest order ready time. F2, the second part of the fitness value, can be obtained after taking the mean value of pallets’ open times. Finally, calculate the left and right I/O point distribution of orders in each pallet and calculate the sub-pallets’ aggregation penalty time F3.
Code String Update Mechanism
- (1)
- Ball-rolling dung beetles
- (2)
- Breeding dung beetles
- (3)
- Small dung beetles
- (4)
- Stealing dung beetles
| Algorithm 1: The individual’s position update procedure. |
| Input: order quantity , population size , current population . |
| Output: updated population . |
| 1. initiate 2. While do 3. 4. 5. if ball-rolling subpopulation 6. if 7. 8. 9. else 10. 11. 12. end if 13. else if breeding subpopulation 14. 15. 16. else if small dung beetle subpopulation 17. 18. 19. else if stealing subpopulation 20. 21. 22. end if 23. 24. 25. end while |
| Return |
4.2.2. Hybrid Initialization Strategy
| Algorithm 2: The population initialization operator. |
| Input: problem instance, problem parameters (order quantity , population size , variable range ). |
| Output: initial population. |
| 1. Calculate the Chebyshev adjacency matrix between all points in the instance 2. Initialize the task sequences, , , 3. 4. While do 5. if 6. , 7. else 8. 9. while do 10. Randomly select from the remaining order pool 11. 12. , , 13. , , 14. for 15. 16. end for 17. 18. , 19. end while 20. if 21. 22. if 23. 24. else 25. end if 26. end if 27. transcode to the double-layer code individual 28. end if 29. end while |
| Return initial population |
4.2.3. Cauchy–Gaussian Mixture Distribution Neighborhood Search Operator
| Algorithm 3: The neighborhood population generation procedure. |
| Input: order quantity , population size , current population . |
| Output: neighborhood population , optimal individual index. |
| 1. Calculate the range of current population’s first-layer values, 2. Initiate 3. , retrieve the optimal individual index 4. While do 5. 6. 7. 8. 9. 10. 11. end while 12. 13. 14. , |
| Return , |
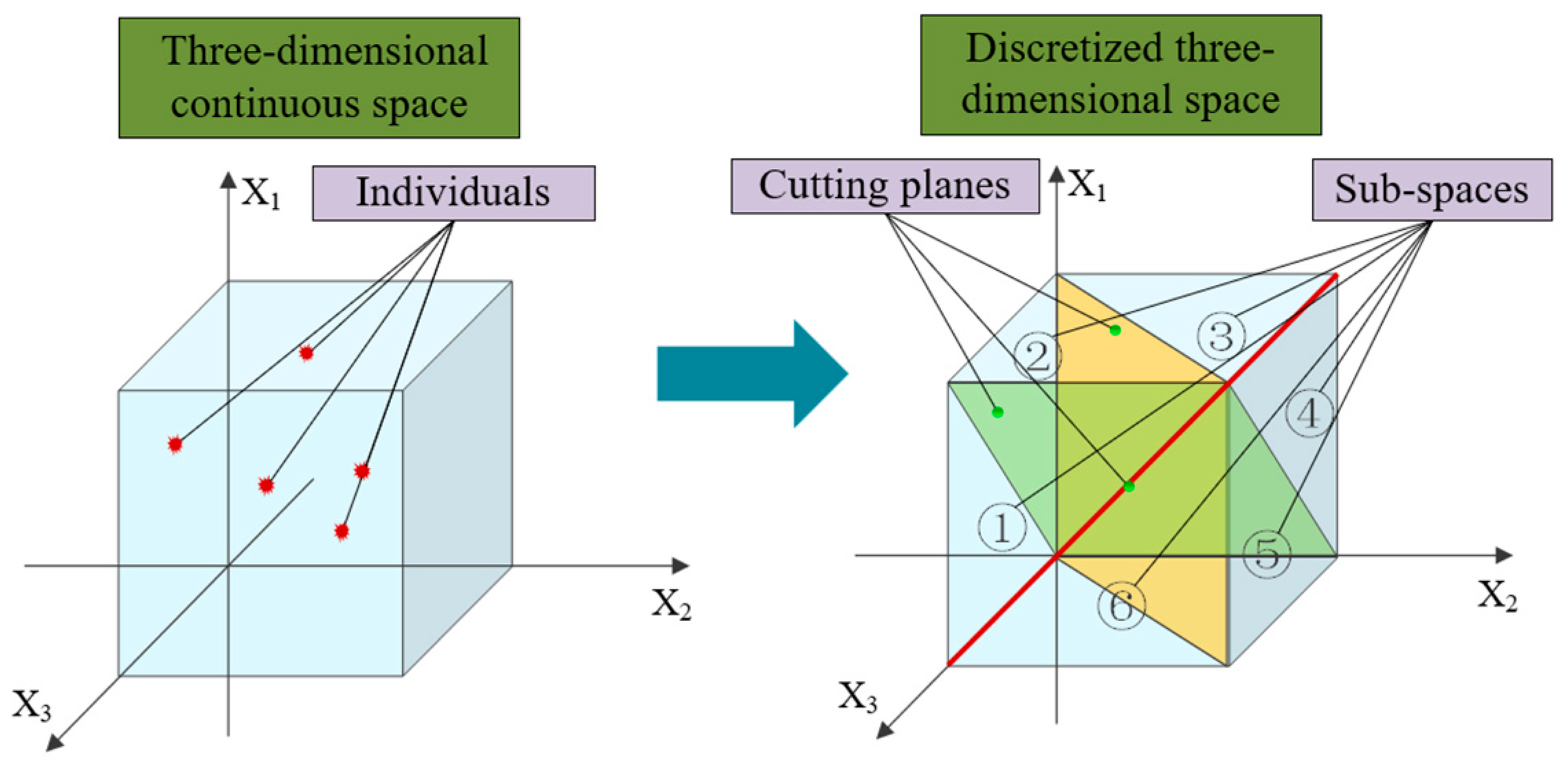
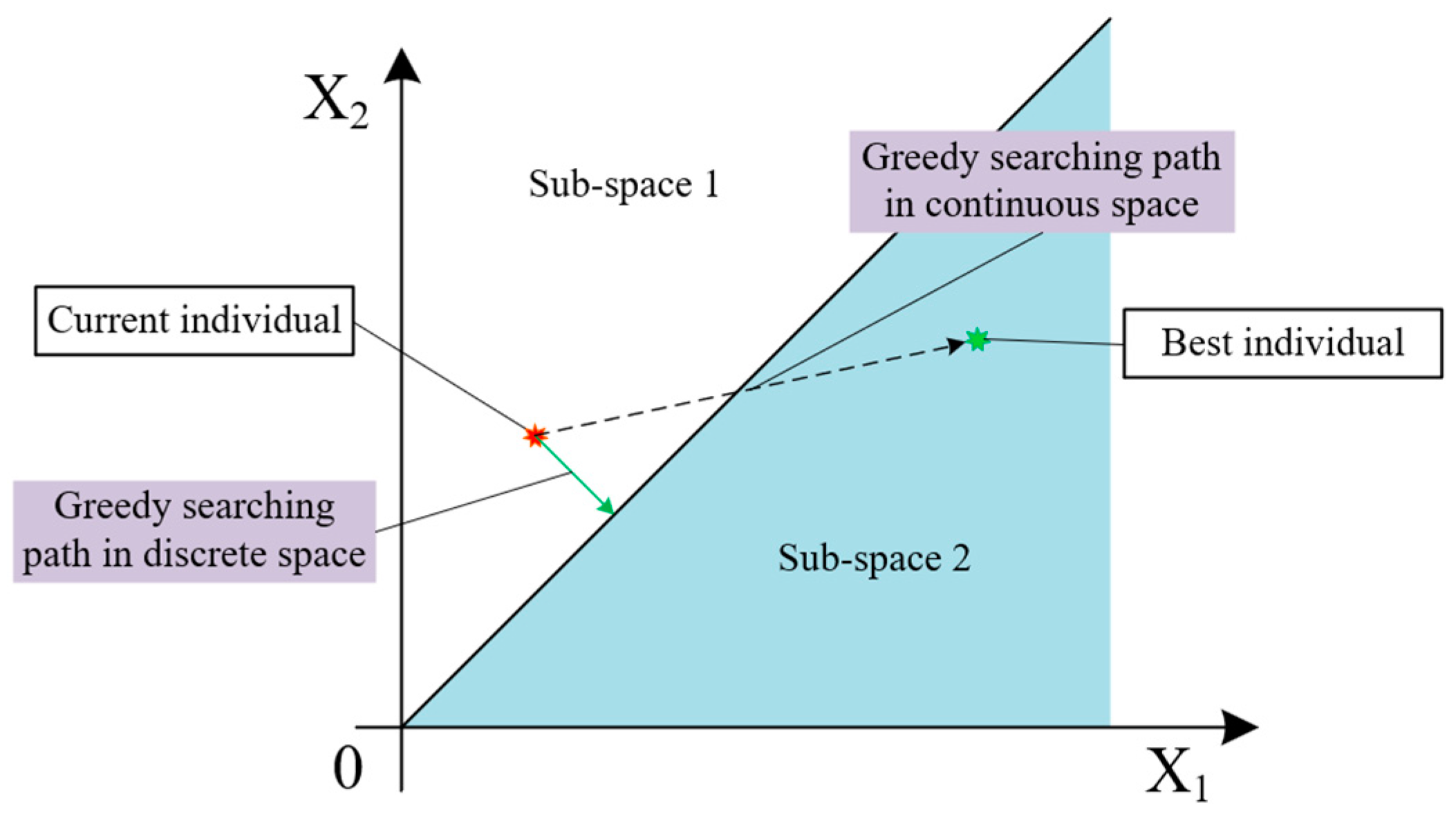
4.2.4. Velocity Revising Strategy Based on Continuous Space Discretization
| Algorithm 4: The individual’s velocity revising procedure. |
| Input: individual’s current first-layer code string , updated first-layer code string , normal vectors’ matrix of the cut planes in -dimensional continuous space . |
| Output: revised first-layer code string . |
| 1. Calculate the current velocity 1. Calculate the BROV code string of and , 2. , contrapuntal subtraction 3. Calculate the distances from individual’s current position to all cut planes 3. if individual ball-rolling subpopulation 4. Deflect the velocity by Equation (34) 2. Enlarge the step size by Equation (35) 3. else 3. Enlarge the step size by Equation (35) 3. end if 3. Calculate the revised position |
| Return |
4.2.5. Other Minor Modifications to DBO
- Improved Dance Strategy of the Dung Beetle
- Local Search Boundary Modification
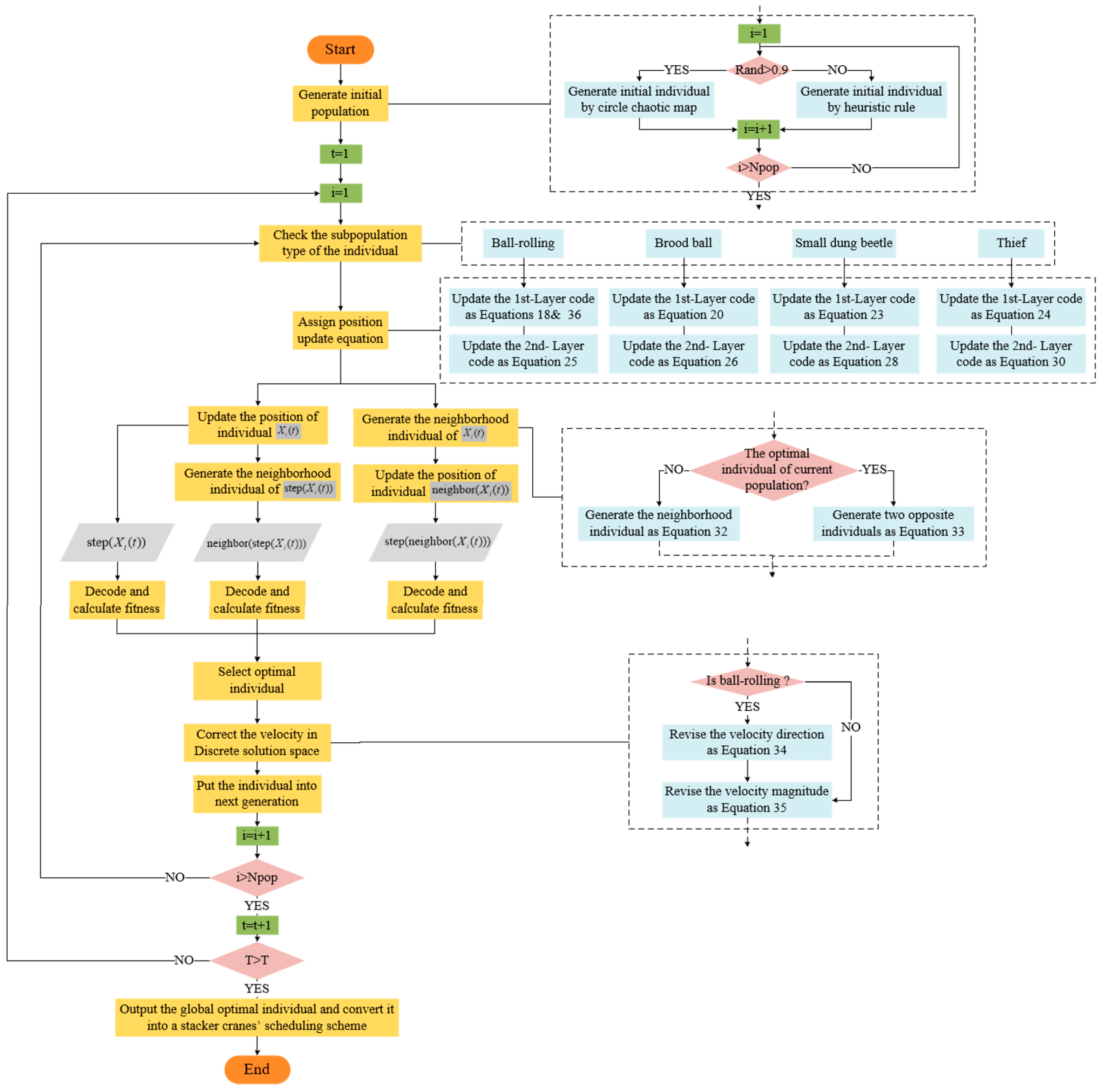
4.3. Algorithm Process of IDBO
5. Results and Discussion
5.1. Experiment Settings
5.1.1. Parameter Setting
5.1.2. Instance Generation
5.2. Sensitivity Analysis of IDBO’s Parameters
5.3. Ablation Study
5.4. Instance Validation
5.5. IDBO’s Performance on Various-Scale Instances
5.6. IDBO’s Performance on Various-Distribution Instances
6. Managerial Implications
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, S.; Wang, Q.; Batta, R.; Nagi, R. An integrated model for site selection and space determination of warehouses. Comput. Oper. Res. 2015, 62, 169–176. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z. Shuttle-Based Storage and Retrieval System: A Literature Review. Sustainability 2022, 14, 14347. [Google Scholar] [CrossRef]
- Azadeh, K.; De Koster, R.; Roy, D. Robotized and Automated Warehouse Systems: Review and Recent Developments. Transp. Sci. 2019, 53, 917–945. [Google Scholar] [CrossRef]
- Boysen, N.; Stephan, K. A survey on single crane scheduling in automated storage/retrieval systems. Eur. J. Oper. Res. 2016, 254, 691–704. [Google Scholar] [CrossRef]
- Guo, P.; Wang, L.; Xue, C.; Wang, Y. Dispatching Rules for Scheduling Twin Automated Gantry Cranes in an Automated Railroad Container Terminal. Arab. J. Sci. Eng. 2020, 45, 2205–2217. [Google Scholar] [CrossRef]
- Carlo, H.J.; Martinez-Acevedo, F.L. Priority rules for twin automated stacking cranes that collaborate. Comput. Ind. Eng. 2015, 89, 23–33. [Google Scholar] [CrossRef]
- Park, T.; Choe, R.; Ok, S.M.; Ryu, K.R. Real-time scheduling for twin RMGs in an automated container yard. OR Spectrum 2010, 32, 593–615. [Google Scholar] [CrossRef]
- Gao, Y.; Chang, D.; Chen, C.-H. A digital twin-based approach for optimizing operation energy consumption at automated container terminals. J. Clean. Prod. 2023, 385, 135782. [Google Scholar] [CrossRef]
- Zey, L.; Briskorn, D.; Boysen, N. Twin-crane scheduling during seaside workload peaks with a dedicated handshake area. J. Sched. 2022, 25, 3–34. [Google Scholar] [CrossRef]
- Han, X.; Wang, Q.; Huang, J. Scheduling cooperative twin automated stacking cranes in automated container terminals. Comput. Ind. Eng. 2019, 128, 553–558. [Google Scholar] [CrossRef]
- Kress, D.; Dornseifer, J.; Jaehn, F. An exact solution approach for scheduling cooperative gantry cranes. Eur. J. Oper. Res. 2019, 273, 82–101. [Google Scholar] [CrossRef]
- Oladugba, A.O.; Gheith, M.; Eltawil, A. A new solution approach for the twin yard crane scheduling problem in automated container terminals. Adv. Eng. Inform. 2023, 57, 102015. [Google Scholar] [CrossRef]
- Fan, H.; Peng, W.; Ma, M.; Yue, L. Storage Space Allocation and Twin Automated Stacking Cranes Scheduling in Automated Container Terminals. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14336–14348. [Google Scholar] [CrossRef]
- Angelelli, E.; Kalinowski, T.; Kapoor, R.; Savelsbergh, M.W. A reclaimer scheduling problem arising in coal stockyard management. J. Sched. 2016, 19, 563–582. [Google Scholar] [CrossRef]
- Xin, J.; Liu, C.; D’Ariano, A.; Liu, S.Q.; Liang, J. Conflict-Free Routing of Twin Reclaimers in the Stockyard Based on a Time-Space Network Model. IEEE Trans. Autom. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P.; Yarlagadda, P.; Eustace, C.; Smith, S. A flexible job shop scheduling approach with operators for coal export terminals. Comput. Oper. Res. 2019, 104, 15–36. [Google Scholar] [CrossRef]
- Kung, Y.; Kobayashi, Y.; Higashi, T.; Sugi, M.; Ota, J. Order scheduling of multiple stacker cranes on common rails in an automated storage/retrieval system. Int. J. Prod. Res. 2014, 52, 1171–1187. [Google Scholar] [CrossRef]
- Briskorn, D.; Emde, S.; Boysen, N. Cooperative twin-crane scheduling. Discret Appl. Math. 2016, 211, 40–57. [Google Scholar] [CrossRef]
- Geng, S.; Wang, L.; Li, D.; Jiang, B.; Su, X. Research on scheduling strategy for automated storage and retrieval system. CAAI T. Intell. Technol. 2022, 7, 522–536. [Google Scholar] [CrossRef]
- Chen, M.; Li, X.; Liu, W.; Wang, Y. Research on Multilevel Coordinational Flexible Scheduling Strategy of One-track Dual-stacker System Oriented towards Response Time on Demand Side. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; Chen, X., Zhao, Q.C., Eds.; IEEE: New York, NY, USA, 2018; pp. 2390–2395. [Google Scholar]
- Erdogan, G.; Battarra, M.; Laporte, G. Scheduling twin robots on a line. Nav. Res. Logist. 2014, 61, 119–130. [Google Scholar] [CrossRef]
- Boysen, N.; Briskorn, D.; Emde, S. A Decomposition Heuristic for the Twin Robots Scheduling Problem. Nav. Res. Logist. 2015, 62, 16–22. [Google Scholar] [CrossRef]
- Jaehn, F.; Wiehl, A. Approximation algorithms for the twin robot scheduling problem. J. Sched. 2020, 23, 117–133. [Google Scholar] [CrossRef]
- Xu, Z.; Chang, D.; Sun, M.; Luo, T. Dynamic Scheduling of Crane by Embedding Deep Reinforcement Learning into a Digital Twin Framework. Information 2022, 13, 286. [Google Scholar] [CrossRef]
- Li, J.; Yang, J.; Xu, B.; Yin, W.; Yang, Y.; Wu, J.; Zhou, Y.; Shen, Y. A Flexible Scheduling for Twin Yard Cranes at Container Terminals Considering Dynamic Cut-Off Time. J. Mar. Sci. Eng. 2022, 10, 675. [Google Scholar] [CrossRef]
- Jin, X.; Mi, N.; Song, W.; Li, Q. Deep Reinforcement Learning for Dynamic Twin Automated Stacking Cranes Scheduling Problem. Electronics 2023, 12, 3288. [Google Scholar] [CrossRef]
- Jin, X.; Mi, N.; Song, W.; Li, Q. Scheduling of twin automated stacking cranes based on Deep Reinforcement Learning. Comput. Ind. Eng. 2024, 191, 110104. [Google Scholar] [CrossRef]
- Lu, H.; Wang, S. A study on multi-ASC scheduling method of automated container terminals based on graph theory. Comput. Ind. Eng. 2019, 129, 404–416. [Google Scholar] [CrossRef]
- Zhao, N.; Fu, Z.; Sun, Y.; Pu, X.; Luo, L. Digital-twin driven energy-efficient multi-crane scheduling and crane number selection in workshops. J. Clean. Prod. 2022, 336, 130175. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Lyu, L.; Jiang, H.; Yang, F. Improved Dung Beetle Optimizer Algorithm with Multi-Strategy for Global Optimization and UAV 3D Path Planning. IEEE Access 2024, 12, 69240–69257. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, H.; Wang, R. Low-Carbon and Energy-Saving Path Optimization Scheduling of Material Distribution in Machining Shop Based on Business Compass Model. Processes 2023, 11, 1960. [Google Scholar] [CrossRef]
- Shen, Q.; Zhang, D.; Xie, M.; He, Q. Multi-Strategy Enhanced Dung Beetle Optimizer and Its Application in Three-Dimensional UAV Path Planning. Symmetry 2023, 15, 1432. [Google Scholar] [CrossRef]
- He, J.; Fu, L. Robot path planning based on improved dung beetle optimizer algorithm. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 235. [Google Scholar] [CrossRef]
- Sun, H.; Lao, Z. Preventive Maintenance for Key Components of Metro Door System Based on Improved Dung Beetle Optimizer Algorithm. J. Fail. Anal. Prev. 2024, 24, 424–435. [Google Scholar] [CrossRef]
- Pan, Y.; Wei, R.; Wang, Z. A Cascaded Controller Design for Switched Reluctance Motor Based on Dung Beetle Optimizer. IEEJ Trans. Electr. Electron. Eng. 2024. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, H.; Liu, M. Applying an Improved Dung Beetle Optimizer Algorithm to Network Traffic Identification. CMC-Comput. Mat. Contin. 2024, 78, 4091–4107. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, Y. Predicting the Mechanical Properties of Heat-Treated Woods Using Optimization-Algorithm-Based BPNN. Forests 2023, 14, 935. [Google Scholar] [CrossRef]
- Qiao, L.; Chen, L.; Li, Y.; Hua, W.; Wang, P.; Cui, Y. Predictions of Aeroengines’ Infrared Radiation Characteristics Based on HKELM Optimized by the Improved Dung Beetle Optimizer. Sensors 2024, 24, 1734. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, H.; Zhou, J. Prediction of the Debonding Failure of Beams Strengthened with FRP through Machine Learning Models. Buildings 2023, 13, 608. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Z.; Zhang, J.; Zhang, T.; Zhang, L.; Chen, H. UAV-assisted task offloading system using dung beetle optimization algorithm & deep reinforcement learning. Ad Hoc Netw. 2024, 156, 103434. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Lin, S.-W.; Lee, Z.-J.; Ying, K.-C.; Lee, C.-Y. Applying hybrid meta-heuristics for capacitated vehicle routing problem. Expert Syst. Appl. 2009, 36, 1505–1512. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Tang, J.; Lu, K.; Tian, Q. Binary Code Ranking with Weighted Hamming Distance. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; IEEE: New York, NY, USA, 2013; pp. 1586–1593. [Google Scholar]
- Arora, S.; Anand, P. Chaotic grasshopper optimization algorithm for global optimization. Neural Comput. Appl. 2019, 31, 4385–4405. [Google Scholar] [CrossRef]
- Bjondal, M.; Jornsten, K. The deregulated electricity market viewed as a bilevel programming problem. J. Glob. Optim. 2005, 33, 465–475. [Google Scholar] [CrossRef]
- Mehlitz, P. Asymptotic regularity for Lipschitzian nonlinear optimization problems with applications to complementarity constrained and bilevel programming. Optimization 2023, 72, 277–320. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Shaban, A.K.M.F.H.; Mirjalili, S. White Shark Optimizer: A new meta-heuristic optimization algorithm. Swarm Evol. Comput. 2020, 54, 100–111. [Google Scholar]
- Alzubaidi, G.A.; Abdulkareem, A.N.N. Elk Herd Optimizer: A new meta-heuristic optimization algorithm. Expert Syst. Appl. 2020, 147, 113179. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- West, E.D. The signed-rank (Wilcoxon) test. Lancet 1969, 1, 526. [Google Scholar] [CrossRef] [PubMed]


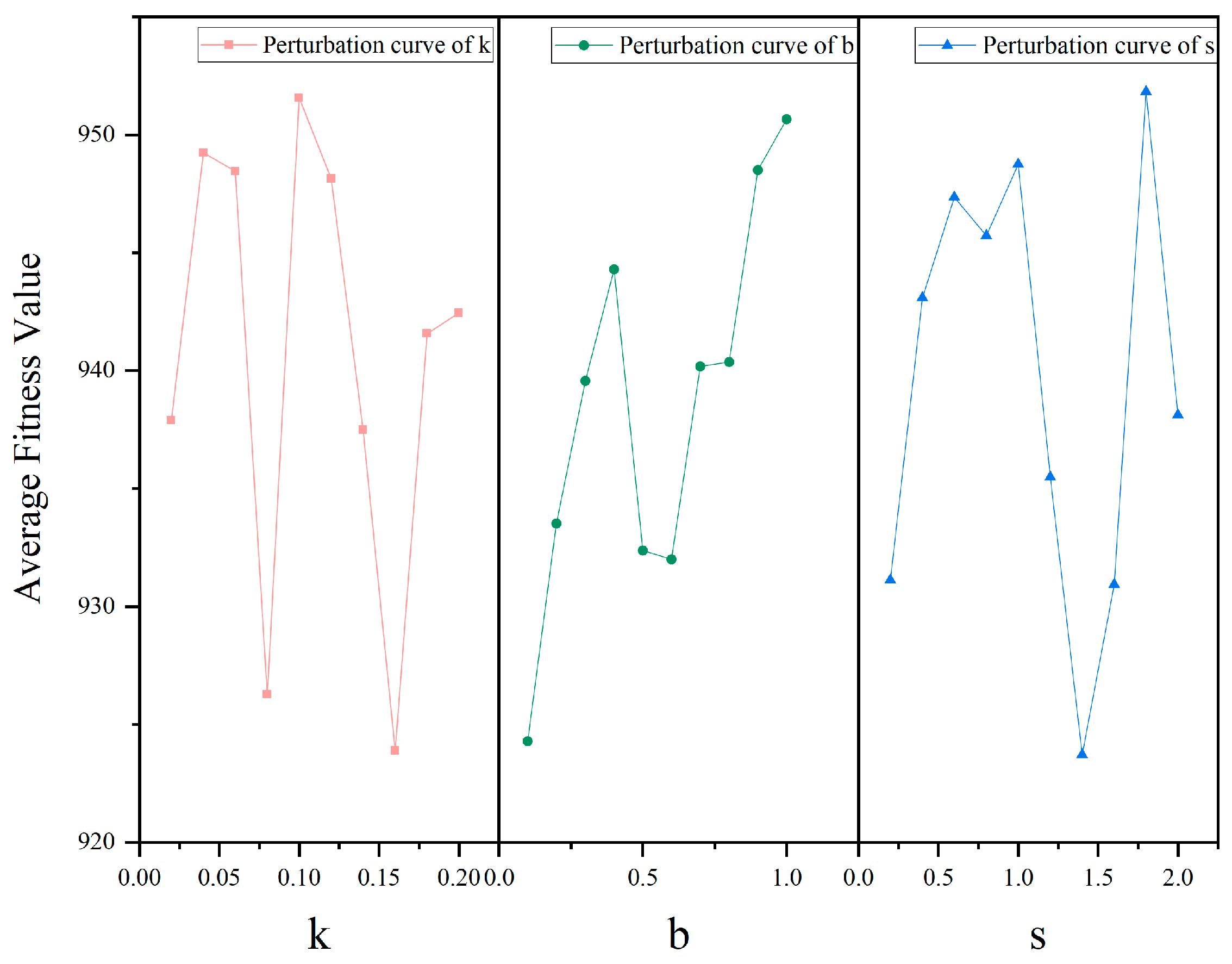
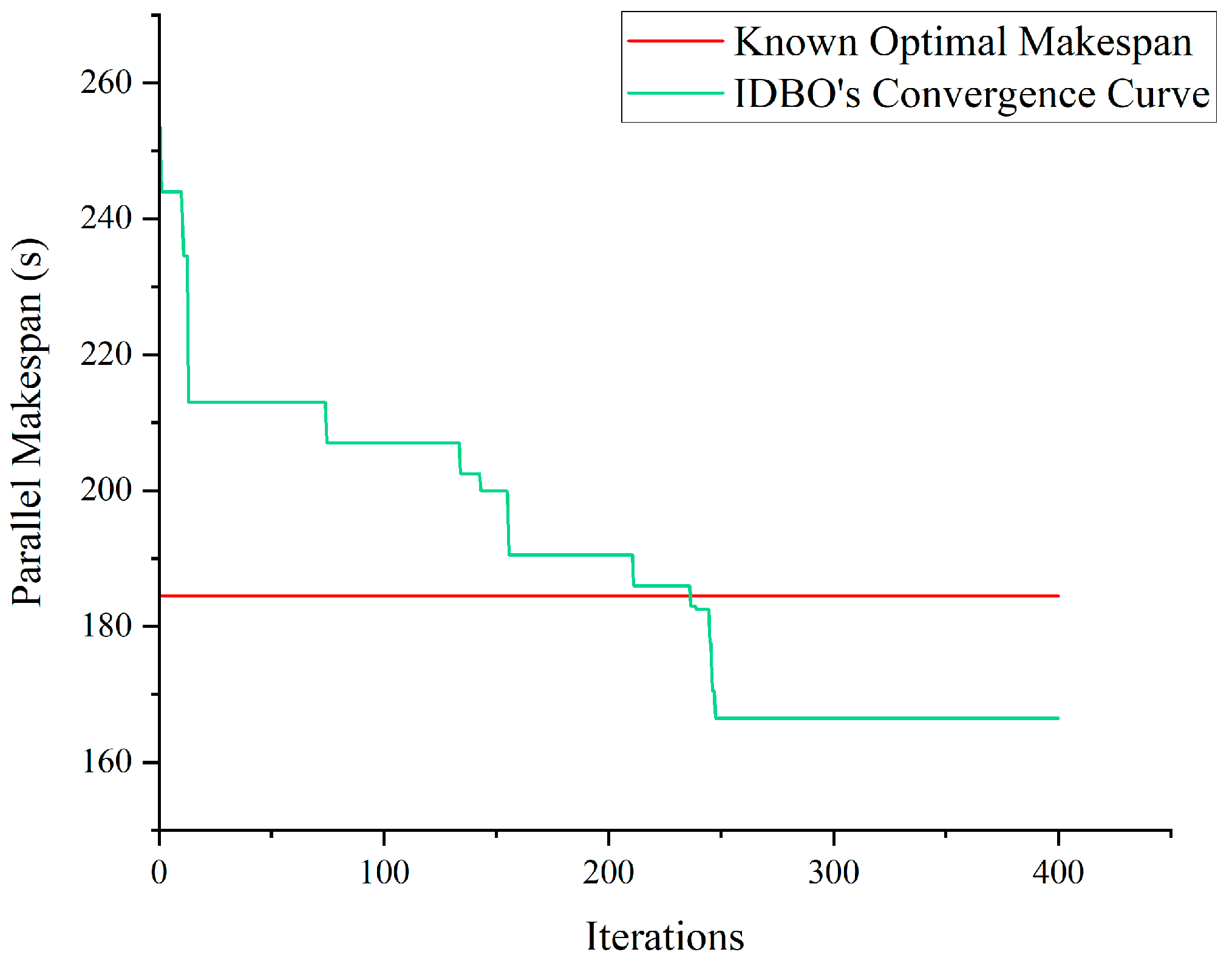
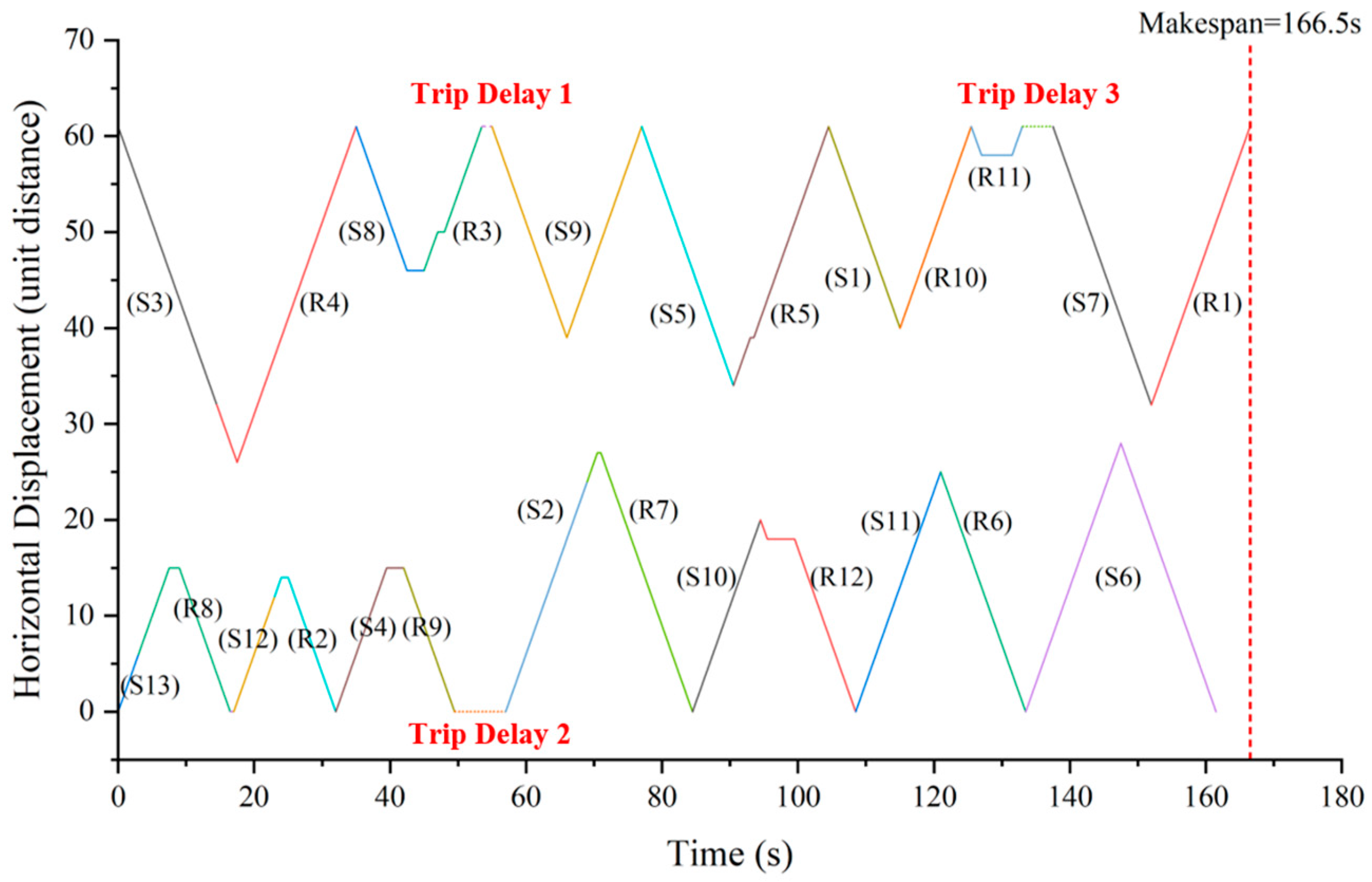
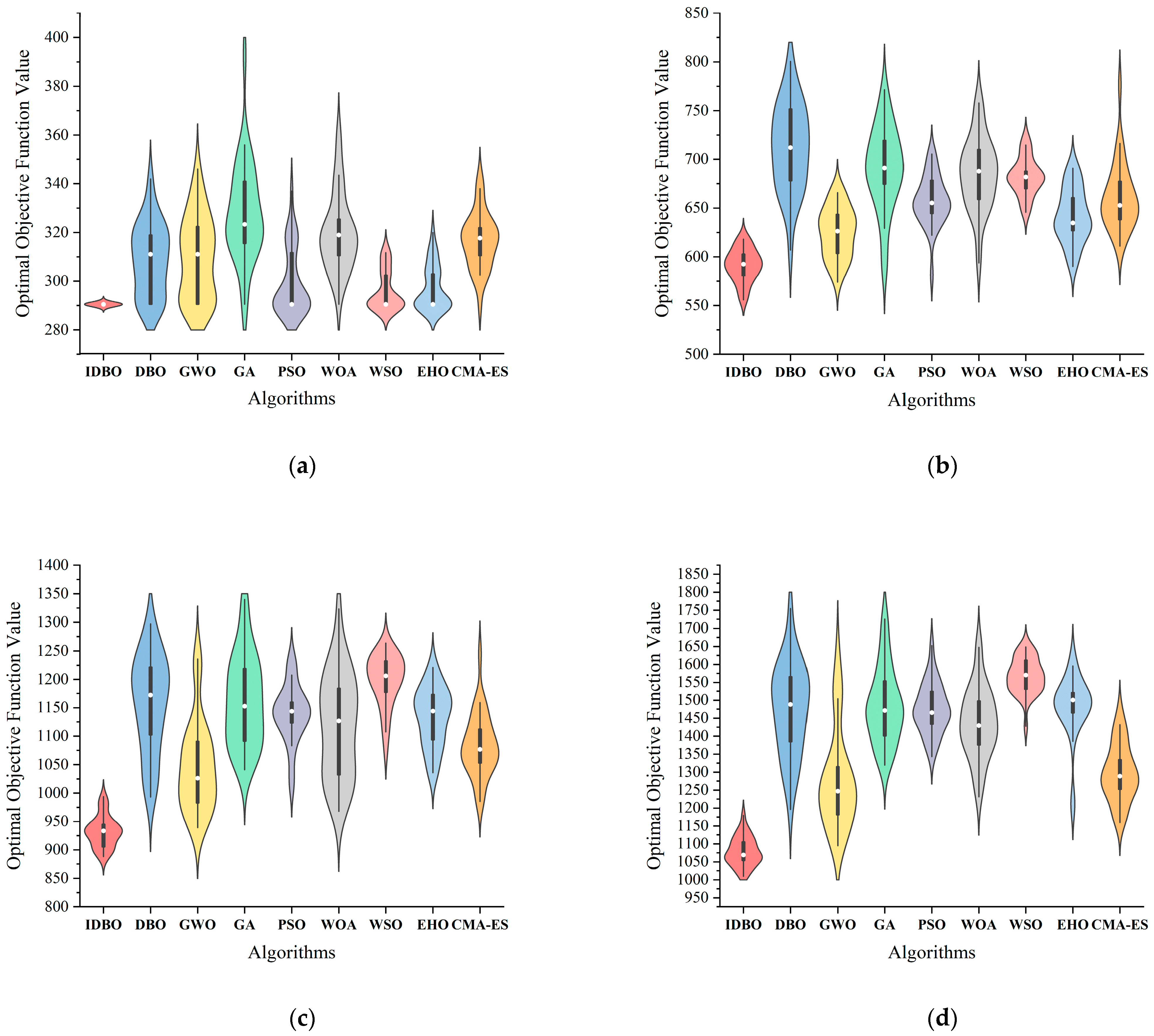
| Notation | Definition |
|---|---|
| Task point set of storage orders | |
| Task point set of retrieval orders | |
| Entire order pool contains all task points | |
| I/O point set, contains left and right I/O points and mirror points as the end of the trip | |
| Point set containing all order points and I/O points | |
| Trip set of the current order pool, where represents left stacker trips and represents right stacker trips | |
| Total time of stacker to go through shelf in horizontal direction | |
| , calculated by Chebyshev distance | |
| , else equals 0 | |
| Parameter | Value |
|---|---|
| Coordinate of left I/O point | (0, 1) |
| Coordinate of right I/O point | (61, 1) |
| Stacker’s horizontal speed | 1 column/s |
| Stacker’s vertical speed | 0.4 layers/s |
| Time of single loading/unloading operation | 5 s |
| Instance Name | Storage Order Content | Retrieval Order Content |
|---|---|---|
| C30 | (29, 9) 1 (53, 4) (55, 8) (16, 4) (8, 4) (28, 3) (17, 5) (27, 6) (33, 1) (51, 6) (1, 9) (5, 3) (45, 2) | (35, 6, 4) 2 (13, 2, 4) (9, 8, 4) (48, 1, 1) (31, 8, 2) (16, 10, 2) (18, 2, 1) (27, 11, 4) (32, 6, 2) (4, 11, 5) (13, 7, 4) (52, 3, 5) (23, 5, 5) (43, 2, 6) (48, 6, 5) (22, 5, 1) (36, 7, 1) |
| D30-1 | (49, 11) (38, 2) (58, 12) (17, 1) (12, 6) (43, 10) (40, 2) (23, 7) (35, 6) (10, 10) (10, 8) (42, 9) (14, 11) (33, 12) | (58, 6, 1) (26, 11, 6) (40, 1, 6) (41, 10, 3) (40, 3, 1) (42, 4, 1) (27, 5, 5) (58, 5, 2) (46, 4, 5) (54, 12, 1) (9, 4, 2) (49, 3, 3) (12, 4, 3) (22, 10, 4) (56, 4, 5) (32, 10, 1) |
| D30-2 | (19, 2) (26, 3) (2, 5) (42, 7) (25, 3) (3, 1) (18, 5) (13, 4) (11, 4) (7, 8) (34, 11) (40, 10) (34, 10) (11, 8) (27, 1) | (5, 12, 5) (40, 11, 1) (11, 11, 6) (55, 6, 4) (13, 9, 3) (34, 2, 5) (33, 5, 6) (27, 5, 6) (25, 7, 3) (40, 8, 4) (13, 7, 4) (33, 4, 1) (26, 8, 2) (59, 11, 6) (27, 5, 3) |
| D30-3 | (13, 1) (29, 12) (31, 6) (4, 5) (3, 8) (34, 11) (52, 3) (39, 7) (33, 5) (30, 5) (57, 4) (21, 9) (43, 10) (25, 3) (17, 3) | (35, 10, 6) (27, 10, 3) (25, 12, 5) (79, 7, 3) (39, 5, 6) (49, 7, 5) (4, 5, 1) (47, 1, 1) (38, 12, 5) (47, 8, 5) (28, 4, 6) (48, 6, 1) (53, 2, 3) (13, 9, 5) (32, 10, 6) |
| P30-1 | (12, 5) (10, 11) (12, 6) (36, 3) (16, 4) (50, 12) (50, 4) (26, 4) (42, 9) (5, 4) (25, 10) (32, 4) (10, 4) (39, 12) (18, 9) (16, 3) (21, 10) (28, 6) (20, 10) (11, 9) (21, 8) (15, 12) (12, 4) (42, 7) | (2, 7, 5) (36, 2, 6) (26, 2, 3) (47, 6, 2) (28, 11, 6) (37, 5, 1) |
| P30-2 | (56, 9) (32, 3) (41, 5) (6, 4) (9, 9) (49, 7) (54, 1) (4, 9) (26, 10) (40, 8) (1, 12) (23, 3) (58, 12) (26, 12) | (6, 4, 1) (15, 6, 4) (3, 11, 5) (30, 10, 6) (54, 5, 2) (2, 9, 3) (55, 8, 6) (59, 9, 3) (32, 2, 5) (44, 2, 4) (59, 8, 3) (11, 5, 5) (4, 5, 3) (17, 6, 6) (40, 7, 4) (11, 2, 2) |
| P30-3 | (14, 2) (32, 7) (42, 9) (50, 6) (23, 3) (12, 6) | (39, 9, 6) (13, 9, 1) (37, 6, 4) (47, 5, 3) (51, 10, 4) (35, 7, 2) (20, 2, 4) (29, 8, 4) (33, 9, 6) (25, 6, 5) (38, 10, 6) (12, 2, 1) (24, 9, 4) (21, 2, 2) (3, 10, 3) (42, 5, 3) (20, 6, 2) (47, 5, 5) (20, 9, 6) (47, 3, 6) (31, 11, 1) (12, 5, 5) (48, 4, 1) (7, 2, 3) |
| NO. | k-Value Disturbance | b-Value Disturbance | s-Value Disturbance | ||||||
|---|---|---|---|---|---|---|---|---|---|
| k | b | s | k | b | s | k | b | s | |
| 1 | 0.02 | 0.3 | 0.5 | 0.1 | 0.1 | 0.5 | 0.1 | 0.3 | 0.2 |
| 2 | 0.04 | 0.3 | 0.5 | 0.1 | 0.2 | 0.5 | 0.1 | 0.3 | 0.4 |
| 3 | 0.06 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.6 |
| 4 | 0.08 | 0.3 | 0.5 | 0.1 | 0.4 | 0.5 | 0.1 | 0.3 | 0.8 |
| 5 | 0.1 | 0.3 | 0.5 | 0.1 | 0.5 | 0.5 | 0.1 | 0.3 | 1 |
| 6 | 0.12 | 0.3 | 0.5 | 0.1 | 0.6 | 0.5 | 0.1 | 0.3 | 1.2 |
| 7 | 0.14 | 0.3 | 0.5 | 0.1 | 0.7 | 0.5 | 0.1 | 0.3 | 1.4 |
| 8 | 0.16 | 0.3 | 0.5 | 0.1 | 0.8 | 0.5 | 0.1 | 0.3 | 1.6 |
| 9 | 0.18 | 0.3 | 0.5 | 0.1 | 0.9 | 0.5 | 0.1 | 0.3 | 1.8 |
| 10 | 0.2 | 0.3 | 0.5 | 0.1 | 1 | 0.5 | 0.1 | 0.3 | 2 |
| Level | Factors | ||
|---|---|---|---|
| k | b | s | |
| 1 | 0.16 | 0.1 | 1.4 |
| 2 | 0.18 | 0.3 | 2 |
| 3 | 0.06 | 0.4 | 0.6 |
| NO. | Parameter Value | AFV | No. | Parameter Value | AFV | No. | Parameter Value | AFV | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k | b | s | k | b | s | k | b | s | ||||||
| 1 | 0.16 | 0.1 | 1.4 | 927.95 | 10 | 0.18 | 0.1 | 1.4 | 915.98 | 19 | 0.06 | 0.1 | 1.4 | 932.07 |
| 2 | 0.16 | 0.1 | 2 | 911.36 | 11 | 0.18 | 0.1 | 2 | 934.35 | 20 | 0.06 | 0.1 | 2 | 934.33 |
| 3 | 0.16 | 0.1 | 0.6 | 942.22 | 12 | 0.18 | 0.1 | 0.6 | 926.15 | 21 | 0.06 | 0.1 | 0.6 | 933.84 |
| 4 | 0.16 | 0.3 | 1.4 | 942.88 | 13 | 0.18 | 0.3 | 1.4 | 931.77 | 22 | 0.06 | 0.3 | 1.4 | 947.6 |
| 5 | 0.16 | 0.3 | 2 | 925.2 | 14 | 0.18 | 0.3 | 2 | 938.73 | 23 | 0.06 | 0.3 | 2 | 940.77 |
| 6 | 0.16 | 0.3 | 0.6 | 941.01 | 15 | 0.18 | 0.3 | 0.6 | 935.61 | 24 | 0.06 | 0.3 | 0.6 | 943.62 |
| 7 | 0.16 | 0.4 | 1.4 | 942.52 | 16 | 0.18 | 0.4 | 1.4 | 941.58 | 25 | 0.06 | 0.4 | 1.4 | 953.43 |
| 8 | 0.16 | 0.4 | 2 | 940.72 | 17 | 0.18 | 0.4 | 2 | 934.87 | 26 | 0.06 | 0.4 | 2 | 951.38 |
| 9 | 0.16 | 0.4 | 0.6 | 949 | 18 | 0.18 | 0.4 | 0.6 | 942.8 | 27 | 0.06 | 0.4 | 0.6 | 946.2 |
| C10 | C20 | C30 | |||||||
| AFV | Gap | ACI | AFV | Gap | ACI | AFV | Gap | ACI | |
| IDBO | 290.5 | - | 33 | 588.53 | - | 252 | 929.48 | - | 291 |
| (w/o) IC | 290.5 | 0.00% | 32 | 595.68 | 1.21% | 283 | 936.19 | 0.72% | 312 |
| (w/o) NSC | 303.4 | 4.44% | 38 | 642.49 | 9.17% | 277 | 989.55 | 6.46% | 285 |
| (w/o) DLCC | 292 | 0.52% | 35 | 648.9 | 10.26% | 265 | 1126.46 | 21.19% | - * |
| (w/o) VRC | 290.5 | 0.00% | 46 | 594.16 | 0.96% | 341 | 927.06 | −0.26% | 397 |
| basic DBO | 314.78 | 8.36% | 245 | 689.66 | 17.18% | 277 | 1136.23 | 22.24% | - * |
| C40 | C50 | C60 | |||||||
| AFV | Gap | ACI | AFV | Gap | ACI | AFV | Gap | ACI | |
| IDBO | 1076.6 | - | 262 | 1476.84 | - | 283 | 1945.68 | - | 276 |
| (w/o) IC | 1094.87 | 1.70% | 307 | 1497.39 | 1.39% | 299 | 1982.45 | 1.89% | 314 |
| (w/o) NSC | 1180.2 | 9.62% | 279 | 1583.26 | 7.21% | 303 | 2134.49 | 9.70% | 282 |
| (w/o) DLCC | 1462.11 | 35.81% | - * | 1959.9 | 32.71% | - * | 2681.39 | 37.81% | - * |
| (w/o) VRC | 1073.36 | −0.30% | 379 | 1490.82 | 0.95% | 434 | 1954.44 | 0.45% | 386 |
| basic DBO | 1489.22 | 38.33% | - * | 1962.95 | 32.92% | - * | 2488.28 | 27.89% | - * |
| Storage Orders | No. | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
| Coordinates | (40, 6) | (24, 8) | (32, 7) | (15, 11) | (34, 4) | (28, 3) | (32, 12) | |
| No. | S8 | S9 | S10 | S11 | S12 | S13 | ||
| Coordinates | (46, 11) | (39, 10) | (20, 4) | (25, 2) | (12, 6) | (6, 3) | ||
| Retrieval Orders | No. | R1 | R2 | R3 | R4 | R5 | R6 | R7 |
| Coordinates | (35, 11) | (14, 8) | (50, 8) | (26, 9) | (39, 7) | (9, 5) | (27, 6) | |
| No. | R8 | R9 | R10 | R11 | R12 | |||
| Coordinates | (15, 9) | (5, 11) | (45, 4) | (58, 7) | (18, 9) | |||
| Optimal Makespan (s) | 184.5 | |||||||
| Left Stacker’s Task Sequence | Trip No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Order | (S13/R8) | (S12/R2) | (S4/R9) | (S2/R7) | (S10/R12) | (S11/R6) | (S6) | |
| Right Stacker’s Task Sequence | Trip No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Order | (S3/R4) | (S8/R3) | (S9) | (S5/R5) | (S1/R10) | (R11) | (S7/R1) |
| Algorithm | Parameter/Operator | Value/Description |
|---|---|---|
| IDBO | {0.16, 0.1, 2} | |
| DBO | {0.1, 0.3, 0.5} | |
| GWO | {0, 2} | |
| GA | {0.8, 0.05} | |
| Encoding mechanism | Double layer | |
| Selection operator | Roulette wheel based on fitness | |
| Crossover operator | Single-point crossover | |
| Mutation operator | Single-point mutation | |
| PSO | {2, 2} | |
| Inertia weight | Linear reduction from 0.9 to 0.1 | |
| Topology | Fully connected | |
| WOA | Linearly decreased from 2 to 0 | |
| WSO | ||
| 4.11 | ||
| EHO | 0.2 | |
| CMA-ES | Default value |
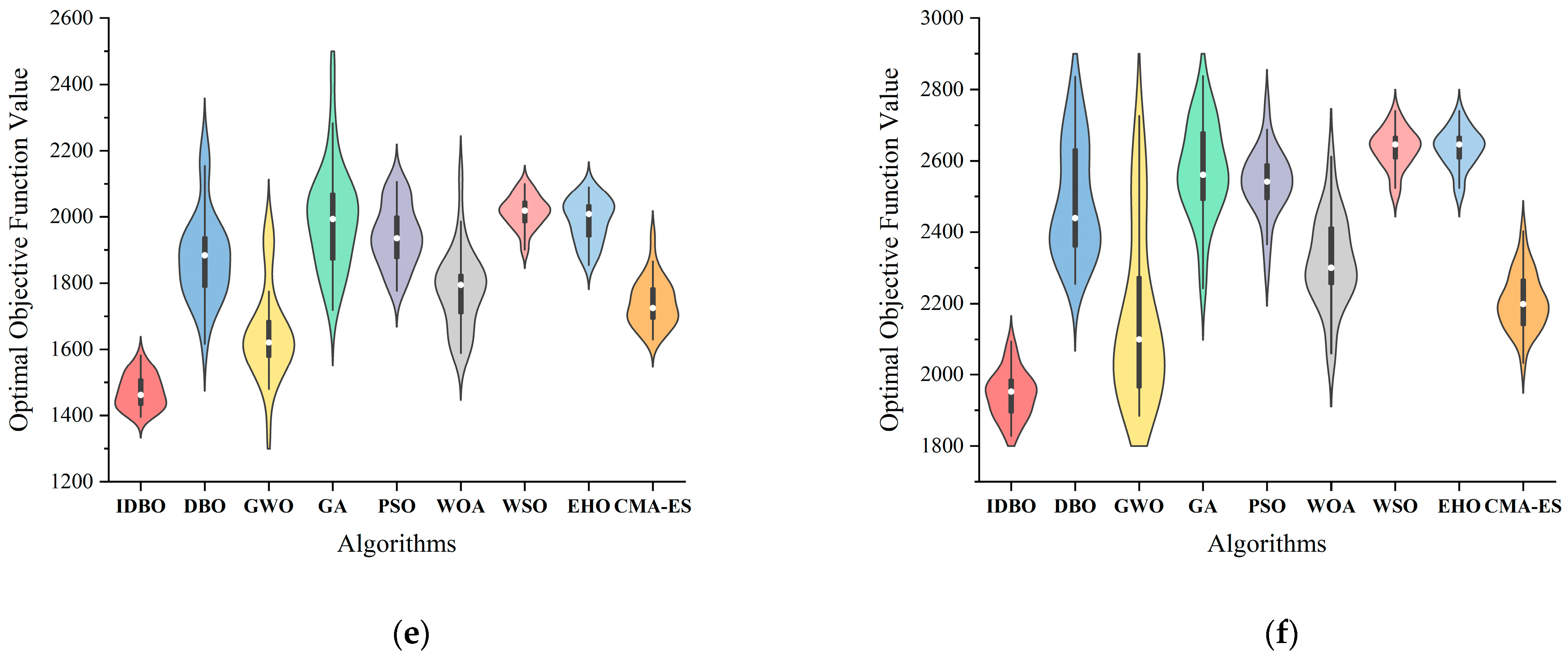
| Algorithm | IDBO | DBO | GWO | GA | PSO | WOA | WSO | EHO | CMA-ES | |
|---|---|---|---|---|---|---|---|---|---|---|
| C10 | AFV | 290.5 | 309.1 | 309.6 | 328.3 | 299.7 | 319.8 | 296.1 | 297.3 | 316.7 |
| Gap | - | 6.0% | 6.2% | 11.5% | 3.1% | 9.2% | 1.9% | 2.3% | 8.3% | |
| p-value | 1 | 3.95 × 10−5 | 8.79 × 10−5 | 2.55 × 10−6 | 9.77 × 10−4 | 2.52 × 10−6 | 4.89 × 10−4 | 2.44 × 10−4 | 2.51 × 10−6 | |
| CT(s) | 3.03 | 0.98 | 0.91 | 0.88 | 0.75 | 0.42 | 0.94 | 1.02 | 0.84 | |
| C20 | AFV | 591.2 | 712.3 | 624.8 | 691.1 | 657.5 | 685.2 | 682.1 | 642.2 | 661.3 |
| Gap | - | 17.0% | 5.4% | 14.5% | 10.1% | 13.7% | 13.3% | 7.9% | 10.6% | |
| p-value | 1 | 1.73 × 10−6 | 5.79 × 10−5 | 1.92 × 10−6 | 2.88 × 10−6 | 2.35 × 10−6 | 1.73 × 10−6 | 2.12 × 10−6 | 1.73 × 10−6 | |
| CT(s) | 4.92 | 2.47 | 1.78 | 1.57 | 0.94 | 0.69 | 1.64 | 1.97 | 1.49 | |
| C30 | AFV | 932.3 | 1158 | 1047.4 | 1161.8 | 1139.8 | 1118.9 | 1198.5 | 1134.4 | 1083.7 |
| Gap | - | 19.5% | 11.0% | 19.8% | 18.2% | 16.7% | 22.2% | 17.8% | 14.0% | |
| p-value | 1 | 1.73 × 10−6 | 2.35 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | |
| CT(s) | 8.03 | 3.28 | 3.1 | 2.11 | 1.08 | 0.96 | 2.14 | 3.04 | 2.37 | |
| C40 | AFV | 1078.7 | 1475.3 | 1277.9 | 1484.2 | 1476.2 | 1436.2 | 1567.5 | 1482.3 | 1297.2 |
| Gap | - | 26.9% | 15.6% | 27.3% | 26.9% | 24.9% | 31.2% | 27.2% | 16.8% | |
| p-value | 1 | 1.73 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | |
| CT(s) | 15.29 | 3.62 | 4.41 | 2.8 | 1.42 | 1.31 | 2.97 | 3.34 | 3.08 | |
| C50 | AFV | 1472.5 | 1877.8 | 1646.4 | 1996 | 1944 | 1779 | 2015.6 | 1989.5 | 1739.1 |
| Gap | - | 21.6% | 10.6% | 26.2% | 24.3% | 17.2% | 26.9% | 26.0% | 15.3% | |
| p-value | 1 | 1.73 × 10−6 | 4.29 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | |
| CT(s) | 23.7 | 4.63 | 5.34 | 3.5 | 1.74 | 1.6 | 3.16 | 3.49 | 3.53 | |
| C60 | AFV | 1945.7 | 2488.3 | 2159.8 | 2571.5 | 2538.5 | 2317.8 | 2634.9 | 2634.9 | 2205.8 |
| Gap | - | 21.8% | 9.9% | 24.3% | 23.4% | 16.1% | 26.2% | 26.2% | 11.8% | |
| p-value | 1 | 1.73 × 10−6 | 8.9 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | |
| CT(s) | 74.26 | 7.54 | 8.83 | 6.52 | 2.01 | 2.45 | 4.59 | 5.06 | 4.29 | |
| Performance | ~ | + | + | + | + | + | + | + | + | |
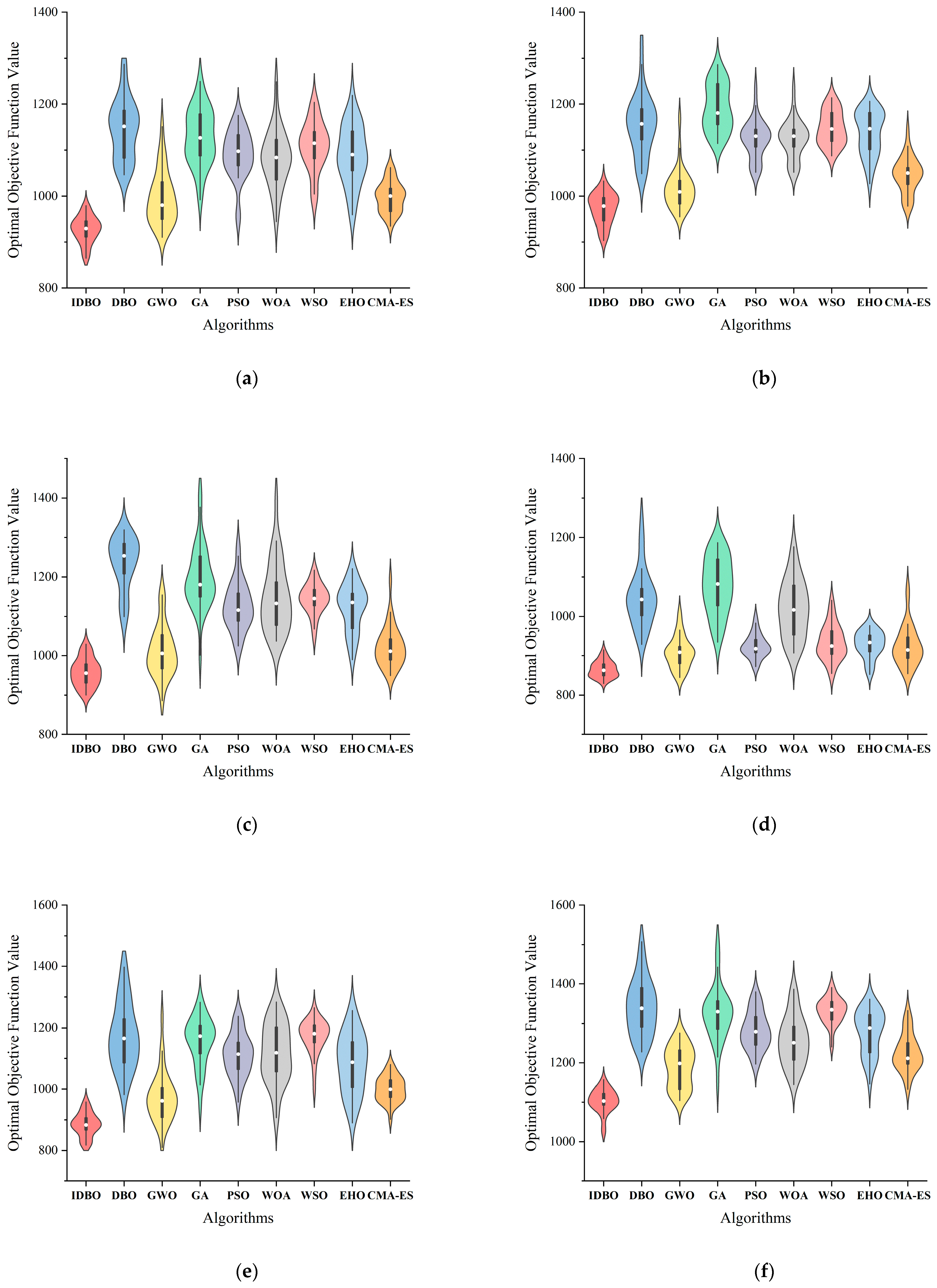
| Algorithm | IDBO | DBO | GWO | GA | PSO | WOA | WSO | EHO | CMA-ES | |
|---|---|---|---|---|---|---|---|---|---|---|
| D30-1 | AFV | 927.3 | 1145.4 | 995.7 | 1128.8 | 1091.6 | 1082.8 | 1109.2 | 1090.1 | 998.2 |
| Gap | - | 19.0% | 6.9% | 17.9% | 15.1% | 14.4% | 16.4% | 14.9% | 7.1% | |
| p-value | 1 | 1.73 × 10−6 | 1.97 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.92 × 10−6 | |
| D30-2 | AFV | 973.1 | 1156.2 | 1015.5 | 1192.2 | 1123 | 1130.91 | 1147.8 | 1137.3 | 1045.77 |
| Gap | - | 15.8% | 4.2% | 18.4% | 13.3% | 14.0% | 15.2% | 14.4% | 6.9% | |
| p-value | 1 | 1.73 × 10−6 | 1.6 × 10−4 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 4.29 × 10−6 | |
| D30-3 | AFV | 957.8 | 1235 | 1011.6 | 1198.1 | 1126.4 | 1148.6 | 1144.3 | 1122.2 | 1023 |
| Gap | - | 22.4% | 5.3% | 20.1% | 15.0% | 16.6% | 16.3% | 14.6% | 6.4% | |
| p-value | 1 | 1.73 × 10−6 | 6.39 × 10−4 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.6 × 10−6 | |
| P30-1 | AFV | 865.7 | 1047.5 | 908.1 | 1078.7 | 924.1 | 1019.4 | 934.3 | 928.4 | 925.23 |
| Gap | - | 17.4% | 4.7% | 19.7% | 6.3% | 15.1% | 7.3% | 6.8% | 6.4% | |
| p-value | 1 | 1.73 × 10−6 | 2.84 × 10−5 | 1.73 × 10−6 | 2.6 × 10−6 | 1.73 × 10−6 | 2.6 × 10−6 | 7.7 × 10−6 | 1.5 × 10−5 | |
| P30-2 | AFV | 884.4 | 1174 | 973.5 | 1156 | 1111.5 | 1118.2 | 1171.4 | 1084.9 | 999.9 |
| Gap | - | 24.7% | 9.2% | 23.5% | 20.4% | 20.9% | 24.5% | 18.5% | 11.6% | |
| p-value | 1 | 1.73 × 10−6 | 1.8 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.92 × 10−6 | |
| P30-3 | AFV | 1103.3 | 1341 | 1189.2 | 1325.7 | 1282 | 1256 | 1331.2 | 1277.5 | 1226.1 |
| Gap | - | 17.7% | 7.2% | 16.8% | 13.9% | 12.2% | 17.1% | 13.6% | 10.0% | |
| p-value | 1 | 1.73 × 10−6 | 3.02 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | |
| Performance | ~ | + | + | + | + | + | + | + | + | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Li, J.; Zhou, L.; Song, D.; Yang, B. An Improved Dung Beetle Optimizer for the Twin Stacker Cranes’ Scheduling Problem. Biomimetics 2024, 9, 683. https://doi.org/10.3390/biomimetics9110683
Chen Y, Li J, Zhou L, Song D, Yang B. An Improved Dung Beetle Optimizer for the Twin Stacker Cranes’ Scheduling Problem. Biomimetics. 2024; 9(11):683. https://doi.org/10.3390/biomimetics9110683
Chicago/Turabian StyleChen, Yidong, Jinghua Li, Lei Zhou, Dening Song, and Boxin Yang. 2024. "An Improved Dung Beetle Optimizer for the Twin Stacker Cranes’ Scheduling Problem" Biomimetics 9, no. 11: 683. https://doi.org/10.3390/biomimetics9110683
APA StyleChen, Y., Li, J., Zhou, L., Song, D., & Yang, B. (2024). An Improved Dung Beetle Optimizer for the Twin Stacker Cranes’ Scheduling Problem. Biomimetics, 9(11), 683. https://doi.org/10.3390/biomimetics9110683







