Leveraging Machine Learning for Optimized Mechanical Properties and 3D Printing of PLA/cHAP for Bone Implant
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Preparation of PLA-cHAP Composites
2.2.2. Composite Filaments Production
2.2.3. Processing of Scaffolds by FDM
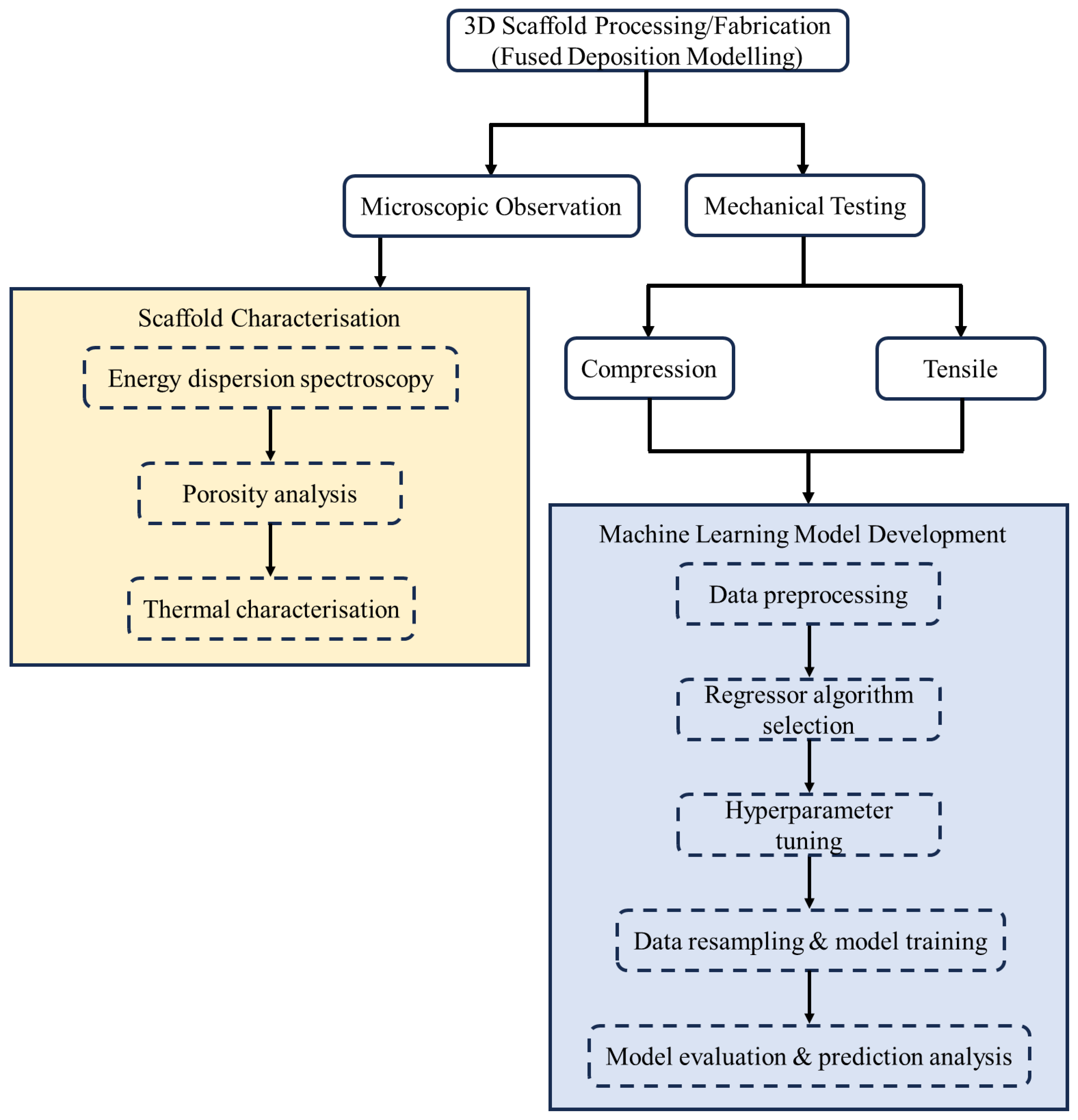
2.3. 3D-Printed Scaffold Characterisation
2.3.1. Microscopic Observation
2.3.2. Thermal Characterisation
2.3.3. Mechanical Tests
2.4. Machine Learning Implementation
2.4.1. Data Description
2.4.2. Data Preprocessing
2.4.3. ML Regressor Algorithm Selection
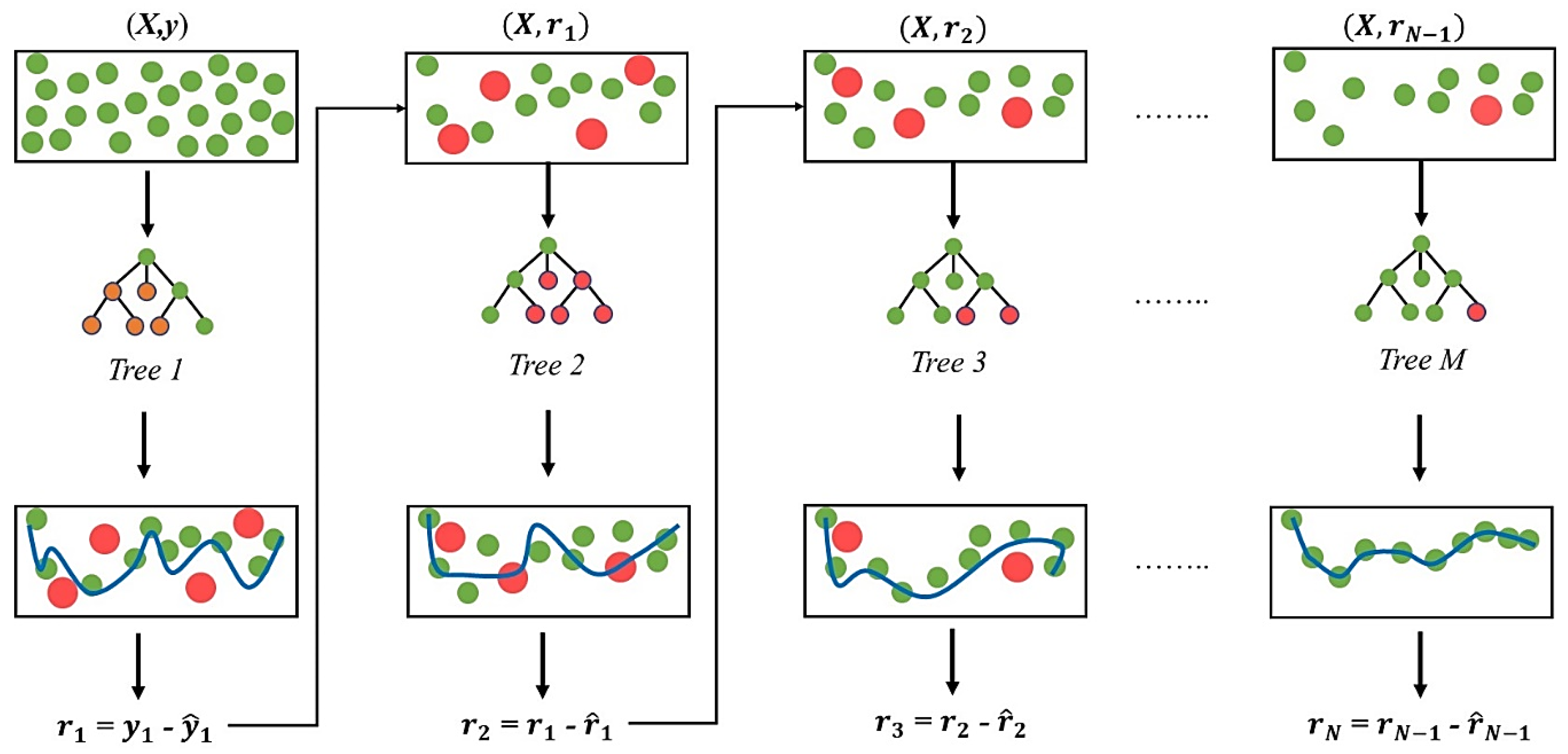
2.4.4. Extreme Gradient Boosting Regressor
2.4.5. K-Nearest Neighbour Regressor
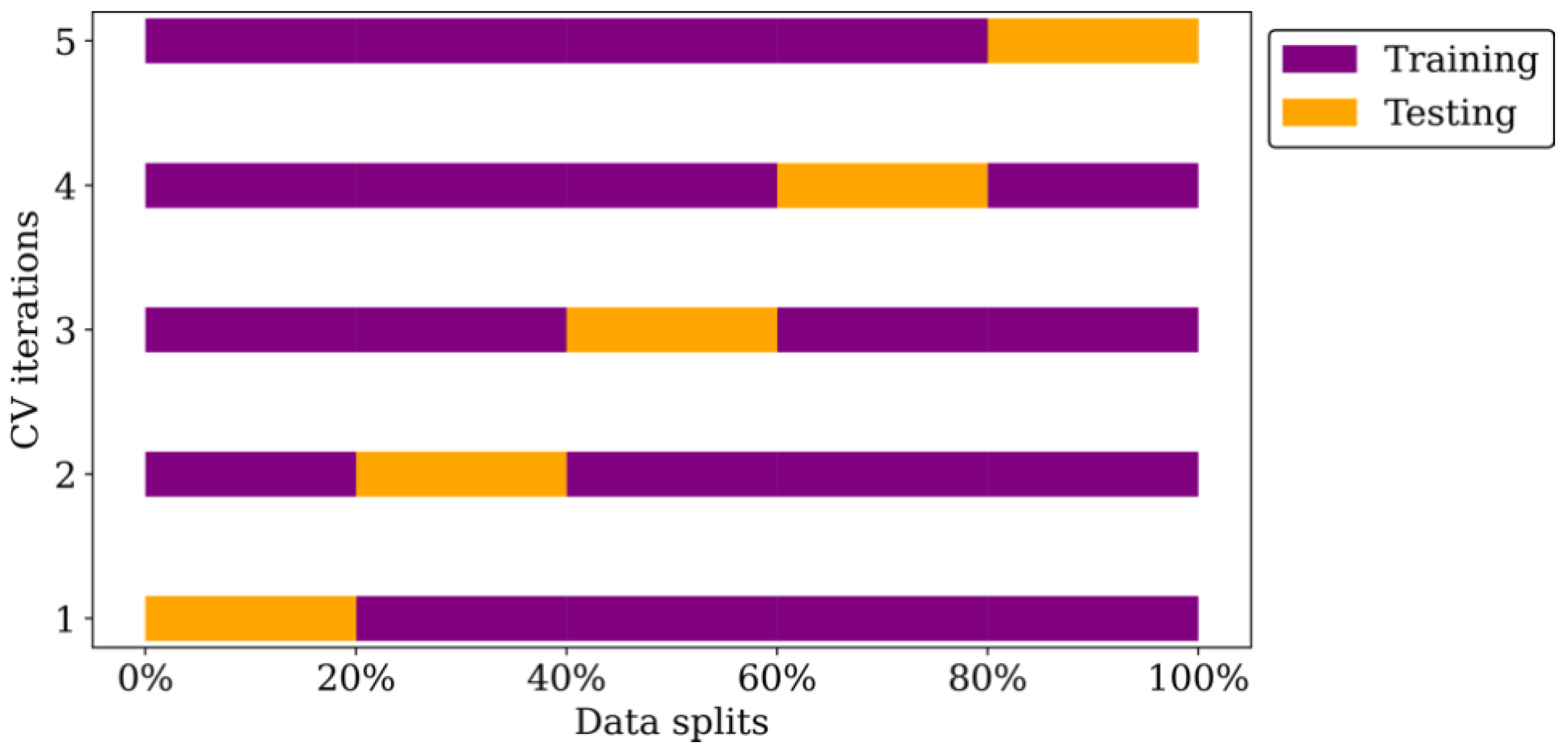
2.4.6. Data Resampling and Model Training
2.4.7. Hyper-Parameter Tuning and Model Training
2.4.8. Model Evaluation
3. Results and Discussion
3.1. Visual and Dimensional Aspects of the Filaments and Scaffolds of PLA/cHAP
3.2. Microstructural Characterisation
3.3. Thermal Stability
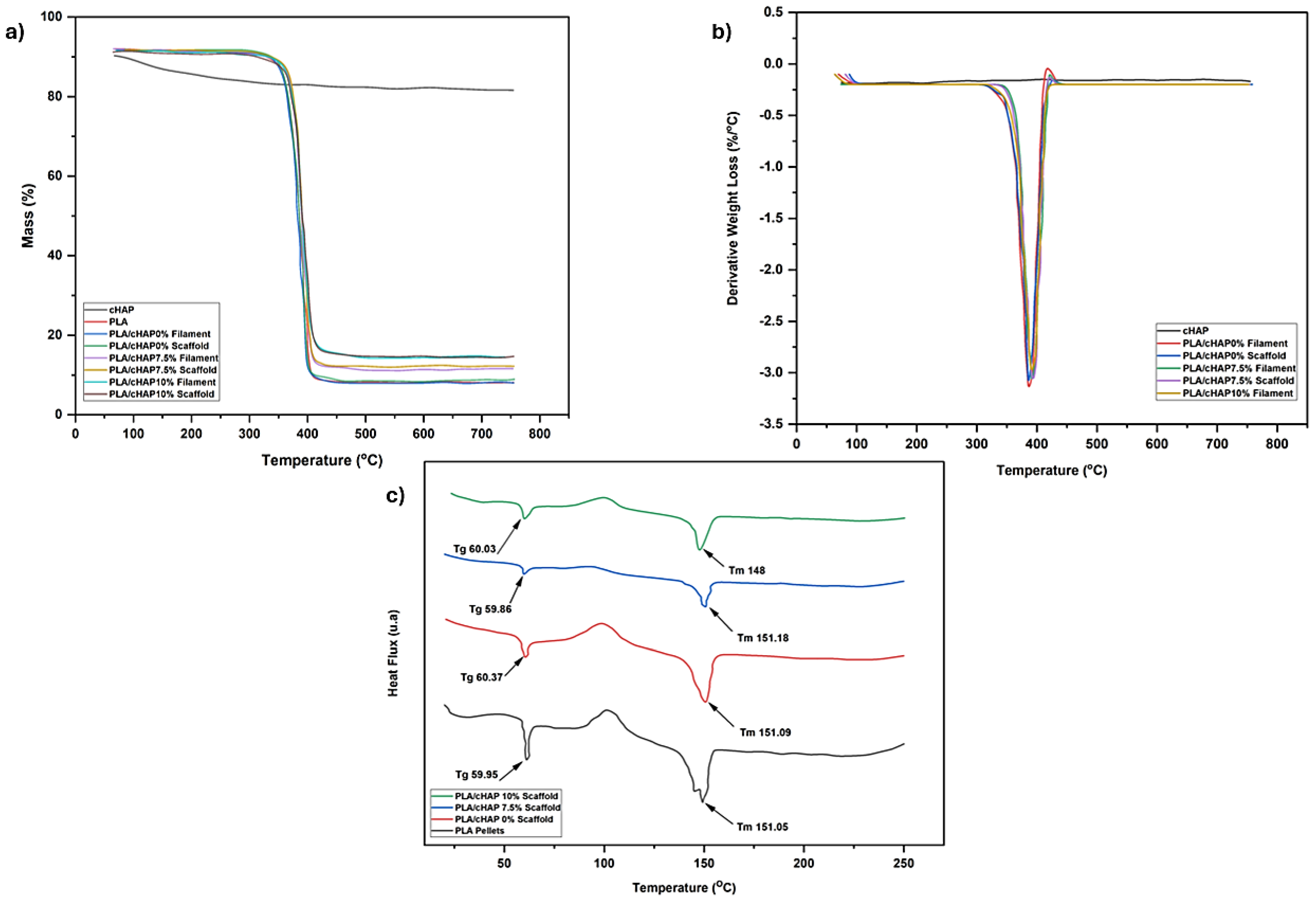
3.3.1. Thermogravimetric Analysis
3.3.2. Differential Scanning Calorimetry
3.4. Mechanical Properties
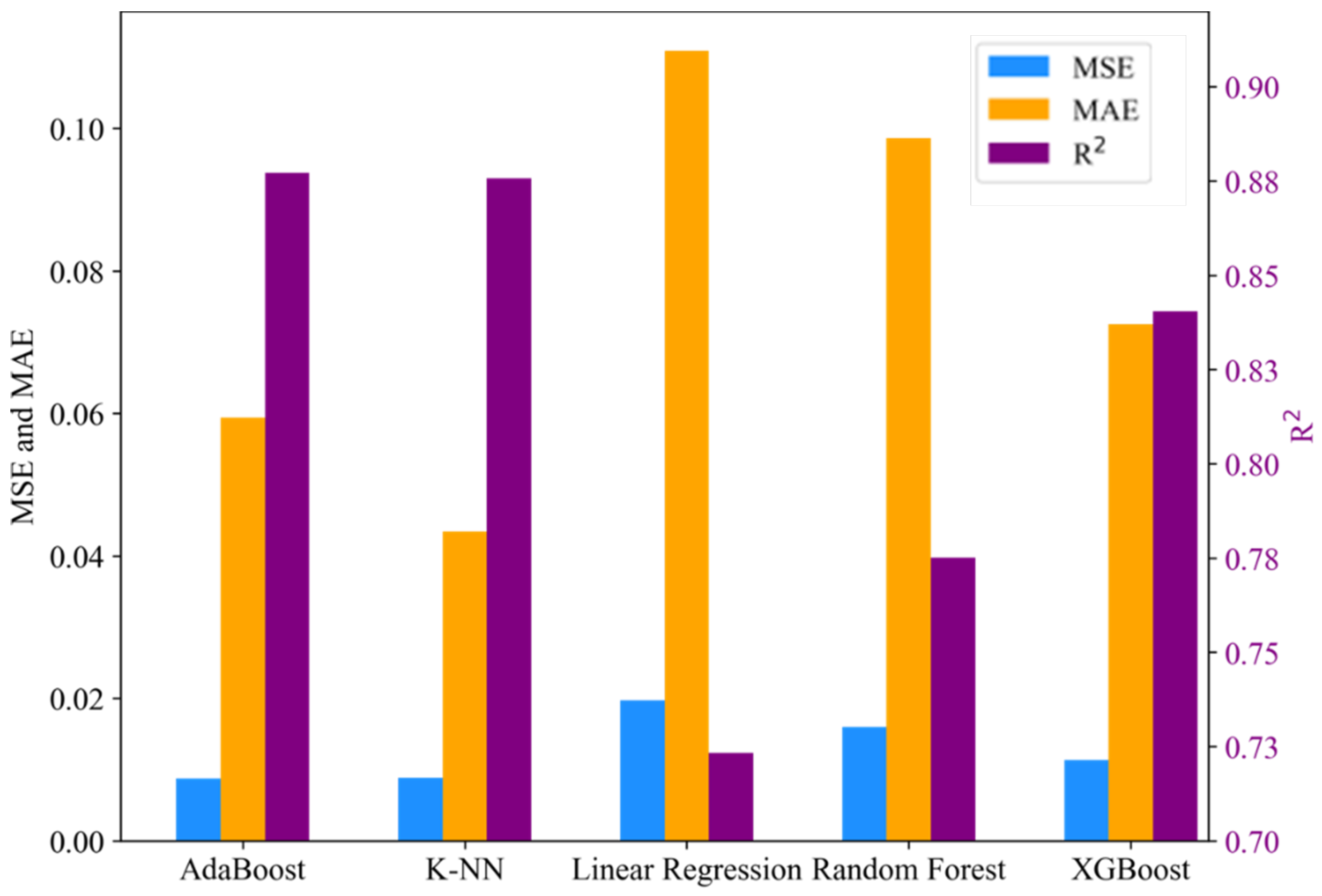
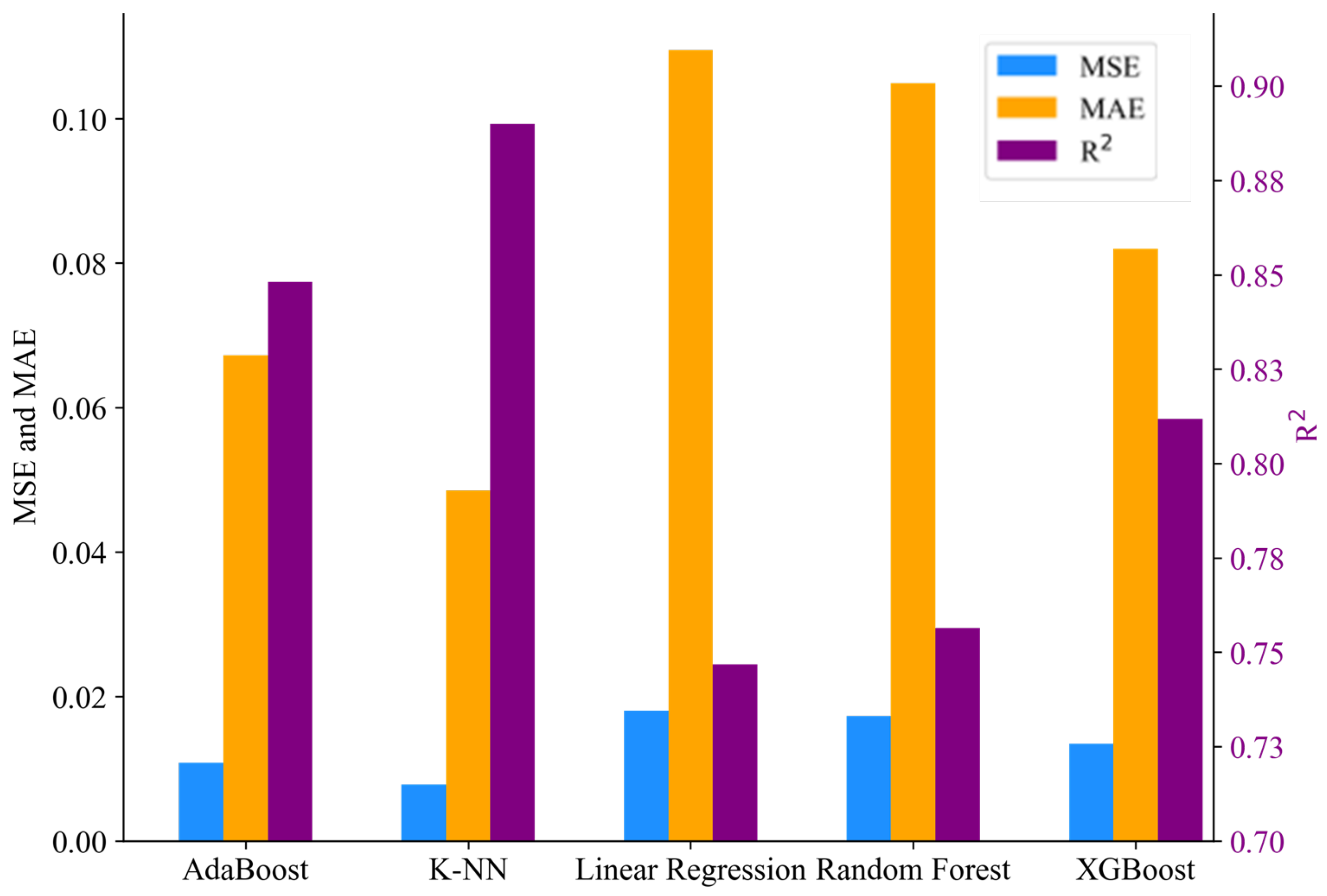
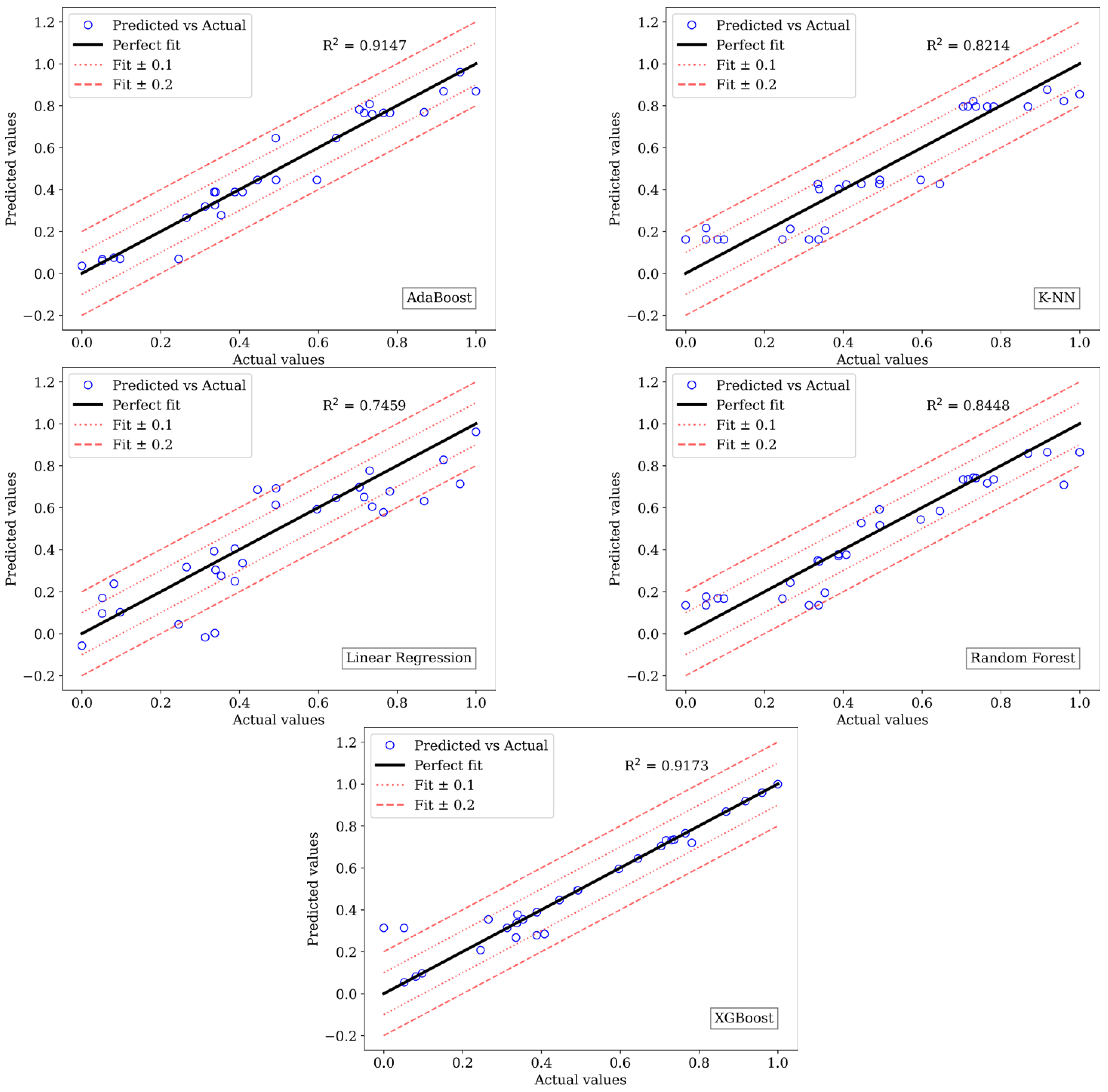
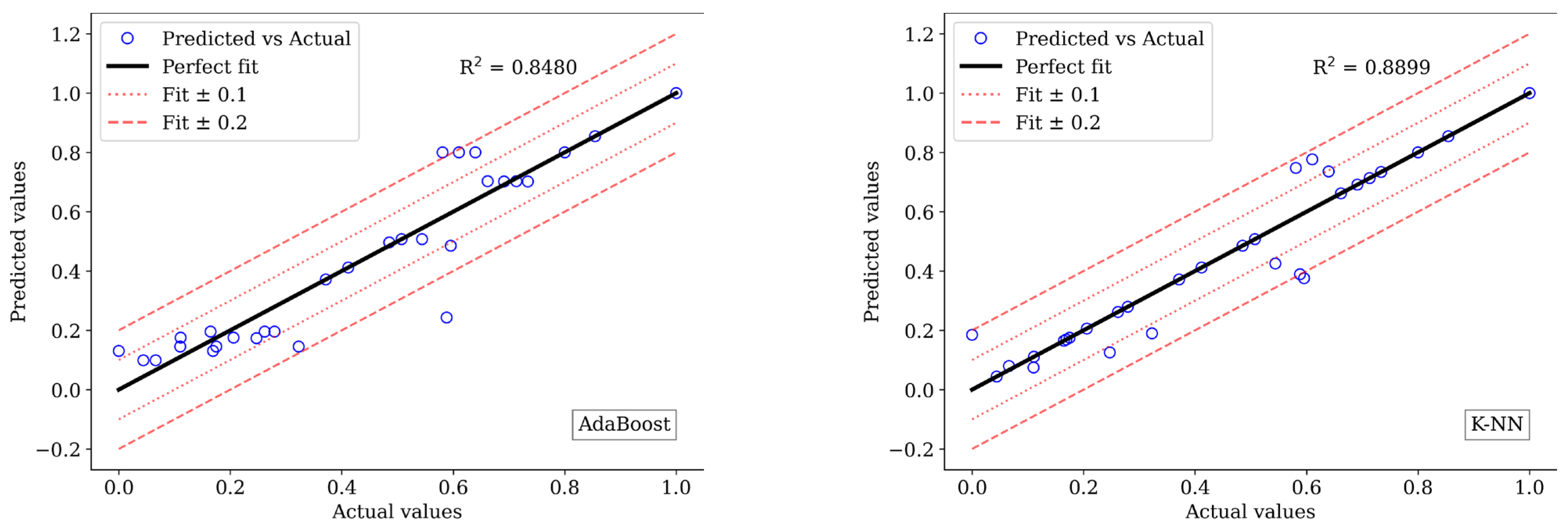
3.5. Machine Learning Analysis
3.5.1. Setup
3.5.2. Performance
3.5.3. Evaluation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lian, Q.; Li, D.C.; Chen, C.; Zhang, W.J.; Liu, Y.X.; He, J.K.; Jin, Z.M. Tissue-engineered soft tissue oriented manufacturing technologies and additive manufacturing. Chin. J. Tissue Eng. Res. 2014, 18, 1263–1269. [Google Scholar] [CrossRef]
- Witek, L.; Colon, R.R.; Wang, M.M.; Torroni, A.; Young, S.; Melville, J.; Lopez, C.D.; Flores, R.L.; Cronstein, B.N.; Coelho, P.G. Tissue-engineered alloplastic scaffolds for reconstruction of alveolar defects. In Handbook of Tissue Engineering Scaffolds: Volume One; Elsevier Ltd.: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- An, J.; Teoh, J.E.M.; Suntornnond, R.; Chua, C.K. Design and 3D Printing of Scaffolds and Tissues. Engineering 2015, 1, 261–268. [Google Scholar] [CrossRef]
- Ruiz-Alonso, S.; Lafuente-Merchan, M.; Ciriza, J.; Saenz-del-Burgo, L.; Pedraz, J.L. Tendon tissue engineering: Cells, growth factors, scaffolds and production techniques. J. Control. Release 2021, 333, 448–486. [Google Scholar] [CrossRef] [PubMed]
- Roseti, L.; Parisi, V.; Petretta, M.; Cavallo, C.; Desando, G.; Bartolotti, I.; Grigolo, B. Scaffolds for Bone Tissue Engineering: State of the art and new perspectives. Mater. Sci. Eng. C 2017, 78, 1246–1262. [Google Scholar] [CrossRef]
- Preethi Soundarya, S.; Haritha Menon, A.; Viji Chandran, S.; Selvamurugan, N. Bone tissue engineering: Scaffold preparation using chitosan and other biomaterials with different design and fabrication techniques. Int. J. Biol. Macromol. 2018, 119, 1228–1239. [Google Scholar] [CrossRef]
- Melchels, F.P.W.; Domingos, M.A.N.; Klein, T.J.; Malda, J.; Bartolo, P.J.; Hutmacher, D.W. Additive manufacturing of tissues and organs. Prog. Polym. Sci. 2012, 37, 1079–1104. [Google Scholar] [CrossRef]
- Qu, H. Additive manufacturing for bone tissue engineering scaffolds. Mater. Today Commun. 2020, 24, 101024. [Google Scholar] [CrossRef]
- Adeniran, O.; Osa-uwagboe, N.; Cong, W.; Ramoni, M. Fabrication Temperature-Related Porosity Effects on the Mechanical Properties of Additively Manufactured CFRP Composites. J. Comp. Sci. 2023, 7, 12. [Google Scholar] [CrossRef]
- Karuth, A.; Alesadi, A.; Xia, W.; Rasulev, B. Predicting glass transition of amorphous polymers by application of cheminformatics and molecular dynamics simulations. Polymer 2021, 218, 123495. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.; Feng, H.; Zhang, S.; Fu, Y. Design and Control for WLR-3P: A Hydraulic Wheel-Legged Robot. Cyborg Bionic Syst. 2023, 4, 25. [Google Scholar] [CrossRef]
- Atay, I.; Yilgör, E.; Sürme, S.; Kavakli, I.H.; Yilgör, I. Critical role of the composition of the cell culture medium on cell attachment and viability on PLA biocomposite scaffolds under in vitro assay conditions. Polymer 2024, 297, 126823. [Google Scholar] [CrossRef]
- Senatov, F.S.; Niaza, K.V.; Zadorozhnyy, M.Y.; Maksimkin, A.V.; Kaloshkin, S.D.; Estrin, Y.Z. Mechanical properties and shape memory effect of 3D-printed PLA-based porous scaffolds. J. Mech. Behav. Biomed. Mater. 2016, 57, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Udu, A.G.; Osa-uwagboe, N.; Olusanmi, A.; Aremu, A.; Khaksar, M.; Dong, H. A machine learning approach to characterise fabrication porosity effects on the mechanical properties of additively manufactured thermoplastic Composites. J. Reinf. Plast. Compos. 2024. [Google Scholar] [CrossRef]
- Czajka, A.; Plichta, A.; Bulski, R.; Pomilovskis, R.; Iuliano, A.; Cygan, T.; Ryszkowska, J. PLA reinforced with modified chokeberry pomace and beetroot pulp fillers. Effect of oligomeric chain extender on the properties of biocomposites. Polymer 2023, 289, 126472. [Google Scholar] [CrossRef]
- Farah, S.; Anderson, D.G.; Langer, R. Physical and mechanical properties of PLA, and their functions in widespread applications—A comprehensive review. Adv. Drug Deliv. Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef] [PubMed]
- Nevado, P.; Lopera, A.; Bezzon, V.; Fulla, M.R.; Palacio, J.; Zaghete, M.A.; Biasotto, G.; Montoya, A.; Rivera, J.; Robledo, S.; et al. Preparation and in vitro evaluation of PLA/biphasic calcium phosphate filaments used for fused deposition modelling of scaffolds. Mater. Sci. Eng. C 2020, 114, 111013. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Y.; Xie, B.; Jin, F.; Ma, L.; Zhang, H.; Li, Y.; Chen, X.; Hou, M.; Gao, J.; et al. Lightweight and drift-free magnetically actuated millirobots via asymmetric laser-induced graphene. Nat. Commun. 2024, 15, 4334. [Google Scholar] [CrossRef]
- Ranjan, N.; Singh, R.; Ahuja, I.S. Preparation of Partial Denture with Nano HAp-PLA Composite Under Cryogenic Grinding Environment Using 3D Printing. In Materials Science and Materials Engineering Encyclopedia of Renewable and Sustainable Materials; Elsevier Ltd.: Amsterdam, The Netherlands, 2020; Volume 4. [Google Scholar] [CrossRef]
- Ignjatović, N.; Tomić, S.; Dakić, M.; Miljković, M.; Plavšić, M.; Uskoković, D. Synthesis and properties of hydroxyapatite/poly-L-lactide composite biomaterials. Biomaterials 1999, 20, 809–816. [Google Scholar] [CrossRef]
- Xiao, L.; Liu, H.; Huang, H.; Wu, S.; Xue, L.; Geng, Z.; Cai, L.; Yan, F. 3D nanofiber scaffolds from 2D electrospun membranes boost cell penetration and positive host response for regenerative medicine. J. Nanobiotechnol. 2024, 22, 322. [Google Scholar] [CrossRef] [PubMed]
- Yüksel, N.; Börklü, H.R.; Sezer, H.K.; Canyurt, O.E. Review of artificial intelligence applications in engineering design perspective. Eng. Appl. Artif. Intell. 2023, 118, 105697. [Google Scholar] [CrossRef]
- Suwardi, A.; Wang, F.K.; Xue, K.; Han, M.Y.; Teo, P.; Wang, P.; Wang, S.; Liu, Y.; Ye, E.; Li, Z.; et al. Machine Learning-Driven Biomaterials Evolution. Adv. Mater. 2022, 34, 2102703. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Gupta, V.; Mudgal, D.; Srivastava, V. Predicting biomechanical properties of additively manufactured polydopamine coated poly lactic acid bone plates using deep learning. Eng. Appl. Artif. Intell. 2023, 124, 106587. [Google Scholar] [CrossRef]
- Xue, X.; Zhang, H.; Liu, H.; Wang, S.; Li, J.; Zhou, Q.; Chen, X.; Ren, X.; Jing, Y.; Deng, Y.; et al. Rational Design of Multifunctional CuS Nanoparticle-PEG Composite Soft Hydrogel-Coated 3D Hard Polycaprolactone Scaffolds for Efficient Bone Regeneration. Adv. Funct. Mater. 2022, 32, 2202470. [Google Scholar] [CrossRef]
- Alakent, B.; Soyer-Uzun, S. Implementation of Statistical Learning Methods to Develop Guidelines for the Design of PLA-Based Composites with High Tensile Strength Values. Ind. Eng. Chem. Res. 2019, 58, 3478–3489. [Google Scholar] [CrossRef]
- Thakur, V.; Kumar, R.; Kumar, R.; Singh, R.; Kumar, V. Hybrid additive manufacturing of highly sustainable Polylactic acid -Carbon Fiber-Polylactic acid sandwiched composite structures: Optimization and machine learning. J. Thermoplast. Compos. Mater. 2024, 37, 466–492. [Google Scholar] [CrossRef]
- Munir, N.; McMorrow, R.; Mulrennan, K.; Whitaker, D.; McLoone, S.; Kellomäki, M.; Talvitie, E.; Lyyra, I.; McAfee, M. Interpretable Machine Learning Methods for Monitoring Polymer Degradation in Extrusion of Polylactic Acid. Polymers 2023, 15, 3566. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, L.; Song, P.; Pei, X.; Sun, H.; Wu, L.; Zhou, C.; Wang, K.; Fan, Y.; Zhang, X. 3D printed bone tissue regenerative PLA/HA scaffolds with comprehensive performance optimizations. Mater. Des. 2021, 201, 109490. [Google Scholar] [CrossRef]
- Nie, T.; Xue, L.; Ge, M.; Ma, H.; Zhang, J. Fabrication of poly(L-lactic acid) tissue engineering scaffolds with precisely controlled gradient structure. Mater. Lett. 2016, 176, 25–28. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Zahedi, S.A.; Adeoye, A.O.M. 3D printing of bone scaffolds with hybrid biomaterials. Compos. B Eng. 2019, 158, 428–436. [Google Scholar] [CrossRef]
- ASTM D638-22; Standard Test Method for Tensile Properties of Plastics 1. Annual Book of ASTM Standards. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- Lee, D.; Kwon, H.J.; Yang, S.; Kim, M.S. Fabrication, testing, and analysis of sandwich structure with composite skin and additive manufactured core. J. Reinf. Plast. Compos. 2021, 40, 654–664. [Google Scholar] [CrossRef]
- López-Vázquez, C.; Hochsztain, E. Extended and updated tables for the Friedman rank test. Commun. Stat. Theory Methods 2019, 48, 268–281. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Osa-uwagboe, N.; Udu, A.G.; Ghalati, M.K.; Silberschmidt, V.V.; Aremu, A.; Dong, H.; Demirci, E. A machine learning-enabled prediction of damage properties for fiber-reinforced polymer composites under out-of-plane loading. Eng. Struct. 2024, 308, 117970. [Google Scholar] [CrossRef]
- Tsamardinos, I.; Greasidou, E.; Borboudakis, G. Bootstrapping the out-of-sample predictions for efficient and accurate cross-validation. Mach. Learn. 2018, 107, 1895–1922. [Google Scholar] [CrossRef] [PubMed]
- Botchkarev, A. A new typology design of performance metrics to measure errors in machine learning regression algorithms. Interdiscip. J. Inf. Knowl. Manag. 2019, 14, 45–76. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, L.; Wang, W.; Zhao, L.; Li, M.; Han, Y.; Wang, L.; Zhang, Z.; Li, J.; Zhou, C.; et al. Fabrication and properties of PLA/nano-HA composite scaffolds with balanced mechanical properties and biological functions for bone tissue engineering application. Nanotechnol. Rev. 2021, 10, 1359–1373. [Google Scholar] [CrossRef]
- Woźna, A.E.; Junka, A.; Hoppe, V.W. Influence of the different composites (Pla/plla/ha/β-tcp) contents manufactured with additive laser technology on the biocompatibility. Acta Bioeng. Biomech. 2021, 23, 169–180. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Zahedi, S.A.; Omigbodun, F.T. A systematic review of polymer composite in biomedical engineering. Eur. Polym. J. 2021, 154, 110534. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, Q.; Wei, Z.; Chen, X.; Shi, Q.; Yu, Z.; Sun, T. An Overview of In Vitro Biological Neural Networks for Robot Intelligence. Cyborg Bionic Syst. 2023, 4, 0001. [Google Scholar] [CrossRef]
- Zhang, S.; Li, F.; Fu, R.; Li, H.; Zou, S.; Ma, N.; Qu, S.; Li, J. A Versatile Continuum Gripping Robot with a Concealable Gripper. Cyborg Bionic Syst. 2023, 4, 0003. [Google Scholar] [CrossRef] [PubMed]
- Zimina, A.; Senatov, F.; Choudhary, R.; Kolesnikov, E.; Anisimova, N.; Kiselevskiy, M.; Orlova, P.; Strukova, N.; Generalova, M.; Manskikh, V.; et al. Biocompatibility and physico-chemical properties of highly porous PLA/HA scaffolds for bone reconstruction. Polymers 2020, 12, 2938. [Google Scholar] [CrossRef] [PubMed]
- Pietrzykowska, E.; Romelczyk-Baishya, B.; Wojnarowicz, J.; Sokolova, M.; Szlazak, K.; Swieszkowski, W.; Locs, J.; Lojkowski, W. Preparation of a ceramic matrix composite made of hydroxyapatite nanoparticles and polylactic acid by consolidation of composite granules. Nanomaterials 2020, 10, 1060. [Google Scholar] [CrossRef]
- Nedaipour, F.; Bagheri, H.; Mohammadi, S. “Polylactic acid-polyethylene glycol-hydroxyapatite composite” an efficient composition for interference screws. Nanocomposites 2020, 6, 99–110. [Google Scholar] [CrossRef]
- Lu, J.; Sun, C.; Yang, K.; Wang, K.; Jiang, Y.; Tusiime, R.; Yang, Y.; Fan, F.; Sun, Z.; Liu, Y.; et al. Properties of polylactic acid reinforced by hydroxyapatite modified nanocellulose. Polymers 2019, 11, 1009. [Google Scholar] [CrossRef]
- Kosowska, K.; Domalik-Pyzik, P.; Krok-Borkowicz, M.; Chłopek, J. Polylactide/hydroxyapatite nonwovens incorporated into chitosan/graphene materials hydrogels to form novel hierarchical scaffolds. Int. J. Mol. Sci. 2020, 21, 2330. [Google Scholar] [CrossRef]
- Zare, R.N.; Doustkhah, E.; Assadi, M.H.N. Three-dimensional bone printing using hydroxyapatite-PLA composite. Mater. Today Proc. 2019, 42, 1531–1533. [Google Scholar] [CrossRef]
- Joyce, M.; Hodgkinson, T.; Lemoine, M.; González-Vázquez, A.; Kelly, D.J.; O’Brien, F.J. Development of a 3D-printed bioabsorbable composite scaffold with mechanical properties suitable for treating large, load-bearingarticular cartilage defects. Eur. Cells Mater. 2023, 45, 158–172. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, F.; Zhai, W.; Cheng, S.; Li, J.; Wang, Y. Unraveling of Advances in 3D-Printed Polymer-Based Bone Scaffolds. Polymers 2022, 14, 566. [Google Scholar] [CrossRef]
- Lee, S.S.; Du, X.; Kim, I.; Ferguson, S.J. Scaffolds for bone-tissue engineering. Matter 2022, 5, 2722–2759. [Google Scholar] [CrossRef]




| Property | Value | ASTM Method |
|---|---|---|
| Relative density (g/cm3). | 1.24 | D792 |
| Stress (MPa) | 36 | D638 |
| Poison ratio | 2.5 | |
| Elastic modulus (GPa) | 3.5 | |
| Tm °C | 151.5 | E2092 |
| Tg °C | 55.1 |
| Composites | Mass of PLA (%) | Mass of cHAP (%) | Volume of Chloroform (l) |
|---|---|---|---|
| PLA/cHAP | 100 | 0 | 4.5 |
| PLA/cHAP | 92.5 | 7.5 | 4.5 |
| PLA/cHAP | 90 | 10 | 4.5 |
| Sample | Degradation Temperature (°C) | |||
|---|---|---|---|---|
| % Final Residue | ||||
| PLA pellets | 320.5 | 387 | 426.8 | 0 |
| PLA/cHAP 0% filament | 318 | 384.2 | 426.9 | 0.11 |
| PLA/cHAP 7.5% filament | 321.7 | 390.5 | 430.8 | 3.95 |
| PLA/cHAP 10% filament | 319 | 389 | 427.9 | 7.67 |
| PLA/cHAP 0% scaffold | 297.7 | 385.3 | 426.2 | 0.27 |
| PLA/cHAP 7.5% scaffold | 320.5 | 390.3 | 431.3 | 4.88 |
| PLA/cHAP 10% scaffold | 320.6 | 390.9 | 431 | 7.75 |
| Calcium hydroxyapatite | 90.33 | |||
| Sample | Second Heating Cycle | |||||
|---|---|---|---|---|---|---|
| (°C) | (°C) | (°C) | (J/g) | (J/g) | (%) | |
| PLA Pellets | 60.03 | 151.05 | - | 2.51 | 2.6 | |
| PLA/cHAP 0% filament | 60.15 | 151.09 | 123.50 | 21.54 | −17.20 | 23.14 |
| PLA/cHAP 7.5% filament | 59.62 | 151.24 | 127.00 | 14.22 | −12.54 | 16.51 |
| PLA/cHAP 10% filament | 58.90 | 150.06 | 115.39 | 22.25 | −22.75 | 26.55 |
| PLA/cHAP 0% scaffold | 60.37 | 150.64 | 122.60 | 22.40 | −24.31 | 24.06 |
| PLA/cHAP 7.5% scaffold | 59.86 | 151.18 | 125.58 | 19.63 | −19.52 | 26.39 |
| PLA/cHAP 10% scaffold | 59.95 | 148.00 | 114.79 | 25.11 | −25.86 | 29.96 |
| Composites | Modulus of Elasticity (GPa) | UTS (MPa) | Compression Strength (MPa) |
|---|---|---|---|
| Human Cancellous Bones [53] | 0.3–3 | 1.5–45 | 2–12 |
| Human Cortical Bones [53] | 4–30 | 27–283 | 96–200 |
| PLA | 3.42 | 36 | 35.9 |
| PLA/cHAP 7.5% | 4.72 | 42.16 | 83.01 |
| PLA/cHAP 10% | 4.86 | 43.88 | 38.81 |
| Model | Compression | Tensile | ||||
|---|---|---|---|---|---|---|
| MSE | MAE | R2 | MSE | MAE | R2 | |
| AdaBoost | 0.0069 | 0.0500 | 0.9147 | 0.0087 | 0.0594 | 0.8772 |
| K-NN | 0.0144 | 0.0964 | 0.8214 | 0.0088 | 0.0434 | 0.8757 |
| Linear Regression | 0.0205 | 0.1159 | 0.7459 | 0.0197 | 0.1109 | 0.7233 |
| Random Forest | 0.0125 | 0.0823 | 0.8448 | 0.0160 | 0.0986 | 0.7751 |
| XGBoost | 0.0067 | 0.0384 | 0.9173 | 0.0113 | 0.0725 | 0.8405 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omigbodun, F.T.; Osa-Uwagboe, N.; Udu, A.G.; Oladapo, B.I. Leveraging Machine Learning for Optimized Mechanical Properties and 3D Printing of PLA/cHAP for Bone Implant. Biomimetics 2024, 9, 587. https://doi.org/10.3390/biomimetics9100587
Omigbodun FT, Osa-Uwagboe N, Udu AG, Oladapo BI. Leveraging Machine Learning for Optimized Mechanical Properties and 3D Printing of PLA/cHAP for Bone Implant. Biomimetics. 2024; 9(10):587. https://doi.org/10.3390/biomimetics9100587
Chicago/Turabian StyleOmigbodun, Francis T., Norman Osa-Uwagboe, Amadi Gabriel Udu, and Bankole I. Oladapo. 2024. "Leveraging Machine Learning for Optimized Mechanical Properties and 3D Printing of PLA/cHAP for Bone Implant" Biomimetics 9, no. 10: 587. https://doi.org/10.3390/biomimetics9100587
APA StyleOmigbodun, F. T., Osa-Uwagboe, N., Udu, A. G., & Oladapo, B. I. (2024). Leveraging Machine Learning for Optimized Mechanical Properties and 3D Printing of PLA/cHAP for Bone Implant. Biomimetics, 9(10), 587. https://doi.org/10.3390/biomimetics9100587








