Figure 1.
Evaluation stages to determine the performance of an metaheuristic.
Figure 1.
Evaluation stages to determine the performance of an metaheuristic.
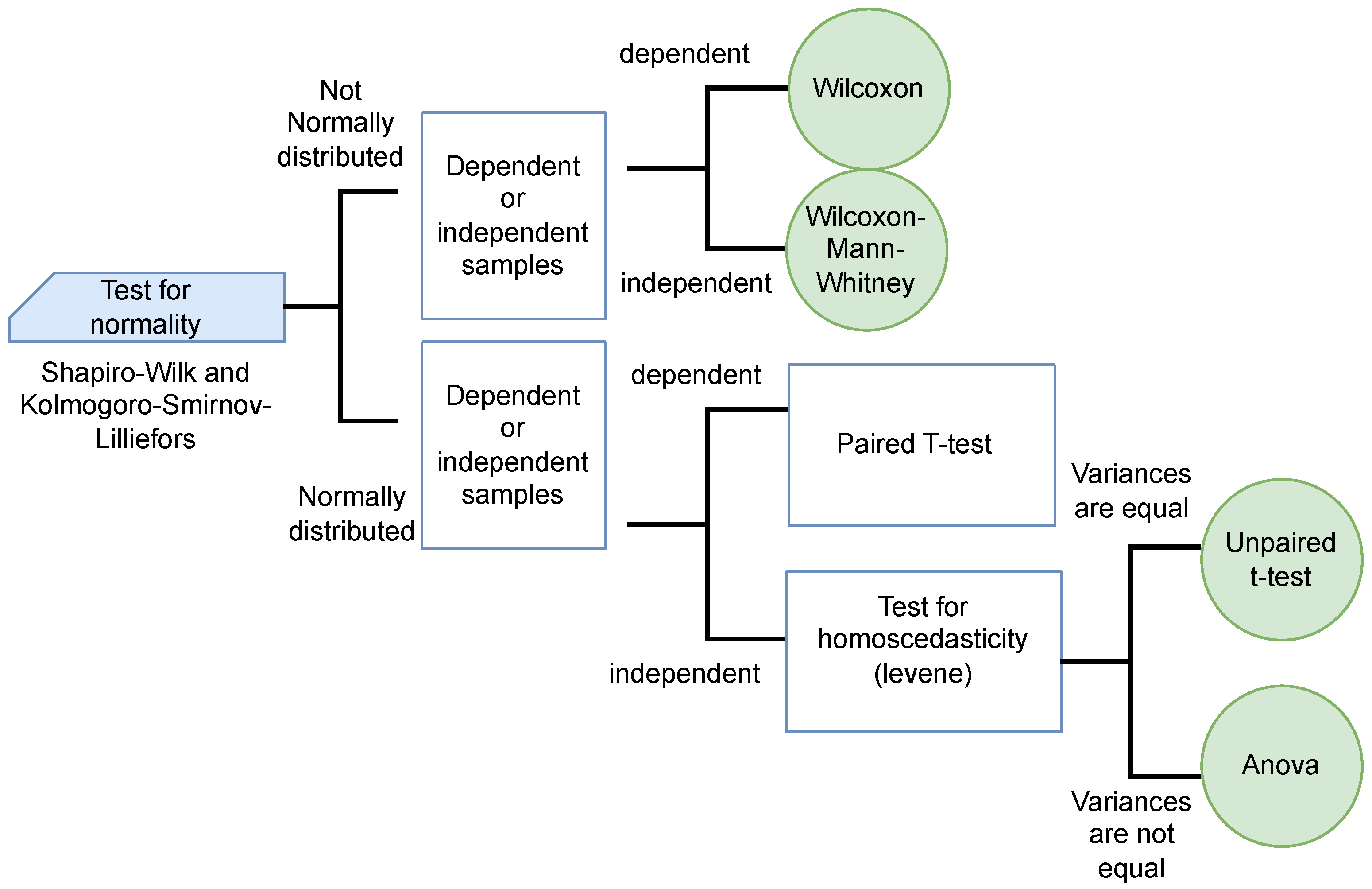
Figure 2.
Statistical significance test.
Figure 2.
Statistical significance test.
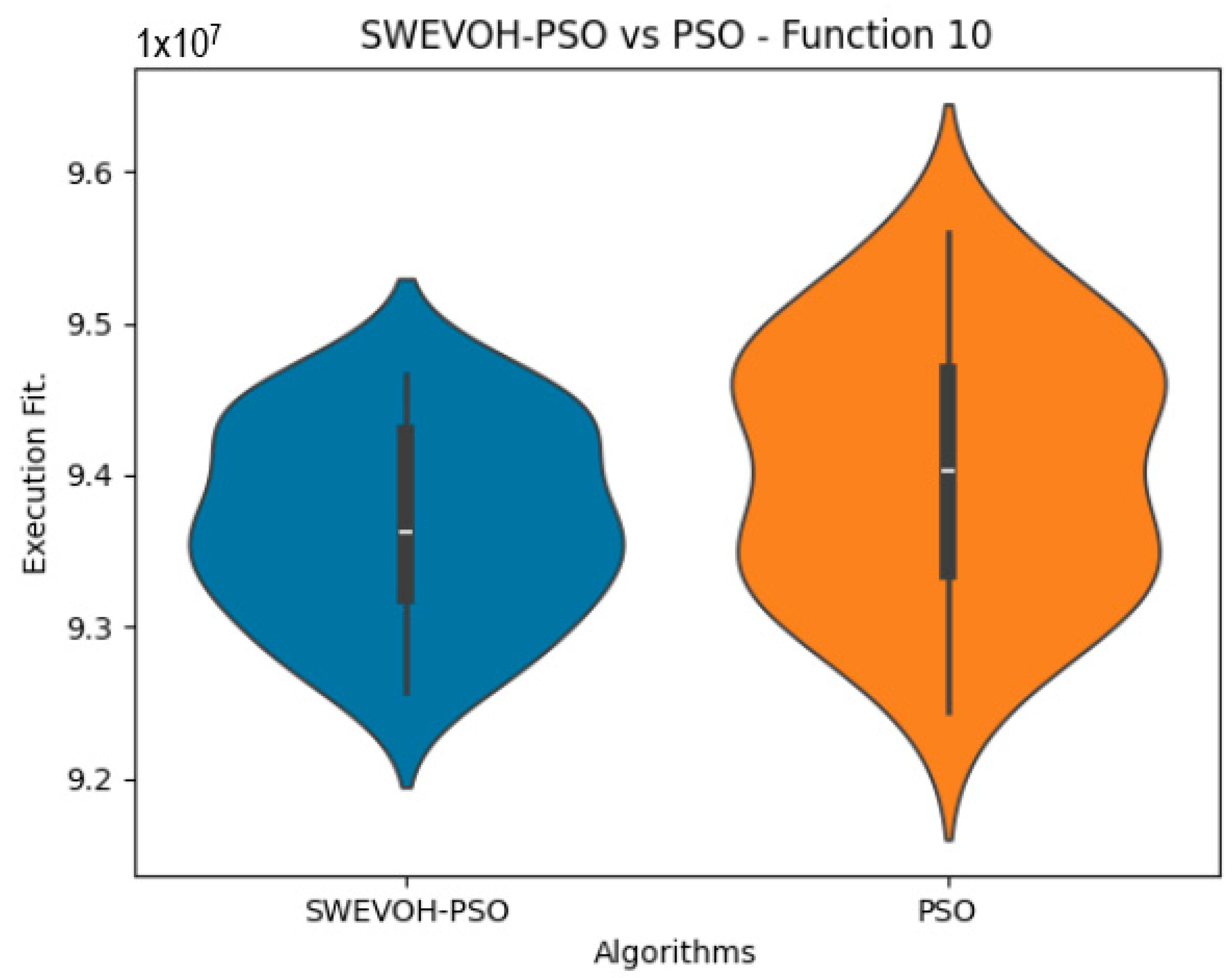
Figure 3.
SWEVO-PSO vs. PSO distribution on F10.
Figure 3.
SWEVO-PSO vs. PSO distribution on F10.
Figure 4.
SWEVO-PSO vs. PSO distribution on F11.
Figure 4.
SWEVO-PSO vs. PSO distribution on F11.
Figure 5.
SWEVO-PSO vs. PSO distribution on F12.
Figure 5.
SWEVO-PSO vs. PSO distribution on F12.
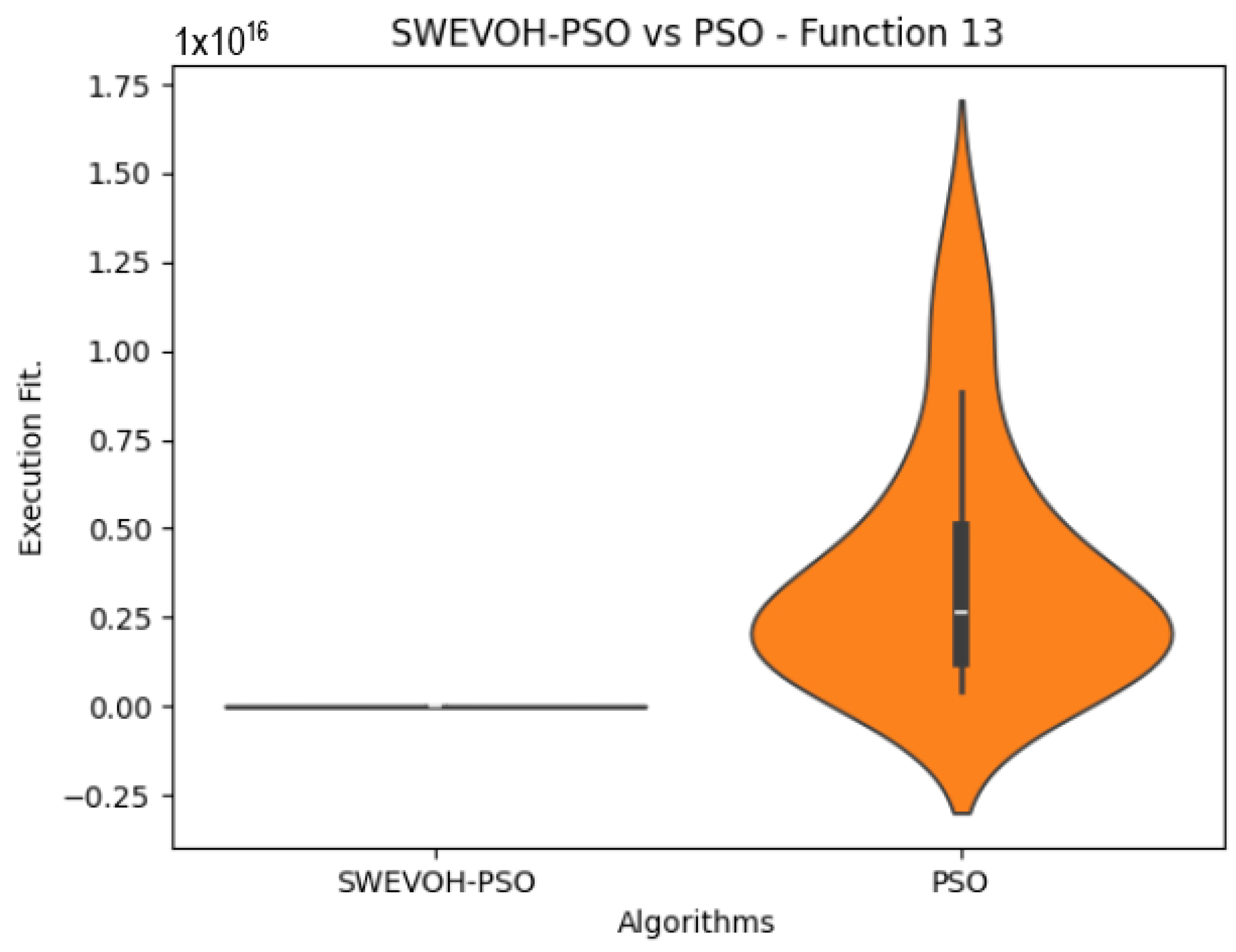
Figure 6.
SWEVO-PSO vs. PSO distribution on F13.
Figure 6.
SWEVO-PSO vs. PSO distribution on F13.
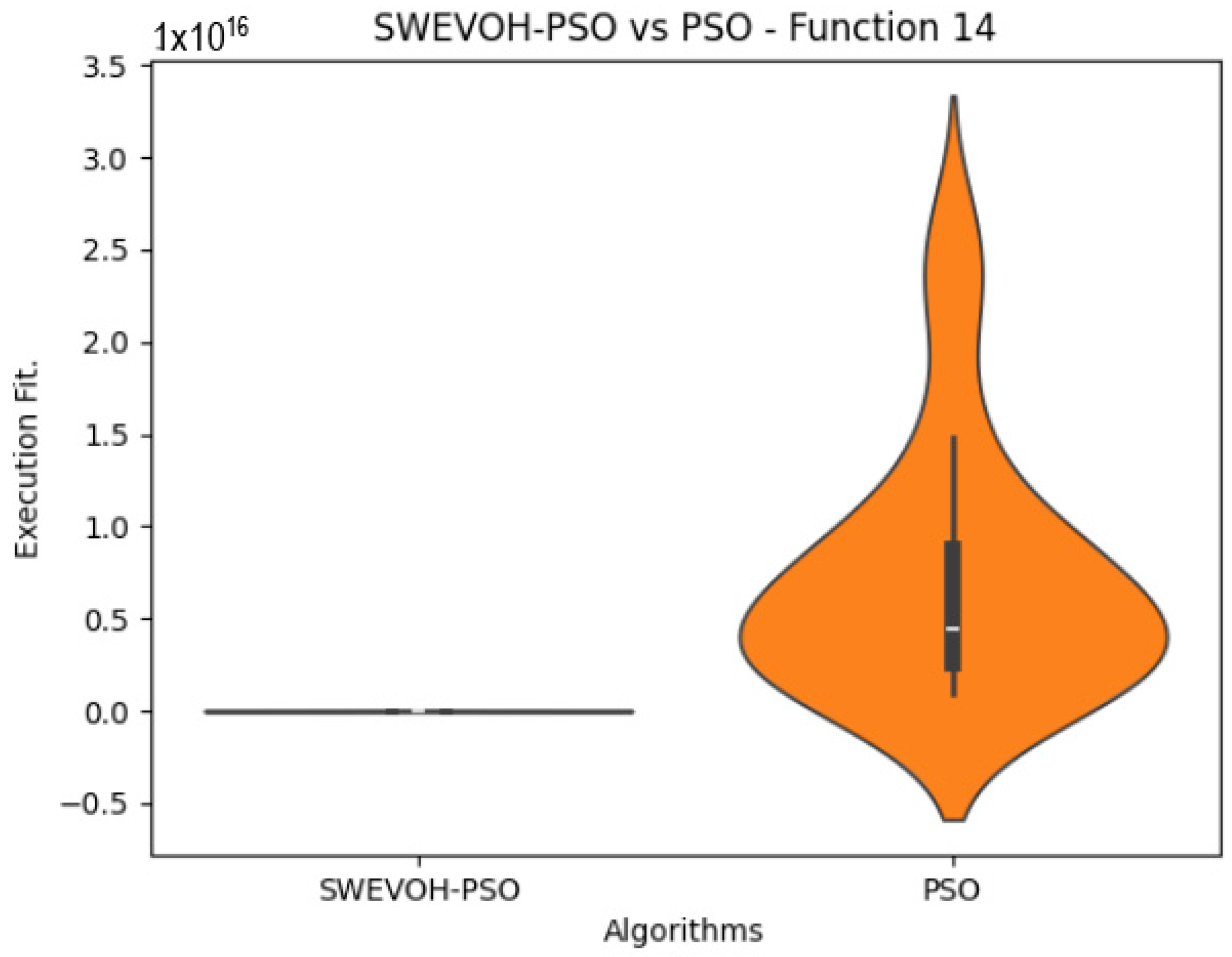
Figure 7.
SWEVO-PSO vs. PSO distribution on F14.
Figure 7.
SWEVO-PSO vs. PSO distribution on F14.
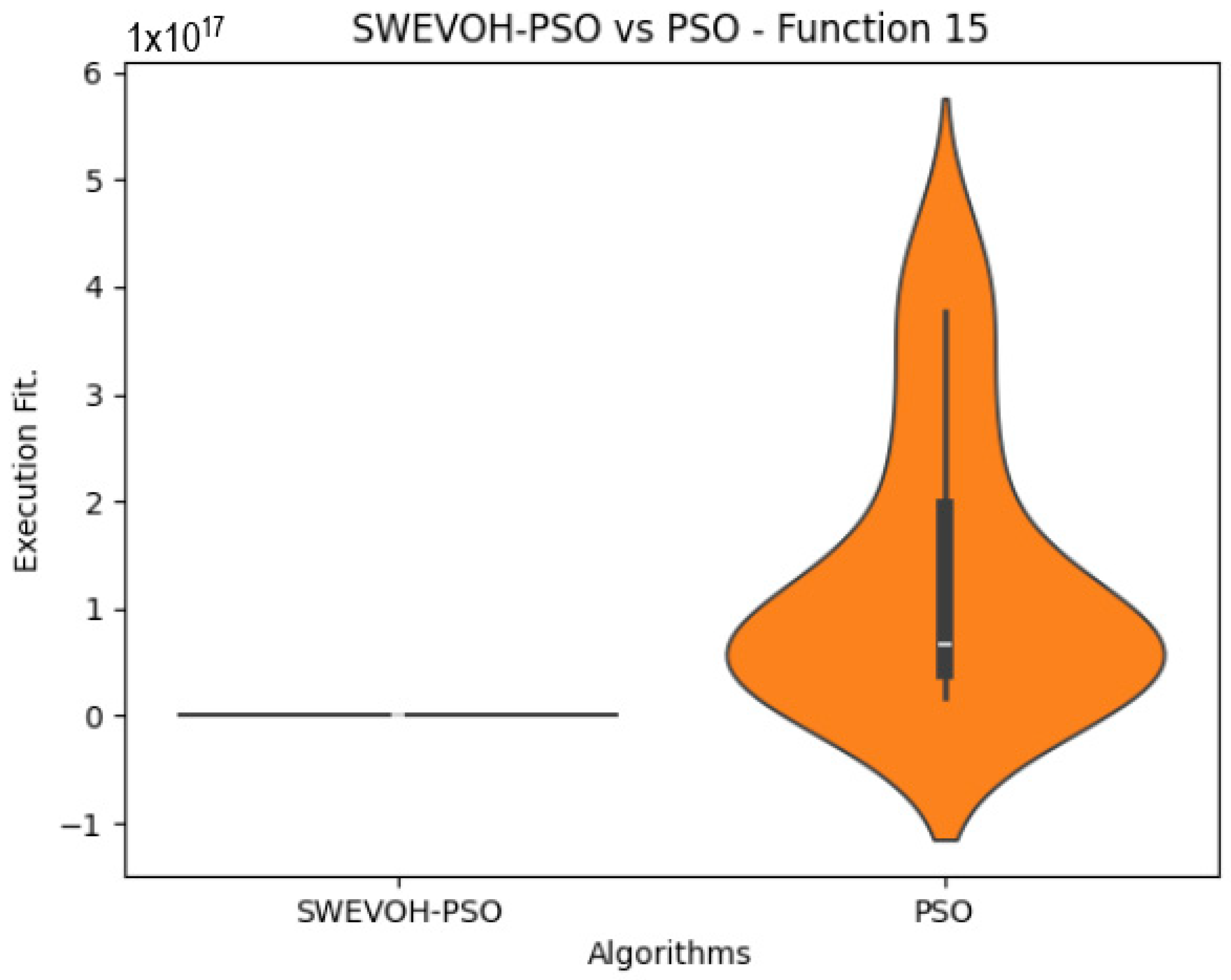
Figure 8.
SWEVO-PSO vs. PSO distribution on F15.
Figure 8.
SWEVO-PSO vs. PSO distribution on F15.
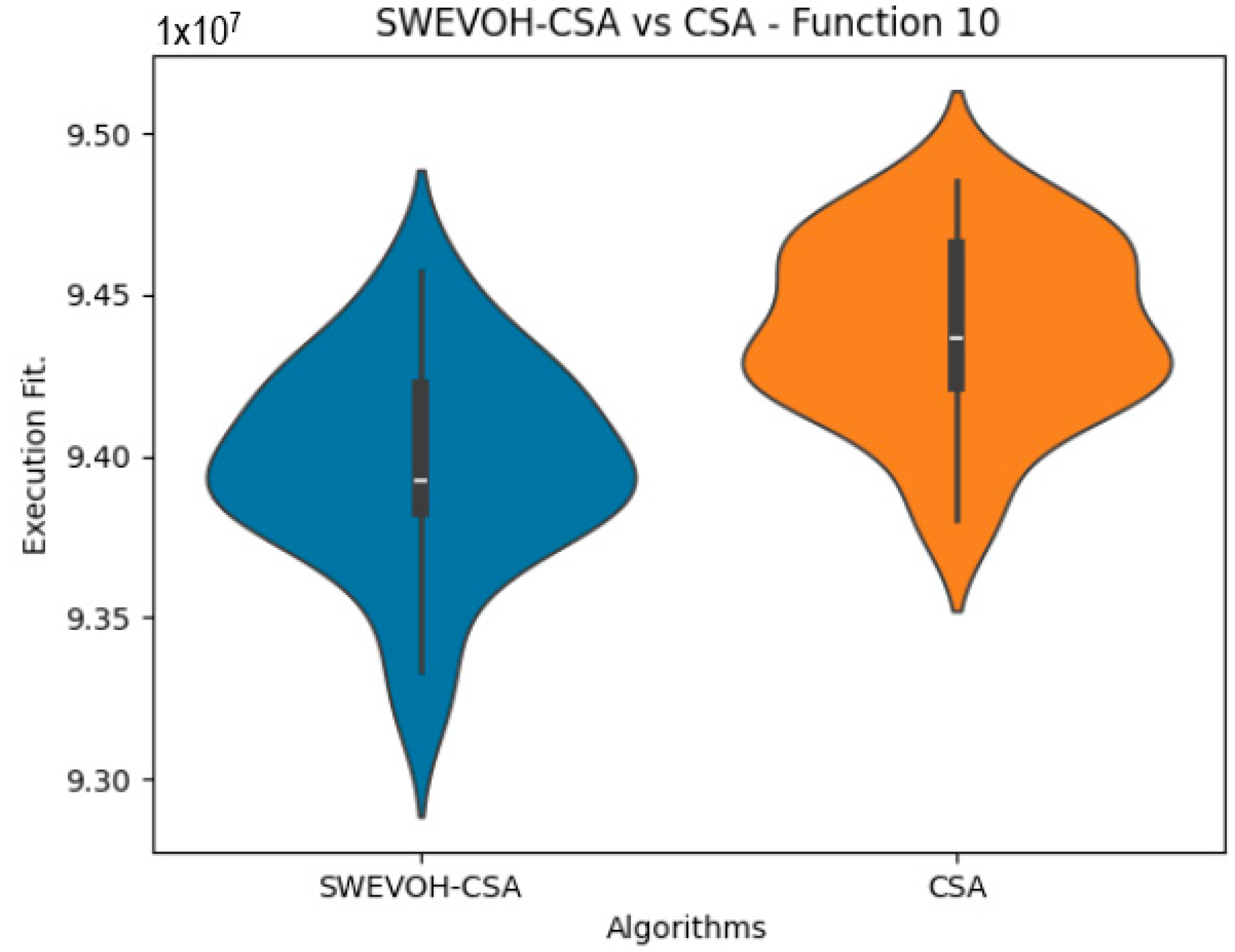
Figure 9.
SWEVO-CSA vs. CSA distribution on F10.
Figure 9.
SWEVO-CSA vs. CSA distribution on F10.
Figure 10.
SWEVO-CSA vs. CSA distribution on F11.
Figure 10.
SWEVO-CSA vs. CSA distribution on F11.
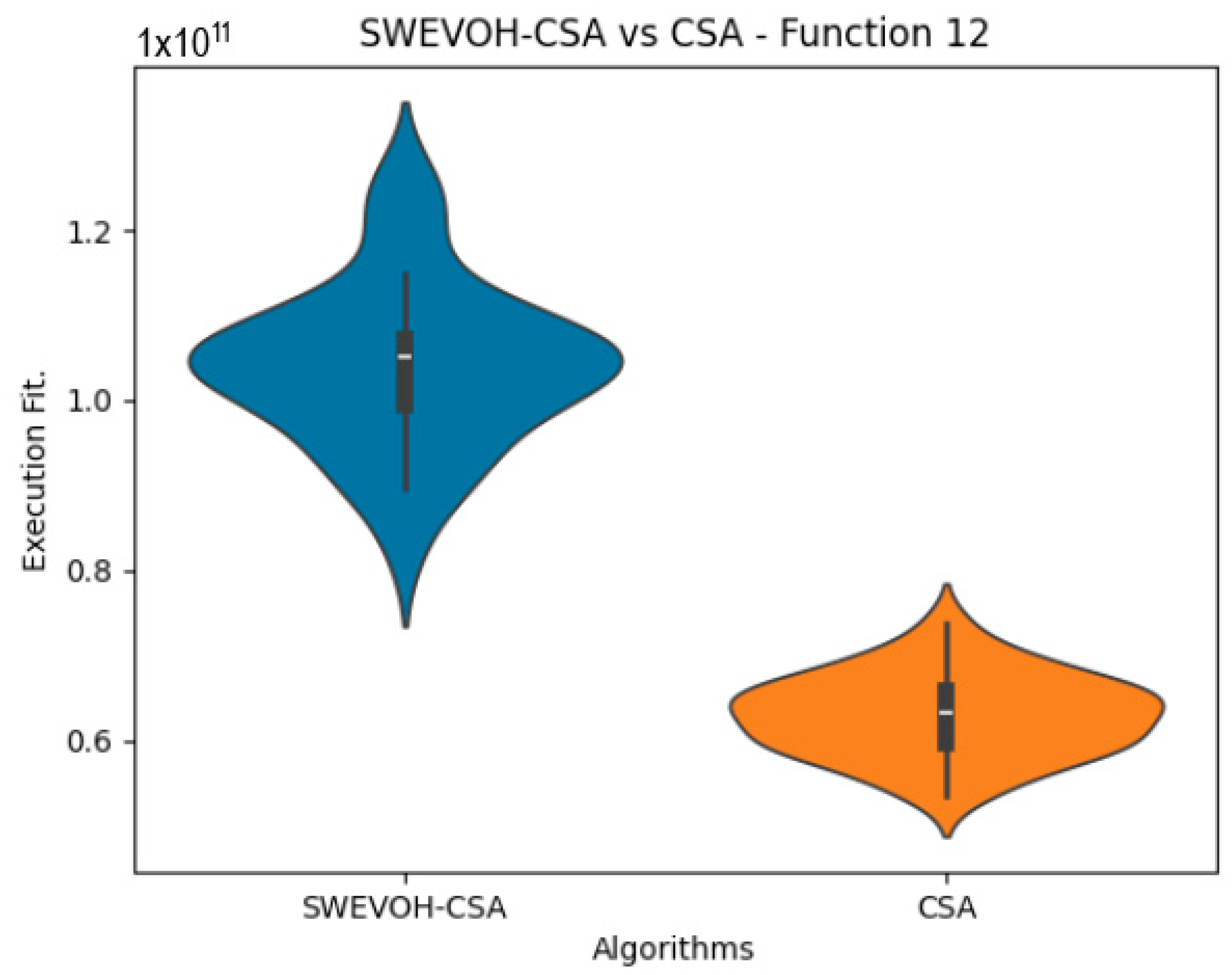
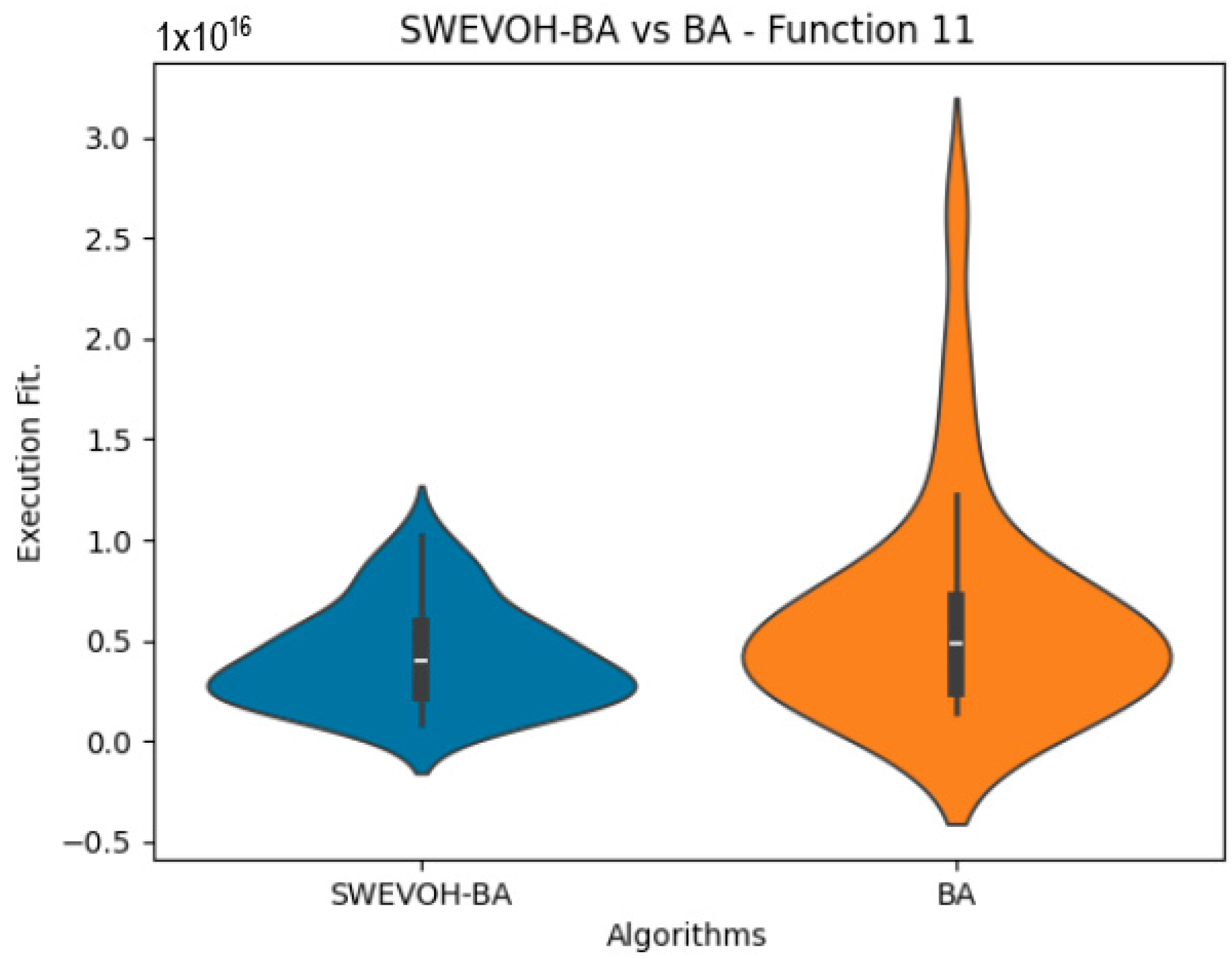
Figure 11.
SWEVO-CSA vs. CSA distribution on F12.
Figure 11.
SWEVO-CSA vs. CSA distribution on F12.
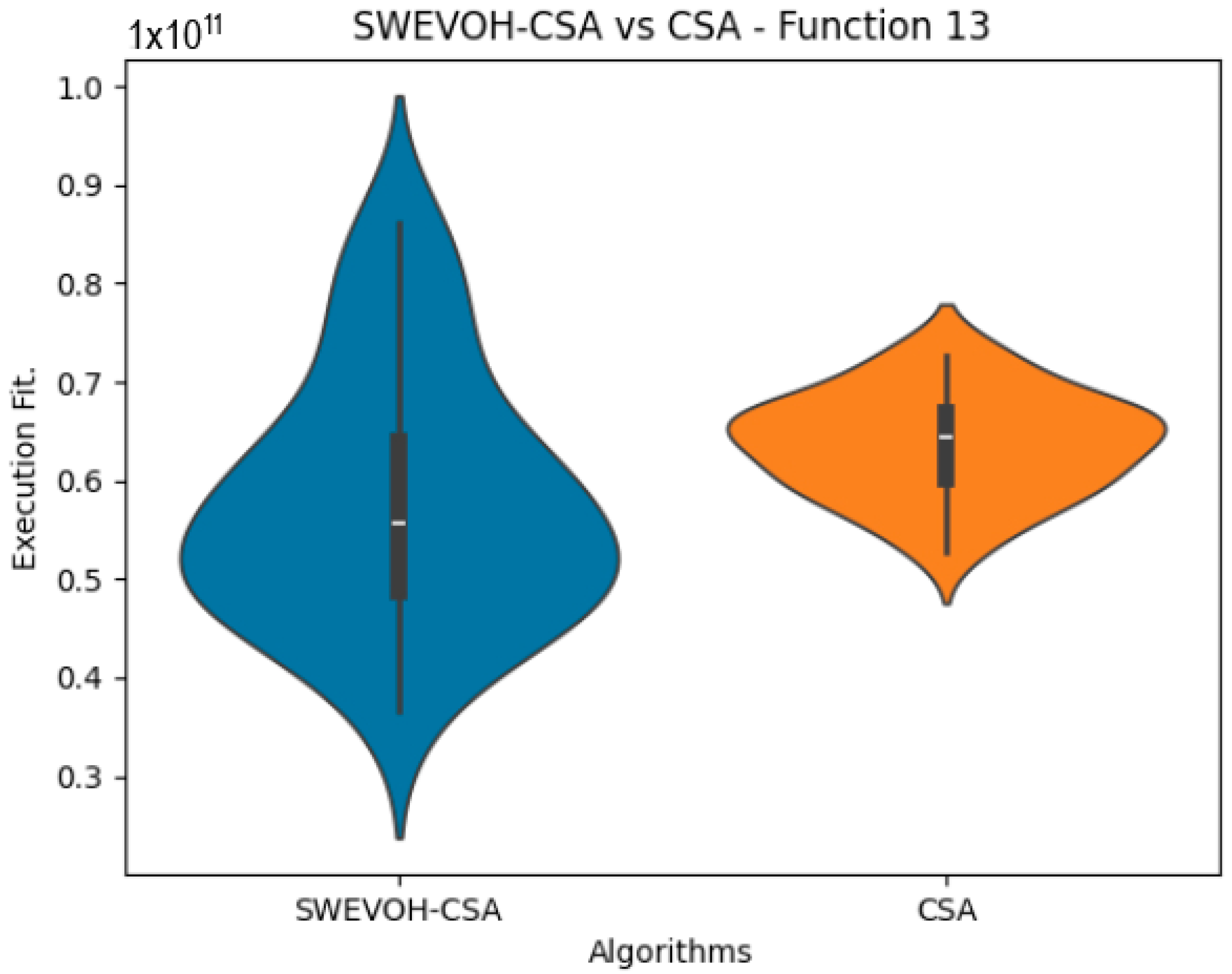
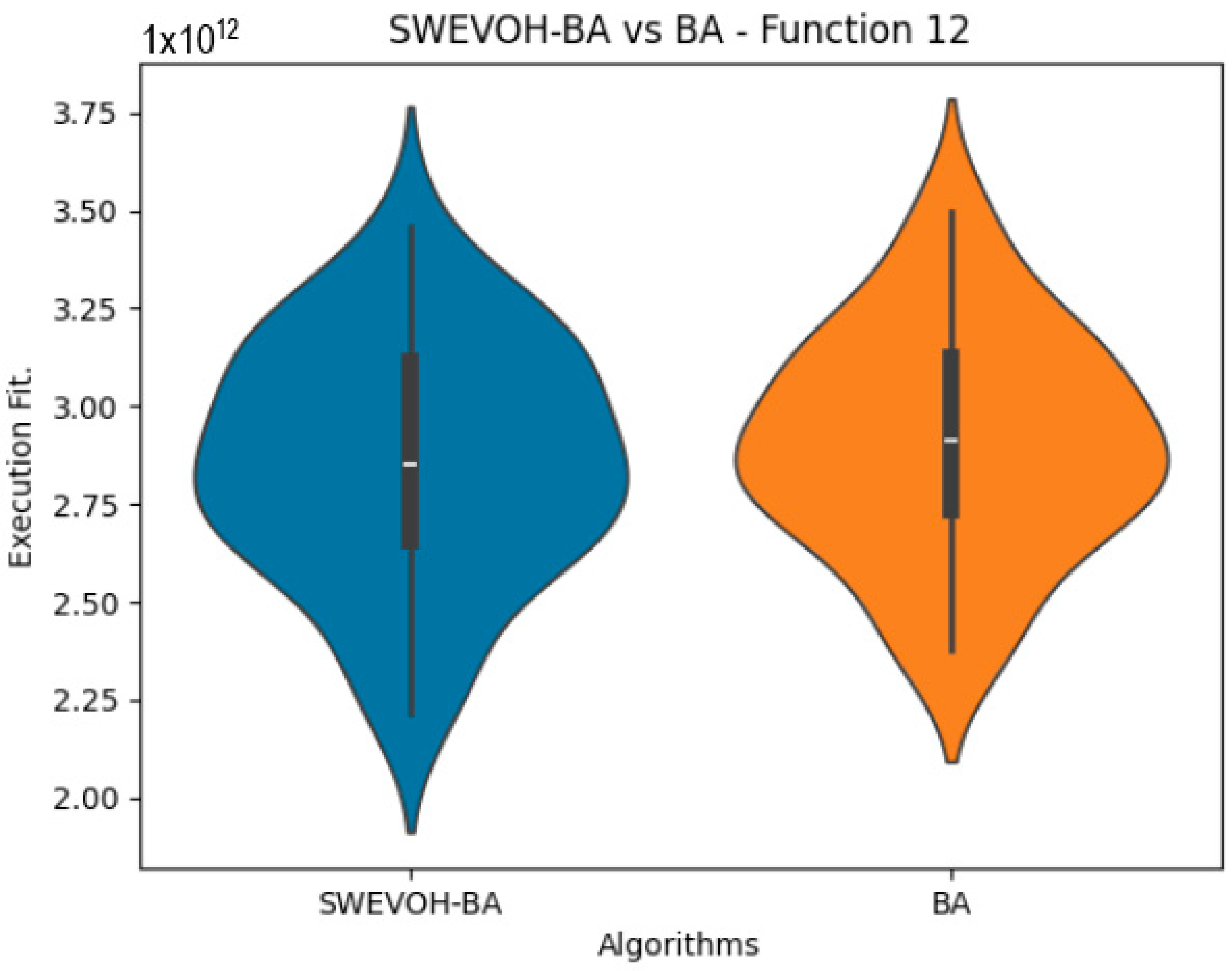
Figure 12.
SWEVO-CSA vs. CSA distribution on F13.
Figure 12.
SWEVO-CSA vs. CSA distribution on F13.
Figure 13.
SWEVO-CSA vs. CSA distribution on F14.
Figure 13.
SWEVO-CSA vs. CSA distribution on F14.
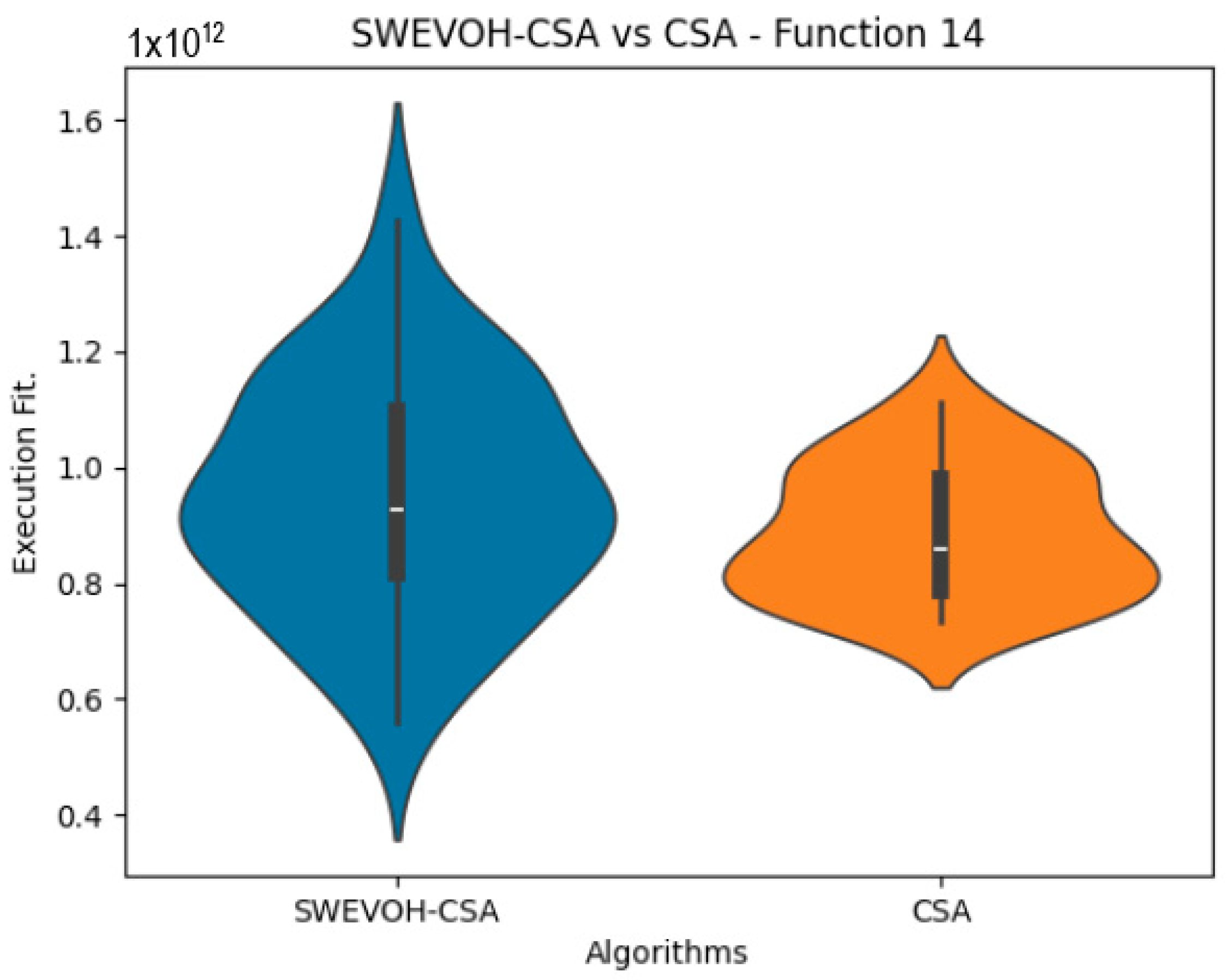
Figure 14.
SWEVO-CSA vs. CSA distribution on F15.
Figure 14.
SWEVO-CSA vs. CSA distribution on F15.
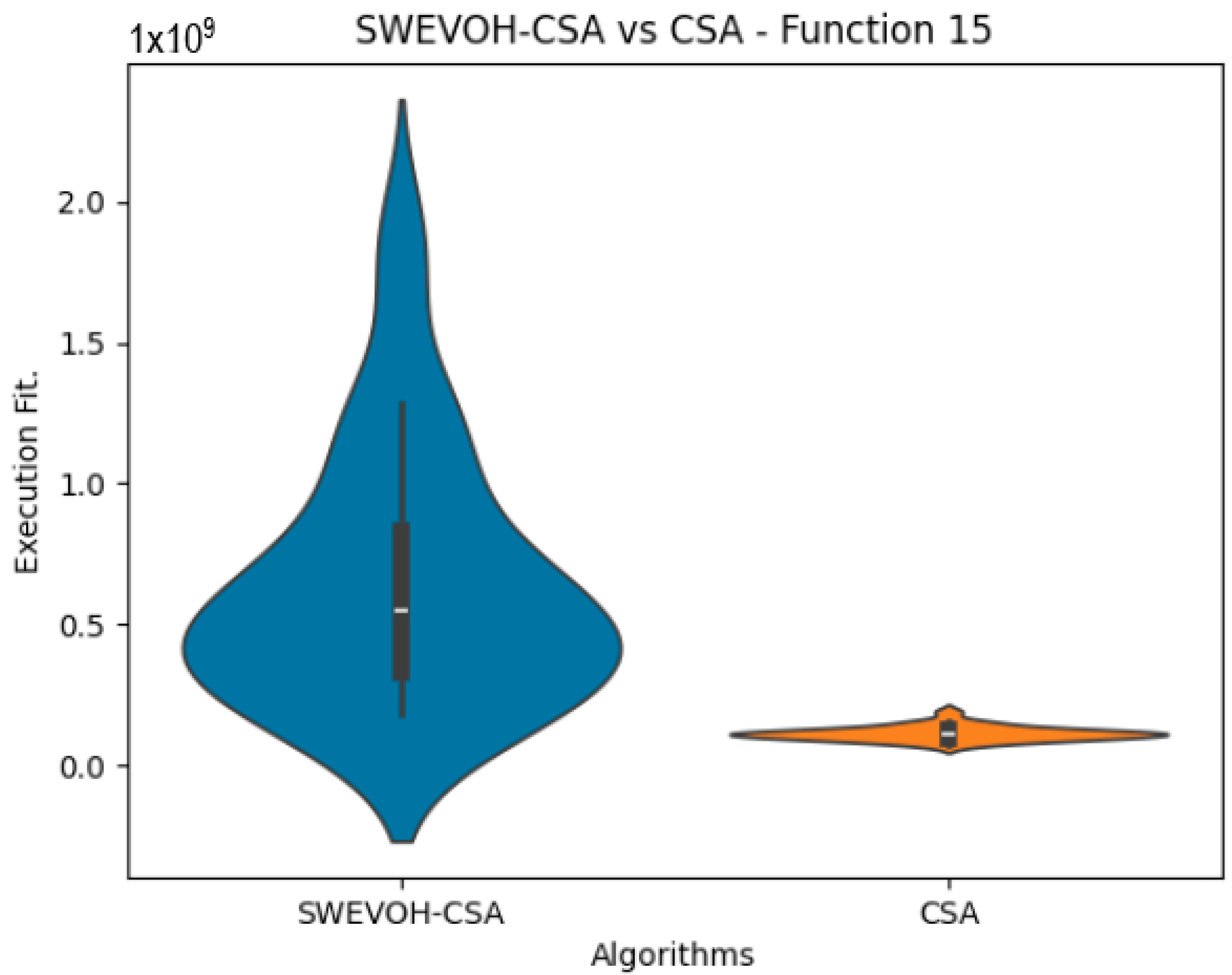
Figure 15.
SWEVO-BA vs. BA distribution on F10.
Figure 15.
SWEVO-BA vs. BA distribution on F10.
Figure 16.
SWEVO-BA vs. BA distribution on F11.
Figure 16.
SWEVO-BA vs. BA distribution on F11.
Figure 17.
SWEVO-BA vs. BA distribution on F12.
Figure 17.
SWEVO-BA vs. BA distribution on F12.
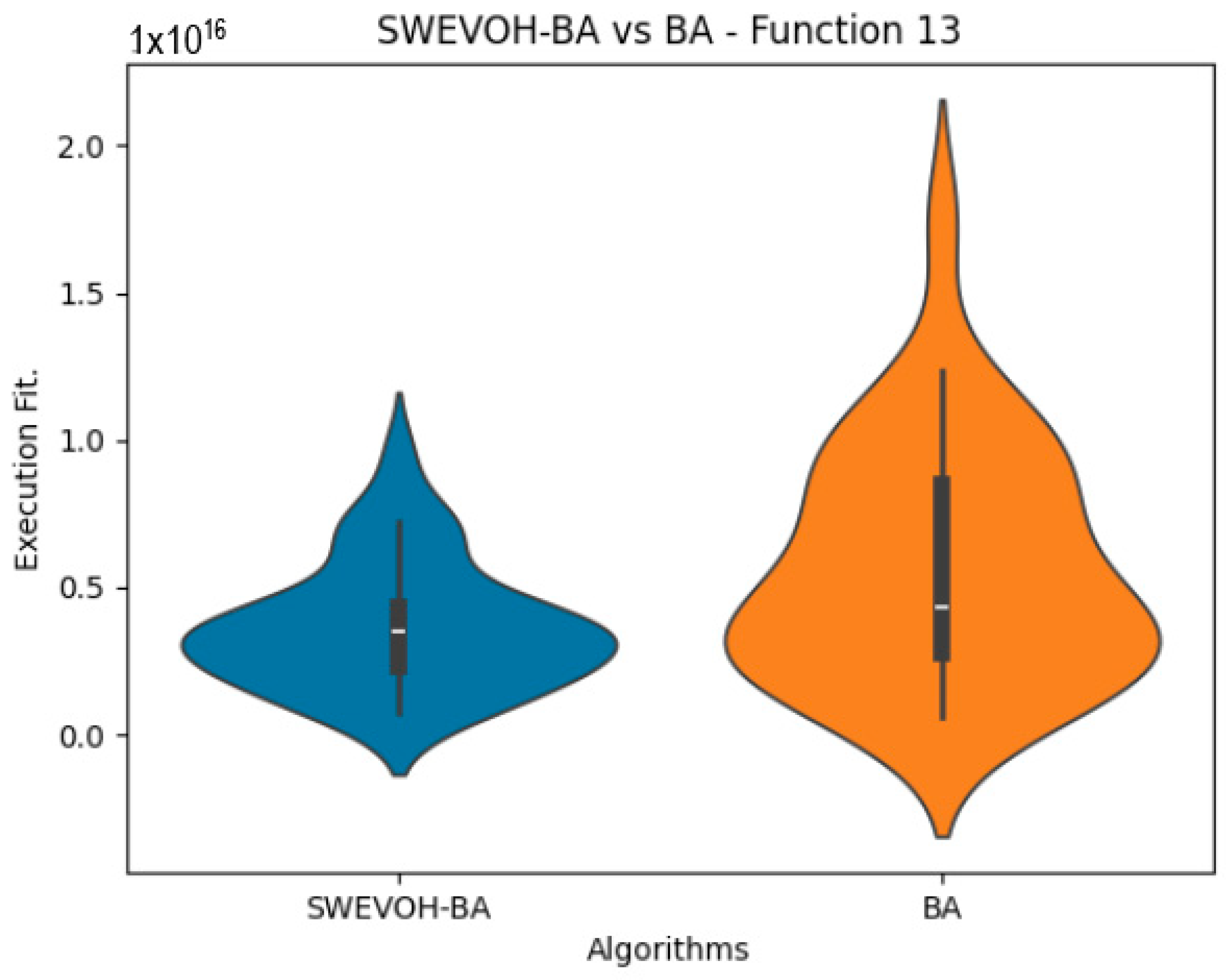
Figure 18.
SWEVO-BA vs. BA distribution on F13.
Figure 18.
SWEVO-BA vs. BA distribution on F13.
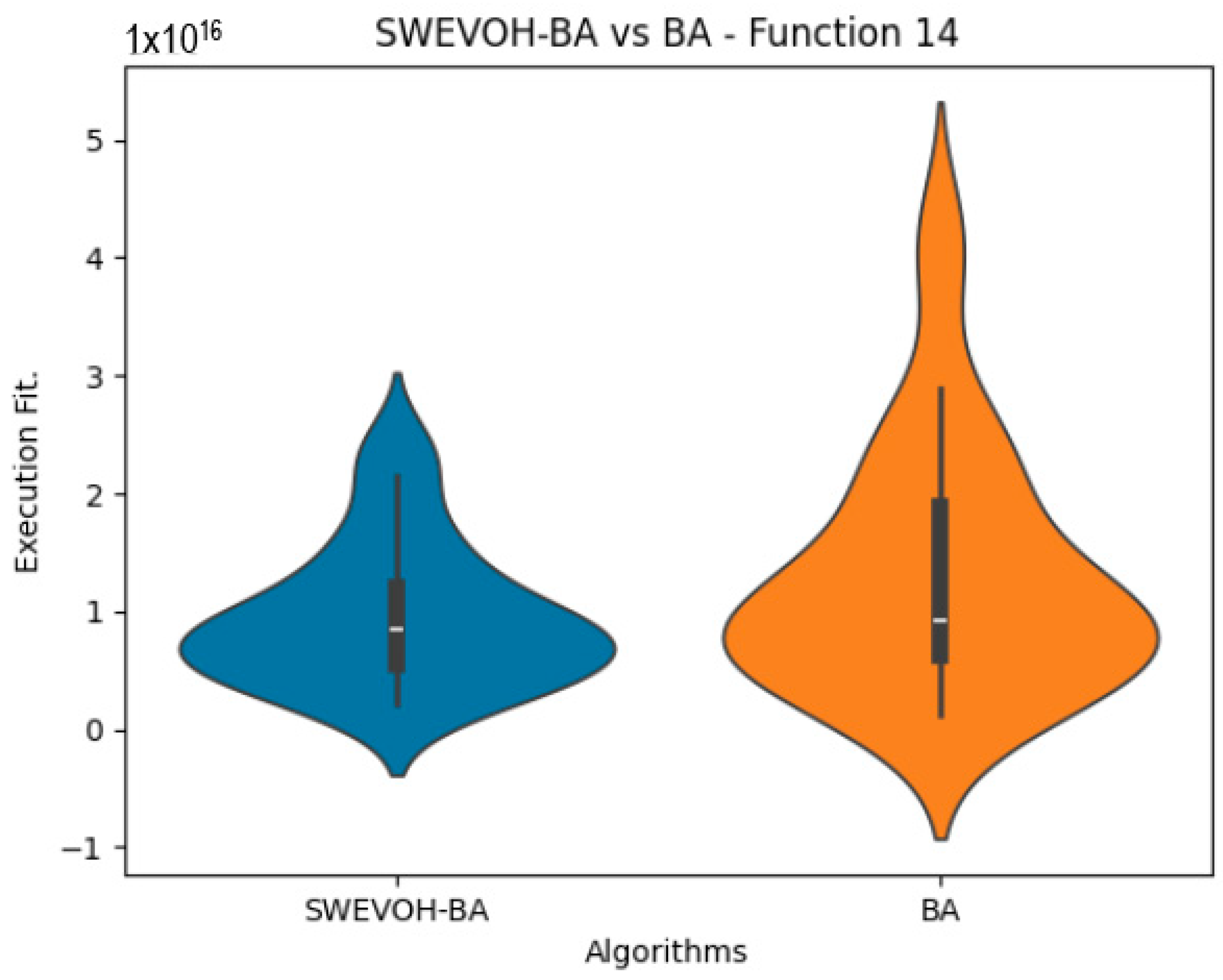
Figure 19.
SWEVO-BA vs. BA distribution on F14.
Figure 19.
SWEVO-BA vs. BA distribution on F14.
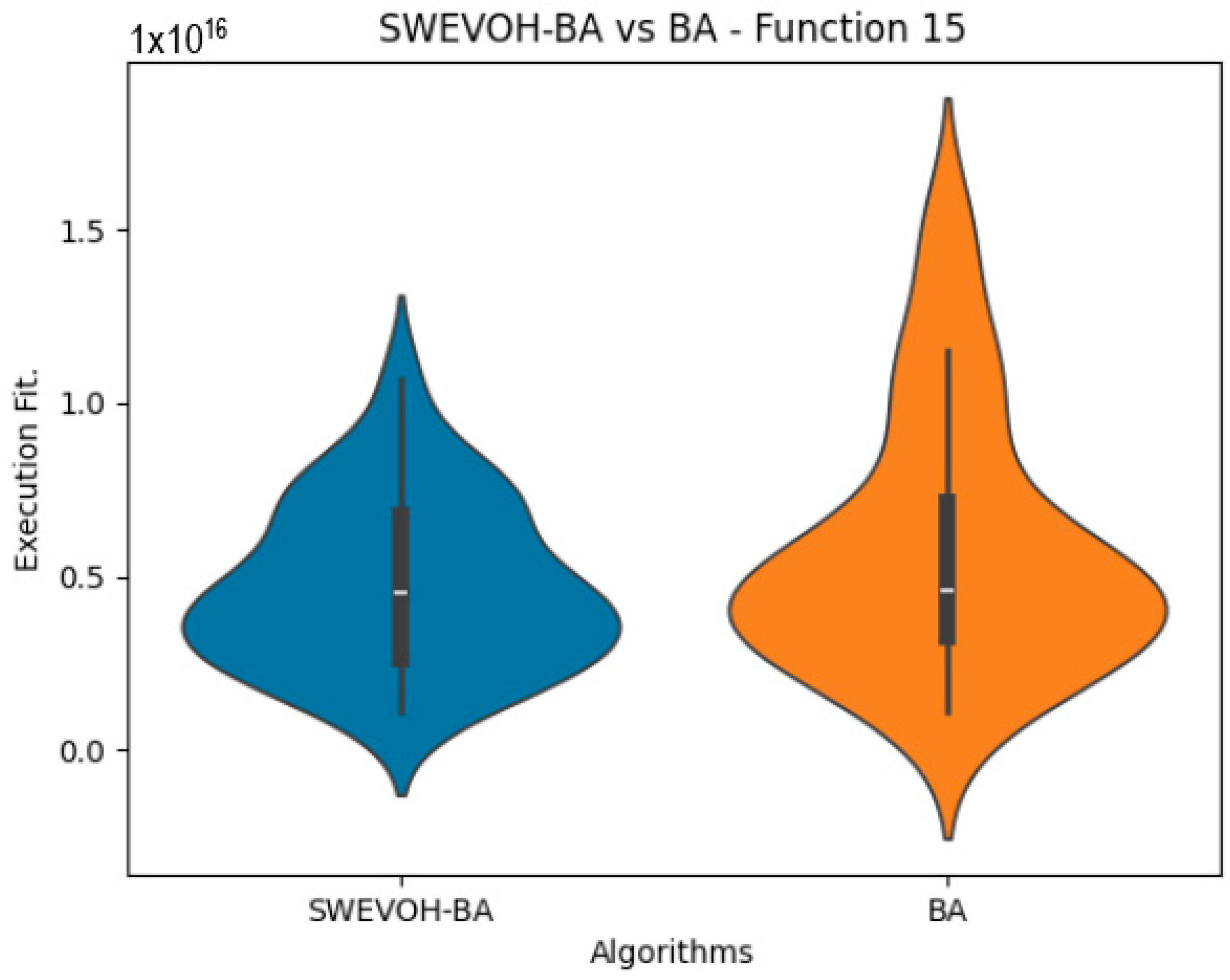
Figure 20.
SWEVO-BA vs. BA distribution on F15.
Figure 20.
SWEVO-BA vs. BA distribution on F15.
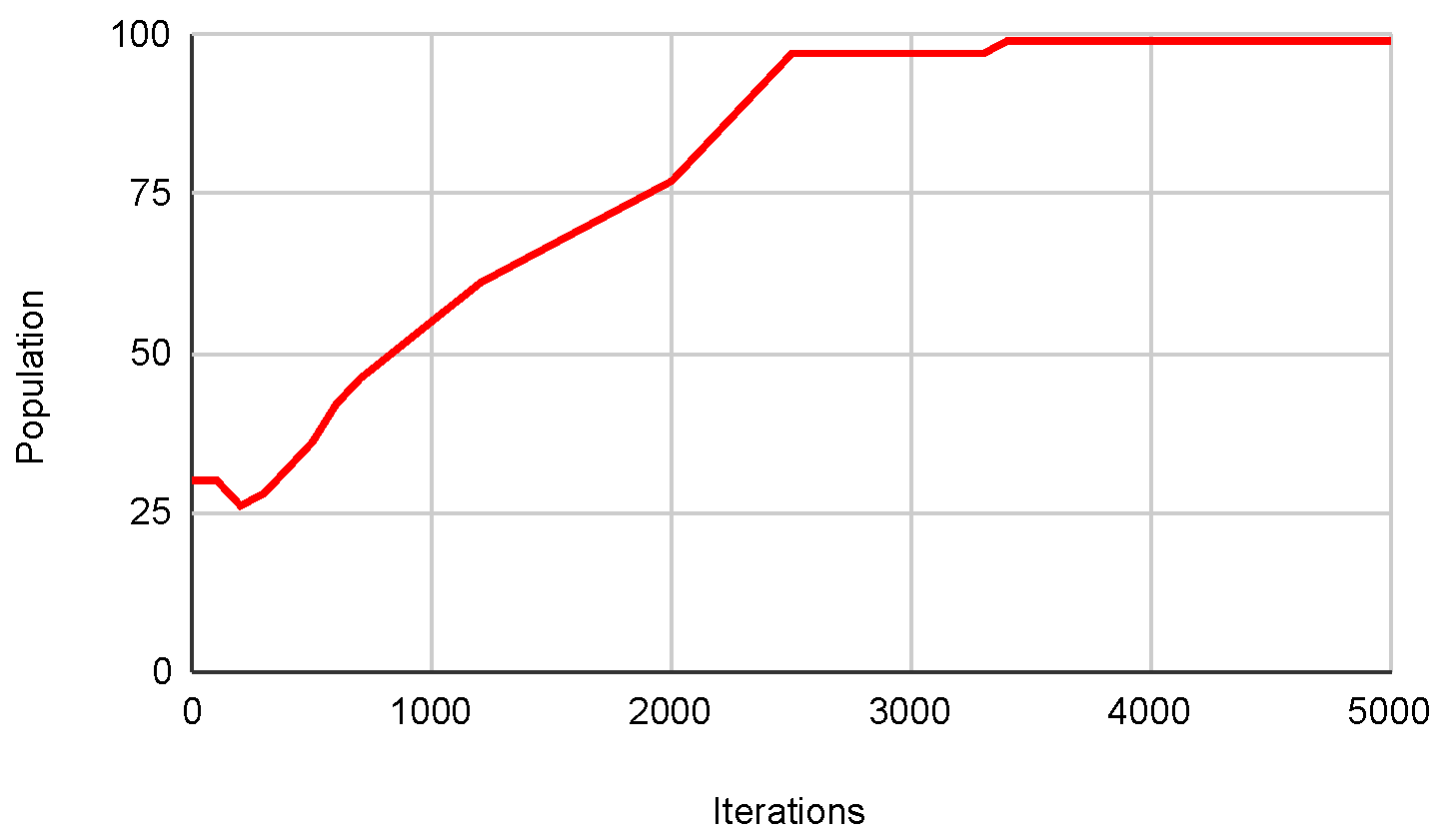
Figure 21.
Pop. in SWEVOH-BA—Func. 2.
Figure 21.
Pop. in SWEVOH-BA—Func. 2.
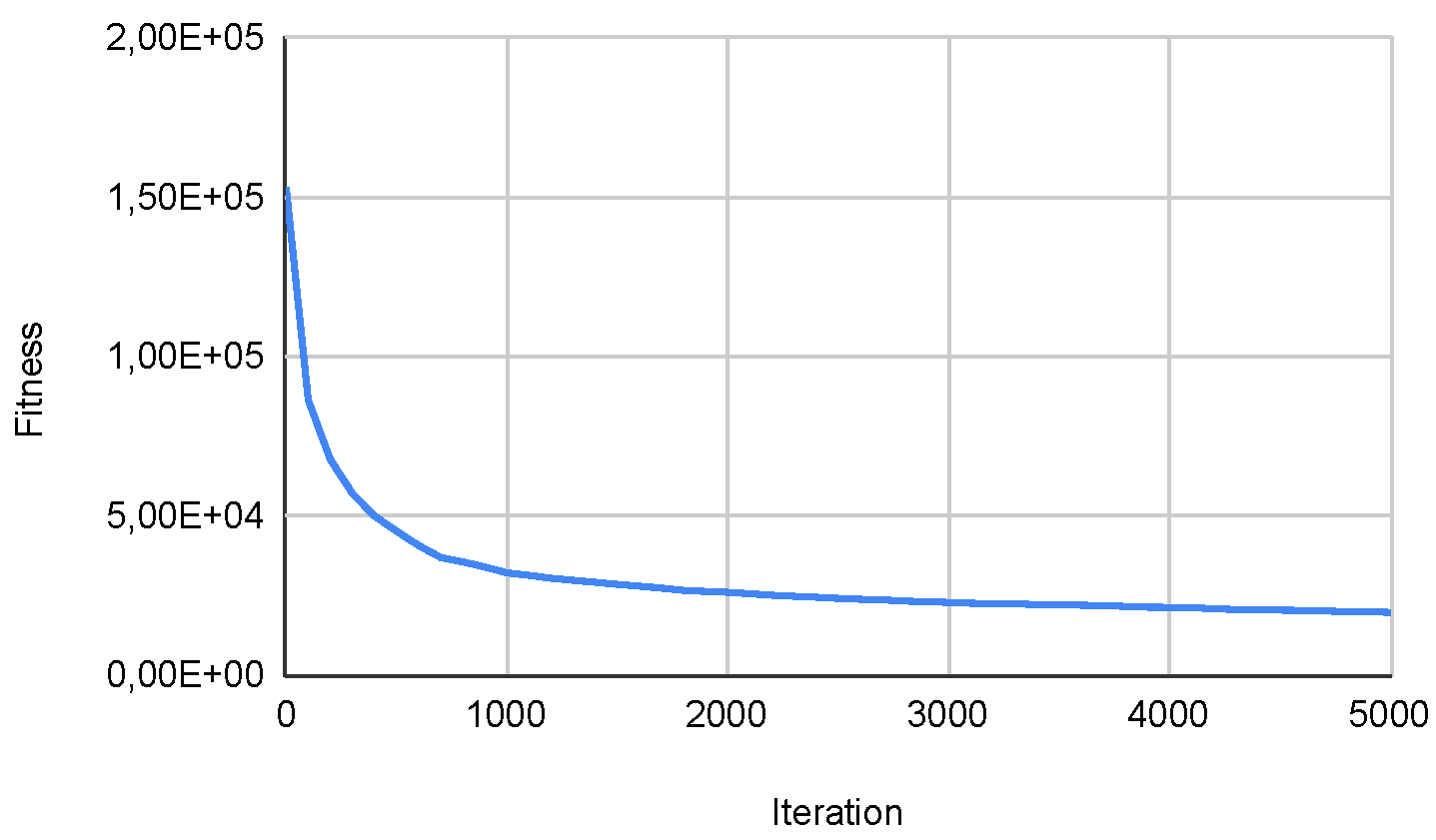
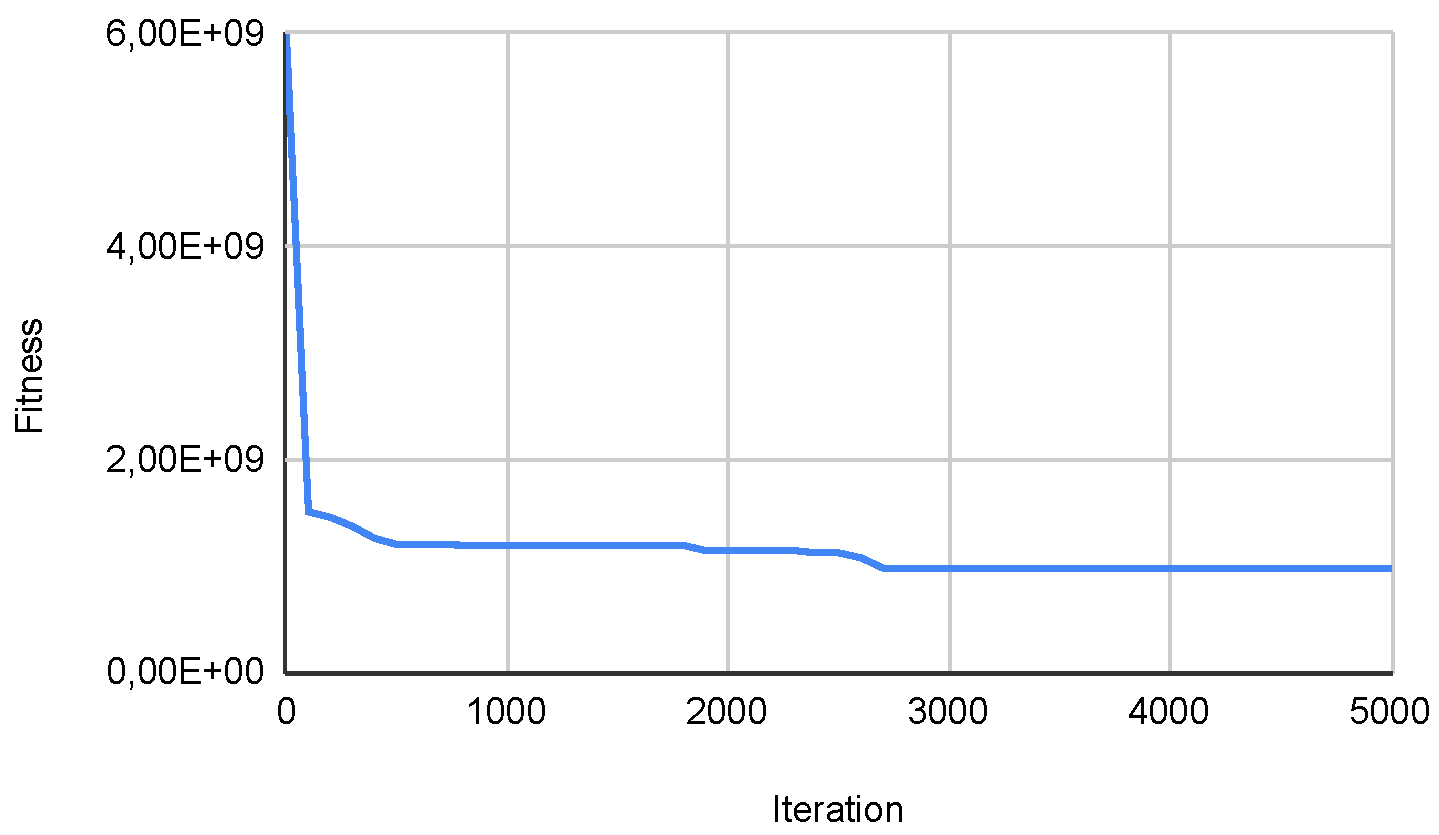
Figure 22.
Convg. in SWEVOH-BA—Func. 2.
Figure 22.
Convg. in SWEVOH-BA—Func. 2.
Figure 23.
Pop. in SWEVOH-CSA—Func. 9.
Figure 23.
Pop. in SWEVOH-CSA—Func. 9.
Figure 24.
Convg. in SWEVOH-CSA—Func. 9.
Figure 24.
Convg. in SWEVOH-CSA—Func. 9.
Table 1.
SWEVOH Parameters for self-tunning population size.
Table 1.
SWEVOH Parameters for self-tunning population size.
| Population Min–Max | Improve % Accepted | Increment Solutions × Cluster | Diff Cluster % Accepted |
|---|
| 10–100 | 10% | 2 | 5% |
Table 2.
SWEVOH CSA Parameters for CEC LSGO.
Table 2.
SWEVOH CSA Parameters for CEC LSGO.
| Population Initial | Abandon Probability | | Max Iterations | and |
|---|
| 30 | 0.25 | 0.01 | 5000 | Acc. to each func. |
Table 3.
SWEVOH BA Parameters for CEC LSGO.
Table 3.
SWEVOH BA Parameters for CEC LSGO.
| Population Initial | Loudness A | Pulse Rate r | | | Max Iterations | and |
|---|
| 30 | 0.95 | 0.1 | 0.9 | 0.5 | 5000 | Acc. to each func. |
Table 4.
SWEVOH PSO Parameters for CEC LSGO.
Table 4.
SWEVOH PSO Parameters for CEC LSGO.
| Population Initial | Max Iterations | and |
|---|
| 30 | 5000 | Acc. to each func. |
Table 5.
Comparison results between Original PSO Algorithm and Autonomous PSO Algorithm.
Table 5.
Comparison results between Original PSO Algorithm and Autonomous PSO Algorithm.
| | Original PSO | Autonomous PSO |
|---|
| Function | Min | Max | Mean | Min | Max | Mean |
|---|
| f1 | 1.69 × | 5.62 × | 2.33 × | 6.63 × | 5.52 × | 7.00 × |
| f2 | 8.51 × | 1.71 × | 9.65 × | 4.25 × | 1.66 × | 6.05 × |
| f3 | 2.15 × | 2.18 × | 2.15 × | 2.13 × | 2.18 × | 2.14 × |
| f4 | 1.94 × | 6.42 × | 8.42 × | 4.10 × | 5.46 × | 5.68 × |
| f5 | 3.03 × | 2.09 × | 4.37 × | 2.49 × | 2.44 × | 4.08 × |
| f6 | 1.05 × | 1.09 × | 1.06 × | 1.04 × | 1.09 × | 1.05 × |
| f7 | 3.74 × | 8.76 × | 1.12 × | 3.12 × | 1.05 × | 9.51 × |
| f8 | 2.51 × | 4.66 × | 3.87 × | 1.10 × | 4.29 × | 2.60 × |
| f9 | 2.34 × | 3.10 × | 3.57 × | 2.06 × | 6.48 × | 3.44 × |
| f10 | 9.24 × | 9.96 × | 9.41 × | 9.09 × | 9.95 × | 9.39 × |
| f11 | 6.55 × | 7.04 × | 8.60 × | 6.83 × | 3.17 × | 4.19 × |
| f12 | 5.86 × | 1.09 × | 6.46 × | 1.75 × | 1.13 × | 1.46 × |
| f13 | 4.30 × | 1.56 × | 2.80 × | 2.00 × | 5.48 × | 3.84 × |
| f14 | 8.90 × | 1.27 × | 9.74 × | 2.00 × | 6.50 × | 4.17 × |
| f15 | 1.64 × | 2.08 × | 3.04 × | 2.61 × | 2.64 × | 2.07 × |
Table 6.
Comparison results between Original Cuckoo Search Algorithm versus Autonomous Cuckoo Search Algorithm.
Table 6.
Comparison results between Original Cuckoo Search Algorithm versus Autonomous Cuckoo Search Algorithm.
| | Original CSA | Autonomous CSA |
|---|
| Function | Min | Max | Mean | Min | Max | Mean |
|---|
| f1 | 2.21 × | 5.88 × | 3.07 × | 3.65 × | 5.67 × | 3.03 × |
| f2 | 2.02 × | 1.67 × | 3.18 × | 1.97 × | 1.70 × | 3.16 × |
| f3 | 2.15 × | 2.18 × | 2.15 × | 2.14 × | 2.18 × | 2.15 × |
| f4 | 3.48 × | 8.15 × | 6.91 × | 2.60 × | 7.74 × | 6.53 × |
| f5 | 1.45 × | 2.33 × | 2.23 × | 9.63 × | 2.24 × | 1.82 × |
| f6 | 1.06 × | 1.09 × | 1.07 × | 1.05 × | 1.09 × | 1.06 × |
| f7 | 2.09 × | 5.67 × | 1.35 × | 1.82 × | 1.19 × | 1.13 × |
| f8 | 3.04 × | 5.95 × | 2.96 × | 1.87 × | 5.07 × | 2.94 × |
| f9 | 1.17 × | 2.44 × | 2.07 × | 7.44 × | 3.24 × | 1.58 × |
| f10 | 9.38 × | 9.95 × | 9.47 × | 9.29 × | 9.93 × | 9.44 × |
| f11 | 1.96 × | 6.58 × | 6.75 × | 2.07 × | 7.34 × | 7.77 × |
| f12 | 5.35 × | 1.08 × | 9.27 × | 7.76 × | 1.10 × | 9.42 × |
| f13 | 5.28 × | 1.91 × | 1.73 × | 3.66 × | 4.11 × | 3.34 × |
| f14 | 7.34 × | 8.14 × | 5.18 × | 5.59 × | 1.46 × | 1.63 × |
| f15 | 7.06 × | 2.13 × | 1.55 × | 1.85 × | 2.18 × | 1.49 × |
Table 7.
Comparison results between Original BA versus SWEVOH -BA.
Table 7.
Comparison results between Original BA versus SWEVOH -BA.
| | Original BAT | Autonomous Bat |
|---|
| Function | Min | Max | Mean | Min | Max | Mean |
|---|
| f1 | 1.71 × | 4.35 × | 2.04 × | 1.59 × | 4.18 × | 2.01 × |
| f2 | 2.86 × | 1.31 × | 3.55 × | 2.55 × | 1.32 × | 3.45 × |
| f3 | 2.16 × | 2.17 × | 2.16 × | 2.16 × | 2.17 × | 2.16 × |
| f4 | 1.49 × | 8.17 × | 6.16 × | 2.16 × | 1.03 × | 5.33 × |
| f5 | 1.15 × | 9.10 × | 1.65 × | 1.12 × | 1.02 × | 1.67 × |
| f6 | 1.06 × | 1.08 × | 1.06 × | 1.06 × | 1.08 × | 1.06 × |
| f7 | 1.49 × | 1.30 × | 6.06 × | 7.55 × | 7.55 × | 5.19 × |
| f8 | 1.96 × | 3.56 × | 2.33 × | 1.74 × | 4.98 × | 2.71 × |
| f9 | 1.02 × | 8.73 × | 1.43 × | 9.79 × | 9.15 × | 1.36 × |
| f10 | 9.39 × | 9.75 × | 9.48 × | 9.36 × | 9.74 × | 9.47 × |
| f11 | 1.41 × | 4.99 × | 3.94 × | 8.98 × | 8.47 × | 4.30 × |
| f12 | 2.38 × | 8.94 × | 3.03 × | 2.22 × | 8.93 × | 3.00 × |
| f13 | 5.75 × | 7.02 × | 4.82 × | 7.85 × | 4.02 × | 3.15 × |
| f14 | 1.18 × | 1.07 × | 7.09 × | 2.18 × | 1.03 × | 6.92 × |
| f15 | 1.10 × | 3.14 × | 3.07 × | 1.09 × | 2.23 × | 3.11 × |
Table 8.
Comparison results in similar hybrid algorithms.
Table 8.
Comparison results in similar hybrid algorithms.
| | Adaptive RSA | CSARSA | CSHADE | SWEVOH-PSO | SWEVOH-CS | SWEVOH-BA |
|---|
| Func. | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std |
|---|
| f1 | 3.61 × | 1.14 × | 2.40 × | 3.45 × | 1.11 × | 1.24 × | 7.00 × | 8.30 × | 3.03 × | 7.81 × | 2.01 × | 3.04 × |
| f2 | 7.96 × | 3.94 × | 5.47 × | 1.19 × | 1.41 × | 9.22 × | 6.05 × | 1.67 × | 3.16 × | 1.97 × | 3.45 × | 1.31 × |
| f3 | 2.14 × | 1.89 × | 2.12 × | 1.05 × | 1.68 × | 6.52 × | 2.14 × | 9.04 × | 2.15 × | 5.61 × | 2.16 × | 1.39 × |
| f4 | 1.24 × | 9.29 × | 5.21 × | 3.28 × | 1.18 × | 1.26 × | 5.68 × | 3.64 × | 6.53 × | 4.63 × | 5.33 × | 6.67 × |
| f5 | 8.63 × | 3.48 × | 5.80 × | 9.49 × | 2.05 × | 3.44 × | 4.08 × | 1.59 × | 1.82 × | 1.70 × | 1.67 × | 9.28 × |
| f6 | 1.06 × | 1.29 × | 1.04 × | 9.18 × | 7.22 × | 3.01 × | 1.05 × | 8.04 × | 1.06 × | 3.52 × | 1.06 × | 2.21 × |
| f7 | 1.87 × | 8.95 × | 4.11 × | 6.76 × | 5.06 × | 1.98 × | 9.51 × | 2.69 × | 1.13 × | 3.05 × | 5.19 × | 4.28 × |
| f8 | 4.42 × | 4.72 × | 3.00 × | 2.47 × | 5.80 × | 4.12 × | 2.60 × | 2.05 × | 2.94 × | 2.66 × | 2.71 × | 3.87 × |
| f9 | 1.03 × | 9.45 × | 5.32 × | 1.56 × | 2.09 × | 2.19 × | 3.44 × | 2.48 × | 1.58 × | 2.14 × | 1.36 × | 7.68 × |
| f10 | 9.48 × | 7.66 × | 9.44 × | 6.81 × | 1.02 × | 4.34 × | 9.39 × | 1.12 × | 9.44 × | 7.76 × | 9.47 × | 5.10 × |
| f11 | 7.29 × | 1.97 × | 1.70 × | 4.62 × | 3.42 × | 1.73 × | 4.19 × | 1.03 × | 7.77 × | 2.07 × | 4.30 × | 4.22 × |
| f12 | 6.34 × | 3.36 × | 2.57 × | 6.39 × | 8.07 × | 2.33 × | 1.46 × | 2.03 × | 9.42 × | 1.58 × | 3.00 × | 8.30 × |
| f13 | 3.58 × | 1.73 × | 3.58 × | 6.87 × | 1.56 × | 6.80 × | 3.84 × | 1.38 × | 3.34 × | 1.04 × | 3.15 × | 2.26 × |
| f14 | 1.89 × | 4.07 × | 7.97 × | 1.82 × | 1.56 × | 8.43 × | 4.17 × | 1.64 × | 1.63 × | 3.93 × | 6.92 × | 5.20 × |
| f15 | 2.50 × | 4.90 × | 9.04 × | 1.17 × | 1.25 × | 5.48 × | 2.07 × | 1.68 × | 1.49 × | 1.29 × | 3.11 × | 1.97 × |
Table 9.
PSO p-values for function 1.
Table 9.
PSO p-values for function 1.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | 7.01 × | × |
Table 10.
PSO p-values for function 2.
Table 10.
PSO p-values for function 2.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | SWS | × |
Table 11.
PSO p-values for function 3.
Table 11.
PSO p-values for function 3.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | 7.01 × |
| PSO | SWS | × |
Table 12.
PSO p-values for function 4.
Table 12.
PSO p-values for function 4.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | 1.86 × |
| PSO | SWS | × |
Table 13.
PSO p-values for function 5.
Table 13.
PSO p-values for function 5.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | 6.21 × |
| PSO | SWS | × |
Table 14.
PSO p-values for function 6.
Table 14.
PSO p-values for function 6.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | 1.67 × |
| PSO | SWS | × |
Table 15.
PSO p-values for function 7.
Table 15.
PSO p-values for function 7.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | SWS | × |
Table 16.
PSO p-values for function 8.
Table 16.
PSO p-values for function 8.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | 1.51 × | × |
Table 17.
PSO p-values for function 9.
Table 17.
PSO p-values for function 9.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | 5.93 × |
| PSO | SWS | × |
Table 18.
PSO p-values for function 10.
Table 18.
PSO p-values for function 10.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | 3.78 × |
| PSO | SWS | × |
Table 19.
PSO p-values for function 11.
Table 19.
PSO p-values for function 11.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | SWS | × |
Table 20.
PSO p-values for function 12.
Table 20.
PSO p-values for function 12.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | 6.97 × | × |
Table 21.
PSO p-values for function 13.
Table 21.
PSO p-values for function 13.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | 2.90 × |
| PSO | SWS | × |
Table 22.
PSO p-values for function 14.
Table 22.
PSO p-values for function 14.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | SWS | × |
Table 23.
PSO p-values for function 15.
Table 23.
PSO p-values for function 15.
| | SWEVOH-PSO | PSO |
|---|
| SWEVOH-PSO | × | SWS |
| PSO | 8.49 × | × |
Table 24.
CSA p-values for function 1.
Table 24.
CSA p-values for function 1.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | 7.01 × | × |
Table 25.
CSA p-values for function 2.
Table 25.
CSA p-values for function 2.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | SWS | × |
Table 26.
CSA p-values for function 3.
Table 26.
CSA p-values for function 3.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | 7.01 × |
| CSA | SWS | × |
Table 27.
CSA p-values for function 4.
Table 27.
CSA p-values for function 4.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | 1.86 × |
| CSA | SWS | × |
Table 28.
CSA p-values for function 5.
Table 28.
CSA p-values for function 5.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | 6.21 × |
| CSA | SWS | × |
Table 29.
CSA p-values for function 6.
Table 29.
CSA p-values for function 6.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | 1.67 × |
| CSA | SWS | × |
Table 30.
CSA p-values for function 7.
Table 30.
CSA p-values for function 7.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | SWS | × |
Table 31.
CSA p-values for function 8.
Table 31.
CSA p-values for function 8.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | 1.51 × | × |
Table 32.
CSA p-values for function 9.
Table 32.
CSA p-values for function 9.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | 5.93 × |
| CSA | SWS | × |
Table 33.
CSA p-values for function 10.
Table 33.
CSA p-values for function 10.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | 3.78 × |
| CSA | SWS | × |
Table 34.
CSA p-values for function 11.
Table 34.
CSA p-values for function 11.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | SWS | × |
Table 35.
CSA p-values for function 12.
Table 35.
CSA p-values for function 12.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | 6.97 × | × |
Table 36.
CSA p-values for function 13.
Table 36.
CSA p-values for function 13.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | 2.90 × |
| CSA | SWS | × |
Table 37.
CSA p-values for function 14.
Table 37.
CSA p-values for function 14.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | SWS | × |
Table 38.
CSA p-values for function 15.
Table 38.
CSA p-values for function 15.
| | SWEVOH-CSA | CSA |
|---|
| SWEVOH-CSA | × | SWS |
| CSA | 8.49 × | × |
Table 39.
BA p-values for function 1.
Table 39.
BA p-values for function 1.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | SWS |
| BA | SWS | × |
Table 40.
BA p-values for function 2.
Table 40.
BA p-values for function 2.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 1.48 × |
| BA | SWS | × |
Table 41.
BA p-values for function 3.
Table 41.
BA p-values for function 3.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 7.43 × |
| BA | SWS | × |
Table 42.
BA p-values for function 4.
Table 42.
BA p-values for function 4.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 3.58 × |
| BA | SWS | × |
Table 43.
BA p-values for function 5.
Table 43.
BA p-values for function 5.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | SWS |
| BA | SWS | × |
Table 44.
BA p-values for function 6.
Table 44.
BA p-values for function 6.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 4.21 × |
| BA | SWS | × |
Table 45.
BA p-values for function 7.
Table 45.
BA p-values for function 7.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 2.96 × |
| BA | SWS | × |
Table 46.
BA p-values for function 8.
Table 46.
BA p-values for function 8.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | SWS |
| BA | SWS | × |
Table 47.
BA p-values for function 9.
Table 47.
BA p-values for function 9.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 4.56 × |
| BA | SWS | × |
Table 48.
BA p-values for function 10.
Table 48.
BA p-values for function 10.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 2.67 × |
| BA | SWS | × |
Table 49.
BA p-values for function 11.
Table 49.
BA p-values for function 11.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | SWS |
| BA | SWS | × |
Table 50.
BA p-values for function 12.
Table 50.
BA p-values for function 12.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | SWS |
| BA | SWS | × |
Table 51.
BA p-values for function 13.
Table 51.
BA p-values for function 13.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | 2.36 × |
| BA | SWS | × |
Table 52.
BA p-values for function 14.
Table 52.
BA p-values for function 14.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | SWS |
| BA | SWS | × |
Table 53.
BA p-values for function 15.
Table 53.
BA p-values for function 15.
| | SWEVOH-BA | BA |
|---|
| SWEVOH-BA | × | SWS |
| BA | SWS | × |