Sine Cosine Algorithm for Elite Individual Collaborative Search and Its Application in Mechanical Optimization Designs
Abstract
:1. Introduction
1.1. The Motivation
1.2. The Contribution
- (1)
- A sine cosine algorithm for elite individual collaborative search was proposed, and SCAEICS exhibits the faster convergence speed, higher convergence accuracy, and effective escape from local optima compared to the SCA;
- (2)
- In the improvement process, the tent chaotic mapping strategy and the hyperbolic tangent function strategy are adopted, which effectively solve the defect of the randomness of the population distribution and balance the global search and local exploitation;
- (3)
- In addition, the concept of the collaborative search of elite individuals is combined with SCA and used to improve the search performance of SCA;
- (4)
- The proposed SCAEICS was validated by 23 benchmark functions, CEC2020 functions, and in two mechanical engineering optimization problems, and it outperformed the basic SCA in terms of convergence performance.
1.3. The Structure of Organization
2. Related Research
3. Basic Sine Cosine Algorithm
3.1. Principle of the Sine Cosine Algorithm
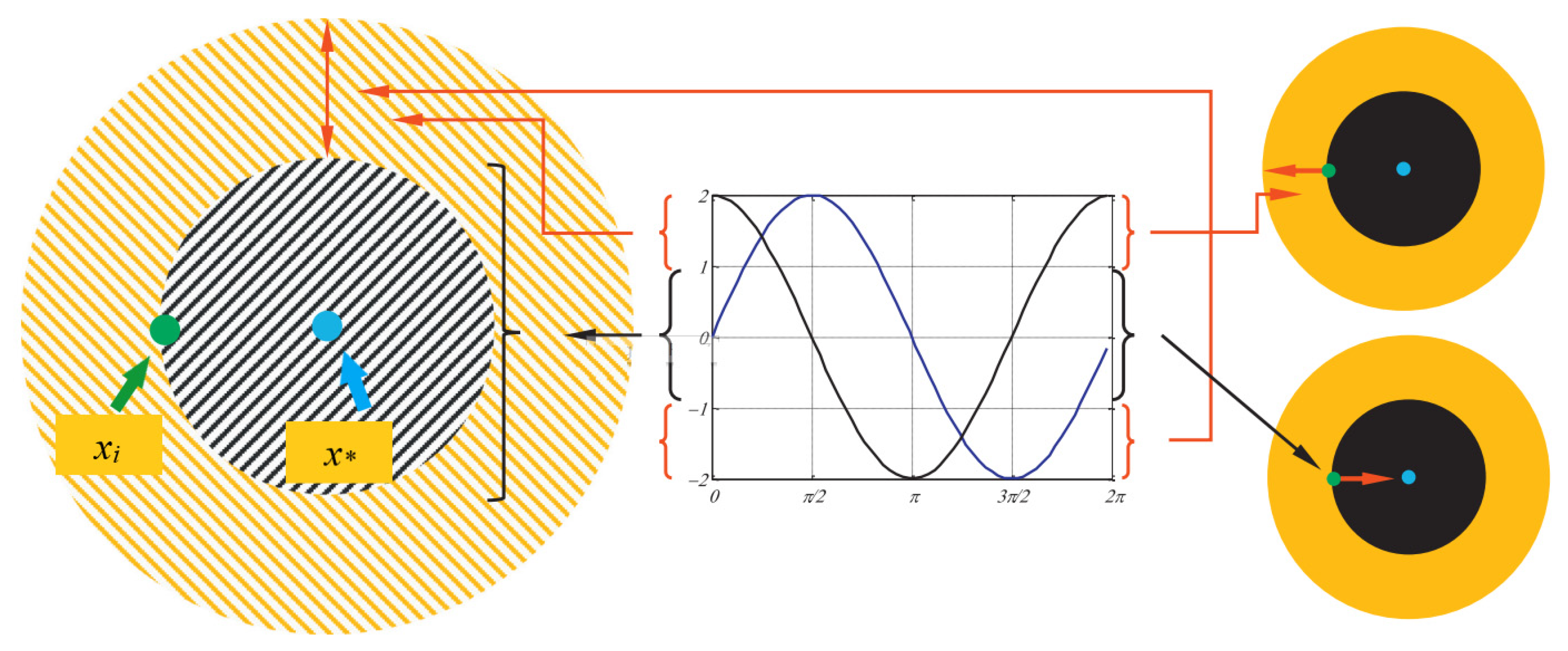
3.2. Disadvantage Analysis of the Sine Cosine Algorithm
4. Sine Cosine Algorithm for Collaborative Search of Elite Individuals
4.1. Modified Strategies of the SCAEICS Algorithm
- (I).
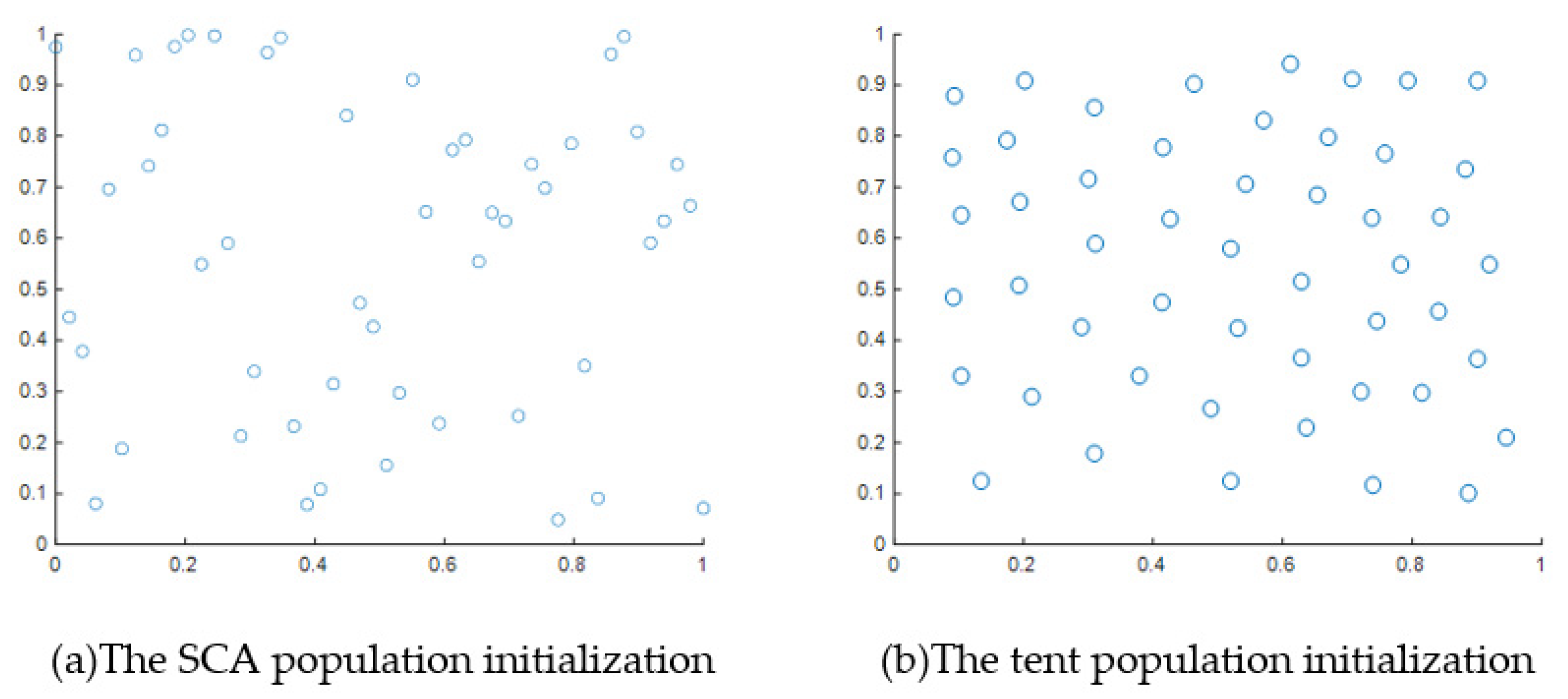
- Tent chaos mapping initialization
- (II).
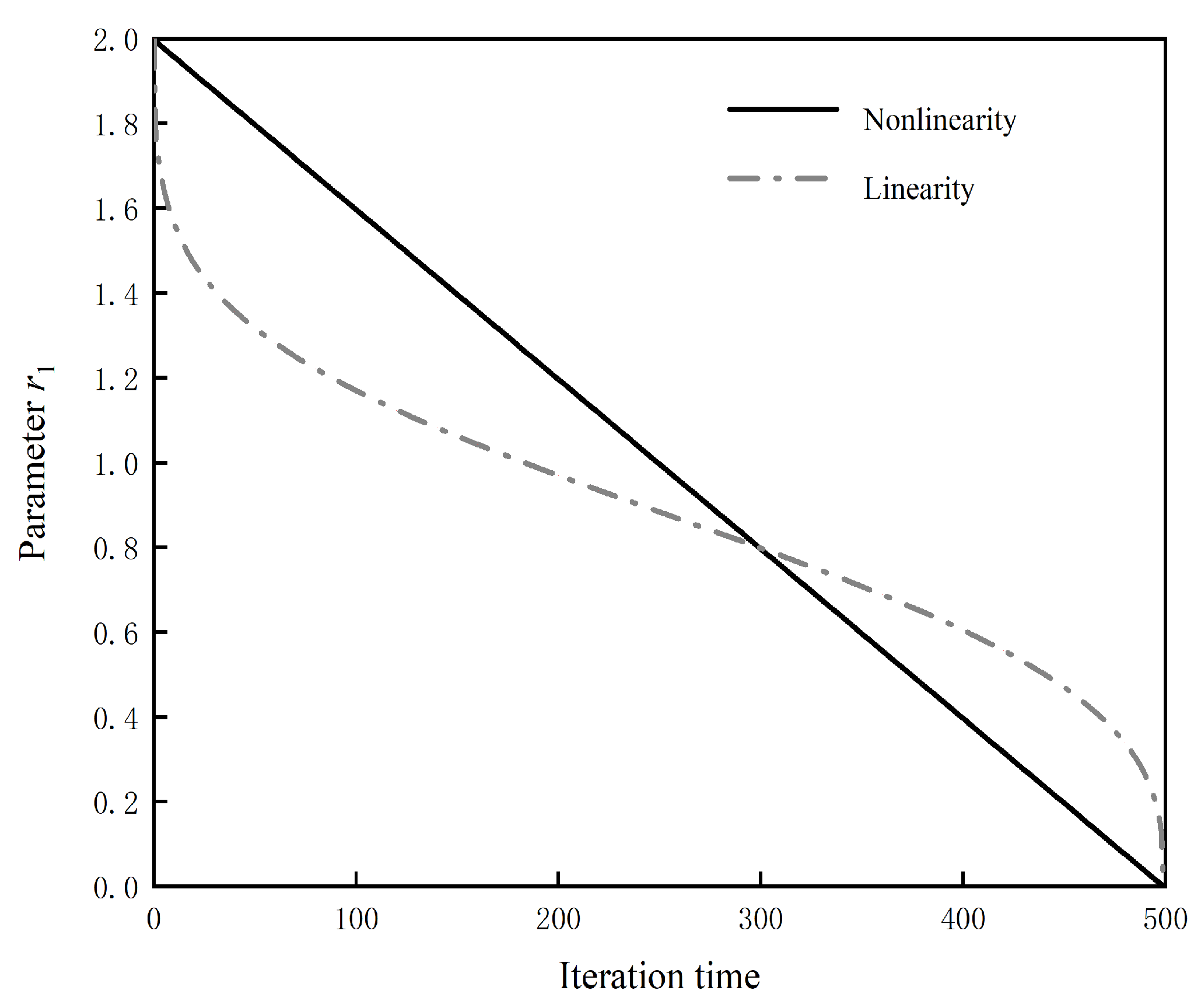
- The hyperbolic tangent function non-linear adjustment control parameter r1
- (III).
- The elite individual collaborative search strategies
- (IV).
- The m-neighborhood locally optimal individual-guided search strategy
- (V).
- The global optimal individual-guided search strategy
- (VI).
- The collaborative search strategy
- (VII).
- The greedy selection strategy
4.2. Algorithm Implementation Steps
4.2.1. Pseudo-Code for the SCAEICS Algorithm
| Algorithm 1: Sine cosine algorithm for the collaborative search of elite individuals (SCAEICS) |
| Enter parameters and initialize. |
| Set the population size N, use the tent chaos mapping strategy to generate the initialized population, (xi, i = 1, 2, …, N), and the maximum number of iterations T. Set the neighborhood individuals m, integer h, and spatial dimension D (where the function f14~f23 is a fixed dimension). |
| Calculate the individual fitness value f(xi), i = 1, 2, …, N) and find the globally optimal individual and its location. |
| t = 0; |
| While (t < T) do |
| Identifying locally optimal individuals and their locations. |
| for i = 1 to N do |
| Calculate the value of the control parameter r1 according to Equation (6). |
| if (t mod 2==0) |
| The SCA search strategy is executed according to Equation (1). |
| else if (h > 0.5) |
| Execute the m-neighborhood locally optimal individual-guided search strategy according to Equation (7). |
| else if |
| Execute the globally optimal individual guided search strategy according to Equation (8). |
| end if |
| end if |
| end if |
| Execute the greedy selection strategy according to Equation (9). |
| end for |
| Updating the current optimal individual and position. |
| t = t + 1; |
| end while |
4.2.2. Flowchart of the SCAEICS Algorithm
4.3. Analysis of Algorithm Convergence and Diversity
5. Simulation Experiments
- (I).
- Benchmark functions and parameter settings
- (II).
- Parameter settings of other algorithms involved in the following comparison
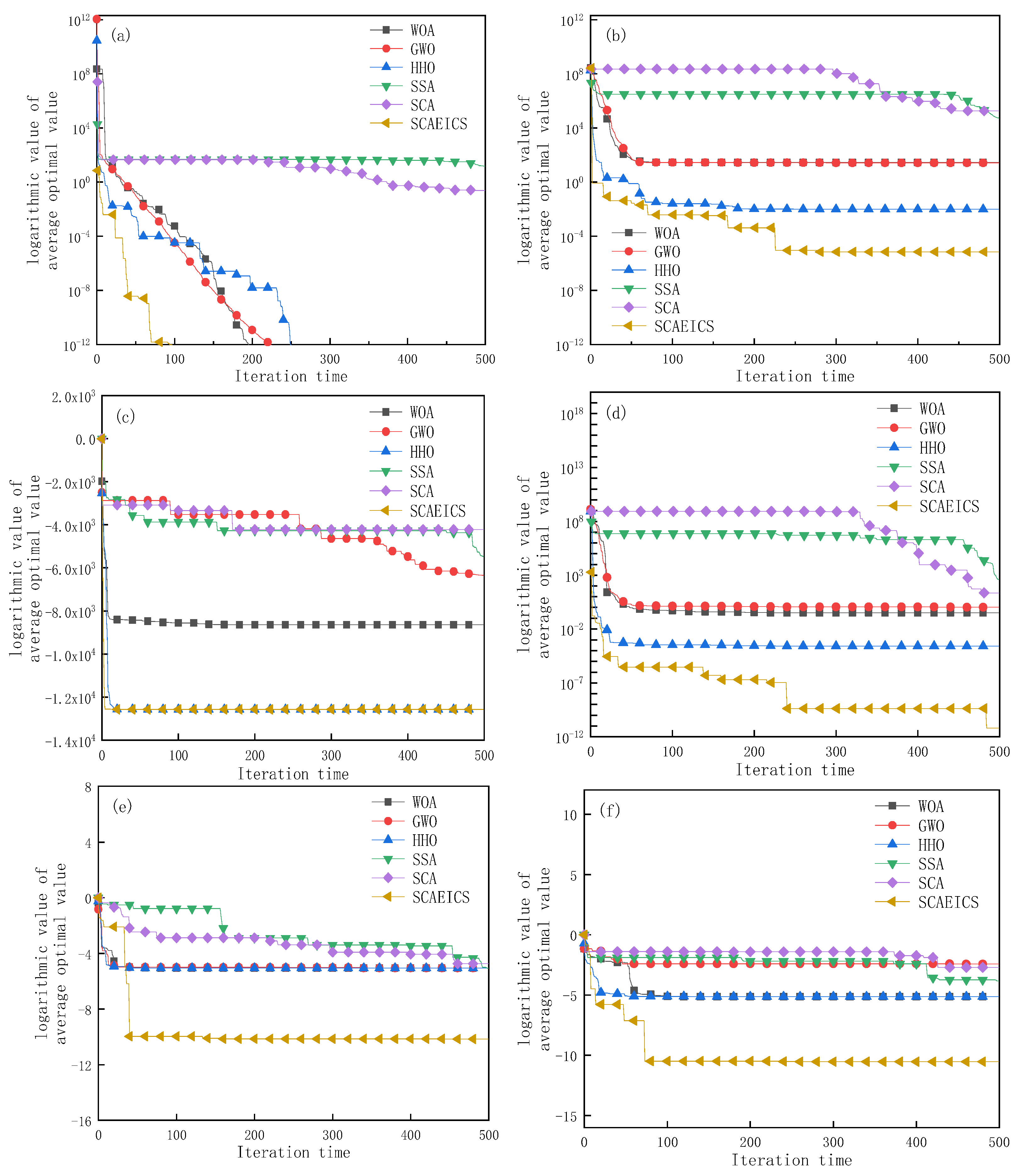
5.1. Comparative Analysis of the SCAEICS with the SCA and Other Intelligent Algorithms
5.2. Comparative Analysis of the SCAEICS with Other Improved Algorithms
5.3. Comparison and Analysis of the SCAEICS with Other Chaos-Based Algorithms
5.4. Analysis of Important Parameters
5.5. Time Complexity Analysis
6. Applications
- (I).
- Mechanical design optimization
- (II).
- Example of mechanical design optimization
- (III).
- Example of optimized design of a cantilever beam
- (IV).
- Modified strategies of SFLACF algorithm: Example of optimized design of a three-rod truss
7. Discussion
7.1. The Practical Managerial Significance (PMS)
7.2. Open Research Questions (ORQ)
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Aaha, B.; Sm, C.; Hf, D.; Ia, D.; Mm, E.; Hc, F. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Arasteh, B.; Sadegi, R.; Arasteh, K.; Gunes, P.; Kiani, F.; Torkamanian-Afshar, M. A bioinspired discrete heuristic algorithm to generate the effective structural model of a program source code. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 101655. [Google Scholar] [CrossRef]
- Amir, S.; Farzad, K. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Kiani, F.; Anka, F.A.; Erenel, F. PSCSO: Enhanced sand cat swarm optimization inspired by the political system to solve complex problems. Adv. Eng. Softw. 2023, 178, 103423. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z.; Mirjalili, S.; Khodadadi, N.; Ge, Q. Quadratic Interpolation Optimization (QIO): A new optimization algorithm based on generalized quadratic interpolation and its applications to real-world engineering problems. Comput. Methods Appl. Mech. Eng. 2023, 417, 116446. [Google Scholar] [CrossRef]
- Nadimi, S.; Mohammad, H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 917–940. [Google Scholar] [CrossRef]
- Yang, W.; Xia, K.; Fan, S.; Wang, L.; Li, T.; Zhang, J.; Feng, Y. A Multi-Strategy Whale Optimization Algorithm and Its Application. Eng. Appl. Artif. Intell. 2022, 108, 111–139. [Google Scholar] [CrossRef]
- Zhang, C.; Han, Y.; Wang, Y.; Li, J.; Gao, K. A Distributed Blocking Flowshop Scheduling with Setup Times Using Multi-Factory Collaboration Iterated Greedy Algorithm. Mathematics 2023, 11, 581. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J.; Fan, H. New method of traffic flow forecasting based on quantum particle swarm optimization strategy for intelligent transportation system. Int. J. Commun. Syst. 2020, 34, e4647.1–e4647.20. [Google Scholar] [CrossRef]
- Arasteh, B.; Fatolahzadeh, A.; Kiani, F. Savalan: Multi objective and homogeneous method for software modules clustering. J. Softw. Evol. Process 2022, 34, e2408. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F.; Allahviranloo, T.; Fernandez-Gamiz, U.; Noeiaghdam, S. Optimal data transmission and pathfinding for WSN and decentralized IoT systems using I-GWO and Ex-GWO algorithms. Alex. Eng. J. 2023, 63, 339–357. [Google Scholar] [CrossRef]
- Kiani, F.; Seyyedabbasi, A.; Nematzadeh, S. Improving the performance of hierarchical wireless sensor networks using the metaheuristic algorithms: Efficient cluster head selection. Sens. Rev. 2021, 41, 368–381. [Google Scholar] [CrossRef]
- Kiani, F.; Randazzo, G.; Yelmen, I.; Seyyedabbasi, A.; Nematzadeh, S.; Anka, F.A.; Erenel, F.; Zontul, M.; Lanza, S.; Muzirafuti, A. A Smart and Mechanized Agricultural Application: From Cultivation to Harvest. Appl. Sci. 2022, 12, 6021. [Google Scholar] [CrossRef]
- Singh, N.; Bhatia, O.S. Optimization of Process Parameters in Die Sinking EDM—A Review. Int. J. Sci. Technol. Eng. 2016, 2, 808–813. [Google Scholar]
- Jaiswal, A.K.; Siddique, M.H.; Paul, A.R.; Samad, A. Surrogate-based design optimization of a centrifugal pump impeller. Eng. Optim. 2022, 54, 1395–1412. [Google Scholar] [CrossRef]
- Shadkam, E. Cuckoo optimization algorithm in reverse logistics: A network design for COVID-19 waste management. Waste Manag. Res. 2022, 40, 458–469. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Kiani, F.; Nematzadeh, S.; Anka, F.A.; Findikli, M.A. Chaotic Sand Cat Swarm Optimization. Mathematics 2023, 11, 2340. [Google Scholar] [CrossRef]
- Duan, J.; Jiang, Z. Joint Scheduling Optimization of a Short-Term Hydrothermal Power System Based on an Elite Collaborative Search Algorithm. Energies 2022, 15, 4633. [Google Scholar] [CrossRef]
- Jiang, Z.; Duan, J.; Xiao, Y.; He, S. Elite collaborative search algorithm and its application in power generation scheduling optimization of cascade reservoirs. J. Hydrol. 2022, 615, 128684. [Google Scholar] [CrossRef]
- Wu, L.; Li, Z.; Ge, W.; Zhao, X. An adaptive differential evolution algorithm with elite gaussian mutation and bare-bones strategy. Math. Biosci. Eng. 2022, 19, 8537–8553. [Google Scholar] [CrossRef]
- Qsha, C.; Hs, B.; Sas, A.; Ms, A. Q-Learning embedded sine cosine algorithm (QLESCA). Expert Syst. Appl. 2022, 193, 0957–0972. [Google Scholar]
- Zhao, Y.Q.; Zou, F.; Chen, D.B. A new bare bone sine cosine algorithm based on neighborhood structure. J. Chang. Norm. Univ. 2019, 88, 16–25. [Google Scholar]
- Hussien, G.; Liang, G.; Chen, H.; Lin, H. A double adaptive random spare reinforced sine cosine algorithm. Comput. Model Eng. 2023, 136, 2267–2289. [Google Scholar] [CrossRef]
- Chao, Z.; Yi, Y. Improved sine cosine algorithm for large-scale optimization problems. J. Shenzhen Univ. Sci. Eng. 2022, 39, 684–692. [Google Scholar]
- Kun, Y.; Qingliang, J.; Zilong, L.; Qin, J.Y. Positioning of characterstic spectral peaks based on improved sine cosine algorithm. Acta Opt. Sin. 2019, 39, 411–417. [Google Scholar]
- Elaziz, M.A.; Oliva, D.; Xiong, S. An Improved Opposition-Based Sine Cosine Algorithm for Global Optimization. Expert Syst. Appl. 2017, 90, 484–500. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M. An improved sine-cosine algorithm based on orthogonal parallel information for global optimization. Soft Comput. Meth. Appl. 2019, 23, 7135–7161. [Google Scholar] [CrossRef]
- Wu, W.; Yuhui, W.; Zhiyun, W. Text feature selection based on sine and cosine algorithm. Comput. Eng. Sci. 2022, 44, 1467–1473. [Google Scholar]
- Verma, D.; Soni, J.; Kalathia, D.; Bhattacharjee, K. Sine cosine algorithm for solving economic load dispatch problem with penetration of renewables. Intern. Swarm Intell. Res. 2022, 13, 1–21. [Google Scholar] [CrossRef]
- Belazi, A.; Jimenomorenilla, A.; Sanchezromero, J.L. Enhanced parallel sine cosine algorithm for constrained and unconstrained optimization. Mathematics 2022, 10, 1166. [Google Scholar] [CrossRef]
- Long, W.; Wu, T.; Liang, X.; Xu, S. Solving high-dimensional global optimization problems using an improved sine cosine algorithm. Expert Syst. Appl. 2019, 123, 108–126. [Google Scholar] [CrossRef]
- Li, C.; Luo, Z.; Song, Z.; Yang, F.; Fan, J.; Liu, P.X. An enhanced brain storm sine cosine algorithm for global optimization problems. IEEE Access 2019, 5, 102–113. [Google Scholar] [CrossRef]
- Cheng, J.; Duan, Z. Cloud model based sine cosine algorithm for solving optimization problems. Evol. Intell. 2019, 12, 503–514. [Google Scholar] [CrossRef]
- Ning, Z.; He, X.; Yang, X.; Zhao, X. Sine cosine algorithm embedded with differential evolution and inertia weight. Trans. Micro. Tech. 2022, 41, 131–135. [Google Scholar]
- Guo, G.; Zhang, N. A hybrid multi-objective firefly-sine cosine algorithm for multi-objective optimization problem. Int. J. Comput. Inf. Eng. 2020, 10, 71–82. [Google Scholar]
- Dida, H.; Charif, F.; Benchabane, A. Image registration of computed tomography of lung infected with COVID-19 using an improved sine cosine algorithm. Med. Biol. Eng. Comput. 2022, 60, 2521–2535. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Guo, Q. Modified whale optimization algorithm based on tent chaotic mapping and its application in structural optimization. KSCE J. Civ. Eng. 2020, 24, 3703–3713. [Google Scholar] [CrossRef]
- Xiao, F.; Honma, Y.; Kono, T. A simple algebraic interface capturing scheme using hyperbolic tangent function. Int. J. Numer. Methods Fluids 2005, 48, 1023–1040. [Google Scholar] [CrossRef]
- Elkhateeb, N.; Badr, R. A novel variable population size artificial bee colony algorithm with convergence analysis for optimal parameter tuning. Int. J. Comput. Intell. Appl. 2017, 16, 175–189. [Google Scholar] [CrossRef]
- Bansal, J.C.; Gopal, A.; Nagar, A.K. Stability analysis of Artificial Bee Colony optimization algorithm. Swarm Evol. Comput. 2018, 41, 9–19. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yun, G.J.; Yang, X.-S.; Talatahari, S. Chaos-enhanced accelerated particle swarm optimization. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 327–340. [Google Scholar] [CrossRef]
- Yuanxia, S.; Xuefeng, Z.; Xin, F.; Xiaoyan, W. A multi-scale sine cosine algorithm for optimization problems. Control Decis. 2022, 37, 2860–2868. [Google Scholar] [CrossRef]
- Wenyan, G.; Yuan, W.; Fang, D.; Ting, L. Alternating sine cosine algorithm based on elite chaotic search strategy. Control Decis. 2019, 34, 1654–1662. [Google Scholar] [CrossRef]
- Kumar, S.; Yildiz, B.S.; Mehta, P.; Panagant, N.; Sait, S.M.; Mirjalili, S.; Yildiz, A.R. Chaotic marine predators algorithm for global optimization of real-world engineering problems. Knowl.-Based Syst. 2023, 261, 110192. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K.; Engelbrecht, A.P. A memory guided sine cosine algorithm for global optimization. Eng. Appl. Artif. Intell. 2020, 93, 476–489. [Google Scholar] [CrossRef]
- Xiaojuan, L.; Lianguo, W. A sine cosine algorithm based on differential evolution. Chin. J. Eng. 2020, 42, 1674–1684. [Google Scholar]
- Yang, J.; Liu, Z.; Zhang, X.; Hu, G. Elite Chaotic Manta Ray Algorithm Integrated with Chaotic Initialization and Opposition-Based Learning. Mathematics 2022, 10, 2960. [Google Scholar] [CrossRef]
- Cong, S. Mechanical optimization design. China’s Foreign Trade 2011, 13, 12–25. [Google Scholar]
- Canbaz, B.; Yannou, B.; Yvars, P.A.B.T.-I. A new framework for collaborative set-based design: Application to the design problem of a hollow cylindrical cantilever beam. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; pp. 1345–1356. [Google Scholar]
- Teknillinen, T.; Konstruktiotekniikan, Y.; Tutkimusraportti, L. Multicriterion compliance minimization and stress-constrained minimum weight design of a three-bar truss. Astrophysical 2011, 6, 321–332. [Google Scholar]

| Functions | Function Name | Dimensionality | Search Space | Theoretical Optimal Value |
|---|---|---|---|---|
| f1 | Sphere | 30 | [−100,100] | 0 |
| f2 | Schwefel 2.22 | 30 | [−10,10] | 0 |
| f3 | Schwefel 1.2 | 30 | [−100,100] | 0 |
| f4 | Schwefel 2.21 | 30 | [−100,100] | 0 |
| f5 | Rosenbrock | 30 | [−30,30] | 0 |
| f6 | Step | 30 | [−100,100] | 0 |
| f7 | quarticWN | 30 | [−1.28,1.28] | 0 |
| f8 | Schwefel 2.26 | 30 | [−500,500] | −12,569.48 |
| f9 | Rastrigin | 30 | [−5.12,5.12] | 0 |
| f10 | Ackley | 30 | [−32,32] | 0 |
| f11 | Griewank | 30 | [−600,600] | 0 |
| f12 | Penalized1 | 30 | [−50,50] | 0 |
| f13 | Penalized2 | 30 | [−50,50] | 0 |
| f14 | Shekel foxholes | 2 | [−65,65] | 1 |
| f15 | Kowalk | 4 | [−5,5] | 0.0003075 |
| f16 | Six_hump camel_back | 2 | [−5,5] | −1.0316 |
| f17 | Branin | 2 | [−5,5] | 0.398 |
| f18 | Goldstein_price | 2 | [0,2] | 3 |
| f19 | Hartman1 | 3 | [0,1] | −3.86 |
| f20 | Hartman2 | 6 | [0,1] | −3.32 |
| f21 | Sheke_5 | 4 | [0,10] | −10.1532 |
| f22 | Sheke_7 | 4 | [0,10] | −10.4028 |
| f23 | Sheke_10 | 4 | [0,10] | −10.5363 |
| Functions | Function Name | Dimensionality | Search Space | Theoretical Optimal Value | |
|---|---|---|---|---|---|
| Unimodal Function | F1 | Shifted and Rotated Bent Cigar Function | 10 | [−100,100] | 100 |
| Basic Functions | F2 | Shifted and Rotated Schwefel’s Function | 10 | [−100,100] | 1100 |
| F3 | Shifted and Rotated Lunacek bi-Rastrigin Function | 10 | [−100,100] | 700 | |
| F4 | Expanded Rosenbrock’s plus Griewangk’s Function | 10 | [−100,100] | 1900 | |
| Hybri Functions | F5 | Hybrid Function 1 | 10 | [−100,100] | 1700 |
| F6 | Hybrid Function 2 | 10 | [−100,100] | 1600 | |
| F7 | Hybrid Function 3 | 10 | [−100,100] | 2100 | |
| Composition Functions | F8 | Composition Function 1 | 10 | [−100,100] | 2200 |
| F9 | Composition Function 2 | 10 | [−100,100] | 2400 | |
| F10 | Composition Function 3 | 10 | [−100,100] | 2500 |
| Algorithms | Parameter Settings |
|---|---|
| WOA | a ∈ [0,2]; b = 1; l ∈ [−2,1] |
| GWO | a ∈ [0,2], r1 ∈ [0,1]; r2 ∈ [0,1] |
| HHO | E0 ∈ [−1,1]; E ∈ [0,1]; r ∈ [0,1]; u ∈ [0,1]; v ∈ [0,1]; β =1.5 |
| SSA | C1 ∈ [2,0]; C2 ∈ [0,1]; C3 ∈ [0,1] |
| SCA | r2 ∈ [0,2π]; r3 ∈ [−2,2]; r4 ∈ [0,1]; a = 2 |
| COSCA | η = 1; astart = 1; aend = 0; pr = 0.1 |
| SCADE | nlim = 50; cr = 0.3; kmax = 3; h = 10; δ2max = 0.6; δ2min = 0.0001; a = 2 |
| MGSCA | r2 ∈ [0,2π]; r3 ∈ [−2,2]; r4 ∈ [0,1]; a = 2 |
| CSCA | r2 ∈ [0,2π]; r3 ∈ [−2,2]; r4 ∈ [0,1] |
| CMRFO | S ∈ 2, p ∈ 0.1 |
| CMPA | r ∈ [0,1], p ∈ 0.5, v ∈ 0.1, u ∈ [0,1], FADs ∈ 0.2 |
| Function | Evaluation Criterion | WOA | GWO | HHO | SSA | SCA | SCAEICS |
|---|---|---|---|---|---|---|---|
| f1 | Ave | 2.02 × 10−72 | 1.39 × 10−27 | 3.95 × 10−96 | 1.70 × 10−7 | 8.10 × 101 | 9.72 × 10−232 |
| Std | 1.09 × 10−71 | 1.59 × 10−27 | 1.66 × 10−95 | 2.11 × 10−7 | 1.15 × 102 | 0 | |
| f2 | Ave | 2.16 × 10−50 | 1.37 × 10−16 | 9.15 × 10−51 | 1.85 | 1.76 × 10−1 | 3.10 × 10−123 |
| Std | 1.10 × 10−49 | 8.53 × 10−17 | 3.99 × 10−50 | 1.59 | 2.57 × 10−1 | 1.69 × 10−122 | |
| f3 | Ave | 4.47 × 104 | 3.16 × 10−5 | 2.85 × 10−80 | 1.57 × 103 | 1.42 × 104 | 3.71 × 10−230 |
| Std | 1.53 × 104 | 1.44 × 10−4 | 1.20 × 10−79 | 1.15 × 103 | 7.42 × 103 | 0 | |
| f4 | Ave | 4.64 × 101 | 9.54 × 10−7 | 2.51 × 10−50 | 1.06 × 101 | 4.80 × 101 | 1.45 × 10−124 |
| Std | 2.86 × 101 | 1.20 × 10−6 | 7.44 × 10−50 | 3.62 | 1.01 × 101 | 7.73 × 10−124 | |
| f5 | Ave | 2.80 × 101 | 2.72 × 101 | 1.19 × 10−2 | 1.13 × 102 | 3.43 × 105 | 3.29 × 10−8 |
| Std | 4.50 × 10−1 | 7.31 × 10−1 | 1.69 × 10−2 | 1.41 × 102 | 5.99 × 105 | 3.77 × 10−8 | |
| f6 | Ave | 3.17 × 10−1 | 7.43 × 10−1 | 9.25 × 10−5 | 2.55 × 10−7 | 1.04 × 102 | 2.62 × 10−10 |
| Std | 1.82 × 10−1 | 4.07 × 10−1 | 1.73 × 10−4 | 3.82 × 10−7 | 1.45 × 102 | 1.12 × 10−9 | |
| f7 | Ave | 3.10 × 10−3 | 2.06 × 10−3 | 1.66 × 10−4 | 1.68 × 10−1 | 3.02 × 10−1 | 7.65 × 10−6 |
| Std | 4.58 × 10−3 | 1.36 × 10−3 | 1.75 × 10−4 | 5.77 × 10−2 | 4.11 × 10−1 | 7.67 × 10−6 | |
| f8 | Ave | −10,672.1305 | −6090.7165 | −12,554.3583 | −6374.5963 | −3785.7654 | −12,569.4865 |
| Std | 1704.9911 | 887.893 | 76.2766 | 743.4421 | 273.8353 | 0.00029551 | |
| f9 | Ave | 0 | 2.30 | 0 | 6.18 × 101 | 5.28 × 101 | 0 |
| Std | 0 | 5.34 | 0 | 1.61 × 101 | 4.14 × 101 | 0 | |
| f10 | Ave | 4.44 × 10−15 | 1.03 × 10−13 | 8.88 × 10−16 | 2.57 | 1.62 × 101 | 8.88 × 10−16 |
| Std | 2.09 × 10−15 | 2.02 × 10−14 | 0 | 8.19 × 10−1 | 7.34 | 0 | |
| f11 | Ave | 1.11 × 10−2 | 6.80 × 10−3 | 0 | 1.57 × 10−2 | 1.60 | 0 |
| Std | 6.07 × 10−2 | 1.31 × 10−2 | 0 | 1.32 × 10−2 | 6.49 × 10−1 | 0 | |
| f12 | Ave | 1.71 × 10−2 | 4.55 × 10−2 | 6.33 × 10−6 | 6.64 | 6.12 × 105 | 1.45 × 10−9 |
| Std | 7.51 × 10−3 | 2.28 × 10−2 | 8.21 × 10−6 | 2.95 | 1.86 × 106 | 2.97 × 10−9 | |
| f13 | Ave | 4.94 × 10−1 | 7.19 × 10−1 | 1.02 × 10−4 | 2.00 × 101 | 1.44 × 106 | 1.69 × 10−10 |
| Std | 2.51 × 10−1 | 2.21 × 10−1 | 1.19 × 10−4 | 1.64 × 101 | 2.02 × 106 | 3.02 × 10−10 | |
| f14 | Ave | 2.57 | 4.98 | 1.33 | 1.16 | 1.33 | 9.98 × 10−1 |
| Std | 2.99 | 4.53 | 9.47 × 10−1 | 4.58 × 10−1 | 7.50 × 10−1 | 1.06 × 10−6 | |
| f15 | Ave | 0.00071818 | 0.0024681 | 0.00034688 | 0.00099878 | 0.001211 | 0.00033444 |
| Std | 0.00054231 | 0.0060734 | 3.251× 10−5 | 0.00028419 | 0.00034186 | 1.84 × 10−4 | |
| f16 | Ave | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| Std | 8.63 × 10−10 | 2.82 × 10−8 | 8.49 × 10−10 | 3.06 × 10−14 | 9.52 × 10−5 | 4.45 × 10−2 | |
| f17 | Ave | 0.39789 | 0.39789 | 0.39789 | 0.39789 | 0.4016 | 0.39789 |
| Std | 1.22 × 10−5 | 2.14 × 10−3 | 7.01 × 10−6 | 2.16 × 10−3 | 2.20 × 10−3 | 8.47 × 10−5 | |
| f18 | Ave | 3.0001 | 3 | 3 | 3.0005 | 3.0003 | 3 |
| Std | 4.93 | 5.05 × 10−5 | 6.38 × 10−7 | 5.01 × 10−4 | 3.71 × 10−4 | 6.49 × 10−7 | |
| f19 | Ave | −3.8582 | −3.8615 | −3.8595 | −3.8626 | −3.8536 | −3.8633 |
| Std | 5.88 × 10−2 | 2.72 × 10−3 | 2.70 × 10−3 | 2.59 × 10−4 | 3.10 × 10−3 | 9.69 × 10−3 | |
| f20 | Ave | −3.1983 | −3.2541 | −3.133 | −3.2072 | −2.8409 | −3.3263 |
| Std | 9.35 × 10−2 | 7.38 × 10−2 | 1.01 × 10−1 | 7.48 × 10−2 | 2.46 × 10−1 | 1.66 × 10−1 | |
| f21 | Ave | −8.4313 | −8.6048 | −5.0507 | −8.3476 | −1.8336 | −10.153 |
| Std | 2.27 | 2.46 | 1.24 | 3.16 | 1.63 | 1.13 × 10−3 | |
| f22 | Ave | −8.1586 | −9.6926 | −5.0821 | −9.4209 | −3.4597 | −10.4024 |
| Std | 3.23 | 1.62 | 1.58 | 2.04 | 1.81 | 3.95 × 10−4 | |
| f23 | Ave | −8.4151 | −10.0841 | −5.2933 | −9.3126 | −3.8672 | −0.5362 |
| Std | 3.14 | 9.79 × 10−1 | 9.83 × 10−1 | 2.40 | 1.03 | 5.24 × 10−4 | |
| Decision result | +/=/− | 2/2/19 | 2/3/18 | 3/7/13 | 3/2/18 | 1/1/21 | -- |
| Function | Evaluation Criterion | WOA | GWO | HHO | SSA | SCA | SCAEICS |
|---|---|---|---|---|---|---|---|
| f1 | Ave | 8.79 × 10−71 | 1.03 × 10−27 | 1.20 × 10−94 | 3.02 × 102 | 7.82 × 101 | 4.79 × 10−224 |
| Std | 3.71 × 10−70 | 1.68 × 10−27 | 6.53 × 10−94 | 8.75 × 101 | 1.24 × 102 | 0 | |
| f2 | Ave | 1.29 × 10−50 | 9.79 × 10−17 | 2.57 × 10−51 | 1.22 × 101 | 2.06 × 10−1 | 4.23 × 10−127 |
| Std | 4.22 × 10−50 | 5.86 × 10−17 | 8.54 × 10−51 | 1.97 | 4.10 × 10−1 | 1.11 × 10−126 | |
| f3 | Ave | 4.33 × 104 | 4.22 × 10−6 | 9.12 × 10−70 | 6.58 × 103 | 1.56 × 104 | 4.11 × 10−234 |
| Std | 1.36 × 104 | 1.08 × 10−5 | 4.99 × 10−69 | 2.85 × 103 | 6.59 × 103 | 0 | |
| f4 | Ave | 5.10 × 101 | 6.11 × 10−7 | 2.04 × 10−48 | 1.84 × 101 | 4.61 × 101 | 3.40 × 10−125 |
| Std | 2.94 × 101 | 6.59 × 10−7 | 9.61 × 10−48 | 3.64 | 1.27 × 101 | 1.84 × 10−124 | |
| f5 | Ave | 2.80 × 101 | 2.68 × 101 | 1.46 × 10−2 | 2.62 × 104 | 5.35 × 105 | 3.77 × 10−8 |
| Std | 3.90 × 10−1 | 5.50 × 10−1 | 1.64 × 10−2 | 2.91 × 104 | 1.70 × 106 | 7.36 × 10−10 | |
| f6 | Ave | 3.84 × 10−1 | 8.13 × 10−1 | 9.96 × 10−5 | 3.20 × 102 | 1.29 × 102 | 2.98 × 10−9 |
| Std | 2.72 × 10−1 | 3.82 × 10−1 | 1.44 × 10−4 | 1.14 × 102 | 1.74 × 102 | 5.37 × 10−9 | |
| f7 | Ave | 2.56 × 10−3 | 1.88 × 10−3 | 1.64 × 10−4 | 3.31 × 10−1 | 2.16 × 10−1 | 9.11 × 10−5 |
| Std | 2.79 × 10−3 | 1.22 × 10−3 | 1.40 × 10−4 | 1.08 × 10−1 | 4.31 × 10−1 | 8.65 × 10−5 | |
| f8 | Ave | −9016.3152 | −6709.0284 | −12569.3642 | −6699.3213 | −3794.8247 | −12569.4851 |
| Std | 1.69 × 103 | 8.88 × 102 | 5.88 × 102 | 7.95 × 102 | 2.45 × 102 | 7.73 × 10−4 | |
| f9 | Ave | 1.89 × 10−15 | 2.21 | 0 | 1.33 × 102 | 5.44 × 101 | 0 |
| Std | 1.04 × 10−14 | 3.79 | 0 | 2.50 × 101 | 4.35 × 101 | 0 | |
| f10 | Ave | 3.85 × 10−15 | 9.94 × 10−14 | 8.88 × 10−16 | 6.37 | 1.42 × 101 | 8.88 × 10−16 |
| Std | 2.81 × 10−15 | 1.96 × 10−14 | 0 | 9.36 × 10−1 | 8.09 | 0 | |
| f11 | Ave | 5.91 × 10−3 | 4.42 × 10−3 | 0 | 3.66 | 1.81 | 0 |
| Std | 3.24 × 10−2 | 8.23 × 10−3 | 0 | 8.74 × 10−1 | 1.10 | 0 | |
| f12 | Ave | 2.25 × 10−2 | 3.74 × 10−2 | 8.11 × 10−6 | 3.61 × 101 | 1.94 × 106 | 3.69 × 10−10 |
| Std | 1.78 × 10−2 | 2.04 × 10−2 | 9.99 × 10−6 | 3.92 × 101 | 9.39 × 106 | 1.01 × 10−9 | |
| f13 | Ave | 5.56 × 10−1 | 5.72 × 10−1 | 7.79 × 10−5 | 2.73 × 103 | 1.57 × 106 | 7.07 × 10−9 |
| Std | 2.20 × 10−1 | 1.77 × 10−1 | 7.82 × 10−5 | 1.05 × 104 | 2.78 × 106 | 1.21 × 10−8 | |
| Decision result | +/=/− | 0/0/13 | 0/0/13 | 1/3/9 | 0/0/13 | 0/0/13 | -- |
| Function | Evaluation Criterion | WOA | GWO | HHO | SSA | SCA | SCAEICS |
|---|---|---|---|---|---|---|---|
| f1 | Ave | 9.88 × 10−74 | 7.23 × 10−28 | 8.49 × 10−96 | 3.18 × 102 | 9.23 × 101 | 2.56 × 10−216 |
| Std | 4.30 × 10−73 | 9.27 × 10−28 | 4.64 × 10−95 | 1.14 × 102 | 1.42 × 102 | 0 | |
| f2 | Ave | 2.23 × 10−51 | 1.13 × 10−16 | 7.58 × 10−51 | 1.23 × 101 | 1.57 × 10−1 | 2.77 × 10−123 |
| Std | 6.13 × 10−51 | 6.47 × 10−17 | 3.98 × 10−50 | 3.13 | 2.01 × 10−1 | 1.38 × 10−122 | |
| f3 | Ave | 4.72 × 104 | 3.15 × 10−5 | 2.58 × 10−70 | 5.94 × 103 | 1.33 × 104 | 1.32 × 10−238 |
| Std | 1.24 × 104 | 9.29 × 10−5 | 1.41 × 10−69 | 2.46 × 103 | 7.85 × 103 | 0 | |
| f4 | Ave | 5.35 × 101 | 6.68 × 10−7 | 5.78 × 10−49 | 1.87 × 101 | 4.46 × 101 | 1.28 × 10−123 |
| Std | 2.48 × 101 | 5.59 × 10−7 | 2.22 × 10−48 | 3.54 | 1.29 × 101 | 6.96 × 10−123 | |
| f5 | Ave | 2.81 × 101 | 2.69 × 101 | 1.02 × 10−2 | 2.59 × 104 | 2.66 × 105 | 1.52 × 10−7 |
| Std | 5.13 × 10−1 | 6.93 × 10−1 | 1.11 × 10−2 | 2.22 × 104 | 4.40 × 105 | 2.04 × 10−7 | |
| f6 | Ave | 3.32 × 10−1 | 7.66 × 10−1 | 1.46 × 10−4 | 3.02 × 102 | 8.19 × 101 | 7.83 × 10−9 |
| Std | 2.07 × 10−1 | 3.71 × 10−1 | 2.17 × 10−4 | 7.90 × 101 | 1.24 × 102 | 1.99 × 10−8 | |
| f7 | Ave | 3.19 × 10−3 | 2.05 × 10−3 | 1.56 × 10−4 | 3.25 × 10−1 | 3.47 × 10−1 | 8.38 × 10−5 |
| Std | 4.50 × 10−3 | 8.65 × 10−4 | 1.62 × 10−4 | 1.43 × 10−1 | 3.00 × 10−1 | 6.56 × 10−5 | |
| f8 | Ave | −12507.8053 | −5308.7488 | −12568.5282 | −5959.9149 | −4434.8286 | −12569.4857 |
| Std | 1.61 × 103 | 9.96 × 102 | 4.08 × 101 | 8.14 × 102 | 2.66 × 102 | 2.63 × 10−4 | |
| f9 | Ave | 0 | 2.55 | 0 | 1.30 × 102 | 6.79 × 101 | 0 |
| Std | 0 | 3.34 | 0 | 2.07 × 101 | 4.15 × 101 | 0 | |
| f10 | Ave | 4.32 × 10−15 | 1.08 × 10−13 | 8.88 × 10−16 | 6.37 | 1.60 × 101 | 8.88 × 10−16 |
| Std | 2.72 × 10−15 | 2.07 × 10−14 | 0 | 8.91 × 10−1 | 7.21 | 0 | |
| f11 | Ave | 1.25 × 10−2 | 3.06 × 10−3 | 0 | 3.60 | 1.89 | 0 |
| Std | 4.79 × 10−2 | 5.85 × 10−3 | 0 | 9.60 × 10−1 | 1.63 | 0 | |
| f12 | Ave | 1.86 × 10−2 | 5.16 × 10−2 | 1.14 × 10−5 | 2.27 × 101 | 4.08 × 105 | 8.64 × 10−10 |
| Std | 1.34 × 10−2 | 3.00 × 10−2 | 1.85 × 10−5 | 1.33 × 101 | 1.16 × 106 | 1.97 × 10−9 | |
| f13 | Ave | 5.31 × 10−1 | 5.71 × 10−1 | 1.04 × 10−4 | 1.23 × 103 | 1.81 × 106 | 6.16 × 10−9 |
| Std | 2.90 × 10−1 | 2.24 × 10−1 | 1.41 × 10−4 | 2.63 × 103 | 3.87 × 106 | 1.39 × 10−8 | |
| Decision result | +/=/− | 0/1/12 | 0/0/13 | 1/4/8 | 0/0/13 | 0/0/13 | -- |
| Function | Evaluation Criterion | COSCA | SCADE | MGSCA | CSCA | SCAEICS |
|---|---|---|---|---|---|---|
| f1 | Ave | 2.44 × 10−78 | 9.58 × 10−95 | 7.62 × 10−23 | 7.49 × 10−2 | 9.72 × 10−232 |
| Std | 3.21 × 10−94 | 4.92 × 10−94 | 1.67 × 10−22 | 1.93 × 10−1 | 0 | |
| f2 | Ave | 1.52 × 10−44 | 6.14 × 10−63 | 1.92 × 10−17 | 5.09 × 10−7 | 3.10 × 10−123 |
| Std | 1.94 × 10−60 | 2.73 × 10−62 | 4.63 × 10−17 | 8.73 × 10−7 | 1.69 × 10−122 | |
| f3 | Ave | 1.78 × 10−15 | 1.93 × 10−4 | 2.80 × 10−3 | 5.83 × 103 | 3.71 × 10−230 |
| Std | 1.45 × 10−30 | 9.81 × 10−4 | 8.78 × 10−3 | 5.29 × 103 | 0 | |
| f4 | Ave | 5.27 × 10−35 | 2.85 × 10−9 | 8.11 × 10−3 | 1.26 × 101 | 1.45 × 10−124 |
| Std | 1.91 × 10−50 | 1.53 × 10−8 | 2.34 × 10−2 | 9.50 | 7.73 × 10−124 | |
| f5 | Ave | 2.84 × 101 | 2.69 × 101 | 2.75 × 101 | 4.17 × 103 | 3.29 × 10−08 |
| Std | 7.94 × 10−16 | 1.47 × 10−1 | 7.07 × 10−1 | 1.80 × 104 | 3.77 × 10−8 | |
| f6 | Ave | 3.82 | 7.54 × 10−5 | 1.39 | 5.09 | 2.62 × 10−10 |
| Std | 7.94 × 10−16 | 9.46 × 10−5 | 5.59 × 10−1 | 9.42 × 10−1 | 1.12 × 10−9 | |
| f7 | Ave | 3.21 × 10−4 | 8.44 × 10−3 | 3.87 × 10−3 | 7.74 × 10−2 | 7.65 × 10−6 |
| Std | 6.06 × 10−21 | 7.37 × 10−3 | 2.65 × 10−3 | 5.34 × 10−2 | 7.67 × 10−6 | |
| f8 | Ave | −3.31 × 103 | −1.20 × 104 | −6.36 × 103 | −3.37 × 103 | −12,569.4865 |
| Std | 2.64 × 10−12 | 2.53 × 102 | 6.41 × 102 | 2.95 × 102 | 0.00029551 | |
| f9 | Ave | 0 | 0 | 2.86 × 10−1 | 4.63 × 101 | 0 |
| Std | 0 | 0 | 8.88 × 10−1 | 4.93 × 101 | 0 | |
| f10 | Ave | 2.48 × 10−15 | 2.13 × 10−15 | 7.39 | 2.89 × 10−2 | 8.88 × 10−16 |
| Std | 7.05 × 10−31 | 1.76 × 10−15 | 9.88 | 7.60 × 10−2 | 0 | |
| f11 | Ave | 0 | 0 | 1.01 × 10−2 | 4.78 × 10−1 | 0 |
| Std | 0 | 0 | 1.85 × 10−2 | 3.69 × 10−1 | 0 | |
| f12 | Ave | 3.68 × 10−1 | 3.45 × 10−5 | 1.00 × 10−1 | 9.39 | 1.45 × 10−9 |
| Std | 1.73 × 10−16 | 1.66 × 10−4 | 4.78 × 10−2 | 4.22 × 101 | 2.97 × 10−9 | |
| f13 | Ave | 2.04 | 8.13 × 10−3 | 1.46 | 6.35 × 102 | 1.69 × 10−10 |
| Std | 1.20 × 10−15 | 2.29 × 10−2 | 3.20 × 10−1 | 3.21 × 103 | 3.02 × 10−10 | |
| f14 | Ave | 3.56 | 9.98 × 10−1 | 1.13 | 2.26 | 9.98 × 10−1 |
| Std | 5.95 × 10−16 | 5.00 × 10−16 | 5.03 × 10−1 | 2.48 | 1.06 × 10−6 | |
| f15 | Ave | 7.87 × 10−04 | 7.52 × 10−4 | 0.0006979 | 0.0006694 | 0.00033444 |
| Std | 7.75 × 10−19 | 1.54 × 10−4 | 3.45 × 10−4 | 2.44 × 10−4 | 1.84 × 10−4 | |
| f16 | Ave | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| Std | 1.09 × 10−16 | 4.44 × 10−16 | 2.04 × 10−8 | 3.05 × 10−5 | 4.45 × 10−2 | |
| f17 | Ave | 0.39789 | 0.39789 | 0.39789 | 0.4003 | 0.39789 |
| Std | 0 | 0 | 4.36 × 10−6 | 2.84 × 10−3 | 8.47 × 10−5 | |
| f18 | Ave | 3 | 3 | 3 | 3.0001 | 3 |
| Std | 7.94 × 10−16 | 3.18 × 10−7 | 4.99 × 10−6 | 1.19 × 10−4 | 6.49 × 10−7 | |
| f19 | Ave | −3.8589 | −3.8628 | −3.8585 | −3.8572 | −3.8633 |
| Std | 1.39 × 10−15 | 7.64 × 10−13 | 3.85 × 10−3 | 3.33 × 10−3 | 9.69 × 10−3 | |
| f20 | Ave | −3.1561 | −3.3119 | −3.1134 | −3.1229 | −3.3263 |
| Std | 9.93 × 10−16 | 3.05 × 10−2 | 1.80 × 10−1 | 7.41 × 10−2 | 1.66 × 10−1 | |
| f21 | Ave | −9.8534 | −9.7526 | −7.3713 | −4.2256 | −10.153 |
| Std | 6.35 × 10−15 | 8.91 × 10−1 | 2.91 | 1.14 | 1.13 × 10−3 | |
| f22 | Ave | −10.3208 | −10.4029 | −8.3904 | −4.4632 | −10.4024 |
| Std | 4.36 × 10−15 | 1.45 | 3.21 | 8.68 × 10−1 | 3.95 × 10−4 | |
| f23 | Ave | −10.4821 | −10.5364 | −8.7732 | −4.5667 | −10.5362 |
| Std | 3.97 × 10−15 | 3.45 × 10−14 | 3.04 | 1.34 | 5.24 × 10−4 | |
| Decision result | +/=/− | 2/6/15 | 2/8/13 | 2/3/18 | 2/2/19 | -- |
| Function | Evaluation Criterion | CMRFO | CMPA | SCA | SCAEICS |
|---|---|---|---|---|---|
| F1 | Ave | 2.56 × 103 | 1.732 × 106 | 5.45 × 1010 | 1.35 × 104 |
| Std | 7.12 × 106 | 1.178 × 106 | 6.69 × 1019 | 3.79 × 105 | |
| F2 | Ave | 8.57 × 103 | 2.191 × 103 | 1.52 × 104 | 4.30 × 103 |
| Std | 9.48 × 105 | 2.191 × 103 | 1.80 × 105 | 2.18 × 102 | |
| F3 | Ave | 1.51 × 103 | 2.191 × 103 | 1.76 × 103 | 1.67 × 103 |
| Std | 6.04 × 104 | 2.191 × 103 | 9.22 × 103 | 1.98 × 103 | |
| F4 | Ave | 1.90 × 103 | 2.191 × 103 | 2.04 × 103 | 1.90 × 103 |
| Std | 0 | 6.347 × 101 | 1.75 × 104 | 1.62 | |
| F5 | Ave | 4.10 × 105 | 2.066 × 103 | 7.65 × 107 | 2.94 × 103 |
| Std | 4.32 × 1010 | 8.949 × 101 | 1.60 × 1015 | 1.34 × 103 | |
| F6 | Ave | 3.36 × 103 | 1.601 × 103 | 6.34 × 103 | 1.60 × 103 |
| Std | 2.07 × 105 | 1.601 × 103 | 4.45 × 105 | 1.10 × 101 | |
| F7 | Ave | 2.36 × 105 | 1.601 × 103 | 2.06 × 107 | 2.53 × 105 |
| Std | 1.79 × 1010 | 6.108 × 101 | 7.40 × 1013 | 4.33 × 104 | |
| F8 | Ave | 8.85 × 103 | 2.295 × 103 | 1.68 × 104 | 2.31 × 103 |
| Std | 9.47 × 106 | 2.472 × 101 | 2.79 × 105 | 4.63 × 101 | |
| F9 | Ave | 3.30 × 103 | 2.575 × 103 | 3.80 × 103 | 2.61 × 103 |
| Std | 1.07 × 104 | 7.444 × 101 | 4.87 × 103 | 4.79 × 101 | |
| F10 | Ave | 3.06 × 103 | 2.897 × 103 | 7.43 × 103 | 2.87 × 103 |
| Std | 1.07 × 103 | 2.338 × 101 | 5.82 × 105 | 1.05 × 101 | |
| Decision result | +/=/− | 1/3/6 | 3/4/3 | 0/0/10 | -- |
| m | f1 (p = 3.3074 × 10−76) | f3 (p = 6.8459 × 10−223) | f6 (p = 1.0364 × 10−141) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Average Optimal Value | Standard Deviation | Rank | Average Optimal Value | Standard Deviation | Rank | Average Optimal Value | Standard Deviation | Rank | |
| 4 | 7.60 × 10−232 | 0 | 1 | 6.78 × 10−205 | 0 | 1 | 7.34 × 10−9 | 1.04 × 10−8 | 3 |
| 5 | 2.06 × 10−181 | 0 | 3 | 7.40 × 10−155 | 1.05 × 10−154 | 3 | 4.24 × 10−11 | 3.92 × 10−11 | 1 |
| 6 | 5.94 × 10−219 | 0 | 2 | 1.42 × 10−203 | 0 | 2 | 9.81 × 10−9 | 1.24 × 10−8 | 2 |
| 7 | 9.01 × 10−170 | 0 | 4 | 2.63 × 10−141 | 3.72 × 10−141 | 4 | 8.59 × 10−10 | 2.05 × 10−10 | 4 |
| m | f8 (p = 1.8302 × 10−72) | f13 (p = 2.3981 × 10−187) | f17 (p = 3.1354 × 10−278) | ||||||
| Average Optimal Value | Standard Deviation | Rank | Average Optimal Value | Standard Deviation | Rank | Average Optimal Value | Standard Deviation | Rank | |
| 4 | −12,569.4857 | 9.44 × 10−4 | 3 | 9.21 × 10−9 | 1.30 × 10−8 | 2 | 3.98 × 10−1 | 4.58 × 10−7 | 2 |
| 5 | −12,569.4866 | 5.78 × 10−4 | 2 | 2.17 × 10−8 | 3.02 × 10−8 | 3 | 3.98 × 10−1 | 1.42 × 10−4 | 4 |
| 6 | −12,569.4866 | 4.61 × 10−4 | 1 | 3.89 × 10−10 | 8.74 × 10−11 | 1 | 3.98 × 10−1 | 1.72 × 10−7 | 1 |
| 7 | −12,569.4852 | 2.34 × 10−3 | 4 | 1.96 × 10−8 | 2.59 × 10−8 | 4 | 3.98 × 10−1 | 6.08 × 10−8 | 3 |
| m | f19 (p = 6.4911 × 10−198) | f21 (p = 3.562 × 10−100) | f23 (p = 1.2524 × 10−142) | ||||||
| Average Optimal Value | Standard Deviation | Rank | Average Optimal Value | Standard Deviation | Rank | Average Optimal Value | Standard Deviation | Rank | |
| 4 | −3.44 | 3.11 × 10−2 | 4 | −10.1531 | 2.73 × 10−4 | 4 | −10.5321 | 3.91 × 10−5 | 4 |
| 5 | −3.68 | 1.69 × 10−1 | 1 | −10.1531 | 7.06 × 10−4 | 2 | −10.5363 | 1.73 × 10−3 | 1 |
| 6 | −3.71 | 7.85 × 10−2 | 2 | −10.1532 | 2.38 × 10−4 | 1 | −10.5362 | 1.14 × 10−3 | 2 |
| 7 | −3.56 | 2.39 × 10−1 | 3 | −10.1521 | 1.46 × 10−4 | 3 | −10.5362 | 9.17 × 10−5 | 3 |
| Algorithms | x1 | x2 | x3 | x4 | x5 | f(x) |
|---|---|---|---|---|---|---|
| WOA | 6.7223 | 5.6496 | 4.86784 | 2.7854 | 1.5343 | 1.7224 |
| GWO | 6.0505 | 5.3133 | 4.4703 | 3.5221 | 2.1857 | 1.3402 |
| HHO | 6.2829 | 5.2835 | 4.4123 | 3.6826 | 2.0938 | 1.3415 |
| SSA | 6.7314 | 4.3729 | 4.4344 | 2.9367 | 4.1988 | 1.8389 |
| SCA | 5.0881 | 5.2855 | 3.5683 | 3.6543 | 3.8544 | 1.4901 |
| SCAEICS | 6.9328 | 5.8733 | 4.9051 | 4.5246 | 2.4903 | 1.3401 |
| Algorithms | Maximum Value | Minimum Value | Standard Deviation | x1 | x2 | f (x) |
|---|---|---|---|---|---|---|
| WOA | 267.7761 | 263.8988 | 1.2117 | 0.7975 | 0.3837 | 265.1009 |
| GWO | 264.2903 | 271.0781 | 2.2715 | 0.8146 | 0.3410 | 267.6625 |
| HHO | 263.8972 | 265.0614 | 0.2509 | 0.7879 | 0.4286 | 264.0875 |
| SSA | 263.8973 | 263.9679 | 0.0160 | 0.7873 | 0.4121 | 263.9181 |
| SCA | 263.929 | 282.8427 | 6.4548 | 0.7935 | 0.3984 | 266.6682 |
| SCAEICS | 263.8962 | 263.9349 | 0.0075 | 0.7816 | 0.3404 | 263.9055 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Wang, L. Sine Cosine Algorithm for Elite Individual Collaborative Search and Its Application in Mechanical Optimization Designs. Biomimetics 2023, 8, 576. https://doi.org/10.3390/biomimetics8080576
Tang J, Wang L. Sine Cosine Algorithm for Elite Individual Collaborative Search and Its Application in Mechanical Optimization Designs. Biomimetics. 2023; 8(8):576. https://doi.org/10.3390/biomimetics8080576
Chicago/Turabian StyleTang, Junjie, and Lianguo Wang. 2023. "Sine Cosine Algorithm for Elite Individual Collaborative Search and Its Application in Mechanical Optimization Designs" Biomimetics 8, no. 8: 576. https://doi.org/10.3390/biomimetics8080576
APA StyleTang, J., & Wang, L. (2023). Sine Cosine Algorithm for Elite Individual Collaborative Search and Its Application in Mechanical Optimization Designs. Biomimetics, 8(8), 576. https://doi.org/10.3390/biomimetics8080576





