Bio-Inspired Sutures: Simulating the Role of Suture Placement in the Mechanical Response of Interlocking Structures
Abstract
:1. Introduction
2. Methods
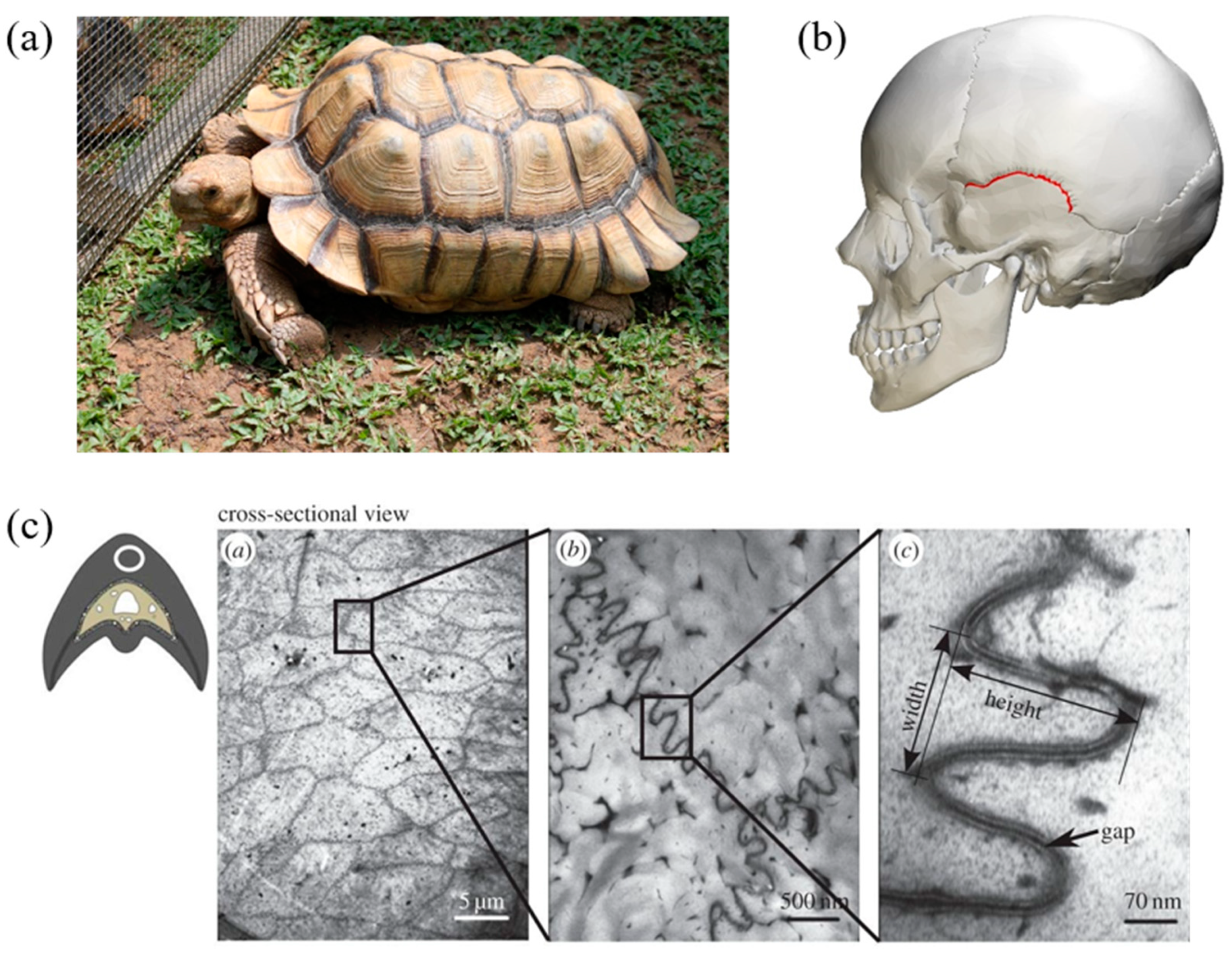
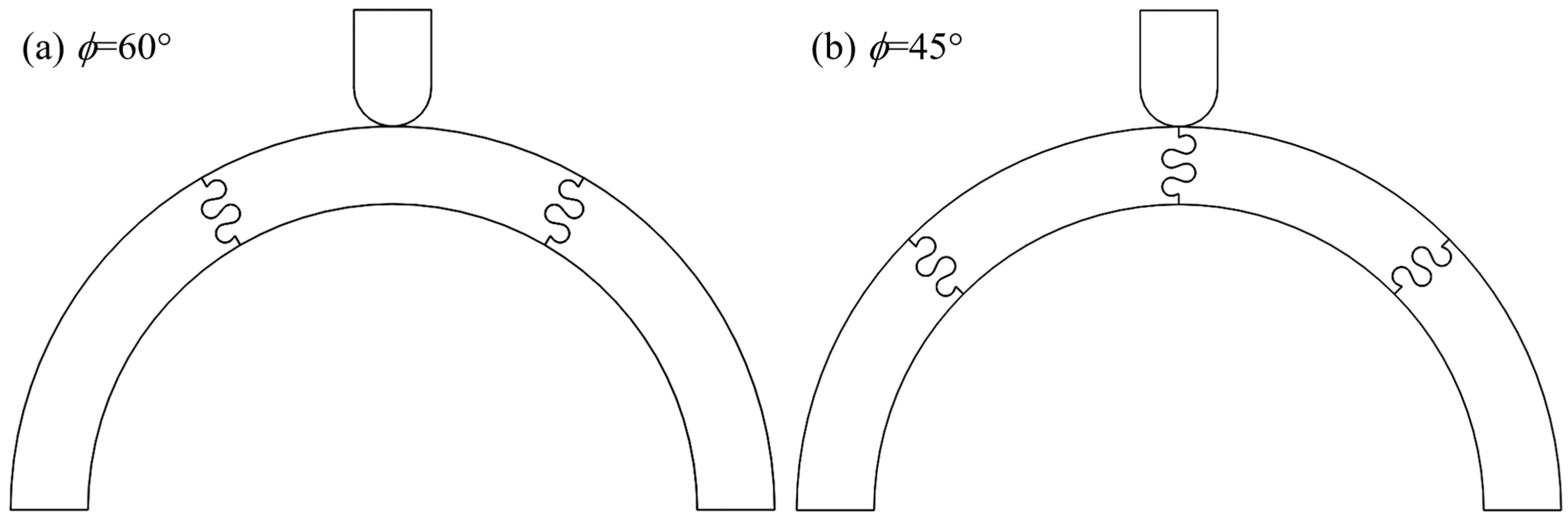
2.1. Archway and Suture Geometries
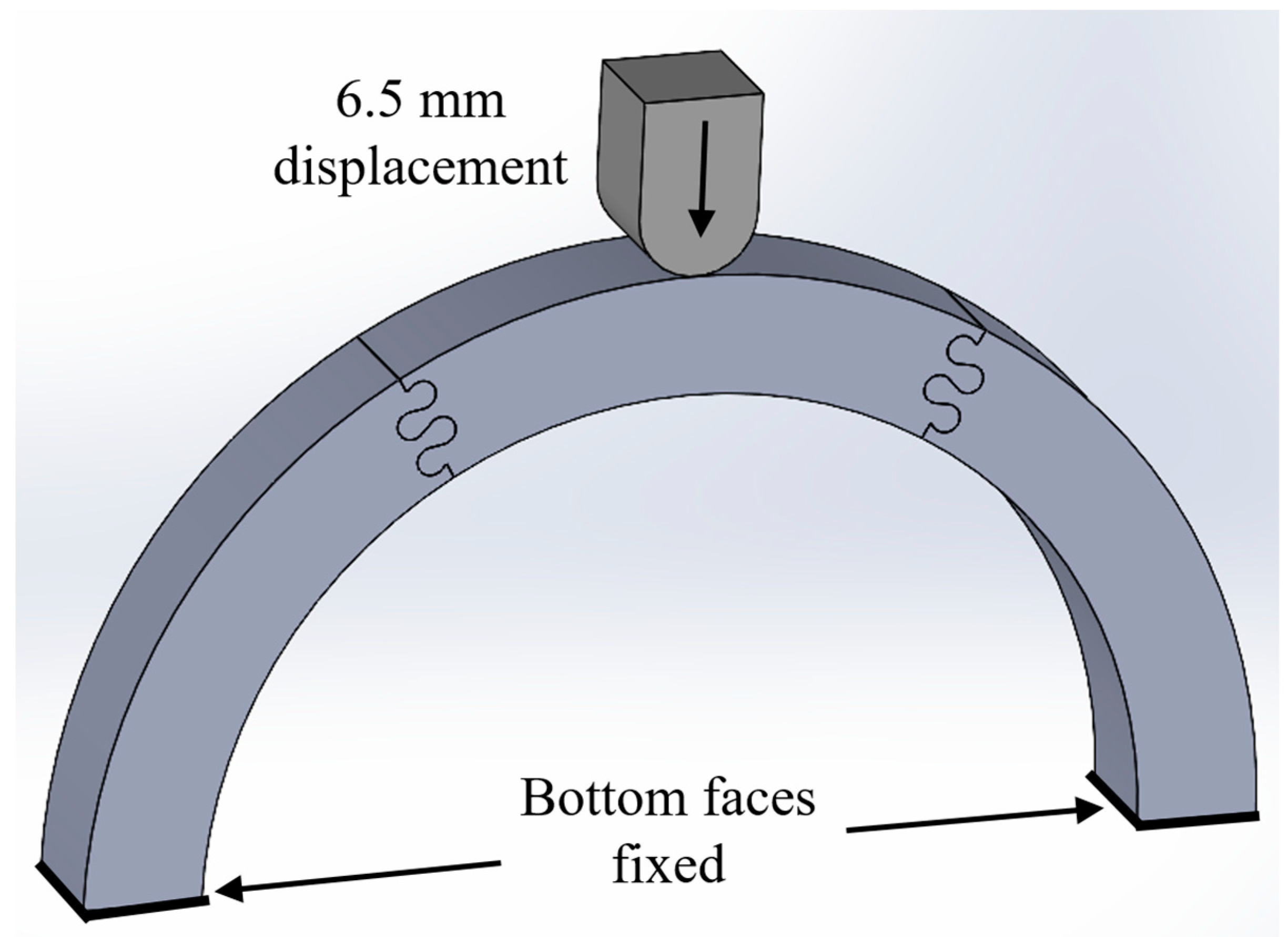
2.2. FEA Setup
3. Results and Discussion
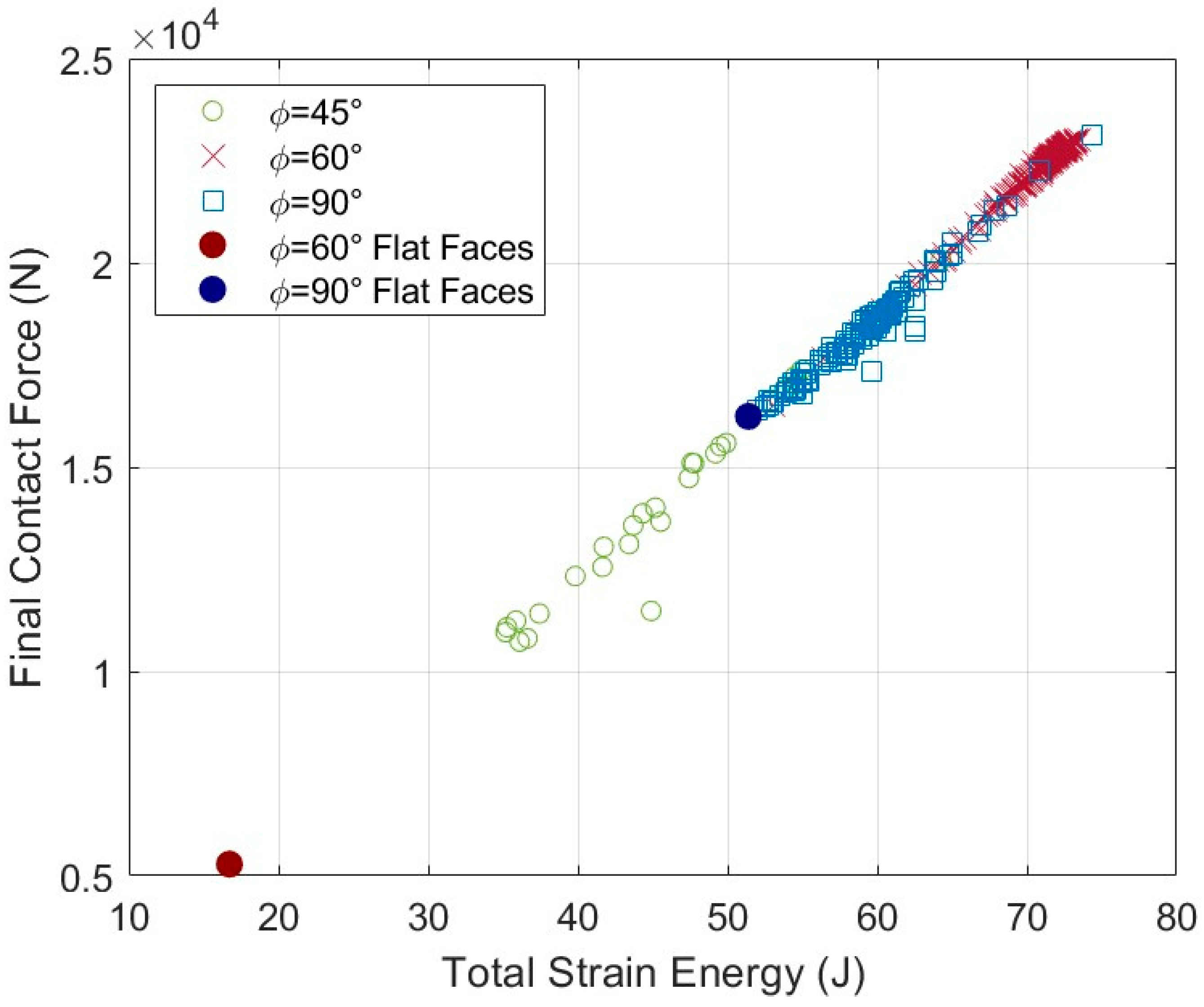
3.1. Base Cases: Verifying the Role of Sutures
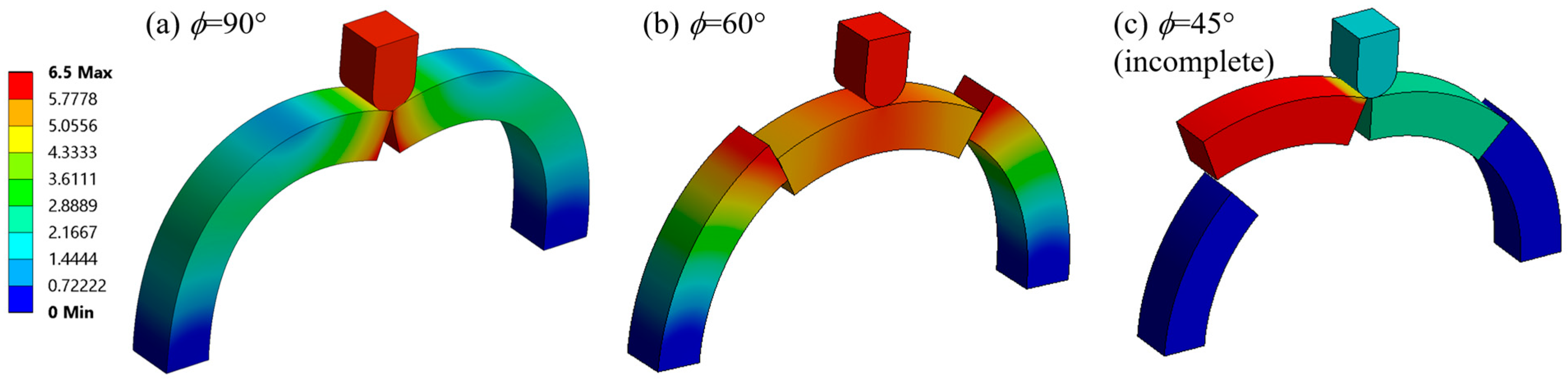
3.2. Comparison of ϕ Values
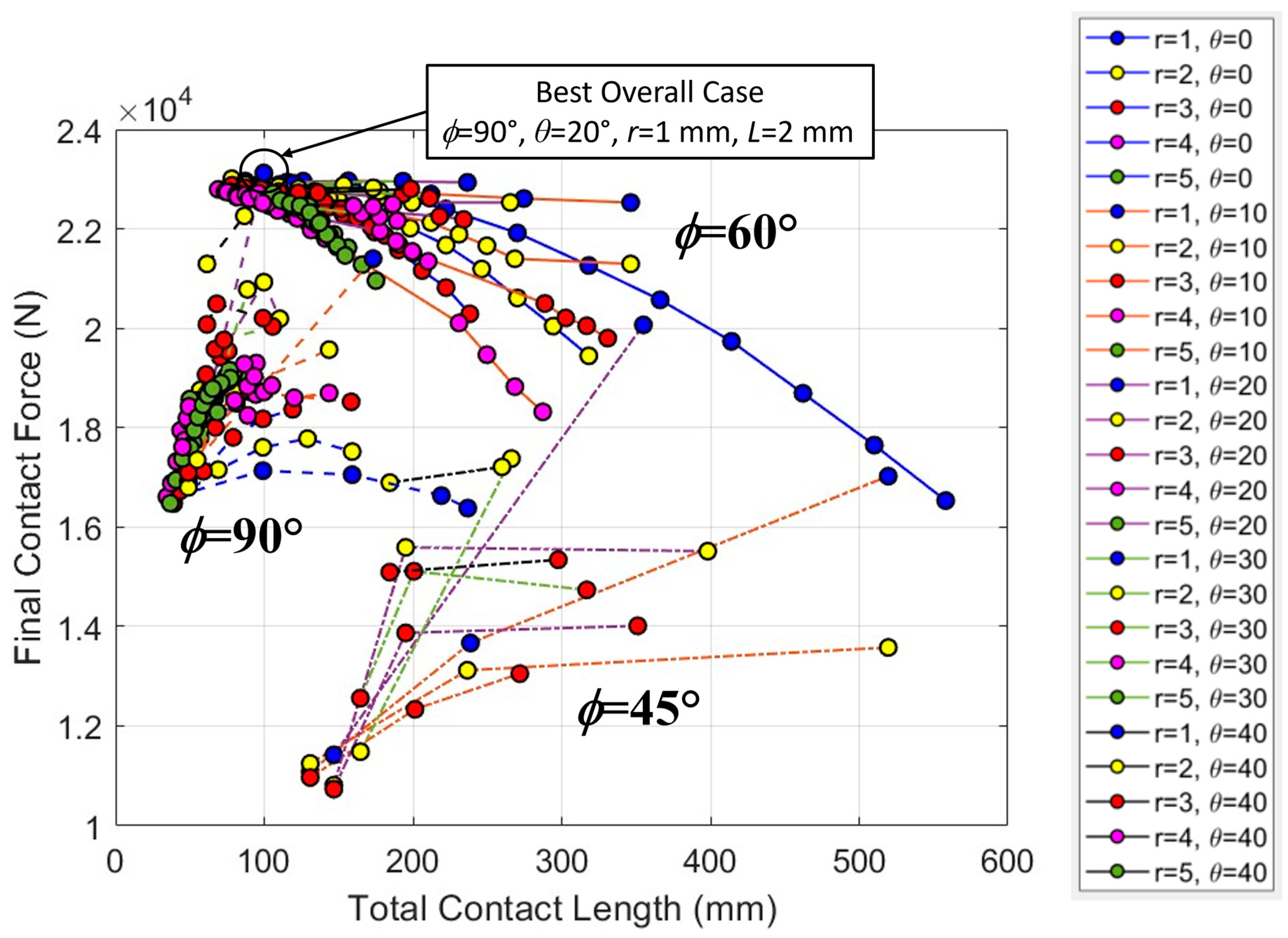
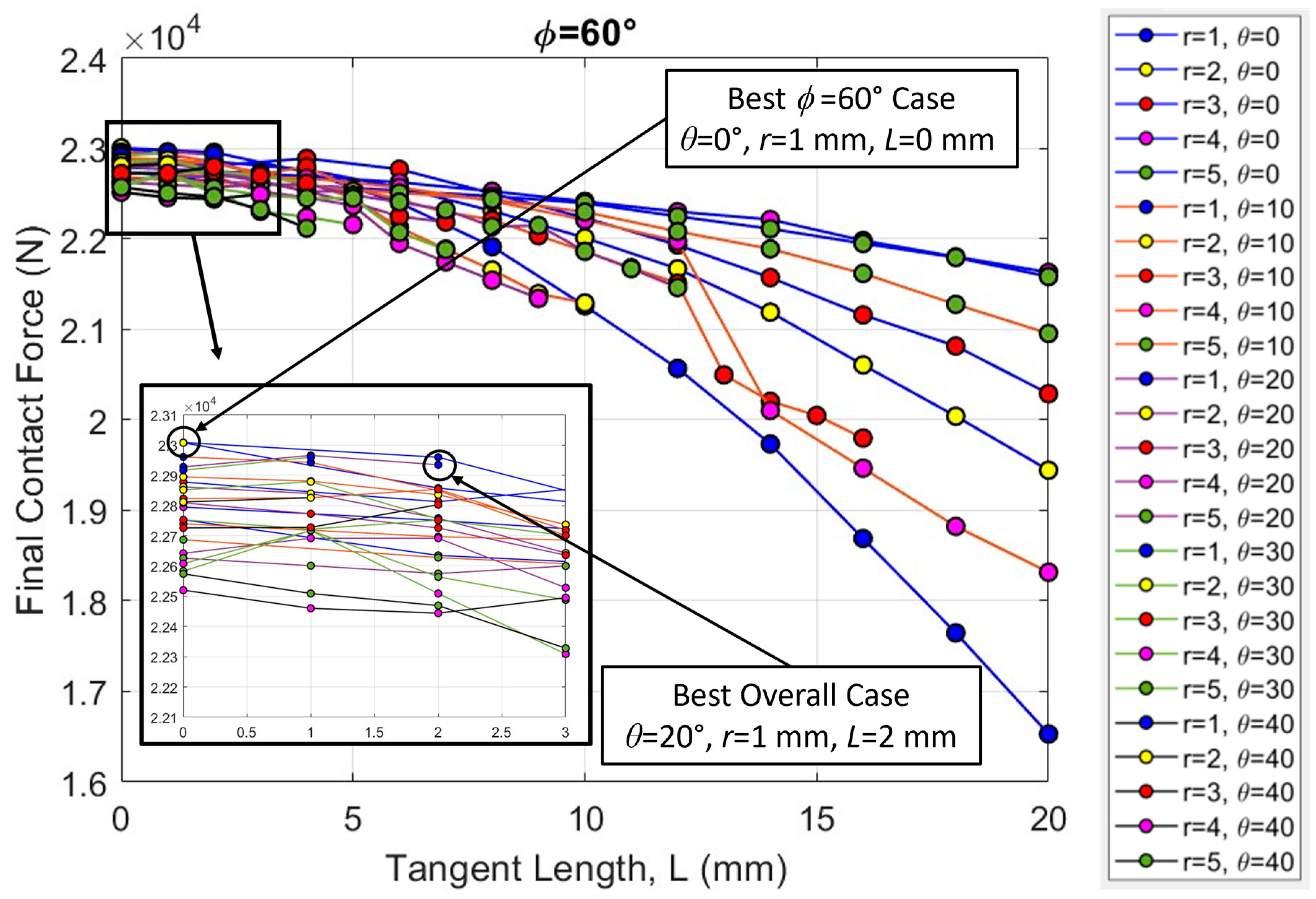
3.3. Increasing Segmentation
3.4. Mid-Segment Indentation
3.5. Reflections on the Role of Sutures in Localizing Strain Energy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- McKittrick, J.; Chen, P.Y.; Tombolato, L.; Novitskaya, E.E.; Trim, M.W.; Hirata, G.A.; Olevsky, E.A.; Horstemeyer, M.F.; Meyers, M.A. Energy Absorbent Natural Materials and Bioinspired Design Strategies: A Review. Mater. Sci. Eng. C 2010, 30, 331–342. [Google Scholar] [CrossRef]
- Chen, D.A.; Ross, B.E.; Klotz, L.E. Lessons from a Coral Reef: Biomimicry for Structural Engineers. J. Struct. Eng. 2015, 141, 02514002. [Google Scholar] [CrossRef]
- Chen, D.A.; Ross, B.E.; Klotz, L.E. Parametric analysis of a spiraled shell: Learning from nature’s adaptable structures. Designs 2018, 2, 46. [Google Scholar] [CrossRef]
- Meyers, M.; Chawla, K. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Miura, T.; Perlyn, C.A.; Kinboshi, M.; Ogihara, N.; Kobayashi-Miura, M.; Morriss-Kay, G.M.; Shiota, K. Mechanism of skull suture maintenance and interdigitation. J. Anat. 2009, 215, 642–655. [Google Scholar] [CrossRef] [PubMed]
- Lee, N.; Horstemeyer, M.F.; Rhee, H.; Nabors, B.; Liao, J.; Williams, L.N. Hierarchical multiscale structure–Property relationships of the red-bellied woodpecker (Melanerpes carolinus) beak. J. R. Soc. Interface 2014, 11, 20140274. [Google Scholar] [CrossRef] [PubMed]
- Krauss, S.; Monsonego-Ornan, E.; Zelzer, E.; Fratzl, P.; Shahar, R. Mechanical function of a complex three-dimensional suture joining the bony elements in the shell of the red-eared slider turtle. Adv. Mater. 2009, 21, 407–412. [Google Scholar] [CrossRef]
- Achrai, B.; Wagner, H.D. The turtle carapace as an optimized multi-scale biological composite armor—A review. J. Mech. Behav. Biomed. Mater. 2017, 73, 50–67. [Google Scholar] [CrossRef] [PubMed]
- Fratzl, P.; Kolednik, O.; Fischer, F.D.; Dean, M.N. The mechanics of tessellations-bioinspired strategies for fracture resistance. Chem. Soc. Rev. 2016, 45, 252–267. [Google Scholar] [CrossRef] [PubMed]
- Hoshizaki, T.B.; Post, A.; Oeur, R.A.; Brien, S.E. Current and Future Concepts in Helmet and Sports Injury Prevention. Neurosurgery 2014, 75, S136–S148. [Google Scholar] [CrossRef] [PubMed]
- Goutnik, M.; Goeckeritz, J.; Sabetta, Z.; Curry, T.; Willman, M.; Willman, J.; Currier Thomas, T.; Lucke-Wold, B. Neurotrauma Prevention Review: Improving Helmet Design and Implementation. Biomechanics 2022, 2, 500–512. [Google Scholar] [CrossRef] [PubMed]
- Jaslow, C.R. Mechanical properties of cranial sutures. J. Biomech. 1990, 23, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Yazdani Sarvestani, H.; Beausoleil, C.; Genest, M.; Ashrafi, B. Architectured Ceramics with Tunable Toughness and Stiffness. Extrem. Mech. Lett. 2020, 39, 100844. [Google Scholar] [CrossRef]
- Li, Y.; Ortiz, C.; Boyce, M.C. A generalized mechanical model for suture interfaces of arbitrary geometry. J. Mech. Phys. Solids 2013, 61, 1144–1167. [Google Scholar] [CrossRef]
- Lin, E.; Li, Y.; Ortiz, C.; Boyce, M.C. 3D printed, bio-inspired prototypes and analytical models for structured suture interfaces with geometrically-tuned deformation and failure behavior. J. Mech. Phys. Solids 2014, 73, 166–182. [Google Scholar] [CrossRef]
- Malik, I.A.; Mirkhalaf, M.; Barthelat, F. Bio-inspired ‘jigsaw’-like interlocking sutures: Modeling, optimization, 3D printing and testing. J. Mech. Phys. Solids 2017, 102, 224–238. [Google Scholar] [CrossRef]
- Malik, I.A.; Barthelat, F. Bioinspired sutured materials for strength and toughness: Pullout mechanisms and geometric enrichments. Int. J. Solids Struct. 2018, 138, 118–133. [Google Scholar] [CrossRef]
- Gibbons, M.M.; Chen, D.A. Bio-Inspired Sutures: Using Finite Element Analysis to Parameterize the Mechanical Response of Dovetail Sutures in Simulated Bending of a Curved Structure. Biomimetics 2022, 7, 82. [Google Scholar] [CrossRef] [PubMed]
- Currey, J.D. The Design of Mineralised Hard Tissues for Their Mechanical Functions. J. Exp. Biol. 1999, 202, 3285–3294. [Google Scholar] [CrossRef] [PubMed]
- Mills, N.J.; Gilchrist, A. Bicycle helmet design. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2006, 220, 167–180. [Google Scholar] [CrossRef]
- Contact Force and Strain Energy Results—Gibbons and Chen. 2023. Available online: https://doi.org/10.6084/m9.figshare.24201420.v1 (accessed on 26 September 2023).

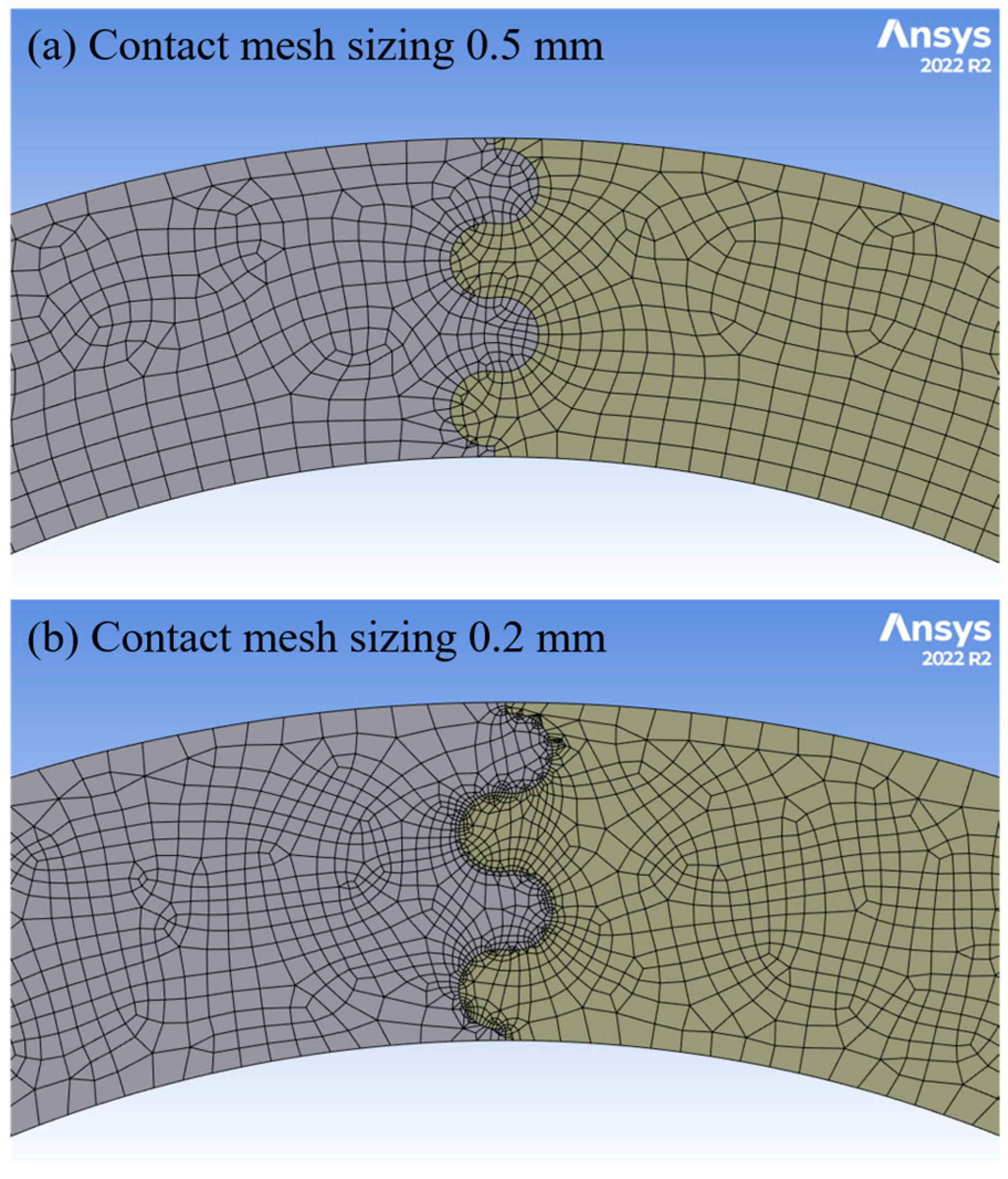



| Mesh Parameters | Nodes (Qty) | Elements (Qty) | CPU Time (s) | Final Contact Force (N) | % Change | Total Strain Energy (J) | % Change | |
|---|---|---|---|---|---|---|---|---|
| Coarse | Global element size: 3 mm | 58,527 | 12,195 | 397 | 22,371 | N/A | 70.674 | N/A |
| Medium | Global element size: 3 mm Contact sizing: 1 mm | 169,030 | 52,490 | 1141 | 22,400 | 0.13% | 70.906 | 0.33% |
| Fine | Global element size: 3 mm Contact sizing: 0.5 mm | 457,715 | 159,522 | 6940 | 22,437 | 0.17% | 71.221 | 0.44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gibbons, M.M.; Chen, D.A. Bio-Inspired Sutures: Simulating the Role of Suture Placement in the Mechanical Response of Interlocking Structures. Biomimetics 2023, 8, 515. https://doi.org/10.3390/biomimetics8070515
Gibbons MM, Chen DA. Bio-Inspired Sutures: Simulating the Role of Suture Placement in the Mechanical Response of Interlocking Structures. Biomimetics. 2023; 8(7):515. https://doi.org/10.3390/biomimetics8070515
Chicago/Turabian StyleGibbons, Melissa M., and Diana A. Chen. 2023. "Bio-Inspired Sutures: Simulating the Role of Suture Placement in the Mechanical Response of Interlocking Structures" Biomimetics 8, no. 7: 515. https://doi.org/10.3390/biomimetics8070515
APA StyleGibbons, M. M., & Chen, D. A. (2023). Bio-Inspired Sutures: Simulating the Role of Suture Placement in the Mechanical Response of Interlocking Structures. Biomimetics, 8(7), 515. https://doi.org/10.3390/biomimetics8070515







