Bioinspired Rigid–Flexible Coupled Adaptive Compliant Motion Control of Robot Gecko for Space Stations
Abstract
:1. Introduction
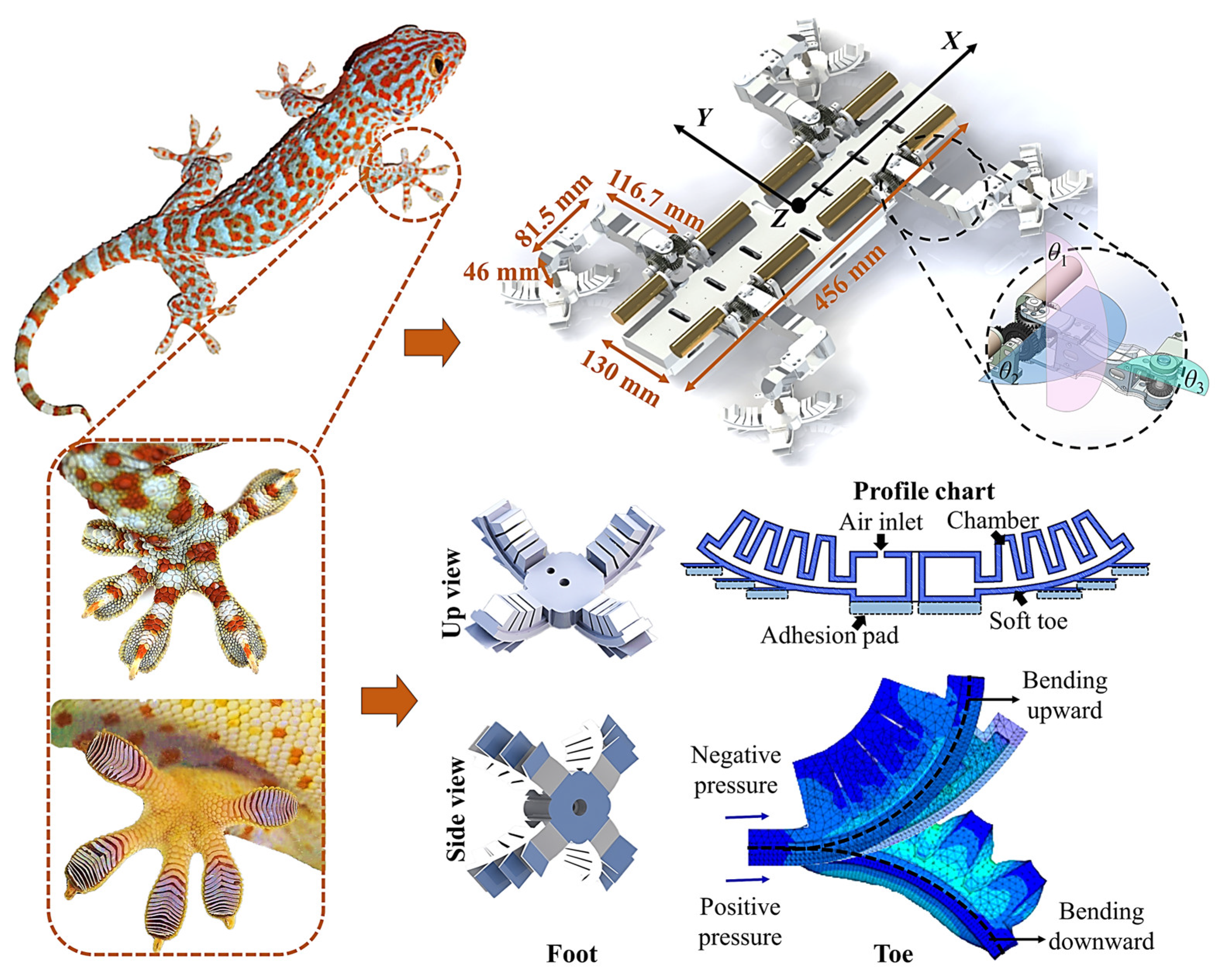
2. Biomimetic Mechanism
3. The Design of the Robot Gecko
3.1. Bionic Mechanical Design
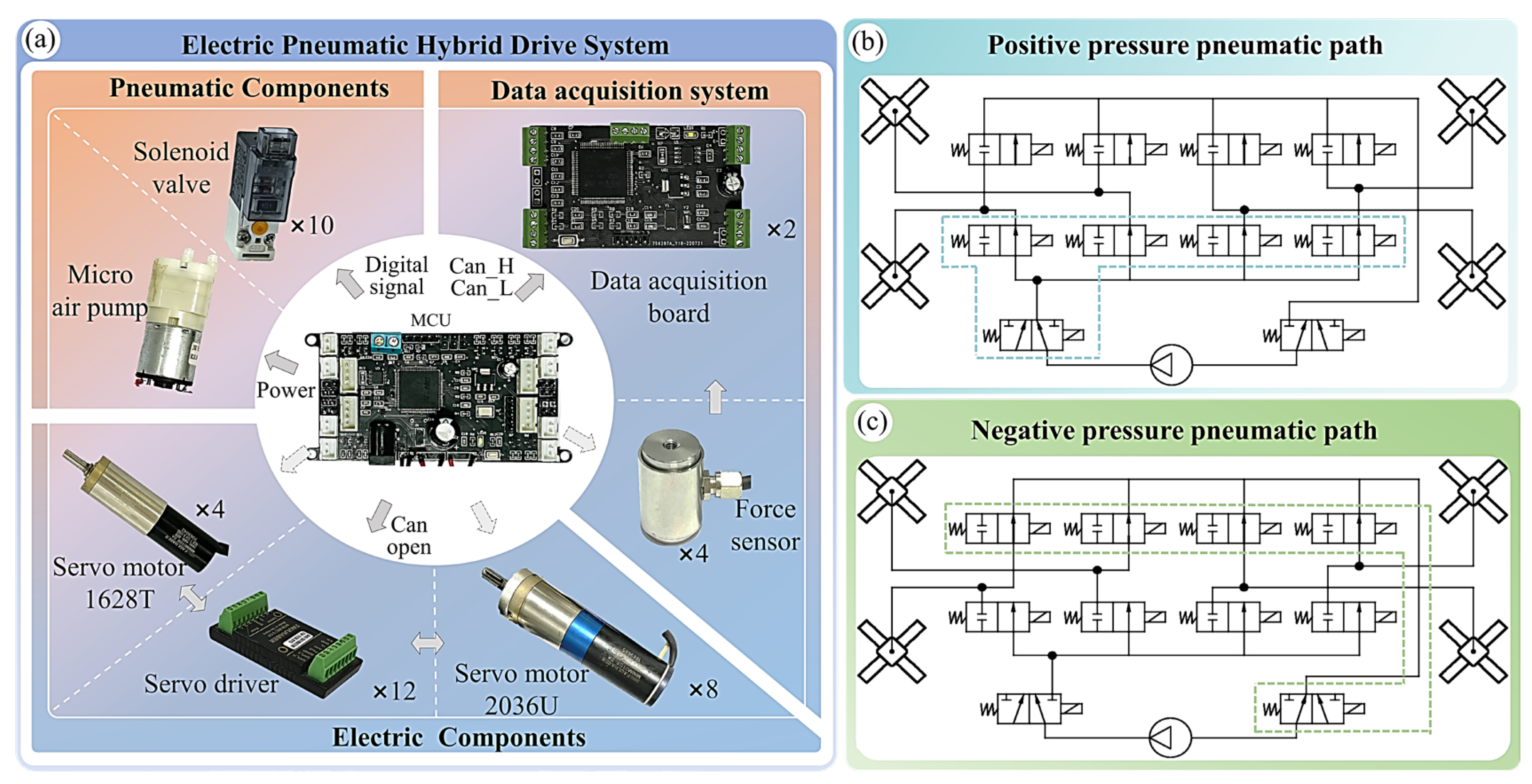
3.2. Biomimetic Hybrid-Driven Design
3.3. Design of Data Acquisition and Control System
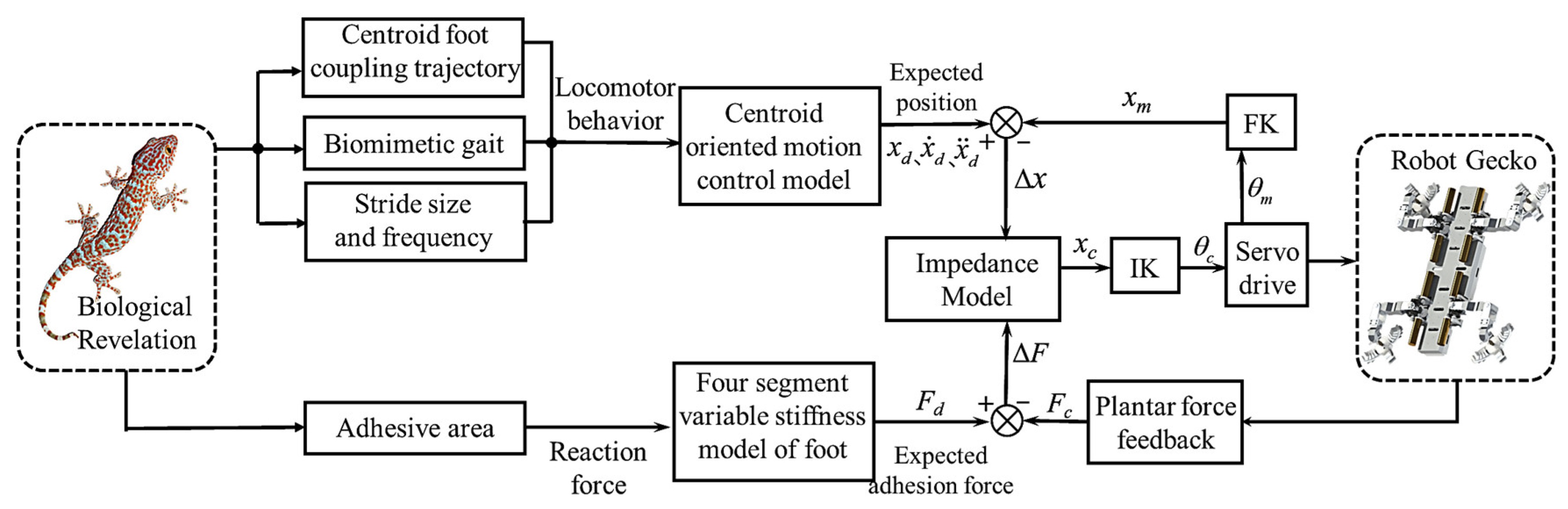
4. Adaptive Active Compliant Control Strategy
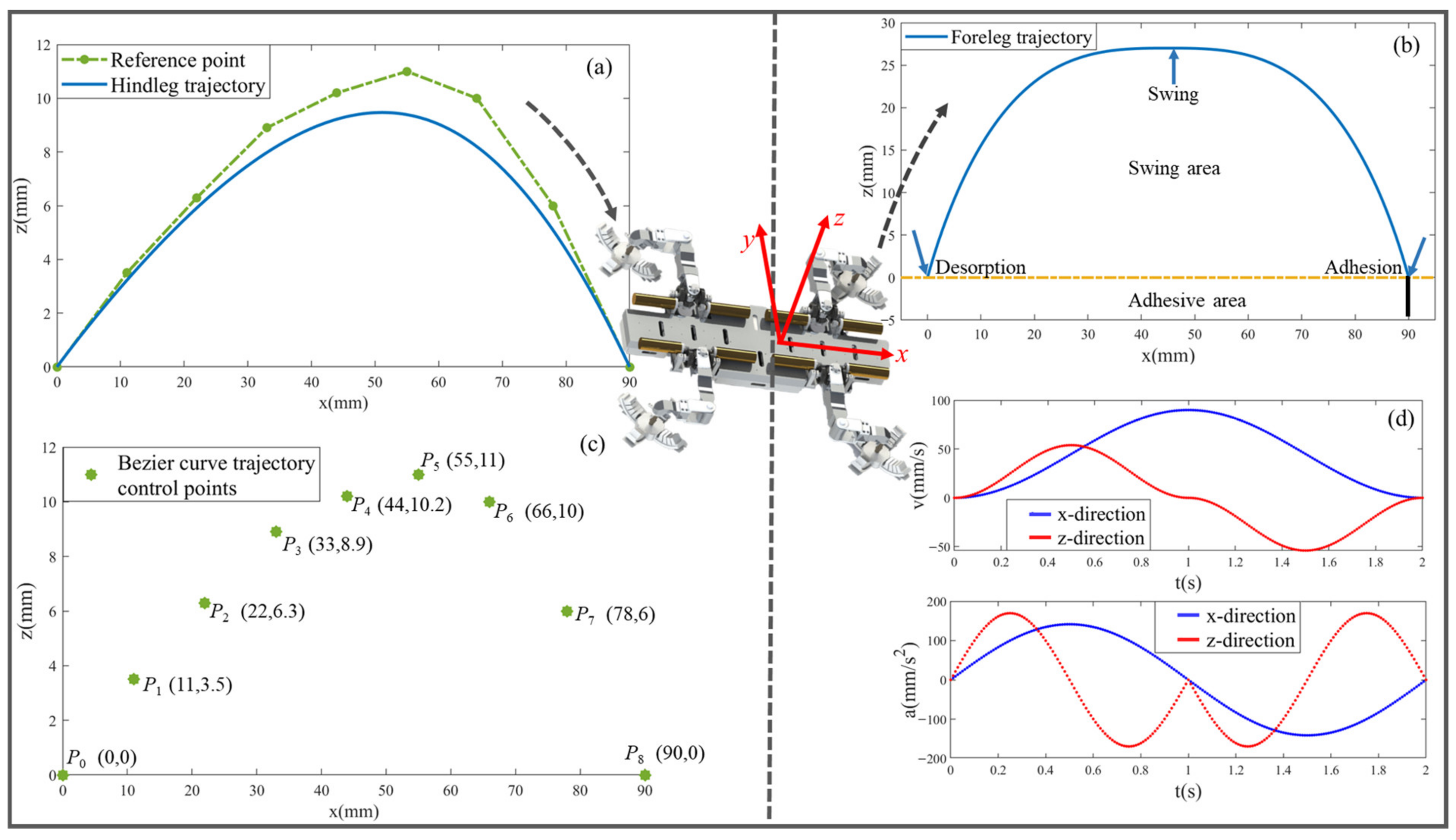
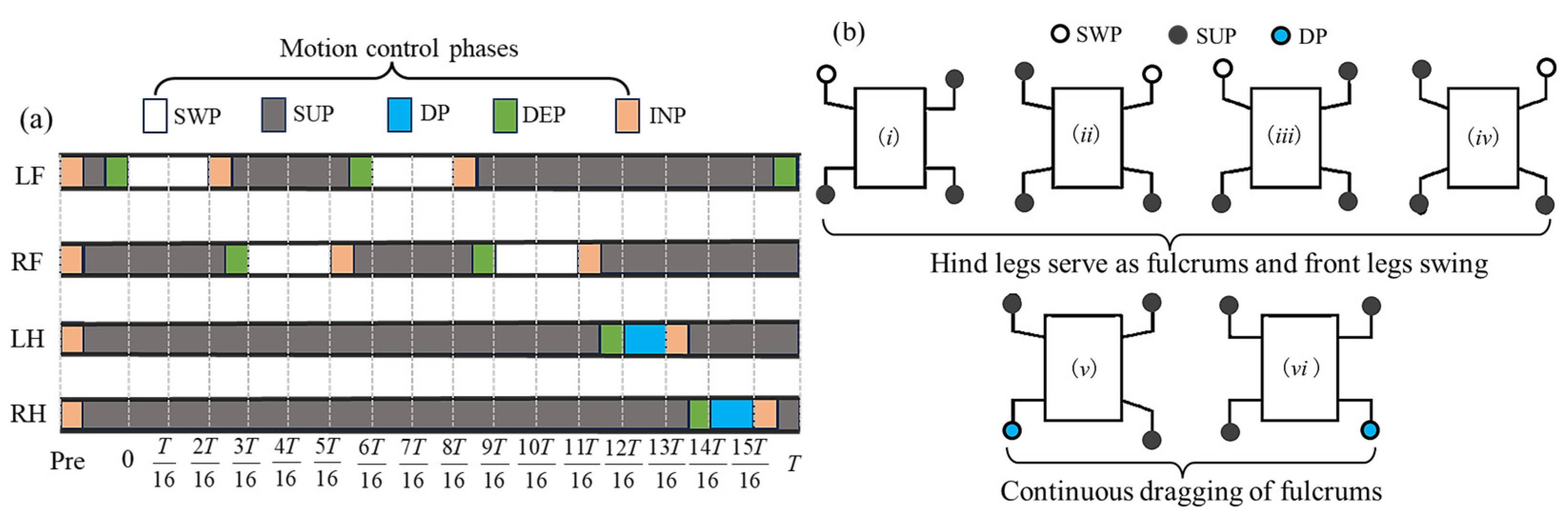
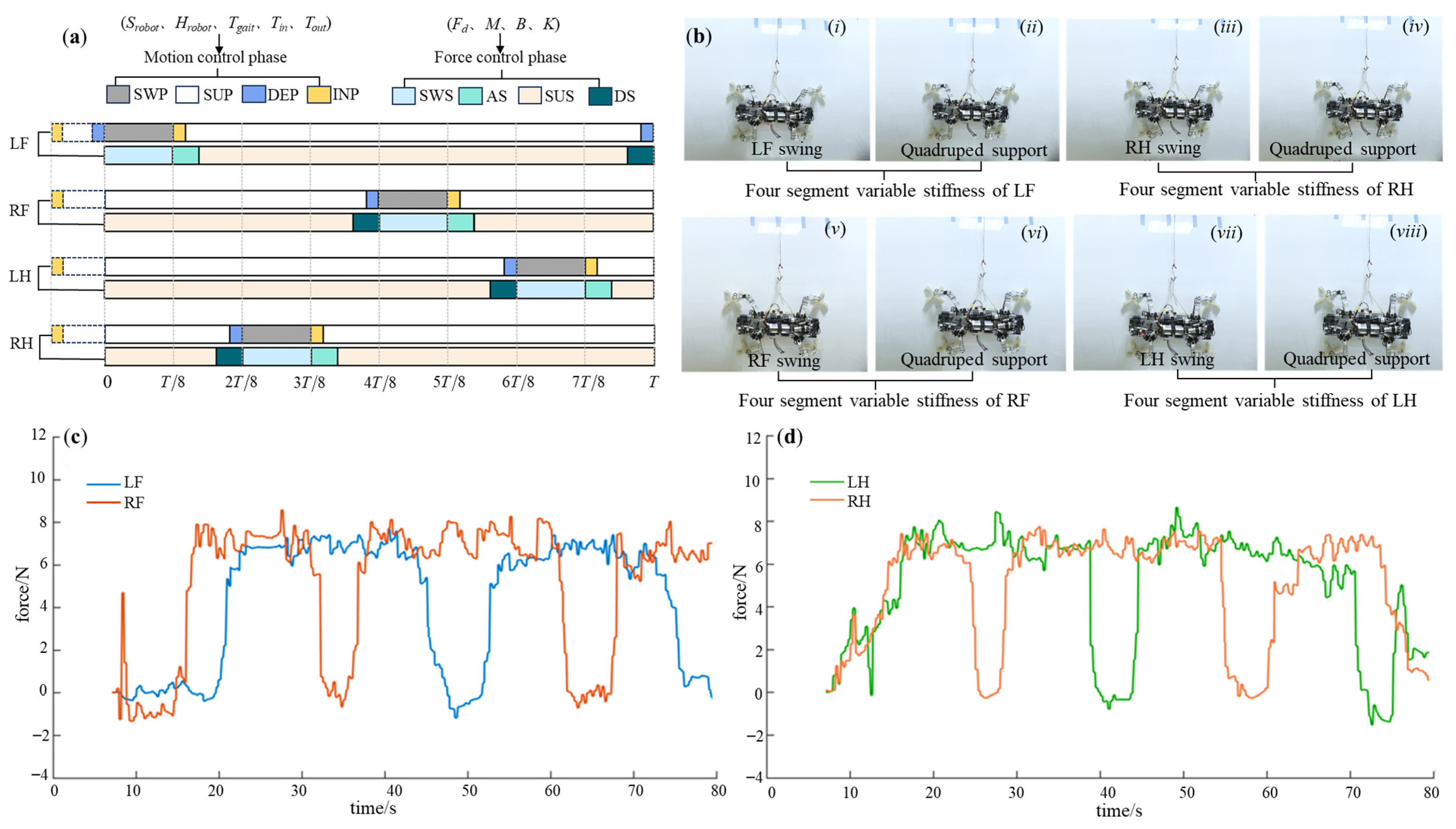
4.1. Motion Planning Based on Bionic Inspiration
4.1.1. Centroid-Foot Coupling Motion Planning
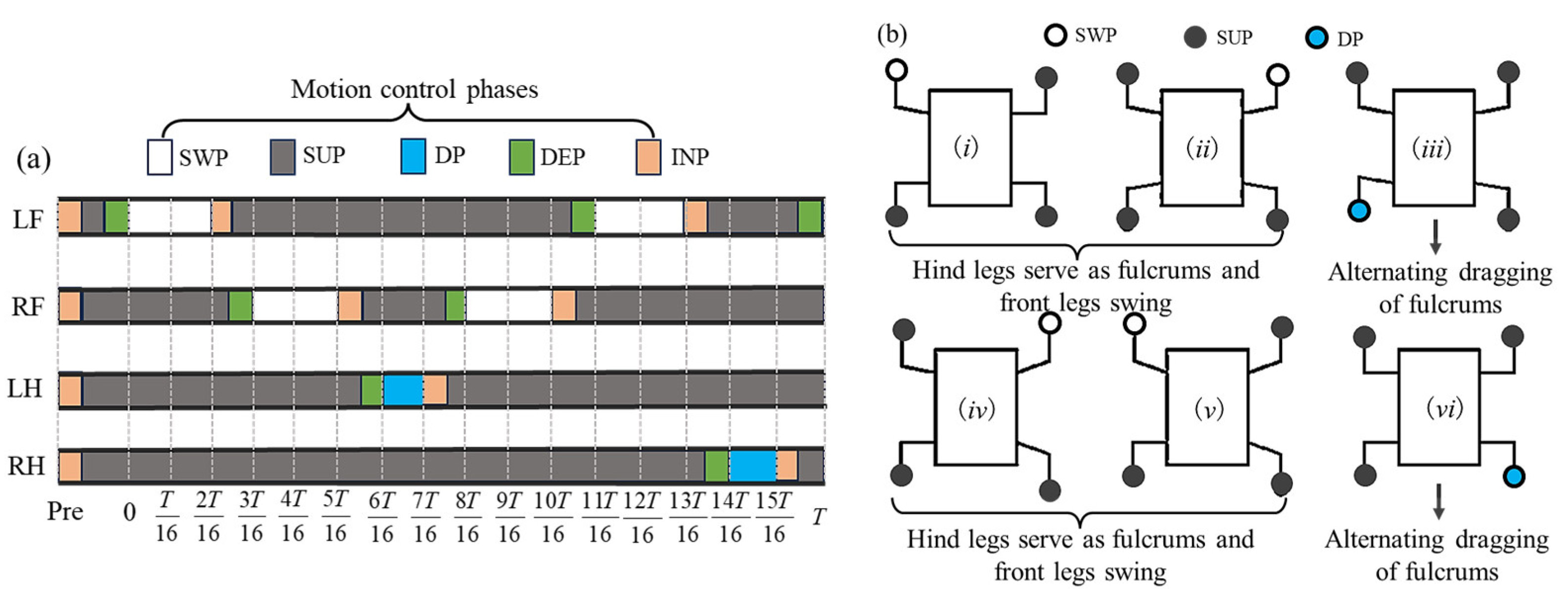
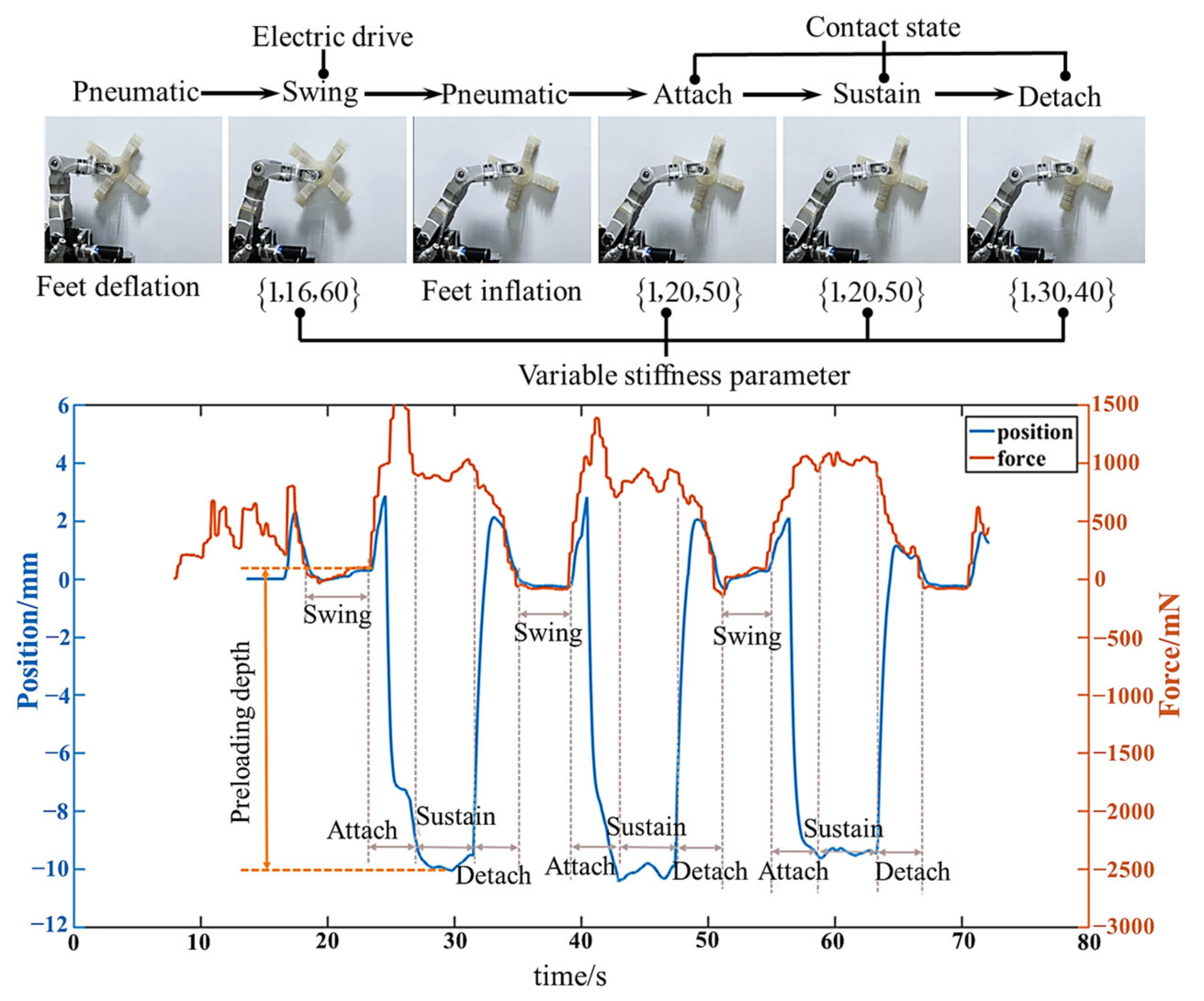
- Attachment segment (AS): The foot finds the landing point and inflates the toes of the foot in response to environmental force feedback. Thus, the attachment process is completed. During this stage, the position of the foot relative to the world coordinate system remains unchanged, relying mainly on the characteristics of the foot for attachment.
- Support segment (SUS): The foot maintains the attachment state. During this stage, the position of the foot remains unchanged.
- Detachment segment (DS): When detachment is required, the foot deflates the toes of the foot to complete detachment. During this stage, the position of foot remains unchanged, relying on the characteristics of the foot, just the same as the attachment segment.
- Swing segment (SWS): After detachment, the foot enters the swing phase, and the single leg takes a step forward. During this stage, the position of the foot changes, and planning in three directions individually is required.
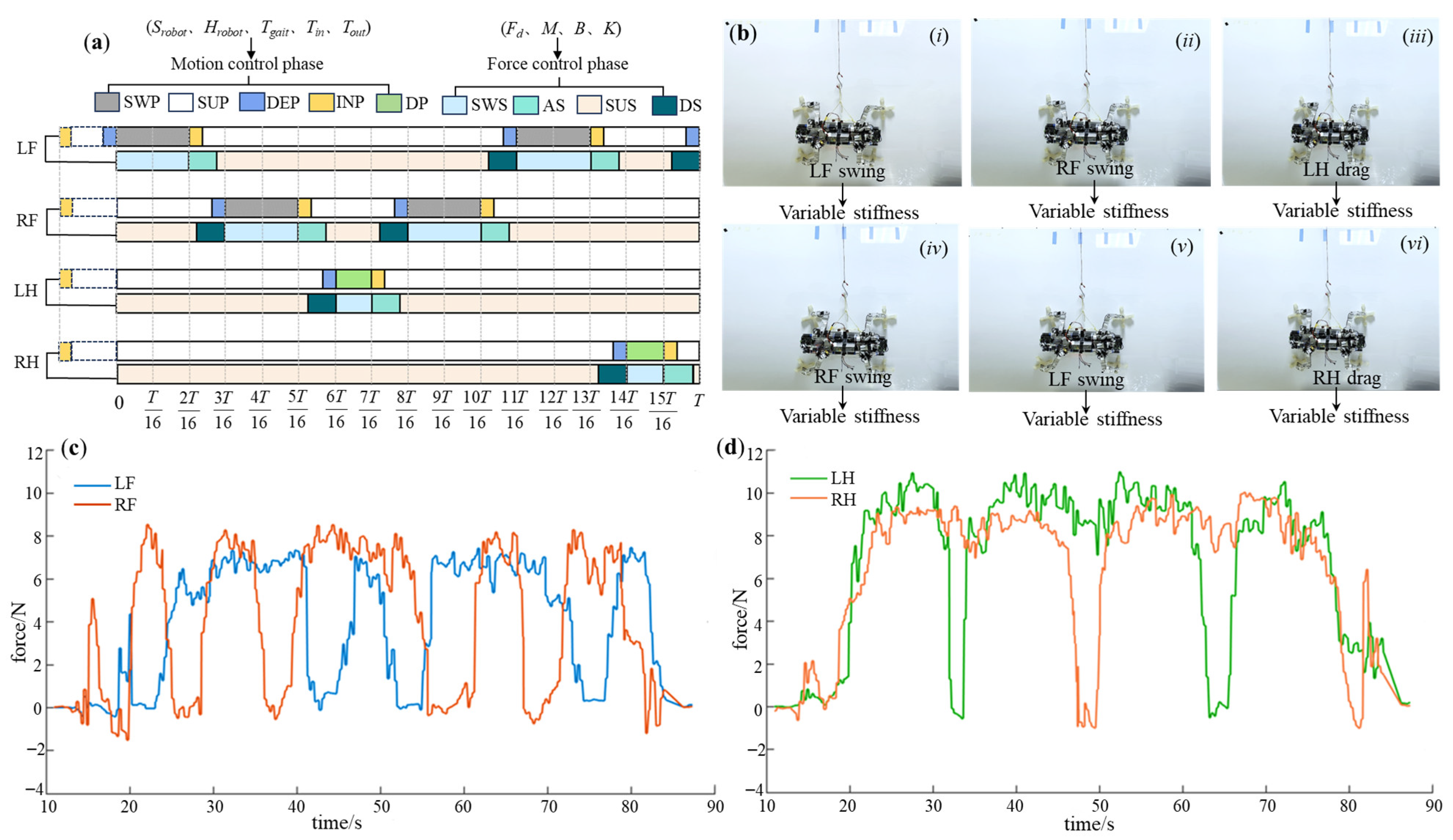
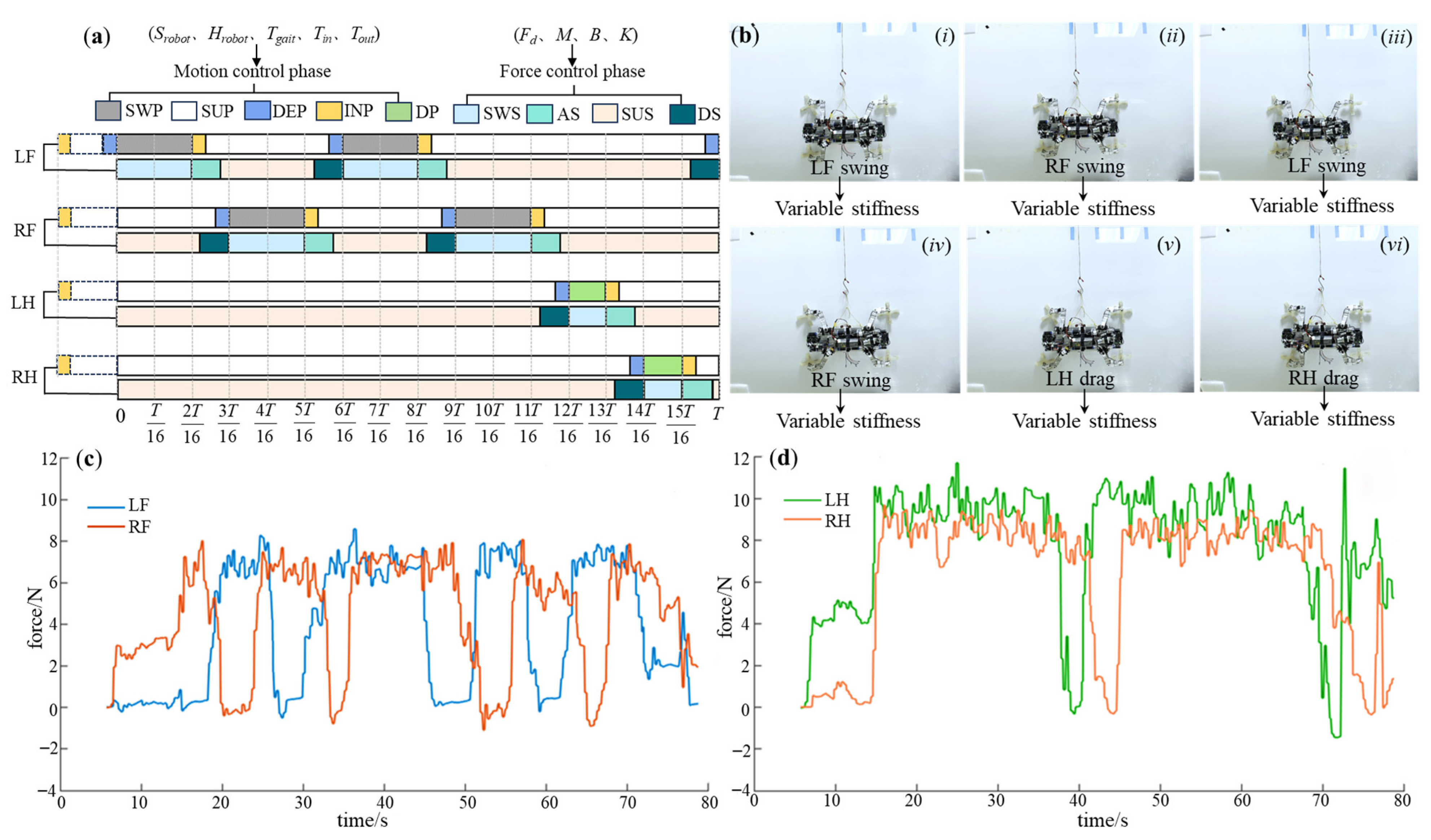
4.1.2. Biomimetic Gait Design for Microgravity
4.2. Adaptive Variable Stiffness Active Compliance Control
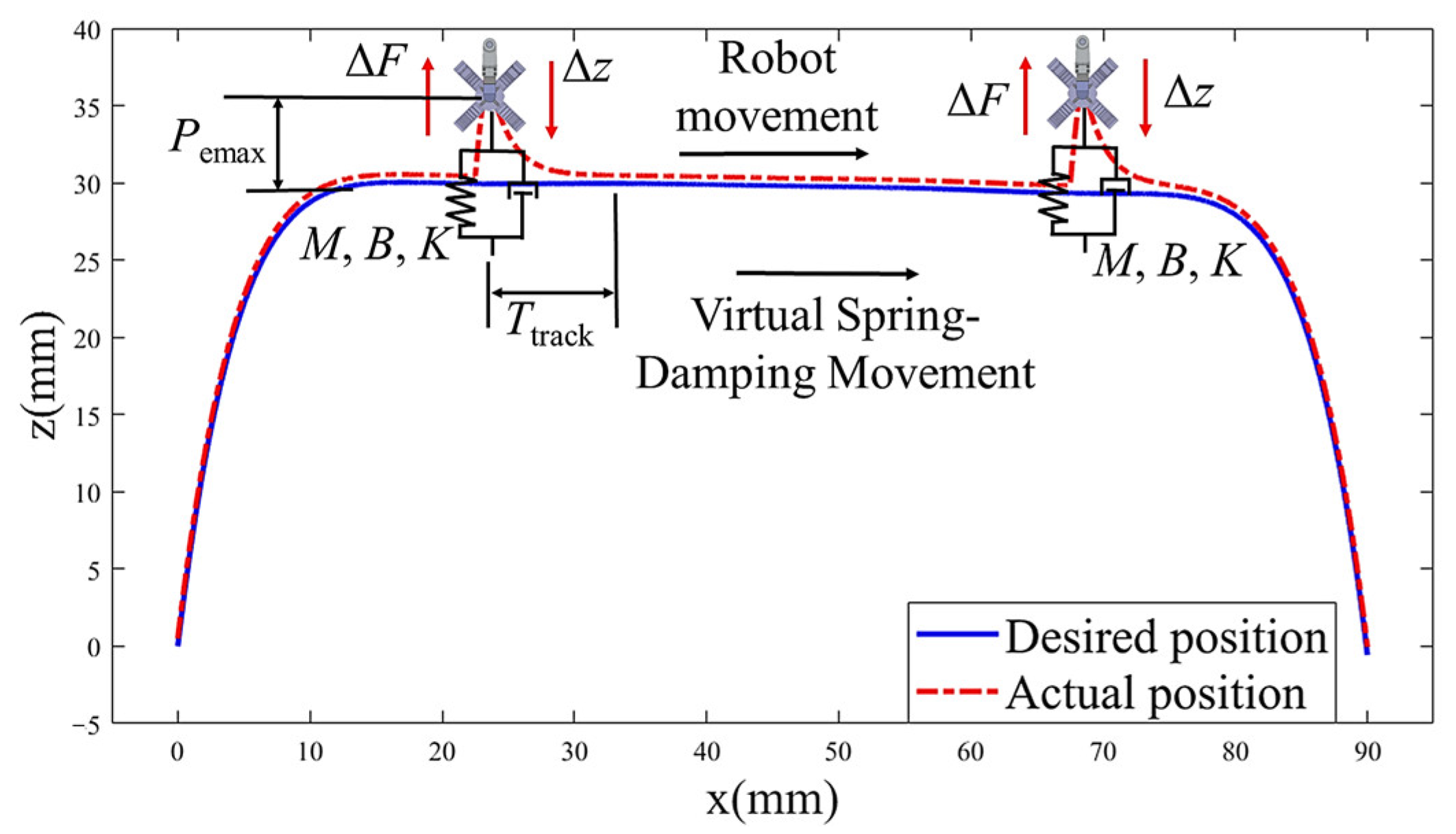
4.2.1. Active Compliance Control
4.2.2. Segmented Variable Stiffness Strategy
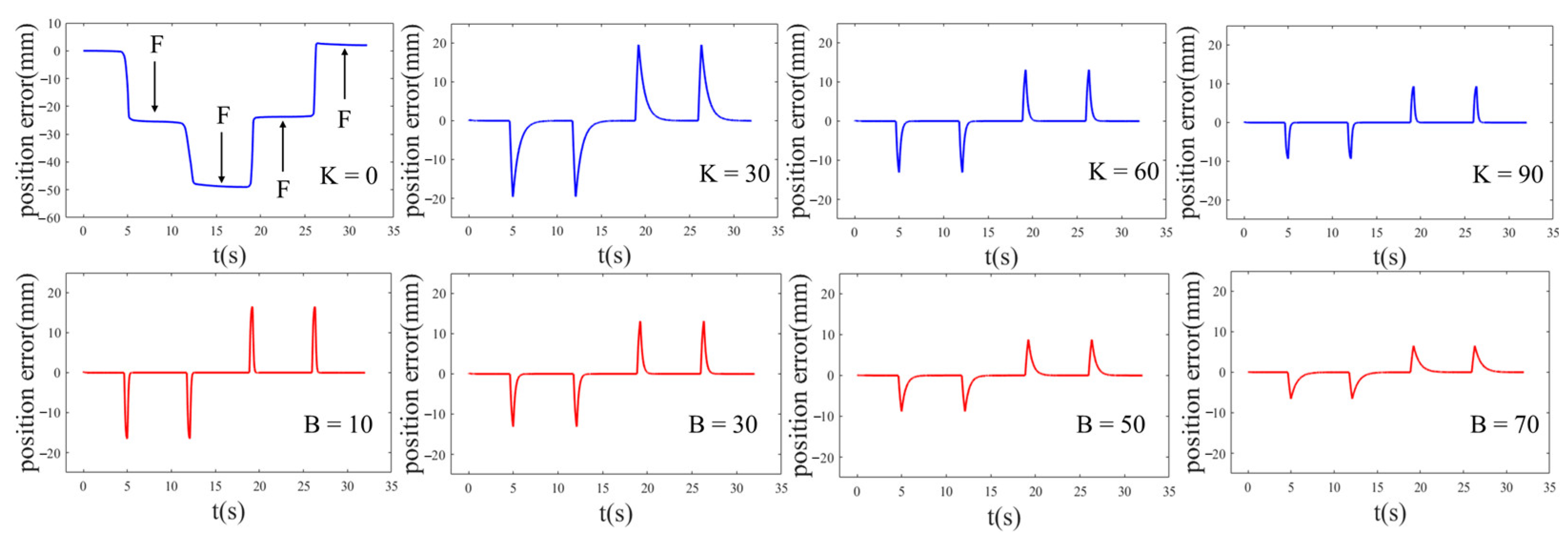
- The actual position deviates due to external disturbing forces. After the disturbance is withdrawn, the actual position starts to follow the desired trajectory;
- With M and B unchanged (M = 1, B = 20), when K = 0, the robot lacks stiffness and does not track the desired position. When K = 30, the position begins to follow, with an average position tracking time of 2.69 s. That is 1.75 s when K = 60, 0.61 s when K = 90. The data shows that under the same external disturbance, the position tracking time decreases with increasing stiffness. The stiffness coefficient affects the position tracking performance;
- With M and K unchanged (M = 1, K = 30), when B = 10, the average position tracking time is 0.53 s. When B = 30, that is 1.02 s, 2.84 s when B = 50, and 3.88 s when B = 70. The data shows that under the same external disturbance, the position tracking time increases with increasing damping. The damping coefficient affects the response speed of position tracking;
- Different stiffness and damping exhibit completely different force control characteristics and are suitable for different application scenarios. When flexible contact is required, stiffness is reduced, while stiffness is increased when disturbance rejection is needed. This reflects the variable stiffness characteristics of the robot motion.
5. Experiments
5.1. Construction of Microgravity Simulation Experimental Platform
5.2. Open-Loop Motion Control Experiment
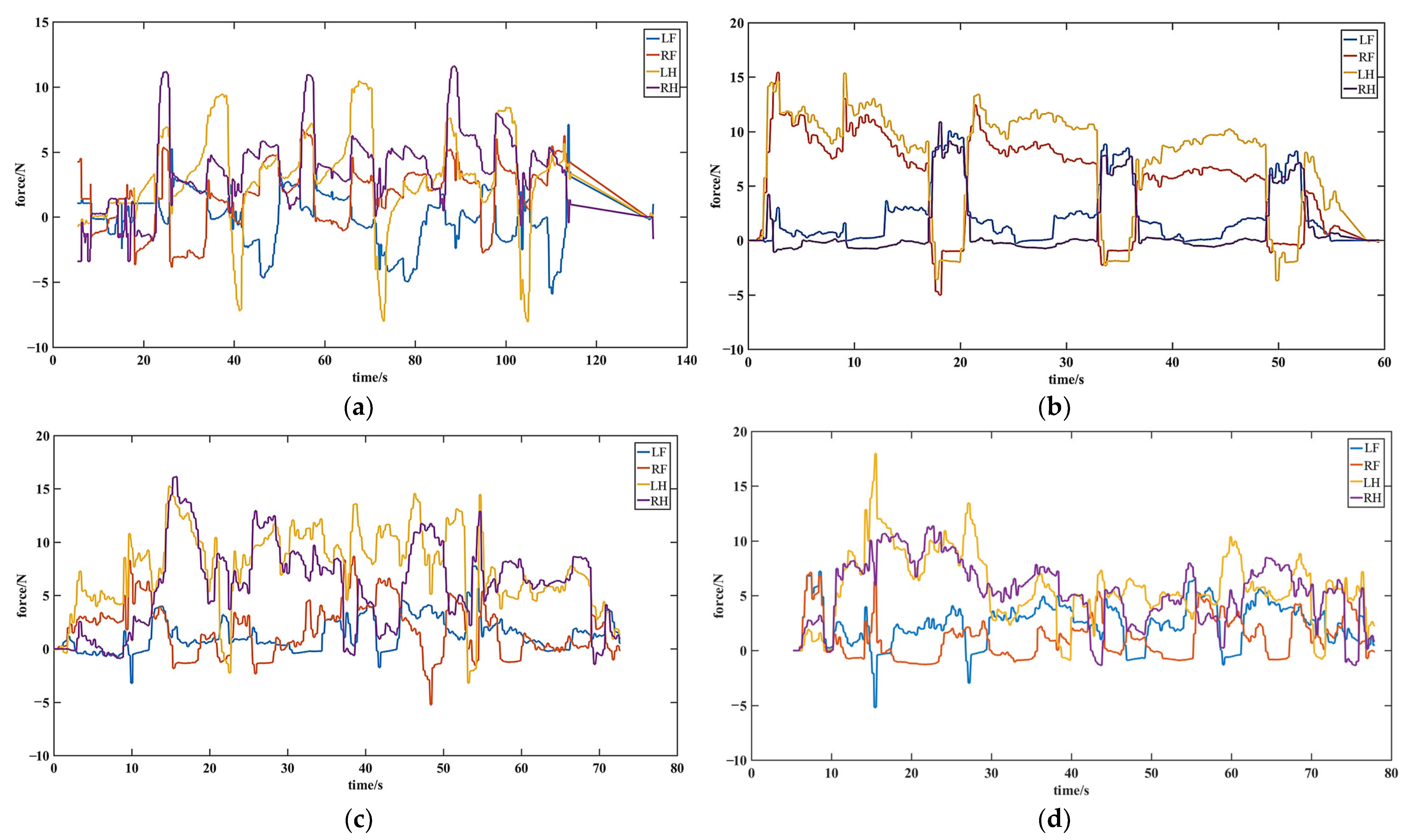
5.3. Static Anti-Interference Experiment
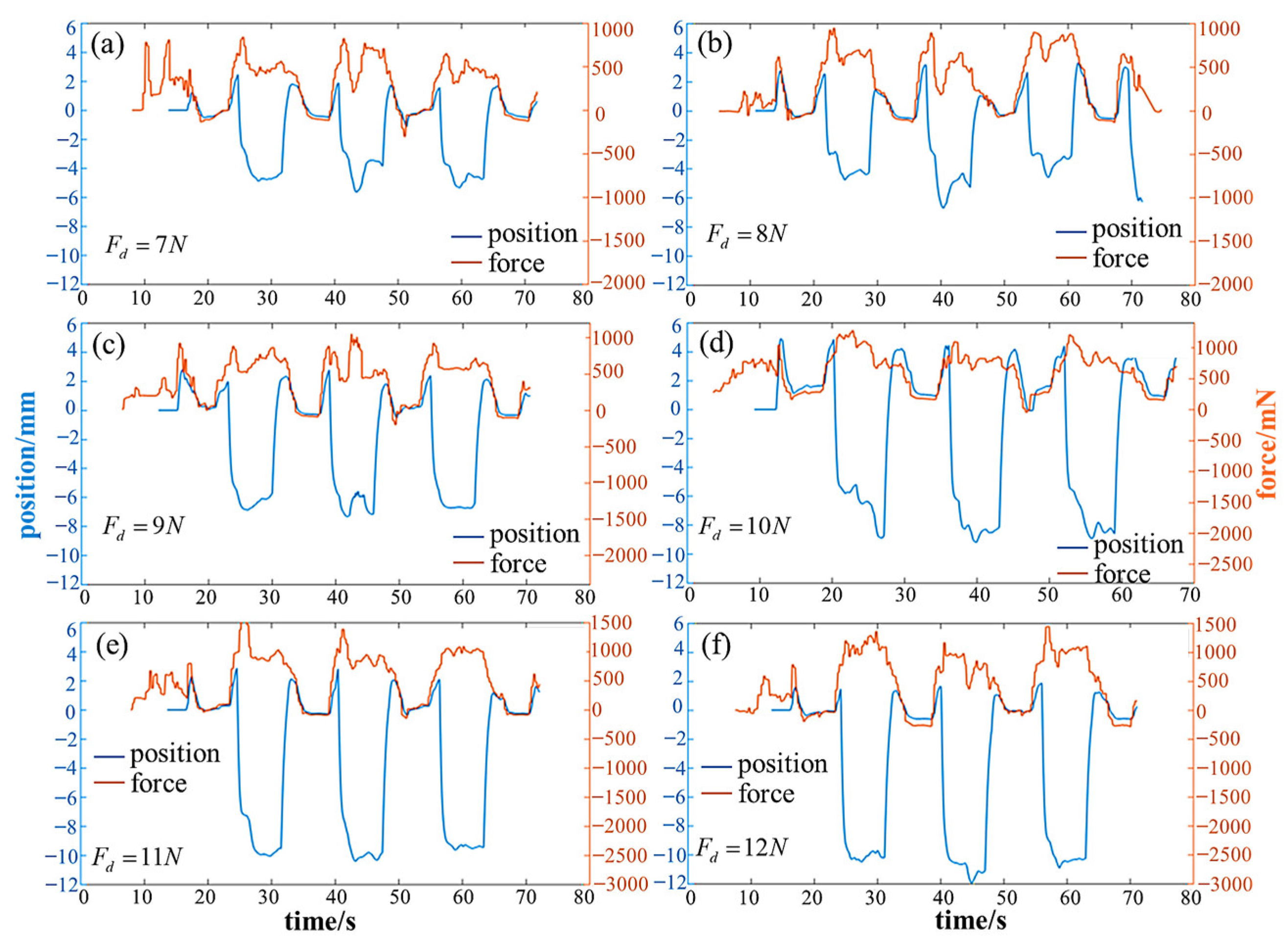
5.4. Segmented Variable Stiffness Experiments
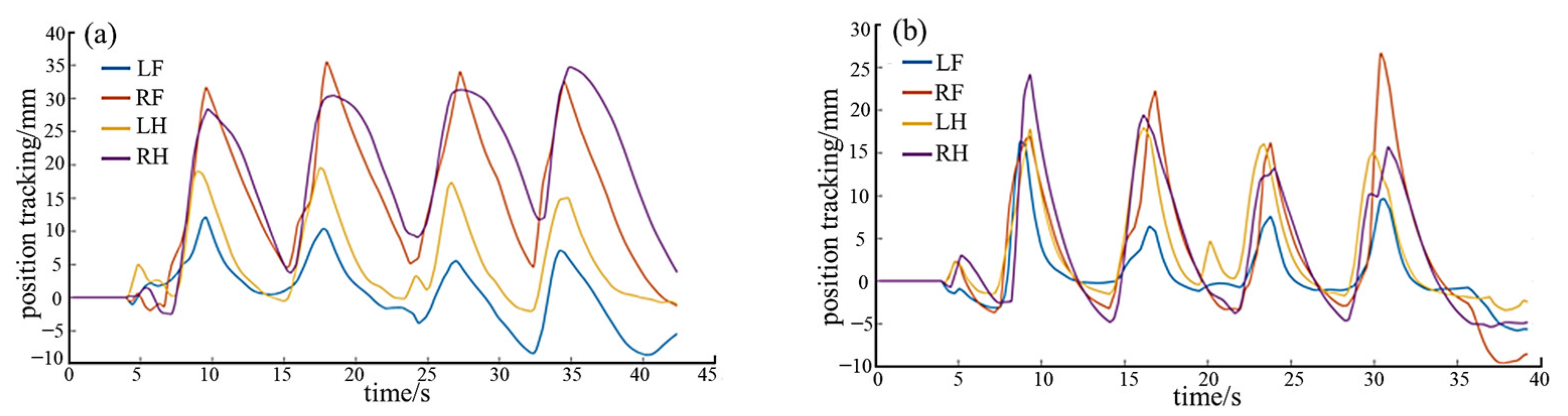
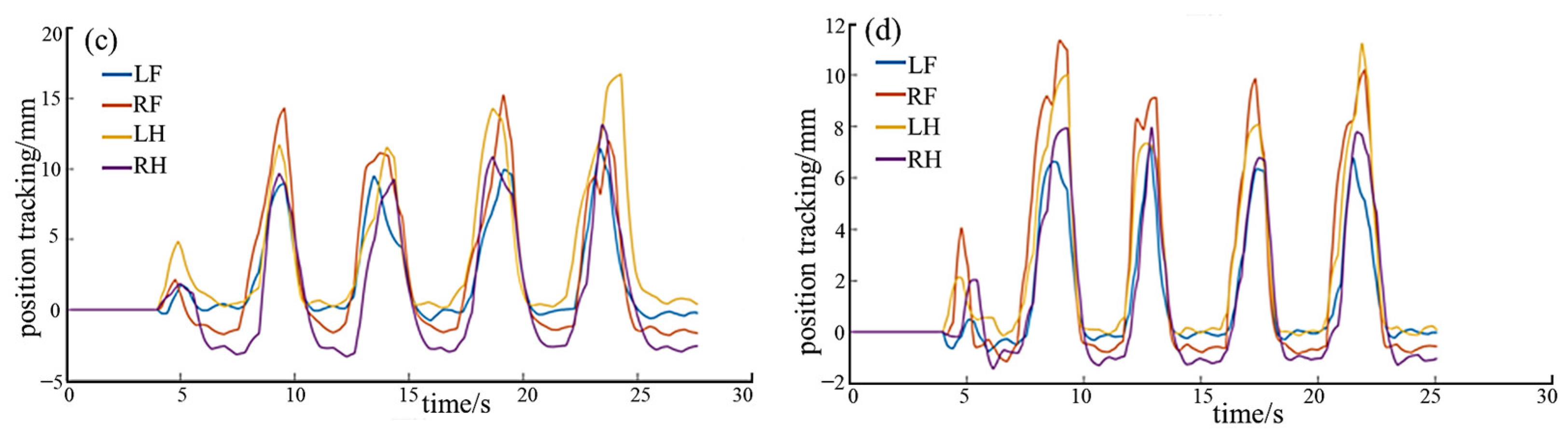
5.5. Adaptive Compliant Motion Control Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, G.; Han, L.L.; Zhang, C.F. Research progress and technical challenges of space robot. Acta Aeronaut. Astronaut. Sin. 2021, 42, 8–32. [Google Scholar]
- Gao, Y.; Chien, S. Review on space robotics: Toward top-level science through space exploration. Sci. Robot. 2017, 2, 5074. [Google Scholar] [CrossRef] [PubMed]
- Dai, Z.D.; Peng, F.J. Research progress of space robots and key technologies of gecko-inspired robots. Chin. Sci. Bull. 2015, 60, 3114–3124. [Google Scholar]
- Song, Y.; Dai, Z.D.; Wang, Z.Y.; Full, R.J. Role of multiple, adjustable toes in distributed control shown by sideways wall-running in geckos. Proc. R. Soc. B Biol. Sci. 2020, 287, 20200123. [Google Scholar] [CrossRef]
- Barabanov, V.M.; Gulimova, V.I.; Berdiev, R.K.; Saveliev, S.V. Individual features of play behavior in thick-toed geckos in weightlessness and normal gravity conditions. Life Sci. Space Res. 2019, 22, 38–46. [Google Scholar] [CrossRef]
- Barabanov, V.M.; Gulimova, V.I.; Berdiev, R.K.; Saveliev, S.V. Object play in thick-toed geckos during a space experiment. J. Ethol. 2015, 33, 109–115. [Google Scholar] [CrossRef]
- Nishi, A.; Wakasugi, Y.; Watanabe, K. Design of a robot capable of moving on a vertical wall. Adv. Robot. 1986, 1, 33–45. [Google Scholar] [CrossRef]
- Nishi, A. Development of wall-climbing robots. Comput. Electr. Eng. 1996, 22, 123–149. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, S.; Bi, Q.S.; Cui, D.; Yan, C.L. Design and Technical Development of Wall-Climbing Robots: A Review. J. Bionic Eng. 2022, 19, 877–901. [Google Scholar] [CrossRef]
- Fang, G.S.; Cheng, J.F. Advances in Climbing Robots for Vertical Structures in the Past Decade: A Review. Biomimetics 2023, 8, 47. [Google Scholar] [CrossRef]
- Nansai, S.; Elara, M.R. A Survey of Wall Climbing Robots: Recent Advances and Challenges. Robotics 2016, 5, 14. [Google Scholar] [CrossRef]
- Kim, S.; Spenko, M.; Trujillo, S.; Heyneman, B.; Santos, D.; Cutkosky, M.R. Smooth Vertical Surface Climbing with Directional Adhesion. IEEE Trans. Robot. 2008, 24, 65–74. [Google Scholar] [CrossRef]
- Li, Y.S.; Ahmed, A.; Sameoto, D. Abigaille II: Toward the development of a spider-inspired climbing robot. Robotica 2012, 30, 79–89. [Google Scholar] [CrossRef]
- Henrey, M.; Ahmed, A.; Bosscariol, P. Abigaille-III: A Versatile, Bioinspired Hexapod for Scaling Smooth Vertical Surfaces. J. Bionic Eng. 2014, 11, 1–17. [Google Scholar] [CrossRef]
- Birkmeyer, P.; Gillies, A.G.; Fearing, R.S. Dynamic Climbing of Near-Vertical Smooth Surfaces. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012; pp. 286–292. [Google Scholar]
- Asbeck, A.T.; Sangbae, K.; McClung, A. Climbing walls with microspines. In Proceedings of the Conference on International Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 4315–4317. [Google Scholar]
- Spenko, M.J.; Haynes, G.C.; Saunders, J.A. Biologically inspired climbing with a hexapedal robot. J. Field Robot. 2008, 25, 223–242. [Google Scholar] [CrossRef]
- Tanaka, Y.; Shirai, Y.; Lin, X. SCALER: A Tough Versatile Quadruped Free-Climber Robot. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Kyoto, Japan, 23–27 October 2022; pp. 5632–5639. [Google Scholar]
- Tavakoli, M.; Lourenço, J.; Viegas, C. The hybrid Omni Climber robot: Wheel based climbing, arm based plane transition, and switchable magnet adhesion. Mechatronics 2016, 36, 136–146. [Google Scholar] [CrossRef]
- Zou, H.; Liu, Z.; Zhao, X. Characteristic Analysis of Wall-Climbing Robot Magnet-Wheel Based on Halbach Array. Light Ind. Mach. 2019, 37, 28–31,42. [Google Scholar]
- Zhou, Q.; Xin, L. Experimental investigation on climbing robot using rotation-flow adsorption unit. Robot. Auton. Syst. 2018, 105, 112–120. [Google Scholar] [CrossRef]
- Chen, R.; Huang, Y.; Tang, Q. An analytical model for electrostatic adhesive dynamics on dielectric substrates. J. Adhes. Sci. Technol. 2017, 31, 1229–1250. [Google Scholar] [CrossRef]
- Koh, K.H.; Sreekumar, M.; Ponnambalam, S.G. Hybrid electrostatic and elastomer adhesion mechanism for wall climbing robot. Mechatronics 2016, 35, 122–135. [Google Scholar] [CrossRef]
- Unver, O.; Uneri, A.; Aydemir, A. Geckobot: A Gecko Inspired Climbing Robot Using Elastomer Adhesives. In Proceedings of the IEEE International Conference on Robotics and Automation ICRA, Orlando, FL, USA, 15–19 May 2006; pp. 2329–2336. [Google Scholar]
- Wang, Z.Y.; Lu, X.B.; Liu, Q. Adhesion performance test and trajectory optimization for gecko-inspired footpad under simulated micro-gravity environment. Chin. Sci. Bull. 2017, 62, 2149–2156. [Google Scholar] [CrossRef]
- Srisuchinnawong, A.; Wang, B.C.; Shao, D.H. Modular Neural Control for Gait Adaptation and Obstacle Avoidance of a Tailless Gecko Robot. J. Intell. Robot. Syst. 2021, 101, 27. [Google Scholar] [CrossRef]
- Wang, B.J.; Xiong, X.F.; Duan, J.J. Compliant Detachment of Wall-Climbing Robot Unaffected by Adhesion State. Appl. Sci. 2021, 11, 5860. [Google Scholar] [CrossRef]
- Wang, B.J.; Wang, Z.Y.; Song, Y.F. A Neural Coordination Strategy for Attachment and Detachment of a Climbing Robot Inspired by Gecko Locomotion. Cyborg Bionic Syst. 2023, 4, 0008. [Google Scholar] [CrossRef]
- Autumn, K.; Liang, Y.A.; Hsieh, S.T. Adhesive force of a single gecko foot-hair. Nature 2000, 405, 681–685. [Google Scholar] [CrossRef]
- Autumn, K.; Gravish, N. Gecko adhesion: Evolutionary nanotechnology. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 1575–1590. [Google Scholar] [CrossRef] [PubMed]
- Autumn, K.; Sitti, M.; Liang, Y.A. Evidence for van der Waals adhesion in gecko setae. Proc. Natl. Acad. Sci. USA 2002, 99, 12251–12256. [Google Scholar] [CrossRef]
- Autumn, K.; Puthoff, J. Properties, principles, and parameters of the gecko adhesive system. In Biological Adhesives; Springer: Cham, Switzerland, 2016; pp. 245–280. [Google Scholar]
- Autumn, K.; Dittomore, A.; Santos, D. Frictional adhesion: A new angle gecko attachment. J. Exp. Biol. 2006, 209, 3569–3579. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, Z.; Ji, A. Biomechanics of gecko locomotion: The patterns of reaction forces on inverted, vertical and horizontal substrates. Bioinspir. Biomim. 2015, 10, 16019. [Google Scholar] [CrossRef]
- Carbone, G.; Pierro, E.; Gorb, S. Origin of the superior adhesive performance of mushroom-shaped micro structured surfaces. Soft Matter 2011, 7, 5545–5552. [Google Scholar] [CrossRef]
- Chen, J.; Ding, N.; Li, Z.; Wang, W. Organic polymer materials in the space environment. Prog. Aerosp. Sci. 2016, 83, 37–56. [Google Scholar] [CrossRef]
- Day, P.; Cutkosky, M.; Mclaughlin, A. Effects of gamma irradiation on adhesion of polymer microstructure-based dry adhesives. Nucl. Technol. 2013, 180, 450–455. [Google Scholar] [CrossRef]
- Henrey, M.; Tellez, J.; Wormnes, K.; Pambaguian, L.; Menon, C. Towards the use of mushroom-capped dry adhesives in outer space: Effects of low pressure and temperature on adhesion strength. Aerosp. Sci. Technol. 2013, 29, 185–190. [Google Scholar] [CrossRef]
- Wang, L.W.; Wang, Z.Y.; Wang, B.C. Reversible Adhesive Bio-Toe with Hierarchical Structure Inspired by Gecko. Biomimetics 2023, 8, 40. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Gorb, S.N.; Dai, Z.D. Control strategies of gecko’s toe in response to reduced gravity. Appl. Sci. 2020, 10, 2257. [Google Scholar] [CrossRef]




| Description | Mark | TG | DG | A-FS | C-FS | ||||
|---|---|---|---|---|---|---|---|---|---|
| Front Legs | Hind Legs | Front Legs | Hind Legs | Front Legs | Hind Legs | Front Legs | Hind Legs | ||
| stride distance | Srobot (mm) | 90 | 90 | 90 | 90 | 45 | 90 | 45 | 90 |
| stride height | Hrobot (mm) | 27 | 27 | 27 | 27 | 27 | 9 | 27 | 9 |
| gait period | Tonegait (s) | 16 | 6 | 32 | 32 | ||||
| foot inflation time | Tin (s) | 0.3 | 0.3 | 0.3 | 0.3 | ||||
| foot deflation time | Tout (s) | 0.5 | 0.5 | 0.5 | 0.5 | ||||
| Stiffness Value | K = 0 | K = 30 | K = 60 | K = 90 |
|---|---|---|---|---|
| MPD (mm) | Not track | 22.27 | 13.53 | 7.93 |
| MRT (s) | Not track | 3.57 | 1.86 | 0.89 |
| Damping Value | B = 10 | B = 30 | B = 50 | B = 70 |
|---|---|---|---|---|
| MPD (mm) | 13.19 | 10.19 | 13.17 | 12.16 |
| MRT (s) | 1.01 | 2.07 | 3.65 | 4.03 |
| Desired Attachment Force (N) | Fd = 7 | Fd = 8 | Fd = 9 | Fd = 10 | Fd = 11 | Fd = 12 |
|---|---|---|---|---|---|---|
| Mean preloading depth (mm) | 4.64 | 5.21 | 6.67 | 8.23 | 9.45 | 10.36 |
| Mean response time (s) | 1.97 | 2.04 | 2.14 | 2.17 | 2.21 | 2.23 |
| Mean force tracking deviation (N) | 1.12 | 1.31 | 1.64 | 1.53 | 1.41 | 1.62 |
| Leg | Fd | {M,B,K} of SWS | {M,B,K} of AS | {M,B,K} of SUS | {M,B,K} of DS |
|---|---|---|---|---|---|
| LF | 8.0 | {1,16,20} | {1,20,50} | {1,20,50} | {1,30,40} |
| RF | 8.0 | {1,16,20} | {1,20,50} | {1,20,50} | {1,30,40} |
| LH | 8.0 | {1,16,20} | {1,20,50} | {1,20,50} | {1,30,40} |
| RH | 8.0 | {1,16,20} | {1,20,50} | {1,20,50} | {1,30,40} |
| Leg | Fd | {M,B,K} of SWS | {M,B,K} of AS | {M,B,K} of SUS | {M,B,K} of DS |
|---|---|---|---|---|---|
| LF | 8.0 | {1,16,60} | {1,20,50} | {1,20,50} | {1,30,40} |
| RF | 8.0 | {1,16,60} | {1,20,50} | {1,20,50} | {1,30,40} |
| LH | 12.0 | {1,16,60} | {1,16,55} | {1,16,55} | {1,25,45} |
| RH | 10.0 | {1,16,60} | {1,16,55} | {1,16,55} | {1,25,45} |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, X.; Liu, S.; Wei, A.; Shi, R.; Dai, Z. Bioinspired Rigid–Flexible Coupled Adaptive Compliant Motion Control of Robot Gecko for Space Stations. Biomimetics 2023, 8, 415. https://doi.org/10.3390/biomimetics8050415
Pei X, Liu S, Wei A, Shi R, Dai Z. Bioinspired Rigid–Flexible Coupled Adaptive Compliant Motion Control of Robot Gecko for Space Stations. Biomimetics. 2023; 8(5):415. https://doi.org/10.3390/biomimetics8050415
Chicago/Turabian StylePei, Xiangli, Shuhao Liu, Anmin Wei, Ruizhuo Shi, and Zhendong Dai. 2023. "Bioinspired Rigid–Flexible Coupled Adaptive Compliant Motion Control of Robot Gecko for Space Stations" Biomimetics 8, no. 5: 415. https://doi.org/10.3390/biomimetics8050415
APA StylePei, X., Liu, S., Wei, A., Shi, R., & Dai, Z. (2023). Bioinspired Rigid–Flexible Coupled Adaptive Compliant Motion Control of Robot Gecko for Space Stations. Biomimetics, 8(5), 415. https://doi.org/10.3390/biomimetics8050415







