Ballistic Behavior of Bioinspired Nacre-like Composites
Abstract
1. Introduction
2. Methods
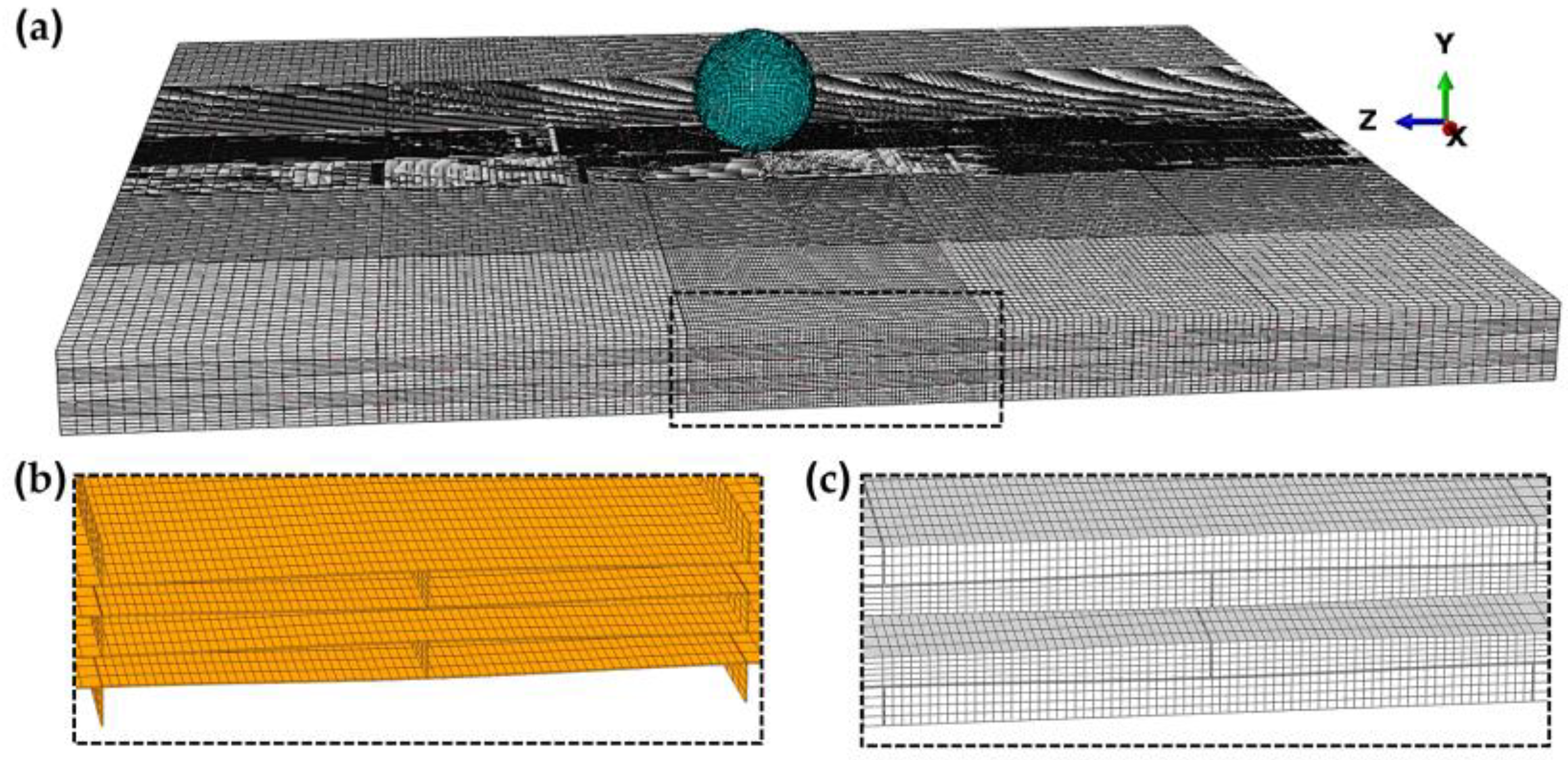
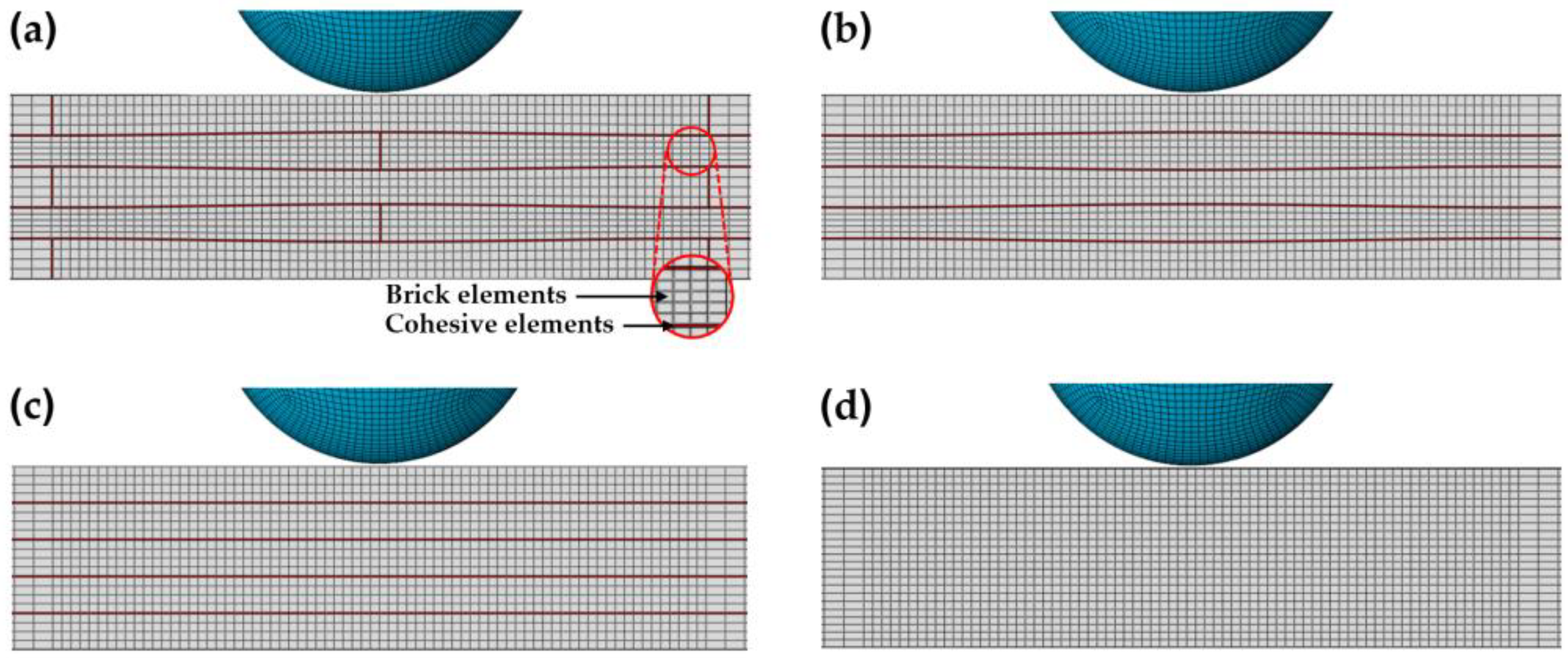
2.1. Nacre-like Composite Plate Configurations
2.2. Finite Element (FE) Model
2.3. Materials
2.3.1. Johnson–Cook Plasticity Model and Fracture Criterion
2.3.2. Constitutive Response of the Cohesive Elements
3. Results and Discussion
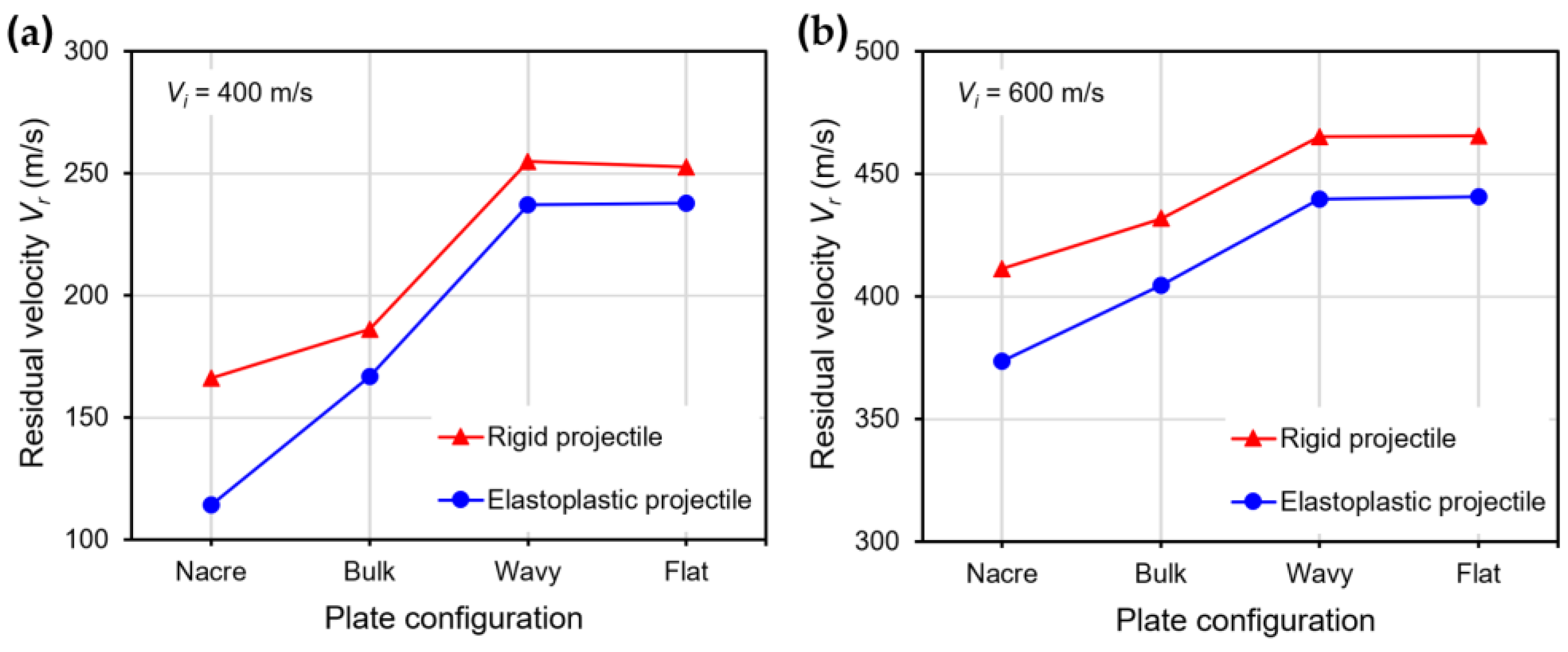
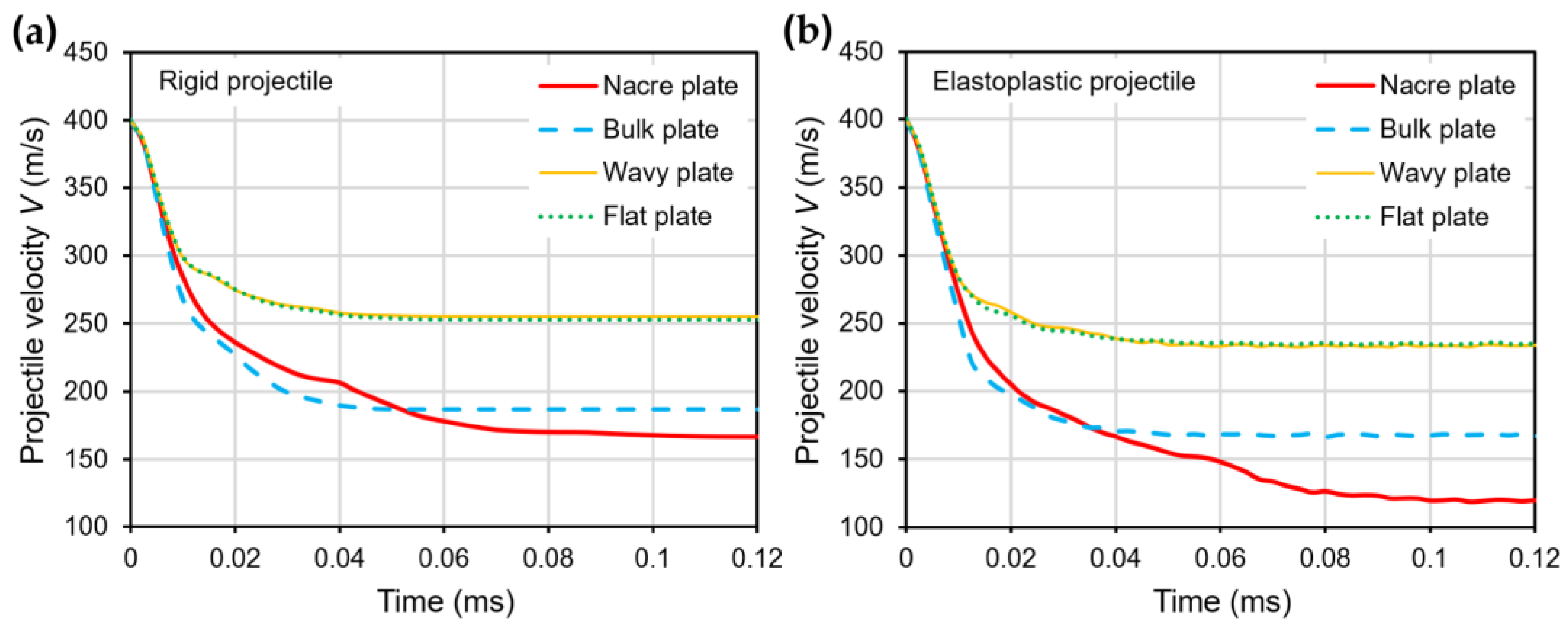
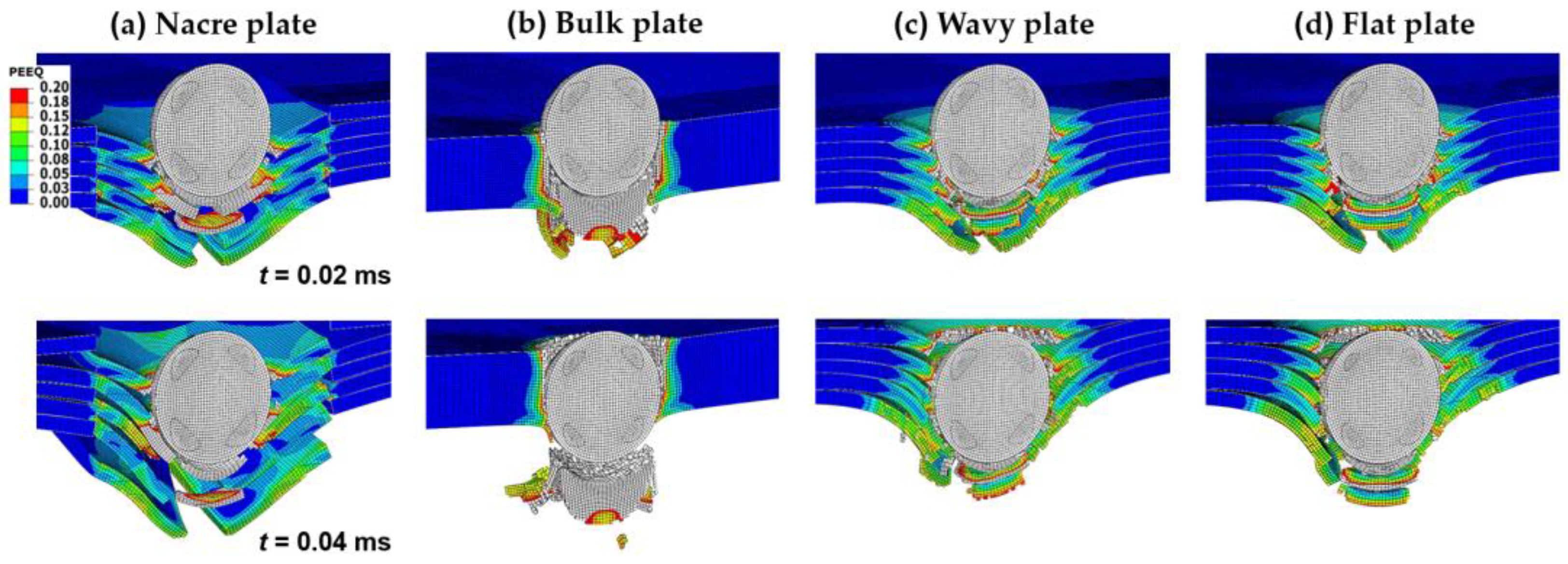
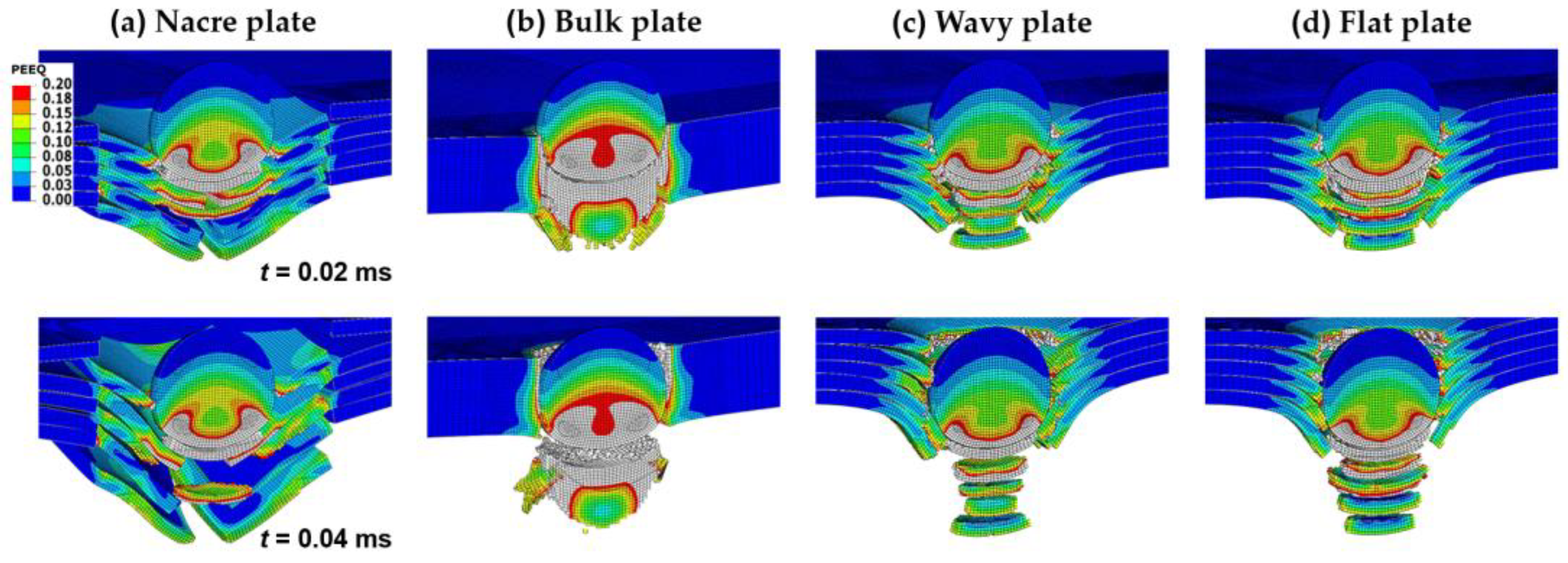
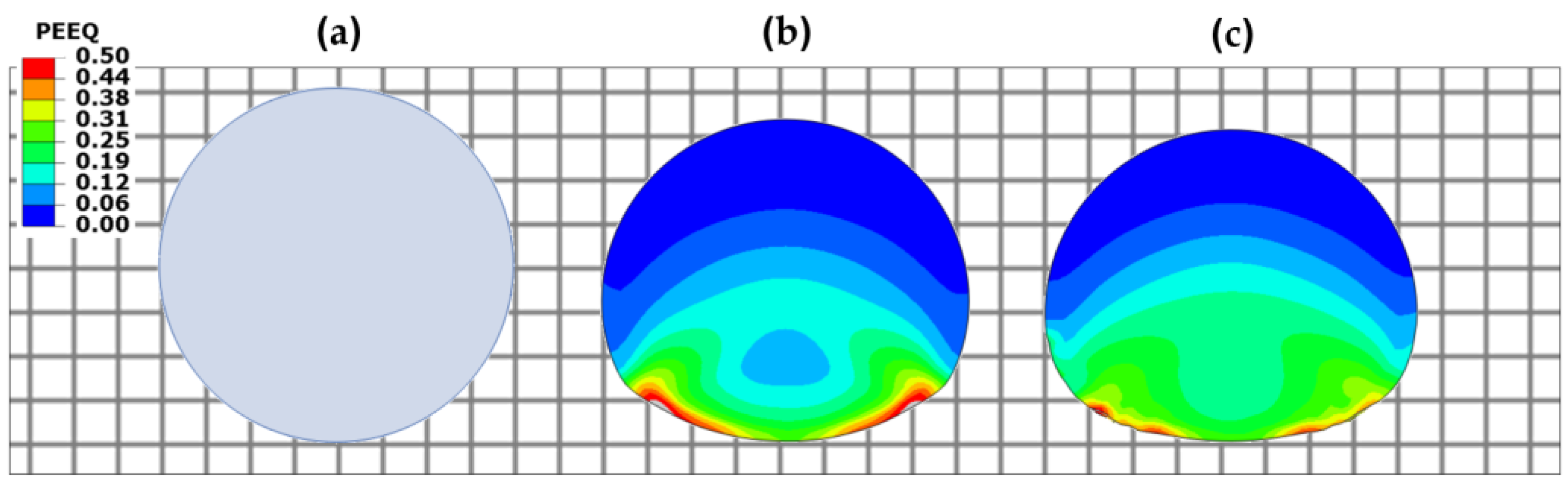
3.1. Ballistic Performance of the Plate Configurations
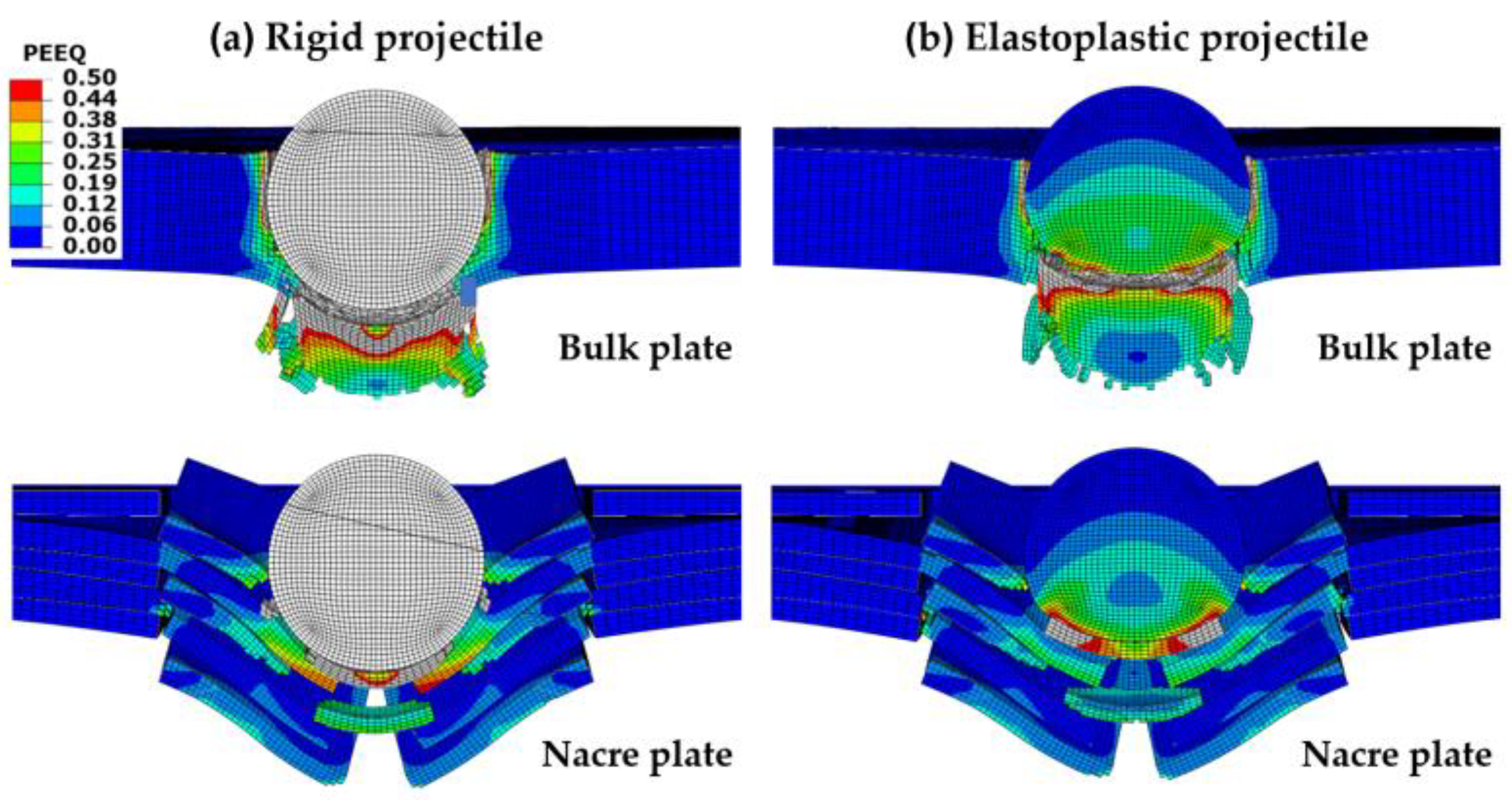
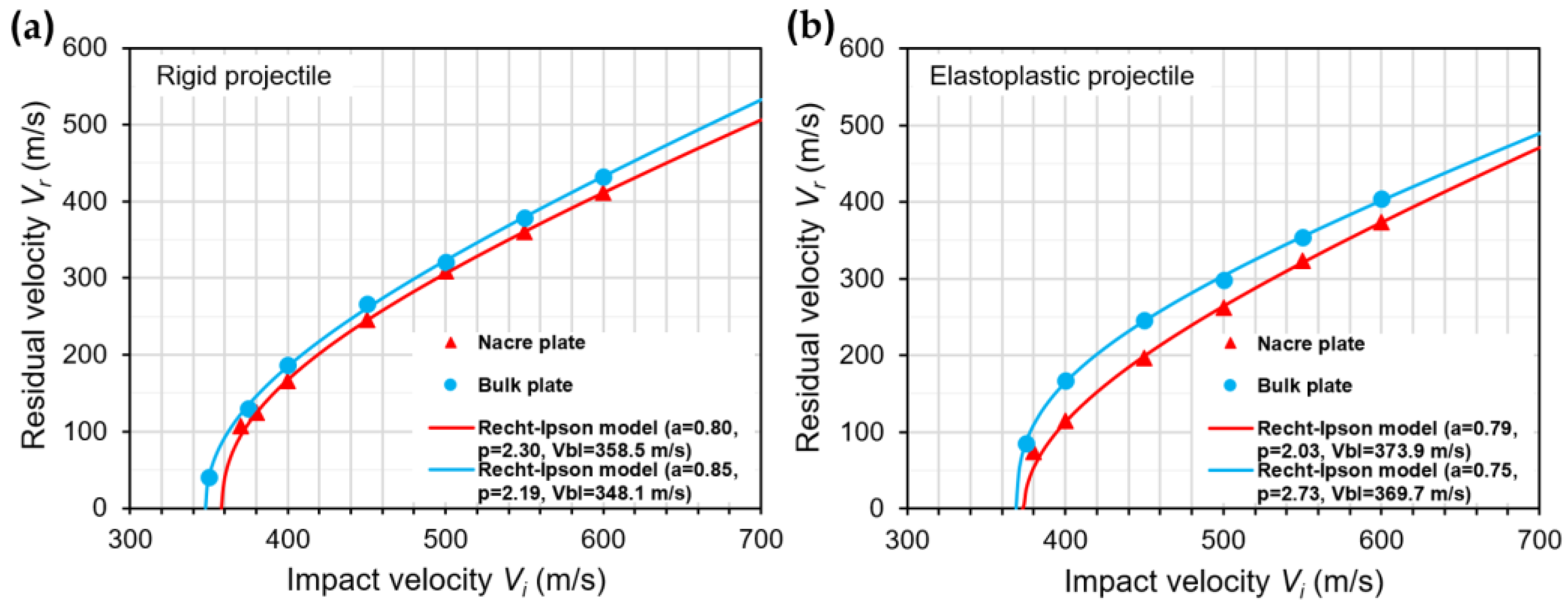
3.2. Effect of the Elastoplastic Behavior of the Projectile on the Ballistic Performance
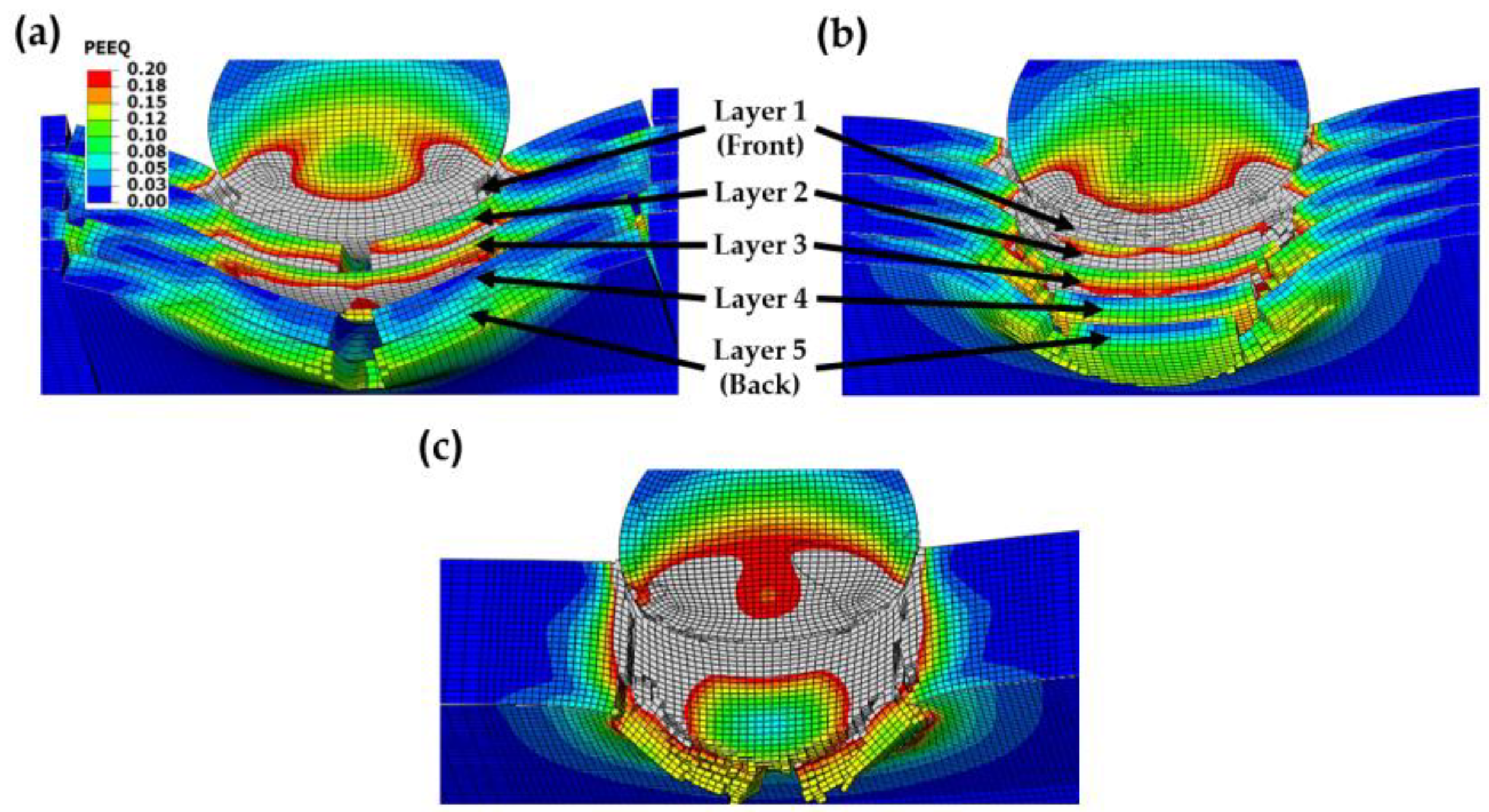
3.3. Results Analysis
3.4. Discussion
4. Conclusions
- The nacre plate exhibited a more ductile failure compared to the brittle failure of the bulk plate.
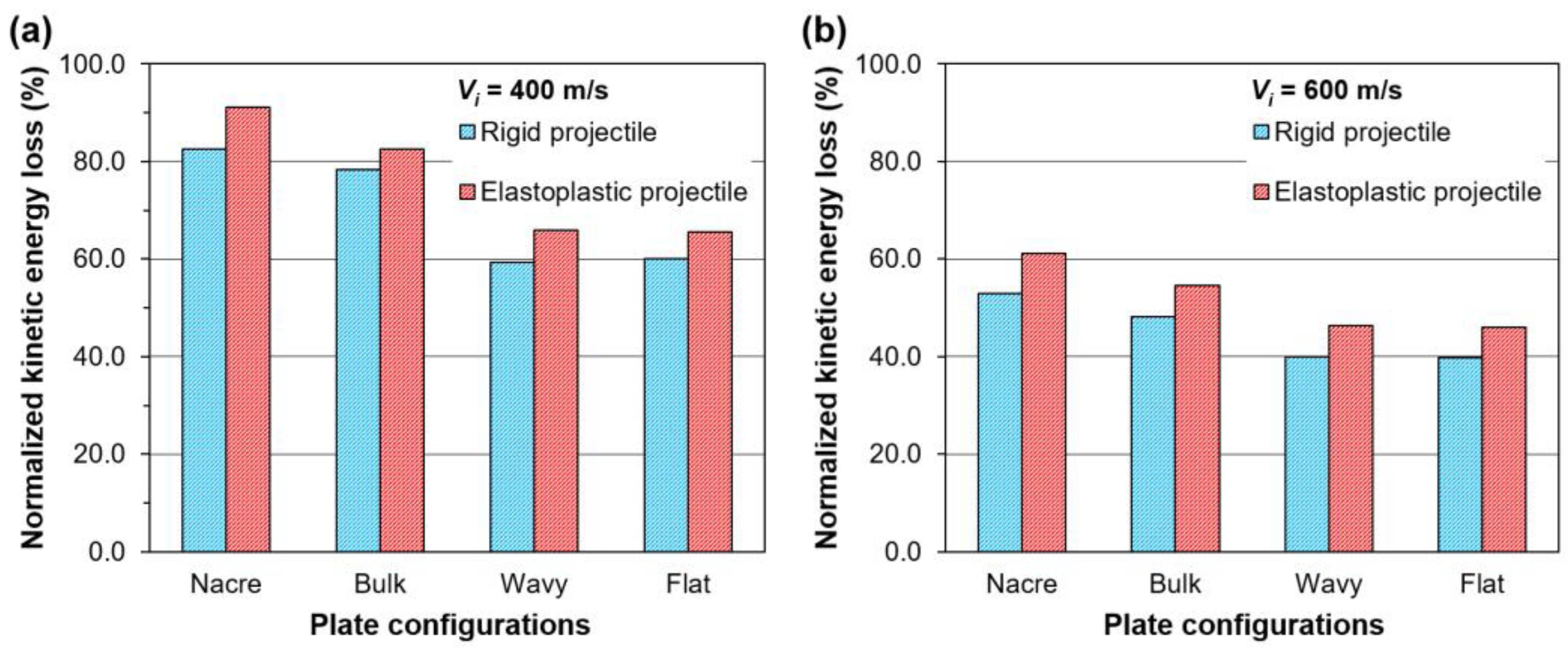
- The nacre plate exhibited better ballistic performance than the plates with continuous layers, showing that using tablets resulted in a larger area of plastic deformation, producing higher impact energy absorption.
- The structural design of the nacre plate produced an improved ballistic performance by enabling localized energy absorption via the plastic deformation of the tablets and globalized energy dissipation due to interface debonding and friction.
- All the plate configurations showed a better ballistic performance when impacted by an elastoplastic projectile compared to the rigid one, which is explained by the plastic deformation of the elastoplastic projectile and the enlarged contact areas between the projectile and the plates, enabling more energy absorption by the plates.
- The numerical results indicated that the nacre-like composites have the potential to be used for ballistic applications; however, further research is required to assess the parameters that affect the mechanical response of the bioinspired composites to achieve an optimal design with improved ballistic performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zaera, R. Ballistic Impacts on Polymer Matrix Composites, Composite Armor, Personal Armor. In Impact Engineering of Composite Structures; Abrate, S., Ed.; Springer: Vienna, Austria, 2011; Volume 526, pp. 305–403. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.-Y.; McKittrick, J.; Meyers, M.A. Biological materials: Functional adaptations and bioinspired designs. Prog. Mater. Sci. 2012, 57, 1492–1704. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Rim, J.E.; Barthelat, F.; Buehler, M.J. Merger of structure and material in nacre and bone—Perspectives on de novo biomimetic materials. Prog. Mater. Sci. 2009, 54, 1059–1100. [Google Scholar] [CrossRef]
- Kakisawa, H.; Sumitomo, T. The toughening mechanism of nacre and structural materials inspired by nacre. Sci. Technol. Adv. Mater. 2011, 12, 064710. [Google Scholar] [CrossRef]
- Tang, B.; Niu, S.; Yang, J.; Shao, C.; Wang, M.; Ni, J.; Zhang, X.; Yang, X. Investigation of Bioinspired Nacreous Structure on Strength and Toughness. Biomimetics 2022, 7, 120. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Bhushan, B. Hierarchical structure and mechanical properties of nacre: A review. RSC Adv. 2012, 2, 7617. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, K.; Ni, Y.; He, L. Anomalous inapplicability of nacre-like architectures as impact-resistant templates in a wide range of impact velocities. Nat. Commun. 2022, 13, 7719. [Google Scholar] [CrossRef]
- Barthelat, F.; Tang, H.; Zavattieri, P.D.; Li, C.M.; Espinosa, H.D. On the mechanics of mother-of-pearl: A key feature in the material hierarchical structure. J. Mech. Phys. Solids 2007, 55, 306–337. [Google Scholar] [CrossRef]
- Yao, H.; Song, Z.; Xu, Z.; Gao, H. Cracks fail to intensify stress in nacreous composites. Compos. Sci. Technol. 2013, 81, 24–29. [Google Scholar] [CrossRef]
- Huang, Z.; Li, H.; Pan, Z.; Wei, Q.; Chao, Y.J.; Li, X. Uncovering high-strain rate protection mechanism in nacre. Sci. Rep. 2011, 1, 148. [Google Scholar] [CrossRef]
- Barthelat, F.; Espinosa, H.D. An Experimental Investigation of Deformation and Fracture of Nacre–Mother of Pearl. Exp. Mech. 2007, 47, 311–324. [Google Scholar] [CrossRef]
- Flores-Johnson, E.A.; Shen, L.; Guiamatsia, I.; Nguyen, G.D. A numerical study of bioinspired nacre-like composite plates under blast loading. Compos. Struct. 2015, 126, 329–336. [Google Scholar] [CrossRef]
- Tran, P.; Ngo, T.D.; Ghazlan, A.; Hui, D. Bimaterial 3D printing and numerical analysis of bio-inspired composite structures under in-plane and transverse loadings. Compos. Part B 2017, 108, 210–223. [Google Scholar] [CrossRef]
- Barthelat, F.; Zhu, D. A novel biomimetic material duplicating the structure and mechanics of natural nacre. J. Mater. Res. 2011, 26, 1203–1215. [Google Scholar] [CrossRef]
- Ko, K.; Jin, S.; Lee, S.E.; Hong, J.-W. Impact resistance of nacre-like composites diversely patterned by 3D printing. Compos. Struct. 2020, 238, 111951. [Google Scholar] [CrossRef]
- Wu, K.; Zheng, Z.; Zhang, S.; He, L.; Yao, H.; Gong, X.; Ni, Y. Interfacial strength-controlled energy dissipation mechanism and optimization in impact-resistant nacreous structure. Mater. Des. 2019, 163, 107532. [Google Scholar] [CrossRef]
- Yin, Z.; Hannard, F.; Barthelat, F. Impact-resistant nacre-like transparent materials. Science 2019, 364, 1260–1263. [Google Scholar] [CrossRef]
- Miao, T.; Shen, L.; Xu, Q.; Flores-Johnson, E.A.; Zhang, J.; Lu, G. Ballistic performance of bioinspired nacre-like aluminium composite plates. Compos. Part B 2019, 177, 107382. [Google Scholar] [CrossRef]
- Knipprath, C.; Bond, I.P.; Trask, R.S. Biologically inspired crack delocalization in a high strain-rate environment. J. R. Soc. Interface 2011, 9, 665–676. [Google Scholar] [CrossRef]
- Yang, H.; Gao, D.; Chen, P.; Lu, G. Numerical Investigation on the Ballistic Performance of Semi-Cylindrical Nacre-like Composite Shells under High-Velocity Impact. Materials 2023, 16, 3699. [Google Scholar] [CrossRef]
- Gao, D.; Chen, P.; Lu, G.; Yang, H. Numerical analysis for impact resistance of nacre-like composites. Mater. Today Commun. 2023, 35, 106031. [Google Scholar] [CrossRef]
- Ghazlan, A.; Ngo, T.; Tan, P.; Tran, P.; Xie, Y.M. A Numerical Modelling Framework for Investigating the Ballistic Performance of Bio-Inspired Body Armours. Biomimetics 2023, 8, 195. [Google Scholar] [CrossRef]
- Flores-Johnson, E.A.; Shen, L.; Guiamatsia, I.; Nguyen, G.D. Numerical investigation of the impact behaviour of bioinspired nacre-like aluminium composite plates. Compos. Sci. Technol. 2014, 96, 13–22. [Google Scholar] [CrossRef]
- ABAQUS. Abaqus Analysis User’s Guide, Version 2016; Dassault Systèmes: Providence, RI, USA, 2015. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; p. 541. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Børvik, T.; Hopperstad, O.S.; Pedersen, K.O. Quasi-brittle fracture during structural impact of AA7075-T651 aluminium plates. Int. J. Impact Eng. 2010, 37, 537–551. [Google Scholar] [CrossRef]
- Flores-Johnson, E.A.; Muránsky, O.; Hamelin, C.J.; Bendeich, P.J.; Edwards, L. Numerical analysis of the effect of weld-induced residual stress and plastic damage on the ballistic performance of welded steel plate. Comput. Mater. Sci. 2012, 58, 131–139. [Google Scholar] [CrossRef]
- Dorogoy, A.; Karp, B.; Rittel, D. A Shear Compression Disk Specimen with Controlled Stress Triaxiality under Quasi-Static Loading. Exp. Mech. 2011, 51, 1545–1557. [Google Scholar] [CrossRef]
- Brar, N.S.; Joshi, V.S.; Harris, B.W. Constitutive model constants for Al7075-T651 and Al7075-T6. AIP Conf. Proc. 2009, 1195, 945–948. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Wang, R.X.; Shayganpur, A.; Sareskani, S.; Spelt, J.K. Analytical peel load prediction as a function of adhesive stress concentration. J. Adhes. 2006, 82, 39–61. [Google Scholar] [CrossRef]
- Recht, R.F.; Ipson, T.W. Ballistic Perforation Dynamics. J. Appl. Mech. 1963, 30, 384–390. [Google Scholar] [CrossRef]
- Dey, S.; Børvik, T.; Teng, X.; Wierzbicki, T.; Hopperstad, O.S. On the ballistic resistance of double-layered steel plates: An experimental and numerical investigation. Int. J. Solids Struct. 2007, 44, 6701–6723. [Google Scholar] [CrossRef]
- Flores-Johnson, E.A.; Saleh, M.; Edwards, L. Ballistic performance of multi-layered metallic plates impacted by a 7.62-mm APM2 projectile. Int. J. Impact Eng. 2011, 38, 1022–1032. [Google Scholar] [CrossRef]
- Ghazlan, A.; Ngo, T.; Van Le, T.; Nguyen, T.; Remennikov, A. Blast performance of a bio-mimetic panel based on the structure of nacre—A numerical study. Compos. Struct. 2020, 234, 111691. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H.; Liu, Y.; Zhang, Z.; Yuan, Y. Nacre-inspired topological design tuning the impact resistant behaviors of composite plates. Compos. Struct. 2022, 299, 116077. [Google Scholar] [CrossRef]
- Bahrami, B.; Mehraban, M.R.; Koloor, S.S.R.; Ayatollahi, M.R. Non-local and local criteria based on the extended finite element method (XFEM) for fracture simulation of anisotropic 3D-printed polymeric components. Rapid Prototyp. J. 2023. [Google Scholar] [CrossRef]
- Khorasani, M.; Leary, M.; Downing, D.; Rogers, J.; Ghasemi, A.; Gibson, I.; Brudler, S.; Rolfe, B.; Brandt, M.; Bateman, S. Numerical and experimental investigations on manufacturability of Al–Si–10Mg thin wall structures made by LB-PBF. Thin-Walled Struct. 2023, 188, 110814. [Google Scholar] [CrossRef]
- Agaliotis, E.M.; Ake-Concha, B.D.; May-Pat, A.; Morales-Arias, J.P.; Bernal, C.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Proust, G.; Koh-Dzul, J.F.; Carrillo, J.G.; et al. Tensile Behavior of 3D Printed Polylactic Acid (PLA) Based Composites Reinforced with Natural Fiber. Polymers 2022, 14, 3976. [Google Scholar] [CrossRef] [PubMed]
| Material Properties | AA 7075 [28] | SS 316L |
|---|---|---|
| Density (kg/m3) | 2700 | 7850 |
| Young’s modulus E (GPa) | 70 | 210 |
| Poisson’s ratio (-) | 0.33 | 0.3 |
| Inelastic heat fraction (-) | 0.9 | 0.9 |
| Specific heat Cp (J/kgK) | 910 | 500 |
| Johnson–Cook Model Parameters | AA 7075 [28] | SS 316L [29] |
|---|---|---|
| A (MPa) | 520 | 238 |
| B (MPa) | 477 | 1202.4 |
| n (-) | 0.52 | 0.675 |
| C (-) | 0.001 | 0.0224 |
| Reference strain rate (s−1) | 5 × 10−4 | 5 × 10−4 |
| m (-) | 1 | 1.083 |
| Reference temperature Tr (K) | 293 | 293 |
| Melting temperature Tm (K) | 893 | 1673 |
| Johnson–Cook Damage Criterion Parameters | AA 7075 [30,31] |
|---|---|
| 0.096 | |
| 0.049 | |
| 3.465 | |
| 0.016 | |
| 1.099 |
| Material Properties | Betamate 1044 [33] |
|---|---|
| (kg/m3) | 1350 |
| Elastic modulus in the normal direction E (GPa) | 3.1 |
| Elastic modulus in the transverse directions G1, G2 (GPa) | 1.55 |
| (MPa) | 85.5 |
| (MPa) | 70 |
| Critical fracture energy in mode I GIC (J/m2) | 1680 |
| Critical fracture energy in mode II GIIC (J/m2) | 3570 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan-Colli, D.G.; Agaliotis, E.M.; Frias-Bastar, D.; Shen, L.; Carrillo, J.G.; Herrera-Franco, P.J.; Flores-Johnson, E.A. Ballistic Behavior of Bioinspired Nacre-like Composites. Biomimetics 2023, 8, 341. https://doi.org/10.3390/biomimetics8040341
Chan-Colli DG, Agaliotis EM, Frias-Bastar D, Shen L, Carrillo JG, Herrera-Franco PJ, Flores-Johnson EA. Ballistic Behavior of Bioinspired Nacre-like Composites. Biomimetics. 2023; 8(4):341. https://doi.org/10.3390/biomimetics8040341
Chicago/Turabian StyleChan-Colli, Danny G., Eliana M. Agaliotis, David Frias-Bastar, Luming Shen, Jose G. Carrillo, Pedro J. Herrera-Franco, and Emmanuel A. Flores-Johnson. 2023. "Ballistic Behavior of Bioinspired Nacre-like Composites" Biomimetics 8, no. 4: 341. https://doi.org/10.3390/biomimetics8040341
APA StyleChan-Colli, D. G., Agaliotis, E. M., Frias-Bastar, D., Shen, L., Carrillo, J. G., Herrera-Franco, P. J., & Flores-Johnson, E. A. (2023). Ballistic Behavior of Bioinspired Nacre-like Composites. Biomimetics, 8(4), 341. https://doi.org/10.3390/biomimetics8040341








