Abstract
The present study introduces a subtraction-average-based optimization algorithm (SAOA), a unique enhanced evolutionary technique for solving engineering optimization problems. The typical SAOA works by subtracting the average of searcher agents from the position of population members in the search space. To increase searching capabilities, this study proposes an improved SAO (ISAO) that incorporates a cooperative learning technique based on the leader solution. First, after considering testing on different standard mathematical benchmark functions, the proposed ISAOA is assessed in comparison to the standard SAOA. The simulation results declare that the proposed ISAOA establishes great superiority over the standard SAOA. Additionally, the proposed ISAOA is adopted to handle power system applications for Thyristor Controlled Series Capacitor (TCSC) allocation-based losses reduction in electrical power grids. The SAOA and the proposed ISAOA are employed to optimally size the TCSCs and simultaneously select their installed transmission lines. Both are compared to two recent algorithms, the Artificial Ecosystem Optimizer (AEO) and AQuila Algorithm (AQA), and two other effective and well-known algorithms, the Grey Wolf Optimizer (GWO) and Particle Swarm Optimizer (PSO). In three separate case studies, the standard IEEE-30 bus system is used for this purpose while considering varying numbers of TCSC devices that will be deployed. The suggested ISAOA’s simulated implementations claim significant power loss reductions for the three analyzed situations compared to the GWO, AEO, PSO, and AQA.
1. Introduction
Optimization is a broad idea used in many sectors of research. An optimization problem constitutes a single issue that possesses more than one viable solution. As a result, the purpose of optimization is to discover the optimal option out of all possible possibilities. The optimization issues are stated mathematically in three parts: objective function, constraints, and decision variables [1]. In the research of optimization, problem solution strategies are classified as deterministic or stochastic [2]. Stochastic techniques solve optimization issues by randomly exploring the searching space and employing arbitrary operators. Such methods build a population of workable solutions to a particular issue before iteratively improving those answers to finally settle on an acceptable solution [3,4,5].
Global optimum is the best response to an optimization issue. Unfortunately, there is no assurance, however, whether the algorithms being used will exactly produce such an optimal solution. As a result, the solution produced by an optimization method for a problem is referred to as a quasi-optimal, which may or may not be equivalent to the global optimum [6]. To organize an effective search in the problem-solving area, metaheuristic techniques must be capable of executing and overseeing queries at the local as well as global levels. The global exploratory investigation leads to an in-depth examination in the space of issue solution and diverts attention from the finest local regions [7]. Local searching, when linked with the concept of exploiting, initiates an exhaustive examination of the most intriguing possibilities for the purpose of converging on possibly better ones. Given the competing goals of discovering and exploiting, establishing an equitable relationship between them throughout the process of searching is critical for the success of metaheuristic techniques [8]. Because of the concept of randomized searching mechanisms, researchers have developed a huge variety of metaheuristic methods. Evolutionary, physics-based, human-based, and swarm-intelligence computational techniques are the four basic types of metaheuristic methods. Evolutionary systems were constructed by representing biological evolutionary qualities such as crossings, mutations, and selections, as detailed in [9,10]. Physical rules drive physics-based techniques, including Archimedes’ optimization algorithm [11], thermal exchange optimization [12], and the equilibrium algorithm (EA) [13,14]. Swarm intelligence computations include the heap-based technique [15], marine predator optimizer [16], grasshopper algorithm [17], jellyfish search optimizer [18], particle swarm optimizer (PSO) [19], artificial bee colony [20], and whale optimization [21]. Several applications are conducted on these optimization frameworks in engineering fields, especially regarding renewable energy. In [22], the ant colony optimizer (ACO) has been intended for training a multilayer feed-forward neural network control system to derive the maximum power point tracking (MPPT) from photovoltaic (PV) arrays supplying an arc welding machine (AWM). In [23], a PSO has been enhanced with a Gauss mapping chaotic component and combined with MPPT for a wind conversion system based on a permanent magnet (PM) synchronous generator to run its tip-to-speed ratio at the optimal level. In [24,25] the ACO algorithm has been adopted to optimally find the tuning parameters of the fractional order proportional integral derivative (FOPID) controller of a PMDC motor that drive a wire-feeder system (WFS) regarding AWM. In [26], a PSO algorithm has been integrated with an MPPT controller depending on the adaptive neuro fuzzy inference system to track the maximum available power from a PV system that utilized for supplying WFS of AWM with varying weather conditions. For dealing with diverse engineering design challenges, an improved artificial ecosystem optimizer has been conducted [27]. The amalgamated fitness-distance architecture facilitates in identifying people who effectively improve the solution quality which was designed to handle engineering design tasks such as hydrostatic thrust bearing, planetary gear train, speed reducer, pressure vessel, and rolling element bearing.
Recently, a technique named SAOA [1] has been presented where its fundamental premise is to update population members’ locations in the search space by deducting the average of searcher agents. This technique is beneficial since it can be easily applied to engineering applications and has minimal parameters that need to be changed. The results of the SAOA were contrasted with more modern approaches and other existing techniques considering several benchmark models [1]. In this paper, an ISAOA is presented to enhance the searching capability. The proposed ISAOA augments the standard SAOA, including a cooperative learning strategy depending on the leader solution. Additionally, the proposed ISAOA is adopted to handle power system applications for Thyristor Controlled Series Capacitor (TCSC) allocation-based loss reductions in electrical power grids.
In order to meet load demand through power export-import agreements, utilities heavily rely on present generation capacity because the installed generating units are often situated distant from load centers. As a result, actual power systems include several connections. The minimization of power system losses is a pivotal technical objective function to enhance the voltage quality for all common coupling system points. It can be optimized using the optimal power flow issue (OPFI) [28], reactive power management [29], ancillary services [30], and flexible alternating current transmission systems (FACTS) devices incorporation [31]. For such supporting strategies, maintaining load flow balance and keeping operating variables within the associated constraints are necessary, including transmission network limitations, voltage restrictions, generator output limitations, and valve restrictions [32]. Researchers have created a number of traditional and metaheuristic optimization methods recently in an effort to solve the OPFI [33]. The traditional approaches include the sequential unconstrained minimization technique [34], interior point approach [35], linear and nonlinear programming, gradient methods, interior-point methods, Newton method, Newton-based method [36], and fuzzy linear frameworks. However, it has been noted that these methods cannot be used for large power systems and do not produce global ideal solutions. Therefore, researchers have attempted to develop metaheuristic methods to sidestep the issues that traditional methods possess. There are diverse population-based heuristics that are used to solve the OPFI, such as the electromagnetism-like mechanism [37], simulated annealing optimization [38], Particle Swarm Optimization (PSO) [39], Gradient-Based Optimization Algorithm (GBOA) [40], and Quantum computing with Moth Flame Technique (QMFT) [41]. In addition, in [42], the TLBO technique has been developed and adopted for solving the allocation optimization problem in power systems of capacitors for the sake of power factor correction. To suitably increase the incorporation of dispersed sources of energy in low-inertia electrical networks, an updated priority-list approach with a Boolean inference coding/decoding method and a feed-forward neural network for determining the subsequent function assessment was hybridized [43]. Priority-based dynamic computing was used in this study to solve the unit commitment issue by simulating various scenarios with growing renewable energy. In [44], a priority list approach based on a genetic algorithm has been presented for investigating the expansion problem of intermittent renewable sources and measuring their effects on the total cost of production, involving renewable generation curtailment and load shedding avoidance while taking into account various types of electricity storage. In [45], Bayesian optimization was adopted with Gaussian process regression for finding the best unit commitment scheduling for coping with the variable and fluctuating behavior of energy from renewable sources. In [46], the Gorilla Troops Technique (GTT) has been employed on the OPFI with IEEE 30 bus system. The GTT includes five strategies for the group behaviors of gorillas which are visiting other gorillas, migrating to a new area, migrating in a certain direction, vying for adult females, and following the silverback. In [47], GTT has been employed on the OPFI with the inclusion of TCSC devices in the system. However, the size and allocation of the TCSC have not been taken into consideration. An Emended Crow Search Algorithm (ECSA) has been employed on the OPFI as depicted in [48] with adjustments to aggregated novel bat algorithm. For the purpose of reducing the costs of energy losses with/without the inclusion of voltage-source-converter stations, a manta-ray foraging optimizer has been designed for electrical grids in Ref. [49].
The significant contributions mentioned in this study are listed below.
- A novel ISAOA is presented.
- The proposed ISAOA establishes great superiority over the standard SAOA after considering testing on different standard mathematical benchmark functions.
- Compared to existing studies, the placement and sizing of TCSC devices are handled to minimize power losses.
- In this context, considering the standard IEEE 30 bus power system, the proposed ISAOA outperforms various SAOA and other recent approaches of GWO, AEO, PSO, and AQA.
- Considering different numbers of TCSC devices, the suggested ISAOA’s precision and quality of solution are demonstrated compared to the others.
2. Novel ISAOA Version: Mathematical Model
This section explains the theory behind the ISAOA technique that has been suggested and a presentation of its mathematical modeling for use in optimization problems.
2.1. Standard SAOA Version
The basic idea behind the standard SAOA is to update the location of population members in the search space by subtracting the average of searcher agents [1]. The search space represents the name given to the set of solutions to each optimization issue. The dimension length of the search space is the number of control variables in the problem being studied. Their numerical values are determined by the positions of the algorithm’s searching individuals consisting of the population size. As a result, every seeking solution or individual is computationally represented employing a vector and comprises data pertaining to the control variables. Random initialization determines the search agents’ initial principal locations in the search space as follows [1]:
where Sai indicates a solution vector agent in the SAOA population, which has a size of solution (Ns). Dim symbolizes the dimensional length regarding the number of control variables. LL indicates the lower limit of the control variables. Range denotes an acceptable interval of the dimensions, which can be expressed as follows [1]:
where UL indicates the higher limit of the control variables.
Each individual investigation seems to be a potential solution to the considered optimization aspect. Therefore, based on each search individual, the problem’s objective function can be assessed. Fiti can be used to represent the evaluated values for the problem’s objective function for each solution vector agent (i). According to the assessed values for the objective function, the optimal solution is determined using the best value generated for the goal function. In addition, the worst solution corresponds to the worst value determined for the goal function.
Mathematical considerations, including mean values, variations in search representative placements, and the sign of the variation between two objective values, served as the foundation for the SAOA’s conception. Because it relies on a special functioning “v” known as the “v-subtraction operator,” the SAOA method for computing the arithmetic mean is wholly original. Therefore, each solution vector agent in the SAOA population is updated related to the following equation [1]:
where Sai,new indicates the new upgraded solution vector agent in the SAOA population. denotes a vector of size Dim, containing numbers inside the range [0, 1] and a normal distribution for each of its elements. indicates the subtraction operation of the two searching solutions (Sai and Sak) from the SAOA population, which can be mathematically represented as follows [1]:
where denotes the Hadamard product symbol. is a randomized vector of size Dim containing numbers from the range [1, 2]. Fiti(Sai) and Fitk(Sak) are the evaluated objective values for solutions (i) and (k), respectively.
After updating each solution vector, the objective value is estimated and assessed. Then, in accordance with (5), this newly created solution replaces the old one if the new solution provides a better objective score as follows [1]:
2.2. Novel ISAOA Version Incorporating a Cooperative Learning Strategy
In an effort to enhance the searching capability, an ISAOA is proposed in this study by incorporating a cooperative learning strategy depending on the leader solution. In the standard SAOA version, as described in the updating mechanism of Equation (3), the change in position of every searching solution (Sai) within the search space is determined by the arithmetic mean of the v-subtraction operator of all the other solution vectors in the population, from it. Using this framework, the exploration characteristics are significant and powerful. On the other side, the exploitation searching characteristics require further enhancement by supporting the local searching mechanism around the best promising area. In order to accomplish that, a cooperative learning strategy is merged in the ISAOA version to provide learning information from the best solution vector as follows:
where indicates the new upgraded solution vector agent in the SAOA population. refers to the best solution in the current iteration; denotes a vector of size Dim, containing numbers inside range [0, 1] and a normal distribution for each of its elements. and represent two random unequal picked from the SAOA population.
In order to provide a balance between the exploration characteristics described in Equation (3) and the augmented exploitation characteristics described in Equation (6), a selection probability (SR) is preserved, which is set to 50%. The abovementioned key phases of the suggested ISAOA are shown in Figure 1.
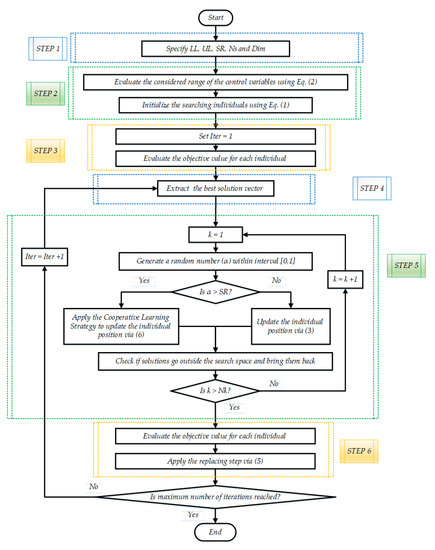
Figure 1.
Key phases of the suggested ISAOA.
3. Experimental Validation of Standard Benchmarking Functions
In this section, an evaluation of the formed ISAOA and the standard SAOA is made in comparison to ten popular, well-known mathematical benchmarks that are listed in Table 1 [50]. While the second function (F2) is multimodal, the first function (F1) represents a unimodal function. Mixed functions are represented by functions (F3–F6), while composite functions are represented by functions (F7–F10). According to the no free lunch theorem, no optimization algorithm is the best for all optimization problems. Therefore, the comparisons involve several problems with distinct features. These simulations were carried out using MATLAB 2017b software.

Table 1.
Definitions in detail of the 10 prevalent benchmarks being considered [50].
The performance analysis of the designed ISAOA and standard SAOA for ten widely used mathematical problems is shown in Table 2. Additionally, Figure 2 presents the most desirable convergent motion characteristics. This table demonstrates the resilience of the produced ISAOA in determining the optimal solution to the majority of the investigated mathematical problems by explicitly showing that the designed ISAOA runs and works better than the standard SAOA in the tested mathematical functions. According to the best-obtained objective, the suggested ISAOA outperforms the standard SAOA for all investigated benchmarks except F6, with a success rate of 90%. In addition, the suggested ISAOA surpasses the regular SAOA for all examined benchmarks, with the exception of F6 and F10, according to the mean achieved objective, with a success rate of 80%. Moreover, the adopted ISAOA surpasses the regular SAOA for all benchmarks examined, with the exception of F6, F8, and F10, with a success rate of 70%, according to the worst attained objective. According to this table, the proposed ISAOA beats the conventional SAOA for the best, mean, worst, and standard deviations in 70% of the benchmark functions’ statistical indices regarding the benchmarks investigated. The success rates attested demonstrate the considerable efficacy of the proposed ISAOA combining the advised cooperative learning technique.

Table 2.
Performance study for the designed ISAOA and standard SAOA on different benchmarks.
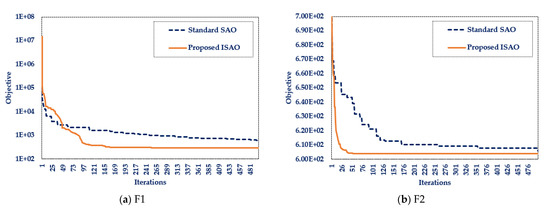
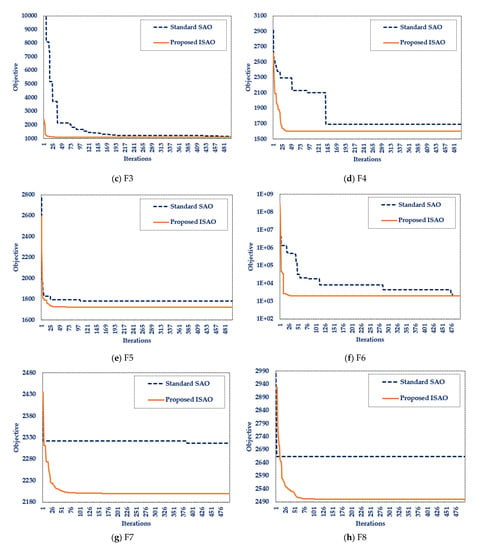
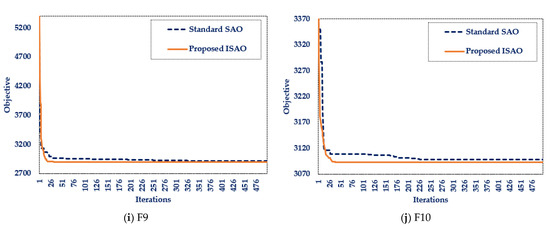
Figure 2.
Benchmarks’ best convergence curves for the designed ISAOA and standard SAOA.
4. TCSC Allocation-Based Loss Minimization in Electrical Power Grids
One of the most well-known FACTS devices in the series is the TCSC, which has a number of benefits, including great performance, rapid response, and low cost. Inductive and capacitive capability compensations are the two reactive operational modes available for TCSC devices. The reactance of the corresponding transmission line can be, consequently, increased or decreased in both modes. TCSC modeling in electrical systems connected in series with a line is shown in Figure 3. It is composed of a capacitance (C) coupled in parallel with an inductance (L), which is modulated by a valve located in anti-parallel conventional thyristors [51,52,53,54].
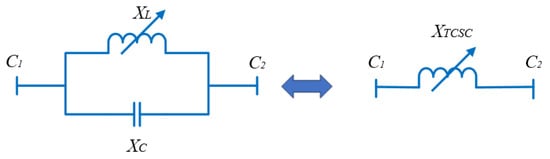
Figure 3.
TCSC modeling.
In order to technically enhance the power grid and the voltage quality in all buses, the primary objective is to minimize the whole grid losses, which can be mathematically represented as illustrated [55]:
where Nbq manifests the number of buses; Gpq points out the transfer conductance among buses p and q; θ signifies the phase angle; V represents the voltage.
To address the TCSC allocation problem, several equality and inequality limitations must be maintained, which are related to control and dependent variables. First, regarding the control variables, the TCSC locations and the regarding reactance compensation have to be satisfied as illustrated in Equations (8) and (9), respectively.
where LineTCSC,p manifests the candidate lines to install TCSC devices; Nlines points out the whole number of lines; NTCSC signifies the number of TCSC devices to be installed; represents the reactance of the regarding lines selected to install TCSC devices.
The TCSC devices are sized to ensure the capacitor bank compensates for 50–70% of the transmission line. Therefore, the maximum limit of capacitor bank compensations is considered 50%, as displayed in Equation (9) which is based on several other previously published articles [46,47,51,52,53,54].
In addition, regarding the control variables, the limitations for the output powers from generators, generators voltage, reactive powers injection from Var sources, and tap settings are handled using Equations (10)–(13), respectively [56,57].
where Ngen represents the total number of generation units; Nt illustrates the total number of transformer units; Nq characterizes the total number of compensating/capacitors units; Pgen illustrates generators’ real power output; Tp denotes the tap changer settings; Vgen gives voltages of the generators; Qc signifies the reactive power injections of switching reactors/capacitors.
Second, regarding the dependent variables, the limitations for the output reactive powers from generators, power flow through the lines, and load bus voltages are handled using Equations (14)–(16), respectively [55].
where Qgen characterizes generator reactive power outputs; Sfl elaborates transmission flow limits; VL shows load bus voltage magnitudes at bus j; NPQ signifies the entire number of load buses.
On the other side, the active and reactive power load balancing equations at each bus must be maintained as equality constraints. These constraints are fully achieved with the convergence of the load flow routine.
5. Simulation Results for Optimal TCSC Allocations in Power Systems
The proposed ISAOA is applied in this section to solve the considered problem of optimal TCSC allocations in power systems to minimize power losses. In this regard, the IEEE standard 30 bus system is considered. The IEEE 30 bus grid is displayed in Figure 4 [58], which consists of 41 branches, 30 buses, 4 tap transformers, and 9 VAr compensators. The whole data set for the generation limitations, lines, and buses are derived from [59]. The maximum generator voltages and tap positions correspond to 1.1 and 0.9 p.u. For load buses, the maximum voltage remains 1.05 and 0.95 p.u., correspondingly. The limits for the generator voltage and tap settings are 1.1000 and 0.9000 p.u., respectively. The voltage limits of load buses are considered to be 1.0500 and 0.9500 p.u., respectively. The proposed ISAOA is contrasted with the standard SAOA and other recent algorithms, which demonstrated previous effective applications such as AEO [60], AQA [61,62], PSO, and GWO [63,64]. The five compared algorithms are applied with the same 50 searching individuals and 300 iterations. They are performed 20 separate times considering three different case studies as follows:
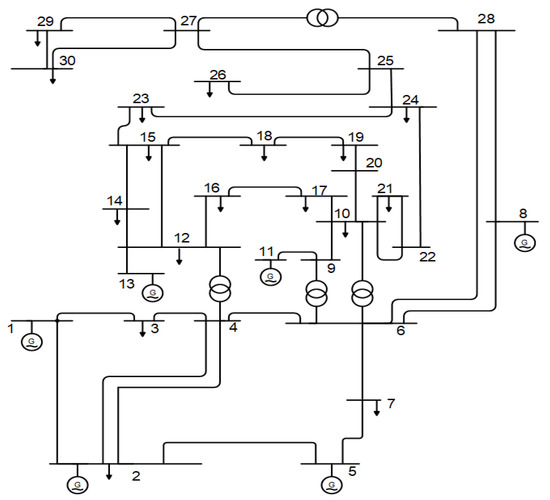
Figure 4.
Schematic diagram of IEEE 30 bus grid [65].
- Case 1: One TCSC to be allocated.
- Case 2: Two TCSCs to be allocated.
- Case 3: Three TCSCs to be allocated.
5.1. Application for Case 1
In this case, one TCSC device must be assigned to the power grid by looking for the best location and size. To reduce power losses, the suggested ISAOA is used in place of the standard SAOA, AEO, AQA, PSO, and GWO.
Table 3 tabulates the optimal control variables related to the compared results in terms of the generator’s voltage and output power, the Var sources injection power, and the tap value, in addition to the placement and sizing of the TCSC device. As illustrated, the suggested ISAOA yields the lowest power losses of 2.8217 MW with the best performance. The proposed ISAOA selects the transmission lines (28-27) with a compensation level of approximately 50% subtraction from the installed line reactance.

Table 3.
TCSC device addition and their compensation levels for Case 1.
According to the proposed ISAOA, the achieved power losses represent a significant reduction percentage of 51.62% compared to the initial case. On the other side, the standard SAOA obtains power losses of 3.061 MW upon installing a TCSC device in series with lines (23-24) with a compensation level of approximately 4.66% addition. The proposed ISAOA derives a significant reduction percentage of 7.81% compared to the SAOA. Additionally, the AEO acquires power losses of 2.884 MW upon connecting a TCSC device in series with lines (28-27) with a compensation level of roughly 49.49% subtraction. Upon adding a TCSC device in series with lines (4-6) with a compensation level of around 35.03% subtraction, the GWO also achieves power losses of 3.035 MW. Additionally, upon connecting a TCSC device in series with lines (6-28) and subtracting a compensation level of roughly 42.017%, the AQA achieves power losses of 2.99 MW. As shown in Table 3, the proposed ISAOA derives the best performance upon acquiring the smallest measurement of the best power losses of 2.8217 MW, respectively. On the other side, the SAOA, AEO, GWO, PSO, and AQA achieve losses of 3.061, 2.844, 3.035, 3.37, and 2.990 MW, respectively.
The suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO converging properties are also shown in Figure 5. As shown, the proposed ISAOA has a high and quick capability to find promising areas. After only fifty iterations, it starts, with precedence compared to the others, searching to minimize the losses of less than 2.83 MW. Despite the AQA converging at an earlier iteration, it becomes stuck in a local optimizing area for more than 150 iterations.
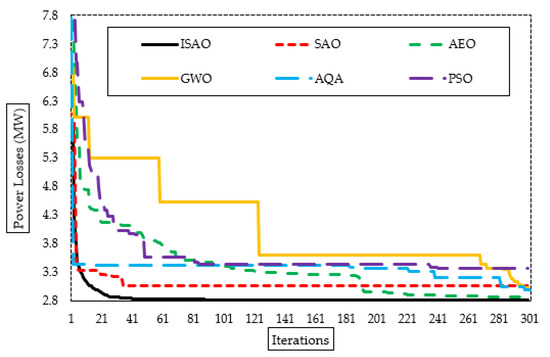
Figure 5.
Convergence characteristics of suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO for Case 1.
Figure 6 shows the bus voltage after installing the candidate TCSC device based on the suggested ISAOA vs. the initial instance to demonstrate a range of voltage enhancements. As can be seen, grid buses have made significant advancements. The last grid bus (No. 30) has the biggest voltage profile rise, increasing from 0.9012 per unit (p.u.) to 1.0696 p.u. with an improvement percentage of 15.74%.
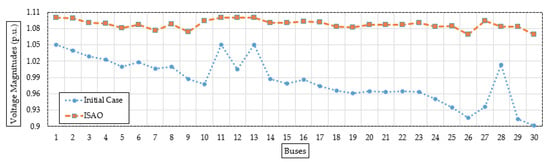
Figure 6.
Bus voltages after installing the candidate TCSC device (Case 1) based on the proposed ISAOA versus the initial case.
To assess the statistical evaluation of the compared techniques, Figure 7 displays the characteristics of the suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO in terms of the best, mean, worst and standard deviation (STD) over the separate runs. As shown, the proposed ISAOA derives the best performance by acquiring the smallest measurements of the best and mean power losses of 2.8217 and 2.93 MW, respectively.
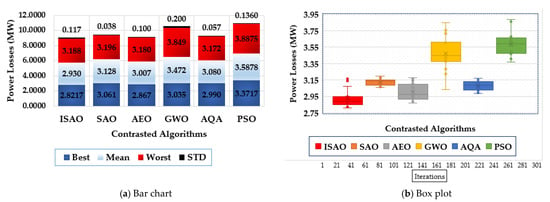
Figure 7.
Statistical characteristics of suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO for Case 1.
5.2. Application for Case 2
Upon choosing the appropriate position and size, two TCSC devices may be connected to the power grid. The proposed ISAOA is employed in place of the conventional SAOA, AEO, AQA, PSO, and GWO in order to minimize power losses. The associated appropriate control variables are shown in Table 4. As shown, the recommended ISAOA produces the highest performance and the lowest power losses of 2.82 MW. It chooses the transmission lines (28-27) and (6-28) with 50% subtraction compensation levels. The conventional SAOA, AEO, GWO, PSO, and AQA, on the other hand, experience power losses of 3.102, 2.867, 3.227, 3.36, and 2.995 MW, respectively.

Table 4.
TCSC device addition and their compensation levels for Case 2.
Figure 8 also displays the proposed ISAOA, standard SAOA, AEO, AQA, PSO, and GWO convergence features. As demonstrated, the suggested ISAOA is highly and quickly capable of identifying interesting locations. After just 75 iterations, it searches for a reduction in power loss below 2.83 MW with primacy over the others. In addition, Figure 9 shows the bus voltage after installing the candidate TCSC devices based on the suggested ISAOA vs. the initial instance to demonstrate the range of voltage enhancements. As can be seen, grid buses have made significant advancements.
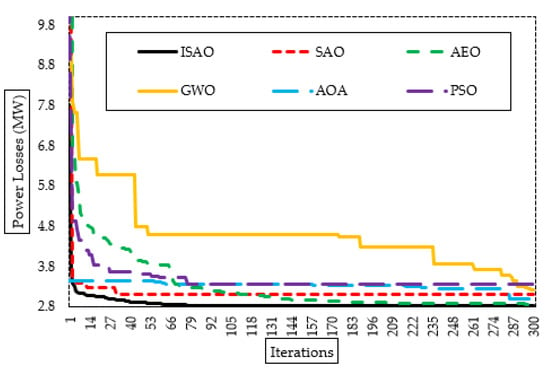
Figure 8.
Convergence characteristics of suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO for Case 2.
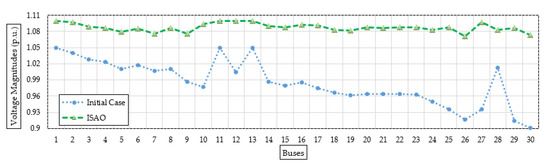
Figure 9.
Bus voltages after installing the candidate TCSC device (Case 2) based on the proposed ISAOA versus the initial case.
Figure 10 shows the features of the proposed ISAOA, conventional SAOA, AEO, AQA, PSO, and GWO across the individual runs to evaluate their statistical assessment. It has been demonstrated that the suggested ISAOA outperforms the competition. According to the best losses, the proposed ISAOA acquires 2.82 MW losses with an improvement of 9.08%, 1.62%, 12.60%, 16.1%, and 5.85%, respectively compared to the standards SAOA, AEO, AQA, PSO, and GWO. In addition, the suggested ISAOA, when compared to the normal SAOA, AEO, AQA, PSO, and GWO, acquires 2.938 MW losses with improvements of 6.39%, 1.66%, 16.08%, 18.8%, and 5.37%, respectively, in line with the mean losses. The designed ISAOA acquires 3.168 MW losses in accordance with the worst losses, with improvements of 0.41%, 1.43%, 24.21%, 21.3%, and 0.40%, respectively, compared to the standard SAOA, AEO, AQA, PSO, and GWO.
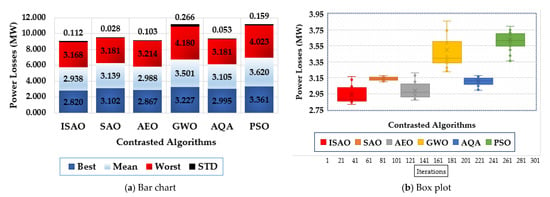
Figure 10.
Statistical characteristics of suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO for Case 2.
5.3. Application for Case 3
In this case, three TCSC devices may be connected to the electrical grid upon selecting the right position and size. In order to reduce power losses, the suggested ISAOA is used in place of the traditional SAOA, AEO, AQA, PSO, and GWO. Table 5 displays the associated suitable control variables. As can be seen, the suggested ISAOA yields the best results and the lowest power loss of 2.821 MW. It selects the transmission lines (6-28), (10-20), and (28-27) with subtraction compensation values of 36.96%, 50%, and 50%, respectively. On the other hand, the standard SAOA, AEO, GWO, PSO, and AQA suffer power losses of 3.036, 2.880, 3.187, 3.328, and 2.969 MW, respectively.

Table 5.
TCSC device addition and their compensation levels for Case 3.
Figure 11 additionally shows the proposed ISAOA, standard SAOA, AEO, AQA, PSO, and GWO convergence features. As demonstrated, the suggested ISAOA is highly and quickly capable of identifying interesting locations. After just 79 iterations, it begins to hunt to decrease the losses below 2.83 MW with precedence over the others.
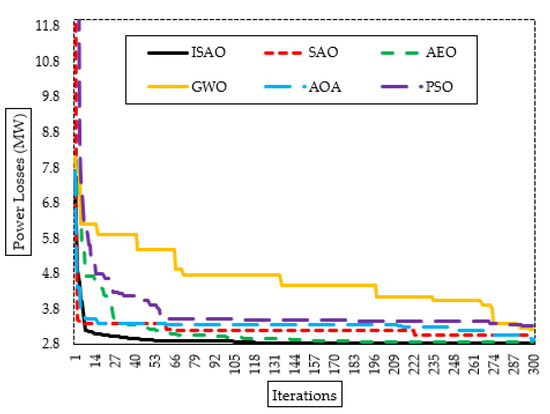
Figure 11.
Convergence characteristics of suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO for Case 3.
To illustrate the range of voltage enhancement, Figure 12 compares the bus voltages before and after installing the proposed TCSC devices based on the indicated ISAOA. Grid buses have progressed significantly, as is evident. The statistical evaluation of the proposed ISAOA, standard SAOA, AEO, AQA, PSO, and GWO is also shown in Figure 13 in terms of the best, mean, worst, and standard deviation (STD) over the individual runs. As it has been demonstrated, the suggested ISAOA achieves the greatest performance by gaining the smallest measurements for the best and mean worst losses, which are, respectively, 2.821 and 2.918.
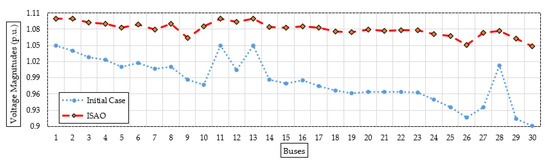
Figure 12.
Bus voltages after installing the candidate TCSC device (Case 3) based on the proposed ISAOA versus the initial case.
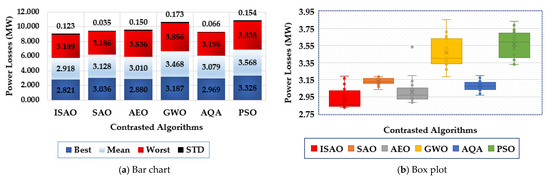
Figure 13.
Statistical characteristics of suggested ISAOA, standard SAOA, AEO, AQA, PSO, and GWO for Case 3.
5.4. Analysis of Increasing the Maximum Compensation Level to 70%
As previously formulated in Equation (9), the TCSC reactance compensation has to be satisfied and limited to 50%. In this section, an analysis of increasing the maximum compensation level to 70% is investigated instead of Equation (9) considering the following constraint:
For this analysis, to reduce power losses, the suggested ISAOA is used, considering maximum compensation levels of 50% and 70%, respectively. The three cases are investigated based on the number of TCSC devices to be allocated, and the related results are stated in Table 6.

Table 6.
TCSC device addition and their compensation levels based on ISAOA for the three cases studied.
As shown, considering the 70% compensation limit, the proposed ISAOA achieves power losses of 2.80645 and 2.775199 for Cases 2 and 3, respectively. On the other side, considering the 50% compensation limit, the proposed ISAOA achieves power losses of 2.820 and 2.821 for Cases 2 and 3, respectively. This output assessment shows more compensation derives more reduction in power losses. The compensation of 70% derives a reduction in power losses of 0.5% and 1.62% for Cases 2 and 3, respectively.
6. Conclusions
This study proposes a novel, improved evolutionary method dubbed the Subtraction-Average-based optimization algorithm. The proposed ISAOA incorporates a cooperative learning strategy depending on the leader solution to enhance the searching capability. The proposed ISAOA shows great superiority in enhancement compared with the standard SAOA with experimental validation of 10 standard benchmarking functions. It beats the conventional SAOA for the best, mean, worst, and standard deviation measurements in 70% of the benchmark functions’ statistical indices regarding the benchmarks investigated. The success rates attested demonstrate the considerable efficacy of the proposed ISAOA combining the advised cooperative learning technique. Further, the TCSC allocation-based loss reduction in electrical power grids is achieved through the development of the ISAOA algorithm. In comparison to the conventional SOA, GWO, AEO, PSO, and AQA, the suggested ISAOA is successfully implemented for the IEEE-30 bus power grid standard. The suggested ISAOA’s simulated implementations assert significant power loss reductions for the three examined cases studied compared to the others. On the basis of the suggested ISAOA for all grid buses, significant improvement is also gained.
The proposed ISAOA derives the best performance by acquiring the smallest measurements of the best power losses of 2.8217, 2.82, and 2.821 MW, respectively, for the three cases studied. In addition, the voltage profiles of all buses are enhanced with an improvement percentage of 15.74%. As a future area of study, the application of more advanced algorithms can be developed and applied with statistical comparisons in order to find highly robust and superior solution quality.
Author Contributions
Conceptualization, G.M.; Data curation, A.G.; Formal analysis, M.A.T. and A.M.S.; Investigation, M.A.T. and A.M.S.; Methodology, G.M.; Software, G.M. and A.M.S.; Supervision, S.A.; Validation, A.M.S.; Visualization, A.M.E.-R. and S.A.; Writing—original draft, A.G. and A.M.S.; Writing—review and editing, A.M.E.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. There are no financial competing interests.
References
- Trojovský, P.; Dehghani, M. Subtraction-Average-Based Optimizer: A New Swarm-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef]
- Jakšić, Z.; Devi, S.; Jakšić, O.; Guha, K. A Comprehensive Review of Bio-Inspired Optimization Algorithms Including Applications in Microelectronics and Nanophotonics. Biomimetics 2023, 8, 278. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Leiva, V. Drawer Algorithm: A New Metaheuristic Approach for Solving Optimization Problems in Engineering. Biomimetics 2023, 8, 239. [Google Scholar] [CrossRef]
- Ben Aribia, H.; El-Rifaie, A.M.; Tolba, M.A.; Shaheen, A.; Moustafa, G.; Elsayed, F.; Elshahed, M. Growth Optimizer for Parameter Identification of Solar Photovoltaic Cells and Modules. Sustainability 2023, 15, 7896. [Google Scholar] [CrossRef]
- Moustafa, G.; Ginidi, A.R.; Elshahed, M.; Shaheen, A.M. Economic environmental operation in bulk AC/DC hybrid interconnected systems via enhanced artificial hummingbird optimizer. Electr. Power Syst. Res. 2023, 222, 109503. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, J.; Chen, Y.; Xue, X.; Sun, S. Binary Restructuring Particle Swarm Optimization and Its Application. Biomimetics 2023, 8, 266. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubalovsky, S.; Trojovsky, P. Tasmanian Devil Optimization: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm. IEEE Access 2022, 10, 19599–19620. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1989th ed.; Addison-Wesley Publishing Company, Inc.: Redwood City, CA, USA, 1989. [Google Scholar]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; Allam, S.M.; Shaheen, A.M.; Nagem, N.A. Optimal allocation of biomass distributed generation in distribution systems using equilibrium algorithm. Int. Trans. Electr. Energy Syst. 2020, 31, e12727. [Google Scholar] [CrossRef]
- Askari, Q.; Saeed, M.; Younas, I. Heap-based optimizer inspired by corporate rank hierarchy for global optimization. Expert Syst. Appl. 2020, 161, 113702. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine predators algorithm: A nature-inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Chou, J.-S.; Truong, D.-N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Babes, B.; Boutaghane, A.; Hamouda, N. A novel nature-inspired maximum power point tracking (MPPT) controller based on ACO-ANN algorithm for photovoltaic (PV) system fed arc welding machines. Neural Comput. Appl. 2022, 34, 299–317. [Google Scholar] [CrossRef]
- Kahla, S.; Bechouat, M.; Amieur, T.; Sedraoui, M.; Babes, B.; Hamouda, N. Maximum power extraction framework using robust fractional-order feedback linearization control and GM-CPSO for PMSG-based WECS. Wind Eng. 2021, 45, 1040–1054. [Google Scholar] [CrossRef]
- Hamouda, N.; Babes, B.; Hamouda, C.; Kahla, S.; Ellinger, T.; Petzoldt, J. Optimal tuning of fractional order proportional-integral-derivative controller for wire feeder system using ant colony optimization. J. Eur. Syst. Autom. 2020, 53, 157–166. [Google Scholar] [CrossRef]
- Hamouda, N.; Babes, B.; Boutaghane, A.; Kahla, S.; Mezaache, M. Optimal tuning of PIλDμ controller for PMDC motor speed control using ant colony optimization algorithm for enhancing robustness of WFSs. In Proceedings of the CCSSP 2020—1st International Conference on Communications, Control Systems and Signal Processing, El Oued, Algeria, 16–17 May 2020. [Google Scholar] [CrossRef]
- Hamouda, N.; Babes, B.; Kahla, S.; Boutaghane, A.; Beddar, A.; Aissa, O. ANFIS Controller Design Using PSO Algorithm for MPPT of Solar PV System Powered Brushless DC Motor Based Wire Feeder Unit. In Proceedings of the 2020 International Conference on Electrical Engineering, ICEE 2020, Istanbul, Turkey, 25–27 September 2020. [Google Scholar] [CrossRef]
- Mahdy, A.; Shaheen, A.; El-Sehiemy, R.; Ginidi, A. Artificial ecosystem optimization by means of fitness distance balance model for engineering design optimization. J. Supercomput. 2023. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Elsayed, A.; Shaheen, A.; Elattar, E.; Ginidi, A. Scheduling of Generation Stations, OLTC Substation Transformers and VAR Sources for Sustainable Power System Operation Using SNS Optimizer. Sustainability 2021, 13, 11947. [Google Scholar] [CrossRef]
- Shokouhandeh, H.; Latif, S.; Irshad, S.; Kamarposhti, M.A.; Colak, I.; Eguchi, K. Optimal Management of Reactive Power Considering Voltage and Location of Control Devices Using Artificial Bee Algorithm. Appl. Sci. 2021, 12, 27. [Google Scholar] [CrossRef]
- Lin, W.-M.; Yang, C.-Y.; Tsai, M.-T.; Wang, Y.-H. Unit Commitment with Ancillary Services in a Day-Ahead Power Market. Appl. Sci. 2021, 11, 5454. [Google Scholar] [CrossRef]
- Behzadpoor, S.; Davoudkhani, I.F.; Abdelaziz, A.Y.; Geem, Z.W.; Hong, J. Power System Stability Enhancement Using Robust FACTS-Based Stabilizer Designed by a Hybrid Optimization Algorithm. Energies 2022, 15, 8754. [Google Scholar] [CrossRef]
- Montoya, O.D. A convex OPF approximation for selecting the best candidate nodes for optimal location of power sources on DC resistive networks. Eng. Sci. Technol. Int. J. 2020, 23, 527–533. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.; Farrag, S.M. Optimal reactive power dispatch using backtracking search algorithm. Aust. J. Electr. Electron. Eng. 2016, 13, 200–210. [Google Scholar] [CrossRef]
- Rahli, M.; Pirotte, P. Optimal load flow using sequential unconstrained minimization technique (SUMT) method under power transmission losses minimization. Electr. Power Syst. Res. 1999, 52, 61–64. [Google Scholar] [CrossRef]
- Yan, X.; Quintana, V. Improving an interior-point-based off by dynamic adjustments of step sizes and tolerances. IEEE Trans. Power Syst. 1999, 14, 709–717. [Google Scholar] [CrossRef]
- Sun, D.I.; Ashley, B.; Brewer, B.; Hughes, A.; Tinney, W.F. Optimal power flow by Newton approach. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 2864–2880. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.-H.; Abido, M.A.; Chaib, A.E. Optimal Power Flow Using an Improved Electromagnetism-like Mechanism Method. Electr. Power Compon. Syst. 2016, 44, 434–449. [Google Scholar] [CrossRef]
- Ziane, I.; Benhamida, F.; Graa, A. Simulated annealing algorithm for combined economic and emission power dispatch using max/max price penalty factor. Neural Comput. Appl. 2017, 28, 197–205. [Google Scholar] [CrossRef]
- Basu, M. Modified particle swarm optimization for nonconvex economic dispatch problems. Int. J. Electr. Power Energy Syst. 2015, 69, 304–312. [Google Scholar] [CrossRef]
- Moustafa, G.; Elshahed, M.; Ginidi, A.R.; Shaheen, A.M.; Mansour, H.S.E. A Gradient-Based Optimizer with a Crossover Operator for Distribution Static VAR Compensator (D-SVC) Sizing and Placement in Electrical Systems. Mathematics 2023, 11, 1077. [Google Scholar] [CrossRef]
- Dabba, A.; Tari, A.; Meftali, S. Hybridization of Moth flame optimization algorithm and quantum computing for gene selection in microarray data. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 2731–2750. [Google Scholar] [CrossRef]
- Bouaraki, M.; Recioui, A. Optimal placement of power factor correction capacitors in power systems using Teaching Learning Based Optimization. Alger. J. Signals Syst. 2017, 2, 102–109. [Google Scholar] [CrossRef]
- Nikolaidis, P.; Poullikkas, A. Evolutionary Priority-Based Dynamic Programming for the Adaptive Integration of Intermittent Distributed Energy Resources in Low-Inertia Power Systems. Eng 2021, 2, 643–660. [Google Scholar] [CrossRef]
- Nikolaidis, P.; Poullikkas, A. Co-optimization of active power curtailment, load shedding and spinning reserve deficits through hybrid approach: Comparison of electrochemical storage technologies. IET Renew. Power Gener. 2022, 16, 92–104. [Google Scholar] [CrossRef]
- Nikolaidis, P.; Chatzis, S. Gaussian process-based Bayesian optimization for data-driven unit commitment. Int. J. Electr. Power Energy Syst. 2021, 130, 106930. [Google Scholar] [CrossRef]
- Shaheen, A.; Ginidi, A.; El-Sehiemy, R.; Elsayed, A.; Elattar, E.; Dorrah, H.T. Developed Gorilla Troops Technique for Optimal Power Flow Problem in Electrical Power Systems. Mathematics 2022, 10, 1636. [Google Scholar] [CrossRef]
- Ginidi, A.; Elattar, E.; Shaheen, A.; Elsayed, A.; El-Sehiemy, R.; Dorrah, H. Optimal Power Flow Incorporating Thyristor-Controlled Series Capacitors Using the Gorilla Troops Algorithm. Int. Trans. Electr. Energy Syst. 2022, 2022, 9448199. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E.E.; Abd-Elrazek, A.S. A Modified Crow Search Optimizer for Solving Non-Linear OPF Problem with Emissions. IEEE Access 2021, 9, 43107–43120. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Elsayed, A.M.; Elattar, E.E. Multi-objective manta ray foraging algorithm for efficient operation of hybrid AC/DC power grids with emission minimisation. IET Gener. Transm. Distrib. 2021, 15, 1314–1336. [Google Scholar] [CrossRef]
- Shen, Y.; Liang, Z.; Kang, H.; Sun, X.; Chen, Q. A modified jso algorithm for solving constrained engineering problems. Symmetry 2021, 13, 63. [Google Scholar] [CrossRef]
- Gupta, C. Book Review: FACTS: Modelling and Simulation in Power Networks. Int. J. Electr. Eng. Educ. 2005, 42, 209–210. [Google Scholar] [CrossRef]
- Sen, K.K.; Sen, M.L. Introduction to FACTS Controllers: Theory, Modeling, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Sakr, W.S.; El-Sehiemy, R.A.; Azmy, A.M. Optimal allocation of TCSCs by adaptive DE algorithm. IET Gener. Transm. Distrib. 2016, 10, 3844–3854. [Google Scholar] [CrossRef]
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A. Adaptive multi objective parallel seeker optimization algorithm for incorporating TCSC devices into optimal power flow framework. IEEE Access 2019, 7, 36934–36947. [Google Scholar] [CrossRef]
- Sarhana, S.; Shaheen, A.; El-Sehiemy, R.; Gafar, M. Optimal Multi-dimension Operation in Power Systems by an Improved Artificial Hummingbird Optimizer. Hum.-Centric Comput. Inf. Sci. 2023, 13, 13. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.M.; El-Sehiemy, R.A.; Gafar, M. Enhanced Teaching Learning-Based Algorithm for Fuel Costs and Losses Minimization in AC-DC Systems. Mathematics 2022, 10, 2337. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.M.; El-Sehiemy, R.A.; Gafar, M. An Enhanced Slime Mould Optimizer That Uses Chaotic Behavior and an Elitist Group for Solving Engineering Problems. Mathematics 2022, 10, 1991. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; El-Sehiemy, R.A.; Ghoneim, S.S.M.; Alharthi, M.M.; Ginidi, A.R. Multi-dimensional energy management based on an optimal power flow model using an improved quasi-reflection jellyfish optimization algorithm. Eng. Optim. 2022, 55, 907–929. [Google Scholar] [CrossRef]
- Ghasemi, M.; Taghizadeh, M.; Ghavidel, S.; Aghaei, J.; Abbasian, A. Solving optimal reactive power dispatch problem using a novel teaching-learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2015, 39, 100–108. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Artificial ecosystem-based optimization: A novel nature-inspired meta-heuristic algorithm. Neural Comput. Appl. 2020, 32, 9383–9425. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Elaziz, M.A.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Shalaby, A.S. Aquila Optimization Algorithm for Wind Energy Potential Assessment Relying on Weibull Parameters Estimation. Wind 2022, 2, 617–635. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mahdy, A.; Shaheen, A.; El-Sehiemy, R.; Ginidi, A.; Al-Gahtani, S.F. Single- and Multi-Objective Optimization Frameworks of Shape Design of Tubular Linear Synchronous Motor. Energies 2023, 16, 2409. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.; El-Sehiemy, R.; Gafar, M. An Augmented Social Network Search Algorithm for Optimal Reactive Power Dispatch Problem. Mathematics 2023, 11, 1236. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).