Vibration State Identification of Hydraulic Units Based on Improved Artificial Rabbits Optimization Algorithm
Abstract
1. Introduction
- The stable operation of hydraulic units is very important for the safe production of hydropower stations. Vibration state monitoring is the premise of analyzing whether the hydraulic unit is operating stably. It is very necessary to improve the identification accuracy of the vibration states of hydraulic units to guarantee the secure operation of the hydraulic units;
- Optimization algorithms are widely used in signal classification and identification. However, many optimization algorithms have some shortcomings. Therefore, according to the shortcomings of the ARO algorithm, this paper proposes an improvement strategy based on the adaptive adjustment of the weight to improve the identification accuracy of the vibration states of the hydraulic units;
- A method of adaptively changing the inertia weight according to the current rabbit population distribution is proposed, which is used to improve the optimization ability of the ARO algorithm;
- A total of 23 benchmark functions are used to test the performance of the IARO algorithm. The experimental results show that the IARO algorithm has good exploration and exploitation abilities;
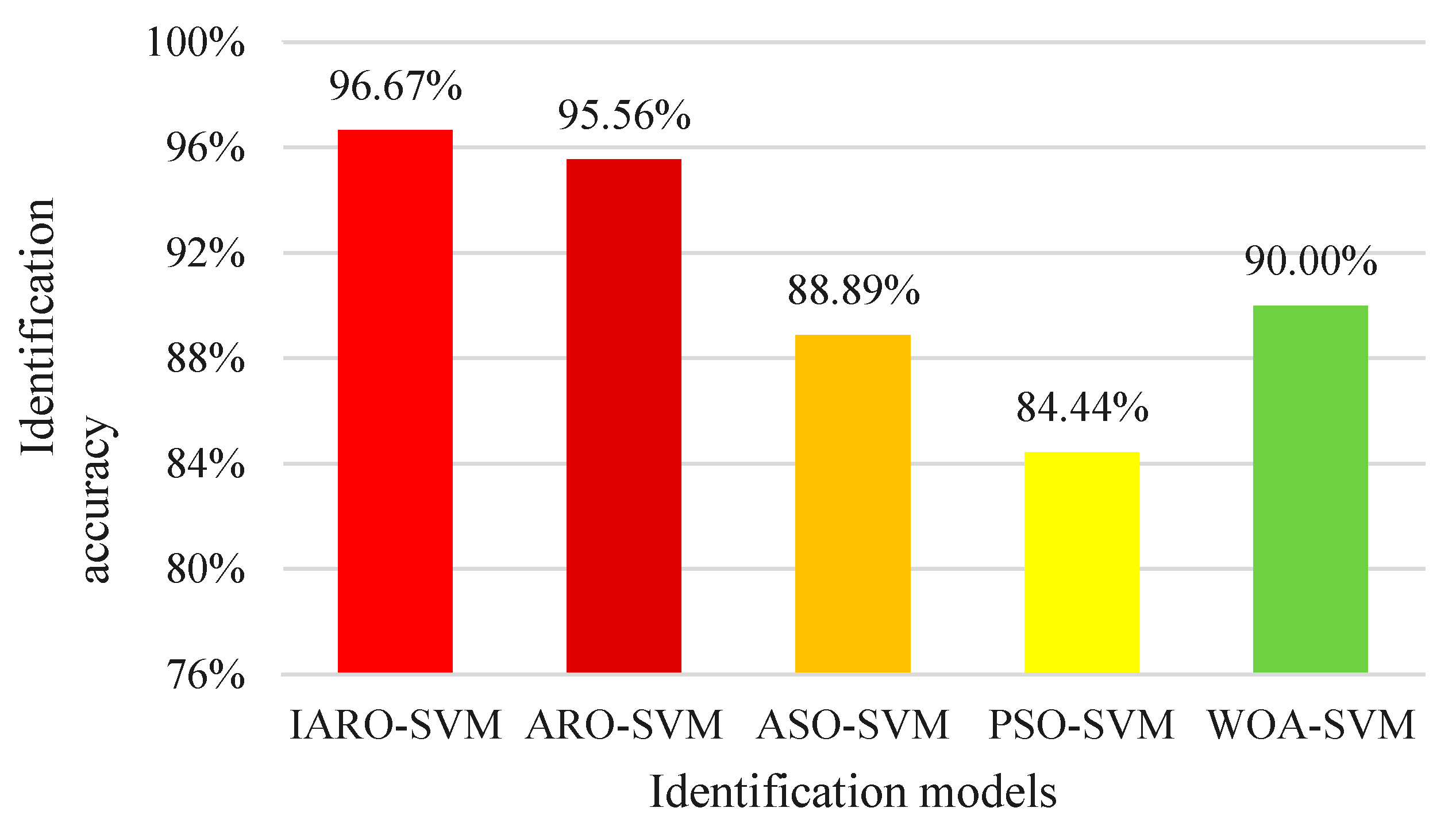
- Through the application of vibration state signals of the hydraulic units, the identification method of SVM optimized by the IARO algorithm is verified. The experimental results show that the IARO-SVM model can well identify the different vibration states of hydraulic units, and provide a guarantee for the stable operation of hydraulic units.
2. The Proposed Method
2.1. Variational Mode Decomposition Algorithm
2.2. Artificial Rabbits Optimization Algorithm
2.2.1. Detour Foraging (Exploration)
2.2.2. Random Hiding (Exploitation)
2.2.3. Energy Shrink (Switch from Exploration to Exploitation)
2.3. Multi-Classification Design of SVM
3. Improvement of Artificial Rabbit Optimization Algorithm
3.1. Adaptive Inertia Weight
3.2. The Specific Procedure of the IARO Algorithm
3.3. Energy Shrink of the IARO Algorithm
4. Experimental Results and Analysis
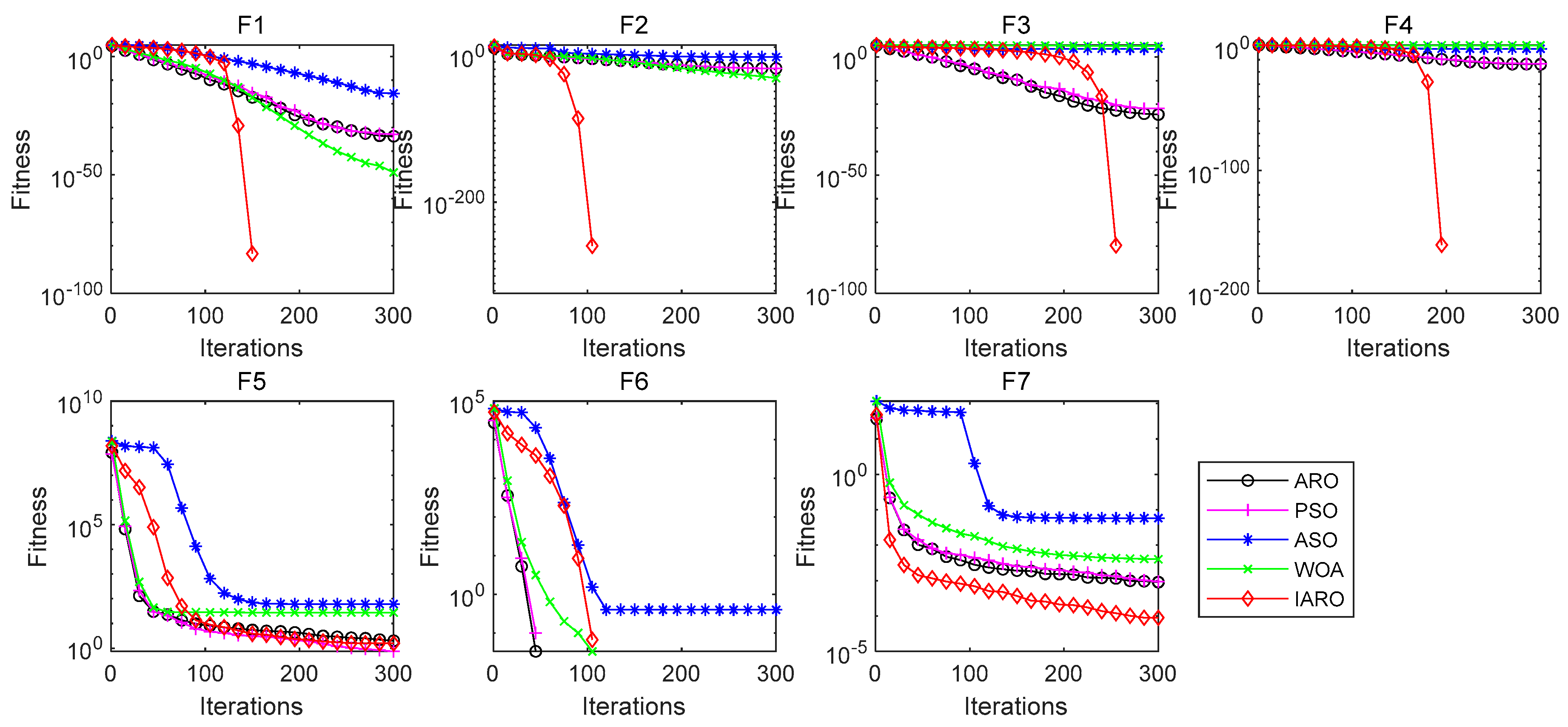
4.1. Exploitation Assessment
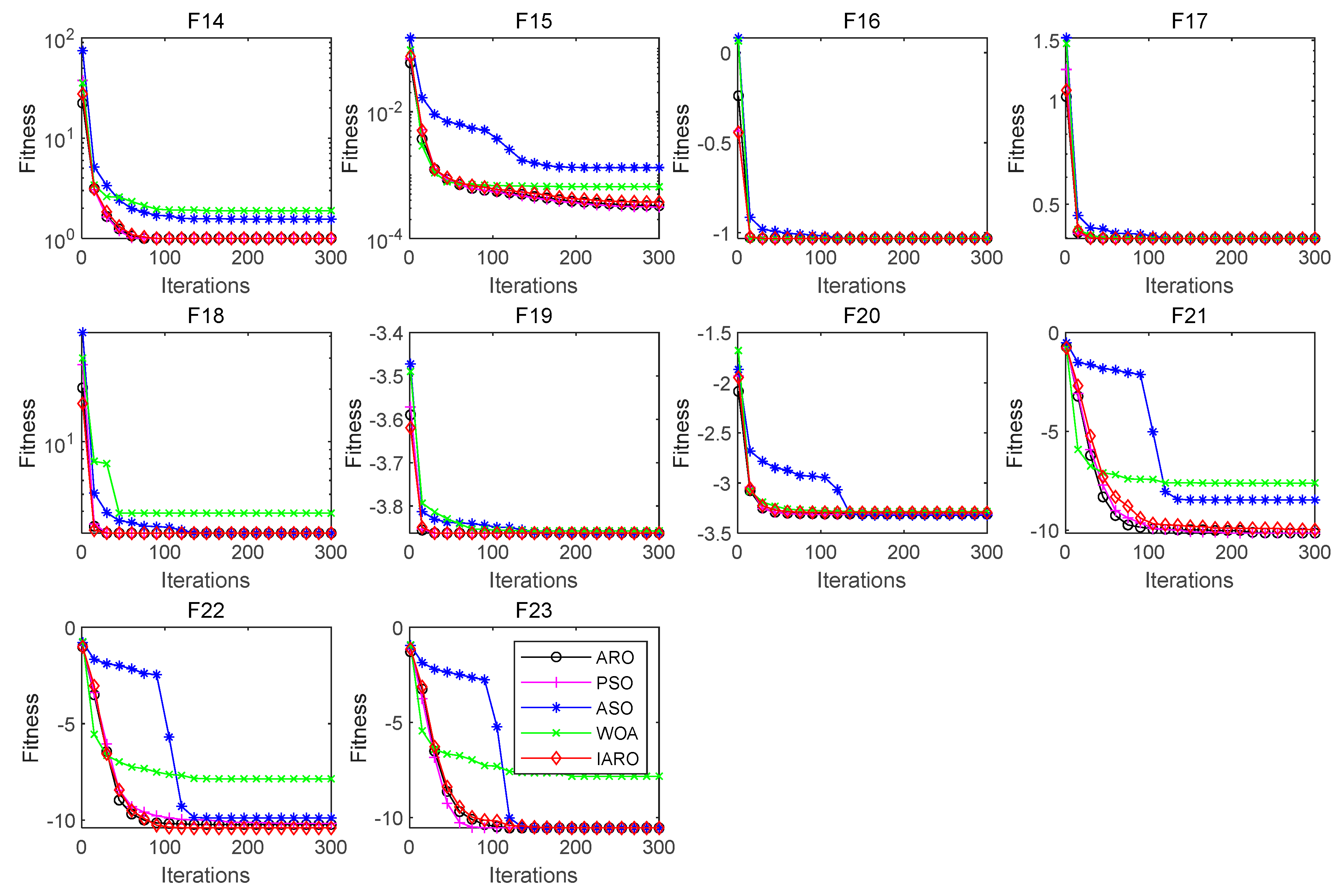
4.2. Exploration Assessment
5. IARO for Vibration State Identification of Hydraulic Units
5.1. Acquisition of Experimental Data
5.2. Vibration Signal Processing and Extraction
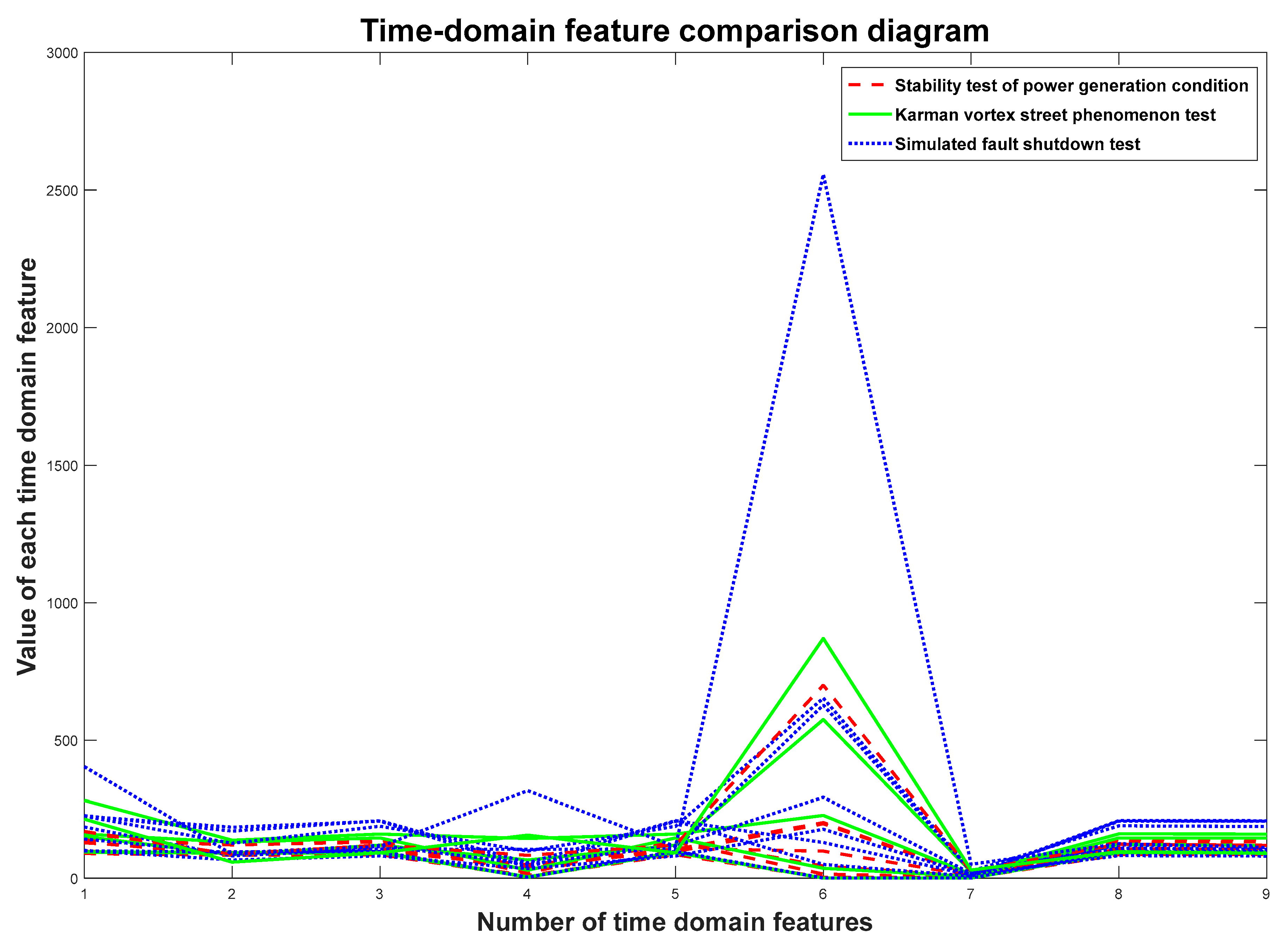
5.3. Feature Vectors Selection
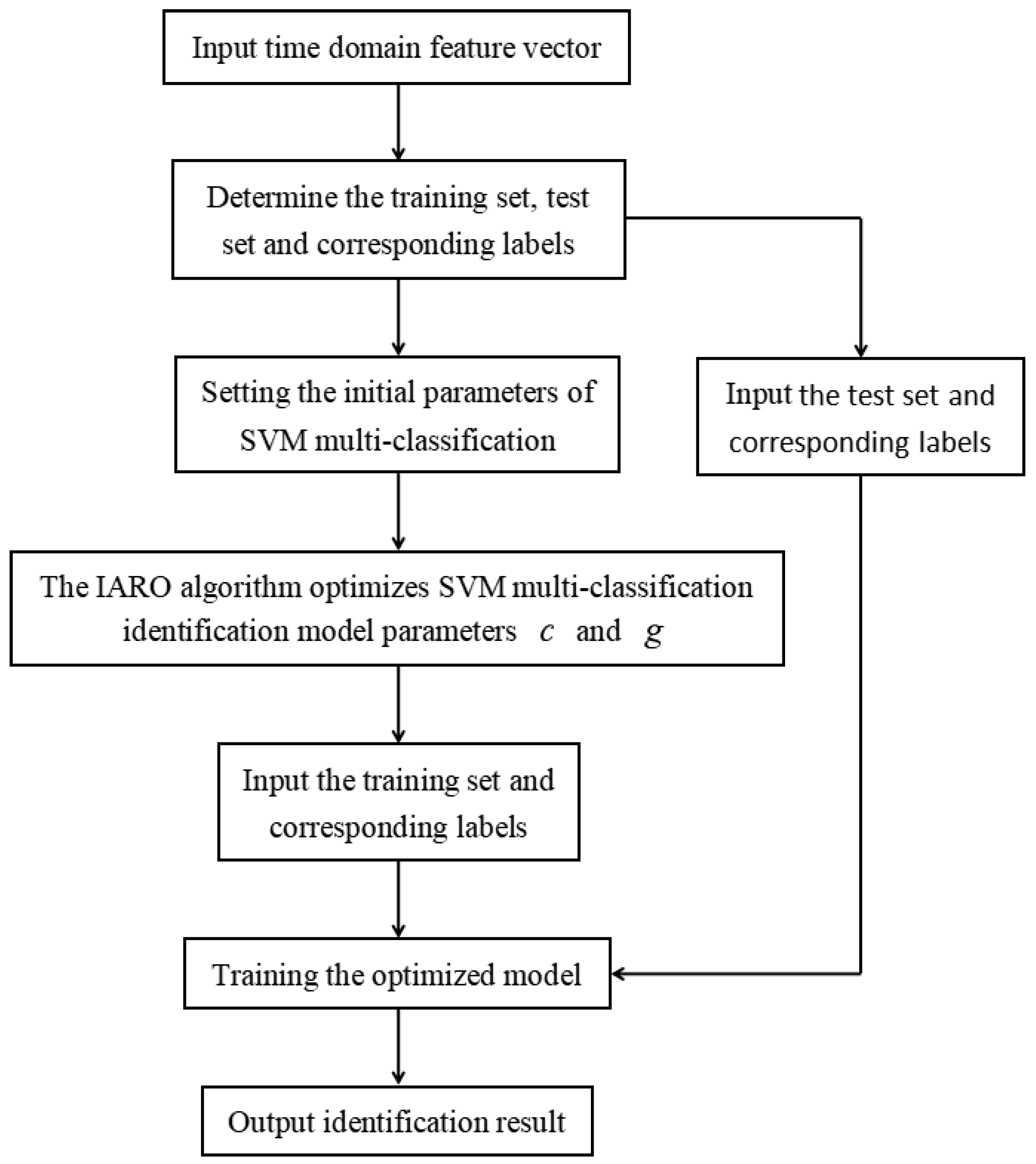
5.4. SVM Classification and Identification Model Construction
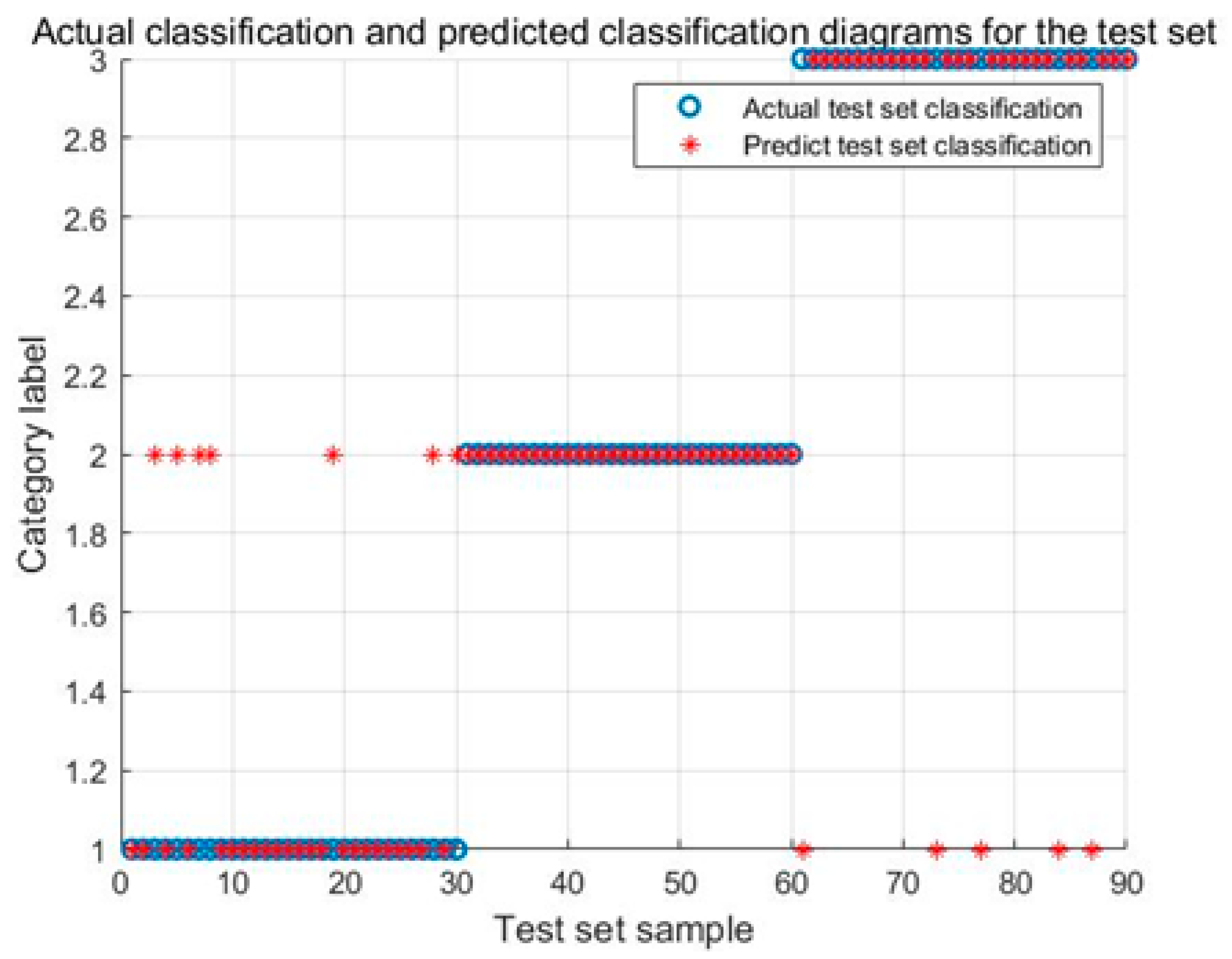
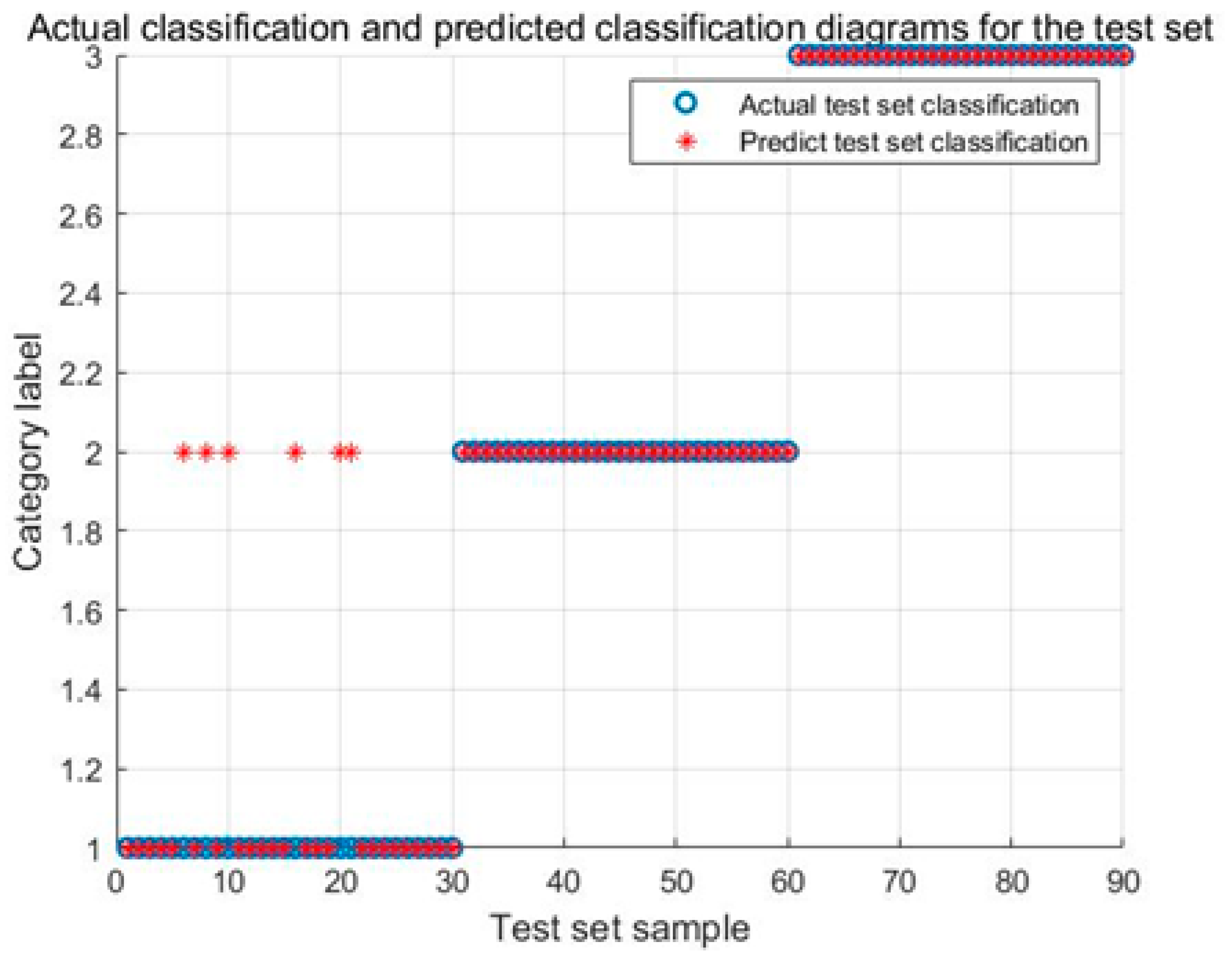
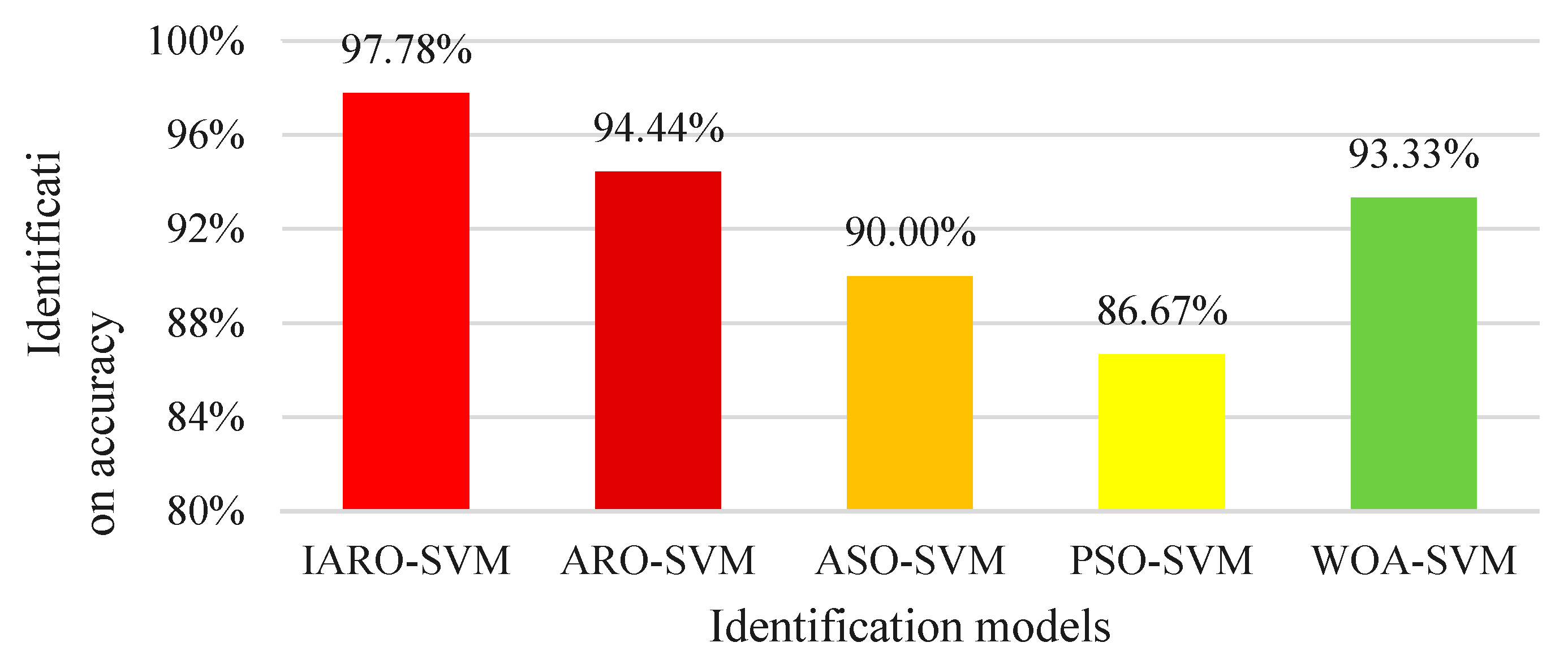
5.5. Validation of the Proposed IARO-SVM Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, P.C.; Wan, Y.; Zhu, H.P.; Hu, B.; Zeng, H.B.; Liu, Y. Vibration measurement method of hydraulic turbine unit based on multi-source information fusion. China Meas. Test 2021, 47, 94–100. [Google Scholar]
- Hu, X.; Wang, X.; Huang, J.Y.; Liu, D.; Xiao, Z.H. Vibration Feature Extraction of Hydropower Unit Based on Variational Mode Decomposition and Complexity Analysis. China Rural Water Hydropower 2019, 1, 188–192. [Google Scholar]
- Seyrek, P.; Şener, B.; Özbayoğlu, A.M.; Unver, H.O. An Evaluation Study of EMD, EEMD, and VMD For Chatter Detection in Milling. Procedia Comput. Sci. 2022, 200, 160–174. [Google Scholar] [CrossRef]
- Joshuva, A.; Kumar, R.S.; Sivakumar, S.; Deenadayalan, G.; Vishnuvardhan, R. An insight on VMD for diagnosing wind turbine blade faults using C4.5 as feature selection and discriminating through multilayer perceptron. Alex. Eng. J. 2020, 59, 3863–3879. [Google Scholar] [CrossRef]
- Wang, Z.J.; He, G.F.; Du, W.H.; Zhou, J.; Han, X.; Wang, J.; He, H.; Guo, X.; Wang, J.; Kou, Y. Application of parameter optimized variational mode decomposition method in fault diagnosis of gearbox. IEEE Access 2019, 7, 44871–44882. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Qaisar, S.M.; Inayatullah Khan, S.; Srinivasan, K.; Krichen, M. Arrhythmia classification using multirate processing metaheuristic optimization and variational mode decomposition. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 26–37. [Google Scholar]
- Mazzeo, M.; De Domenico, D.; Quaranta, G.; Santoro, R. Automatic modal identification of bridges based on free vibration response and variational mode decomposition technique. Eng. Struct. 2023, 280, 115665. [Google Scholar] [CrossRef]
- Liu, W.; Liang, T.; Li, T.; Wen, J. Variable conditions rolling bearing fault diagnosis based on SHO-VMD decomposition and multi-feature parameters. Mach. Tool Hydraul. 2022, 50, 185–193. [Google Scholar]
- Ni, Q.; Ji, J.C.; Feng, K.; Halkon, B. A fault information-guided variational mode decomposition (FIVMD) method for rolling element bearings diagnosis. Mech. Syst. Signal Process. 2022, 164, 108216. [Google Scholar] [CrossRef]
- Hatiegan, C.; Padureanu, I.; Jurcu, M.; Nedeloni, M.D.; Hamat, C.O.; Chioncel, C.P.; Trocaru, S.; Vasile, O.; Bădescu, O.; Micliuc, D. Vibration analysis of a hydro generator for different operating regimes. IOP Conf. Ser. Mater. Sci. Eng. 2017, 163, 012030. [Google Scholar] [CrossRef]
- Jose, J.T.; Das, J.; Mishra, S.K.; Wrat, G. Early detection and classification of internal leakage in boom actuator of mobile hydraulic machines using SVM. Eng. Appl. Artif. Intell. 2021, 106, 104492. [Google Scholar] [CrossRef]
- Jena, D.P.; Panigrahi, S.N.; Rajesh, K. Gear fault identification and localization using analytic wavelet transform of vibration signal. Measurement 2013, 46, 1115–1124. [Google Scholar] [CrossRef]
- Alsaiari, A.O.; Moustafa, E.B.; Alhumade, H.; Abulkhair, H.; Elshiekh, A.H. A coupled artificial neural network with artificial rabbits optimizer for predicting water productivity of different designs of solar stills. Adv. Eng. Softw. 2023, 175, 103315. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Springer: Cham, Switzerland, 2018; pp. 451–455. [Google Scholar]
- Khalil, A.E.; Boghdady, T.A.; Alham, M.H.; Ibrahim, D.K. Enhancing the Conventional Controllers for Load Frequency Control of Isolated Microgrids Using Proposed Multi-Objective Formulation Via Artificial Rabbits Optimization Algorithm. IEEE Access 2023, 11, 3472–3493. [Google Scholar] [CrossRef]
- Pei, J.F.; Yan, A.; Peng, J.; Zhao, J.X. Fault Diagnosis of reciprocating pump based on acoustic signal MFDFA and SFLA-SVM algorithms. Mach. Des. Manuf. 2020, 4, 199–203, 207. [Google Scholar]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Wang, Q.Q.; Wang, R.S.; Xiong, X.R. Optical fiber perimeter vibration signal recognition based on SVD and MPSO-SVM. Syst. Eng. Electron. 2020, 42, 1652–1661. [Google Scholar]
- Wang, Z.; He, X.; Shen, H.; Fan, S.; Zeng, Y. Multi-source information fusion to identify water supply pipe leakage based on SVM and VMD. Inf. Process. Manag. 2022, 59, 102819. [Google Scholar] [CrossRef]
- Li, S.; Kong, X.; Yue, L.; Liu, C.; Khan, M.A.; Yang, Z.; Zhang, H. Short-term electrical load forecasting using hybrid model of manta ray foraging optimization and support vector regression. J. Clean. Prod. 2023, 388, 135856. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.Z.; Fu, X.H.; Bi, W.H. An extraction and recognition method of the distributed optical fiber vibration signal based on EMD-AWPP and HOSA-SVM algorithm. Spectrosc. Spectr. Anal. 2016, 36, 577–582. [Google Scholar]
- Saari, J.; Strömbergsson, D.; Lundberg, J.; Thomson, A. Detection and identification of windmill bearing faults using a one-class support vector machine (SVM). Measurement 2019, 137, 287–301. [Google Scholar] [CrossRef]
- Ruan, J.; Wang, X.; Zhou, T.; Peng, X.; Deng, Y.; Yang, Q. Fault identification of high voltage circuit breaker trip mechanism based on PSR and SVM. IET Gener. Transm. Distrib. 2022, 17, 1179–1189. [Google Scholar]
- Li, Y.J.; Zhang, J.P.; Li, Y.G. Wear state recognition of rolling bearings based on VMD-HMM. J. Vib. Shock. 2018, 37, 61–67. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Lan, J.F.; Zhou, Y.H.; Gao, Z.L.; JIANG, B.; LI, C.S. A model for predicting the deterioration trend of hydropower units based on machine learning. J. Hydroelectr. Eng. 2022, 41, 135–144. [Google Scholar]
- Jiang, X.X.; Song, Q.Y.; Du, G.F.; Huang, W.G.; Zhu, Z.K. A review on research and application of variational mode decomposition. Chin. J. Sci. Instrum. 2023, 01, 1–24. Available online: https://kns.cnki.net/kcms/detail/11.2179.th.20221031.0957.012.html (accessed on 1 November 2022).
- Yang, H.B.; Liu, S.L.; Zhang, H.L. Adaptive estimation of VMD modes number based on cross correlation coefficient. J. Vibroengineering 2017, 19, 1185–1196. [Google Scholar] [CrossRef]
- Wang, L.Y.; Cao, Q.J.; Zhang, Z.X.; Mirjalili, S.; Zhao, W.G. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Ding, Y.M.; Liu, J.Z.; Xu, X.D.; Zhang, W.X.; Yang, Z.P. Recognition of Pantograph Vibration Interference Signal Based on SVM Classification. J. China Railw. Soc. 2021, 43, 38–45. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Zhang, W.; Ma, Z.H. Classification and Recognition Method for Bearing Fault based on IFOA-SVM. J. Mech. Transm. 2021, 45, 148–156. [Google Scholar]
- Kong, Z.; Yang, Q.F.; Zhao, J.; Xiong, J.J. Adaptive Adjustment of Weights and Search Strategies-Based Whale Optimization Algorithm. J. Northeast. Univ. (Nat. Sci.) 2020, 41, 35–43. [Google Scholar]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Wu, Y.; Gu, Z.F.; Liu, G.H.; You, L.S.; Wang, R.L. Selection of Assembly and Disassembly Mode of Main Equipment in Zhanghewan Pumped Storage Power Station. Mech. Electr. Tech. Hydropower Stn. 2018, 41, 12–15. [Google Scholar]
- Yang, X.J. Engineering Design of Zhanghewan Pumped Storage Power Station; China Water & Power Press: Beijing, China, 2018; pp. 445–451. [Google Scholar]
- Zhang, J. The K Value Determination Method of VMD in Signal Decomposition. J. Lanzhou Univ. Arts Sci. (Nat. Sci.) 2022, 36, 75–79. [Google Scholar]
- Huang, N.; Wu, Y.; Cai, G.; Zhu, H.; Yu, C.; Jiang, L.; Zhang, Y.; Zhang, J.; Xing, E. Short-term wind speed forecast with low loss of information based on feature generation of OSVD. IEEE Access 2019, 7, 81027–81046. [Google Scholar] [CrossRef]
- Batista, G.C.; Oliveira, D.L.; Saotome, O.; Silva, W.L.S. A low-power asynchronous hardware implementation of a novel SVM classifier, with an application in a speech recognition system. Microelectron. J. 2020, 105, 104907. [Google Scholar] [CrossRef]
- Aiswarya, R.; Nair, D.S.; Rajeev, T.; Vinod, V. A novel SVM based adaptive scheme for accurate fault identification in microgrid. Electr. Power Syst. Res. 2023, 221, 109439. [Google Scholar]







| Name | Function | D | Range | |
|---|---|---|---|---|
| Sphere | 30 | 0 | ||
| Schwefel 2.22 | 30 | 0 | ||
| Schwefel 1.2 | 30 | 0 | ||
| Schwefel 2.21 | 30 | 0 | ||
| Rosenbrock | 30 | 0 | ||
| Step | 30 | 0 | ||
| Quartic | 30 | 0 |
| Name | Function | D | Range | |
|---|---|---|---|---|
| Schwefel | 30 | |||
| Rastrigin | 30 | 0 | ||
| Ackley | 30 | 0 | ||
| Griewank | 30 | 0 | ||
| Penalized | 30 | 0 | ||
| Penalized 2 | 30 | 0 |
| Name | Function | D | Range | |
|---|---|---|---|---|
| Foxholes | 2 | |||
| Kowalik | 4 | |||
| Six Hump Camel | 2 | |||
| Branin | 2 | |||
| Goldstein-Price | 2 | |||
| Hartman 3 | 3 | |||
| Hartman 6 | 6 | |||
| Shekel 5 | 4 | |||
| Shekel 7 | 4 | |||
| Shekel 10 | 4 |
| NO. | INDEX | IARO | ARO | PSO | ASO | WOA |
|---|---|---|---|---|---|---|
| F1 | Mean | 0 | 1.89 × 10−34 | 9.08 × 10−50 | 1.47 × 10−33 | 2.31 × 10−16 |
| Std | 0 | 6.59 × 10−34 | 4.78 × 10−49 | 7.15 × 10−33 | 2.68 × 10−16 | |
| Worst | 0 | 3.07 × 10−33 | 2.62 × 10−48 | 3.93 × 10−32 | 1.03 × 10−15 | |
| Best | 0 | 1.89 × 10−34 | 9.08 × 10−50 | 1.47 × 10−33 | 2.31 × 10−16 | |
| F2 | Mean | 0 | 1.04 × 10−19 | 1.09 × 10−32 | 1.56 × 10−19 | 3.12 × 10−4 |
| Std | 0 | 2.18 × 10−19 | 3.06 × 10−32 | 3.24 × 10−19 | 1.02 × 10−3 | |
| Worst | 0 | 8.70 × 10−19 | 1.61 × 10−31 | 1.12 × 10−18 | 4.18 × 10−3 | |
| Best | 0 | 1.04 × 10−19 | 1.09 × 10−32 | 1.56 × 10−19 | 3.12 × 10−4 | |
| F3 | Mean | 0 | 4.82 × 10−25 | 4.98 × 10+4 | 1.52 × 10−22 | 3.13 × 10+3 |
| Std | 0 | 1.45 × 10−24 | 1.54 × 10+4 | 8.21 × 10−22 | 9.39 × 10+2 | |
| Worst | 0 | 7.70 × 10−24 | 8.59 × 10+4 | 4.50 × 10−21 | 5.16 × 10+3 | |
| Best | 0 | 4.82 × 10−25 | 4.98 × 10+4 | 1.52 × 10−22 | 3.13 × 10+3 | |
| F4 | Mean | 0 | 1.78 × 10−14 | 4.35 × 10+1 | 5.01 × 10−14 | 8.70 × 10−2 |
| Std | 0 | 5.07 × 10−14 | 3.20 × 10+1 | 2.16 × 10−13 | 1.68 × 10−1 | |
| Worst | 0 | 2.14 × 10−13 | 8.788 × 10+1 | 1.18 × 10−12 | 7.08 × 10−1 | |
| Best | 0 | 1.78 × 10−14 | 4.35 × 10+1 | 5.01 × 10−14 | 8.70 × 10−2 | |
| F5 | Mean | 1.55 × 10+0 | 2.01 × 10+0 | 2.80 × 10+1 | 7.43 × 10−1 | 6.16 × 10+1 |
| Std | 3.16 × 10+0 | 5.10 × 10+0 | 3.34 × 10−1 | 9.57 × 10−1 | 9.49 × 10+1 | |
| Worst | 1.50 × 10+1 | 2.69 × 10+1 | 2.87 × 10+1 | 4.68 × 10+0 | 5.31 × 10+2 | |
| Best | 1.55 × 10+0 | 2.01 × 10+0 | 2.80 × 10+1 | 7.43 × 10−1 | 6.16 × 10+1 | |
| F6 | Mean | 0 | 0 | 0 | 0 | 4.0 × 10−1 |
| Std | 0 | 0 | 0 | 0 | 8.14 × 10−1 | |
| Worst | 0 | 0 | 0 | 0 | 4 | |
| Best | 0 | 0 | 0 | 0 | 4.0 × 10−1 | |
| F7 | Mean | 8.92 × 10−5 | 9.02 × 10−4 | 4.04 × 10−3 | 9.43 × 10−4 | 5.78 × 10−2 |
| Std | 9.76 × 10−5 | 5.93 × 10−4 | 3.76 × 10−3 | 6.21 × 10−4 | 2.14 × 10−2 | |
| Worst | 4.35 × 10−4 | 2.37 × 10−3 | 1.50 × 10−2 | 2.59 × 10−3 | 1.17 × 10−1 | |
| Best | 8.92 × 10−5 | 9.02 × 10−4 | 4.04 × 10−3 | 9.43 × 10−4 | 5.78 × 10−2 |
| NO. | INDEX | IARO | ARO | PSO | ASO | WOA |
|---|---|---|---|---|---|---|
| F8 | Mean | −9.90 × 10+3 | −1.02 × 10+4 | −1.02 × 10+4 | −1.02 × 10+4 | −7.18 × 10+3 |
| Std | 4.68 × 10+2 | 5.09 × 10+2 | 1.73 × 10+3 | 5.68 × 10+2 | 6.89 × 10+2 | |
| Worst | −9.03 × 10+3 | −8.79 × 10+3 | −7.79 × 10+3 | −8.98 × 10+3 | −5.88 × 10+3 | |
| Best | −9.90 × 10+3 | −1.02 × 10+4 | −1.02 × 10+4 | −1.02 × 10+4 | −7.18 × 10+3 | |
| F9 | Mean | 0 | 0 | 0 | 0 | 3.09 × 10+1 |
| Std | 0 | 0 | 0 | 0 | 9.33 | |
| Worst | 0 | 0 | 0 | 0 | 4.78 × 10+1 | |
| Best | 0 | 0 | 0 | 0 | 3.09 × 10+1 | |
| F10 | Mean | 8.88 × 10−16 | 8.88 × 10−16 | 5.27 × 10−15 | 1.01 × 10−15 | 7.98 × 10−9 |
| Std | 0 | 0 | 2.22 × 10−15 | 6.49 × 10−16 | 4.43 × 10−9 | |
| Worst | 8.88 × 10−16 | 8.88 × 10−16 | 7.99 × 10−15 | 4.44 × 10−15 | 2.36 × 10−8 | |
| Best | 8.88 × 10−16 | 8.88 × 10−16 | 5.27 × 10−15 | 1.01 × 10−15 | 7.98 × 10−9 | |
| F11 | Mean | 0 | 0 | 4.86 × 10−3 | 0.00 × 10+0 | 1.31 × 10−3 |
| Std | 0 | 0 | 2.66 × 10−2 | 0 | 4.51 × 10−3 | |
| Worst | 0 | 0 | 1.46 × 10−1 | 0 | 2.21 × 10−2 | |
| Best | 0 | 0 | 4.86 × 10−3 | 0 | 1.31 × 10−3 | |
| F12 | Mean | 5.22 × 10−3 | 4.51 × 10−4 | 1.62 × 10−2 | 5.13 × 10−4 | 2.11 × 10−2 |
| Std | 3.73 × 10−3 | 4.31 × 10−4 | 9.48 × 10−3 | 3.14 × 10−4 | 4.29 × 10−2 | |
| Worst | 1.68 × 10−2 | 2.44 × 10−3 | 3.78 × 10−2 | 1.62 × 10−3 | 1.30 × 10−1 | |
| Best | 5.22 × 10−3 | 4.51 × 10−4 | 1.62 × 10−2 | 5.13 × 10−4 | 2.11 × 10−2 | |
| F13 | Mean | 4.61 × 10−2 | 8.14 × 10−3 | 4.26 × 10−1 | 6.03 × 10−3 | 7.33 × 10−3 |
| Std | 3.64 × 10−2 | 1.09 × 10−2 | 2.05 × 10−1 | 9.97 × 10−3 | 1.94 × 10−2 | |
| Worst | 1.37 × 10−1 | 4.47 × 10−2 | 8.31 × 10−1 | 4.59 × 10−2 | 9.89 × 10−2 | |
| Best | 4.61 × 10−2 | 8.14 × 10−3 | 4.26 × 10−1 | 6.03 × 10−3 | 7.33 × 10−3 |
| NO. | INDEX | IARO | ARO | PSO | ASO | WOA |
|---|---|---|---|---|---|---|
| F14 | Mean | 9.98 × 10−1 | 9.98 × 10−1 | 1.8859 | 9.98 × 10−1 | 1.5523 |
| Std | 7.14 × 10−17 | 7.14 × 10−17 | 1.88 | 8.25 × 10−17 | 6.76 × 10−1 | |
| Worst | 9.98 × 10−1 | 9.98 × 10−1 | 10.76 | 9.98 × 10−1 | 3.1209 | |
| Best | 9.98 × 10−1 | 9.98 × 10−1 | 1.8859 | 9.98 × 10−1 | 1.5523 | |
| F15 | Mean | 3.76 × 10−4 | 3.27 × 10−4 | 6.53 × 10−4 | 3.12 × 10−4 | 1.31 × 10−3 |
| Std | 8.24 × 10−5 | 3.56 × 10−5 | 4.16 × 10−4 | 7.47 × 10−6 | 1.02 × 10−3 | |
| Worst | 6.44 × 10−4 | 4.59 × 10−4 | 2.25 × 10−3 | 3.37 × 10−4 | 6.49 × 10−3 | |
| Best | 3.76 × 10−4 | 3.27 × 10−4 | 6.53 × 10−4 | 3.12 × 10−4 | 1.31 × 10−3 | |
| F16 | Mean | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| Std | 5.17 × 10−16 | 5.56 × 10−16 | 1.93 × 10−9 | 5.30 × 10−16 | 5.98 × 10−16 | |
| Worst | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | |
| Best | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | |
| F17 | Mean | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| Std | 0 | 6.97 × 10−14 | 7.68 × 10−6 | 8.21 × 10−14 | 0 | |
| Worst | 3.98 × 10−1 | 0.3979 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | |
| Best | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | |
| F18 | Mean | 3.0000 | 3.0000 | 3.9003 | 3.0000 | 3.0000 |
| Std | 1.50 × 10−15 | 5.34 × 10−16 | 4.93 × 10−1 | 1.34 × 10−15 | 1.61 × 10−15 | |
| Worst | 3.0000 | 3.0000 | 30.0077 | 3.0000 | 3.0000 | |
| Best | 3.0000 | 3.0000 | 3.9003 | 3.0000 | 3.0000 | |
| F19 | Mean | −3.8628 | −3.8628 | −3.8576 | −3.8628 | −3.8628 |
| Std | 2.52 × 10−15 | 2.49 × 10−15 | 9.09 × 10−3 | 2.46 × 10−15 | 2.60 × 10−15 | |
| Worst | −3.8628 | −3.8628 | −3.8235 | −3.8628 | −3.8628 | |
| Best | −3.8628 | −3.8628 | −3.8576 | −3.8628 | −3.8628 | |
| F20 | Mean | −3.2943 | −3.3101 | −3.2848 | −3.3141 | −3.3220 |
| Std | 5.11 × 10−2 | 3.63 × 10−2 | 6.57 × 10−2 | 3.02 × 10−2 | 1.36 × 10−15 | |
| Worst | −3.2031 | −3.2031 | −3.0778 | −3.2031 | −3.3220 | |
| Best | −3.2943 | −3.3101 | −3.2848 | −3.3141 | −3.3220 | |
| F21 | Mean | −9.9787 | −10.1531 | −7.6137 | −10.1530 | −8.47 |
| Std | 8.37 × 10−1 | 8.12 × 10−4 | 3.0335 | 1.27 × 10−3 | 3.1122 | |
| Worst | −5.5962 | −10.1488 | −2.6296 | −10.1463 | −2.6829 | |
| Best | −9.9787 | −10.1531 | −7.6137 | −10.1530 | −8.4749 | |
| F22 | Mean | −10.4029 | −10.2258 | −7.8582 | −10.1794 | −9.8929 |
| Std | 1.38 × 10−10 | 9.70 × 10−1 | 2.86 | 1.22 | 1.942 | |
| Worst | −10.4029 | −5.0877 | −2.7642 | −3.7243 | −2.7519 | |
| Best | −10.4029 | −10.2258 | −7.8582 | −10.1794 | −9.8929 | |
| F23 | Mean | −10.5364 | −10.5364 | −7.8230 | −10.5364 | −10.5364 |
| Std | 6.00 × 10−5 | 2.54 × 10−7 | 3.1920 | 2.03 × 10−11 | 1.32 × 10−15 | |
| Worst | −10.5361 | −10.5364 | −2.4216 | −10.5364 | −10.5364 | |
| Best | −10.5364 | −10.5364 | −7.8230 | −10.5364 | −10.5364 |
| Vibration State | Measuring Point Position | Experimental Point | Direction | Category Label |
|---|---|---|---|---|
| Stability test of power generation condition | upper guide bearing | 1 | X | 1 |
| upper guide bearing | 2 | Y | ||
| water guide bearing | 3 | X | ||
| water guide bearing | 4 | Y | ||
| lower guide bearing | 5 | X | ||
| lower guide bearing | 6 | Y | ||
| Karman vortex street phenomenon test | upper guide bearing | 1 | X | 2 |
| upper guide bearing | 2 | Y | ||
| water guide bearing | 3 | X | ||
| water guide bearing | 4 | Y | ||
| lower guide bearing | 5 | X | ||
| lower guide bearing | 6 | Y | ||
| Simulated fault shutdown test | upper guide bearing | 1 | X | 3 |
| upper guide bearing | 2 | Y | ||
| water guide bearing | 3 | X | ||
| water guide bearing | 4 | Y | ||
| lower guide bearing | 5 | X | ||
| lower guide bearing | 6 | Y |
| Vibration State | Measuring Point Position and Direction | Number of Decomposition Layers () | Update Steps () |
|---|---|---|---|
| Stability test of power generation condition | upper guide bearing, X direction | 13 | 0.0043 |
| upper guide bearing, Y direction | 12 | 0.0312 | |
| water guide bearing, X direction | 13 | 0.0012 | |
| water guide bearing, Y direction | 12 | 0.0315 | |
| lower guide bearing, X direction | 12 | 0.0314 | |
| lower guide bearing, Y direction | 12 | 0.0068 | |
| Karman vortex street phenomenon test | upper guide bearing, X direction | 14 | 0.0192 |
| upper guide bearing, Y direction | 13 | 0.0321 | |
| water guide bearing, X direction | 12 | 0.0077 | |
| water guide bearing, Y direction | 12 | 0.1331 | |
| lower guide bearing, X direction | 15 | 0.0205 | |
| lower guide bearing, Y direction | 11 | 0.0474 | |
| Simulated fault shutdown test | upper guide bearing, X direction | 12 | 0.0318 |
| upper guide bearing, Y direction | 15 | 0.0483 | |
| water guide bearing, X direction | 10 | 0.3245 | |
| water guide bearing, Y direction | 12 | 0.0505 | |
| lower guide bearing, X direction | 14 | 0.0230 | |
| lower guide bearing, Y direction | 12 | 0.0053 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.; Wang, L.; Zhao, W.; Yuan, Z.; Liu, A.; Gao, Y.; Ye, R. Vibration State Identification of Hydraulic Units Based on Improved Artificial Rabbits Optimization Algorithm. Biomimetics 2023, 8, 243. https://doi.org/10.3390/biomimetics8020243
Cao Q, Wang L, Zhao W, Yuan Z, Liu A, Gao Y, Ye R. Vibration State Identification of Hydraulic Units Based on Improved Artificial Rabbits Optimization Algorithm. Biomimetics. 2023; 8(2):243. https://doi.org/10.3390/biomimetics8020243
Chicago/Turabian StyleCao, Qingjiao, Liying Wang, Weiguo Zhao, Zhouxiang Yuan, Anran Liu, Yanfeng Gao, and Runfeng Ye. 2023. "Vibration State Identification of Hydraulic Units Based on Improved Artificial Rabbits Optimization Algorithm" Biomimetics 8, no. 2: 243. https://doi.org/10.3390/biomimetics8020243
APA StyleCao, Q., Wang, L., Zhao, W., Yuan, Z., Liu, A., Gao, Y., & Ye, R. (2023). Vibration State Identification of Hydraulic Units Based on Improved Artificial Rabbits Optimization Algorithm. Biomimetics, 8(2), 243. https://doi.org/10.3390/biomimetics8020243






