Augmented Harris Hawks Optimizer with Gradient-Based-Like Optimization: Inverse Design of All-Dielectric Meta-Gratings
Abstract
1. Introduction
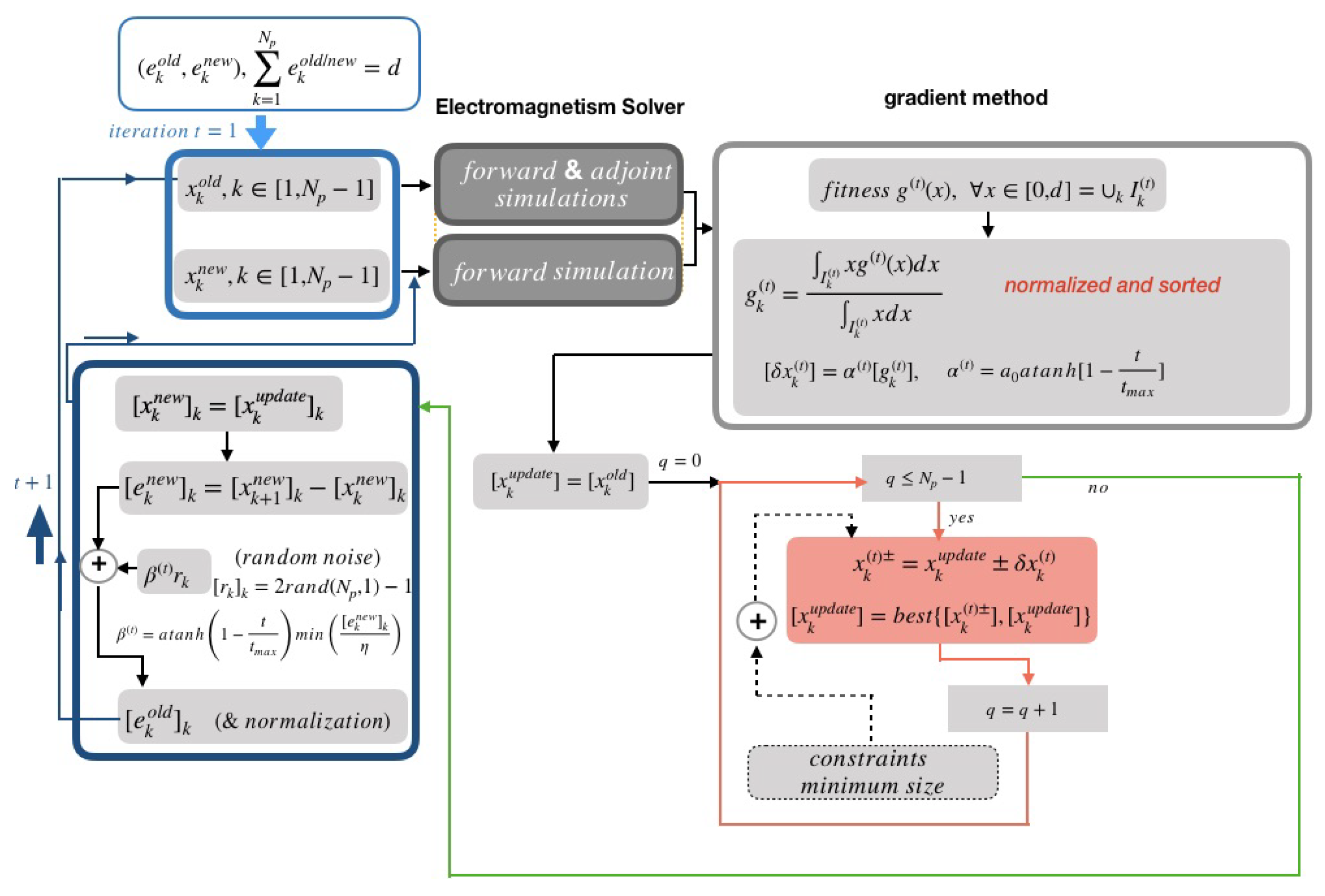
2. The Gradient-Based-Like (GBL) Optimization Method
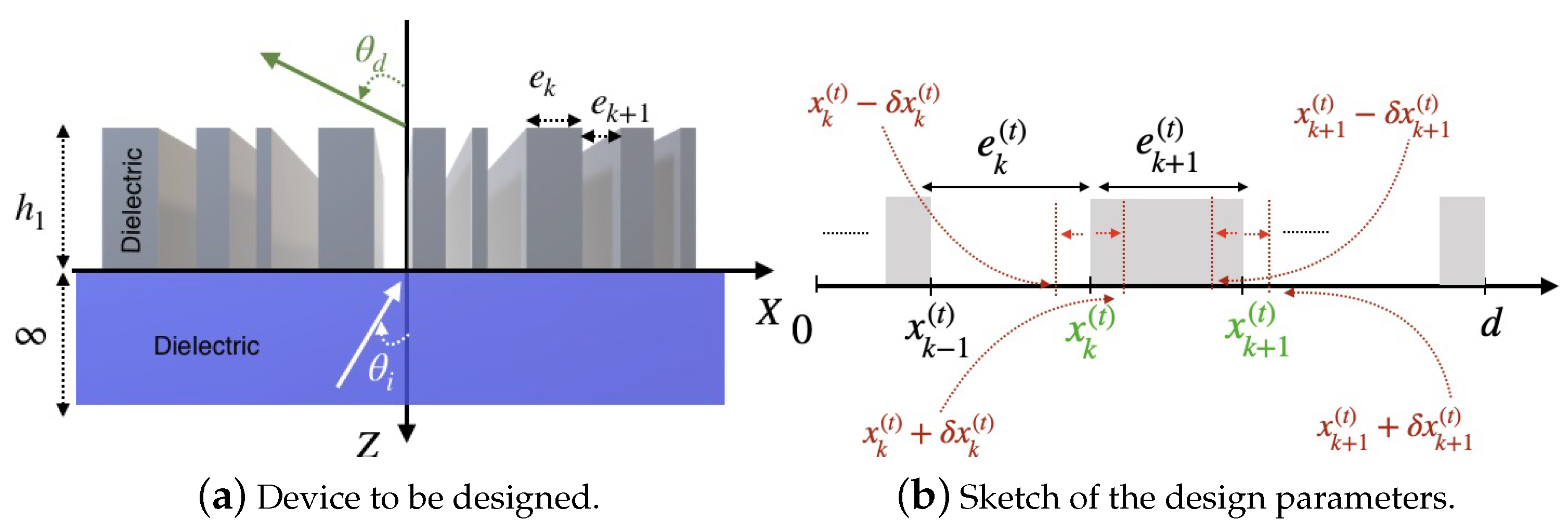
2.1. Initialization
2.2. Evaluation of the Fitness of the Design Parameters
2.3. Best Current Pattern Update
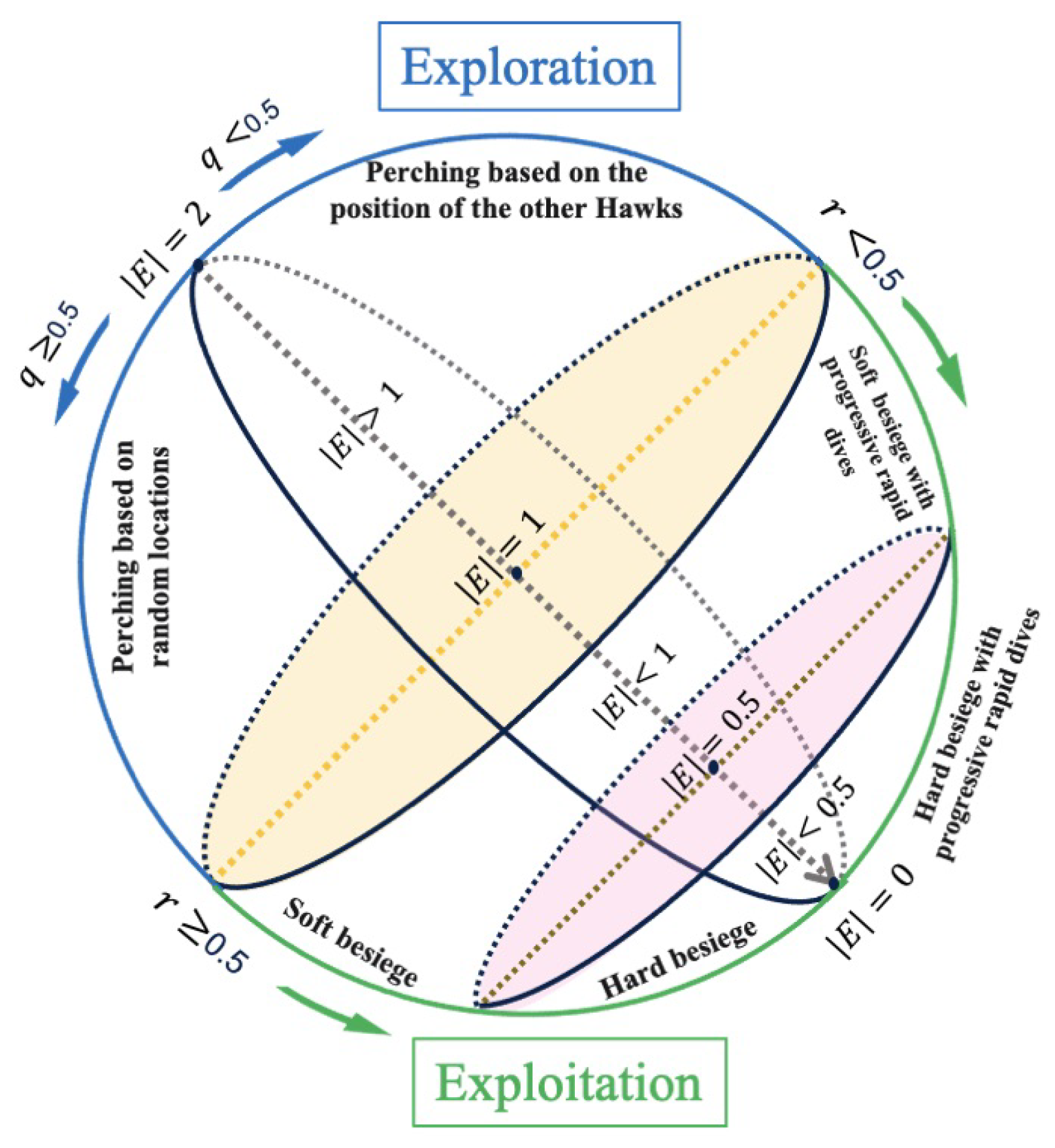
3. Harris Hawks Optimizer
3.1. Exploration Phase
3.2. Exploitation Phase ()
- 1.
- When , hawks consider the prey to still have enough energy to escape, and thus, a soft besiege strategy is applied. In this case, locations are updated as follows:with , , a random number in and the parameter simulates the random jump strength of the prey during the escape procedure in each iteration. represents the updated location of the hawk at iteration , denotes the position of the prey at iteration t.
- 2.
- When , hawks apply a more aggressive strategy, a hard besiege, to capture the prey, as they believe the prey to be too tired to escape. The location update equation for this phase can be written as:with always being the difference between the positions of the prey and the hawk.
- 3.
- In the exploitation phase, hawks can also perform some progressive rapid dives based on the Levy flight (LF) function. The LF function is defined as:where u, v are random values within , and is a default constant set to in this paper. The term is calculated as:where denotes the gamma function. Rapid dives can be performed with either soft or hard besieges. The hawks’ location at iteration is evaluated based on the following equation:
- In the case of a soft besiege with progressive rapid dives
- In the case of a hard besiege with progressive rapid dives
in both cases , where D denotes the dimension of the problem and S is a random vector with size .
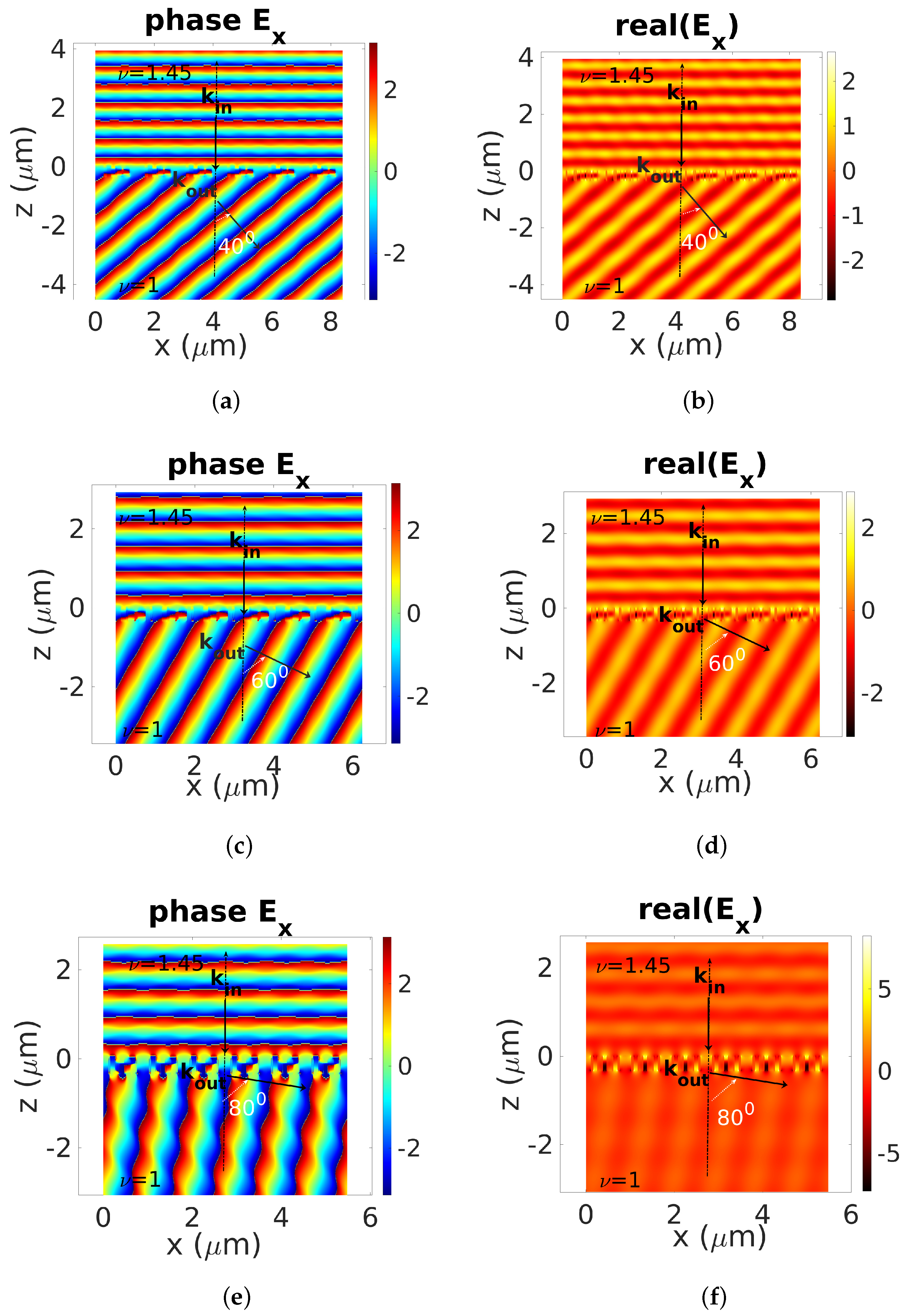
4. Results and Discussion
5. Conclusions and Outlook
Funding
Data Availability Statement
Conflicts of Interest
References
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Andrei, N.A. SQP Algorithm for Large-Scale Constrained Optimization: SNOPT. In Continuous Nonlinear Optimization for Engineering Applications in GAMS Technology; Springer Optimization and Its Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 1, 66–73. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; Volume 1, pp. 39–43. [Google Scholar]
- Dorigo, M.; Caro, G.D. Ant colony optimization: A new metaheuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1470–1477. [Google Scholar]
- Stornand, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolves optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whales optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Senthilnath, J.; Dokania, A.; Kulkarni, S.; Omkar, S.N. Harris hawks optimization for multi-objective optimization in power system engineering. Appl. Soft Comput. 2020, 97, 106739. [Google Scholar]
- Baskar, S.; Krishnakumar, K. Harris hawks optimization algorithm for segmentation of MRI brain images. Multimed. Tools Appl. 2021, 80, 17909–17926. [Google Scholar]
- Zhang, H.; Cao, Z. Multimodal optimization and its application in image segmentation based on Harris hawks optimization. Soft Comput. 2021, 25, 5019–5033. [Google Scholar]
- Sharma, R.; Singh, S.N. An improved Harris hawks optimization with multi-verse optimizer for optimal power flow solution. Int. J. Electr. Power Energy Syst. 2021, 128, 106775. [Google Scholar]
- Mohajeri, S.; Beheshti, S.M. A novel approach for feature selection based on Harris hawks optimization. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 3939–3950. [Google Scholar]
- Lim, J.H.; Lee, K.Y. Optimal design of shell-and-tube heat exchanger using Harris hawks optimization. Appl. Therm. Eng. 2020, 179, 115656. [Google Scholar]
- Qin, N.; Yang, D. Joint base station placement and user association in heterogeneous networks using Harris hawks optimization. Wirel. Netw. 2020, 26, 5089–5101. [Google Scholar]
- Kaveh, A.; Khayatazad, M. A new optimization method: Ray Optimization. Comput. Struct. 2012, 112, 76–82. [Google Scholar]
- Song, J.; Li, X.; Zhou, Y.; Li, S. Enhancing the performance of Harris Hawks optimization via persistent-trigonometric-differences mechanism and enhanced energy factor. Soft Comput. 2021, 25, 14089–14116. [Google Scholar]
- Edee, K. Biomimicry-Gradient-Based Algorithm as Applied to Photonic Devices Design: Inverse Design of Flat Plasmonic Metalenses. Appl. Sci. 2021, 11, 5436. [Google Scholar] [CrossRef]
- Frandsen, L.H.; Harpøth, A.; Borel, P.I.; Kristensen, M.; Jensen, J.S.; Sigmund, O. Broadband photonic crystal waveguide 60∘ bend obtained utilizing topology optimization. Opt. Express 2004, 12, 5916–5921. [Google Scholar] [CrossRef] [PubMed]
- Borel, P.I.; Harpøth, A.; Frandsen, L.H.; Kristensen, M.; Shi, P.; Jensen, J.S.; Sigmund, O. Topology optimization and fabrication of photonic crystal structures. Opt. Express 2004, 12, 1996–2001. [Google Scholar] [CrossRef]
- Lu, J.; Vuckovic, J. Nanophotonic computational design. Opt. Express 2013, 21, 13351–13367. [Google Scholar] [CrossRef]
- Xiao, T.P.; Cifci, O.S.; Bhargava, S.; Chen, H.; Gissibl, T.; Zhou, W.; Giessen, H.; Toussaint, K.C.; Yablonovitch, E.; Braun, P.V. Diffractive spectral-splitting optical element designed by adjoint-based electromagnetic optimization and fabricated by femtosecond 3D direct laser writing. ACS Photonics 2016, 3, 886–894. [Google Scholar] [CrossRef]
- Sell, D.; Yang, J.; Doshay, S.; Yang, R.; Fan, J.-A. Large-angle, multifunctional metagratings based on freeform multimode geometries. Nano Lett. 2017, 17, 3752–3757. [Google Scholar] [CrossRef]
- Hughes, T.W.; Minkov, M.; Williamson, I.A.D.; Fan, S. Adjoint Method and Inverse Design for Nonlinear Nanophotonic Devices. ACS Photonics 2018, 5, 4781–4787. [Google Scholar] [CrossRef]
- Lin, Z.; Groever, B.; Capasso, F.; Rodriguez, A.W.; Lončar, M. Topology-optimized multilayered metaoptics. Phys. Rev. Appl. 2018, 9, 044030. [Google Scholar] [CrossRef]
- Phan, T.; Sell, D.; Wang, E.W.; Doshay, S.; Edee, K.; Yang, J.; Fan, J.A. High-efficiency, large-area, topology-optimized metasurfaces. Light. Sci. Appl. 2019, 8, 48. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.W.; Sell, D.; Phan, T.; Fan, J.-A. Robust design of topology-optimized metasurfaces. Opt. Mater. Express 2019, 9, 469–482. [Google Scholar] [CrossRef]
- Edee, K. Modal method based on subsectional Gegenbauer polynomial expansion for lamellar grating. J. Opt. Soc. Am. A 2011, 28, 2006–2013. [Google Scholar] [CrossRef]
- Edee, K.; Fenniche, I.; Granet, G.; Guizal, B. Modal method based on subsectional Gegenbauer polynomial expansion for lamellar gratings: Weighting function, convergence and stability. Prog. Electromagn. Res. 2013, 133, 17–35. [Google Scholar] [CrossRef]
- Edee, K.; Guizal, B. Modal method based on subsectional Gegenbauer polynomial expansion for nonperiodic structures: Complex coordinates implementation. J. Opt. Soc. Am. A 2013, 30, 631–639. [Google Scholar] [CrossRef]
- Edee, K.; Plumey, J.P. Plumey Numerical scheme for the modal method based on subsectional Gegenbauer polynomial expansion: Application to biperiodic binary grating. J. Opt. Soc. Am. A 2015, 31, 402–410. [Google Scholar] [CrossRef]
- Edee, K.; Plumey, J.P.; Guizal, B. Unified Numerical Formalism of Modal Methods in Computational Electromagnetics and Latest Advances: Applications in Plasmonics. Adv. Imaging Electron Phys. 2016, 197, 45–103. [Google Scholar]
- Knop, K. Rigorous diffraction theory for transmission phase gratings with deep rectangular grooves. J. Opt. Soc. Am. A 1978, 68, 1206–1210. [Google Scholar] [CrossRef]
- Granet, G.; Guizal, B. Efficient implementation of the coupled-wave method for metallic lamellar gratings in TM polarization. J. Opt. Soc. Am. A 1996, 13, 1019–1023. [Google Scholar] [CrossRef]
- Lalanne, P.; Morris, G.M. Highly improved convergence of the coupled-wave method for TM polarization. J. Opt. Soc. Am. A 1996, 13, 779–784. [Google Scholar] [CrossRef]
- Li, L. Use of Fourier series in the analysis of discontinuous periodic structures. J. Opt. Soc. Am. A 1996, 13, 1870–1876. [Google Scholar] [CrossRef]
- Granet, G. Reformulation of the lamellar grating problem through the concept of adaptive spatial resolution. J. Opt. Soc. Am. A 1999, 16, 2510–2516. [Google Scholar] [CrossRef]
- Jiang, J.; Fan, J.-A. Global Optimization of Dielectric Metasurfaces Using a Physics-Driven Neural Network. Nano Lett. 2019, 8, 5366–5372. [Google Scholar] [CrossRef]
- Jiang, J.; Lupoiu, R.; Wang, E.W.; Sell, D.; Hugonin, J.P.; Lalanne, P.; Fan, J.A. MetaNet: A new paradigm for data sharing in photonics research. Opt. Express 2020, 28, 13670. [Google Scholar] [CrossRef]
- Edee, K. Topology optimization of photonics devices: Fluctuation-trend analysis concept; random initial conditions with Gaussian and Durden-Vesecky power density bandlimited spectra. J. Opt. Soc. Am. B 2020, 37, 2111–2120. [Google Scholar] [CrossRef]
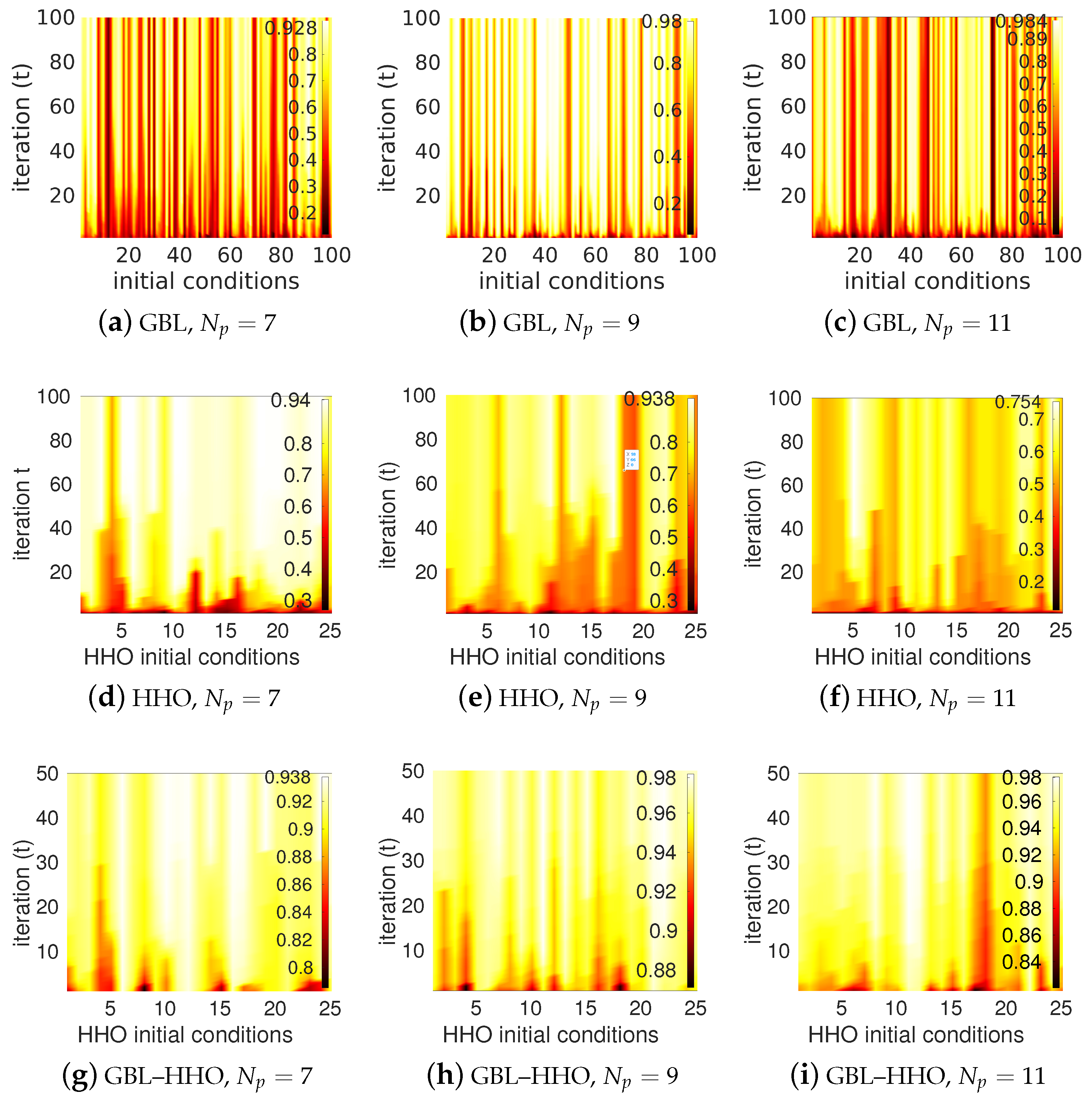
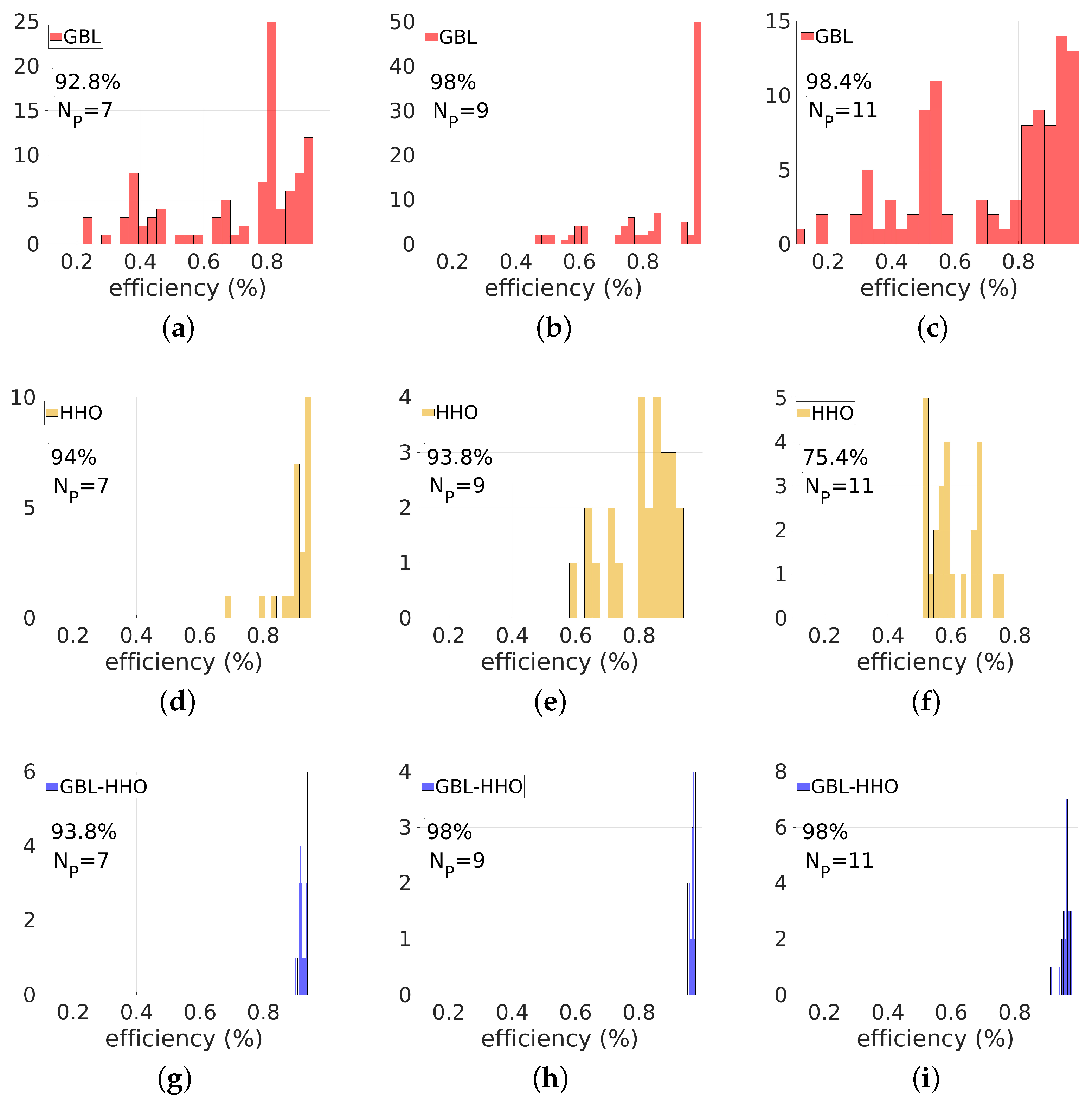


| Method | GBL | HHO | GBL–HHO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 7 | 7 | 11 | 7 | 7 | 11 | 7 | 7 | 11 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edee, K. Augmented Harris Hawks Optimizer with Gradient-Based-Like Optimization: Inverse Design of All-Dielectric Meta-Gratings. Biomimetics 2023, 8, 179. https://doi.org/10.3390/biomimetics8020179
Edee K. Augmented Harris Hawks Optimizer with Gradient-Based-Like Optimization: Inverse Design of All-Dielectric Meta-Gratings. Biomimetics. 2023; 8(2):179. https://doi.org/10.3390/biomimetics8020179
Chicago/Turabian StyleEdee, Kofi. 2023. "Augmented Harris Hawks Optimizer with Gradient-Based-Like Optimization: Inverse Design of All-Dielectric Meta-Gratings" Biomimetics 8, no. 2: 179. https://doi.org/10.3390/biomimetics8020179
APA StyleEdee, K. (2023). Augmented Harris Hawks Optimizer with Gradient-Based-Like Optimization: Inverse Design of All-Dielectric Meta-Gratings. Biomimetics, 8(2), 179. https://doi.org/10.3390/biomimetics8020179








