Abstract
In this study, we investigate the contact electrification properties of glycine, cysteine, and dimethyl siloxane on silicon dioxide (SiO2) surfaces using density functional theory calculations. Molecule contacting through the sulfhydryl group has stronger adhesion to the SiO2-O and SiO2-OH surfaces. The SiOH/SiO2-Si system has the largest adhesion energy in all molecule/SiO2-Si contact systems and charge transfers from the molecule to the SiO2-O and SiO2-Si surfaces. The molecule/SiO2-OH systems have a reverse charge transfer direction. Molecules with their sulfhydryl and hydroxyl groups facing the SiO2-O and SiO2-OH surfaces have more transferred charges. The NH2/SiO2-Si system has a larger transferred charge than other molecule/SiO2-Si systems. The direction of charge transfer is determined by the Bader charge of the isolated surface atoms. The respective energy difference in the lowest unoccupied occupied molecular orbitals between contacting atoms influences the charge transfer. The respective energy difference in the highest occupied molecular orbitals reflects the electron attraction and affects charge transfer. Finally, the quantitative relationship between the transferred charge and energy gaps is established to evaluate the charge transfer. The findings propose a new perspective and in-depth understanding of contact electrification and shed light on the bio-inspired adhesive materials design and fabrication for engineering applications.
1. Introduction
Geckos have the extraordinary motion ability to temporarily and reversibly adhere to nearly all surface topographies [1,2,3]. The adhesive mechanism of geckos is believed to be dominated by the van der Waals interactions between the submicron-sized spatulae and the substrate [4,5]. By mimicking the outstanding adhesive capabilities of the gecko, researchers have fabricated different kinds of gecko-inspired artificial adhesives based on polymer materials (e.g., polyvinylsiloxane, polyurethane, polydimethylsiloxane) [6,7,8,9]. However, the mechanism of gecko adhesion and the physical origin of the adhesion-induced surface properties have been subjects of debate, especially for the improvement of the adhesion of bionic materials [10,11]. Meanwhile, it is well known that contact electrification is one kind of surface effect and almost all substances exhibit a contact electrification effect in daily life, which cannot be ignored in the study of interface adhesion. Izadi et al. measured the tribocharge and shearing forces of geckos’ footpads and found that interfacial contact electrification contributes effectively to gecko adhesion [12]. Song et al. synchronously measured interfacial tribocharge and contact forces and found that the tribocharge at the footpads of free locomotion geckos is related to contact forces [13]. In addition, geckos’ hairy attachments are easily positively tribo-charged, and thus electrostatic interaction is increasingly invoked to elucidate the adhesion of geckos [11,14]. Hence, we need to consider the presence and contribution of contact electrification in the adhesion effects of gecko and gecko-inspired materials.
Given the perspective above, what causes the contact electrification of gecko setae and gecko-inspired polymeric adhesive materials? In recent years, our understanding of contact electrification mechanisms has developed rapidly with scanning probe microscopy and first-principles calculations [15,16,17]. There are a certain number of studies on the fundament of contact electrification for polymers, and some distinct viewpoints have been raised. For example, the effective work function and tunneling effect are proposed to explain the charge transfer between polymer surfaces [18,19,20]. Meanwhile, Lowell et al. developed the high-energy state theory that electron transfers from high-energy states to lower-energy states achieve an equilibrium state for polymers [21]. A recent study has also confirmed that the interfacial barrier rather than the effective work function difference is the more fundamental parameter to polymer contact electrification [22]. In addition, some researchers believe that the interface contact electrification is related to the difference in the electronic attraction of the surfaces for polymers, rather than the potential barrier [23]. To date, our understanding of the contact electrification mechanism for polymers is far from enough. Hence, a systematic study of the underlying mechanisms of polymer contact electrification based on the electron transfer model is essential for a better understanding of the interfacial adhesion properties of polymer adhesive materials.
Accordingly, the study of contact electrification of gecko setae or polymer adhesives is an essential prerequisite for the research of the mechanisms of biological adhesion and the bio-inspired design of artificial adhesives [24]. Studies on simple adhesion systems (amino acids of geckos’ proteins and monomers of polymeric adhesive materials) are necessary for a thorough understanding of actual adhesion systems. Researchers have found that the prevalent proteins in the gecko setae are mostly glycine-rich or cysteine-rich [25,26,27]. The study of glycine and cysteine interfacial charge transfer would give a deep understanding of contact electrification for geckos. Numerous studies have shown that the contact electrification performance of polymers is also affected by the characteristics of the functional groups and the chemical structure of the polymer. By attaching different functional groups to the surfaces of the polyethylene terephthalate (PET) films, researchers can tune the electron loss or gain ability of the PET surface more easily during contact electrification [28]. Li et al. proposed that the contact electrification on both polymer–polymer and polymer–liquid interfaces can be explained by the electron cloud overlapping and electron-withdrawing ability of functional groups [29]. Thus, studies on the relationships between different functional groups of polymers and contact electrification are necessary for a better understanding of the interfacial effect of gecko toes and gecko-inspired dry adhesives.
In this study, we study the contact electrification performance of amino acids (glycine and cysteine) and monomers of polymeric adhesive materials on the SiO2 surface at the atomic scale. SiO2 is one of the essential dielectric materials in the natural environment of gecko activities and physical property measurements [30,31,32]. The charge transfer between different functional groups of polymers and the SiO2 surface is systematically studied to deeply understand the contact electrification mechanism using the first-principles calculation. The results of this work provide useful theoretical knowledge which is very important for a better understanding of contact electrification and adhesion property of gecko seta and bio-inspired adhesive materials at the SiO2 surface, and shed light on the design and application of bio-inspired adhesive materials and structures.
2. Methodology
All of the DFT calculations in the present work are carried out by the Vienna Ab initio simulation package (VASP) with the projected augmented wave (PAW) method [33,34,35,36]. The exchange-correlation effects are described by the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation [37]. The DFT-D3 method of Grimme is used to correct the effect of van der Waals interactions between the molecule and silicon oxide (quartz) surfaces [38]. For calculations of molecule and surface with a dipole moment, the dipole correction is used. The electronic kinetic energy cutoff of 520 eV is used in the calculations. The k-point mesh of 3 × 3 × 1 Monkhorst–Pack is used in all calculations [39]. The convergence standard is set as follows: the interatomic force is less than 0.01 eV/Å, and the energy change per atom is less than 10−5 eV. The vacuum layer in the model is more than 20 Å along the z-direction to avoid the mirror self-interaction.
To simulate the interfacial structure, the contact model of the SiO2(001) substrate, molecule, and vacuum layer is adopted in this study. The bulk structure of α-SiO2 has hexagonal symmetry (P3121). Previous calculations found that the fully hydroxylated SiO2 surface is the most stable one [40]. As various types of interface structures can be generated in molecule/SiO2 contact models, the O-terminated, OH-terminated, and Si-terminated SiO2(001) are all investigated. The O-terminated (Si-terminated) SiO2 is modeled by a slab containing five (six) Si atomic layers and twelve O atomic layers. The O atoms at the bottom are passivated by H. The atomic structure of the O-terminated systems is built by the removal of the top surface Si atoms from the Si-terminated systems. The atomic structure of the OH-terminated is constructed by hydroxylating the top surface O atoms from the O-terminated systems. The interfacial properties are calculated using a 3 × 3 SiO2(001) supercell. Thus, the O-terminated (Si-terminated) SiO2 contains 45 (54) Si atoms, 108 O atoms, and 18 H atoms, and the OH-terminated SiO2 contains 45 Si atoms, 108 O atoms, and 36 H atoms (Figure S1). The SiO2 surface is first fully relaxed prior to interfacial calculations. For O-terminated or OH-terminated (Si-terminated) SiO2 and molecule contact systems, the bottom ten (eleven) atomic layers are fixed in their bulk positions during relax calculations.
The fact that contact electrification is likely to be related to the molecular structure of the polymer. Hence, in our calculations, the different functional groups of amino acids and monomers of adhesive materials should be considered. A glycine (Gly) molecule has three active sites, carbonyl oxygen (C=O), hydroxyl oxygen (OH), and amino nitrogen (NH2) groups. A cysteine (Cys) molecule has the above-mentioned groups and an extra sulfhydryl sulfur (SH) group. In addition to the above functional groups, since the most common polymeric adhesive materials partly differ through their sidechains, we decided to add the silanol group of dimethyl siloxane (C2H8OSi, DMS), which represents the constituent repeating unit of adhesive polydimethylsiloxane material in the theoretical calculations. Therefore, the most common functional groups of gecko toes and polymer adhesive materials have been considered. The molecule structure is modeled as the Gly, Cys, or DMS molecule in a 14.73 × 12.756 × 40 Å cell, which is the size of the SiO2(001) slab for calculations. In calculations, molecules are placed above the top site of the surface atoms of the SiO2(001) surface via five related active sites. The molecules have ten or more atoms which involve a number of degrees of freedom in the simulation. Therefore, we have limited our calculations to the models described as the contact atom of SiO2 surface (topmost O atom of O-terminated and OH-terminated SiO2(001) surface and topmost Si atom of Si-terminated SiO2(001) surface) contact atom (O, N or S atom) of the molecule. The corresponding two adjacent atoms (C or Si atom) have the same coordinates in the x-axis and y-axis to ensure the top site’s relationship, which is kept frozen at the x-axis and y-axis in the relax calculations. The graphical representations of the initial configurations of molecule-SiO2(001) systems are shown in Figure 1.
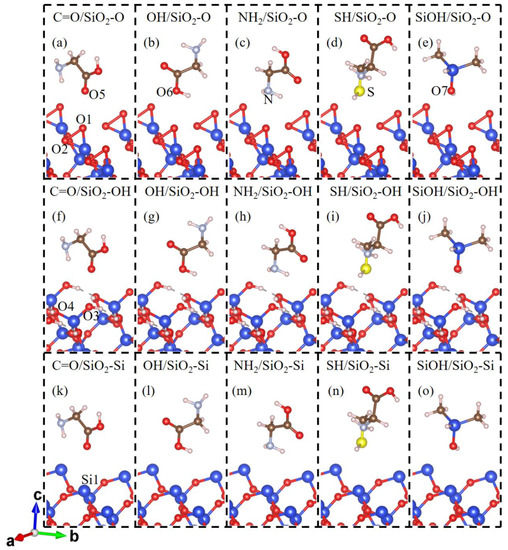
Figure 1.
The initial contact conformation for (a) C=O group of glycine; (b) OH group of glycine; (c) NH2 group of glycine; (d) SH group of cysteine; (e) SiOH group of dimethyl siloxane molecule on the O-terminated SiO2(001) (SiO2-O) surface; (f) C=O; (g) OH; (h) NH2; (i) SH; (j) SiOH groups on the OH-terminated SiO2(001) (SiO2-OH) surface; (k) C=O; (l) OH; (m) NH2; (n) SH; and (o) SiOH group on the Si-terminated SiO2(001) (SiO2-Si) surface. The Si, O, H, C, N, and S atoms are drawn in blue, red, white, brown, light blue, and yellow, respectively.
To quantify the adhesion energy between SiO2(001) surface and molecule, Eb is obtained for various cases of the study:
where E is the total energy of the contact systems, and Esub (Emo) is the total energy of the isolated SiO2(001) (molecule).
Eb = E − Esub − Emo,
The quantitative estimation of the charge density differences along the z-direction is defined as:
where n(z) is the xy-plane-averaged charge density of the systems, and nsub (nmo) is the xy-plane-averaged charge density of the isolated SiO2 (molecule).
Δn(z) = n(z) − nsub(z) − nmo(z),
Moreover, the amount of transferred charge is obtained by integrating Δn(z) from the interfacial node z0 (the position of the electrostatic potential peak at the interface) to the vacuum. Thus, the transferred charge Q is defined as:
where −e is the charge of an electron, and z0 is the interfacial point between the SiO2 substrate and the molecule, which is discussed below.
3. Results and Discussion
The characteristic parameters including interfacial distance, adhesion energy, and the transferred charge of 15 molecule/SiO2 configurations are listed in Table 1. The interfacial distances on the SiO2-OH surface are slightly larger than that on the SiO2-O surface for the molecule with the same group, which are all about 3.0 Å. The equilibrium interfacial atomic distances for the molecule/SiO2-Si systems are about 3.6 Å or larger. For most contact systems, the distances are approximately equal to the sums of the corresponding van der Waals atomic radius of interfacial atoms except the SH/SiO2-O and SH/SiO2-OH systems (~3.0 Å v.s. 3.32 Å), indicating the possible stronger interfacial interaction and charge transfer in the SH/SiO2-O and SH/SiO2-OH systems.

Table 1.
The interfacial distances deq, adhesion energy Eb, and charge transfer q of molecules Gly, Cys, and DMS contacted with SiO2 slab, respectively. Positive (negative) q represents that charge transfers from SiO2 (molecule) to molecule (SiO2) surface.
To quantitatively evaluate the interfacial adhesion, we calculate the adhesion energy of the molecule/SiO2 systems (Table 1). Adhesion energy is the result of the interaction of several factors, including hydrogen bonds, van der Waals interaction, and electrostatic interaction. The negative adhesion energy indicates an attraction interaction. The results indicate that the order of adhesion energy for molecule groups binding to the SiO2-O or SiO2-OH surface is SH > SiOH > NH2 > C=O > OH. The SH group of cysteine and SiO2-O or SiO2-OH contact model has strong adhesion energy. While for the molecule/SiO2-Si systems, the order of adhesion energy is SiOH > NH2 > SH > OH > C=O, that is, contact with the SiOH group of siloxane facing the SiO2-Si surface has strong adhesion energy. When the molecule contacts the SiO2-Si surface, the NH2 group of glycine has a larger adhesion energy than the SH group of cysteine. Furthermore, when glycine contacts the different SiO2 surfaces, the NH2 group of glycine has the largest adhesion energy. This indicates that the most possible contact site of the Gly/SiO2 system is the amino group of glycine, which agrees with experimental results that glycine is specifically adsorbed on silica surfaces through its moiety [41]. Thus, for the different molecule/SiO2 contact systems, the SH group of cysteine, the SiOH group of siloxane, and the NH2 group have a larger adhesion energy, and it can be inferred that SH and SiOH groups may to some extent enhance the interfacial adhesion. Furthermore, the effect of hydrogen bonds on interfacial adhesion energy is also investigated, since the network of hydrogen bonds can reveal the interactional complementarity between the amino acid and specific contact sites for the contact models [42,43]. Considering the electronegativity of interfacial O, N, and S atoms, it is inferred that interfacial H atoms can interact with interfacial O, N, and S atoms in the form of hydrogen. It is clear that molecule/SiO2-OH systems can form more hydrogen bonds than molecule/SiO2-O systems through the same group, leading to larger adhesion energy than that of most of the molecule/SiO2-O systems. For instance, the adhesion energy of the C=O/SiO2-O is −0.0568 eV, which is less than that of the C=O/SiO2-OH contact system (−0.0888 eV).
To clarify the contact electrification mechanism of gecko toes and bio-inspired adhesive materials, we investigate the charge transfer and charge redistribution at the molecule and SiO2 interfaces. The charge density differences in the molecules contacting SiO2 surfaces are shown in Figure 2. For molecule and SiO2 contact systems, charge accumulations and depletions appear not only in the vicinity of the contacting O or Si atoms of the SiO2 substrate but also around the adjacent O or Si atoms, which indicates the delocalization charge distribution between the molecule and SiO2 substrate. As displayed in Figure 2a–e, the SiO2-O substrate acquires electrons from Gly, Cys, and DMS molecules, forming a charge accumulation region around interfacial O atoms of the SiO2 surface and charge depletion regions around the interfacial atoms of molecules. In the molecule/SiO2-OH systems (Figure 2f–j), there is significant charge accumulation around the molecule and charge depletion around the surface atoms of the SiO2-OH surface, indicating electrons transfer from the SiO2 surface to the molecules. Meanwhile, owing to the existence of interfacial hydrogen bonding, the H atom of molecules or SiO2 surface and the O, N or S atom of Gly, Cys, or DMS have an interaction with each other and form a charge depletion region at the interface as shown in Figure 2c,e,f–j. For the molecule/SiO2-Si systems (Figure 2k–o), charge density differences indicate that the charge on the SiO2 surface increases and that on the molecule side decreases when in contact. That is, the electrons transfer from the molecule to the SiO2 surface side.
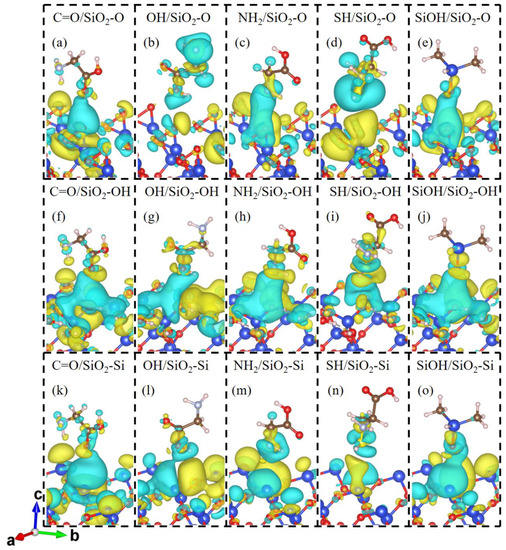
Figure 2.
Charge density difference for the contact systems of (a) C=O/SiO2-O, (b) OH/SiO2-O, (c) NH2/SiO2-O, (d) SH/SiO2-O, (e) SiOH/SiO2-O, (f) C=O/SiO2-OH, (g) OH/SiO2-OH, (h) NH2/SiO2-OH, (i) SH/SiO2-OH, (j) SiOH/SiO2-OH, (k) C=O/SiO2-Si, (l) OH/SiO2-Si, (m) NH2/SiO2-Si, (n) SH/SiO2-Si, and (o) SiOH/SiO2-Si. The blue and yellow domains show the electron depleted and accumulated regions, respectively. The value of the iso-surface is set to 2 × 10−4 e/bhor3 for the OH/SiO2-O and SH/SiO2-O systems. The value of the iso-surface is set to 8 × 10−5 e/bhor3 for other contact systems.
Quantitative variations of charges at the interface in all contact systems are further calculated using the plane-averaged charge density differences that numerically account for the charge transfer. Figure 3b,d,f exhibit the variation of charge density differences along the z-direction for C=O/SiO2-O, C=O/SiO2-OH, and C=O/SiO2-Si contact systems, respectively. The plane-average electrostatic potential is calculated to confirm the interfacial dividing point z0 along the z-direction of the systems (Figure 3a,c,e). The dividing point z0 locates the position of the electrostatic potential peak at the interface, which is marked in the red dotted line in Figure 3. For the C=O/SiO2-O and C=O/SiO2-Si contact systems, the maximum value of the SiO2 side positive peak is larger than that of the glycine positive peak. While for the C=O/SiO2-OH systems, the maximum value of the glycine positive peak is larger than that of the SiO2 side. To some extent, these results further illustrate that the accumulation of charge density tends to locate at the molecule (SiO2) side in the C=O/SiO2-OH (C=O/SiO2-O and C=O/SiO2-Si) contact systems. The plane-averaged charge density differences in other molecule/SiO2 contact systems are shown in Figures S2–S5. Thus, for the molecule/SiO2-O and molecule/SiO2-Si contact systems, the charge in the molecule side tends to decrease and more charge gathers at the SiO2 atoms’ top positions, leading to the molecule to SiO2 surface charge transfer direction. Meanwhile, for the molecule/SiO2-OH contact systems, charge transfers from the SiO2 side to the molecule side.
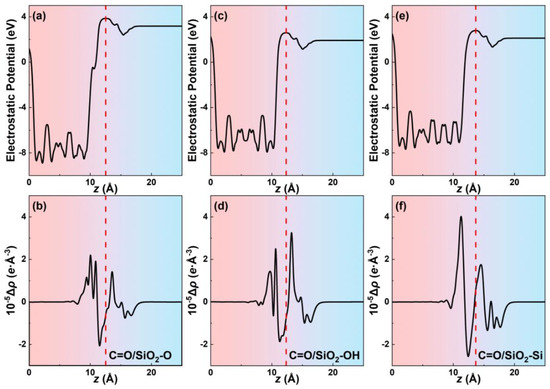
Figure 3.
The plane-average electrostatic potentials along the z direction of the (a) C=O/SiO2-O, (c) C=O/SiO2-OH, and (e) C=O/SiO2-Si systems. The plane-average charge density differences along the z direction of the (b) C=O/SiO2-O, (d) C=O/SiO2-OH, and (f) C=O/SiO2-Si systems.
The transferred charge Q is calculated as the calculation formula mentioned above, and the corresponding values of Q are listed in Table 1. Charge transfers from molecule to SiO2 surface when the molecule contacts with the SiO2-O or SiO2-Si substrates. The molecule/SiO2-OH systems have a contrary charge transfer direction. The interfacial hydrogen bonds limit the charge transfer and make the less-transferred charge of the molecule/SiO2-OH systems when compared with the molecule/SiO2-O systems. Moreover, owing to the unpaired electrons of O atoms, the saturated (OH-terminated) SiO2 surfaces have a more limited charge transfer than the O-terminated SiO2 surfaces. Under the effect of these two factors, the amounts of transferred charge for the molecule/SiO2-O systems are larger than the molecule/SiO2-OH systems. The value of Q is in the order of SH > OH > NH2 > SiOH > C=O for the molecule/SiO2-O systems. The sequence of Q for the molecule/SiO2-OH systems is SH > OH > SiOH > NH2 > C=O. Thus, the transferred charge Q of the SH/SiO2-O and OH/SiO2-O (SH/SiO2-OH and OH/SiO2-OH) contact systems is larger than other molecule/SiO2-O (molecule/SiO2-OH) systems. The transferred charge Q of different molecule/SiO2-Si systems is in an order of NH2 > C=O > SiOH > OH > SH, that is, the NH2/SiO2-Si system has the largest transferred charge in all molecule/SiO2-Si systems. The transferred charges of the SH/SiO2-O and SH/SiO2-OH systems are −0.09641 e and 0.00798 e, respectively, which are much larger than that of other molecule/SiO2-O and molecule/SiO2-OH systems. The difference between the electronegativity of the interfacial O atom and the S atom may affect the charge transfer. Meanwhile, combined with the hydrogen bond and van der Waals interaction, the interfacial charge transfer affects the interfacial interactions and finally affects the interfacial adhesion energy.
To explore the determinant of the direction of interfacial charge transfer, we carry out the Bader Charge Analysis of the single contact atom in the free molecule and the isolated SiO2 surfaces (Figure 4). When in contact, charge trends transfer from the surface with more charges to the surface with fewer charges. Thus, charge transfers from the molecule to the SiO2-O and SiO2-Si surface after contact (see light orange and light cyan region in Figure 4), and charge tends to transfer from the SiO2-OH surface to the molecule side (see the light magenta region in Figure 4) to balance the interface charge. However, for the SH/SiO2-O contact system (see the red dotted box in Figure 4), the charge transfer direction cannot be directly obtained by comparing the amounts of the variation of charge for the contact atoms. We may think that charge transfers from the SiO2-O surface to the cysteine side (Figure 4). However, the charge transfer direction is from molecule to SiO2 surface for the SH/SiO2-O system. Thus, the charge transfer mechanism of the SH/SiO2-O system needs to be further investigated. The charge transfer behavior of the SH/SiO2-O system is considered by detailed Bader Charge Analysis. The O1 atom in the isolated SiO2 obtains 0.730997 e, which is smaller than that of the contact system (0.782837 e). The S atom in the isolated cysteine obtains a larger charge than that of the system (0.067708 vs. −0.013996 e). The changes in Bader charge for contact (O1 and S) atoms further prove that charge transfers from cysteine to the SiO2-O surface. These things considered, we tried to find the effect of interfacial structure on charge transfer. The length of the O1 and O2 bond on the SiO2-O surface is 1.72 Å, which is larger than the bond length of O1–O2 (1.64 Å) for SiO2-O substrate in other systems, indicating the weaker interaction between the interfacial O atoms. The interaction between the O1 atom and S atom of cysteine strengthens, and charge trends transfer from the larger radius S atom to the smaller radius O atom, leading to the increasing charge transfer at the interface. Thus, charge transfers from the cysteine molecule to the SiO2-O surface, which agrees with other molecule/SiO2 contact systems.
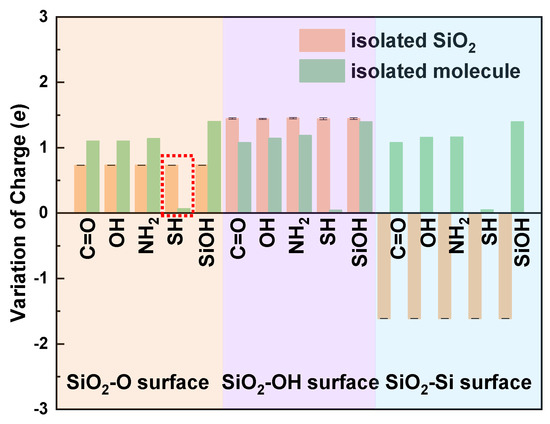
Figure 4.
Bader charge analysis on atoms at the isolated SiO2 surface and the molecule.
To gain insight into the nature of contact electrification between molecules and different SiO2 surfaces, we calculate the total density of states (TDOS) of these contact systems. Figure 5 shows that the contact between the molecule and SiO2 substrate causes the states to shift toward the lower energy levels after contact, indicating the stabilization of contact systems. For the molecule/SiO2-O and molecule/SiO2-Si contact systems, the contribution of molecular contact and charge transfer to electronic orbit can change the minimum of the conduction band of contact systems, which narrows the bandgap of the contact system. Similarly, for the molecule/SiO2-OH contact systems, the impurity state induced by the molecule is located below the conduction band, which causes the band gap of the contact system to become narrower after contact. To further explore the direction of charge transfer and contact electrification mechanism of molecule/SiO2 contact systems, the high-energy states originated by the TDOS of the isolated SiO2 substrate and the molecule are considered. The high-energy state electrons above the Fermi level influence the charge transfer and the difference in the high-energy state electrons (first peak of the density of states energy) of isolated surfaces can be used to further confirm the direction of charge transfer. The first peak of isolated SiO2-O substrate density of states energy (DOS) above the Fermi level in the energy range of [0.9 eV, 2.4 eV], and the first peak of free molecule DOS above the Fermi level in the energy range of [3.7 eV, 4.3 eV] or [5.3 eV, 5.6eV] (Figure 5a–e). The energy of high-energy states for the free molecule is larger than that of the isolated SiO2-O slab. Thus, higher energy state electrons of molecules tend to transfer to the SiO2-O substrate. For the molecule/SiO2-Si system (Figure 5k–o), the first peak of isolated SiO2-Si substrate and free molecule DOS above the Fermi level is in the range of [3.0 eV, 3.4 eV] and [3.4 eV, 4.0 eV] (or [5.3 eV, 5.6 eV]). We can find the same energy states magnitude distribution of isolated surfaces above the Fermi energy, meaning the same interfacial charge transfer direction (from molecule to SiO2-Si substrate). As shown in Figure 5f–j, the energy of the first peak above the Fermi energy for the free molecule is less than that of isolated SiO2-OH slabs, causing charge transfers from the SiO2-OH surface to glycine, which leads to the reversed charge transfer direction from molecule/SiO2-O and molecule/SiO2-Si contact systems. Thus, the direction of interfacial charge transfer is further confirmed by the energy difference in the high-energy state electrons above the Fermi level.
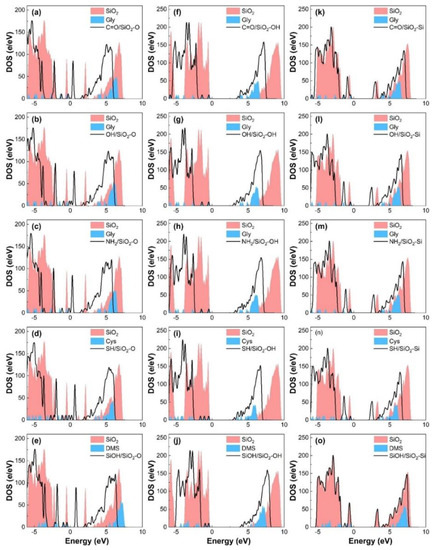
Figure 5.
DOS of SiO2-O substrate with (black solid line) and without (red shadow) molecules’ (a) C=O, (b) OH, (c) NH2, (d) SH, and (e) SiOH group contact. DOS of SiO2-OH substrate with (black solid line) and without (red shadow) molecules’ (f) C=O, (g) OH, (h) NH2, (i) SH, and (j) SiOH group contact. DOS of SiO2-Si substrate with (black solid line) and without (red shadow) molecules’ (k) C=O, (l) OH, (m) NH2, (n) SH, and (o) SiOH group contact. The blue shadow denotes the DOS of the corresponding isolated molecule. The Fermi level is set to zero.
In order to understand the contact electrification property and the mechanism of the charge transfer at the interface, the electronic energy level for the considered complexes is analyzed. The valence band maximum (VBM) and conduction band minimum (CBM) of SiO2 surface atoms are calculated to describe the electronic energy. Their equivalent in a molecule is the energies of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), respectively. These parameters are vital ingredients that define the electronic structure and control processes of charge transfer across interfaces. The HOMO and LUMO of the molecular contact atom are marked as HOMO1 and LUMO1, and the VBM and CBM of the SiO2 contact atom are marked as HOMO2 and LUMO2, which are marked in Figure 6a–c and Figure S6, and all included in Table S1. The energy of the LUMO is partially occupied and is used to accept the transferable electrons. The values of LUMO1 and LUMO2 are different; when the systems contact, electrons transfer from the larger LUMO to the smaller LUMO. When the molecule contacts the SiO2-Si surface, electron transition will first happen from HOMO1 to LUMO1 in the molecule itself, then electrons will transfer from the LUMO1 of the molecule to LUMO2 of the SiO2, making the interface more energetically stable (Figure 6f). As shown in Figure 2, charge accumulations or depletions appear around the adjacent atoms of the SiO2 substrate, not just at the two contacting atoms. The HOMO3 and LUMO3 of the SiO2 interfacial neighboring atom should also be considered. Thus, electrons further transfer from LUMO2 to LUMO3. Meanwhile, LUMO3 is larger than LUMO2, indicating the hindrance of interfacial charge transfer and reducing the amount of transferred charge. The electron transition mechanism of the molecule/SiO2-O and molecule/SiO2-OH systems are similar to the molecule/SiO2-Si systems. For the molecule/SiO2-O systems (Figure 6d), the value of LUMO1 of the molecule is larger than the LUMO2 of SiO2. So, when contacting each other, electrons first transfer from HOMO1 to LUMO1 in the molecule itself, and then electrons transfer from LUMO1 to LUMO2 between interfaces. Furthermore, the value of LUMO2 is equal to LUMO3, which means that obtained charge is easy to transfer from LUMO2 to LUMO3 at the SiO2 surface leading to the non-local charge distribution, as shown in Figure 2a. For the molecule/SiO2-OH system (Figure 6e), the value of LUMO1 is less than LUMO2. Electrons transfer from HOMO2 to LUMO2 in the SiO2 itself, and then electrons transfer from LUMO2 to LUMO1. Meanwhile, LUMO3 is larger than LUMO2, which represents that charge will transfer from adjacent atoms to the contact atoms owing to the electron depletion of the contact O atom on the SiO2 surface.
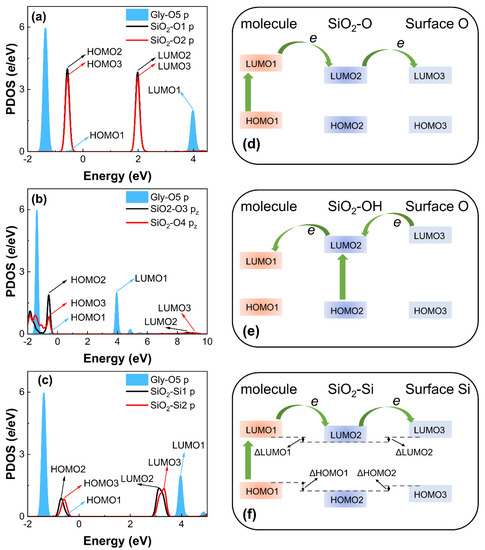
Figure 6.
The PDOS electrons of the contact and neighbor atoms in (a) Gly and SiO2-O surface, (b) Gly and SiO2-OH surface, and (c) Gly and SiO2-Si surface before contact. The black curve shows the PDOS of contact O1, O3, and Si1 atoms in SiO2 surface. The red curve shows the PDOS of neighbor O2, O4, and Si2 (adjacent Si atom) atoms in SiO2 surface. The blue shadow denotes the PDOS of corresponding contact O5, O6, N, S and O7 atoms in isolated molecule. Fermi level is set to zero. Schematic diagrams of charge transfer mechanism of (d) molecule/SiO2-O, (e) molecule/SiO2-OH, and (f) molecule/SiO2-Si contact systems.
Table 1 (ΔHOMO1) is defined as ΔLUMO1 = LUMO1 − LUMO2 (ΔHOMO1 = HOMO1 − HOMO2) and specific data are included in Table S2. The energy gap and energy levels are central to the definition of carrier injection and extraction at the interfaces [44]. Thus, in this paper, the energy gaps ΔLUMO1 and ΔHOMO1 reflect the charge transfer direction and the ability to attract electrons of the two contact atoms, respectively. As mentioned above, charge accumulations or depletions appear around the SiO2 substrate after contact. The energy gap between the contact atom and the adjacent atom in the SiO2 surface should also be considered. Then, the energy gap ΔLUMO2 (ΔHOMO2) is defined as ΔLUMO2 = LUMO2 − LUMO3 (ΔHOMO2 = HOMO2 − HOMO3) to further elaborate the effect of SiO2 surface charge distribution to interfacial charge transfer and the electronic attraction. Thus, the relation between transferred charge q and the energy gaps (ΔLUMO1, ΔHOMO1, ΔLUMO2, and ΔHOMO2) can be established by considering a correlation analysis.
A multiple linear regression (MLR) model is used to model the charge transfer in terms of parameters of ΔLUMO1, ΔHOMO1, ΔLUMO2, and ΔHOMO2. If Q > 0, charge transfer Q has a negative association with the response variable ln(|Q|), if Q < 0, Q is proportional to ln(|Q|). Q and ln(|Q|) do not exhibit monotonic behavior. So, the positive and negative sign for the below MLR equation (for monotonicity of Q and ln(|Q|)) is used for the mathematical meaning rather than the physical meaning.
The obtained MLR equation is as follow:
ln(|Q|) = ±(−6.11 + 0.23ΔLUMO1 + 5.08ΔHOMO1 − 28.22ΔLUMO2 + 55.11ΔHOMO2),
The coefficient of determination (R2) for the prediction capability of the MLR model is obtained as 95.39%. ΔLUMO2 has a negative effect on charge transfer, indicating the hindrance of charge transfer or the relatively localized charge distribution, while ΔLUMO1, ΔHOMO1, and ΔHOMO2 have a positive effect. ΔLUMO1 determines the direction of charge transfer and, even more, affects the interfacial charge interaction. The coefficients of ΔLUMO1 and ΔHOMO1 are equal to 0.23 and 5.08, respectively. Meanwhile, the value of ΔLUMO1 is nearly an order of magnitude larger than ΔHOMO1 for the same contact system (Table S2), which indicates that the coefficients of independent variables ΔLUMO1 and ΔHOMO1 have a similar positive effect on charge transfer. For some contact systems, ΔLUMO2 and ΔHOMO2 are very small negative numbers, and then the relatively large value of the coefficients will hinder the charge transfer and the redistribution of electrons on the SiO2 surface. Therefore, we can obtain a quantitative relation between the transferred charge and energy gap to evaluate the contact electrification of polymers. This demonstrates that when molecules (Gly, Cys, and DMS) come into contact with SiO2, ΔLUMO1 determines the charge transfer direction at the interface, ΔLUMO2 affects the charge transfer at the SiO2, and ΔHOMO1 and ΔHOMO2 show that the charge transfer in contact electrification is closely related to the electron attraction from the contact surfaces and atoms.
4. Conclusions
In this paper, the electronic behaviors and charge transfer at the contact interfaces of molecule/SiO2 systems are studied using density functional theory calculations. The different contact configurations of molecule groups and SiO2 surfaces are analyzed. When the molecule contacts the SiO2-O and SiO2-OH surfaces through the sulfhydryl group, stronger adhesion energy is obtained in comparison to carbonyl, hydroxyl, amino, and silanol groups. The SiOH/SiO2-Si contact model has stronger adhesion energy than other molecule/SiO2-Si systems. Furthermore, for the different Gly/SiO2 systems, the NH2 group of glycine has the largest adhesion energy, respectively. Charge transfers from molecule to SiO2-O and SiO2-Si surfaces. Meanwhile, the charge transfer direction reverses for the molecule/SiO2-OH contact systems. The sulfhydryl or hydroxyl groups of the molecule contacting the SiO2-OH and SiO2-OH surfaces have the larger transferred charge. For the molecule/SiO2-Si systems, the NH2/SiO2-Si system has the largest transferred charge. The direction of the transferred charge is determined by the Bader charge of the isolated contact atoms. In addition, charge tends to transfer from the surface with more charge to the surface with less charge. The charge transfer direction can be further demonstrated by the energy difference in the high-energy state electrons of the molecule and the SiO2 surface above the Fermi level. Further investigation indicates that electrons transfer from the HOMO to the LUMO of the molecule or SiO2 itself, then electrons transfer from the higher LUMO to the lower LUMO, and finally, electrons transfer between the LUMO2 and LUMO3 of atoms in SiO2 surface, making the interface more energetically stable after contact. The energy gap represented by ΔLUMO1 and ΔLUMO2 signifies the charge transfer direction. ΔHOMO1 and ΔHOMO2 reflect the electronic attraction and interfacial charge transfer. Thus, the amount of the transferred charge can be related to the energy gaps (ΔLUMO1, ΔHOMO1, ΔLUMO2, and ΔHOMO2) between the contacting surfaces, and then charge transfer Q can be evaluated by the quantitative relationship of these four parameters to predict the interfacial charge transfer behavior. Thus, this study provides a more accurate method to estimate the relations between charge transfer and the variations of energy states for the polymers’ contact electrification. Insights into the interaction between Gly, Cys, or DMS and SiO2 may therefore give some important guidance to the further study of contact electrification and adhesion modulation of gecko and bioinspired dry adhesives.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/biomimetics7040216/s1. Figure S1. The initial conformation of the isolated (a) SiO2-O, (b) SiO2-OH, (c) SiO2-Si surface, respectively; Figure S2. The plane-average electrostatic potentials along the z direction of the (a) OH/SiO2-O, (c) OH/SiO2-OH, (e) OH/SiO2-Si systems. The plane-average charge density differences along the z direction of the (b) OH/SiO2-O, (d) OH/SiO2-OH, (f) OH/SiO2-Si systems; Figure S3. The plane-average electrostatic potentials along the z direction of the (a) NH2/SiO2-O, (c) NH2/SiO2-OH, (e) NH2/SiO2-Si systems. The plane-average charge density differences along the z direction of the (b) NH2/SiO2-O, (d) NH2/SiO2-OH, (f) NH2/SiO2-Si systems; Figure S4. The plane-average electrostatic potentials along the z direction of the (a) SH/SiO2-O, (c) SH/SiO2-OH, (e) SH/SiO2-Si systems. The plane-average charge density differences along the z direction of the (b) SH/SiO2-O, (d) SH/SiO2-OH, (f) SH/SiO2-Si systems; Figure S5. The plane-average electrostatic potentials along the z direction of the (a) SiOH/SiO2-O, (c) SiOH/SiO2-OH, (e) SiOH/SiO2-Si systems. The plane-average charge density differences along the z direction of the (b) SiOH/SiO2-O, (d) SiOH/SiO2-OH, (f) SiOH/SiO2-Si systems; Figure S6. The PDOS electrons of the contact and neighbor atoms in (a) Gly-OH and SiO2-O surface, (b) Gly-NH2 and SiO2-O surface, (c) Cys-SH and SiO2-O surface, (d) DMS-SiOH and SiO2-O surface, (e) Gly-OH and SiO2-OH surface, (f) Gly-NH2 and SiO2-OH surface, (g) Cys-SH and SiO2-OH surface, (h) DMS-SiOH and SiO2-OH surface, (i) Gly-OH and SiO2-Si surface, (j) Gly-NH2 and SiO2-Si surface, (k) Cys-SH and SiO2-Si surface, and (l) DMS-SiOH and SiO2-Si surface, before contact. The black curve shows the PDOS of contact O1, O3, and Si1 atoms in SiO2 surface, respectively. The red curve shows the PDOS of neighbor O2, O4, and Si2 (adjacent Si atom) atoms in SiO2 surface, respectively. The blue shadow denotes the PDOS of corresponding contact O5, O6, N, S and O7 atoms in isolated molecule, respectively. Fermi level is set to zero; Table S1. High energy state of molecule’s contact atom LUMO1, low energy state of molecule’s contact atom HOMO1, high energy state of contact atom in SiO2 slab LUMO2, low energy state of contact atom in SiO2 slab HOMO2, high energy state of the adjacent atom to SiO2 interfacial atom LUMO3, low energy state of the adjacent atom to SiO2 interfacial atom HOMO3; Table S2. ΔLUMO1 is the difference of the high energy state between the molecule contact atom and SiO2 contact atom, which is defined as ΔLUMO1=LUMO1-LUMO2. ΔHOMO1 is the difference of the low energy state between the molecule contact atom and SiO2 contact atom, which is defined as ΔHOMO1=HOMO1-HOMO2. ΔLUMO2 is the difference of the high energy state between the SiO2 contact atom and the adjacent atom, which is defined as ΔLUMO2=LUMO2-LUMO3. ΔHOMO2 is the difference of the low energy state between the SiO2 contact atom and the adjacent atom, which is defined as ΔHOMO2=HOMO2-HOMO3. q is the transferred charge between the interface. ln|q| is the natural logarithm of the absolute values of q. The sign of the ln|q| is related its physical meaning and ±ln|q| is negatively correlated with q.
Author Contributions
Conceptualization, L.W. and Z.D.; methodology, L.W., Z.D. and J.T.; validation, L.W. and J.T.; investigation, L.W. and J.T.; resources, L.W. and Z.D.; data curation, L.W., J.T., K.K. and M.H.; writing—original draft preparation, L.W., J.T. and K.K.; writing—review and editing, L.W. and J.T.; funding acquisition L.W. and Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62233008 (Zhendong Dai), 52075249 (Linfeng Wang), 51505217 (Linfeng Wang), and 51705247 (Linfeng Wang).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The computational data on the results reported in this manuscript are available upon official request to the corresponding authors.
Acknowledgments
The authors gratefully acknowledge the support from the Center for High Performance Computing of Nanjing University of Aeronautics and Astronautics.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Autumn, K.; Gravish, N. Gecko adhesion: Evolutionary nanotechnology. Philos. Trans. R. Soc. A 2008, 366, 1575–1590. [Google Scholar] [CrossRef]
- Nam, K.; Seo, T.W.; Kim, B.; Jeon, D.; Cho, K.J.; Kim, J. Kinematic analysis and experimental verification on the locomotion of gecko. J. Bionic Eng. 2009, 6, 246–254. [Google Scholar] [CrossRef]
- Autumn, K.; Hansen, W. Ultrahydrophobicity indicates a non-adhesive default state in gecko setae. J. Comp. Physiol. A 2006, 192, 1205–1212. [Google Scholar] [CrossRef] [PubMed]
- Autumn, K.; Liang, Y.A.; Hsieh, S.T.; Zesch, W.; Chan, W.P.; Kenny, T.W.; Fearing, R.; Full, R.J. Adhesive force of a single gecko foot-hair. Nature 2000, 405, 681–685. [Google Scholar] [CrossRef] [PubMed]
- Autumn, K.; Peattie, A.M. Mechanisms of adhesion in geckos. Integr. Comp. Biol. 2002, 42, 1081–1090. [Google Scholar] [CrossRef]
- Gorb, S.; Varenberg, M.; Peressadko, A.; Tuma, J. Biomimetic mushroom-shaped fibrillar adhesive microstructure. J. R. Soc. Interface 2007, 4, 271–275. [Google Scholar] [CrossRef]
- Murphy, M.P.; Kim, S.; Sitti, M. Enhanced adhesion by gecko-inspired hierarchical fibrillar adhesives. ACS Appl. Mater. Interfaces 2009, 1, 849–855. [Google Scholar] [CrossRef]
- Soltannia, B.; Sameoto, D. Strong, reversible underwater adhesion via gecko-inspired hydrophobic fibers. ACS Appl. Mater. Interfaces 2015, 6, 21995–22003. [Google Scholar] [CrossRef]
- Li, X.S.; Tao, D.S.; Lu, H.Y.; Bai, P.P.; Liu, Z.Y.; Ma, L.R.; Meng, Y.G.; Tian, Y. Recent developments in gecko-inspired dry adhesive surfaces from fabrication to application. Surf. Topogr. Metrol. 2019, 7, 023001. [Google Scholar] [CrossRef]
- Russell, A.P.; Stark, A.Y.; Higham, T.E. The Integrative Biology of Gecko Adhesion: Historical Review, Current Understanding, and Grand Challenges. Integr. Comp. Biol. 2019, 59, 101–116. [Google Scholar] [CrossRef]
- Izadi, H.; Penlidis, A. Polymeric bio-inspired dry adhesives: Van der Waals or electrostatic interactions? Macromol. React. Eng. 2013, 7, 588–608. [Google Scholar] [CrossRef]
- Izadi, H.; Stewart, K.M.E.; Penlidis, A. Role of contact electrification and electrostatic interactions in gecko adhesion. J. R. Soc. Interface 2014, 11, 20140371. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.Y.; Zhou, J.; Li, Y.; Dai, Z.D. Synchronous measurement of tribocharge and force at the footpads of freely moving animals. Friction 2018, 6, 75–83. [Google Scholar] [CrossRef]
- Arzt, E.; Gorb, S.; Spolenak, R. From micro to nano contacts in biological attachment devices. Proc. Natl. Acad. Sci. USA 2003, 100, 10603–10606. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Wang, A.C. On the origin of contact-electrification. Mater. Today 2019, 30, 34–51. [Google Scholar] [CrossRef]
- Zou, H.Y.; Zhang, Y.; Guo, L.T.; Wang, P.H.; He, X.; Dai, G.Z.; Zheng, H.W.; Chen, C.Y.; Wang, A.C.; Xu, C.; et al. Quantifying the triboelectric series. Nat. Commun. 2019, 10, 1427. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.N.; Yin, N.; Wu, Z.S.; Pan, S.H.; Wang, D.A. Research methods of contact electrification: Theoretical simulation and experiment. Nano Energy 2021, 79, 105501. [Google Scholar] [CrossRef]
- Cole, B.N.; Baum, M.R.; Mobbs, F.R. An investigation of electrostatic charging effects in highspeed gas-solids pipe flows. Proc. Inst. Mech. Eng. 1969, 184, 77–83. [Google Scholar]
- Zhou, Y.S.; Liu, Y.; Zhu, G.; Lin, Z.H.; Pan, C.; Jing, Q.; Wang, Z.L. In situ quantitative study of nanoscale triboelectrification and patterning. Nano Lett. 2013, 13, 2771–2776. [Google Scholar] [CrossRef]
- Lowell, J. Tunnelling between metals and insulators and its role in contact electrification. J. Phys. D Appl. Phys. 1979, 12, 1541–1554. [Google Scholar] [CrossRef]
- Lowell, J.; Truscott, W.S. Triboelectrification of identical insulators. 2. Theory and further experiments. J. Phys. D Appl. Phys. 1986, 19, 1281–1298. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.L.; Li, H.; Wang, F.; Yang, W.; Hu, Y.Q. Insights into the mechanisms of metal-polymer contact electrification for triboelectric nanogenerator via first-principles investigations. Nano Energy 2018, 48, 607–616. [Google Scholar] [CrossRef]
- Wang, L.F.; Dong, Y.; Tao, J.; Ma, T.B.; Dai, Z.D. Study of the mechanisms of contact electrification and charge transfer between polytetrafluoroethylene and metals. J. Phys. D Appl. Phys. 2020, 53, 285302. [Google Scholar] [CrossRef]
- Tao, J.; Wang, L.F.; Li, J.; Dai, Z.D. Contact electrification and adhesion between carbon nanotube and graphene on metal surfaces: Insights from first-principles study. J. Bionic Eng. 2021, 19, 103–112. [Google Scholar] [CrossRef]
- Rizzo, N.W.; Gardner, K.H.; Walls, D.J.; Keiper-Hrynko, N.M.; Ganzke, T.S.; Hallahan, D.L. Characterization of the structure and composition of gecko adhesive setae. J. R. Soc. Interface 2006, 3, 441–451. [Google Scholar] [CrossRef] [PubMed]
- Hallahan, D.L.; Keiper-Hrynko, N.M.; Shang, T.Q.; Ganzke, T.S.; Toni, M.; Dalla Valle, L.; Alibardi, L. Analysis of gene expression in gecko digital adhesive pads indicates significant production of cysteine- and glycine-rich beta-keratin. J. Exp. Zool. Part B 2010, 312, 58–73. [Google Scholar] [CrossRef]
- Alibardi, L. Immunolocalization of specific keratin associated beta-proteins (beta-keratins) in the adhesive setae of Gekko gecko. Tissue Cell 2013, 45, 231–240. [Google Scholar] [CrossRef]
- Shin, S.H.; Kwon, Y.H.; Kim, Y.H.; Jung, J.Y.; Lee, M.H.; Nah, J. Triboelectric charging sequence induced by surface functionalization as a method to fabricate high performance triboelectric generators. ACS Nano 2015, 9, 4621–4627. [Google Scholar] [CrossRef]
- Li, S.Y.; Nie, J.H.; Shi, Y.X.; Tao, X.L.; Wang, F.; Tian, J.W.; Lin, S.Q.; Chen, X.Y.; Wang, Z.L. Contributions of different functional groups to contact electrification of polymers. Adv. Mater. 2020, 32, 2001307. [Google Scholar] [CrossRef]
- Han, B.; Zhang, Q.F.; Wu, J.P.; Han, B.; Karwacki, E.J.; Derecskei, A.; Xiao, M.C.; Lei, X.J.; O’Neill, M.L.; Cheng, H.S. On the Mechanisms of SiO2 Thin-Film Growth by the Full Atomic Layer Deposition Process Using Bis(t-butylamino)silane on the Hydroxylated SiO2 Surface. J. Phys. Chem. C 2012, 116, 947–952. [Google Scholar] [CrossRef]
- Huang, L.; Han, B.; Han, B.; Derecskei, A.; Xiao, M.C.; Lei, X.J.; O’Neill, M.L.; Pearlstein, R.M.; Chandra, H.; Cheng, H.S. First-Principles Study of a Full Cycle of Atomic Layer Deposition of SiO2 Thin Films with Di(sec-butylamino)silane and Ozone. J. Phys. Chem. C 2013, 117, 19454–19463. [Google Scholar]
- Rimola, A.; Sodupe, M.; Tosoni, S.; Civalleri, B.; Ugliengo, P. Interaction of Glycine with Isolated Hydroxyl Groups at the Silica Surface: First Principles B3LYP Periodic Simulation. Langmuir 2006, 22, 6593–6604. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Zhuravlev, L.T. The surface chemistry of amorphous silica. Zhuravlev model. Colloids Surf. A 2000, 173, 1–38. [Google Scholar] [CrossRef]
- Meng, M.; Stievano, L.; Lambert, J.F. Adsorption and thermal condensation mechanisms of amino acids on oxide supports. 1. Glycine on silica. Langmuir 2004, 20, 914–923. [Google Scholar] [CrossRef] [PubMed]
- Stievano, L.; Piao, L.Y.; Lopes, I.; Meng, M.; Costa, D.; Lambert, J.F. Glycine and iysine adsorption and reactivity on the surface of amorphous silica. Eur. J. Mineral. 2007, 19, 321–331. [Google Scholar] [CrossRef]
- Rimola, A.; Tosoni, S.; Sodupe, M.; Ugliengo, P. Does silica surface catalyse peptide bond formation? New insights from first-principles calculations. ChemPhysChem 2006, 7, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Kahn, A. Fermi level, work function and vacuum level. Mater. Horiz. 2016, 3, 7–10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).