Analysis of Kinematic Characteristics of Saanen Goat Spine under Multi-Slope
Abstract
1. Introduction
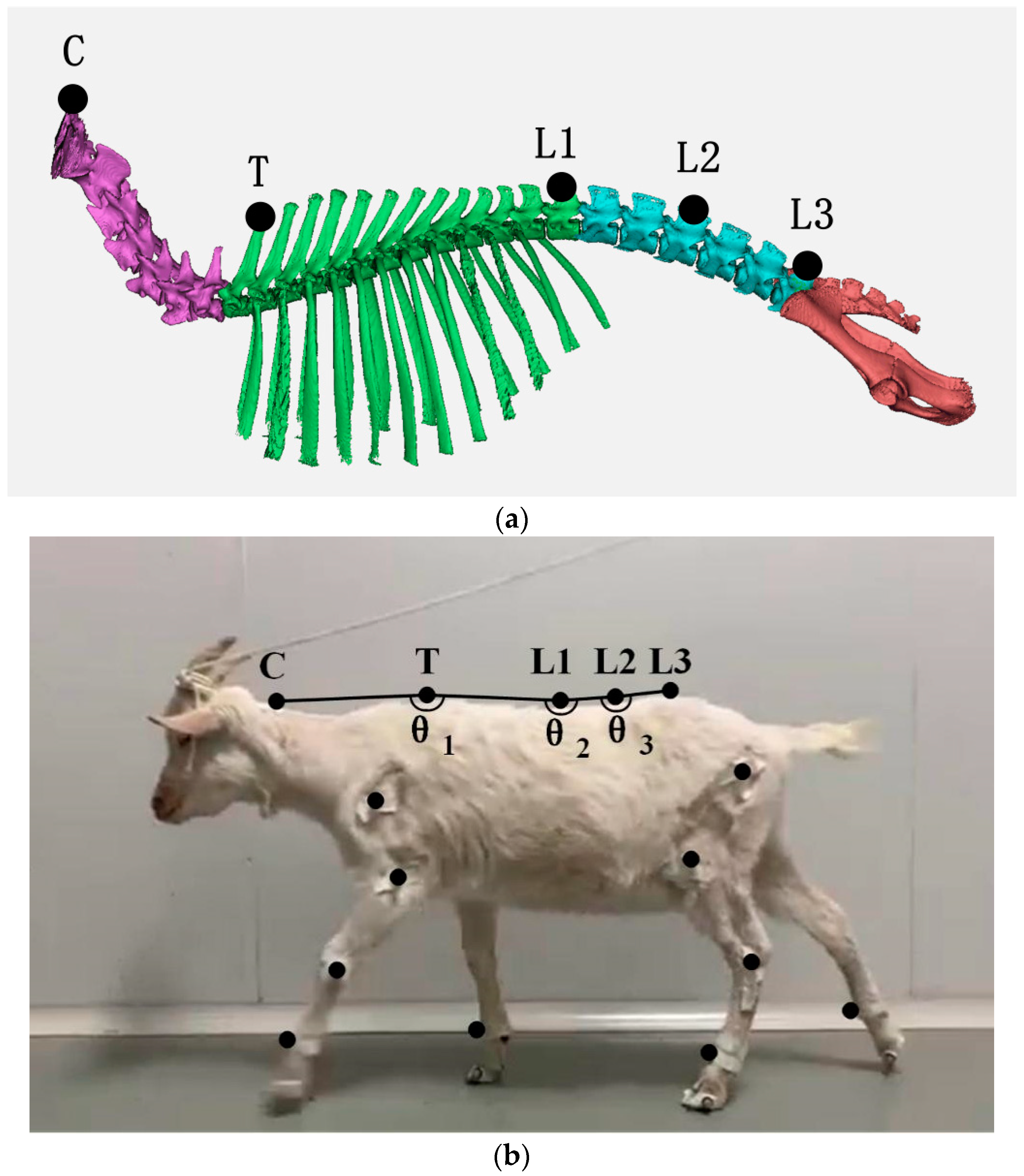
2. Materials and Methods
3. Results
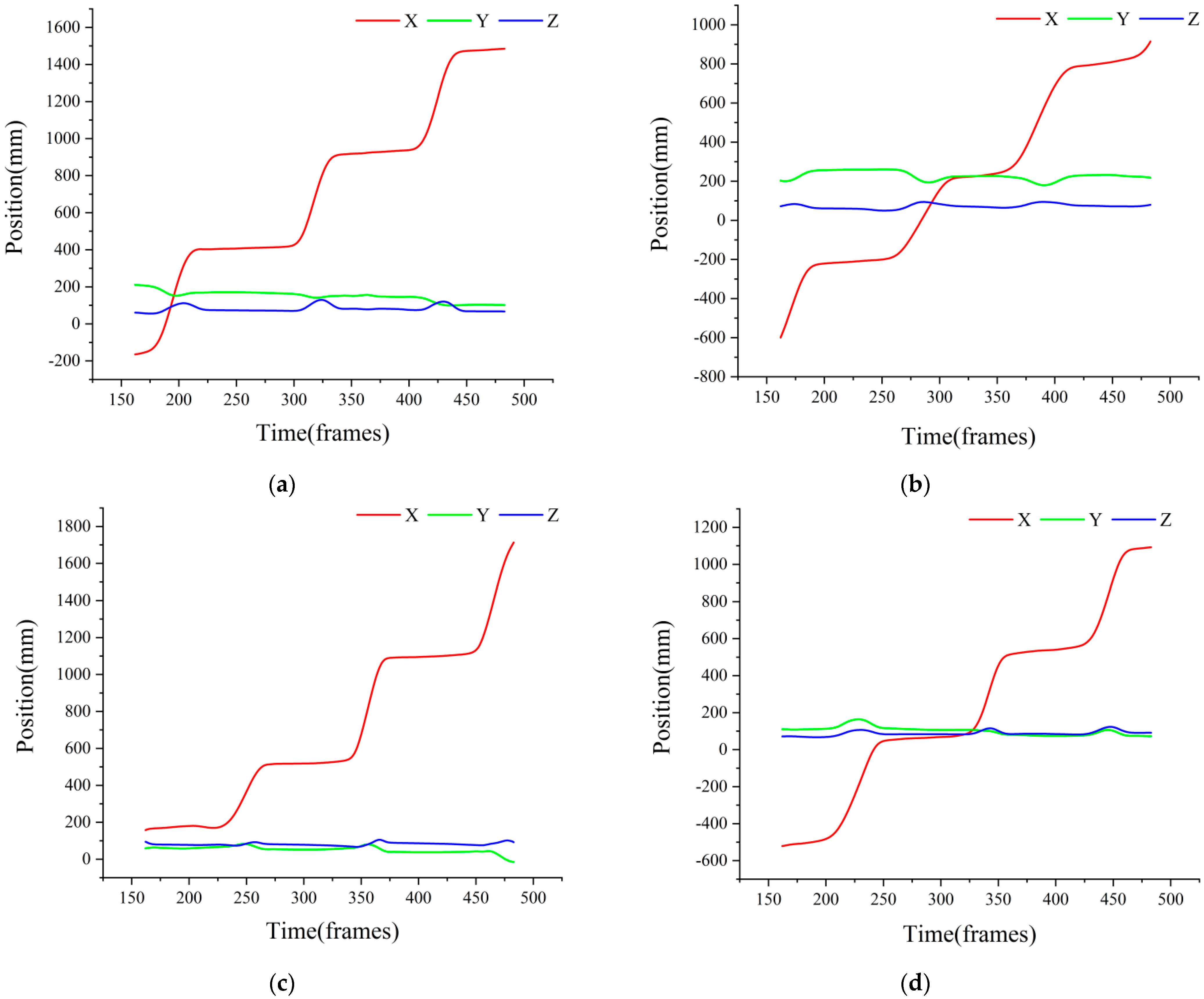
3.1. Analysis of the Motion of Each Part of Spine
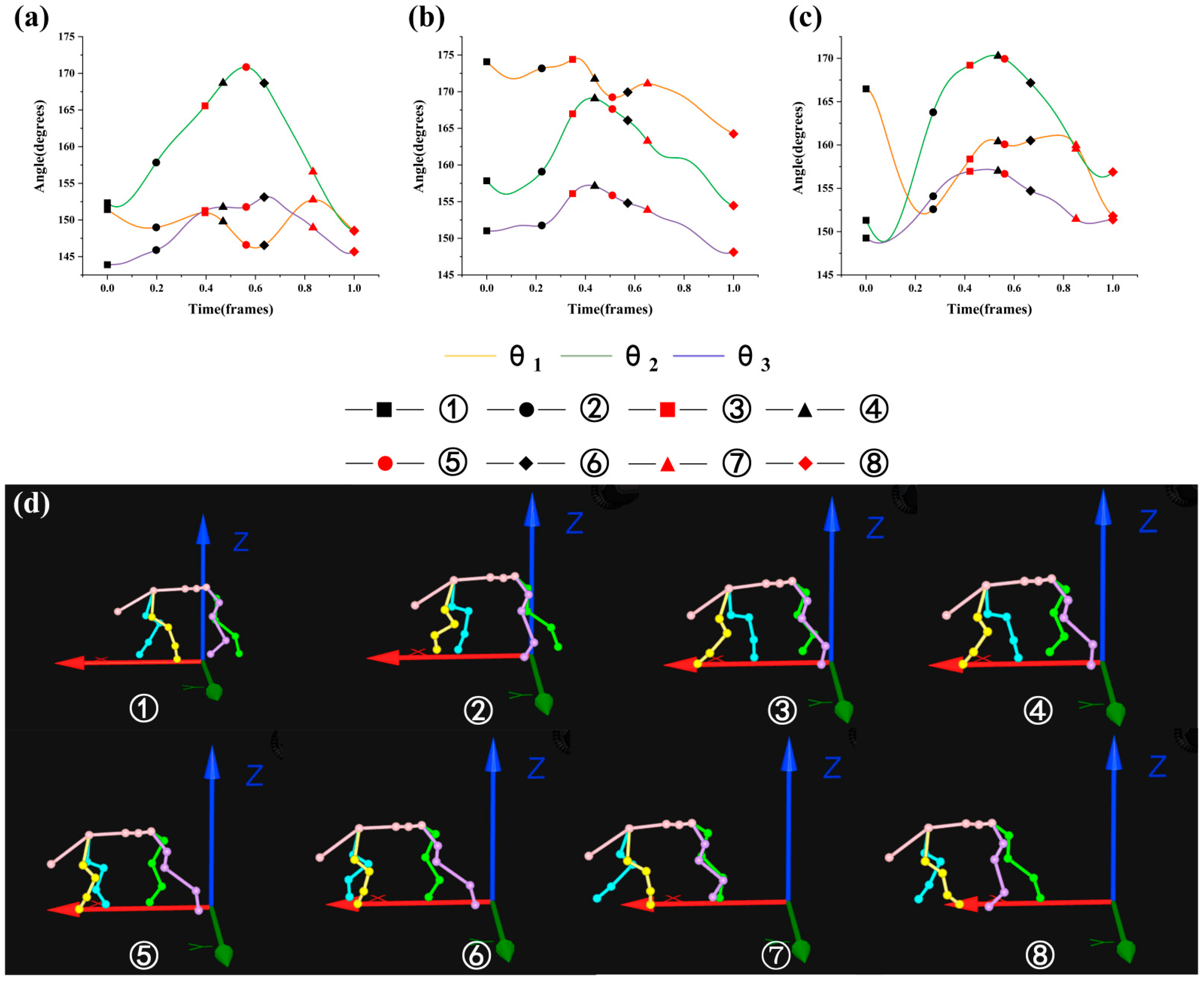
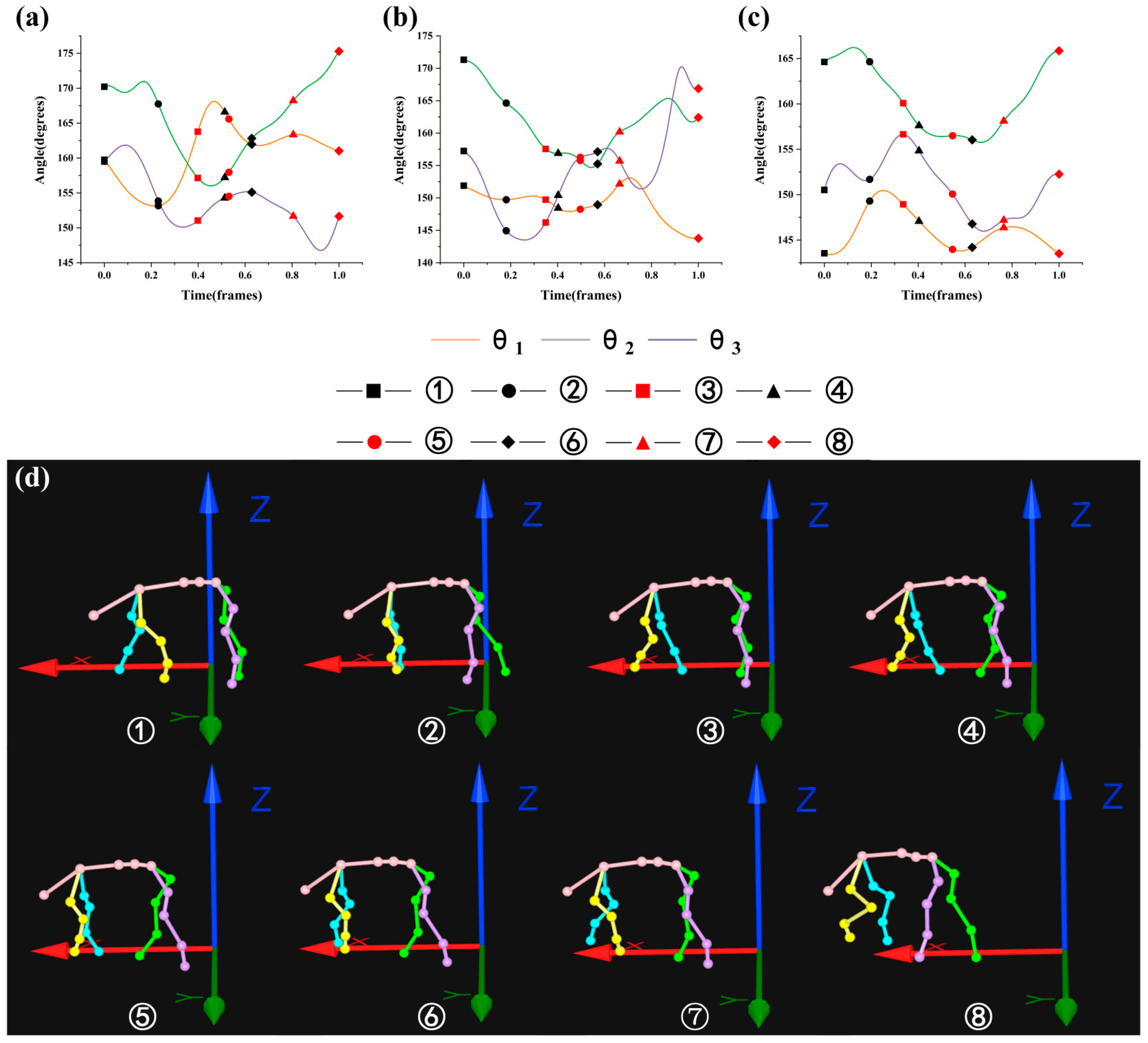
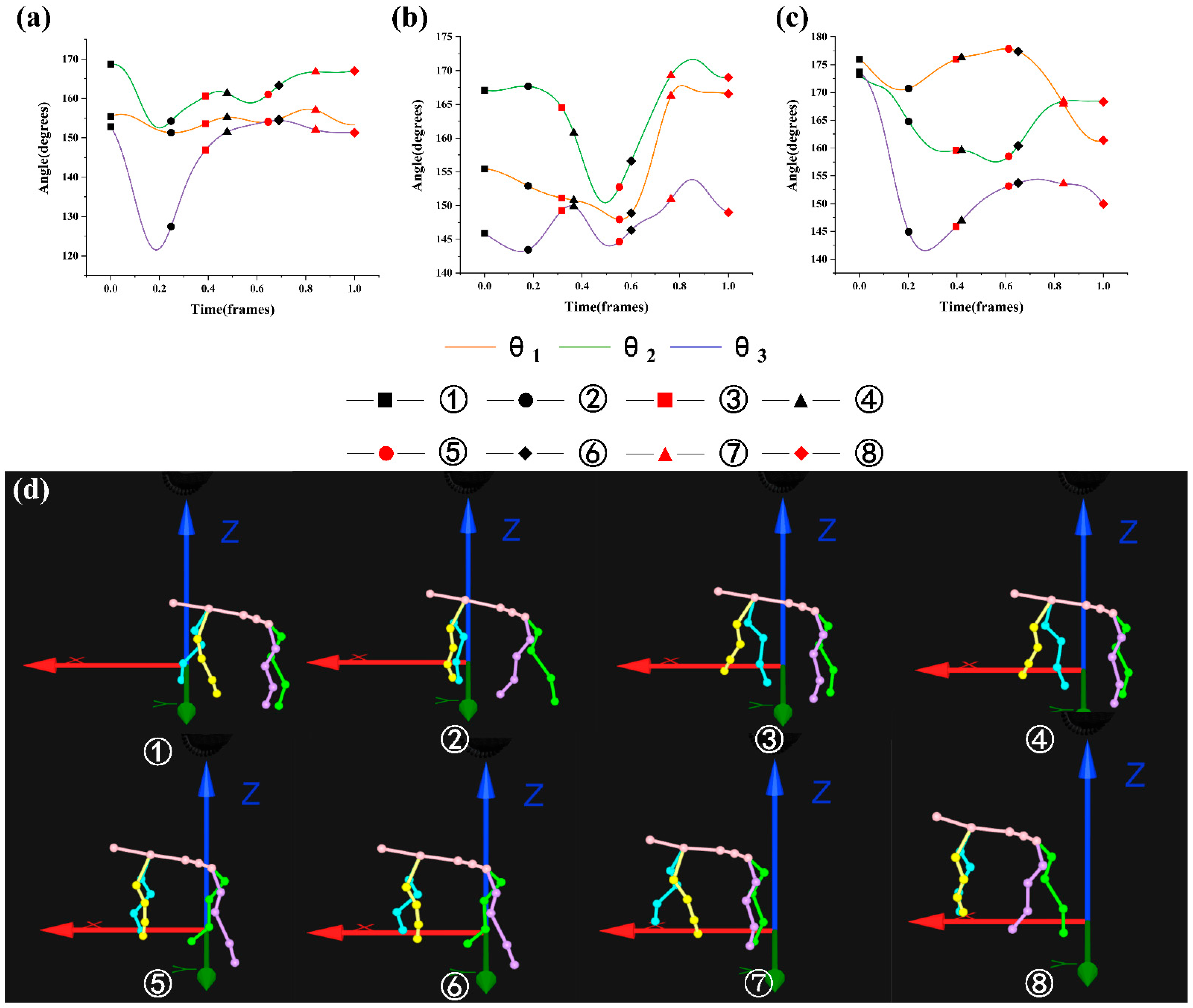
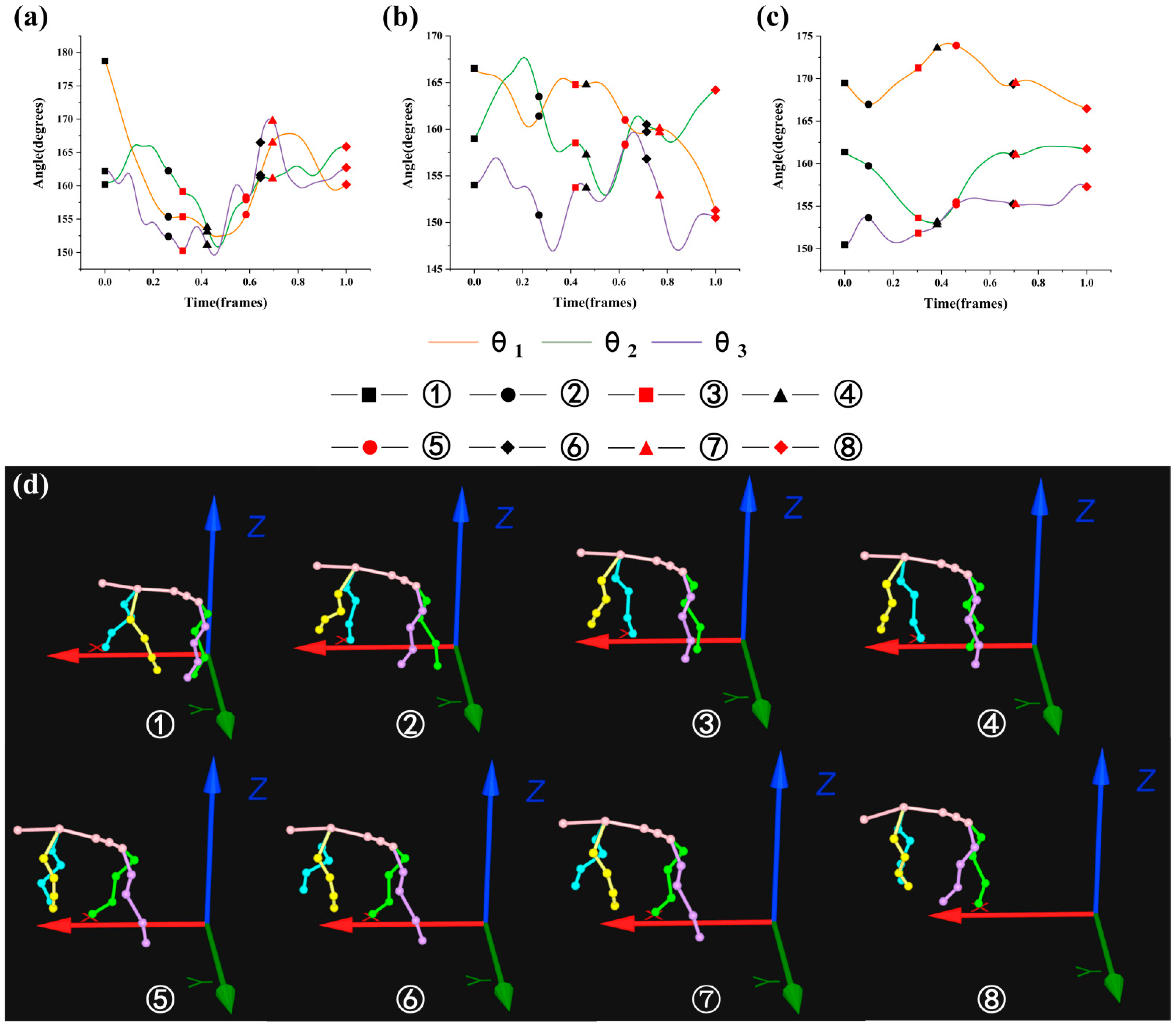
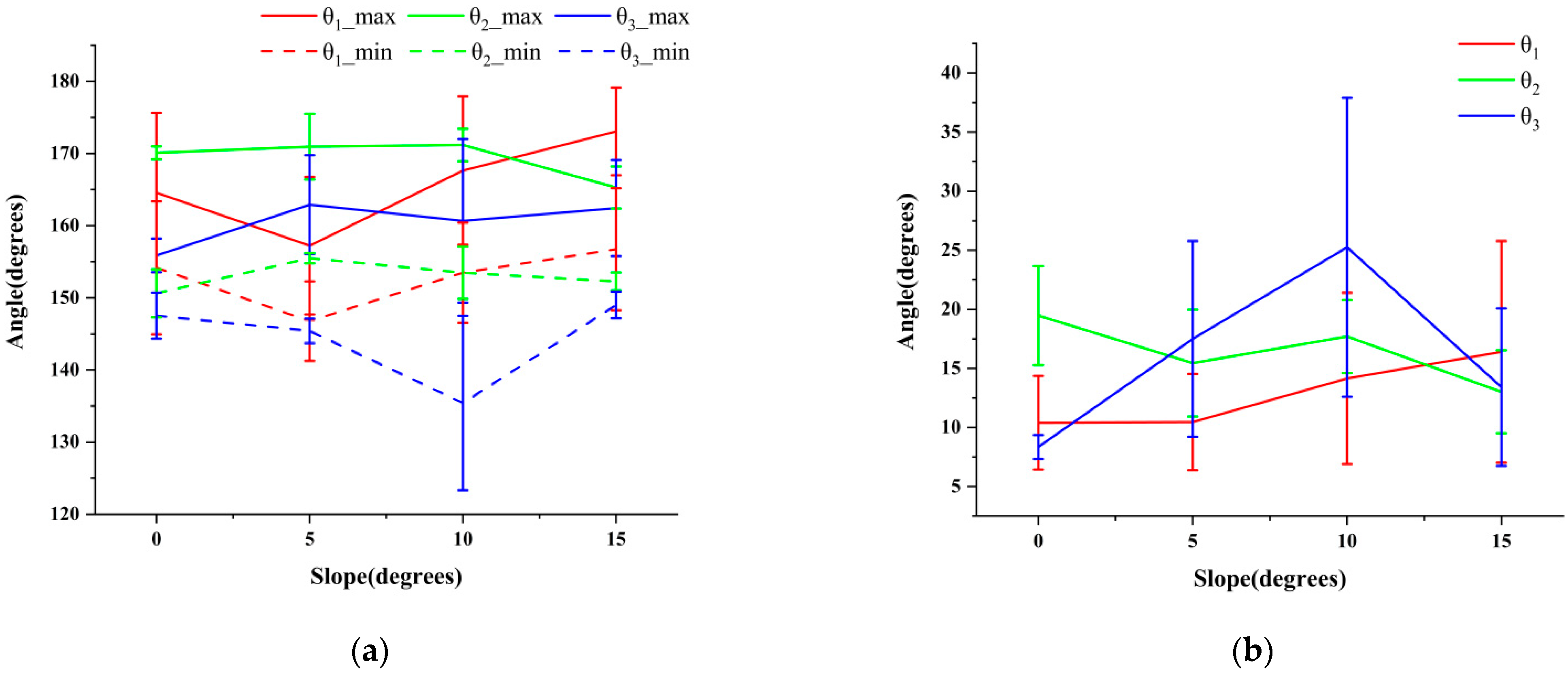
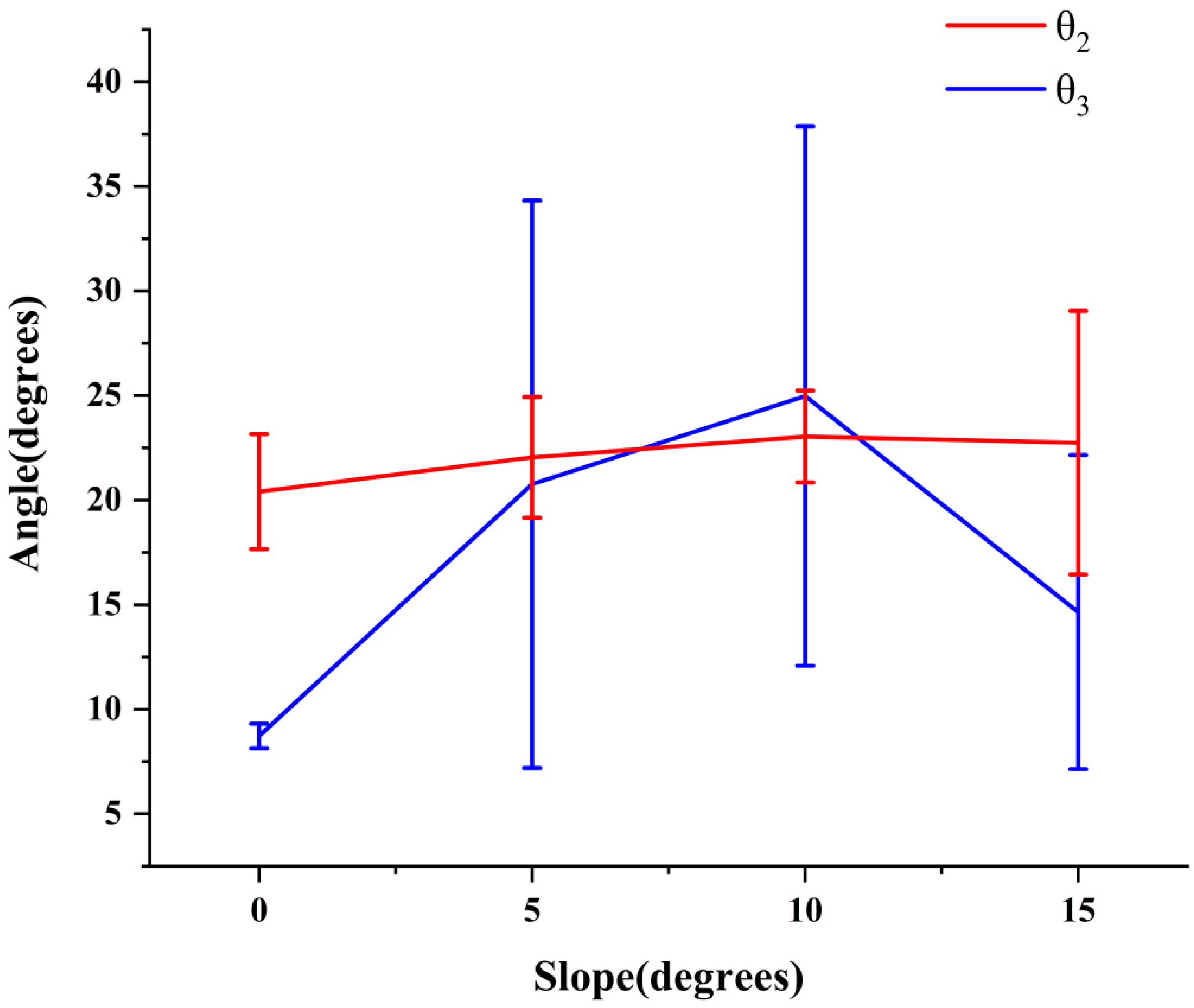
3.2. Analysis of the Maximin and Variation Range of θ1, θ2, and θ3
3.3. Analysis of Motion of Thoracic and Lumbar Vertebrae under Different Slopes
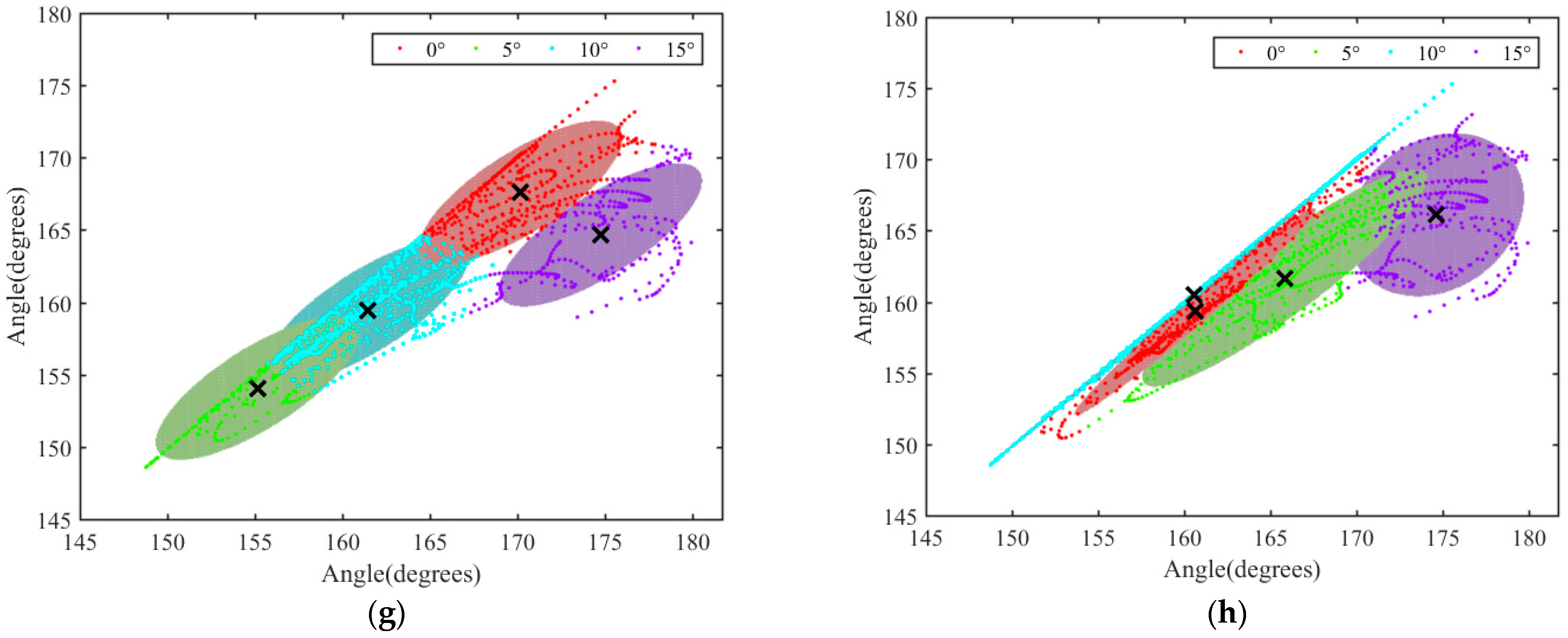
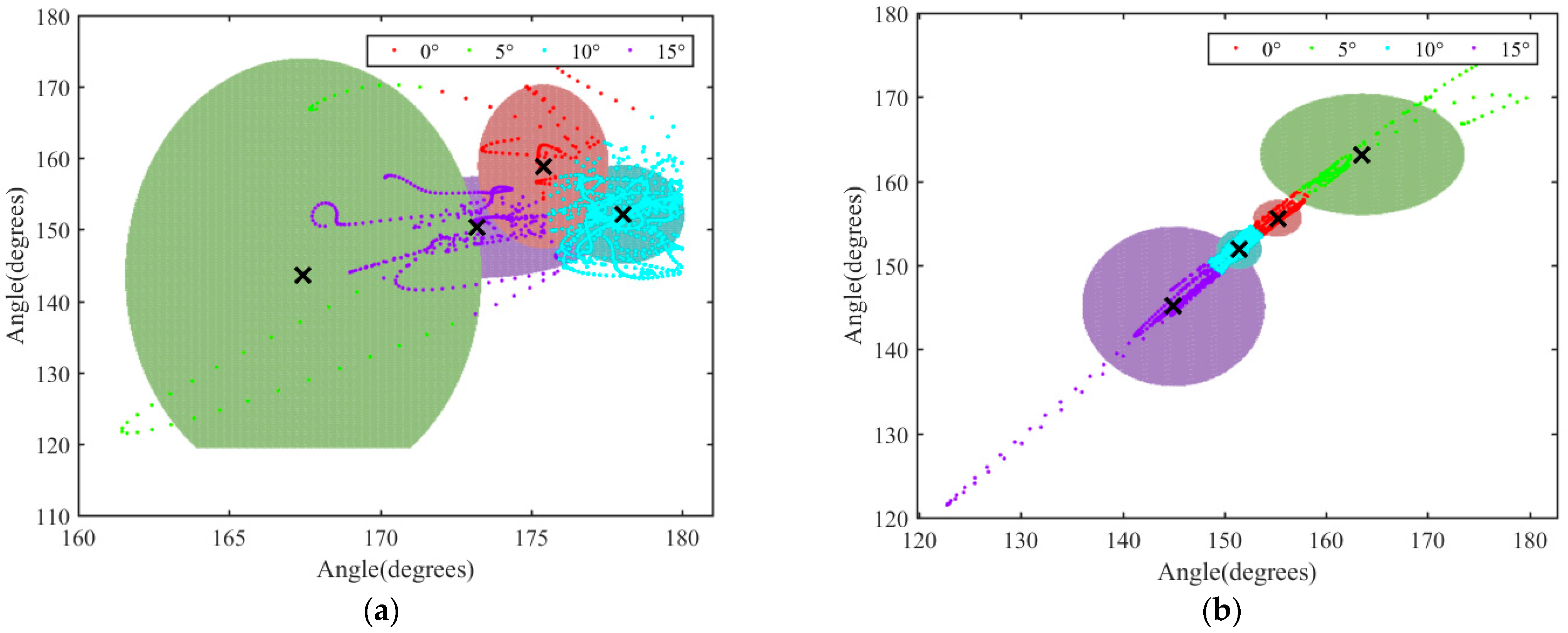
3.4. Analysis of the Variation Range of θ2 and θ3 in the XY Plane
3.5. Construction of Spine Spatial Curve Models for Eight Movements at 10°
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Bao, Y.N.; Yu, W.; Zhang, J.M.; Li, C.; Xie, X.R. Mechanism of spine motion about contact time in quadruped running. Chin. J. Mech. Eng. 2019, 32, 18. [Google Scholar] [CrossRef]
- Lei, J.T.; Zhang, Y.W.; Rao, J.J. Research progress of rigid-flexible coupling bionic spine of quadruped robot. Sci. Technol. Rev. 2020, 38, 35–48. [Google Scholar]
- Galbusera, F.; Bassani, T. The spine: A strong, stable, and flexible structure with biomimetics potential. Biomimetics 2019, 4, 60. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Jiang, P.; Bai, L.; Lin, L.H.; Liao, J.W.; Pan, J.C. Review on bionics mechanism and structure of flexible spine for quadruped robots. Mach. Des. Res. 2018, 34, 37–43. [Google Scholar]
- Hildebrand, M. Motions of the running cheetah and horse. J. Mammlogy 1959, 40, 481–495. [Google Scholar] [CrossRef]
- Hackert, R. Dynamics of Pikas’ Half-Bound: Spinal Flexion Contributes to Dynamic Stability. Ph.D. Thesis, Friedrich-Schiller-University Jena, Jena, Germany, 2003. [Google Scholar]
- Schiilling, N.; Hackert, R. Sagittal spine movements of small therian mammals during asymmetrical gaits. J. Exp. Biol. 2006, 209, 3925–3939. [Google Scholar] [CrossRef] [PubMed]
- Fisher, C.; Shield, S.; Patel, A. The effect of spine morphology on rapid acceleration in quadruped robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Chen, D.L.; Li, N.J.; Wang, H.; Chen, L. Effect of flexible spine motion on energy efficiency in quadruped running. J. Bionic Eng. 2017, 14, 716–725. [Google Scholar] [CrossRef]
- Zhang, X.L.; Tan, X.K.; Wu, H.B. Design and application of passive compliant spine of quadruped robot with variable stiffness. J. Beijing Jiaotong Univ. 2018, 42, 111–118. [Google Scholar]
- Zhao, Y.S. Kinematics Characteristics and Simulation Analysis of Goat Trunk. Master’s Thesis, Jilin University, Changchun, China, June 2021. [Google Scholar]
- Wei, X.H. Dynamics and Galloping Mechanism of the Galloping Bionic Quadrupedal Robots. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, March 2018. [Google Scholar]
- Li, N.J. Effect of Gait Parameters and Spine Stiffness on Energy Use Efficiency of Quadruped Robot with Spine Joint. Master’s Thesis, Harbin Engineering University, Harbin, China, March 2018. [Google Scholar]
- Borisova, O.; Borisov, I.; Kolyubin, S.; Stramigioli, S. Design of galloping robots with elastic spine: Tracking relations between dynamic model parameters based on motion analysis of a real cheetah. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar]
- Zhang, S.S.; Rong, X.W.; Li, Y.B.; Li, B. Static gait planning method for quadruped robots on rough terrains. J. Jilin Univ. (Eng. Technol. Ed.) 2018, 46, 1287–1296. [Google Scholar]
- Zhang, F.; Wang, Y.F.; Teng, S.; Zheng, L.M.; Wang, J.J.; Chen, Z.J. Development of agricultural bionic four-legged robot: Effect of head movement adjustment on the stability of goats. Int. J. Agric. Biol. Eng. 2019, 46, 10–15. [Google Scholar] [CrossRef]
- Zhang, F.; Zheng, L.M.; Wang, W.; Wang, Y.F.; Wang, J.J. Development of agricultural bionic mechanisms: Investigation of the effect of joint angle and pressure on the stability of goats moving on sloping lands. Int. J. Agric. Biol. Eng. 2018, 11, 35–41. [Google Scholar] [CrossRef]
- Van Engelen, S.J.P.M.; Van Der Veen, A.J.; De Boer, A.; Ellenbroek, M.H.M.; Smit, T.H.; Van Royen, B.J.; Van Dieen, J.H. The feasibility of modal testing for measurement of the dynamic characteristics of goat vertebral motion segments. J. Biomech. 2011, 44, 1478–1483. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Valentin, S.; Licka, T.F. Spinal motion and muscle activity during active trunk movements–comparing sheep and humans adopting upright and quadrupedal postures. PLoS ONE 2016, 11, e0146362. [Google Scholar] [CrossRef] [PubMed]
- DeVries, N.A.; Gandhi, A.A.; Fredericks, D.C.; Grosland, N.M.; Smucker, J.D. Biomechanical analysis of the intact and destabilized sheep cervical spine. Spinel 2012, 37, E957–E963. [Google Scholar] [CrossRef] [PubMed]
- McDonald, C.P.; Bachison, C.C.; Chang, V.; Bartol, S.W.; Bey, M.J. Three-dimensional dynamic in vivo motion of the cervical spine: Assessment of measurement accuracy and preliminary findings. Spine J. 2010, 10, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Li, H.L.; Zhang, L.P. Summary of clustering research in time series data mining. J. Univ. Electron. Sci. Technol. China 2022, 51, 98–106. [Google Scholar]
- Zhen, R.; Shi, Z.Q. Ship Trajectory clustering method based on Gaussian Mixture Model. Ship Eng. 2021, 43, 139–143. [Google Scholar]


| Group | xn | SSE | R2 | Adjusted-R2 | RMSE |
|---|---|---|---|---|---|
| 1 | x | 299.67 | 0.9550 | 0.9399 | 9.995 |
| x2 | 297.03 | 0.9553 | 0.9107 | 12.187 | |
| x3 | 159.53 | 0.9760 | 0.9041 | 12.631 | |
| 2 | x | 1308.00 | 0.9511 | 0.9348 | 20.880 |
| x2 | 715.62 | 0.9732 | 0.9465 | 18.916 | |
| x3 | 318.17 | 0.9881 | 0.9524 | 17.837 | |
| 3 | x | 70.32 | 0.9946 | 0.9928 | 4.842 |
| x2 | 66.71 | 0.9949 | 0.9898 | 5.775 | |
| x3 | 0.33 | 1.0000 | 0.9999 | 0.573 |
| Group | xn | SSE | R2 | Adjusted-R2 | RMSE |
|---|---|---|---|---|---|
| 1 | x | 3955.00 | 0.6583 | 0.5444 | 36.310 |
| x2 | 133.00 | 0.9885 | 0.9770 | 8.155 | |
| x3 | 5.19 | 0.9996 | 0.9982 | 2.279 | |
| 2 | x | 4320.00 | 0.6119 | 0.4825 | 37.950 |
| x2 | 55.82 | 0.9950 | 0.9900 | 5.283 | |
| x3 | 0.59 | 0.9999 | 0.9998 | 0.765 | |
| 3 | x | 255.70 | 0.9487 | 0.9316 | 9.232 |
| x2 | 33.49 | 0.9933 | 0.9866 | 4.092 | |
| x3 | 0.05 | 1.0000 | 1.0000 | 0.214 |
| Group | 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|---|
| Movements | SSE | Adjusted-R2 | SSE | Adjusted-R2 | SSE | Adjusted-R2 | |
| ① | 292.5584 | 0.9950 | 373.9871 | 0.9884 | 33.8155 | 0.9984 | |
| ② | 995.2212 | 0.9888 | 502.3968 | 0.9881 | 244.2641 | 0.9927 | |
| ③ | 551.2280 | 0.9946 | 444.4963 | 0.9909 | 352.6374 | 0.9924 | |
| ④ | 374.7172 | 0.9965 | 468.5899 | 0.9907 | 352.1559 | 0.9927 | |
| ⑤ | 387.7880 | 0.9967 | 801.4724 | 0.9854 | 330.8916 | 0.9956 | |
| ⑥ | 346.9201 | 0.9971 | 733.1521 | 0.9866 | 304.8748 | 0.9963 | |
| ⑦ | 159.6307 | 0.9988 | 196.8156 | 0.9977 | 311.9123 | 0.9975 | |
| ⑧ | 132.3038 | 0.9991 | 184.2575 | 0.9987 | 291.8196 | 0.9981 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Cui, X.; Wang, S.; Sun, H.; Wang, J.; Wang, X.; Fu, S.; Guo, Z. Analysis of Kinematic Characteristics of Saanen Goat Spine under Multi-Slope. Biomimetics 2022, 7, 181. https://doi.org/10.3390/biomimetics7040181
Zhang F, Cui X, Wang S, Sun H, Wang J, Wang X, Fu S, Guo Z. Analysis of Kinematic Characteristics of Saanen Goat Spine under Multi-Slope. Biomimetics. 2022; 7(4):181. https://doi.org/10.3390/biomimetics7040181
Chicago/Turabian StyleZhang, Fu, Xiahua Cui, Shunqing Wang, Haoxuan Sun, Jiajia Wang, Xinyue Wang, Sanling Fu, and Zhijun Guo. 2022. "Analysis of Kinematic Characteristics of Saanen Goat Spine under Multi-Slope" Biomimetics 7, no. 4: 181. https://doi.org/10.3390/biomimetics7040181
APA StyleZhang, F., Cui, X., Wang, S., Sun, H., Wang, J., Wang, X., Fu, S., & Guo, Z. (2022). Analysis of Kinematic Characteristics of Saanen Goat Spine under Multi-Slope. Biomimetics, 7(4), 181. https://doi.org/10.3390/biomimetics7040181







