Load Balancing Based on Firefly and Ant Colony Optimization Algorithms for Parallel Computing
Abstract
1. Introduction
2. Related Work
3. Background and Problem Statement
3.1. Background
3.1.1. Parallel Computing
3.1.2. Gragh and Bioinspired Algorithms
3.2. Problem Statement
4. Methods and Models
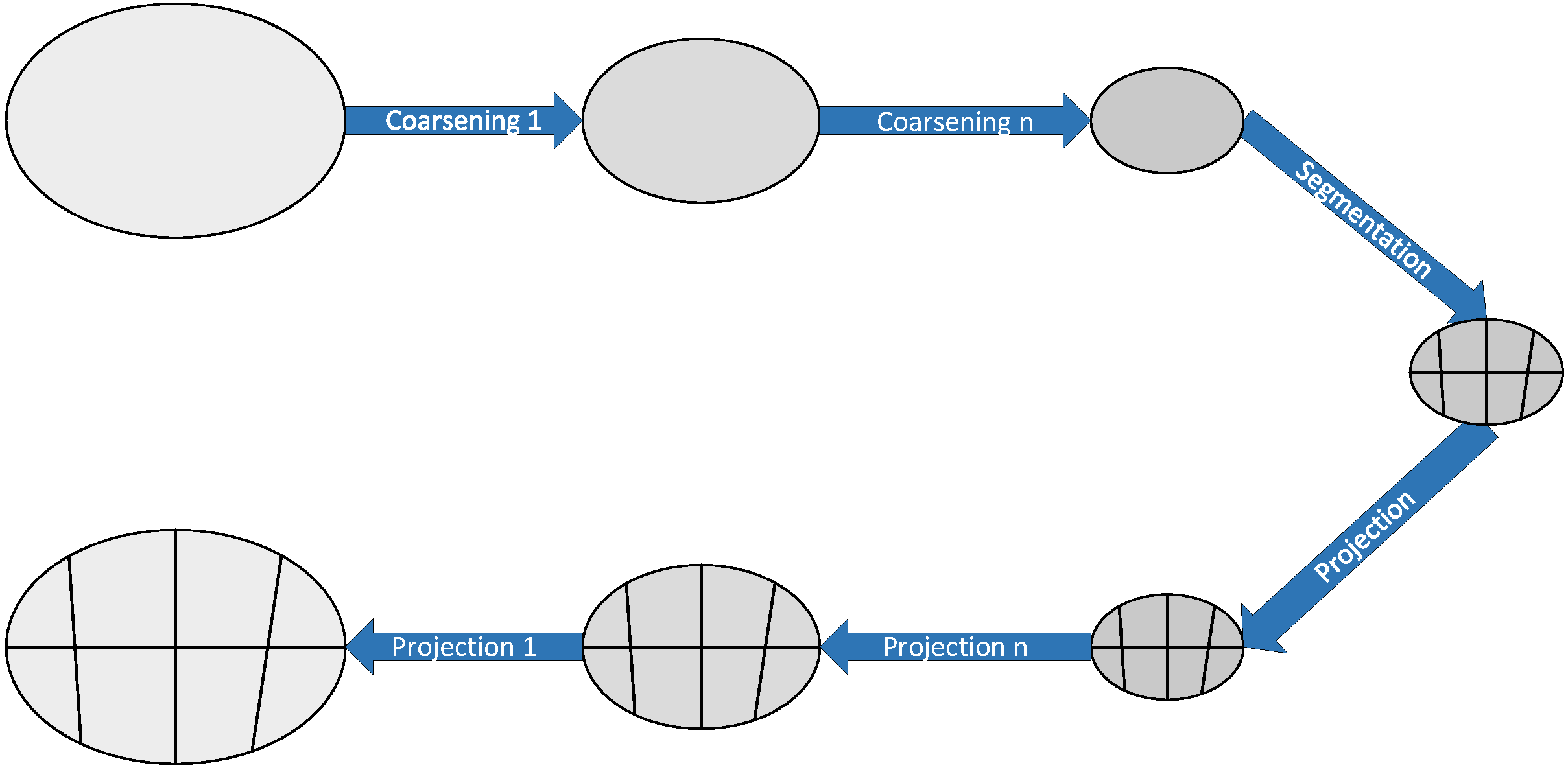
4.1. Multi-Level Algorithm for Partitioning Graphs
4.2. Firefly Algorithm
4.3. Ant Colony Optimization
5. Proposed Method
5.1. The FaCO Principle
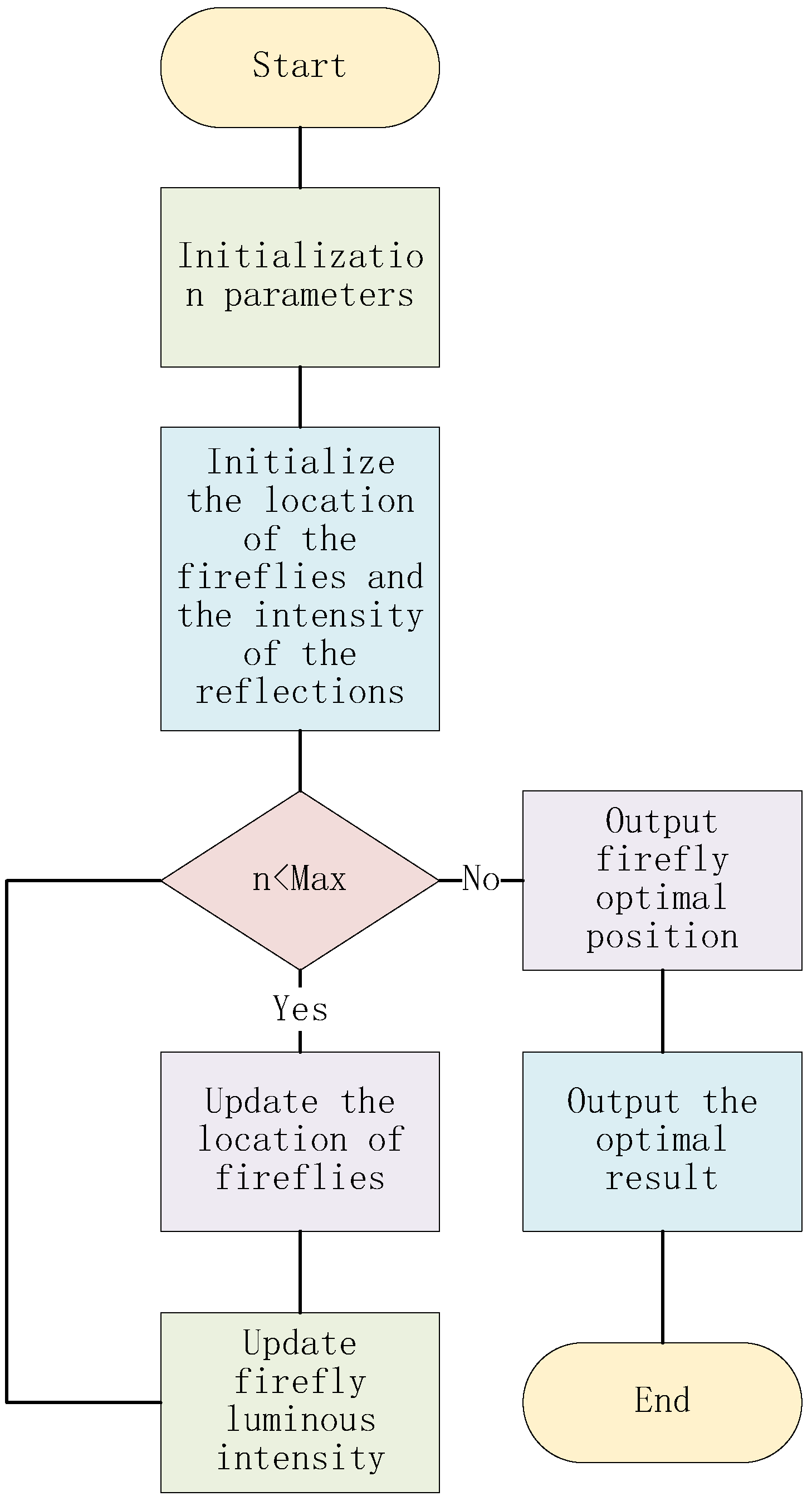
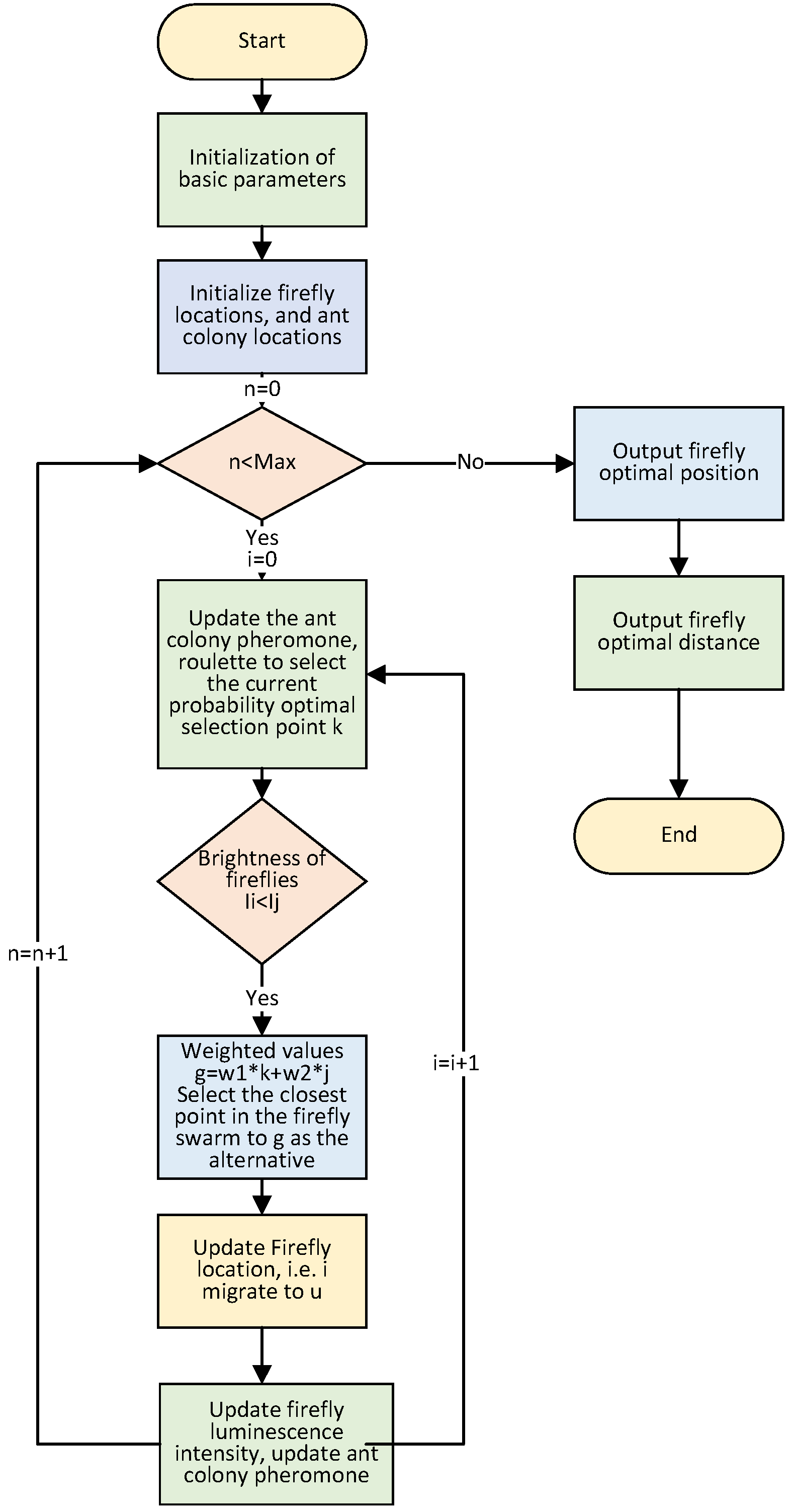
5.2. Algorithm Flow
5.2.1. Algorithm Logic Diagram
5.2.2. Algorithm Pseudocode
| Algorithm 1 FaCO algorithm. |
| Input: m, I, , , p, Q, , ′, , Max ▹ Initialization parameters Output: global extreme value points and optimal individual values
|
5.2.3. Algorithm Flow Chart
6. Experiment and Analysis
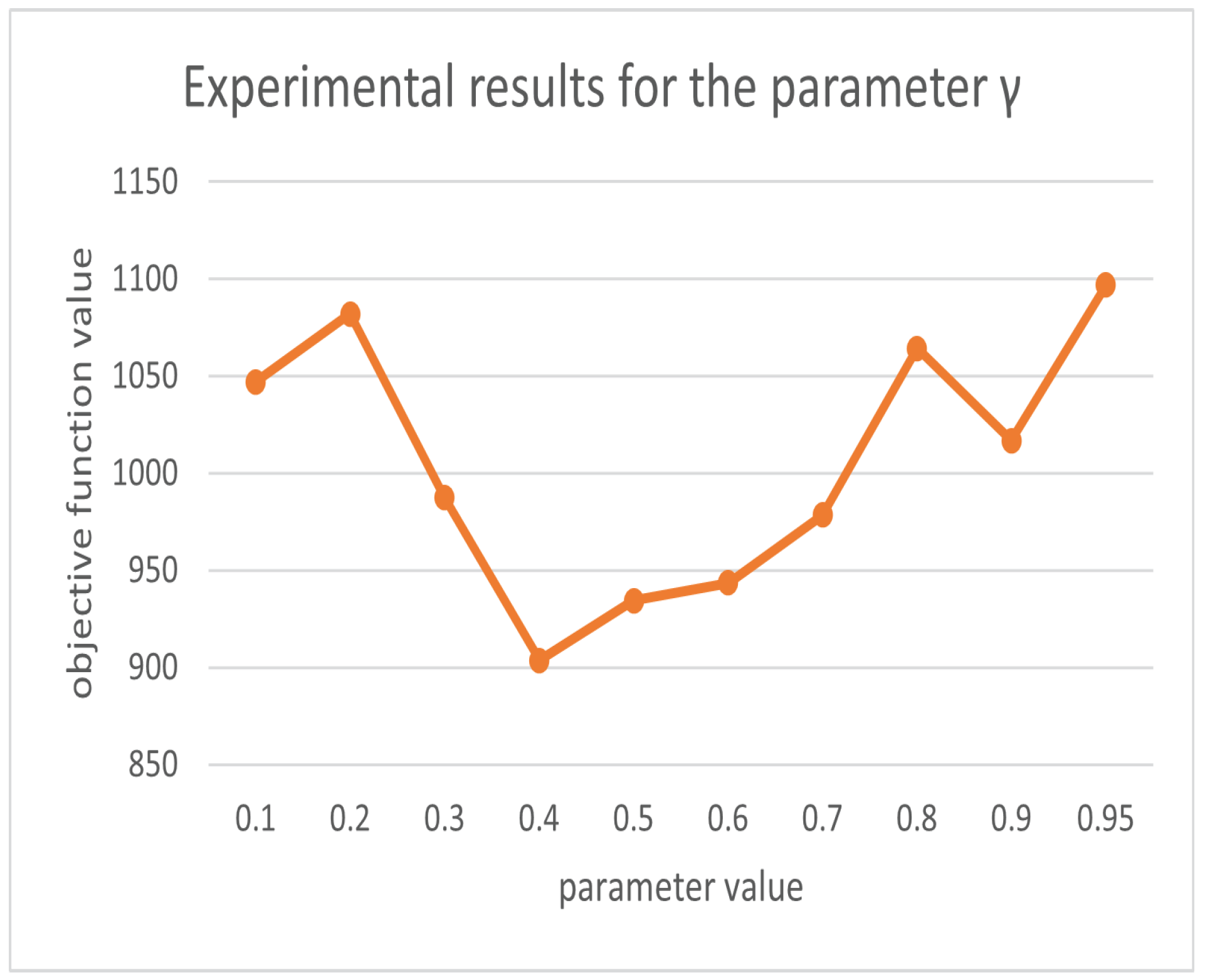
6.1. Parameter Setting
6.2. Experiment Analysis
7. Conclusions
8. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kusmayadi, A.; Suyono, E.A.; Nagarajan, D.; Chang, J.S.; Yen, H.W. Application of computational fluid dynamics (CFD) on the raceway design for the cultivation of microalgae: A review. J. Ind. Microbiol. Biotechnol. 2020, 47, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Wang, Y. A novel task load balancing algorithm in the large-scale CFD with multi-zone structured grids. Comput. Eng. Sci. 2014, 36, 1213–1220. [Google Scholar]
- Streng, M. Load Balancing for Computational Fluid Dynamics Calculations; Springer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Ytterström, A. A Tool for Partitioning Structured Multiblock Meshes for Parallel Computational Mechanics. Int. J. High Perform. Comput. Appl. 1997, 11, 336–343. [Google Scholar] [CrossRef]
- Hendrickson, B.A.; Leland, R.W. A Multi-Level Algorithm for Partitioning Graphs. Comput. Eng. Sci. 2014, 36, 1213–1220. [Google Scholar]
- Oh, B.S.; Cho, J.; Choi, B.; Choi, H.W.; Kim, M.S.; Lee, G. Application of heuristic algorithms for design optimization of industrial heat pump. Int. J. Refrig. 2022, 134, 1–15. [Google Scholar] [CrossRef]
- Castillon, L.F.; Bedriñana, M.F. Transmission Network Reconfiguration in Restoration Process Based on Constructive Heuristic Algorithms. J. Control Autom. Electr. Syst. 2022, 33, 929–938. [Google Scholar] [CrossRef]
- Spirov, A.V.; Myasnikova, E.M. Heuristic algorithms in evolutionary computation and modular organization of biological macromolecules: Applications to in vitro evolution. PLoS ONE 2022, 17, e0260497. [Google Scholar] [CrossRef]
- Zuo, L.; Shu, L.; Dong, S.; Zhu, C.; Hara, T. A multi-objective optimization scheduling method based on the ant colony algorithm in cloud computing. IEEE Access 2015, 3, 2687–2699. [Google Scholar] [CrossRef]
- Li, H.; Zhao, T.; Li, N.; Cai, Q.; Du, J. Feature Matching of Multi-view 3D Models Based on Hash Binary Encoding. Neural Netw. World 2017, 27, 95–105. [Google Scholar] [CrossRef]
- Li, H.; Liu, X.; Lai, L.; Cai, Q.; Du, J. An Area Weighted Surface Sampling Method for 3D Model Retrieval. Chin. J. Electron. 2014, 23, 484–488. [Google Scholar]
- Li, H.; Zheng, Y.; Wu, X.; Cai, Q. 3D Model Generation and Reconstruction Using Conditional Generative Adversarial Network. Int. J. Comput. Intell. Syst. 2019, 12, 697–705. [Google Scholar] [CrossRef]
- Li, H.; Sun, L.; Dong, S.; Zhu, X.; Cai, Q.; Du, J. Efficient 3D Object Retrieval Based on Compact Views and Hamming Embedding. IEEE Access 2018, 6, 31854–31861. [Google Scholar] [CrossRef]
- Kernighan, B.W.; Lin, S. An efficient heuristic procedure for partitioning graphs. Bell Syst. Tech. J. 1970, 49, 291–307. [Google Scholar] [CrossRef]
- Hou, X.; Yang, C.; Liu, D. Hybrid load balancing algorithm based on osmotic artificial bee colony and ant colony optimization. Appl. Res. Comput. 2021, 38, 440–443. [Google Scholar]
- Muteeh, A.; Sardaraz, M.; Tahir, M. MrLBA: Multi-resource load balancing algorithm for cloud computing using ant colony optimization. Cluster Compu. 2021, 24, 3135–3145. [Google Scholar] [CrossRef]
- Zeng, G.; Li, H.; Wang, X.; Li, N. Point cloud up-sampling network with multi-level spatial local feature aggregation. Comput. Electr. Eng. 2021, 94, 107337. [Google Scholar] [CrossRef]
- Li, H.; Zeng, G.; Cao, J.; Cai, Q. Multi-view-based siamese convolutional neural network for 3D object retrieval. Comput. Electr. Eng. 2019, 78, 11–21. [Google Scholar] [CrossRef]
- Kannan, K.S.; Sunitha, G.; Deepa, S.N.; Babu, D.V.; Avanija, J. A multi-objective load balancing and power minimization in cloud using bio-inspired algorithms. Comput. Electr. Eng. 2022, 102, 108225. [Google Scholar] [CrossRef]
- Li, J.; Han, Y. A hybrid multi-objective artificial bee colony algorithm for flexible task scheduling problems in cloud computing system. Cluster Comput. 2020, 23, 2483–2499. [Google Scholar] [CrossRef]
- Manasrah, A.M.; Hanan, B.A. Workflow Scheduling Using Hybrid GA-PSO Algorithm in Cloud Computing. Wirel. Commun. Mob. Comput. 2018, 2018, 1934784. [Google Scholar] [CrossRef]
- Tapale, M.T.; Goudar, R.H.; Birje, M.N.; Patil, R.S. Utility based load balancing using firefly algorithm in cloud. J. Data Inf. Manag. 2022, 2, 215–224. [Google Scholar] [CrossRef]
- Cheng, C.; Xu, Y.; Daniels, G. Efficient Management and Application of Human Resources Based on Genetic Ant Colony Algorithm. J. Sens. 2022, 2022, 9903319. [Google Scholar] [CrossRef]
- Skinderowicz, R. Improving Ant Colony Optimization efficiency for solving large TSP instances. Appl. Soft Comput. 2022, 120, 108653. [Google Scholar] [CrossRef]
- Ma, T.; Gao, S.; Chen, C.; Song, X. Multitarget Tracking Algorithm Based on Adaptive Network Graph Segmentation in the Presence of Measurement Origin Uncertainty. Sensors 2018, 18, 3791. [Google Scholar] [CrossRef]
- Zeng, S. Research of Multilevel Hypergraph Partitioning Algorithms and Its Application in Large-scale Parallel CFD Computations. Natl. Univ. Def. Technol. 2013, 17, e0260497. [Google Scholar]
- Wang, X.; Ren, H.; Guo, X. A novel discrete firefly algorithm for Bayesian network structure learning. Knowl.-Based Syst. 2022, 242, 108426. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Y.; Zhang, J. Parameter Analysis and Simulation Experiment of Ant Colony Optimization on Small-scale TSP Problem. IOP Conf. Ser. Mater. Sci. Eng. 2020, 768, 072095. [Google Scholar] [CrossRef]
- Renu, J.; Ramesh, K. Modified Ant System Solving TSP Problem. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2019, 8, 328–331. [Google Scholar]
- Hima Bindu, G.B.; Ramani, K.; Shoba Bindu, C. Optimized Resource Scheduling using the Meta Heuristic Algorithm in Cloud Computing. IAENG Int. J. Comput. Sci. 2020, 47, 360–366. [Google Scholar]
- Liu, Z.; Du, G.; Zhou, S.; Lu, H.; Ji, H. Analysis of Internet Financial Risks Based on Deep Learning and BP Neural Network. Comput. Econ. 2022, 59, 1481–1499. [Google Scholar] [CrossRef]
- Zhuo, H.; Chen, Q. Firefly algorithm parameter analysis and optimization. Inf. Technol. Netw. Secur. 2019, 38, 60–66. [Google Scholar]
- Li, Y. Study of Firefly algorithm parameters. Logist. Eng. Manag. 2015, 37, 195–197. [Google Scholar]
- Xiang, Y. Study of parameter setting in ant colony algorithm–TSP as an example. Mod. Inf. Technol. 2020, 4, 95–98, 102. [Google Scholar]
- Li, H.; Wei, Y.; Huang, Y.; Cai, Q.; Du, J. Visual analytics of cellular signaling data. Multimed. Tools Appl. 2019, 78, 29447–29461. [Google Scholar] [CrossRef]
- Zheng, Y.; Zeng, G.; Li, H.; Cai, Q.; Du, J. Colorful 3D Reconstruction at High Resolution Using Multi-View Representation. J. Vis. Commun. Image Represent. 2022, 85, 103486. [Google Scholar] [CrossRef]





| Name of Parameter | Meaning of Parameters | Remarks | Experimental Values |
|---|---|---|---|
| m | Firefly population size | 1.5 times the number of cities | 60 |
| I | Absolute brightness of fireflies | Objective function value correlation; the better the value of the objective function, the higher the brightness of their own | Determined by the initial position of the firefly |
| The maximum attractiveness of fireflies | The maximum attractiveness of fireflies when | Generally set to 1 | |
| Firefly light absorption coefficient | 0.4 | ||
| p | Colony population size | 1.5 times the number of cities | 60 |
| Q | Colony pheromone constant | Usually takes the value of [10, 1000] | 20 |
| Colony pheromone factor | Range usually: [0.5, 1] | 0.5 | |
| ′ | Ant colony heuristic function factor | Range of values: [0, 5] | 2 |
| Ant colony pheromone volatility factor | Range of values usually: [0.4, 0.7] | 0.69 | |
| Max | Maximum number of iterations | 1000 | |
| r | Distance between two points | ||
| Ant colony position update weight | 0.35 | ||
| Firefly position update weight | 0.65 |
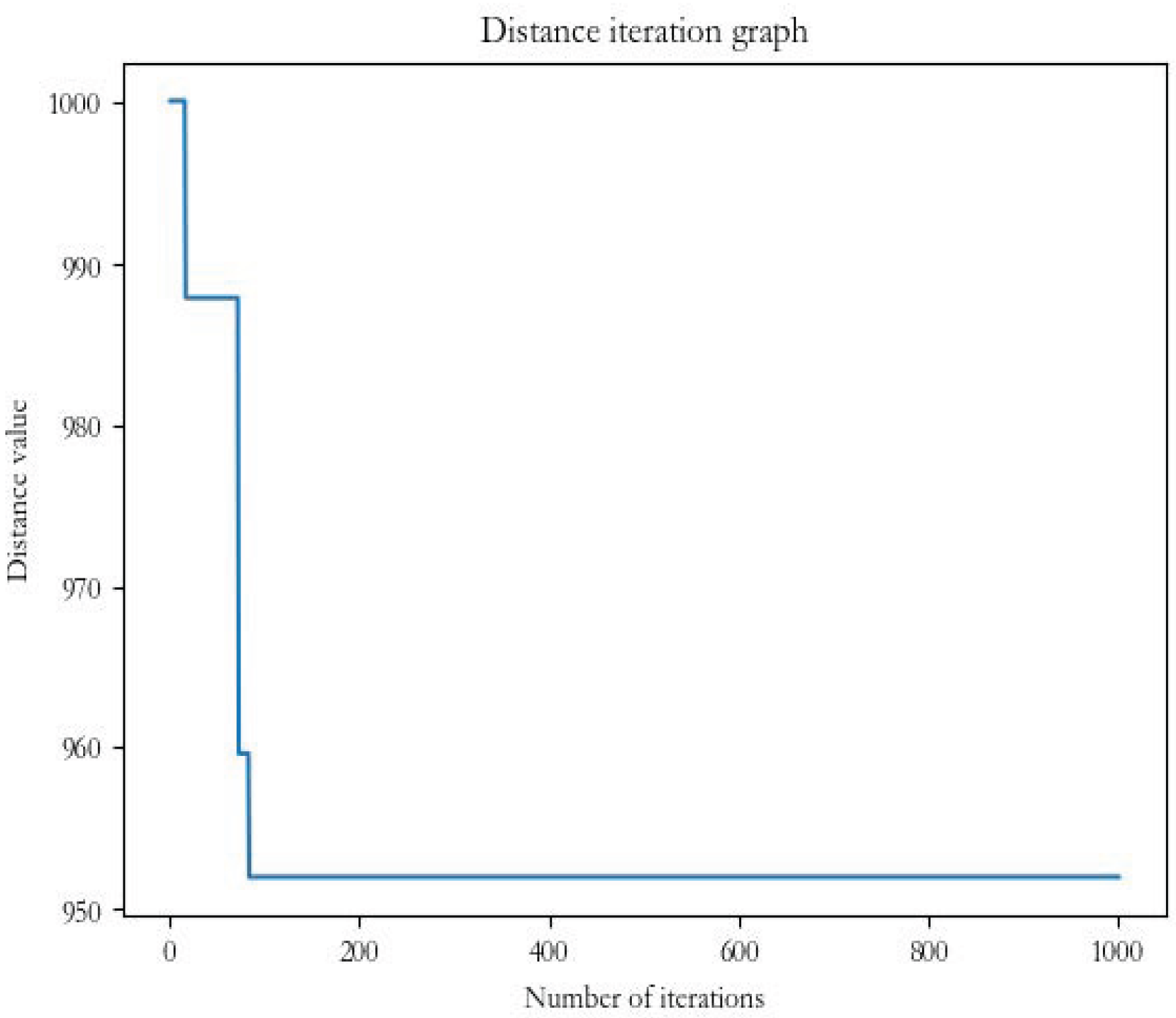
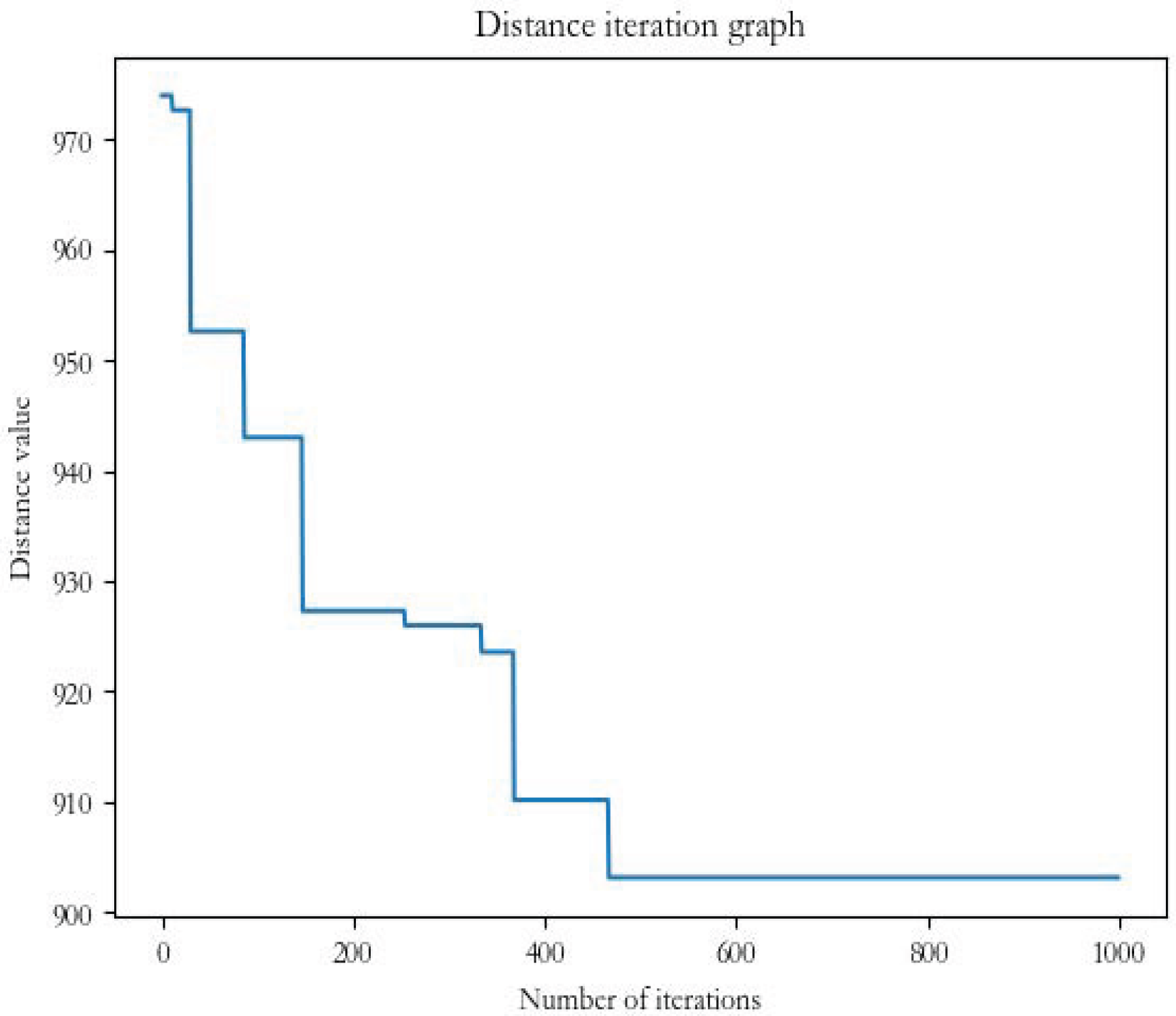
| TSP Arithmetic Example | Firefly Algorithm Results | FaCO Algorithm Results | Particle Swarm Algorithm Results | Genetic Algorithm |
|---|---|---|---|---|
| Burma14 | 44.129 | 30.8785 | 32.7 | 30.847 |
| Oliver30 | 956.26 | 864.37 | 897.4 | 906.57 |
| eil51 | 1436.788 | 807.175 | 823.6 | 842.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, J.; Sun, Y.; Li, H. Load Balancing Based on Firefly and Ant Colony Optimization Algorithms for Parallel Computing. Biomimetics 2022, 7, 168. https://doi.org/10.3390/biomimetics7040168
Li Y, Li J, Sun Y, Li H. Load Balancing Based on Firefly and Ant Colony Optimization Algorithms for Parallel Computing. Biomimetics. 2022; 7(4):168. https://doi.org/10.3390/biomimetics7040168
Chicago/Turabian StyleLi, Yong, Jinxing Li, Yu Sun, and Haisheng Li. 2022. "Load Balancing Based on Firefly and Ant Colony Optimization Algorithms for Parallel Computing" Biomimetics 7, no. 4: 168. https://doi.org/10.3390/biomimetics7040168
APA StyleLi, Y., Li, J., Sun, Y., & Li, H. (2022). Load Balancing Based on Firefly and Ant Colony Optimization Algorithms for Parallel Computing. Biomimetics, 7(4), 168. https://doi.org/10.3390/biomimetics7040168





