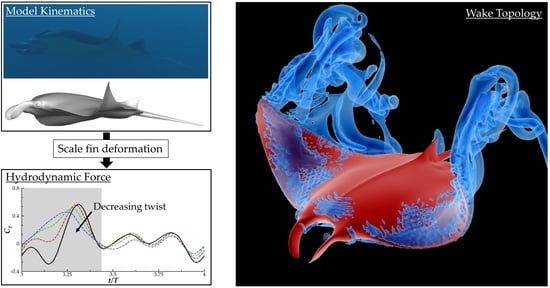
Bio-Inspired Propulsion: Towards Understanding the Role of Pectoral Fin Kinematics in Manta-like Swimming
Abstract
:1. Introduction
2. Materials and Methods
2.1. 3D Manta Ray Model Kinematics
2.2. Numerical Methods and Simulation Setup
3. Results and Discussions
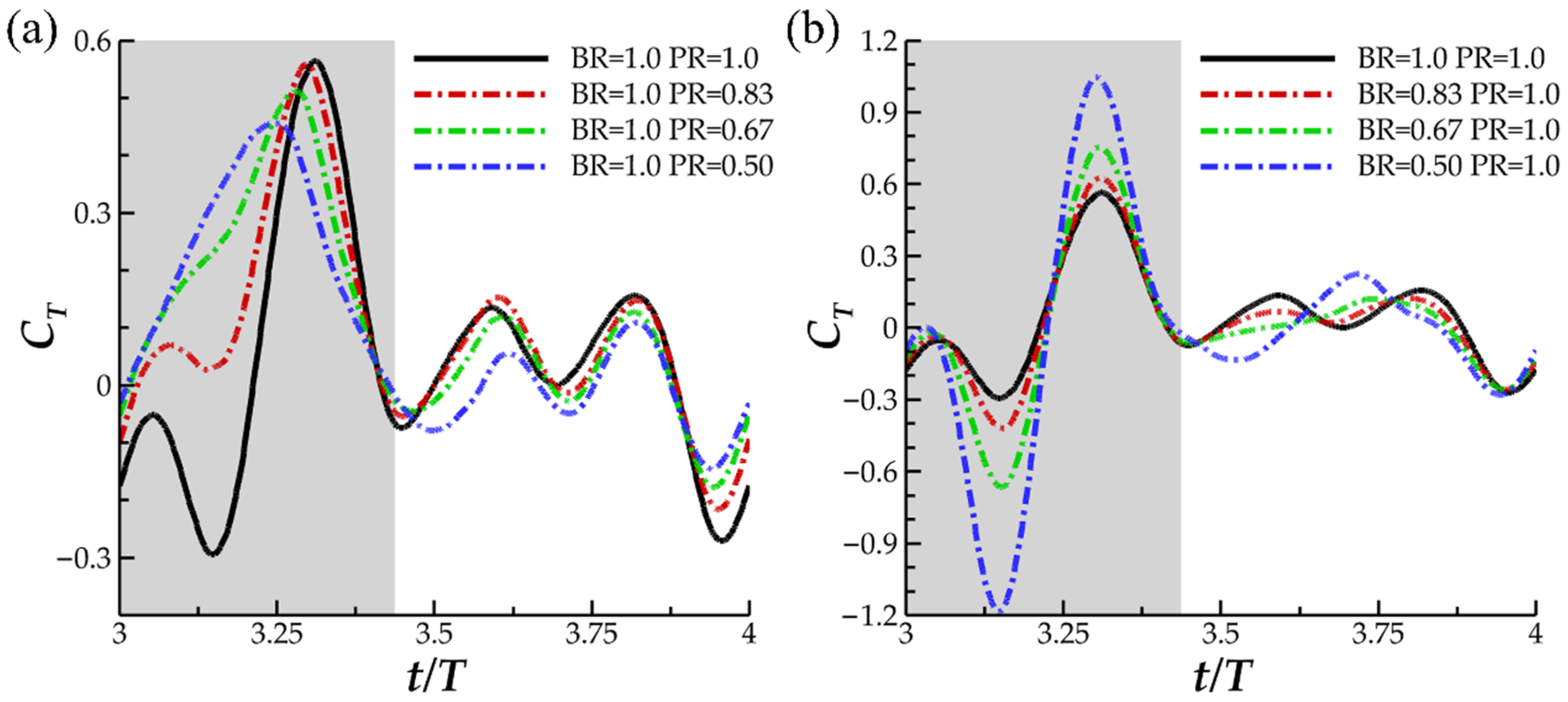
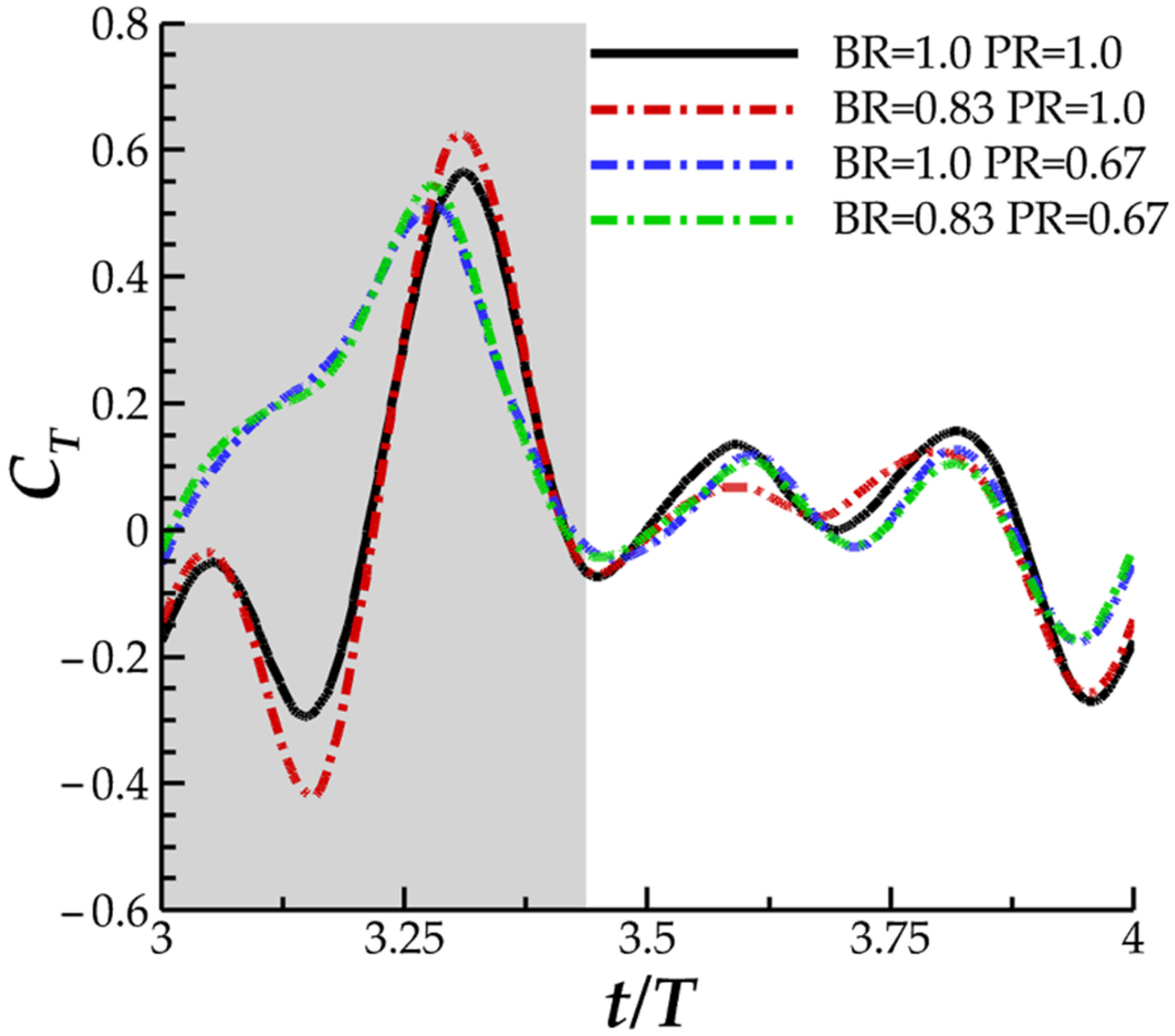
3.1. Comparison of Hydrodynamic Performance for Varying Bending and Pitching
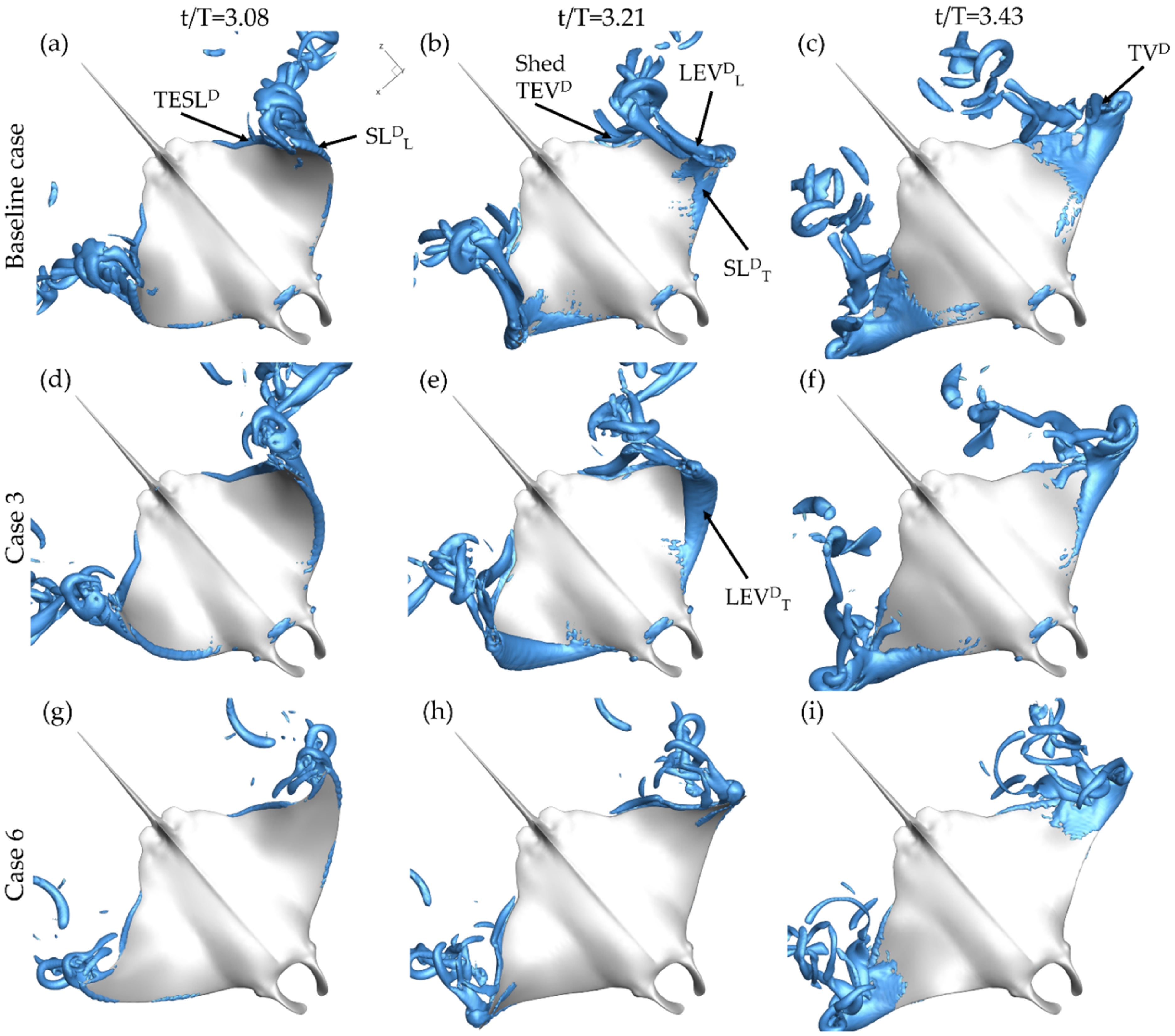
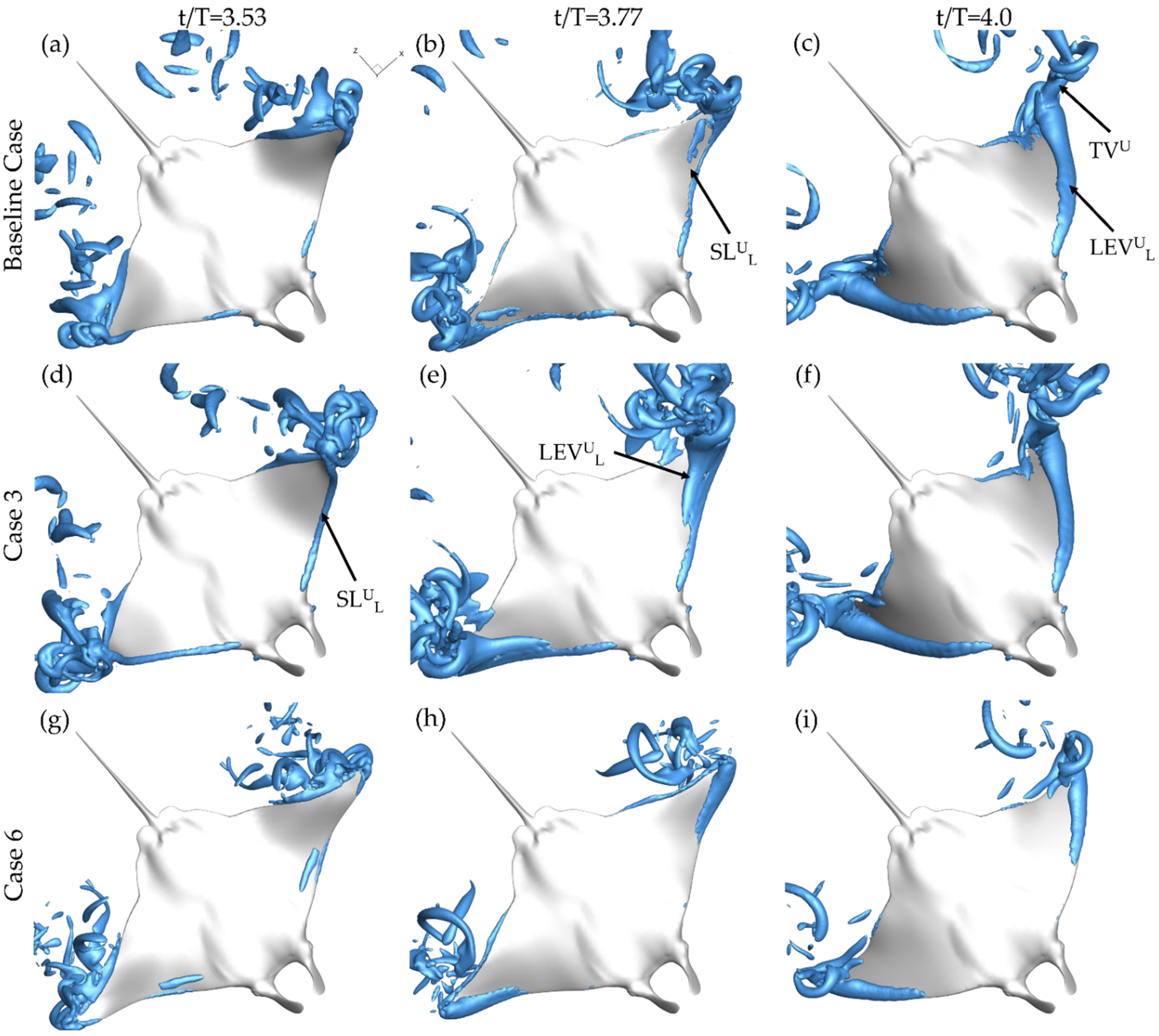
3.2. Comparison of Vortex Topology
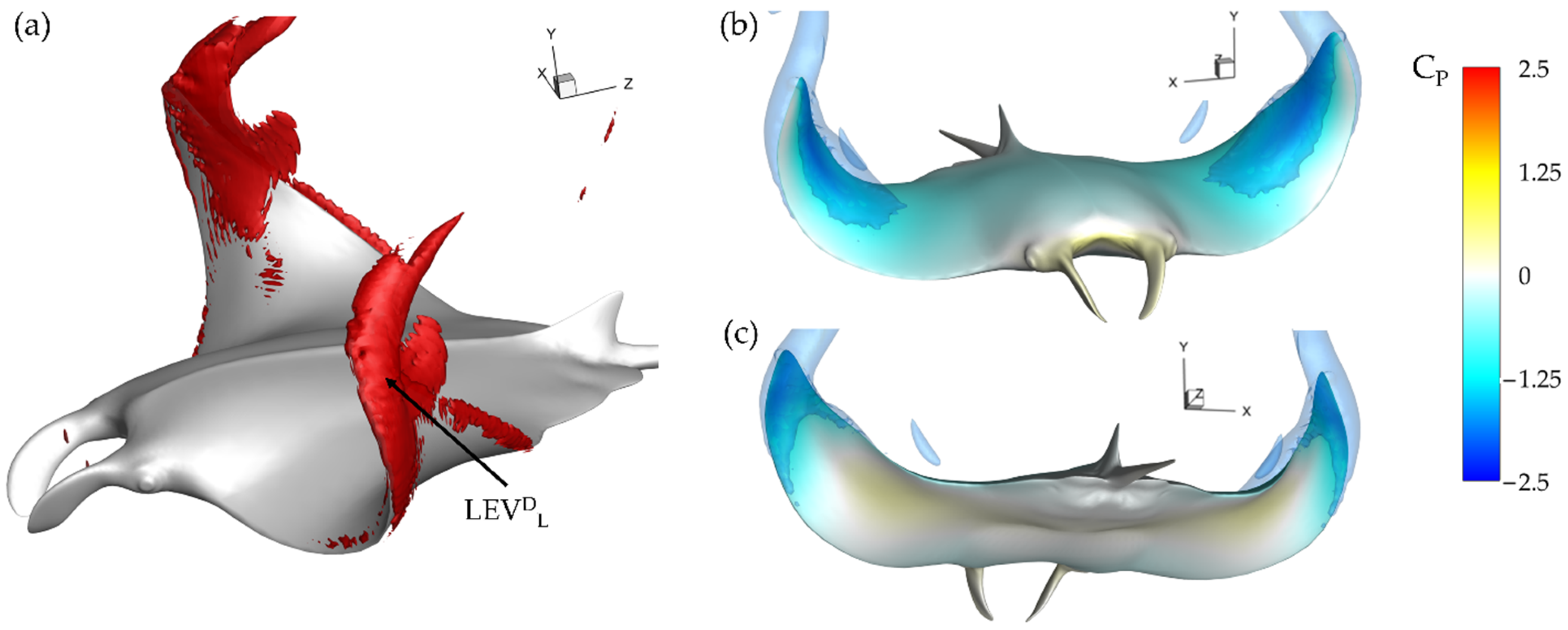
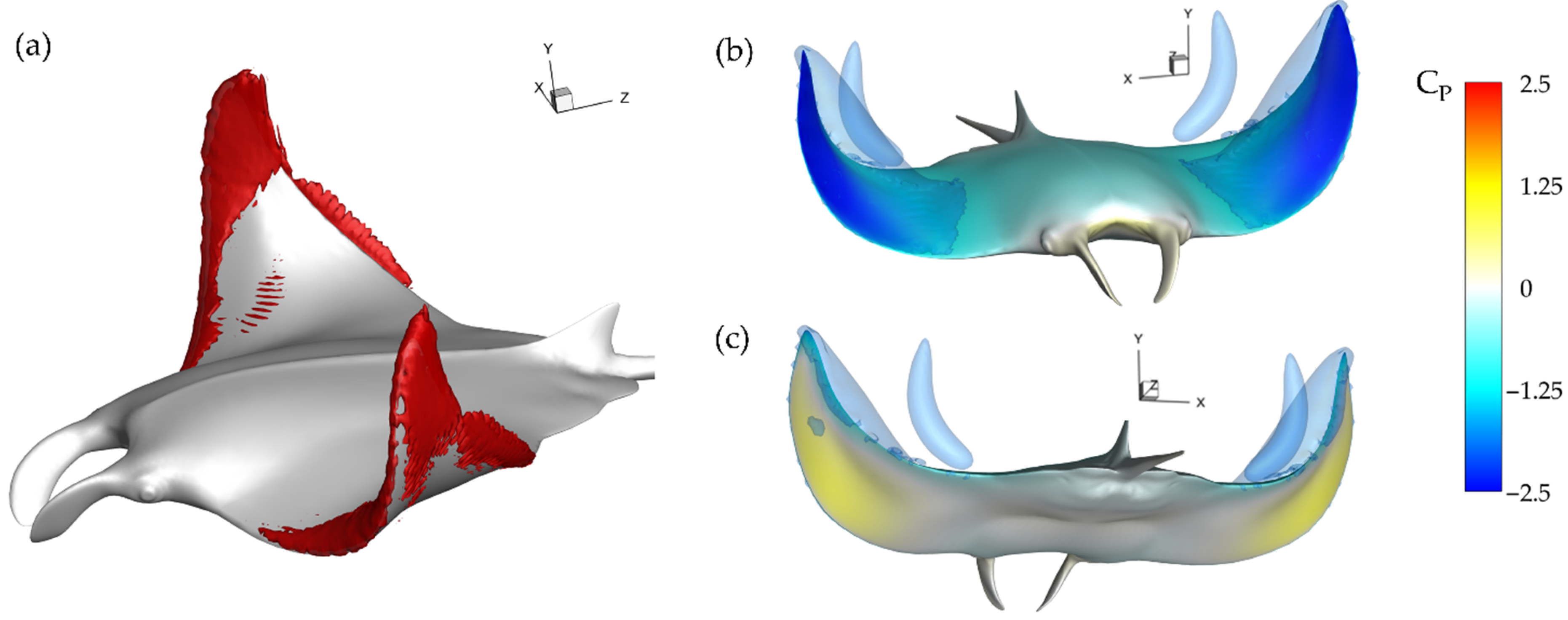
3.3. Impact of LEV and AV Formation on Hydrodynamic Surface Pressure
3.4. Hydrodynamic Performance and Surface Forces of Simultaneous Bending and Pitching Variation Case
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- White, C.H.; Lauder, G.V.; Bart-Smith, H. Tunabot Flex: A tuna-inspired robot with body flexibility improves high-performance swimming. Bioinspir. Biomim. 2021, 16, 026019. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Um, T.I.; Bart-Smith, H. Bio-inspired robotic manta ray powered by ionic polymer-metal composite artificial muscles. Int. J. Smart Nano Mater. 2012, 3, 296–308. [Google Scholar] [CrossRef] [Green Version]
- Fish, F.E. Advantages of aquatic animals as models for bio-inspired drones over present AUV technology. Bioinspir. Biomim. 2020, 15, 025001. [Google Scholar] [CrossRef] [PubMed]
- Gray, J. Studies in animal locomotion. J. Exp. Biol. 1939, 16, 9–17. [Google Scholar] [CrossRef]
- Liu, G.; Ren, Y.; Dong, H.; Akanyeti, O.; Liao, J.C.; Lauder, G.V. Computational analysis of vortex dynamics and performance enhancement due to body-fin and fin-fin interactions in fish-like locomotion. J. Fluid Mech. 2017, 829, 65–88. [Google Scholar] [CrossRef] [Green Version]
- Han, P.; Lauder, G.V.; Dong, H. Hydrodynamics of median-fin interactions in fish-like locomotion: Effects of fin shape and movement. Phys. Fluids 2020, 32, 011902. [Google Scholar] [CrossRef]
- Zhong, Q.; Dong, H.; Quinn, D.B. How dorsal fin sharpness affects swimming speed and economy. J. Fluid Mech. 2019, 878, 370–385. [Google Scholar] [CrossRef]
- Dewar, H.; Mous, P.; Domeier, M.; Muljadi, A.; Pet, J.; Whitty, J. Movements and site fidelity of the giant manta ray, Manta birostris, in the Komodo Marine Park, Indonesia. Mar. Biol. 2008, 155, 121–133. [Google Scholar] [CrossRef]
- Rosenberger, L.J.; Westneat, M.W. Functional morphology of undulatory pectoral fin locomotion in the stingray Taeniura lymma (Chondrichthyes: Dasyatidae). J. Exp. Biol. 1999, 202, 3523–3539. [Google Scholar] [CrossRef]
- Rosenberger, L.J.; Museum, F.; Drive, S.L.S. Pectoral Fin Locomotion in Batoid Fishes: Undulation Versus Oscillation. J. Exp. Biol. 2001, 204, 379–394. [Google Scholar] [CrossRef]
- Moored, K.W.; Smith, W.; Hester, J.M.; Chang, W.; Bart-Smith, H. Investigating the thrust production of a myliobatoid-lnspired oscillating wing. In CIMTEC 2008—Proceedings of the 3rd International Conference on Smart Materials 2, Structures and System—Mining Smartness from Nature, Acireale, Sicily, 8–13 June 2008; Trans Tech Publications Ltd.: Bäch, Switzerland, 2008; Volume 58, pp. 25–30. [Google Scholar] [CrossRef]
- Bottom, R.G.; Borazjani, I.; Blevins, E.L.; Lauder, G.V. Hydrodynamics of swimming in stingrays: Numerical simulations and the role of the leading-edge vortex. J. Fluid Mech. 2016, 788, 407–443. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Huang, Q.G.; Pan, G.; Yang, L.M.; Huang, W.X. Vortex dynamics and hydrodynamic performance enhancement mechanism in batoid fish oscillatory swimming. J. Fluid Mech. 2022, 930, A28. [Google Scholar] [CrossRef]
- Russo, R.S.; Blemker, S.S.; Fish, F.E.; Bart-Smith, H. Biomechanical model of batoid (skates and rays) pectoral fins predicts the influence of skeletal structure on fin kinematics: Implications for bio-inspired design. Bioinspir. Biomim. 2015, 10, 046002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bianchi, G.; Cinquemani, S.; Schito, P.; Resta, F. A numerical nodel for the analysis of the locomotion of a cownose ray. J. Fluids Eng. 2022, 144, 1–13. [Google Scholar] [CrossRef]
- Thekkethil, N.; Sharma, A.; Agrawal, A. Three-dimensional biological hydrodynamics study on various types of batoid fishlike locomotion. Phys. Rev. Fluids 2020, 5, 1–26. [Google Scholar] [CrossRef]
- Fish, F.E.; Schreiber, C.M.; Moored, K.W.; Liu, G.; Dong, H.; Bart-Smith, H. Hydrodynamic performance of aquatic flapping: Efficiency of underwater flight in the manta. Aerospace 2016, 3, 20. [Google Scholar] [CrossRef] [Green Version]
- Fish, F.E.; Kolpas, A.; Crossett, A.; Dudas, M.A.; Moored, K.W.; Bart-Smith, H. Kinematics of swimming of the manta ray: Three-dimensional analysis of open-water maneuverability. J. Exp. Biol. 2018, 221, 166041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fish, F.E.; Dong, H.; Zhu, J.; Bart-Smith, H. Swimming kinematics of mobuliform rays: Oscillatory winged propulsion by large pelagic batoids. Mar. Technol. Soc. J. 2017, 51, 35–47. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, L.; Chen, W. Investigation in wave number of rajiform swimmers. In Proceedings of the 2015 IEEE International Conference on Information and Automation 2015, ICIA 2015—In Conjunction with 2015 IEEE International Conference on Automation and Logistics, Lijiang, China, 10 August 2015; pp. 359–363. [Google Scholar] [CrossRef]
- Tu, Y.; Wang, J.; Hu, H.; Dong, H. Twist morphing effect on propulsive performance of bioinspired pitching-rolling plates. In Proceedings of the AIAA Scitech 2020 Forum, 1 PartF, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Ren, Y.; Dong, H. Low-dimensional modeling and aerodynamics of flexible wings in flapping flight. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef] [Green Version]
- Kang, C.K.; Aono, H.; Baik, Y.S.; Bernal, L.P.; Shyy, W. Fluid dynamics of pitching and plunging flat plate at intermediate Reynolds numbers. AIAA J. 2013, 51, 315–329. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Ren, Y.; Dong, H. Effects of surface morphing on the wake structure and performance of flapping plates. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–12. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, G.; Dong, H. Effects of surface morphing on the wake structure and performance of pitching-rolling plates. In Proceedings of the 53rd AIAA Aerospace Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef] [Green Version]
- Jia, K.; Wei, M. Optimization of flexible flapping wings for thrust and efficiency. In Proceedings of the AIAA Aviation 2021 Forum, Chicago, IL, USA, 2–6 August 2021. [Google Scholar] [CrossRef]
- Wang, J.; Ren, Y.; Li, C.; Dong, H. Computational investigation of wing-body interaction and its lift enhancement effect in hummingbird forward flight. Bioinspir. Biomim. 2019, 14, 046010. [Google Scholar] [CrossRef]
- Wang, J.; Wainwright, D.K.; Lindengren, R.E.; Lauder, G.V.; Dong, H. Tuna locomotion: A computational hydrodynamic analysis of finlet function. J. R. Soc. Interface 2020, 17, 20190590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.M.; Vargas, A.; von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C.; Dong, H.; Liu, G. Effects of a dynamic trailing-edge flap on the aerodynamic performance and flow structures in hovering flight. J. Fluids Struct. 2015, 58, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Dong, H.; Zhao, K. A balance between aerodynamic and olfactory performance during flight in Drosophila. Nat. Commun. 2018, 9, 3215. [Google Scholar] [CrossRef] [Green Version]
- Han, P.; Pan, Y.; Liu, G.; Dong, H. Propulsive performance and vortex wakes of multiple tandem foils pitching in-line. J. Fluids Struct. 2022, 108, 103422. [Google Scholar] [CrossRef]
- Ullah Khalid, M.S.; Wang, J.; Akhtar, I.; Dong, H.; Liu, M. Modal decompositions of the kinematics of Crevalle jack and the fluid-caudal fin interaction. Bioinspir. Biomim. 2020, 16, 016018. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Dong, H. Computational analysis of hydrodynamic interactions in a high-density fish school. Phys. Fluids 2020, 32, 121901. [Google Scholar] [CrossRef]
- Kelly, J.; Han, P.; Dong, H.; Buren, T. Van. Wake structures and effect of hydrofoil shapes in efficient flapping propulsion. Am. Soc. Mech. Eng. Fluids Eng. Div. Publ. FEDSM 2021, 3, 1–7. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Deshmukh, A.T.; Xia, J.; Reuss, M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Euler-Lagrange computational fluid dynamics for bioreactor scale down: An analysis of organism lifelines. Eng. Life Sci. 2016, 16, 652–663. [Google Scholar] [CrossRef] [Green Version]
- Hathway, E.A.; Noakes, C.J.; Sleigh, P.A.; Fletcher, L.A. CFD simulation of airborne pathogen transport due to human activities. Build. Environ. 2011, 46, 2500. [Google Scholar] [CrossRef]
- Zhang, W.; Pan, Y.; Gong, Y.; Dong, H.; Xi, J. A versatile IBM-based amr method for studying human snoring. In Proceedings of the American Society of Mechanical Engineers, Fluids Engineering Division (Publication) FEDSM, Virtual, 10–12 August 2021. [Google Scholar] [CrossRef]
- Liu, G.; Ren, Y.; Zhu, J.; Bart-Smith, H.; Dong, H. Thrust producing mechanisms in ray-inspired underwater vehicle propulsion. Theor. Appl. Mech. Lett. 2015, 5, 54–57. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Chen, L.; Bi, S.; Li, G.; Zhang, H. Bionic Flapping Pectoral Fin with Controllable Spatial Deformation. J. Bionic Eng. 2019, 16, 916–930. [Google Scholar] [CrossRef]


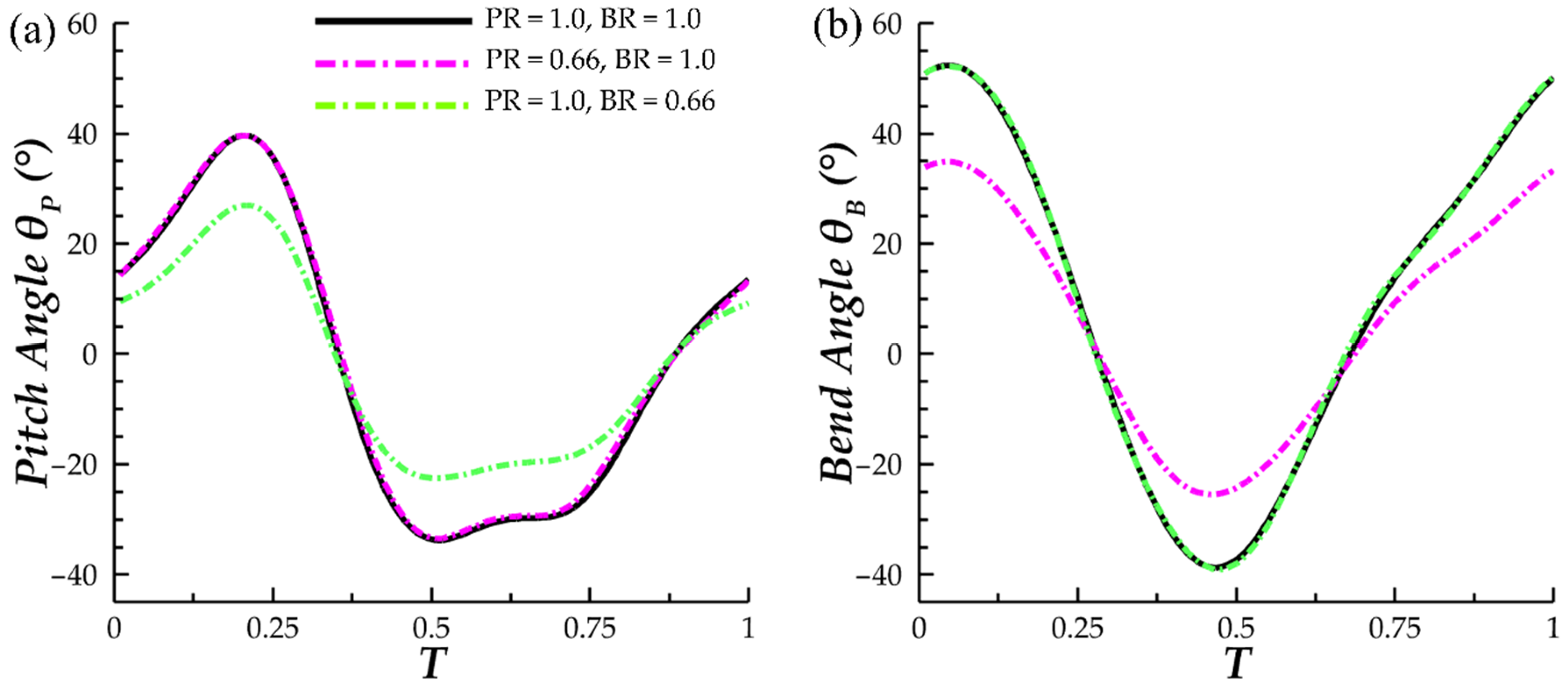



| Baseline | Fixed BR, Vary PR | Fixed PR, Vary BR | Case 7 | ||||
|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | ||
| BR = 1.0 | BR = 1.0 | BR = 1.0 | BR = 1.0 | BR = 0.83 | BR = 67 | BR = 0.5 | BR = 0.83 |
| PR = 1.0 | PR = 0.83 | PR = 0.67 | PR = 0.50 | PR = 1.0 | PR = 1.0 | PR = 1.0 | PR = 0.67 |
| BR and PR | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normalized | 2.27 | 2.71 | 2.34 | 0.65 | 0.14 | −0.53 | |||||||
| Upstroke | Downstroke | 0.90 | 0.10 | 0.97 | 0.03 | 1.11 | −0.11 | 1.12 | −0.12 | 3.04 | −2.04 | 0.31 | 0.69 |
| Normalized | 1.04 | 1.14 | 1.32 | 0.96 | 1.02 | 1.29 | |||||||
| Normalized | 2.19 | 2.36 | 1.76 | 0.68 | 0.13 | -- | |||||||
| BR and PR | Case 2 | Case 4 | Case 7 |
|---|---|---|---|
| Normalized | 2.71 | 0.65 | 2.66 |
| Normalized | 1.14 | 0.96 | 0.93 |
| Normalized | 2.36 | 0.68 | 2.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menzer, A.; Gong, Y.; Fish, F.E.; Dong, H. Bio-Inspired Propulsion: Towards Understanding the Role of Pectoral Fin Kinematics in Manta-like Swimming. Biomimetics 2022, 7, 45. https://doi.org/10.3390/biomimetics7020045
Menzer A, Gong Y, Fish FE, Dong H. Bio-Inspired Propulsion: Towards Understanding the Role of Pectoral Fin Kinematics in Manta-like Swimming. Biomimetics. 2022; 7(2):45. https://doi.org/10.3390/biomimetics7020045
Chicago/Turabian StyleMenzer, Alec, Yuchen Gong, Frank E. Fish, and Haibo Dong. 2022. "Bio-Inspired Propulsion: Towards Understanding the Role of Pectoral Fin Kinematics in Manta-like Swimming" Biomimetics 7, no. 2: 45. https://doi.org/10.3390/biomimetics7020045
APA StyleMenzer, A., Gong, Y., Fish, F. E., & Dong, H. (2022). Bio-Inspired Propulsion: Towards Understanding the Role of Pectoral Fin Kinematics in Manta-like Swimming. Biomimetics, 7(2), 45. https://doi.org/10.3390/biomimetics7020045