EvoSeg: Automated Electron Microscopy Segmentation through Random Forests and Evolutionary Optimization
Abstract
1. Introduction
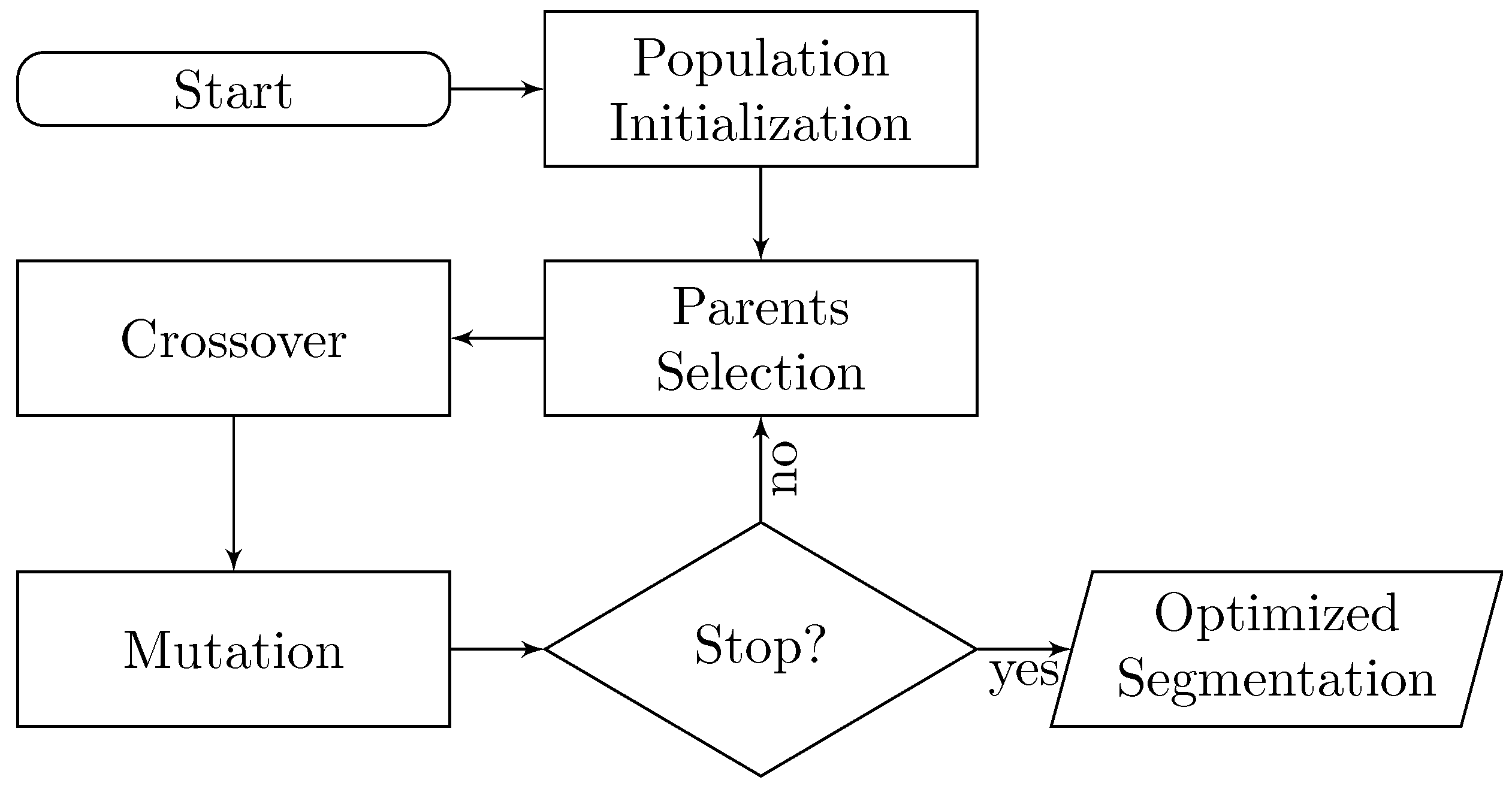
2. EvoSeg: Evolutionary-Optimized Segmentation
- A way of determining if a segmentation is good or bad. In other words, is a segmentation result close to being biologically correct?
- Once we can discriminate good segmentation results, we need a method to create segmentation candidates to explore the space, and keep traversing the regions of the space that are biologically relevant.
2.1. Crossover
2.2. Mutation
2.2.1. Merge Operation
2.2.2. Split Operation
2.3. Ideal Segmentation Classifier
- Number of segments: Directly derived from the expected number of protein units in the macromolecule.
- Volume of segment: Proportion of the total macromolecule volume in voxels, captured by each segment.
- Topology of segments: Euler–Poincaré Characteristic is used to encode invariant shape details of segments.
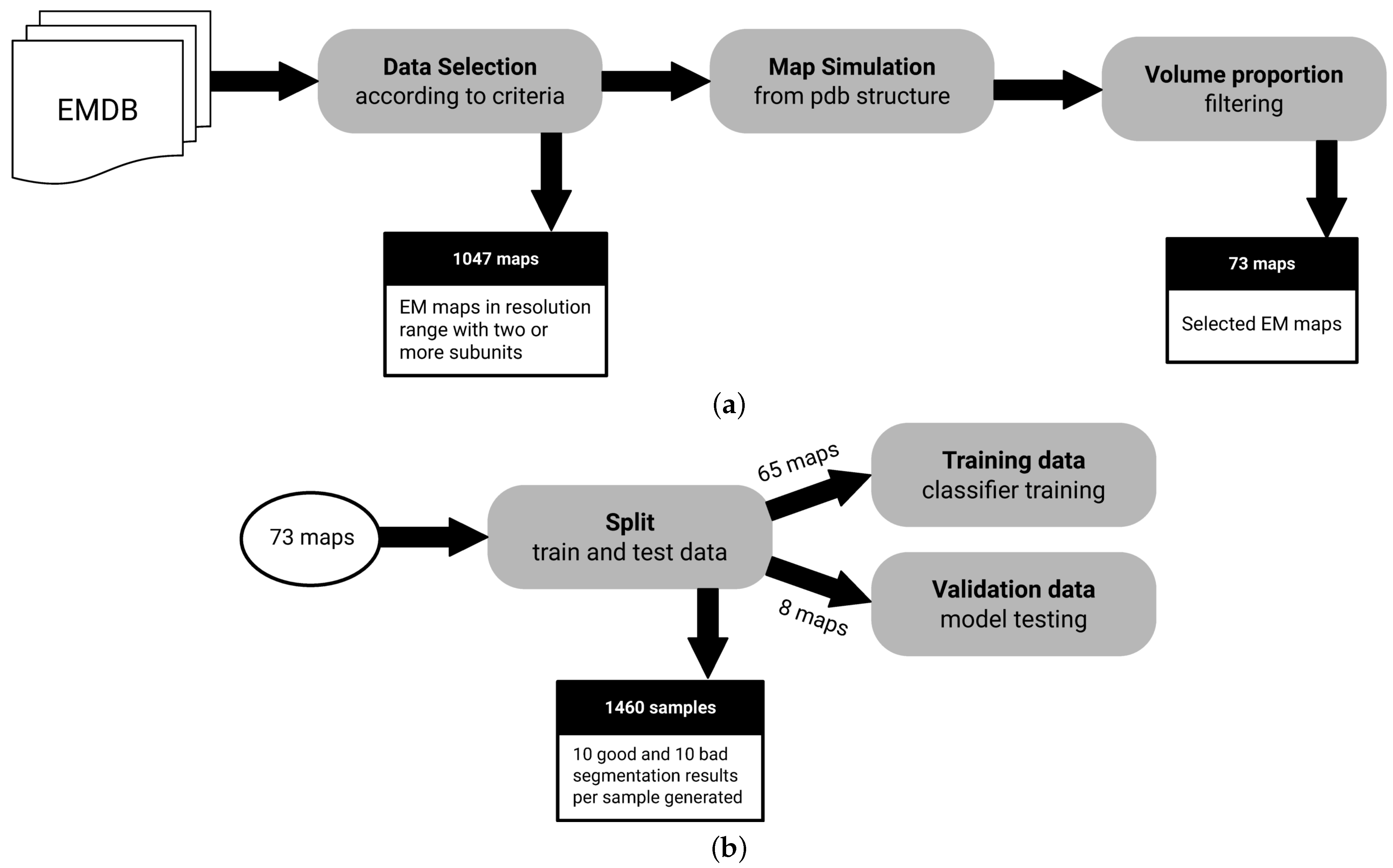
2.4. Data
- Macromolecules with at least 2 subunits: We need macromolecules with more than a single subunit, as we want to assess segmentation performance.
- Macromolecules in a resolution range of Å to Å: It is possible to derive structures from maps with resolutions below Å. On the other hand, lower resolutions above Å may not have enough signal for predictive purposes.
- Macromolecules with an associated atomic structure: It is necessary for ground truth annotation.
3. Performance Measures
3.1. Matching IoU
3.2. Homogeneity
3.3. Proportion of Estimated Segments
3.4. Consistency
4. Results
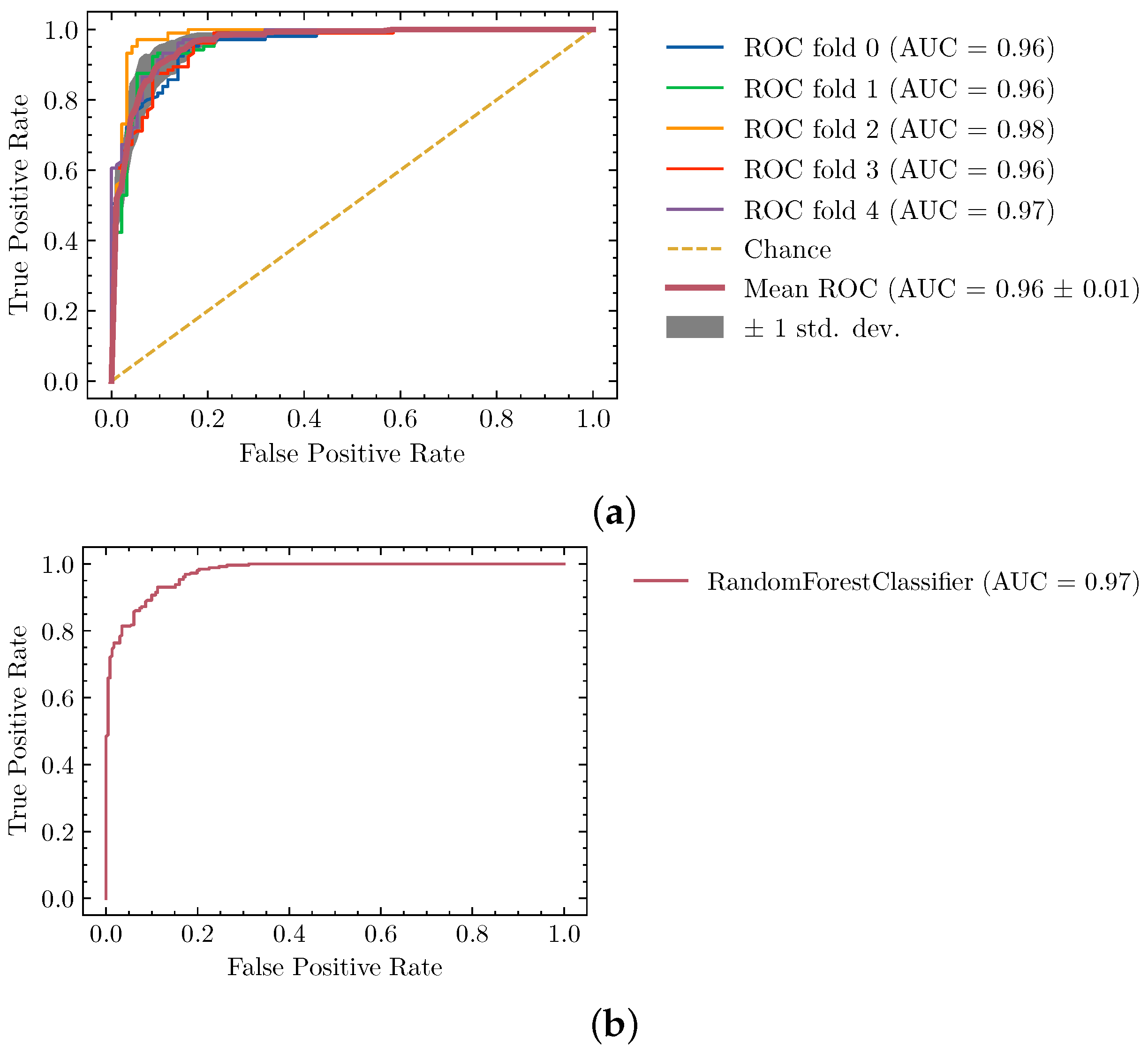
4.1. Ideal Segmentation Classifier
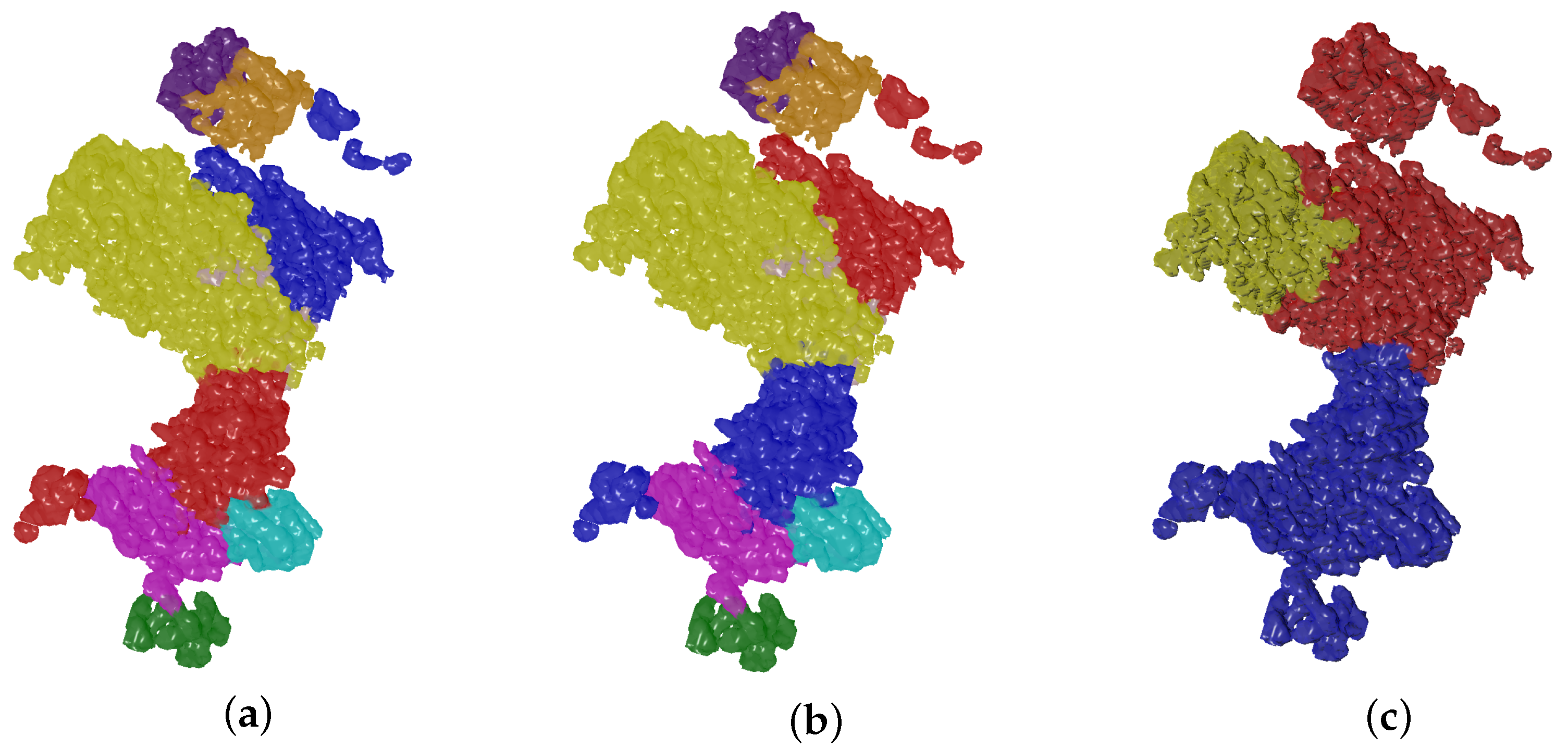
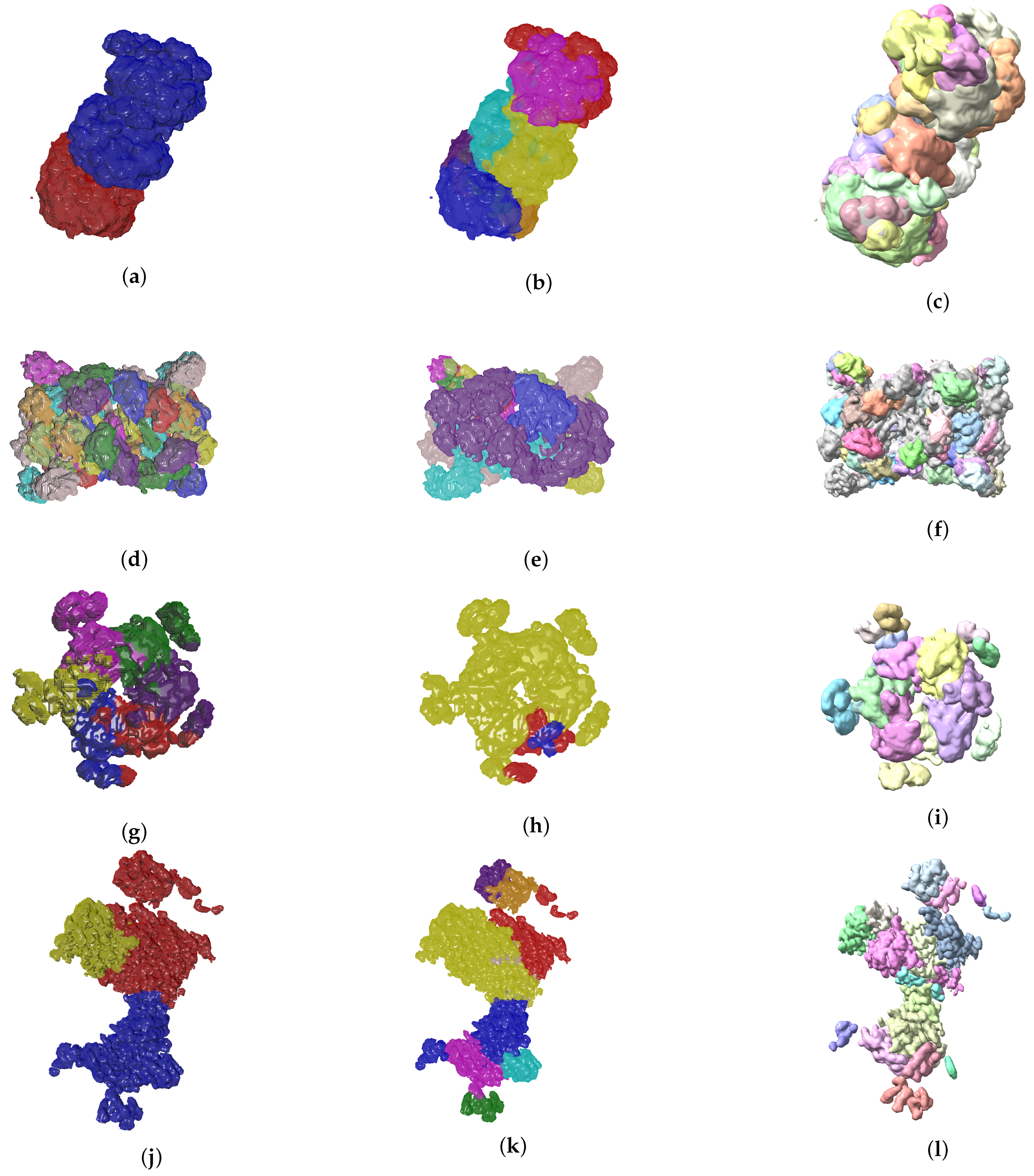
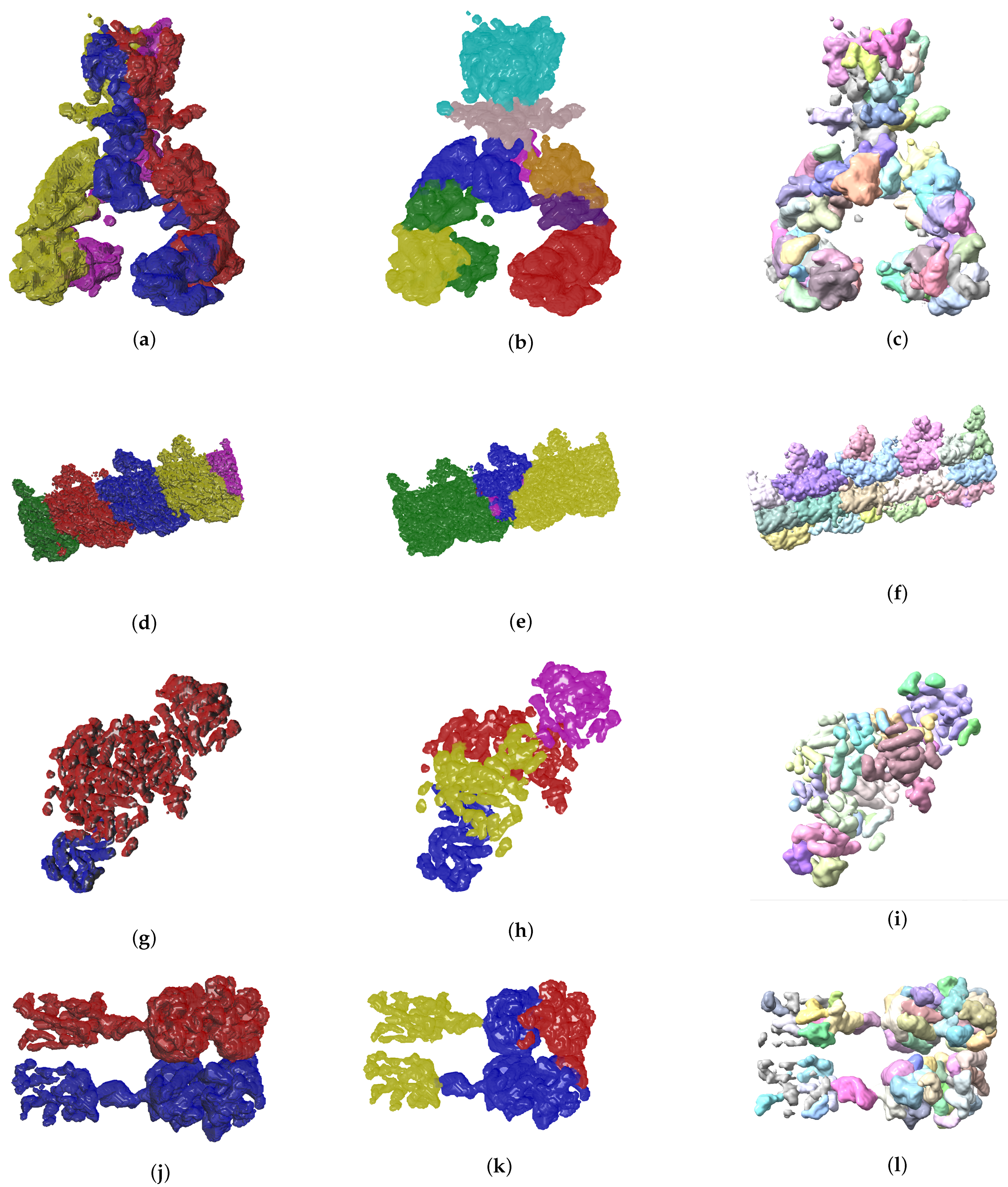
4.2. Evolutionary-Optimized Segmentation Validation
- The ground truth protein units
- Our segmentation results
- Segger results with baseline configuration
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EM | Electron Microscopy |
| PDB | Protein Data Bank |
| EvoSeg | Evolutionary-Optimized Segmentation |
References
- Zhang, K.; Pintilie, G.D.; Li, S.; Schmid, M.F.; Chiu, W. Resolving Individual-Atom of Protein Complex using Commonly Available 300-kV Cryo-electron Microscopes. bioRxiv 2020. [Google Scholar] [CrossRef]
- Nakane, T.; Kotecha, A.; Sente, A.; McMullan, G.; Masiulis, S.; Brown, P.M.; Grigoras, I.T.; Malinauskaite, L.; Malinauskas, T.; Miehling, J.; et al. Single-particle cryo-EM at atomic resolution. bioRxiv 2020. [Google Scholar] [CrossRef]
- Yip, K.M.; Fischer, N.; Paknia, E.; Chari, A.; Stark, H. Atomic-resolution protein structure determination by cryo-EM. Nature 2020, 587, 157–161. [Google Scholar] [CrossRef]
- EMStats: EMDB Statistics. Available online: https://www.ebi.ac.uk/pdbe/emdb/statistics_sp_res.html/ (accessed on 5 April 2021).
- Baker, M.L.; Baker, M.R.; Hryc, C.F.; Ju, T.; Chiu, W. Gorgon and pathwalking: macromolecular modeling tools for subnanometer resolution density maps. Biopolymers 2012, 97, 655–668. [Google Scholar] [CrossRef]
- Baker, M.L.; Ju, T.; Chiu, W. Identification of secondary structure elements in intermediate-resolution density maps. Structure 2007, 15, 7–19. [Google Scholar] [CrossRef]
- Jiang, W.; Baker, M.L.; Ludtke, S.J.; Chiu, W. Bridging the information gap: computational tools for intermediate resolution structure interpretation. J. Mol. Biol. 2001, 308, 1033–1044. [Google Scholar] [CrossRef]
- Kong, Y.; Ma, J. A structural-informatics approach for mining beta-sheets: locating sheets in intermediate-resolution density maps. J. Mol. Biol. 2003, 332, 399–413. [Google Scholar] [CrossRef]
- Kong, Y.; Zhang, X.; Baker, T.S.; Ma, J. A Structural-informatics approach for tracing beta-sheets: building pseudo-C(alpha) traces for beta-strands in intermediate-resolution density maps. J. Mol. Biol. 2004, 339, 117–130. [Google Scholar] [CrossRef] [PubMed]
- Terashi, G.; Kagaya, Y.; Kihara, D. MAINMASTseg: Automated Map Segmentation Method for Cryo-EM Density Maps with Symmetry. J. Chem. Inf. Model. 2020, 60, 2634–2643. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Jebril, R.; Nasr, K.A. Segmentation-Based Feature Extraction for Cryo-Electron Microscopy at Medium Resolution; ACM: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Ng, A.; Si, D. Beta-Barrel Detection for Medium Resolution Cryo-Electron Microscopy Density Maps Using Genetic Algorithms and Ray Tracing. J. Comput. Biol. 2018, 25, 326–336. [Google Scholar] [CrossRef] [PubMed]
- Si, D.; Ji, S.; Nasr, K.A.; He, J. A Machine Learning Approach for the Identification of Protein Secondary Structure Elements from Electron Cryo-Microscopy Density Maps. Biopolymers 2012, 97. [Google Scholar] [CrossRef]
- Bajaj, C.; Goswami, S.; Zhang, Q. Detection of secondary and supersecondary structures of proteins from cryo-electron microscopy. J. Struct. Biol. 2012, 177. [Google Scholar] [CrossRef][Green Version]
- Subramaniya, S.R.M.V.; Terashi, G.; Kihara, D. Protein secondary structure detection in intermediate-resolution cryo-EM maps using deep learning. Nat. Methods 2019, 16. [Google Scholar] [CrossRef]
- He, J.; Huang, S.Y. Full-length de novo protein structure determination from cryo-EM maps using deep learning. bioRxiv 2021. [Google Scholar] [CrossRef]
- Wang, X.; Alnabati, E.; Aderinwale, T.W.; Subramaniya, S.R.M.V.; Terashi, G.; Kihara, D. Emap2sec+: Detecting Protein and DNA/RNA Structures in Cryo-EM Maps of Intermediate Resolution Using Deep Learning. bioRxiv 2020. [Google Scholar] [CrossRef]
- Mostosi, P.; Schindelin, H.; Kollmannsberger, P.; Thorn, A. Haruspex: A Neural Network for the Automatic Identification of Oligonucleotides and Protein Secondary Structure in Cryo-Electron Microscopy Maps. Angew. Chem. Int. Ed. 2020, 59, 14788–14795. [Google Scholar] [CrossRef]
- Lindert, S.; Stewart, P.L.; Meiler, J. Hybrid approaches: applying computational methods in cryo-electron microscopy. Curr. Opin. Struct. Biol. 2009, 19, 218–225. [Google Scholar] [CrossRef] [PubMed]
- Beck, M.; Topf, M.; Frazier, Z.; Tjong, H.; Xu, M.; Zhang, S.; Alber, F. Exploring the spatial and temporal organization of a cell’s proteome. J. Struct. Biol. 2011, 173, 483–496. [Google Scholar] [CrossRef] [PubMed]
- Dou, H.; Burrows, D.W.; Baker, M.L.; Ju, T. Flexible Fitting of Atomic Models into Cryo-EM Density Maps Guided by Helix Correspondences. Biophys. J. 2017, 112, 2479–2493. [Google Scholar] [CrossRef]
- Topf, M.; Baker, M.L.; John, B.; Chiu, W.; Sali, A. Structural characterization of components of protein assemblies by comparative modeling and electron cryo-microscopy. J. Struct. Biol. 2005, 149, 191–203. [Google Scholar] [CrossRef]
- Fabiola, F.; Chapman, M.S. Fitting of High-Resolution Structures into Electron Microscopy Reconstruction Images. Structure 2005, 13, 389–400. [Google Scholar] [CrossRef]
- Beck, F.; Unverdorben, P.; Bohn, S.; Schweitzer, A.; Pfeifer, G.; Sakata, E.; Nickell, S.; Plitzko, J.M.; Villa, E.; Baumeister, W.; et al. Near-atomic resolution structural model of the yeast 26S proteasome. Proc. Natl. Acad. Sci. USA 2012, 109. [Google Scholar] [CrossRef]
- Hryc, C.F.; Chen, D.H.; Afonine, P.V.; Jakana, J.; Wang, Z.; Haase-Pettingell, C.; Jiang, W.; Adams, P.D.; King, J.A.; Schmid, M.F.; et al. Accurate model annotation of a near-atomic resolution cryo-EM map. Proc. Natl. Acad. Sci. USA 2017, 114. [Google Scholar] [CrossRef] [PubMed]
- Burley, S.K.; Berman, H.M.; Bhikadiya, C.; Bi, C.; Chen, L.; Costanzo, L.D.; Christie, C.; Duarte, J.M.; Dutta, S.; Feng, Z.; et al. Protein Data Bank: The single global archive for 3D macromolecular structure data. Nucleic Acids Res. 2019, 47. [Google Scholar] [CrossRef]
- Lawson, C.L.; Patwardhan, A.; Baker, M.L.; Hryc, C.; Garcia, E.S.; Hudson, B.P.; Lagerstedt, I.; Ludtke, S.J.; Pintilie, G.; Sala, R.; et al. EMDataBank unified data resource for 3DEM. Nucleic Acids Res. 2016, 44. [Google Scholar] [CrossRef] [PubMed]
- Baker, M.L.; Yu, Z.; Chiu, W.; Bajaj, C. Automated segmentation of molecular subunits in electron cryomicroscopy density maps. J. Struct. Biol. 2006, 156. [Google Scholar] [CrossRef] [PubMed]
- Terwilliger, T.C.; Adams, P.D.; Afonine, P.V.; Sobolev, O.V. A fully automatic method yielding initial models from high-resolution cryo-electron microscopy maps. Nat. Methods 2018, 15. [Google Scholar] [CrossRef]
- Volkmann, N. A novel three-dimensional variant of the watershed transform for segmentation of electron density maps. J. Struct. Biol. 2002, 138. [Google Scholar] [CrossRef]
- Patwardhan, A.; Brandt, R.; Butcher, S.J.; Collinson, L.; Gault, D.; Grünewald, K.; Hecksel, C.; Huiskonen, J.T.; Iudin, A.; Jones, M.L.; et al. Building bridges between cellular and molecular structural biology. eLife 2017, 6. [Google Scholar] [CrossRef]
- Pintilie, G.D.; Zhang, J.; Goddard, T.D.; Chiu, W.; Gossard, D.C. Quantitative analysis of cryo-EM density map segmentation by watershed and scale-space filtering, and fitting of structures by alignment to regions. J. Struct. Biol. 2010, 170. [Google Scholar] [CrossRef]
- Manuel, Z.C.; Luis, C.V.; José, S.B.; Julio, V.M.; Daisuke, K.; Juan, E.R. Matching of EM Map Segments to Structurally-Relevant Bio-molecular Regions; Springer: Berlin/Heidelberg, Germany, 2020; pp. 464–478. [Google Scholar]
- Vincent, L.; Soille, P. Watersheds in digital spaces: an efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13. [Google Scholar] [CrossRef]
- Derivaux, S.; Lefevre, S.; Wemmert, C.; Korczak, J. On Machine Learning in Watershed Segmentation. In Proceedings of the 2007 IEEE Workshop on Machine Learning for Signal Processing, Hessaloniki, Greece, 27–29 August 2007. [Google Scholar] [CrossRef]
- Maulik, U. Medical Image Segmentation Using Genetic Algorithms. IEEE Trans. Inf. Technol. Biomed. 2009, 13. [Google Scholar] [CrossRef] [PubMed]
- Javadpour, A.; Mohammadi, A. Improving brain magnetic resonance image (MRI) segmentation via a novel algorithm based on genetic and regional growth. J. Biomed. Phys. Eng. 2016, 6, 95. [Google Scholar]
- Arnab, A.; Torr, P.H.S. Pixelwise Instance Segmentation With a Dynamically Instantiated Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Meng, E.C.; Couch, G.S.; Croll, T.I.; Morris, J.H.; Ferrin, T.E. UCSF ChimeraX: Structure visualization for researchers, educators, and developers. Protein Sci. 2021, 30. [Google Scholar] [CrossRef] [PubMed]
- Esquivel-Rodríguez, J.; Yang, Y.D.; Kihara, D. Multi-LZerD: Multiple protein docking for asymmetric complexes. Proteins 2012, 7, 1818–1833. [Google Scholar] [CrossRef] [PubMed]
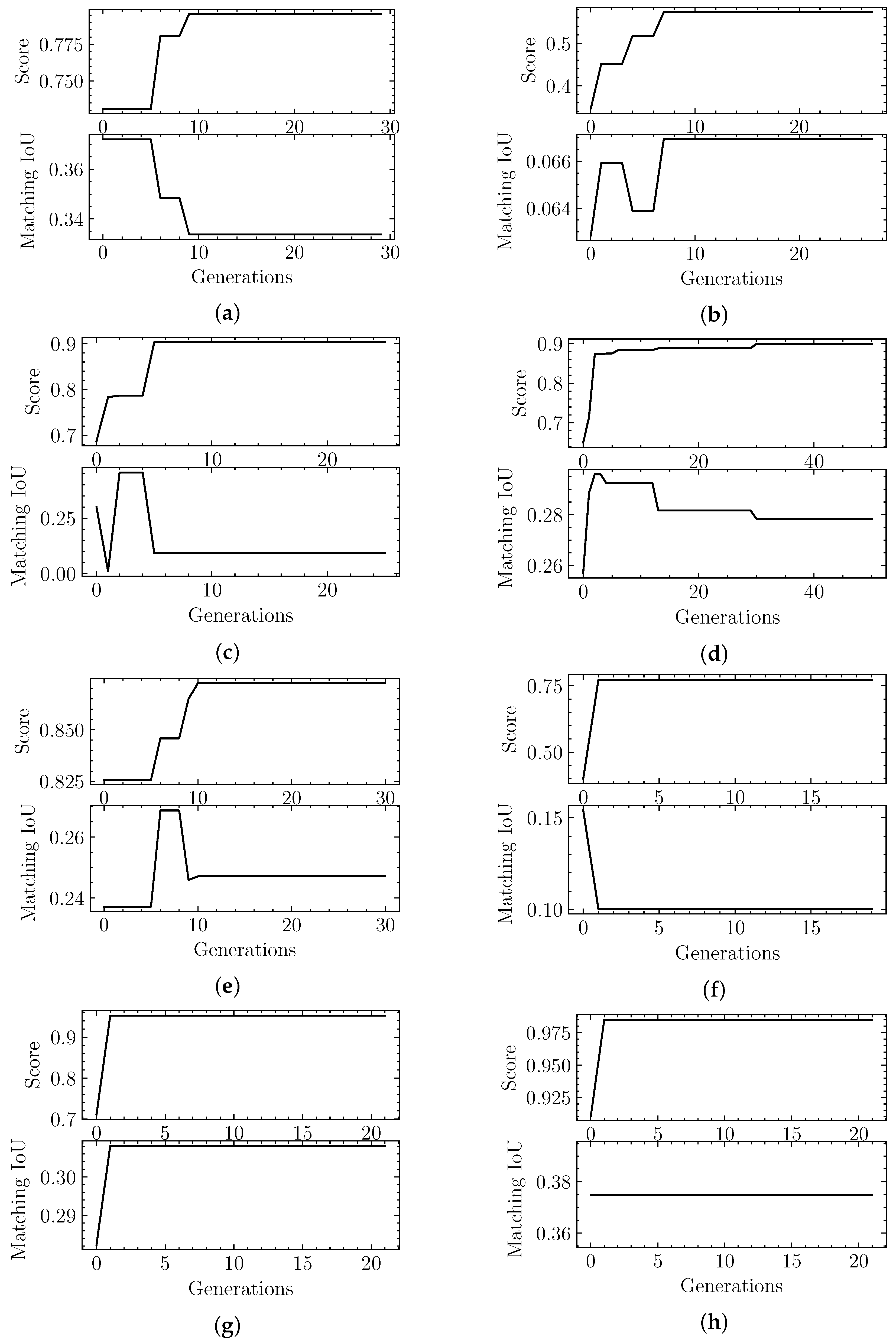
| Model | Area under ROC | Parameters |
|---|---|---|
| Logistic Regression | 0.77 | C: 10, dual: False, max_iter: 120, penalty: l2 |
| SVM | 0.79 | C: 0.1, gamma: 1, kernel: rbf |
| MLP | 0.78 | activation: relu, alpha: 0.0001,hidden_layer_sizes: 100, learning_rate: constant, solver: adam |
| Random Forests | 0.83 | max_features: auto, n_estimators: 1200 |
| Sample | Score | Matching IoU | Segger IoU | H | C | P |
|---|---|---|---|---|---|---|
| EMD-7090 | 0.98 | 0.07 | 0.00 | 0.08 | 9 | 8.00 |
| EMD-4670 | 0.57 | 0.08 | 0.06 | 0.25 | 1 | 3.35 |
| EMD-0044 | 0.90 | 0.09 | 0.05 | 0.20 | 1 | 4.33 |
| EMD-0790 | 0.87 | 0.11 | 0.00 | 0.14 | 5 | 5.00 |
| EMD-8528 | 0.77 | 0.10 | 0.07 | 0.28 | 2 | 2.60 |
| EMD-3206 | 0.95 | 0.15 | 0.02 | 0.35 | 4 | 2.50 |
| EMD-3573 | 0.90 | 0.19 | 0.14 | 0.52 | 1 | 1.67 |
| EMD-20824 | 0.98 | 0.23 | 0.00 | 0.40 | 3 | 3.00 |
| Sample | Matching IoU | Segger IoU |
|---|---|---|
| EMD-7090 | 0.33 | 0.32 |
| EMD-4670 | 0.07 | 0.07 |
| EMD-0044 | 0.28 | 0.32 |
| EMD-0790 | 0.25 | 0.13 |
| EMD-8528 | 0.10 | 0.10 |
| EMD-3206 | 0.31 | 0.26 |
| EMD-3573 | 0.09 | 0.44 |
| EMD-20824 | 0.37 | 0.08 |
| Sample | EvoSeg | Segger | Ground Truth |
|---|---|---|---|
| EMD-7090 | 9 | 32 | 2 |
| EMD-4670 | 44 | 293 | 54 |
| EMD-0044 | 9 | 18 | 3 |
| EMD-0790 | 9 | 91 | 4 |
| EMD-8528 | 5 | 25 | 5 |
| EMD-3206 | 4 | 31 | 2 |
| EMD-3573 | 3 | 19 | 6 |
| EMD-20824 | 3 | 81 | 2 |
| Sample | Result 1 IoU | Result 1 Max Score | Result 2 IoU | Result 2 Max Score |
|---|---|---|---|---|
| EMD-7090 | 0.33 | 0.98 | 0.53 | 0.94 |
| EMD-4670 | 0.07 | 0.57 | 0.08 | 0.55 |
| EMD-0044 | 0.28 | 0.90 | 0.33 | 0.94 |
| EMD-0790 | 0.25 | 0.87 | 0.29 | 0.96 |
| EMD-8528 | 0.10 | 0.77 | 0.17 | 0.62 |
| EMD-3206 | 0.31 | 0.95 | 0.38 | 0.98 |
| EMD-3573 | 0.09 | 0.90 | 0.45 | 0.85 |
| EMD-20824 | 0.37 | 0.98 | 0.37 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zumbado-Corrales, M.; Esquivel-Rodríguez, J. EvoSeg: Automated Electron Microscopy Segmentation through Random Forests and Evolutionary Optimization. Biomimetics 2021, 6, 37. https://doi.org/10.3390/biomimetics6020037
Zumbado-Corrales M, Esquivel-Rodríguez J. EvoSeg: Automated Electron Microscopy Segmentation through Random Forests and Evolutionary Optimization. Biomimetics. 2021; 6(2):37. https://doi.org/10.3390/biomimetics6020037
Chicago/Turabian StyleZumbado-Corrales, Manuel, and Juan Esquivel-Rodríguez. 2021. "EvoSeg: Automated Electron Microscopy Segmentation through Random Forests and Evolutionary Optimization" Biomimetics 6, no. 2: 37. https://doi.org/10.3390/biomimetics6020037
APA StyleZumbado-Corrales, M., & Esquivel-Rodríguez, J. (2021). EvoSeg: Automated Electron Microscopy Segmentation through Random Forests and Evolutionary Optimization. Biomimetics, 6(2), 37. https://doi.org/10.3390/biomimetics6020037






