Design and Analysis of a Variable Inertia Spatial Robotic Tail for Dynamic Stabilization
Abstract
1. Introduction
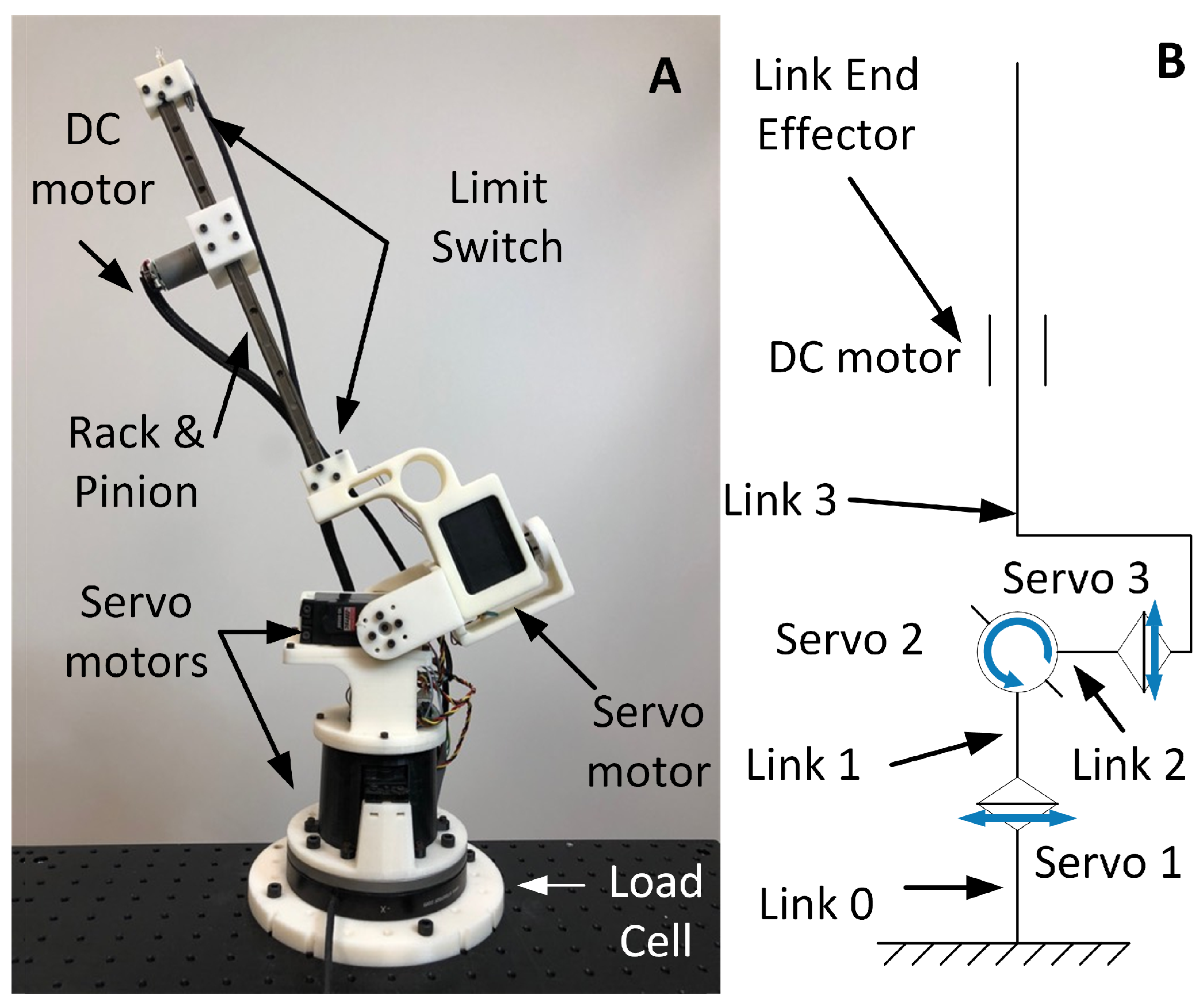
2. Mechanical and Mechatronic Design
2.1. Mechanical Design
2.2. Mechatronics Design
3. System Modeling
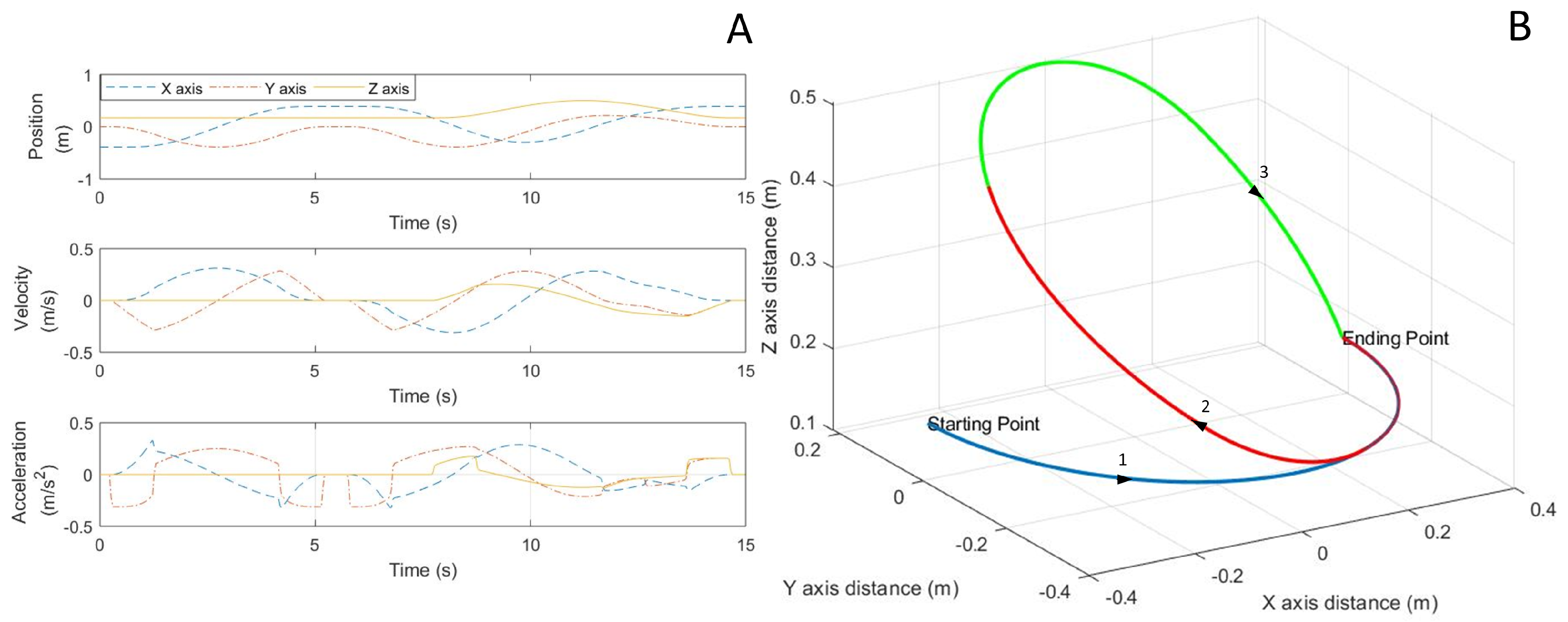
3.1. Kinematic Modeling
3.2. Dynamics Modeling
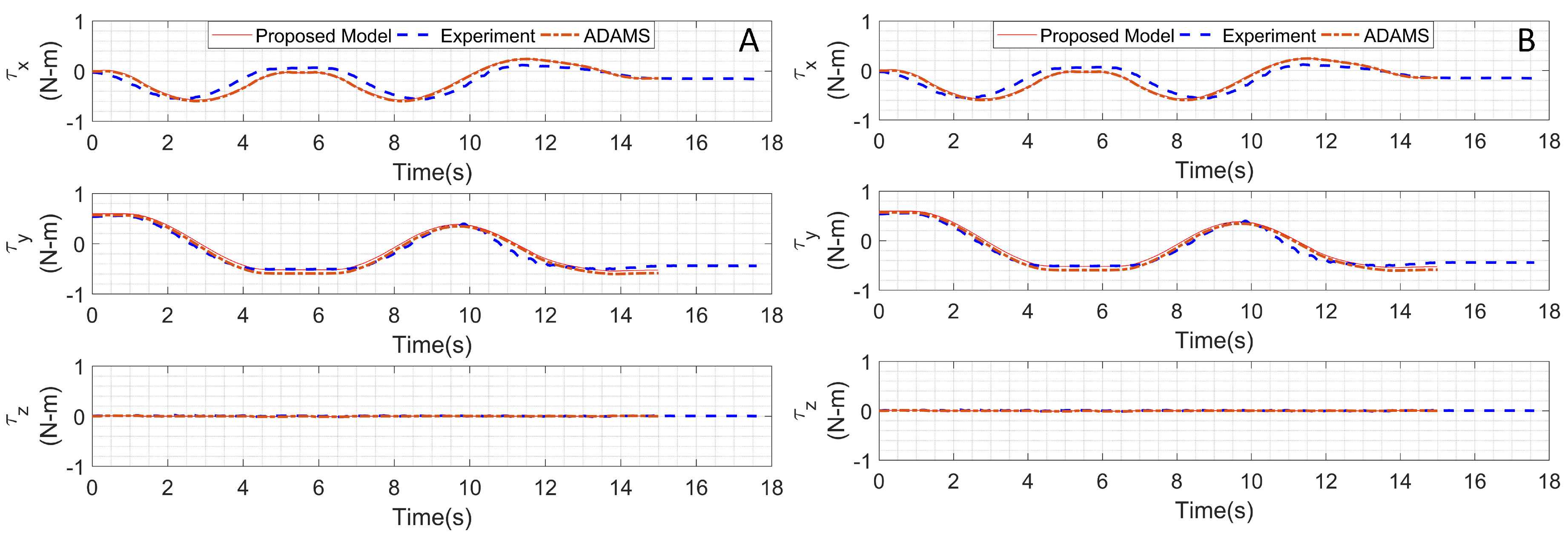
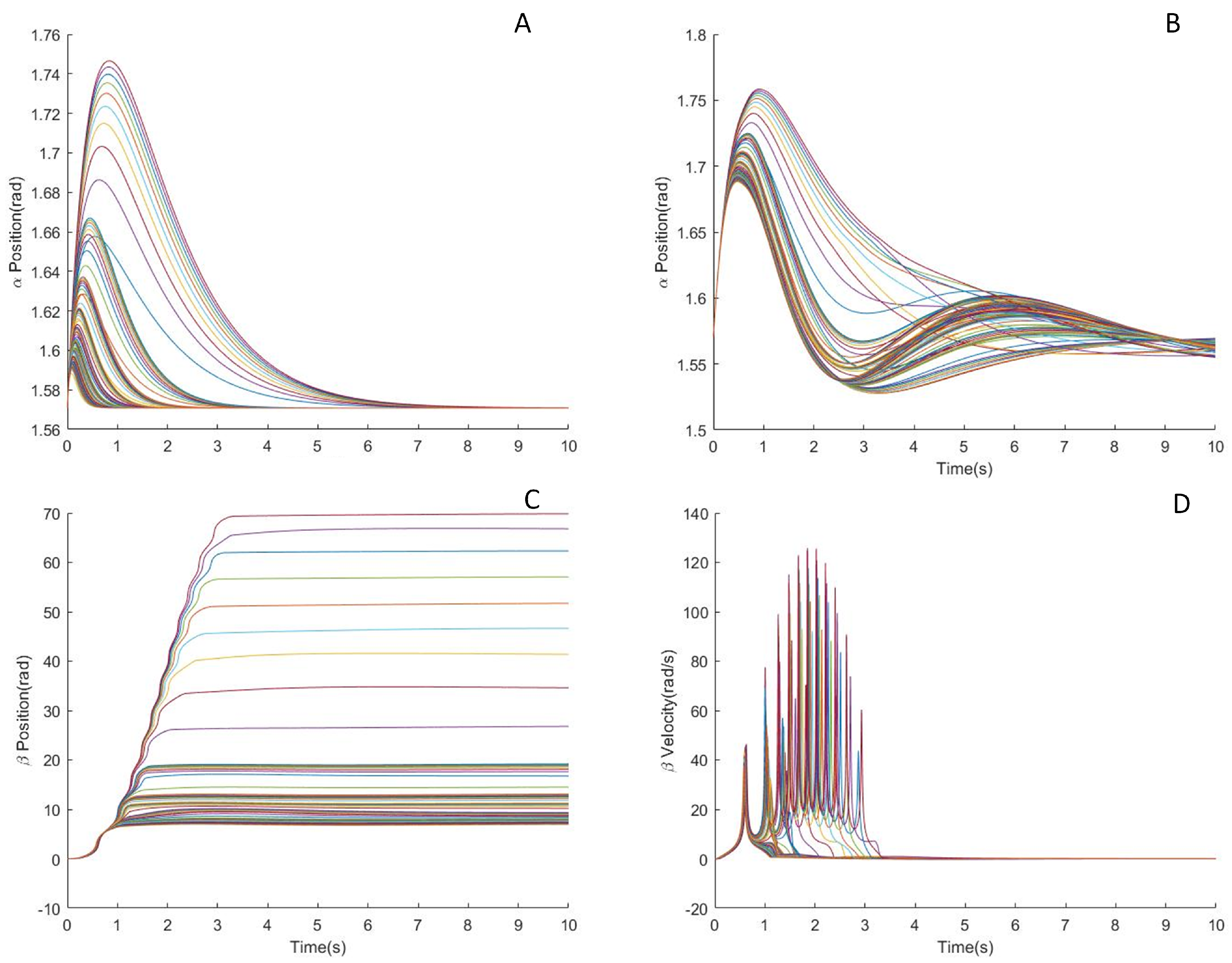
4. Validation of Dynamic Model and Simulation Results
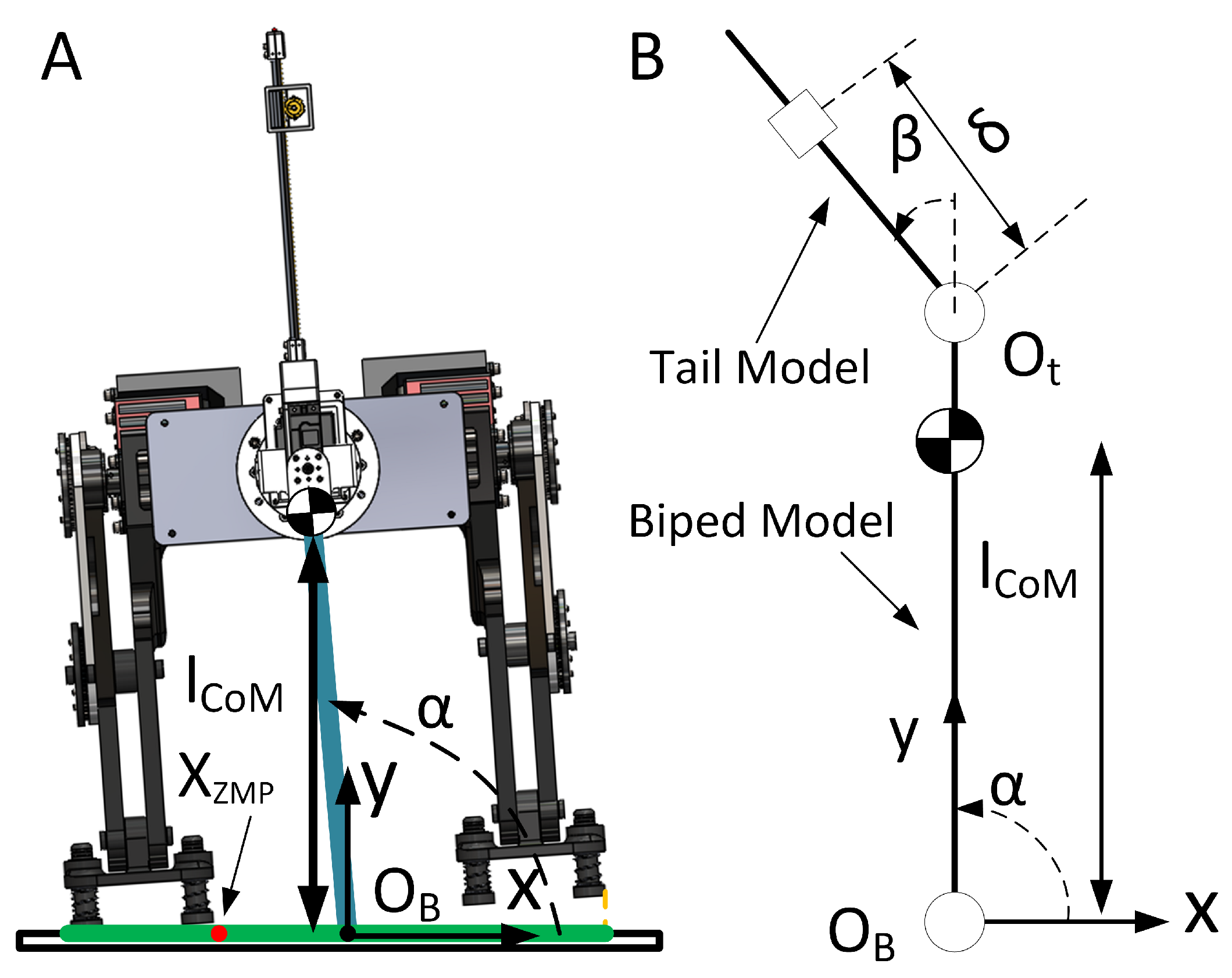
5. Robot Stabilization Using the Robotic Tail
5.1. Biped Robot-Tail System
5.2. Trajectory Planner
5.3. Virtual Torque Estimator
5.4. Model Based Controller
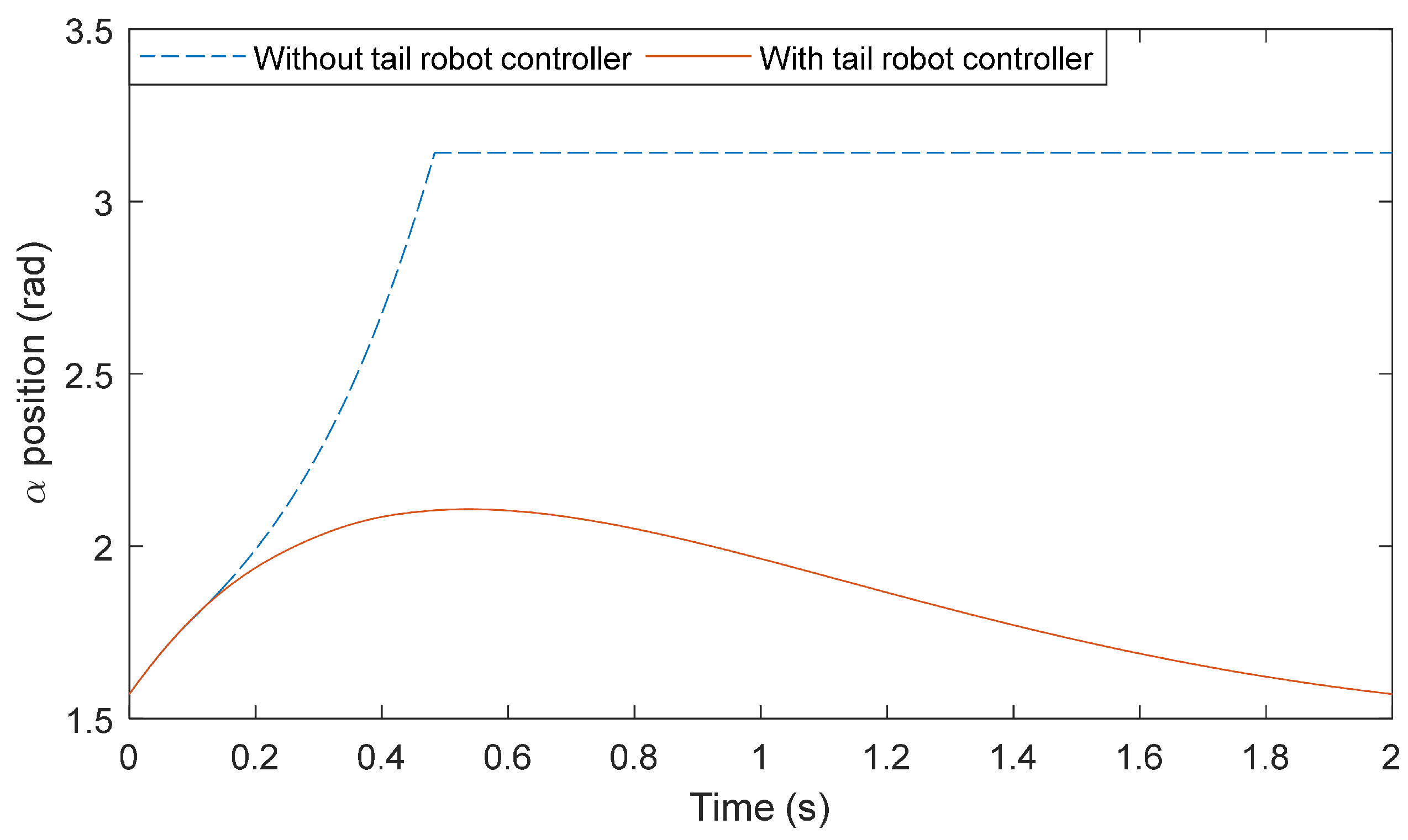
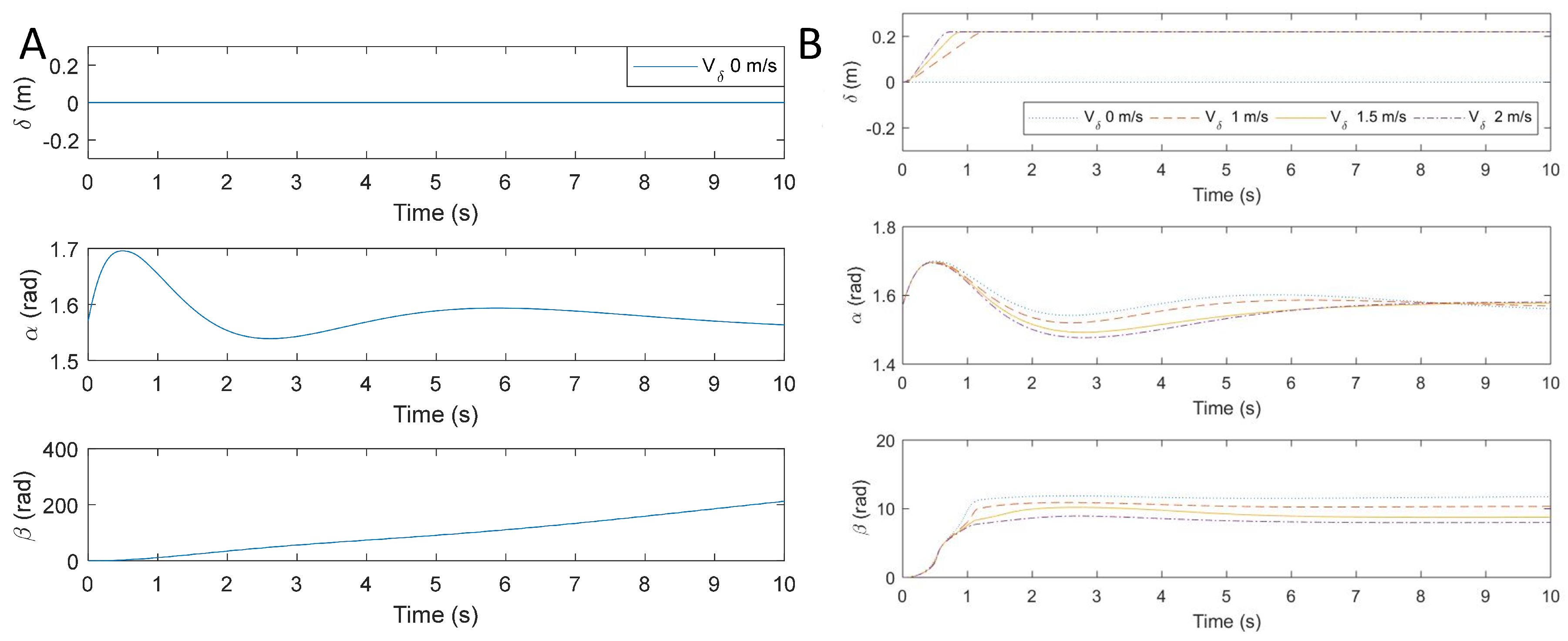
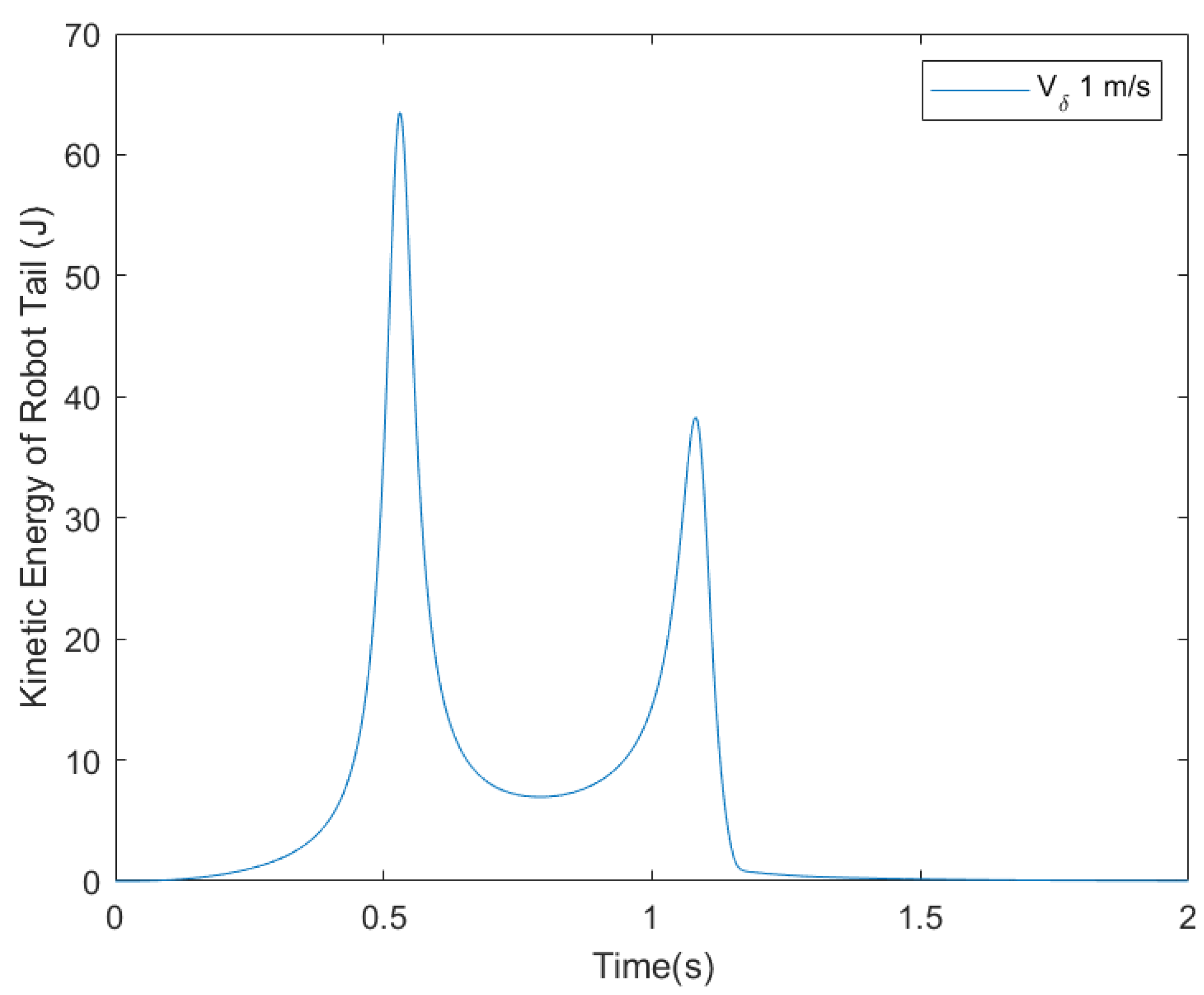
5.5. Controller Performance
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alexander, R.M.; Vernon, A. The mechanics of hopping by kangaroos (Macropodidae). J. Zool. 2009, 177, 265–303. [Google Scholar] [CrossRef]
- HICKMAN, G.C. The mammalian tail: A review of functions. Mammal Rev. 1979, 9, 143–157. [Google Scholar] [CrossRef]
- Yang, L.; Su, Y.; Xiao, Q. Numerical study of propulsion mechanism for oscillating rigid and flexible tuna-tails. J. Bionic Eng. 2011, 8, 406–417. [Google Scholar] [CrossRef]
- Jusufi, A.; Goldman, D.I.; Revzen, S.; Full, R.J. Active tails enhance arboreal acrobatics in geckos. Proc. Natl. Acad. Sci. USA 2008, 105, 4215–4219. [Google Scholar] [CrossRef] [PubMed]
- Libby, T.; Moore, T.Y.; Chang-Siu, E.; Li, D.; Cohen, D.J.; Jusufi, A.; Full, R.J. Tail-assisted pitch control in lizards, robots and dinosaurs. Nature 2012, 481, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Jusufi, A.; Kawano, D.T.; Libby, T.; Full, R.J. Righting and turning in mid-air using appendage inertia: Reptile tails, analytical models and bio-inspired robots. Bioinspir. Biomim. 2010, 5, 045001. [Google Scholar] [CrossRef] [PubMed]
- Bartholomew, G.A.; Caswell, H.H. Locomotion in Kangaroo Rats and Its Adaptive Significance. J. Mammal. 1951, 32, 155. [Google Scholar] [CrossRef]
- Liu, G.H.; Lin, H.Y.; Lin, H.Y.; Chen, S.T.; Lin, P.C. A Bio-Inspired Hopping Kangaroo Robot with an Active Tail. J. Bionic Eng. 2014, 11, 541–555. [Google Scholar] [CrossRef]
- Patel, A.; Braae, M. Rapid turning at high-speed: Inspirations from the cheetah’s tail. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 5506–5511. [Google Scholar] [CrossRef]
- Patel, A.; Boje, E. On the Conical Motion of a Two-Degree-of-Freedom Tail Inspired by the Cheetah. IEEE Trans. Robot. 2015, 31, 1555–1560. [Google Scholar] [CrossRef]
- Dharmawan, A.G.; Koh, D.C.Y.; Soh, G.S.; Foong, S.; Bouffanais, R.; Wood, K.L. Tail Design of A Miniature Two-Wheg Climbing Robot for External Transitioning. In Mechanisms and Machine Science; Springer: Dordrecht, The Netherlands, 2019; Volume 73, pp. 2139–2148. [Google Scholar] [CrossRef]
- Suarez, A.; Grau, P.; Heredia, G.; Ollero, A. Winged Aerial Manipulation Robot with Dual Arm and Tail. Appl. Sci. 2020, 10, 4783. [Google Scholar] [CrossRef]
- Rone, W.S.; Ben-Tzvi, P. Continuum Robotic Tail Loading Analysis for Mobile Robot Stabilization and Maneuvering. In Volume 5A: 38th Mechanisms and Robotics Conference; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 5A. [Google Scholar] [CrossRef]
- Saab, W.; Rone, W.S.; Ben-Tzvi, P. Discrete modular serpentine robotic tail: Design, analysis and experimentation. Robotica 2018, 36, 994–1018. [Google Scholar] [CrossRef]
- Rone, W.S.; Ben-Tzvi, P. Mechanics Modeling of Multisegment Rod-Driven Continuum Robots. J. Mech. Robot. 2014, 6. [Google Scholar] [CrossRef]
- Singh, A.; Libby, T.; Fuller, S.B. Rapid Inertial Reorientation of an Aerial Insect-sized Robot Using a Piezo-actuated Tail. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4154–4160. [Google Scholar] [CrossRef]
- Berenguer, F.; Monasterio-Huelin, F. Zappa, a Quasi-Passive Biped Walking Robot with a Tail: Modeling, Behavior, and Kinematic Estimation Using Accelerometers. IEEE Trans. Ind. Electron. 2008, 55, 3281–3289. [Google Scholar] [CrossRef]
- Briggs, R.; Lee, J.; Haberland, M.; Kim, S. Tails in biomimetic design: Analysis, simulation, and experiment. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1473–1480. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Ben-Tzvi, P. A Cable Length Invariant Robotic Tail Using a Circular Shape Universal Joint Mechanism. J. Mech. Robot. 2019, 11. [Google Scholar] [CrossRef]
- Transeth, A.A.; Pettersen, K.Y.; Liljebäck, P. A survey on snake robot modeling and locomotion. Robotica 2009, 27, 999–1015. [Google Scholar] [CrossRef]
- Jazar, R.N. Theory of Applied Robotics; Springer: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Saab, W.; Rone, W.S.; Ben-Tzvi, P. Robotic Modular Leg: Design, Analysis, and Experimentation. J. Mech. Robot. 2017, 9. [Google Scholar] [CrossRef]
- Fernandes, C.; Gurvits, L.; Li, Z. Attitude Control of a Space Platform/Manipulator System Using Internal Motion. Int. J. Robot. Res. 1994, 13, 289–304. [Google Scholar] [CrossRef]
- Chang-Siu, E.; Libby, T.; Tomizuka, M.; Full, R.J. A lizard-inspired active tail enables rapid maneuvers and dynamic stabilization in a terrestrial robot. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1887–1894. [Google Scholar] [CrossRef]
- Keo, L.; Yamakita, M. Controlling balancer and steering for bicycle stabilization. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 4541–4546. [Google Scholar] [CrossRef]
- Alcaraz-Jiménez, J.; Herrero-Pérez, D.; Martínez-Barberá, H. Robust feedback control of ZMP-based gait for the humanoid robot Nao. Int. J. Robot. Res. 2013, 32, 1074–1088. [Google Scholar] [CrossRef]
- Ugurlu, B. Bipedal Motion Planning Based on Composite Rigid Body Angular Momentum Resolution. Ph.D. Thesis, Yokohama National University, Yokohama, Japan, 2010. [Google Scholar]




| i | a | d | ||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 90 | 0 | |
| 2 | 0 | 90 | 0 | |
| 3 | 0 | 90 | 0 | |
| 4 | 0 | 0 | 0 |
| Parameter | Length (m) | Mass (kg) |
|---|---|---|
| Link0 | ||
| Link1 | ||
| Link2 | ||
| Link3 | ||
| Total Mass of Tail | − | |
| Mass of End Effector | − |
| Parameter | Unit |
|---|---|
| Height of Biped Robot | 0.482 (m) |
| 0.382 (m) | |
| Mass of Biped Robot | 15.88 (Kg) |
| Mass of End Effector | 0.83 (Kg) |
| Total Mass of Biped Robot –Tail system | 18.3 (Kg) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Ren, H.; Kumar, A.; Ben-Tzvi, P. Design and Analysis of a Variable Inertia Spatial Robotic Tail for Dynamic Stabilization. Biomimetics 2020, 5, 55. https://doi.org/10.3390/biomimetics5040055
Wang X, Ren H, Kumar A, Ben-Tzvi P. Design and Analysis of a Variable Inertia Spatial Robotic Tail for Dynamic Stabilization. Biomimetics. 2020; 5(4):55. https://doi.org/10.3390/biomimetics5040055
Chicago/Turabian StyleWang, Xinran, Hailin Ren, Anil Kumar, and Pinhas Ben-Tzvi. 2020. "Design and Analysis of a Variable Inertia Spatial Robotic Tail for Dynamic Stabilization" Biomimetics 5, no. 4: 55. https://doi.org/10.3390/biomimetics5040055
APA StyleWang, X., Ren, H., Kumar, A., & Ben-Tzvi, P. (2020). Design and Analysis of a Variable Inertia Spatial Robotic Tail for Dynamic Stabilization. Biomimetics, 5(4), 55. https://doi.org/10.3390/biomimetics5040055







