IAROA: An Enhanced Attraction–Repulsion Optimisation Algorithm Fusing Multiple Strategies for Mechanical Optimisation Design
Abstract
1. Introduction
- (1)
- Based on the defects in the primordial AROA algorithm, an improved attraction–rejection optimisation algorithm called IAROA is raised by importing the EDO strategy, DLH strategy, the PAS strategy, and the CDICP strategy.
- (2)
- Some of the typical, recently raised, highly cited, CEC ranking, and refined classical intelligent algorithms are elected as the contrasting algorithms. The experiments are carried out in the 30D, 50D, and 100D CEC2017 test environments, respectively. The outcomes demonstrate that the IAROA algorithm exhibits remarkable superiority in most of the functions in the CEC2017 test set.
- (3)
- IAROA is applied in six engineering design issues of varying complexity, including Alkylation Unit, Industrial refrigeration System, Speed Reducer, Robot gripper problem, and Himmelblau’s Function, and 12 highly cited optimisation algorithms were also picked for contrast.
2. Theory
2.1. Overview of the Attraction–Repulsion Algorithm
2.1.1. Initialisation
2.1.2. Attraction and Repulsion
2.1.3. Attracted by the Optimal Solution
2.1.4. Local Search Operator
2.1.5. Population-Based Operations
2.2. Improved Attraction–Repulsion Algorithm
- (1)
- EDO strategy to enable a more uniform spread of the primary population and to acquire a high-quality starting population.
- (2)
- DLH strategy which scales up the trade-off among local exploitation and global search, while retaining the multiplicity of solutions.
- (3)
- CDICP strategy, which increases the reliability of the algorithm search and the variety of candidate solutions, thus effectively preventing the algorithm from converging to the local optimum prematurely.
- (4)
- PAS strategy to raise the overall running efficiency of the algorithm, both to expedite the convergence procedure and to ensure that the ultimately optimal solution is gained with a higher degree of precision.
2.2.1. Elite Dynamic Opposite Learning Strategy (EDO)
2.2.2. Dimension Learning-Based Hunting Search Strategy
2.2.3. Cauchy Distribution Inverse Cumulative Perturbation Strategy
2.2.4. Pheromone Adjustment Strategy (PAS)
2.2.5. Steps of the Improved Attraction–Repulsion Optimisation Algorithm
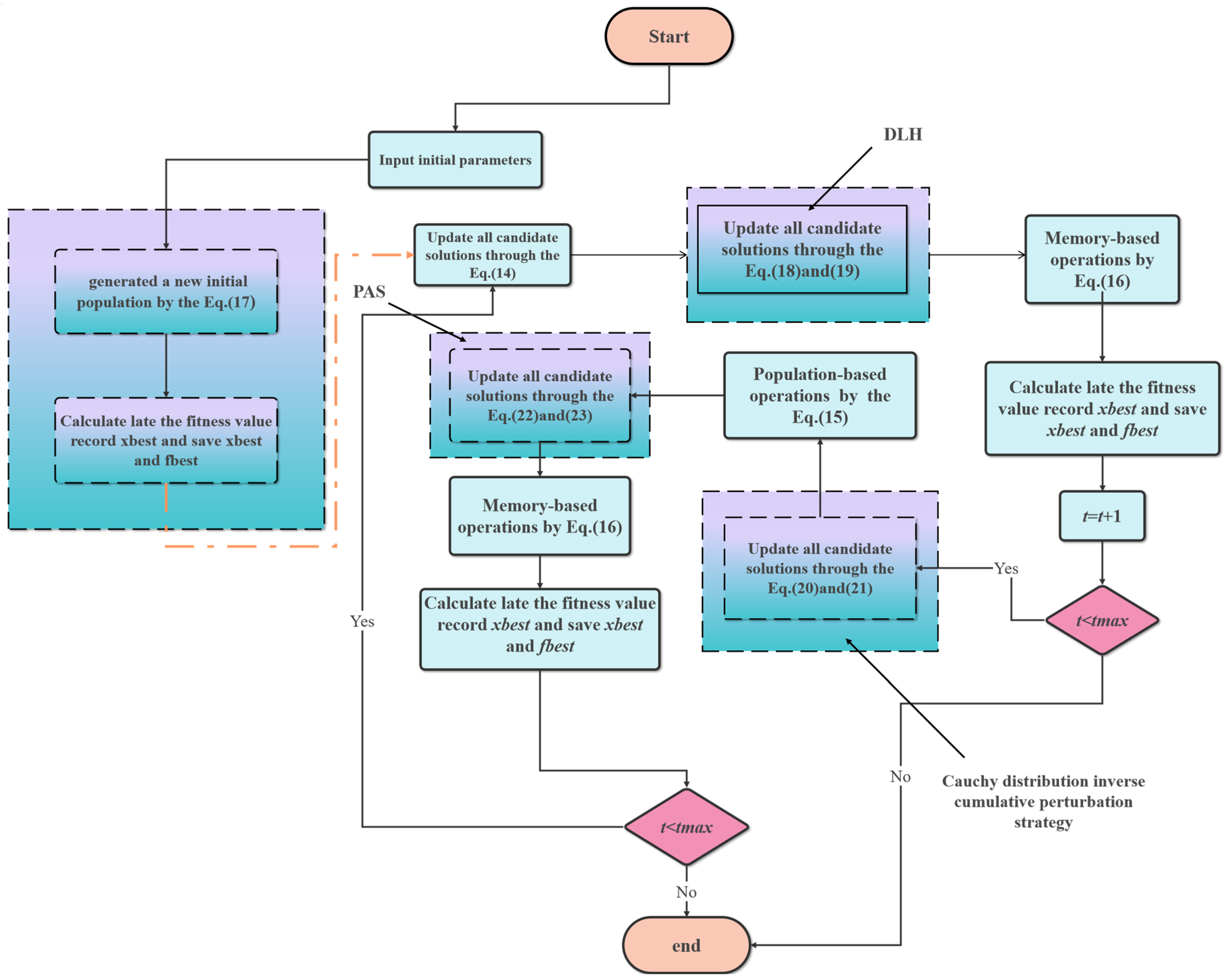
| Algorithm 1: IAROA algorithm |
 |
2.3. Time Complexity of the IAROA Algorithm
2.4. Test Functions and Comparison Algorithms
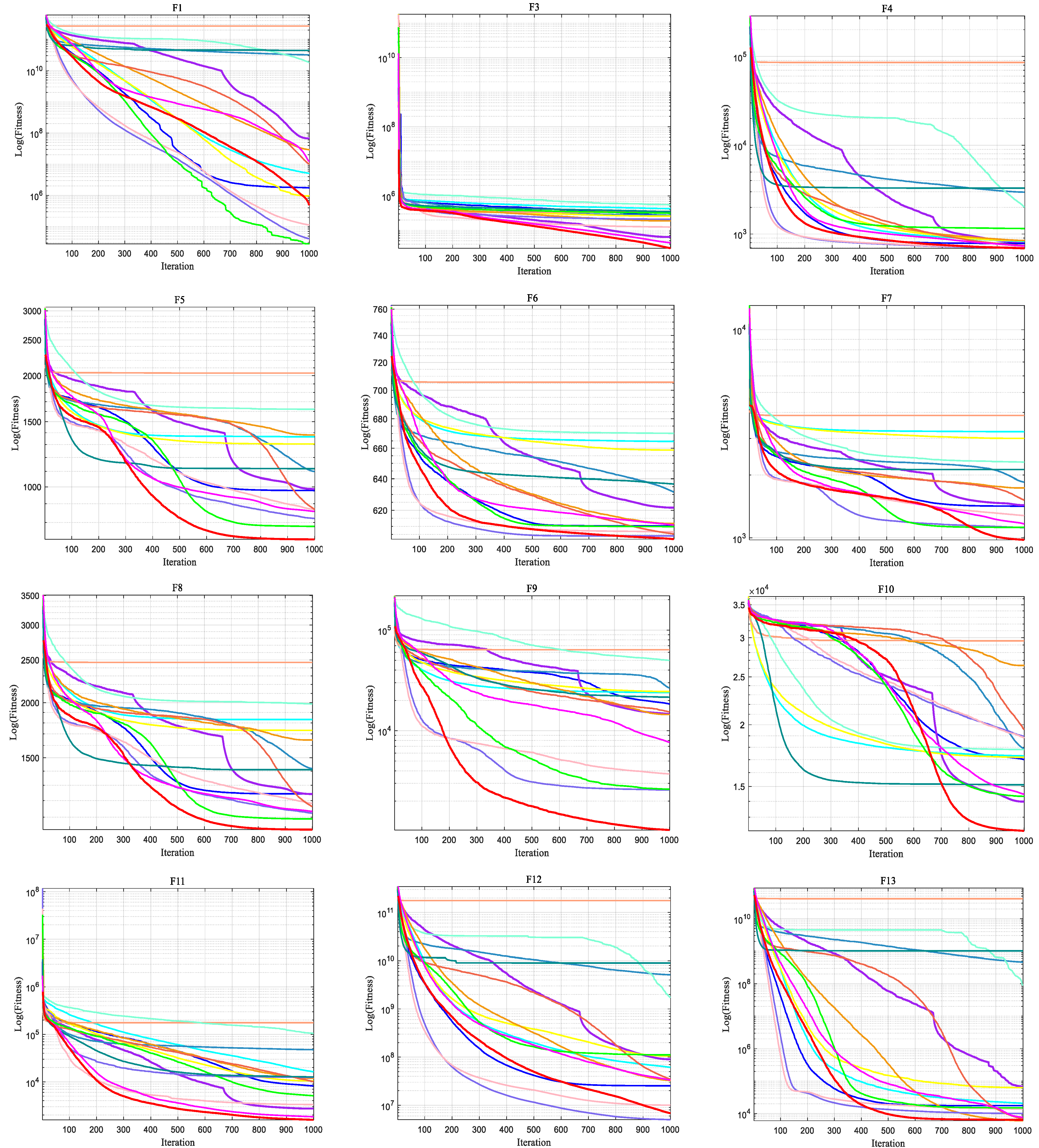
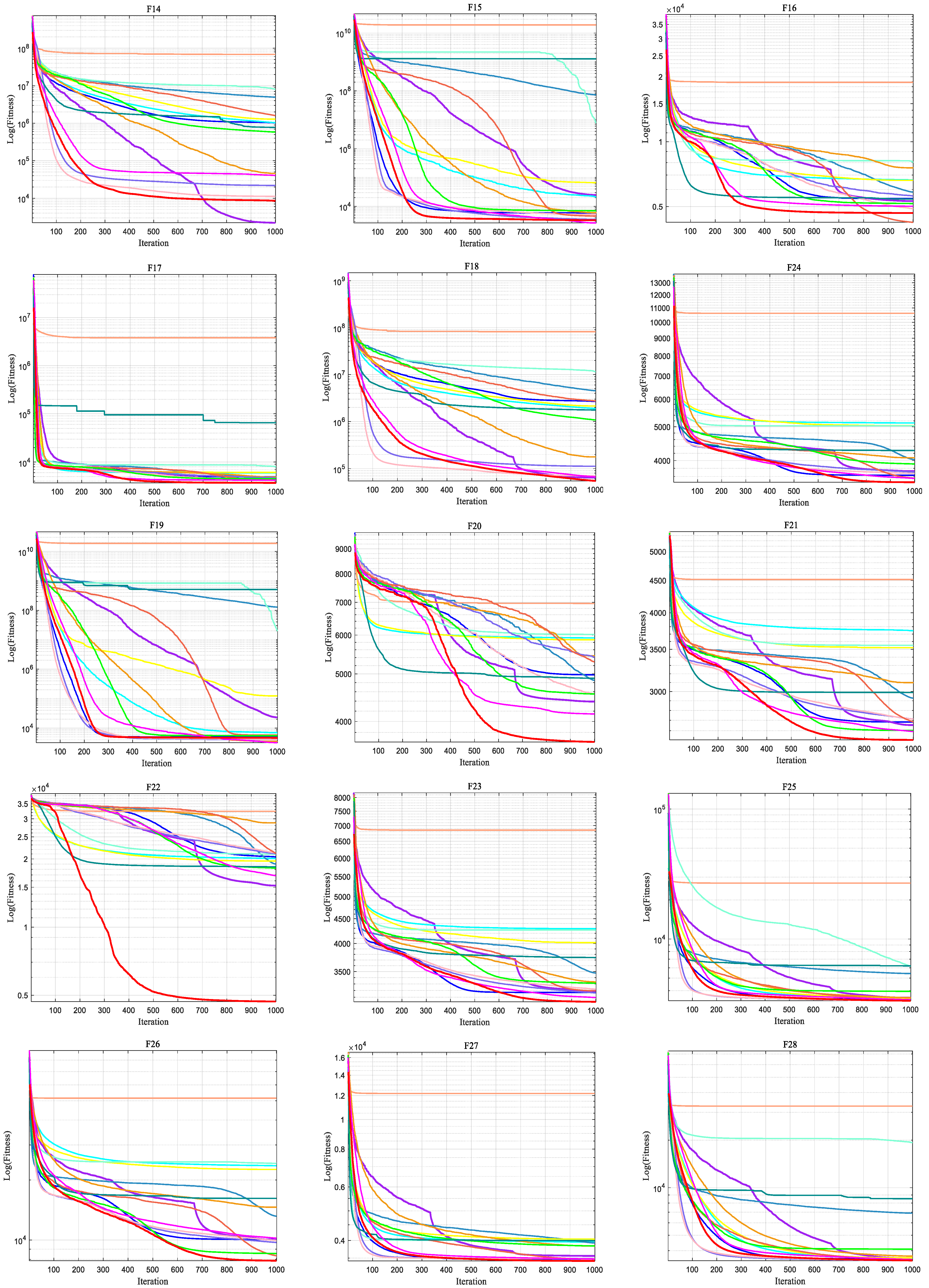
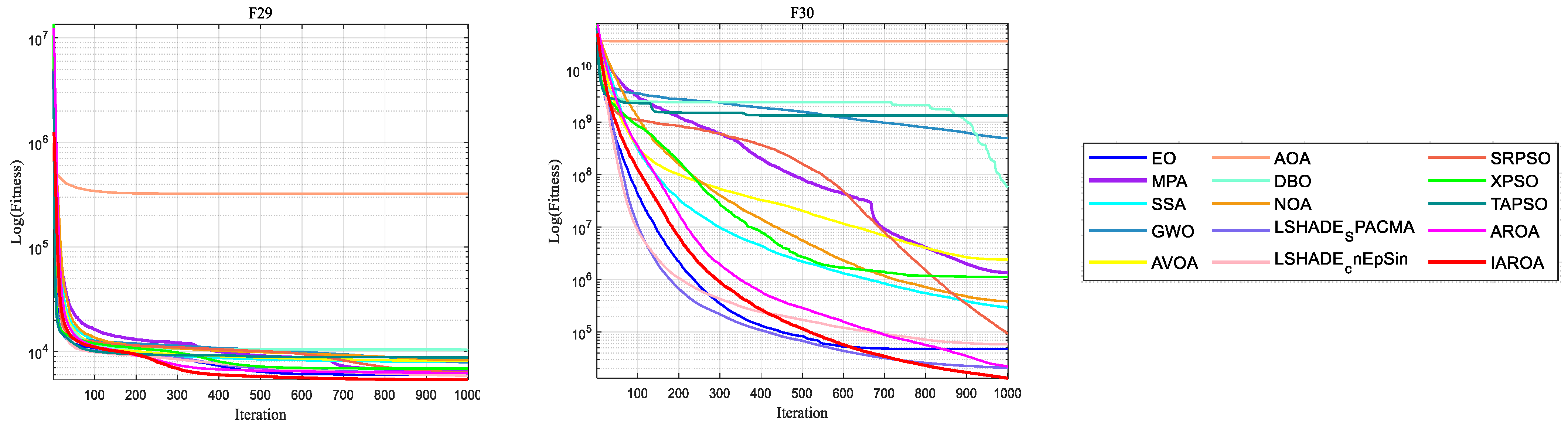
2.5. Analysis of Optimisation Results Under the CEC2017 Test Set
- (1)
- Single-peak shift-rotation functions (F1 and F3) have a global unique optimal solution and are ideal tools for inspecting algorithm development capabilities.
- (2)
- Multi-peak shift-rotation functions (F4–F10) have multiple local optimum solutions and are suitable for testing the discovery ability of the algorithms.
- (3)
- Hybrid functions (F11–F20) enable a comprehensive assessment of the algorithm’s ability to trade off between development and discovery due to their complex mathematical spatial properties.
- (4)
- Composite functions (F21–F30) incorporate the hybrid function as a basic function.
2.5.1. Optimisation Accuracy Analysis
2.5.2. Convergence Analysis
2.5.3. Box Plot Analysis
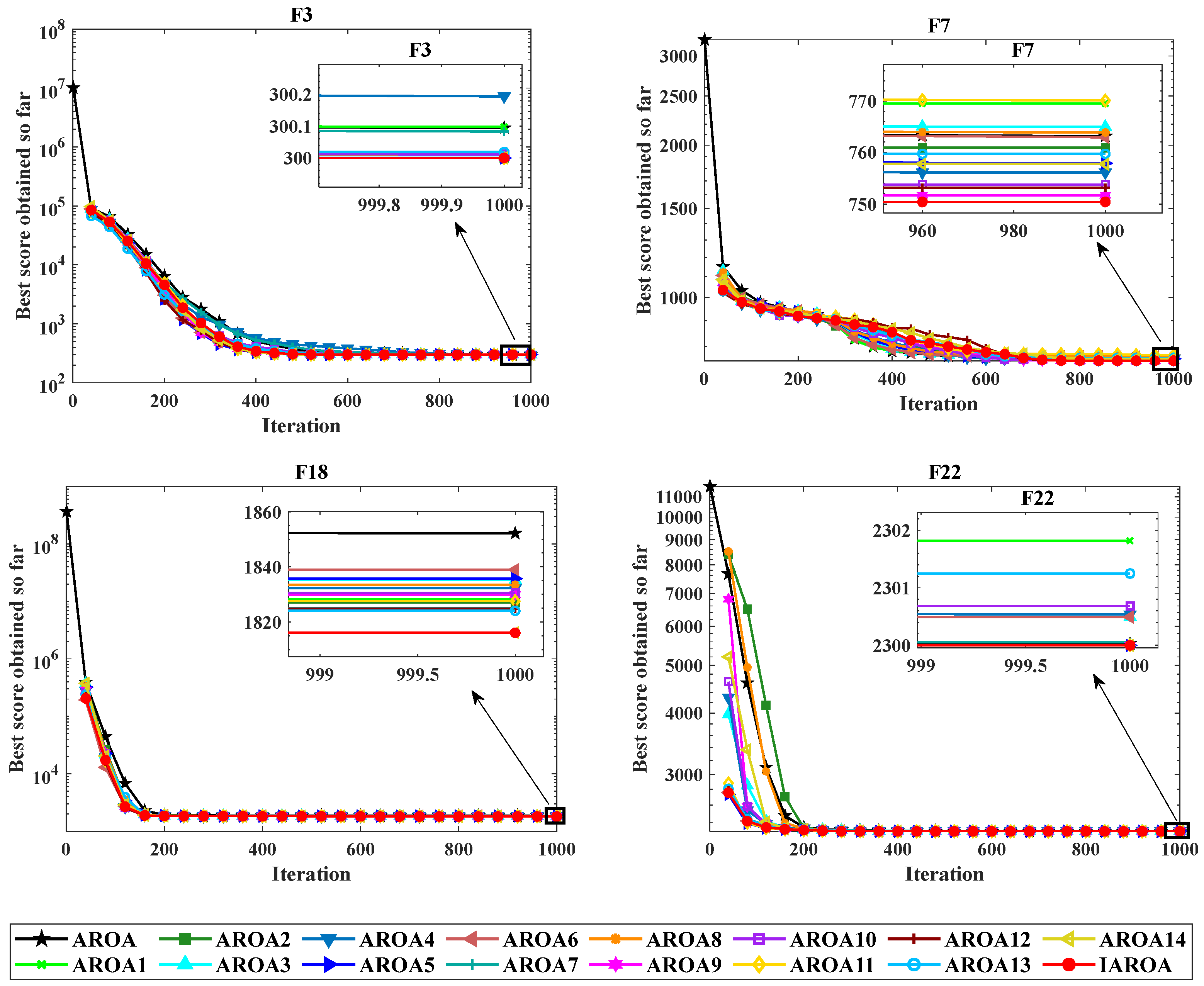
2.6. Ablation Experiment
3. Practice
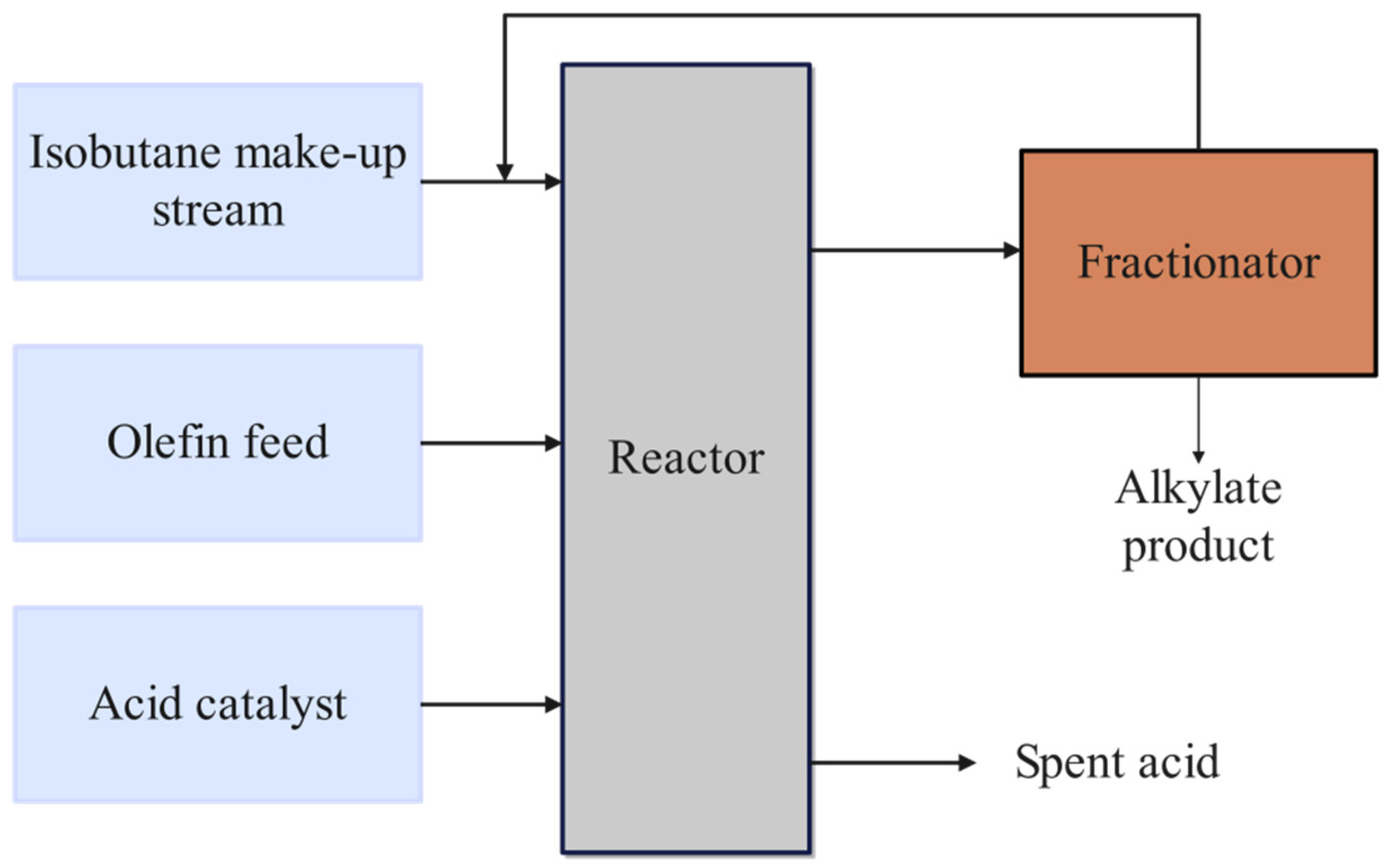
3.1. Industrial Chemical Processes
Alkylation Unit
3.2. Mechanical Engineering Issues
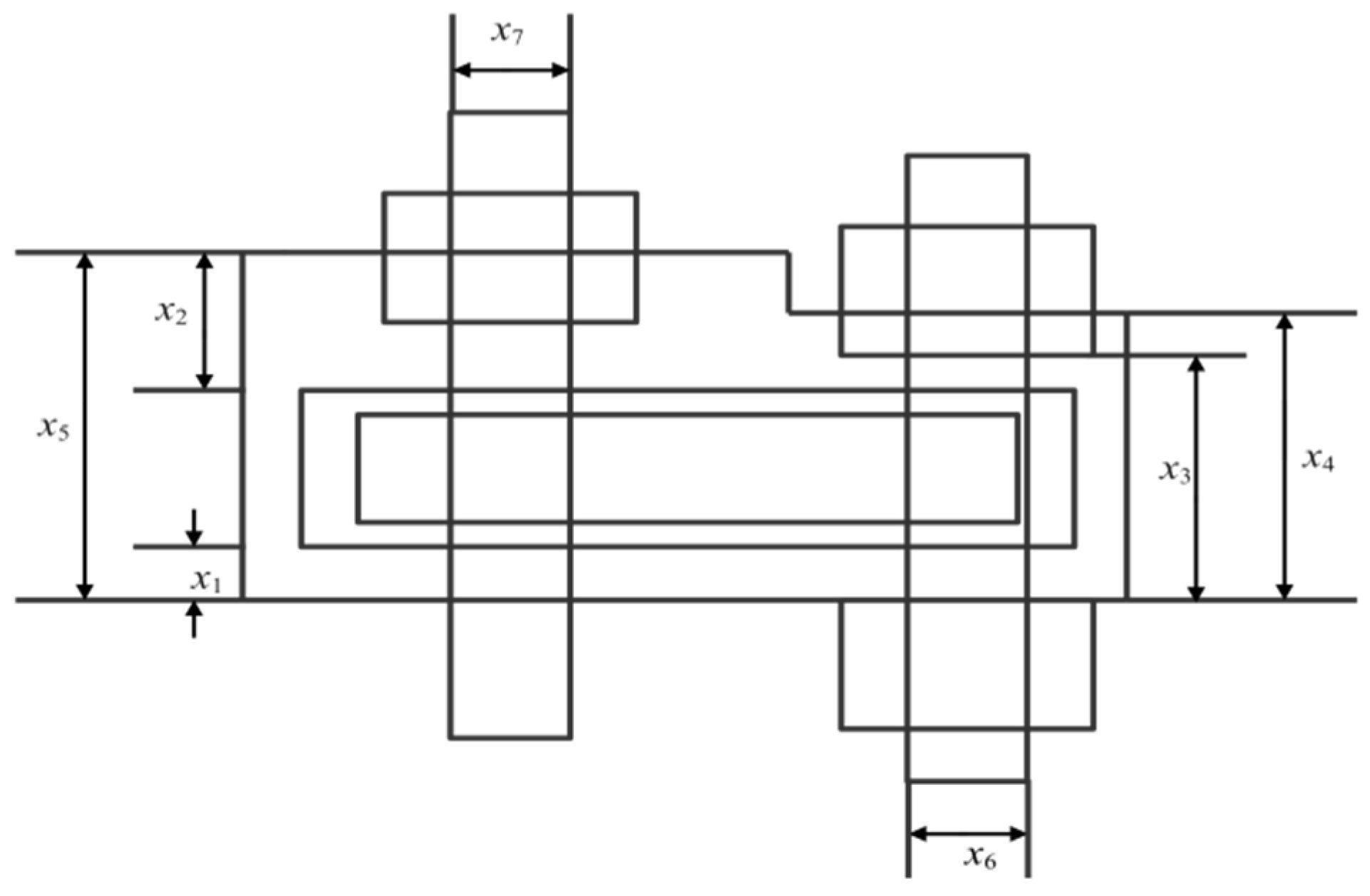
3.2.1. Speed Reducer

3.2.2. Industrial Refrigeration System
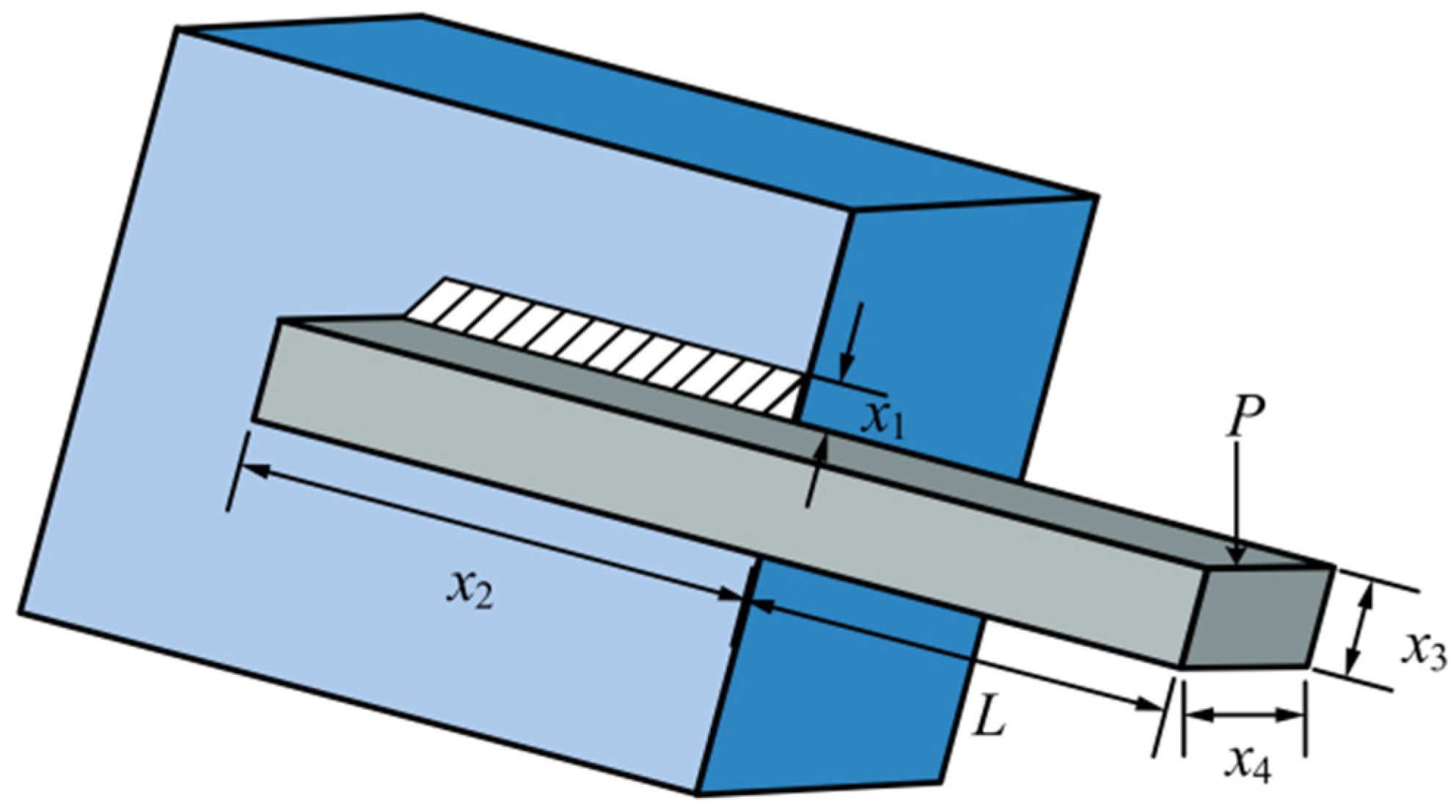
3.2.3. Welded Beam Design
3.2.4. Robot Gripper Problem

3.2.5. Himmelblau Function
4. Conclusions and Expectations
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Corriveau, G.; Guilbault, R.; Tahan, A.; Sabourin, R. Bayesian network as an adaptive parameter setting approach for genetic algorithms. Complex Intell. Syst. 2016, 2, 1–22. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Chun, J.S.; Jung, H.K.; Hahn, S.Y. A study on comparison of optimization performances between immune algorithm and other heuristic algorithms. IEEE Trans. Magn. 1998, 34, 2972–2975. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.M.; Chakrabortty, R.K. Light spectrum optimizer: A novel physics-inspired metaheuristic optimization algorithm. Mathematics 2022, 10, 3466. [Google Scholar] [CrossRef]
- Sayed, G.I.; Darwish, A.; Hassanien, A.E. Quantum multiverse optimization algorithm for optimization problems. Neural Comput. Appl. 2019, 31, 2763–2780. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Khodadadi, N.; Mirjalili, S. Mountain gazelle optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Adv. Eng. Softw. 2022, 174, 103282. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Proceedings of the International Symposium on Stochastic Algorithms, Sapporo, Japan, 26–28 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Hu, G.; Cheng, M.; Houssein, E.H.; Hussien, A.G.; Abualigah, L. SDO: A novel sled dog-inspired optimizer for solving engineering problems. Adv. Eng. Inform. 2024, 62, 102783. [Google Scholar] [CrossRef]
- Trojovský, P. A new human-based metaheuristic algorithm for solving optimization problems based on preschool education. Sci. Rep. 2023, 13, 21472. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Truong, D.N.; Chou, J.S. Metaheuristic algorithm inspired by enterprise development for global optimization and structural engineering problems with frequency constraints. Eng. Struct. 2024, 318, 118679. [Google Scholar] [CrossRef]
- Tian, Z.; Gai, M. Football team training algorithm: A novel sport-inspired meta-heuristic optimization algorithm for global optimization. Expert Syst. Appl. 2024, 245, 123088. [Google Scholar] [CrossRef]
- Cymerys, K.; Oszust, M. Attraction-repulsion optimization algorithm for global optimization problems. Swarm Evol. Comput. 2024, 84, 101459. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization; Technical Report; Nanyang Technological University Singapore: Singapore, 2016; pp. 1–34. [Google Scholar]
- Xu, Y.; Yang, Z.; Li, X.; Kang, H.; Yang, X. Dynamic opposite learning enhanced teaching-learning-based optimization. Knowl.-Based Syst. 2020, 188, 104966. [Google Scholar] [CrossRef]
- Li, Y.; Peng, T.; Hua, L.; Ji, C.; Ma, H.; Nazir, M.S.; Zhang, C. Research and application of an evolutionary deep learning model based on improved grey wolf optimization algorithm and DBN-ELM for AQI prediction. Sustain. Cities Soc. 2022, 87, 104209. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.S.; Li, X.D.; Zhang, M.; Hao, W.K. Harris hawk optimization algorithm based on Cauchy distribution inverse cumulative function and tangent flight operator. Appl. Intell. 2022, 52, 10999–11026. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia-San Sebastián, Spain, 5–8 June 2017; IEEE: New York, NY, USA, 2017; pp. 372–379. [Google Scholar]
- Mohamed, A.W.; Hadi, A.A.; Fattouh, A.M.; Jambi, K.M. LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia-San Sebastián, Spain, 5–8 June 2017; IEEE: New York, NY, USA, 2017; pp. 145–152. [Google Scholar]
- He, Z.; Liu, T.; Liu, H. Improved particle swarm optimization algorithms for aerodynamic shape optimization of high-speed train. Adv. Eng. Softw. 2022, 173, 103242. [Google Scholar] [CrossRef]
- Tanweer, M.R.; Suresh, S.; Sundararajan, N. Improved SRPSO algorithm for solving CEC 2015 computationally expensive numerical optimization problems. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; IEEE: New York, NY, USA, 2015; pp. 1943–1949. [Google Scholar]
- Xia, X.; Gui, L.; He, G.; Wei, B.; Zhang, Y.; Yu, F.; Wu, H.; Zhan, Z.-H. An expanded particle swarm optimization based on multi-exemplar and forgetting ability. Inf. Sci. 2020, 508, 105–120. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; Yu, F.; Wu, H.; Wei, B.; Zhang, Y.L.; Zhan, Z.H. Triple archives particle swarm optimization. IEEE Trans. Cybern. 2019, 50, 4862–4875. [Google Scholar] [CrossRef] [PubMed]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Supraba, A.; Musfirah, M.; Sjachrun, R.A.M.; Wahyono, E. The Students’ Response Toward Indirect Corrective Feedback Used By The Lecturer In Teaching Writing At Cokroaminoto Palopo University. DEIKTIS J. Pendidik. Bhs. Dan Sastra 2021, 1, 148–158. [Google Scholar] [CrossRef]
- Han, Z.; Han, C.; Lin, S.; Dong, X.; Shi, H. Flexible flow shop scheduling method with public buffer. Processes 2019, 7, 681. [Google Scholar] [CrossRef]
- Hu, G.; He, P.; Jia, H.; Houssein, E.H.; Abualigah, L. PDPSO: Priority-driven search particle swarm optimization with dynamic candidate solutions management strategy for solving higher-dimensional complex engineering problems. Comput. Methods Appl. Mech. Eng. 2025, 446, 118318. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern goshawk optimization: A new swarm-based algorithm for solving optimization problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Andrei, N. Nonlinear Optimization Applications Using the GAMS Technology; Springer: New York, NY, USA, 2013. [Google Scholar]
- Pant, M.; Thangaraj, R.; Singh, V.P. Optimization of mechanical design problems using improved differential evolution algorithm. Int. J. Recent Trends Eng. 2009, 1, 21. [Google Scholar]
- Hu, G.; Gong, C.; Li, X.; Xu, Z. CGKOA: An enhanced Kepler optimization algorithm for multi-domain optimization problems. Comput. Methods Appl. Mech. Eng. 2024, 425, 116964. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y. Enhancing the performance of differential evolution with covariance matrix self-adaptation. Appl. Soft Comput. 2018, 64, 227–243. [Google Scholar] [CrossRef]
- Wang, K.; Guo, M.; Dai, C.; Li, Z. Information-decision searching algorithm: Theory and applications for solving engineering optimization problems. Inf. Sci. 2022, 607, 1465–1531. [Google Scholar] [CrossRef]
- Himmelblau, D.M. Applied Nonlinear Programming; McGraw-Hill: Columbus, OH, USA, 2018. [Google Scholar]
- Hu, G.; Song, K.; Abdel-salam, M. Sub-population evolutionary particle swarm optimization with dynamic fitness-distance balance and elite reverse learning for engineering design problems. Adv. Eng. Softw. 2025, 202, 103866. [Google Scholar] [CrossRef]




| Arithmetic | Parameterisation |
|---|---|
| AROA | c = 0.95, fr1 = 0.15, fr2 = 0.15, p1 = 0.6, p2 = 0.8, ef = 0.4, tr1 = 0.9, tr2 = 0.85, tr3 = 0.9 |
| IAROA | c = 0.98, fr1 = 0.15, fr2 = 0.15, p1 = 0.6, p2 = 0.8, ef = 0.2, tr1 = 0.9, tr2 = 0.85, tr3 = 0.9 |
| MPA | FADs = 0.2, P = 0.5 |
| EO | a1 = 2, a2 = 1, GP = 0.5 |
| SSA | P_percent = 0.2 |
| AVOA | p1= 0.6, p2 = 0.4, p3 = 0.6, alpha = 0.8, betha = 0.2, gamma = 2.5 |
| AOA | MOA_max = 1, MOA_min = 0.2, µ = 0.5, a = 5 |
| NOA | Alpha = 0.05, Pa2 = 0.2, Prb = 0.2 |
| DBO | P_percent = 0.2, |
| LSHADE_SPACMA | L_Rate = 0.8, num_prbs = 30 |
| LSHADE_cnEpSin | µF = 0.5, µCR = 0.5, H = 5, pb = 0.4, ps = 0.5 |
| SRPSO | ϖmin = 0.5, ϖmax = 1.05, c1 = 1.49445, c2 = 1.49445 |
| XPSO | elite_ratio = 0.5 |
| TAPSO | tatio = 0.5 |
| Arithmetic | Best | Mean | Worst | Std |
|---|---|---|---|---|
| IAROA | −4529.119739 | −4529.118781 | −4529.104906 | 0.002852721 |
| AROA | −4529.119724 | −4333.335038 | 321.1617524 | 891.8735161 |
| EO | −4528.336676 | 1.85265E+12 | 5.55795E+13 | 1.01474E+13 |
| MPA | −4529.119356 | −4528.975121 | −4526.301432 | 0.532510698 |
| SSA | −4520.736764 | 1.75014E+17 | 5.24861E+18 | 9.5825E+17 |
| GWO | −4507.618354 | 1.22554E+18 | 1.41438E+19 | 3.43021E+18 |
| AVOA | −4339.874892 | 1.71088E+17 | 5.1306E+18 | 9.36702E+17 |
| AOA | 5.25688E+17 | 9.81415E+20 | 8.48024E+21 | 1.90575E+21 |
| DBO | −4526.325004 | 9.45899E+18 | 2.47028E+20 | 4.49258E+19 |
| NOA | −4491.895714 | −4238.302978 | −2996.590641 | 357.074788 |
| SRPSO | 242.7751343 | 7.29395E+15 | 5.65979E+16 | 1.58177E+16 |
| XPSO | 307.5008681 | 1.72755E+15 | 1.22294E+16 | 3.29314E+15 |
| TAPSO | 95.76530005 | 5.64566E+19 | 1.63764E+21 | 2.98727E+20 |
| Arithmetic | Norm | Best | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | ||
| IAROA | 2000.0000 | 0.0000 | 2576.4003 | 0.0000 | 58.1607 | 1.2600 | 41.2298 | −4529.1197 |
| AROA | 2000.0000 | 0.0000 | 2576.2814 | 0.0000 | 58.1602 | 1.2595 | 41.0656 | −4529.1197 |
| EO | 2000.0000 | 0.0000 | 2520.7881 | 0.0000 | 57.9240 | 1.0236 | 41.0957 | −4528.3367 |
| MPA | 2000.0000 | 0.0000 | 2576.6928 | 0.0000 | 58.1620 | 1.2613 | 41.6599 | −4529.1194 |
| SSA | 2000.0000 | 0.0000 | 2393.8182 | 0.0000 | 57.3913 | 0.5062 | 39.3992 | −4520.7368 |
| GWO | 2000.0000 | 0.0000 | 2846.6975 | 0.0000 | 59.3727 | 2.5429 | 45.0267 | −4507.6184 |
| AVOA | 1978.1237 | 0.0000 | 3245.5427 | 0.0000 | 61.5237 | 5.2220 | 52.0448 | −4339.8749 |
| AOA | 1370.2034 | 0.0000 | 2000.0000 | 0.0000 | 60.4692 | 2.9016 | 118.3750 | 5.257E+17 |
| DBO | 2000.0000 | 0.0000 | 2471.1994 | 0.0000 | 57.7148 | 0.8180 | 40.0673 | −4526.3250 |
| NOA | 2000.0000 | 0.0000 | 2898.0294 | 0.0000 | 59.6468 | 2.8014 | 45.6220 | −4491.8957 |
| SRPSO | 1546.5284 | 99.9386 | 2489.1299 | 89.1439 | 91.0258 | 5.2212 | 141.4753 | 242.7751 |
| XPSO | 1255.2243 | 83.1251 | 2122.5650 | 88.9856 | 93.2456 | 12.9129 | 145.2599 | 307.5009 |
| TAPSO | 1212.0246 | 99.9832 | 2000.0000 | 92.2010 | 94.3667 | 14.2142 | 148.5907 | 95.7653 |
| Arithmetic | Best | Mean | Worst | Std |
|---|---|---|---|---|
| IAROA | 2994.424465757 | 2994.424465757 | 2994.424465757 | 8.27383E−13 |
| AROA | 2994.424465796 | 2994.428042917 | 2994.462009308 | 0.007962375 |
| EO | 2994.424467407 | 2994.940560954 | 3007.389939194 | 2.394794727 |
| MPA | 2994.432990414 | 2994.464360154 | 2994.552827818 | 0.032564995 |
| SSA | 2994.424465757 | 2994.424465761 | 2994.424465816 | 0.000000013 |
| GWO | 3005.081581813 | 3012.799534176 | 3027.361758088 | 6.172417742 |
| AVOA | 2994.485468413 | 3001.600561104 | 3012.584810106 | 4.779087615 |
| AOA | 3089.654773885 | 3168.842990181 | 3227.788857380 | 43.609182558 |
| DBO | 2994.424465757 | 3059.233600655 | 3202.582182010 | 61.362527570 |
| NOA | 2994.424478453 | 2994.424560776 | 2994.424773818 | 0.000072466 |
| SRPSO | 2994.424502755 | 2994.424588091 | 2994.424802393 | 0.000068117 |
| XPSO | 3010.085574331 | 3023.140078015 | 3028.962368880 | 4.128647703 |
| TAPSO | 2994.424465757 | 3084.211466321 | 4302.119178611 | 259.168749641 |
| Arithmetic | Norm | Best | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | ||
| IAROA | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| AROA | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| EO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424467 |
| MPA | 3.500003 | 0.700000 | 17.000002 | 7.300000 | 7.715535 | 3.350545 | 5.286656 | 2994.432990 |
| SSA | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| GWO | 3.503537 | 0.700000 | 17.000000 | 7.467445 | 7.851442 | 3.352099 | 5.293569 | 3005.081582 |
| AVOA | 3.500000 | 0.700000 | 17.000000 | 7.302007 | 7.717221 | 3.350545 | 5.286655 | 2994.485468 |
| AOA | 3.600000 | 0.700000 | 17.000000 | 8.300000 | 8.300000 | 3.375762 | 5.329721 | 3089.654774 |
| DBO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| NOA | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424478 |
| SRPSO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424503 |
| XPSO | 3.501907 | 0.700329 | 17.002960 | 7.715093 | 7.885609 | 3.357101 | 5.292655 | 3010.085574 |
| TAPSO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| Arithmetic | Best | Mean | Worst | Std |
|---|---|---|---|---|
| IAROA | 0.032213002 | 0.036734092 | 0.156321137 | 0.022643996 |
| AROA | 0.032232241 | 1.56031E+14 | 9.36186E+14 | 3.54861E+14 |
| EO | 0.032220672 | 9.36186E+13 | 9.36186E+14 | 2.85657E+14 |
| MPA | 0.033126578 | 0.045639262 | 0.070884567 | 0.009299800 |
| SSA | 0.03221639 | 2.18444E+14 | 9.36186E+14 | 4.02732E+14 |
| GWO | 0.04034639 | 2.19203E+14 | 9.42846E+14 | 4.04133E+14 |
| AVOA | 0.042434402 | 6.86537E+14 | 9.36187E+14 | 4.21075E+14 |
| AOA | 5.098532627 | 4.67991E+14 | 1.682E+15 | 5.97876E+14 |
| DBO | 0.044763203 | 7.79872E+14 | 3.38785E+15 | 7.14765E+14 |
| NOA | 0.032670028 | 0.049593042 | 0.078531071 | 0.014427310 |
| SRPSO | 0.050958848 | 9.36186E+13 | 9.36186E+14 | 2.85657E+14 |
| XPSO | 0.499612786 | 4.74863E+13 | 1.42459E+15 | 2.60093E+14 |
| TAPSO | 0.032226552 | 1.01416E+15 | 9.12181E+15 | 1.91438E+15 |
| Arithmetic | Norm | ||||||
|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| IAROA | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 1.524000 |
| AROA | 0.001000 | 0.001000 | 0.001001 | 0.001000 | 0.001000 | 0.001001 | 1.524129 |
| EO | 0.001000 | 0.001000 | 0.001000 | 0.001003 | 0.001000 | 0.001000 | 1.524003 |
| MPA | 0.001000 | 0.001238 | 0.001015 | 0.001109 | 0.001088 | 0.001144 | 1.524008 |
| SSA | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 1.524001 |
| GWO | 0.001000 | 0.001129 | 0.001123 | 0.001195 | 0.003270 | 0.001181 | 1.524347 |
| AVOA | 0.001000 | 0.001000 | 0.001000 | 0.002072 | 0.001000 | 0.002144 | 1.524001 |
| AOA | 0.001000 | 0.001000 | 0.001000 | 1.679435 | 0.169433 | 1.727573 | 5.000000 |
| DBO | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 1.524000 |
| NOA | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 1.524038 |
| SRPSO | 0.001001 | 0.001072 | 0.001718 | 0.001499 | 0.001305 | 0.001031 | 1.545509 |
| XPSO | 0.000000 | 0.001293 | 0.002440 | 0.089629 | 0.877626 | 0.094048 | 2.783794 |
| TAPSO | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 0.001000 | 1.524000 |
| Norm | Best | ||||||
| x8 | x9 | x10 | x11 | x12 | x13 | x14 | |
| 1.524000 | 5.000000 | 2.000000 | 0.001000 | 0.001000 | 0.007293 | 0.087556 | 0.032213002 |
| 1.524278 | 4.999994 | 2.000334 | 0.001010 | 0.001010 | 0.007326 | 0.087951 | 0.032232241 |
| 1.524041 | 4.999927 | 2.000003 | 0.001000 | 0.001000 | 0.007292 | 0.087537 | 0.032220672 |
| 1.524005 | 5.000000 | 2.000139 | 0.001019 | 0.001016 | 0.007348 | 0.088213 | 0.033126578 |
| 1.524004 | 4.999997 | 2.000009 | 0.001000 | 0.001000 | 0.007292 | 0.087543 | 0.03221639 |
| 1.524921 | 4.985041 | 2.013069 | 0.005317 | 0.005052 | 0.015337 | 0.183778 | 0.04034639 |
| 1.524001 | 4.933572 | 2.328689 | 0.007956 | 0.005692 | 0.017713 | 0.212635 | 0.042434402 |
| 2.277239 | 3.416799 | 2.374662 | 0.001000 | 0.001000 | 0.002130 | 0.008816 | 5.098532627 |
| 1.524000 | 5.000000 | 5.000000 | 0.002072 | 0.002072 | 0.015851 | 0.190286 | 0.044763203 |
| 1.528605 | 4.970139 | 2.015543 | 0.001003 | 0.001000 | 0.007315 | 0.087398 | 0.032670028 |
| 1.534080 | 4.744826 | 4.191221 | 0.005251 | 0.004998 | 0.021267 | 0.252935 | 0.050958848 |
| 3.399624 | 2.524434 | 2.778828 | 0.149176 | 0.030801 | 0.024767 | 0.204583 | 0.499612786 |
| Arithmetic | Best | Mean | Worst | Std |
|---|---|---|---|---|
| IAROA | 1.6702177263 | 1.670217726 | 1.670217726 | 3.81709E−13 |
| AROA | 1.6702177264 | 1.670509295 | 1.674240477 | 0.000792958 |
| EO | 1.6702179939 | 1.671599635 | 1.697186403 | 0.004923826 |
| MPA | 1.6702185592 | 1.670226507 | 1.670242132 | 0.000006517 |
| SSA | 1.6702178503 | 1.779812944 | 2.262797186 | 0.148506619 |
| GWO | 1.6712384796 | 1.676213570 | 1.697783459 | 0.005098199 |
| AVOA | 1.6736509403 | 1.758871592 | 1.816849475 | 0.051331019 |
| AOA | 1.9338394264 | 2.339173265 | 2.742053530 | 0.191872482 |
| DBO | 1.6702306649 | 1.754227932 | 1.902804769 | 0.072558174 |
| NOA | 1.6702197253 | 1.670244842 | 1.670346272 | 2.93581E−05 |
| SRPSO | 1.6702187308 | 1.670411051 | 1.673644428 | 0.000631020 |
| XPSO | 1.6702177263 | 1.670240491 | 1.670717093 | 9.15251E−05 |
| TAPSO | 1.6702178263 | 2.014143679 | 5.453527824 | 0.713119231 |
| Arithmetic | Norm | Best | |||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | ||
| IAROA | 0.19883230722 | 3.33736529865 | 9.19202432248 | 0.19883230722 | 1.67021772630 |
| AROA | 0.19883230718 | 3.33736529935 | 9.19202432278 | 0.19883230722 | 1.67021772640 |
| EO | 0.19883231922 | 3.33736478516 | 9.19202537600 | 0.19883232586 | 1.67021799390 |
| MPA | 0.19883198519 | 3.33737379241 | 9.19202575982 | 0.19883230055 | 1.67021855920 |
| SSA | 0.19883233882 | 3.33736492830 | 9.19202356992 | 0.19883233999 | 1.67021785030 |
| GWO | 0.19821666038 | 3.35150485273 | 9.19247421285 | 0.19883104333 | 1.67123847960 |
| AVOA | 0.19937272345 | 3.33255027593 | 9.17231614750 | 0.19968767089 | 1.67365094030 |
| AOA | 0.12500000000 | 5.50547860699 | 10.00000000000 | 0.19594970586 | 1.93383942640 |
| DBO | 0.19883154106 | 3.33734606069 | 9.19215184203 | 0.19883171314 | 1.67023066490 |
| NOA | 0.19883190377 | 3.33737354767 | 9.19202287301 | 0.19883253486 | 1.67021972530 |
| SRPSO | 0.19883170350 | 3.33737819322 | 9.19202411741 | 0.19883233679 | 1.67021873080 |
| XPSO | 0.19883230722 | 3.33736529865 | 9.19202432248 | 0.19883230722 | 1.67021772630 |
| TAPSO | 0.19883231440 | 3.33736530865 | 9.19202379059 | 0.19883233024 | 1.67021782630 |
| Arithmetic | Best | Mean | Worst | Std |
|---|---|---|---|---|
| IAROA | −30,665.538671784 | −30,665.538671784 | −30,665.538671784 | 8.9876841E−12 |
| AROA | −30,665.538671784 | −30,665.538661737 | −30,665.538518081 | 3.5086010E−05 |
| EO | −30,665.538671783 | −30,665.524005855 | −30,665.315217247 | 0.042360026 |
| MPA | −30,665.538566739 | −30,665.538095716 | −30,665.537366849 | 0.000325091 |
| SSA | −30,665.538671784 | −30,665.538647089 | −30,665.538285515 | 9.1271724E−05 |
| GWO | −30,662.724520364 | −30,657.279460554 | −30,641.165298064 | 4.795902492 |
| AVOA | −30,665.537797521 | −30,661.905410462 | −30,609.047187836 | 10.961911294 |
| AOA | −30,573.492828232 | −29,587.801638904 | −28,883.198992723 | 405.704030987 |
| DBO | −30,665.538671784 | −30,659.523848894 | −30,491.114101749 | 31.815822115 |
| NOA | −30,665.537122546 | −30,665.529190299 | −30,665.495723935 | 0.011777849 |
| SRPSO | −30,665.535954249 | −30,659.819894304 | −30,495.698990493 | 30.997549900 |
| XPSO | −30,644.778298218 | −30,612.308790981 | −30,529.963003225 | 23.667554290 |
| TAPSO | −30,665.538671784 | −30,607.422932739 | −29,893.249053707 | 189.359224254 |
| Arithmetic | Norm | Best | ||||
|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | ||
| IAROA | 78.0000000 | 33.0000000 | 29.9952560 | 45.0000000 | 36.7758129 | −30,665.5386718 |
| AROA | 78.0000000 | 33.0000000 | 29.9952560 | 45.0000000 | 36.7758129 | −30,665.5386718 |
| EO | 78.0000000 | 33.0000000 | 29.9952560 | 45.0000000 | 36.7758129 | −30,665.5386718 |
| MPA | 78.0000000 | 33.0000000 | 29.9952565 | 45.0000000 | 36.7758122 | −30,665.5385667 |
| SSA | 78.0000000 | 33.0000000 | 29.9952560 | 45.0000000 | 36.7758129 | −30,665.5386718 |
| GWO | 78.0000000 | 33.0000000 | 30.0066260 | 45.0000000 | 36.7629096 | −30,662.7245204 |
| AVOA | 78.0000000 | 33.0000015 | 29.9952616 | 45.0000000 | 36.7757988 | −30,665.5377975 |
| AOA | 78.0000000 | 33.0000000 | 30.2498287 | 45.0000000 | 36.9272888 | −30,573.4928282 |
| DBO | 78.0000000 | 33.0000000 | 29.9952560 | 45.0000000 | 36.7758129 | −30,665.5386718 |
| NOA | 78.0000000 | 33.0000005 | 29.9952607 | 45.0000000 | 36.7758137 | −30,665.5371225 |
| SRPSO | 78.0000184 | 33.0000045 | 29.9952664 | 45.0000000 | 36.7757842 | −30,665.5359542 |
| XPSO | 78.0136130 | 33.0715995 | 30.0817785 | 44.9701113 | 36.6528608 | −30,644.7782982 |
| TAPSO | 78.0000000 | 33.0000000 | 29.9952560 | 45.0000000 | 36.7758129 | −30,665.5386718 |
| Arithmetic | Best | Mean | Worst | Std |
|---|---|---|---|---|
| IAROA | 2.543790469 | 2.589878551 | 3.036007330 | 0.097775114 |
| AROA | 2.543968130 | 2.876128644 | 3.651941325 | 0.303358096 |
| EO | 2.547173857 | 3.498080150 | 5.966433367 | 0.752739873 |
| MPA | 2.546031208 | 2.838837273 | 3.153007707 | 0.175297596 |
| SSA | 2.792611983 | 6.313794528 | 72.686677135 | 12.588411554 |
| GWO | 3.092374187 | 3.823935171 | 4.564037027 | 0.376625847 |
| AVOA | 2.591978421 | 4.156581140 | 6.767453071 | 0.931277604 |
| AOA | 3.705794959 | 5.111113547 | 16.101476709 | 2.264300497 |
| DBO | 2.552505703 | 4.789698560 | 8.338582727 | 1.435788140 |
| NOA | 3.061661302 | 3.444272265 | 3.781554059 | 0.175854864 |
| SRPSO | 3.354019627 | 3.983458789 | 4.941396283 | 0.351937577 |
| XPSO | 3.036056335 | 4.425171790 | 5.368783114 | 0.512379516 |
| TAPSO | 2.644273848 | 6.579609477 | 49.625244808 | 9.957733009 |
| Arithmetic | Norm | Best | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | ||
| IAROA | 150.0000 | 149.8828 | 200.0000 | 0.0000 | 149.9999 | 100.9430 | 2.2974 | 2.543790469 |
| AROA | 150.0000 | 149.8825 | 200.0000 | 0.0003 | 150.0000 | 100.9528 | 2.2978 | 2.543968130 |
| EO | 150.0000 | 149.8810 | 200.0000 | 0.0000 | 150.0000 | 101.1322 | 2.3172 | 2.547173857 |
| MPA | 149.9669 | 149.8394 | 200.0000 | 0.0094 | 149.1333 | 101.0302 | 2.2982 | 2.546031208 |
| SSA | 148.9886 | 141.6340 | 200.0000 | 7.0801 | 136.4111 | 110.8249 | 2.3244 | 2.792611983 |
| GWO | 149.8509 | 149.7731 | 199.1393 | 0.0000 | 25.6465 | 103.5958 | 1.6901 | 3.092374187 |
| AVOA | 150.0000 | 149.8724 | 200.0000 | 0.0000 | 150.0000 | 102.3170 | 2.3702 | 2.591978421 |
| AOA | 150.0000 | 98.6045 | 200.0000 | 50.0000 | 150.0000 | 129.6142 | 2.8907 | 3.705794959 |
| DBO | 150.0000 | 149.8779 | 200.0000 | 0.0000 | 136.4369 | 101.4306 | 2.2325 | 2.552505703 |
| NOA | 148.1264 | 139.7663 | 199.8558 | 7.6498 | 143.0177 | 125.3845 | 2.4155 | 3.061661302 |
| SRPSO | 149.9801 | 123.2550 | 184.1166 | 26.2918 | 149.4296 | 115.4428 | 2.7775 | 3.354019627 |
| XPSO | 143.0801 | 138.5940 | 191.5218 | 4.1952 | 15.9860 | 110.4247 | 1.6847 | 3.036056335 |
| TAPSO | 150.0000 | 142.5250 | 200.0000 | 7.3194 | 149.9913 | 103.5358 | 2.4202 | 2.644273848 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Jiang, Z.; Hu, G.; Hussien, A.G. IAROA: An Enhanced Attraction–Repulsion Optimisation Algorithm Fusing Multiple Strategies for Mechanical Optimisation Design. Biomimetics 2025, 10, 628. https://doi.org/10.3390/biomimetics10090628
Zhang N, Jiang Z, Hu G, Hussien AG. IAROA: An Enhanced Attraction–Repulsion Optimisation Algorithm Fusing Multiple Strategies for Mechanical Optimisation Design. Biomimetics. 2025; 10(9):628. https://doi.org/10.3390/biomimetics10090628
Chicago/Turabian StyleZhang, Na, Ziwei Jiang, Gang Hu, and Abdelazim G. Hussien. 2025. "IAROA: An Enhanced Attraction–Repulsion Optimisation Algorithm Fusing Multiple Strategies for Mechanical Optimisation Design" Biomimetics 10, no. 9: 628. https://doi.org/10.3390/biomimetics10090628
APA StyleZhang, N., Jiang, Z., Hu, G., & Hussien, A. G. (2025). IAROA: An Enhanced Attraction–Repulsion Optimisation Algorithm Fusing Multiple Strategies for Mechanical Optimisation Design. Biomimetics, 10(9), 628. https://doi.org/10.3390/biomimetics10090628








