Graduate Student Evolutionary Algorithm: A Novel Metaheuristic Algorithm for 3D UAV and Robot Path Planning
Abstract
1. Introduction
- A review of the existing relevant literature on the subject and a discussion of its strengths and weaknesses.
- Proposed a novel Graduate Student Evolutionary Algorithm (GSEA).
- Compare the performance of the proposed algorithm with 11 new classical algorithms on 42 test functions in two test sets, CEC2017 and CEC2022.
- The algorithms proposed in this paper are utilized to solve real-life path planning problems, such as UAV path planning and robot path planning problems.
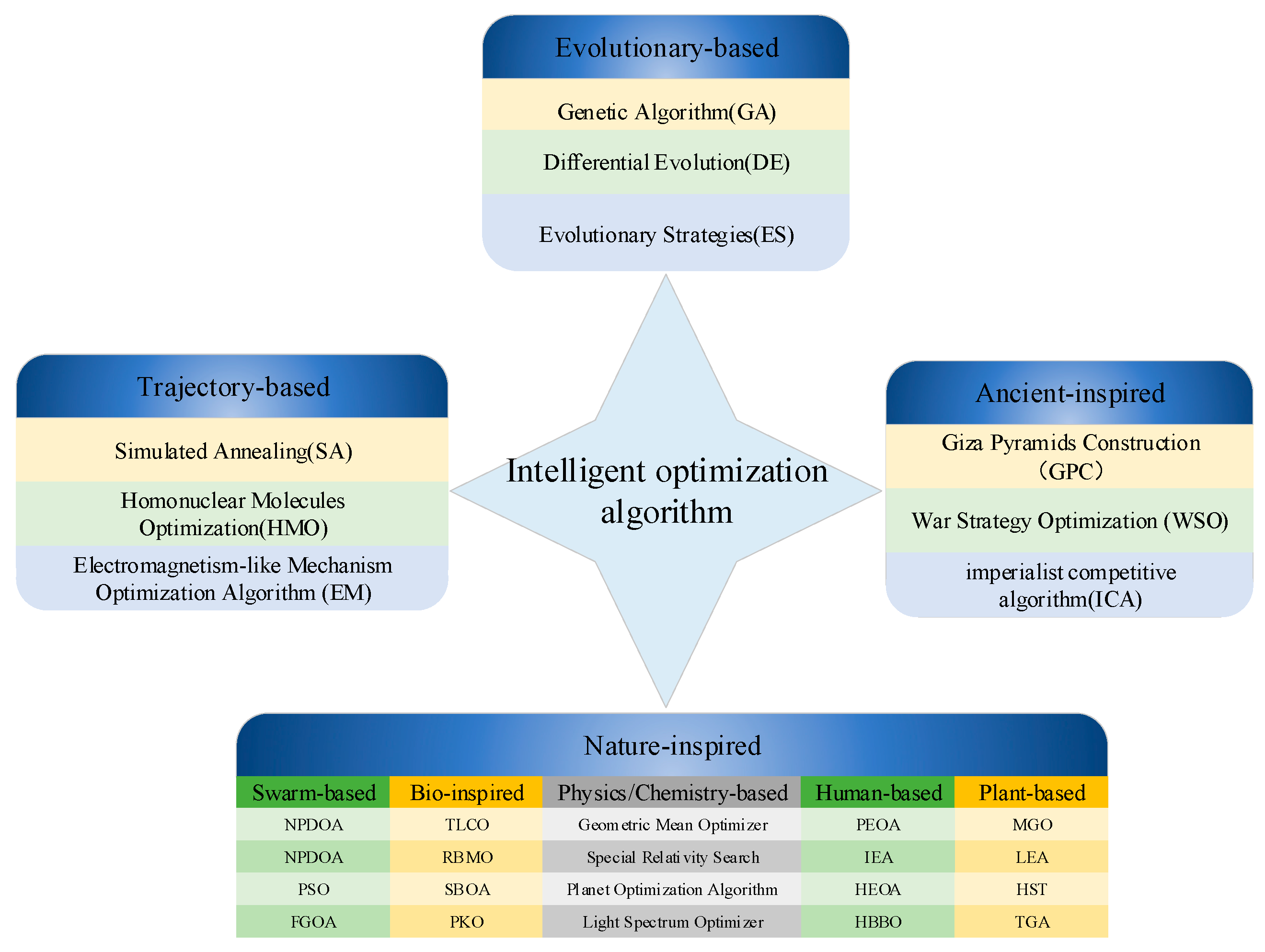
2. Literature Review
3. The Graduate Student Evolutionary Algorithm (GSEA)
3.1. Inspiration
3.2. Mathematical Modeling of GSEA
3.2.1. Initialization Stage-Examination/Preservation
3.2.2. Finding Research Directions
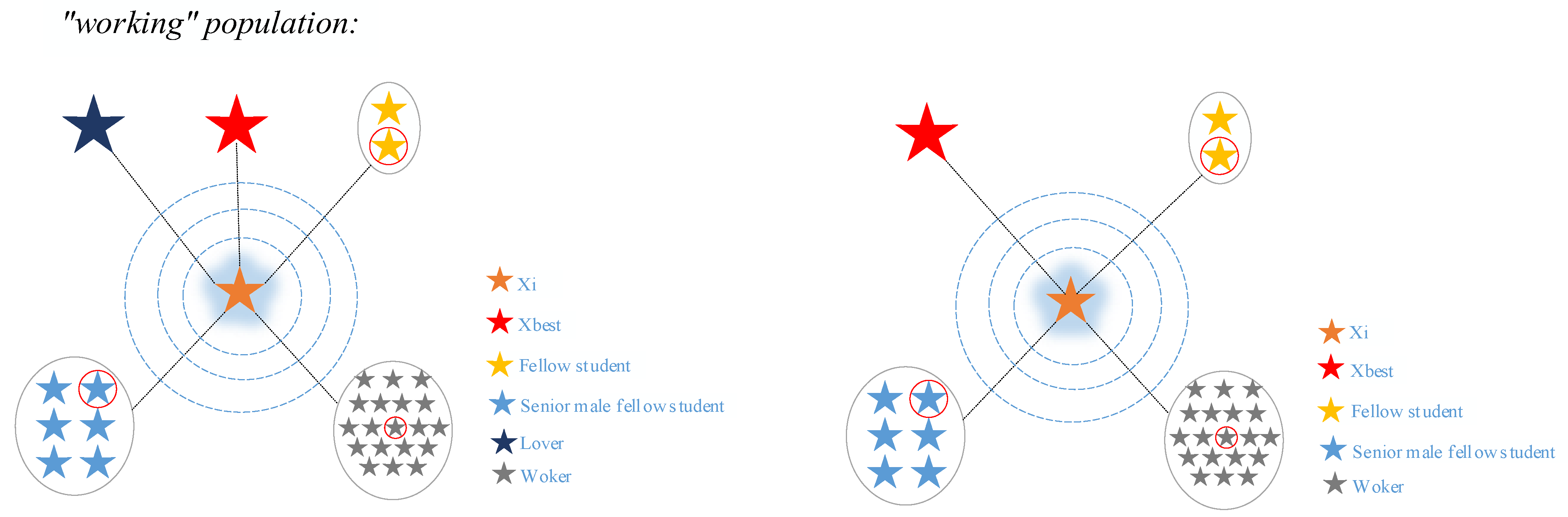
3.2.3. Study Intensively
3.2.4. Knowledge Accumulation
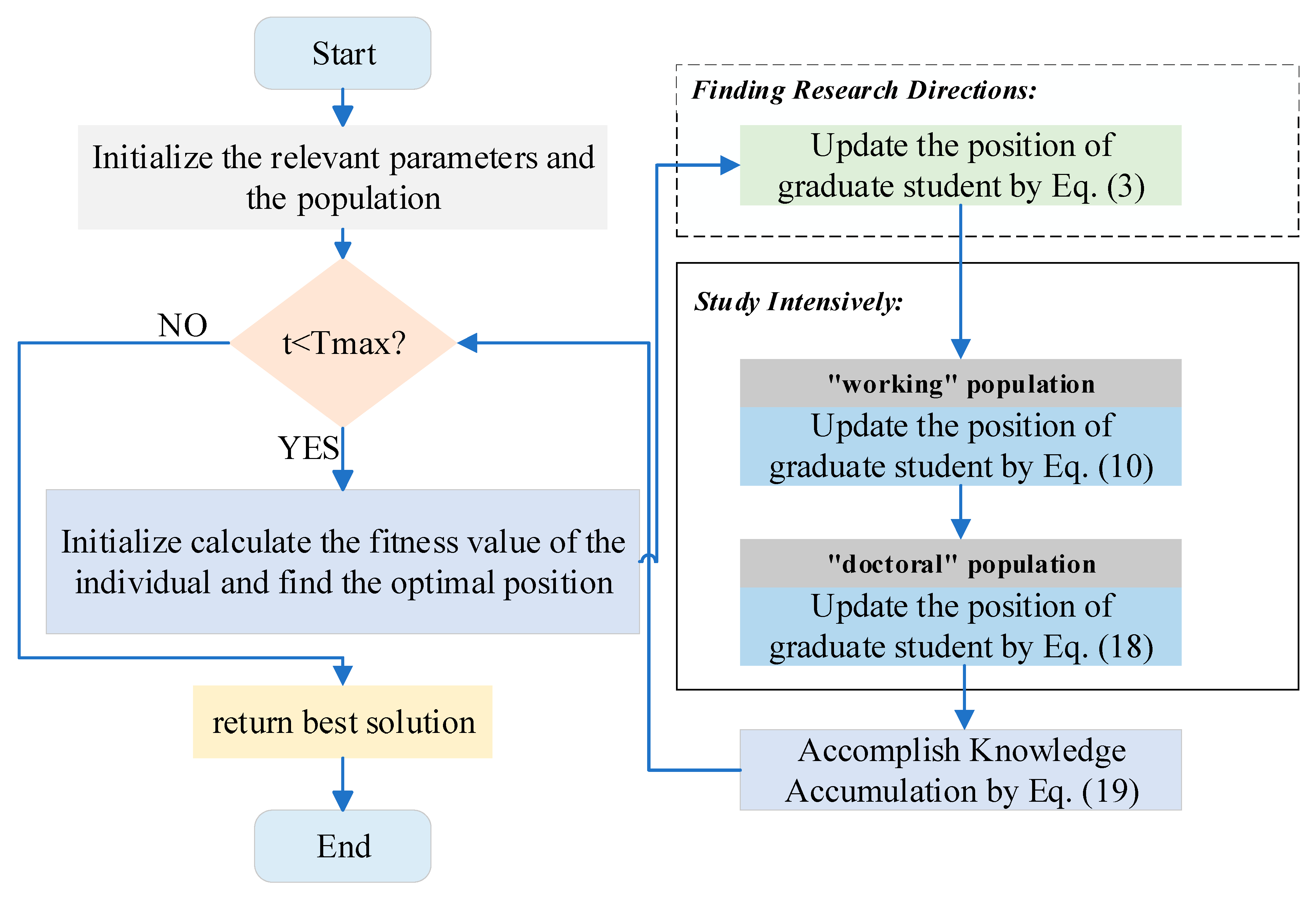
| Algorithm 1: the pseudo-code of the GSEA |
| 1: Begin 2: Initialize the relevant parameters 4: Calculate the fitness of each graduate student 5: Update the best solution 6: Finding Research Directions: 7: Update the position of graduate student by Equation (3) 8: Study Intensively: 9: “working” population: 10: Update the position of graduate student by Equation (10) 11: “doctoral” population: 12: Update the position of graduate student by Equation (18) and accomplish Knowledge Accumulation by Equation (19) 14: End while 15: return best solution 16: end |
3.3. Algorithm Convergence Analysis
3.3.1. GSEA’s Markov Model
3.3.2. GSEA Convergence Analysis
- (a)
- if , then.
- (b)
- For any Borel subset of , , then, , and is the sequence generated by algorithm, specifically , where is the probability measure of the solution at step of the algorithm.
3.4. Time Complexity Analysis
4. Numerical Optimization Experiments
4.1. Benchmark Test Functions
4.2. Competitor Algorithms and Parameters Setting
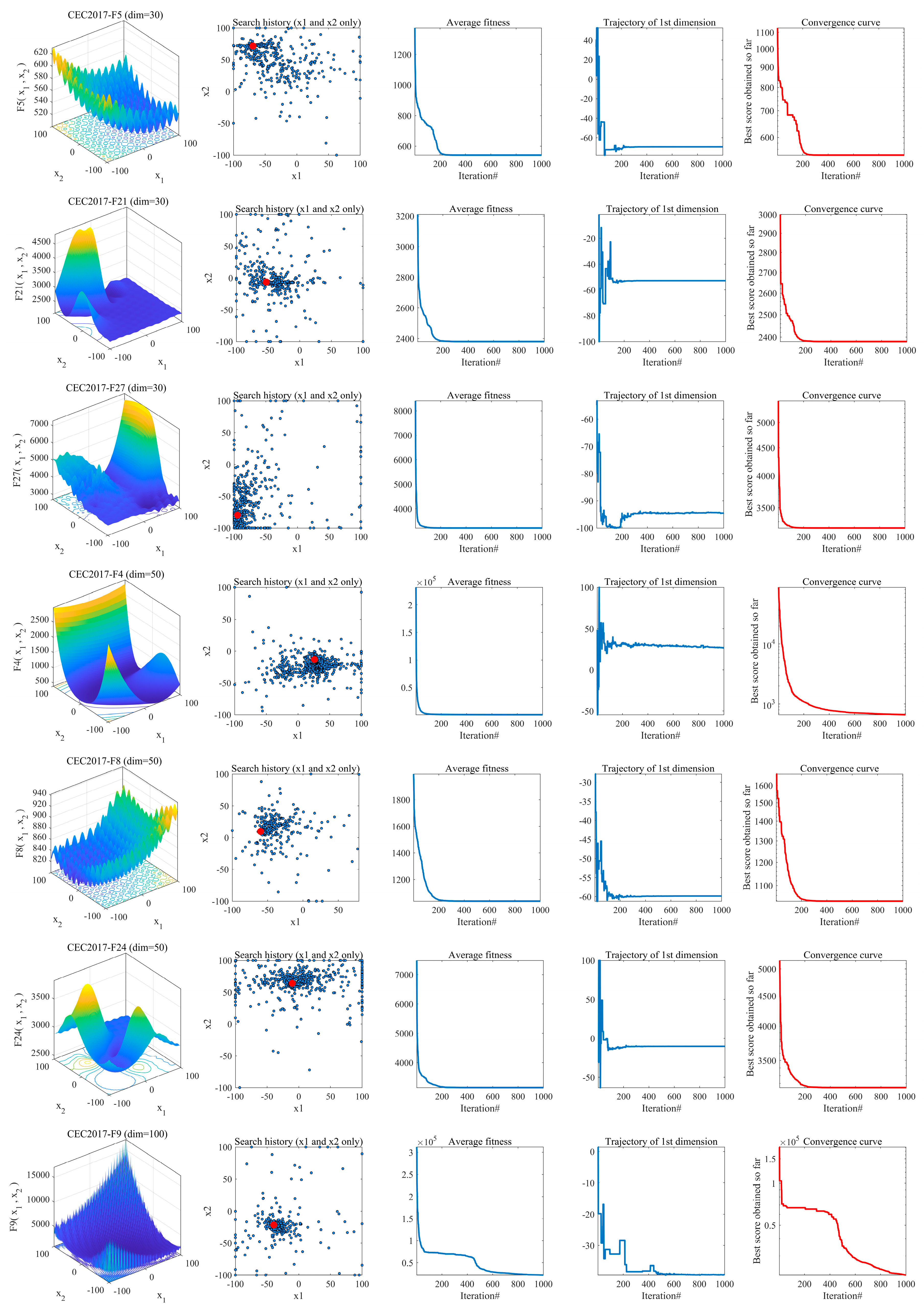
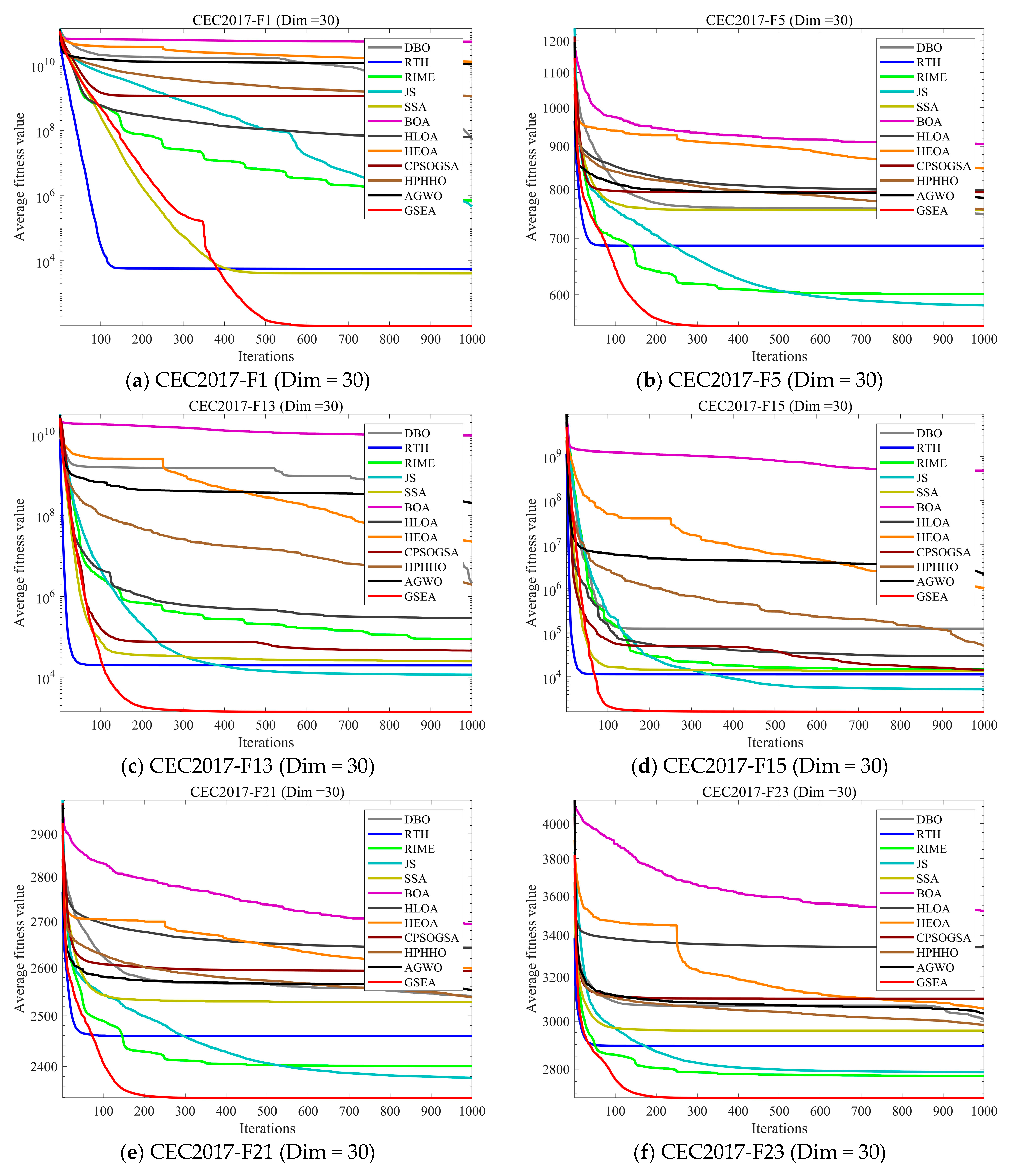
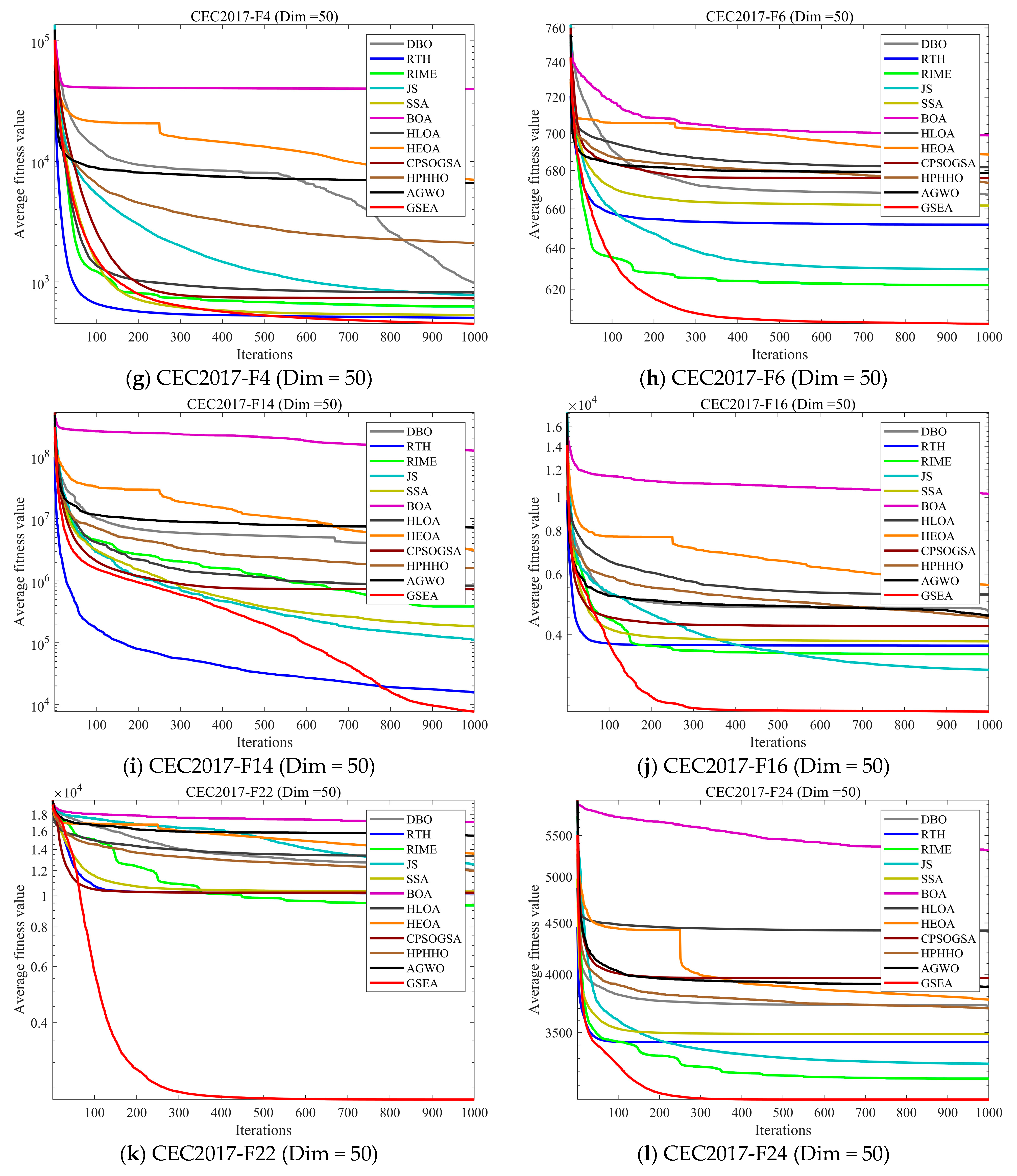
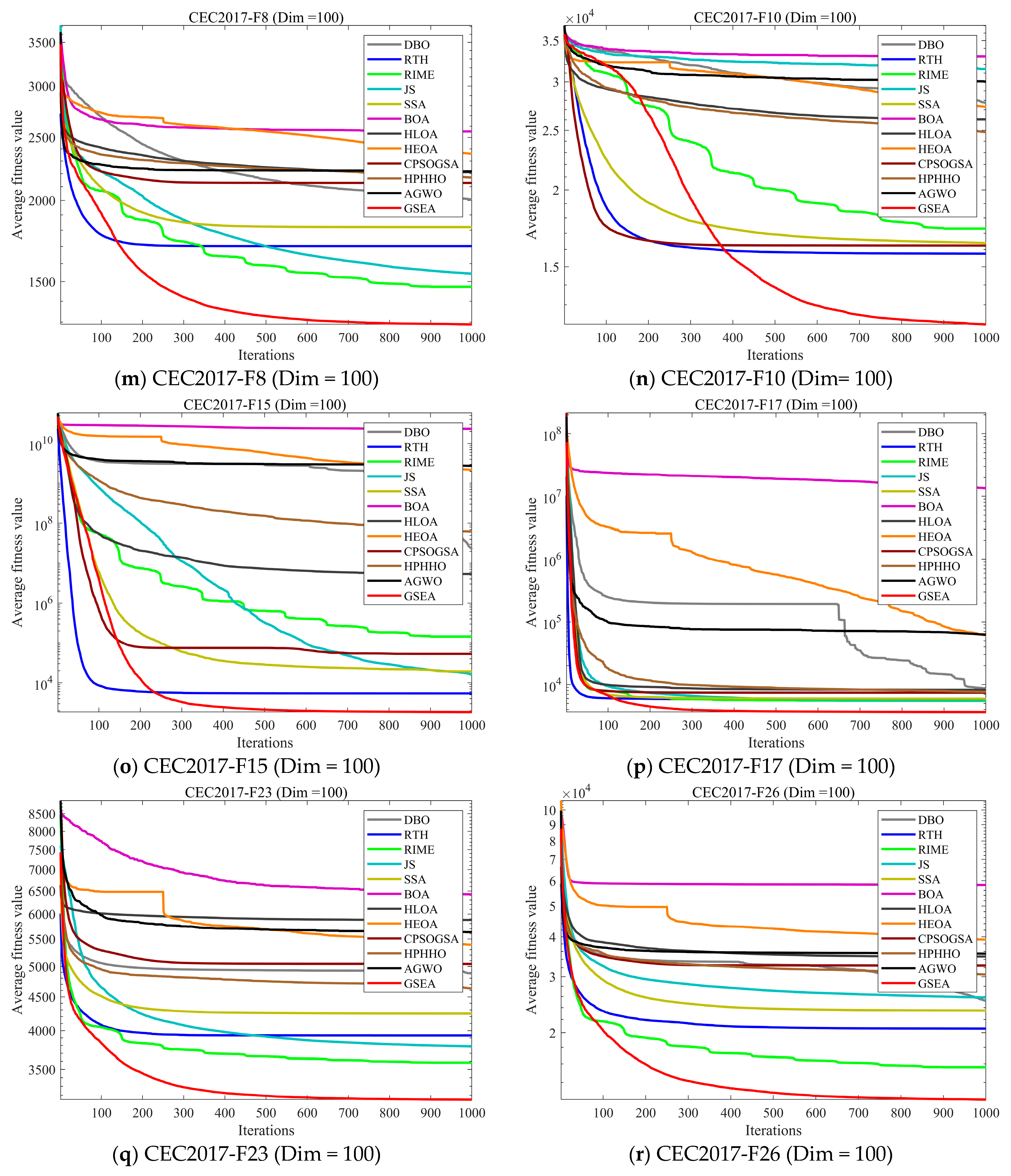
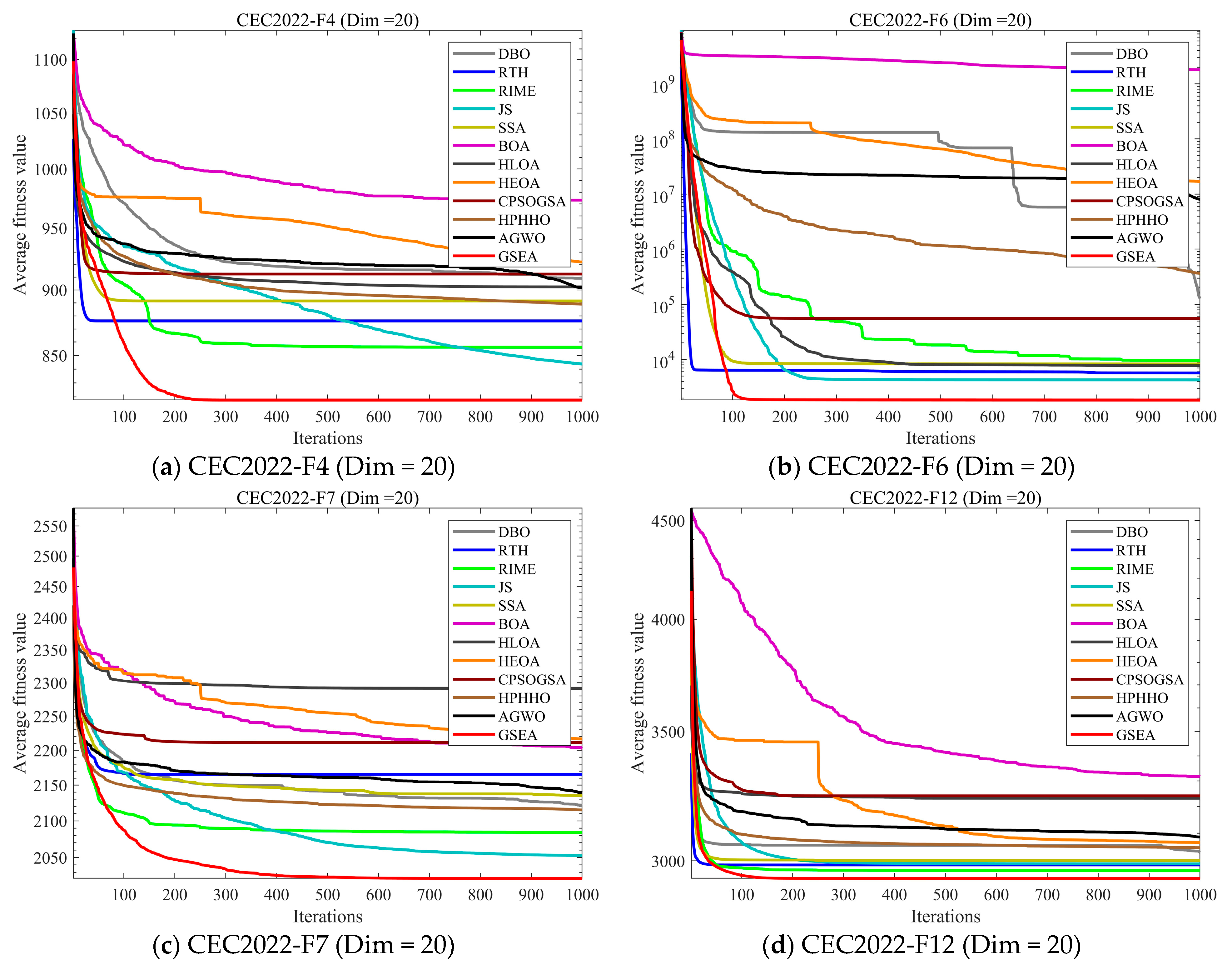
4.3. Analysis of the Convergence Behavior
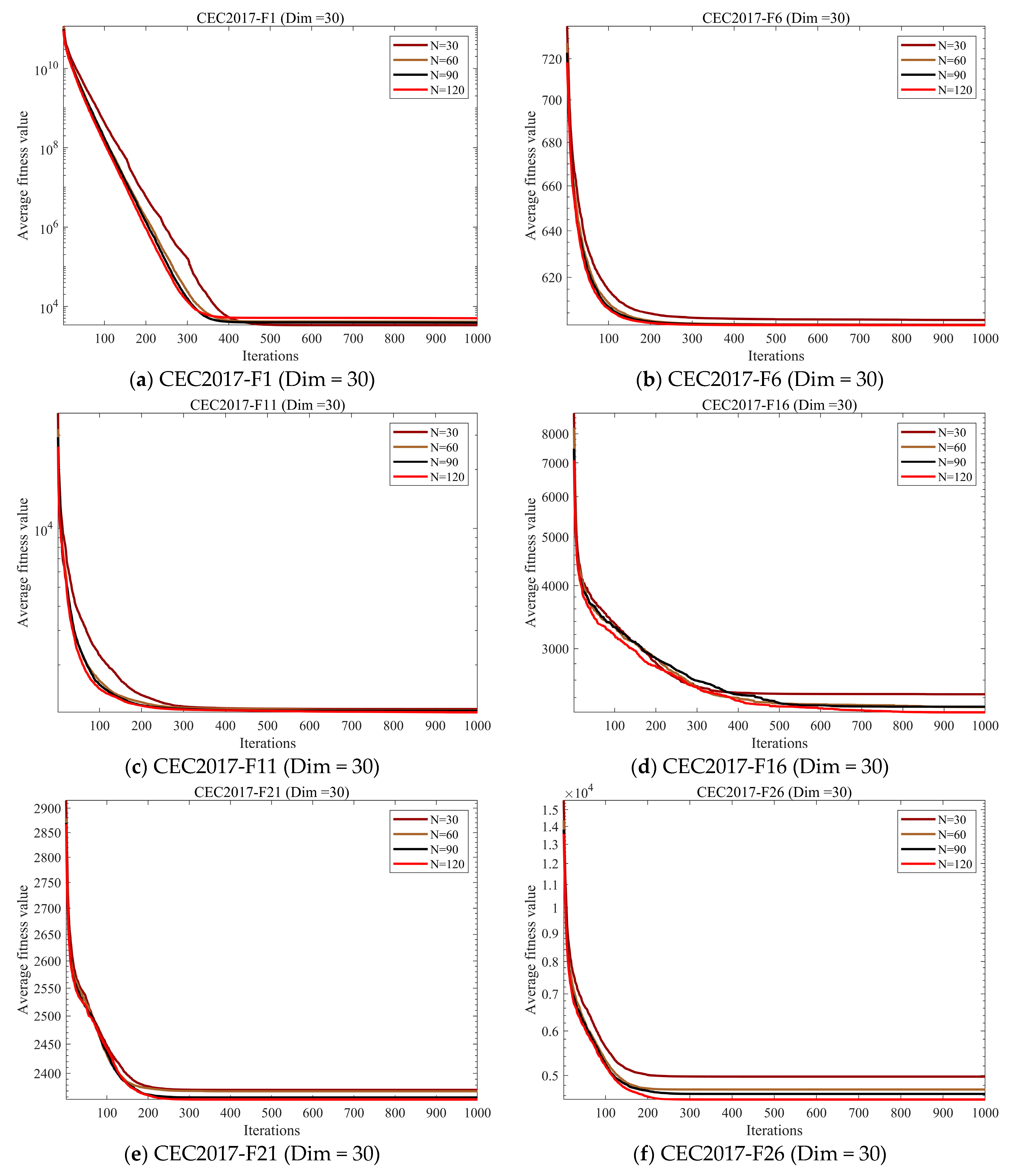
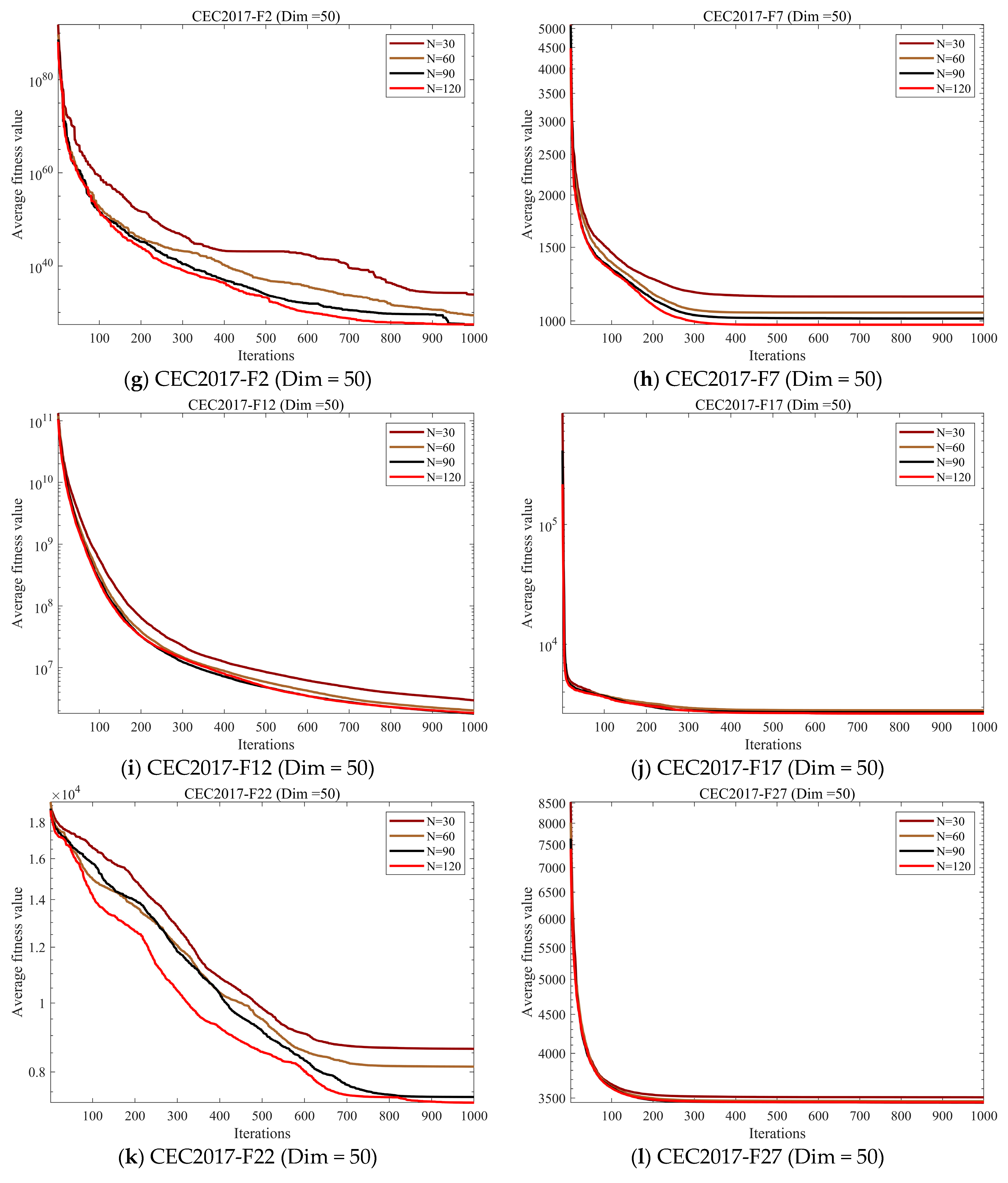
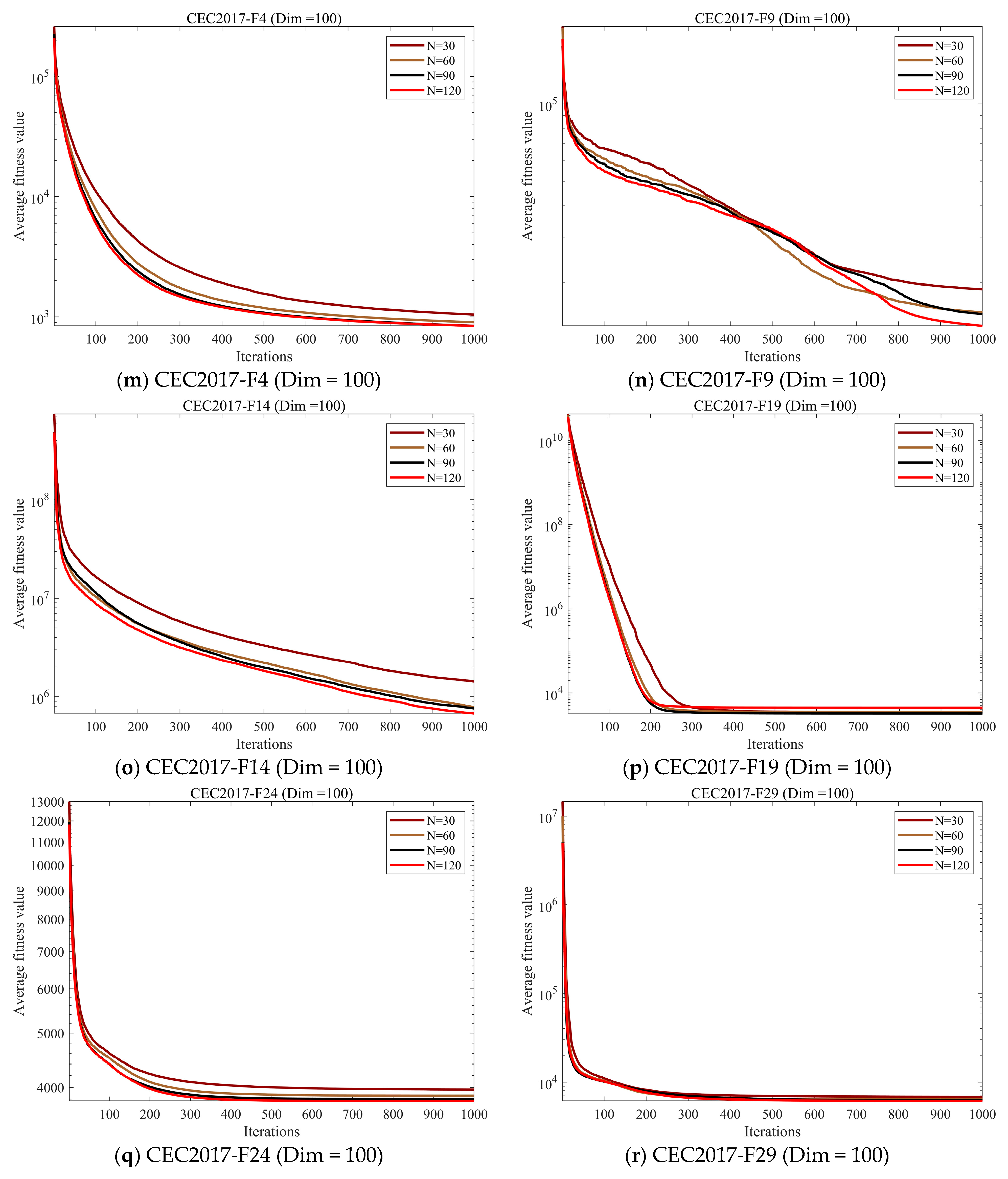
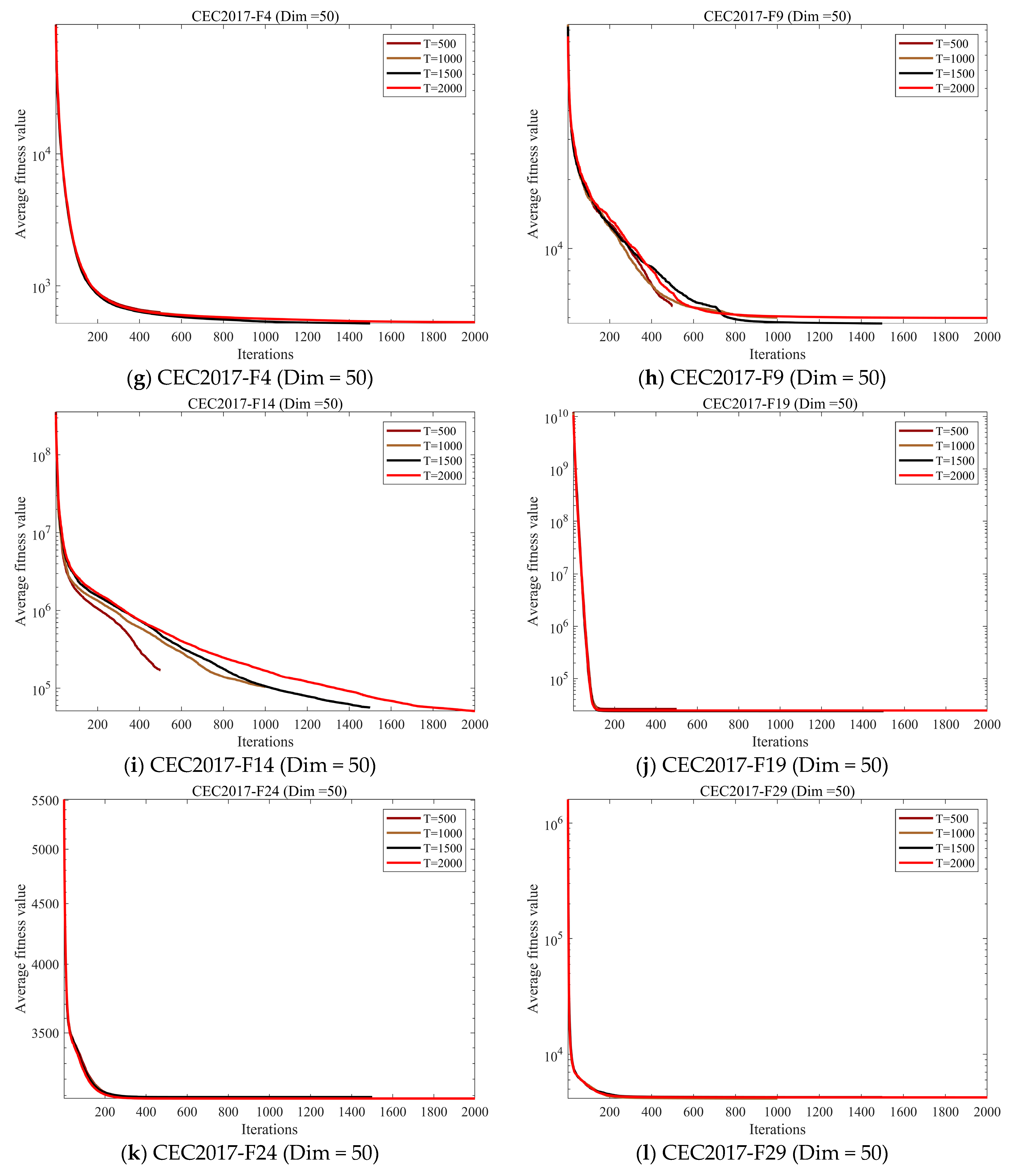
4.4. Parameter Sensitivity Analysis
4.4.1. Population Size Sensitivity Analysis
4.4.2. Sensitivity Analysis of Iteration Count
4.5. Quantitative Evaluation
4.5.1. Compare Using CEC 2017 Test Functions
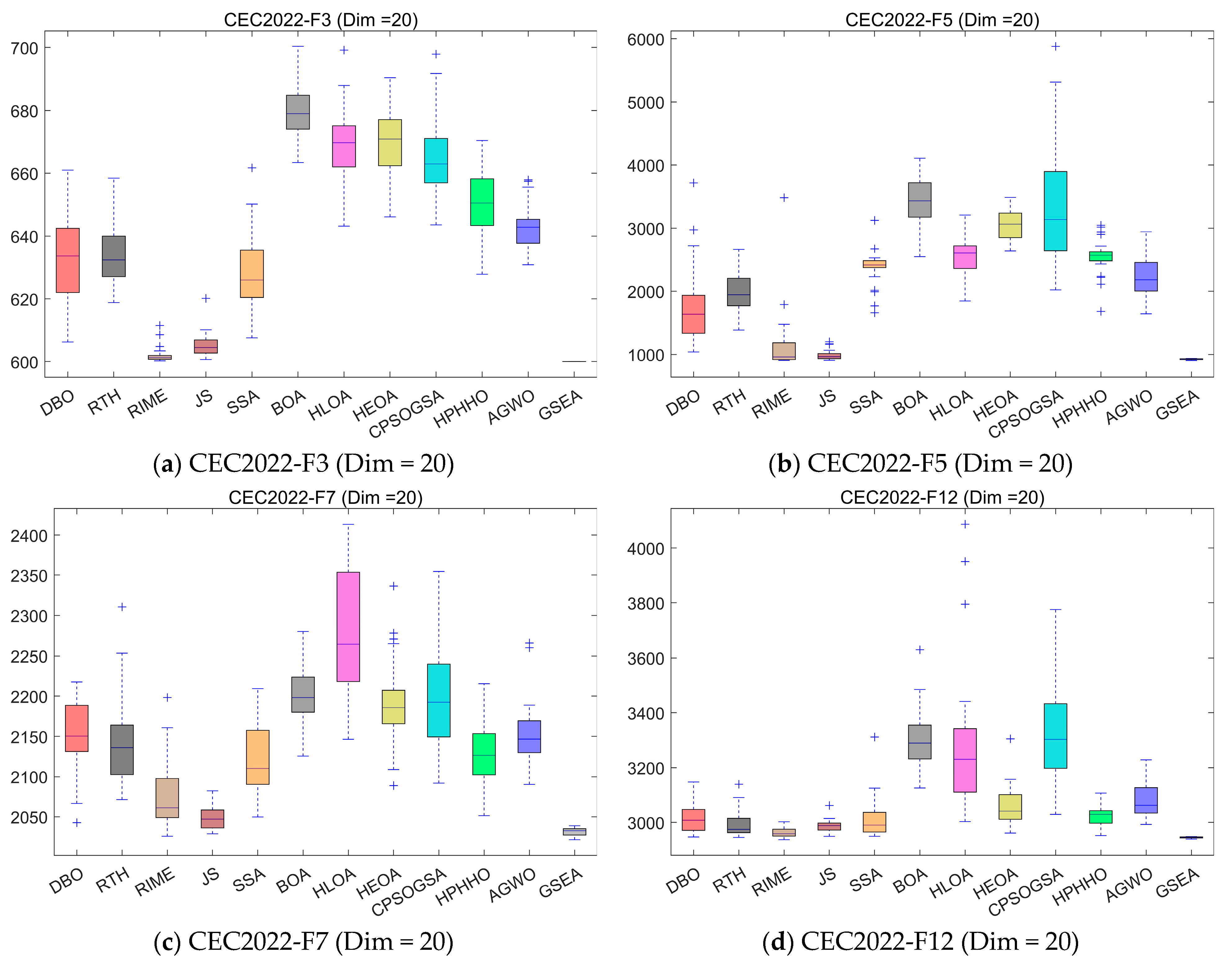
4.5.2. Compare Using CEC 2022 Test Functions
4.6. Statistical Analysis
4.6.1. Wilcoxon Rank Sum Test
4.6.2. Friedman Mean Rank Test
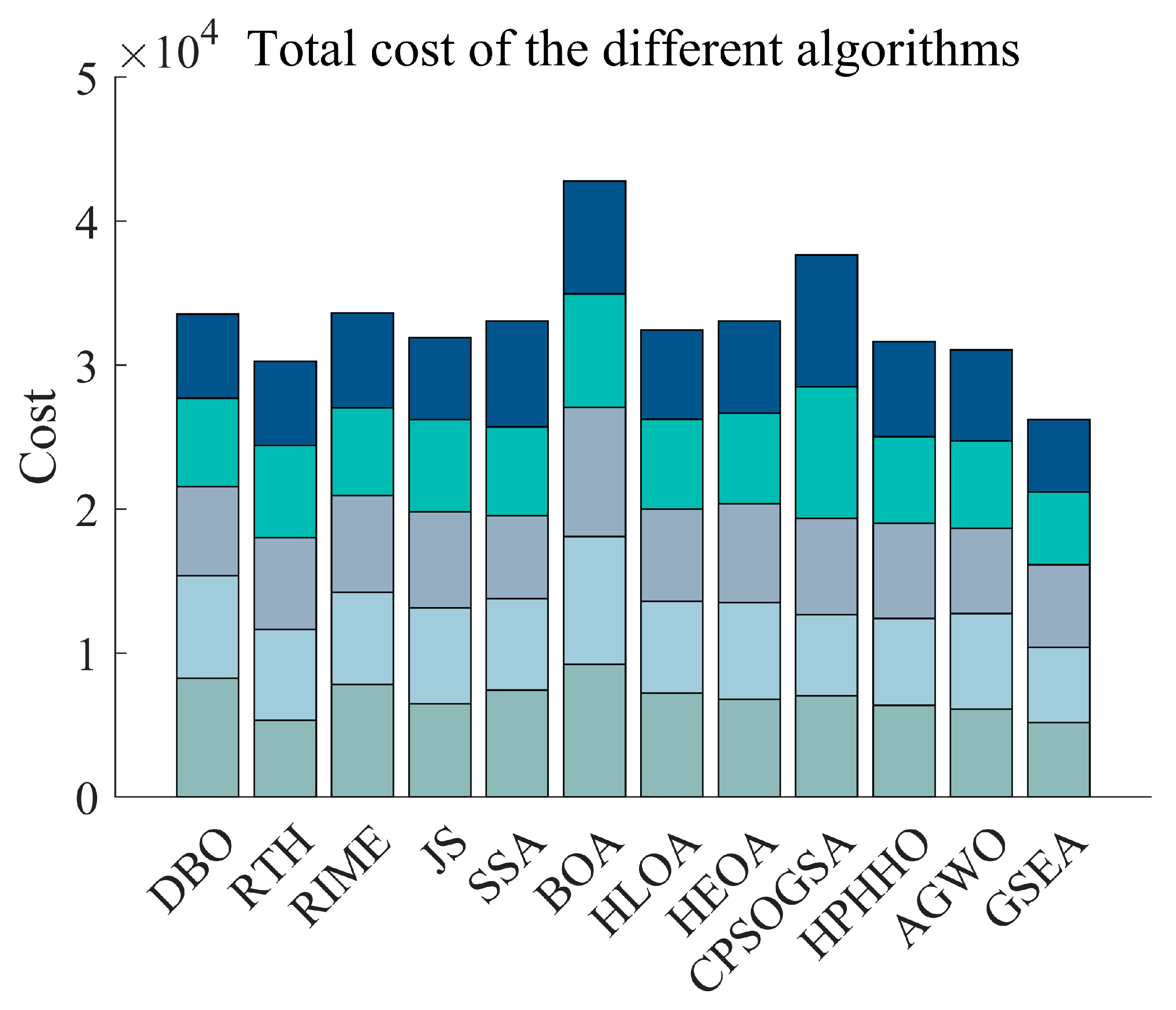
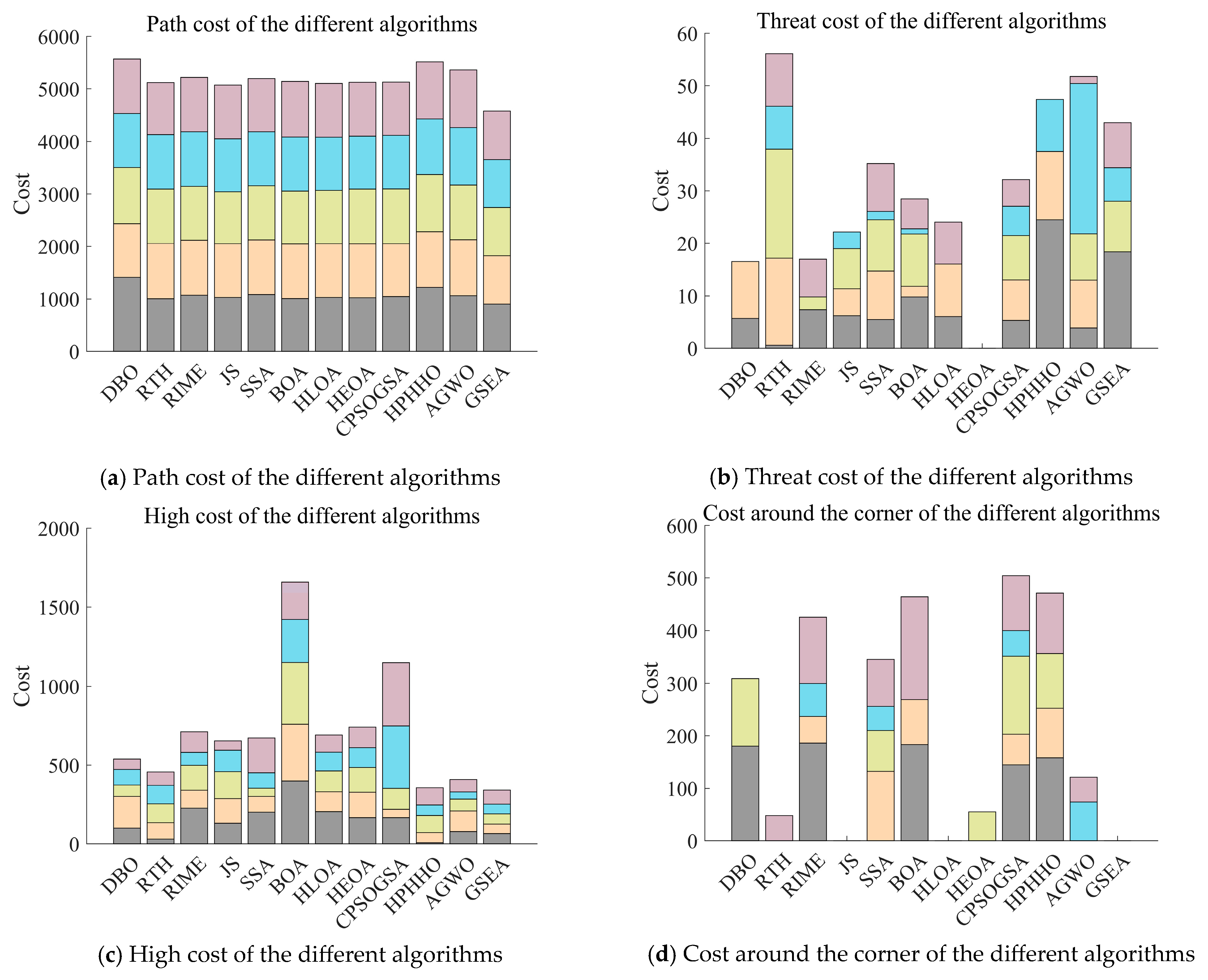
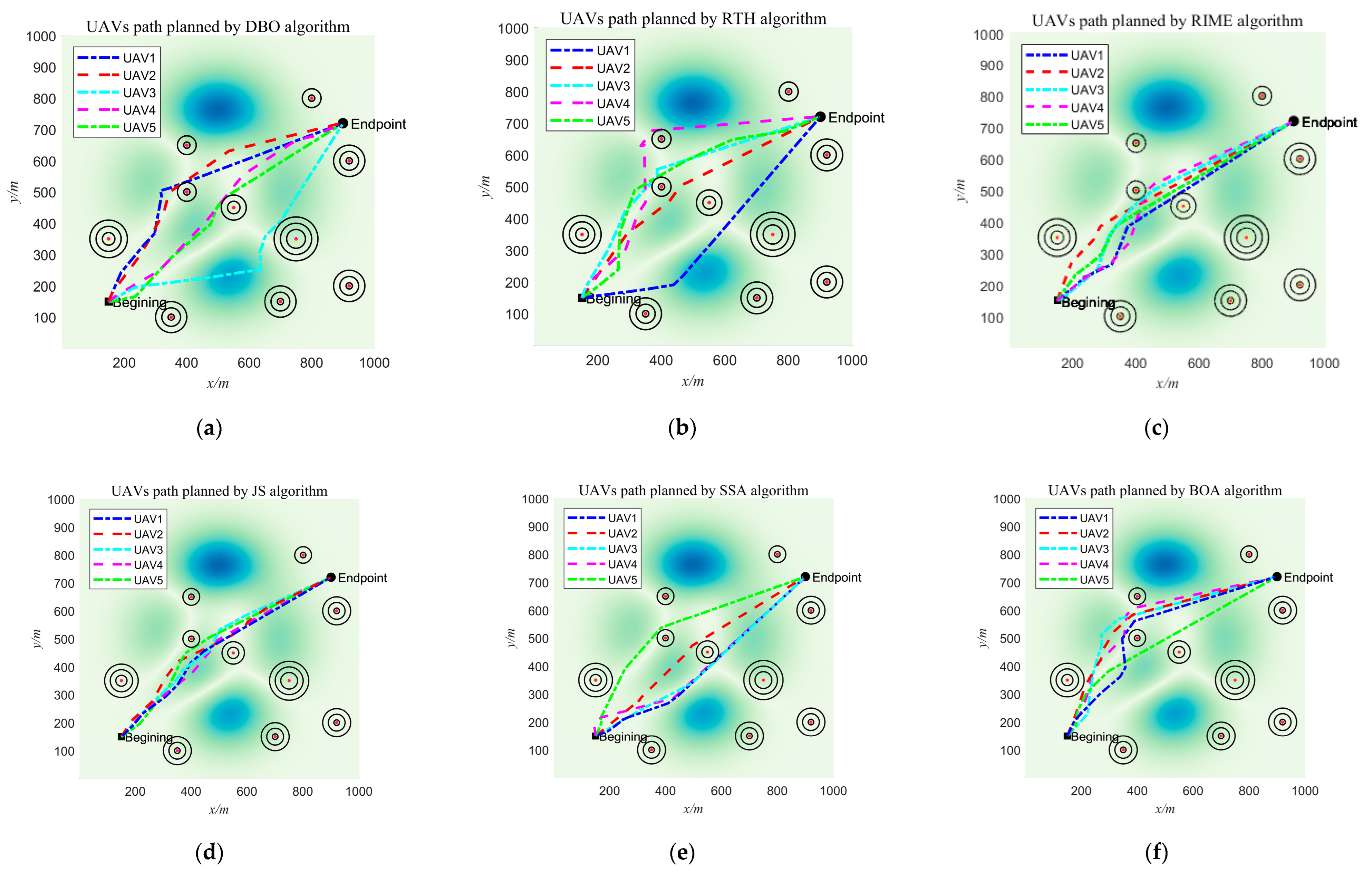
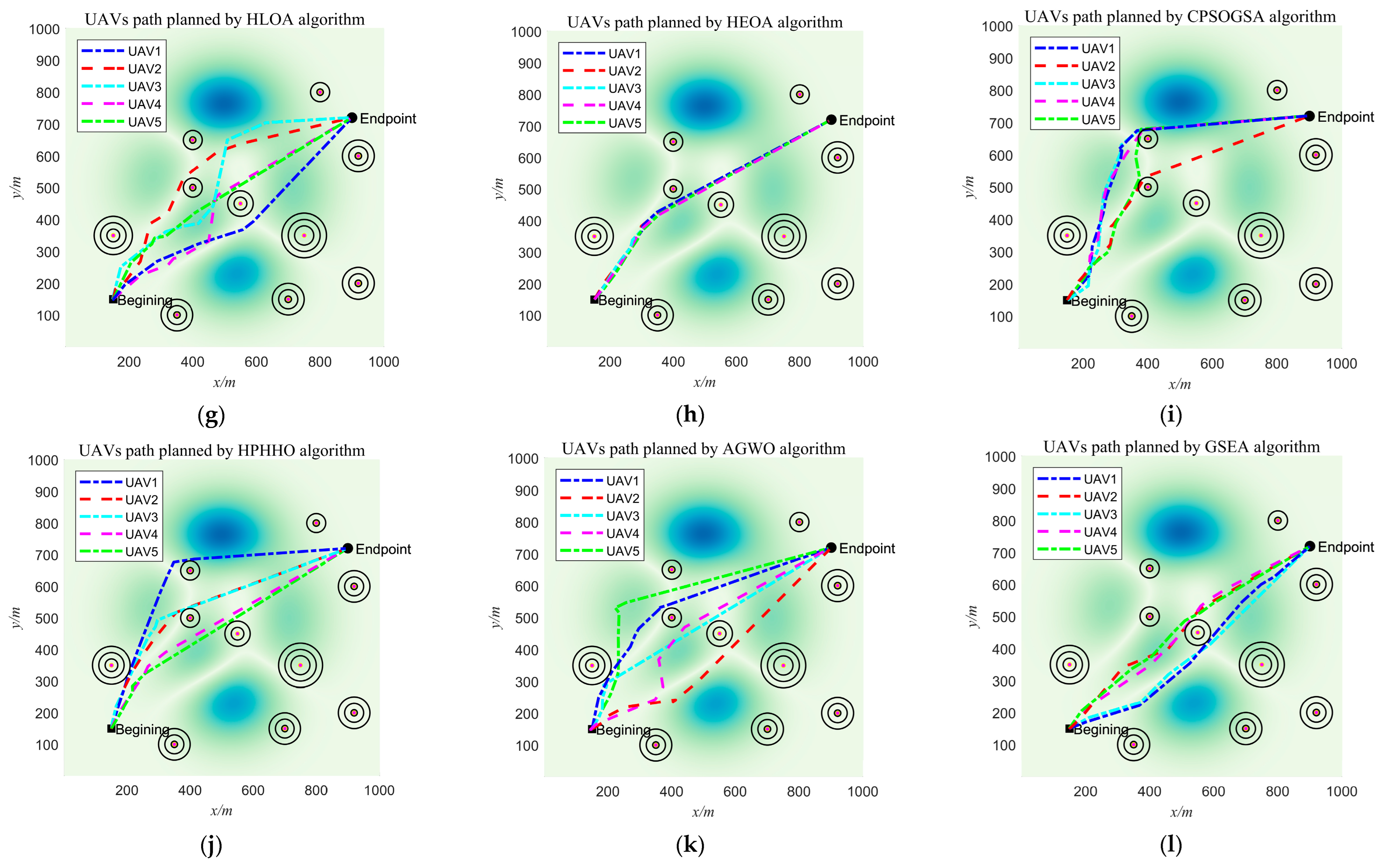
5. 3D UAV/Robot Path Planning
5.1. 3D UAV Path Planning
5.1.1. Modeling of the UAV Flight Environment
5.1.2. Modeling of UAV Flight Cost Function
- Path Shortest Constraints
- 2.
- Threat minimization constraints
- 3.
- Flight level constraints
- 4.
- Flight angle constraints
- 5.
- Multi-factor flight cost function
5.1.3. Analysis of Experimental Results
5.2. Mobile Robot Path Planning
5.2.1. Environmental Mathematical Model
5.2.2. Analysis of the Results of the Dynamic Map Experiment
6. Conclusions and Prospects
- We plan to combine reinforcement learning with algorithms to enhance the adaptive and self-learning capabilities of the algorithms, so that the algorithms are able to learn while running, and to improve the adaptability of the algorithms in solving problems.
- We plan to further extend the application area of this algorithm to a wider range of domains, including cloud resource scheduling, fault diagnosis, 3D reconstruction, and so on.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, X.; He, F.; Li, L.; Zhang, L.; Xiao, G. A Route Network Planning Method for Urban Air Delivery. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102872. [Google Scholar] [CrossRef]
- Chern, C.; Wang, H.; Huang, K. A Heuristic Master Planning Algorithm for Recycling Supply Chain Management. J. Intell. Manuf. 2017, 28, 985–1003. [Google Scholar] [CrossRef]
- Luo, J.; Wang, Z.; Xia, M.; Wu, L.; Tian, Y.; Chen, Y. Path Planning for UAV Communication Networks: Related Technologies, Solutions, and Opportunities. ACM Comput. Surv. 2023, 55, 193. [Google Scholar] [CrossRef]
- Lyu, D.; Chen, Z.; Cai, Z.; Piao, S. Robot Path Planning by Leveraging the Graph-Encoded Floyd Algorithm. Future Gener. Comput. Syst. 2021, 122, 204–208. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path Planning Techniques for Mobile Robots: Review and Prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Hao, G.; Lv, Q.; Huang, Z.; Zhao, H.; Chen, W. UAV Path Planning Based on Improved Artificial Potential Field Method. Aerospace 2023, 10, 562. [Google Scholar] [CrossRef]
- Liu, C.; Mao, Q.; Chu, X.; Xie, S. An Improved A-Star Algorithm Considering Water Current, Traffic Separation and Berthing for Vessel Path Planning. Appl. Sci. 2019, 9, 1057. [Google Scholar] [CrossRef]
- Jiang, J.; Yahya, W.; Ananta, M. Load Balancing and Multicasting Using the Extended Dijkstra’s Algorithm in Software Defined Networking. In Intelligent Systems and Applications; Chu, W., Chao, H., Yang, S., Eds.; IOS Press: Amsterdam, The Netherlands, 2015; Volume 274, pp. 2123–2132. [Google Scholar]
- Shi, K.; Denny, J.; Amato, N. Spark PRM: Using RRTs Within PRMs to Efficiently Explore Narrow Passages. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4659–4666. [Google Scholar]
- Liao, B.; Hua, Y.; Wan, F.; Zhu, S.; Zong, Y.; Qing, X. Stack-RRT*: A Random Tree Expansion Algorithm for Smooth Path Planning. Int. J. Control Autom. Syst. 2023, 21, 993–1004. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P. Heterogeneous Comprehensive Learning Particle Swarm Optimization with Enhanced Exploration and Exploitation. Swarm Evol. Comput. 2015, 24, 11–24. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Zhang, Q. Alpha Evolution: An Efficient Evolutionary Algorithm with Evolution Path Adaptation and Matrix Generation. Eng. Appl. Artif. Intell. 2024, 137, 109202. [Google Scholar] [CrossRef]
- Ouyang, K.; Fu, S.; Chen, Y.; Cai, Q.; Heidari, A.A.; Chen, H. Escape: An Optimization Method Based on Crowd Evacuation Behaviors. Artif. Intell. Rev. 2024, 58, 19. [Google Scholar] [CrossRef]
- Minh, H.-L.; Sang-To, T.; Abdel Wahab, M.; Cuong-Le, T. A New Metaheuristic Optimization Based on K-Means Clustering Algorithm and Its Application to Structural Damage Identification. Knowl. Based Syst. 2022, 251, 109189. [Google Scholar] [CrossRef]
- Alsattar, H.; Zaidan, A.; Zaidan, B. Novel Meta-Heuristic Bald Eagle Search Optimisation Algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.; Gandomi, A. A Survey of Learning-Based Intelligent Optimization Algorithms. Arch. Comput. Methods Eng. 2021, 28, 3781–3799. [Google Scholar] [CrossRef]
- Ning, Z.; Sun, S.; Wang, X.; Guo, L.; Guo, S.; Hu, X.; Hu, B.; Kwok, R. Blockchain-Enabled Intelligent Transportation Systems: A Distributed Crowdsensing Framework. IEEE Trans. Mob. Comput. 2022, 21, 4201–4217. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-Objective Optimization Methods and Application in Energy Saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A. Artificial Fish Swarm Algorithm: A Survey of the State-of-the-Art, Hybridization, Combinatorial and Indicative Applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P. Ensemble Particle Swarm Optimizer. Appl. Soft Comput. 2017, 55, 533–548. [Google Scholar] [CrossRef]
- Chen, M.; Wu, Q.; Jiang, C. A Modified Ant Optimization Algorithm for Path Planning of UCAV. Appl. Soft Comput. 2008, 8, 1712–1718. [Google Scholar] [CrossRef]
- Jan, G.; Chang, K.; Parberry, I. Optimal Path Planning for Mobile Robot Navigation. IEEE ASME Trans. Mechatron. 2008, 13, 451–460. [Google Scholar] [CrossRef]
- Duan, H.; Liu, S.; Wu, J. Novel Intelligent Water Drops Optimization Approach to Single UCAV Smooth Trajectory Planning. Aerosp. Sci. Technol. 2009, 13, 442–449. [Google Scholar] [CrossRef]
- Garcia, M.; Montiel, O.; Castillo, O.; Sepúlveda, R.; Melin, P. Path Planning for Autonomous Mobile Robot Navigation with Ant Colony Optimization and Fuzzy Cost Function Evaluation. Appl. Soft Comput. 2009, 9, 1102–1110. [Google Scholar] [CrossRef]
- Kala, R.; Shukla, A.; Tiwari, R. Fusion of Probabilistic A* Algorithm and Fuzzy Inference System for Robotic Path Planning. Artif. Intell. Rev. 2010, 33, 307–327. [Google Scholar] [CrossRef]
- Xu, C.; Duan, H.; Liu, F. Chaotic Artificial Bee Colony Approach to Uninhabited Combat Air Vehicle (UCAV) Path Planning. Aerosp. Sci. Technol. 2010, 14, 535–541. [Google Scholar] [CrossRef]
- Soulignac, M. Feasible and Optimal Path Planning in Strong Current Fields. IEEE Trans. Robot. 2011, 27, 89–98. [Google Scholar] [CrossRef]
- Wang, C.; Hwang, R.; Ting, C. UbiPaPaGo: Context-Aware Path Planning. Expert Syst. Appl. 2011, 38, 4150–4161. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y. A New Vibrational Genetic Algorithm Enhanced with a Voronoi Diagram for Path Planning of Autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55. [Google Scholar] [CrossRef]
- Kala, R. Multi-Robot Path Planning Using Co-Evolutionary Genetic Programming. Expert Syst. Appl. 2012, 39, 3817–3831. [Google Scholar] [CrossRef]
- Davoodi, M.; Panahi, F.; Mohades, A.; Hashemi, S. Multi-Objective Path Planning in Discrete Space. Appl. Soft Comput. 2013, 13, 709–720. [Google Scholar] [CrossRef]
- Fu, Y.; Ding, M.; Zhou, C.; Hu, H. Route Planning for Unmanned Aerial Vehicle (UAV) on the Sea Using Hybrid Differential Evolution and Quantum-Behaved Particle Swarm Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1451–1465. [Google Scholar] [CrossRef]
- Zhu, W.; Duan, H. Chaotic Predator-Prey Biogeography-Based Optimization Approach for UCAV Path Planning. Aerosp. Sci. Technol. 2014, 32, 153–161. [Google Scholar] [CrossRef]
- Asl, A.; Menhaj, M.; Sajedin, A. Control of Leader-Follower Formation and Path Planning of Mobile Robots Using Asexual Reproduction Optimization (ARO). Appl. Soft Comput. 2014, 14, 563–576. [Google Scholar] [CrossRef]
- Zhu, Z.; Xiao, J.; Li, J.; Wang, F.; Zhang, Q. Global Path Planning of Wheeled Robots Using Multi-Objective Memetic Algorithms. Integr. Comput. Aided Eng. 2015, 22, 387–404. [Google Scholar] [CrossRef]
- Mo, H.; Xu, L. Research of Biogeography Particle Swarm Optimization for Robot Path Planning. Neurocomputing 2015, 148, 91–99. [Google Scholar] [CrossRef]
- Oral, T.; Polat, F. MOD* Lite: An Incremental Path Planning Algorithm Taking Care of Multiple Objectives. IEEE Trans. Cybern. 2016, 46, 245–257. [Google Scholar] [CrossRef]
- Li, J.; Deng, G.; Luo, C.; Lin, Q.; Yan, Q.; Ming, Z. A Hybrid Path Planning Method in Unmanned Air/Ground Vehicle (UAV/UGV) Cooperative Systems. IEEE Trans. Veh. Technol. 2016, 65, 9585–9596. [Google Scholar] [CrossRef]
- Tong, J.; Wu, C.; Jiang, H.; Yu, Y.; Rao, X. Optimizing the Path of Seedling Low-Density Transplanting by Using Greedy Genetic Algorithm. Comput. Electron. Agric. 2017, 142, 356–368. [Google Scholar] [CrossRef]
- Mac, T.; Copot, C.; Tran, D.; De Keyser, R. A Hierarchical Global Path Planning Approach for Mobile Robots Based on Multi-Objective Particle Swarm Optimization. Appl. Soft Comput. 2017, 59, 68–76. [Google Scholar] [CrossRef]
- Wu, X.; Bai, W.; Xie, Y.; Sun, X.; Deng, C.; Cui, H. A Hybrid Algorithm of Particle Swarm Optimization, Metropolis Criterion and RTS Smoother for Path Planning of UAVs. Appl. Soft Comput. 2018, 73, 735–747. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, M.; Yan, X. Multi-Objective Path Planning for Unmanned Surface Vehicle with Currents Effects. ISA Trans. 2018, 75, 137–156. [Google Scholar] [CrossRef]
- Yang, H.; Qi, J.; Miao, Y.; Sun, H.; Li, J. A New Robot Navigation Algorithm Based on a Double-Layer Ant Algorithm and Trajectory Optimization. IEEE Trans. Ind. Electron. 2019, 66, 8557–8566. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-Objective Multi-Robot Path Planning in Continuous Environment Using an Enhanced Genetic Algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Ajeil, F.; Ibraheem, I.; Sahib, M.; Humaidi, A. Multi-Objective Path Planning of an Autonomous Mobile Robot Using Hybrid PSO-MFB Optimization Algorithm. Appl. Soft Comput. 2020, 89, 106076. [Google Scholar] [CrossRef]
- Liu, L.; Luo, S.; Guo, F.; Tan, S. Multi-Point Shortest Path Planning Based on an Improved Discrete Bat Algorithm. Appl. Soft Comput. 2020, 95, 106498. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path Planning Optimization of Indoor Mobile Robot Based on Adaptive Ant Colony Algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, L.; You, T.; Ning, X. An Adaptive Clustering-Based Algorithm for Automatic Path Planning of Heterogeneous UAVs. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16842–16853. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, L.; Zhou, X.; Zhou, Y.; Sun, Y.; Zhu, W.; Chen, H.; Deng, W.; Chen, H.; Zhao, H. Multi-Strategy Particle Swarm and Ant Colony Hybrid Optimization for Airport Taxiway Planning Problem. Inf. Sci. 2022, 612, 576–593. [Google Scholar] [CrossRef]
- Chen, J.; Ling, F.; Zhang, Y.; You, T.; Liu, Y.; Du, X. Coverage Path Planning of Heterogeneous Unmanned Aerial Vehicles Based on Ant Colony System. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Wang, J.; Chen, H.; Deng, W. Adaptive Cylinder Vector Particle Swarm Optimization with Differential Evolution for UAV Path Planning. Eng. Appl. Artif. Intell. 2023, 121, 105942. [Google Scholar] [CrossRef]
- Lin, S.; Liu, A.; Wang, J.; Kong, X. An Intelligence-Based Hybrid PSO-SA for Mobile Robot Path Planning in Warehouse. J. Comput. Sci. 2023, 67, 101938. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Han, G.; Qian, Y.; Li, Z. A Collaborative Path Planning Method for Heterogeneous Autonomous Marine Vehicles. IEEE Internet Things J. 2024, 11, 1465–1480. [Google Scholar] [CrossRef]
- Zhang, R.; Chai, R.; Chai, S.; Xia, Y.; Tsourdos, A. Design and Practical Implementation of a High Efficiency Two-Layer Trajectory Planning Method for AGV. IEEE Trans. Ind. Electron. 2024, 71, 1811–1822. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A Survey on New Generation Metaheuristic Algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N.; Liang, J.J.; Qu, B.Y. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017. [Google Scholar]
- Kumar, A.; Price, K.V.; Mohamed, A.W.; Hadi, A.A. Problem Definitions and Evaluation Criteria for the CEC 2022 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization; Nanyang Technological University: Singapore, 2022. [Google Scholar]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Ferahtia, S.; Houari, A.; Rezk, H.; Djerioui, A.; Machmoum, M.; Motahhir, S.; Ait-Ahmed, M. Red-Tailed Hawk Algorithm for Numerical Optimization and Real-World Problems. Sci. Rep. 2023, 13, 12950. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Jafari, Z.; Navin, A.; Zamanifar, A. Task Scheduling Approach in Fog and Cloud Computing Using Jellyfish Search (JS) Optimizer and Improved Harris Hawks Optimization (IHHO) Algorithm Enhanced by Deep Learning. Clust. Comput. 2024, 27, 8939–8963. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Peraza-Vázquez, H.; Peña-Delgado, A.; Merino-Treviño, M.; Morales-Cepeda, A.B.; Sinha, N. A Novel Metaheuristic Inspired by Horned Lizard Defense Tactics. Artif. Intell. Rev. 2024, 57, 59. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly Optimization Algorithm: A Novel Approach for Global Optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G. Human Evolutionary Optimization Algorithm. Expert Syst. Appl. 2024, 241, 122638. [Google Scholar] [CrossRef]
- Dao, F.; Zou, Y.; Zeng, Y.; Qian, J.; Li, X. An Intelligent CPSOGSA-Based Mixed H2/H∞ Robust Controller for the Multi-Hydro-Turbine Governing System with Sharing Common Penstock. Renew. Energy 2023, 206, 481–497. [Google Scholar] [CrossRef]
- Su, Y.; Dai, Y.; Liu, Y. A Hybrid Parallel Harris Hawks Optimization Algorithm for Reusable Launch Vehicle Reentry Trajectory Optimization with No-Fly Zones. Soft Comput. 2021, 25, 14597–14617. [Google Scholar] [CrossRef]
- Ma, C.; Huang, H.; Fan, Q.; Wei, J.; Du, Y.; Gao, W. Grey Wolf Optimizer Based on Aquila Exploration Method. Expert Syst. Appl. 2022, 205, 117629. [Google Scholar] [CrossRef]
- Zhang, Q.; Bing, W.; Wei, L.; Wang, H. Chicken Swarm Optimization Algorithm Based on Quantum Behavior and Its Convergence Analysis. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; Fu, J., Sun, J., Eds.; IEEE: New York, NY, USA, 2020; pp. 2107–2112. [Google Scholar]
- Huan, T.T.; Kulkarni, A.J.; Kanesan, J.; Huang, C.J.; Abraham, A. Ideology Algorithm: A Socio-Inspired Optimization Methodology. Neural Comput. Appl. 2017, 28, 845–876. [Google Scholar] [CrossRef]
- López-Vázquez, C.; Hochsztain, E. Extended and Updated Tables for the Friedman Rank Test. Commun. Stat. Theory Methods 2019, 48, 268–281. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, Z.; Liu, Y. Survey on Computational-Intelligence-Based UAV Path Planning. Knowl. Based Syst. 2018, 158, 54–64. [Google Scholar] [CrossRef]
- Dam, T.; Chalvatzaki, G.; Peters, J.; Pajarinen, J. Monte-Carlo Robot Path Planning. IEEE Robot. Autom. Lett. 2022, 7, 11213–11220. [Google Scholar] [CrossRef]


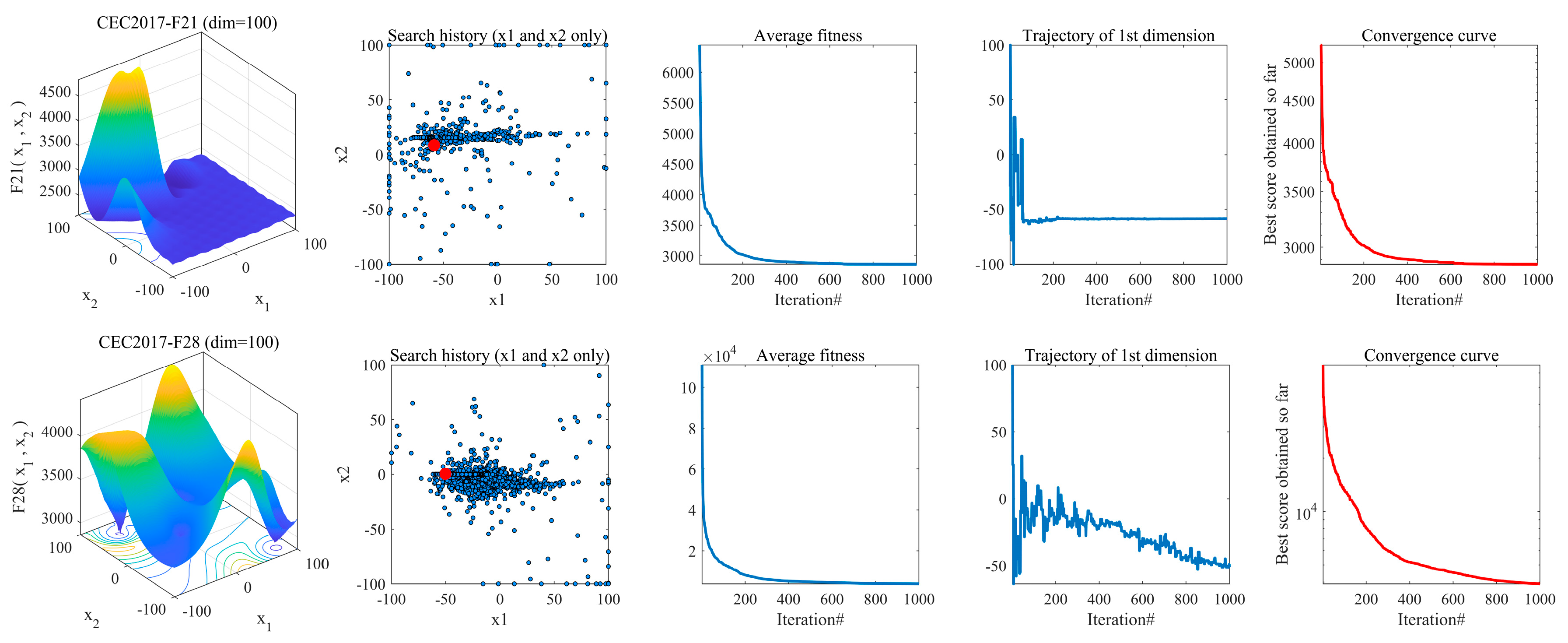



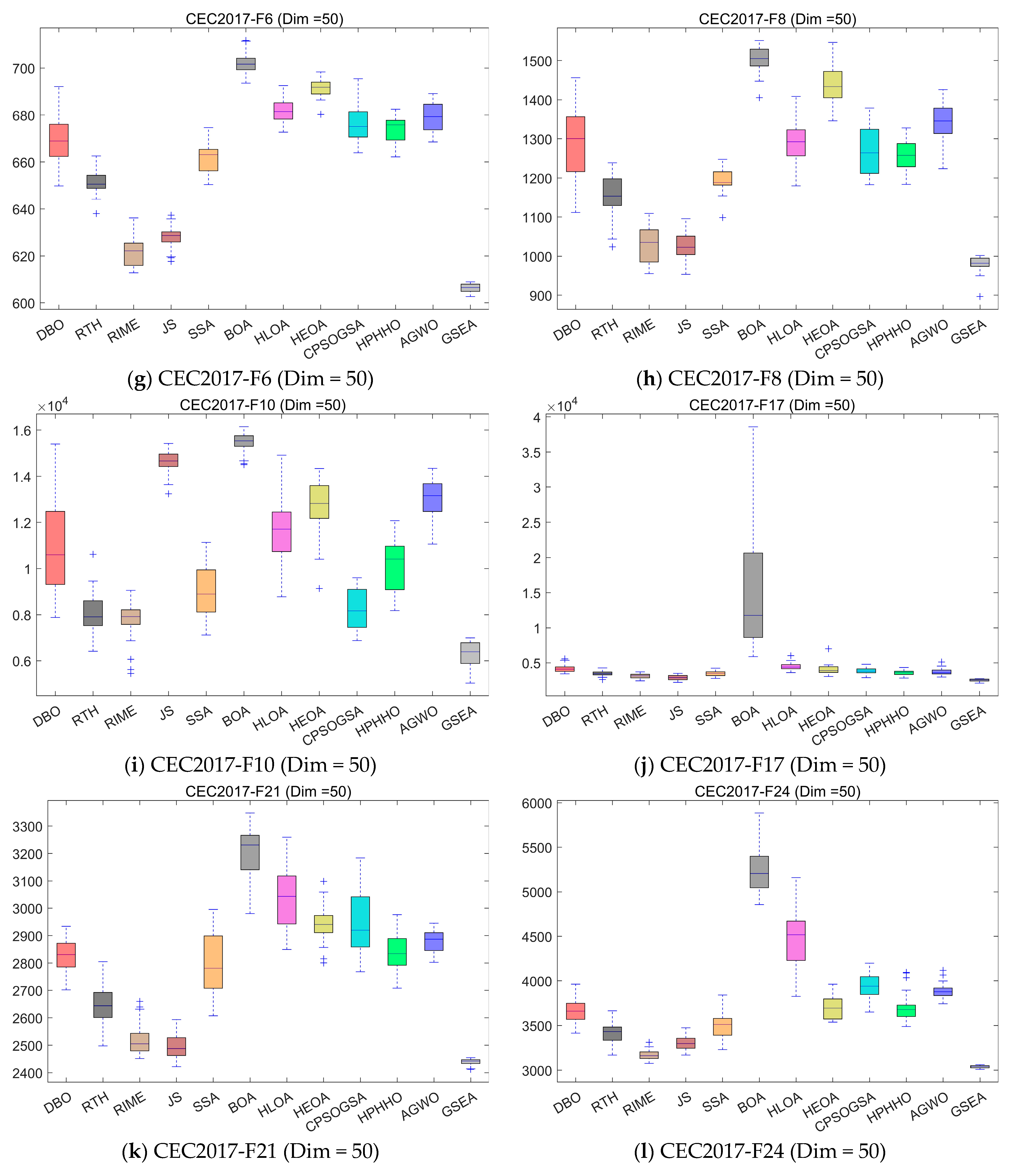
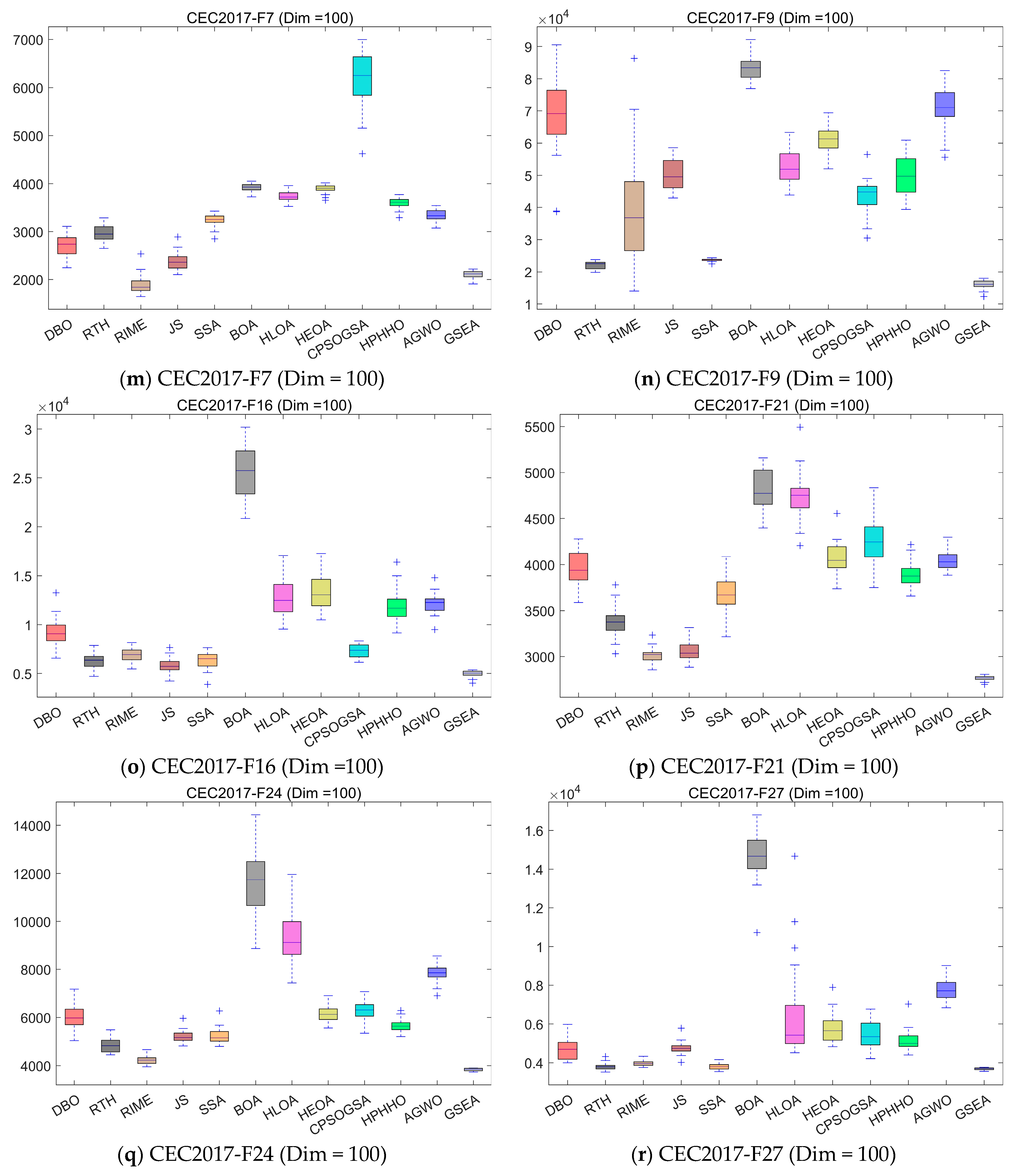


| No. | Functions | Search Range | Dim | fmin |
|---|---|---|---|---|
| Unimodal functions | ||||
| F1 | Shifted and Rotated Bent Cigar Function | [−100, 100] | 30/50/100 | 100 |
| F3 | Shifted and Rotated Zakharov Function | [−100, 100] | 30/50/100 | 300 |
| Simple multimodal functions | ||||
| F4 | Shifted and Rotated Rosenbrock’s Function | [−100, 100] | 30/50/100 | 400 |
| F5 | Shifted and Rotated Rastrigin’s Function | [−100, 100] | 30/50/100 | 500 |
| F6 | Shifted and Rotated Expanded Scaffer’s F6 Function | [−100, 100] | 30/50/100 | 600 |
| F7 | Shifted and Rotated Lunacek Bi_Rastrigin’s Function | [−100, 100] | 30/50/100 | 700 |
| F8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | [−100, 100] | 30/50/100 | 800 |
| F9 | Shifted and Rotated Levy Function | [−100, 100] | 30/50/100 | 900 |
| F10 | Shifted and Rotated Schwefel’s Function | [−100, 100] | 30/50/100 | 1000 |
| Hybrid functions | ||||
| F11 | Hybrid Function 1 (N = 3) | [−100, 100] | 30/50/100 | 1100 |
| F12 | Hybrid Function 2 (N = 3) | [−100, 100] | 30/50/100 | 1200 |
| F13 | Hybrid Function 3 (N = 3) | [−100, 100] | 30/50/100 | 1300 |
| F14 | Hybrid Function 4 (N = 4) | [−100, 100] | 30/50/100 | 1400 |
| F15 | Hybrid Function 5 (N = 4) | [−100, 100] | 30/50/100 | 1500 |
| F16 | Hybrid Function 6 (N = 4) | [−100, 100] | 30/50/100 | 1600 |
| F17 | Hybrid Function 6 (N = 5) | [−100, 100] | 30/50/100 | 1700 |
| F18 | Hybrid Function 6 (N = 5) | [−100, 100] | 30/50/100 | 1800 |
| F19 | Hybrid Function 6 (N = 5) | [−100, 100] | 30/50/100 | 1900 |
| F20 | Hybrid Function 6 (N = 6) | [−100, 100] | 30/50/100 | 2000 |
| Composition functions | ||||
| F21 | Composition Function 1 (N = 3) | [−100, 100] | 30/50/100 | 2100 |
| F22 | Composition Function 2 (N = 3) | [−100, 100] | 30/50/100 | 2200 |
| F23 | Composition Function 3 (N = 4) | [−100, 100] | 30/50/100 | 2300 |
| F24 | Composition Function 4 (N = 4) | [−100, 100] | 30/50/100 | 2400 |
| F25 | Composition Function 5 (N = 5) | [−100, 100] | 30/50/100 | 2500 |
| F26 | Composition Function 6 (N = 5) | [−100, 100] | 30/50/100 | 2600 |
| F27 | Composition Function 7 (N = 6) | [−100, 100] | 30/50/100 | 2700 |
| F28 | Composition Function 8 (N = 6) | [−100, 100] | 30/50/100 | 2800 |
| F29 | Composition Function 9 (N = 3) | [−100, 100] | 30/50/100 | 2900 |
| F30 | Composition Function 10 (N = 3) | [−100, 100] | 30/50/100 | 3000 |
| No. | Functions | Search Range | Dim | fmin |
|---|---|---|---|---|
| Unimodal function | ||||
| F1 | Shifted and full Rotated Zakharov Function | [−100, 100] | 20 | 300 |
| Basic Functions | ||||
| F2 | Shifted and full Rotated Rosenbrock’s Function | [−100, 100] | 20 | 400 |
| F3 | Shifted and full Expanded Schaffer’s f6 Function | [−100, 100] | 20 | 600 |
| F4 | Shifted and full Rotated Non-Continuous Rastrigin’s Function | [−100, 100] | 20 | 800 |
| F5 | Shifted and full Rotated Levy Function | [−100, 100] | 20 | 900 |
| Hybrid functions | ||||
| F6 | Hybrid Function 1 (N = 3) | [−100, 100] | 20 | 1800 |
| F7 | Hybrid Function 2 (N = 6) | [−100, 100] | 20 | 2000 |
| F8 | Hybrid Function 3 (N = 5) | [−100, 100] | 20 | 2200 |
| Composition functions | ||||
| F9 | Composition Function 1 (N = 5) | [−100, 100] | 20 | 2300 |
| F10 | Composition Function 2 (N = 4) | [−100, 100] | 20 | 2400 |
| F11 | Composition Function 3 (N = 5) | [−100, 100] | 20 | 2600 |
| F12 | Composition Function 5 (N = 6) | [−100, 100] | 20 | 2700 |
| Algorithm | Name of the Parameter | Value of the Parameter | n | T | References |
|---|---|---|---|---|---|
| DBO | 0.2 | 30 | 1000 | [59] | |
| RTH | 15, 1.5, 0.5 | 30 | 1000 | [60] | |
| RIME | 5 | 30 | 1000 | [61] | |
| JS | 1 | 30 | 1000 | [62] | |
| SSA | 0.2 | 30 | 1000 | [63] | |
| BOA | 0.8 | 30 | 1000 | [64] | |
| HLOA | 0.5 | 30 | 1000 | [65] | |
| HEOA | 0.6, 0.4, 0.4, 0.1 | 30 | 1000 | [66] | |
| CPSOGSA | 2.05, 2.05 | 30 | 1000 | [67] | |
| HPHHO | 0.5, 0.9, 0.5, 1.5, [0, 2] | 30 | 1000 | [68] | |
| AGWO | 0.8, 0.5 | 30 | 1000 | [69] |
| ID | Items | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO | GSEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017-F1 | Ave | 3.5917E+07 | 6.1849E+03 | 6.0357E+05 | 6.9582E+05 | 6.5229E+03 | 4.9600E+10 | 4.6001E+07 | 1.2816E+10 | 3.4255E+05 | 1.2277E+09 | 1.2039E+10 | 4.0225E+02 |
| Std | 3.2062E+07 | 6.6127E+03 | 2.2575E+05 | 1.6078E+06 | 7.2584E+03 | 6.9918E+09 | 2.6820E+07 | 4.6810E+09 | 1.7892E+06 | 5.5768E+08 | 2.9583E+09 | 2.8337E+02 | |
| CEC2017-F2 | Ave | 6.6797E+31 | 2.7192E+18 | 3.7714E+13 | 6.5759E+17 | 1.0930E+13 | 6.1868E+53 | 1.6693E+37 | 1.1474E+41 | 1.1034E+30 | 1.0000E+20 | 2.3096E+35 | 9.7396E+08 |
| Std | 3.6241E+32 | 1.4771E+19 | 6.5857E+13 | 2.1034E+18 | 2.3375E+13 | 3.2655E+54 | 7.2150E+37 | 6.2847E+41 | 2.8391E+30 | 0.0000E+00 | 1.0855E+36 | 1.7532E+09 | |
| CEC2017-F3 | Ave | 7.4586E+04 | 3.0000E+02 | 1.2443E+04 | 4.1394E+04 | 2.9344E+04 | 7.8200E+04 | 2.0451E+04 | 6.5972E+04 | 1.1454E+05 | 3.6085E+04 | 6.5946E+04 | 8.5211E+03 |
| Std | 1.2693E+04 | 1.3717E-03 | 3.8797E+03 | 7.8544E+03 | 5.5459E+03 | 6.6435E+03 | 7.7203E+03 | 7.3365E+03 | 3.8327E+04 | 9.2223E+03 | 1.0467E+04 | 2.3263E+03 | |
| CEC2017-F4 | Ave | 5.9364E+02 | 4.4586E+02 | 5.0961E+02 | 5.2508E+02 | 4.9426E+02 | 2.1605E+04 | 5.5261E+02 | 1.6348E+03 | 5.1909E+02 | 6.6115E+02 | 1.5416E+03 | 4.6809E+02 |
| Std | 8.2621E+01 | 3.5587E+01 | 2.5032E+01 | 3.0601E+01 | 2.6146E+01 | 3.2577E+03 | 4.4405E+01 | 6.1414E+02 | 3.9820E+01 | 1.0991E+02 | 7.0115E+02 | 2.7255E+01 | |
| CEC2017-F5 | Ave | 7.5526E+02 | 6.8351E+02 | 5.9539E+02 | 5.8809E+02 | 7.5090E+02 | 9.1177E+02 | 8.0822E+02 | 8.4022E+02 | 8.0885E+02 | 7.5711E+02 | 7.7489E+02 | 5.6961E+02 |
| Std | 6.1758E+01 | 3.4393E+01 | 2.3437E+01 | 2.3026E+01 | 5.6826E+01 | 2.3200E+01 | 4.4307E+01 | 3.8428E+01 | 5.0587E+01 | 3.7713E+01 | 3.1465E+01 | 8.3017E+00 | |
| CEC2017-F6 | Ave | 6.5089E+02 | 6.4137E+02 | 6.0908E+02 | 6.1478E+02 | 6.4483E+02 | 6.8593E+02 | 6.7477E+02 | 6.7251E+02 | 6.6710E+02 | 6.5787E+02 | 6.5869E+02 | 6.0056E+02 |
| Std | 9.0743E+00 | 8.1505E+00 | 5.5324E+00 | 4.4188E+00 | 1.2300E+01 | 7.2815E+00 | 1.0748E+01 | 7.1028E+00 | 7.9285E+00 | 6.7616E+00 | 7.5579E+00 | 3.3184E-01 | |
| CEC2017-F7 | Ave | 1.0015E+03 | 1.0978E+03 | 8.3888E+02 | 8.7526E+02 | 1.2550E+03 | 1.3826E+03 | 1.3348E+03 | 1.3572E+03 | 1.5970E+03 | 1.2013E+03 | 1.1168E+03 | 8.3243E+02 |
| Std | 9.0008E+01 | 8.7582E+01 | 2.8198E+01 | 5.0293E+01 | 8.4973E+01 | 3.7165E+01 | 4.9569E+01 | 8.0332E+01 | 2.2772E+02 | 9.8517E+01 | 4.5043E+01 | 1.2611E+01 | |
| CEC2017-F8 | Ave | 1.0332E+03 | 9.4357E+02 | 9.0109E+02 | 8.7773E+02 | 9.7130E+02 | 1.1397E+03 | 1.0047E+03 | 1.0820E+03 | 1.0210E+03 | 9.9495E+02 | 1.0150E+03 | 8.6552E+02 |
| Std | 5.3794E+01 | 3.1697E+01 | 3.1601E+01 | 2.2869E+01 | 2.9512E+01 | 2.1955E+01 | 3.6856E+01 | 2.9766E+01 | 4.2480E+01 | 2.2913E+01 | 2.5096E+01 | 8.3413E+00 | |
| CEC2017-F9 | Ave | 5.6889E+03 | 4.1045E+03 | 2.7125E+03 | 1.8943E+03 | 5.1297E+03 | 1.1171E+04 | 6.7049E+03 | 8.1965E+03 | 7.4810E+03 | 6.1328E+03 | 6.5537E+03 | 1.1884E+03 |
| Std | 1.7680E+03 | 6.5502E+02 | 1.5904E+03 | 6.9700E+02 | 5.7480E+02 | 1.0251E+03 | 1.0567E+03 | 1.3461E+03 | 1.8736E+03 | 5.6936E+02 | 1.0645E+03 | 1.2470E+02 | |
| CEC2017-F10 | Ave | 6.4907E+03 | 5.2775E+03 | 4.2618E+03 | 8.1459E+03 | 5.2330E+03 | 9.0118E+03 | 6.6383E+03 | 7.4159E+03 | 5.1057E+03 | 5.6050E+03 | 7.1174E+03 | 3.8609E+03 |
| Std | 9.8029E+02 | 6.4865E+02 | 6.1824E+02 | 6.1961E+02 | 6.3391E+02 | 3.2088E+02 | 9.2365E+02 | 6.3230E+02 | 6.6812E+02 | 6.1456E+02 | 8.7168E+02 | 4.1218E+02 | |
| CEC2017-F11 | Ave | 1.5945E+03 | 1.2438E+03 | 1.2762E+03 | 1.2294E+03 | 1.3100E+03 | 7.6172E+03 | 1.3846E+03 | 3.8948E+03 | 1.2639E+03 | 1.4813E+03 | 4.1183E+03 | 1.1383E+03 |
| Std | 2.6798E+02 | 4.7806E+01 | 4.7345E+01 | 3.7960E+01 | 6.8238E+01 | 2.1249E+03 | 7.1983E+01 | 1.2975E+03 | 5.6351E+01 | 1.0429E+02 | 1.7348E+03 | 1.4089E+01 | |
| CEC2017-F12 | Ave | 4.7778E+07 | 3.2377E+04 | 1.1018E+07 | 1.1476E+06 | 6.6517E+05 | 1.3761E+10 | 1.8383E+07 | 3.2692E+08 | 3.1597E+06 | 8.5914E+07 | 5.7649E+08 | 1.3743E+05 |
| Std | 7.4876E+07 | 1.5838E+04 | 1.0673E+07 | 9.3309E+05 | 5.4980E+05 | 4.1771E+09 | 1.6878E+07 | 2.0065E+08 | 4.1918E+06 | 5.7737E+07 | 4.4606E+08 | 6.8600E+04 | |
| CEC2017-F13 | Ave | 4.5835E+06 | 2.0645E+04 | 6.2328E+04 | 1.0369E+04 | 1.6544E+05 | 1.1639E+10 | 7.7669E+05 | 5.5986E+06 | 5.4152E+04 | 1.1039E+06 | 1.1234E+08 | 3.1487E+03 |
| Std | 7.9353E+06 | 2.2344E+04 | 8.5956E+04 | 9.6460E+03 | 8.1151E+05 | 4.7243E+09 | 1.7000E+06 | 1.1422E+07 | 2.9687E+04 | 1.3036E+06 | 1.9572E+08 | 1.3943E+03 | |
| CEC2017-F14 | Ave | 1.8232E+05 | 2.1765E+03 | 6.5564E+04 | 1.6559E+04 | 4.3685E+04 | 4.0150E+06 | 1.0391E+05 | 1.1401E+06 | 8.9122E+04 | 3.4026E+05 | 7.9721E+05 | 3.8242E+03 |
| Std | 2.2334E+05 | 6.6556E+02 | 6.0435E+04 | 1.4086E+04 | 3.1281E+04 | 3.1546E+06 | 1.5342E+05 | 8.6343E+05 | 1.1784E+05 | 3.3438E+05 | 7.9360E+05 | 1.0997E+03 | |
| CEC2017-F15 | Ave | 9.3324E+04 | 9.6126E+03 | 1.2122E+04 | 5.7000E+03 | 1.2874E+04 | 5.4226E+08 | 1.2495E+05 | 6.7504E+05 | 1.9950E+04 | 4.1997E+04 | 2.2551E+06 | 2.8888E+03 |
| Std | 8.5410E+04 | 1.1606E+04 | 1.1084E+04 | 4.0784E+03 | 1.6466E+04 | 4.2597E+08 | 5.2038E+05 | 7.1902E+05 | 1.2791E+04 | 3.4167E+04 | 3.7172E+06 | 9.6464E+02 | |
| CEC2017-F16 | Ave | 3.4018E+03 | 2.8265E+03 | 2.6325E+03 | 2.4724E+03 | 2.9970E+03 | 7.6177E+03 | 3.8453E+03 | 3.7639E+03 | 3.2760E+03 | 3.0066E+03 | 3.3388E+03 | 2.1513E+03 |
| Std | 4.0297E+02 | 2.9317E+02 | 2.7966E+02 | 2.7851E+02 | 3.4795E+02 | 2.4171E+03 | 6.6316E+02 | 8.3133E+02 | 3.4030E+02 | 4.1709E+02 | 3.0521E+02 | 1.6421E+02 | |
| CEC2017-F17 | Ave | 2.5946E+03 | 2.4975E+03 | 2.1263E+03 | 1.9309E+03 | 2.5055E+03 | 1.3328E+04 | 2.9229E+03 | 2.6109E+03 | 2.6344E+03 | 2.3552E+03 | 2.3982E+03 | 1.8188E+03 |
| Std | 3.1361E+02 | 2.8548E+02 | 2.2926E+02 | 1.2367E+02 | 2.9816E+02 | 1.8505E+04 | 3.4021E+02 | 2.8533E+02 | 2.6746E+02 | 2.6904E+02 | 2.5625E+02 | 6.3493E+01 | |
| CEC2017-F18 | Ave | 3.3070E+06 | 2.5114E+04 | 8.0717E+05 | 6.3591E+05 | 3.3263E+05 | 6.9863E+07 | 5.5877E+05 | 6.0215E+06 | 9.0152E+05 | 1.4525E+06 | 5.1933E+06 | 5.3281E+04 |
| Std | 4.4027E+06 | 3.3420E+04 | 5.9211E+05 | 6.8027E+05 | 3.0403E+05 | 9.1958E+07 | 5.9755E+05 | 5.1486E+06 | 1.0288E+06 | 1.1923E+06 | 7.7429E+06 | 2.2037E+04 | |
| CEC2017-F19 | Ave | 5.7797E+06 | 7.0364E+03 | 2.0534E+04 | 7.8626E+03 | 9.9326E+03 | 5.1978E+08 | 6.4581E+04 | 5.3768E+06 | 1.2615E+04 | 1.1514E+06 | 1.0284E+07 | 2.3419E+03 |
| Std | 1.8557E+07 | 6.4845E+03 | 1.9772E+04 | 6.4607E+03 | 1.3840E+04 | 3.5941E+08 | 8.9073E+04 | 2.8668E+06 | 1.4688E+04 | 1.8548E+06 | 2.6679E+07 | 3.6972E+02 | |
| CEC2017-F20 | Ave | 2.6207E+03 | 2.6932E+03 | 2.4926E+03 | 2.3648E+03 | 2.7817E+03 | 3.0188E+03 | 3.0744E+03 | 2.8113E+03 | 2.9834E+03 | 2.5838E+03 | 2.7129E+03 | 2.1342E+03 |
| Std | 1.9840E+02 | 2.1949E+02 | 2.0727E+02 | 1.3261E+02 | 1.8385E+02 | 1.2865E+02 | 2.7287E+02 | 2.1902E+02 | 2.5557E+02 | 1.8983E+02 | 1.9281E+02 | 4.9219E+01 | |
| CEC2017-F21 | Ave | 2.5673E+03 | 2.4647E+03 | 2.4019E+03 | 2.3754E+03 | 2.5150E+03 | 2.7161E+03 | 2.6546E+03 | 2.5906E+03 | 2.5663E+03 | 2.5318E+03 | 2.5541E+03 | 2.3598E+03 |
| Std | 4.5157E+01 | 3.9287E+01 | 3.2599E+01 | 1.7421E+01 | 3.9573E+01 | 6.6462E+01 | 5.6610E+01 | 3.4566E+01 | 4.1545E+01 | 4.0631E+01 | 2.9194E+01 | 8.3140E+00 | |
| CEC2017-F22 | Ave | 5.0790E+03 | 4.5211E+03 | 4.8287E+03 | 2.3116E+03 | 6.0563E+03 | 6.9834E+03 | 7.8902E+03 | 7.3159E+03 | 6.5842E+03 | 4.8203E+03 | 6.1318E+03 | 2.3000E+03 |
| Std | 2.2161E+03 | 2.3253E+03 | 1.9119E+03 | 8.5503E+00 | 2.0360E+03 | 1.0948E+03 | 1.5992E+03 | 1.8105E+03 | 1.3761E+03 | 2.5442E+03 | 2.4781E+03 | 1.6707E-07 | |
| CEC2017-F23 | Ave | 3.0296E+03 | 2.8944E+03 | 2.7731E+03 | 2.7889E+03 | 2.9384E+03 | 3.4644E+03 | 3.3652E+03 | 3.1291E+03 | 3.1166E+03 | 2.9709E+03 | 3.0236E+03 | 2.7012E+03 |
| Std | 6.1993E+01 | 6.3111E+01 | 3.1507E+01 | 4.0008E+01 | 7.4832E+01 | 1.5564E+02 | 1.6653E+02 | 1.3445E+02 | 9.5442E+01 | 8.6136E+01 | 6.2097E+01 | 1.1623E+01 | |
| CEC2017-F24 | Ave | 3.1734E+03 | 3.0416E+03 | 2.9306E+03 | 2.9594E+03 | 3.0736E+03 | 4.0549E+03 | 3.5411E+03 | 3.1954E+03 | 3.3024E+03 | 3.1792E+03 | 3.2496E+03 | 2.8724E+03 |
| Std | 6.7364E+01 | 8.1154E+01 | 2.7556E+01 | 3.8451E+01 | 8.2529E+01 | 2.5318E+02 | 1.9413E+02 | 8.5994E+01 | 8.9352E+01 | 9.1974E+01 | 3.8932E+01 | 8.1961E+00 | |
| CEC2017-F25 | Ave | 2.9523E+03 | 2.8974E+03 | 2.9048E+03 | 2.9311E+03 | 2.9024E+03 | 5.7927E+03 | 2.9785E+03 | 3.2093E+03 | 2.9302E+03 | 3.0373E+03 | 3.1781E+03 | 2.8855E+03 |
| Std | 4.7761E+01 | 1.5562E+01 | 2.4442E+01 | 2.7927E+01 | 2.0983E+01 | 5.1615E+02 | 3.6628E+01 | 7.7617E+01 | 2.8245E+01 | 3.4916E+01 | 6.9337E+01 | 1.7607E+00 | |
| CEC2017-F26 | Ave | 6.7026E+03 | 5.4904E+03 | 4.7558E+03 | 4.7805E+03 | 6.2757E+03 | 1.1801E+04 | 9.0860E+03 | 8.3385E+03 | 7.6901E+03 | 6.7037E+03 | 7.3690E+03 | 4.2848E+03 |
| Std | 1.1183E+03 | 1.6497E+03 | 6.1238E+02 | 1.3148E+03 | 1.1782E+03 | 7.7475E+02 | 1.3958E+03 | 1.0271E+03 | 9.1567E+02 | 1.4655E+03 | 8.7087E+02 | 6.0534E+02 | |
| CEC2017-F27 | Ave | 3.3558E+03 | 3.2661E+03 | 3.2366E+03 | 3.2944E+03 | 3.2864E+03 | 4.2856E+03 | 3.7557E+03 | 3.4462E+03 | 3.5855E+03 | 3.3434E+03 | 3.4654E+03 | 3.2191E+03 |
| Std | 8.5092E+01 | 4.5819E+01 | 1.3575E+01 | 2.9849E+01 | 6.1784E+01 | 3.2111E+02 | 3.4559E+02 | 1.0326E+02 | 3.0558E+02 | 7.7061E+01 | 8.7042E+01 | 5.0881E+00 | |
| CEC2017-F28 | Ave | 3.4628E+03 | 3.1452E+03 | 3.2732E+03 | 3.3129E+03 | 3.2078E+03 | 8.2799E+03 | 3.3093E+03 | 4.1391E+03 | 3.2688E+03 | 3.4136E+03 | 3.8814E+03 | 3.2038E+03 |
| Std | 2.9725E+02 | 5.9412E+01 | 5.3291E+01 | 3.6568E+01 | 2.8021E+01 | 4.8780E+02 | 3.1389E+01 | 3.2287E+02 | 2.7164E+01 | 6.8985E+01 | 2.1212E+02 | 4.6917E+00 | |
| CEC2017-F29 | Ave | 4.5364E+03 | 4.2239E+03 | 3.9469E+03 | 3.8814E+03 | 4.1996E+03 | 1.5177E+04 | 5.8414E+03 | 5.3726E+03 | 4.5657E+03 | 4.3456E+03 | 4.6519E+03 | 3.4934E+03 |
| Std | 3.4669E+02 | 4.1072E+02 | 2.5985E+02 | 2.0379E+02 | 3.1400E+02 | 1.1299E+04 | 8.0940E+02 | 4.7225E+02 | 3.2454E+02 | 3.1564E+02 | 2.7251E+02 | 8.9152E+01 | |
| CEC2017-F30 | Ave | 4.6413E+06 | 1.0560E+04 | 2.5265E+05 | 1.1828E+04 | 5.2803E+04 | 1.7058E+09 | 1.2929E+06 | 5.4702E+07 | 3.0454E+05 | 9.5511E+06 | 3.6086E+07 | 6.4192E+03 |
| Std | 6.1151E+06 | 3.4820E+03 | 2.4365E+05 | 6.0650E+03 | 2.1211E+05 | 9.7107E+08 | 1.5223E+06 | 3.2007E+07 | 2.8669E+05 | 8.6288E+06 | 2.5334E+07 | 4.2602E+02 |
| ID | Items | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO | GSEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017-F1 | Ave | 1.0352E+09 | 3.2161E+03 | 7.1385E+06 | 3.9286E+08 | 3.1403E+03 | 1.0622E+11 | 4.2916E+08 | 4.0038E+10 | 1.4358E+09 | 1.5493E+10 | 3.6850E+10 | 4.4609E+02 |
| Std | 9.3957E+08 | 3.9047E+03 | 2.1754E+06 | 4.1611E+08 | 2.8676E+03 | 8.3616E+09 | 2.8012E+08 | 1.1552E+10 | 5.7344E+09 | 3.5209E+09 | 6.7610E+09 | 1.9159E+02 | |
| CEC2017-F2 | Ave | 3.2029E+63 | 2.9854E+39 | 2.0236E+34 | 1.6378E+48 | 1.9626E+40 | 3.4676E+95 | 7.4192E+70 | 1.7139E+66 | 7.1803E+66 | 1.0000E+20 | 3.1678E+62 | 4.3605E+26 |
| Std | 9.6579E+63 | 1.6219E+40 | 1.0203E+35 | 8.9589E+48 | 1.0749E+41 | 1.8990E+96 | 3.1499E+71 | 7.8659E+66 | 2.9251E+67 | 0.0000E+00 | 1.5725E+63 | 8.0303E+26 | |
| CEC2017-F3 | Ave | 2.1568E+05 | 5.5802E+03 | 1.2470E+05 | 1.4889E+05 | 1.7460E+05 | 2.8095E+05 | 1.3525E+05 | 1.7482E+05 | 3.0591E+05 | 1.0549E+05 | 1.4787E+05 | 6.1603E+04 |
| Std | 4.2777E+04 | 3.5797E+03 | 2.9843E+04 | 1.9991E+04 | 3.4714E+04 | 8.8415E+04 | 3.8760E+04 | 1.3825E+04 | 7.4187E+04 | 1.2338E+04 | 1.6639E+04 | 7.7734E+03 | |
| CEC2017-F4 | Ave | 9.1675E+02 | 5.0510E+02 | 6.5293E+02 | 7.7879E+02 | 5.5288E+02 | 4.0188E+04 | 8.1116E+02 | 6.9184E+03 | 8.1777E+02 | 2.0776E+03 | 6.8747E+03 | 4.8824E+02 |
| Std | 2.3022E+02 | 5.4255E+01 | 4.8902E+01 | 1.2080E+02 | 5.8859E+01 | 4.3740E+03 | 8.0391E+01 | 2.8567E+03 | 3.6449E+02 | 6.6221E+02 | 1.7430E+03 | 2.2595E+01 | |
| CEC2017-F5 | Ave | 9.5303E+02 | 8.3198E+02 | 7.2401E+02 | 7.0518E+02 | 8.7615E+02 | 1.1765E+03 | 9.6972E+02 | 1.1150E+03 | 1.0397E+03 | 9.5410E+02 | 1.0218E+03 | 6.7779E+02 |
| Std | 1.0843E+02 | 4.0545E+01 | 3.9602E+01 | 4.0864E+01 | 2.1345E+01 | 2.5705E+01 | 5.4718E+01 | 3.4069E+01 | 7.0686E+01 | 3.0949E+01 | 3.6743E+01 | 2.3191E+01 | |
| CEC2017-F6 | Ave | 6.6504E+02 | 6.5160E+02 | 6.2203E+02 | 6.2785E+02 | 6.6165E+02 | 7.0143E+02 | 6.8070E+02 | 6.9013E+02 | 6.7580E+02 | 6.7246E+02 | 6.7840E+02 | 6.0643E+02 |
| Std | 9.7807E+00 | 6.0098E+00 | 6.2915E+00 | 6.2143E+00 | 6.1545E+00 | 5.9034E+00 | 5.2271E+00 | 5.5256E+00 | 7.7145E+00 | 6.2558E+00 | 6.8335E+00 | 1.4370E+00 | |
| CEC2017-F7 | Ave | 1.3740E+03 | 1.5154E+03 | 1.0423E+03 | 1.1650E+03 | 1.7255E+03 | 2.0016E+03 | 1.8648E+03 | 1.9847E+03 | 2.6491E+03 | 1.7626E+03 | 1.5560E+03 | 1.0410E+03 |
| Std | 1.2956E+02 | 1.1950E+02 | 5.3130E+01 | 9.6066E+01 | 6.7790E+01 | 4.4162E+01 | 1.0374E+02 | 5.9994E+01 | 3.7037E+02 | 8.5481E+01 | 9.1653E+01 | 3.7898E+01 | |
| CEC2017-F8 | Ave | 1.2973E+03 | 1.1368E+03 | 1.0153E+03 | 1.0218E+03 | 1.2008E+03 | 1.4982E+03 | 1.3115E+03 | 1.4356E+03 | 1.2469E+03 | 1.2398E+03 | 1.3435E+03 | 9.8620E+02 |
| Std | 1.0933E+02 | 5.6533E+01 | 4.1938E+01 | 5.0005E+01 | 2.7193E+01 | 2.3887E+01 | 5.6435E+01 | 5.2063E+01 | 6.0933E+01 | 3.3870E+01 | 3.1327E+01 | 2.5278E+01 | |
| CEC2017-F9 | Ave | 2.4320E+04 | 1.1296E+04 | 8.3007E+03 | 1.1234E+04 | 1.3236E+04 | 3.7858E+04 | 2.0464E+04 | 2.7827E+04 | 2.0335E+04 | 2.0881E+04 | 2.8482E+04 | 3.4789E+03 |
| Std | 7.5348E+03 | 1.4133E+03 | 2.5273E+03 | 3.4037E+03 | 9.5044E+02 | 3.1599E+03 | 2.5714E+03 | 2.5525E+03 | 2.8774E+03 | 2.8641E+03 | 4.3008E+03 | 5.1594E+02 | |
| CEC2017-F10 | Ave | 1.0504E+04 | 7.8925E+03 | 7.7969E+03 | 1.4483E+04 | 8.5374E+03 | 1.5417E+04 | 1.2199E+04 | 1.2730E+04 | 8.5482E+03 | 1.0091E+04 | 1.2737E+04 | 6.2196E+03 |
| Std | 2.3513E+03 | 8.6017E+02 | 9.0606E+02 | 1.1231E+03 | 9.7740E+02 | 5.8959E+02 | 1.7146E+03 | 1.0735E+03 | 9.9953E+02 | 9.9906E+02 | 1.0379E+03 | 4.5311E+02 | |
| CEC2017-F11 | Ave | 2.7119E+03 | 1.3451E+03 | 1.5745E+03 | 1.4777E+03 | 1.3396E+03 | 2.4730E+04 | 1.8778E+03 | 7.5888E+03 | 2.2804E+03 | 2.6504E+03 | 1.1051E+04 | 1.2171E+03 |
| Std | 1.8394E+03 | 5.8714E+01 | 6.9800E+01 | 1.2607E+02 | 6.7504E+01 | 2.2268E+03 | 2.3543E+02 | 2.4675E+03 | 8.9118E+02 | 7.3693E+02 | 2.9820E+03 | 1.7055E+01 | |
| CEC2017-F12 | Ave | 4.8326E+08 | 5.8183E+05 | 8.9582E+07 | 1.2793E+07 | 5.4751E+06 | 7.5060E+10 | 2.3138E+08 | 7.1195E+09 | 7.9147E+07 | 1.0887E+09 | 1.0649E+10 | 1.2731E+06 |
| Std | 3.9342E+08 | 3.1466E+05 | 5.5210E+07 | 7.4613E+06 | 3.2971E+06 | 1.7716E+10 | 1.2616E+08 | 4.3108E+09 | 7.1754E+07 | 6.6137E+08 | 4.1960E+09 | 3.6383E+05 | |
| CEC2017-F13 | Ave | 3.1255E+07 | 1.2317E+04 | 2.2464E+05 | 1.1294E+04 | 3.1074E+04 | 4.6553E+10 | 5.2266E+06 | 2.8933E+08 | 3.4393E+07 | 6.8029E+07 | 1.2549E+09 | 1.7241E+03 |
| Std | 4.0098E+07 | 1.1358E+04 | 1.1961E+05 | 4.0974E+03 | 2.2281E+04 | 1.5421E+10 | 1.1219E+07 | 2.6016E+08 | 1.4323E+08 | 5.5911E+07 | 1.6585E+09 | 1.5837E+02 | |
| CEC2017-F14 | Ave | 3.3000E+06 | 1.2958E+04 | 3.2793E+05 | 1.0941E+05 | 1.8649E+05 | 1.1641E+08 | 8.3068E+05 | 4.4256E+06 | 4.3093E+05 | 1.5483E+06 | 6.4363E+06 | 3.3864E+04 |
| Std | 3.3751E+06 | 1.1567E+04 | 1.7036E+05 | 7.3093E+04 | 9.3692E+04 | 9.7642E+07 | 6.3074E+05 | 4.0197E+06 | 4.6680E+05 | 1.2849E+06 | 6.7554E+06 | 1.5060E+04 | |
| CEC2017-F15 | Ave | 1.0960E+07 | 1.3334E+04 | 6.9838E+04 | 8.1999E+03 | 1.8482E+04 | 8.0067E+09 | 6.3597E+04 | 1.3699E+08 | 4.9566E+04 | 2.7621E+06 | 3.3705E+08 | 2.7232E+03 |
| Std | 2.4443E+07 | 8.0469E+03 | 6.7527E+04 | 5.8804E+03 | 9.3018E+03 | 3.0972E+09 | 5.2037E+04 | 2.9544E+08 | 2.9908E+04 | 2.5022E+06 | 3.7444E+08 | 1.0236E+03 | |
| CEC2017-F16 | Ave | 4.6348E+03 | 3.6274E+03 | 3.6090E+03 | 3.1898E+03 | 3.9060E+03 | 1.0713E+04 | 5.1683E+03 | 5.7867E+03 | 4.1334E+03 | 4.4630E+03 | 4.5154E+03 | 2.7306E+03 |
| Std | 6.0851E+02 | 5.3328E+02 | 4.1176E+02 | 3.8306E+02 | 5.8464E+02 | 1.6169E+03 | 9.3909E+02 | 1.0480E+03 | 5.1136E+02 | 6.0936E+02 | 3.6187E+02 | 1.7466E+02 | |
| CEC2017-F17 | Ave | 4.1503E+03 | 3.5704E+03 | 3.2972E+03 | 3.0422E+03 | 3.5216E+03 | 1.5537E+04 | 4.2942E+03 | 4.1595E+03 | 3.6957E+03 | 3.6251E+03 | 3.8077E+03 | 2.5426E+03 |
| Std | 5.0739E+02 | 3.5587E+02 | 3.0186E+02 | 3.1803E+02 | 4.1516E+02 | 6.3220E+03 | 4.7755E+02 | 8.0323E+02 | 4.2740E+02 | 3.2539E+02 | 3.4347E+02 | 1.3471E+02 | |
| CEC2017-F18 | Ave | 5.8481E+06 | 8.2453E+04 | 4.1977E+06 | 1.2855E+06 | 1.6793E+06 | 1.9793E+08 | 3.7043E+06 | 4.0702E+07 | 1.9157E+06 | 5.6233E+06 | 2.6131E+07 | 3.4990E+05 |
| Std | 5.7943E+06 | 6.3640E+04 | 3.2709E+06 | 8.0108E+05 | 1.1048E+06 | 1.2105E+08 | 3.0243E+06 | 2.6595E+07 | 1.6006E+06 | 5.3235E+06 | 2.2625E+07 | 1.2933E+05 | |
| CEC2017-F19 | Ave | 6.7889E+06 | 1.6356E+04 | 5.7468E+04 | 2.0330E+04 | 1.8006E+04 | 3.5071E+09 | 6.1812E+05 | 4.6626E+07 | 6.2080E+04 | 1.9101E+06 | 9.8785E+07 | 1.5215E+04 |
| Std | 1.2886E+07 | 9.5971E+03 | 6.8413E+04 | 9.0598E+03 | 1.4015E+04 | 2.0846E+09 | 6.5308E+05 | 6.4513E+07 | 7.2921E+04 | 1.7683E+06 | 1.3836E+08 | 3.9835E+03 | |
| CEC2017-F20 | Ave | 3.6740E+03 | 3.3841E+03 | 3.1957E+03 | 3.5108E+03 | 3.5472E+03 | 4.2816E+03 | 4.0122E+03 | 3.7994E+03 | 3.4803E+03 | 3.3138E+03 | 3.5047E+03 | 2.6304E+03 |
| Std | 3.3425E+02 | 3.0516E+02 | 3.1522E+02 | 4.0165E+02 | 3.7616E+02 | 1.8820E+02 | 4.1729E+02 | 2.5299E+02 | 2.7657E+02 | 2.3818E+02 | 2.4491E+02 | 8.8962E+01 | |
| CEC2017-F21 | Ave | 2.8693E+03 | 2.6489E+03 | 2.5292E+03 | 2.4797E+03 | 2.7645E+03 | 3.2051E+03 | 3.0519E+03 | 2.9390E+03 | 2.9432E+03 | 2.8309E+03 | 2.8580E+03 | 2.4428E+03 |
| Std | 9.0938E+01 | 8.3208E+01 | 3.8230E+01 | 4.6725E+01 | 8.9440E+01 | 6.3510E+01 | 1.4251E+02 | 7.6021E+01 | 1.0086E+02 | 5.1720E+01 | 4.2587E+01 | 1.2042E+01 | |
| CEC2017-F22 | Ave | 1.2699E+04 | 1.0026E+04 | 9.3826E+03 | 1.5073E+04 | 1.0328E+04 | 1.7066E+04 | 1.3782E+04 | 1.3569E+04 | 1.0347E+04 | 1.2190E+04 | 1.5565E+04 | 7.2353E+03 |
| Std | 2.1914E+03 | 1.0156E+03 | 9.5927E+02 | 2.8653E+03 | 9.9450E+02 | 5.9999E+02 | 1.2246E+03 | 1.1354E+03 | 9.7496E+02 | 1.1287E+03 | 9.2705E+02 | 2.0428E+03 | |
| CEC2017-F23 | Ave | 3.4903E+03 | 3.2556E+03 | 3.0043E+03 | 3.1005E+03 | 3.3268E+03 | 4.5273E+03 | 4.2223E+03 | 3.6917E+03 | 3.6133E+03 | 3.4506E+03 | 3.6239E+03 | 2.8783E+03 |
| Std | 1.9103E+02 | 1.2819E+02 | 5.5002E+01 | 6.7197E+01 | 1.2897E+02 | 2.2521E+02 | 3.3075E+02 | 1.5214E+02 | 1.5027E+02 | 1.1162E+02 | 9.1596E+01 | 2.0576E+01 | |
| CEC2017-F24 | Ave | 3.6902E+03 | 3.4589E+03 | 3.1400E+03 | 3.2842E+03 | 3.4945E+03 | 5.3011E+03 | 4.2858E+03 | 3.7587E+03 | 3.9791E+03 | 3.6822E+03 | 3.8826E+03 | 3.0336E+03 |
| Std | 1.5132E+02 | 1.3762E+02 | 5.5073E+01 | 6.1681E+01 | 1.3687E+02 | 2.1638E+02 | 3.2067E+02 | 1.5259E+02 | 1.3753E+02 | 1.0555E+02 | 1.0000E+02 | 1.3021E+01 | |
| CEC2017-F25 | Ave | 3.4477E+03 | 3.0490E+03 | 3.1224E+03 | 3.2814E+03 | 3.0708E+03 | 1.6107E+04 | 3.2646E+03 | 6.6959E+03 | 3.1638E+03 | 4.1441E+03 | 5.6631E+03 | 3.0842E+03 |
| Std | 8.2391E+02 | 3.5363E+01 | 4.6769E+01 | 6.8841E+01 | 3.4888E+01 | 1.1315E+03 | 8.0439E+01 | 1.0450E+03 | 5.1007E+01 | 3.9994E+02 | 6.7586E+02 | 1.5704E+01 | |
| CEC2017-F26 | Ave | 9.5904E+03 | 9.2908E+03 | 6.5900E+03 | 8.9797E+03 | 6.5277E+03 | 1.7662E+04 | 1.3578E+04 | 1.3923E+04 | 1.2779E+04 | 1.1563E+04 | 1.2352E+04 | 6.3971E+03 |
| Std | 2.0118E+03 | 2.8295E+03 | 4.0099E+02 | 1.1139E+03 | 3.7663E+03 | 6.4046E+02 | 1.3468E+03 | 8.8759E+02 | 1.3113E+03 | 1.8854E+03 | 9.9242E+02 | 6.2839E+02 | |
| CEC2017-F27 | Ave | 4.0151E+03 | 3.6802E+03 | 3.5969E+03 | 3.8349E+03 | 3.6655E+03 | 6.6795E+03 | 4.9700E+03 | 4.3278E+03 | 4.8187E+03 | 3.9428E+03 | 4.9153E+03 | 3.4169E+03 |
| Std | 2.0410E+02 | 2.1842E+02 | 1.0596E+02 | 1.4625E+02 | 1.8132E+02 | 8.1138E+02 | 6.4202E+02 | 4.5814E+02 | 4.5829E+02 | 2.2137E+02 | 2.6956E+02 | 3.6372E+01 | |
| CEC2017-F28 | Ave | 5.7445E+03 | 3.2917E+03 | 3.3748E+03 | 3.8343E+03 | 3.3245E+03 | 1.4639E+04 | 3.5839E+03 | 6.6665E+03 | 3.6776E+03 | 4.7988E+03 | 6.6848E+03 | 3.3345E+03 |
| Std | 2.2784E+03 | 2.2899E+01 | 3.6776E+01 | 1.8664E+02 | 3.3998E+01 | 1.2293E+03 | 1.1752E+02 | 6.7297E+02 | 4.4803E+02 | 3.5689E+02 | 6.9041E+02 | 1.7773E+01 | |
| CEC2017-F29 | Ave | 6.3772E+03 | 4.9379E+03 | 4.8263E+03 | 4.6316E+03 | 5.0490E+03 | 4.0237E+05 | 8.4154E+03 | 8.4488E+03 | 6.4267E+03 | 6.4179E+03 | 7.4581E+03 | 3.8256E+03 |
| Std | 1.1055E+03 | 5.2502E+02 | 3.5890E+02 | 3.3468E+02 | 5.0886E+02 | 3.0695E+05 | 1.0611E+03 | 1.3692E+03 | 7.4359E+02 | 8.6325E+02 | 5.9816E+02 | 1.5359E+02 | |
| CEC2017-F30 | Ave | 3.8667E+07 | 9.5036E+05 | 3.1747E+07 | 4.1280E+06 | 1.6750E+06 | 6.8739E+09 | 8.7219E+07 | 4.0034E+08 | 5.9862E+07 | 1.7739E+08 | 3.7760E+08 | 8.1160E+05 |
| Std | 4.7184E+07 | 2.2367E+05 | 1.4933E+07 | 1.7022E+06 | 8.6338E+05 | 2.8884E+09 | 5.3803E+07 | 1.9373E+08 | 1.6879E+07 | 7.7781E+07 | 2.0162E+08 | 4.4879E+04 |
| ID | Items | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO | GSEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017-F1 | Ave | 3.7741E+10 | 9.3622E+03 | 1.6095E+08 | 2.2829E+10 | 4.3604E+06 | 2.5971E+11 | 4.6850E+09 | 1.5313E+11 | 8.9245E+09 | 8.1796E+10 | 1.5065E+11 | 5.1680E+07 |
| Std | 4.7516E+10 | 9.2640E+03 | 4.3176E+07 | 7.2752E+09 | 1.7900E+06 | 1.7040E+10 | 1.1209E+09 | 2.4565E+10 | 5.9123E+09 | 1.0287E+10 | 7.6575E+09 | 1.9743E+07 | |
| CEC2017-F2 | Ave | 1.7132E+98 | 5.2459E+99 | 1.3942E+98 | 2.8180E+91 | 1.8297E+99 | 2.8919E+97 | 4.6577E+62 | 1.5007E+59 | 2.1132E+59 | 1.0000E+20 | 2.4429E+53 | 6.7940E+92 |
| Std | 6.5535E+04 | 2.8733E+96 | 6.1034E+98 | 1.4676E+92 | 1.0016E+99 | 6.5535E+04 | 6.5535E+04 | 6.5535E+04 | 6.5535E+04 | 0.0000E+00 | 6.5535E+04 | 1.4631E+93 | |
| CEC2017-F3 | Ave | 5.4424E+05 | 1.1380E+05 | 5.8502E+05 | 4.2076E+05 | 6.4783E+05 | 4.4140E+05 | 3.2000E+05 | 3.4566E+05 | 7.7347E+05 | 2.8242E+05 | 3.3240E+05 | 2.6632E+05 |
| Std | 2.6340E+05 | 2.8092E+04 | 8.2293E+04 | 3.7860E+04 | 1.2169E+05 | 1.3686E+05 | 5.5478E+04 | 1.1643E+04 | 1.1236E+05 | 1.7577E+04 | 1.4264E+04 | 1.7881E+04 | |
| CEC2017-F4 | Ave | 6.9133E+03 | 6.9633E+02 | 9.8020E+02 | 2.8309E+03 | 7.7506E+02 | 1.1459E+05 | 1.7954E+03 | 2.4296E+04 | 2.8003E+03 | 1.1263E+04 | 2.3194E+04 | 9.2873E+02 |
| Std | 1.2434E+04 | 4.4245E+01 | 1.0624E+02 | 8.6067E+02 | 5.2382E+01 | 1.1336E+04 | 2.3721E+02 | 5.4852E+03 | 8.2008E+02 | 2.1331E+03 | 3.0761E+03 | 3.2239E+01 | |
| CEC2017-F5 | Ave | 1.6657E+03 | 1.2878E+03 | 1.1668E+03 | 1.1899E+03 | 1.3694E+03 | 2.0864E+03 | 1.7429E+03 | 1.8931E+03 | 1.7758E+03 | 1.6885E+03 | 1.8151E+03 | 1.0690E+03 |
| Std | 2.6519E+02 | 6.6986E+01 | 8.9348E+01 | 7.2374E+01 | 4.1429E+01 | 3.4605E+01 | 5.4926E+01 | 8.7535E+01 | 1.4242E+02 | 5.6955E+01 | 5.7904E+01 | 4.5420E+01 | |
| CEC2017-F6 | Ave | 6.7421E+02 | 6.5607E+02 | 6.4701E+02 | 6.4818E+02 | 6.6369E+02 | 7.1106E+02 | 6.9351E+02 | 7.0109E+02 | 6.8271E+02 | 6.8710E+02 | 6.9496E+02 | 6.2828E+02 |
| Std | 1.1894E+01 | 2.9144E+00 | 7.3504E+00 | 4.6355E+00 | 1.7247E+00 | 3.6568E+00 | 5.5434E+00 | 4.6054E+00 | 6.6987E+00 | 4.6228E+00 | 4.0835E+00 | 2.4833E+00 | |
| CEC2017-F7 | Ave | 2.8156E+03 | 2.9540E+03 | 1.8037E+03 | 2.4108E+03 | 3.2575E+03 | 3.9502E+03 | 3.7351E+03 | 3.8912E+03 | 6.4037E+03 | 3.5966E+03 | 3.2973E+03 | 2.1029E+03 |
| Std | 2.2959E+02 | 2.0155E+02 | 1.3406E+02 | 2.2711E+02 | 7.9562E+01 | 6.2015E+01 | 1.1859E+02 | 1.0196E+02 | 6.1556E+02 | 1.1456E+02 | 1.2289E+02 | 9.4693E+01 | |
| CEC2017-F8 | Ave | 2.1822E+03 | 1.6966E+03 | 1.5102E+03 | 1.5652E+03 | 1.8291E+03 | 2.5463E+03 | 2.1731E+03 | 2.3859E+03 | 2.1311E+03 | 2.1633E+03 | 2.2112E+03 | 1.3833E+03 |
| Std | 2.1396E+02 | 9.0453E+01 | 1.0053E+02 | 9.3559E+01 | 6.2331E+01 | 4.5090E+01 | 1.0978E+02 | 8.2236E+01 | 1.5516E+02 | 6.6627E+01 | 6.8888E+01 | 4.3439E+01 | |
| CEC2017-F9 | Ave | 6.8042E+04 | 2.2361E+04 | 4.0491E+04 | 5.0424E+04 | 2.3751E+04 | 8.2785E+04 | 5.2846E+04 | 6.0265E+04 | 4.4332E+04 | 4.6198E+04 | 7.2449E+04 | 1.5249E+04 |
| Std | 1.6803E+04 | 1.1042E+03 | 8.5029E+03 | 6.6348E+03 | 2.7445E+02 | 4.2639E+03 | 5.8394E+03 | 4.1681E+03 | 5.9732E+03 | 7.0455E+03 | 4.9522E+03 | 1.2320E+03 | |
| CEC2017-F10 | Ave | 2.6312E+04 | 1.5355E+04 | 1.7792E+04 | 3.1382E+04 | 1.6843E+04 | 3.2902E+04 | 2.7016E+04 | 2.7334E+04 | 1.6259E+04 | 2.5017E+04 | 2.9920E+04 | 1.3832E+04 |
| Std | 5.4735E+03 | 1.3807E+03 | 1.7501E+03 | 8.4885E+02 | 9.0378E+02 | 5.7391E+02 | 2.2921E+03 | 1.6001E+03 | 1.0401E+03 | 1.9119E+03 | 1.5764E+03 | 7.1653E+02 | |
| CEC2017-F11 | Ave | 1.5331E+05 | 2.3891E+03 | 1.2028E+04 | 4.4372E+04 | 2.3982E+04 | 4.0625E+05 | 4.2843E+04 | 1.6209E+05 | 1.2679E+05 | 5.5122E+04 | 1.2799E+05 | 9.9883E+03 |
| Std | 4.4585E+04 | 3.1134E+02 | 2.3490E+03 | 9.1415E+03 | 8.1507E+03 | 1.6445E+05 | 1.5387E+04 | 2.2752E+04 | 2.8559E+04 | 1.2667E+04 | 1.5551E+04 | 2.3321E+03 | |
| CEC2017-F12 | Ave | 3.2008E+09 | 4.5429E+06 | 8.5127E+08 | 1.4202E+09 | 6.6691E+07 | 1.9490E+11 | 1.6389E+09 | 5.2860E+10 | 1.7862E+09 | 1.7404E+10 | 5.8726E+10 | 1.8643E+07 |
| Std | 1.1773E+09 | 2.3800E+06 | 3.2538E+08 | 1.6535E+09 | 3.3893E+07 | 1.8490E+10 | 3.4040E+08 | 1.9316E+10 | 2.3506E+09 | 6.3638E+09 | 7.8971E+09 | 3.5585E+06 | |
| CEC2017-F13 | Ave | 1.3483E+08 | 9.6719E+03 | 1.0408E+06 | 2.4923E+05 | 3.3477E+04 | 4.4541E+10 | 3.4870E+07 | 8.8051E+09 | 2.1159E+07 | 8.9859E+08 | 9.8440E+09 | 3.2568E+03 |
| Std | 1.0904E+08 | 7.1030E+03 | 3.3615E+06 | 4.7698E+05 | 1.0727E+04 | 6.0516E+09 | 2.9711E+07 | 4.4813E+09 | 8.0229E+07 | 5.5160E+08 | 2.4917E+09 | 5.0889E+02 | |
| CEC2017-F14 | Ave | 1.4795E+07 | 9.7513E+04 | 5.0287E+06 | 2.6422E+06 | 1.1918E+06 | 1.5375E+08 | 7.2412E+06 | 2.0206E+07 | 2.5964E+06 | 7.3815E+06 | 1.7691E+07 | 7.2234E+05 |
| Std | 1.2972E+07 | 4.2834E+04 | 2.2676E+06 | 1.5004E+06 | 3.8870E+05 | 1.0607E+08 | 3.5462E+06 | 6.3584E+06 | 1.3462E+06 | 2.7645E+06 | 9.2974E+06 | 1.5964E+05 | |
| CEC2017-F15 | Ave | 3.6432E+07 | 4.7873E+03 | 1.5744E+05 | 1.0979E+04 | 1.8580E+04 | 2.4003E+10 | 2.9509E+06 | 1.9978E+09 | 7.4699E+07 | 4.2517E+07 | 2.4498E+09 | 2.0960E+03 |
| Std | 6.0229E+07 | 3.0480E+03 | 7.3711E+04 | 4.8197E+03 | 1.3826E+04 | 5.0247E+09 | 2.2615E+06 | 1.6840E+09 | 2.9264E+08 | 3.1691E+07 | 1.2774E+09 | 1.9246E+02 | |
| CEC2017-F16 | Ave | 8.8817E+03 | 6.0057E+03 | 7.3212E+03 | 6.0450E+03 | 6.1237E+03 | 2.5294E+04 | 1.1967E+04 | 1.3273E+04 | 7.6745E+03 | 1.2012E+04 | 1.2298E+04 | 4.8827E+03 |
| Std | 1.5732E+03 | 5.4388E+02 | 8.1512E+02 | 5.5322E+02 | 8.8622E+02 | 2.5032E+03 | 2.3505E+03 | 2.3399E+03 | 1.1457E+03 | 1.3494E+03 | 1.2170E+03 | 3.0899E+02 | |
| CEC2017-F17 | Ave | 8.6115E+03 | 5.6965E+03 | 5.6847E+03 | 5.4166E+03 | 5.8796E+03 | 1.4022E+07 | 8.2918E+03 | 1.2224E+05 | 6.4418E+03 | 7.5301E+03 | 3.5455E+04 | 4.1546E+03 |
| Std | 1.0254E+03 | 5.8976E+02 | 6.4490E+02 | 7.2660E+02 | 8.0145E+02 | 1.5226E+07 | 1.0896E+03 | 1.1800E+05 | 6.6432E+02 | 1.0677E+03 | 2.7556E+04 | 2.7901E+02 | |
| CEC2017-F18 | Ave | 1.8516E+07 | 3.6427E+05 | 7.9899E+06 | 3.0602E+06 | 1.8895E+06 | 2.9652E+08 | 6.0773E+06 | 2.0003E+07 | 3.2473E+06 | 8.2509E+06 | 1.8330E+07 | 1.1908E+06 |
| Std | 1.2223E+07 | 1.7419E+05 | 3.8223E+06 | 1.5694E+06 | 7.1396E+05 | 1.6321E+08 | 2.2448E+06 | 7.2124E+06 | 1.8659E+06 | 4.0101E+06 | 9.3858E+06 | 3.2142E+05 | |
| CEC2017-F19 | Ave | 3.7834E+07 | 6.6971E+03 | 1.0015E+07 | 2.0434E+04 | 4.0813E+04 | 2.4997E+10 | 1.1309E+07 | 2.1694E+09 | 3.9452E+07 | 6.2133E+07 | 2.4660E+09 | 2.1667E+03 |
| Std | 2.8663E+07 | 6.9467E+03 | 6.4866E+06 | 1.7275E+04 | 1.8338E+05 | 5.3550E+09 | 6.3303E+06 | 2.8292E+09 | 2.1123E+08 | 4.8957E+07 | 1.1766E+09 | 8.7004E+01 | |
| CEC2017-F20 | Ave | 7.0832E+03 | 5.3214E+03 | 5.7362E+03 | 7.0886E+03 | 6.1858E+03 | 7.9850E+03 | 6.8670E+03 | 6.4167E+03 | 5.9821E+03 | 5.6618E+03 | 6.8189E+03 | 4.0916E+03 |
| Std | 6.1165E+02 | 3.7677E+02 | 4.2628E+02 | 4.2225E+02 | 5.3417E+02 | 3.0431E+02 | 6.5856E+02 | 4.7141E+02 | 4.9027E+02 | 5.9565E+02 | 7.9273E+02 | 2.5690E+02 | |
| CEC2017-F21 | Ave | 3.9333E+03 | 3.4171E+03 | 3.0377E+03 | 3.0399E+03 | 3.6520E+03 | 4.8590E+03 | 4.7141E+03 | 4.0945E+03 | 4.1716E+03 | 3.9013E+03 | 3.9960E+03 | 2.7993E+03 |
| Std | 1.3836E+02 | 1.7054E+02 | 9.3171E+01 | 1.0453E+02 | 2.2023E+02 | 1.5530E+02 | 2.8166E+02 | 1.9428E+02 | 2.5161E+02 | 1.7446E+02 | 8.9596E+01 | 3.0838E+01 | |
| CEC2017-F22 | Ave | 2.7274E+04 | 1.9370E+04 | 1.9648E+04 | 3.3465E+04 | 1.8920E+04 | 3.5346E+04 | 2.9693E+04 | 3.1076E+04 | 1.9285E+04 | 2.7957E+04 | 3.2381E+04 | 1.7051E+04 |
| Std | 4.5762E+03 | 1.1735E+03 | 1.4358E+03 | 1.3332E+03 | 1.3232E+03 | 5.7492E+02 | 2.2482E+03 | 1.5258E+03 | 1.2452E+03 | 1.6235E+03 | 1.8328E+03 | 7.7487E+02 | |
| CEC2017-F23 | Ave | 4.8622E+03 | 3.8428E+03 | 3.5706E+03 | 3.7991E+03 | 4.1981E+03 | 6.3690E+03 | 5.9034E+03 | 5.4108E+03 | 5.0623E+03 | 4.6981E+03 | 5.5965E+03 | 3.2128E+03 |
| Std | 2.6091E+02 | 2.0169E+02 | 7.7406E+01 | 1.0784E+02 | 2.0957E+02 | 2.1071E+02 | 5.0044E+02 | 3.6167E+02 | 2.7963E+02 | 1.2169E+02 | 2.7529E+02 | 2.7133E+01 | |
| CEC2017-F24 | Ave | 6.0474E+03 | 4.8598E+03 | 4.2584E+03 | 5.1409E+03 | 5.1994E+03 | 1.1693E+04 | 9.3033E+03 | 6.2693E+03 | 6.3613E+03 | 5.7482E+03 | 7.7947E+03 | 3.8653E+03 |
| Std | 4.4876E+02 | 3.4733E+02 | 1.6745E+02 | 2.3693E+02 | 3.3327E+02 | 1.3404E+03 | 9.6539E+02 | 4.1543E+02 | 3.6617E+02 | 2.8075E+02 | 3.9206E+02 | 3.3967E+01 | |
| CEC2017-F25 | Ave | 6.3395E+03 | 3.3372E+03 | 3.6928E+03 | 5.0256E+03 | 3.4466E+03 | 2.9846E+04 | 4.4040E+03 | 1.5371E+04 | 4.4188E+03 | 8.0854E+03 | 1.2802E+04 | 3.5914E+03 |
| Std | 3.6573E+03 | 6.0971E+01 | 9.0182E+01 | 5.2140E+02 | 5.8697E+01 | 1.7783E+03 | 2.3609E+02 | 1.9303E+03 | 6.7576E+02 | 9.1110E+02 | 1.1301E+03 | 3.9826E+01 | |
| CEC2017-F26 | Ave | 2.3080E+04 | 2.1829E+04 | 1.5541E+04 | 2.6015E+04 | 2.1353E+04 | 5.7365E+04 | 3.5399E+04 | 3.8982E+04 | 3.2976E+04 | 3.0194E+04 | 3.4265E+04 | 1.4427E+04 |
| Std | 2.7695E+03 | 4.4402E+03 | 1.5883E+03 | 2.2593E+03 | 7.5145E+03 | 2.5656E+03 | 4.7589E+03 | 2.8668E+03 | 2.2870E+03 | 2.9804E+03 | 2.2204E+03 | 1.0678E+03 | |
| CEC2017-F27 | Ave | 4.5468E+03 | 3.7568E+03 | 4.0075E+03 | 4.7552E+03 | 3.8662E+03 | 1.4749E+04 | 5.5640E+03 | 5.7912E+03 | 5.6353E+03 | 5.1517E+03 | 7.7398E+03 | 3.6803E+03 |
| Std | 4.2616E+02 | 1.2114E+02 | 1.8239E+02 | 2.4119E+02 | 2.6306E+02 | 1.1102E+03 | 1.2346E+03 | 1.0124E+03 | 7.2997E+02 | 3.8866E+02 | 5.7527E+02 | 4.0223E+01 | |
| CEC2017-F28 | Ave | 1.8040E+04 | 3.4270E+03 | 3.7789E+03 | 7.7971E+03 | 3.5421E+03 | 3.7097E+04 | 4.5781E+03 | 1.6663E+04 | 5.0271E+03 | 1.0195E+04 | 1.7705E+04 | 3.8489E+03 |
| Std | 7.5206E+03 | 4.0098E+01 | 7.8350E+01 | 1.3046E+03 | 4.2129E+01 | 1.6352E+03 | 2.7820E+02 | 1.4137E+03 | 1.0037E+03 | 1.3855E+03 | 1.3688E+03 | 4.8847E+01 | |
| CEC2017-F29 | Ave | 1.1109E+04 | 7.3613E+03 | 9.2764E+03 | 8.8529E+03 | 7.5123E+03 | 1.0042E+06 | 1.5229E+04 | 2.4583E+04 | 1.1399E+04 | 1.3503E+04 | 1.9403E+04 | 6.1195E+03 |
| Std | 1.4593E+03 | 7.1043E+02 | 9.0598E+02 | 7.5812E+02 | 6.9042E+02 | 4.9959E+05 | 1.9541E+03 | 9.6814E+03 | 1.0793E+03 | 1.2170E+03 | 5.5657E+03 | 3.1404E+02 | |
| CEC2017-F30 | Ave | 1.1358E+08 | 1.8219E+04 | 1.2176E+08 | 1.1559E+07 | 2.5928E+05 | 3.9497E+10 | 2.2493E+08 | 6.7101E+09 | 8.4726E+07 | 1.0296E+09 | 8.4744E+09 | 1.6474E+04 |
| Std | 5.5941E+07 | 1.8578E+04 | 4.9197E+07 | 7.1841E+06 | 1.7823E+05 | 5.8794E+09 | 1.0004E+08 | 4.5735E+09 | 2.7473E+08 | 3.6580E+08 | 2.8481E+09 | 3.4078E+03 |
| ID | Item | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO | GSEA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2022-F1 | Ave | 2.2632E+04 | 3.0000E+02 | 3.4451E+02 | 4.5165E+03 | 8.6142E+02 | 5.7833E+04 | 2.9129E+03 | 2.2482E+04 | 1.5747E+04 | 4.2001E+03 | 1.6793E+04 | 3.0542E+02 |
| Std | 8.2006E+03 | 3.6696E-12 | 3.5968E+01 | 2.3327E+03 | 8.1398E+02 | 2.0962E+04 | 3.0949E+03 | 6.2065E+03 | 8.9789E+03 | 2.2055E+03 | 5.2073E+03 | 4.3804E+00 | |
| CEC2022-F2 | Ave | 4.8911E+02 | 4.3661E+02 | 4.5350E+02 | 4.7405E+02 | 4.5202E+02 | 3.1285E+03 | 4.9017E+02 | 6.9407E+02 | 4.5746E+02 | 5.1939E+02 | 6.2980E+02 | 4.4357E+02 |
| Std | 4.4569E+01 | 2.0731E+01 | 1.6571E+01 | 3.1620E+01 | 1.3499E+01 | 7.6408E+02 | 4.3587E+01 | 1.2367E+02 | 1.1994E+01 | 4.8463E+01 | 7.4426E+01 | 4.5723E+00 | |
| CEC2022-F3 | Ave | 6.3271E+02 | 6.3528E+02 | 6.0145E+02 | 6.0497E+02 | 6.2393E+02 | 6.7804E+02 | 6.7103E+02 | 6.6721E+02 | 6.6340E+02 | 6.4706E+02 | 6.4551E+02 | 6.0002E+02 |
| Std | 1.0491E+01 | 9.7860E+00 | 6.9795E-01 | 3.4140E+00 | 1.0302E+01 | 7.5421E+00 | 1.2067E+01 | 8.4464E+00 | 1.3623E+01 | 1.2419E+01 | 9.1849E+00 | 1.6808E-02 | |
| CEC2022-F4 | Ave | 9.0868E+02 | 8.7031E+02 | 8.5838E+02 | 8.4940E+02 | 8.9704E+02 | 9.7196E+02 | 9.0728E+02 | 9.2770E+02 | 9.1908E+02 | 8.9108E+02 | 9.0132E+02 | 8.2793E+02 |
| Std | 3.1312E+01 | 1.6612E+01 | 1.8332E+01 | 2.2150E+01 | 2.1521E+01 | 1.4313E+01 | 3.5283E+01 | 1.9865E+01 | 3.2720E+01 | 1.3102E+01 | 2.0313E+01 | 5.4930E+00 | |
| CEC2022-F5 | Ave | 1.8116E+03 | 2.0157E+03 | 9.7582E+02 | 9.6405E+02 | 2.3987E+03 | 3.4875E+03 | 2.6876E+03 | 3.0023E+03 | 3.3935E+03 | 2.4379E+03 | 2.2980E+03 | 9.2937E+02 |
| Std | 4.5550E+02 | 3.1317E+02 | 8.3288E+01 | 5.8730E+01 | 2.3254E+02 | 4.4448E+02 | 6.8010E+02 | 2.9825E+02 | 7.0962E+02 | 4.0638E+02 | 5.1083E+02 | 1.2945E+01 | |
| CEC2022-F6 | Ave | 4.2982E+05 | 5.2415E+03 | 7.8094E+03 | 4.2611E+03 | 7.9926E+03 | 1.5406E+09 | 7.0369E+03 | 1.9797E+07 | 5.0775E+03 | 3.4346E+05 | 1.0194E+07 | 1.9845E+03 |
| Std | 1.3209E+06 | 3.6723E+03 | 5.0500E+03 | 3.1217E+03 | 7.6208E+03 | 9.1185E+08 | 5.5854E+03 | 3.5237E+07 | 3.4558E+03 | 4.5859E+05 | 1.3152E+07 | 9.9873E+01 | |
| CEC2022-F7 | Ave | 2.1248E+03 | 2.1496E+03 | 2.0616E+03 | 2.0485E+03 | 2.1268E+03 | 2.1956E+03 | 2.2925E+03 | 2.2216E+03 | 2.2217E+03 | 2.1270E+03 | 2.1698E+03 | 2.0300E+03 |
| Std | 4.7496E+01 | 5.9726E+01 | 3.3797E+01 | 1.7062E+01 | 5.0252E+01 | 3.1332E+01 | 1.0567E+02 | 4.3500E+01 | 7.8271E+01 | 3.9048E+01 | 4.0362E+01 | 7.4381E+00 | |
| CEC2022-F8 | Ave | 2.2776E+03 | 2.3004E+03 | 2.2399E+03 | 2.2318E+03 | 2.2737E+03 | 3.6831E+03 | 2.5650E+03 | 2.2470E+03 | 2.3880E+03 | 2.2422E+03 | 2.2635E+03 | 2.2214E+03 |
| Std | 7.1586E+01 | 8.4764E+01 | 3.7708E+01 | 5.0085E+00 | 6.3813E+01 | 1.4909E+03 | 1.9812E+02 | 2.9131E+01 | 1.2108E+02 | 2.2944E+01 | 4.8786E+01 | 3.1045E-01 | |
| CEC2022-F9 | Ave | 2.5019E+03 | 2.4808E+03 | 2.4810E+03 | 2.4811E+03 | 2.4808E+03 | 3.7860E+03 | 2.4871E+03 | 2.6039E+03 | 2.4875E+03 | 2.5021E+03 | 2.5847E+03 | 2.4808E+03 |
| Std | 2.0006E+01 | 4.1214E-12 | 2.1034E-01 | 1.7760E+00 | 6.7475E-03 | 3.7048E+02 | 9.4733E+00 | 7.2234E+01 | 2.0191E+01 | 1.5809E+01 | 4.2147E+01 | 4.1544E-11 | |
| CEC2022-F10 | Ave | 3.0134E+03 | 4.0646E+03 | 2.6984E+03 | 2.5309E+03 | 3.8103E+03 | 3.9689E+03 | 5.0980E+03 | 4.7306E+03 | 4.8883E+03 | 2.5012E+03 | 4.4874E+03 | 2.5006E+03 |
| Std | 8.9619E+02 | 9.6291E+02 | 2.0600E+02 | 7.0620E+01 | 7.2216E+02 | 2.0144E+03 | 8.1759E+02 | 1.2110E+03 | 7.0893E+02 | 2.6204E-01 | 1.3488E+03 | 5.4741E-02 | |
| CEC2022-F11 | Ave | 3.0960E+03 | 2.9133E+03 | 2.9196E+03 | 2.9163E+03 | 2.8907E+03 | 8.9661E+03 | 2.9888E+03 | 5.9755E+03 | 3.0732E+03 | 3.3935E+03 | 4.5286E+03 | 2.9000E+03 |
| Std | 2.1675E+02 | 7.3030E+01 | 1.1331E+02 | 1.2685E+02 | 1.2427E+02 | 5.6268E+02 | 9.4961E+01 | 1.3525E+03 | 4.4038E+02 | 7.4606E+02 | 4.8452E+02 | 1.2582E-12 | |
| CEC2022-F12 | Ave | 3.0489E+03 | 2.9838E+03 | 2.9640E+03 | 2.9931E+03 | 3.0054E+03 | 3.3382E+03 | 3.2465E+03 | 3.0514E+03 | 3.2464E+03 | 3.0228E+03 | 3.1070E+03 | 2.9434E+03 |
| Std | 5.6634E+01 | 3.8805E+01 | 1.8155E+01 | 3.1643E+01 | 5.8409E+01 | 1.1029E+02 | 1.5949E+02 | 6.4514E+01 | 1.6311E+02 | 4.7989E+01 | 1.0612E+02 | 2.8107E+00 |
| Function | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199E-11 | 8.8411E-07 | 3.0199E-11 | 3.0199E-11 | 7.0430E-07 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 7.0881E-08 | 3.0199E-11 | 3.0199E-11 |
| F2 | 3.0199E-11 | 2.4386E-09 | 3.0199E-11 | 3.0199E-11 | 1.4643E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 1.2118E-12 | 3.0199E-11 |
| F3 | 3.0199E-11 | 3.0199E-11 | 9.7917E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 8.1527E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F4 | 3.0199E-11 | 5.2640E-04 | 7.7725E-09 | 1.3111E-08 | 2.1265E-04 | 3.0199E-11 | 1.3289E-10 | 3.0199E-11 | 9.5139E-06 | 3.0199E-11 | 3.0199E-11 |
| F5 | 3.0199E-11 | 3.0199E-11 | 4.0840E-05 | 1.1058E-04 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F6 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F7 | 3.3384E-11 | 3.0199E-11 | 7.1719E-01 | 3.1573E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F8 | 3.0199E-11 | 3.0199E-11 | 1.5581E-08 | 8.2357E-02 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F9 | 3.0199E-11 | 3.0199E-11 | 1.8500E-08 | 3.1573E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F10 | 3.6897E-11 | 5.5727E-10 | 7.2884E-03 | 3.0199E-11 | 8.1014E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 5.5727E-10 | 3.0199E-11 | 3.0199E-11 |
| F11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 4.5043E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F12 | 3.0199E-11 | 8.4848E-09 | 3.0199E-11 | 6.6955E-11 | 1.4918E-06 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.4742E-10 | 3.0199E-11 | 3.0199E-11 |
| F13 | 3.0199E-11 | 7.7387E-06 | 3.0199E-11 | 1.1058E-04 | 1.6947E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F14 | 1.6132E-10 | 7.6950E-08 | 3.0199E-11 | 3.6459E-08 | 3.0199E-11 | 3.0199E-11 | 1.7769E-10 | 3.0199E-11 | 2.3715E-10 | 3.0199E-11 | 3.0199E-11 |
| F15 | 3.0199E-11 | 1.0233E-01 | 5.5999E-07 | 1.2362E-03 | 4.6390E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 8.9934E-11 | 3.0199E-11 | 3.0199E-11 |
| F16 | 3.0199E-11 | 8.1527E-11 | 3.1967E-09 | 5.8587E-06 | 1.3289E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.8202E-10 | 3.0199E-11 |
| F17 | 3.0199E-11 | 3.0199E-11 | 1.2023E-08 | 5.2650E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 8.1527E-11 | 3.0199E-11 |
| F18 | 3.1589E-10 | 2.4327E-05 | 3.0199E-11 | 9.9186E-11 | 2.2273E-09 | 3.0199E-11 | 9.9186E-11 | 3.0199E-11 | 3.6897E-11 | 3.0199E-11 | 3.0199E-11 |
| F19 | 3.0199E-11 | 1.0907E-05 | 8.3520E-08 | 7.5991E-07 | 1.2860E-06 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 1.0937E-10 | 3.0199E-11 | 3.0199E-11 |
| F20 | 3.0199E-11 | 3.0199E-11 | 8.8910E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F21 | 3.0199E-11 | 3.0199E-11 | 1.2870E-09 | 3.1821E-04 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F22 | 3.0199E-11 | 7.9555E-03 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F23 | 3.0199E-11 | 3.0199E-11 | 9.9186E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F24 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F25 | 6.6955E-11 | 1.8608E-06 | 2.1544E-10 | 3.0199E-11 | 3.1830E-03 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F26 | 4.1997E-10 | 2.0054E-04 | 1.8682E-05 | 1.1711E-02 | 4.9980E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.9648E-08 | 3.0199E-11 |
| F27 | 3.0199E-11 | 2.9215E-09 | 3.0103E-07 | 3.0199E-11 | 3.8202E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F28 | 3.0199E-11 | 2.4990E-03 | 3.0199E-11 | 3.0199E-11 | 9.1171E-01 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 8.1014E-10 | 3.0199E-11 | 3.0199E-11 |
| F29 | 3.0199E-11 | 8.1527E-11 | 6.0658E-11 | 7.3803E-10 | 3.3384E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F30 | 3.0199E-11 | 2.3168E-06 | 3.0199E-11 | 8.8910E-10 | 5.4617E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| Function | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199E-11 | 2.3768E-07 | 3.0199E-11 | 3.0199E-11 | 4.3531E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F2 | 3.0199E-11 | 3.3242E-06 | 3.0199E-11 | 3.0199E-11 | 4.6159E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 1.2118E-12 | 3.0199E-11 |
| F3 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F4 | 3.0199E-11 | 1.1536E-01 | 3.0199E-11 | 3.0199E-11 | 4.1178E-06 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F5 | 3.0199E-11 | 3.0199E-11 | 1.5292E-05 | 5.3221E-03 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F6 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F7 | 3.0199E-11 | 3.0199E-11 | 9.7052E-01 | 7.0881E-08 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F8 | 3.0199E-11 | 6.0658E-11 | 2.2658E-03 | 1.7666E-03 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F9 | 3.0199E-11 | 3.0199E-11 | 1.2870E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F10 | 3.0199E-11 | 1.4110E-09 | 5.5727E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 1.7769E-10 | 3.0199E-11 | 3.0199E-11 |
| F11 | 3.0199E-11 | 8.1527E-11 | 3.0199E-11 | 3.0199E-11 | 1.2057E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F12 | 3.0199E-11 | 2.1947E-08 | 3.0199E-11 | 3.0199E-11 | 1.4110E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F13 | 3.0199E-11 | 4.0772E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F14 | 3.0199E-11 | 5.1857E-07 | 8.1527E-11 | 3.9648E-08 | 1.8567E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F15 | 3.0199E-11 | 1.0105E-08 | 3.0199E-11 | 6.7362E-06 | 1.9568E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F16 | 3.0199E-11 | 8.1527E-11 | 3.1589E-10 | 2.5721E-07 | 3.8202E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F17 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 4.1825E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F18 | 4.0772E-11 | 2.3715E-10 | 1.3289E-10 | 3.6459E-08 | 4.1997E-10 | 3.0199E-11 | 8.4848E-09 | 3.0199E-11 | 2.2273E-09 | 3.0199E-11 | 3.0199E-11 |
| F19 | 3.3384E-11 | 7.8446E-01 | 1.2541E-07 | 3.6439E-02 | 9.9410E-01 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 7.7387E-06 | 3.0199E-11 | 3.0199E-11 |
| F20 | 3.0199E-11 | 3.0199E-11 | 3.8202E-10 | 4.5726E-09 | 4.5043E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F21 | 3.0199E-11 | 1.7769E-10 | 3.0199E-11 | 3.5638E-04 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F22 | 3.0199E-11 | 2.3715E-10 | 1.8500E-08 | 3.1967E-09 | 1.0937E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 2.6099E-10 | 3.0199E-11 | 3.0199E-11 |
| F23 | 3.0199E-11 | 3.0199E-11 | 6.6955E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F24 | 3.0199E-11 | 3.0199E-11 | 4.5043E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F25 | 3.0199E-11 | 9.5139E-06 | 5.5611E-04 | 3.0199E-11 | 3.1830E-01 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F26 | 7.1186E-09 | 1.1077E-06 | 2.5188E-01 | 3.0199E-11 | 1.0000E+00 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 5.0723E-10 | 3.0199E-11 |
| F27 | 3.0199E-11 | 3.8249E-09 | 2.2273E-09 | 3.0199E-11 | 1.4110E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F28 | 3.0199E-11 | 1.0105E-08 | 3.8349E-06 | 3.0199E-11 | 8.1200E-04 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F29 | 3.0199E-11 | 4.9752E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F30 | 3.0199E-11 | 1.6798E-03 | 3.0199E-11 | 3.0199E-11 | 3.4742E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| Function | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199E-11 | 3.0199E-11 | 3.6897E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F2 | 3.0199E-11 | 1.6813E-04 | 8.9934E-11 | 3.0199E-11 | 3.1967E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 1.2118E-12 | 3.0199E-11 |
| F3 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.5708E-06 | 3.0199E-11 | 3.0199E-11 | 2.0523E-03 | 3.0199E-11 |
| F4 | 3.0199E-11 | 3.0199E-11 | 3.6439E-02 | 3.0199E-11 | 3.6897E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F5 | 3.0199E-11 | 3.0199E-11 | 4.8011E-07 | 6.5183E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F6 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F7 | 3.0199E-11 | 3.0199E-11 | 1.5465E-09 | 3.0811E-08 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F8 | 3.0199E-11 | 7.3891E-11 | 1.2860E-06 | 4.5043E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F9 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F10 | 3.0199E-11 | 1.6351E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 2.3715E-10 | 3.0199E-11 | 3.0199E-11 |
| F11 | 3.0199E-11 | 3.0199E-11 | 3.1830E-03 | 3.0199E-11 | 9.9186E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F12 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F13 | 3.0199E-11 | 4.9752E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F14 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 2.3168E-06 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 7.1186E-09 | 3.0199E-11 | 3.0199E-11 |
| F15 | 3.0199E-11 | 3.4971E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F16 | 3.0199E-11 | 5.5727E-10 | 3.0199E-11 | 1.6132E-10 | 3.3520E-08 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F17 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 7.3803E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F18 | 3.0199E-11 | 1.0937E-10 | 3.0199E-11 | 5.4617E-09 | 4.2175E-04 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 1.8500E-08 | 3.0199E-11 | 3.0199E-11 |
| F19 | 3.0199E-11 | 6.6955E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F20 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F21 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F22 | 3.0199E-11 | 2.9215E-09 | 3.4971E-09 | 3.0199E-11 | 1.4733E-07 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 4.9980E-09 | 3.0199E-11 | 3.0199E-11 |
| F23 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F24 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F25 | 3.0199E-11 | 3.0199E-11 | 1.7479E-05 | 3.0199E-11 | 2.3715E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F26 | 3.0199E-11 | 5.5727E-10 | 2.7548E-03 | 3.0199E-11 | 1.1077E-06 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F27 | 3.8202E-10 | 7.9590E-03 | 9.9186E-11 | 3.0199E-11 | 4.2259E-03 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F28 | 3.0199E-11 | 3.0199E-11 | 3.3681E-05 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F29 | 3.0199E-11 | 1.4110E-09 | 3.0199E-11 | 3.0199E-11 | 2.8716E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F30 | 3.0199E-11 | 8.7710E-02 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| Function | DBO | RTH | RIME | JS | SSA | BOA | HLOA | HEOA | CPSOGSA | HPHHO | AGWO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199E-11 | 2.9543E-11 | 2.8716E-10 | 3.0199E-11 | 5.0723E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F2 | 3.0199E-11 | 5.5498E-02 | 9.2603E-09 | 3.3384E-11 | 7.1186E-09 | 3.0199E-11 | 5.4617E-09 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F3 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F4 | 3.0180E-11 | 3.0180E-11 | 2.8700E-10 | 3.8297E-05 | 3.0180E-11 | 3.0180E-11 | 3.0180E-11 | 3.0180E-11 | 3.0180E-11 | 3.0180E-11 | 3.0180E-11 |
| F5 | 3.0199E-11 | 3.0199E-11 | 4.0330E-03 | 2.1566E-03 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F6 | 3.0199E-11 | 1.0666E-07 | 3.0199E-11 | 3.5923E-05 | 6.0459E-07 | 3.0199E-11 | 7.3803E-10 | 3.0199E-11 | 5.4617E-09 | 3.0199E-11 | 3.0199E-11 |
| F7 | 2.6099E-10 | 3.0199E-11 | 5.5999E-07 | 4.4205E-06 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F8 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 2.3715E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F9 | 3.0104E-11 | 4.0950E-11 | 3.0104E-11 | 3.0104E-11 | 1.3140E-01 | 3.0104E-11 | 3.0104E-11 | 3.0104E-11 | 3.0104E-11 | 3.0104E-11 | 3.0104E-11 |
| F10 | 8.1527E-11 | 3.0199E-11 | 5.5999E-07 | 3.3384E-11 | 5.5727E-10 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| F11 | 1.5693E-11 | 3.0236E-09 | 5.1735E-09 | 5.1735E-09 | 7.7464E-07 | 1.5693E-11 | 3.1458E-10 | 1.5693E-11 | 1.5693E-11 | 3.1458E-10 | 1.5693E-11 |
| F12 | 3.0199E-11 | 1.4643E-10 | 3.6459E-08 | 3.0199E-11 | 4.5043E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 | 3.0199E-11 |
| Suites | CEC2017 | CEC2022 | ||||||
|---|---|---|---|---|---|---|---|---|
| Dimensions | 30 | 50 | 100 | 20 | ||||
| Algorithms | ||||||||
| DBO | 7.60 | 8 | 7.60 | 8 | 7.73 | 9 | 7.25 | 7 |
| RTH | 3.17 | 2 | 2.93 | 2 | 2.27 | 2 | 3.92 | 4 |
| RIME | 3.77 | 4 | 3.67 | 3 | 4.13 | 4 | 3.58 | 3 |
| JS | 3.60 | 3 | 4.40 | 5 | 5.37 | 5 | 3.50 | 2 |
| SSA | 4.60 | 5 | 4.30 | 4 | 3.97 | 3 | 4.75 | 5 |
| BOA | 11.83 | 12 | 11.93 | 12 | 11.80 | 12 | 11.42 | 12 |
| HLOA | 8.70 | 9 | 8.37 | 9 | 7.67 | 8 | 8.75 | 9 |
| HEOA | 10.07 | 11 | 10.07 | 11 | 9.93 | 11 | 9.92 | 11 |
| CPSOGSA | 7.43 | 7 | 6.97 | 6 | 6.67 | 6 | 8.33 | 8 |
| HPHHO | 7.10 | 6 | 7.03 | 7 | 7.17 | 7 | 6.58 | 6 |
| AGWO | 8.90 | 10 | 9.40 | 10 | 9.70 | 10 | 8.83 | 10 |
| GSEA | 1.23 | 1 | 1.33 | 1 | 1.60 | 1 | 1.17 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, S.; Wu, Y.; Fu, Z. Graduate Student Evolutionary Algorithm: A Novel Metaheuristic Algorithm for 3D UAV and Robot Path Planning. Biomimetics 2025, 10, 616. https://doi.org/10.3390/biomimetics10090616
Liu X, Li S, Wu Y, Fu Z. Graduate Student Evolutionary Algorithm: A Novel Metaheuristic Algorithm for 3D UAV and Robot Path Planning. Biomimetics. 2025; 10(9):616. https://doi.org/10.3390/biomimetics10090616
Chicago/Turabian StyleLiu, Xiaoxuan, Shaobo Li, Yongming Wu, and Zijun Fu. 2025. "Graduate Student Evolutionary Algorithm: A Novel Metaheuristic Algorithm for 3D UAV and Robot Path Planning" Biomimetics 10, no. 9: 616. https://doi.org/10.3390/biomimetics10090616
APA StyleLiu, X., Li, S., Wu, Y., & Fu, Z. (2025). Graduate Student Evolutionary Algorithm: A Novel Metaheuristic Algorithm for 3D UAV and Robot Path Planning. Biomimetics, 10(9), 616. https://doi.org/10.3390/biomimetics10090616







