Effect of Substrate Compliance on the Jumping Mechanism of the Tree Frog (Polypedates dennys)
Abstract
1. Introduction
2. Materials and Methods
2.1. Performance Testing Apparatus
2.2. Experiment Setup
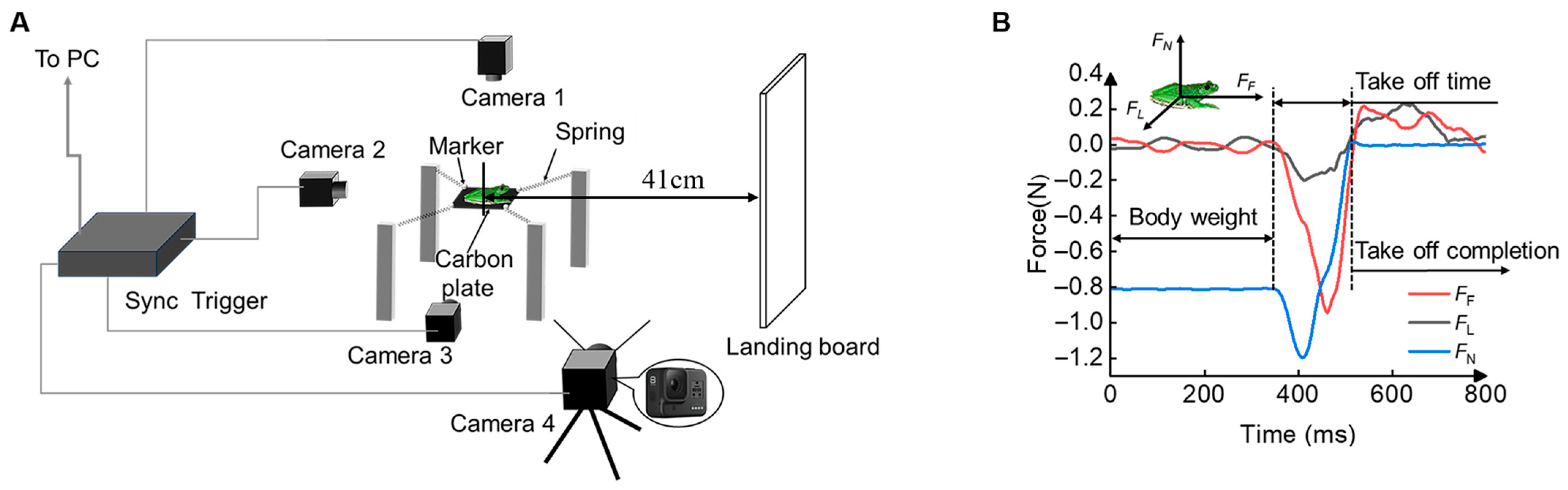
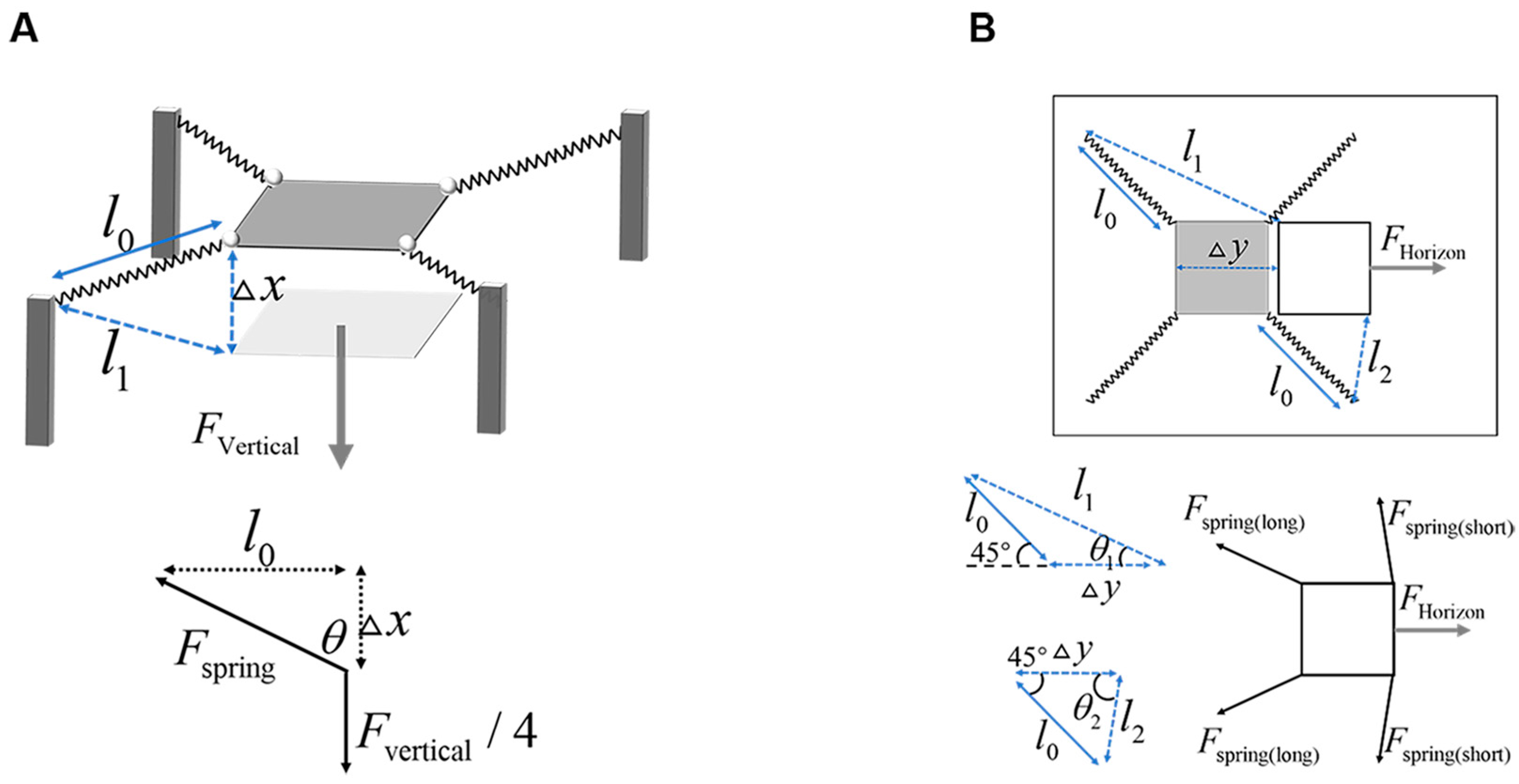
2.3. Analyses
3. Results
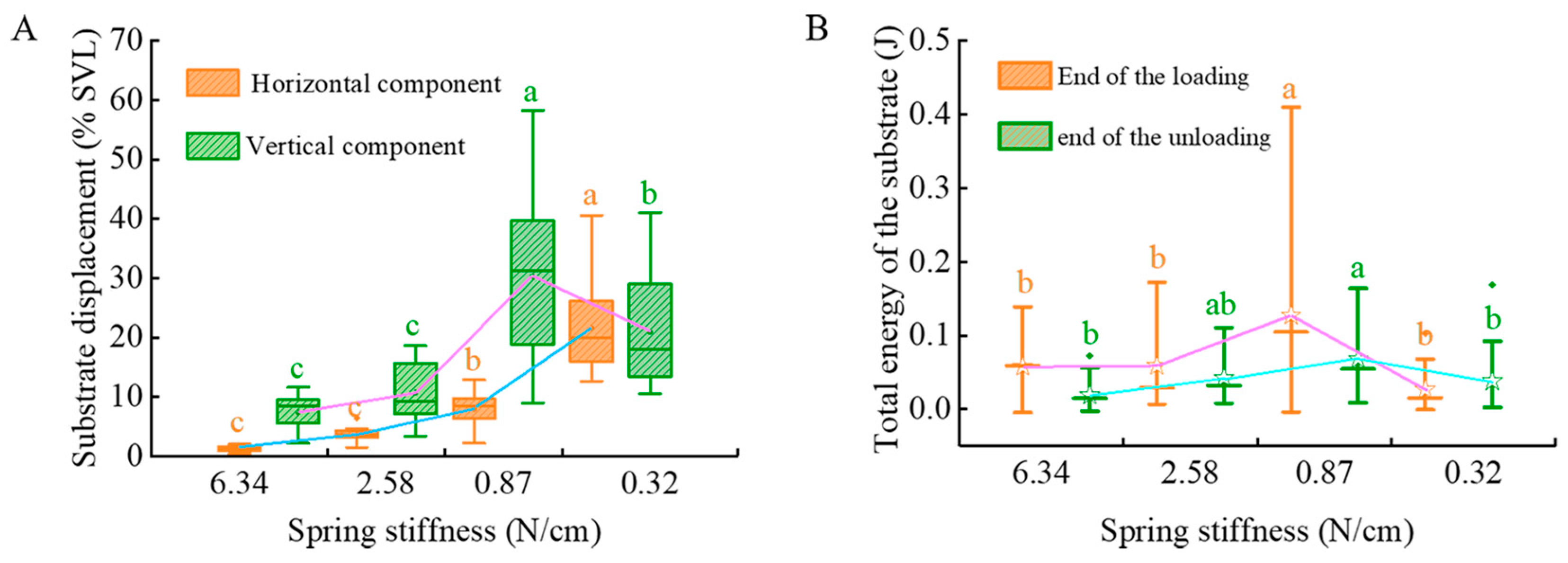
3.1. Substrate Parameter Analysis
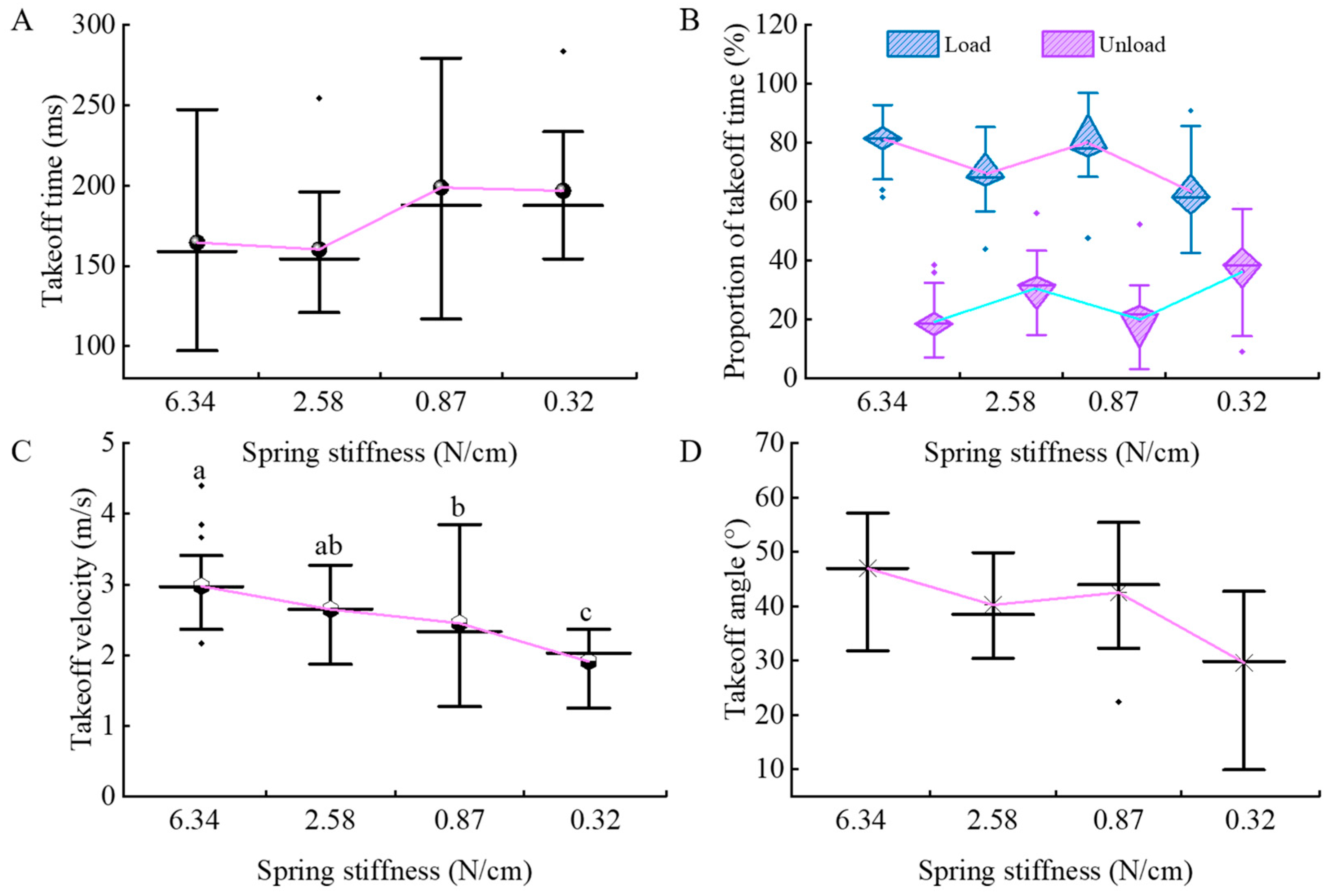
3.2. Kinematic Parameter Analysis of Tree Frogs
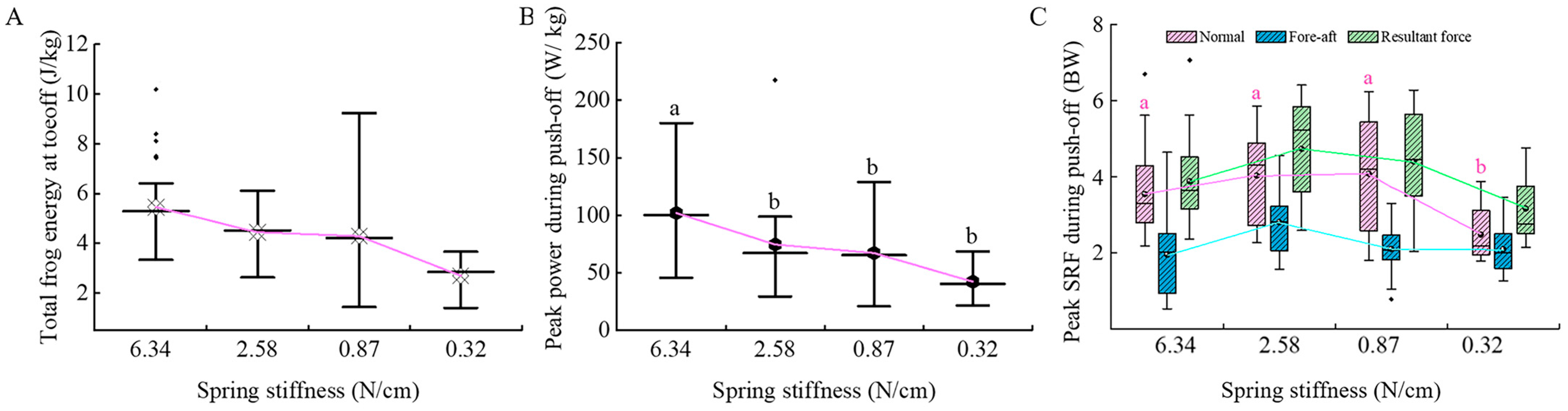
3.3. Dynamic Parameter Analysis of Tree Frogs
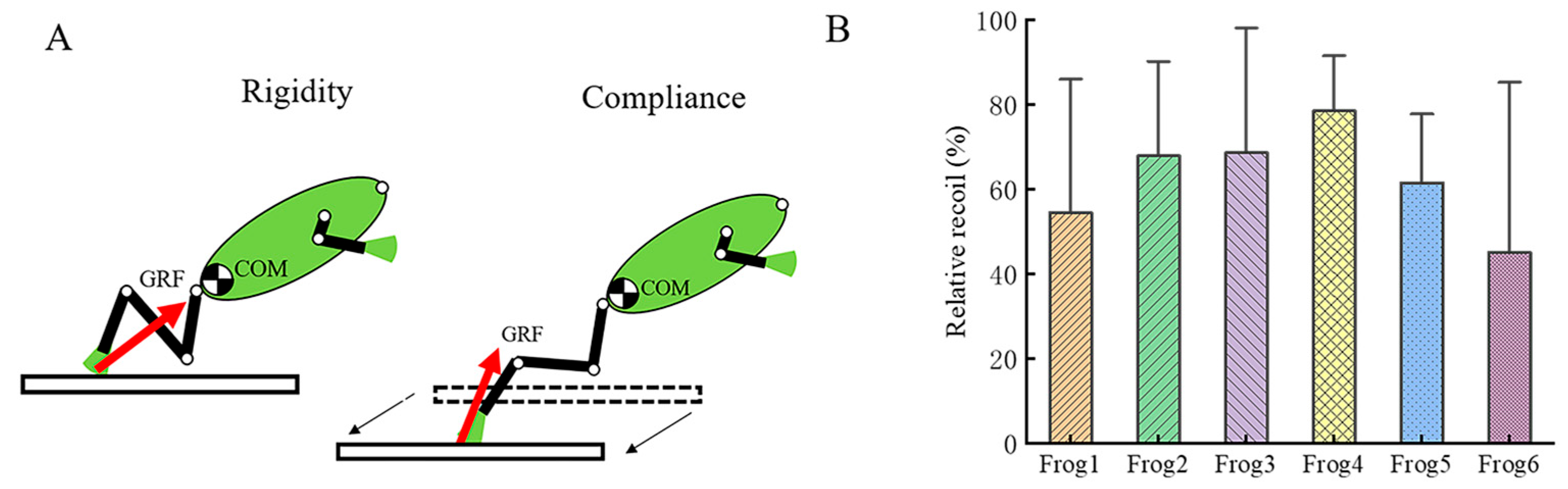
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| COM | Center of Mass |
| SVL | Snout–Vent Length |
| BW | Body Weight |
References
- Blob, R.W.; Diamond, K.M.; Lagarde, R.; Maie, T.; Moody, K.N.; Palecek, A.M.; Ward, J.L.; Schoenfuss, H.L. Integrating Biomechanics in Evolutionary Studies, with Examples from the Amphidromous Goby Model System. J. Exp. Biol. 2023, 226, jeb244942. [Google Scholar] [CrossRef] [PubMed]
- Gregorič, M.; Agnarsson, I.; Blackledge, T.A.; Kuntner, M. How Did the Spider Cross the River? Behavioral Adaptations for River-Bridging Webs in Caerostris darwini (Araneae: Araneidae). PLoS ONE 2011, 6, e26847. [Google Scholar] [CrossRef]
- Rothier, P.S.; Fabre, A.; Benson, R.B.J.; Martinez, Q.; Fabre, P.; Hedrick, B.P.; Herrel, A. Of Flippers and Wings: The Locomotor Environment as a Driver of the Evolution of Forelimb Morphological Diversity in Mammals. Funct. Ecol. 2024, 38, 2231–2246. [Google Scholar] [CrossRef]
- Ostridge, H.J.; Fontsere, C.; Lizano, E.; Soto, D.C.; Saxena, V.; Alvarez-Estape, M.; Barratt, C.D.; Gratton, P.; Bocksberger, G.; Lester, J.D.; et al. Local Genetic Adaptation to Habitat in Wild Chimpanzees. Science 2025, 387, eadn7954. [Google Scholar] [CrossRef]
- Korff, W.L.; McHenry, M.J. Environmental Differences in Substrate Mechanics Do Not Affect Sprinting Performance in Sand Lizards (Uma scoparia and Callisaurus draconoides). J. Exp. Biol. 2011, 214, 122–130. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Shen, M.; Ma, Z.; Zhou, X. Research Progress on Bionic Water Strider Robots. J. Bionic. Eng. 2024, 21, 635–652. [Google Scholar] [CrossRef]
- Yao, C.; Zhou, Y.; Wang, J.; Jiang, L. Bioinspired Universal Approaches for Cavity Regulation during Cylinder Impact Processes for Drag Reduction in Aqueous Media: Macrogeometry Vanquishing Wettability. ACS Appl. Mater. Interfaces 2021, 13, 38808–38815. [Google Scholar] [CrossRef]
- Bush, J.W.M.; Hu, D.L. WALKING ON WATER: Biolocomotion at the Interface. Annu. Rev. Fluid Mech. 2006, 38, 339–369. [Google Scholar] [CrossRef]
- Voigt, D.; De Souza, E.J.; Kovalev, A.; Gorb, S. Inter- and Intraspecific Differences in Leaf Beetle Attachment on Rigid and Compliant Substrates. J. Zool. 2019, 307, 1–8. [Google Scholar] [CrossRef]
- Thorpe, S.K.S.; Crompton, R.H.; Alexander, R.M. Orangutans Use Compliant Branches to Lower the Energetic Cost of Locomotion. Biol. Lett. 2007, 3, 253–256. [Google Scholar] [CrossRef]
- Higham, T.E.; Russell, A.P.; Niklas, K.J. Leaping Lizards Landing on Leaves: Escape-Induced Jumps in the Rainforest Canopy Challenge the Adhesive Limits of Geckos. J. R. Soc. Interface 2017, 14, 20170156. [Google Scholar] [CrossRef]
- Byrnes, G.; Jayne, B.C. Substrate Diameter and Compliance Affect the Gripping Strategies and Locomotor Mode of Climbing Boa Constrictors. J. Exp. Biol. 2010, 213, 4249–4256. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kuo, C.-Y.; Gillis, G.B.; Irschick, D.J. Loading Effects on Jump Performance in Green Anole Lizards, Anolis carolinensis. J. Exp. Biol. 2011, 214, 2073–2079. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ribak, G.; Reingold, S.; Weihs, D. The Effect of Natural Substrates on Jump Height in Click-beetles. Funct. Ecol. 2012, 26, 493–499. [Google Scholar] [CrossRef]
- Crandell, K.E.; Smith, A.F.; Crino, O.L.; Tobalske, B.W. Coping with Compliance during Take-off and Landing in the Diamond Dove (Geopelia cuneata). PLoS ONE 2018, 13, e0199662. [Google Scholar] [CrossRef]
- Gilman, C.A.; Irschick, D.J. Foils of Flexion: The Effects of Perch Compliance on Lizard Locomotion and Perch Choice in the Wild. Funct. Ecol. 2013, 27, 374–381. [Google Scholar] [CrossRef]
- Boulinguez-Ambroise, G.; Dunham, N.; Phelps, T.; Mazonas, T.; Nguyen, P.; Bradley-Cronkwright, M.; Boyer, D.M.; Yapuncich, G.S.; Zeininger, A.; Schmitt, D.; et al. Jumping Performance in Tree Squirrels: Insights into Primate Evolution. J. Hum. Evol. 2023, 180, 103386. [Google Scholar] [CrossRef]
- Mo, X.; Romano, D.; Miraglia, M.; Ge, W.; Stefanini, C. Effect of Substrates’ Compliance on the Jumping Mechanism of Locusta migratoria. Front. Bioeng. Biotechnol. 2020, 8, 661. [Google Scholar] [CrossRef]
- Bijma, N.N.; Gorb, S.N.; Kleinteich, T. Landing on Branches in the Frog Trachycephalus resinifictrix (Anura: Hylidae). J. Comp. Physiol. A 2016, 202, 267–276. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, R.; Qiu, Y.; Chen, J.; Dai, Z.; Wu, H.; Gorb, S.N. Tree Frogs (Polypedates dennysi) Landing on Horizontal Perches: The Effects of Perch Diameter. J. Exp. Biol. 2024, 227, jeb246931. [Google Scholar] [CrossRef]
- Endlein, T.; Ji, A.; Samuel, D.; Yao, N.; Wang, Z.; Barnes, W.J.P.; Federle, W.; Kappl, M.; Dai, Z. Sticking like Sticky Tape: Tree Frogs Use Friction Forces to Enhance Attachment on Overhanging Surfaces. J. R. Soc. Interface 2013, 10, 20120838. [Google Scholar] [CrossRef]
- Endlein, T.; Ji, A.; Yuan, S.; Hill, I.; Wang, H.; Barnes, W.J.P.; Dai, Z.; Sitti, M. The Use of Clamping Grips and Friction Pads by Tree Frogs for Climbing Curved Surfaces. Proc. R. Soc. B 2017, 284, 20162867. [Google Scholar] [CrossRef] [PubMed]
- Herrel, A.; Perrenoud, M.; Decamps, T.; Abdala, V.; Manzano, A.; Pouydebat, E. The Effect of Substrate Diameter and Incline on Locomotion in an Arboreal Frog. J. Exp. Biol. 2013, 216, 3599–3605. [Google Scholar] [CrossRef] [PubMed]
- Federle, W.; Barnes, W.J.P.; Baumgartner, W.; Drechsler, P.; Smith, J.M. Wet but Not Slippery: Boundary Friction in Tree Frog Adhesive Toe Pads. J. R. Soc. Interface 2006, 3, 689–697. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Wang, Z.; Song, Y.; Liu, S.; Dai, Z. Tree Frogs Alter Their Behavioral Strategies While Landing On Vertical Perches. J. Exp. Zool. A Ecol. Integr. Physiol. 2025, 343, 15–24. [Google Scholar] [CrossRef]
- Meng, F.; Liu, Q.; Wang, X.; Tan, D.; Xue, L.; Barnes, W.J.P. Tree Frog Adhesion Biomimetics: Opportunities for the Development of New, Smart Adhesives That Adhere under Wet Conditions. Phil. Trans. R. Soc. A 2019, 377, 20190131. [Google Scholar] [CrossRef]
- Reynaga, C.M.; Eaton, C.E.; Strong, G.A.; Azizi, E. Compliant Substrates Disrupt Elastic Energy Storage in Jumping Tree Frogs. Integr. Comp. Biol. 2019, 59, 1535–1545. [Google Scholar] [CrossRef]
- Astley, H.C.; Haruta, A.; Roberts, T.J. Robust Jumping Performance and Elastic Energy Recovery from Compliant Perches in Tree Frogs. J. Exp. Biol. 2015, 218, 3360–3363. [Google Scholar] [CrossRef]
- Hedrick, T.L. Software Techniques for Two- and Three-Dimensional Kinematic Measurements of Biological and Biomimetic Systems. Bioinspir. Biomim. 2008, 3, 034001. [Google Scholar] [CrossRef]
- Porro, L.B.; Collings, A.J.; Eberhard, E.A.; Chadwick, K.P.; Richards, C.T. Inverse Dynamic Modelling of Jumping in the Red-Legged Running Frog Kassina maculata. J. Exp. Biol. 2017, 220, 1882–1893. [Google Scholar] [CrossRef]
- Richards, C.T.; Porro, L.B.; Collings, A.J. Kinematic Control of Extreme Jump Angles in the Red Leg Running Frog (Kassina maculata). J. Exp. Biol. 2017, 220, 1894–1904. [Google Scholar] [CrossRef]
- Bonser, R.H.C.; Norman, A.P.; Rayner, J.M.V. Does Substrate Quality Influence Take-off Decisions in Common Starlings? Funct. Ecol. 1999, 13, 102–105. [Google Scholar] [CrossRef]
- Channon, A.J.; Günther, M.M.; Crompton, R.H.; D’Août, K.; Preuschoft, H.; Vereecke, E.E. The Effect of Substrate Compliance on the Biomechanics of Gibbon Leaps. J. Exp. Biol. 2011, 214, 687–696. [Google Scholar] [CrossRef] [PubMed]
- Hunt, N.H.; Jinn, J.; Jacobs, L.F.; Full, R.J. Acrobatic Squirrels Learn to Leap and Land on Tree Branches without Falling. Science 2021, 373, 697–700. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Byun, J.; Kim, J.-K.; Choi, W.-Y.; Jakobsen, K.; Jakobsen, J.; Lee, D.-Y.; Cho, K.-J. Bioinspired Dual-Morphing Stretchable Origami. Sci. Robot. 2019, 4, eaay3493. [Google Scholar] [CrossRef]
- Faber, J.A.; Arrieta, A.F.; Studart, A.R. Bioinspired Spring Origami. Science 2018, 359, 1386–1391. [Google Scholar] [CrossRef]
- Merces, L.; Ferro, L.M.M.; Thomas, A.; Karnaushenko, D.D.; Luo, Y.; Egunov, A.I.; Zhang, W.; Bandari, V.K.; Lee, Y.; McCaskill, J.S.; et al. Bio-Inspired Dynamically Morphing Microelectronics toward High-Density Energy Applications and Intelligent Biomedical Implants. Adv. Mater. 2024, 36, 2313327. [Google Scholar] [CrossRef]

| Spring Stiffness (N/cm) | Horizontal Stiffness (N/cm) | Vertical Stiffness (N/cm) |
|---|---|---|
| 6.34 | 11.41 | 2.33 |
| 2.58 | 4.64 | 0.96 |
| 0.87 | 1.56 | 0.37 |
| 0.32 | 0.57 | 0.18 |
| 0.11 | 0.19 | 0.11 |
| 0.03 | 0.04 | 0.08 |
| Spring Stiffness (N/cm) | Load (BW) | Measurement Result (BW) | Relative Error |
|---|---|---|---|
| 6.34 | 1 | 0.89 ± 0.02 | 11% |
| 2.58 | 1 | 0.96 ± 0.04 | 4% |
| 0.87 | 1 | 0.91 ± 0.01 | 9% |
| 0.32 | 1 | 0.87 ± 0.01 | 13% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Zhang, B.; Wang, Z.; Dai, Z. Effect of Substrate Compliance on the Jumping Mechanism of the Tree Frog (Polypedates dennys). Biomimetics 2025, 10, 604. https://doi.org/10.3390/biomimetics10090604
Zhou R, Zhang B, Wang Z, Dai Z. Effect of Substrate Compliance on the Jumping Mechanism of the Tree Frog (Polypedates dennys). Biomimetics. 2025; 10(9):604. https://doi.org/10.3390/biomimetics10090604
Chicago/Turabian StyleZhou, Rui, Baowen Zhang, Zhouyi Wang, and Zhendong Dai. 2025. "Effect of Substrate Compliance on the Jumping Mechanism of the Tree Frog (Polypedates dennys)" Biomimetics 10, no. 9: 604. https://doi.org/10.3390/biomimetics10090604
APA StyleZhou, R., Zhang, B., Wang, Z., & Dai, Z. (2025). Effect of Substrate Compliance on the Jumping Mechanism of the Tree Frog (Polypedates dennys). Biomimetics, 10(9), 604. https://doi.org/10.3390/biomimetics10090604







