Research on Target Localization Method for Underwater Robot Based on the Bionic Lateral Line System of Fish
Abstract
1. Introduction
2. Target Positioning Theoretical Model Based on Flow Field Perception
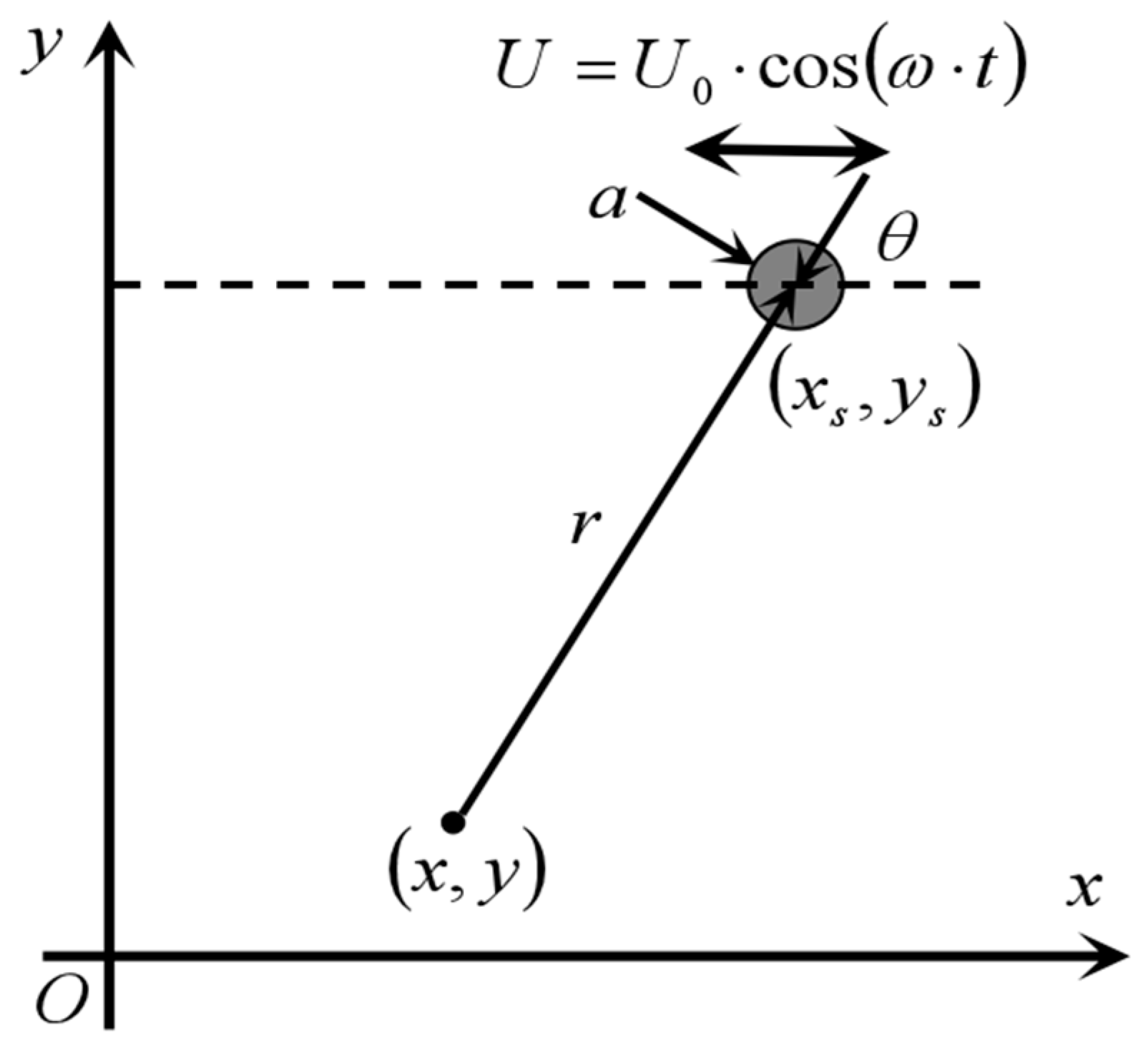
2.1. Equivalent Dipole Model for Underwater Moving Targets
2.2. Simulation Validation of an Equivalent Dipole Localization Model
3. Positioning Methods for Equivalent Modelling of Underwater Targets
3.1. Least Squares Based Target Location Function
3.2. Target Positioning Optimisation Algorithm Based on the Quasi-Newton Method
4. Analysis of Target Positioning Results
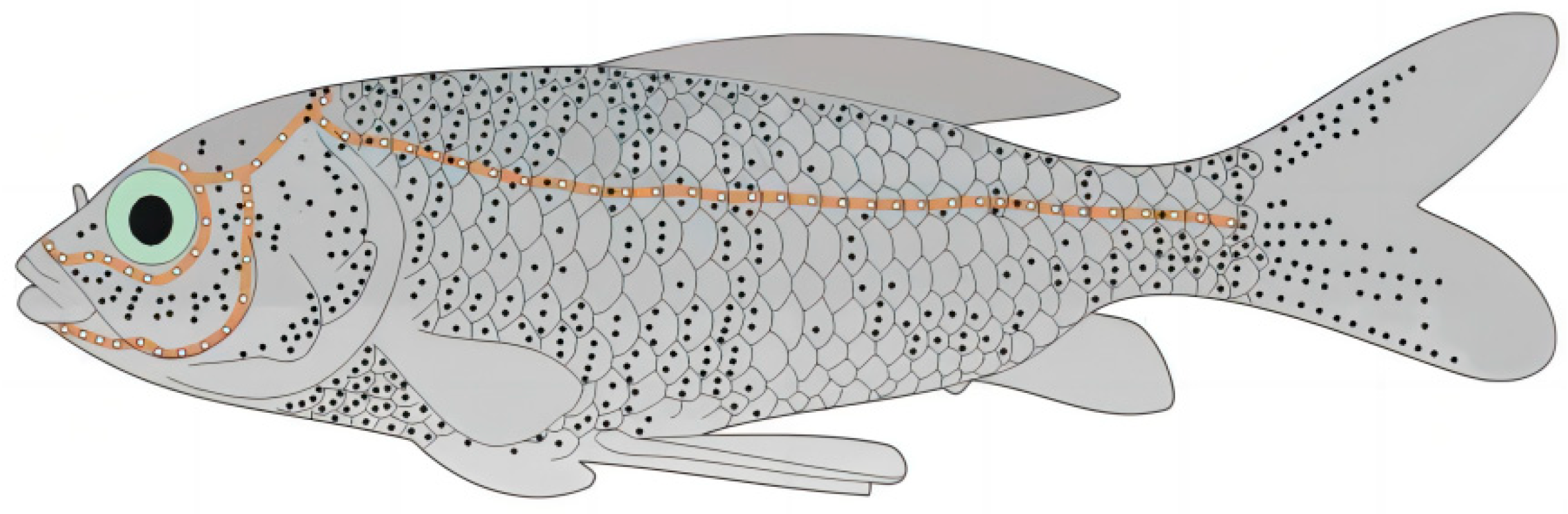
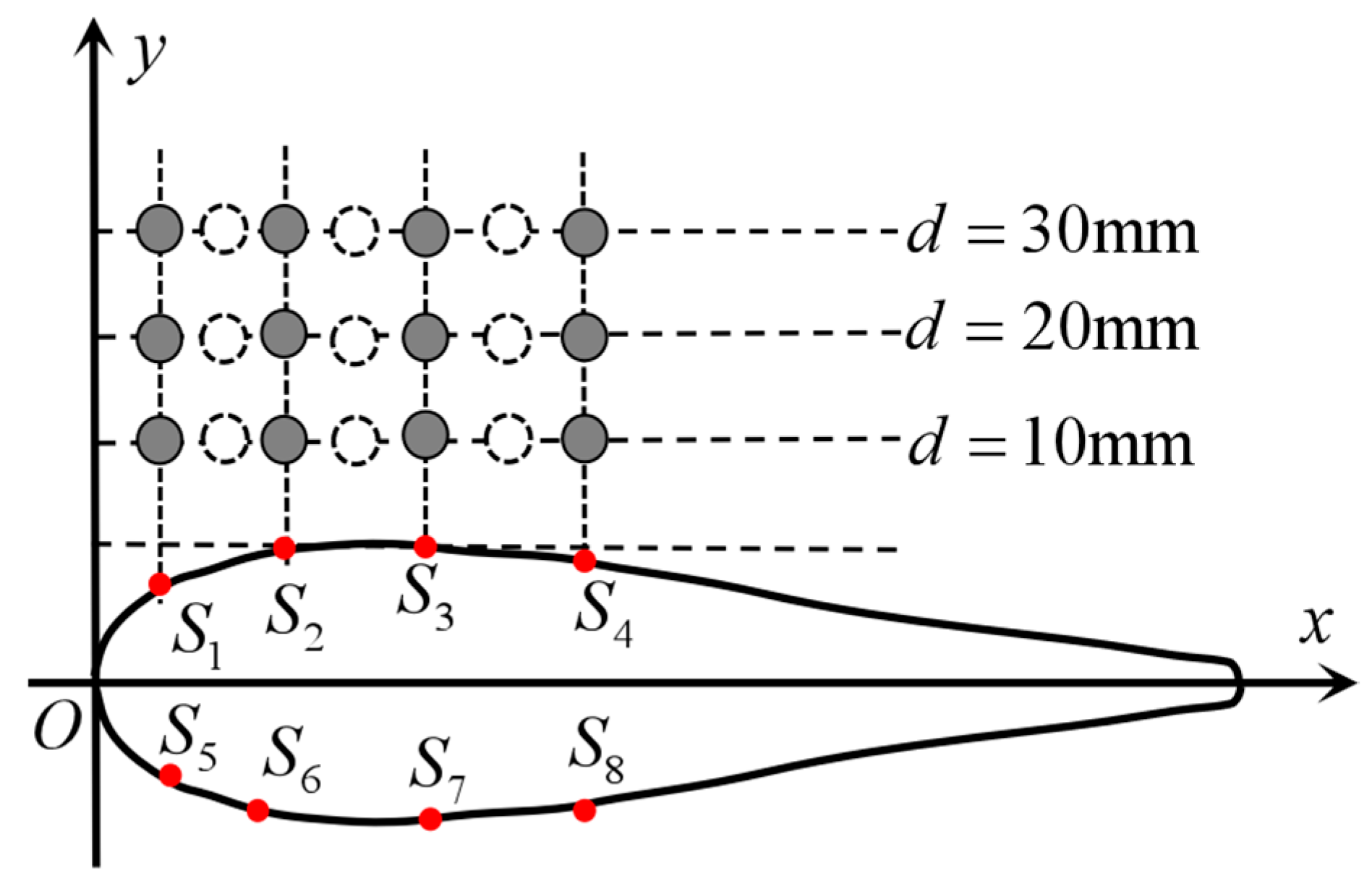
4.1. Lateral Line Perception Array Model
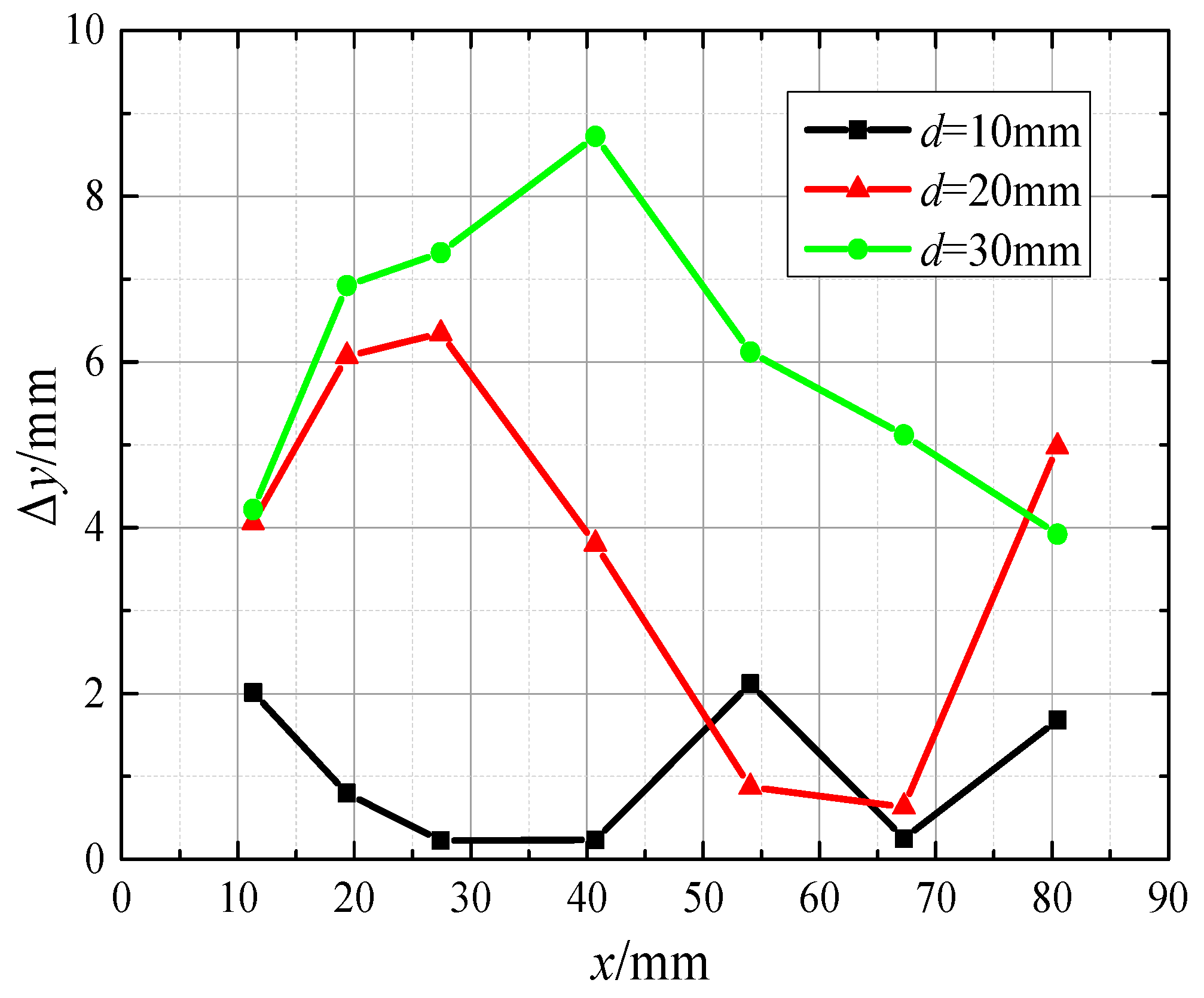
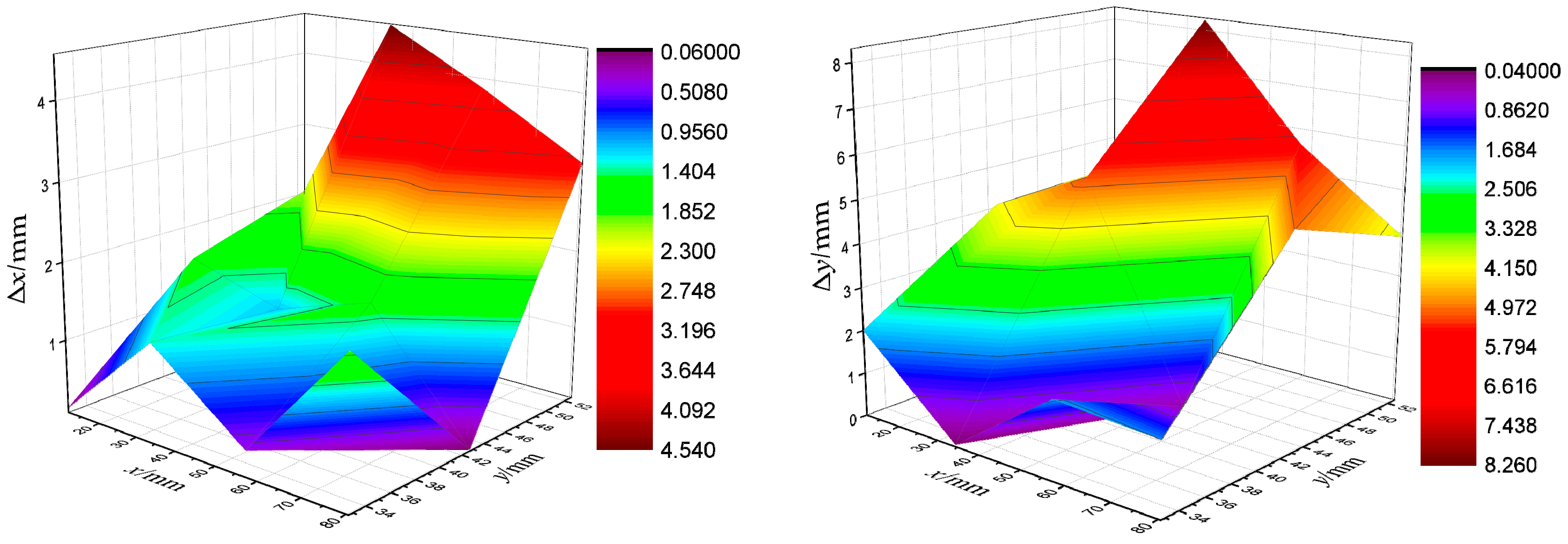
4.2. Error Analysis of Targeting Results
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cong, Y.; Gu, C.J.; Zhang, T.; Gao, Y.J. Underwater robot sensing technology: A survey. Fundam. Res. 2021, 1, 337–345. [Google Scholar] [CrossRef]
- Ge, X.; Zhao, J.; Cheng, Y.; Yang, J.; Geng, H. An intelligent positioning method for underwater vehicle under hydroacoustic noises. Ad Hoc Netw. 2025, 178, 103963. [Google Scholar] [CrossRef]
- Qiu, F.; Guo, D. Regularized constrained total least squares localization for underwater acoustic sensor networks using angle-delay-doppler measurements. Ad Hoc Netw. 2025, 170, 103768. [Google Scholar] [CrossRef]
- Ge, X.; Zhou, H.; Zhao, J.; Li, X.; Liu, X.; Li, J.; Luo, C. Robust positioning estimation for underwater acoustics targets with use of multi-particle swarm optimization. J. Mar. Sci. Eng. 2024, 12, 185. [Google Scholar] [CrossRef]
- Tang, G.; Yang, T.; Yang, Y.; Zhao, Q.; Xu, M.; Xie, G. Relative localization and dynamic tracking of underwater robots based on 3D-AprilTag. J. Mar. Sci. Eng. 2025, 13, 833. [Google Scholar] [CrossRef]
- Kumar, M.; Mondal, S. Recent developments on target tracking problem: A review. Ocean Eng. 2021, 236, 109588. [Google Scholar] [CrossRef]
- Zhang, C.; Xiao, F. Overview of data acquisition technology in underwater acoustic detection. Procedia Comput. Sci. 2021, 188, 130–136. [Google Scholar] [CrossRef]
- Nash, J.Z.; Bond, J.; Case, M.; McCarthy, I.; Mowat, R.; Pierce, I.; Teahan, W. Tracking the fine scale movements of fish using autonomous maritime robotics: A systematic state of the art review. Ocean Eng. 2021, 229, 108650. [Google Scholar] [CrossRef]
- Hu, Q.; Liu, Y.; Zhao, Z.; Zhu, Z. Research progress of bionic artificial lateral line detection technology for underwater unmanned clusters. J. Underw. Unmanned Syst. 2019, 27, 114–122. [Google Scholar]
- Zhang, W.; Wang, N.; Wei, S.; Du, X.; Yan, Z. Overview of the current development status and key technologies of underwater unmanned submersible vehicle clusters. J. Harbin Eng. Univ. 2020, 41, 289–297. [Google Scholar]
- Zhang, L.; Li, C.; Sun, H. Object detection/tracking toward underwater photographs by remotely operated vehicles (ROVs). Future Gener. Comput. Syst. 2022, 126, 163–168. [Google Scholar] [CrossRef]
- Wang, N.; Wang, Y.Y.; Meng, J.E. Review on deep learning techniques for marine object recognition: Architectures and algorithms. Control Eng. Pract. 2022, 118, 104458. [Google Scholar] [CrossRef]
- Bucci, A.; Zacchini, L.; Franchi, M.; Ridolfi, A.; Allotta, B. Comparison of feature detection and outlier removal strategies in a mono visual odometry algorithm for underwater navigation. Appl. Ocean Res. 2022, 118, 102961. [Google Scholar] [CrossRef]
- Gite, P.; Shrivastava, A.; Krishna, K.M.; Kusumadevi, G.; Dilip, R.; Potdar, R.M. Under water motion tracking and monitoring using wireless sensor network and machine learning. Mater. Today Proc. 2022, 80, 3511–3516. [Google Scholar] [CrossRef]
- Park, D.; Kwak, K.; Kim, J.; Li, J.-H.; Chung, W.K. Underwater localization using received signal strength of electromagnetic wave with obstacle penetration effects. IFAC Pap. Online 2019, 52, 372–377. [Google Scholar] [CrossRef]
- García-Vega, A.; Fuentes-Pérez, J.F.; Fukuda, S.; Kruusmaa, M.; Sanz-Ronda, F.J.; Tuhtan, J.A. Artificial lateral line for aquatic habitat modelling: An example for lefua echigonia. Ecol. Inform. 2021, 65, 101388. [Google Scholar] [CrossRef]
- Brian, M.M. Lateral line: From water waves to brain waves. Curr. Biol. 2021, 31, 344–347. [Google Scholar] [CrossRef]
- Peloggia, J.; Münch, D.; Meneses, G.P.; Romero-Carvajal, A.; Lush, M.E.; Lawson, N.D.; McClain, M.; Pan, Y.A.; Piotrowski, T. Adaptive cell invasion maintains lateral line organ homeostasis in response to environmental changes. Dev. Cell 2021, 56, 1296–1312. [Google Scholar] [CrossRef]
- Nguyen, N. High-Resolution Source Imaging with Bio-Inspired Sensing Systems; University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2011. [Google Scholar]
- Schmitz, A.; Bleckmann, H.; Mogdans, J. Organization of the superficial neuromast system in goldfish, carassius auratus. J. Morphol. 2008, 269, 751–761. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, J.M.; Atema, J. Flow sensing in sharks: Lateral line contributions to navigation and prey capture. In Flow Sensing in Air and Water; Bleckmann, H., Mogdans, J., Coombs, S.L., Eds.; Springer: New York, NY, USA, 2014; pp. 127–146. [Google Scholar]
- Hanke, W. Natural hydrodynamic stimuli. In Flow Sensing in Air and Water; Bleckmann, H., MogdansCoombs, S.L., Eds.; Springer: New York, NY, USA, 2014; pp. 3–29. [Google Scholar]
- Ahrari, A.; Lei, H.; Sharif, M.A.; Deb, K.; Tan, X. Reliable underwater dipole source characterization in 3D space by an optimally designed artificial line system. Bioinspir. Biomim. 2017, 12, 036010. [Google Scholar] [CrossRef]
- Ji, M.J.; Zhang, Y.; Zheng, X.; Lin, X.; Liu, G.; Qiu, J. Resolution improvement of dipole source localization for artificial lateral lines based on multiple signal classification. Bioinspir. Biomim. 2018, 14, 016016. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, X.D.; Ji, M.J.; Lin, X.; Qiu, J.; Liu, G.J. Orientation recognition of underwater translational target based on fish lateral line perception principle and deep learning. J. Mech. Eng. 2020, 56, 231–239. [Google Scholar]
- Lin, X.; Wu, J.; Qin, Q. A novel obstacle localization method for an underwater robot based on the flow field. J. Mar. Sci. Eng. 2019, 7, 437. [Google Scholar] [CrossRef]
- Hassan, E.S. Mathematical description of the stimuli to the lateral line system of fish derived from a three-dimensional flow field analysis I: The cases of moving in open water and of gliding towards a plane surface. Biol. Cybern. 1992, 66, 443–452. [Google Scholar] [CrossRef]
- Hassan, E.S. Mathematical description of the stimuli to the lateral line system of fish derived from a three-dimensional flow field analysis II: The case of gliding alongside or above a plane surface. Biol. Cybern. 1992, 66, 453–461. [Google Scholar] [CrossRef]
- Hassan, E.S. Mathematical description of the stimuli to the lateral line system of fish, derived from a three-dimensional flow field analysis III: The case of an oscillating sphere near the fish. Biol. Cybern. 1993, 69, 525–538. [Google Scholar] [CrossRef]
- Zhang, N.; Shen, H.; Yao, H. Numerical simulation and validation of submarine resistance and flow field and numerical optimization of boat type. Ship Mech. 2005, 9, 13. [Google Scholar]
- Lin, X.; Xu, H.; Wang, H.; Sun, P.; Yang, E.; Zan, G. Research on an Underwater Target Classification Method Based on the Spatial–Temporal Characteristics of a Flow Field. Water 2025, 17, 2006. [Google Scholar] [CrossRef]







| Comparative Parameters | Experimental Group | Simulation Group | Relative Error |
|---|---|---|---|
| 2.716 | 2.681 | 1.29% |
| Number | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| X-axis coordinate | 11.31 mm | 27.44 mm | 54.05 mm | 80.47 mm |
| Y-axis coordinate | 15.33 mm | 20.48 mm | 22.68 mm | 19.78 mm |
| normal angle | 116.5° | 100.5° | 2.0° | 10.5° |
| Component | Parameters | Symbol | Numerical Value |
|---|---|---|---|
| Computational domain | Length × Width × Height | L×W×H | 3500 × 1000 × 1000 mm |
| Distance from water surface | D | 500 mm | |
| Vibrating ball | Small ball diameter | a | 50.8 mm |
| Vibration direction | // | Horizontal plane X-axis direction | |
| Vibration frequency | f | 45 Hz | |
| Vibration amplitude | s | 10 mm | |
| Robotic fish model | Length | L | 180 mm |
| Number of sampling points | Ns | 4 × 2 rows | |
| Signal acquisition | Time step | 5 × 10−4 s | |
| Data length | t | 20 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Yang, E.; Zan, G.; Xu, H.; Wang, H.; Sun, P. Research on Target Localization Method for Underwater Robot Based on the Bionic Lateral Line System of Fish. Biomimetics 2025, 10, 593. https://doi.org/10.3390/biomimetics10090593
Lin X, Yang E, Zan G, Xu H, Wang H, Sun P. Research on Target Localization Method for Underwater Robot Based on the Bionic Lateral Line System of Fish. Biomimetics. 2025; 10(9):593. https://doi.org/10.3390/biomimetics10090593
Chicago/Turabian StyleLin, Xinghua, Enyu Yang, Guozhen Zan, Hang Xu, Hao Wang, and Peilong Sun. 2025. "Research on Target Localization Method for Underwater Robot Based on the Bionic Lateral Line System of Fish" Biomimetics 10, no. 9: 593. https://doi.org/10.3390/biomimetics10090593
APA StyleLin, X., Yang, E., Zan, G., Xu, H., Wang, H., & Sun, P. (2025). Research on Target Localization Method for Underwater Robot Based on the Bionic Lateral Line System of Fish. Biomimetics, 10(9), 593. https://doi.org/10.3390/biomimetics10090593







