Multi-Strategy Improved Red-Billed Blue Magpie Optimization Algorithm and Its Applications
Abstract
1. Introduction
2. Red-Billed Blue Magpie Optimization Algorithm
2.1. Initial Population
2.2. Search for Food
2.3. Attacking Prey
2.4. Food Storage
3. Improved Optimization Algorithm for Red-Billed Blue Magpie
3.1. Adaptive T-Distribution-Based Sinh–Cosh Search Strategy
3.2. Neighborhood-Guided Reinforcement Strategy
3.3. Crossover Strategy
3.3.1. Horizontal Crossing
3.3.2. Vertical Crossing
3.4. The Pseudocode of SWRBMO Algorithm
| Algorithm 1 The pseudocode of the SWRBMO algorithm |
| Input: The dimension D, maximum number of iterations T, and population size N |
| Output: Global optimal solution Global optimal solution |
| 1: Procedure SWRBMO |
| 2: Initialize the key parameters T, D, N, t, and α |
| 3: While t < T +1 |
| 4: Calculate the position of each individual |
| 5: Update the optimal solution |
| 6: Exploration: |
| 7: for i = 1: N |
| 8: if rand < α |
| 9: Modify the individual’s position using Equation (17) |
| 10: else |
| 11: Modify the individual’s position using Equation (18) |
| 12: end if |
| 13: Exploitation: |
| 14: if rand < α |
| 15: Modify the magpie’s coordinates using Equation (19) |
| 16: else |
| 17: Update the magpie’s location using Equation (20) |
| 18: end if |
| 19: Execute the Crossover Strategy using Equations (21)–(23) |
| 20: end for |
| 21: Refresh the food storage, using Equation (9) |
| 22: t = t + 1 |
| 23: end while |
| 24: Return best solution |
3.5. Time Complexity Analysis
4. Algorithm Performance Test and Analysis
4.1. Experimental Design and Parameter Settings
4.1.1. Division of the Experimental Stages
4.1.2. Experimental Parameters and Environment
4.2. Effectiveness Analysis of the Improvement Strategy
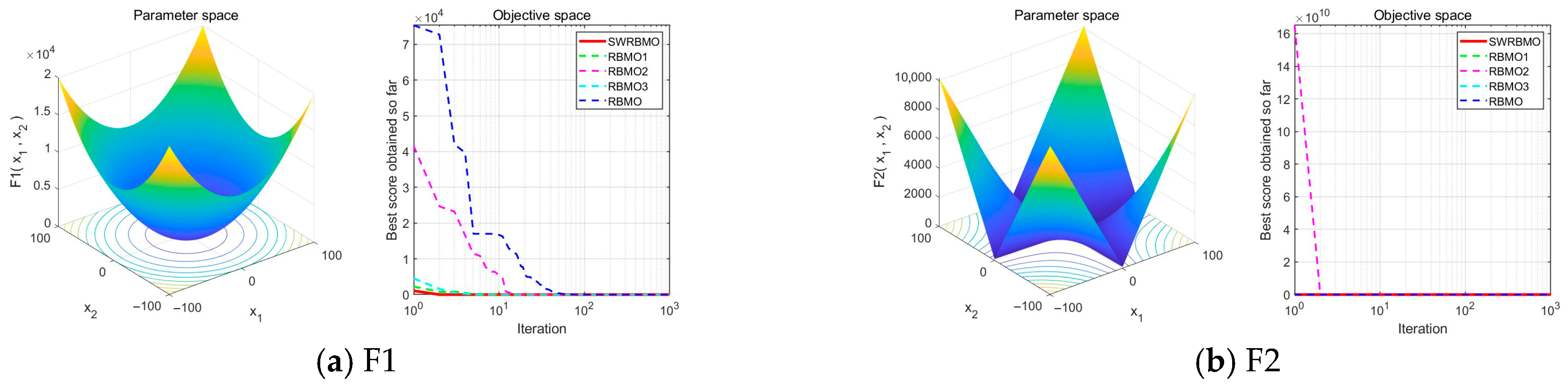
4.2.1. Selection of Test Functions
4.2.2. Effectiveness Analysis of Different Improvement Strategies
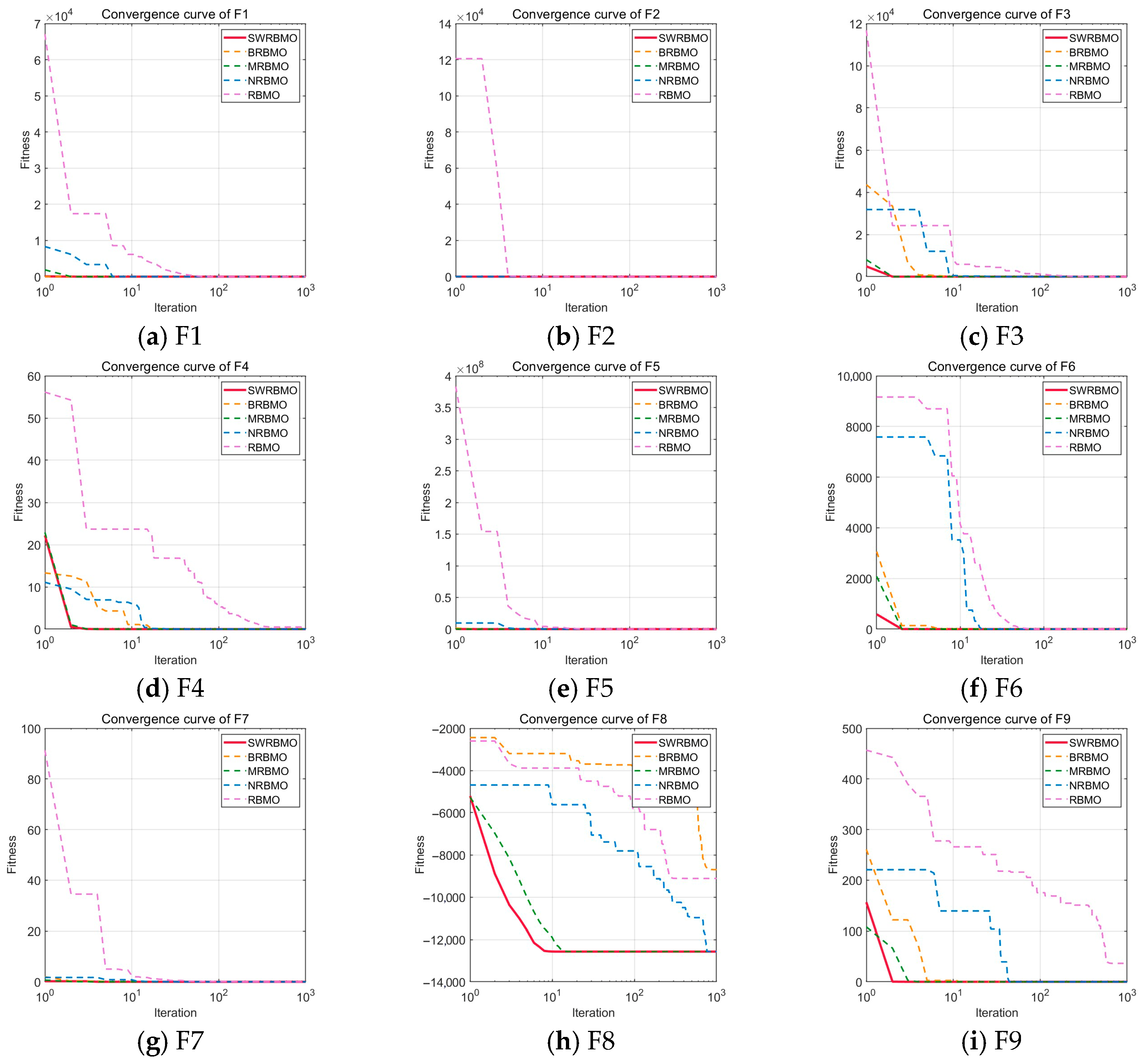
4.3. Ablation Study
4.4. Comparison and Analysis of SWRBMO Optimization Results with Other Optimization Algorithms
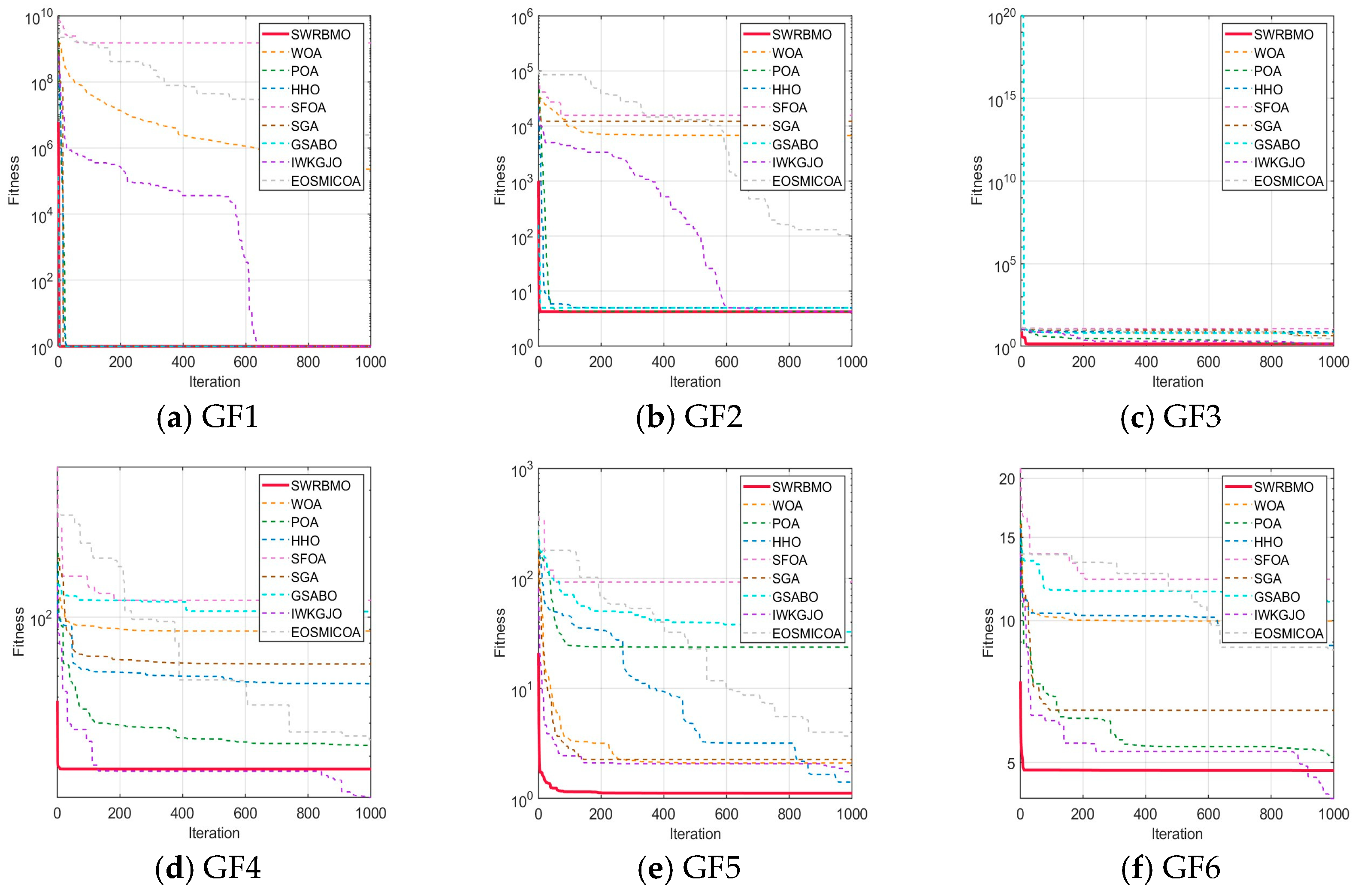
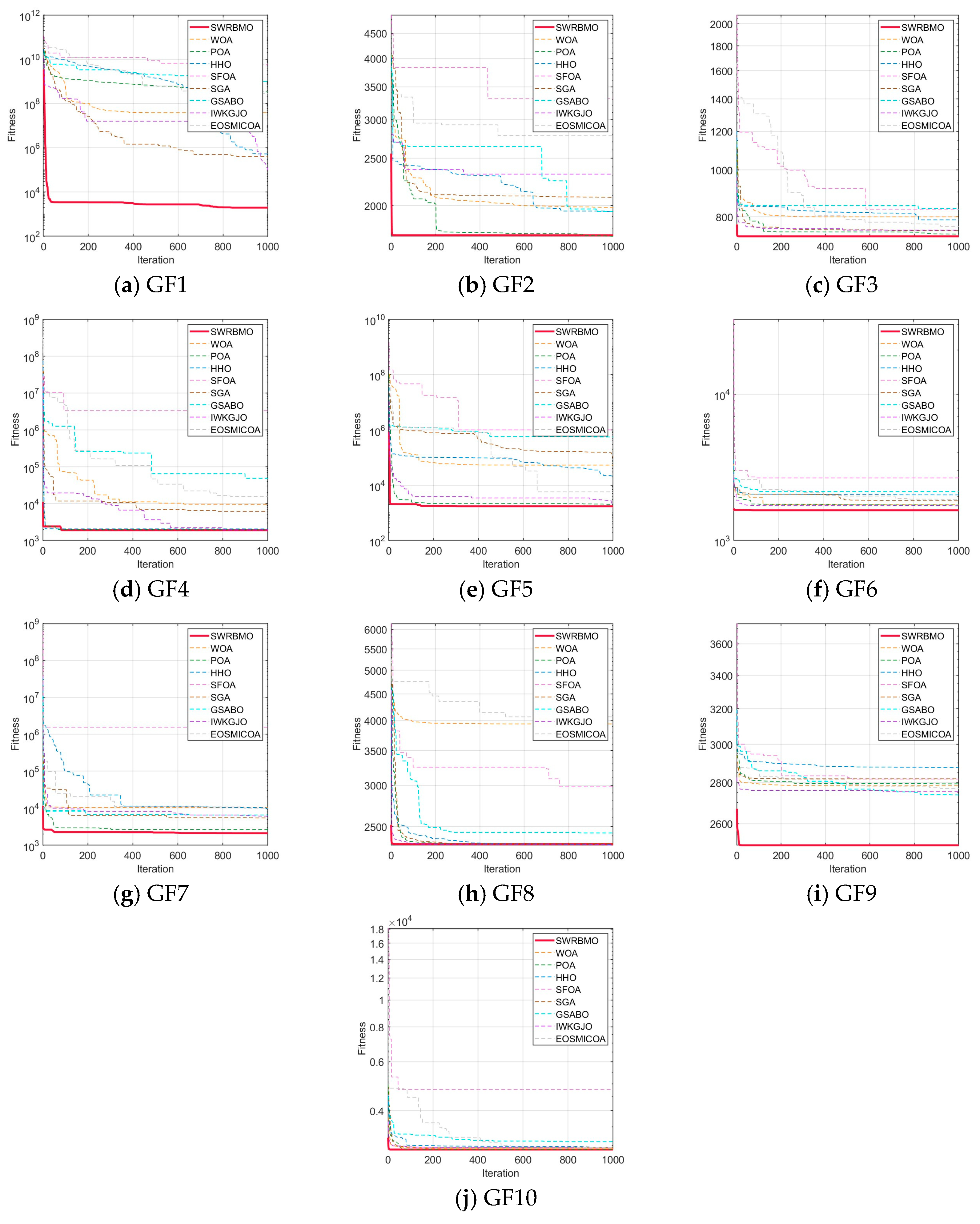
4.4.1. Performance Analysis Using the CEC2019 Test Function Suite
4.4.2. Performance Analysis Using the CEC2021 Test Function Suite
4.5. Wilcoxon Rank-Sum Test
4.5.1. Wilcoxon Rank-Sum Test on CEC2005
4.5.2. Wilcoxon Rank-Sum Test on CEC2019
4.5.3. Wilcoxon Rank-Sum Test on CEC2021
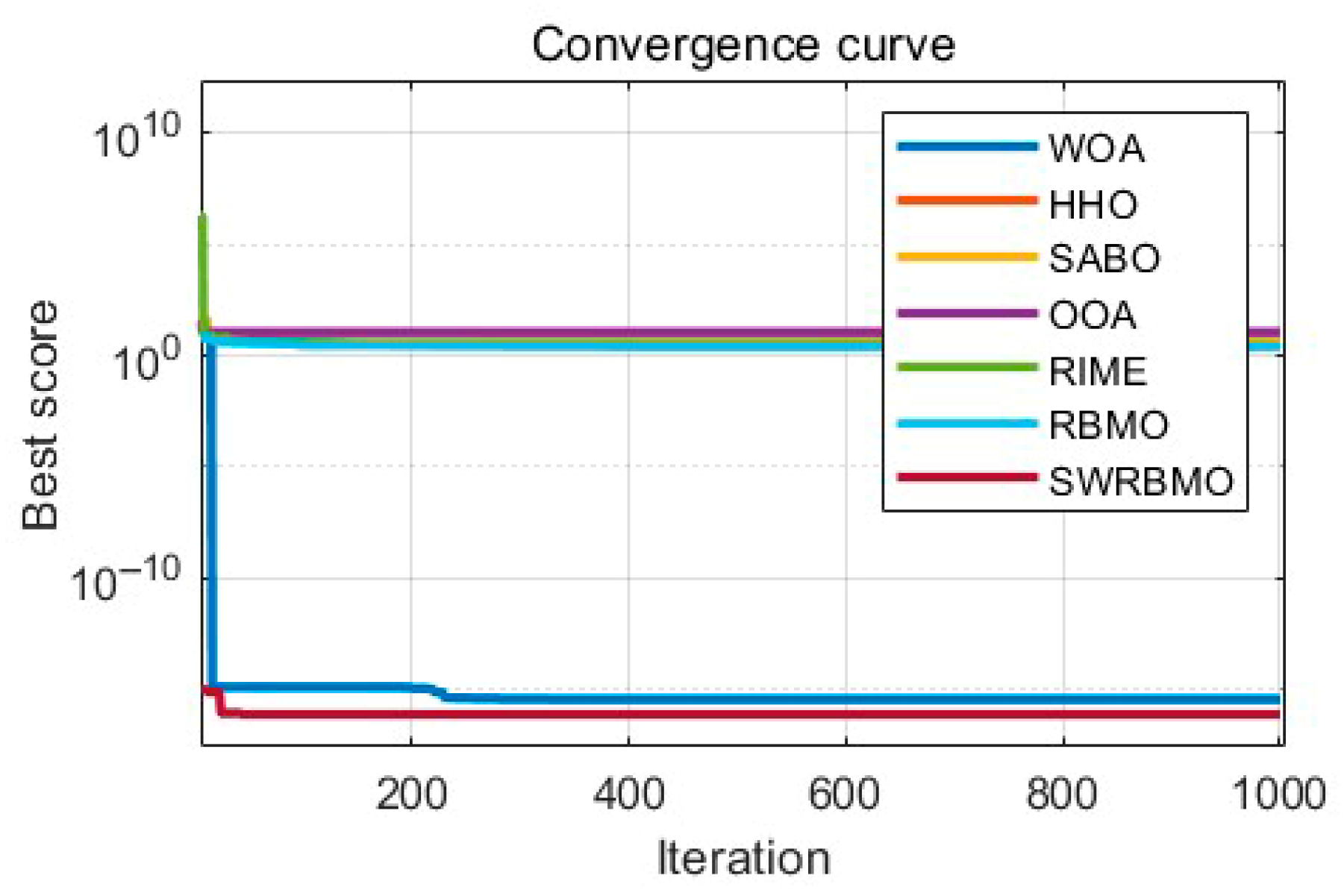
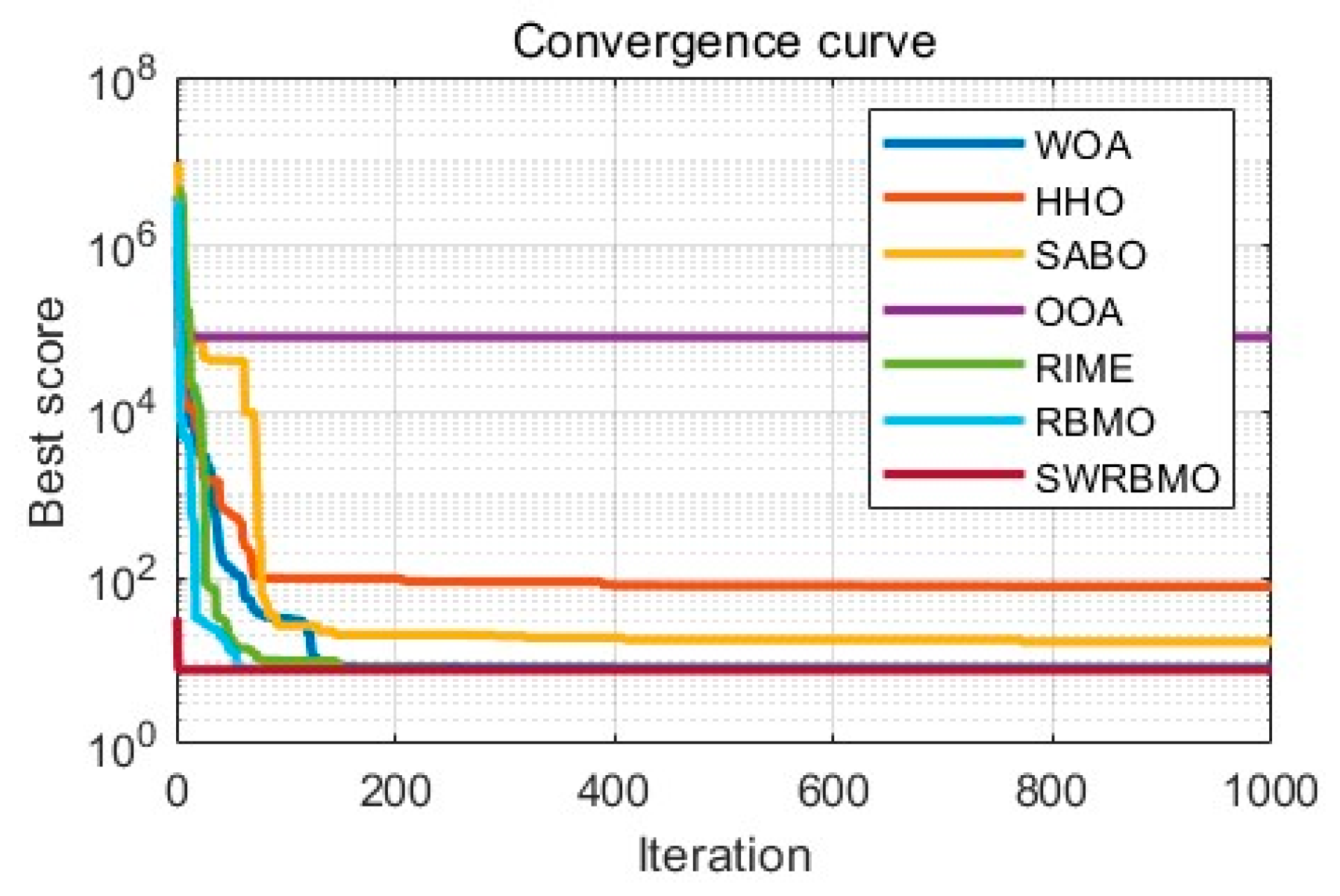
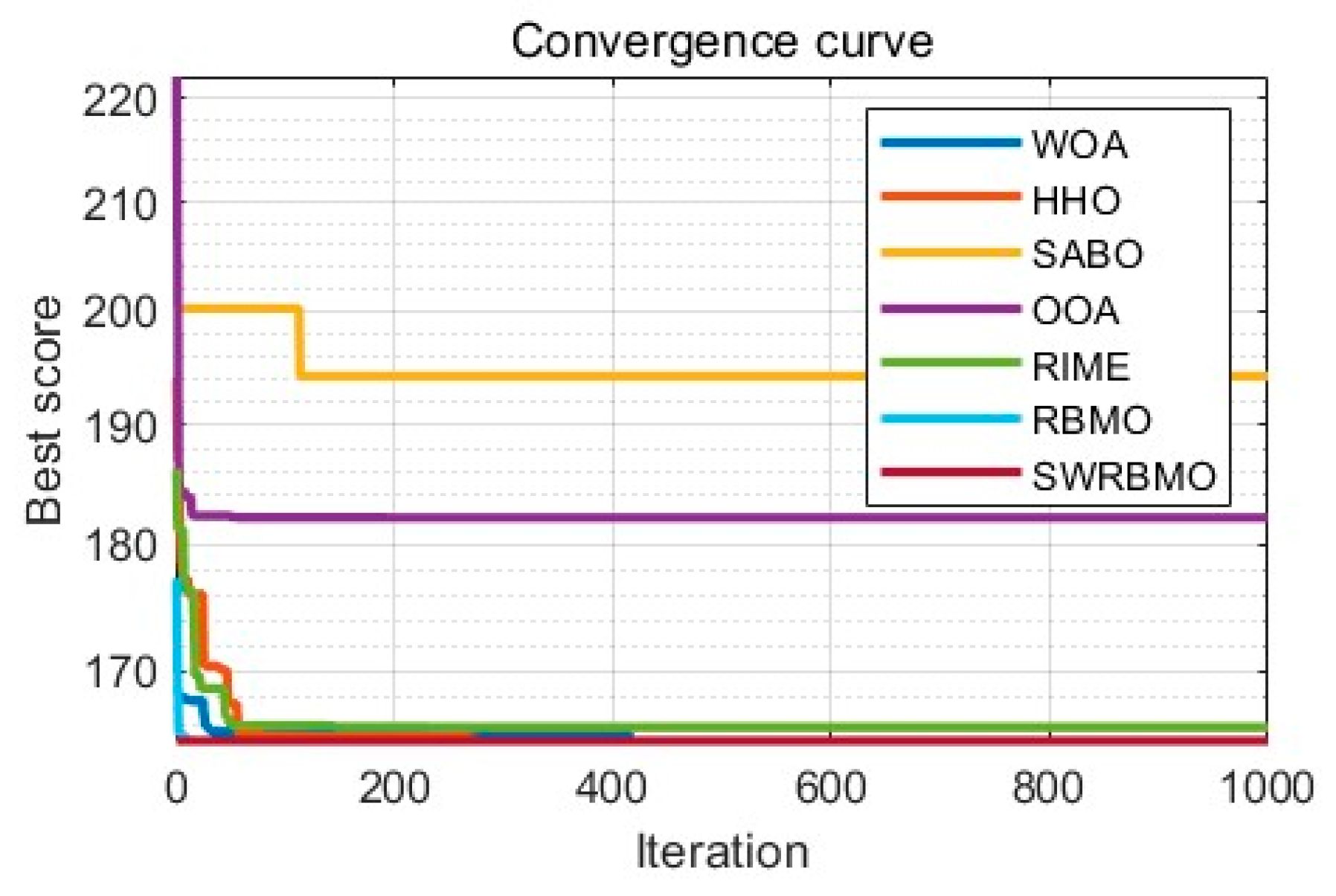
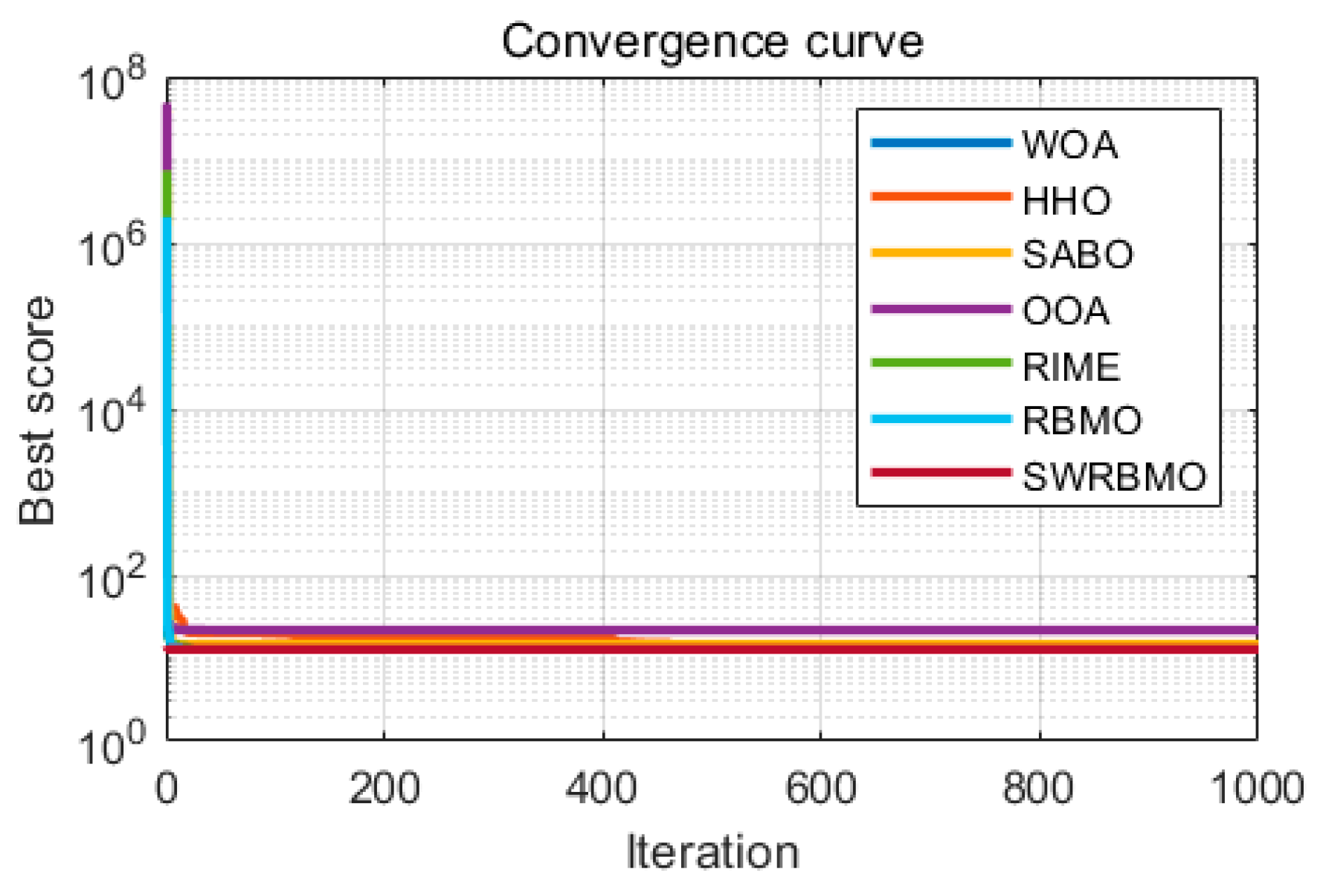
5. Excellent Engineering Applications Based on SWRBMO
5.1. Robot Gripper Problem
5.2. Industrial Refrigeration System Problem
5.3. Reinforced Concrete Beam Design Problem
5.4. Step Cone Pulley Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahkar, F.T. Battle Royale Optimization Algorithm. Neural Comput. Appl. 2021, 33, 1139–1157. [Google Scholar] [CrossRef]
- Li, J.-Y.; Zhan, Z.-H.; Tan, K.C.; Zhang, J. A Meta-Knowledge Transfer-Based Differential Evolution for Multitask Optimization. IEEE Trans. Evol. Comput. 2022, 26, 719–734. [Google Scholar] [CrossRef]
- Yankai, W.; Shilong, W.; Dong, L.; Chunfeng, S.; Bo, Y. An Improved Multi-Objective Whale Optimization Algorithm for the Hybrid Flow Shop Scheduling Problem Considering Device Dynamic Reconfiguration Processes. Expert Syst. Appl. 2021, 174, 114793. [Google Scholar] [CrossRef]
- Yang, B.; Liang, B.; Qian, Y.; Zheng, R.; Su, S.; Guo, Z.; Jiang, L. Parameter Identification of PEMFC via Feedforward Neural Network-Pelican Optimization Algorithm. Appl. Energy 2024, 361, 122857. [Google Scholar] [CrossRef]
- Song, X.; Ma, H.; Zhang, Y.; Gong, D.; Guo, Y.; Hu, Y. A Streaming Feature Selection Method Based on Dynamic Feature Clustering and Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2024. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly Optimization Algorithm: A Novel Approach for Global Optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Pourhaji Kazem, A.A. Black Widow Optimization Algorithm: A Novel Meta-Heuristic Approach for Solving Engineering Optimization Problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Ye, M.; Zhou, H.; Yang, H.; Hu, B.; Wang, X. Multi-Strategy Improved Dung Beetle Optimization Algorithm and Its Applications. Biomimetics 2024, 9, 291. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Lee, H.W.; Zhang, J.H. Probabilistic Load Flow Evaluation With Hybrid Latin Hypercube Sampling and Cholesky Decomposition. IEEE Trans. Power Syst. 2009, 24, 661–667. [Google Scholar] [CrossRef]
- Fu, H.; Liu, H. Improved sparrow search algorithm with multi-strategy integration and its application. Control. Decis. 2022, 37, 87–96. [Google Scholar] [CrossRef]
- Fu, S.; Li, K.; Huang, H.; Ma, C.; Fan, Q.; Zhu, Y. Red-Billed Blue Magpie Optimizer: A Novel Metaheuristic Algorithm for 2D/3D UAV Path Planning and Engineering Design Problems. Artif. Intell. Rev. 2024, 57, 134. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Agwa, A.M. Red-Billed Blue Magpie Optimizer for Electrical Characterization of Fuel Cells with Prioritizing Estimated Parameters. Technologies 2024, 12, 156. [Google Scholar] [CrossRef]
- Lu, B.; Xie, Z.; Wei, J.; Gu, Y.; Yan, Y.; Li, Z.; Pan, S.; Cheong, N.; Chen, Y.; Zhou, R. MRBMO: An Enhanced Red-Billed Blue Magpie Optimization Algorithm for Solving Numerical Optimization Challenges. Symmetry 2025, 17, 1295. [Google Scholar] [CrossRef]
- Sharma, A. Improved Red-Billed Blue Magpie Optimizer for Unmanned Aerial Vehicle Path Planning. In Proceedings of the 2024 International Conference on Computational Intelligence and Network Systems (CINS), Dubai, United Arab Emirates, 28–29 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Morozov, A.Y.; Kuzenkov, O.A.; Sandhu, S.K. Global Optimisation in Hilbert Spaces Using the Survival of the Fittest Algorithm. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106007. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Bai, J.; Li, Y.; Zheng, M.; Khatir, S.; Benaissa, B.; Abualigah, L.; Abdel Wahab, M. A Sinh Cosh Optimizer. Knowl.-Based Syst. 2023, 282, 111081. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, P. Whale Optimization Algorithm with Improved Multi-Strategy. Comput. Eng. Appl. 2024, 61, 83. [Google Scholar] [CrossRef]
- Liu, K.; Zhao, L.L.; Wang, H. Whale Optimization Algorithm Based on Elite Opposition-Based and Crisscross Optimization. J. Chin. Comput. Syst. 2020, 41, 2092–2097. [Google Scholar]
- Gaviano, M.; Kvasov, D.E.; Lera, D.; Sergeyev, Y.D. Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans. Math. Softw. 2003, 29, 469–480. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, X.; Zhang, J.; Mirjalili, S. Superb Fairy-Wren Optimization Algorithm: A Novel Metaheuristic Algorithm for Solving Feature Selection Problems. Clust. Comput. 2025, 28, 1–62. [Google Scholar] [CrossRef]
- Tian, A.-Q.; Liu, F.-F.; Lv, H.-X. Snow Geese Algorithm: A Novel Migration-Inspired Meta-Heuristic Algorithm for Constrained Engineering Optimization Problems. Appl. Math. Model. 2024, 126, 327–347. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Q.; Du, Z. Sand Cat Swarm Optimization Algorithm and Its Application Integrating Elite Decentralization and Crossbar Strategy. Sci. Rep. 2024, 14, 8927. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Q.; Wang, Z.; Du, Z.; Jin, Z. An Improved Golden Jackal Optimization Algorithm Based on Mixed Strategies. Mathematics 2024, 12, 1506. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, S.; Li, M.; Guo, Y. Multi-strategy chimp optimization algorithm and its application of engineering problem. Comput. Eng. Appl. 2022, 58, 174–183. [Google Scholar]
- Zhong, R.; Yu, J.; Zhang, C.; Munetomo, M. SRIME: A Strengthened RIME with Latin Hypercube Sampling and Embedded Distance-Based Selection for Engineering Optimization Problems. Neural Comput. Appl. 2024, 36, 6721–6740. [Google Scholar] [CrossRef]
- Kumar, A.; Wu, G.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A Test-Suite of Non-Convex Constrained Optimization Problems from the Real-World and Some Baseline Results. Swarm Evol. Comput. 2020, 56, 100693. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Subtraction-Average-Based Optimizer: A New Swarm-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, M.; Trojovský, P. Osprey Optimization Algorithm: A New Bio-Inspired Metaheuristic Algorithm for Solving Engineering Optimization Problems. Front. Mech. Eng. 2023, 13, 8775. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]




| Algorithm | Inspiration Source | Main Strategy/Improvement | Strengths | Limitations |
|---|---|---|---|---|
| DE | Natural selection and genetic evolution mechanisms | Differential mutation and recombination | Strong global exploration via differential mutation | High cost of calculation, parameter sensitive |
| PSO | Group behaviors of bird flocks and fish schools | Individual and global best memory mechanism | Simple implementation, fast convergence speed | Low diversity at later stages, easy to fall into local optima, parameter sensitive |
| SSA | The foraging and anti-predation behaviors of sparrows | Detection and early warning mechanism | Strong global search capability | Poor convergence accuracy, easy to fall into local optima, sensitive to parameter setting |
| RBMO | Cooperative hunting of red-billed blue magpies | Environment-feedback-driven dynamic coordination | Strong adaptability, few parameters, good population diversity | Poor convergence accuracy; easy to fall into local optima |
| MDBO | The natural behavior of dung beetles, combined with improved strategies | Latin Hypercube Sampling, mean differential variation, lens imaging reverse learning and dimension-by-dimension optimization | Superior performance in terms of optimization accuracy, stability, and convergence speed | In certain complex scenarios, MDBO still faces challenges in obtaining the theoretically optimal solution |
| SWRBMO | Cooperative hunting of red-billed blue magpies, combined with improved strategies | Adaptive T-distribution-based sinh–cosh search strategy, neighborhood-guided reinforcement strategy and crossover strategy | Improved global search, faster convergence, higher robustness | The application of SWRBMO in certain complex scenarios requires further investigation |
| Function | Function Name | Dimension | Domain | Optimum Value |
|---|---|---|---|---|
| Sphere | 30/100 | [−100, 100] | 0 | |
| Schwefel’s problem 2.22 | 30/100 | [−10, 10] | 0 | |
| Schwefel’s problem 1.2 | 30/100 | [−100, 100] | 0 | |
| Schwefel’s problem 2.21 | 30/100 | [−100, 100] | 0 | |
| Generalized Rosenbrock function | 30/100 | [−30, 30] | 0 | |
| Step function | 30/100 | [−100, 100] | 0 | |
| Quartic function | 30/100 | [−1.28, 1.28] | 0 | |
| Generalized Schwefel problem 2.26 | 30/100 | [−500, 500] | −418.98 | |
| Generalized Rastrigin Function | 30/100 | [−5.12, 5.12] | 0 | |
| Ackley’s function | 30/100 | [−32, 32] | 0 | |
| Generalized Criewank function | 30/100 | [−600, 600] | 0 | |
| Generalized penalized function 1 | 30/100 | [−50, 50] | 0 | |
| Generalized penalized function 2 | 30/100 | [−50, 50] | 0 | |
| Shekell’s foxhole function | 2 | [−65, 65] | 0 | |
| Kowalik’s function | 4 | [−5, 5] | 0.1484 |
| Function | Algorithm | D = 30 | D = 100 | ||||
|---|---|---|---|---|---|---|---|
| Best | Mean | Std | Best | Mean | Std | ||
| F1 | SWRBMO | 0 | 0 | 0 | 0 | 0 | 0 |
| RBMO1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO3 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO | 2.119 × 10−12 | 4.328 × 10−10 | 8.708 × 10−10 | 7.837 | 8.600 × 10 | 6.821 × 10 | |
| F2 | SWRBMO | 0 | 0 | 0 | 0 | 0 | 0 |
| RBMO1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO3 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO | 2.678 × 10−7 | 5.218 × 10−6 | 5.701 × 10−6 | 1.683 | 7.587 | 6.355 | |
| F3 | SWRBMO | 0 | 0 | 0 | 0 | 0 | 0 |
| RBMO1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO3 | 0 | 0 | 0 | 4.860 × 10 | 2.636 × 102 | 1.546 × 102 | |
| RBMO | 1.481 | 6.354 | 4.948 | 4.392 × 103 | 9.835 × 103 | 3.580 × 103 | |
| F4 | SWRBMO | 0 | 0 | 0 | 0 | 0 | 0 |
| RBMO1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO3 | 0 | 0 | 0 | 2.483 × 10−5 | 1.367 × 10−4 | 9.041 × 10−5 | |
| RBMO | 1.978 × 10−1 | 7.501 × 10−1 | 4.057 × 10−1 | 9.980 | 1.417 × 10 | 1.883 | |
| F5 | SWRBMO | 1.736 × 10 | 1.841 × 10 | 4.375 × 10−1 | 9.187 × 10 | 9.233 × 10 | 1.965 × 10−1 |
| RBMO1 | 2.216 × 10 | 2.326 × 10 | 7.388 × 10−1 | 9.352 × 10 | 9.476 × 10 | 6.550 × 10−1 | |
| RBMO2 | 2.581 × 10 | 2.649 × 10 | 3.579 × 10−1 | 9.651 × 10 | 9.746 × 10 | 6.132 × 10−1 | |
| RBMO3 | 6.599 × 10−5 | 9.146 | 1.198 × 10 | 3.724 × 10−2 | 1.129 × 102 | 7.385 × 10 | |
| RBMO | 2.003 × 10 | 4.240 × 10 | 3.510 × 10 | 1.542 × 103 | 4.811 × 103 | 2.890 × 103 | |
| F6 | SWRBMO | 0 | 0 | 0 | 0 | 0 | 0 |
| RBMO1 | 6.968 × 10−10 | 4.120 × 10−8 | 1.136 × 10−7 | 5.016 × 10−2 | 2.825 × 10−1 | 2.154 × 10−1 | |
| RBMO2 | 3.690 × 10−5 | 3.019 × 10−2 | 1.136 × 10−1 | 3.810 | 5.587 | 1.119 | |
| RBMO3 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO | 1.825 × 10−12 | 1.092 × 10−9 | 2.374 × 10−9 | 2.022 × 10 | 7.623 × 10 | 8.510 × 10 | |
| F7 | SWRBMO | 1.509 × 10−4 | 1.320 × 10−3 | 1.170 × 10−3 | 1.208 × 10−5 | 1.325 × 10−3 | 1.282 × 10−3 |
| RBMO1 | 9.051 × 10−6 | 5.423 × 10−5 | 5.658 × 10−5 | 9.934 × 10−7 | 5.295 × 10−5 | 4.426 × 10−5 | |
| RBMO2 | 2.442 × 10−5 | 3.520× 10−5 | 3.409 × 10−4 | 1.799 × 10−5 | 2.474 × 10−4 | 2.158 × 10−4 | |
| RBMO3 | 1.008 × 10−2 | 2.160 × 10−2 | 7.055 × 10−3 | 1.084 × 10−1 | 1.885 × 10−1 | 4.892 × 10−2 | |
| RBMO | 3.384 × 10−3 | 1.188 × 10−2 | 7.101 × 10−3 | 1.565 × 10−1 | 4.141 × 10−1 | 2.360 × 10−1 | |
| F8 | SWRBMO | −1.257 × 104 | −1.257 × 104 | 5.394 × 10−12 | −4.190 × 104 | −4.190 × 104 | 2.879 × 10−11 |
| RBMO1 | −1.209 × 104 | −9.857 × 103 | 1.060 × 103 | −3.378 × 104 | −2.775 × 104 | 2.899 × 103 | |
| RBMO2 | −8.578 × 103 | −7.483 × 103 | 6.211 × 102 | −2.641 × 104 | −2.172 × 104 | 2.126 × 103 | |
| RBMO3 | −1.257 × 104 | −1.257 × 104 | 3.411 × 10−12 | −4.190 × 104 | −4.190 × 104 | 2.027 × 10−11 | |
| RBMO | −9.888 × 103 | −9.023 × 103 | 6.979 × 102 | −2.902 × 104 | −2.517 × 104 | 2.502 × 103 | |
| F9 | SWRBMO | 0 | 0 | 0 | 0 | 0 | 0 |
| RBMO1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO3 | 0 | 2.463 × 10−14 | 3.859 × 10−14 | 1.137 × 10−12 | 1.709 × 10−12 | 3.589 × 10−13 | |
| RBMO | 2.215 × 10 | 4.560 × 10 | 1.596 × 10 | 1.352 × 102 | 3.060 × 102 | 5.919 × 10 | |
| F10 | SWRBMO | 4.441 × 10−16 | 4.441 × 10−16 | 0 | 4.441 × 10−16 | 4.441 × 10−16 | 0 |
| RBMO1 | 4.441 × 10−16 | 4.441 × 10−16 | 0 | 4.441 × 10−16 | 4.441 × 10−16 | 0 | |
| RBMO2 | 4.441 × 10−16 | 4.441 × 10−16 | 0 | 4.441 × 10−16 | 4.441 × 10−16 | 0 | |
| RBMO3 | 7.550 × 10−15 | 1.039 × 10−14 | 5.144 × 10−15 | 9.281 × 10−14 | 1.351 × 10−13 | 1.622 × 10−14 | |
| RBMO | 8.881 × 10−7 | 3.420 × 10−1 | 5.848 × 10−1 | 2.823 | 5.086 | 1.041 | |
| F11 | SWRBMO | 0 | 0 | 0 | 0 | 0 | 0 |
| RBMO1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| RBMO3 | 0 | 1.780 × 10−2 | 4.550 × 10−2 | 0 | 0 | 0 | |
| RBMO | 6.242 × 10−12 | 1.304 × 10−2 | 2.088 × 10−2 | 1.099 | 1.634 | 4.901 × 10−1 | |
| F12 | SWRBMO | 1.571 × 10−32 | 1.571 × 10−32 | 5.567 × 10−48 | 4.712 × 10−33 | 4.712 × 10−33 | 1.392 × 10−48 |
| RBMO1 | 2.247 × 10−11 | 4.160 × 10−9 | 1.750 × 10−8 | 4.298 × 10−4 | 2.820 × 10−3 | 1.965 × 10−3 | |
| RBMO2 | 1.283 × 10−6 | 5.491 × 10−3 | 1.914 × 10−2 | 3.542 × 10−2 | 7.365 × 10−2 | 2.658 × 10−2 | |
| RBMO3 | 1.571 × 10−32 | 1.571 × 10−32 | 5.567 × 10−48 | 4.712 × 10−33 | 4.712 × 10−33 | 1.392 × 10−48 | |
| RBMO | 3.964 × 10−11 | 1.013 × 10−1 | 2.281 × 10−1 | 2.902 | 7.073 | 3.223 | |
| F13 | SWRBMO | 1.350 × 10−32 | 1.350 × 10−32 | 5.567 × 10−48 | 1.350 × 10−32 | 1.350 × 10−32 | 5.567 × 10−48 |
| RBMO1 | 1.399 × 10−9 | 2.583 × 10−2 | 3.680 × 10−2 | 1.220 | 5.025 | 3.704 | |
| RBMO2 | 1.093 × 10−3 | 5.568 × 10−1 | 7.302 × 10−1 | 5.298 | 9.506 | 1.101 | |
| RBMO3 | 1.350 × 10−32 | 1.350 × 10−32 | 5.567 × 10−48 | 1.350 × 10−32 | 1.350 × 10−32 | 5.567 × 10−48 | |
| RBMO | 7.926 × 10−12 | 4.395 × 10−3 | 5.475 × 10−3 | 6.060 × 10 | 1.103 × 102 | 3.142 × 10 | |
| Function | Algorithm | Best | Mean | Std | Function | Best | Mean | Std |
|---|---|---|---|---|---|---|---|---|
| F14 | SWRBMO | 9.980 × 10−1 | 9.980 × 10−1 | 0 | F15 | 3.075 × 10−4 | 3.075 × 10−4 | 8.860 × 10−15 |
| RBMO1 | 9.980 × 10−1 | 9.980 × 10−1 | 0 | 3.075 × 10−4 | 4.380 × 10−3 | 8.276 × 10−3 | ||
| RBMO2 | 9.980 × 10−1 | 1.064 | 2.567 × 10−1 | 3.075 × 10−4 | 3.251 × 10−3 | 6.963 × 10−3 | ||
| RBMO3 | 9.980 × 10−1 | 1.392 | 1.525 | 3.075 × 10−4 | 4.296 × 10−4 | 3.222 × 10−4 | ||
| RBMO | 9.980 × 10−1 | 9.980 × 10−1 | 0 | 3.075 × 10−4 | 4.502 × 10−3 | 8.217 × 10−3 |
| Function | Algorithm | Best | Mean | Std | Function | Best | Mean | Std |
|---|---|---|---|---|---|---|---|---|
| F1 | SRWRBO | 0 | 0 | 0 | F7 | 1.509 × 10−4 | 1.320 × 10−3 | 1.170 × 10−3 |
| BRBMO | 0 | 0 | 0 | 8.520 × 10−6 | 7.360 × 10−5 | 4.970 × 10−5 | ||
| MRBMO | 0 | 0 | 0 | 1.600 × 10−4 | 8.320 × 10−4 | 7.270 × 10−4 | ||
| NRBMO | 0 | 0 | 0 | 1.760 × 10−5 | 2.270 × 10−4 | 2.640 × 10−4 | ||
| RBMO | 2.119 × 10−12 | 4.328 × 10−10 | 8.708 × 10−10 | 3.384 × 10−3 | 1.188 × 10−2 | 7.101 × 10−3 | ||
| F2 | SRWRBO | 0 | 0 | 0 | F8 | −1.257 × 104 | −1.257 × 104 | −5.394 × 10−12 |
| BRBMO | 0 | 0 | 0 | −1.100 × 104 | −1.000 × 104 | 8.208 × 102 | ||
| MRBMO | 0 | 0 | 0 | −1.260 × 104 | −1.260 × 104 | 3.330 × 10−12 | ||
| NRBMO | 0 | 0 | 0 | −1.260 × 104 | −1.260 × 104 | 4.670 × 10−12 | ||
| RBMO | 2.678 × 10−7 | 5.218 × 10−6 | 5.701 × 10−6 | −9.888 × 103 | −9.023 × 103 | 6.979 × 102 | ||
| F3 | SRWRBMO | 0 | 0 | 0 | F9 | 0 | 0 | 0 |
| BRBMO | 0 | 0 | 0 | 0 | 0 | 0 | ||
| MRBMO | 0 | 0 | 0 | 0 | 0 | 0 | ||
| NRBMO | 0 | 0 | 0 | 0 | 0 | 0 | ||
| RBMO | 1.481 | 6.354 | 4.948 | 2.215 × 10 | 4.560 × 10 | 1.596 × 10 | ||
| F4 | SRWRBMO | 0 | 0 | 0 | F10 | 4.441 × 10−16 | 4.441 × 10−16 | 0 |
| BRBMO | 0 | 0 | 0 | 4.441 × 10−16 | 4.441 × 10−16 | 0 | ||
| MRBMO | 0 | 0 | 0 | 4.441 × 10−16 | 4.441 × 10−16 | 0 | ||
| NRBMO | 0 | 0 | 0 | 4.441 × 10−16 | 4.441 × 10−16 | 0 | ||
| RBMO | 1.978 × 10−1 | 7.501 × 10−1 | 4.057 × 10−1 | 8.881 × 10−7 | 3.420 × 10−1 | 5.848 × 10−1 | ||
| F5 | SRWRBMO | 1.736 × 10 | 1.841 × 10 | 4.375 × 10−1 | F11 | 0 | 0 | 0 |
| BRBMO | 2.142 × 10 | 2.312 × 10 | 5.252 × 10−1 | 0 | 0 | 0 | ||
| MRBMO | 1.717 × 10 | 1.828 × 10 | 5.492 × 10−1 | 0 | 0 | 0 | ||
| NRBMO | 4.930 × 10−17 | 2.242 × 10−3 | 5.995 × 10−3 | 0 | 0 | 0 | ||
| RBMO | 2.003 × 10 | 4.240 × 10 | 3.510 × 10 | 6.242 × 10−12 | 1.304 × 10−2 | 2.088 × 10−2 | ||
| F6 | SRWRBMO | 0 | 0 | 0 | F12 | 1.571 × 10−32 | 1.571 × 10−32 | 5.567 × 10−48 |
| BRBMO | 1.360 × 10−10 | 1.860 × 10−9 | 1.820 × 10−9 | 6.761 × 10−11 | 3.961 × 10−10 | 3.638 × 10−10 | ||
| MRBMO | 0 | 0 | 0 | 1.571 × 10−32 | 1.571 × 10−32 | 5.567 × 10−48 | ||
| NRBMO | 0 | 0 | 0 | 1.571 × 10−32 | 1.571 × 10−32 | 5.567 × 10−48 | ||
| RBMO | 1.825 × 10−12 | 1.092 × 10−9 | 2.374 × 10−9 | 3.964 × 10−11 | 1.013 × 10−1 | 2.281 × 10−1 |
| Function | SWRBMO | WOA | POA | HHO | SFOA | SGA | GSABO | IWKGJO | EOSMICOA | |
|---|---|---|---|---|---|---|---|---|---|---|
| GF1 | Best | 1 | 3.255 × 104 | 1 | 1 | 5.117 × 107 | 1 | 1 | 1 | 1 |
| Mean | 1 | 7.539 × 106 | 1 | 1 | 6.441 × 108 | 1 | 1 | 1.064 | 1.836 × 106 | |
| std | 0 | 1.018 × 107 | 0 | 0 | 3.856 × 108 | 0 | 0 | 2.928 × 10−1 | 3.634 × 106 | |
| GF2 | Best | 4.205 | 2.853 × 103 | 4.238 | 4.814 | 4.175 × 103 | 8.461 × 103 | 5.000 | 4.246 | 6.090 |
| Mean | 4.388 | 6.659 × 103 | 4.325 | 4.987 | 2.208 × 104 | 1.710 × 104 | 5.000 | 4.541 | 6.543 × 102 | |
| std | 1.445 × 10−1 | 2.914 × 103 | 8.439 × 10−2 | 4.785 × 10−2 | 6.656 × 103 | 5.936 × 103 | 0 | 3.251 × 10−1 | 9.026 × 102 | |
| GF3 | Best | 1 | 1.230 | 1.002 | 2.549 | 1.024 × 10 | 2.157 | 3.365 | 1.034 | 2.221 |
| Mean | 1.802 | 4.289 | 1.979 | 4.741 | 1.147 × 10 | 4.205 | 1.070 × 1020 | 2.620 | 4.233 | |
| std | 1.610 | 2.045 | 9.180 × 10−1 | 1.463 | 5.710 × 10−1 | 1.445 | 8.680 × 1019 | 1.722 | 1.125 | |
| GF4 | Best | 1.393 × 10 | 2.009 × 10 | 1.991 × 10 | 2.401 × 10 | 4.572 × 10 | 1.530 × 10 | 6.201 × 10 | 4.287 | 3.333 × 10 |
| Mean | 3.868 × 10 | 4.861 × 10 | 3.960 × 10 | 5.123 × 10 | 1.155 × 102 | 5.096 × 10 | 1.009 × 102 | 1.984 × 10 | 4.370 × 10 | |
| std | 1.550 × 10 | 1.650 × 10 | 1.268 × 10 | 1.726 × 10 | 3.309 × 10 | 1.605 × 10 | 1.385 × 10 | 8.876 | 7.660 | |
| GF5 | Best | 1.126 | 1.522 | 1.618 | 1.714 | 1.662 × 10 | 1.416 | 1.730 × 10 | 1.196 | 3.003 |
| Mean | 1.508 | 2.219 | 6.903 | 1.979 | 1.216 × 102 | 1.891 | 5.241 × 10 | 1.588 | 4.612 | |
| std | 3.203 × 10−1 | 5.225 × 10−1 | 1.182 × 10 | 2.179 × 10−1 | 5.593 × 10 | 3.531 × 10−1 | 2.528 × 10 | 3.475 × 10−1 | 2.607 | |
| GF6 | Best | 2.545 | 6.126 | 2.996 | 4.815 | 9.774 | 2.880 | 9.273 | 1.645 | 4.715 |
| Mean | 2.484 | 9.066 | 4.934 | 7.637 | 1.293 × 10 | 7.071 | 1.060 × 10 | 2.815 | 6.763 | |
| std | 1.604 | 1.440 | 1.529 | 1.683 | 1.284 | 1.996 | 6.392 × 10−1 | 8.334 × 10−1 | 1.384 | |
| GF7 | Best | 2.801 × 10 | 5.316 × 102 | 4.955 × 102 | 7.017 × 102 | 1.400 × 103 | 7.762 × 102 | 1.228 × 103 | 2.529 × 102 | 1.214 × 103 |
| Mean | 7.341 × 102 | 1.520 × 103 | 9.116 × 102 | 1.063 × 103 | 2.238 × 103 | 1.301 × 103 | 1.685 × 103 | 7.828 × 102 | 1.640 × 103 | |
| std | 2.335 × 102 | 4.891 × 102 | 2.622 × 102 | 2.373 × 102 | 3.414 × 102 | 2.611 × 102 | 2.508 × 102 | 2.383 × 102 | 2.445 × 102 | |
| GF8 | Best | 2.613 | 4.138 | 3.552 | 4.290 | 4.744 | 3.836 | 4.227 | 3.140 | 4.321 |
| Mean | 2.561 | 4.611 | 4.111 | 4.827 | 5.251 | 4.478 | 4.828 | 3.850 | 4.668 | |
| std | 3.758 | 2.601 × 10−1 | 2.964 × 10−1 | 2.286 × 10−1 | 2.146 × 10−1 | 3.724 × 10−1 | 2.222 × 10−1 | 3.411 × 10−1 | 2.193 × 10−1 | |
| GF9 | Best | 1.075 | 1.166 | 1.087 | 1.121 | 1.671 | 1.080 | 1.303 | 1.080 | 1.187 |
| Mean | 1.230 | 1.415 | 1.349 | 1.427 | 4.560 | 1.317 | 3.276 | 1.292 | 1.318 | |
| std | 9.958 × 10−2 | 2.079 × 10−1 | 5.488 × 10−1 | 2.056 × 10−1 | 9.820 × 10−1 | 1.710 × 10−1 | 9.375 × 10−1 | 7.500 × 10−2 | 9.260 × 10−2 | |
| GF10 | Best | 2.100 × 10 | 2.104 × 10 | 1.409 × 10 | 2.100 × 10 | 2.130 × 10 | 2.100 × 10 | 2.120 × 10 | 1.630 | 2.125 × 10 |
| Mean | 2.100 × 10 | 2.127 × 10 | 2.062 × 10 | 2.117 × 10 | 2.180 × 10 | 2.110 × 10 | 2.140 × 10 | 1.880 × 10 | 2.149 × 10 | |
| std | 4.062 × 10−3 | 1.482 × 10−1 | 1.808 | 9.136 × 10−2 | 1.518 × 10−1 | 1.238 × 10−1 | 1.103 × 10−1 | 6.539 | 1.147 × 10−1 | |
| Function | SWRBMO | WOA | POA | HHO | SFOA | SGA | GSABO | IWKGJO | EOSMICOA | |
|---|---|---|---|---|---|---|---|---|---|---|
| GF1 | Best | 1.344 × 102 | 5.497 × 105 | 3.730 × 104 | 1.415 × 105 | 1.860 × 109 | 2.039 × 104 | 9.400 × 108 | 1.107 × 104 | 1.335 × 108 |
| Mean | 2.533 × 103 | 1.306 × 107 | 1.220 × 108 | 4.584 × 105 | 1.125 × 1010 | 4.398 × 105 | 4.231 × 109 | 1.036 × 105 | 3.857 × 108 | |
| std | 2.268 × 103 | 2.101 × 107 | 2.120 × 108 | 1.734 × 105 | 5.627 × 109 | 1.412 × 106 | 2.213 × 109 | 9.840 × 104 | 2.271 × 108 | |
| GF2 | Best | 1.254 × 103 | 1.693 × 103 | 1.280 × 103 | 1.550 × 103 | 2.696 × 103 | 1.639 × 103 | 2.016 × 103 | 1.367 × 103 | 2.067 × 103 |
| Mean | 1.806 × 103 | 2.298 × 103 | 1.810 × 103 | 2.022 × 103 | 3.305 × 103 | 2.190 × 103 | 2.609 × 103 | 1.810 × 103 | 2.599 × 103 | |
| std | 2.663 × 102 | 2.485 × 102 | 2.240 × 102 | 2.351 × 102 | 1.933 × 102 | 3.024 × 102 | 2.230 × 102 | 3.584 × 102 | 2.259 × 102 | |
| GF3 | Best | 7.230 × 102 | 7.287 × 102 | 7.270 × 102 | 7.550 × 102 | 8.393 × 102 | 7.337 × 102 | 7.658 × 102 | 7.233 × 102 | 7.484 × 102 |
| Mean | 7.408 × 102 | 7.825 × 102 | 7.620 × 102 | 7.953 × 102 | 1.015 × 103 | 7.646 × 102 | 8.231 × 102 | 7.412 × 102 | 7.643 × 102 | |
| std | 2.230 × 10 | 3.136 × 10 | 2.060 × 10 | 2.099 × 10 | 1.467 × 102 | 1.726 × 10 | 1.665 × 10 | 1.026 × 10 | 1.073 × 10 | |
| GF4 | Best | 1.901 × 103 | 2.112 × 103 | 1.910 × 103 | 2.083 × 103 | 1.185 × 104 | 1.967 × 103 | 2.567 × 103 | 1.916 × 103 | 7.824 × 103 |
| Mean | 3.631 × 103 | 5.325 × 104 | 1.950 × 103 | 1.443 × 104 | 8.702 × 106 | 8.563 × 103 | 1.157 × 104 | 5.271 × 103 | 2.030 × 104 | |
| std | 3.677 × 103 | 8.330 × 104 | 3.870 × 103 | 1.331 × 104 | 2.232 × 107 | 7.984 × 103 | 1.037 × 104 | 4.970 × 103 | 6.796 × 103 | |
| GF5 | Best | 1.714 × 103 | 9.532 × 103 | 2.000 × 103 | 3.078 × 103 | 3.940 × 104 | 3.441 × 103 | 1.354 × 105 | 1.820 × 103 | 3.029 × 103 |
| Mean | 2.373 × 103 | 3.206 × 105 | 2.990 × 103 | 6.438 × 104 | 9.657 × 106 | 3.196 × 104 | 7.253 × 105 | 2.366 × 103 | 3.055 × 104 | |
| std | 2.123 × 103 | 3.284 × 105 | 1.660 × 103 | 8.021 × 104 | 1.935 × 107 | 2.910 × 104 | 1.995 × 105 | 3.804 × 102 | 3.586 × 104 | |
| GF6 | Best | 1.600 × 103 | 1.624 × 103 | 1.600 × 103 | 1.622 × 103 | 1.906 × 103 | 1.620 × 103 | 1.764 × 103 | 1.606 × 103 | 1.636 × 103 |
| Mean | 1.806 × 103 | 1.893 × 103 | 1.770 × 103 | 1.885 × 103 | 2.348 × 103 | 1.822 × 103 | 2.078 × 103 | 1.724 × 103 | 1.844 × 103 | |
| std | 1.355 × 102 | 1.519 × 102 | 1.250 × 102 | 1.539 × 102 | 2.327 × 102 | 1.519 × 102 | 1.071 × 102 | 1.302 × 102 | 1.100 × 102 | |
| GF7 | Best | 2.243 × 103 | 2.780 × 103 | 2.140 × 103 | 3.724 × 103 | 1.054 × 104 | 2.753 × 103 | 6.052 × 103 | 2.541 × 103 | 3.011 × 103 |
| Mean | 6.928 × 103 | 9.828 × 103 | 2.490 × 103 | 1.018 × 104 | 8.654 × 105 | 8.043 × 103 | 1.466 × 104 | 8.138 × 103 | 8.997 × 103 | |
| std | 5.581 × 103 | 5.965 × 103 | 2.750 × 102 | 5.019 × 103 | 1.422 × 106 | 4.392 × 103 | 6.762 × 103 | 3.779 × 103 | 3.416 × 103 | |
| GF8 | Best | 2.242 × 103 | 2.268 × 103 | 2.300 × 103 | 2.275 × 103 | 2.365 × 103 | 2.303 × 103 | 2.386 × 103 | 2.301 × 103 | 2.338 × 103 |
| Mean | 2.311 × 103 | 2.400 × 103 | 2.340 × 103 | 2.393 × 103 | 3.326 × 103 | 2.311 × 103 | 2.762 × 103 | 2.316 × 103 | 3.867 × 103 | |
| std | 1.448 × 10 | 3.264 × 102 | 4.560 × 10 | 3.118 × 102 | 6.144 × 102 | 4.964 | 4.070 × 102 | 3.100 | 5.415 × 102 | |
| GF9 | Best | 2.500 × 103 | 2.560 × 103 | 2.500 × 103 | 2.501 × 103 | 2.804 × 103 | 2.502 × 103 | 2.624 × 103 | 2.501 × 103 | 2.760 × 103 |
| Mean | 2.760 × 103 | 2.772 × 103 | 2.650 × 103 | 2.810 × 103 | 2.848 × 103 | 2.757 × 103 | 2.849 × 103 | 2.739 × 103 | 2.772 × 103 | |
| std | 5.093 × 10 | 4.602 × 10 | 1.330 × 102 | 7.255 × 10 | 3.828 × 10 | 8.842 × 10 | 1.012 × 102 | 5.023 × 10 | 8.472 | |
| GF10 | Best | 2.898 × 103 | 2.691 × 103 | 2.900 × 103 | 2.898 × 103 | 2.953 × 103 | 2.899 × 103 | 2.981 × 103 | 2.898 × 103 | 2.929 × 103 |
| Mean | 2.923 × 103 | 2.941 × 103 | 2.940 × 103 | 2.935 × 103 | 3.884 × 103 | 2.940 × 103 | 3.369 × 103 | 2.930 × 103 | 2.956 × 103 | |
| std | 2.304 × 10 | 5.136 × 10 | 2.890 × 10 | 3.020 × 10 | 6.205 × 102 | 3.317 × 10 | 2.457 × 102 | 2.360 × 10 | 1.854 × 10 | |
| Function | SWRBMO- WOA | SWRBMO- POA | SWRBMO- HHO | SWRBMO- SFOA | SWRBMO- SGA | SWRBMO- GSABO | SWRBMO-IWKGJO | SWRBMO-EOSMICOA |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1 | 1 | 1.212 × 10−12 |
| F2 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.657 × 10−11 | 1.212 × 10−12 | 1.212 × 10−12 |
| F3 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1 | 1.104 × 10−2 | 1.212 × 10−12 |
| F4 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 4.574 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 |
| F5 | 3.020 × 10−11 | 3.020 × 10−11 | 6.066 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 1.329 × 10−10 | 3.020 × 10−11 | 3.020 × 10−11 |
| F6 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 |
| F7 | 7.845 × 10−1 | 4.311 × 10−8 | 1.429 × 10−8 | 3.020 × 10−11 | 5.395 × 10−1 | 1.695 × 10−9 | 4.200 × 10−10 | 6.669 × 10−3 |
| F8 | 1.666 × 10−11 | 1.666 × 10−11 | 1.666 × 10−11 | 1.639 × 10−11 | 1.666 × 10−11 | 1.666 × 10−11 | 1.666 × 10−11 | 1.666 × 10−11 |
| F9 | 1 | 1 | 1 | 1.212 × 10−12 | 1.212 × 10−12 | 1 | 1 | 3.337 × 10−1 |
| F10 | 2.641 × 10−5 | 8.986 × 10−11 | 1 | 1.212 × 10−12 | 1.212 × 10−12 | 1 | 1 | 1.212 × 10−12 |
| F11 | 1.104 × 10−2 | 1 | 1 | 1.212 × 10−12 | 1.212 × 10−12 | 1 | 3.337 × 10−1 | 1.104 × 10−2 |
| F12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 |
| F13 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 |
| F14 | 2.364 × 10−12 | 1.607 × 10−1 | 2.364 × 10−12 | 2.364 × 10−12 | 2.364 × 10−12 | 2.364 × 10−12 | 2.364 × 10−12 | 2.364 × 10−12 |
| F15 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1.212 × 10−12 | 1 | 1 | 1.212 × 10−12 |
| +/=/− | 13/0/2 | 12/0/3 | 12/0/3 | 15/0/0 | 14/0/1 | 9/0/6 | 10/0/5 | 14/0/1 |
| Function | SWRBMO- WOA | SWRBMO- POA | SWRBMO- HHO | SWRBMO- SFOA | SWRBMO- SGA | SWRBMO- GSABO | SWRBMO-IWKGJO | SWRBMO-EOSMICOA |
|---|---|---|---|---|---|---|---|---|
| GF1 | 1.212 × 10−12 | 1 | 1 | 1.210 × 10−12 | 1 | 1 | 4.574 × 10−12 | 1.210 × 10−12 |
| GF2 | 3.020 × 10−11 | 5.264 × 10−4 | 1.015 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 1.212 × 10−12 | 2.704 × 10−2 | 3.020 × 10−11 |
| GF3 | 3.020 × 10−11 | 5.573 × 10−10 | 5.573 × 10−10 | 3.020 × 10−11 | 8.480 × 10−9 | 3.020 × 10−11 | 8.485 × 10−9 | 5.570 × 10−10 |
| GF4 | 1.606 × 10−6 | 1.501 × 10−2 | 1.337 × 10−5 | 3.020 × 10−11 | 3.770 × 10−4 | 8.153 × 10−11 | 8.771 × 10−2 | 4.860 × 10−3 |
| GF5 | 1.698 × 10−8 | 1.558 × 10−8 | 3.352 × 10−8 | 3.020 × 10−11 | 6.770 × 10−5 | 3.020 × 10−11 | 9.069 × 10−3 | 3.020 × 10−11 |
| GF6 | 4.183 × 10−9 | 5.943 × 10−2 | 8.146 × 10−5 | 5.490 × 10−11 | 4.080 × 10−5 | 3.020 × 10−11 | 3.831 × 10−5 | 1.250 × 10−5 |
| GF7 | 1.558 × 10−8 | 4.856 × 10−3 | 2.034 × 10−9 | 3.020 × 10−11 | 4.310 × 10−8 | 6.066 × 10−11 | 9.117 × 10−1 | 3.020 × 10−11 |
| GF8 | 8.485 × 10−9 | 6.353 × 10−2 | 2.439 × 10−9 | 3.330 × 10−11 | 3.830 × 10−6 | 1.857 × 10−9 | 4.637 × 10−3 | 4.570 × 10−9 |
| GF9 | 1.383 × 10−2 | 8.684 × 10−3 | 4.459 × 10−4 | 3.020 × 10−11 | 3.632 × 10−1 | 4.975 × 10−11 | 1.250 × 10−5 | 2.010 × 10−1 |
| GF10 | 3.020 × 10−11 | 9.514 × 10−6 | 6.722 × 10−10 | 3.020 × 10−11 | 2.230 × 10−9 | 3.020 × 10−11 | 1.360 × 10−7 | 3.020 × 10−11 |
| +/=/− | 10/0/0 | 9/0/1 | 9/0/1 | 10/0/0 | 8/0/2 | 9/0/1 | 8/0/2 | 9/0/1 |
| Function | SWRBMO- WOA | SWRBMO- POA | SWRBMO- HHO | SWRBMO- SFOA | SWRBMO- SGA | SWRBMO- GSABO | SWRBMO-IWKGJO | SWRBMO-EOSMICOA |
|---|---|---|---|---|---|---|---|---|
| GF1 | 1.212 × 10−12 | 1.210 × 10−12 | 1.210 × 10−12 | 3.311 × 10−20 | 3.311 × 10−20 | 3.371 × 10−2 | 1 | 1.212 × 10−12 |
| GF2 | 1.089 × 10−2 | 2.142 × 10−2 | 4.550 × 10−2 | 3.311 × 10−20 | 3.311 × 10−20 | 2.158 × 10−2 | 1 | 2.853 × 10−4 |
| GF3 | 1 | 1 | 2.620 × 10−3 | 3.311 × 10−20 | 3.311 × 10−20 | 1 | 1 | 1.212 × 10−12 |
| GF4 | 2.158 × 10−2 | 1.104 × 10−2 | 1 | 3.311 × 10−20 | 3.311 × 10−20 | 1 | 1.370 × 10−3 | 1.608 × 10−1 |
| GF5 | 1.212 × 10−12 | 1.210 × 10−12 | 1.210 × 10−12 | 3.311 × 10−20 | 3.311 × 10−20 | 1.608 × 10−2 | 7.850 × 10−3 | 1.212 × 10−12 |
| GF6 | 3.018 × 10−11 | 3.020 × 10−11 | 2.060 × 10−1 | 7.064 × 10−18 | 7.064 × 10−18 | 3.020 × 10−11 | 3.430 × 10−6 | 3.018 × 10−11 |
| GF7 | 2.954 × 10−11 | 2.800 × 10−11 | 2.520 × 10−5 | 6.930 × 10−18 | 6.930 × 10−18 | 6.220 × 10−11 | 8.682 × 10−3 | 3.020 × 10−11 |
| GF8 | 1 | 3.337 × 10−1 | 1 | 3.311 × 10−20 | 3.311 × 10−20 | 1 | 1 | 1 |
| GF9 | 1.930 × 10−11 | 1.780 × 10−11 | 3.020 × 10−11 | 7.066 × 10−18 | 7.066 × 10−18 | 3.020 × 10−11 | 1.892 × 10−4 | 3.020 × 10−11 |
| GF10 | 3.020 × 10−11 | 3.020 × 10−11 | 3.020 × 10−11 | 7.064 × 10−18 | 7.064 × 10−18 | 3.020 × 10−11 | 3.020 × 10−11 | 3.018 × 10−11 |
| +/=/− | 8/0/2 | 8/0/2 | 7/0/3 | 10/0/0 | 10/0/0 | 8/0/2 | 6/0/4 | 8/0/2 |
| Algorithm | Result | |||||||
|---|---|---|---|---|---|---|---|---|
| WOA | 100.64 | 31.39 | 100.00 | 0.00 | 10.00 | 100.00 | 1.00 | 3.43 × 10−16 |
| HHO | 149.93 | 94.19 | 106.04 | 39.01 | 55.00 | 183.57 | 2.77 | 9.52 × 10 |
| SABO | 146.50 | 115.87 | 171.86 | 19.45 | 143.92 | 181.63 | 2.95 | 5.52 × 10 |
| OOA | 130.03 | 78.89 | 146.72 | 48.38 | 102.96 | 150.36 | 3.03 | 1.16 × 10 |
| RIME | 146.95 | 146.62 | 191.93 | 0.13 | 145.98 | 106.44 | 2.39 | 2.82 × 10 |
| RBMO | 150.00 | 148.16 | 200.00 | 1.72 | 149.94 | 100.00 | 2.36 | 2.53 × 10 |
| SWRBMO | 100.00 | 38.19 | 200.00 | 0.00 | 10.00 | 100.00 | 1.44 | 7.27 × 10−17 |
| Algorithm | WOA | HHO | SABO | OOA | RIME | RBMO | SWRBMO |
|---|---|---|---|---|---|---|---|
| Result | 25.88 | 16.61 | 9.10 | 7.80 | 7.91 | 7.73 | 7.71 |
| Algorithm | Result | |||
|---|---|---|---|---|
| WOA | 8.000 | 29.689 | 7.867 | 1.65 × 102 |
| HHO | 8.000 | 29.577 | 7.867 | 1.65 × 102 |
| SABO | 8.000 | 30.967 | 8.006 | 1.72 × 102 |
| OOA | 7.582 | 30.511 | 7.710 | 1.66 × 102 |
| RIME | 7.999 | 29.623 | 7.869 | 1.65 × 102 |
| RBMO | 8.000 | 29.954 | 7.867 | 1.65 × 102 |
| SWRBMO | 8.000 | 29.390 | 7.867 | 1.64 × 102 |
| Algorithm | Result | |||||
|---|---|---|---|---|---|---|
| WOA | 41.000 | 56.000 | 74.000 | 89.000 | 89.000 | 7.078 × 1084 |
| HHO | 41.000 | 56.000 | 75.000 | 90.000 | 90.000 | 6.806 × 1080 |
| SABO | 41.000 | 56.000 | 75.000 | 90.000 | 90.000 | 6.455 × 1094 |
| OOA | 43.000 | 56.000 | 85.000 | 87.000 | 87.000 | 6.265 × 1097 |
| RIME | 39.000 | 53.000 | 71.000 | 85.000 | 90.000 | 1.395 × 1090 |
| RBMO | 40.000 | 55.000 | 74.000 | 88.000 | 86.000 | 1.842 × 1080 |
| SWRBMO | 41.000 | 56.000 | 75.000 | 90.000 | 85.000 | 1.712 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhi, J.; Wang, X.; Shi, B. Multi-Strategy Improved Red-Billed Blue Magpie Optimization Algorithm and Its Applications. Biomimetics 2025, 10, 592. https://doi.org/10.3390/biomimetics10090592
Li Y, Zhi J, Wang X, Shi B. Multi-Strategy Improved Red-Billed Blue Magpie Optimization Algorithm and Its Applications. Biomimetics. 2025; 10(9):592. https://doi.org/10.3390/biomimetics10090592
Chicago/Turabian StyleLi, Yancang, Jiaqi Zhi, Xinle Wang, and Binli Shi. 2025. "Multi-Strategy Improved Red-Billed Blue Magpie Optimization Algorithm and Its Applications" Biomimetics 10, no. 9: 592. https://doi.org/10.3390/biomimetics10090592
APA StyleLi, Y., Zhi, J., Wang, X., & Shi, B. (2025). Multi-Strategy Improved Red-Billed Blue Magpie Optimization Algorithm and Its Applications. Biomimetics, 10(9), 592. https://doi.org/10.3390/biomimetics10090592






