Novel Greylag Goose Optimization Algorithm with Evolutionary Game Theory (EGGO)
Abstract
1. Introduction
2. Materials and Methods
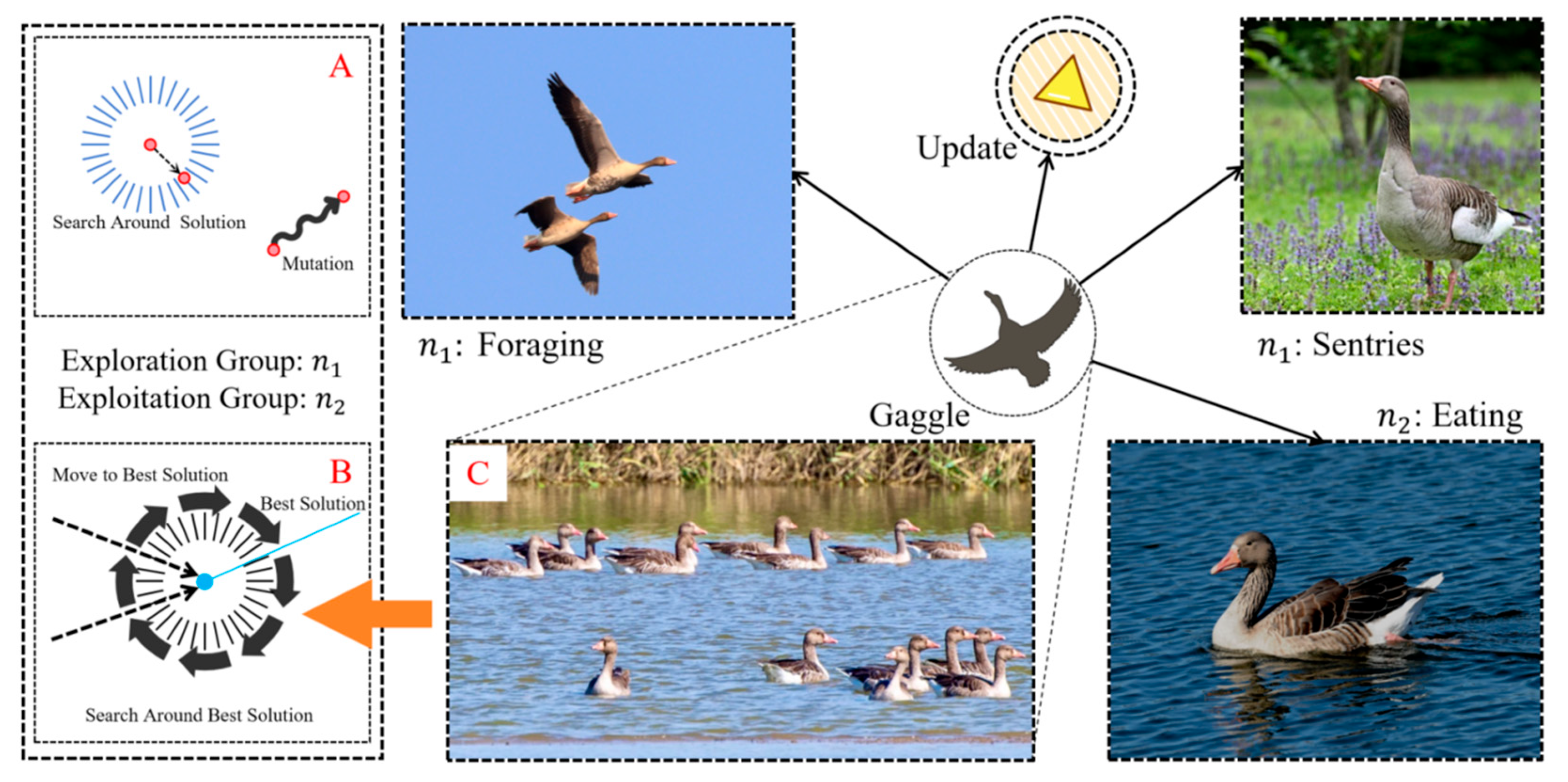
2.1. Overview of the Greylag Goose Optimization Algorithm
2.2. Improvement of Greylag Goose Optimization Based on Evolutionary Game Theory (EGGO)
2.2.1. Strategy Selection and Update
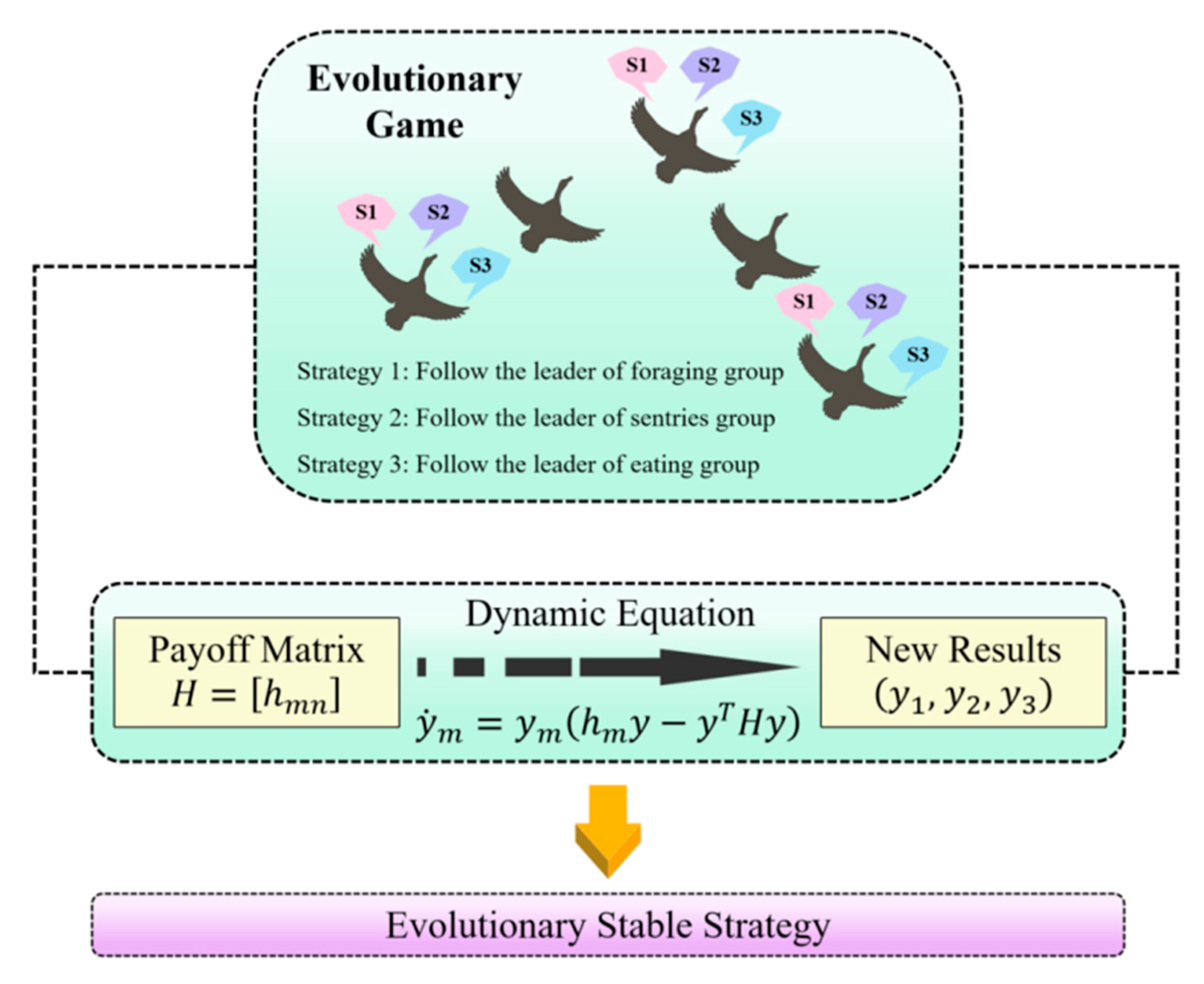
2.2.2. Fitness Assessment and Evolutionary Stable Strategy (ESS)
- (1)
- Each greylag goose is mapped to a player in the evolutionary game.
- (2)
- The three operators are regarded as three available strategies S1, S2, and S3, with the state space , where represents the proportion of strategy m in the population.
- (3)
- The average behavior obtained by following a specific strategy constitutes the payoff matrix H.
2.3. Lyapunov Stability Theory
2.3.1. Dynamic System Modeling
- Strategy similarity: increased reduces if strategies and mm exploit overlapping regions.
- Resource dilution: a fixed population size implies that a higher diminishes resources available to strategy .
2.3.2. Lyapunov Stability Proof
- (1)
- is positive definite within the strategy space;
- (2)
- , and only when (ESS), then .
2.4. EGGO Algorithm Model and Analysis
2.4.1. Mathematical Model
2.4.2. Analysis of Algorithm Complexity
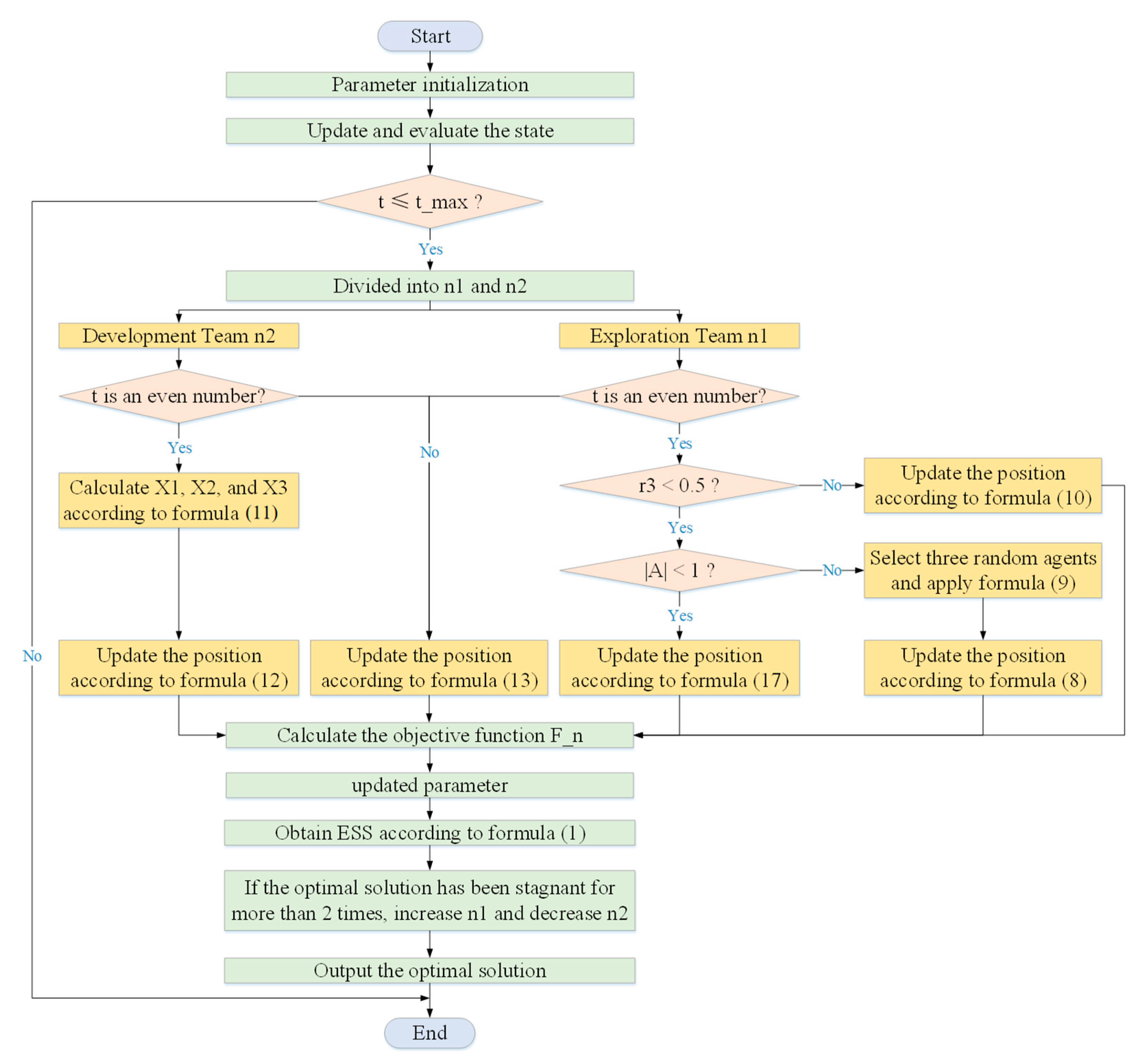
2.4.3. Algorithm Pseudocode and Flowchart
| Algorithm 1 Pseudocode of EGGO |
| 1. Initialize EGGO population , size , iterations , and objective function |
| 2. Initialize EGGO parameters, |
| 3. Calculate objective function for each agent |
| 4. Set best agent position |
| 5. Update solutions in exploration group () and exploitation group () |
| 6. while do |
| 7. Initialize the transition factor , strategy proportion |
| 8. Divide the exploration group members into three parts |
| 9. Calculate the average fitness values of each part , , and . |
| 10. Initialize the payoff matrix |
| 11. Update the strategy proportion based on Equation (1) |
| 12. for () do |
| 13. if () then |
| 14. if () then |
| 15. if () then |
| 16. Update position of current search agent as Equation (7) |
| 17. else |
| 18. Select three random search agents , , and |
| 19. Update (z) by the exponential form of Equation (9) |
| 20. Update position of current search agent as Equation (8) |
| 21. end if |
| 22. else |
| 23. Update position of current search agent as Equation (10) |
| 24. end if |
| 25. else |
| 26. Update position of current search agent as Equation (13) |
| 27. end if |
| 28. end for |
| 29. for () do |
| 30. if () then |
| 31. Calculate , , and by the Equation (11) |
| 32. Update individual position as Equation (12) |
| 33. else |
| 34. Update position of current search agent as Equation (13) |
| 35. end if |
| 36. end for |
| 37. Calculate objective function for each agent |
| 38. Update parameters |
| 39. Set |
| 40. Adjust beyond the search space solutions |
| 41. if (Best is same as previous two iterations) then |
| 42. Increase solutions of exploration group () |
| 43. Decrease solutions of exploitation group () |
| 44. end if |
| 45. end while |
| 46. Return best agent |
3. Results
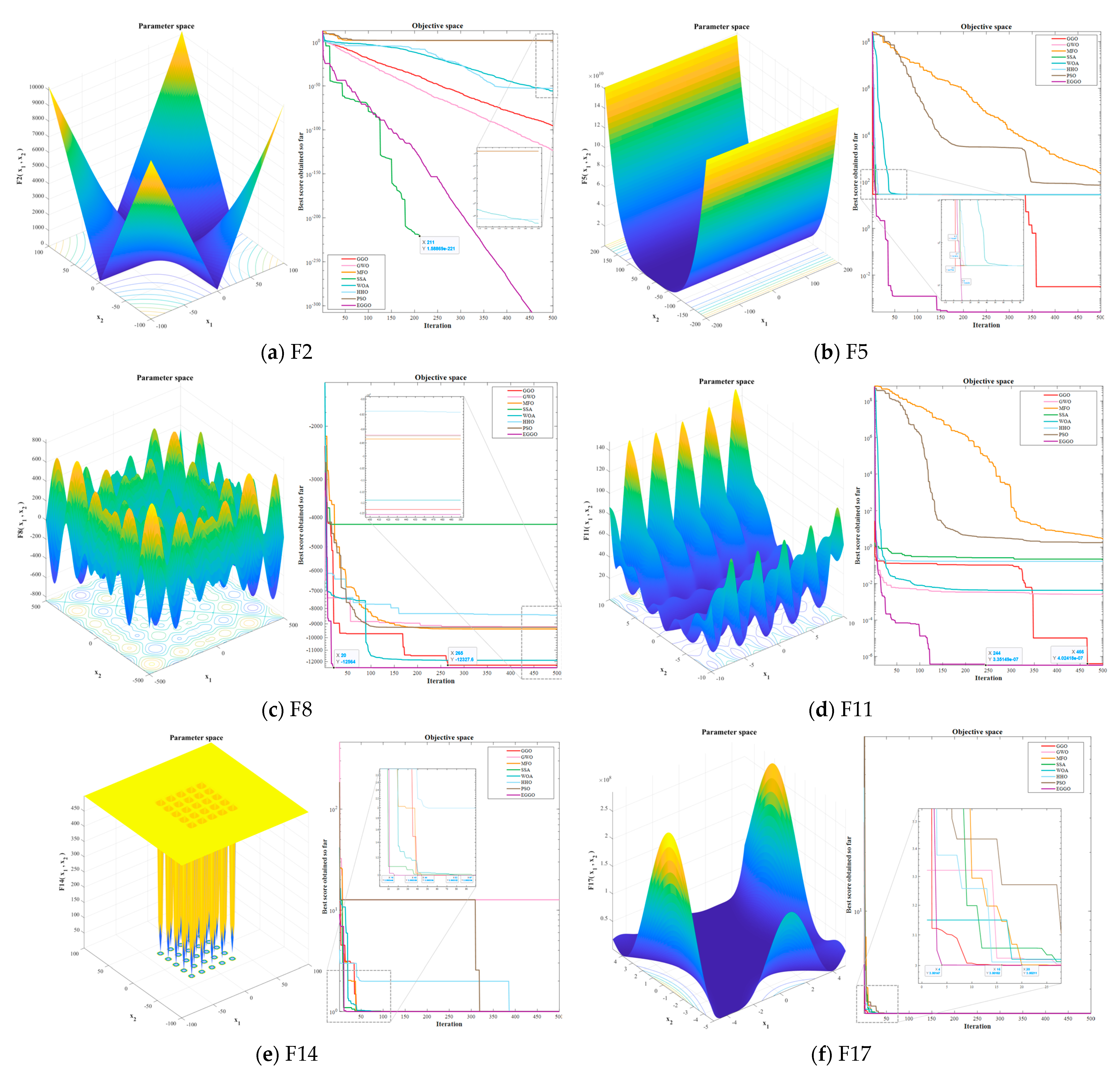
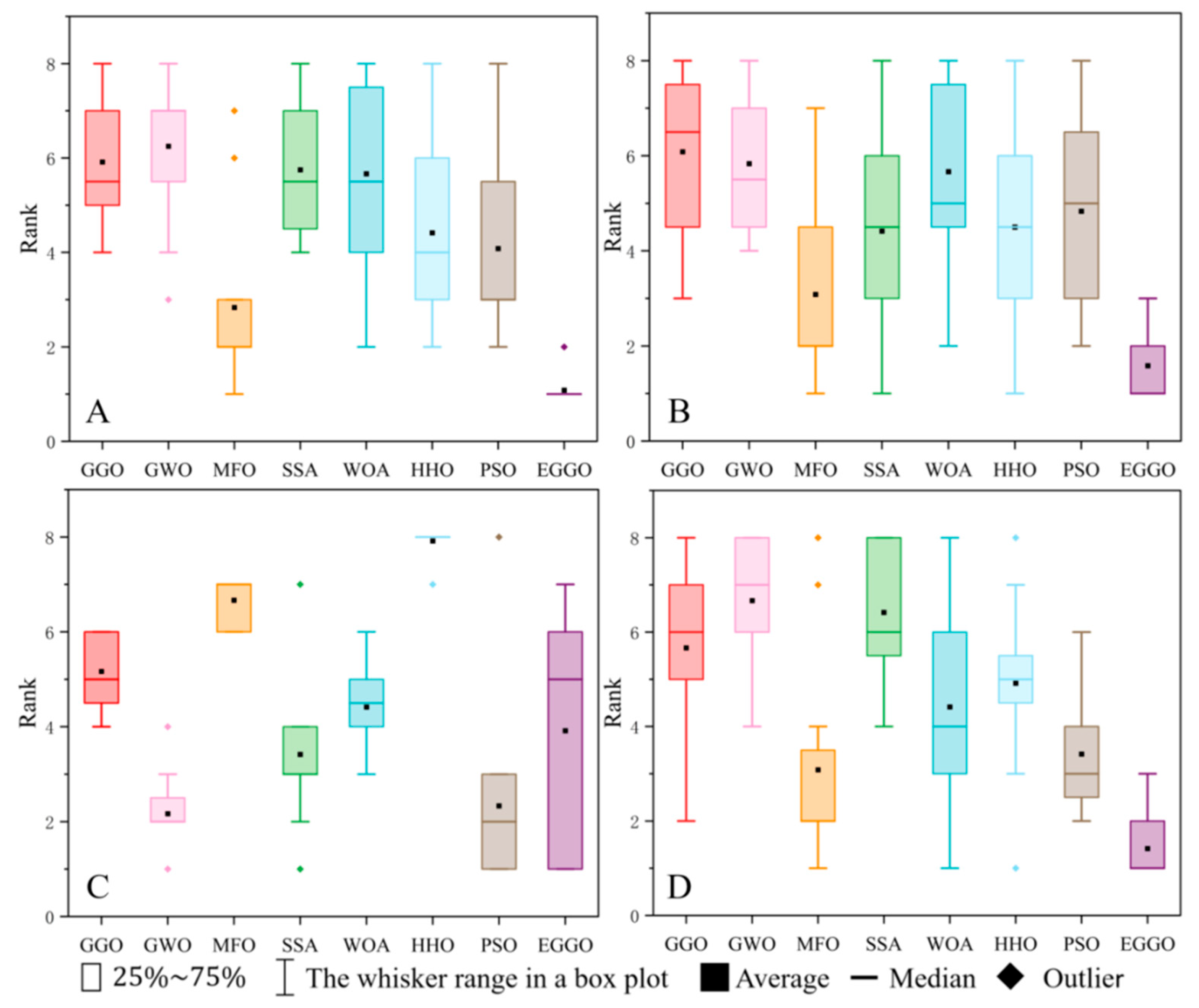
3.1. Comparison and Analysis of Test Functions
3.1.1. Benchmark Test Functions
3.1.2. CEC 2022 Test Suite
3.2. Engineering Applications of EGGO
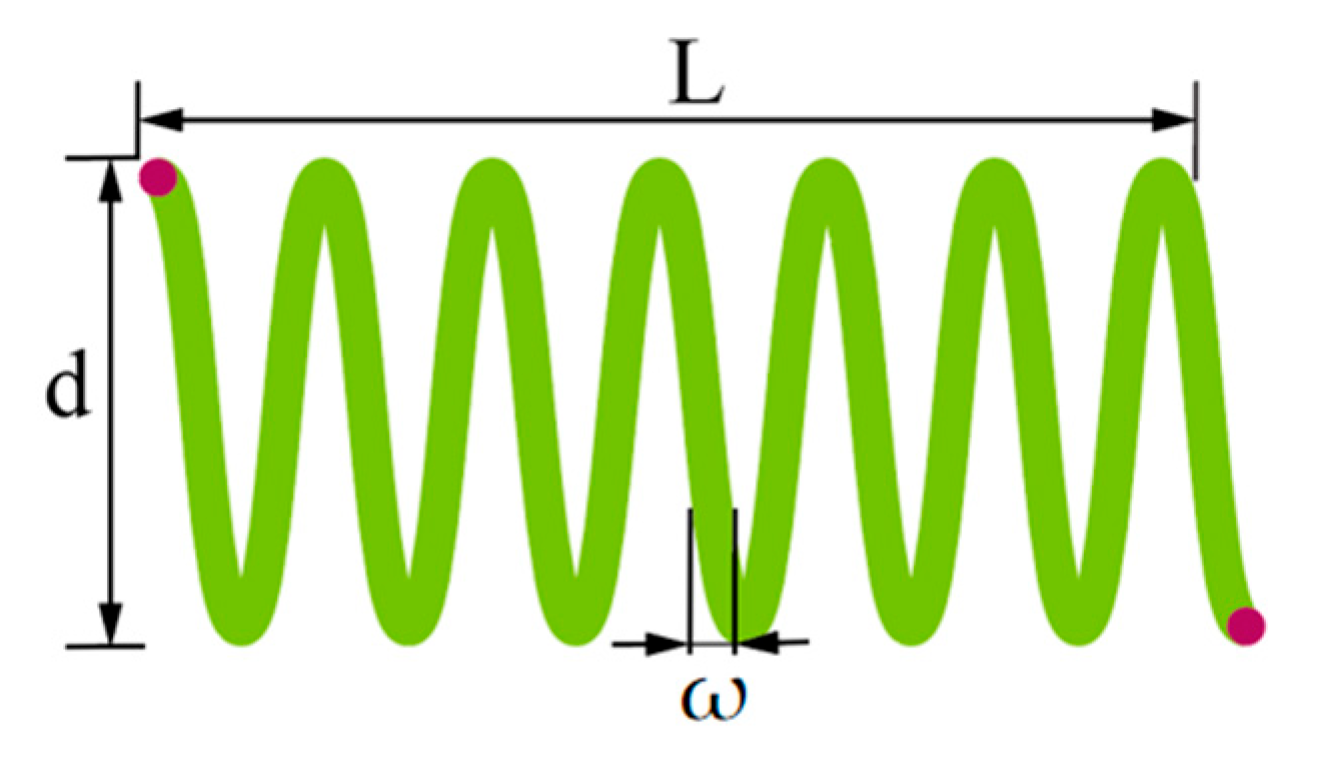
3.2.1. Tension/Compression Spring Design Problem
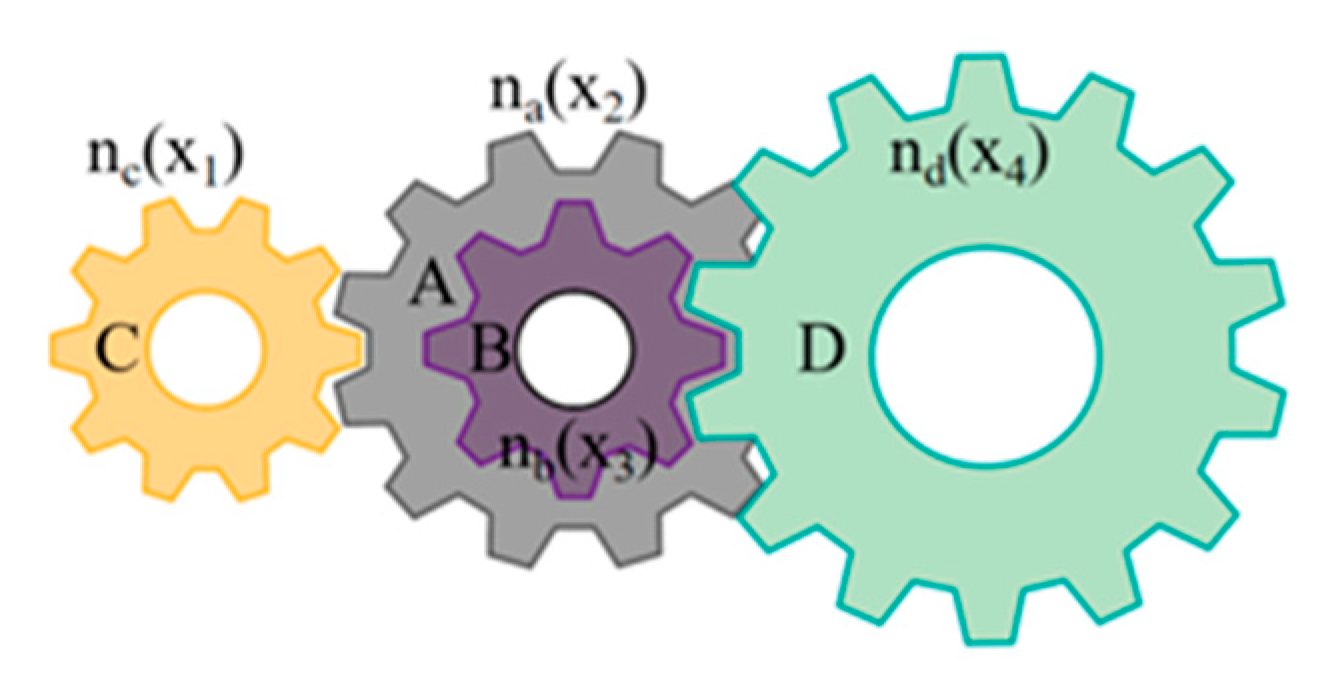
3.2.2. Gear Train Design Problem
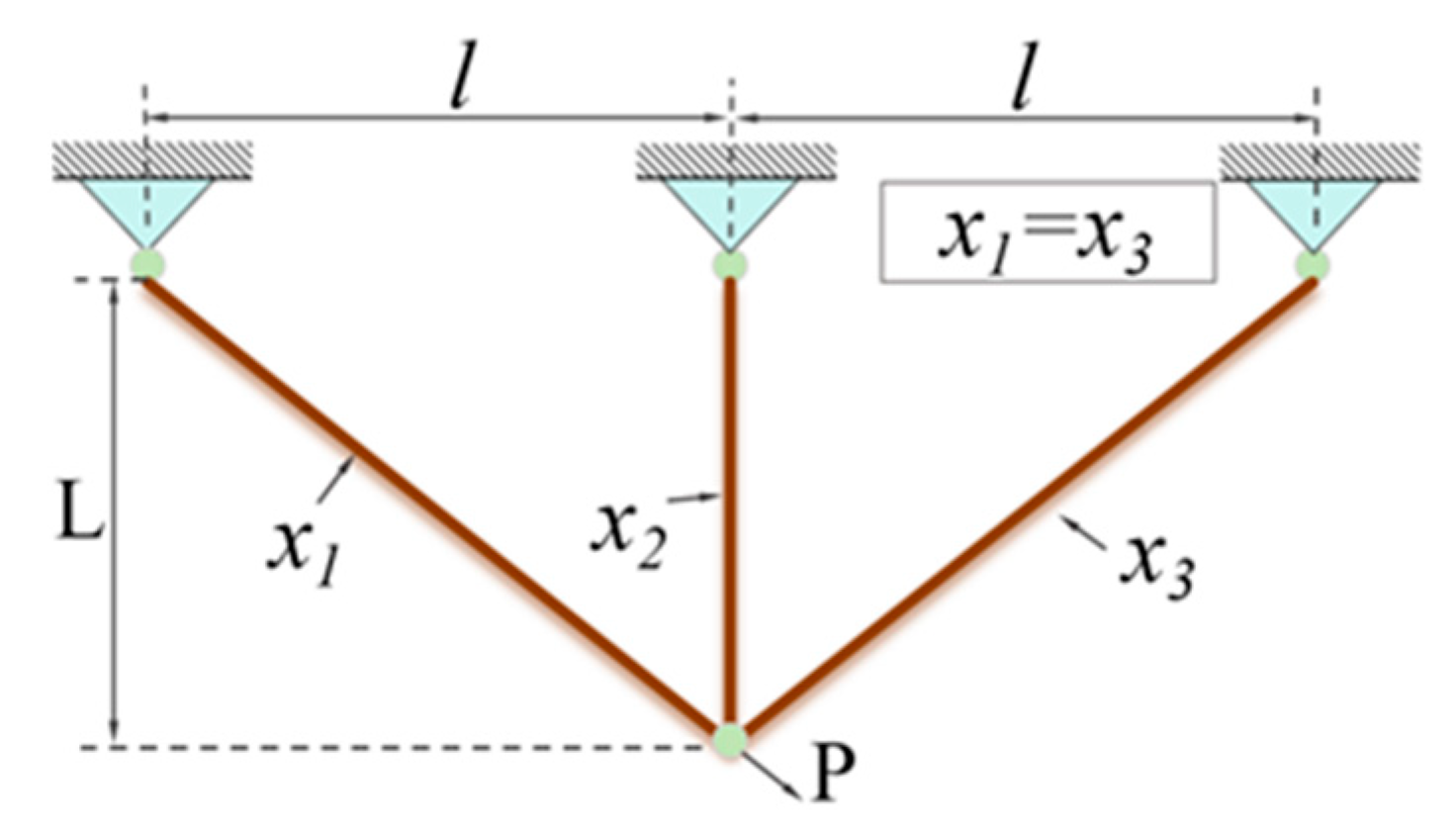
3.2.3. Three-Bar Truss Design Problem
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qin, S.; Liu, J.; Bai, X.; Hu, G. A Multi-Strategy Improvement Secretary Bird Optimization Algorithm for Engineering Optimization Problems. Biomimetics 2024, 9, 478. [Google Scholar] [CrossRef]
- Zhang, C.; Song, Z.; Yang, Y.; Zhang, C.; Guo, Y. A Decomposition-Based Multi-Objective Flying Foxes Optimization Algorithm and Its Applications. Biomimetics 2024, 9, 417. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Casella, G.; Murino, T.; Bottani, E. A modified binary bat algorithm for machine loading in flexible manufacturing systems: A case study. Int. J. Syst. Sci. Oper. Logist. 2024, 11, 2381828. [Google Scholar] [CrossRef]
- Fevrier, V.; Oscar, C.; Patricia, M. Bio-Inspired Algorithms and Its Applications for Optimization in Fuzzy Clustering. Algorithms 2021, 14, 122. [Google Scholar] [CrossRef]
- Mohammadi, A.; Sheikholeslam, F.; Mirjalili, S. Nature-Inspired Metaheuristic Search Algorithms for Optimizing BenchmarkProblems: Inclined Planes System Optimization to State-of-the-Art Methods. Arch. Computat. Methods Eng. 2023, 30, 331–389. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G.; Gambardella, L.M. Ant Algorithms for Discrete Optimization. Artif. Life 1999, 5, 137–172. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Khodadadi, N.; Mirjalili, S.; Abdelhamid, A.A.; Eid, M.M.; Ibrahim, A. Greylag Goose Optimization: Nature-inspired optimization algorithm. Expert Syst. Appl. 2024, 238, 122147. [Google Scholar] [CrossRef]
- Xu, M.; Cao, L.; Lu, D.; Hu, Z.; Yue, Y. Application of Swarm Intelligence Optimization Algorithms in Image Processing: A Comprehensive Review of Analysis, Synthesis, and Optimization. Biomimetics 2023, 8, 235. [Google Scholar] [CrossRef]
- Liu, J.; Shi, J.; Hao, F.; Dai, M. A novel enhanced global exploration whale optimization algorithm based on Lévy flights and judgment mechanism for global continuous optimization problems. Eng. Comput. 2023, 39, 2433–2461. [Google Scholar] [CrossRef]
- Chu, J.; Yu, X.; Yang, S.; Qiu, J.; Wang, Q. Architecture entropy sampling-based evolutionary neural architecture search and its application in osteoporosis diagnosis. Complex Intell. Syst. 2023, 9, 213–231. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, T.; Liu, Z. A whale optimization algorithm based on quadratic interpolation for high-dimensional global optimization problems. Appl. Soft Comput. 2019, 85, 105744. [Google Scholar] [CrossRef]
- Khosrowshahi, H.N.; Aghdasi, H.S.; Salehpour, P. A refined Greylag Goose optimization method for effective IoT service allocation in edge computing systems. Sci. Rep. 2025, 15, 15729. [Google Scholar] [CrossRef]
- Alharbi, A.H.; Khafaga, D.S.; El-Kenawy, E.-S.M.; Eid, M.M.; Ibrahim, A.; Abualigah, L.; Khodadadi, N.; Abdelhamid, A.A. Optimizing electric vehicle paths to charging stations using parallel greylag goose algorithm and Restricted Boltzmann Machines. Front. Energy Res. 2024, 12, 1401330. [Google Scholar] [CrossRef]
- Saqr, A.E.S.; Saraya, M.S.; El-Kenawy, E.S.M. Enhancing CO2 emissions prediction for electric vehicles using Greylag Goose Optimization and machine learning. Sci. Rep. 2025, 15, 16612. [Google Scholar] [CrossRef]
- Mashru, N.; Tejani, G.G.; Patel, P. Reliability-based multi-objective optimization of trusses with greylag goose algorithm. Evol. Intell. 2025, 18, 25. [Google Scholar] [CrossRef]
- Gürses, D.; Mehta, P.; Sait, S.M.; Yildiz, A.R. Enhanced Greylag Goose optimizer for solving constrained engineering design problems. Mater. Test. 2025, 67, 900–909. [Google Scholar] [CrossRef]
- Cheng, L.; Huang, P.; Zhang, M.; Yang, R.; Wang, Y. Optimizing Electricity Markets Through Game-Theoretical Methods: Strategic and Policy Implications for Power Purchasing and Generation Enterprises. Mathematics 2025, 13, 373. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Song, L.; Zhang, Y.; Gu, L.; Zhao, X. Wild Geese Migration Optimization Algorithm: A New Meta-Heuristic Algorithm for Solving Inverse Kinematics of Robot. Comput. Intell. Neurosci. 2022, 2022, 5191758. [Google Scholar] [CrossRef]
- El-Sherbiny, A.; Elhosseini, M.A.; Haikal, A.Y. A new ABC variant for solving inverse kinematics problem in 5 DOF robot arm. Appl. Soft Comput. J. 2018, 73, 24–38. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35, Erratum in Eng. Comput. 2013, 29, 245. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. J. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Guedria, N.B. Improved accelerated PSO algorithm for mechanical engineering optimization problems. Appl. Soft Comput. 2016, 40, 455–467. [Google Scholar] [CrossRef]
- Ma, L.; Wang, C.; Xie, N.G.; Shi, M.; Ye, Y.; Wang, L. Moth-flame optimization algorithm based on diversity and mutation strategy. Appl. Intell. 2021, 51, 1–37. [Google Scholar] [CrossRef]
- Belegundu, A.D.; Arora, J.S. A study of mathematical programming methods for structural optimization. Part I: Theory. Int. J. Numer. Methods Eng. 1985, 21, 1583–1599. [Google Scholar] [CrossRef]
- Moosavi SH, S.; Bardsiri, K.V. Poor and rich optimization algorithm: A new human-based and multi populations algorithm. Eng. Appl. Artif. Intell. 2019, 86, 165–181. [Google Scholar] [CrossRef]
- Xu, X.; Hu, Z.; Su, Q.; Li, Y.; Dai, J. Multivariable grey prediction evolution algorithm: A new metaheuristic. Appl. Soft Comput. J. 2020, 89, 106086. [Google Scholar] [CrossRef]



| Algorithm | Parameter(s) | Value(s) |
|---|---|---|
| GGO | ||
| GWO | 2 to 0 | |
| MFO | −1 to −2 | |
| SSA | 0.7 | |
| 0.2 | ||
| 0.8 | ||
| 0.3 | ||
| HHO | 2 to 0 | |
| PSO | 0.9, 0.6 | |
| 2, 2 | ||
| EGGO | ||
| Type | No. | Functions | Dimension | |
|---|---|---|---|---|
| Unimodal | 1 | Shifted and fully rotated Zakharov’s function | 10 and 20 | 300 |
| Multimodal | 2 | Shifted and fully rotated Rosenbrock’s function | 10 and 20 | 400 |
| 3 | Shifted and fully rotated expanded Schaffer’s F6 function | 10 and 20 | 600 | |
| 4 | Shifted and fully rotated non-continuous Rastrigin’s function | 10 and 20 | 800 | |
| 5 | Shifted and fully rotated Levy’s function | 10 and 20 | 900 | |
| Hybrid | 6 | Hybrid function 1 (N = 3) | 10 and 20 | 1800 |
| 7 | Hybrid function 2 (N = 6) | 10 and 20 | 2000 | |
| 8 | Hybrid function 3 (N = 5) | 10 and 20 | 2200 | |
| Composition | 9 | Composition function 1 (N = 5) | 10 and 20 | 2300 |
| 10 | Composition function 2 (N = 4) | 10 and 20 | 2400 | |
| 11 | Composition function 3 (N = 5) | 10 and 20 | 2600 | |
| 12 | Composition function 4 (N = 6) | 10 and 20 | 2700 |
| Function | GGO | GWO | ||||||
| Ave. | Std. | Time | Best | Ave. | Std. | Time | Best | |
| F1 | 8.9718 × 103 | 1.5981 × 104 | 5.5247 × 10−3 | 2.7181 × 103 | 1.3111 × 104 | 4.2103 × 103 | 4.5857 × 10−3 | 5.2255 × 103 |
| F2 | 5.7769 × 102 | 1.0435 × 102 | 5.0988 × 10−3 | 4.3759 × 102 | 6.7885 × 102 | 1.8679 × 102 | 4.6382 × 10−3 | 4.4534 × 102 |
| F3 | 6.4261 × 102 | 1.1480 × 101 | 1.1234 × 10−2 | 6.2053 × 102 | 6.3172 × 102 | 9.4214 × 100 | 1.0332 × 10−2 | 6.1625 × 102 |
| F4 | 8.4191 × 102 | 1.0476 × 101 | 7.5605 × 10−3 | 8.2221 × 102 | 8.4370 × 102 | 1.1005 × 101 | 6.5427 × 10−3 | 8.2070 × 102 |
| F5 | 1.4666 × 103 | 2.1263 × 102 | 7.8058 × 10−3 | 1.0897 × 103 | 1.2911 × 103 | 2.3521 × 102 | 6.6609 × 10−3 | 9.5376 × 102 |
| F6 | 8.8523 × 105 | 1.7495 × 106 | 5.9593 × 10−3 | 3.3302 × 103 | 3.1509 × 106 | 7.1051 × 106 | 5.6340 × 10−3 | 2.9283 × 103 |
| F7 | 2.0917 × 103 | 2.8859 × 101 | 6.0866 × 10−2 | 2.0438 × 103 | 2.0877 × 103 | 3.2519 × 101 | 1.1995 × 10−2 | 2.0457 × 103 |
| F8 | 2.2397 × 103 | 1.2090 × 101 | 2.0055 × 10−2 | 2.2204 × 103 | 2.2390 × 103 | 2.3285 × 101 | 1.5010 × 10−2 | 2.2247 × 103 |
| F9 | 2.6888 × 103 | 4.8706 × 101 | 1.3135 × 10−2 | 2.5514 × 103 | 2.7271 × 103 | 5.9966 × 101 | 1.1441 × 10−2 | 2.5818 × 103 |
| F10 | 2.5896 × 103 | 8.5976 × 101 | 1.2604 × 10−2 | 2.5007 × 103 | 2.7194 × 103 | 3.6536 × 102 | 1.1074 × 10−2 | 2.5037 × 103 |
| F11 | 3.2998 × 103 | 4.1118 × 102 | 2.0037 × 10−2 | 2.8391 × 103 | 4.0570 × 103 | 3.8145 × 102 | 1.6217 × 10−2 | 3.1253 × 103 |
| F12 | 2.8958 × 103 | 3.6440 × 101 | 6.6573 × 10−2 | 2.8694 × 103 | 2.9202 × 103 | 3.4289 × 101 | 1.6469 × 10−2 | 2.8729 × 103 |
| Function | MFO | SSA | ||||||
| Ave. | Std. | Time | Best | Ave. | Std. | Time | Best | |
| F1 | 1.1746 × 104 | 6.4984 × 103 | 7.9990 × 10−3 | 2.2914 × 103 | 6.8049 × 103 | 2.3104 × 103 | 4.7821 × 10−3 | 1.0998 × 103 |
| F2 | 4.1524 × 102 | 1.7718 × 101 | 7.9137 × 10−3 | 4.0764 × 102 | 5.0932 × 102 | 6.4575 × 101 | 4.7256 × 10−3 | 4.3617 × 102 |
| F3 | 6.0385 × 102 | 4.1744 × 100 | 1.3584 × 10−2 | 6.0074 × 102 | 6.3476 × 102 | 8.7952 × 100 | 9.9959 × 10−3 | 6.2033 × 102 |
| F4 | 8.3243 × 102 | 1.4684 × 101 | 9.8440 × 10−3 | 8.2561 × 102 | 8.4346 × 102 | 9.8422 × 100 | 6.5236 × 10−3 | 8.3317 × 102 |
| F5 | 9.9985 × 102 | 1.3416 × 102 | 1.0137 × 10−2 | 9.0080 × 102 | 1.3829 × 103 | 2.4189 × 102 | 6.7142 × 10−3 | 1.0154 × 103 |
| F6 | 4.4705 × 103 | 2.0481 × 103 | 1.0395 × 10−2 | 1.9312 × 103 | 9.6276 × 106 | 7.6058 × 106 | 5.8453 × 10−3 | 2.0961 × 105 |
| F7 | 2.0280 × 103 | 1.0856 × 101 | 1.5446 × 10−2 | 2.0212 × 103 | 2.0812 × 103 | 1.8711 × 101 | 1.1743 × 10−2 | 2.0442 × 103 |
| F8 | 2.2253 × 103 | 5.0467 × 100 | 1.7968 × 10−2 | 2.2044 × 103 | 2.2432 × 103 | 7.5604 × 100 | 1.4752 × 10−2 | 2.2302 × 103 |
| F9 | 2.5359 × 103 | 1.9028 × 101 | 1.5121 × 10−2 | 2.5293 × 103 | 2.6328 × 103 | 4.2446 × 101 | 1.1410 × 10−2 | 2.5370 × 103 |
| F10 | 2.5092 × 103 | 3.1289 × 101 | 1.4872 × 10−2 | 2.5004 × 103 | 2.5710 × 103 | 7.7876 × 101 | 1.0658 × 10−2 | 2.5016 × 103 |
| F11 | 3.2059 × 103 | 3.0766 × 102 | 1.9802 × 10−2 | 2.7544 × 103 | 3.0473 × 103 | 2.8749 × 102 | 1.5646 × 10−2 | 2.7994 × 103 |
| F12 | 2.9037 × 103 | 3.8110 × 101 | 2.9144 × 10−2 | 2.8715 × 103 | 2.8801 × 103 | 1.6583 × 101 | 1.6196 × 10−2 | 2.8676 × 103 |
| Function | WOA | HHO | ||||||
| Ave. | Std. | Time | Best | Ave. | Std. | Time | Best | |
| F1 | 3.3560 × 104 | 1.4314 × 104 | 5.1796 × 10−3 | 6.4874 × 103 | 6.2245 × 103 | 1.4228 × 103 | 1.4660 × 10−2 | 2.1536 × 103 |
| F2 | 5.2604 × 102 | 1.1783 × 102 | 5.1717 × 10−3 | 4.1115 × 102 | 5.3526 × 102 | 1.0068 × 102 | 1.3786 × 10−2 | 4.1830 × 102 |
| F3 | 6.4022 × 102 | 1.3011 × 101 | 1.0706 × 10−2 | 6.1425 × 102 | 6.4120 × 102 | 1.1798 × 101 | 2.7284 × 10−2 | 6.1749 × 102 |
| F4 | 8.4883 × 102 | 1.3810 × 101 | 6.9401 × 10−3 | 8.2021 × 102 | 8.2818 × 102 | 8.4948E+00 | 1.9141 × 10−2 | 8.1322 × 102 |
| F5 | 1.5849 × 103 | 3.5923 × 102 | 7.1641 × 10−3 | 1.0663 × 103 | 1.4879 × 103 | 1.9571 × 102 | 1.9885 × 10−2 | 1.0407 × 103 |
| F6 | 7.5709 × 104 | 3.0266 × 105 | 5.7107 × 10−3 | 2.5663 × 103 | 1.6960 × 104 | 1.5749 × 104 | 1.6687 × 10−2 | 2.4769 × 103 |
| F7 | 2.0915 × 103 | 3.3568 × 101 | 1.2637 × 10−2 | 2.0425 × 103 | 2.0799 × 103 | 3.7449 × 101 | 3.2018 × 10−2 | 2.0288 × 103 |
| F8 | 2.2453 × 103 | 2.2034 × 101 | 1.5100 × 10−2 | 2.2271 × 103 | 2.2365 × 103 | 1.1173 × 101 | 3.8780 × 10−2 | 2.2220 × 103 |
| F9 | 2.6465 × 103 | 5.0501 × 101 | 1.1429 × 10−2 | 2.5445 × 103 | 2.6576 × 103 | 4.7668 × 101 | 2.8653 × 10−2 | 2.5412 × 103 |
| F10 | 2.6658 × 103 | 3.0651 × 102 | 1.1056 × 10−2 | 2.5004 × 103 | 2.6260 × 103 | 1.7383 × 102 | 2.7131 × 10−2 | 2.5010 × 103 |
| F11 | 3.3174 × 103 | 4.1017 × 102 | 1.6037 × 10−2 | 2.7653 × 103 | 3.1280 × 103 | 3.2571 × 102 | 3.6550 × 10−2 | 2.7317 × 103 |
| F12 | 2.9193 × 103 | 4.3466 × 101 | 1.6161 × 10−2 | 2.8682 × 103 | 2.9453 × 103 | 6.4707 × 101 | 4.0554 × 10−2 | 2.8705 × 103 |
| Function | PSO | EGGO | ||||||
| Ave. | Std. | Time | Best | Ave. | Std. | Time | Best | |
| F1 | 9.7990 × 103 | 5.9490 × 103 | 4.5264 × 10−3 | 2.6880 × 103 | 9.0246 × 103 | 2.1287 × 103 | 1.5709 × 10−2 | 2.1574 × 103 |
| F2 | 4.4942 × 102 | 6.2600 × 101 | 4.5352 × 10−3 | 4.0791 × 102 | 4.1372 × 102 | 1.5217 × 101 | 1.6228 × 10−2 | 4.0991 × 102 |
| F3 | 6.0719 × 102 | 5.6420 × 100 | 1.0123 × 10−2 | 6.3648 × 102 | 6.0295 × 102 | 3.8314 × 100 | 2.1082 × 10−2 | 6.0067 × 102 |
| F4 | 8.3708 × 102 | 1.2480 × 101 | 6.2257 × 10−3 | 8.1230 × 102 | 8.2084 × 102 | 7.9549 × 100 | 1.7677 × 10−2 | 8.0714 × 102 |
| F5 | 9.9364 × 102 | 2.0986 × 102 | 6.4482 × 10−3 | 9.0027 × 102 | 1.1621 × 103 | 1.1416 × 102 | 1.7785 × 10−2 | 9.0007 × 102 |
| F6 | 6.1313 × 103 | 2.2224 × 103 | 5.1812 × 10−3 | 1.8941 × 103 | 4.4205 × 103 | 1.8767 × 103 | 1.7495 × 10−2 | 1.8541 × 103 |
| F7 | 2.0381 × 103 | 3.3524 × 101 | 1.1919 × 10−2 | 2.0213 × 103 | 2.0265 × 103 | 8.6546 × 100 | 1.1643 × 10−2 | 2.0182 × 103 |
| F8 | 2.2308 × 103 | 1.8176 × 101 | 1.4598 × 10−2 | 2.2068 × 103 | 2.2253 × 103 | 4.0303 × 100 | 1.6902 × 10−2 | 2.2043 × 103 |
| F9 | 2.5650 × 103 | 6.2866 × 101 | 1.0617 × 10−2 | 2.5293 × 103 | 2.5227 × 103 | 1.1393 × 101 | 1.1867 × 10−2 | 2.5172 × 103 |
| F10 | 2.6067 × 103 | 1.8315 × 102 | 1.0071 × 10−2 | 2.5008 × 103 | 2.5336 × 103 | 5.1820 × 101 | 1.2894 × 10−2 | 2.5021 × 103 |
| F11 | 3.4855 × 103 | 4.5981 × 102 | 3.0300 × 10−2 | 2.8209 × 103 | 2.9557 × 103 | 2.7451 × 102 | 1.5464 × 10−2 | 2.6972 × 103 |
| F12 | 2.8724 × 103 | 1.2959 × 101 | 1.5298 × 10−2 | 2.8624 × 103 | 2.8634 × 103 | 1.3006 × 100 | 1.9950 × 10−2 | 2.8597 × 103 |
| Function | GGO | GWO | ||||||
| Ave. | Std. | Time | Best | Ave | std | Time | Best | |
| F1 | 5.9176 × 104 | 3.3688 × 104 | 6.4054 × 10−3 | 1.7561 × 104 | 5.2474 × 104 | 1.7347 × 104 | 5.8229 × 10−3 | 2.1648 × 104 |
| F2 | 1.6682 × 103 | 5.1504 × 102 | 6.2956 × 10−3 | 8.6866 × 102 | 1.6142 × 103 | 6.6266 × 102 | 5.5554 × 10−3 | 8.3519 × 102 |
| F3 | 6.7649 × 102 | 1.1363 × 101 | 1.7646 × 10−2 | 6.4770 × 102 | 6.6671 × 102 | 1.2263 × 101 | 1.6815 × 10−2 | 6.3532 × 102 |
| F4 | 9.5411 × 102 | 1.9946 × 101 | 1.0233 × 10−2 | 9.1132 × 102 | 9.5686 × 102 | 1.9856 × 101 | 9.2864 × 10−3 | 9.1853 × 102 |
| F5 | 3.4490 × 103 | 4.3306 × 102 | 1.0047 × 10−2 | 2.2112 × 103 | 3.3415 × 103 | 5.7951 × 102 | 9.2455 × 10−3 | 1.8887 × 103 |
| F6 | 6.4271 × 108 | 5.5643 × 108 | 7.0105 × 10−3 | 2.0092E+07 | 6.5769 × 108 | 6.1897 × 108 | 6.2666 × 10−3 | 4.9632E+07 |
| F7 | 2.2067 × 103 | 5.7969 × 101 | 2.0988 × 10−2 | 2.1064 × 103 | 2.2292 × 103 | 5.8759 × 101 | 1.9661 × 10−2 | 2.1208 × 103 |
| F8 | 2.3474 × 103 | 1.2507 × 102 | 2.4538 × 10−2 | 2.2328 × 103 | 2.3625 × 103 | 1.1567 × 102 | 2.2600 × 10−2 | 2.2329 × 103 |
| F9 | 2.9256 × 103 | 1.6498 × 102 | 2.3938 × 10−2 | 2.6696 × 103 | 2.8730 × 103 | 1.2788 × 102 | 2.1279 × 10−2 | 2.6940 × 103 |
| F10 | 5.4755 × 103 | 1.8551 × 103 | 1.8726 × 10−2 | 2.5362 × 103 | 6.2215 × 103 | 1.2073 × 103 | 1.6678 × 10−2 | 2.6349 × 103 |
| F11 | 7.8689 × 103 | 8.6044 × 102 | 3.2313 × 10−2 | 5.6132 × 103 | 8.7527 × 103 | 7.8209 × 102 | 2.7213 × 10−2 | 6.6834 × 103 |
| F12 | 3.1950 × 103 | 1.4512 × 102 | 3.4304 × 10−2 | 2.9730 × 103 | 3.3076 × 103 | 1.8595 × 102 | 3.0777 × 10−2 | 3.0239 × 103 |
| Function | MFO | SSA | ||||||
| Ave. | Std. | Time | Best | Ave | std | Time | Best | |
| F1 | 6.1231 × 104 | 1.1673 × 104 | 1.2524 × 10−2 | 3.3050 × 104 | 7.9260 × 104 | 3.1556 × 104 | 1.7645 × 10−2 | 3.5907 × 104 |
| F2 | 5.4734 × 102 | 6.0904 × 101 | 1.1413 × 10−2 | 4.6990 × 102 | 1.0300 × 103 | 2.1787 × 102 | 5.7990 × 10−3 | 5.9555 × 102 |
| F3 | 6.2558 × 102 | 7.3784 × 100 | 2.2844 × 10−2 | 6.1151 × 102 | 6.6635 × 102 | 1.1044 × 101 | 1.6953E × 10−2 | 6.3920 × 102 |
| F4 | 9.0440 × 102 | 2.1010 × 101 | 1.5567 × 10−2 | 8.6080 × 102 | 9.6325 × 102 | 1.4271 × 101 | 9.3094 × 10−3 | 9.3560 × 102 |
| F5 | 3.0670 × 103 | 1.0176 × 103 | 1.5547 × 10−2 | 1.5266 × 103 | 3.6631 × 103 | 4.6332 × 102 | 9.6323 × 10−3 | 2.2913 × 103 |
| F6 | 8.9806 × 106 | 3.2434 × 107 | 1.2335 × 10−2 | 3.7945 × 104 | 1.4716 × 108 | 1.0144 × 108 | 6.6011 × 10−3 | 2.7310 × 107 |
| F7 | 2.1225 × 103 | 5.0527 × 101 | 2.6023 × 10−2 | 2.0362 × 103 | 2.2096 × 103 | 6.4204 × 101 | 2.0051 × 10−2 | 2.0982 × 103 |
| F8 | 2.2556 × 103 | 3.7816 × 101 | 2.9029 × 10−2 | 2.2275 × 103 | 2.3669 × 103 | 7.0686 × 101 | 2.2952 × 10−2 | 2.2473 × 103 |
| F9 | 2.4995 × 103 | 1.5796 × 101 | 2.7036 × 10−2 | 2.4817 × 103 | 2.6849 × 103 | 5.8066 × 101 | 2.1603 × 10−2 | 2.5745 × 103 |
| F10 | 3.6510 × 103 | 1.1102 × 103 | 2.2880 × 10−2 | 2.5030 × 103 | 5.3046 × 103 | 2.0359 × 103 | 1.7008 × 10−2 | 2.5315 × 103 |
| F11 | 1.6579 × 104 | 8.2847 × 103 | 3.3437 × 10−2 | 8.6969 × 103 | 6.9695 × 103 | 4.7637 × 102 | 2.7133 × 10−2 | 5.6653 × 103 |
| F12 | 3.0669 × 103 | 1.3933 × 101 | 4.4198 × 10−2 | 2.9818 × 103 | 3.1248 × 103 | 9.3803 × 101 | 3.0523 × 10−2 | 2.9939 × 103 |
| Function | WOA | HHO | ||||||
| Ave. | Std. | Time | Best | Ave | std | Time | Best | |
| F1 | 5.4916 × 104 | 1.8629 × 104 | 6.4459 × 10−3 | 1.6798 × 104 | 5.0829 × 104 | 1.5932 × 104 | 1.8694 × 10−2 | 2.1948 × 104 |
| F2 | 8.5476 × 102 | 1.6965 × 102 | 6.3828 × 10−3 | 5.8846 × 102 | 8.7254 × 102 | 1.5400 × 102 | 1.6184 × 10−2 | 6.3827 × 102 |
| F3 | 6.7819 × 102 | 1.2832 × 101 | 1.7020 × 10−2 | 6.5280 × 102 | 6.6708 × 102 | 1.0961 × 101 | 4.4547 × 10−2 | 6.3088 × 102 |
| F4 | 9.5966 × 102 | 2.6966 × 101 | 9.8217 × 10−3 | 8.9240 × 102 | 8.9961 × 102 | 1.4888 × 101 | 2.5623 × 10−2 | 8.6119 × 102 |
| F5 | 4.5437 × 103 | 1.3793 × 103 | 1.0117 × 10−2 | 2.2502 × 103 | 3.1558 × 103 | 3.7781 × 102 | 2.8117 × 10−2 | 2.1695 × 103 |
| F6 | 7.1896 × 107 | 8.2773 × 107 | 7.3713 × 10−3 | 3.3799 × 105 | 1.7839 × 107 | 3.7642 × 107 | 1.9376 × 10−2 | 3.5391 × 105 |
| F7 | 2.2575 × 103 | 8.9587 × 101 | 2.0146 × 10−2 | 2.1066 × 103 | 2.2271 × 103 | 7.2493 × 101 | 5.3109 × 10−2 | 2.1327 × 103 |
| F8 | 2.3488 × 103 | 1.2004 × 102 | 2.3399 × 10−2 | 2.2304 × 103 | 2.3335 × 103 | 1.0893 × 102 | 5.8203 × 10−2 | 2.2318 × 103 |
| F9 | 2.6565 × 103 | 6.8495 × 101 | 2.1379 × 10−2 | 2.5218 × 103 | 2.7010 × 103 | 7.2822 × 101 | 5.0356 × 10−2 | 2.5664 × 103 |
| F10 | 5.5397 × 103 | 1.3492 × 103 | 1.7146 × 10−2 | 2.5106 × 103 | 4.8006 × 103 | 1.7619 × 103 | 4.3705 × 10−2 | 2.5284 × 103 |
| F11 | 5.6536 × 103 | 5.8157 × 102 | 2.7628 × 10−2 | 4.3616 × 103 | 6.2412 × 103 | 9.0108 × 102 | 6.2003 × 10−2 | 4.1782 × 103 |
| F12 | 3.1741 × 103 | 1.3144 × 102 | 3.0692 × 10−2 | 3.0187 × 103 | 3.3290 × 103 | 2.0010 × 102 | 7.5187 × 10−2 | 3.0188 × 103 |
| Function | PSO | EGGO | ||||||
| Ave. | Std. | Time | Best | Ave | std | Time | Best | |
| F1 | 6.8451 × 104 | 2.0562 × 104 | 5.8537 × 10−3 | 2.9053 × 104 | 3.7418 × 104 | 1.1689 × 104 | 5.8202 × 10−3 | 1.7921 × 104 |
| F2 | 7.1217 × 102 | 2.2996 × 102 | 1.6870 × 10−2 | 4.4896 × 102 | 5.1170 × 102 | 4.5991 × 101 | 5.7311 × 10−3 | 4.3560 × 102 |
| F3 | 6.2776 × 102 | 8.8523 × 100 | 1.6637 × 10−2 | 6.1328 × 102 | 6.2367 × 102 | 6.7724 × 100 | 1.5967 × 10−2 | 6.1260 × 102 |
| F4 | 9.4195 × 102 | 2.6359 × 101 | 9.0505 × 10−3 | 8.9326 × 102 | 8.7182 × 102 | 1.7680 × 101 | 1.6379 × 10−2 | 8.4077 × 102 |
| F5 | 3.7861 × 103 | 1.5398 × 103 | 9.2301 × 10−3 | 1.6896 × 103 | 2.7219 × 103 | 3.9913 × 102 | 9.1869 × 10−3 | 1.5199 × 103 |
| F6 | 9.6455 × 106 | 1.6462 × 107 | 6.5599 × 10−3 | 4.0381 × 103 | 1.3426 × 106 | 8.2665 × 105 | 1.7603 × 10−2 | 2.1938 × 103 |
| F7 | 2.1349 × 103 | 4.5206 × 101 | 1.9406 × 10−2 | 2.0655 × 103 | 2.1184 × 103 | 3.6514 × 101 | 2.1295 × 10−2 | 2.0420 × 103 |
| F8 | 2.3038 × 103 | 7.3715 × 101 | 2.2781 × 10−2 | 2.2305 × 103 | 2.2486 × 103 | 2.4609 × 101 | 1.9803 × 10−2 | 2.2183 × 103 |
| F9 | 2.5862 × 103 | 9.3564 × 101 | 2.0743 × 10−2 | 2.4819 × 103 | 2.5060 × 103 | 5.1559 × 101 | 2.3087 × 10−2 | 2.4649 × 103 |
| F10 | 4.3177 × 103 | 1.1727 × 103 | 1.6412 × 10−2 | 2.5212 × 103 | 3.5931 × 103 | 1.0167 × 103 | 1.7544 × 10−2 | 2.5028 × 103 |
| F11 | 1.8980 × 104 | 1.9458 × 104 | 2.7436 × 10−2 | 4.4370 × 103 | 5.5911 × 103 | 5.8405 × 102 | 3.1106 × 10−2 | 4.2239 × 103 |
| F12 | 3.0249 × 103 | 4.5139 × 101 | 2.9727 × 10−2 | 2.9527 × 103 | 2.9533 × 103 | 7.9448 × 100 | 3.7432 × 10−2 | 2.9411 × 103 |
| Algorithm | Optimal Values for Variables | f | ||||||
|---|---|---|---|---|---|---|---|---|
| w | d | L | g1 | g2 | g3 | g4 | ||
| GGO | 0.05178 | 0.35885 | 11.171 | −3.52 × 10−4 | −1.33 × 10−4 | −4.0555 | −0.7262 | 0.0126724 |
| PSO | 0.0527 | 0.3809 | 10.03011 | −0.0011 | −0.0013 | −4.0863 | −0.7109 | 0.0127263 |
| GWO | 0.05173 | 0.35749 | 11.2594 | −6.99 × 10−4 | −4.80 × 10−4 | −4.0492 | −0.7272 | 0.0126845 |
| SSA | 0.0507 | 0.3319 | 12.98 | −5.31 × 10−4 | −0.0035 | −3.9801 | −0.7449 | 0.0127801 |
| WOA | 0.05173 | 0.35764 | 11.24 | −2.32 × 10−4 | −1.43 × 10−4 | −4.0537 | −0.7271 | 0.0126712 |
| MFO | 0.05172 | 0.35746 | 11.31 | −0.0057 | −5.64 × 10−6 | −4.0265 | −0.7272 | 0.0127269 |
| HHO | 0.05173 | 0.3576 | 11.242 | −7.48 × 10−5 | −2.33 × 10−4 | −4.0539 | −0.7271 | 0.0126717 |
| EGGO | 0.05178 | 0.35884 | 11.1704 | −2.06 × 10−4 | −1.56 × 10−4 | −4.0561 | −0.7263 | 0.0126703 |
| Algorithm | Optimal Values for Variables | Optimum Cost | |||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | ||
| EGGO | 43 | 19 | 16 | 49 | 2.700857 × 10−12 |
| GMO | 43 | 19 | 16 | 49 | 2.700857 × 10−12 |
| KABC | 50.4259 | 22.3987 | 16.7082 | 51.4394 | 0 |
| IAPSO | 43 | 19 | 16 | 49 | 2.700857 × 10−12 |
| MBA | 43 | 19 | 16 | 49 | 2.700857 × 10−12 |
| ALO | 43 | 19 | 16 | 49 | 2.7009 × 10−12 |
| Algorithm | Optimal Values for Variables | Optimum Cost | |
|---|---|---|---|
| x1 | x2 | ||
| EGGO | 0.78868624 | 0.40823425 | 263.8958434 |
| GMO | 0.7886775 | 0.4082415 | 263.8958434 |
| KABC | 0.7886 | 0.4084 | 263.8959 |
| DMMFO | 0.788687421 | 0.408213541 | 263.8958435 |
| GOA | 0.7888976 | 0.4076196 | 263.895881 |
| ALO | 0.788662816000317 | 0.408283133832901 | 263.8958434 |
| CS | 0.78867 | 0.40902 | 263.9716 |
| GSA | 0.7886751284 | 0.4082483080 | 263.8958434 |
| MBA | 0.7885650 | 0.4085597 | 263.8958522 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Yao, Y.; Yang, Y.; Zang, Z.; Zhang, X.; Zhang, Y.; Yu, Z. Novel Greylag Goose Optimization Algorithm with Evolutionary Game Theory (EGGO). Biomimetics 2025, 10, 545. https://doi.org/10.3390/biomimetics10080545
Wang L, Yao Y, Yang Y, Zang Z, Zhang X, Zhang Y, Yu Z. Novel Greylag Goose Optimization Algorithm with Evolutionary Game Theory (EGGO). Biomimetics. 2025; 10(8):545. https://doi.org/10.3390/biomimetics10080545
Chicago/Turabian StyleWang, Lei, Yuqi Yao, Yuanting Yang, Zihao Zang, Xinming Zhang, Yiwen Zhang, and Zhenglei Yu. 2025. "Novel Greylag Goose Optimization Algorithm with Evolutionary Game Theory (EGGO)" Biomimetics 10, no. 8: 545. https://doi.org/10.3390/biomimetics10080545
APA StyleWang, L., Yao, Y., Yang, Y., Zang, Z., Zhang, X., Zhang, Y., & Yu, Z. (2025). Novel Greylag Goose Optimization Algorithm with Evolutionary Game Theory (EGGO). Biomimetics, 10(8), 545. https://doi.org/10.3390/biomimetics10080545






