Multi-AUV Dynamic Cooperative Path Planning with Hybrid Particle Swarm and Dynamic Window Algorithm in Three-Dimensional Terrain and Ocean Current Environment
Abstract
1. Introduction
2. Underwater Environment Modeling
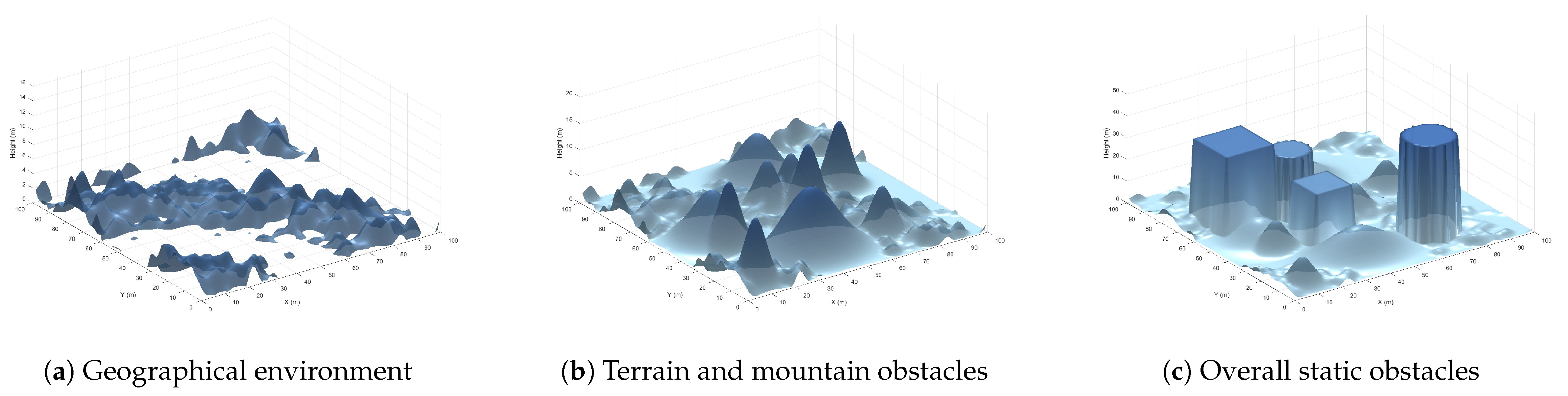
2.1. Underwater Terrain Environment Modeling
2.2. Obstacle Modeling
2.2.1. Static Obstacle Modeling
2.2.2. Dynamic Obstacle Modeling
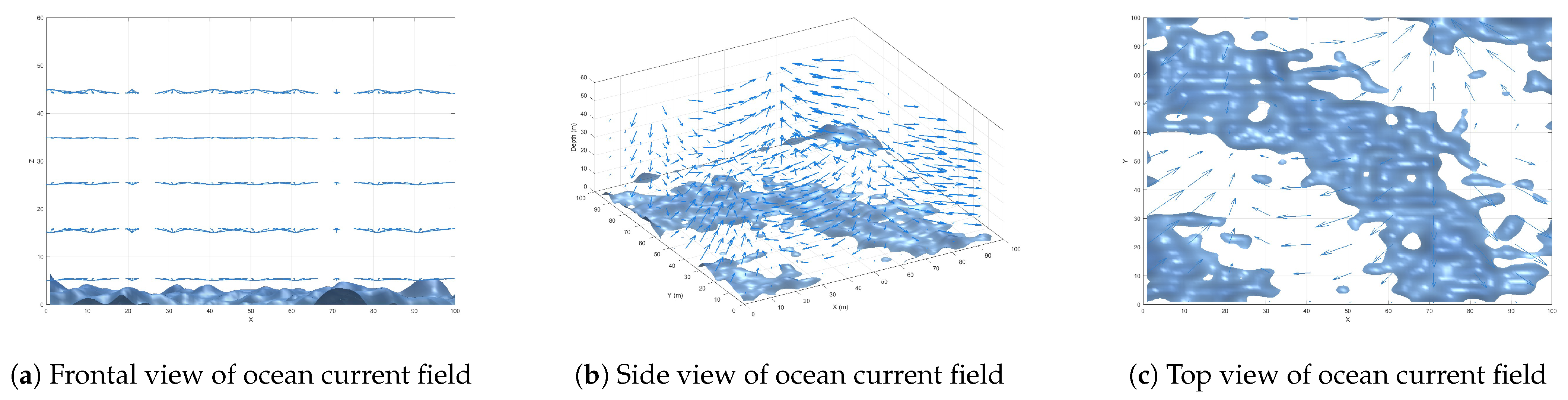
2.3. Ocean Current Model with Complex Vortices
3. Improved Multi-Objective Particle Swarm Optimization Algorithm
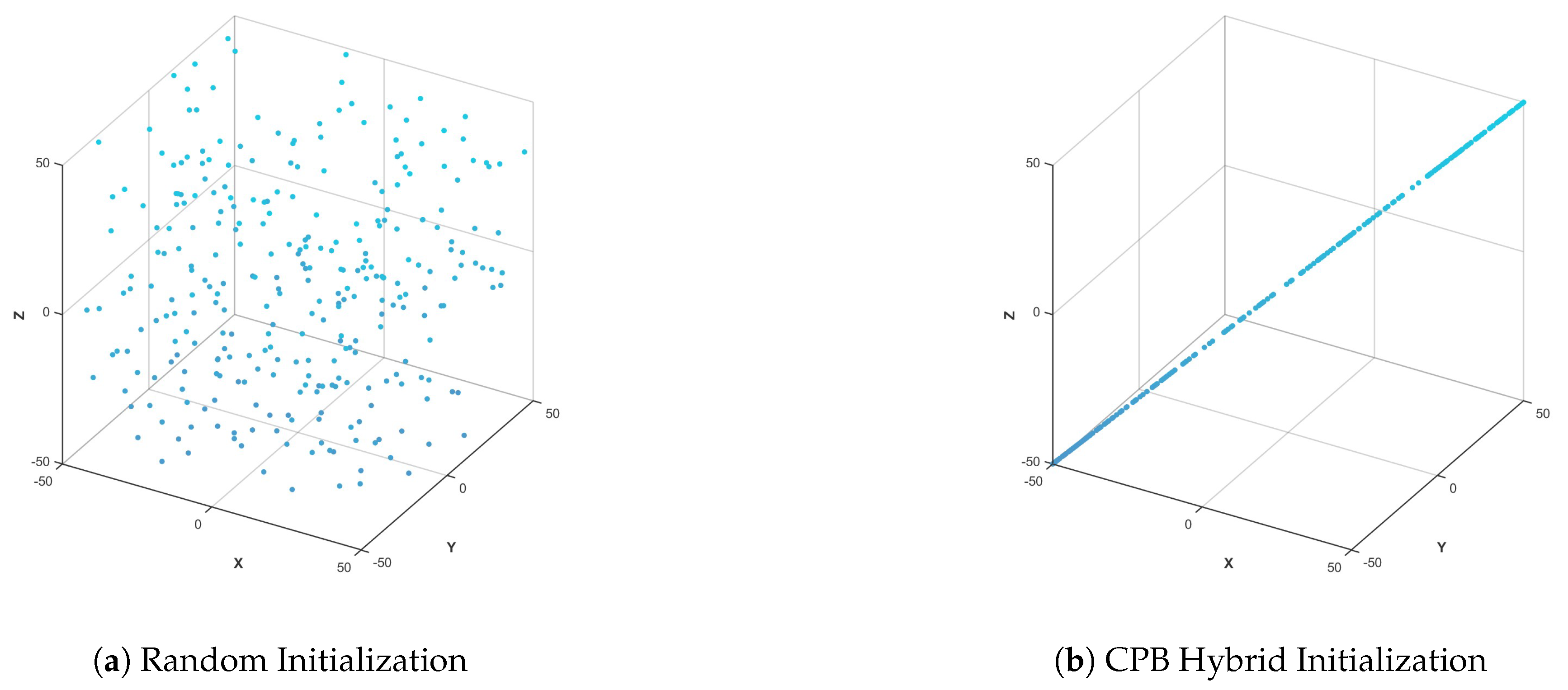
3.1. The Initialization Method of Hybrid Particle Swarm Based on CPB Method
3.1.1. Hybrid Chaotic Initialization
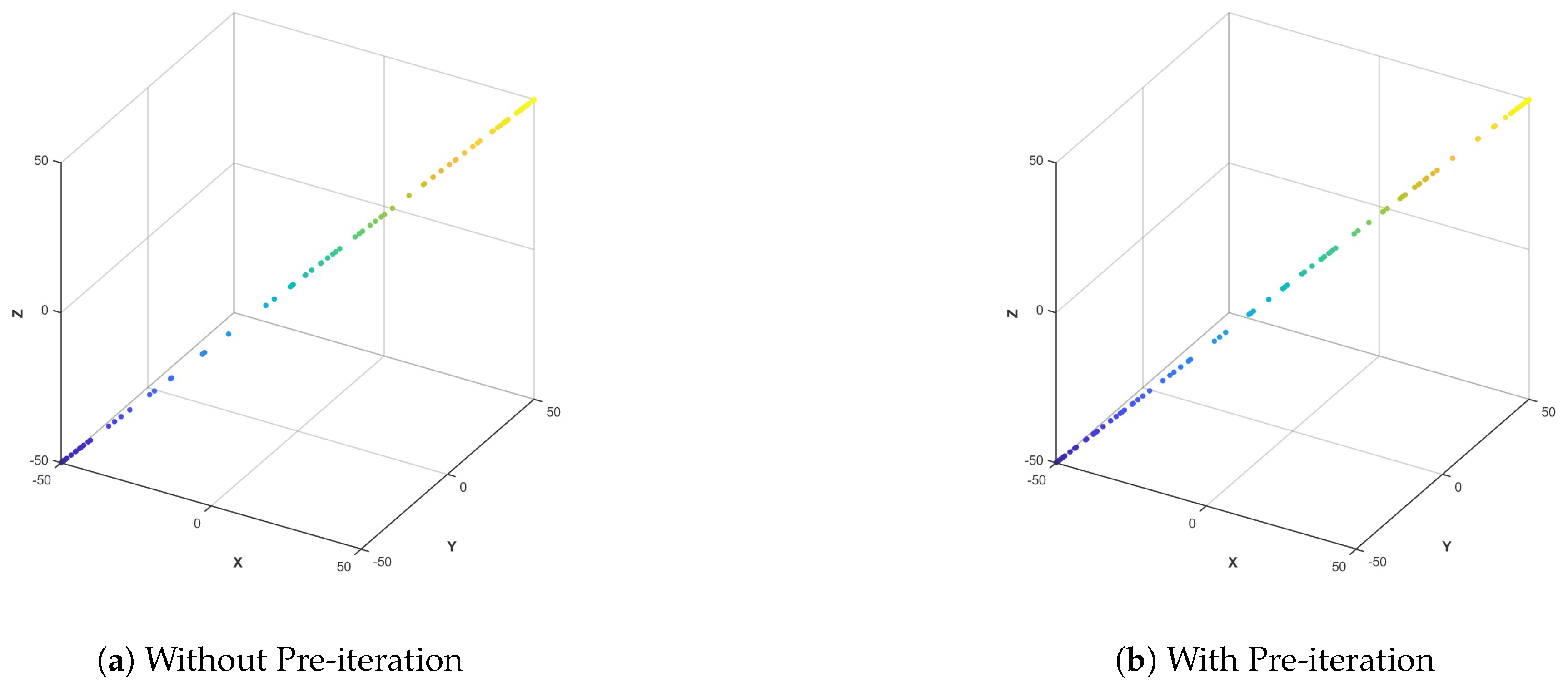
3.1.2. Pre-Iterative Transient Elimination
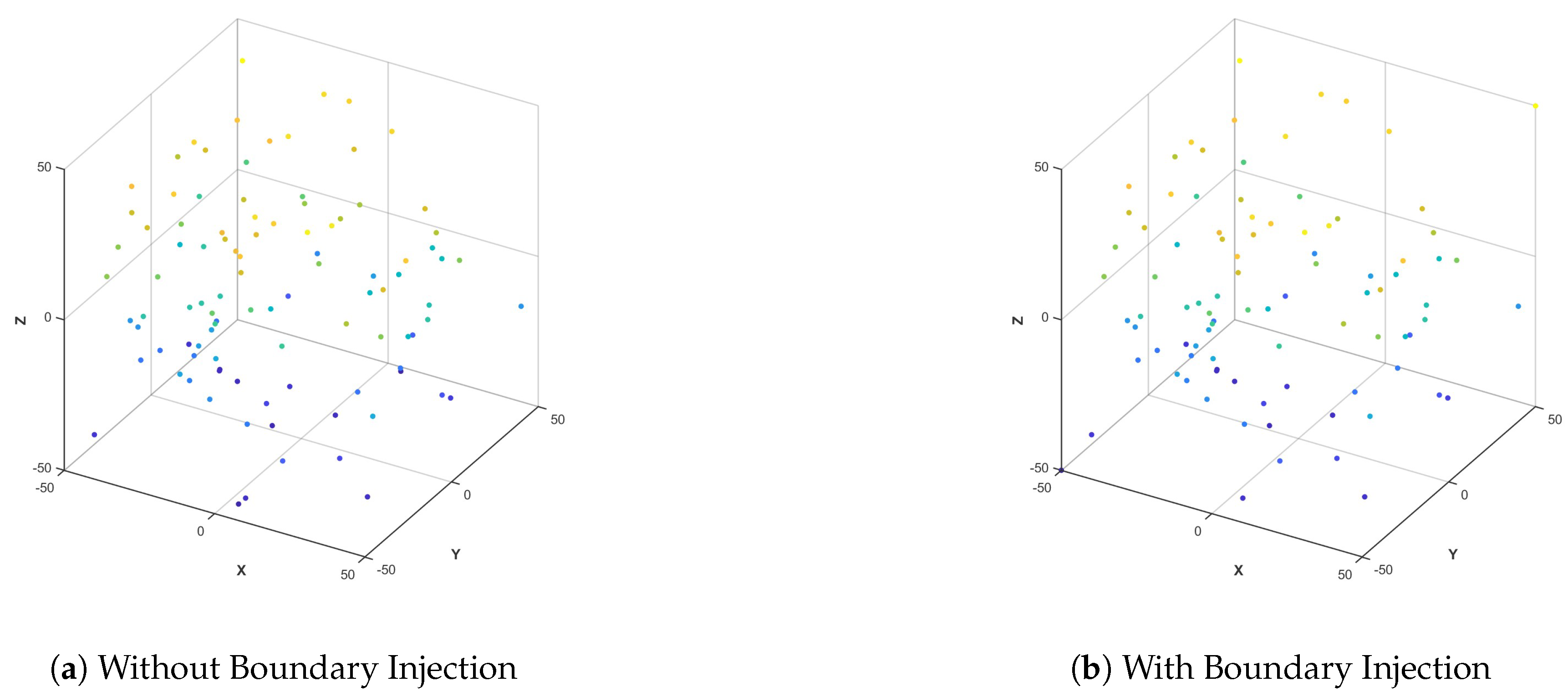
3.1.3. Boundary Particle Injection
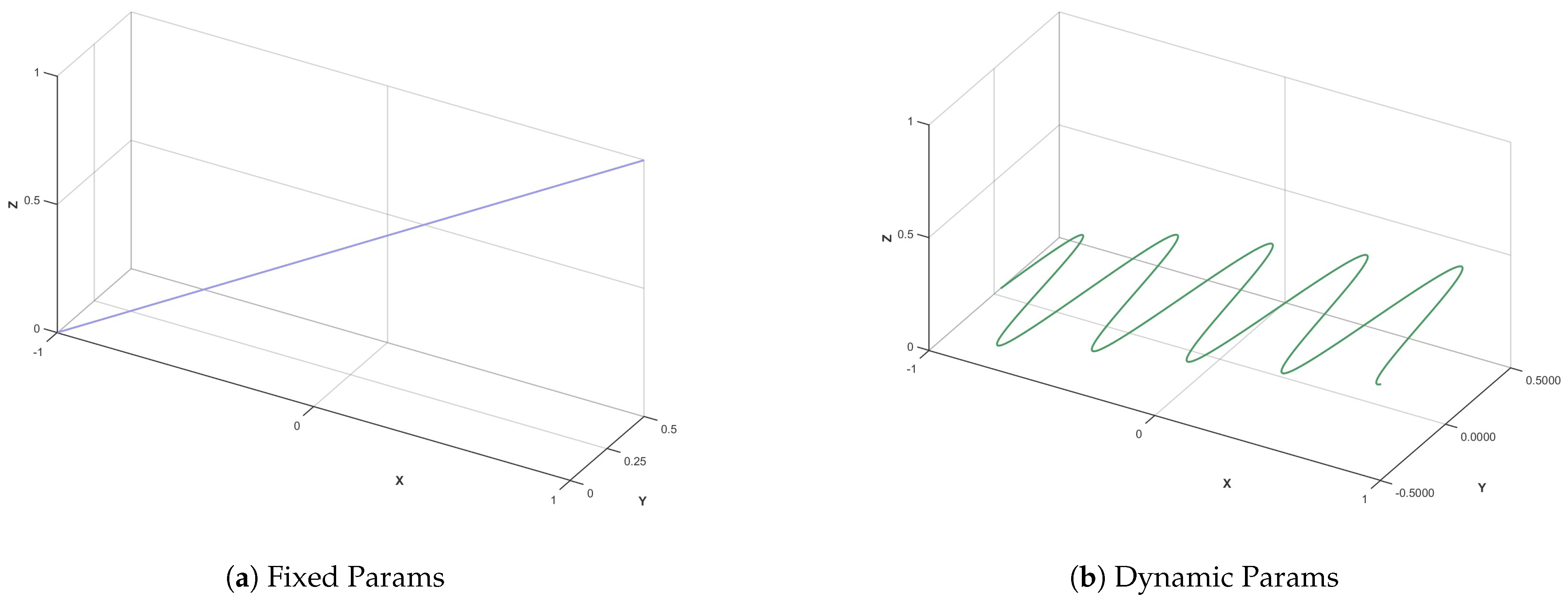
3.2. Dynamic Adaptive Parameter Adjustment
3.3. Hybrid Perturbation Strategy
3.3.1. Levy Flight Disturbance
3.3.2. Differential Mutation Strategy
4. Improved Dynamic Window Approach
4.1. Adaptive Dynamic Window Generation
4.2. Multi-Objective Optimization Cost Function
4.3. Trajectory Prediction and Correction Mechanism
5. Multi-AUV Cooperative Path Planning Based on Improved PSO-DWA
5.1. Multi-Stage Planning Framework Design
5.2. Reconstruction of Multi-Objective Optimization Functions
5.3. Collaborative Path Smoothing Enhancement
5.4. Dynamic Window Collaborative Expansion
5.5. Computational Complexity and Scalability Analysis
5.6. Flowchart of Multi-AUVs Path Planning Based on IMOPSO Algorithm
| Algorithm 1: Hybrid Global-Local Path Planning for Multi-AUV. |
 |
6. Simulation Result and Analysis
6.1. Initialization Comparison Experiment
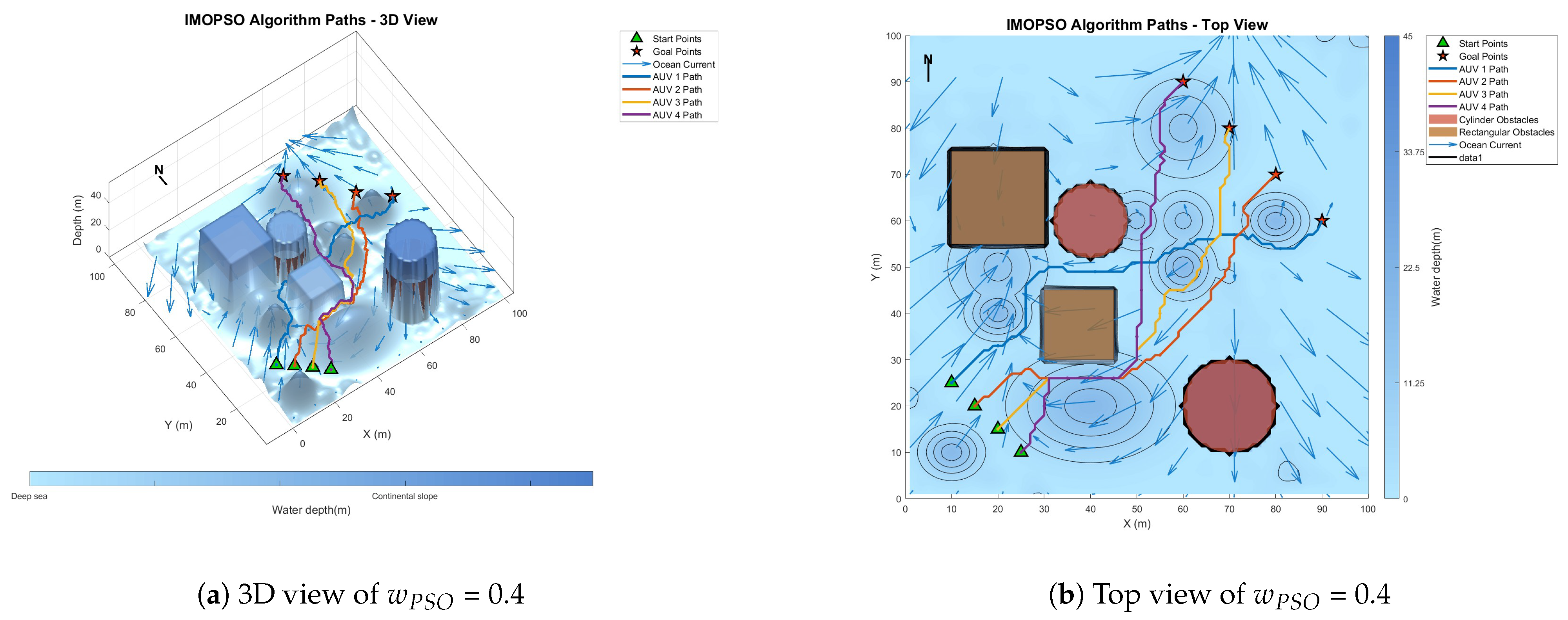
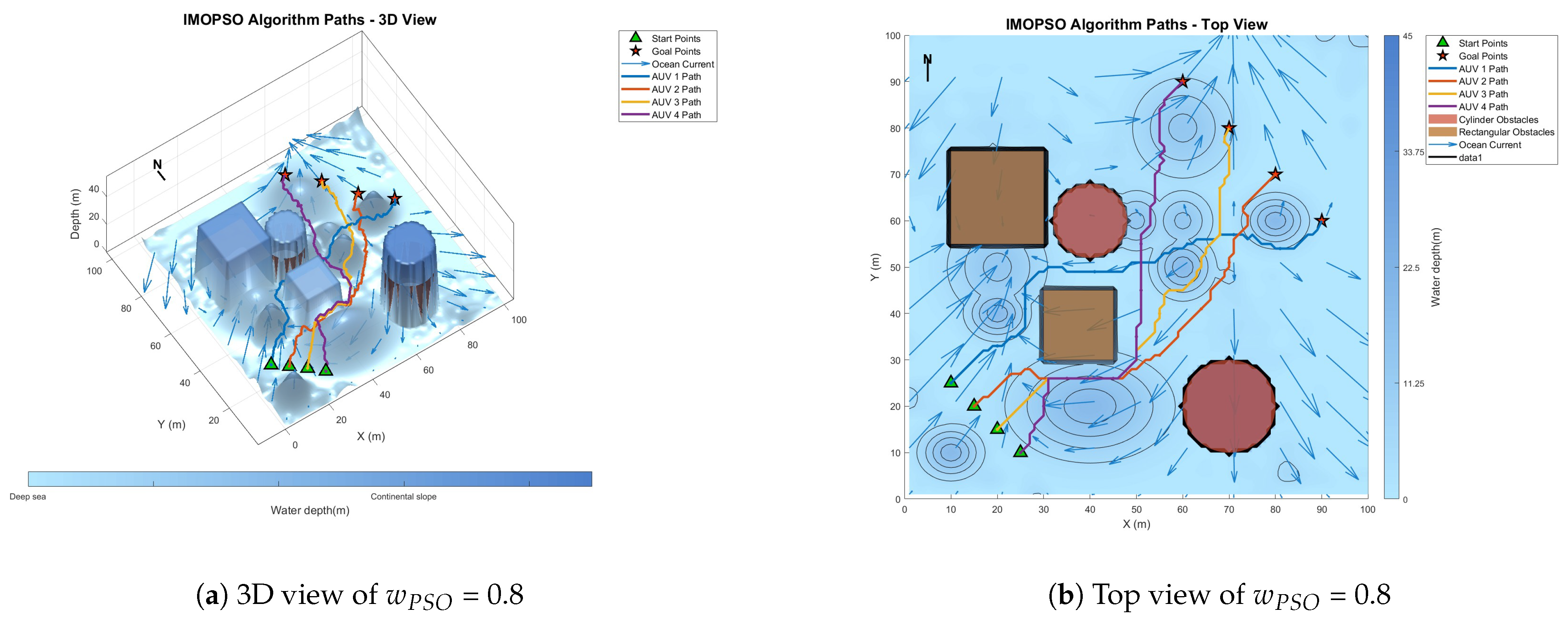
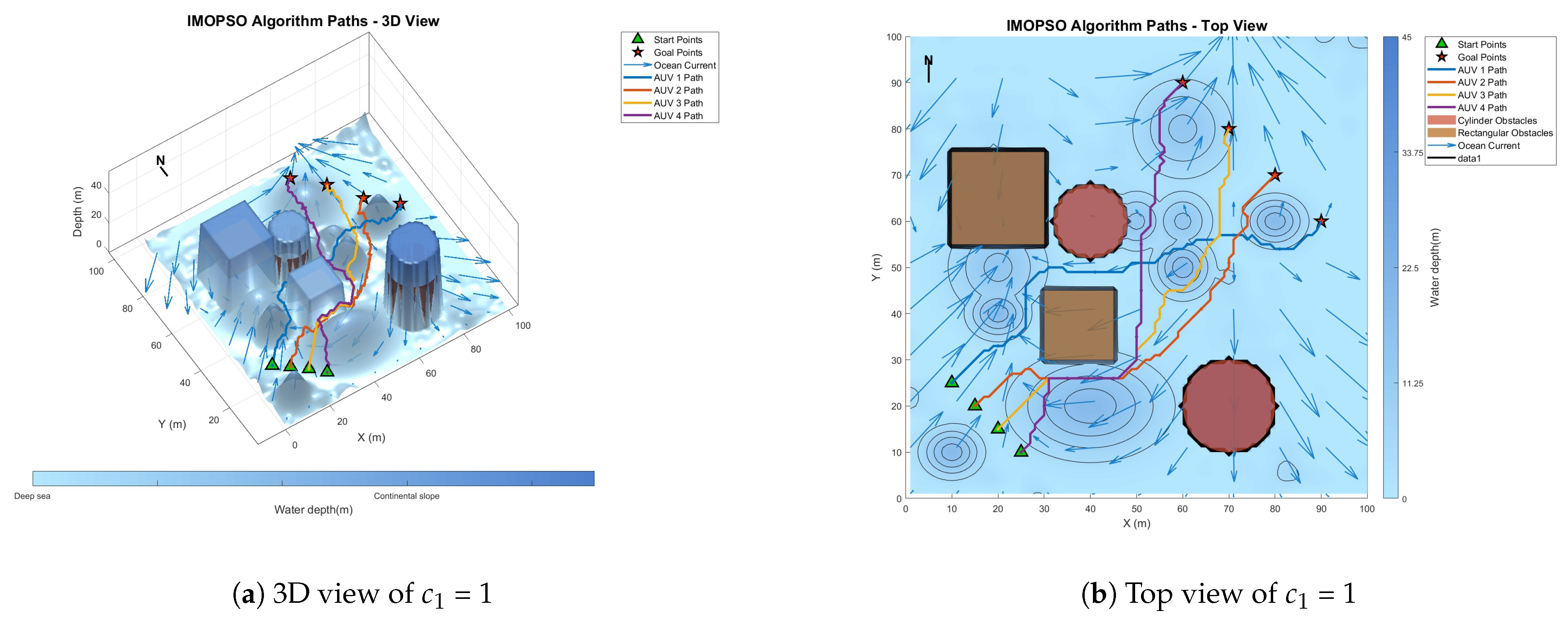
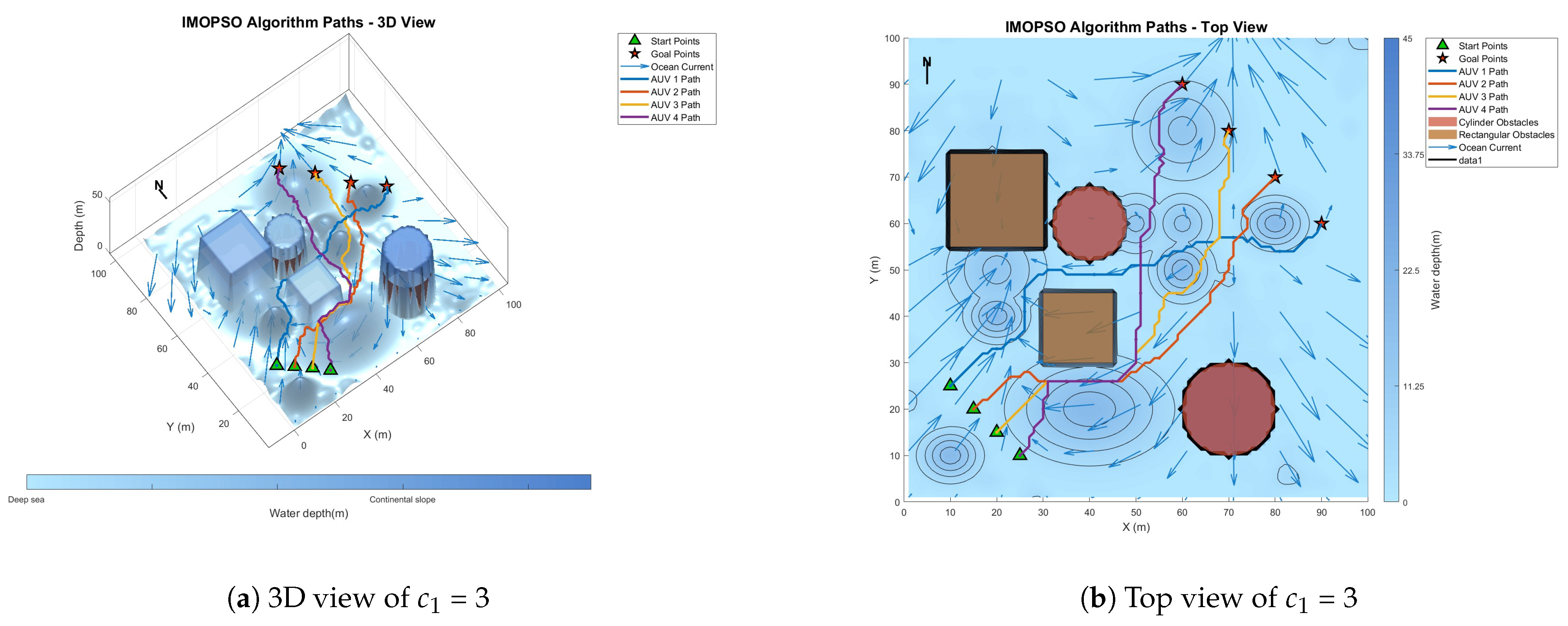
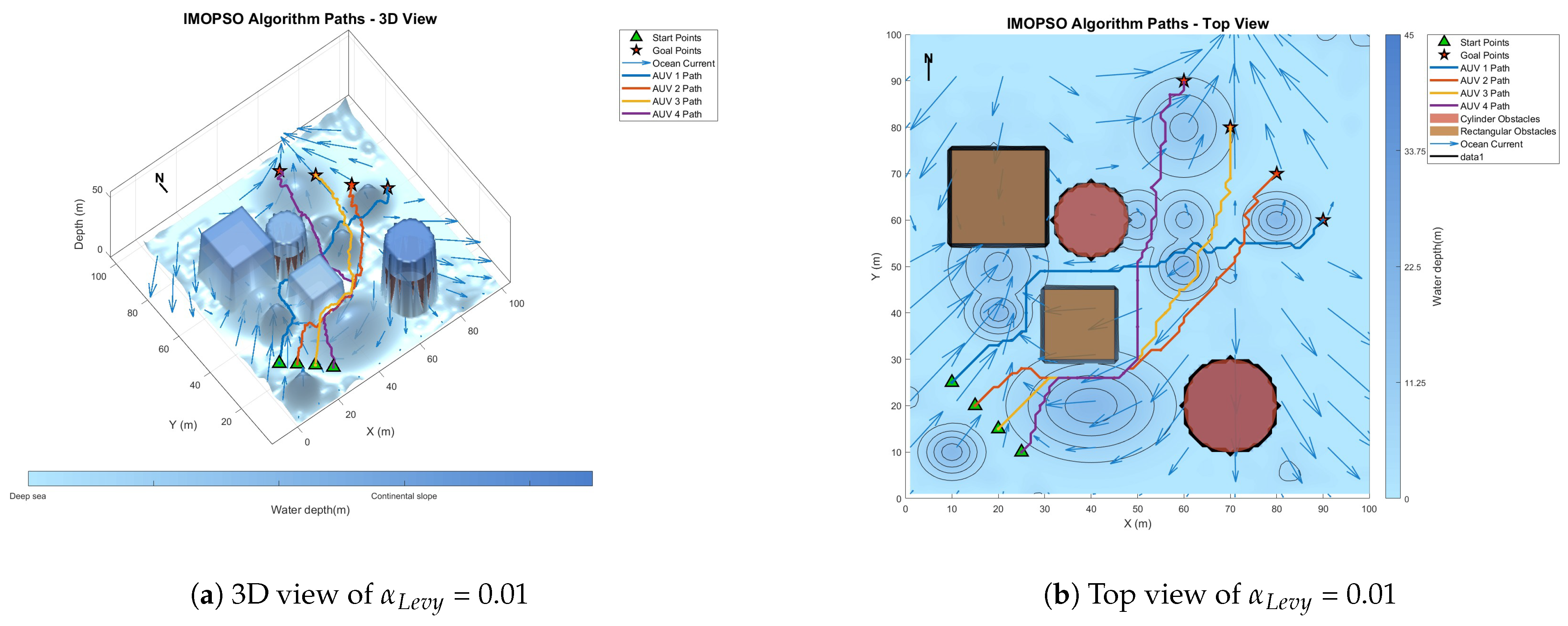
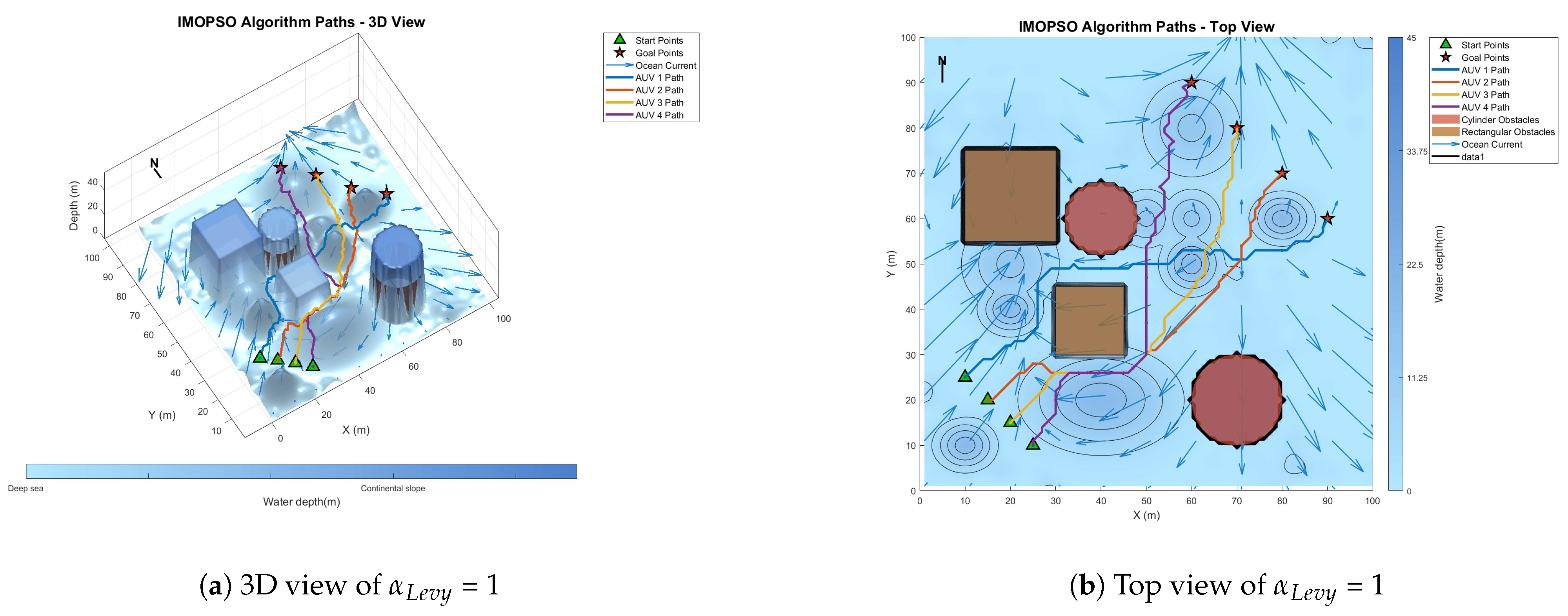
6.2. Parameter Sensitivity Analysis
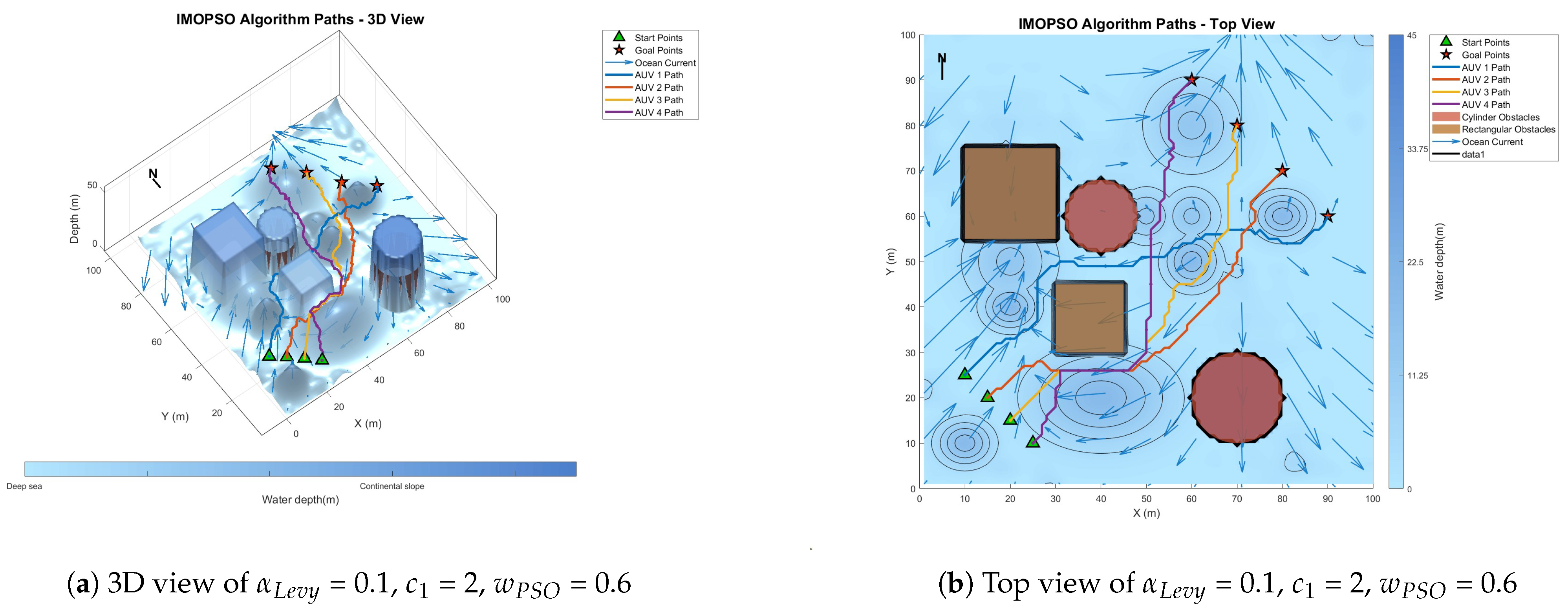
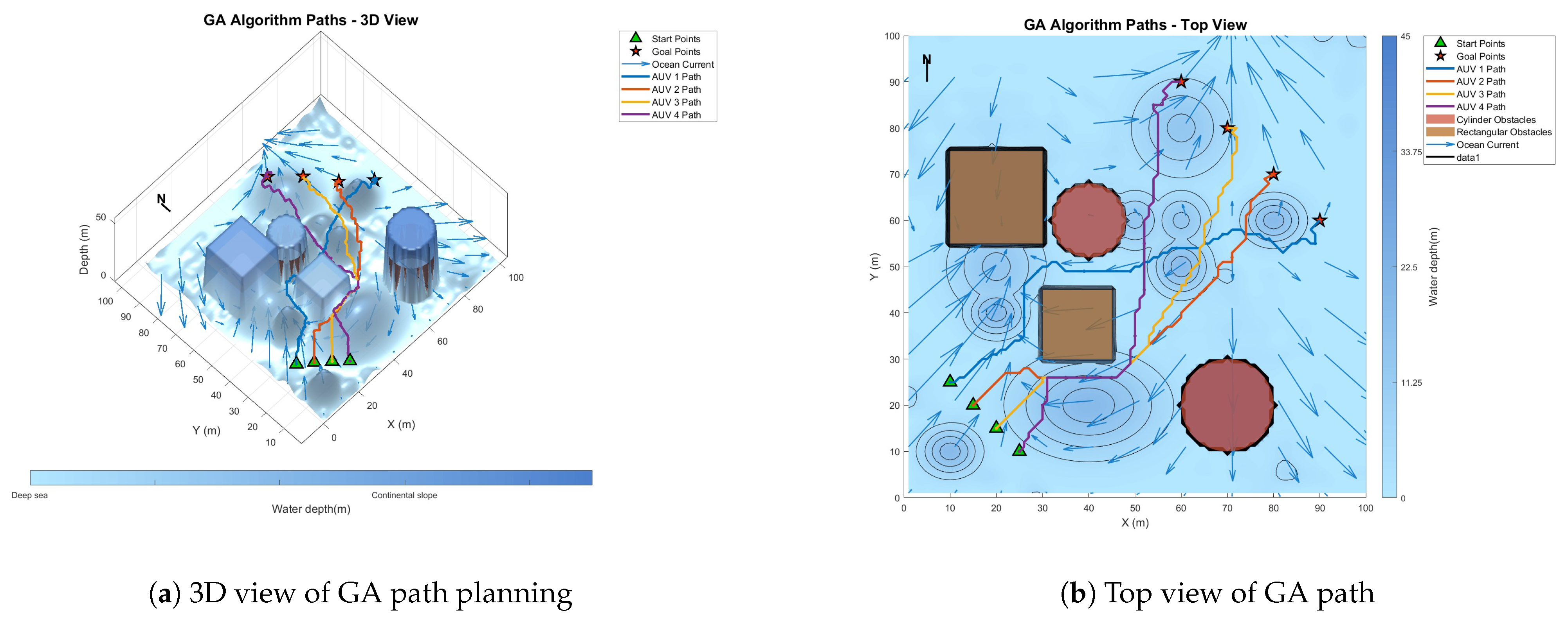
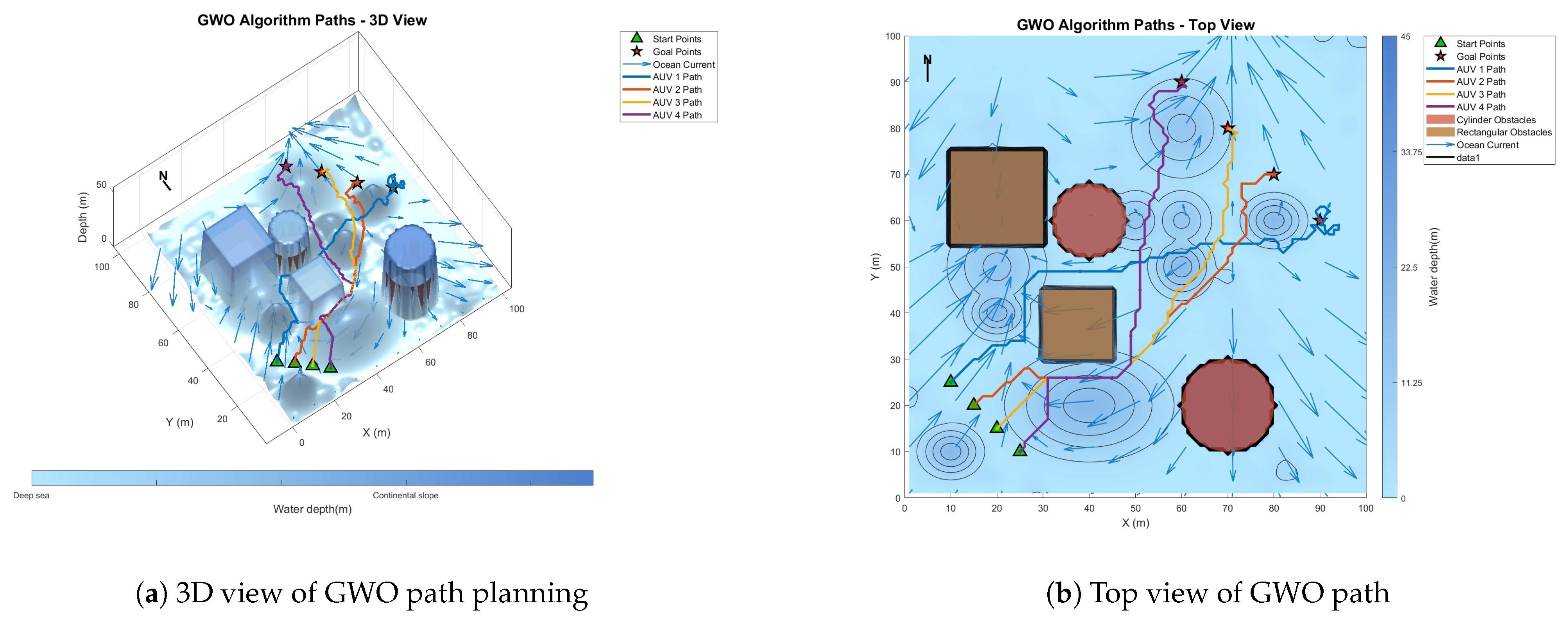
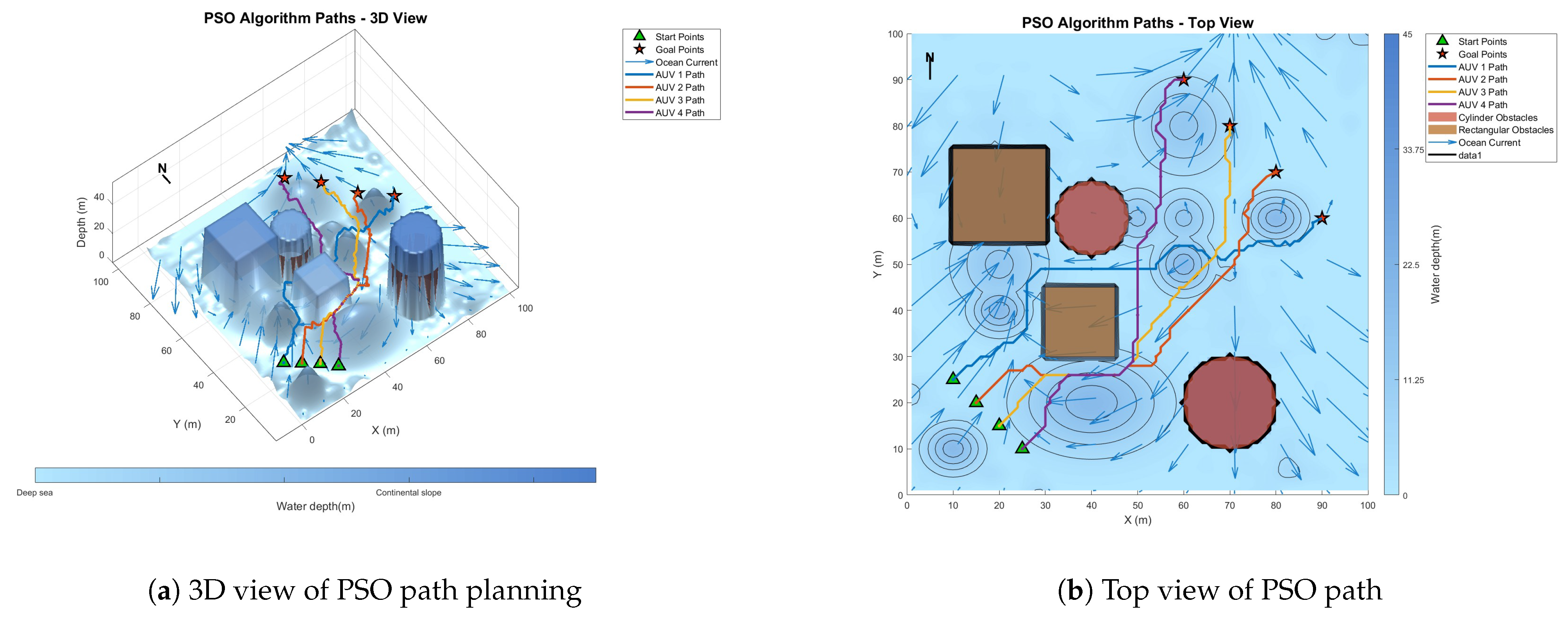
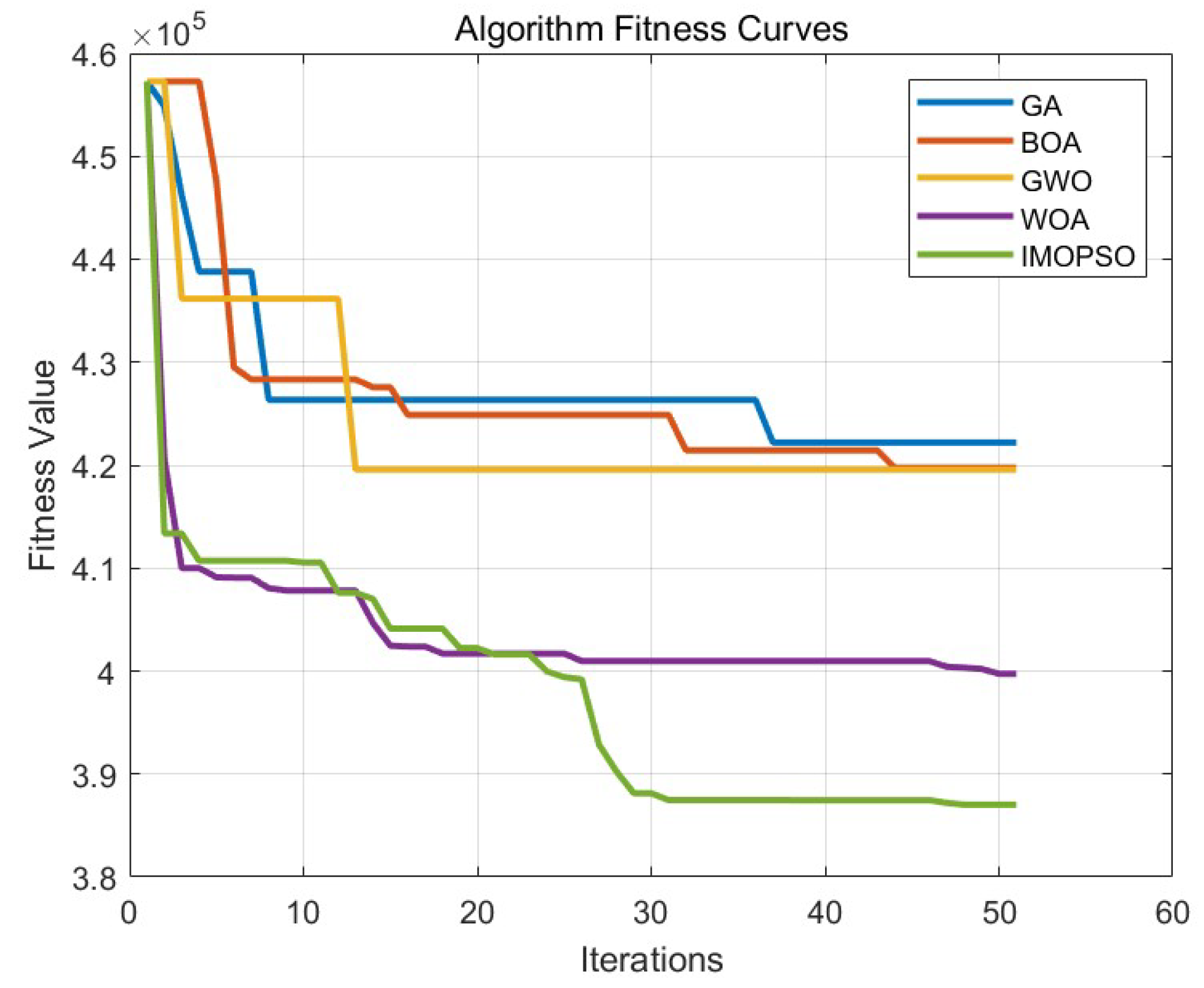
6.3. Comparative Experiment on Path Planning of IMOPSO Algorithm
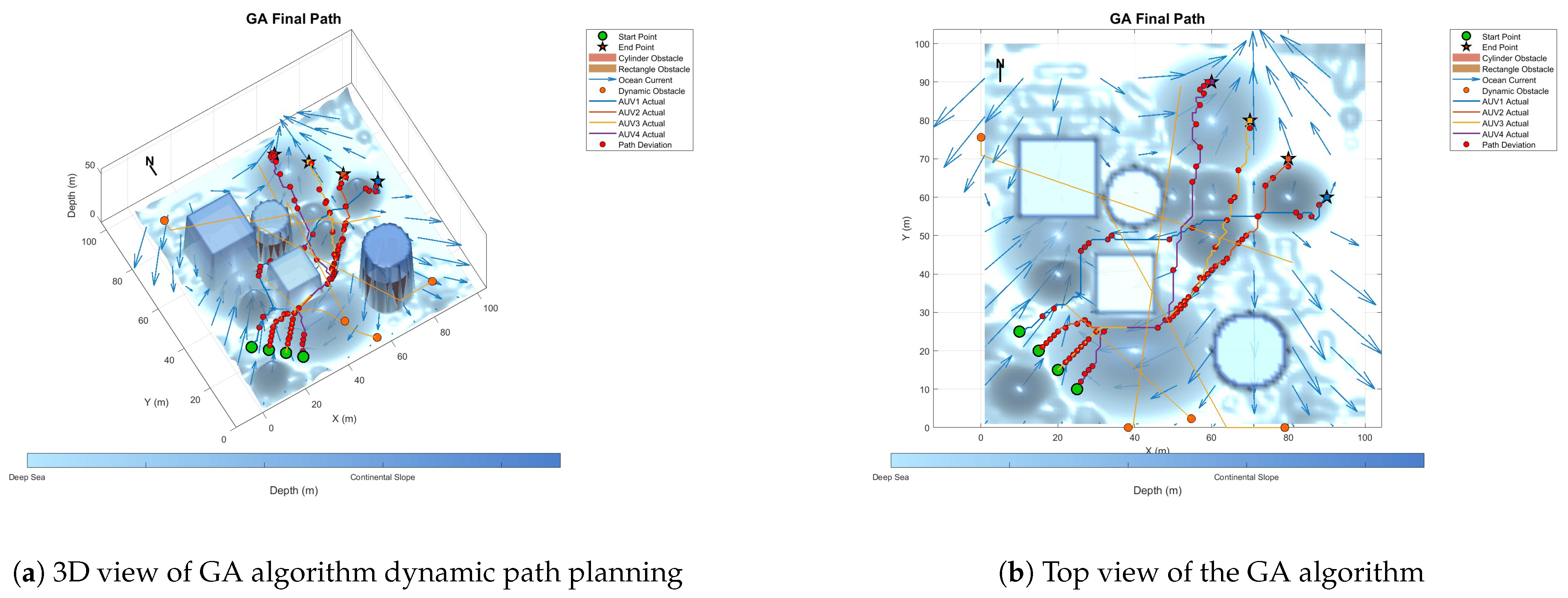
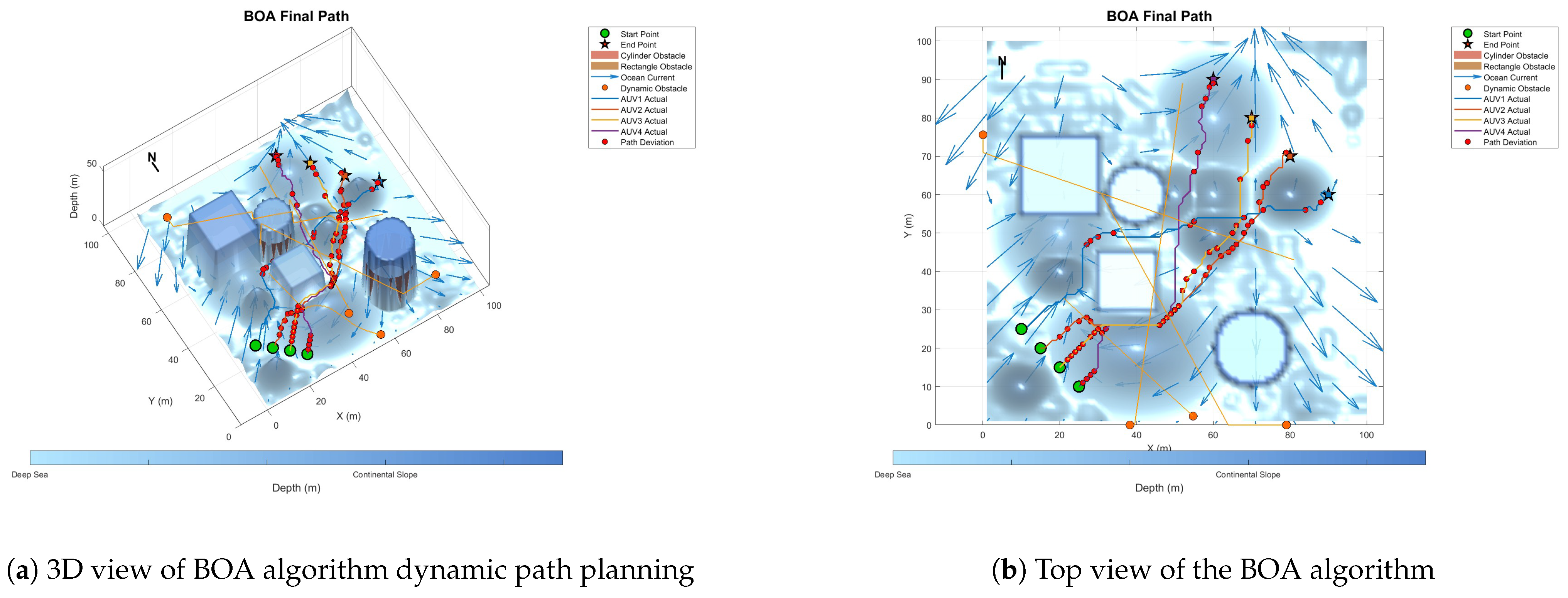
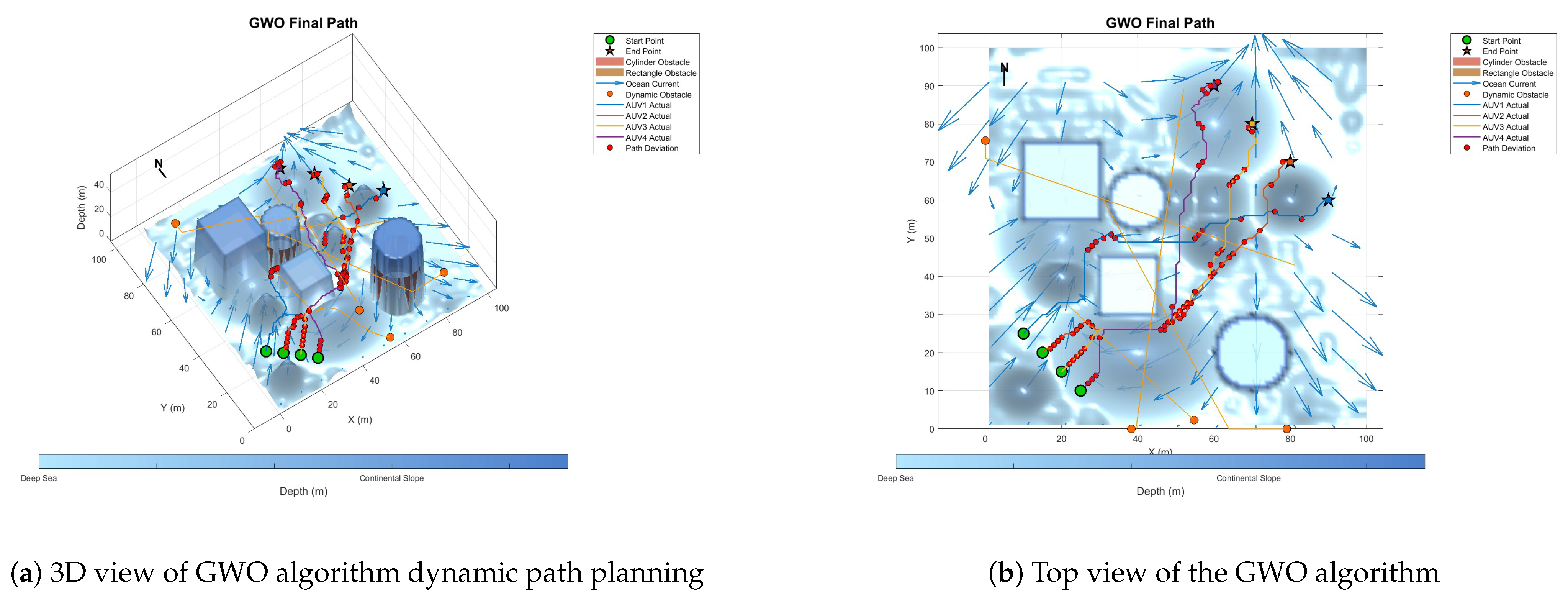
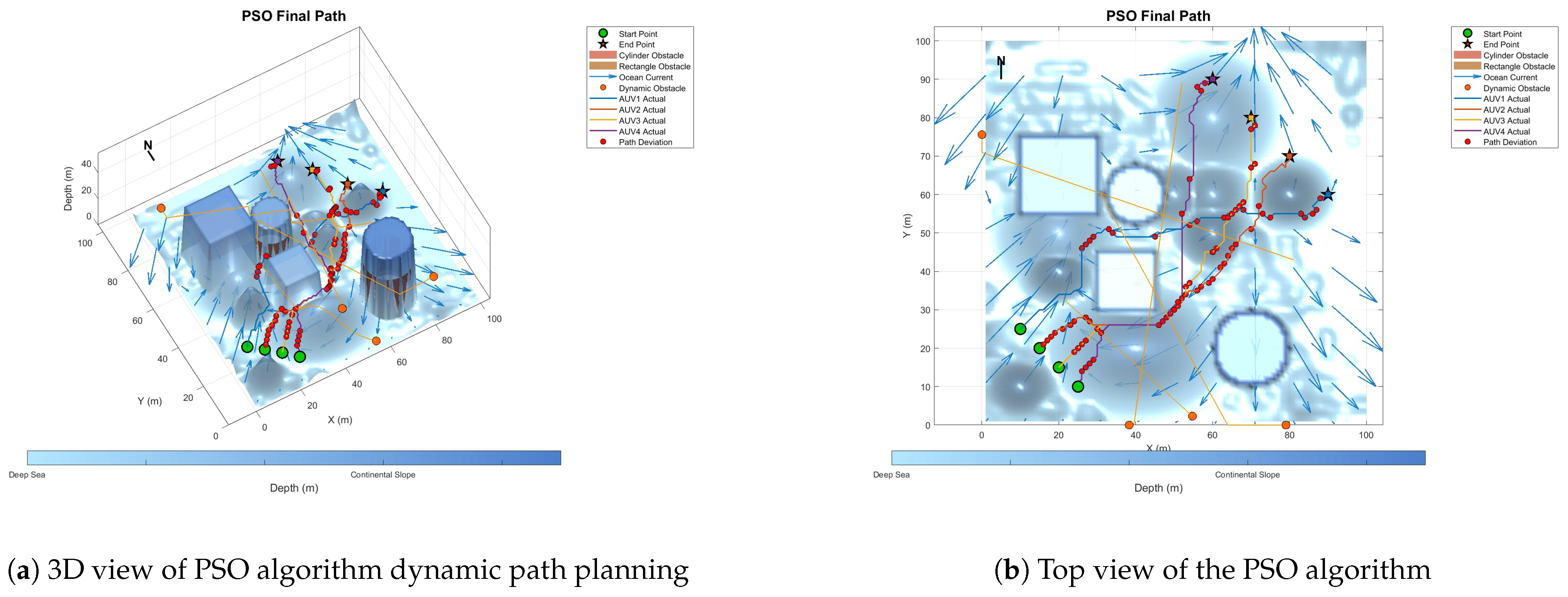
6.4. Multi-AUV Dynamic Cooperative Path-Planning Experiment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| PSO | Particle Swarm Optimization |
| DWA | Dynamic Window Approach |
| GA | Genetic Algorithm |
References
- Wu, W.; Zhang, W.; Du, X.; Li, Z.; Wang, Q. Homing tracking control of autonomous underwater vehicle based on adaptive integral event-triggered nonlinear model predictive control. Ocean Eng. 2023, 277, 114243. [Google Scholar] [CrossRef]
- Li, B.; Mao, J.; Yin, S.; Fu, L.; Wang, Y. Path Planning of Multi-Objective Underwater Robot Based on Improved Sparrow Search Algorithm in Complex Marine Environment. J. Mar. Sci. Eng. 2022, 10, 1695. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Švestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic Roadmaps for Path Planning in High-Dimensional Configuration Spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Nashua, NH, USA, 2012. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Tang, R.; Qi, L.; Ye, S.; Li, C.; Ni, T.; Guo, J.; Liu, H.; Li, Y.; Zuo, D.; Shi, J. Three-Dimensional Path Planning for AUVs Based on Interval Multi-Objective Secretary Bird Optimization Algorithm. Symmetry 2025, 17, 993. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Yao, M.; Fan, G. A Self-Adaptive Improved Slime Mold Algorithm for Multi-UAV Path Planning. Drones 2025, 9, 219. [Google Scholar] [CrossRef]
- Puente-Castro, A.; Rivero, D.; Pedrosa, E.; Pereira, A.; Lau, N.; Fernandez-Blanco, E. Q-Learning based system for Path Planning with Unmanned Aerial Vehicles swarms in obstacle environments. Expert Syst. Appl. 2024, 235, 121240. [Google Scholar] [CrossRef]
- Liu, H.; Shen, Y.; Yu, S.J.; Gao, Z.J.; Wu, T. Deep Reinforcement Learning for Mobile Robot Path Planning. J. Theory Pract. Eng. Sci. 2024, 4, 37–44. [Google Scholar] [CrossRef]
- Tao, B.; Kim, J.H. Deep reinforcement learning-based local path planning in dynamic environments for mobile robot. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102254. [Google Scholar] [CrossRef]
- Babakhani, A.; Jahanbakhshi, M.R.; Parsa, H. Autonomous Underwater Vehicle Motion Planning in Realistic Ocean Environments Using Penalty Function-Particle Swarm Optimization Technique. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1303–1318. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Qi, J.; He, J. AUV underwater 3D path planning based on particle swarm optimization-adaptive step-size cuckoo search algorithm. In Proceedings of the 2022 11th International Conference on Networks, Communication and Computing, Beijing, China, 9–11 December 2023; pp. 215–225. [Google Scholar] [CrossRef]
- Zhi, L.W.; Zuo, Y. Collaborative Path Planning of Multiple AUVs Based on Adaptive Multi-Population PSO. J. Mar. Sci. Eng. 2024, 12, 223. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.; Ding, S.; Liang, D.; He, H. A novel particle swarm optimization algorithm with Lévy flight and orthogonal learning. Swarm Evol. Comput. 2022, 75, 101207. [Google Scholar] [CrossRef]
- Liu, Y.X.; Vogiatzis, C.; Yoshida, R.; Morman, E. Solving reward-collecting problems with UAVs: A comparison of online optimization and Q-learning. arXiv 2021, arXiv:2112.00141. [Google Scholar] [CrossRef]
- Chen, J.S.; Xu, L.H.; Ebel, H.; Eberhard, P. An Online Optimization-Based Trajectory Planning Approach for Cooperative Landing Tasks. arXiv 2025, arXiv:2502.13823. [Google Scholar]
- Fox, D.; Burgard, W.; Thrun, S. The Dynamic Window Approach to Collision Avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Wu, S.; Chen, T. Underwater Path Planning of UUV Based on UDWA. In Proceedings of the 2022 IEEE Intl Conf on Dependable, Autonomic and Secure Computing, Intl Conf on Pervasive Intelligence and Computing, Intl Conf on Cloud and Big Data Computing, Intl Conf on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), Falerna, Italy, 12–15 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, H.; Wang, D.; Zhang, Y.; Yan, T.; He, B. Real-time Obstacle Avoidance for AUV Based on Reinforcement Learning and Dynamic Window Approach. In Proceedings of the Global Oceans 2020: Singapore—U.S. Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Reynolds, A.M.; Rhodes, C.J. The Lévy flight paradigm: Random search patterns and mechanisms. Ecology 2009, 90, 877–887. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zhang, S.; Zheng, R.; Dong, S. Five-Tiered Route Planner for Multi-AUV Accessing Fixed Nodes in Uncertain Ocean Environments. arXiv 2023, arXiv:2311.06579. [Google Scholar] [CrossRef]
- Lin, Y.H.; Huang, L.C.; Chen, S.Y.; Yu, C.M. The optimal route planning for inspection task of autonomous underwater vehicle composed of MOPSO-based dynamic routing algorithm in currents. Appl. Ocean Res. 2018, 75, 178–192. [Google Scholar] [CrossRef]
- Sutantyo, D.; Levi, P.; Möslinger, C.; Read, M. Collective-adaptive Lévy flight for underwater multi-robot exploration. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 456–462. [Google Scholar] [CrossRef]
- Shen, Z. 3-D Coverage Path Planning for Underwater Terrain Mapping. Master’s Thesis, University of Connecticut, Storrs, CT, USA, 2017. [Google Scholar]
- Mu, X.; Gao, W. Coverage Path Planning for Multi-AUV Considering Ocean Currents and Sonar Performance. Front. Mar. Sci. 2025, 11, 1483122. [Google Scholar] [CrossRef]
- Yang, L.; Bi, K.; He, Y.; Han, Z. Multi-rotor UAV Track Planning Based on Improved Artificial Potential Field. In Proceedings of the 11th International Conference on Modelling, Identification and Control (ICMIC2019), Tianjin, China, 13–15 July 2019; Springer: Singapore, 2019; pp. 1291–1302. [Google Scholar] [CrossRef]
- Srivastava, S.; Michael, N. Efficient, Multifidelity Perceptual Representations via Hierarchical Gaussian Mixture Models. IEEE Trans. Robot. 2019, 35, 248–260. [Google Scholar] [CrossRef]
- Couzin, I.D.; Krause, J.; James, R.; Ruxton, G.D.; Franks, N.R. Collective Memory and Spatial Sorting in Animal Groups. J. Theor. Biol. 2002, 218, 1–11. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yan, X.; Wang, W.; Huang, C.; Li, L. A new path planning method for AUV based on the Navier–Stokes equations for ocean currents. Math. Comput. Simul. 2024, 222, 199–208. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Hameed, A.; Alosaimi, W.; Alyami, H. A New Initialization Approach in Particle Swarm Optimization for Global Optimization Problems. Comput. Intell. Neurosci. 2021, 2021, 6628889. [Google Scholar] [CrossRef]
- Chu, H.; Yi, J.; Yang, F. Chaos Particle Swarm Optimization Enhancement Algorithm for UAV Safe Path Planning. Appl. Sci. 2022, 12, 8977. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, K.; Zheng, B.; Ning, H.; Zhou, Y.; Peng, Q.; Li, Z. A CML-ECA Chaotic Image Encryption System Based on Multi-Source Perturbation Mechanism and Dynamic DNA Encoding. Symmetry 2025, 17, 1042. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, D.; Wang, X.; Rong, X.; Zhang, R. 2D Logistic-Adjusted-Chebyshev map for visual color image encryption. J. Inf. Secur. Appl. 2021, 60, 102854. [Google Scholar] [CrossRef]
- Hahn, B. Enhancing Obstacle Avoidance in Dynamic Window Approach via Dynamic Obstacle Behavior Prediction. Actuators 2025, 14, 207. [Google Scholar] [CrossRef]
- Hong, L.; Song, C.; Yang, P.; Cui, W. Two-Layer Path Planner for AUVs Based on the Improved AAF-RRT Algorithm. J. Mar. Sci. Appl. 2022, 21, 102–115. [Google Scholar] [CrossRef]




| Parameter Name | Parameter Definition | Value |
|---|---|---|
| T | Maximum Iterations | 100 |
| num_particles | Population size | 100 |
| knot_num | Path Nodes | 10 |
| N | Cubic spline interpolation points | 200 |
| Maximum inertia weight | 0.9 | |
| Minimum inertia weight | 0.4 | |
| lower boundary control factor | 1 | |
| upper boundary control factor | 1.5 | |
| lower boundary control factor | 1 | |
| upper boundary control factor | 1.5 | |
| Maximum difference weight | 0.5 | |
| Minimum difference weight | 0.1 | |
| Initial perturbation amplitude for local search | 1 | |
| Exponential decay coefficient | 4 | |
| k | Control parameter of sine chaotic perturbation | 1200 |
| Initial perturbation amplitude | 10 | |
| Base angular velocity resolution | 0.1 | |
| K | Velocity samples per step | 50 |
| System response time | 0.5 | |
| Minimum static safety margin | 3 | |
| Multi-AUV safety distance | 5 | |
| Communication distance | 50 | |
| Velocity sensitivity factor | 0.8 | |
| Maximum jerk limit | 2.0 | |
| Prediction horizon steps | 10 | |
| Prediction-correction factor | 0.7 |
| Parameters | Value | Iteration Count | Path Length | Energy |
|---|---|---|---|---|
| 1 | 38 | 562.4 | 215.7 | |
| 2 | 22 | 541.1 | 197.9 | |
| 3 | 18 | 548.3 | 206.5 | |
| 0.01 | 18 | 558.2 | 208.3 | |
| 0.1 | 24 | 542.7 | 199.1 | |
| 1 | 29 | 551.6 | 211.8 | |
| 0.4 | 32 | 552.9 | 205.4 | |
| 0.6 | 23 | 543.3 | 200.2 | |
| 0.8 | 27 | 547.5 | 209.7 |
| Algorithm | Path Length | Energy | Smoothness | Threat Penalty | Total Fitness |
|---|---|---|---|---|---|
| GA | 560.08 | 213.57 | 1.811 | 4214.24 | 422,197.93 |
| BOA | 536.04 | 184.48 | 1.569 | 4190.34 | 419,754.35 |
| GWO | 589.83 | 220.64 | 1.865 | 4187.64 | 419,574.23 |
| PSO | 549.54 | 190.54 | 1.472 | 3991.32 | 399,736.68 |
| IMOPSO | 463.84 | 200.28 | 1.562 | 3862.72 | 387,020.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Lv, Z. Multi-AUV Dynamic Cooperative Path Planning with Hybrid Particle Swarm and Dynamic Window Algorithm in Three-Dimensional Terrain and Ocean Current Environment. Biomimetics 2025, 10, 536. https://doi.org/10.3390/biomimetics10080536
Sun B, Lv Z. Multi-AUV Dynamic Cooperative Path Planning with Hybrid Particle Swarm and Dynamic Window Algorithm in Three-Dimensional Terrain and Ocean Current Environment. Biomimetics. 2025; 10(8):536. https://doi.org/10.3390/biomimetics10080536
Chicago/Turabian StyleSun, Bing, and Ziang Lv. 2025. "Multi-AUV Dynamic Cooperative Path Planning with Hybrid Particle Swarm and Dynamic Window Algorithm in Three-Dimensional Terrain and Ocean Current Environment" Biomimetics 10, no. 8: 536. https://doi.org/10.3390/biomimetics10080536
APA StyleSun, B., & Lv, Z. (2025). Multi-AUV Dynamic Cooperative Path Planning with Hybrid Particle Swarm and Dynamic Window Algorithm in Three-Dimensional Terrain and Ocean Current Environment. Biomimetics, 10(8), 536. https://doi.org/10.3390/biomimetics10080536






