Grid-Based Path Planning of Agricultural Robots Driven by Multi-Strategy Collaborative Evolution Honey Badger Algorithm
Abstract
1. Introduction
2. Related Work
2.1. Honey Badger Optimisation Algorithm
2.1.1. Population Initialisation
2.1.2. Odour Intensity Setting
2.1.3. Density Factor Setting
2.1.4. Digging Mode
2.1.5. Honey Mode
2.2. Set of Enhancement Strategies
- Good Point Set-based Population Initialization Strategy.
- (1)
- Square root sequence method
- (2)
- Prime number representation
- (3)
- Cyclotomic field method
- Decentralised Boundary Constraint Handling Strategy
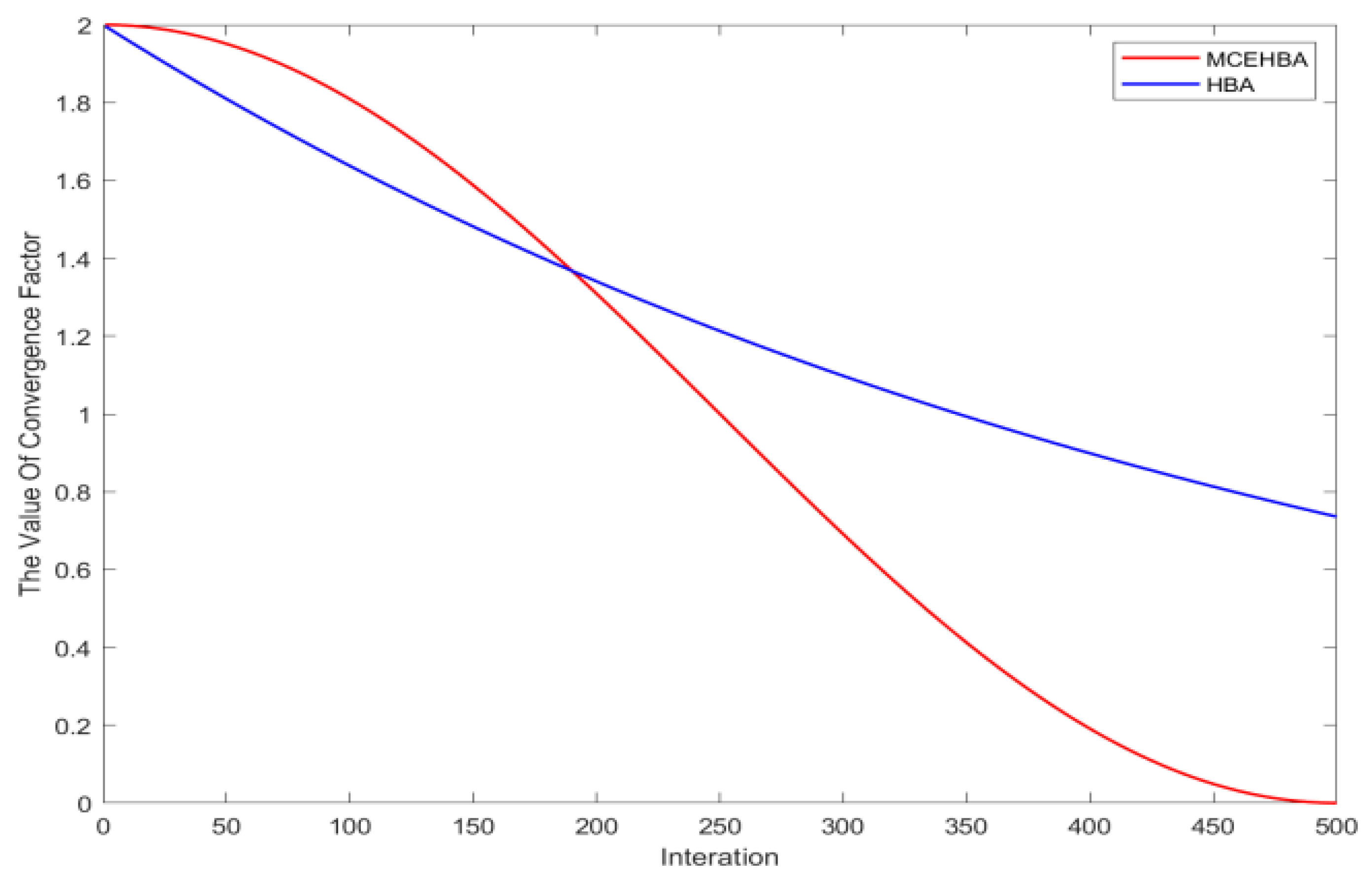
- Sinusoidal function-based nonlinear convergence factor
- Differential Evolution Strategy
- Gravity-Centred Opposition-Based Learning Strategy
3. Algorithm Design and Structure
3.1. Good Point Set-Based Population Initialization Strategy
3.2. Decentralised Boundary Constraint Handling Strategy
3.3. Nonlinear Convergence Factors Based on Sinusoidal Functions
3.4. Differential Evolution Strategy
3.5. Gravity-Centred Opposition-Based Learning Strategy
3.6. Time Complexity Analysis and Pseudocode
| Algorithm 1. The pseudocode of MCEHBA |
| Start MCEHBA; Input: Set the population parameter size , the population dimension , the maximun number of iterations , upper and lower bounds The initial population X is generated via good point set initialisation (Equations (12) and (13)); Evaluate the fitness values of the initial population and designate the optimal value as ; While t < Max do; Update the convergence factor using Equation (15); Update odour concentration using Equation (2); For I = 1: N do; Update the value of F using Equation (6); For j = 1:D do; If r < 0.5 Update the position of the individual using Equation (7) Else Update the position of the individual using Equation (8); End End Using Equation (14) for out-of-bounds processing; Evaluating the adaptation value of the new individual, if the adaptation value is better than the corresponding individual in X, the new individual overwrites the original individual; Individuals were differentially varied using the Equations (16)–(18); Evaluating the adaptation value of the new individual, if the adaptation value is better than the corresponding individual in X, the new individual overwrites the original individual; End Using Equation (14) for out-of-bounds processing; Evaluate adaptation values for new populations and update ; Perform the Gravity-Centred Opposition-Based Learning Strategy using the Equations (19) and (20) Evaluate the new fitness value of the population, keeping the current optimal solution vector with the optimal fitness value End Output: Solution vectors and optimisation results. End MCEHBA |
4. Algorithm Experimentation and Testing
4.1. Test Functions and Parameter Settings
4.2. Analysis of the Effectiveness of Optimization Strategies
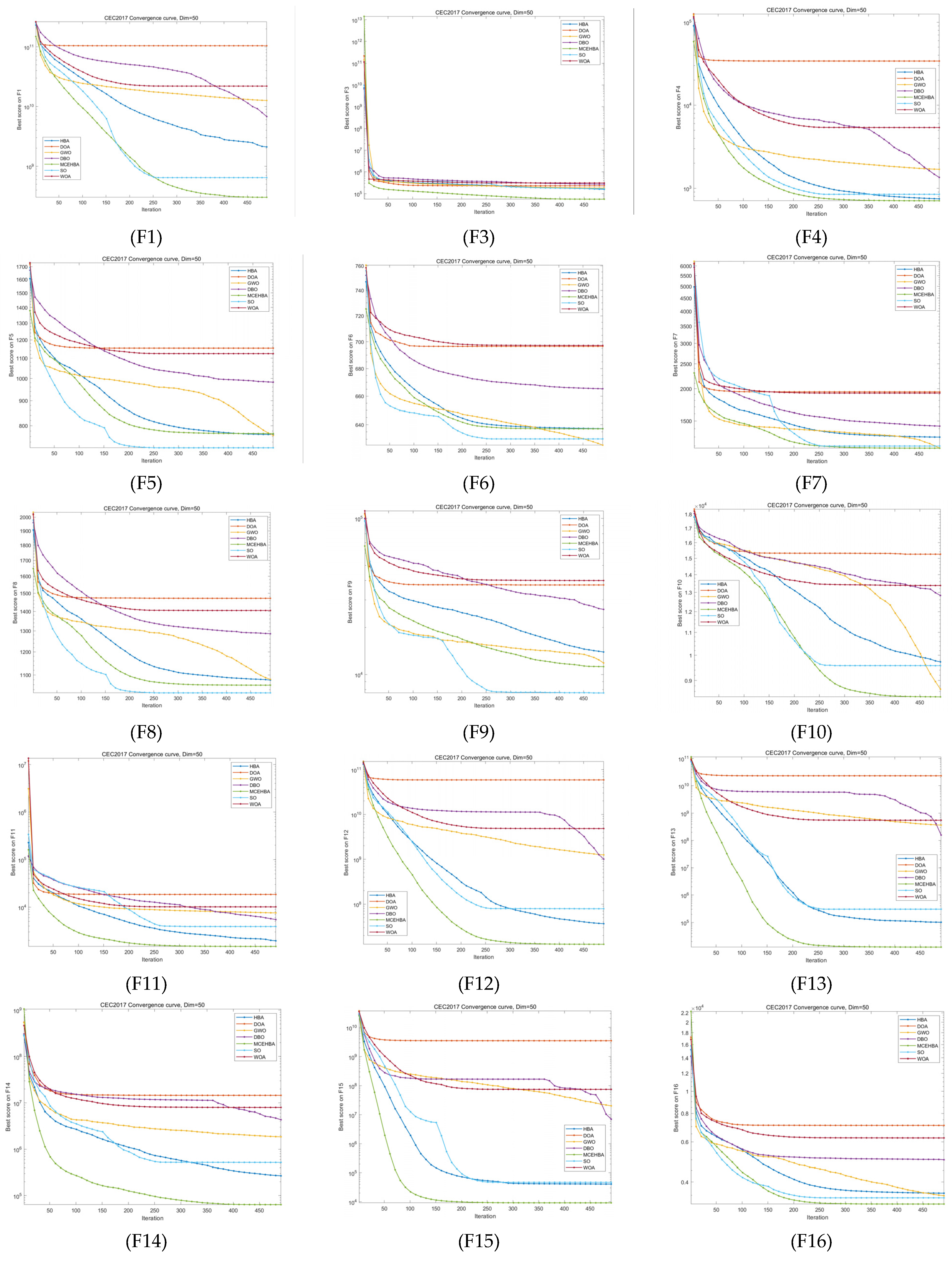
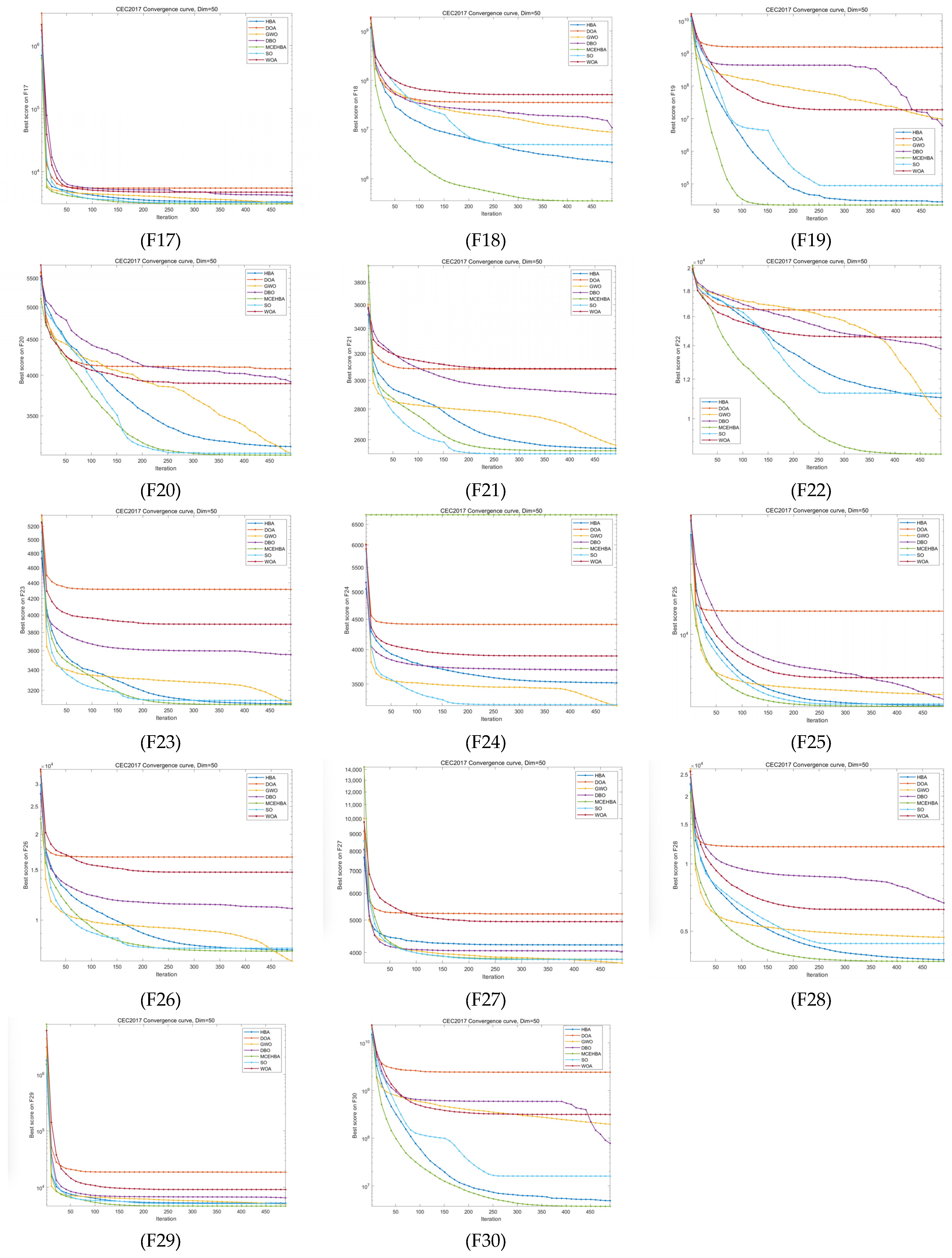
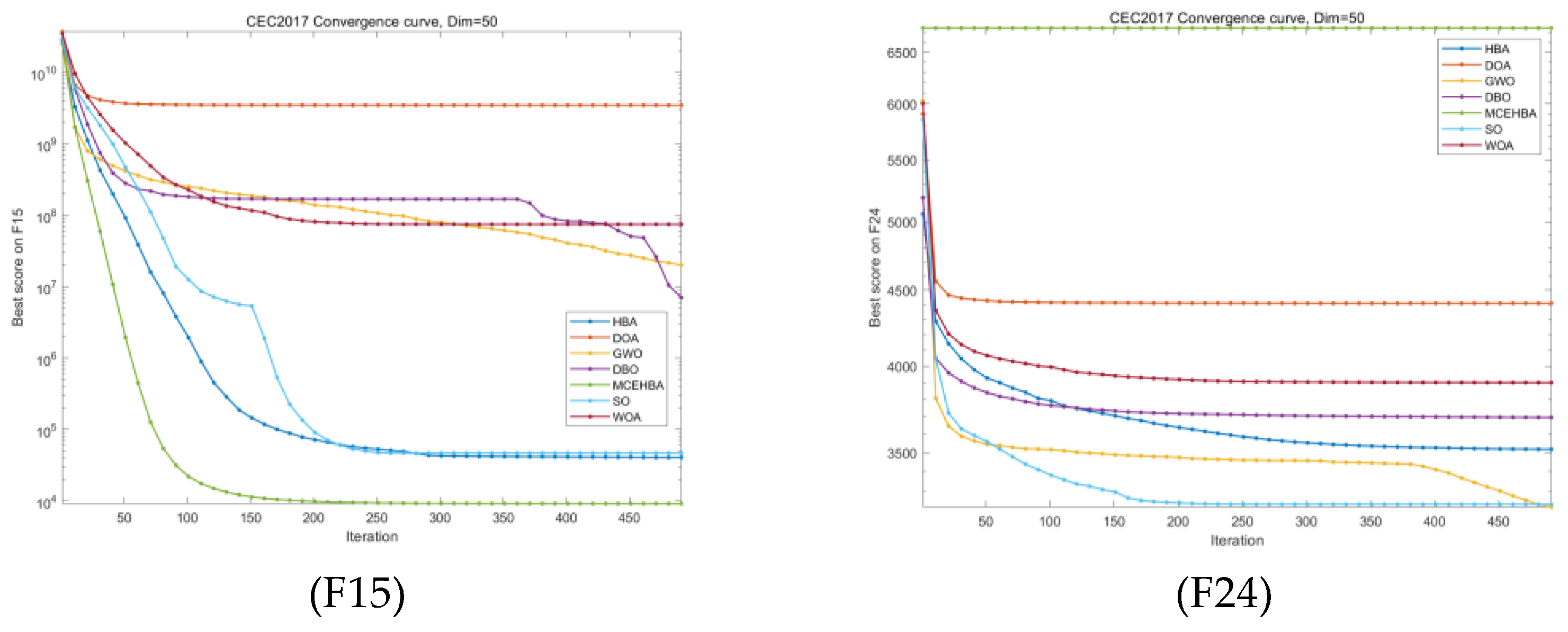
4.3. Comparison with Other Excellent Swarm Intelligence Algorithms
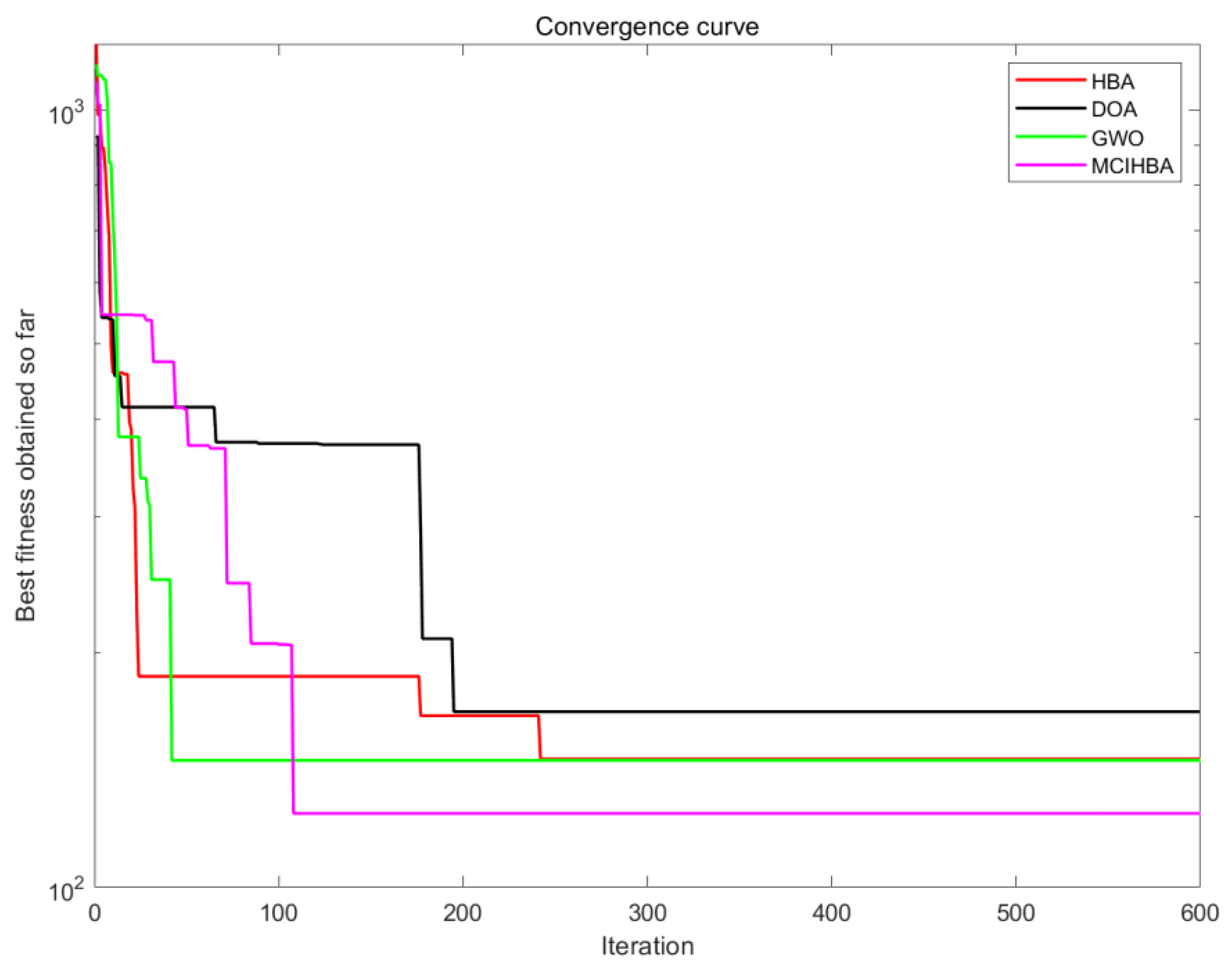
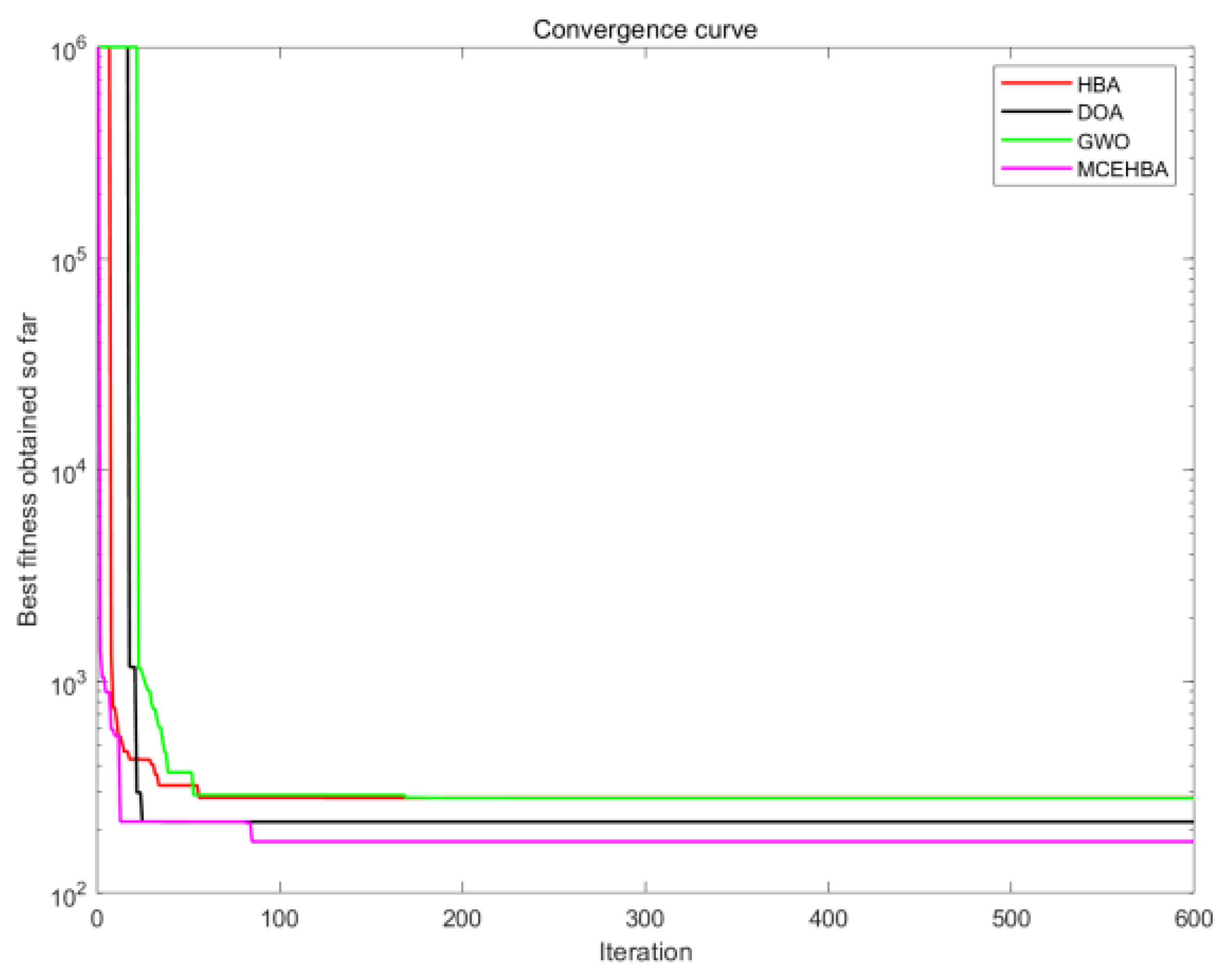
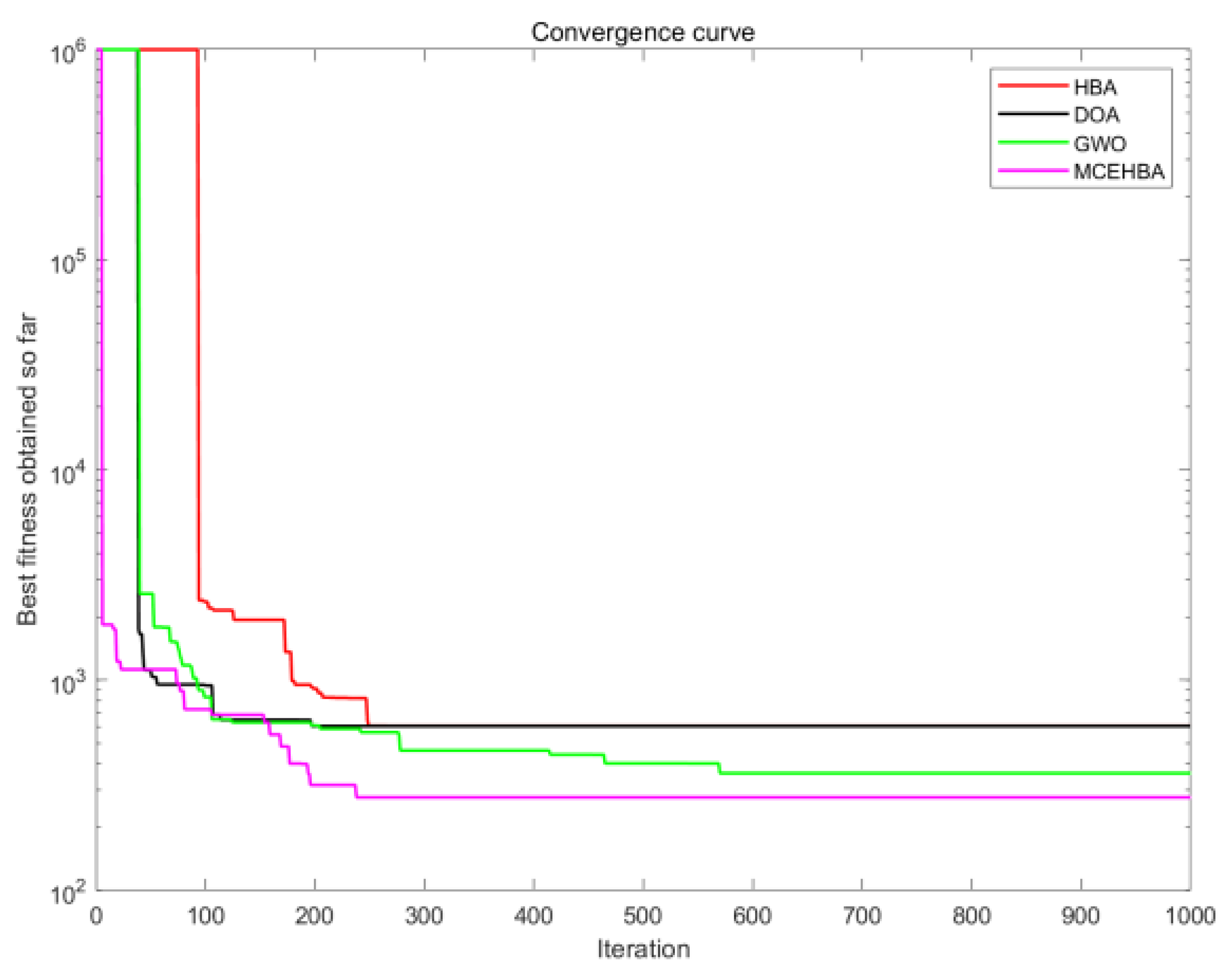
4.4. Convergence Analysis
4.5. Feldman Test
4.6. Engineering Applications
- (1)
- Welding beam design problem
- (2)
- Reducer design problem
- (3)
- Cantilever Beam Design Problem
5. Mobile Robot Path Planning Based on Grid Method
5.1. Procedure
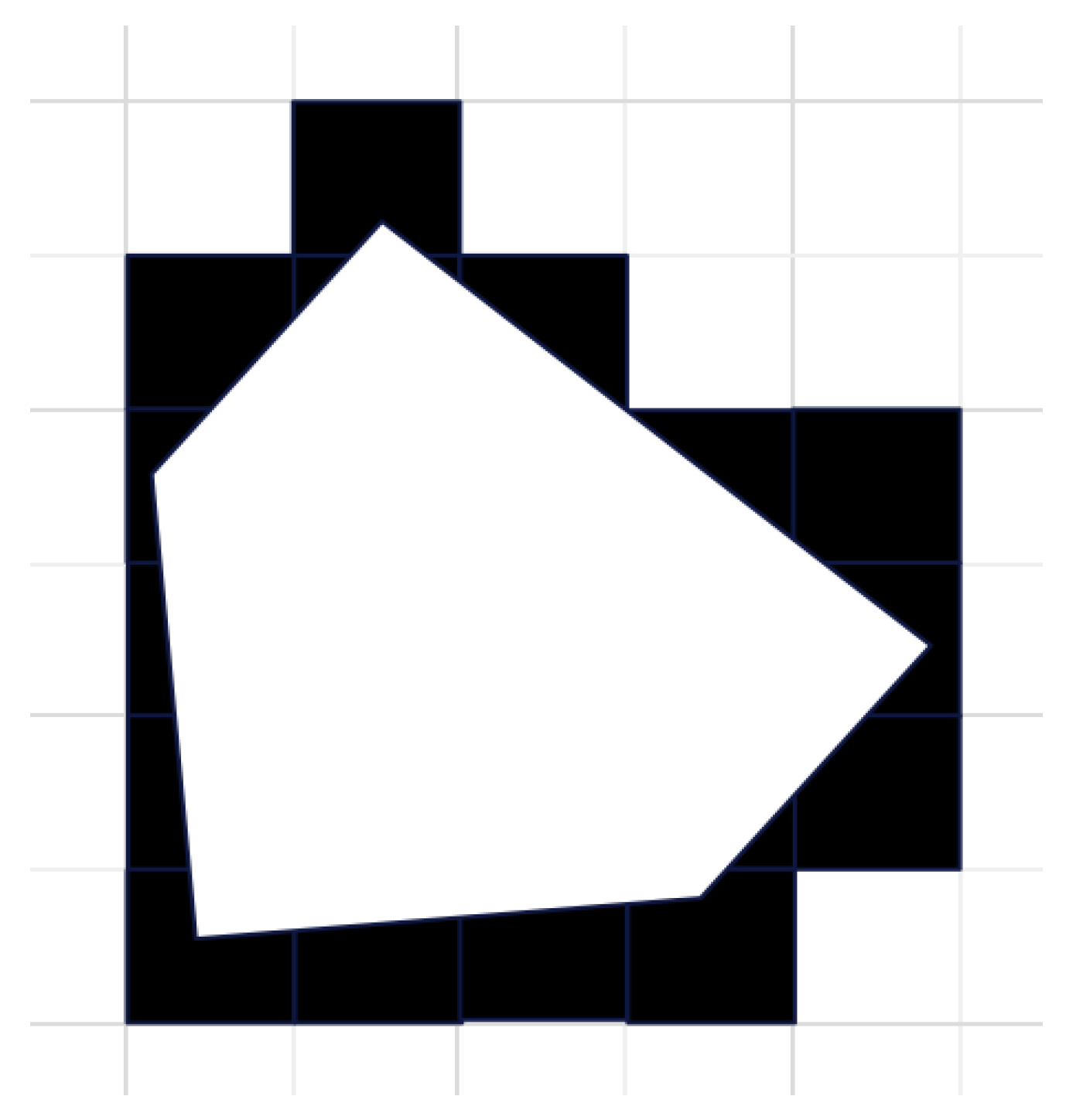
5.1.1. Generate Obstacle Field
5.1.2. Design of Objective Function Functions and Constraints
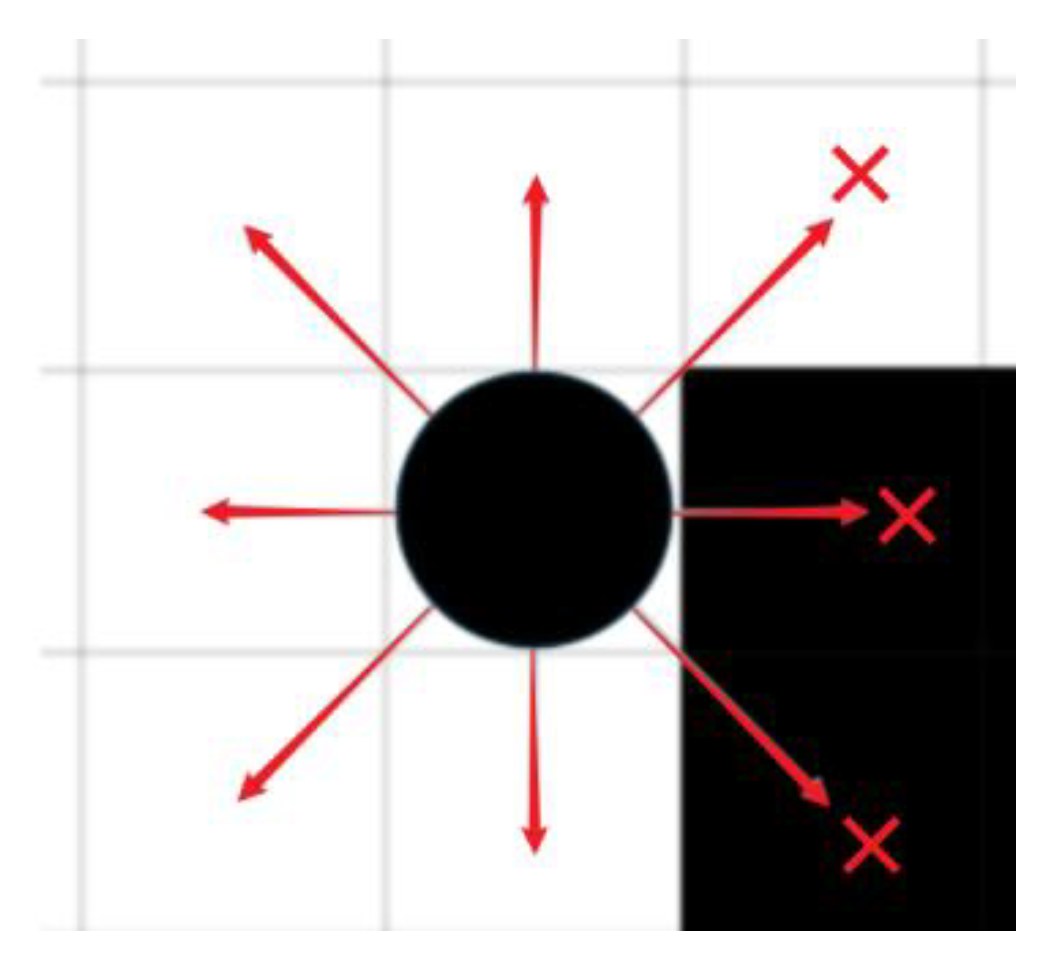
5.1.3. Improvement of Neighbourhood Search Strategies
5.2. Program Setting and Parameter Setting
5.3. Simulation Results and Analysis
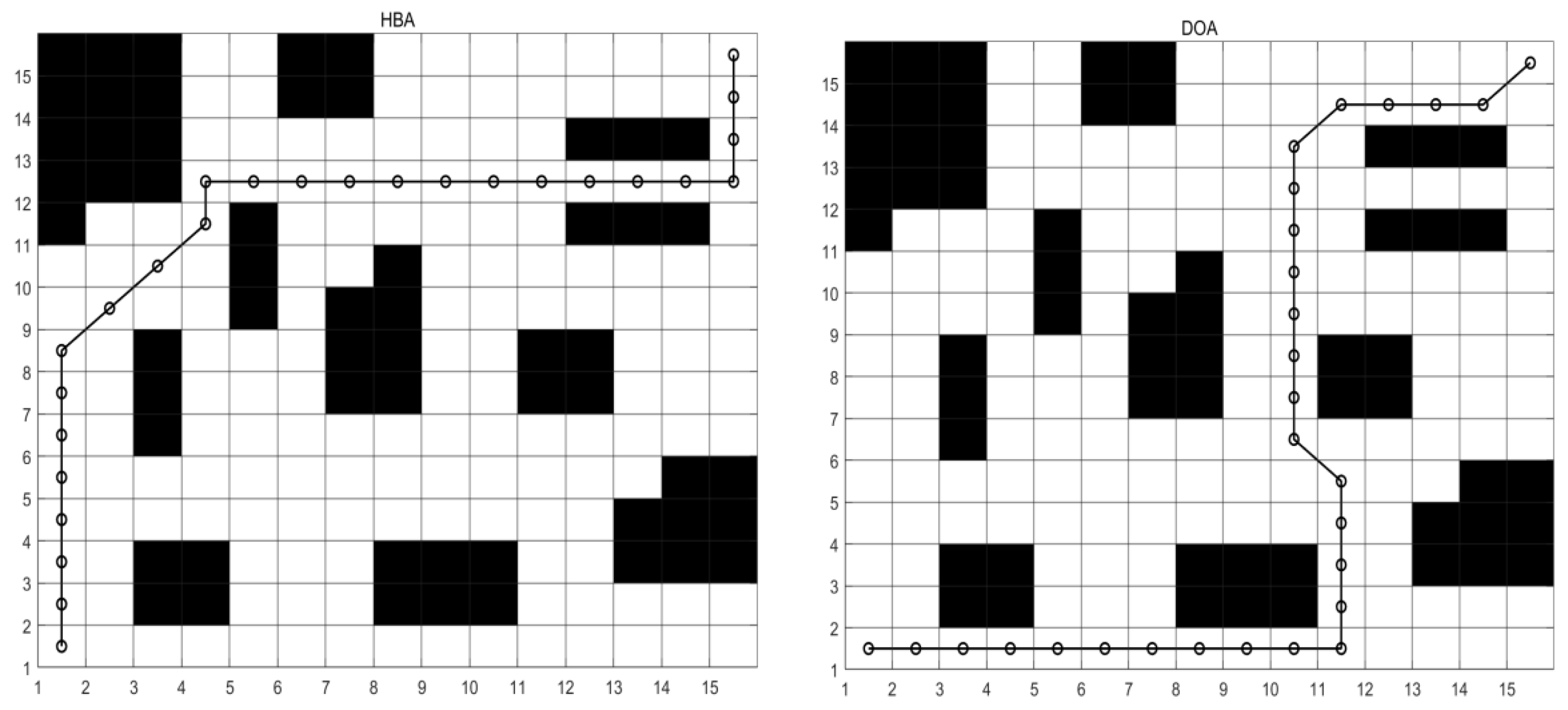
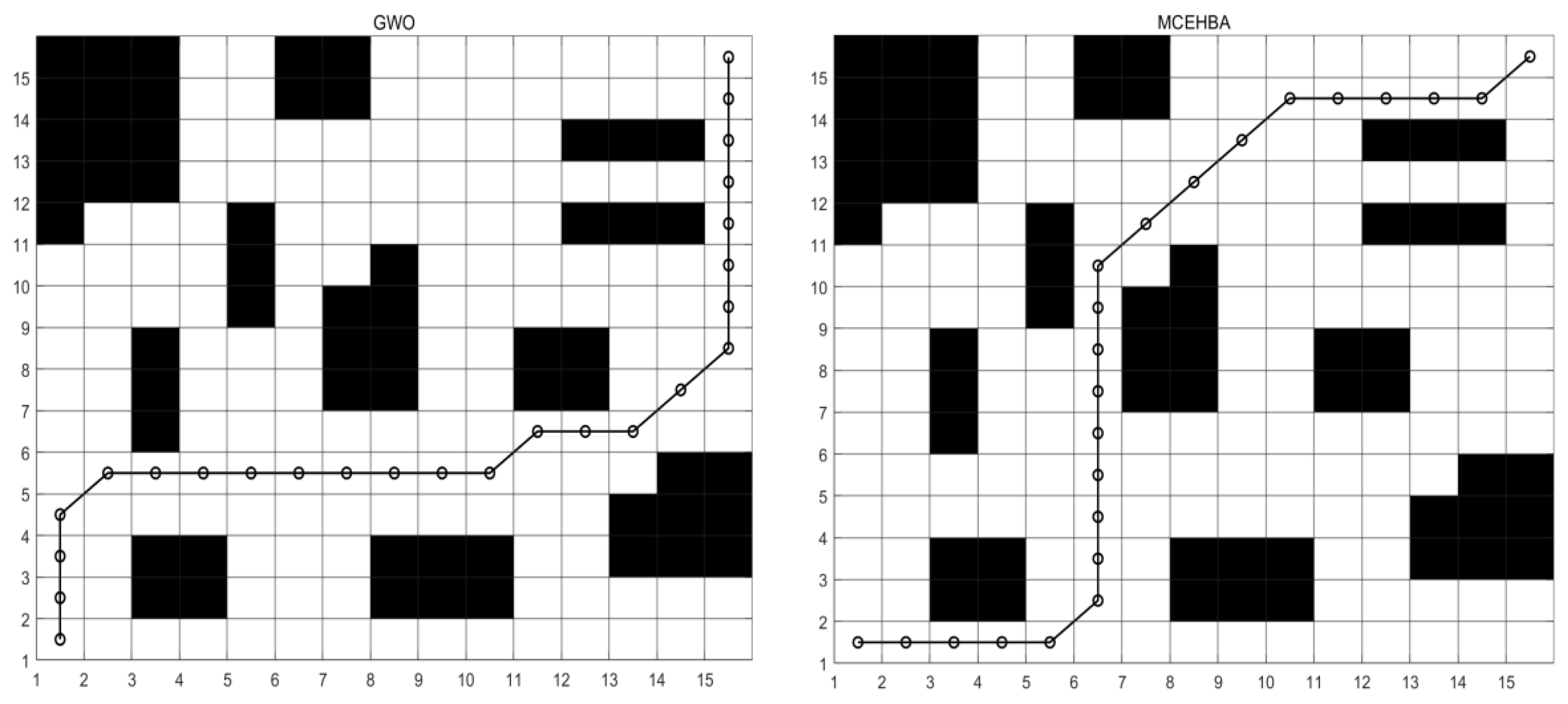
5.3.1. Analysis of Results for Map M1
5.3.2. Analysis of Results for Map M2
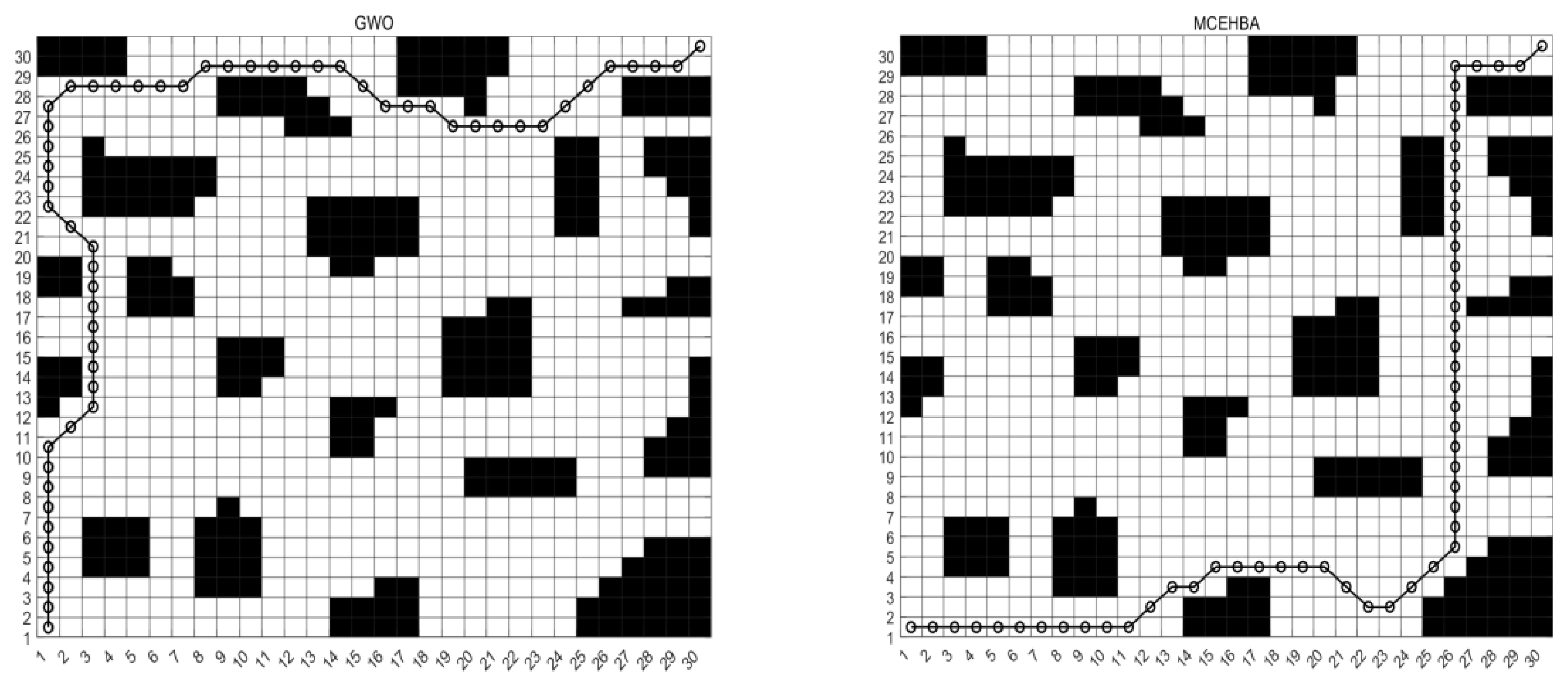
5.3.3. Analysis of Results for Map M3
6. Discussion
6.1. Experimental Result
6.2. Application to Engineering Problems
6.3. Experimental Analysis of Mobile Robot Path Planning
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Function | Algorithm | Mean | Std | Max | Min |
|---|---|---|---|---|---|
| F1 | HBA | 1.3862 × 106 | 4.8147 × 1012 | 1.1311 × 107 | 4.9457 × 104 |
| HBA Variant1 | 4.8878 × 107 | 8.0296 × 1015 | 4.8894 × 108 | 5.0715 × 106 | |
| HBA Variant2 | 4.0339 × 107 | 3.3164 × 1015 | 3.2462 × 108 | 6.1327 × 106 | |
| HBA Variant3 | 5.0328 × 107 | 4.1998 × 1015 | 3.3773 × 108 | 7.0629 × 106 | |
| HBA Variant4 | 9.1174 × 105 | 1.3859 × 1012 | 5.8414 × 106 | 3.8087 × 104 | |
| HBA Variant5 | 7.3168 × 105 | 8.2264 × 1011 | 4.2273 × 106 | 5.3006 × 104 | |
| F3 | HBA | 3.7048 × 104 | 9.0918 × 107 | 5.2058 × 104 | 2.0063 × 104 |
| HBA Variant1 | 4.8771 × 104 | 9.3261 × 107 | 6.3413 × 104 | 3.1881 × 104 | |
| HBA Variant2 | 5.0196 × 104 | 7.7317 × 107 | 6.8128 × 104 | 3.0939 × 104 | |
| HBA Variant3 | 4.4646 × 104 | 5.7147 × 107 | 6.0493 × 104 | 2.7099 × 104 | |
| HBA Variant4 | 6.5007 × 103 | 5.4666 × 106 | 1.1888 × 104 | 2.4813 × 103 | |
| HBA Variant5 | 6.9880 × 103 | 1.0537 × 107 | 1.6645 × 104 | 2.1950 × 103 | |
| F4 | HBA | 5.2316 × 102 | 1.3850 × 103 | 6.2472 × 102 | 4.6852 × 102 |
| HBA Variant1 | 5.4563 × 102 | 1.9361 × 103 | 6.6362 × 102 | 4.8365 × 102 | |
| HBA Variant2 | 5.3965 × 102 | 1.5247 × 103 | 6.1992 × 102 | 4.7020 × 102 | |
| HBA Variant3 | 5.4881 × 102 | 2.2237 × 103 | 7.0534 × 102 | 4.2635 × 102 | |
| HBA Variant4 | 5.2034 × 102 | 1.2148 × 103 | 6.0435 × 102 | 4.0503 × 102 | |
| HBA Variant5 | 5.1885 × 102 | 9.0008 × 102 | 5.8219 × 102 | 4.0139 × 102 | |
| F5 | HBA | 6.2384 × 102 | 4.9642 × 102 | 6.8025 × 102 | 5.7998 × 102 |
| HBA Variant1 | 6.4277 × 102 | 8.2536 × 102 | 6.9012 × 102 | 5.9075 × 102 | |
| HBA Variant2 | 6.4284 × 102 | 1.0954 × 103 | 7.3800 × 102 | 6.0166 × 102 | |
| HBA Variant3 | 6.5350 × 102 | 9.9217 × 102 | 7.5263 × 102 | 5.9910 × 102 | |
| HBA Variant4 | 6.3692 × 102 | 1.2028 × 103 | 7.1593 × 102 | 5.7404 × 102 | |
| HBA Variant5 | 6.3508 × 102 | 1.9502 × 103 | 7.6182 × 102 | 5.7465 × 102 | |
| F6 | HBA | 6.2329 × 102 | 1.0543 × 102 | 6.4516 × 102 | 6.0785 × 102 |
| HBA Variant1 | 6.2155 × 102 | 4.7340 × 101 | 6.3697 × 102 | 6.1053 × 102 | |
| HBA Variant2 | 6.2129 × 102 | 5.7471 × 101 | 6.3922 × 102 | 6.1061 × 102 | |
| HBA Variant3 | 6.1946 × 102 | 7.3767 × 101 | 6.3982 × 102 | 6.0672 × 102 | |
| HBA Variant4 | 6.1869 × 102 | 7.0832 × 101 | 6.4035 × 102 | 6.0391 × 102 | |
| HBA Variant5 | 6.1705 × 102 | 7.6460 × 101 | 6.3763 × 102 | 6.0541 × 102 | |
| F7 | HBA | 9.4520 × 102 | 6.4003 × 103 | 1.2714 × 103 | 8.4463 × 102 |
| HBA Variant1 | 9.4074 × 102 | 3.3671 × 103 | 1.1298 × 103 | 8.5869 × 102 | |
| HBA Variant2 | 9.5635 × 102 | 5.7762 × 103 | 1.2194 × 103 | 8.4625 × 102 | |
| HBA Variant3 | 9.4375 × 102 | 1.6664 × 103 | 1.0176 × 103 | 8.5138 × 102 | |
| HBA Variant4 | 9.1803 × 102 | 2.6011 × 103 | 1.0267 × 103 | 8.3085 × 102 | |
| HBA Variant5 | 9.0054 × 102 | 2.4875 × 103 | 1.0136 × 103 | 8.1588 × 102 | |
| F8 | HBA | 9.1245 × 102 | 5.4565 × 102 | 9.5539 × 102 | 8.6413 × 102 |
| HBA Variant1 | 9.1016 × 102 | 3.8984 × 102 | 9.4795 × 102 | 8.7267 × 102 | |
| HBA Variant2 | 9.1394 × 102 | 5.7920 × 102 | 9.8906 × 102 | 8.7454 × 102 | |
| HBA Variant3 | 9.1793 × 102 | 4.4043 × 102 | 9.7127 × 102 | 8.7245 × 102 | |
| HBA Variant4 | 9.1202 × 102 | 8.8778 × 102 | 9.8209 × 102 | 8.5786 × 102 | |
| HBA Variant5 | 9.1194 × 102 | 6.8054 × 102 | 9.7719 × 102 | 8.5808 × 102 | |
| F9 | HBA | 2.9927 × 103 | 6.4966 × 105 | 4.5387 × 103 | 1.5269 × 103 |
| HBA Variant1 | 3.4181 × 103 | 1.3978 × 106 | 6.3487 × 103 | 1.1017 × 103 | |
| HBA Variant2 | 3.7441 × 103 | 1.3693 × 106 | 6.0017 × 103 | 1.9450 × 103 | |
| HBA Variant3 | 3.8789 × 103 | 1.3828 × 106 | 5.8075 × 103 | 2.2791 × 103 | |
| HBA Variant4 | 3.3905 × 103 | 1.8256 × 106 | 6.8447 × 103 | 1.2144 × 103 | |
| HBA Variant5 | 2.4121 × 103 | 1.0466 × 106 | 5.5315 × 103 | 1.1435 × 103 | |
| F10 | HBA | 5.9393 × 103 | 9.5724 × 105 | 8.3012 × 103 | 3.7704 × 103 |
| HBA Variant1 | 5.8671 × 103 | 8.2237 × 105 | 7.5143 × 103 | 3.9979 × 103 | |
| HBA Variant2 | 7.3379 × 103 | 1.4038 × 106 | 9.8564 × 103 | 4.9224 × 103 | |
| HBA Variant3 | 5.8188 × 103 | 8.1045 × 105 | 7.5033 × 103 | 4.1155 × 103 | |
| HBA Variant4 | 4.7215 × 103 | 5.3222 × 105 | 7.1113 × 103 | 3.4016 × 103 | |
| HBA Variant5 | 4.8939 × 103 | 4.7606 × 105 | 6.2447 × 103 | 3.0554 × 103 | |
| F11 | HBA | 1.3115 × 103 | 5.7245 × 103 | 1.4789 × 103 | 1.1946 × 103 |
| HBA Variant1 | 1.3585 × 103 | 7.7381 × 103 | 1.6103 × 103 | 1.2321 × 103 | |
| HBA Variant2 | 1.3467 × 103 | 5.6262 × 103 | 1.5377 × 103 | 1.2325 × 103 | |
| HBA Variant3 | 1.2577 × 103 | 1.9689 × 103 | 1.3783 × 103 | 1.1653 × 103 | |
| HBA Variant4 | 1.2158 × 103 | 1.6123 × 103 | 1.2944 × 103 | 1.1444 × 103 | |
| HBA Variant5 | 1.2134 × 103 | 1.5446 × 103 | 1.3017 × 103 | 1.1377 × 103 | |
| F12 | HBA | 1.2043 × 106 | 1.5928 × 1012 | 5.4333 × 106 | 1.7308 × 105 |
| HBA Variant1 | 6.8348 × 106 | 4.9101 × 1014 | 1.2371 × 108 | 2.2405 × 105 | |
| HBA Variant2 | 3.3645 × 106 | 6.3026 × 1012 | 1.0333 × 107 | 2.5984 × 105 | |
| HBA Variant3 | 2.4005 × 106 | 2.9158 × 1012 | 6.7546 × 106 | 2.6643 × 105 | |
| HBA Variant4 | 4.6747 × 105 | 1.7247 × 1011 | 1.5554 × 106 | 1.0682 × 104 | |
| HBA Variant5 | 5.3736 × 105 | 5.9009 × 1011 | 3.7682 × 106 | 5.5324 × 104 | |
| F13 | HBA | 6.4088 × 104 | 4.3024 × 109 | 3.1612 × 105 | 7.1596 × 103 |
| HBA Variant1 | 6.7227 × 104 | 4.4099 × 109 | 2.4106 × 105 | 1.0873 × 104 | |
| HBA Variant2 | 2.1013 × 105 | 6.8448 × 1011 | 4.5757 × 106 | 4.7554 × 103 | |
| HBA Variant3 | 1.5114 × 104 | 2.1075 × 108 | 6.3275 × 104 | 2.4979 × 103 | |
| HBA Variant4 | 7.4475 × 103 | 4.6140 × 107 | 2.6650 × 104 | 1.7433 × 103 | |
| HBA Variant5 | 9.4799 × 103 | 7.2872 × 107 | 3.6726 × 104 | 1.8155 × 103 | |
| F14 | HBA | 1.1243 × 105 | 9.5711 × 1010 | 1.6729 × 106 | 2.5775 × 103 |
| HBA Variant1 | 3.0269 × 104 | 5.1048 × 108 | 9.5841 × 104 | 3.8666 × 103 | |
| HBA Variant2 | 6.7335 × 104 | 4.5896 × 109 | 2.5758 × 105 | 2.2304 × 103 | |
| HBA Variant3 | 4.5414 × 104 | 2.5430 × 109 | 2.2691 × 105 | 2.3393 × 103 | |
| HBA Variant4 | 1.9726 × 103 | 1.5684 × 106 | 8.5177 × 103 | 1.5848 × 103 | |
| HBA Variant5 | 2.9346 × 103 | 8.9711 × 106 | 1.3585 × 104 | 1.5480 × 103 | |
| F15 | HBA | 2.5842 × 104 | 5.7854 × 108 | 9.4914 × 104 | 2.1140 × 103 |
| HBA Variant1 | 2.7514 × 104 | 2.1072 × 109 | 2.2660 × 105 | 3.5501 × 103 | |
| HBA Variant2 | 1.8958 × 104 | 5.0565 × 108 | 1.0730 × 105 | 2.0780 × 103 | |
| HBA Variant3 | 3.7794 × 103 | 8.0703 × 106 | 1.1690 × 104 | 1.6300 × 103 | |
| HBA Variant4 | 5.8591 × 103 | 5.7937 × 107 | 4.0340 × 104 | 1.7376 × 103 | |
| HBA Variant5 | 5.0200 × 103 | 4.3765 × 107 | 2.9498 × 104 | 1.7804 × 103 | |
| F16 | HBA | 2.6382 × 103 | 6.8473 × 104 | 3.1965 × 103 | 2.1707 × 103 |
| HBA Variant1 | 2.7042 × 103 | 7.1696 × 104 | 3.1817 × 103 | 2.1106 × 103 | |
| HBA Variant2 | 2.8302 × 103 | 1.9730 × 105 | 3.6613 × 103 | 1.8779 × 103 | |
| HBA Variant3 | 2.7613 × 103 | 8.6274 × 104 | 3.4019 × 103 | 2.1135 × 103 | |
| HBA Variant4 | 2.5731 × 103 | 1.0722 × 105 | 3.3434 × 103 | 1.8458 × 103 | |
| HBA Variant5 | 2.5246 × 103 | 9.6061 × 104 | 3.4188 × 103 | 2.0343 × 103 | |
| F17 | HBA | 2.3734 × 103 | 5.1266 × 104 | 2.8894 × 103 | 1.8822 × 103 |
| HBA Variant1 | 2.2832 × 103 | 5.9338 × 104 | 2.6967 × 103 | 1.8164 × 103 | |
| HBA Variant2 | 2.3493 × 103 | 3.0839 × 104 | 2.7949 × 103 | 2.0998 × 103 | |
| HBA Variant3 | 2.1143 × 103 | 3.1636 × 104 | 2.4514 × 103 | 1.8072 × 103 | |
| HBA Variant4 | 2.0742 × 103 | 2.9886 × 104 | 2.4795 × 103 | 1.7934 × 103 | |
| HBA Variant5 | 2.0522 × 103 | 3.8103 × 104 | 2.4773 × 103 | 1.7818 × 103 | |
| F18 | HBA | 4.8340 × 105 | 1.7652 × 1011 | 1.9252 × 106 | 4.3467 × 104 |
| HBA Variant1 | 7.0416 × 105 | 3.9114 × 1011 | 2.2578 × 106 | 1.1225 × 105 | |
| HBA Variant2 | 6.7983 × 105 | 5.6122 × 1011 | 2.8533 × 106 | 1.2226 × 105 | |
| HBA Variant3 | 5.4733 × 105 | 2.4949 × 1011 | 2.2294 × 106 | 9.9536 × 104 | |
| HBA Variant4 | 8.1649 × 104 | 9.7781 × 109 | 5.5578 × 105 | 2.4019 × 104 | |
| HBA Variant5 | 5.7601 × 104 | 1.0501 × 109 | 1.2279 × 105 | 1.0667 × 104 | |
| F19 | HBA | 9.2271 × 103 | 7.0112 × 107 | 3.6353 × 104 | 2.0802 × 103 |
| HBA Variant1 | 1.3638 × 104 | 2.0499 × 108 | 5.6795 × 104 | 2.0454 × 103 | |
| HBA Variant2 | 8.1209 × 103 | 4.1089 × 107 | 2.8318 × 104 | 2.1483 × 103 | |
| HBA Variant3 | 7.1488 × 103 | 5.2206 × 107 | 2.9141 × 104 | 2.0006 × 103 | |
| HBA Variant4 | 7.0894 × 103 | 1.8557 × 107 | 1.9631 × 104 | 2.3233 × 103 | |
| HBA Variant5 | 5.7822 × 103 | 1.7429 × 107 | 2.1258 × 104 | 1.9565 × 103 | |
| F20 | HBA | 2.5873 × 103 | 4.0495 × 104 | 2.9609 × 103 | 2.1565 × 103 |
| HBA Variant1 | 2.5826 × 103 | 6.4201 × 104 | 3.2215 × 103 | 2.2328 × 103 | |
| HBA Variant2 | 2.6036 × 103 | 6.8734 × 104 | 3.2394 × 103 | 2.2626 × 103 | |
| HBA Variant3 | 2.5301 × 103 | 5.2664 × 104 | 3.0441 × 103 | 2.1717 × 103 | |
| HBA Variant4 | 2.4494 × 103 | 2.6022 × 104 | 2.7886 × 103 | 2.1900 × 103 | |
| HBA Variant5 | 2.3716 × 103 | 2.3915 × 104 | 2.7345 × 103 | 2.1297 × 103 | |
| F21 | HBA | 2.4151 × 103 | 8.9075 × 102 | 2.4915 × 103 | 2.3705 × 103 |
| HBA Variant1 | 2.4129 × 103 | 1.1507 × 103 | 2.5017 × 103 | 2.3514 × 103 | |
| HBA Variant2 | 2.4338 × 103 | 1.0399 × 103 | 2.5019 × 103 | 2.3771 × 103 | |
| HBA Variant3 | 2.4171 × 103 | 7.1525 × 102 | 2.4723 × 103 | 2.3654 × 103 | |
| HBA Variant4 | 2.4060 × 103 | 1.9445 × 103 | 2.4567 × 103 | 2.2119 × 103 | |
| HBA Variant5 | 2.4001 × 103 | 2.1691 × 103 | 2.4604 × 103 | 2.2049 × 103 | |
| F22 | HBA | 4.3976 × 103 | 7.0546 × 106 | 9.6617 × 103 | 2.3036 × 103 |
| HBA Variant1 | 4.6452 × 103 | 7.5198 × 106 | 1.0017 × 104 | 2.3234 × 103 | |
| HBA Variant2 | 5.3374 × 103 | 6.3039 × 106 | 9.1000 × 103 | 2.3193 × 103 | |
| HBA Variant3 | 2.3491 × 103 | 2.5846 × 103 | 2.5795 × 103 | 2.3175 × 103 | |
| HBA Variant4 | 2.5636 × 103 | 9.0240 × 105 | 6.2373 × 103 | 2.3031 × 103 | |
| HBA Variant5 | 2.3100 × 103 | 1.9024 × 101 | 2.3224 × 103 | 2.3040 × 103 | |
| F23 | HBA | 2.8036 × 103 | 2.7949 × 103 | 2.9676 × 103 | 2.7197 × 103 |
| HBA Variant1 | 2.7958 × 103 | 3.0289 × 103 | 2.9880 × 103 | 2.7296 × 103 | |
| HBA Variant2 | 2.8103 × 103 | 1.9534 × 103 | 2.9221 × 103 | 2.7305 × 103 | |
| HBA Variant3 | 2.7762 × 103 | 1.0173 × 103 | 2.8377 × 103 | 2.7135 × 103 | |
| HBA Variant4 | 2.7923 × 103 | 2.3161 × 103 | 2.8983 × 103 | 2.7143 × 103 | |
| HBA Variant5 | 2.8092 × 103 | 3.3510 × 103 | 2.9459 × 103 | 2.7040 × 103 | |
| F24 | HBA | 3.1134 × 103 | 4.6835 × 104 | 3.6330 × 103 | 2.9171 × 103 |
| HBA Variant1 | 3.0394 × 103 | 3.0111 × 104 | 3.5665 × 103 | 2.8937 × 103 | |
| HBA Variant2 | 4.6886 × 103 | 8.5570 × 10−25 | 4.6886 × 103 | 4.6886 × 103 | |
| HBA Variant3 | 4.6886 × 103 | 8.5570 × 10−25 | 4.6886 × 103 | 4.6886 × 103 | |
| HBA Variant4 | 4.6886 × 103 | 8.5570 × 10−25 | 4.6886 × 103 | 4.6886 × 103 | |
| HBA Variant5 | 4.6886 × 103 | 8.5570 × 10−25 | 4.6886 × 103 | 4.6886 × 103 | |
| F25 | HBA | 2.9225 × 103 | 4.1271 × 102 | 2.9615 × 103 | 2.8866 × 103 |
| HBA Variant1 | 2.9364 × 103 | 6.6324 × 102 | 3.0001 × 103 | 2.9014 × 103 | |
| HBA Variant2 | 2.9328 × 103 | 8.2271 × 102 | 2.9966 × 103 | 2.8914 × 103 | |
| HBA Variant3 | 2.9496 × 103 | 7.8584 × 102 | 2.9949 × 103 | 2.9002 × 103 | |
| HBA Variant4 | 2.9063 × 103 | 2.6469 × 102 | 2.9519 × 103 | 2.8843 × 103 | |
| HBA Variant5 | 2.9152 × 103 | 6.1532 × 102 | 2.9763 × 103 | 2.8862 × 103 | |
| F26 | HBA | 4.6724 × 103 | 9.7823 × 105 | 6.2253 × 103 | 2.8146 × 103 |
| HBA Variant1 | 4.8338 × 103 | 7.4366 × 105 | 6.3587 × 103 | 2.9037 × 103 | |
| HBA Variant2 | 2.4117 × 104 | 1.2322 × 10−22 | 2.4117 × 104 | 2.4117 × 104 | |
| HBA Variant3 | 4.7731 × 103 | 1.2321 × 106 | 7.0976 × 103 | 3.0021 × 103 | |
| HBA Variant4 | 4.6017 × 103 | 2.0687 × 106 | 7.0404 × 103 | 2.8131 × 103 | |
| HBA Variant5 | 3.9026 × 103 | 1.3160 × 106 | 6.0779 × 103 | 2.8174 × 103 | |
| F27 | HBA | 3.3714 × 103 | 2.6669 × 104 | 3.8894 × 103 | 3.2263 × 103 |
| HBA Variant1 | 3.4460 × 103 | 5.9532 × 104 | 4.4299 × 103 | 3.2246 × 103 | |
| HBA Variant2 | 3.2997 × 103 | 1.2106 × 104 | 3.5876 × 103 | 3.1987 × 103 | |
| HBA Variant3 | 3.2843 × 103 | 1.0950 × 103 | 3.3657 × 103 | 3.2212 × 103 | |
| HBA Variant4 | 3.2792 × 103 | 8.2332 × 102 | 3.3409 × 103 | 3.2285 × 103 | |
| HBA Variant5 | 3.2785 × 103 | 3.1194 × 103 | 3.5381 × 103 | 3.2105 × 103 | |
| F28 | HBA | 3.2870 × 103 | 1.6450 × 103 | 3.4106 × 103 | 3.2216 × 103 |
| HBA Variant1 | 3.3152 × 103 | 1.5978 × 103 | 3.4204 × 103 | 3.2261 × 103 | |
| HBA Variant2 | 3.3107 × 103 | 1.0332 × 103 | 3.3848 × 103 | 3.2335 × 103 | |
| HBA Variant3 | 3.3304 × 103 | 1.9616 × 103 | 3.4000 × 103 | 3.2391 × 103 | |
| HBA Variant4 | 3.2792 × 103 | 1.5306 × 103 | 3.4003 × 103 | 3.2088 × 103 | |
| HBA Variant5 | 3.2645 × 103 | 1.1055 × 103 | 3.3257 × 103 | 3.2088 × 103 | |
| F29 | HBA | 4.3643 × 103 | 1.7400 × 106 | 1.0994 × 104 | 3.5567 × 103 |
| HBA Variant1 | 4.1885 × 103 | 1.5076 × 105 | 5.2167 × 103 | 3.6182 × 103 | |
| HBA Variant2 | 4.0393 × 103 | 1.4524 × 105 | 4.9735 × 103 | 3.5628 × 103 | |
| HBA Variant3 | 3.9796 × 103 | 7.4547 × 104 | 4.7002 × 103 | 3.4926 × 103 | |
| HBA Variant4 | 3.7984 × 103 | 4.6123 × 104 | 4.2896 × 103 | 3.4504 × 103 | |
| HBA Variant5 | 3.8086 × 103 | 3.5469 × 104 | 4.3234 × 103 | 3.4742 × 103 | |
| F30 | HBA | 5.4288 × 104 | 1.2039 × 1010 | 6.2052 × 105 | 9.9590 × 103 |
| HBA Variant1 | 1.4352 × 105 | 8.2639 × 1010 | 1.5853 × 106 | 1.7359 × 104 | |
| HBA Variant2 | 4.8320 × 104 | 1.4924 × 109 | 1.7983 × 105 | 9.6910 × 103 | |
| HBA Variant3 | 8.4822 × 104 | 5.4871 × 109 | 2.7330 × 105 | 9.7172 × 103 | |
| HBA Variant4 | 2.0187 × 104 | 9.6273 × 107 | 5.3792 × 104 | 8.3677 × 103 | |
| HBA Variant5 | 1.6601 × 104 | 3.9915 × 107 | 3.2941 × 104 | 7.9474 × 103 |
| Function | Algorithm | Mean | Std | Max | Min |
|---|---|---|---|---|---|
| F1 | HBA | 1.5420 × 109 | 2.9319 × 1018 | 7.9273 × 109 | 9.2268 × 107 |
| HBA Variant1 | 4.3994 × 109 | 7.6230 × 1018 | 1.5690 × 1010 | 1.0936 × 109 | |
| HBA Variant2 | 4.0562 × 109 | 5.7323 × 1018 | 9.8912 × 109 | 8.4821 × 108 | |
| HBA Variant3 | 5.1972 × 109 | 6.9166 × 1018 | 1.1306 × 1010 | 1.1365 × 109 | |
| HBA Variant4 | 4.4176 × 108 | 1.3714 × 1017 | 1.4332 × 109 | 5.2124 × 107 | |
| HBA Variant5 | 3.0458 × 108 | 1.5907 × 1017 | 1.8927 × 109 | 3.9061 × 107 | |
| F3 | HBA | 1.4753 × 105 | 7.0925 × 108 | 2.2454 × 105 | 1.0379 × 105 |
| HBA Variant1 | 1.6343 × 105 | 8.3193 × 108 | 2.3151 × 105 | 1.1614 × 105 | |
| HBA Variant2 | 1.5175 × 105 | 9.5785 × 108 | 2.4312 × 105 | 8.8770 × 104 | |
| HBA Variant3 | 1.4264 × 105 | 5.2094 × 108 | 1.8500 × 105 | 9.4709 × 104 | |
| HBA Variant4 | 5.9437 × 104 | 1.7746 × 108 | 8.4280 × 104 | 3.0618 × 104 | |
| HBA Variant5 | 5.5989 × 104 | 1.0850 × 108 | 7.2889 × 104 | 3.5091 × 104 | |
| F4 | HBA | 7.7198 × 102 | 2.0837 × 104 | 1.3419 × 103 | 6.0247 × 102 |
| HBA Variant1 | 1.0104 × 103 | 1.3296 × 105 | 2.2274 × 103 | 7.1127 × 102 | |
| HBA Variant2 | 9.8891 × 102 | 8.3409 × 104 | 2.0985 × 103 | 6.9623 × 102 | |
| HBA Variant3 | 1.2230 × 103 | 2.6035 × 105 | 3.0537 × 103 | 7.5173 × 102 | |
| HBA Variant4 | 7.3932 × 102 | 8.9809 × 103 | 9.7770 × 102 | 5.4338 × 102 | |
| HBA Variant5 | 7.5184 × 102 | 1.1592 × 104 | 1.0542 × 103 | 5.4453 × 102 | |
| F5 | HBA | 7.6510 × 102 | 2.0036 × 103 | 8.5816 × 102 | 6.6816 × 102 |
| HBA Variant1 | 8.2566 × 102 | 1.7193 × 103 | 8.8534 × 102 | 7.0449 × 102 | |
| HBA Variant2 | 8.2287 × 102 | 9.0853 × 102 | 9.0802 × 102 | 7.6766 × 102 | |
| HBA Variant3 | 8.0607 × 102 | 1.8046 × 103 | 9.0061 × 102 | 7.0756 × 102 | |
| HBA Variant4 | 7.7148 × 102 | 9.6918 × 102 | 8.2090 × 102 | 7.1495 × 102 | |
| HBA Variant5 | 7.7220 × 102 | 2.1177 × 103 | 8.4962 × 102 | 6.6483 × 102 | |
| F6 | HBA | 6.3560 × 102 | 7.7635 × 101 | 6.5176 × 102 | 6.2020 × 102 |
| HBA Variant1 | 6.3521 × 102 | 7.4970 × 101 | 6.5313 × 102 | 6.1879 × 102 | |
| HBA Variant2 | 6.3863 × 102 | 6.7670 × 101 | 6.5881 × 102 | 6.1851 × 102 | |
| HBA Variant3 | 6.4141 × 102 | 1.3547 × 102 | 6.6539 × 102 | 6.2207 × 102 | |
| HBA Variant4 | 6.3937 × 102 | 2.0099 × 102 | 6.6938 × 102 | 6.1710 × 102 | |
| HBA Variant5 | 6.3457 × 102 | 6.8766 × 101 | 6.5506 × 102 | 6.2216 × 102 | |
| F7 | HBA | 1.2864 × 103 | 1.3353 × 104 | 1.4854 × 103 | 1.0840 × 103 |
| HBA Variant1 | 1.3178 × 103 | 1.3195 × 104 | 1.4863 × 103 | 1.0658 × 103 | |
| HBA Variant2 | 1.3133 × 103 | 1.1777 × 104 | 1.5370 × 103 | 1.1239 × 103 | |
| HBA Variant3 | 1.2948 × 103 | 1.4598 × 104 | 1.6446 × 103 | 1.0943 × 103 | |
| HBA Variant4 | 1.2080 × 103 | 6.5671 × 103 | 1.4140 × 103 | 1.0325 × 103 | |
| HBA Variant5 | 1.1949 × 103 | 8.0008 × 103 | 1.3444 × 103 | 1.0191 × 103 | |
| F8 | HBA | 1.0802 × 103 | 1.7468 × 103 | 1.1971 × 103 | 1.0087 × 103 |
| HBA Variant1 | 1.1228 × 103 | 2.0112 × 103 | 1.2130 × 103 | 1.0288 × 103 | |
| HBA Variant2 | 1.1278 × 103 | 2.7601 × 103 | 1.2709 × 103 | 1.0460 × 103 | |
| HBA Variant3 | 1.1109 × 103 | 1.8336 × 103 | 1.2031 × 103 | 1.0142 × 103 | |
| HBA Variant4 | 1.0775 × 103 | 2.5188 × 103 | 1.2244 × 103 | 9.7147 × 102 | |
| HBA Variant5 | 1.0529 × 103 | 2.1677 × 103 | 1.1424 × 103 | 9.2712 × 102 | |
| F9 | HBA | 1.4373 × 104 | 3.8445 × 107 | 3.7539 × 104 | 7.0875 × 103 |
| HBA Variant1 | 1.6236 × 104 | 2.6071 × 107 | 2.5698 × 104 | 5.9126 × 103 | |
| HBA Variant2 | 1.6445 × 104 | 4.1049 × 107 | 3.1185 × 104 | 4.8276 × 103 | |
| HBA Variant3 | 1.6441 × 104 | 2.0685 × 107 | 2.4615 × 104 | 7.3867 × 103 | |
| HBA Variant4 | 1.1794 × 104 | 3.3485 × 107 | 2.9591 × 104 | 4.2652 × 103 | |
| HBA Variant5 | 1.1379 × 104 | 2.0399 × 107 | 2.2884 × 104 | 4.7137 × 103 | |
| F10 | HBA | 9.5957 × 103 | 4.2257 × 106 | 1.5352 × 104 | 6.7203 × 103 |
| HBA Variant1 | 1.0738 × 104 | 3.6324 × 106 | 1.4632 × 104 | 8.1139 × 103 | |
| HBA Variant2 | 1.0524 × 104 | 2.8773 × 106 | 1.4944 × 104 | 8.0319 × 103 | |
| HBA Variant3 | 1.0225 × 104 | 2.0784 × 106 | 1.3294 × 104 | 7.7728 × 103 | |
| HBA Variant4 | 8.5074 × 103 | 1.2849 × 106 | 1.0628 × 104 | 6.1257 × 103 | |
| HBA Variant5 | 8.1310 × 103 | 1.3567 × 106 | 1.0104 × 104 | 6.2622 × 103 | |
| F11 | HBA | 1.6647 × 103 | 3.5324 × 104 | 2.1881 × 103 | 1.4236 × 103 |
| HBA Variant1 | 2.3969 × 103 | 6.3243 × 105 | 4.5283 × 103 | 1.5908 × 103 | |
| HBA Variant2 | 2.6247 × 103 | 8.3169 × 105 | 4.9510 × 103 | 1.6606 × 103 | |
| HBA Variant3 | 2.6781 × 103 | 9.8280 × 105 | 4.6356 × 103 | 1.5248 × 103 | |
| HBA Variant4 | 1.4810 × 103 | 1.3372 × 104 | 1.8681 × 103 | 1.3237 × 103 | |
| HBA Variant5 | 1.4753 × 103 | 1.0159 × 104 | 1.6648 × 103 | 1.3264 × 103 | |
| F12 | HBA | 2.7615 × 107 | 6.0681 × 1014 | 1.3201 × 108 | 4.4241 × 106 |
| HBA Variant1 | 9.1168 × 107 | 8.8000 × 1015 | 5.1703 × 108 | 2.0054 × 107 | |
| HBA Variant2 | 8.2548 × 107 | 2.1362 × 1015 | 2.0503 × 108 | 1.8564 × 107 | |
| HBA Variant3 | 5.9247 × 107 | 2.2496 × 1015 | 2.6457 × 108 | 1.2663 × 107 | |
| HBA Variant4 | 1.5537 × 107 | 6.9737 × 1013 | 3.6939 × 107 | 2.8920 × 106 | |
| HBA Variant5 | 1.4543 × 107 | 2.6946 × 1014 | 8.8085 × 107 | 2.4369 × 106 | |
| F13 | HBA | 8.4991 × 104 | 5.3884 × 109 | 3.7841 × 105 | 9.8553 × 103 |
| HBA Variant1 | 2.1660 × 105 | 4.3302 × 1010 | 1.1016 × 106 | 4.7312 × 104 | |
| HBA Variant2 | 4.0434 × 105 | 6.4108 × 1011 | 4.2599 × 106 | 2.9266 × 104 | |
| HBA Variant3 | 6.0195 × 104 | 3.1417 × 109 | 3.0138 × 105 | 1.4066 × 104 | |
| HBA Variant4 | 1.6954 × 104 | 2.9294 × 108 | 9.6964 × 104 | 4.9999 × 103 | |
| HBA Variant5 | 1.3275 × 104 | 6.3661 × 107 | 2.8982 × 104 | 4.4306 × 103 | |
| F14 | HBA | 1.1906 × 106 | 2.1680 × 1013 | 2.5754 × 107 | 1.7225 × 104 |
| HBA Variant1 | 1.3705 × 106 | 1.0488 × 1013 | 1.5497 × 107 | 3.2540 × 104 | |
| HBA Variant2 | 6.8941 × 105 | 7.1502 × 1011 | 4.2049 × 106 | 2.9088 × 104 | |
| HBA Variant3 | 5.3568 × 105 | 4.4727 × 1011 | 3.0549 × 106 | 3.6012 × 104 | |
| HBA Variant4 | 5.6948 × 104 | 3.0634 × 109 | 2.4267 × 105 | 2.1121 × 103 | |
| HBA Variant5 | 6.0714 × 104 | 5.2733 × 109 | 3.1058 × 105 | 4.8267 × 103 | |
| F15 | HBA | 3.2531 × 104 | 3.5808 × 108 | 7.5185 × 104 | 4.2814 × 103 |
| HBA Variant1 | 6.0829 × 104 | 2.2671 × 109 | 2.0867 × 105 | 1.6457 × 104 | |
| HBA Variant2 | 5.1395 × 104 | 9.5142 × 108 | 1.1345 × 105 | 1.3603 × 104 | |
| HBA Variant3 | 1.2195 × 104 | 4.7574 × 107 | 2.3958 × 104 | 3.0609 × 103 | |
| HBA Variant4 | 1.2893 × 104 | 5.5510 × 107 | 3.3343 × 104 | 2.2830 × 103 | |
| HBA Variant5 | 1.2561 × 104 | 3.6241 × 107 | 2.0081 × 104 | 2.8071 × 103 | |
| F16 | HBA | 3.5332 × 103 | 2.8950 × 105 | 4.5469 × 103 | 2.3564 × 103 |
| HBA Variant1 | 3.7011 × 103 | 2.3320 × 105 | 4.6593 × 103 | 2.9155 × 103 | |
| HBA Variant2 | 3.7689 × 103 | 1.7089 × 105 | 4.6377 × 103 | 2.9405 × 103 | |
| HBA Variant3 | 3.4917 × 103 | 2.4914 × 105 | 4.7043 × 103 | 2.4389 × 103 | |
| HBA Variant4 | 3.2869 × 103 | 1.3733 × 105 | 3.9777 × 103 | 2.6596 × 103 | |
| HBA Variant5 | 3.4083 × 103 | 2.0681 × 105 | 4.4871 × 103 | 2.6545 × 103 | |
| F17 | HBA | 3.3505 × 103 | 1.6089 × 105 | 4.2245 × 103 | 2.7226 × 103 |
| HBA Variant1 | 3.3817 × 103 | 1.1554 × 105 | 4.0499 × 103 | 2.6649 × 103 | |
| HBA Variant2 | 3.3873 × 103 | 1.7320 × 105 | 4.1500 × 103 | 2.6241 × 103 | |
| HBA Variant3 | 3.1655 × 103 | 1.5801 × 105 | 3.9809 × 103 | 2.5251 × 103 | |
| HBA Variant4 | 3.0138 × 103 | 9.8325 × 104 | 3.6547 × 103 | 2.3185 × 103 | |
| HBA Variant5 | 2.9825 × 103 | 1.0718 × 105 | 3.5434 × 103 | 2.1352 × 103 | |
| F18 | HBA | 2.3957 × 106 | 3.2514 × 1012 | 7.5405 × 106 | 1.4852 × 105 |
| HBA Variant1 | 1.9991 × 106 | 3.4318 × 1012 | 7.8341 × 106 | 2.9004 × 105 | |
| HBA Variant2 | 2.9983 × 106 | 4.5396 × 1012 | 9.2974 × 106 | 2.5223 × 105 | |
| HBA Variant3 | 4.6479 × 106 | 1.4414 × 1013 | 1.3091 × 107 | 4.3063 × 105 | |
| HBA Variant4 | 4.7599 × 105 | 2.4964 × 1011 | 2.5893 × 106 | 5.0458 × 104 | |
| HBA Variant5 | 3.4289 × 105 | 1.2778 × 1011 | 1.6395 × 106 | 8.5556 × 104 | |
| F19 | HBA | 2.0517 × 104 | 1.7408 × 108 | 4.4102 × 104 | 2.3485 × 103 |
| HBA Variant1 | 4.0120 × 104 | 2.4844 × 109 | 2.9001 × 105 | 4.2240 × 103 | |
| HBA Variant2 | 2.7690 × 104 | 2.6446 × 108 | 6.9020 × 104 | 5.7685 × 103 | |
| HBA Variant3 | 2.6046 × 104 | 1.0823 × 108 | 4.2168 × 104 | 9.6255 × 103 | |
| HBA Variant4 | 2.0617 × 104 | 1.0728 × 108 | 4.2961 × 104 | 5.6065 × 103 | |
| HBA Variant5 | 2.1263 × 104 | 9.6453 × 107 | 3.8900 × 104 | 5.2193 × 103 | |
| F20 | HBA | 3.1946 × 103 | 1.6368 × 105 | 4.1407 × 103 | 2.5176 × 103 |
| HBA Variant1 | 3.2834 × 103 | 1.3258 × 105 | 4.4361 × 103 | 2.5626 × 103 | |
| HBA Variant2 | 3.4128 × 103 | 1.2776 × 105 | 4.0172 × 103 | 2.6198 × 103 | |
| HBA Variant3 | 3.3963 × 103 | 9.0278 × 104 | 3.9169 × 103 | 2.8710 × 103 | |
| HBA Variant4 | 3.2345 × 103 | 8.9664 × 104 | 3.7715 × 103 | 2.7102 × 103 | |
| HBA Variant5 | 3.1219 × 103 | 1.2596 × 105 | 3.9370 × 103 | 2.3455 × 103 | |
| F21 | HBA | 2.5611 × 103 | 2.8997 × 103 | 2.6928 × 103 | 2.4711 × 103 |
| HBA Variant1 | 2.5820 × 103 | 2.6362 × 103 | 2.7207 × 103 | 2.4582 × 103 | |
| HBA Variant2 | 2.5963 × 103 | 2.6197 × 103 | 2.7350 × 103 | 2.5133 × 103 | |
| HBA Variant3 | 2.5724 × 103 | 2.1062 × 103 | 2.6653 × 103 | 2.5027 × 103 | |
| HBA Variant4 | 2.5306 × 103 | 1.9981 × 103 | 2.6323 × 103 | 2.4547 × 103 | |
| HBA Variant5 | 2.5418 × 103 | 1.5864 × 103 | 2.6752 × 103 | 2.4739 × 103 | |
| F22 | HBA | 1.1105 × 104 | 4.4696 × 106 | 1.4451 × 104 | 3.9381 × 103 |
| HBA Variant1 | 1.2229 × 104 | 2.2453 × 106 | 1.5538 × 104 | 8.7929 × 103 | |
| HBA Variant2 | 1.2140 × 104 | 5.5609 × 106 | 1.5778 × 104 | 2.7543 × 103 | |
| HBA Variant3 | 9.0497 × 103 | 1.5793 × 107 | 1.4149 × 104 | 2.5039 × 103 | |
| HBA Variant4 | 8.6397 × 103 | 1.2757 × 107 | 1.2323 × 104 | 2.3966 × 103 | |
| HBA Variant5 | 8.8657 × 103 | 1.0709 × 107 | 1.3459 × 104 | 2.3911 × 103 | |
| F23 | HBA | 3.0873 × 103 | 8.9441 × 103 | 3.3933 × 103 | 2.9124 × 103 |
| HBA Variant1 | 3.0757 × 103 | 3.7157 × 103 | 3.2409 × 103 | 2.9663 × 103 | |
| HBA Variant2 | 3.0787 × 103 | 4.8742 × 103 | 3.2467 × 103 | 2.9272 × 103 | |
| HBA Variant3 | 3.0714 × 103 | 4.2311 × 103 | 3.2085 × 103 | 2.9328 × 103 | |
| HBA Variant4 | 3.0757 × 103 | 4.6087 × 103 | 3.2279 × 103 | 2.9790 × 103 | |
| HBA Variant5 | 3.0728 × 103 | 7.2032 × 103 | 3.2729 × 103 | 2.9227 × 103 | |
| F24 | HBA | 3.5490 × 103 | 2.1112 × 105 | 4.5566 × 103 | 3.1240 × 103 |
| HBA Variant1 | 3.4566 × 103 | 1.5542 × 105 | 4.5077 × 103 | 3.1018 × 103 | |
| HBA Variant2 | 6.7454 × 103 | 8.5570 × 10−25 | 6.7454 × 103 | 6.7454 × 103 | |
| HBA Variant3 | 6.7454 × 103 | 8.5570 × 10−25 | 6.7454 × 103 | 6.7454 × 103 | |
| HBA Variant4 | 6.7454 × 103 | 8.5570 × 10−25 | 6.7454 × 103 | 6.7454 × 103 | |
| HBA Variant5 | 6.7454 × 103 | 8.5570 × 10−25 | 6.7454 × 103 | 6.7454 × 103 | |
| F25 | HBA | 3.2832 × 103 | 1.0837 × 104 | 3.5738 × 103 | 3.1453 × 103 |
| HBA Variant1 | 3.4689 × 103 | 4.0923 × 104 | 3.9423 × 103 | 3.1541 × 103 | |
| HBA Variant2 | 3.4378 × 103 | 3.6545 × 104 | 3.9504 × 103 | 3.2091 × 103 | |
| HBA Variant3 | 3.6478 × 103 | 1.0866 × 105 | 4.9441 × 103 | 3.3252 × 103 | |
| HBA Variant4 | 3.2442 × 103 | 5.2472 × 103 | 3.4784 × 103 | 3.1244 × 103 | |
| HBA Variant5 | 3.2287 × 103 | 4.5178 × 103 | 3.3893 × 103 | 3.1160 × 103 | |
| F26 | HBA | 7.9672 × 103 | 2.4340 × 106 | 1.1381 × 104 | 5.7900 × 103 |
| HBA Variant1 | 7.4303 × 103 | 2.3268 × 106 | 1.0814 × 104 | 4.5991 × 103 | |
| HBA Variant2 | 7.4800 × 103 | 5.8024 × 106 | 1.2326 × 104 | 4.4648 × 103 | |
| HBA Variant3 | 8.0229 × 103 | 4.6671 × 106 | 1.1135 × 104 | 4.4430 × 103 | |
| HBA Variant4 | 6.8605 × 103 | 6.9379 × 106 | 1.2266 × 104 | 3.8720 × 103 | |
| HBA Variant5 | 7.7758 × 103 | 6.0474 × 106 | 1.1017 × 104 | 4.0915 × 103 | |
| F27 | HBA | 4.3209 × 103 | 2.9043 × 105 | 5.5419 × 103 | 3.6089 × 103 |
| HBA Variant1 | 4.2962 × 103 | 3.8208 × 105 | 5.6456 × 103 | 3.4706 × 103 | |
| HBA Variant2 | 4.0895 × 103 | 2.8326 × 105 | 5.4600 × 103 | 3.4020 × 103 | |
| HBA Variant3 | 3.8483 × 103 | 1.2146 × 104 | 4.0791 × 103 | 3.6599 × 103 | |
| HBA Variant4 | 3.8045 × 103 | 2.2544 × 104 | 4.2022 × 103 | 3.5012 × 103 | |
| HBA Variant5 | 3.7640 × 103 | 1.8584 × 104 | 3.9939 × 103 | 3.4823 × 103 | |
| F28 | HBA | 3.7327 × 103 | 3.4854 × 104 | 4.1442 × 103 | 3.4188 × 103 |
| HBA Variant1 | 4.0870 × 103 | 9.3854 × 104 | 5.0798 × 103 | 3.7310 × 103 | |
| HBA Variant2 | 3.9699 × 103 | 4.9022 × 104 | 4.4602 × 103 | 3.5150 × 103 | |
| HBA Variant3 | 4.2053 × 103 | 6.4014 × 104 | 4.6087 × 103 | 3.7526 × 103 | |
| HBA Variant4 | 3.6998 × 103 | 1.8153 × 104 | 4.1499 × 103 | 3.4594 × 103 | |
| HBA Variant5 | 3.6399 × 103 | 1.3522 × 104 | 3.9809 × 103 | 3.4785 × 103 | |
| F29 | HBA | 5.4823 × 103 | 1.7973 × 106 | 1.0828 × 104 | 4.0879 × 103 |
| HBA Variant1 | 5.1122 × 103 | 2.3084 × 105 | 6.0240 × 103 | 4.3307 × 103 | |
| HBA Variant2 | 5.1476 × 103 | 4.0645 × 105 | 7.4233 × 103 | 4.1184 × 103 | |
| HBA Variant3 | 4.7388 × 103 | 1.2051 × 105 | 5.5547 × 103 | 4.1877 × 103 | |
| HBA Variant4 | 4.7174 × 103 | 2.0623 × 105 | 5.8894 × 103 | 3.8441 × 103 | |
| HBA Variant5 | 4.5941 × 103 | 1.4672 × 105 | 5.4513 × 103 | 3.8514 × 103 | |
| F30 | HBA | 3.9299 × 106 | 5.6959 × 1012 | 1.2116 × 107 | 1.4320 × 106 |
| HBA Variant1 | 8.4490 × 106 | 5.9644 × 1013 | 3.4072 × 107 | 1.7421 × 106 | |
| HBA Variant2 | 6.6050 × 106 | 1.4232 × 1013 | 1.6934 × 107 | 2.1936 × 106 | |
| HBA Variant3 | 1.1878 × 107 | 1.5381 × 1013 | 1.9686 × 107 | 5.7392 × 106 | |
| HBA Variant4 | 3.5455 × 106 | 1.5670 × 1012 | 6.1212 × 106 | 1.1612 × 106 | |
| HBA Variant5 | 3.4745 × 106 | 1.1059 × 1012 | 6.1616 × 106 | 1.8977 × 106 |
Appendix B
| Function | Algorithm | Mean | Std | Max | Min | ||||
|---|---|---|---|---|---|---|---|---|---|
| F1 | HBA | 2.0695 × 109 | 9.6826 × 1018 | 1.3714 × 1010 | 6.4449 × 107 | ||||
| DOA | 1.0438 × 1011 | 2.5244 × 1020 | 1.2827 × 1011 | 6.6255 × 1010 | |||||
| GWO | 1.2594 × 1010 | 2.2319 × 1019 | 2.1692 × 1010 | 3.4475 × 109 | |||||
| DBO | 5.9421 × 109 | 9.8738 × 1019 | 5.7089 × 1010 | 9.0608 × 108 | |||||
| MCEHBA | 3.0151 × 108 | 1.1446 × 1017 | 1.3671 × 109 | 5.8205 × 107 | |||||
| SO | 6.4625 × 108 | 1.0172 × 1017 | 1.3921 × 109 | 1.3060 × 108 | |||||
| WOA | 2.1963 × 1010 | 1.9271 × 1019 | 3.5304 × 1010 | 1.3665 × 1010 | |||||
| F3 | HBA | 1.5706 × 105 | 1.3487 × 109 | 2.7029 × 105 | 1.0058 × 105 | ||||
| DOA | 2.3091 × 105 | 8.3189 × 109 | 4.8942 × 105 | 1.1008 × 105 | |||||
| GWO | 1.7940 × 105 | 1.1015 × 109 | 2.5563 × 105 | 1.2113 × 105 | |||||
| DBO | 2.7257 × 105 | 5.2314 × 109 | 4.7108 × 105 | 1.5910 × 105 | |||||
| MCEHBA | 5.5508 × 104 | 1.5894 × 108 | 7.6003 × 104 | 3.1126 × 104 | |||||
| SO | 1.6541 × 105 | 2.4918 × 108 | 1.9985 × 105 | 1.3531 × 105 | |||||
| WOA | 3.0980 × 105 | 1.0300 × 1010 | 5.3352 × 105 | 1.7710 × 105 | |||||
| F4 | HBA | 7.4283 × 102 | 1.7178 × 104 | 1.0367 × 103 | 5.5817 × 102 | ||||
| DOA | 3.4009 × 104 | 4.4147 × 107 | 4.8306 × 104 | 2.4124 × 104 | |||||
| GWO | 1.6875 × 103 | 6.6577 × 105 | 4.2350 × 103 | 8.4732 × 102 | |||||
| DBO | 1.2434 × 103 | 1.1671 × 105 | 1.9619 × 103 | 8.0600 × 102 | |||||
| MCEHBA | 7.0617 × 102 | 5.9397 × 103 | 9.1396 × 102 | 6.2034 × 102 | |||||
| SO | 8.4528 × 102 | 1.6074 × 104 | 1.1310 × 103 | 6.5909 × 102 | |||||
| WOA | 5.3971 × 103 | 1.9613 × 106 | 8.0861 × 103 | 3.1167 × 103 | |||||
| F5 | HBA | 7.6667 × 102 | 1.5566 × 103 | 8.3910 × 102 | 6.7183 × 102 | ||||
| DOA | 1.1536 × 103 | 1.6404 × 103 | 1.2607 × 103 | 1.0801 × 103 | |||||
| GWO | 7.6005 × 102 | 2.1647 × 103 | 9.3831 × 102 | 7.0265 × 102 | |||||
| DBO | 9.7916 × 102 | 1.2220 × 104 | 1.1769 × 103 | 7.7662 × 102 | |||||
| MCEHBA | 7.7058 × 102 | 1.9386 × 103 | 8.5794 × 102 | 6.8246 × 102 | |||||
| SO | 7.2024 × 102 | 1.5009 × 103 | 7.9200 × 102 | 6.6156 × 102 | |||||
| WOA | 1.1240 × 103 | 6.7551 × 103 | 1.3454 × 103 | 1.0081 × 103 | |||||
| F6 | HBA | 6.3727 × 102 | 4.3875 × 101 | 6.5432 × 102 | 6.2087 × 102 | ||||
| DOA | 6.9656 × 102 | 5.6702 × 101 | 7.1091 × 102 | 6.8242 × 102 | |||||
| GWO | 6.2472 × 102 | 4.1318 × 101 | 6.4022 × 102 | 6.1545 × 102 | |||||
| DBO | 6.6527 × 102 | 1.5776 × 102 | 6.9550 × 102 | 6.4523 × 102 | |||||
| MCEHBA | 6.3717 × 102 | 1.5688 × 102 | 6.6948 × 102 | 6.1700 × 102 | |||||
| SO | 6.3021 × 102 | 3.5214 × 101 | 6.4034 × 102 | 6.1780 × 102 | |||||
| WOA | 6.9722 × 102 | 1.4061 × 102 | 7.2598 × 102 | 6.7444 × 102 | |||||
| F7 | HBA | 1.2973 × 103 | 1.2179 × 104 | 1.6039 × 103 | 1.1025 × 103 | ||||
| DOA | 1.9435 × 103 | 6.5751 × 103 | 2.0931 × 103 | 1.8171 × 103 | |||||
| GWO | 1.1638 × 103 | 6.2606 × 103 | 1.4355 × 103 | 1.0261 × 103 | |||||
| DBO | 1.4291 × 103 | 2.4198 × 104 | 1.8517 × 103 | 1.1113 × 103 | |||||
| MCEHBA | 1.1760 × 103 | 5.4324 × 103 | 1.3022 × 103 | 1.0176 × 103 | |||||
| SO | 1.1988 × 103 | 4.6494 × 103 | 1.3824 × 103 | 1.0852 × 103 | |||||
| WOA | 1.9229 × 103 | 8.4357 × 103 | 2.1126 × 103 | 1.7596 × 103 | |||||
| F8 | HBA | 1.0785 × 103 | 2.7494 × 103 | 1.1773 × 103 | 9.5582 × 102 | ||||
| DOA | 1.4712 × 103 | 2.1400 × 103 | 1.6063 × 103 | 1.3955 × 103 | |||||
| GWO | 1.0782 × 103 | 4.1308 × 103 | 1.3394 × 103 | 9.8528 × 102 | |||||
| DBO | 1.2838 × 103 | 1.0788 × 104 | 1.4265 × 103 | 1.0698 × 103 | |||||
| MCEHBA | 1.0580 × 103 | 2.2009 × 103 | 1.1339 × 103 | 9.6571 × 102 | |||||
| SO | 1.0275 × 103 | 1.3184 × 103 | 1.1254 × 103 | 9.5484 × 102 | |||||
| WOA | 1.4047 × 103 | 3.6591 × 103 | 1.5188 × 103 | 1.2902 × 103 | |||||
| F9 | HBA | 1.3767 × 104 | 3.8521 × 107 | 3.0583 × 104 | 4.8583 × 103 | ||||
| DOA | 3.7493 × 104 | 2.4412 × 107 | 4.5304 × 104 | 2.6496 × 104 | |||||
| GWO | 1.1363 × 104 | 2.0975 × 107 | 1.9915 × 104 | 5.2280 × 103 | |||||
| DBO | 2.5564 × 104 | 6.1261 × 107 | 4.2696 × 104 | 1.5372 × 104 | |||||
| MCEHBA | 1.1230 × 104 | 3.0131 × 107 | 2.5183 × 104 | 4.0967 × 103 | |||||
| SO | 7.6076 × 103 | 1.2313 × 107 | 1.5197 × 104 | 2.3628 × 103 | |||||
| WOA | 4.0029 × 104 | 1.5322 × 108 | 8.5441 × 104 | 2.2259 × 104 | |||||
| F10 | HBA | 9.7063 × 103 | 3.2627 × 106 | 1.3139 × 104 | 5.2862 × 103 | ||||
| DOA | 1.5243 × 104 | 6.4593 × 105 | 1.6674 × 104 | 1.3936 × 104 | |||||
| GWO | 8.5431 × 103 | 3.7485 × 106 | 1.4410 × 104 | 6.0348 × 103 | |||||
| DBO | 1.2748 × 104 | 4.5587 × 106 | 1.5436 × 104 | 8.8599 × 103 | |||||
| MCEHBA | 8.4038 × 103 | 1.3621 × 106 | 1.0923 × 104 | 6.2255 × 103 | |||||
| SO | 9.5753 × 103 | 8.3289 × 106 | 1.5049 × 104 | 5.7094 × 103 | |||||
| WOA | 1.3379 × 104 | 1.1311 × 106 | 1.5296 × 104 | 1.0445 × 104 | |||||
| F11 | HBA | 1.9376 × 103 | 4.5137 × 105 | 4.3160 × 103 | 1.4191 × 103 | ||||
| DOA | 1.8455 × 104 | 2.7414 × 107 | 2.8226 × 104 | 8.0883 × 103 | |||||
| GWO | 7.5577 × 103 | 8.6312 × 106 | 1.3895 × 104 | 3.0690 × 103 | |||||
| DBO | 5.2983 × 103 | 1.8423 × 107 | 2.1878 × 104 | 1.8497 × 103 | |||||
| MCEHBA | 1.4878 × 103 | 1.1965 × 104 | 1.8242 × 103 | 1.3257 × 103 | |||||
| SO | 3.8917 × 103 | 3.4065 × 106 | 1.0371 × 104 | 2.1241 × 103 | |||||
| WOA | 1.0126 × 104 | 1.0178 × 107 | 1.7890 × 104 | 4.9503 × 103 | |||||
| F12 | HBA | 3.6192 × 107 | 7.0996 × 1014 | 1.0180 × 108 | 4.7769 × 106 | ||||
| DOA | 5.8910 × 1010 | 4.2124 × 1020 | 1.0692 × 1011 | 2.3828 × 1010 | |||||
| GWO | 1.2380 × 109 | 2.2000 × 1018 | 6.2847 × 109 | 5.2333 × 107 | |||||
| DBO | 8.1675 × 108 | 3.3697 × 1017 | 2.9919 × 109 | 1.5457 × 108 | |||||
| MCEHBA | 1.2762 × 107 | 7.9364 × 1013 | 3.8917 × 107 | 1.8567 × 106 | |||||
| SO | 7.9088 × 107 | 6.6592 × 1015 | 4.3995 × 108 | 1.5001 × 107 | |||||
| WOA | 4.8373 × 109 | 3.0510 × 1018 | 7.7991 × 109 | 1.8251 × 109 | |||||
| F13 | HBA | 1.0076 × 105 | 3.4754 × 109 | 2.1554 × 105 | 2.2365 × 104 | ||||
| DOA | 2.3085 × 1010 | 1.5727 × 1020 | 5.9541 × 1010 | 4.1498 × 109 | |||||
| GWO | 3.6060 × 108 | 8.4572 × 1017 | 5.1473 × 109 | 4.5409 × 106 | |||||
| DBO | 8.2913 × 107 | 8.2025 × 1015 | 3.0945 × 108 | 1.2640 × 105 | |||||
| MCEHBA | 1.2486 × 104 | 6.2022 × 107 | 3.9766 × 104 | 3.9028 × 103 | |||||
| SO | 3.0123 × 105 | 1.0623 × 1011 | 1.8065 × 106 | 5.0275 × 104 | |||||
| WOA | 5.5104 × 108 | 1.2157 × 1017 | 1.7401 × 109 | 7.6550 × 107 | |||||
| F14 | HBA | 2.6441 × 105 | 2.8387 × 1010 | 7.5839 × 105 | 4.5580 × 104 | ||||
| DOA | 1.4532 × 107 | 5.4954 × 1014 | 8.5563 × 107 | 3.3523 × 104 | |||||
| GWO | 1.8488 × 106 | 2.7895 × 1012 | 5.2927 × 106 | 1.9769 × 105 | |||||
| DBO | 3.9729 × 106 | 1.8197 × 1013 | 1.7824 × 107 | 5.9855 × 104 | |||||
| MCEHBA | 6.3779 × 104 | 4.1637 × 109 | 3.1160 × 105 | 3.7074 × 103 | |||||
| SO | 5.1979 × 105 | 2.6820 × 1011 | 2.7332 × 106 | 7.5631 × 104 | |||||
| WOA | 7.9599 × 106 | 5.7445 × 1013 | 3.9736 × 107 | 4.9366 × 105 | |||||
| F15 | HBA | 4.0678 × 104 | 2.2019 × 109 | 2.4045 × 105 | 5.0204 × 103 | ||||
| DOA | 3.4611 × 109 | 1.8443 × 1019 | 1.8913 × 1010 | 4.5036 × 107 | |||||
| GWO | 1.9239 × 107 | 6.3586 × 1014 | 7.9121 × 107 | 5.6575 × 104 | |||||
| DBO | 4.8553 × 106 | 2.4732 × 1014 | 7.2855 × 107 | 5.9004 × 104 | |||||
| MCEHBA | 9.1818 × 103 | 3.9379 × 107 | 2.0357 × 104 | 2.0441 × 103 | |||||
| SO | 4.6860 × 104 | 8.5759 × 108 | 1.1708 × 105 | 4.2541 × 103 | |||||
| WOA | 7.4570 × 107 | 8.6787 × 1015 | 4.5828 × 108 | 7.6281 × 105 | |||||
| F16 | HBA | 3.5708 × 103 | 4.5209 × 105 | 5.8189 × 103 | 2.6745 × 103 | ||||
| DOA | 7.0838 × 103 | 1.3451 × 106 | 9.7159 × 103 | 4.8215 × 103 | |||||
| GWO | 3.4694 × 103 | 2.4019 × 105 | 5.0294 × 103 | 2.5597 × 103 | |||||
| DBO | 4.9771 × 103 | 5.2101 × 105 | 6.6480 × 103 | 3.7289 × 103 | |||||
| MCEHBA | 3.2015 × 103 | 1.9294 × 105 | 4.1826 × 103 | 2.3215 × 103 | |||||
| SO | 3.4092 × 103 | 1.6490 × 105 | 4.3649 × 103 | 2.6668 × 103 | |||||
| WOA | 6.2405 × 103 | 8.8968 × 105 | 9.0786 × 103 | 4.0811 × 103 | |||||
| F17 | HBA | 3.2996 × 103 | 1.2072 × 105 | 4.1872 × 103 | 2.7605 × 103 | ||||
| DOA | 5.4714 × 103 | 2.2282 × 106 | 9.3809 × 103 | 3.6994 × 103 | |||||
| GWO | 3.1178 × 103 | 1.8199 × 105 | 4.5644 × 103 | 2.5062 × 103 | |||||
| DBO | 4.1529 × 103 | 2.3130 × 105 | 5.4883 × 103 | 3.3170 × 103 | |||||
| MCEHBA | 3.0752 × 103 | 1.6050 × 105 | 3.9915 × 103 | 2.3002 × 103 | |||||
| SO | 3.2381 × 103 | 9.9343 × 104 | 3.8158 × 103 | 2.5248 × 103 | |||||
| WOA | 4.7223 × 103 | 4.8338 × 105 | 7.0092 × 103 | 3.7371 × 103 | |||||
| F18 | HBA | 2.1217 × 106 | 2.5551 × 1012 | 5.8486 × 106 | 1.7950 × 105 | ||||
| DOA | 3.5250 × 107 | 1.7680 × 1015 | 1.8717 × 108 | 1.8303 × 106 | |||||
| GWO | 8.7644 × 106 | 8.2128 × 1013 | 3.5027 × 107 | 1.1957 × 106 | |||||
| DBO | 1.0367 × 107 | 1.1557 × 1014 | 4.7302 × 107 | 5.9310 × 105 | |||||
| MCEHBA | 3.5468 × 105 | 8.6724 × 1010 | 1.1641 × 106 | 8.2333 × 104 | |||||
| SO | 4.8839 × 106 | 1.4405 × 1013 | 1.9429 × 107 | 7.4322 × 105 | |||||
| WOA | 5.1177 × 107 | 1.3608 × 1015 | 1.2894 × 108 | 5.9922 × 106 | |||||
| F19 | HBA | 2.8039 × 104 | 2.7450 × 108 | 7.9135 × 104 | 2.8711 × 103 | ||||
| DOA | 1.5286 × 109 | 3.1373 × 1018 | 6.5365 × 109 | 4.0989 × 107 | |||||
| GWO | 9.3333 × 106 | 3.8836 × 1014 | 9.9661 × 107 | 3.0220 × 104 | |||||
| DBO | 5.4440 × 106 | 5.5496 × 1013 | 3.0609 × 107 | 1.0943 × 104 | |||||
| MCEHBA | 2.2402 × 104 | 8.1896 × 107 | 3.9542 × 104 | 3.3165 × 103 | |||||
| SO | 8.8793 × 104 | 1.5720 × 1010 | 5.2019 × 105 | 1.0263 × 104 | |||||
| WOA | 1.8582 × 107 | 2.0438 × 1014 | 5.4746 × 107 | 2.3078 × 106 | |||||
| F20 | HBA | 3.1633 × 103 | 1.4159 × 105 | 3.9113 × 103 | 2.5381 × 103 | ||||
| DOA | 4.0864 × 103 | 1.9512 × 105 | 4.7238 × 103 | 3.0278 × 103 | |||||
| GWO | 3.0793 × 103 | 2.6499 × 105 | 4.5893 × 103 | 2.4050 × 103 | |||||
| DBO | 3.8803 × 103 | 1.4151 × 105 | 4.4910 × 103 | 2.9201 × 103 | |||||
| MCEHBA | 3.0766 × 103 | 1.0183 × 105 | 3.6793 × 103 | 2.4521 × 103 | |||||
| SO | 3.0955 × 103 | 1.2972 × 105 | 3.8858 × 103 | 2.4166 × 103 | |||||
| WOA | 3.8920 × 103 | 1.0398 × 105 | 4.7996 × 103 | 3.5111 × 103 | |||||
| F21 | HBA | 2.5451 × 103 | 3.0189 × 103 | 2.6801 × 103 | 2.4574 × 103 | ||||
| DOA | 3.0837 × 103 | 7.0114 × 103 | 3.2242 × 103 | 2.9423 × 103 | |||||
| GWO | 2.5619 × 103 | 4.9131 × 103 | 2.7780 × 103 | 2.4641 × 103 | |||||
| DBO | 2.9001 × 103 | 4.9919 × 103 | 3.1072 × 103 | 2.7719 × 103 | |||||
| MCEHBA | 2.5319 × 103 | 2.3959 × 103 | 2.6503 × 103 | 2.4635 × 103 | |||||
| SO | 2.5134 × 103 | 2.4706 × 103 | 2.6238 × 103 | 2.4386 × 103 | |||||
| WOA | 3.0859 × 103 | 1.3253 × 104 | 3.3909 × 103 | 2.8869 × 103 | |||||
| F22 | HBA | 1.1000 × 104 | 4.3324 × 106 | 1.3129 × 104 | 2.3968 × 103 | ||||
| DOA | 1.6487 × 104 | 1.2901 × 106 | 1.8579 × 104 | 1.3293 × 104 | |||||
| GWO | 9.9687 × 103 | 2.4335 × 106 | 1.7011 × 104 | 7.9810 × 103 | |||||
| DBO | 1.3687 × 104 | 5.1047 × 106 | 1.7422 × 104 | 1.0563 × 104 | |||||
| MCEHBA | 8.4953 × 103 | 1.4123 × 107 | 1.2723 × 104 | 2.4037 × 103 | |||||
| SO | 1.1245 × 104 | 5.7034 × 106 | 1.6743 × 104 | 7.3617 × 103 | |||||
| WOA | 1.4553 × 104 | 1.3447 × 106 | 1.6379 × 104 | 1.2222 × 104 | |||||
| F23 | HBA | 3.0746 × 103 | 5.3817 × 103 | 3.2255 × 103 | 2.9554 × 103 | ||||
| DOA | 4.3155 × 103 | 5.0739 × 104 | 4.8585 × 103 | 3.9820 × 103 | |||||
| GWO | 3.0760 × 103 | 1.1909 × 104 | 3.3819 × 103 | 2.9284 × 103 | |||||
| DBO | 3.5518 × 103 | 2.3814 × 104 | 3.9166 × 103 | 3.2630 × 103 | |||||
| MCEHBA | 3.0670 × 103 | 4.1148 × 103 | 3.2254 × 103 | 2.9697 × 103 | |||||
| SO | 3.1065 × 103 | 3.4693 × 103 | 3.2582 × 103 | 2.9658 × 103 | |||||
| WOA | 3.8924 × 103 | 4.1123 × 104 | 4.4624 × 103 | 3.5643 × 103 | |||||
| F24 | HBA | 3.5167 × 103 | 1.4935 × 105 | 4.3594 × 103 | 3.0860 × 103 | ||||
| DOA | 4.4084 × 103 | 6.8246 × 104 | 5.0670 × 103 | 3.9802 × 103 | |||||
| GWO | 3.2099 × 103 | 7.9998 × 103 | 3.4637 × 103 | 3.1145 × 103 | |||||
| DBO | 3.6900 × 103 | 2.1060 × 104 | 3.9248 × 103 | 3.2991 × 103 | |||||
| MCEHBA | 6.7454 × 103 | 8.5570 × 10−25 | 6.7454 × 103 | 6.7454 × 103 | |||||
| SO | 3.2313 × 103 | 5.1095 × 103 | 3.3725 × 103 | 3.1187 × 103 | |||||
| WOA | 3.9003 × 103 | 2.3072 × 104 | 4.1971 × 103 | 3.6089 × 103 | |||||
| F25 | HBA | 3.2809 × 103 | 1.6262 × 104 | 3.6830 × 103 | 3.1145 × 103 | ||||
| DOA | 1.4334 × 104 | 3.6255 × 106 | 1.8531 × 104 | 1.0860 × 104 | |||||
| GWO | 3.8879 × 103 | 2.1725 × 105 | 5.5553 × 103 | 3.4002 × 103 | |||||
| DBO | 3.5123 × 103 | 1.2209 × 105 | 4.8302 × 103 | 3.1551 × 103 | |||||
| MCEHBA | 3.2339 × 103 | 4.1405 × 103 | 3.3574 × 103 | 3.1021 × 103 | |||||
| SO | 3.3542 × 103 | 1.3627 × 104 | 3.6467 × 103 | 3.1538 × 103 | |||||
| WOA | 5.0654 × 103 | 3.6823 × 105 | 6.6509 × 103 | 4.0059 × 103 | |||||
| F26 | HBA | 7.8675 × 103 | 2.0682 × 106 | 1.1250 × 104 | 6.2028 × 103 | ||||
| DOA | 1.6630 × 104 | 8.9848 × 105 | 1.8678 × 104 | 1.4722 × 104 | |||||
| GWO | 7.1346 × 103 | 4.9210 × 105 | 9.2298 × 103 | 6.2458 × 103 | |||||
| DBO | 1.0873 × 104 | 1.2957 × 106 | 1.3326 × 104 | 8.6845 × 103 | |||||
| MCEHBA | 7.7973 × 103 | 5.8060 × 106 | 1.1323 × 104 | 3.9799 × 103 | |||||
| SO | 7.9832 × 103 | 4.3799 × 105 | 9.5427 × 103 | 6.7647 × 103 | |||||
| WOA | 1.4719 × 104 | 1.5514 × 106 | 1.7939 × 104 | 1.2144 × 104 | |||||
| F27 | HBA | 4.2178 × 103 | 3.1739 × 105 | 5.4107 × 103 | 3.5331 × 103 | ||||
| DOA | 5.2141 × 103 | 5.1956 × 105 | 7.4950 × 103 | 4.2194 × 103 | |||||
| GWO | 3.7172 × 103 | 8.9873 × 103 | 3.9398 × 103 | 3.5325 × 103 | |||||
| DBO | 4.0118 × 103 | 6.4224 × 104 | 4.4752 × 103 | 3.4333 × 103 | |||||
| MCEHBA | 3.8229 × 103 | 3.8791 × 104 | 4.2638 × 103 | 3.4168 × 103 | |||||
| SO | 3.8177 × 103 | 1.1290 × 104 | 3.9954 × 103 | 3.5502 × 103 | |||||
| WOA | 4.9443 × 103 | 3.8168 × 105 | 6.3568 × 103 | 3.9880 × 103 | |||||
| F28 | HBA | 3.7229 × 103 | 5.1602 × 104 | 4.3789 × 103 | 3.4129 × 103 | ||||
| DOA | 1.1909 × 104 | 3.0423 × 106 | 1.6718 × 104 | 9.1833 × 103 | |||||
| GWO | 4.6919 × 103 | 2.2993 × 105 | 5.8259 × 103 | 3.8690 × 103 | |||||
| DBO | 6.5732 × 103 | 4.6599 × 106 | 1.0470 × 104 | 3.7894 × 103 | |||||
| MCEHBA | 3.6634 × 103 | 1.5300 × 104 | 3.9826 × 103 | 3.3781 × 103 | |||||
| SO | 4.4034 × 103 | 2.3813 × 105 | 5.5741 × 103 | 3.6568 × 103 | |||||
| WOA | 6.2543 × 103 | 2.4056 × 105 | 7.2452 × 103 | 5.1703 × 103 | |||||
| F29 | HBA | 5.2623 × 103 | 9.7129 × 105 | 8.6210 × 103 | 4.0839 × 103 | ||||
| DOA | 1.8576 × 104 | 2.1655 × 108 | 8.7528 × 104 | 7.7126 × 103 | |||||
| GWO | 5.0178 × 103 | 1.5663 × 105 | 6.2638 × 103 | 4.4799 × 103 | |||||
| DBO | 6.4521 × 103 | 1.1656 × 106 | 9.8359 × 103 | 4.7972 × 103 | |||||
| MCEHBA | 4.6496 × 103 | 1.8310 × 105 | 5.5785 × 103 | 3.8298 × 103 | |||||
| SO | 5.1542 × 103 | 1.1580 × 105 | 5.9198 × 103 | 4.3836 × 103 | |||||
| WOA | 9.1519 × 103 | 2.6801 × 106 | 1.2052 × 104 | 6.5662 × 103 | |||||
| F30 | HBA | 4.8784 × 106 | 1.5349 × 1013 | 1.9193 × 107 | 1.4177 × 106 | ||||
| DOA | 2.4332 × 109 | 4.4774 × 1018 | 1.0983 × 1010 | 3.1077 × 108 | |||||
| GWO | 1.9402 × 108 | 1.1396 × 1016 | 6.0845 × 108 | 6.9103 × 107 | |||||
| DBO | 5.8819 × 107 | 4.2998 × 1015 | 3.4509 × 108 | 9.7465 × 106 | |||||
| MCEHBA | 3.7144 × 106 | 2.2500 × 1012 | 9.1977 × 106 | 1.7939 × 106 | |||||
| SO | 1.6104 × 107 | 8.3876 × 1013 | 3.8096 × 107 | 5.1475 × 106 | |||||
| WOA | 3.1454 × 108 | 1.4429 × 1016 | 6.7171 × 108 | 9.2151 × 107 | |||||
| result | 20/29 | 15/29 | 20/29 | 16/29 | |||||
Appendix C
References
- Osman, M.J.; Idris, N.H.; Salleh, M.R.M.; Majid, Z.; Ismail, Z.; Othman, N. Utilizing Machine Learning to Determine User Interface Elements in Agricultural Mobile Location-Based Services. IOP Conf. Ser. Earth Environ. Sci. 2024, 1412, 012025. [Google Scholar] [CrossRef]
- Shao, W.; Wu, Y.; Fan, D. A review of path planning technology for mobile robots. J. Tongling Vocat. Tech. Coll. 2018, 17, 57–60. [Google Scholar]
- Zhai, R.; Xiao, P.; Shu, D.; Sun, Y.; Jiang, M. Application of Improved Butterfly Optimization Algorithm in Mobile Robot Path Planning. Electronics 2023, 12, 3424. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Cai, Z. Research and development of path planning algorithms. Control Eng. 2017, 24, 1473–1480. [Google Scholar]
- Zhao, Q. Research on the Kinetic Characteristics of Oil Tea Bud Collection Manipulator. Ph.D. Thesis, Central South Forestry University of Science and Technology, Changsha, China, 2024. [Google Scholar] [CrossRef]
- Li, S.; Song, Q.; Li, Z.; Zhang, X.; Zhe, L. A review of genetic algorithm in robot path planning. Sci. Technol. Eng. 2020, 20, 423–431. [Google Scholar]
- Han, Y.; Yu, M. A review on the application of particle swarm optimization algorithm in robot path planning. Manuf. Technol. Mach. Tools 2024, 85–90. [Google Scholar] [CrossRef]
- Zhang, S.; Pu, J.; Si, Y.; Sun, L. Application of Ant Colony Optimization Algorithm in Path Planning of Mobile Robots. Comput. Eng. Appl. 2020, 56, 10–19. [Google Scholar]
- Qiu, G.; Deng, J.; Li, J.; Wang, W. Hybrid Clustering-Enhanced Brain Storm Optimization Algorithm for Efficient Multi-Robot Path Planning. Biomimetics 2025, 10, 347. [Google Scholar] [CrossRef]
- Ou, Y.; Yin, P.; Mo, L. An Improved Grey Wolf Optimizer and Its Application in Robot Path Planning. Biomimetics 2023, 8, 84. [Google Scholar] [CrossRef]
- Yang, Z. Improved Particle Swarm Optimization Algorithm for Mobile Robot Path Planning. Front. Comput. Intell. Syst. 2024, 9, 8–13. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Bansal, K.A.; Sangtani, S.V.; Bhukya, N.M. Optimal configuration and sensitivity analysis of hybrid nanogrid for futuristic residential application using honey badger algorithm. Energy Convers. Manag. 2024, 315, 118784. [Google Scholar]
- Jia, H.; Rao, H.; Wang, Z.; Wen, C.; Su, Y. Three-dimensional path planning for unmanned aerial vehicles based on improved honey badger algorithm. J. Longyan Coll. 2022, 40, 18–25. [Google Scholar]
- Geetha, M.; Sekar, C.G.; Marichelvam, M.K. A Hybrid Honey Badger Algorithm to Solve Energy-Efficient Hybrid Flow Shop Scheduling Problems. Processes 2025, 13, 174. [Google Scholar] [CrossRef]
- Qu, Y.; Tu, J.; Chen, K.; Jin, S. An assembly tolerance analysis method based on good point set. Mech. Des. Manuf. 2019, 115–118. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, C.A. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Song, T.; Zhang, L. Moth-flame optimisation algorithm incorporating centre of gravity reverse variation. Intell. Comput. Appl. 2020, 10, 104–107+115. [Google Scholar]
- Peraza-Vázquez, H.; Peña-Delgado, A.F.; Echavarría-Castillo, G.; Morales-Cepeda, A.B.; Velasco-Álvarez, J.; Ruiz-Perez, F. A Bio-Inspired Method for Engineering Design Optimization Inspired by Dingoes Hunting Strategies. Math. Probl. Eng. 2021, 2021, 9107547. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, M.S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]






| Average Nearest-Neighbour Distance | Distance Standard Deviation | Minimum Inter-Individual Distance | Spatial Coverage Ratio | ||
|---|---|---|---|---|---|
| Dim = 3 | Good Point Set-based Population Initialization | 2.884 | 0.56188 | 2.2361 | 1 |
| Random Initialization | 2.4683 | 1.0468 | 0.43957 | 1 | |
| Dim = 5 | Good Point Set-based Population Initialization | 7.0292 | 0.78513 | 5.4772 | 1 |
| Random Initialization | 5.8595 | 1.8657 | 2.3788 | 0.9375 | |
| Dim = 10 | Good Point Set-based Population Initialization | 13.612 | 1.6305 | 11.314 | 0.09375 |
| Random Initialization | 13.085 | 2.1067 | 9.1448 | 0.09082 |
| Number of Runs | Average Number of Crossings | Maximum Number of Crossings |
|---|---|---|
| 1 | 3.1960 | 222 |
| 2 | 2.8670 | 244 |
| 3 | 3.3050 | 205 |
| 4 | 3.49320 | 217 |
| 5 | 3.8010 | 260 |
| Mean | Std | Max | Min | |
|---|---|---|---|---|
| HBA_Variant1 | 11 | 9 | 10 | 7 |
| HBA_Variant2 | 13 | 18 | 10 | 12 |
| HBA_Variant3 | 20 | 19 | 14 | 18 |
| HBA_Variant4 | 25 | 18 | 21 | 23 |
| HBA_Variant5 | 20 | 17 | 15 | 15 |
| Mean | Std | Max | Min | |
|---|---|---|---|---|
| HBA_Variant1 | 7 | 15 | 8 | 8 |
| HBA_Variant2 | 15 | 18 | 11 | 18 |
| HBA_Variant3 | 19 | 15 | 18 | 13 |
| HBA_Variant4 | 26 | 20 | 19 | 25 |
| HBA_Variant5 | 20 | 17 | 17 | 14 |
| Mean | Std | Max | Min | |
|---|---|---|---|---|
| F1~F3 | 2 | 1 | 2 | 2 |
| F4~F10 | 2 | 1 | 3 | 1 |
| F11~F20 | 10 | 8 | 9 | 8 |
| F21~F30 | 6 | 5 | 6 | 5 |
| Algorithm | HBA | DOA | GWO | DBO | MCEHBA | SO | WOA |
|---|---|---|---|---|---|---|---|
| Average rank | 2.9310 | 6.7586 | 3.2414 | 4.6897 | 1.6207 | 2.6552 | 6.1034 |
| Algorithms | x1 | x2 | x3 | x4 | Optima Quality |
|---|---|---|---|---|---|
| DBO | 0.201 | 2.942 | 10.000 | 0.201 | 1.77317 |
| GWO | 0.204 | 3.265 | 9.034 | 0.206 | 1.69554 |
| SO | 0.205 | 3.242 | 9.038 | 0.206 | 1.69342 |
| DOA | 0.206 | 3.237 | 9.036 | 0.206 | 1.69315 |
| HBA | 0.206 | 3.221 | 9.079 | 0.206 | 1.69612 |
| MCEHBA | 0.206 | 3.235 | 9.037 | 0.206 | 1.69277 |
| Algorithms | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Optima Quality |
|---|---|---|---|---|---|---|---|---|
| DBO | 3.600 | 0.700 | 17.000 | 7.300 | 8.300 | 3.350 | 5.287 | 3.04671 × 103 |
| GWO | 3.503 | 0.700 | 17.000 | 7.520 | 7.896 | 3.374 | 5.288 | 3.00843 × 103 |
| SO | 3.500 | 0.700 | 17.000 | 7.300 | 7.715 | 3.350 | 5.287 | 2.99453 × 103 |
| DOA | 3.500 | 0.700 | 17.000 | 7.300 | 7.717 | 3.350 | 5.287 | 2.99450 × 103 |
| HBA | 3.500 | 0.700 | 17.000 | 7.300 | 7.715 | 3.350 | 5.287 | 2.99456 × 103 |
| MCEHBA | 3.500 | 0.700 | 17.000 | 7.300 | 7.715 | 3.350 | 5.287 | 2.99447 × 103 |
| WOA | 3.500 | 0.700 | 20.672 | 7.622 | 8.043 | 3.807 | 5.500 | 3.97481 × 103 |
| Algorithms | x1 | x2 | x3 | x4 | x5 | Optima Quality |
|---|---|---|---|---|---|---|
| DBO | 5.99684 | 5.30211 | 4.50314 | 3.49623 | 2.17610 | 1.34000 |
| GWO | 5.98316 | 5.32172 | 4.48639 | 3.53607 | 2.14826 | 1.34008 |
| SO | 6.04859 | 5.29833 | 4.48870 | 3.50432 | 2.13451 | 1.34001 |
| DOA | 5.13085 | 4.37832 | 8.55756 | 6.79829 | 2.63024 | 1.71570 |
| HBA | 6.03167 | 5.32599 | 4.47873 | 3.48725 | 2.15043 | 1.33998 |
| MCEHBA | 6.01602 | 5.30917 | 4.49433 | 3.50147 | 2.15267 | 1.33996 |
| WOA | 6.20937 | 5.57908 | 4.87091 | 2.80830 | 2.68476 | 1.38231 |
| Map | Grid Specification | Start Position | End Position | Number of Obstacles | Obstacles Percent |
|---|---|---|---|---|---|
| M1 | 15 × 15 | 58 | 26% | ||
| M2 | 20 × 20 | 109 | 27% | ||
| M3 | 30 × 30 | 231 | 26% |
| Algorithm | Mean | Std | Best | Worst |
|---|---|---|---|---|
| HBA | 183.33 | 1056.90 | 146.24 | 232.83 |
| DOA | 256.72 | 3996.19 | 168.24 | 317.90 |
| GWO | 158.34 | 358.93 | 145.66 | 189.07 |
| MCEHBA | 140.95 | 508.53 | 124.49 | 165.66 |
| Algorithm | Mean | Std | Best | Worst |
|---|---|---|---|---|
| HBA | 369.75 | 12,698.14 | 281.66 | 543.90 |
| DOA | 351.78 | 21,816.96 | 217.07 | 493.31 |
| GWO | 291.35 | 479.20 | 280.49 | 330.00 |
| MCEHBA | 208.67 | 352.80 | 175.07 | 217.07 |
| Algorithm | Mean | Std | Best | Worst |
|---|---|---|---|---|
| HBA | 748.23 | 42,414.43 | 605.56 | 1067.60 |
| DOA | 761.85 | 23,951.88 | 604.63 | 995.21 |
| GWO | 469.16 | 10,036.71 | 360.38 | 611.80 |
| MCEHBA | 465.00 | 17,319.76 | 276.73 | 619.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Shao, P. Grid-Based Path Planning of Agricultural Robots Driven by Multi-Strategy Collaborative Evolution Honey Badger Algorithm. Biomimetics 2025, 10, 535. https://doi.org/10.3390/biomimetics10080535
Hu Y, Shao P. Grid-Based Path Planning of Agricultural Robots Driven by Multi-Strategy Collaborative Evolution Honey Badger Algorithm. Biomimetics. 2025; 10(8):535. https://doi.org/10.3390/biomimetics10080535
Chicago/Turabian StyleHu, Yunyu, and Peng Shao. 2025. "Grid-Based Path Planning of Agricultural Robots Driven by Multi-Strategy Collaborative Evolution Honey Badger Algorithm" Biomimetics 10, no. 8: 535. https://doi.org/10.3390/biomimetics10080535
APA StyleHu, Y., & Shao, P. (2025). Grid-Based Path Planning of Agricultural Robots Driven by Multi-Strategy Collaborative Evolution Honey Badger Algorithm. Biomimetics, 10(8), 535. https://doi.org/10.3390/biomimetics10080535







