Design and Experimental Validation of a Multimodal Snake Robot with Elliptical Wheels
Abstract
1. Introduction
- Development of a Versatile Snake Robot: This study presents an improved design for a novel snake robot, JiAo-II, which integrates the advantages of both wheeled locomotion and body-based locomotion. The elliptical wheel mechanism retains the cylindrical profile of the robot body while enabling efficient self-propelled motion. Moreover, it allows seamless transitions between different locomotion modes, significantly enhancing the robot’s adaptability to diverse terrain conditions.
- Experimental Validation and Performance Evaluation: A comprehensive experimental platform was established to systematically evaluate the performance of JiAo-II across various typical tasks, including grass traversal, gap crossing, slope ascending, pipe navigation, and cylindrical climbing. In addition, the influence of key parameters, such as the wheel duty cycle and horizontal and vertical body undulations, on locomotion speed and stability was analyzed. Experimental results demonstrate that JiAo-II exhibits strong terrain adaptability and holds significant potential for practical engineering applications.
2. Mechanical Design and Implementation
2.1. Design Concept
- The design of the snake wheels should align with the robot’s originally defined cylindrical body, without causing significant alterations to its overall external shape.
- During motion, the contact point of the wheels with the ground should be located below the robot’s body, allowing the wheels to lift the entire or part of the body off the ground.
- To meet the constraints of limited internal space, the robot’s transmission system must be compactly arranged while ensuring efficiency and reliability.
- To ensure dynamic stability during wheeled locomotion, the structural design should provide a sufficiently large support area between the robot and the ground, effectively preventing tipping or instability.
2.2. Module Design and Implementation
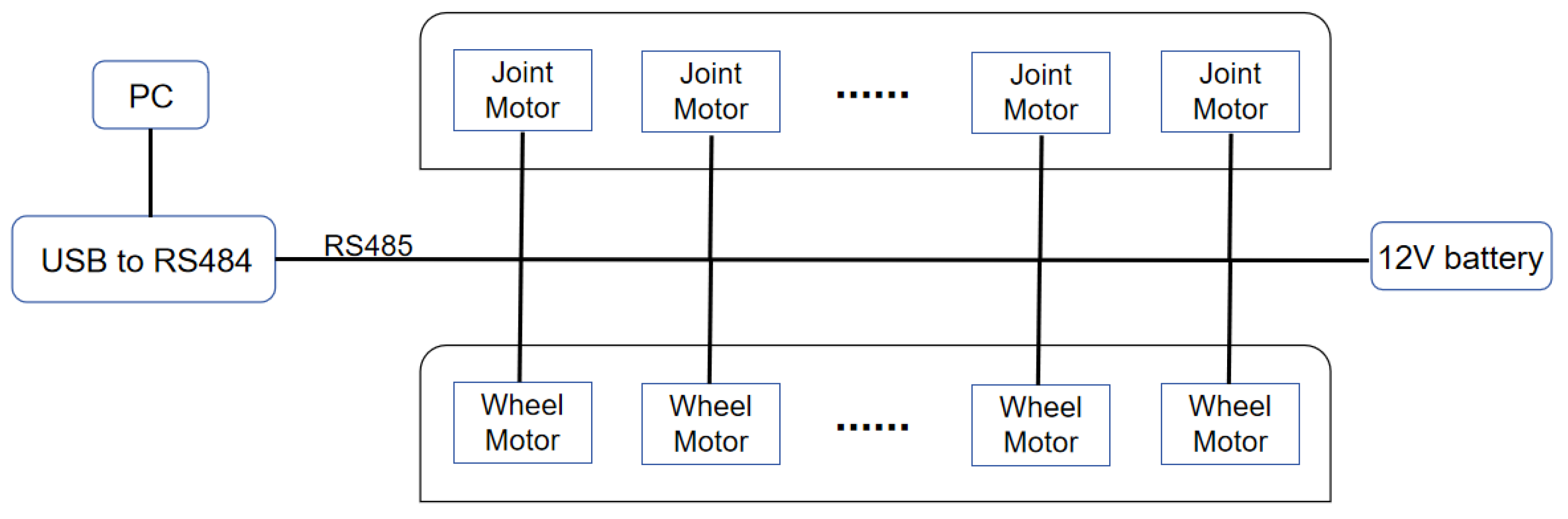
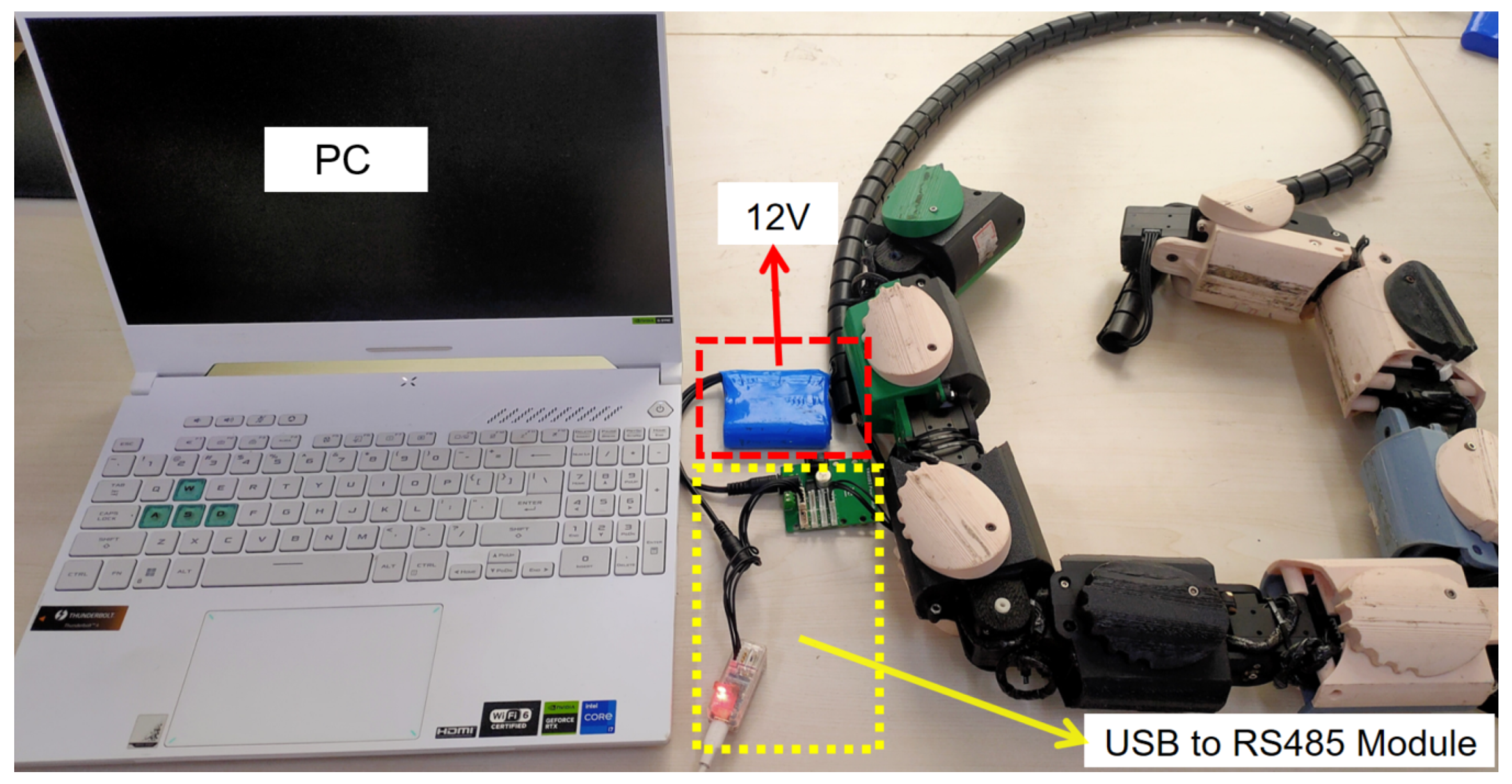
2.3. System Design and Implementation
3. Control Law
3.1. Wheeled Locomotion Control
- All wheels have the same duty factor.
- The motion phases of the corresponding legs on the left and right sides are synchronized.
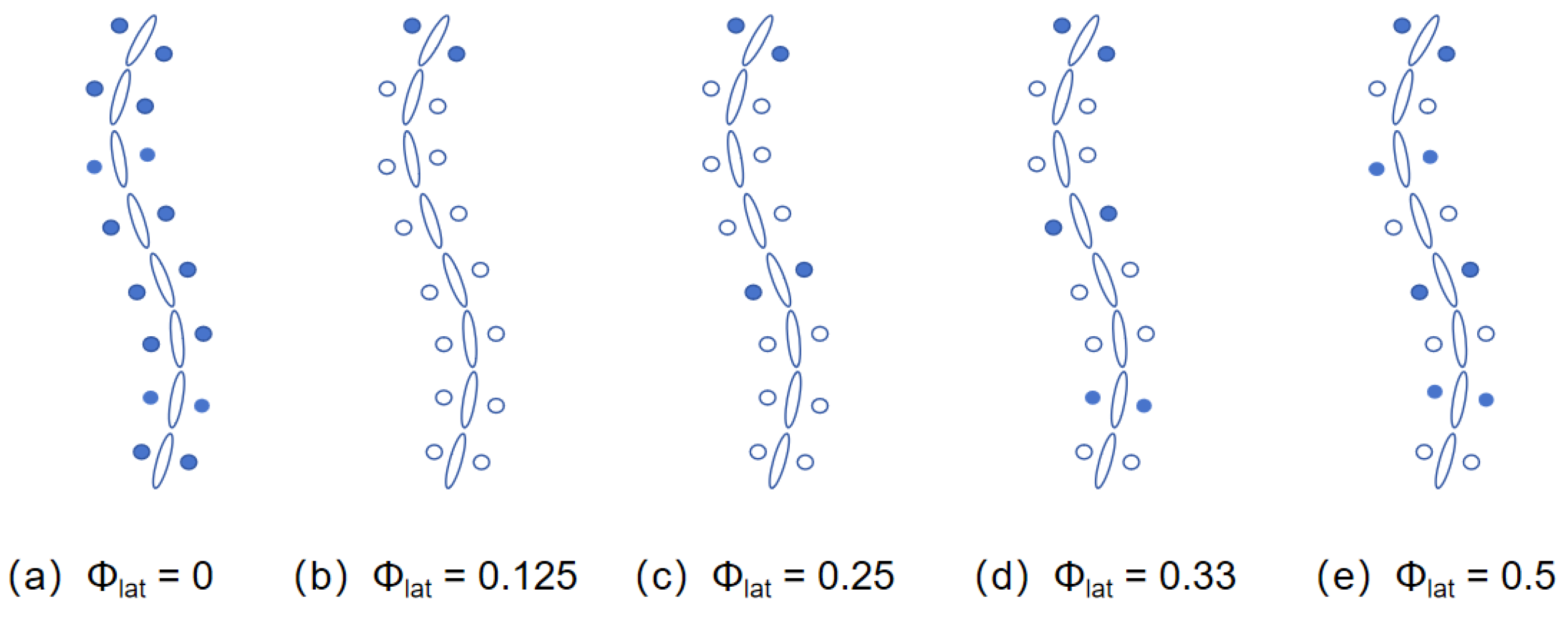
- The lateral phase lag is consistent between the left and right sides.
3.2. Body-Based Locomotion Control
3.2.1. Helix Rolling Gait
- : Tangent vector, representing the direction of the curve’s tangent.
- : Normal vector, representing the direction of the curve’s normal.
- : Binormal vector, which is the cross product of and .
3.2.2. Lateral Rolling Gait
3.2.3. Compliant Control
- is the joint angle of the robot,
- is the mass matrix of the robot,
- is the Coriolis force term,
- represents the gravitational term,
- is the control torque applied to the robot.
3.3. Wheel–Body Coordinated Locomotion Control
- Amplitude for even and odd modules, respectively;
- Angular frequency for even and odd modules, respectively;
- Phase modulation coefficient for even and odd modules, respectively;
- Offset or baseline shift for even and odd modules, respectively.
4. Experiments
4.1. Wheeled Locomotion Experiment
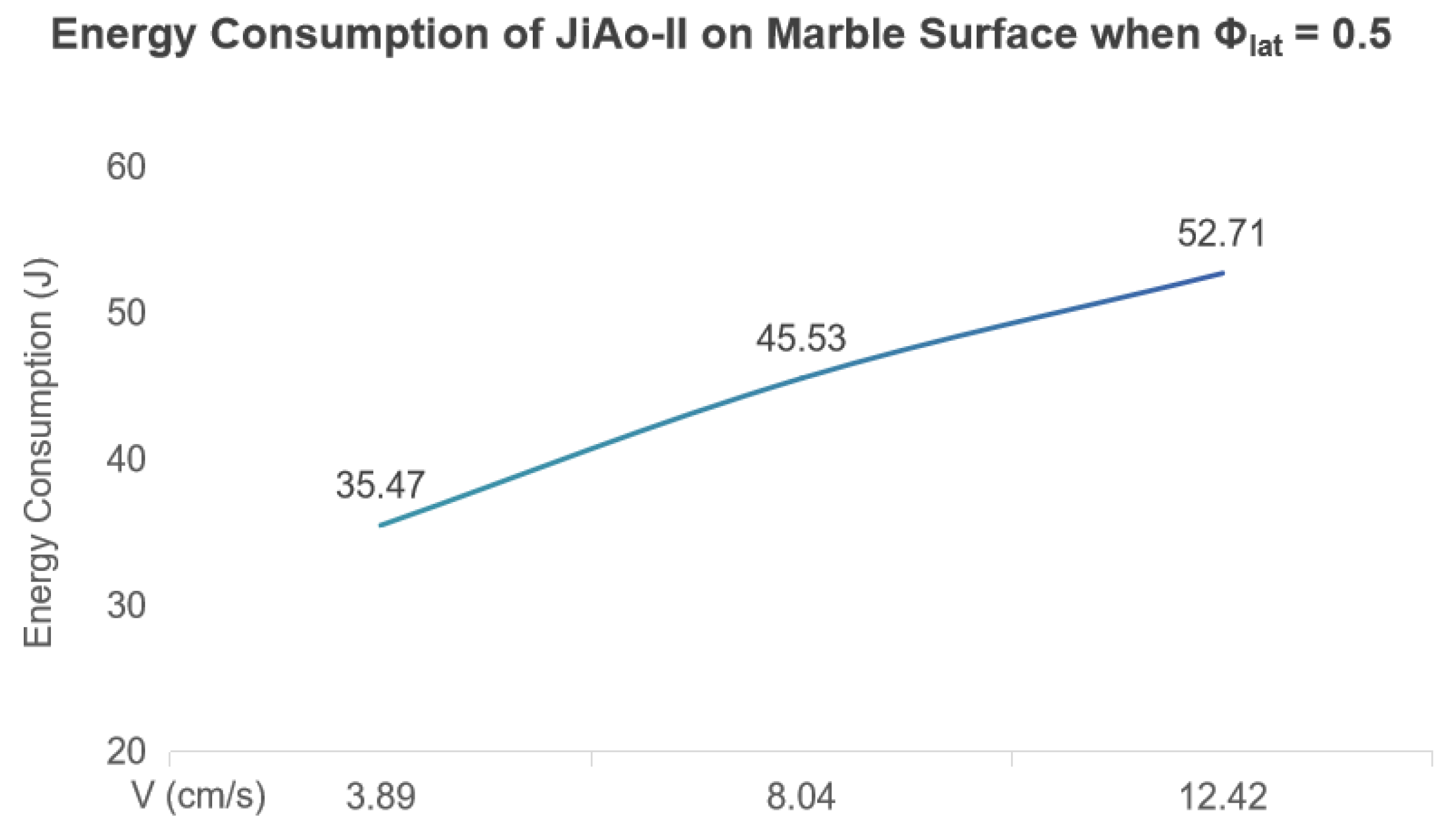
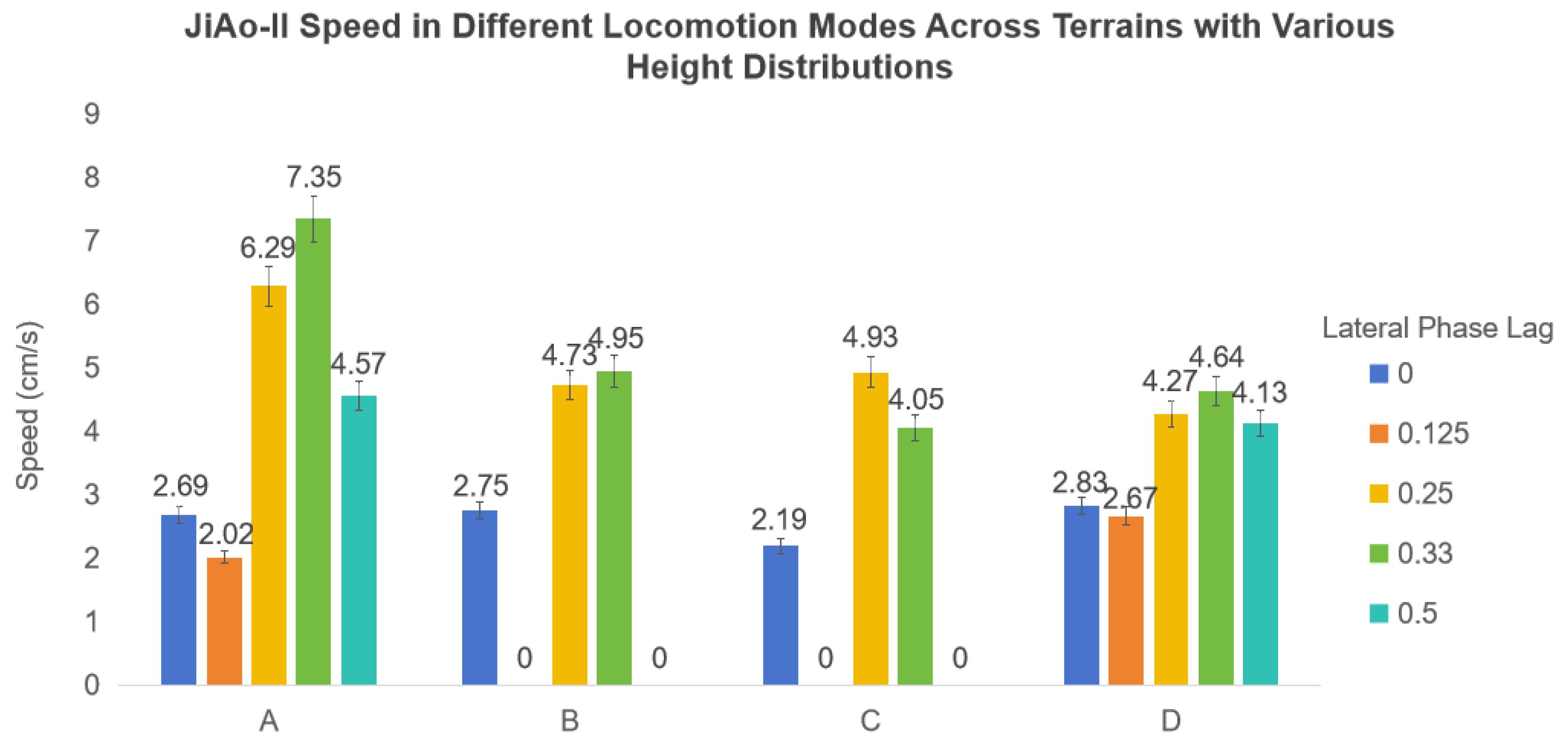
4.1.1. Wheeled Locomotion on Different Terrains
4.1.2. Gap Crossing
- Initial Phase (Figure 13a): JiAo-II began moving steadily towards the gap in wheeled locomotion mode.
- Approaching the Gap (Figure 13b): As the robot neared the edge, the front joints actively raised in preparation for the crossing. The unlifted elliptical wheels continued to provide propulsion, moving the robot forward and shifting its center of gravity for the transition.
- Transition Phase (Figure 13c): Once the first module successfully crossed the gap and landed, it quickly returned to its normal support state, followed by the remaining modules crossing in sequence.
- Completion Phase (Figure 13d): The robot resumed its wheeled locomotion mode, completing the task.
4.2. Body-Based Locomotion Experiment
4.2.1. Cylindrical Climbing
4.2.2. Pipe Navigation
4.3. Wheel–Body Coordinated Locomotion Experiment
4.3.1. Slope Climbing
4.3.2. Simple Obstacle Crossing
4.3.3. Rough Terrain Traversal
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lipkin, K.; Brown, I.; Peck, A.; Choset, H.; Rembisz, J.; Gianfortoni, P.; Naaktgeboren, A. Differentiable and piecewise differentiable gaits for snake robots. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1864–1869. [Google Scholar] [CrossRef]
- Chirikjian, G.; Burdick, J. The kinematics of hyper-redundant robot locomotion. IEEE Trans. Robot. Autom. 1995, 11, 781–793. [Google Scholar] [CrossRef]
- Yamada, H.S. Development of amphibious snake-like robot acm-r5. In Proceedings of the The 36th International Symposium on Robotics (ISR 2005), Tokyo, Japan, 29 November–1 December 2005. [Google Scholar]
- Hirose, S.; Yamada, H. Snake-like robots [tutorial]. IEEE Robot. Autom. Mag. 2009, 16, 88–98. [Google Scholar] [CrossRef]
- Takemori, T.; Tanaka, M.; Matsuno, F. Gait Design for a Snake Robot by Connecting Curve Segments and Experimental Demonstration. IEEE Trans. Robot. 2018, 34, 1384–1391. [Google Scholar] [CrossRef]
- Takemori, T.; Tanaka, M.; Matsuno, F. Adaptive helical rolling of a snake robot to a straight pipe with irregular cross-sectional shape. IEEE Trans. Robot. 2022, 39, 437–451. [Google Scholar] [CrossRef]
- Ono, M.; Thakker, R.; Georgiev, N.; Gavrilov, P.; Archanian, A.; Drevinskas, T.; Daddi, G.; Paton, M.; Melikyan, H.; Pailevanian, T.; et al. To boldly go where no robots have gone before–part 1: Eels robot to spearhead a new one-shot exploration paradigm with in-situ adaptation. In Proceedings of the AIAA Scitech 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 1746. [Google Scholar]
- Hatton, R.L.; Choset, H. Generating gaits for snake robots: Annealed chain fitting and keyframe wave extraction. Auton. Robot. 2010, 28, 271–281. [Google Scholar] [CrossRef]
- Zhen, W.; Gong, C.; Choset, H. Modeling rolling gaits of a snake robot. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3741–3746. [Google Scholar]
- Li, L.; Ma, S.; Tokuda, I.; Asano, F.; Nokata, M.; Tian, Y.; Du, L. Generation of efficient rectilinear gait based on dynamic morphological computation and its theoretical analysis. IEEE Robot. Autom. Lett. 2021, 6, 841–848. [Google Scholar] [CrossRef]
- Hirose, S.; Morishima, A. Design and Control of a Mobile Robot with an Articulated Body. Int. J. Robot. Res. 1990, 9, 99–114. [Google Scholar] [CrossRef]
- Fjerdingen, S.A.; Liljebäck, P.; Transeth, A.A. A snake-like robot for internal inspection of complex pipe structures (PIKo). In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 5665–5671. [Google Scholar] [CrossRef]
- Takaoka, S.; Yamada, H.; Hirose, S. Snake-like active wheel robot ACM-R4. 1 with joint torque sensor and limiter. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 1081–1086. [Google Scholar]
- Kouno, K.; Yamada, H.; Hirose, S. Development of active-joint active-wheel high traversability snake-like robot ACM-R4. 2. J. Robot. Mechatronics 2013, 25, 559–566. [Google Scholar] [CrossRef]
- Kamegawa, T.; Yarnasaki, T.; Igarashi, H.; Matsuno, F. Development of the snake-like rescue robot “kohga”. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Proceedings ICRA ’04. Volume 5, pp. 5081–5086. [Google Scholar] [CrossRef]
- Ito, K.; Maruyama, H. Semi-autonomous serially connected multi-crawler robot for search and rescue. Adv. Robot. 2016, 30, 489–503. [Google Scholar] [CrossRef]
- Chong, B.; O Aydin, Y.; Rieser, J.M.; Sartoretti, G.; Wang, T.; Whitman, J.; Kaba, A.; Aydin, E.; McFarland, C.; Diaz Cruz, K.; et al. A general locomotion control framework for multi-legged locomotors. Bioinspir. Biomim. 2022, 17, 046015. [Google Scholar] [CrossRef] [PubMed]
- Chong, B.; He, J.; Li, S.; Erickson, E.; Diaz, K.; Wang, T.; Soto, D.; Goldman, D.I. Self-propulsion via slipping: Frictional swimming in multilegged locomotors. Proc. Natl. Acad. Sci. USA 2023, 120, e2213698120. [Google Scholar] [CrossRef] [PubMed]
- Chong, B.; He, J.; Soto, D.; Wang, T.; Irvine, D.; Blekherman, G.; Goldman, D.I. Multilegged matter transport: A framework for locomotion on noisy landscapes. Science 2023, 380, 509–515. [Google Scholar] [CrossRef] [PubMed]
- Saranli, U.; Buehler, M.; Koditschek, D.E. RHex: A simple and highly mobile hexapod robot. Int. J. Robot. Res. 2001, 20, 616–631. [Google Scholar] [CrossRef]
- Hildebrand, M. Symmetrical Gaits of Horses. Science 1965, 150, 701–708. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Zhang, Y.; Zheng, W.; Jiang, C.; Xiao, X. Design, control and experiment of a snake-like robot with gripper. In Proceedings of the 2020 17th International Conference on Ubiquitous Robots (UR), Kyoto, Japan, 22–26 June 2020; pp. 50–55. [Google Scholar]
- Travers, M.J.; Whitman, J.; Schiebel, P.E.; Goldman, D.I.; Choset, H. Shape-Based Compliance in Locomotion. Robot. Sci. Syst. 2016, 12. [Google Scholar] [CrossRef]
- Whitman, J.; Ruscelli, F.; Travers, M.; Choset, H. Shape-based compliant control with variable coordination centralization on a snake robot. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 5165–5170. [Google Scholar]
- Gabrielli, G. What price speed? Specific power required for propulsion of vehicles. Mech. Eng. 1950, 775–781. [Google Scholar]
- He, J.; Chong, B.; Xu, Z.; Ha, S.; Goldman, D.I. Learning to enhance multi-legged robot on rugged landscapes. arXiv 2024, arXiv:2409.09473. [Google Scholar]
- He, J.; Chong, B.; Lin, J.; Xu, Z.; Bagheri, H.; Flores, E.; Goldman, D.I. Probabilistic approach to feedback control enhances multi-legged locomotion on rugged landscapes. IEEE Trans. Robot. 2025, 1–18. [Google Scholar] [CrossRef]














| Related Work | Image | Tree Climbing | Helix Rolling | Lateral Rolling | Gap Crossing |
|---|---|---|---|---|---|
| Takemori et al., 2022 [6] |  | ✓ | ✓ | ✓ | × |
| Hatton et al., 2010 [8] |  | ✓ | ✓ | ✓ | × |
| Takaoka et al., 2011 [13] |  | × | × | ✓ | ✓ |
| Kamegawa et al., 2004 [15] |  | × | × | × | ✓ |
| Chong et al., 2023 [19] |  | × | × | × | ✓ |
| Proposed method |  | ✓ | ✓ | ✓ | ✓ |
| Subject | Type | Parameter |
|---|---|---|
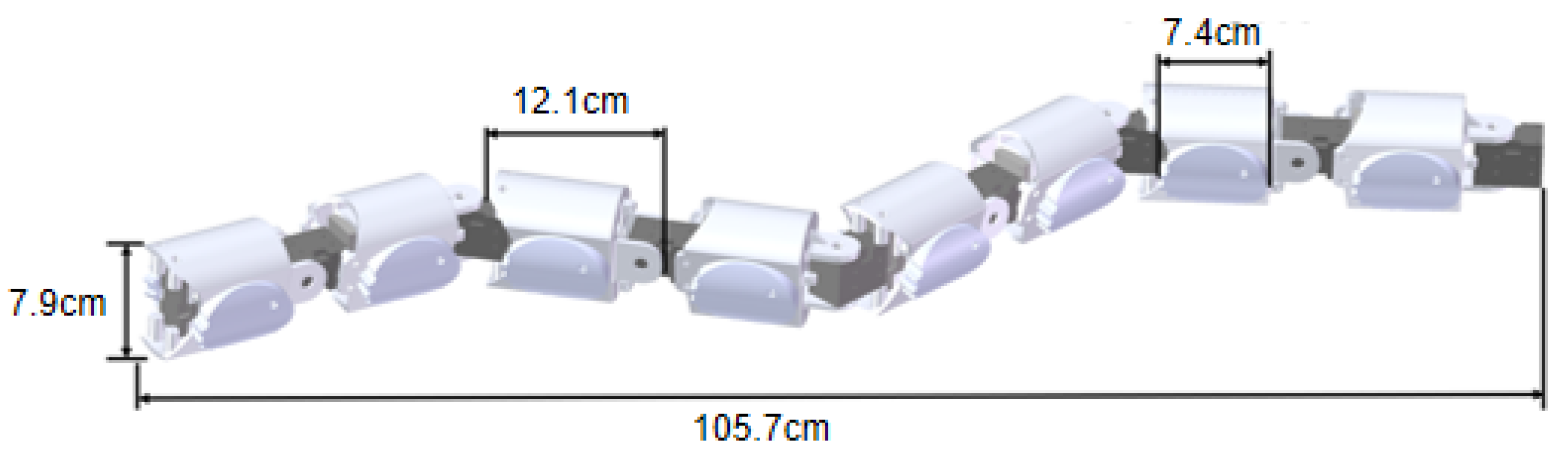
| Unit module | Diameter | 7.9 cm |
| Length | 12.1 cm | |
| Mass | 0.278 kg | |
| Snake robot | Length | 105.7 cm |
| Mass | 2.231 kg | |
| Motor | Model | Dynamixel XH430-W350-R |
| Stall Torque | 4.1 Nm |
| Locomotion Mode | Body-Based Locomotion | Wheeled Locomotion | ||||
|---|---|---|---|---|---|---|
| Helix Rolling Gait | ||||||
| Speed (cm/s) | 0.90 | 3.43 | 2.55 | 5.43 | 5.83 | 5.11 |
| Lateral Phase Lag | 0 | 0.125 | 0.25 | 0.33 | 0.5 |
|---|---|---|---|---|---|
| Speed (cm/s) | 2.01 | 1.89 | 3.84 | 3.35 | 3.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Zhao, Z.; Qi, L.; Sumantri, M.A.; Liu, H.; Li, J.; Zheng, K.; Wang, J. Design and Experimental Validation of a Multimodal Snake Robot with Elliptical Wheels. Biomimetics 2025, 10, 532. https://doi.org/10.3390/biomimetics10080532
Xiao X, Zhao Z, Qi L, Sumantri MA, Liu H, Li J, Zheng K, Wang J. Design and Experimental Validation of a Multimodal Snake Robot with Elliptical Wheels. Biomimetics. 2025; 10(8):532. https://doi.org/10.3390/biomimetics10080532
Chicago/Turabian StyleXiao, Xuan, Zizhu Zhao, Lianzhi Qi, Michael Albert Sumantri, Hengwei Liu, Jianqin Li, Keyang Zheng, and Jianming Wang. 2025. "Design and Experimental Validation of a Multimodal Snake Robot with Elliptical Wheels" Biomimetics 10, no. 8: 532. https://doi.org/10.3390/biomimetics10080532
APA StyleXiao, X., Zhao, Z., Qi, L., Sumantri, M. A., Liu, H., Li, J., Zheng, K., & Wang, J. (2025). Design and Experimental Validation of a Multimodal Snake Robot with Elliptical Wheels. Biomimetics, 10(8), 532. https://doi.org/10.3390/biomimetics10080532






