Explainable Reinforcement Learning for the Initial Design Optimization of Compressors Inspired by the Black-Winged Kite
Abstract
1. Introduction
- (1)
- This study significantly expands the optimization space by introducing more key design variables. Compared with the limited parameters usually focused on in the existing work, this method can simultaneously deal with 25 multi-dimensional design variables, including inlet airflow angle, tip diameter, load factor, etc. It makes the initial design of compressor more flexible, comprehensive, and closer to the actual needs of complex engineering.
- (2)
- The decision tree distillation technique is firstly introduced into the compressor initial design to enhance the design explainability. The improved DDPG algorithm is used to optimize the initial parameters. The key design features are revealed by SHAP value analysis. And the explainable design rules are extracted by the decision tree inspired by black-winged kite. This new paradigm of “Intelligent Optimization-Rule Extraction” not only optimizes the performance of compressor but also transforms the data-driven intelligent optimization into explainable engineering experience. This application perspective provides a new thinking for compressor design that combines high performance and transparency.
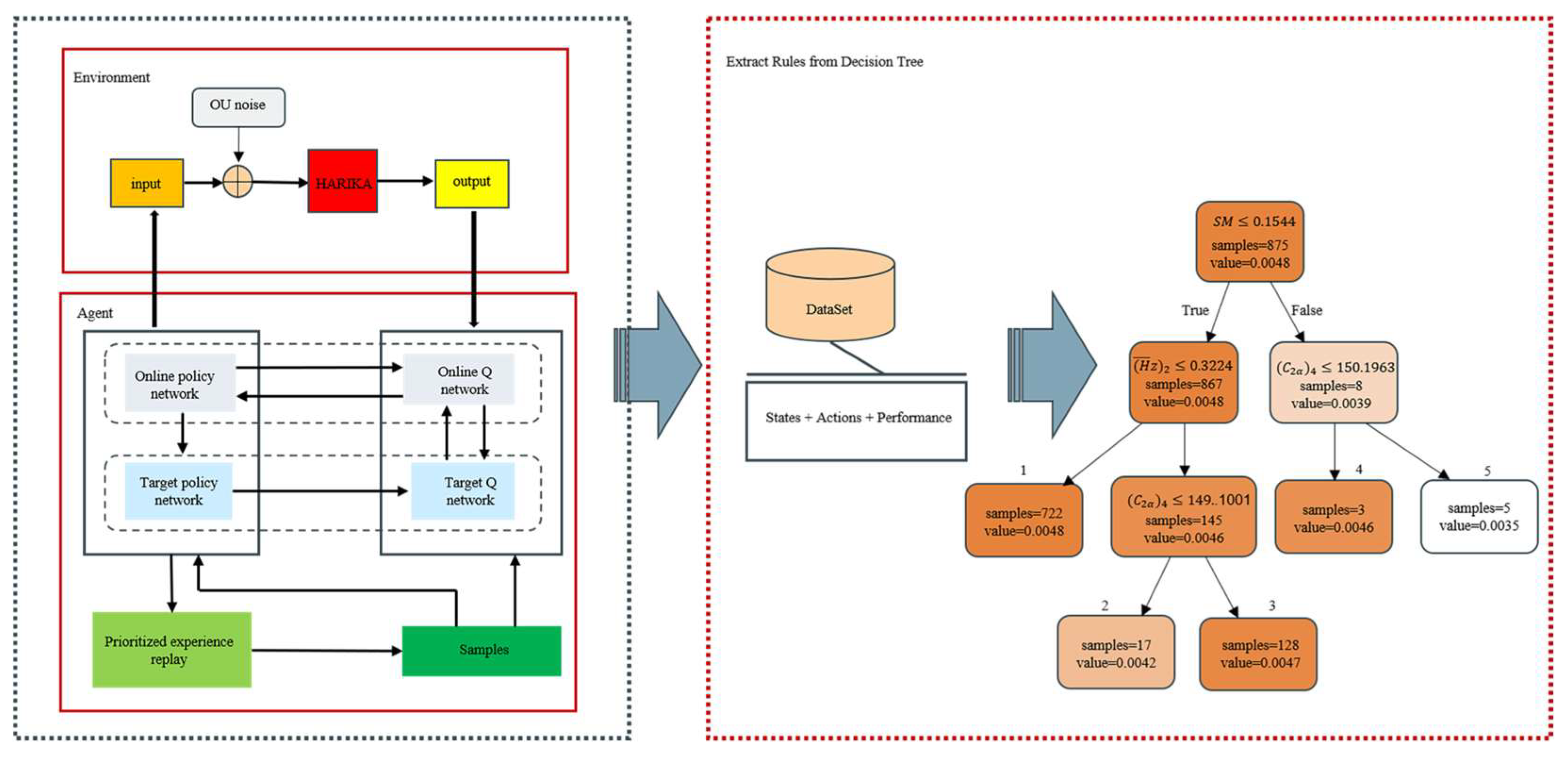
2. Reinforcement Learning Architecture
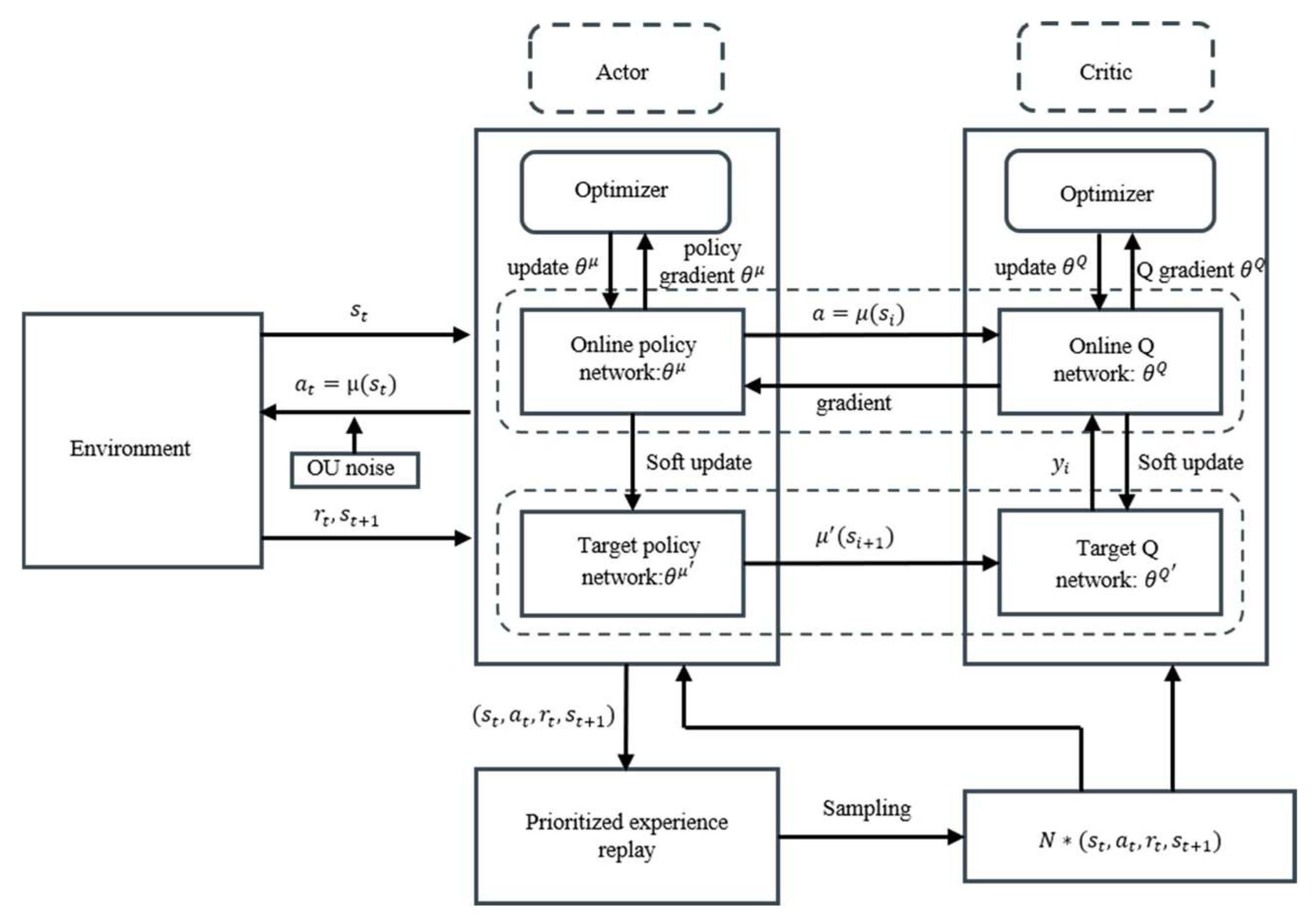
2.1. Deep Deterministic Policy Gradient
- (1)
- Actor–Critic
- (2)
- Dual-network architecture
- (3)
- Noise exploration
- (4)
- Soft update for target network parameters
2.2. Prioritized Experience Replay
- (1)
- The probability of a sample being sampled should be positively correlated with the sample priority.
- (2)
- Each sample should have a chance to be sampled, i.e., the probability of being sampled is greater than 0.
3. Explainability for Intelligent Design
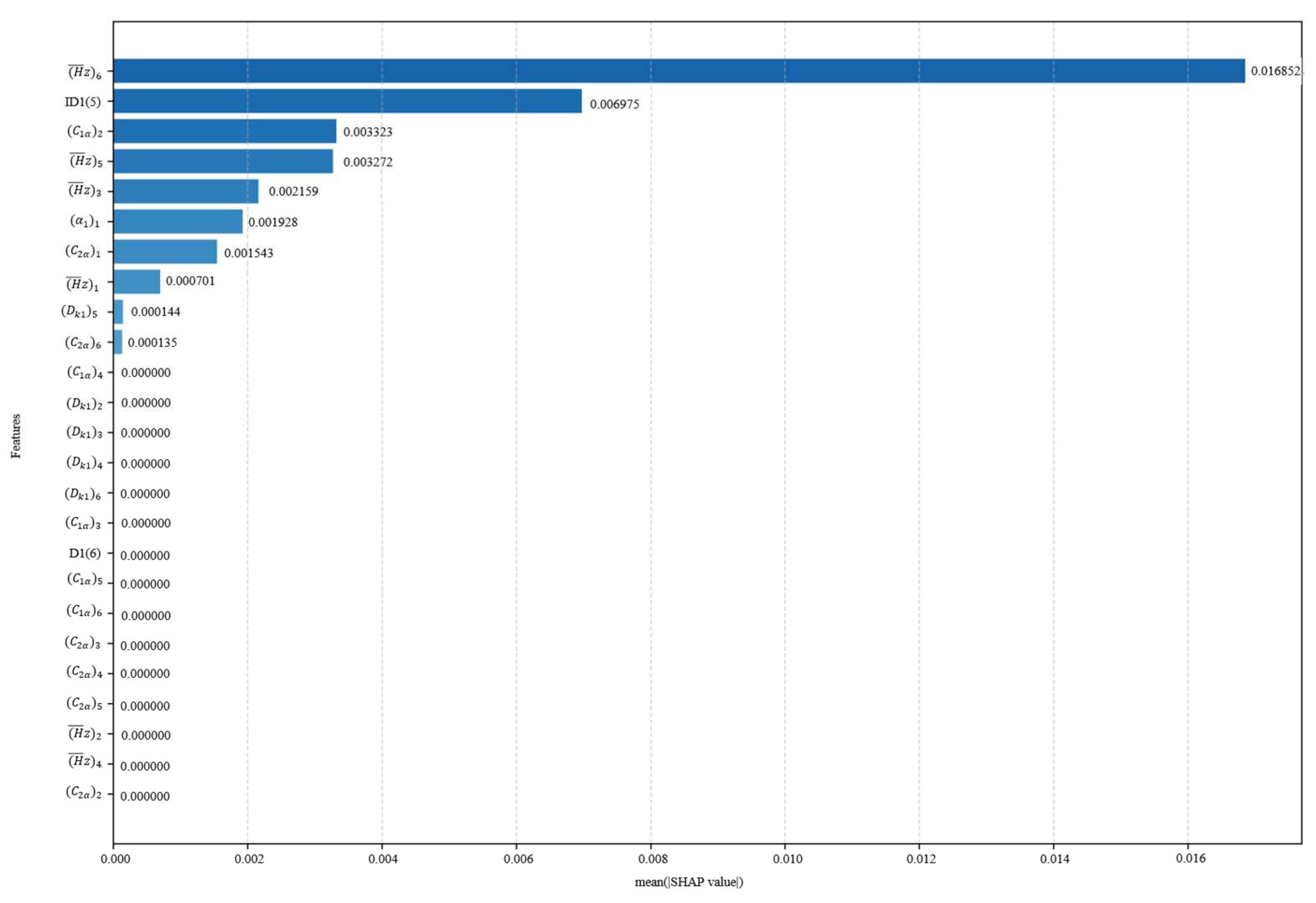
3.1. SHAP Analysis
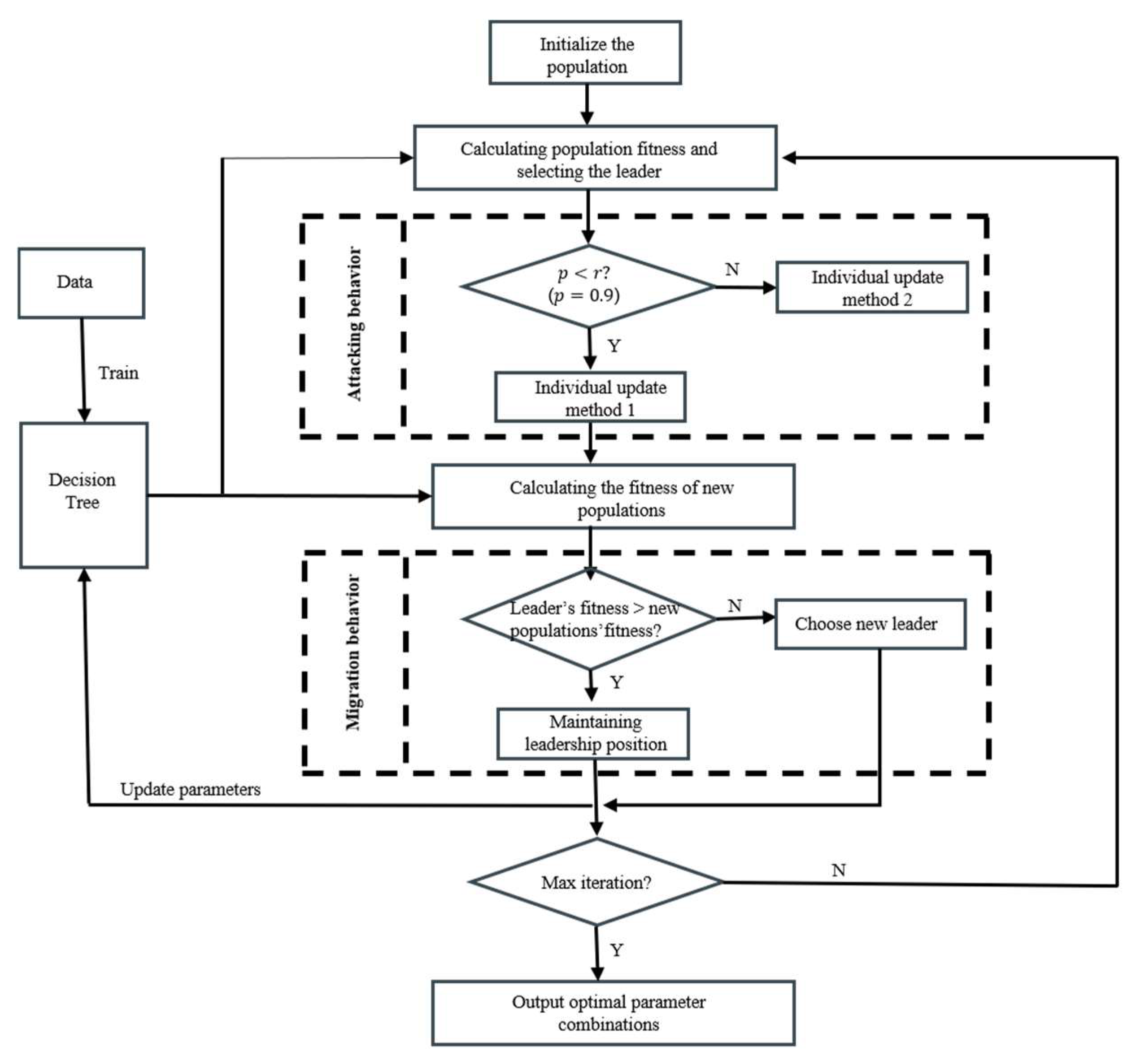
3.2. Decision Tree
3.2.1. Fundamental Theory
3.2.2. Decision Tree Tuning by BKA
4. Filtering Platform on Initial Design Options for Compressor
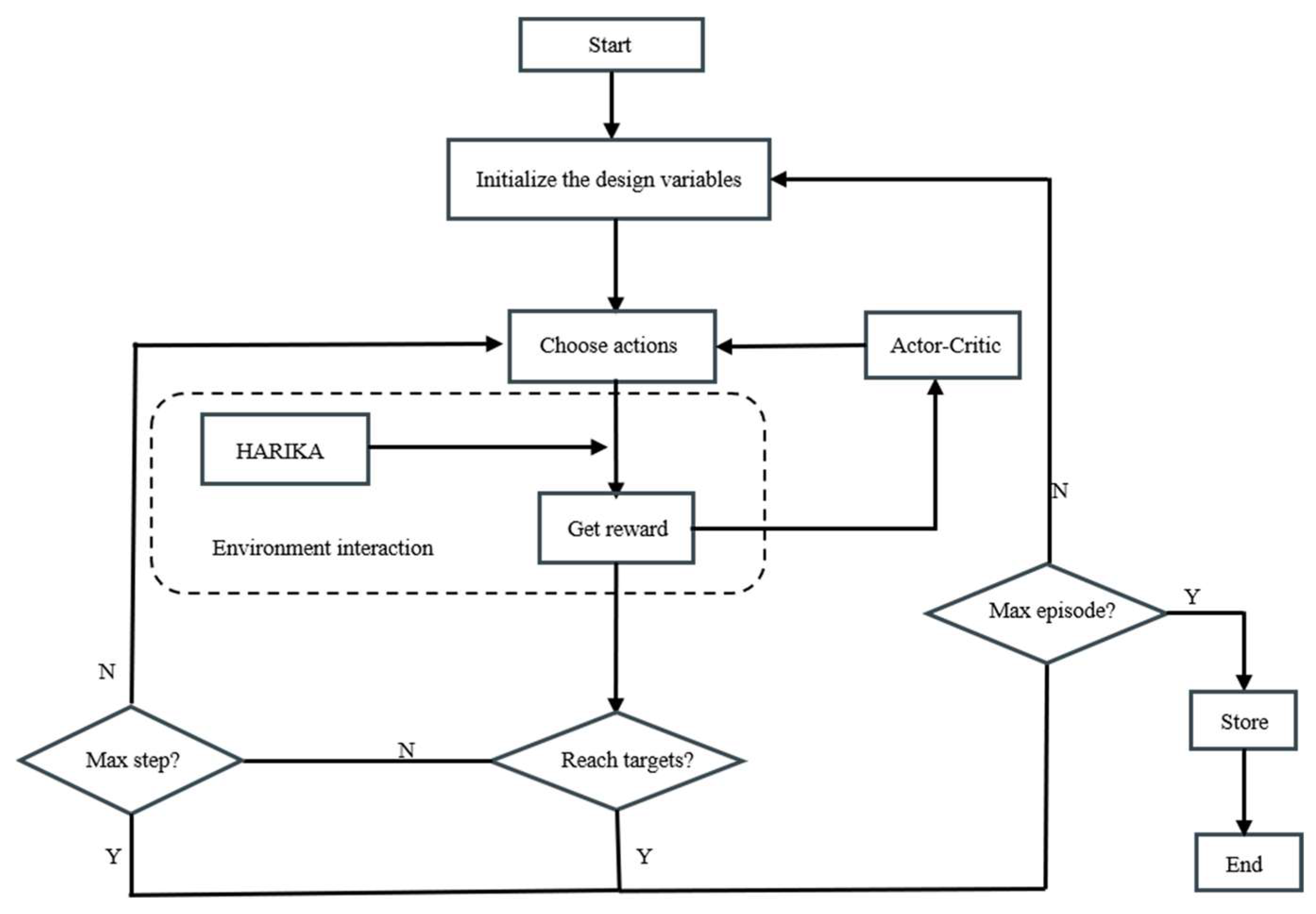
4.1. Algorithm Settings
- (1)
- Environment. The HARIKA program is selected as the environment to interact with the agent. The inputs to HARIKA include design requirements and design variables. The design requirements include the given inlet total pressure, total temperature, pressure ratio, flow rate, etc. And the design variables include the tip diameter, rotational speed, and load coefficients, which need to be determined.
- (2)
- States. According to the design requirements, the inlet airflow angle, the tip diameters of each stage, the inlet axial velocity of each stage rotor, the outlet axial velocity of each stage rotor, the load factors of each stage, the reaction, and the reaction increment are selected as the design variables, which affect the aerodynamic performance to a large extent. The definitions and the values of these parameters are shown in Table 1. The state of DDPG is set as a one-dimensional array of these 25 variables, and the value of each variable in the array is equal to the value of the corresponding design variable.
- (3)
- Actions. The values of the 25 design variables are defined as actions, and the action array is the same size as the state array with 25 variables.
- (4)
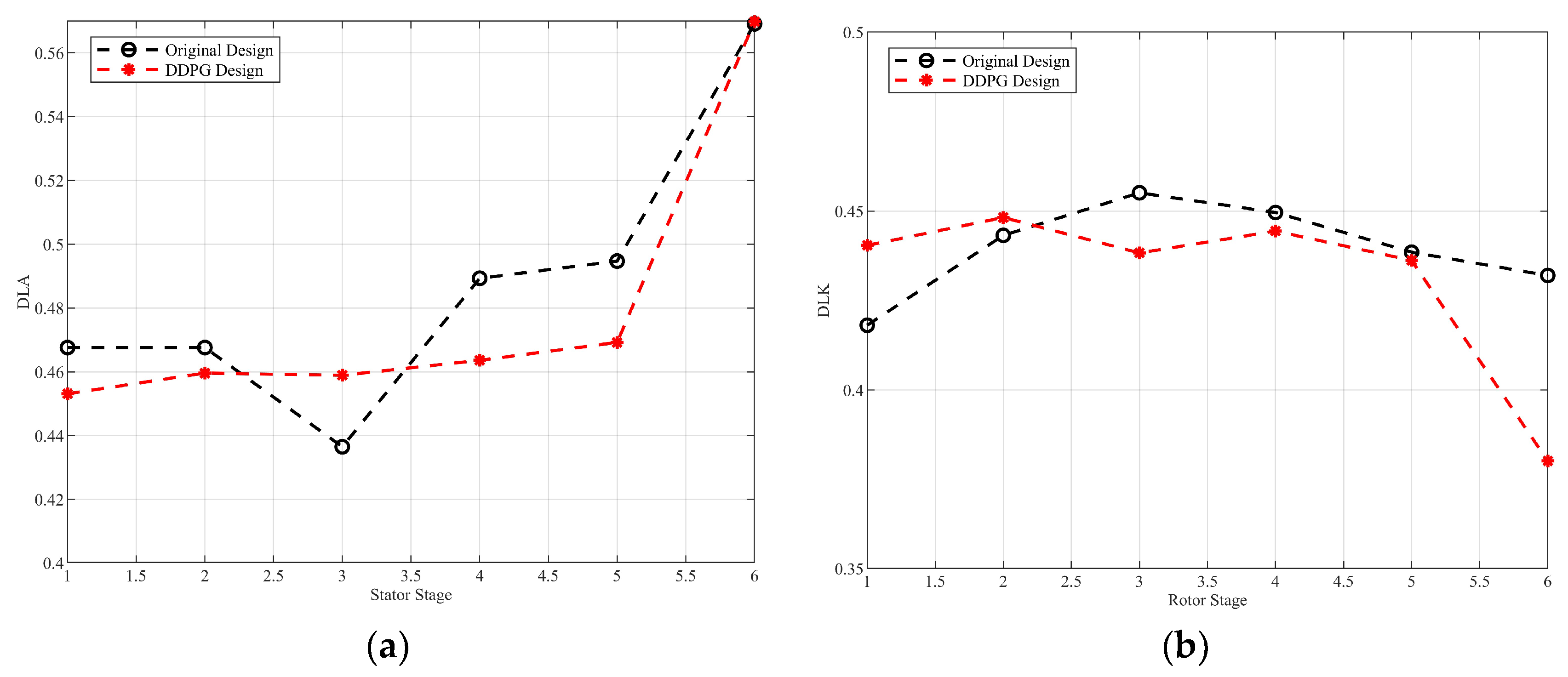
- Rewards. The compressor efficiency at the design speed can be obtained by calculating with the HARIKA program, as well as the surge margin. The formula for the surge margin is defined as,where π is the pressure ratio, G is the flow rate, the subscript o represents the operating point, and s represents the surge point.The D factor is a key parameter in the compressor aerodynamic design to measure the degree of diffusion of the airflow within the cascade. The larger the D factor, the more severe the deceleration of the airflow in the cascade. The boundary layer is prone to separating with a large D factor, resulting in a loss of efficiency or stalling. The DLK as the D factor of the rotor is used to assess the risk of separation of the suction surfaces of the rotor blades and directly affects the stall margin of the rotor. The DLA as the D factor of the stator is used to control the boundary layer development, which affects the secondary flow and total pressure loss in the endwall. In the design of a six-stage compressor, DLA is set as less than 0.57.During the design process, the target is to obtain the greatest possible efficiency and margin, with satisfying the constraints leading to the design of a multi-constraint reward function aswhere is the efficiency and are the two penalty terms related to the surge margin and the D-factor, respectively. and are the two indicator functions, which are only effective if the constraints are not satisfied. , and are the weighting coefficients.
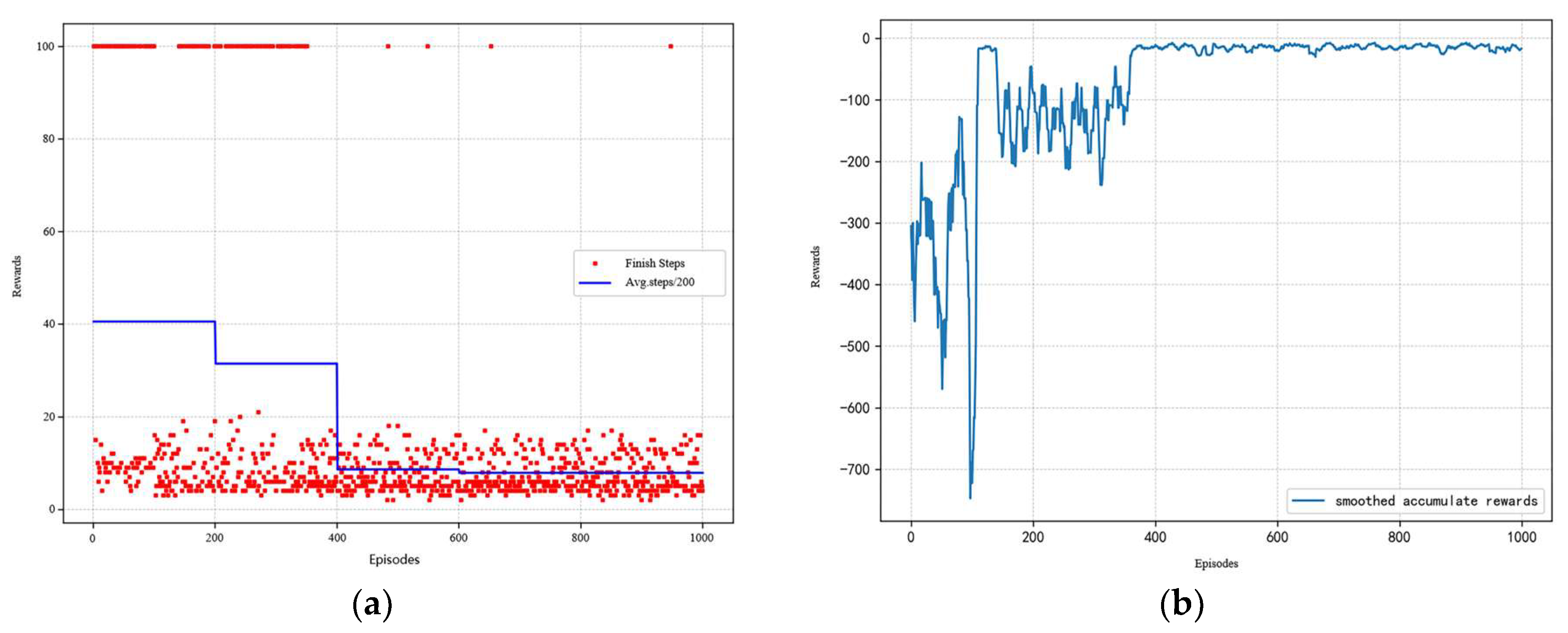
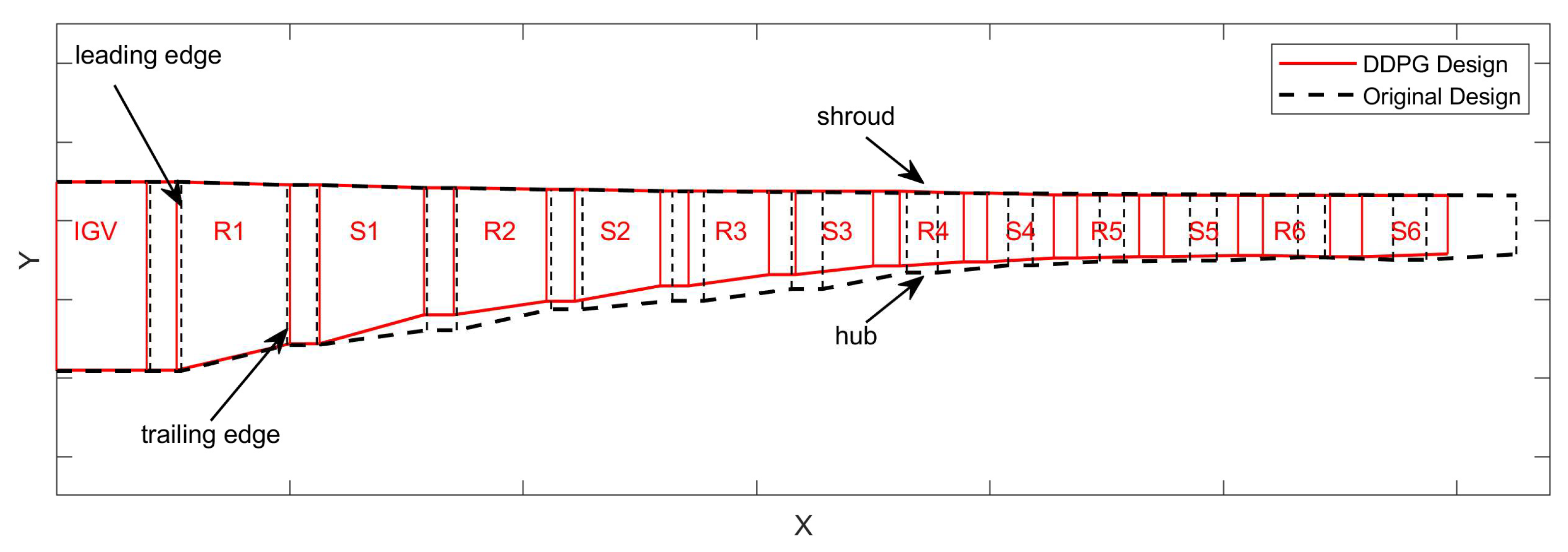
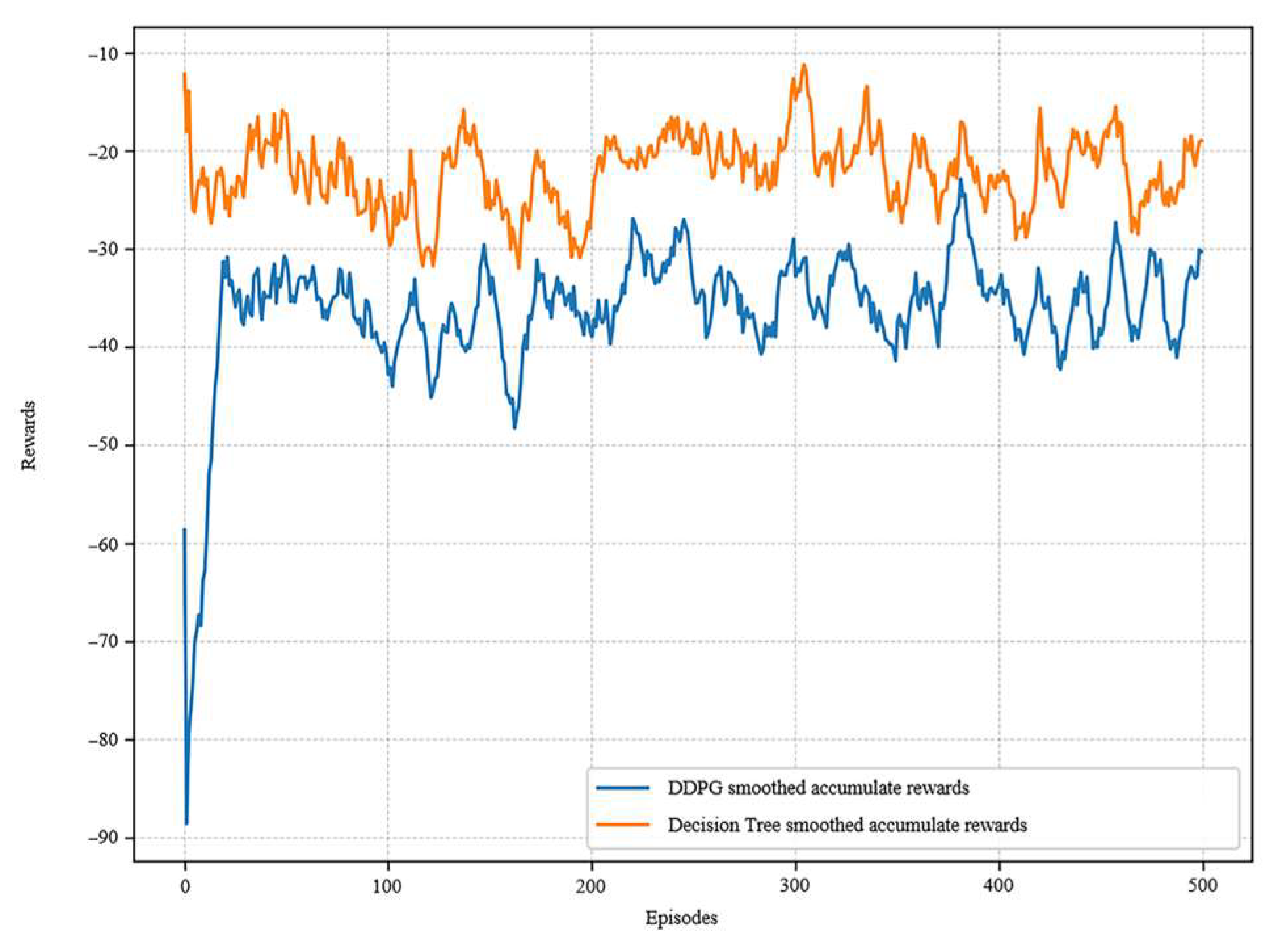
4.2. Optimization Results
5. Model Explanation and Rule Extraction
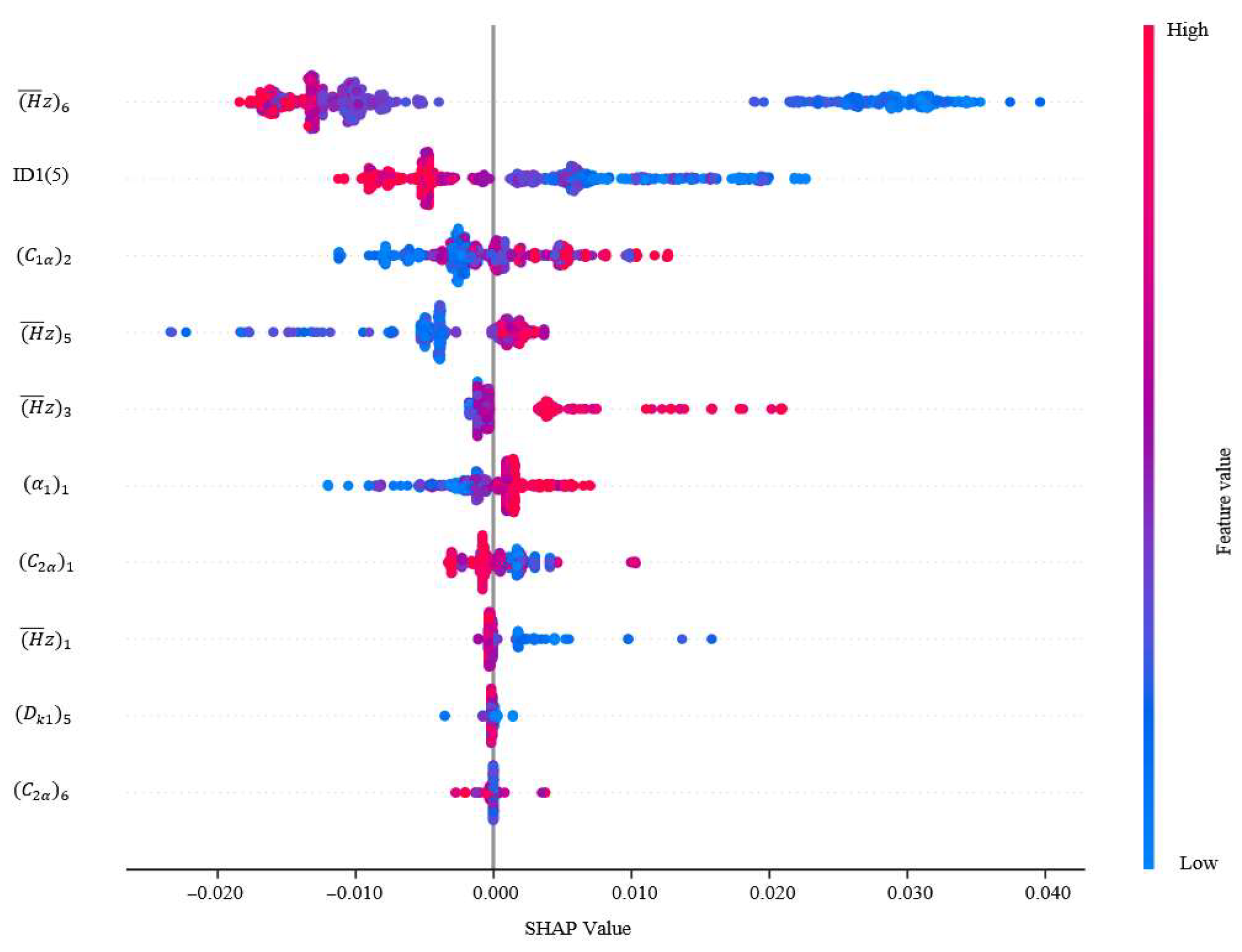
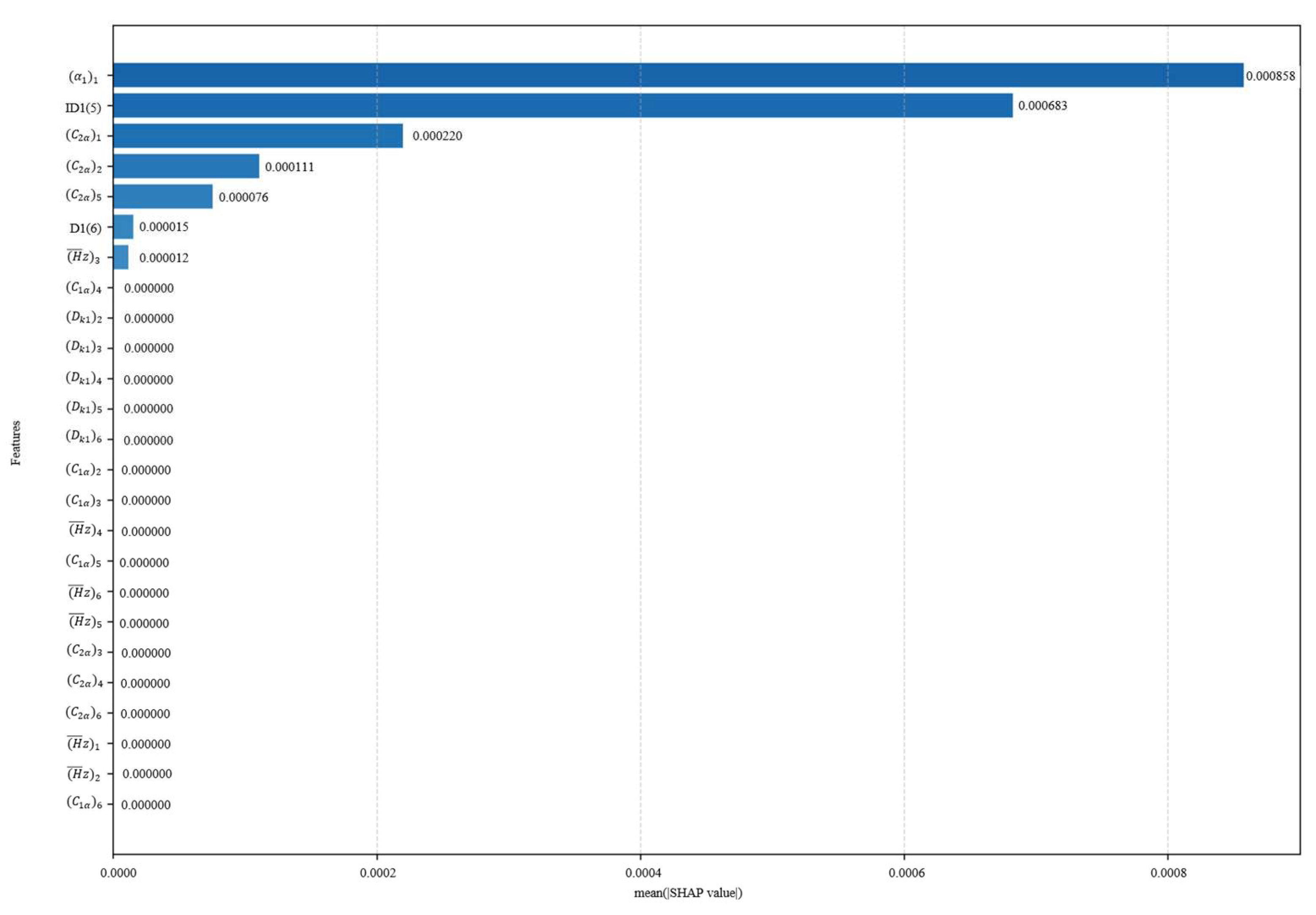
5.1. SHAP Analysis of Key Design Parameters on Compressor Performance
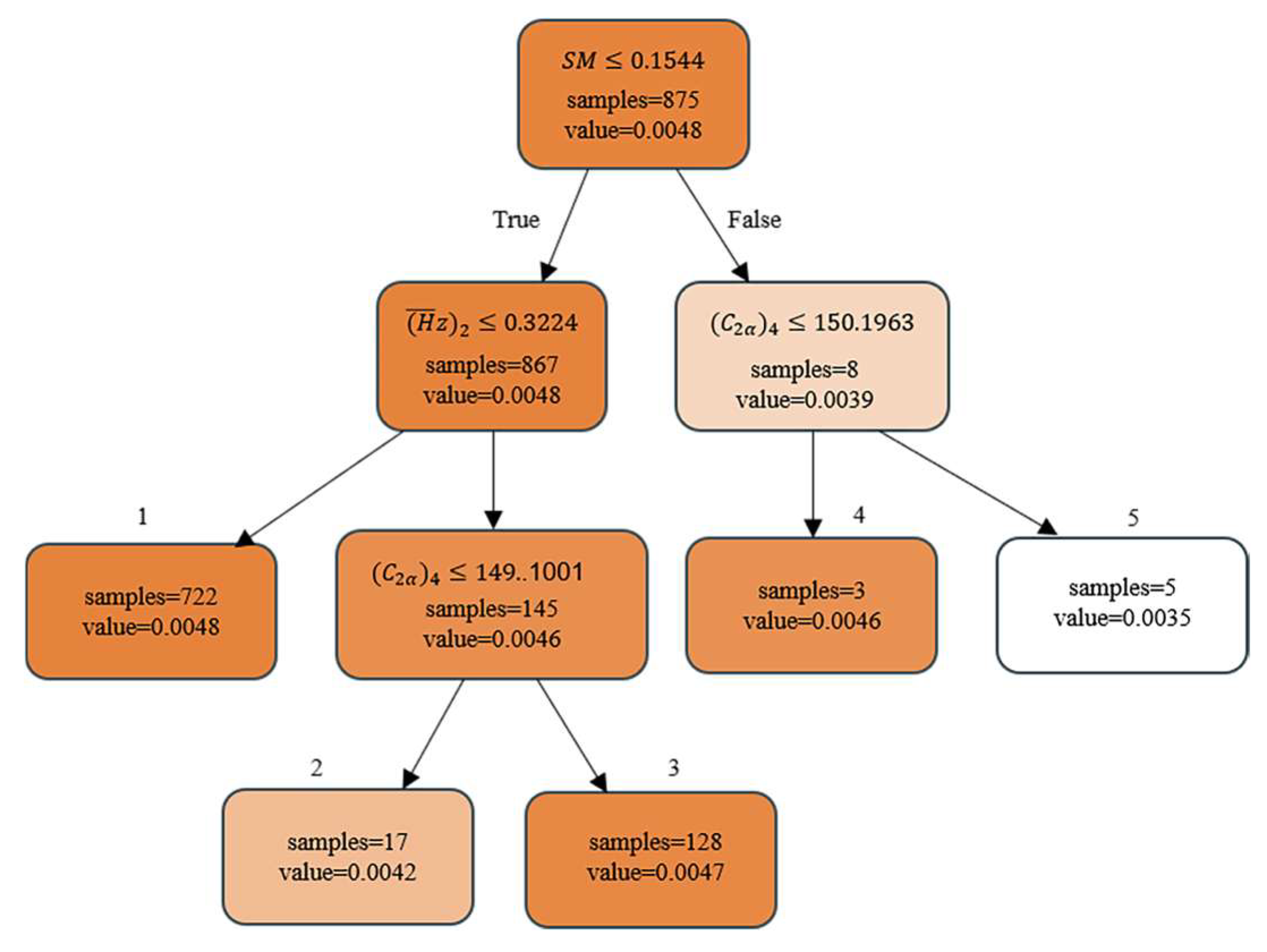
5.2. Decision Tree Rule Extraction for Initial Design
5.3. Rule Validation
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ransom, D.; Srinivasan, R. Machine Learning Application to Centrifugal Compressor Design. In Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition. Volume 12D: Turbomachinery—Multidisciplinary Design Approaches, Optimization, and Uncertainty Quantification; Radial Turbomachinery Aerodynamics; Unsteady Flows in Turbomachinery, London, UK, 24–28 June 2024; American Society of Mechanical Engineers: London, UK, 2024. [Google Scholar]
- Bourabia, L.; Abed, C.B.; Cerdoun, M.; Khalfallah, S.; Deligant, M.; Khelladi, S.; Chettibi, T. Aerodynamic preliminary design optimization of a centrifugal compressor turbocharger based on one-dimensional mean-line model. Eng. Comput. 2021, 38, 3438–3469. [Google Scholar] [CrossRef]
- Ma, Y.; Du, Z.; Xu, Q. Enhancing accuracy of one-dimensional characteristic predictions for axial compressors using deep learning. Eng. Appl. Artif. Intell. 2025, 149, 110533. [Google Scholar] [CrossRef]
- Yan, W.; Zheng, Q.; Chi, Z.; Jiang, B. Improving the accuracy of one-dimensional analysis in axial compressor performance pre-diction. Phys. Fluids 2025, 3, 37. [Google Scholar]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 2023, 231, 120495. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Pro-cess. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Dworschak, F.; Dietze, S.; Wittmann, M.; Schleich, B.; Wartzack, S. Reinforcement learning for engineering design automation. Adv. Eng. Inform. 2022, 52, 101612. [Google Scholar] [CrossRef]
- Sabzevari, M.; Szedmak, S.; Penttilä, M.; Jouhten, P.; Rousu, J. Strain design optimization using reinforcement learning. PLoS Comput. Biol. 2022, 18, e1010177. [Google Scholar] [CrossRef]
- Brown, N.K.; Garland, A.P.; Fadel, G.M.; Li, G. Deep reinforcement learning for engineering design through topology optimization of elementally discretized design domains. Mater. Des. 2022, 218, 110672. [Google Scholar] [CrossRef]
- Qin, S.; Wang, S.; Wang, L.; Wang, C.; Sun, G.; Zhong, Y. Multi-Objective Optimization of Cascade Blade Profile Based on Rein-forcement Learning. Appl. Sci. 2020, 11, 106. [Google Scholar] [CrossRef]
- Xu, X.; Huang, X.; Bi, D.; Zhou, M. An Intellectual Aerodynamic Design Method for Compressors Based on Deep Reinforcement Learning. Aerospace 2023, 10, 171. [Google Scholar] [CrossRef]
- Song, D.; Shen, J.; Ma, T.; Xu, F. Multi-objective acoustic sensor placement optimization for crack detection of compressor blade based on reinforcement learning. Mech. Syst. Signal Process. 2023, 197, 110350. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Z.; Ji, R.; Zhang, T. Deep reinforcement learning based active surge control for aeroengine compressors. Chin. J. Aeronaut. 2024, 37, 418–438. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Cheng, J. Mean line aerodynamic design of an axial compressor using a novel design approach based on rein-forcement learning. Proc. IMechE Part G J. Aerosp. Eng. 2022, 236, 2433–2446. [Google Scholar] [CrossRef]
- Lunderg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; p. 30. [Google Scholar]
- Vasilev, N.; Mincheva, Z.; Nikolov, V. Decision Tree Extraction using Trained Neural Network. In Proceedings of the SMARTGREENS—9th International Conference on Smart Cities and Green ICT Systems, Online, 2–4 May 2020; pp. 194–200. [Google Scholar]
- de Oña, J.; López, G.; Abellán, J. Extracting decision rules from police accident reports through decision trees. Accid. Anal. Prev. 2013, 50, 1151–1160. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, P.; Liang, K.; He, Y.; Ma, S. An alarm and fault association rule extraction method for power equipment based on explainable decision tree. In Proceedings of the 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021; pp. 442–446. [Google Scholar]
- Silva, A.; Gombolay, M.; Killian, T.; Jimenez, I.; Son, S. Optimization methods for interpretable differentiable decision trees applied to reinforcement learning. In Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics (AISTATS 2020), online, 26–28 August 2020; pp. 1855–1865. [Google Scholar]
- Coppens, Y.; Efthymiadis, K.; Lenaerts, T.; Nowé, A. Distilling deep reinforcement learning policies in soft decision trees. In Proceedings of the IJCAI 2019 Workshop on Explainable Artificial Intelligence, Cotai, Macao, 11 August 2019; pp. 1–6. [Google Scholar]
- Zhu, Y.; Yin, X.; Chen, C. Extracting decision tree from trained deep reinforcement learning in traffic signal control. IEEE Trans. Comput. Soc. Syst. 2022, 10, 1997–2007. [Google Scholar] [CrossRef]
- Otterlo, M.V.; Wiering, M. Reinforcement Learning and Markov Decision Processes; Springer: Heidelberg/Berlin, Germany, 2012; pp. 3–42. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 22–24 June 2014; pp. 387–395. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. In Proceedings of the IEEE International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Hou, Y.; Liu, L.; Wei, Q.; Xu, X.; Chen, C. A novel DDPG method with prioritized experience replay. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 316–321. [Google Scholar]
- Mosca, E.; Szigeti, F.; Tragianni, S.; Gallagher, D.; Groh, G. SHAP-based explanation methods: A review for NLP interpretability. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 4593–4603. [Google Scholar]
- Yuan, H.; Yu, H.; Wang, J.; Li, K.; Ji, S. On explainability of graph neural networks via subgraph explorations. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 12241–12252. [Google Scholar]
- Chen, H.; Zheng, G.; Ji, Y. Generating hierarchial explanations on text classification via feature interaction detection. arXiv 2020, arXiv:2004.02015. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; Routledge: London, UK, 2017; pp. 216–247. [Google Scholar]
- Rodrigues, L.R. A hybrid multi-population metaheuristic applied to load-sharing optimization of gas compressor stations. Comput. Electr. Eng. 2022, 97, 107632. [Google Scholar] [CrossRef]
- Sattar, D.; Salim, R. A smart metaheuristic algorithm for solving engineering problems. Eng. Comput. 2021, 37, 2389–2417. [Google Scholar] [CrossRef]
- Zhang, M.; Kong, P.; Xia, A.; Tuo, W.; Lu, Y.; Wang, S. Aerodynamic system machine learning modeling with gray wolf op-timization support vector regression and instability identification strategy of wavelet singular spectrum. Biomimetics 2023, 8, 132. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, W.; Hu, X.; Qu, L.; Zang, H. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artifi. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Zhong, Y. Mean Line Performance Calculation and Optimization of Multi-Stage Axial Compressor. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2014. [Google Scholar]
- Chen, J.; Liu, T. Numerical study on aerodynamic design of 5-stage axial compressor. J. Eng. Thermophys. 2010, 6, 943–946. [Google Scholar]



| Definition | Design Variable | Ranges |
|---|---|---|
| Inlet airflow angle | (°) | 55–70 |
| (m) | 0.40–0.43 | |
| (m/s) | 110–170 | |
| (m/s) | 110–170 | |
| 0.2–0.35 | ||
| Reaction | 0.5–0.8 | |
| Reaction increment | 0–0.025 |
| Design Variables | Original Design | DDPG Design |
|---|---|---|
| (°) | 73 | 65.71 |
| (m/s) | 136.8 | 153.52 |
| (m/s) | 136.8 | 157.54 |
| (m/s) | 151.3 | 157.11 |
| (m/s) | 143.7 | 151.46 |
| (m/s) | 129.5 | 132.83 |
| (m/s) | 130.9 | 134.36 |
| (m/s) | 134.9 | 145.34 |
| (m/s) | 132.7 | 151.83 |
| (m/s) | 146.3 | 148.24 |
| (m/s) | 130 | 137.1 |
| (m/s) | 113 | 118.54 |
| 0.25 | 0.2807 | |
| 0.28 | 0.3076 | |
| 0.27 | 0.3055 | |
| 0.27 | 0.2932 | |
| 0.24 | 0.2711 | |
| 0.23 | 0.2195 | |
| 0.62 | 0.6654 | |
| 0.05 | 0.0212 |
| Design Rules |
|---|
| ① THEN value = 0.0048 |
| ② THEN value = 0.0042 |
| ③ THEN value = 0.0047 |
| ④ THEN value = 0.0046 |
| ⑤ > 150.1963 THEN value = 0.0035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Miao, Z.; Nan, X.; Ma, N.; Liu, R. Explainable Reinforcement Learning for the Initial Design Optimization of Compressors Inspired by the Black-Winged Kite. Biomimetics 2025, 10, 497. https://doi.org/10.3390/biomimetics10080497
Zhang M, Miao Z, Nan X, Ma N, Liu R. Explainable Reinforcement Learning for the Initial Design Optimization of Compressors Inspired by the Black-Winged Kite. Biomimetics. 2025; 10(8):497. https://doi.org/10.3390/biomimetics10080497
Chicago/Turabian StyleZhang, Mingming, Zhuang Miao, Xi Nan, Ning Ma, and Ruoyang Liu. 2025. "Explainable Reinforcement Learning for the Initial Design Optimization of Compressors Inspired by the Black-Winged Kite" Biomimetics 10, no. 8: 497. https://doi.org/10.3390/biomimetics10080497
APA StyleZhang, M., Miao, Z., Nan, X., Ma, N., & Liu, R. (2025). Explainable Reinforcement Learning for the Initial Design Optimization of Compressors Inspired by the Black-Winged Kite. Biomimetics, 10(8), 497. https://doi.org/10.3390/biomimetics10080497




