Design and Implementation of a Biomimetic Underwater Robot Propulsion System Inspired by Bullfrog Hind Leg Movements
Abstract
1. Introduction
2. Analysis of Bullfrog Movement
2.1. Experimental Protocol Design
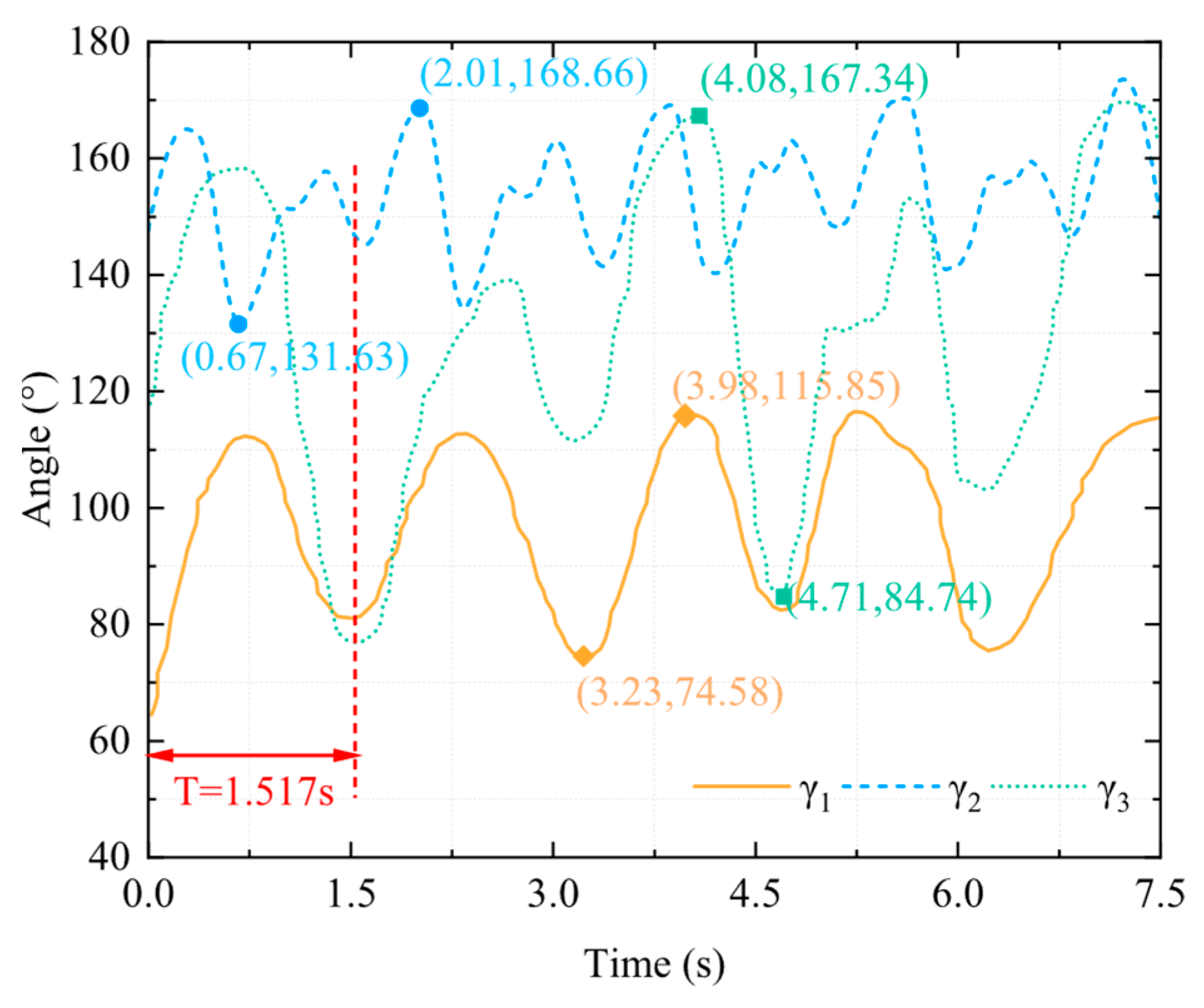
2.2. Experimental and Test Data
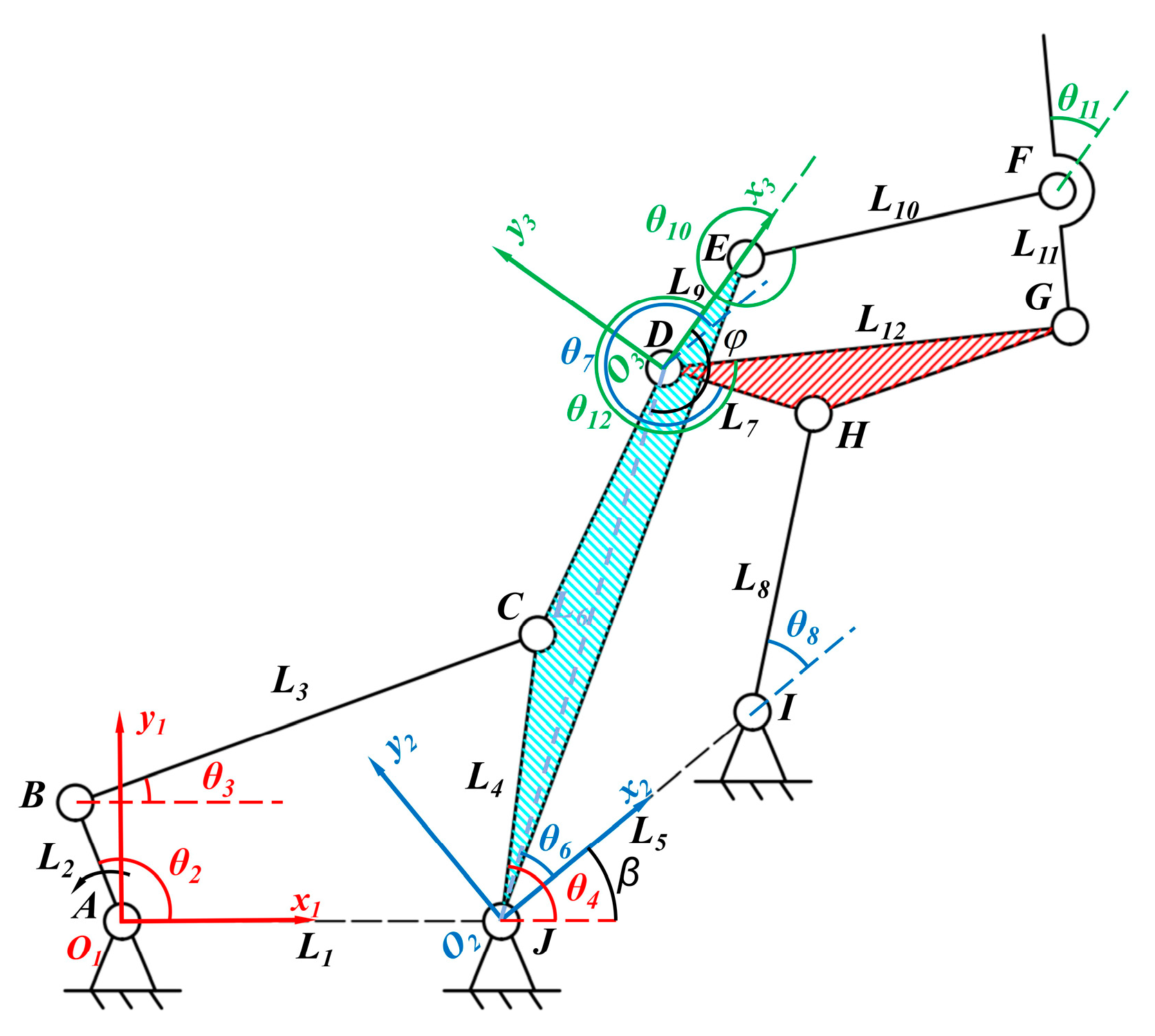
3. Mechanical Design of Bionic Bullfrog Hindlimb
4. Bionic Bullfrog Experiment and Analysis
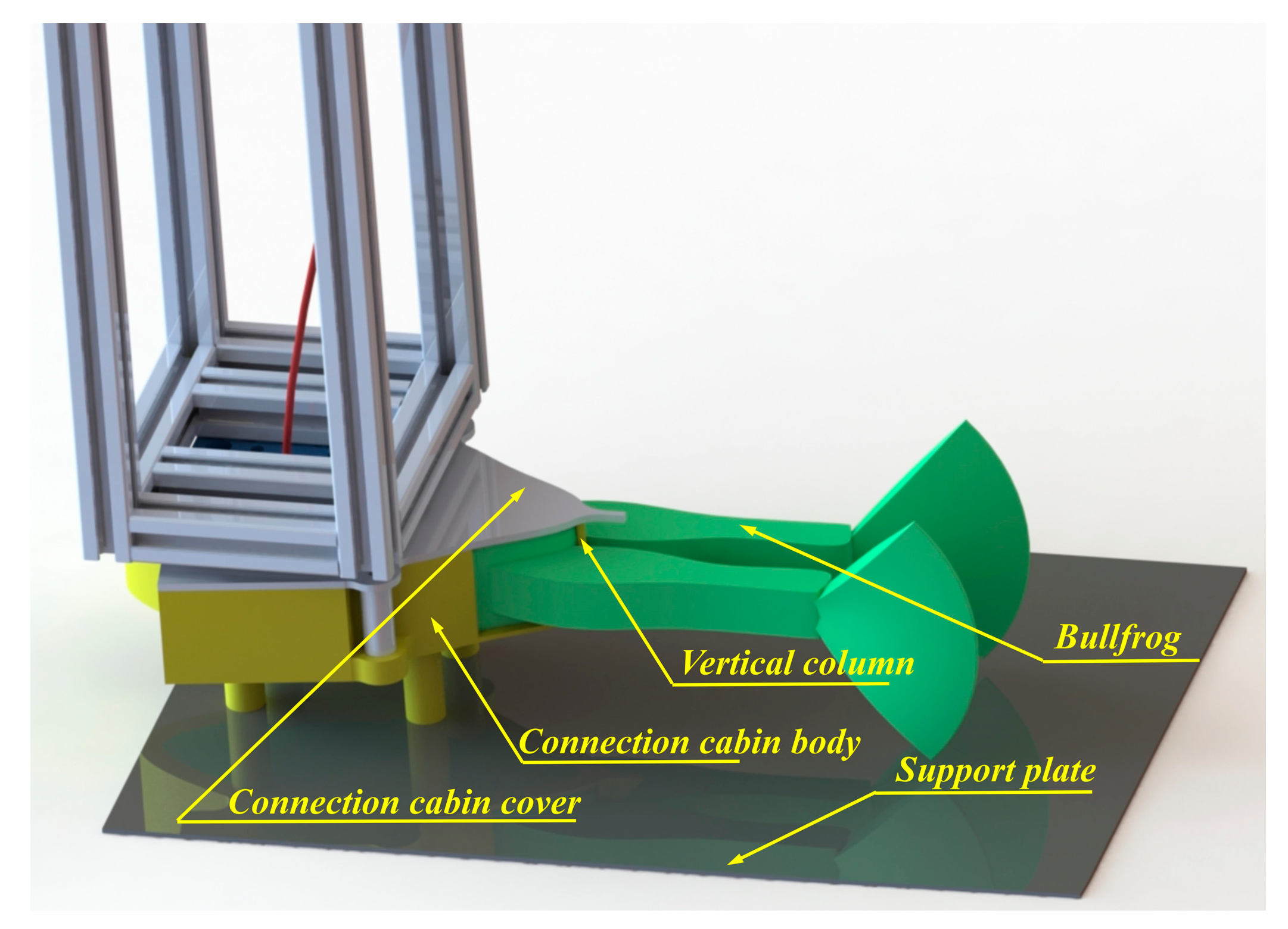
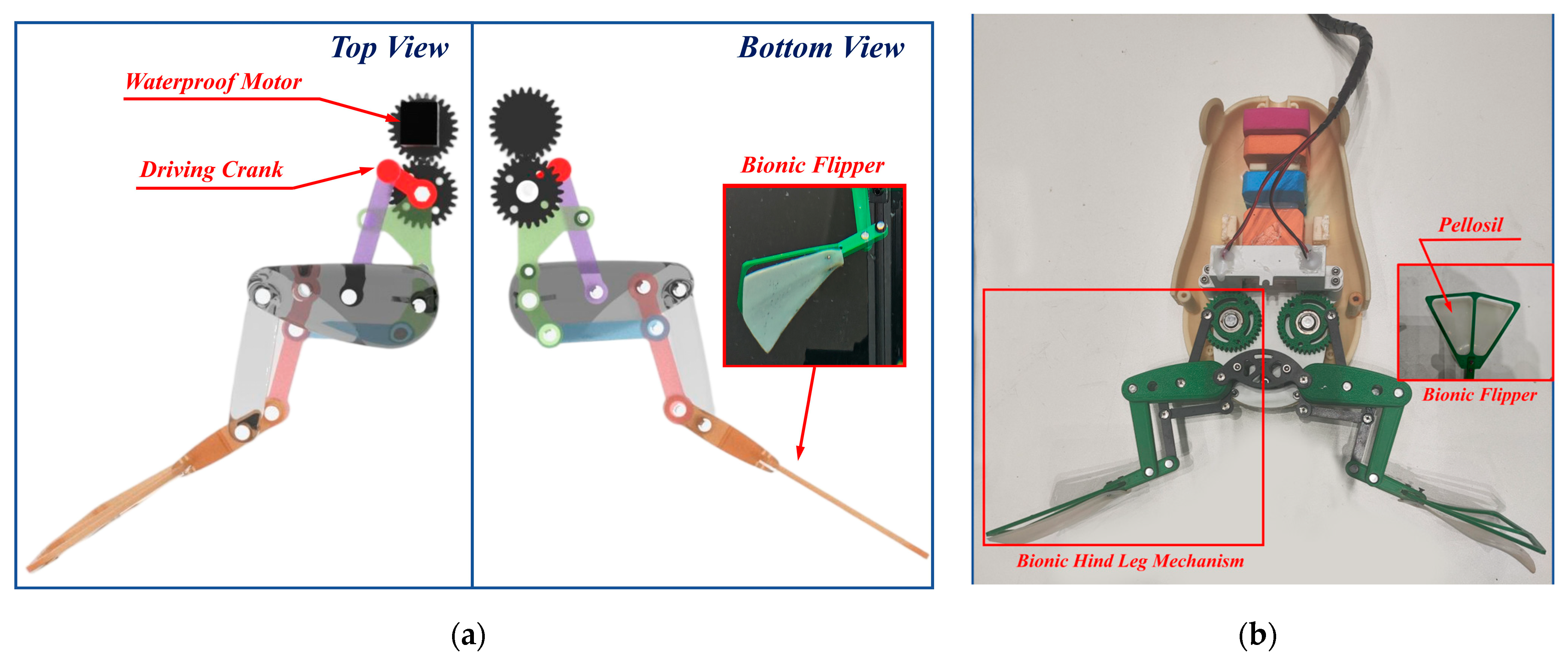
4.1. Experimental Prototype Design of a Bionic Bullfrog Hind Limb Propulsion System
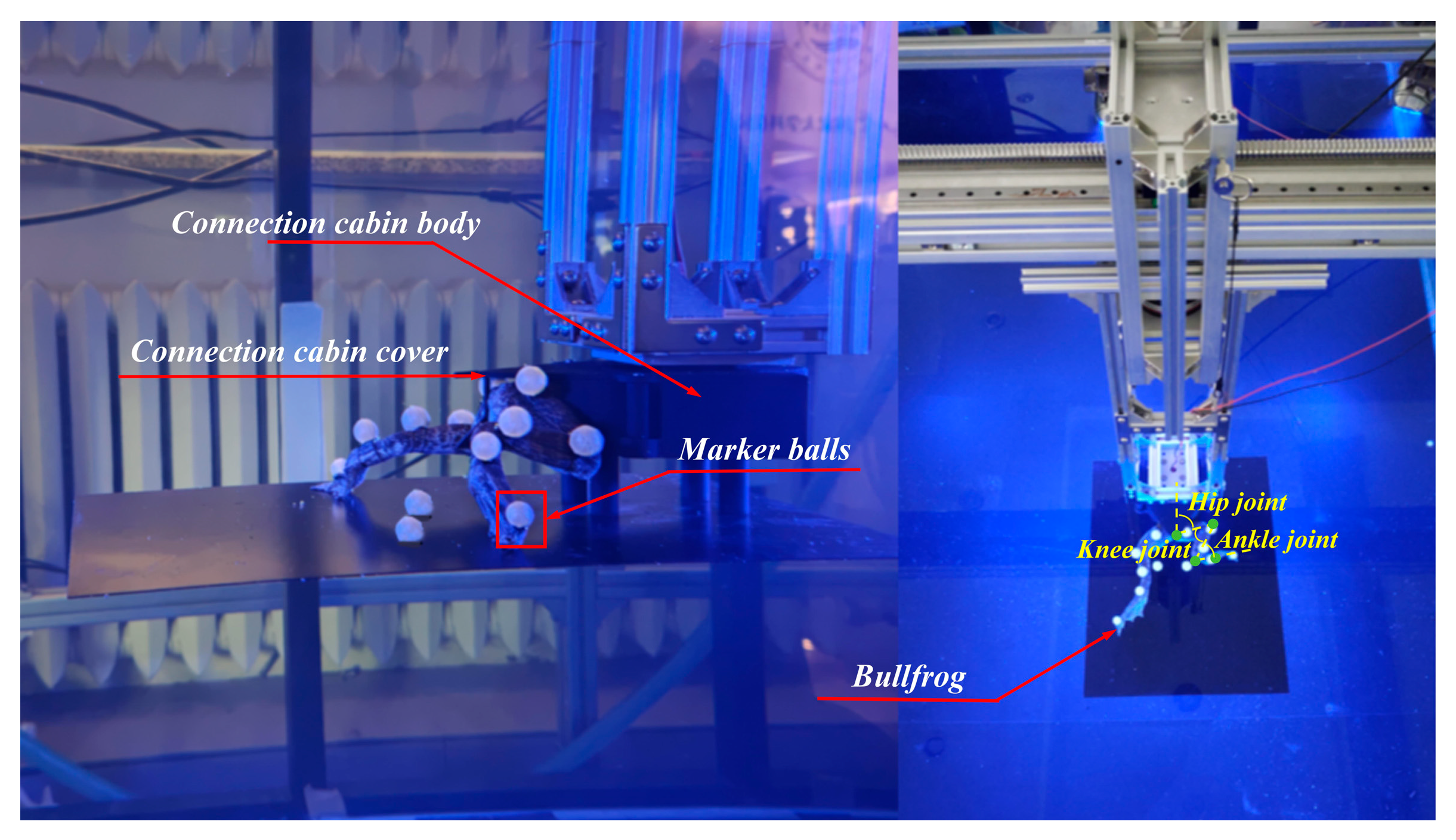
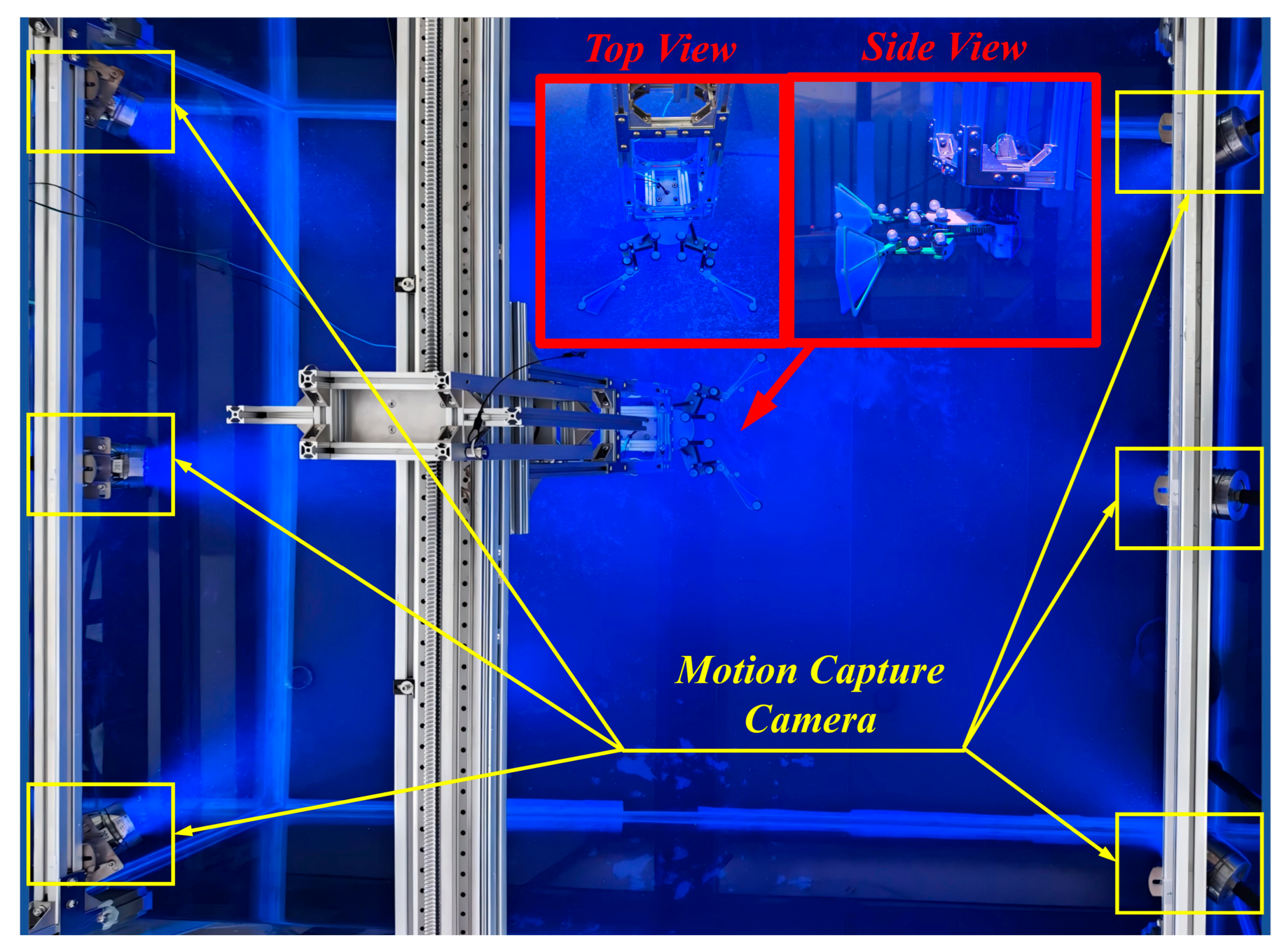
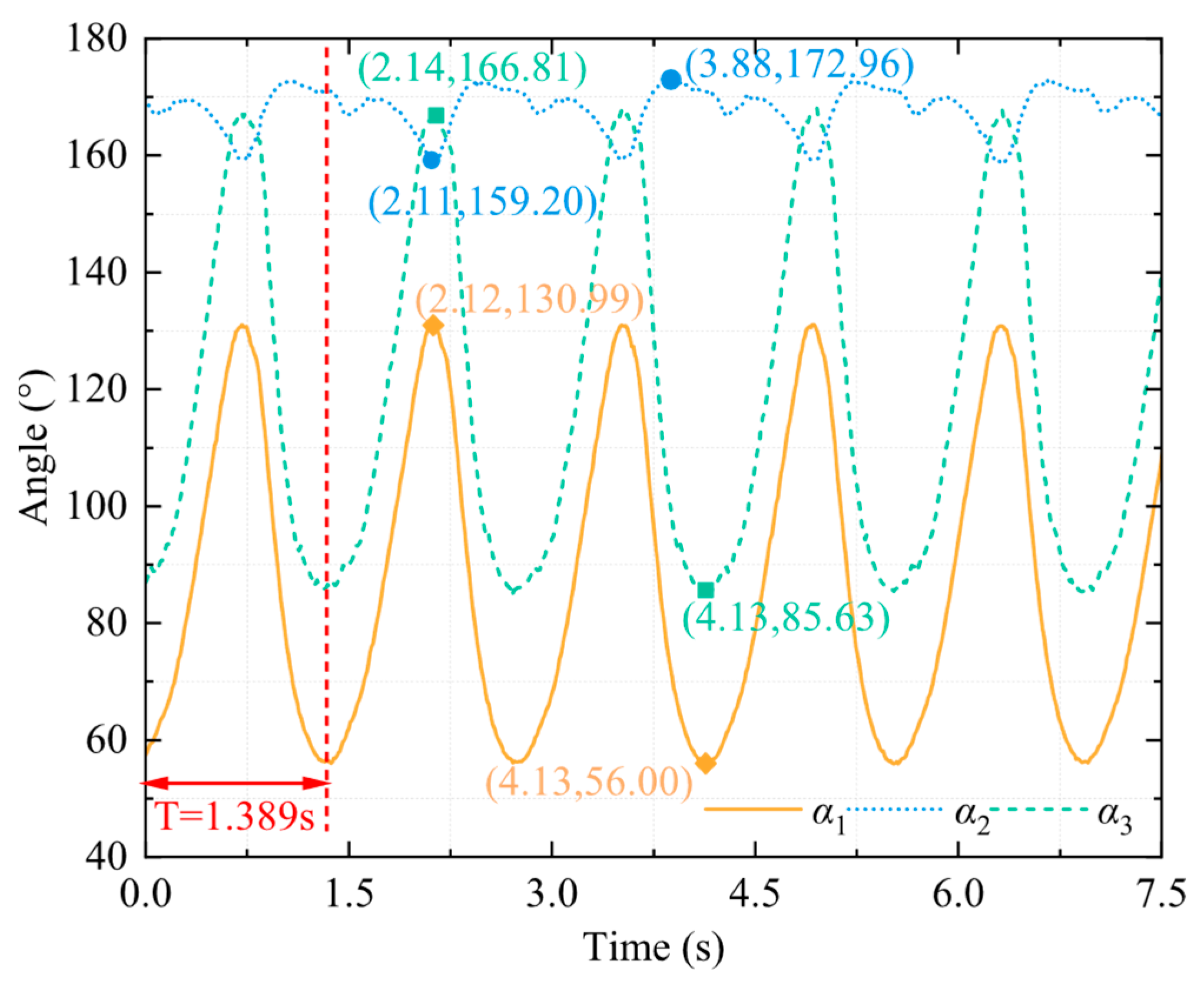
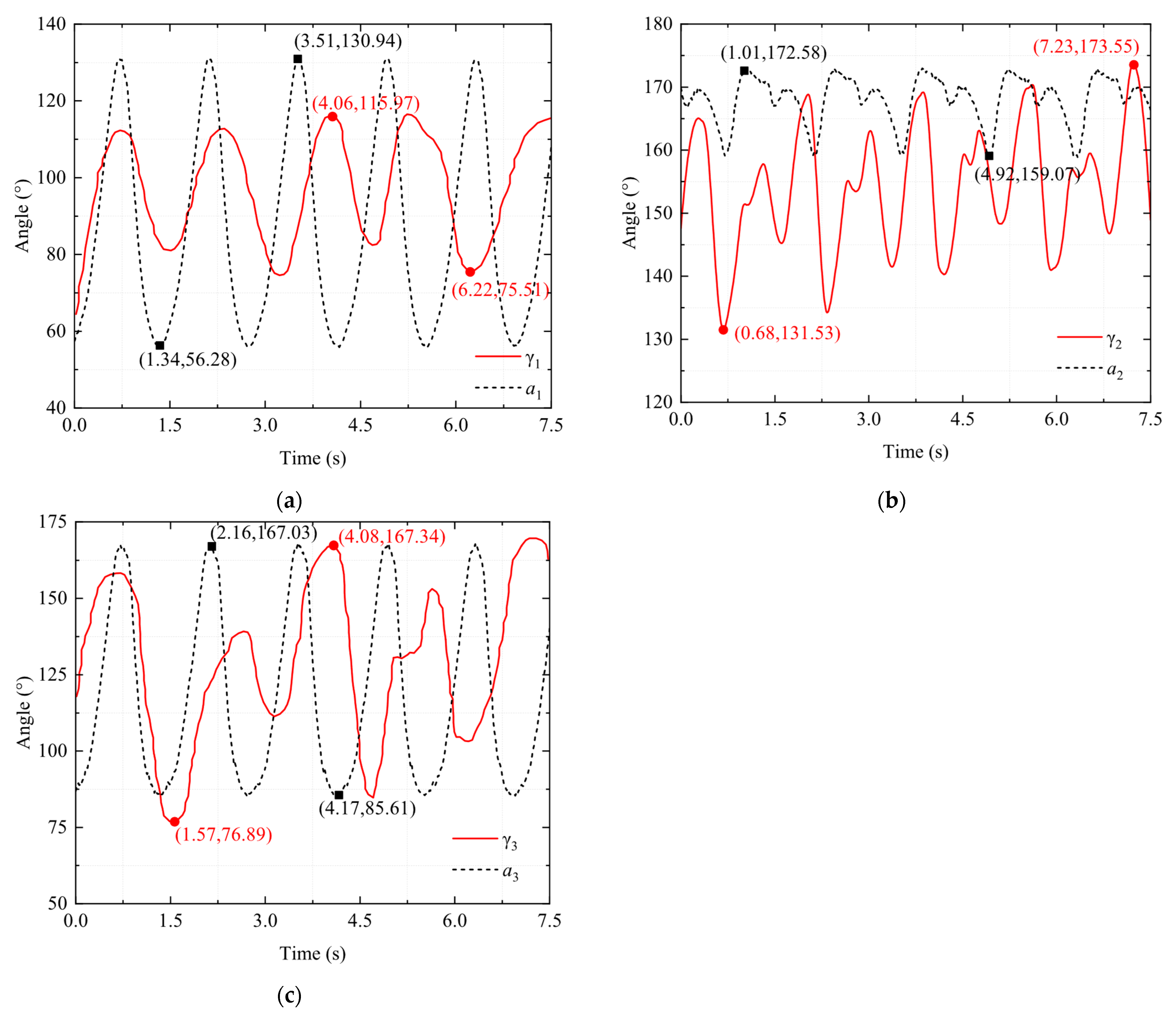
4.2. Motion Capture Experiment on the Hind Legs of a Bionic Bullfrog
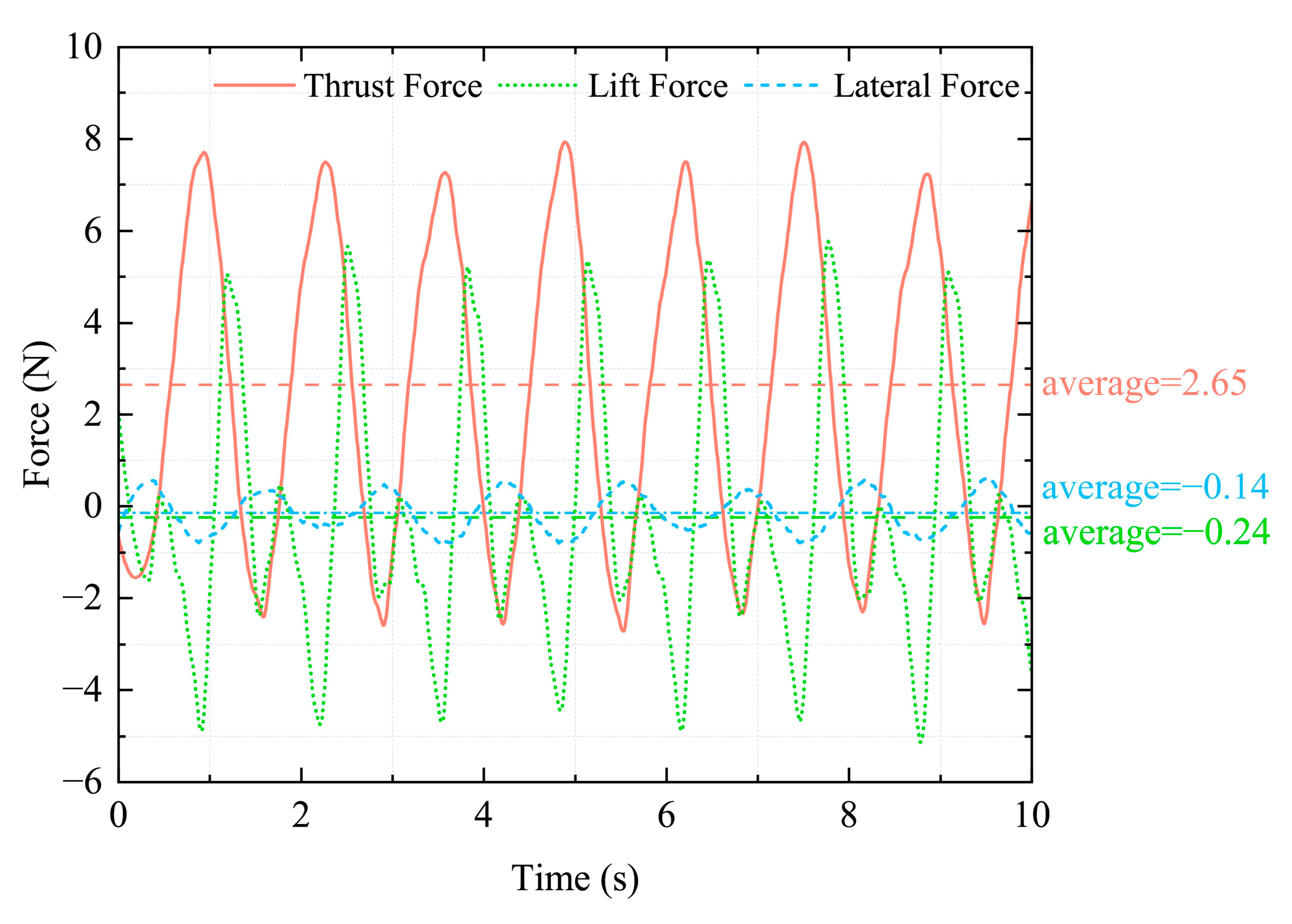
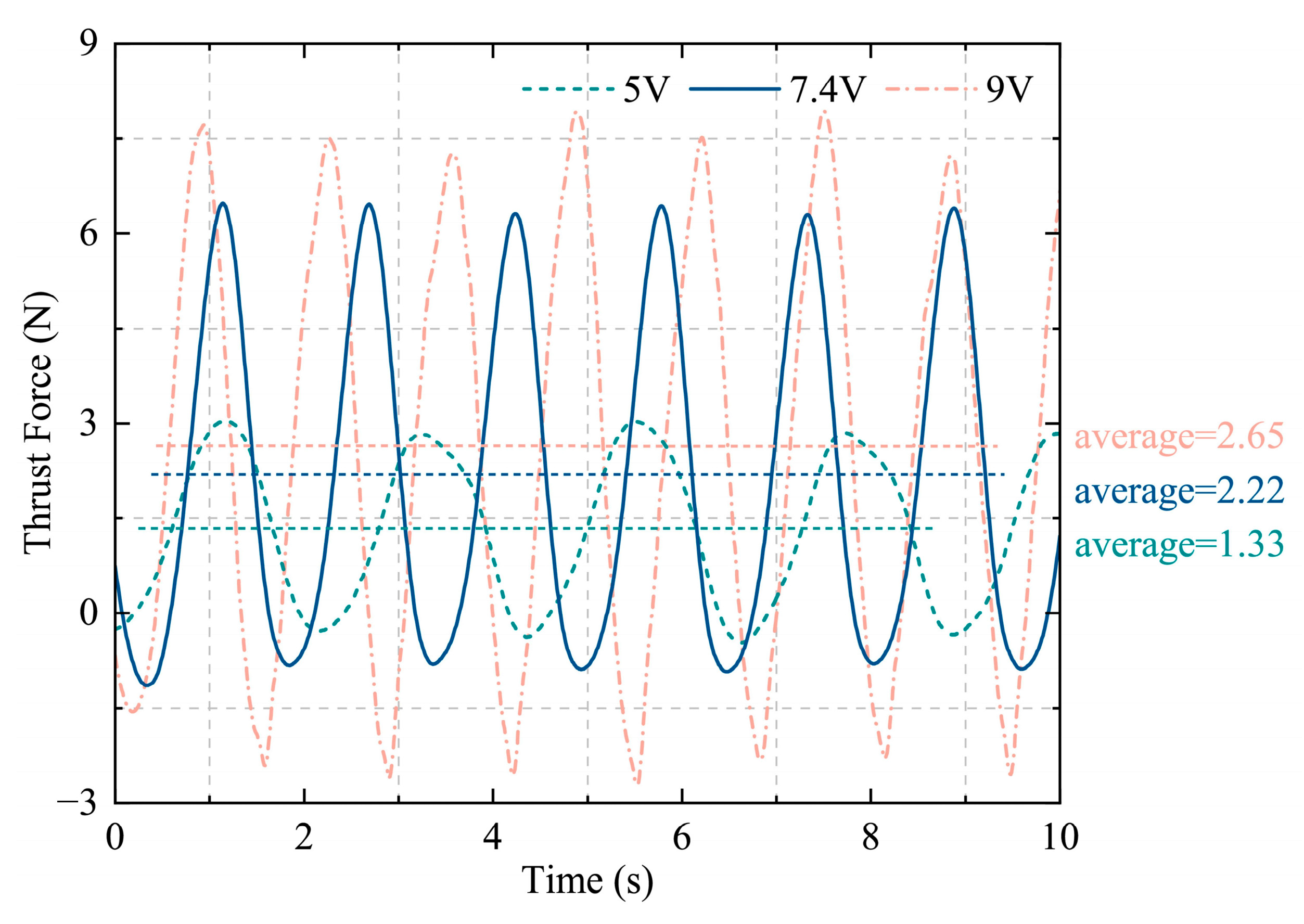
4.3. Six-Dimensional Force Experiment on the Hind Legs of a Bionic Bullfrog
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, X.-R.; Chen, L.-B. An Underwater Explorer Remotely Operated Vehicle: Unraveling the Secrets of the Ocean. IEEE Potentials 2023, 42, 31–36. [Google Scholar] [CrossRef]
- Chen, Z.; Jiao, W.; Ren, K.; Yu, J.; Tian, Y.; Chen, K.; Zhang, X. A Survey of Research Status on the Environmental Adaptation Technologies for Marine Robots. Ocean Eng. 2023, 286, 115650. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, J.; Hong, J.; Hu, D.; Yang, Y.; Guo, S. A Novel Undulatory Propulsion Strategy for Underwater Robots. J. Bionic Eng. 2021, 18, 812–823. [Google Scholar] [CrossRef]
- Bao, H.; Zhang, Y.; Song, M.; Kong, Q.; Hu, X.; An, X. A Review of Underwater Vehicle Motion Stability. Ocean Eng. 2023, 287, 115735. [Google Scholar] [CrossRef]
- Liu, K.; Ding, M.; Pan, B.; Yu, P.; Lu, D.; Chen, S.; Zhang, S.; Wang, G. A Maneuverable Underwater Vehicle for Near-Seabed Observation. Nat. Commun. 2024, 15, 10284. [Google Scholar] [CrossRef]
- Xu, D.; Yan, Z.; Xie, H.; Lu, L.; Xiao, Z.; Han, B. Demand-Driven Optimization Method for Thruster Configuration of Underwater Vehicles Considering Capability Boundary and System Efficiency. Ocean Eng. 2024, 310, 118749. [Google Scholar] [CrossRef]
- Picardi, G.; Astolfi, A.; Chatzievangelou, D.; Aguzzi, J.; Calisti, M. Underwater Legged Robotics: Review and Perspectives. Bioinspir. Biomim. 2023, 18, 031001. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Dong, C.; Zhang, Z.; Tian, Q.; Sun, A.; Yuan, L.; Zhang, L. Review of Multi-Fin Propulsion and Functional Materials of Underwater Bionic Robotic Fish. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 7350–7367. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, Z.; Guo, Q.; Wang, W.; Liu, H.; Liu, A.; Ge, Z.; Yu, H.; Yang, W. An Underwater Bionic Snake Soft Robot with Tunable Deformation and Motion Based on Composite Materials. Adv. Mater. Technol. 2023, 8, 2202012. [Google Scholar] [CrossRef]
- Chen, L.; Hu, Q.; Zhang, H.; Tong, B.; Shi, X.; Jiang, C.; Sun, L. Research on Underwater Motion Modeling and Closed-Loop Control of Bionic Undulating Fin Robot. Ocean Eng. 2024, 299, 117400. [Google Scholar] [CrossRef]
- Li, Q.; Chen, T.; Chen, Y.; Wang, Z. An Underwater Bionic Crab Soft Robot with Multidirectional Controllable Motion Ability. Ocean Eng. 2023, 278, 114412. [Google Scholar] [CrossRef]
- Wright, M.; Xiao, Q.; Dai, S.; Post, M.; Yue, H.; Sarkar, B. Design and Development of Modular Magnetic Bio-Inspired Autonomous Underwater Robot—MMBAUV. Ocean Eng. 2023, 273, 113968. [Google Scholar] [CrossRef]
- Bianchi, G.; Cinquemani, S.; Resta, F. Bio-Inspired Design of an Underwater Robot Exploiting Fin Undulation Propulsion. Appl. Sci. 2021, 11, 2556. [Google Scholar] [CrossRef]
- Xiong, X.; Xu, H.; Chen, S.; Wang, H.; You, C.; Wu, Y. A Bio-Inspired Underwater Robot Inspired by Jellyfish. In Proceedings of the ASME/BATH 2023 Symposium on Fluid Power and Motion Control, Sarasota, FL, USA, 16–18 October 2023; American Society of Mechanical Engineers: Sarasota, FL, USA, 2023; p. V001T01A021. [Google Scholar]
- Sameh, A.; Elhenidy, A. Bio-Inspired Underwater Robotic Vehicle for Marine Exploration and AI-Powered Fish Detection. Res. Sq. 2025; preprint. [Google Scholar] [CrossRef]
- Soto, K.; Hess, I.; Schrader, B.; He, S.; Musgrave, P. Improving Swimming Performance in Soft Robotic Fish with Distributed Muscles and Embedded Kinematic Sensing. In Proceedings of the 2025 IEEE 8th International Conference on Soft Robotics (RoboSoft), Lausanne, Switzerland, 22–26 April 2025; pp. 1–6. [Google Scholar]
- Ding, H.; Gao, Q.; Zhu, Y.; Shi, H.; Chen, K.; Chen, R. Experimental Study on Navigation Performance of Bionic Underwater Vehicle Inspired by Sea Turtle. Ocean Eng. 2024, 310, 118700. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Wang, T.; Zhang, B. Research and Experiments on Electromagnetic-Driven Multi-Joint Bionic Fish. Robotica 2022, 40, 720–746. [Google Scholar] [CrossRef]
- Xia, Q.; Li, H.; Song, N.; Wu, Z.; Wang, X.; Sun, X.; Zhang, S.; Yang, C. Research on Flexible Collapsible Fluid-Driven Bionic Robotic Fish. Ocean Eng. 2023, 276, 114203. [Google Scholar] [CrossRef]
- Baines, R.; Fish, F.; Kramer-Bottiglio, R. Amphibious Robotic Propulsive Mechanisms: Current Technologies and Open Challenges. In Bioinspired Sensing, Actuation, and Control in Underwater Soft Robotic Systems; Paley, D.A., Wereley, N.M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 41–69. ISBN 978-3-030-50475-5. [Google Scholar]
- Lock, R.J.; Burgess, S.C.; Vaidyanathan, R. Multi-Modal Locomotion: From Animal to Application. Bioinspir. Biomim. 2013, 9, 011001. [Google Scholar] [CrossRef]
- Stamhuis, E.J.; Nauwelaerts, S. Propulsive Force Calculations in Swimming Frogs II. Application of a Vortex Ring Model to DPIV Data. J. Exp. Biol. 2005, 208, 1445–1451. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, X.; Liu, W.; Qi, L.; Wang, Y.; Wang, Y. Design and Analysis of a Novel Swimming Mechanism Inspired from Frogs. J. Intell. Robot. Syst. 2022, 105, 23. [Google Scholar] [CrossRef]
- Wang, S.; Fan, J.; Pan, Y.; Liu, G.; Liu, Y. Design and Analysis of Adaptive Flipper With Origami Structure for Frog-Inspired Swimming Robot. IEEE Robot. Autom. Lett. 2024, 9, 1262–1269. [Google Scholar] [CrossRef]
- Pan, Y.; Fan, J.; Liu, G.; Liu, Y.; Zhao, J. Design and Kinematic Analysis of a Rope-Driven Linkage Frog-like Swimming Robot with Multidirectional Controllable Motion. Ocean Eng. 2024, 291, 116430. [Google Scholar] [CrossRef]
- Fan, J.; Wang, S.; Yu, Q.; Zhu, Y. Swimming Performance of the Frog-Inspired Soft Robot. Soft Robot. 2020, 7, 615–626. [Google Scholar] [CrossRef]
- Fan, J.; Wang, S.; Wang, Y.; Li, G.; Zhao, J.; Liu, G. Research on Frog-Inspired Swimming Robot Driven by Pneumatic Muscles. Robotica 2022, 40, 1527–1537. [Google Scholar] [CrossRef]
- Soomro, A.M.; Memon, F.H.; Lee, J.-W.; Ahmed, F.; Kim, K.H.; Kim, Y.S.; Choi, K.H. Fully 3D Printed Multi-Material Soft Bio-Inspired Frog for Underwater Synchronous Swimming. Int. J. Mech. Sci. 2021, 210, 106725. [Google Scholar] [CrossRef]
- Vera, M.C.; Ferretti, J.L.; Cointry, G.R.; Abdala, V. Hind Limb Muscles Influence the Architectural Properties of Long Bones in Frogs. J. Anat. 2022, 241, 702–715. [Google Scholar] [CrossRef]
- Jizhuang, F.; Wei, Z.; Bowen, Y.; Gangfeng, L. Propulsive Efficiency of Frog Swimming with Different Feet and Swimming Patterns. Biol. Open 2017, 6, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Dobos, T.J.; Bench, R.W.G.; McKinnon, C.D.; Brady, A.; Boddy, K.J.; Holmes, M.W.R.; Sonne, M.W.L. Validation of pitchAITM Markerless Motion Capture Using Marker-Based 3D Motion Capture. Sports Biomech. 2022, 24, 587–607. [Google Scholar] [CrossRef]
- Nagaraju, D.S.; Krupakaran, R.L.; Sripadh, C.; Nitin, G.; Joy Joseph Emmanuel, G. Mechanical Properties of 3D Printed Specimen Using FDM (Fused Deposition Modelling) and SLA (Stereolithography) Technologies. Mater. Today Proc. 2023, S2214785323049040. [Google Scholar] [CrossRef]
- Gadallah, N.; Wanees, A.S. Friction Stir Spot Welding. In Advances in Architecture, Engineering and Technology; Rosso, F., Fabiani, C., Altan, H., Amer, M., Eds.; Advances in Science, Technology & Innovation; Springer International Publishing: Cham, Switzerland, 2022; pp. 245–256. ISBN 978-3-030-86912-0. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Y.; Wang, Y.; Fu, Y.; Ma, M.; Zhong, Y.; Yu, T. Design and Implementation of a Biomimetic Underwater Robot Propulsion System Inspired by Bullfrog Hind Leg Movements. Biomimetics 2025, 10, 498. https://doi.org/10.3390/biomimetics10080498
Chu Y, Wang Y, Fu Y, Ma M, Zhong Y, Yu T. Design and Implementation of a Biomimetic Underwater Robot Propulsion System Inspired by Bullfrog Hind Leg Movements. Biomimetics. 2025; 10(8):498. https://doi.org/10.3390/biomimetics10080498
Chicago/Turabian StyleChu, Yichen, Yahui Wang, Yanhui Fu, Mingxu Ma, Yunan Zhong, and Tianbiao Yu. 2025. "Design and Implementation of a Biomimetic Underwater Robot Propulsion System Inspired by Bullfrog Hind Leg Movements" Biomimetics 10, no. 8: 498. https://doi.org/10.3390/biomimetics10080498
APA StyleChu, Y., Wang, Y., Fu, Y., Ma, M., Zhong, Y., & Yu, T. (2025). Design and Implementation of a Biomimetic Underwater Robot Propulsion System Inspired by Bullfrog Hind Leg Movements. Biomimetics, 10(8), 498. https://doi.org/10.3390/biomimetics10080498




