Coordinated Dual-Fin Actuation of Bionic Ocean Sunfish Robot for Multi-Modal Locomotion
Abstract
1. Introduction
- 1.
- We present the design and validation of an ocean sunfish-inspired robotic fish that is propelled by only two actuators and requires no auxiliary mechanisms. This contribution demonstrates the feasibility of achieving function-structure decoupling by imitating a specific biological architecture.
- 2.
- We systematically showcase the multi-modal locomotion performance of the robot, particularly its high stability, agility, 3-D maneuverability, and its signature capability for proactive ascent under conditions of negative buoyancy.
- 3.
- We validate that coordinated dual-fin propulsion can serve as a unified mechanism to flexibly generate diverse motion patterns, offering a novel approach for the design of minimalist underwater robots.
2. Robot Design and Dual-Fin Actuation
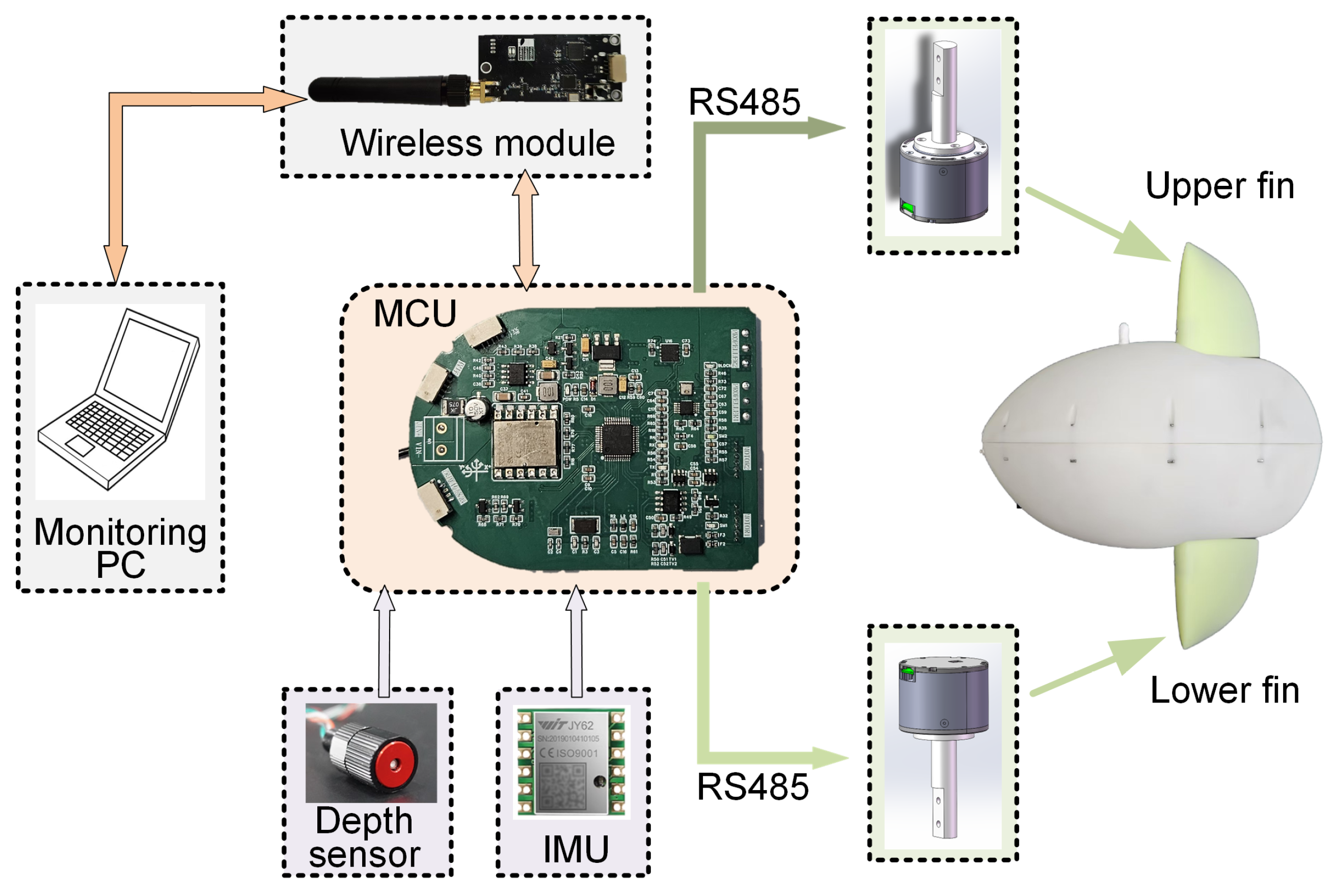
2.1. Robot Prototype Design
2.2. Dual-Fin Cooperation Strategies
3. 2-D Motion Experimental Results
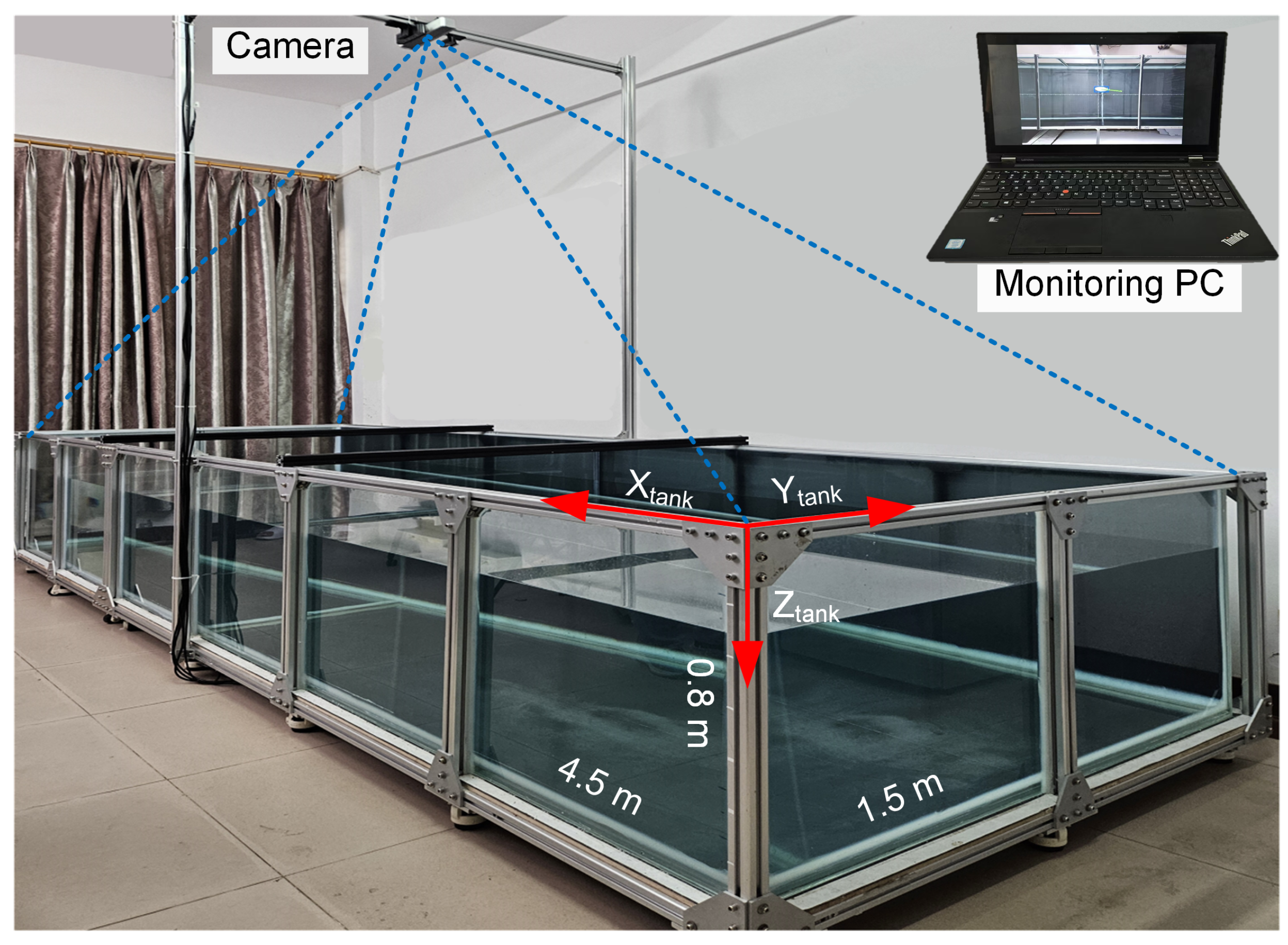
3.1. Experiment Setup
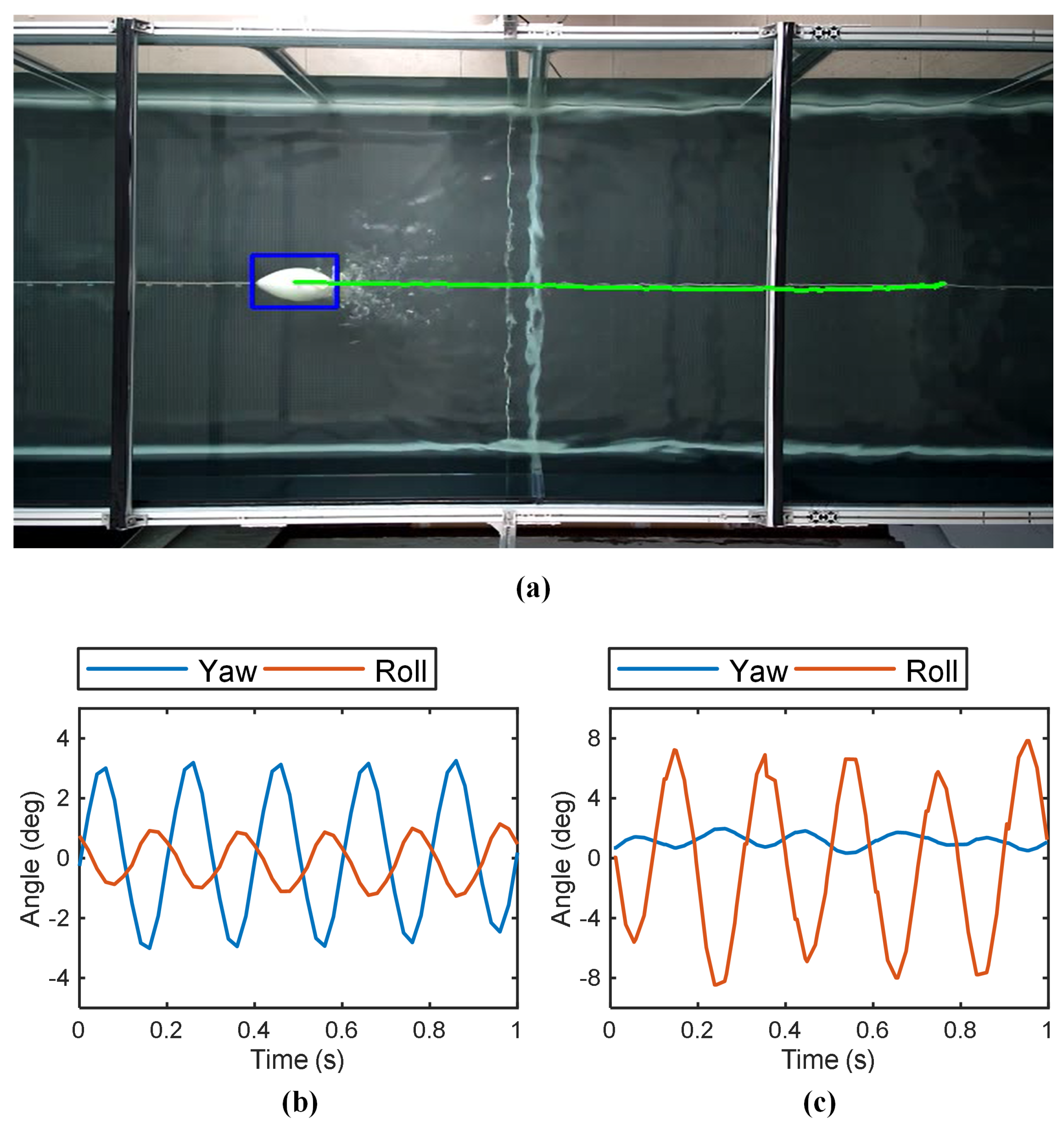
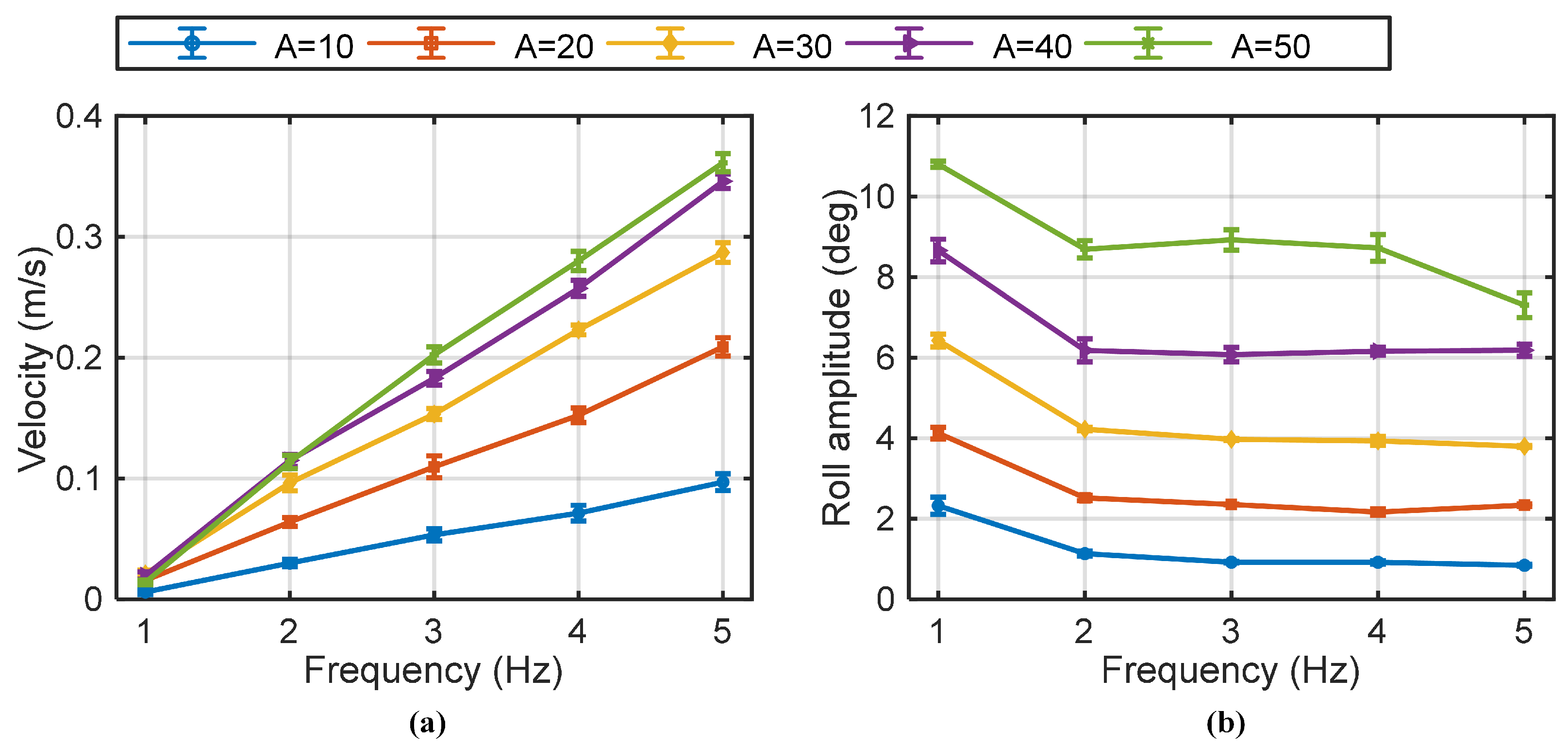
3.2. Cruising-Straight Experiments
- (1)
- In-phase flapping gait
- (2)
- Anti-phase flapping gait
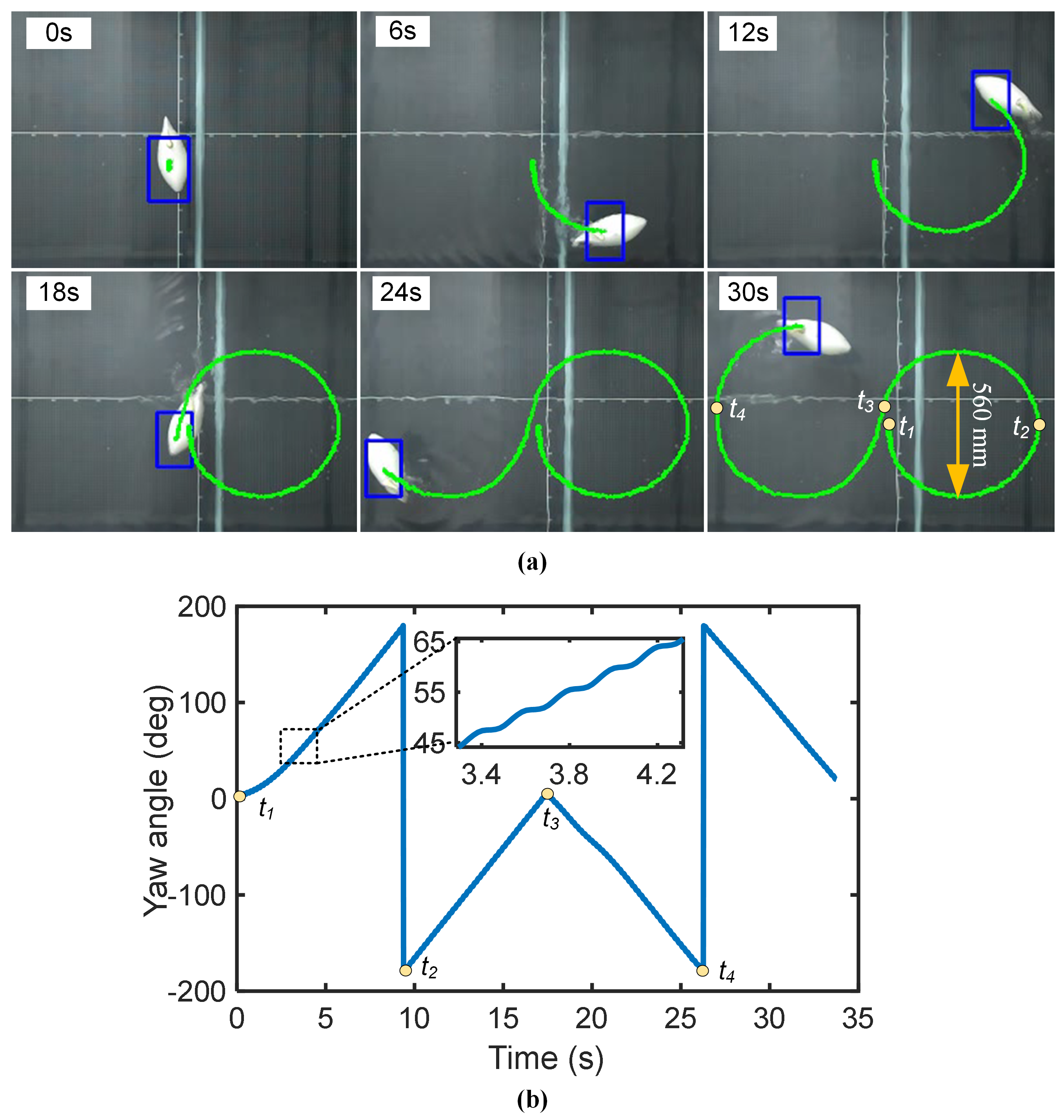
3.3. Cruising-Turn Experiment
4. 3-D Motion Experimental Results
4.1. Experiment Setup
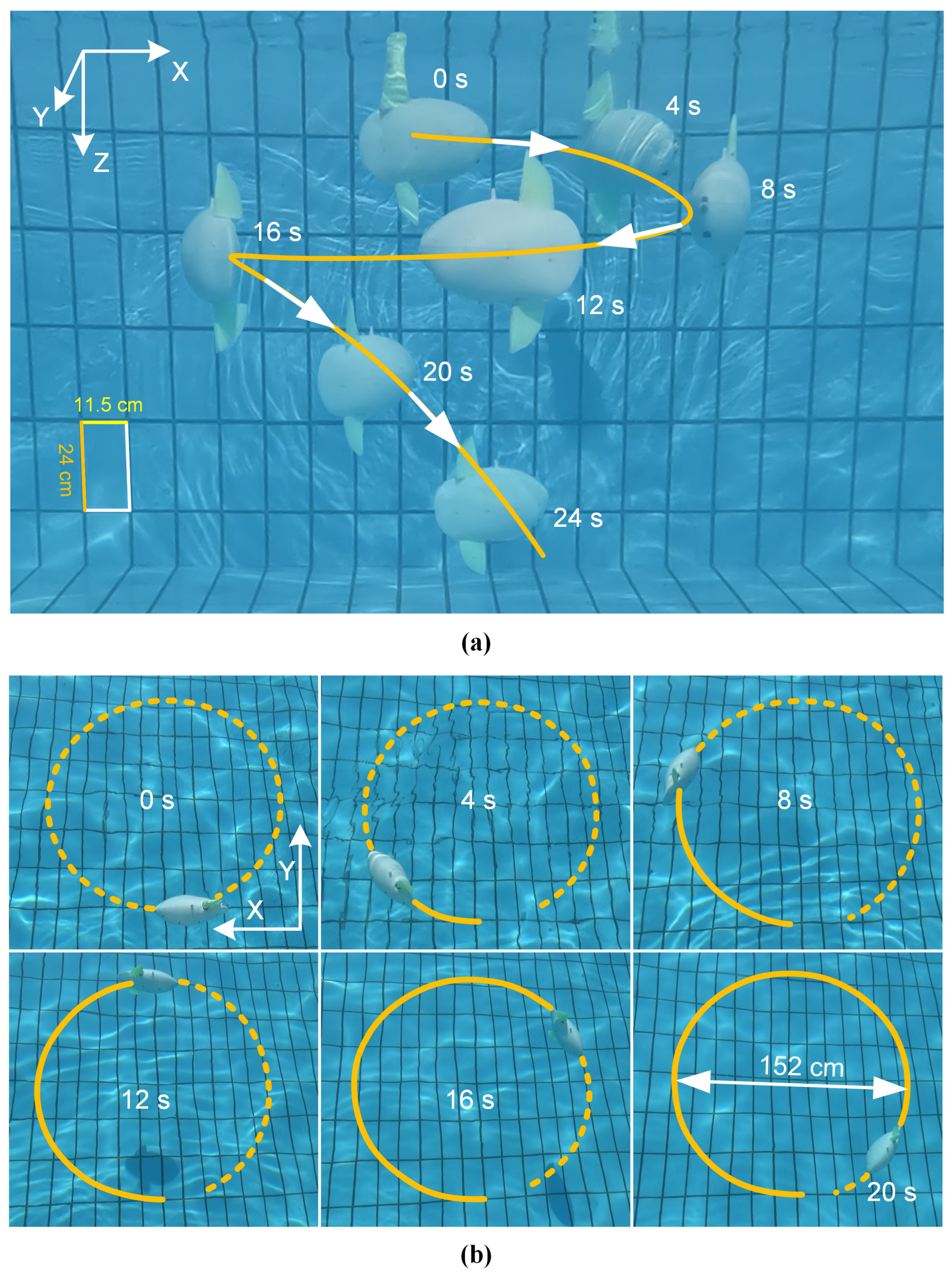
4.2. Descending and Proactive Ascending
- (1)
- Activate the lower fin to descend
- (2)
- Activate the upper fin to proactively ascend
4.3. Spiral Motion
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Wake Vortex Structure in CFD

References
- Sun, B.; Li, W.; Wang, Z.; Zhu, Y.; He, Q.; Guan, X.; Dai, G.; Yuan, D.; Li, A.; Cui, W.; et al. Recent progress in modeling and control of bio-inspired fish robots. J. Mar. Sci. Eng. 2022, 10, 773. [Google Scholar] [CrossRef]
- Amal, P.; Nair, A.R.; Arunav, H.; Raj, R.; Akhil, V.; Tawk, C.; Shankar, K.V. Bioinspiration and biomimetics in marine robotics: A review on current applications and future trends. Bioinspir. Biomim. 2024, 19, 031002. [Google Scholar]
- Wei, D.; Hu, S.; Zhou, Y.; Ren, X.; Huo, X.; Yin, J.; Wu, Z. A magnetically actuated miniature robotic fish with the flexible tail fin. IEEE Robot. Autom. Lett. 2023, 8, 6099–6106. [Google Scholar] [CrossRef]
- Zhang, T.; Tian, R.; Yang, H.; Wang, C.; Sun, J.; Zhang, S.; Xie, G. From simulation to reality: A learning framework for fish-like robots to perform control tasks. IEEE Trans. Robot. 2022, 38, 3861–3878. [Google Scholar] [CrossRef]
- Chen, L.; Cai, Y.; Bi, S. Central pattern generator (CPG)-based locomotion control and hydrodynamic experiments of synergistical interaction between pectoral fins and caudal fin for boxfish-like robot. Biomimetics 2023, 8, 380. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Chen, L.; Ma, X.; Bi, S.; Wang, B.; Li, T. Analysis of heading stability due to interactions between pectoral and caudal fins in robotic boxfish locomotion. J. Bionic Eng. 2023, 20, 390–405. [Google Scholar] [CrossRef]
- Yu, J.; Su, Z.; Wu, Z.; Tan, M. Development of a fast-swimming dolphin robot capable of leaping. IEEE/ASME Trans. Mechatron. 2016, 21, 2307–2316. [Google Scholar] [CrossRef]
- Wu, Z.; Yu, J.; Yuan, J.; Tan, M. Towards a gliding robotic dolphin: Design, modeling, and experiments. IEEE/ASME Trans. Mechatron. 2019, 24, 260–270. [Google Scholar] [CrossRef]
- Zhong, Y.; Hong, Z.; Li, Y.; Yu, J. A general kinematic model of fish locomotion enables robot fish to master multiple swimming motions. IEEE Trans. Robot. 2023, 40, 750–763. [Google Scholar] [CrossRef]
- Lu, B.; Zhou, C.; Wang, J.; Zhang, Z.; Tan, M. Toward swimming speed optimization of a multi-flexible robotic fish with low cost of transport. IEEE Trans. Autom. Sci. Eng. 2023, 21, 2804–2815. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, C.; Tan, W.; Zhang, Y.; Yang, L.; Chen, W.; Wang, F.; Tian, J.; Liu, L. Soft robotic fish actuated by bionic muscle with embedded sensing for self-adaptive multiple modes swimming. IEEE Trans. Robot. 2025, 41, 1329–1345. [Google Scholar] [CrossRef]
- Zhang, S.; Qian, Y.; Liao, P.; Qin, F.; Yang, J. Design and control of an agile robotic fish with integrative biomimetic mechanisms. IEEE/ASME Trans. Mechatron. 2016, 21, 1846–1857. [Google Scholar] [CrossRef]
- Liao, P.; Zhang, S.; Sun, D. A dual caudal-fin miniature robotic fish with an integrated oscillation and jet propulsive mechanism. Bioinspir. Biomim. 2018, 13, 036007. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Li, Z.; Du, R. A novel robot fish with wire-driven active body and compliant tail. IEEE/ASME Trans. Mechatron. 2017, 22, 1633–1643. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Y.; Zeng, R.; Gan, B.; Zhang, M.; Li, H.; Qu, S.; Zhou, H. A bioinspired multimotion modality underwater microrobot. Sci. Adv. 2025, 11, eadu2527. [Google Scholar] [CrossRef] [PubMed]
- Katzschmann, R.K.; DelPreto, J.; MacCurdy, R.; Rus, D. Exploration of underwater life with an acoustically controlled soft robotic fish. Sci. Robot. 2018, 3, eaar3449. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Li, K.; Qiu, Y.; Liang, M.; Wang, L.; Yang, S.X.; Ji, A. Cooperative motion mechanism of a bionic sailfish robot with high motion performance. IEEE Robot. Autom. Lett. 2024, 9, 6592–6599. [Google Scholar] [CrossRef]
- Li, S.; Wu, Z.; Dai, S.; Wang, J.; Tan, M.; Yu, J. Tight-space maneuvering of a hybrid-driven robotic fish using backstepping-based adaptive control. IEEE/ASME Trans. Mechatron. 2023, 29, 3219–3231. [Google Scholar] [CrossRef]
- Kim, T.; Kim, J.; Yu, S.C. Development of bioinspired multimodal underwater robot “hero-blue” for walking, swimming, and crawling. IEEE Trans. Robot. 2024, 40, 1421–1438. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, Q.; Yang, J.; Wang, C. Design, modeling, and experiment of underactuated flexible gliding robotic fish. IEEE/ASME Trans. Mechatron. 2023, 29, 2266–2276. [Google Scholar] [CrossRef]
- Wang, Y.; Chu, H.; Ma, R.; Bai, X.; Cheng, L.; Wang, S.; Tan, M. Learning-Based Discontinuous Path Following Control for a Biomimetic Underwater Vehicle. Research 2024, 7, 0299. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tang, C.; Wang, S.; Cheng, L.; Wang, R.; Tan, M.; Hou, Z. Target tracking control of a biomimetic underwater vehicle through deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3741–3752. [Google Scholar] [CrossRef] [PubMed]
- Hong, Z.; Wang, Q.; Zhong, Y. Parameters optimization of body wave control method for multi-joint robotic fish based on deep reinforcement learning. In Proceedings of the 2022 IEEE International Conference on Robotics and Biomimetics (ROBIO), Xishuangbanna, China, 5–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 604–609. [Google Scholar]
- Tong, R.; Wu, Z.; Li, S.; Chen, D.; Wang, J.; Tan, M.; Yu, J. Design and modeling of an integral molding flexible tail for robotic fish. IEEE/ASME Trans. Mechatron. 2024, 30, 1322–1332. [Google Scholar] [CrossRef]
- Lin, Y.H.; Siddall, R.; Schwab, F.; Fukushima, T.; Banerjee, H.; Baek, Y.; Vogt, D.; Park, Y.L.; Jusufi, A. Modeling and control of a soft robotic fish with integrated soft sensing. Adv. Intell. Syst. 2023, 5, 2000244. [Google Scholar] [CrossRef]
- Sfakiotakis, M.; Lane, D.M.; Davies, J.B.C. Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Eng. 1999, 24, 237–252. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Y.; Wu, Z.; Ma, L.; Guo, M.; Li, Z.; Li, Y. A comprehensive review on fish-inspired robots. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221103707. [Google Scholar] [CrossRef]
- Salazar, R.; Fuentes, V.; Abdelkefi, A. Classification of biological and bioinspired aquatic systems: A review. Ocean. Eng. 2018, 148, 75–114. [Google Scholar] [CrossRef]
- Berlinger, F.; Gauci, M.; Nagpal, R. Implicit coordination for 3D underwater collective behaviors in a fish-inspired robot swarm. Sci. Robot. 2021, 6, eabd8668. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Li, Z.; Du, R. Robot fish with two-DOF pectoral fins and a wire-driven caudal fin. Adv. Robot. 2018, 32, 25–36. [Google Scholar] [CrossRef]
- Berlinger, F.; Dusek, J.; Gauci, M.; Nagpal, R. Robust maneuverability of a miniature, low-cost underwater robot using multiple fin actuation. IEEE Robot. Autom. Lett. 2017, 3, 140–147. [Google Scholar] [CrossRef]
- Clark, A.J.; Tan, X.; McKinley, P.K. Evolutionary multiobjective design of a flexible caudal fin for robotic fish. Bioinspir. Biomim. 2015, 10, 065006. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, F.; Mondada, F.; Bonnet, F.; Mondada, F. State of the Art in Fish Behavioral Studies Using Robots and Robotic-Fish Design. In Shoaling with Fish: Using Miniature Robotic Agents to Close the Interaction Loop with Groups of Zebrafish Danio Rerio; Springer: Berlin/Heidelberg, Germany, 2019; pp. 13–19. [Google Scholar]
- Han, J.; Fu, Z.; Zhang, Y.; Shi, L.; Kang, R.; Dai, J.S.; Song, Z. Undulatory motion of sailfish-like robot via a new single-degree-of-freedom modularized spatial mechanism. Mech. Mach. Theory 2024, 191, 105502. [Google Scholar] [CrossRef]
- Ng, T.J.; Chen, N.; Zhang, F. Snapp: An agile robotic fish with 3-D maneuverability for open water swim. IEEE Robot. Autom. Lett. 2023, 8, 6499–6506. [Google Scholar] [CrossRef]
- Mintchev, S.; Ranzani, R.; Fabiani, F.; Stefanini, C. Towards docking for small scale underwater robots. Auton. Robot. 2015, 38, 283–299. [Google Scholar] [CrossRef]
- Berlinger, F.; Saadat, M.; Haj-Hariri, H.; Lauder, G.; Nagpal, R. Fish-like three-dimensional swimming with an autonomous, multi-fin, and biomimetic robot. Bioinspir. Biomim. 2021, 16, 026018. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Wang, J.; Wu, Z.; Tan, M.; Yu, J. Autonomous vision-based navigation and stability augmentation control of a biomimetic robotic hammerhead shark. IEEE Trans. Autom. Sci. Eng. 2023, 21, 3319–3331. [Google Scholar] [CrossRef]
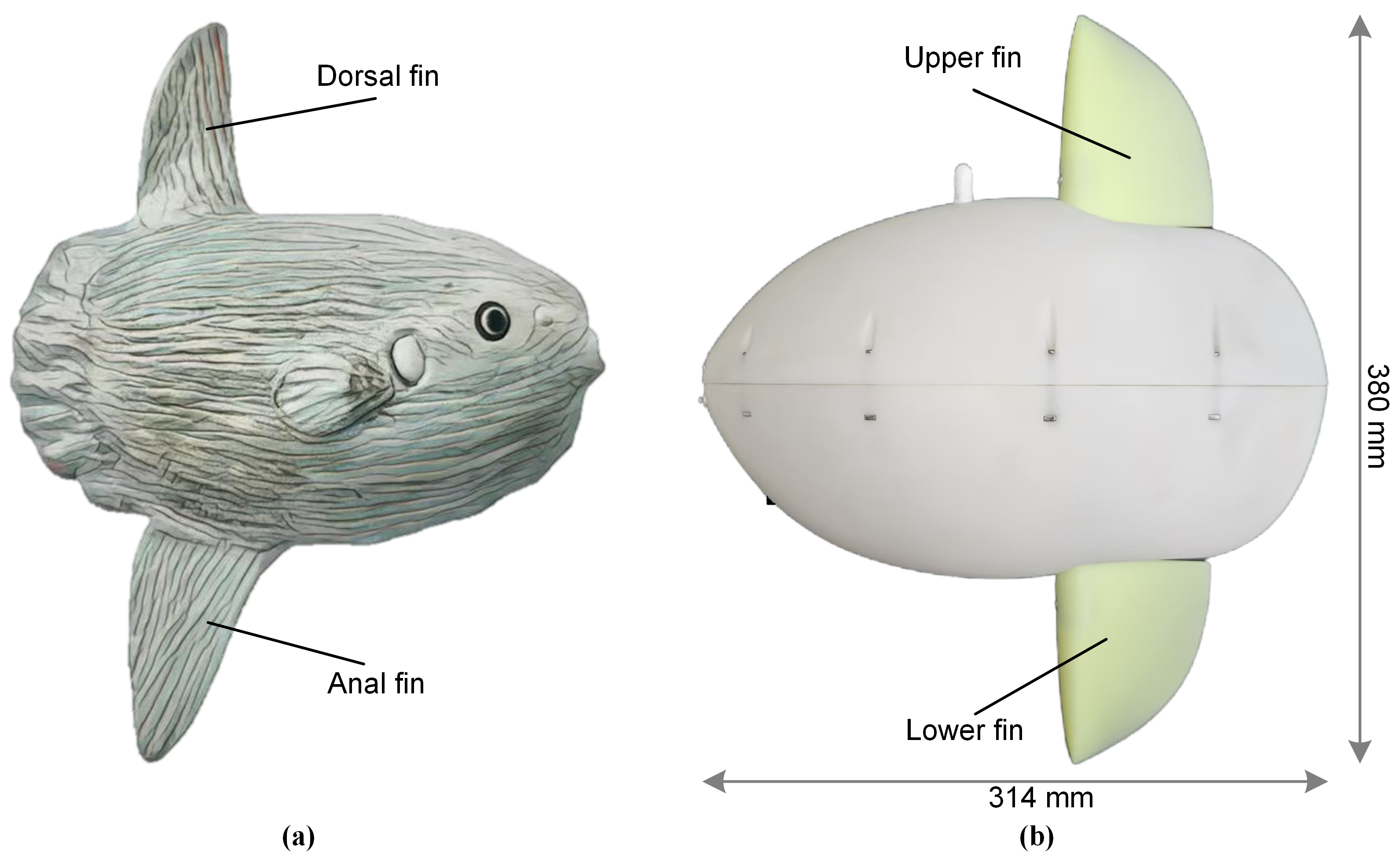





| Items | Characteristics |
|---|---|
| Dimensions | 314 mm (L) × 124 mm (W) × 380 mm (H) |
| Mass | 3322 g |
| Motors | 2 × 4.5 N·m |
| Micro-controller unit | STM32F103 |
| Communication module | 433 MHz |
| Battery | 22.2 V-6S-4000 mAh |
| Attitude sensor | JY61P |
| Depth sensor | MS5837-30BA |
| Swimming Motions | Flapping Amplitude | Flapping Frequency | Initial Phase | Angular Offset |
|---|---|---|---|---|
| Cruising | ||||
| Turning | ||||
| Descending | ||||
| Proactive ascending | ||||
| Spiraling descend | ||||
| Spiraling ascend |
| Offset Fin(s) | Average Descending Speed | Average Spiral Radius |
|---|---|---|
| Upper fin | 7.7 cm/s (0.25 BL/s) | 116 cm (3.69 BL) |
| Lower fin | 9.1 cm/s (0.29 BL/s) | 94 cm (2.99 BL) |
| Double fins | 9.6 cm/s (0.31 BL/s) | 54 cm (1.72 BL) |
| Robotic Fish | Max. Speed (Locomotion Mode) | Min. Turning Radius | 3-D Motion/ Actuators |
|---|---|---|---|
| Boxfish-like robot [5] | 1.07 BL/s (MPF) | Not specified | Yes/4 |
| Dual caudal fins robot [12,13] | 1.21 BL/s (BCF) | 0.23 BL (with pectoral fins) | Yes/4 |
| SoFi [16] | 0.5 BL/s (BCF) | 1.66 BL | Yes/4 |
| Bionic sailfish robot [17] | 1.6 BL/s (BCF) | 0.39 BL (with dorsal fin) | Yes/4 |
| Sailfish robot [34] | 0.54 BL/s (BCF) | 2.16 BL | Yes/3 |
| Snapp [35] | 1.7 BL/s (BCF) | 0.96 BL | Yes/3 |
| Finbot [31,37] | 1 BL/s (BCF) | 1.2 BL/0.5 BL (without/with pectoral fins) | Yes/4 |
| Robotic shark [38] | 0.8 BL/s (BCF) | 0.2 BL (with pectoral fins) | Yes/7 |
| Our robotic fish | 1.16 BL/s (MPF) | 0.89 BL (without auxiliary fins) | Yes/2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Huang, Z.; Liu, Q.; Song, Z.; Shen, Y.; Huang, M. Coordinated Dual-Fin Actuation of Bionic Ocean Sunfish Robot for Multi-Modal Locomotion. Biomimetics 2025, 10, 489. https://doi.org/10.3390/biomimetics10080489
Huang L, Huang Z, Liu Q, Song Z, Shen Y, Huang M. Coordinated Dual-Fin Actuation of Bionic Ocean Sunfish Robot for Multi-Modal Locomotion. Biomimetics. 2025; 10(8):489. https://doi.org/10.3390/biomimetics10080489
Chicago/Turabian StyleHuang, Lidong, Zhong Huang, Quanchao Liu, Zhihao Song, Yayi Shen, and Mengxing Huang. 2025. "Coordinated Dual-Fin Actuation of Bionic Ocean Sunfish Robot for Multi-Modal Locomotion" Biomimetics 10, no. 8: 489. https://doi.org/10.3390/biomimetics10080489
APA StyleHuang, L., Huang, Z., Liu, Q., Song, Z., Shen, Y., & Huang, M. (2025). Coordinated Dual-Fin Actuation of Bionic Ocean Sunfish Robot for Multi-Modal Locomotion. Biomimetics, 10(8), 489. https://doi.org/10.3390/biomimetics10080489






