Multiline Laser Interferometry for Non-Contact Dynamic Morphing of Hierarchical Surfaces
Abstract
1. Introduction
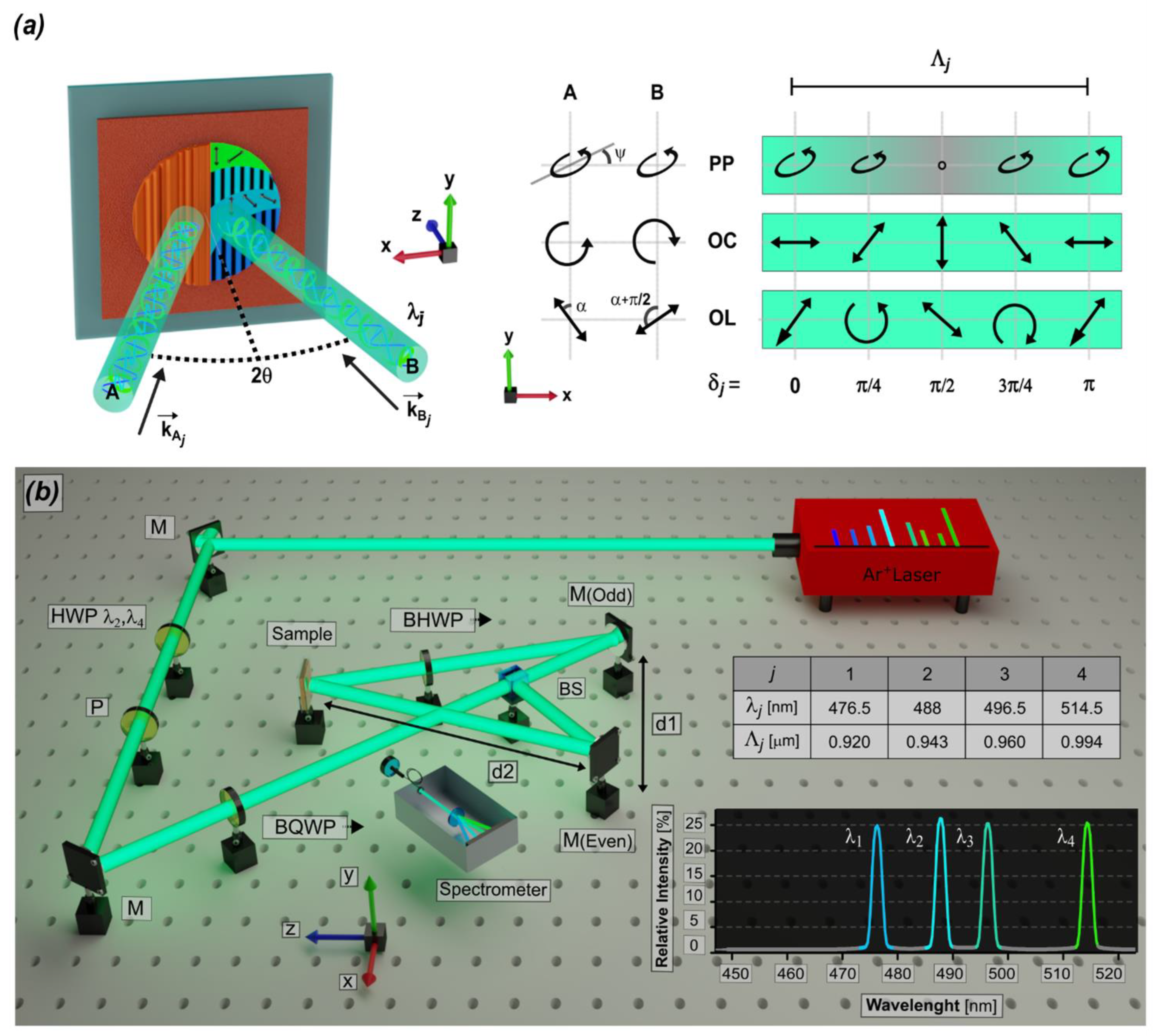
2. Multiline Laser Interferometry
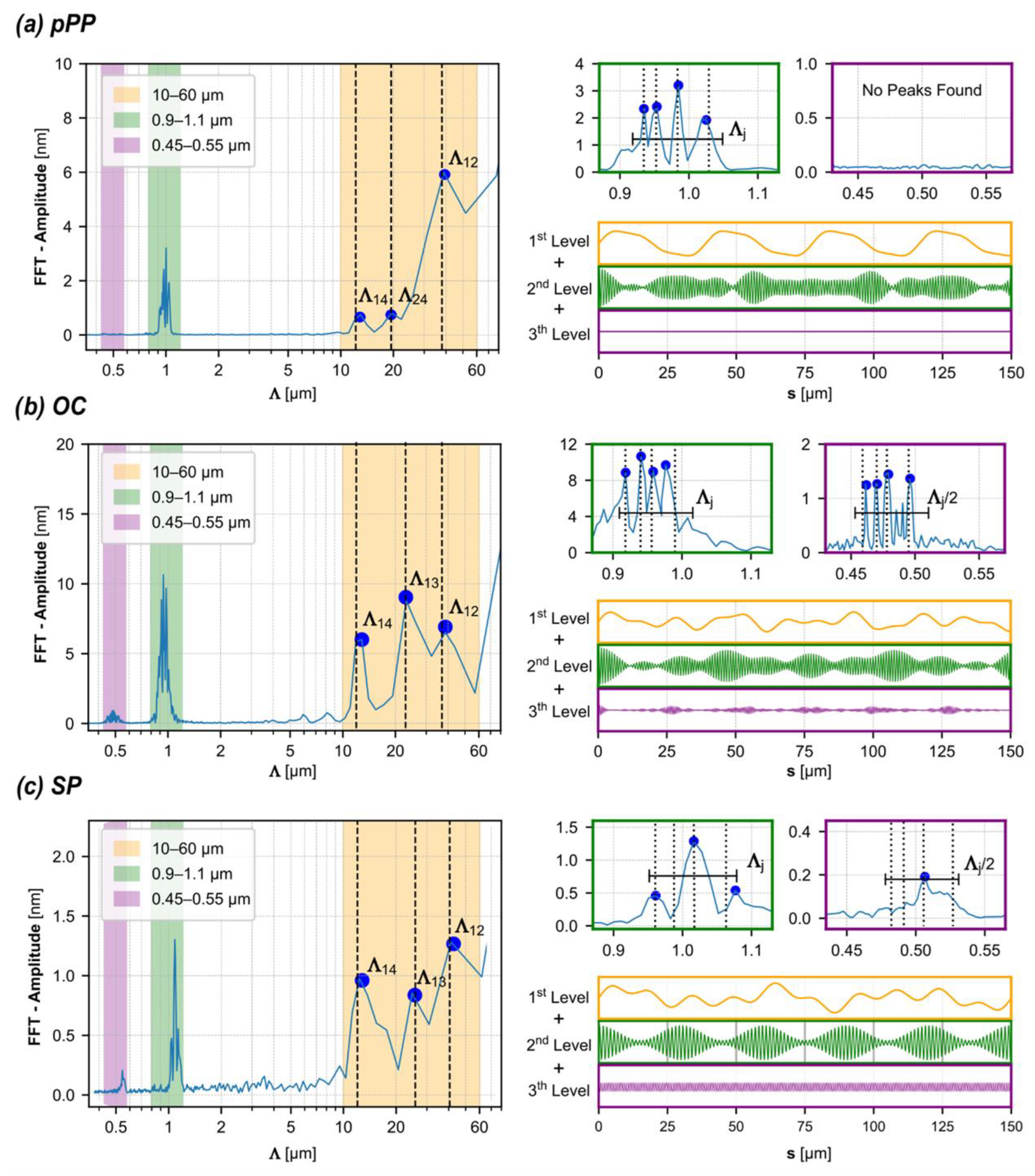
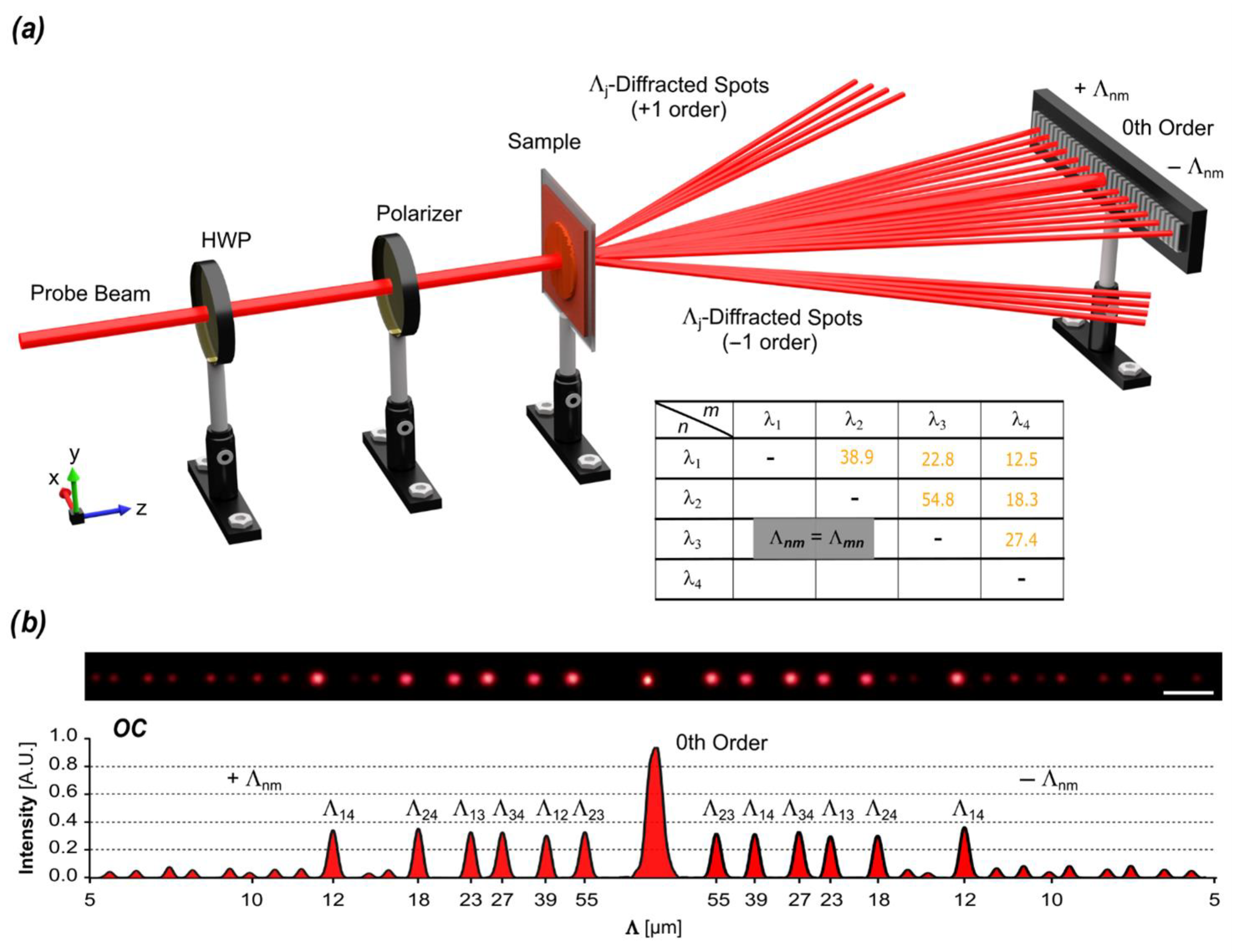
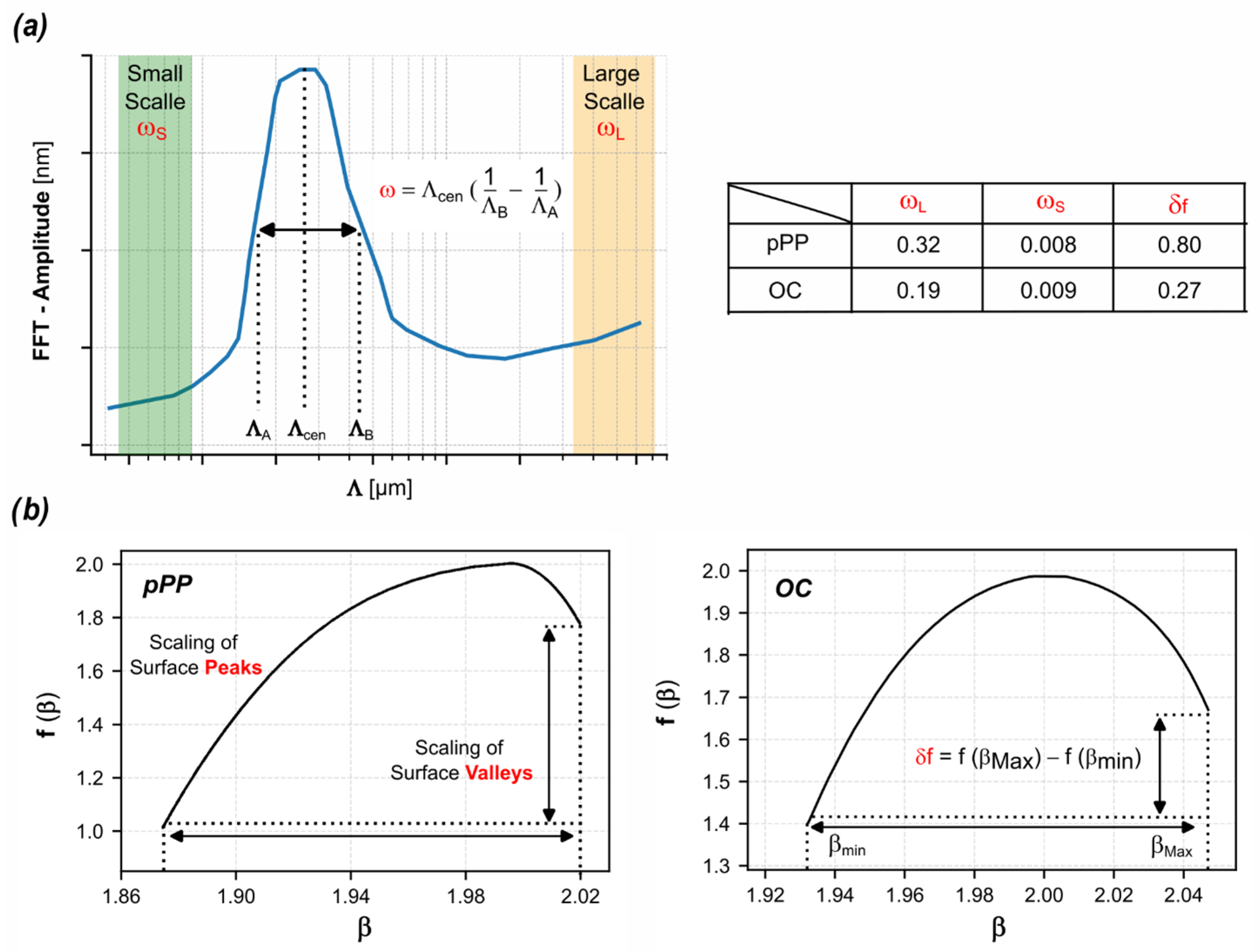
3. Surface Photo-Morphing of Complex Hierarchical Design
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arzt, E.; Quan, H.; McMeeking, R.M.; Hensel, R. Functional surface microstructures inspired by nature—From adhesion and wetting principles to sustainable new devices. Prog. Mater. Sci. 2021, 120, 100823. [Google Scholar] [CrossRef]
- Xia, Z. Biomimetic Principles and Design of Advanced Engineering Materials; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Barthlott, W.; Mail, M.; Bhushan, B.; Koch, K. Plant surfaces: Structures and functions for biomimetic innovations. Nanomicro Lett. 2017, 9, 23. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Bhushan, B.; Tong, J. Structural coloration in nature. RSC Adv. 2013, 3, 14862. [Google Scholar] [CrossRef]
- Chen, C.; Airoldi, C.A.; Lugo, C.A.; Bay, R.K.; Glover, B.J.; Crosby, A.J. Flower inspiration: Broad-angle structural color through tunable hierarchical wrinkles in thin film multilayers. Adv. Funct. Mater. 2021, 31, 2006256. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, D.; Lv, T.; Lai, H.; Zhang, E.; Kang, H.; Wang, Y.; Liu, P.; Liu, Y.; Du, Y.; et al. Superhydrophobic shape memory polymer arrays with switchable isotropic/anisotropic wetting. Adv. Funct. Mater. 2018, 28, 1705002. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, L.; Wang, C.; Li, C.; Lin, N.; Niu, S.; Han, Z.; Duan, J. Bioinspired Near-Full Transmittance MgF2 Window for Infrared Detection in Extremely Complex Environments. ACS Appl. Mater. Interfaces 2023, 15, 30985–30997. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Luo, J.; Li, K.; Wang, C.; Li, Z.; Wang, M.; Jiang, Z.; Veiko, V.P.; Duan, J. Ultrafast laser welding of transparent materials: From principles to applications. Int. J. Extrem. Manuf. 2025, 7, 032001. [Google Scholar] [CrossRef]
- McNamara, L.E.; Burchmore, R.; Riehle, M.O.; Herzyk, P.; Biggs, M.J.P.; Wilkinson, C.D.W.; Curtis, A.S.G.; Dalby, M.J. The role of microtopography in cellular mechanotransduction. Biomaterials 2012, 33, 2835–2847. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; He, X.; Yuan, C.; Cao, P.; Bai, X. Antifouling applications and fabrications of biomimetic micro-structured surfaces: A review. J. Adv. Res. 2024, 59, 201–221. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Gou, X.; Zhang, J.; Liang, J.; Yang, L.; Wang, S.; Chen, F. A review of smart superwetting surfaces based on shape-memory micro/nanostructures. Small 2023, 19, 2206463. [Google Scholar] [CrossRef] [PubMed]
- Chivate, A.; Zhou, C. Additive manufacturing of micropatterned functional surfaces: A review. Int. J. Extreme Manuf. 2024, 6, 042004. [Google Scholar] [CrossRef]
- Daghigh Shirazi, H.; Dong, Y.; Niskanen, J.; Fedele, C.; Priimagi, A.; Jokinen, V.P.; Vapaavuori, J. Multiscale hierarchical surface patterns by coupling optical patterning and thermal shrinkage. ACS Appl. Mater. Interfaces 2021, 13, 15563–15571. [Google Scholar] [CrossRef] [PubMed]
- Gentili, D.; Cavallini, M. Opportunity of patterning in chemistry. Chem. Eur. J. 2024, 30, e202401219. [Google Scholar] [CrossRef] [PubMed]
- Stratakis, E.; Bonse, J.; Heitz, J.; Siegel, J.; Tsibidis, G.D.; Skoulas, E.; Papadopoulos, A.; Mimidis, A.; Joel, A.-C.; Comanns, P.; et al. Laser engineering of biomimetic surfaces. Mater. Sci. Eng. R Rep. 2020, 141, 100562. [Google Scholar] [CrossRef]
- Aboal-Castro, L.; Radziunas-Salinas, Y.; Pita-Vilar, M.; Carnero, B.; Mikos, A.G.; Alvarez-Lorenzo, C.; Flores-Arias, M.T.; Diaz-Gomez, L. Laser-assisted micropatterned 3D printed scaffolds with customizable surface topography and porosity for modulation of cell function. Adv. Healthc. Mater. 2025, 14, 2403992. [Google Scholar] [CrossRef] [PubMed]
- del Barrio, J.; Sánchez-Somolinos, C. Light to shape the future: From photolithography to 4D printing. Adv. Opt. Mater. 2019, 7, 1900598. [Google Scholar] [CrossRef]
- Qiao, W.; Huang, W.; Liu, Y.; Li, X.; Chen, L.-S.; Tang, J.-X. Toward scalable flexible nanomanufacturing for photonic structures and devices. Adv. Mater. 2016, 28, 10353–10380. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Ku, Z.; Lee, S.C.; Brueck, S.R.J. Nanostructures and functional materials fabricated by interferometric lithography. Adv. Mater. 2011, 23, 147–179. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Zheng, Y. Moiré metamaterials and metasurfaces. Adv. Opt. Mater. 2018, 6, 1701057. [Google Scholar] [CrossRef]
- Lasagni, A.F.; Alamri, S.; Aguilar-Morales, A.I.; Rößler, F.; Voisiat, B.; Kunze, T. Biomimetic surface structuring using laser based interferometric methods. Appl. Sci. 2018, 8, 1260. [Google Scholar] [CrossRef]
- Strobelt, J.; Santer, S.; Abourahma, H.; Music, M.; Farzan, Z.; Nezamis, P.; Leon, R.; McGee, D.J. Photomechanical azopolymers and digital polarization optics: A versatile platform for surface microstructure fabrication. ACS Appl. Opt. Mater. 2025. [Google Scholar] [CrossRef]
- Wang, H.; Deng, D.; Zhai, Z.; Yao, Y. Laser-processed functional surface structures for multi-functional applications—A review. J. Manuf. Process. 2024, 116, 247–283. [Google Scholar] [CrossRef]
- Liu, R.; Cao, L.; Liu, D.; Wang, L.; Saeed, S.; Wang, Z. Laser interference lithography—A method for the fabrication of controlled periodic structures. Nanomaterials 2023, 13, 1818. [Google Scholar] [CrossRef] [PubMed]
- Loebner, S.; Yadav, B.; Lomadze, N.; Tverdokhleb, N.; Donner, H.; Saphiannikova, M.; Santer, S. Local direction of optomechanical stress in azobenzene containing polymers during surface relief grating formation. Macromol. Mater. Eng. 2022, 307, 2100990. [Google Scholar] [CrossRef]
- Nedelchev, L.; Mateev, G.; Strijkova, V.; Salgueiriño, V.; Schmool, D.S.; Berberova-Buhova, N.; Stoykova, E.; Nazarova, D. Tunable Polarization and Surface Relief Holographic Gratings in Azopolymer Nanocomposites with Incorporated Goethite (α-FeOOH) Nanorods. Photonics 2021, 8, 306. [Google Scholar] [CrossRef]
- Pagidi, S.; Vishwanath, S.K.; Luo, D.; Dhara, S.; Manda, R. Unconventional photo-control of structural features using elliptically polarized light. Laser Photonics Rev. 2025, 19, 2401085. [Google Scholar] [CrossRef]
- Audia, B.; Tone, C.M.; Pagliusi, P.; Mazzulla, A.; Cipparrone, G. Hierarchical Fourier surfaces via broadband laser vectorial interferometry. ACS Photonics 2023, 10, 3060–3069. [Google Scholar] [CrossRef]
- Yager, K.G.; Barrett, C.J. Novel photo-switching using azobenzene functional materials. J. Photochem. Photobiol. A Chem. 2006, 182, 250–261. [Google Scholar] [CrossRef]
- Li, X.; Huang, H.; Wang, X. Optical erasure and reconfiguration of surface-relief-gratings of azo polymer and azo molecular glass: A comparative study on soft-lithographic duplicates. Adv. Photonics Res. 2023, 4, 2200077. [Google Scholar] [CrossRef]
- Priimagi, A.; Shevchenko, A. Azopolymer-based micro-and nanopatterning for photonic applications. J. Polym. Sci. B Polym. Phys. 2014, 52, 163–182. [Google Scholar] [CrossRef]
- Reda, F.; Salvatore, M.; Januariyasa, I.K.; Borbone, F.; Oscurato, S.L. Holographic photo-morphing of polymer surfaces for reprogrammable diffractive optics. In Proceedings of the MOEMS and Miniaturized Systems XXIV, San Francisco, CA, USA, 25–30 January 2025; Volume 13382. [Google Scholar]
- Oscurato, S.L.; Reda, F.; Salvatore, M.; Borbone, F.; Maddalena, P.; Ambrosio, A. Large-scale multiplexed azopolymer gratings with engineered diffraction behavior. Adv. Mater. Interfaces 2021, 8, 2101375. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Horie, Y.; Faraji-Dana, M.; Faraon, A. Angle-multiplexed metasurfaces: Encoding independent wavefronts in a single metasurface under different illumination angles. Phys. Rev. X 2017, 7, 041056. [Google Scholar] [CrossRef]
- Audia, B.; Pagliusi, P.; Mazzulla, A.; Cipparrone, G. Highly resolved and cross-talk free multiplexed holograms via broadband vectorial interferometry. Adv. Opt. Mater. 2023, 11, 2300275. [Google Scholar] [CrossRef]
- Lagugné Labarthet, F.; Buffeteau, T.; Sourisseau, C. Analyses of the diffraction efficiencies, birefringence, and surface relief gratings on azobenzene-containing polymer films. J. Phys. Chem. B 1998, 102, 2654–2662. [Google Scholar] [CrossRef]
- Yadavalli, N.S.; Saphiannikova, M.; Lomadze, N.; Goldenberg, L.M.; Santer, S. Structuring of photosensitive material below diffraction limit using far field irradiation. Appl. Phys. A Mater. Sci. Process. 2013, 113, 263–272. [Google Scholar] [CrossRef]
- Lefin, P.; Fiorini, C.; Nunzi, J.-M. Anisotropy of the photoinduced translation diffusion of azo-dyes. Opt. Mater. 1998, 9, 323–328. [Google Scholar] [CrossRef]
- Barrett, C.J.; Rochon, P.L.; Natansohn, A.L. Model of laser driven mass transport in thin films of dye-functionalized polymers. J. Chem. Phys. 1998, 109, 1505–1516. [Google Scholar] [CrossRef]
- Kumar, J.; Li, L.; Jiang, X.L.; Kim, D.Y.; Lee, T.S.; Tripathy, S. Gradient force: The mechanism for surface relief grating formation in azobenzene functionalized polymers. Appl. Phys. Lett. 1998, 72, 2096–2098. [Google Scholar] [CrossRef]
- Audia, B.; Pagliusi, P.; Provenzano, C.; Roche, A.; Oriol, L.; Cipparrone, G. Influence of photoanisotropies on light-controllable structuration of azopolymer surface. ACS Appl. Polym. Mater. 2020, 2, 1597–1604. [Google Scholar] [CrossRef]
- Tverdokhleb, N.; Loebner, S.; Yadav, B.; Santer, S.; Saphiannikova, M.V. Viscoplastic modeling of surface relief grating growth on isotropic and preoriented azopolymer films. Polymers 2023, 15, 463. [Google Scholar] [CrossRef] [PubMed]
- Jelken, J.; Henkel, C.; Santer, S. Formation of half-period surface relief gratings in azobenzene containing polymer films. Appl. Phys. B 2020, 126, 149. [Google Scholar] [CrossRef]
- Pagliusi, P.; Audia, B.; Provenzano, C.; Piñol, M.; Oriol, L.; Cipparrone, G. Tunable surface patterning of azopolymer by vectorial holography: The role of photoanisotropies in the driving force. ACS Appl. Mater. Interfaces 2019, 11, 34471–34477. [Google Scholar] [CrossRef] [PubMed]
- Nikolova, L.; Ramanujam, P.S. Polarization Holography; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Papavieros, G.; Constantoudis, V.; Vouroutzis, N.; Gogolides, E. Quantitative characterization of hierarchical multiscale surfaces of micro and nanostructured materials. Nanotechnology 2023, 34, 405702. [Google Scholar] [CrossRef] [PubMed]
- Constantoudis, V.; Ioannou-Sougleridis, I.; Dimou, A.; Ninou, A.; Chatzichristidi, M.; Makarona, E. A symmetry-based approach to the characterization of complex surface morphologies: Application in CuO and NiO nanostructures. Micro Nano Eng. 2022, 16, 100148. [Google Scholar] [CrossRef]
- Xiong, J.; Yin, K.; Li, K.; Wu, S.-T. Holographic optical elements for augmented reality: Principles, present status, and future perspectives. Adv. Photonics Res. 2021, 2, 2000049. [Google Scholar] [CrossRef]
- Campbell, M.; Sharp, D.N.; Harrison, M.T.; Denning, R.G.; Turberfield, A.J. Fabrication of photonic crystals for the visible spectrum by holographic lithography. Nature 2000, 404, 53–56. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Audia, B.; Tone, C.M.; Pagliusi, P.; Mazzulla, A.; Papavieros, G.; Constantoudis, V.; Cipparrone, G. Multiline Laser Interferometry for Non-Contact Dynamic Morphing of Hierarchical Surfaces. Biomimetics 2025, 10, 486. https://doi.org/10.3390/biomimetics10080486
Audia B, Tone CM, Pagliusi P, Mazzulla A, Papavieros G, Constantoudis V, Cipparrone G. Multiline Laser Interferometry for Non-Contact Dynamic Morphing of Hierarchical Surfaces. Biomimetics. 2025; 10(8):486. https://doi.org/10.3390/biomimetics10080486
Chicago/Turabian StyleAudia, Biagio, Caterina Maria Tone, Pasquale Pagliusi, Alfredo Mazzulla, George Papavieros, Vassilios Constantoudis, and Gabriella Cipparrone. 2025. "Multiline Laser Interferometry for Non-Contact Dynamic Morphing of Hierarchical Surfaces" Biomimetics 10, no. 8: 486. https://doi.org/10.3390/biomimetics10080486
APA StyleAudia, B., Tone, C. M., Pagliusi, P., Mazzulla, A., Papavieros, G., Constantoudis, V., & Cipparrone, G. (2025). Multiline Laser Interferometry for Non-Contact Dynamic Morphing of Hierarchical Surfaces. Biomimetics, 10(8), 486. https://doi.org/10.3390/biomimetics10080486








