Chaotic Mountain Gazelle Optimizer Improved by Multiple Oppositional-Based Learning Variants for Theoretical Thermal Design Optimization of Heat Exchangers Using Nanofluids
Abstract
1. Introduction
- Proposing a novel framework for initial population generation that integrates chaotic Latin Hypercube Sampling with the foundational principles of Opposition-Based Learning.
- Evaluating the optimization efficiency of twenty-one different chaotic Mountain Gazelle Algorithms and determining which chaotic method produces the most accurate predictions.
- Developing an innovative dexterous mutation scheme utilizing two efficient variants of an Opposition-Based Learning search mechanism, coordinated by an adaptive switch mechanism, and incorporating this manipulative search equation into the Chaos-Assisted Mountain Gazelle Optimizer.
- Maintaining the thermal design of shell and tube heat exchangers involves working with various nanoparticles in the tube bundle through the proposed enhanced Mountain Gazelle Optimizer.
2. Fundamentals of Mountain Gazelle Optimizer
2.1. Territorial Solitary Males
2.2. Maternity Herds
2.3. Bachelor Male Herds
2.4. Migration for Searching Food
3. Chaotic Mountain Gazelle Optimization Algorithm
Decision Process of the Best-Performing Chaotic Mountain Gazelle Algorithm Variant
4. Improved Mountain Gazelle Optimization Algorithm
4.1. Population Initialization with Chaos-Induced Hybrid Latin Hyper Cube Sampling and Opposition-Based Learning
4.2. Hybrid Chaotic Quasi-Opposition-Based Learning and Quasi-Dynamic Opposition-Based Learning Search Mechanism
| Algorithm 1: Hybrid population initialization scheme |
| Inputs: Population size–N, Problem dimension–D, |
| Upper and lower limits of the search space (up and low) |
| Initialize: N-sized D-Dimensional X population defined within the search limits Employ: logistic map induced LHS to generate evenly distributed population members XLHS = LHS (low, up, N, D, chx) Produce: opposite points (XOP) of X population using Equation (10) Combine: population individuals of X, XOP, and XLHS and select the fittest N solutions (XBESTN) between the competitive candidates |
| Output: The best N solutions (XBESTN) to be used for the iterative process |
| Algorithm 2: Hybrid Opposition-Based Learning Procedure (HOBL) |
| Inputs: Evolving population—X; Chebyshev chaotic numbers—chx |
| Lower and upper limits of the search space (low and up) |
| 1 [N, D] = size (X) 2 for i = 1 to N 3 for j = 1 to D 4 5 6 if 7 8 9 else 10 11 12 end 13 end 14 end |
| 15 XALL = [XQOBL;XDOPP] // Combine two populations 16 XALL = boundary (XALL) // Apply boundary check mechanism 17 XBESTN1 = sort (XALL,1:N) // Select the fittest N individuals |
| Output: XBESTN1 |
4.3. Hybridization of Quasi-Dynamic Opposite Learning Search Mechanism (QDOPP) with a Novel Trigonometric Random Number Generator and Adaptive Fitness-Based Perturbation Scheme
| Algorithm 3: Adaptive Fitness-Driven Perturbation algorithm—AFDP |
| Inputs: Population members—X; objective function—fobj () |
| [N,D] = size (X) // Determine the population size N and problem dimension D Calculate: the diversity of the population Diver using Equation (22) Decide: the best individual among the current population—fbest Initialize: the operator performance scores–So |
| for i = 1 to N // each population member in X Calculate: the normalized fitness gap using Equation (21) Compute: the adaptive scale factor using Equation (23) Determine: the operator selection probability–pro from the current scores using Equation (27) if rand(0,1) < pro// Randomly select the operator according to pro o = 1 // Consider perturbation based on Gaussian distribution vecrand (xi) = Gaussian(1,D) else o = 2 // Consider perturbation based on Cauchy distribution vecrand (xi) = Cauchy(1,D) end Obtain: the updated population member xnew,i using Equation (24) Perform: boundary check on xnew,i to verify solution feasibility Evaluate: the fitness value of xnew,i − fobj(xnew,i) if fobj (xnew,i) < fobj (xi) // Accept candidate if improvement is observed xi = xnew,i Δi = fobj (xi) − fobj (xnew,i) // Employ Equation (25) to calculate improvement So = So + Δi // Update the operator score (So) else So = So • 0.99 // Po—Penalize the operator if no improvement occurs end end |
| Output: XUPTD—updated population members |
| Algorithm 4: Hybrid ISSM-RNG induced QDOPP–AFDP algorithm (AFD-QDOPP) |
| Inputs: Population individuals—X; objective function—fobj () Lower and upper bounds (low and up) |
| 1 [N, D] = size (X) 2 Generate: N-sized D-dimensional random number sequences using ISSM-RNG 3 for i = 1 to N 4 for j = 1 to D 5 6 7 if 8 9 else |
| 10 11 12 end 13 end 14 end 15 Employ: boundary check mechanism to repair infeasible solution in XQDOPP |
| 16 XUPDT = AFDP (XQDOPP, fobj) 17 Amend: the violated solutions in XUPDT |
| 18 XALL2 = [XQDOPP; XUPDT] 19 XBESTN2 = sort (XALL2,1:N) |
| 20 Output: XBESTN2 |
4.4. Majority Voting Adaptive Switch Mechanism
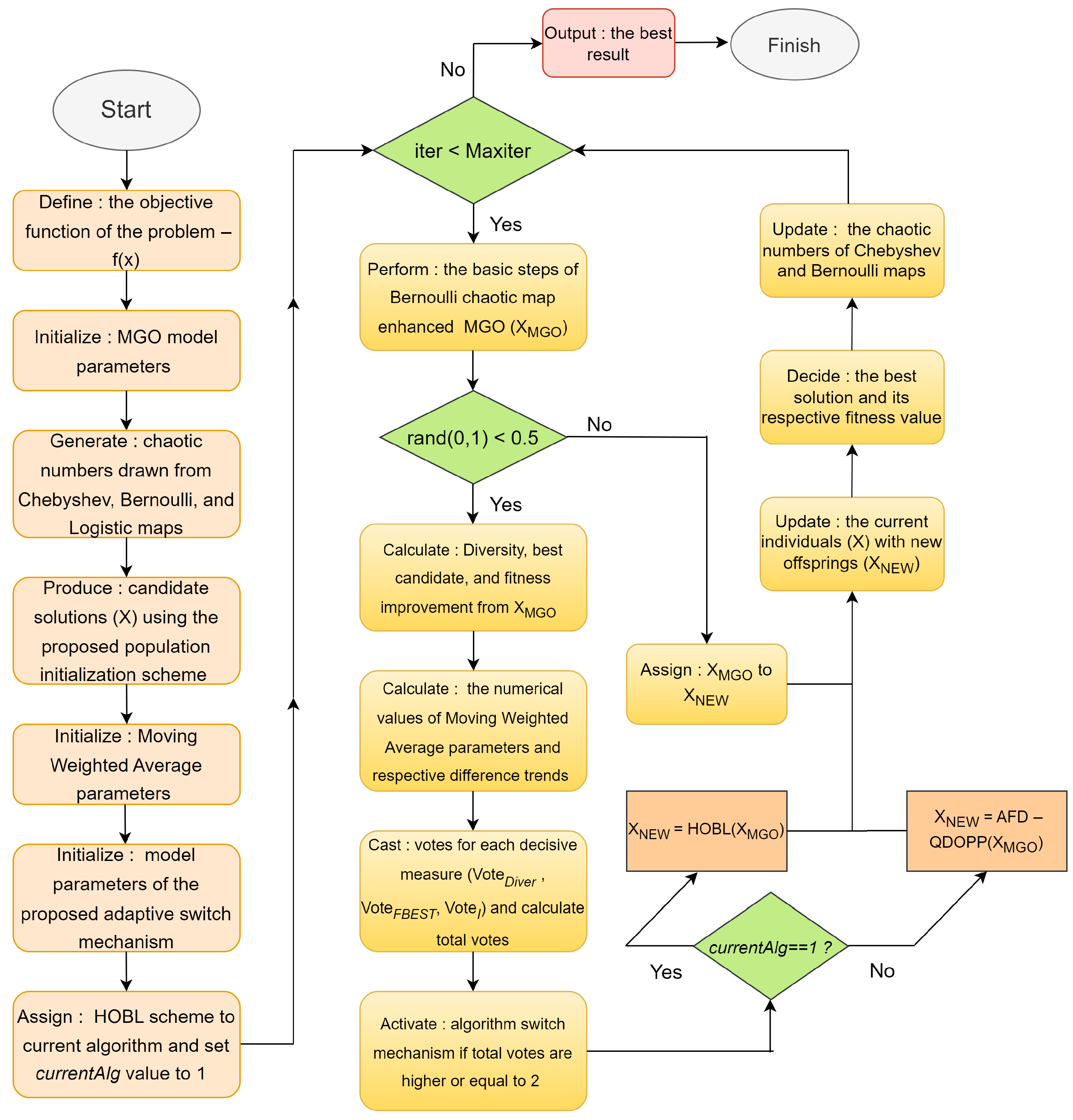
4.5. Hybrid Chaos Induced Integrated Quasi-Dynamic Opposition-Based Learning (HCQDOPP)-Enhanced Mountain Gazelle Optimizer
| Algorithm 5: HCQDOPP enhanced MGO optimizer |
| Inputs: Objective function—fobj(); problem size—N; problem dimension—D Upper and lower bounds (up and low), maximum number of iterations (Maxiter) |
| Initialize: evolvable population X using Algorithm 1 Initialize: the model parameters of the running algorithms |
| Initialize: the responsible metrics for the adaptive switch mechanism Calculate: the population diversity (Diver) using Equation (22) Decide: the best individual (XBEST) and its respective fitness value fbest Set: the current fitness improvement to zero (I = 0) Initialize: Moving Weighted Average parameter values defined for each metric MWADiver = Diver, MWAfbest = fbest, MWAI = I Initialize: chaotic numbers generated by the Chebyshev, Bernoulli, and logistic maps Assign: HOBL to the current switchable procedure and set currentAlg = 1 Set: iteration counter to 1 (iter = 1) |
| While (iter ≤ Maxiter) do Run: Bernoulli map improved MGO algorithm [XMGO, XBEST, fbest] = MGO(X) if rand(0,1) < 0.5 Calculate: Population diversity using XMGO through Equation (22) Diveriter = Diversity (XMGO) Use: fbest to decide on fitness quality fbestiter = fbest Compute: Fitness improvement I through Equation (28) I = if iter > 1 ? max(0, fbestprev − fbestiter): 0 Apply: Equation (32) to calculate the numerical value of smoothing factor αiter |
| Update: MWADiver, MWAfbest, MWAI using Equation (29) to Equation (31) Compute: the difference trends by using Equation (33) to Equation (35) Cast: votes for each decisive metric Calculate: the total votes Activate: the switching mechanism if necessary conditions are met ≥ 2 ? 3–currentAlg Store: the previous MWA metric values and fbest for the upcoming iteration , , fbestprev = fbestiter Apply: the current algorithm according to currentAlg value if currentAlg == 1 then XNEW = HOBL(XMGO) else XNEW = AFD-QDOPP(XMGO) end else Assign: XMGO to XNEW end Activate: boundary search mechanism Update: X population from the newly generated members of XNEW Determine: the best solution vector XBEST and its respective fitness value fbest Update: chaotic sequences generated by Bernoulli and Chebyshev maps Increment: iteration counter (iter = iter + 1) end |
| Output: XBEST, fbest |
4.6. Time Complexity of the HCQDOPP Algorithm
5. Simulation Results and Discussion
5.1. Benchmark Problems
5.2. Parameter Settings of the Comparative Algorithms
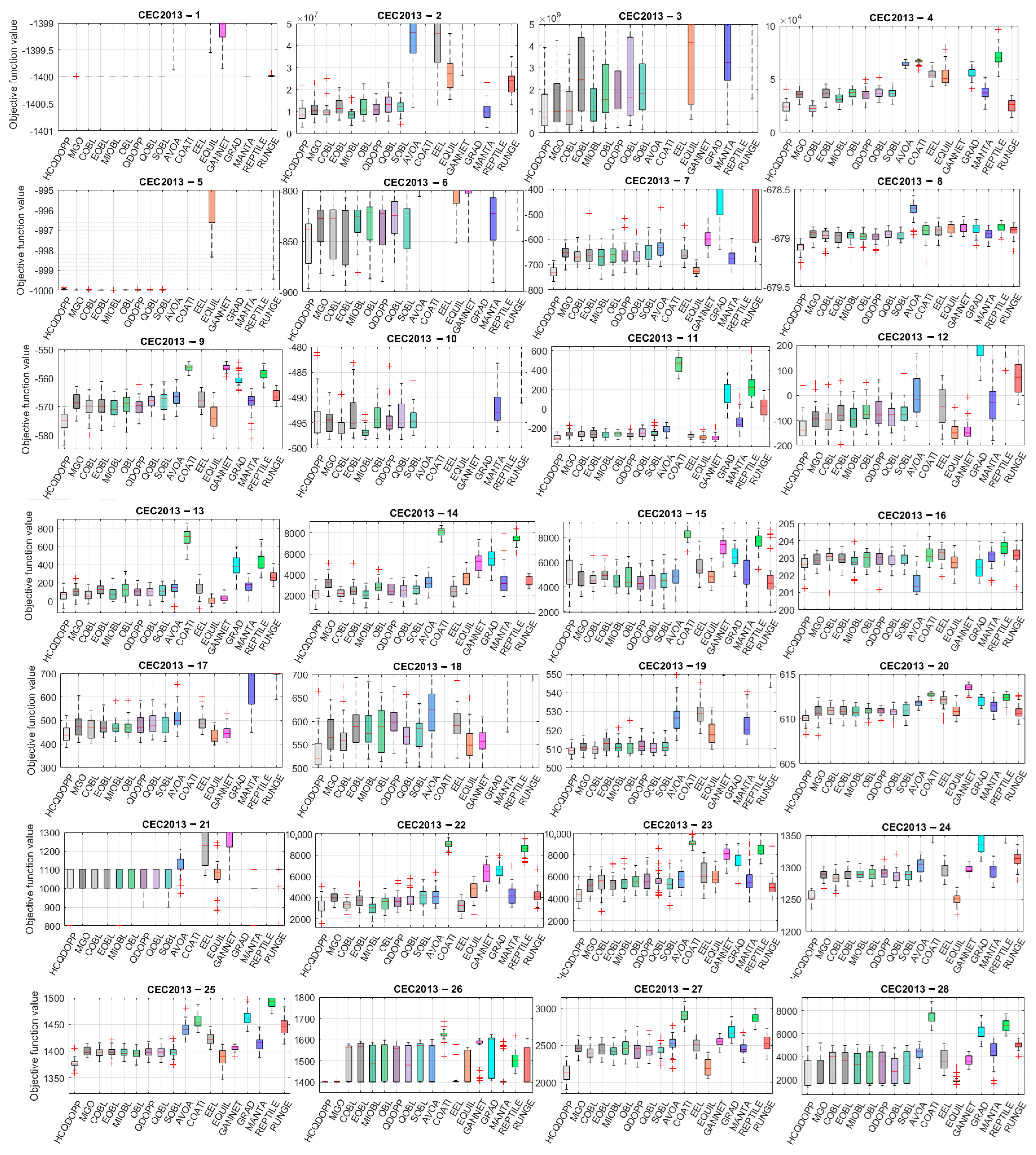
5.3. Comparison of the Statistical Results
5.4. Scalability Analysis and Statistical Test Results
5.5. Performance Assessment on CEC2006 Constrained Test Problems
6. A Complex Real-World Optimization Case: A Shell and Tube Heat Exchanger Design Operated with Nanofluids
6.1. Representative Heat Transfer Model
6.2. Optimization Results and Related Discussion
7. Conclusive Remarks
- When ranking points of the competitive chaotic Mountain Gazelle Optimization algorithm variants are averaged to a mean ranking point for each optimization problem, it is seen that integration of the chaotic numbers produced from the CH02 (Bernoulli map) yields the best predictive results of the employed forty-eight unimodal and multimodal test problems with different problem dimensionalities.
- The proposed intelligently guided manipulation scheme has significantly improved the solution diversity within the population, thanks to the unpredictable yet conducive features of the Opposition-Based Learning, Quasi-Dynamic Opposition-Based Learning, and Quasi Opposition-Based Learning methods, all three of which have complementary capabilities that can eliminate the algorithmic disadvantages of each method by the created synergy between them during the hybridization process. Numerical simulations demonstrate that shaping these three innovative learning schemes into a solid, structured form renders them so dexterous and prolific that the proposed search strategy has acquired the ability to explore unexplored regions of the search space without incurring excessive computational costs. Comprehensive evaluations of the proposed mutation scheme’s versatility suggest that it can enhance the overall optimization performance of any metaheuristic optimizer, thereby demonstrating the method’s efficiency on a global scale.
- It is also understood that Opposition-Based Learning has been proven effective in improving metaheuristic algorithms for optimizing complex structural design problems, such as finding the optimal configuration of a shell and tube heat exchanger or other challenging real-world design cases. The highly randomized characteristics of these improved methods make it effortless to obtain optimal solutions to complex design problems with high nonlinearity and binding, restrictive constraints.
- A detailed investigation of the influences of streaming nanofluids in the tubes of a shell-and-tube heat exchanger indicates that suspended nanoparticles in the refrigerant fluid can increase the tube-side heat transfer rates to some degree. However, it can also increase the tube-side pressure drop rates, which necessitates carefully weighing the optimum amount of nanoparticles in the nanofluid, as both the tube-side heat transfer coefficient and pressure drop rates directly affect the total cost of a heat exchanger.
- Among the six available design alternatives, a heat exchanger configuration operating with a water + SiO2 nanofluid on the tube side yields the minimum total cost rate, thanks to its superior thermophysical properties.
- As a reasonable future projection inspired by this research study, it would be beneficial for metaheuristic algorithm developers to focus on the mutation equations based on the integration of two or more oppositional learning search mechanism variants since they are capable of making abrupt movements in the search space to avoid the local optimum points encountered throughout the iterative process.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bar-Cohen, Y. Biomimetics: Nature-Based Innovation; CEC Press: Moon Township, PA, USA, 2012. [Google Scholar]
- Bhushan, B. Biomimetics: Lessons from Nature—An Overview. Philos. Trans. R. Soc. A 2009, 367, 1445–1486. [Google Scholar] [CrossRef] [PubMed]
- Vincent, J.F.V.; Bogatyreva, O.A.; Bogatyrev, N.R.; Bowyer, A.; Pahl, A.K. Biomimetics: Its Practice and Theory. J. R. Soc. Interface 2006, 3, 471–482. [Google Scholar] [CrossRef] [PubMed]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- de Castro, L.N.; Timmis, J. Artificial Immune Systems: A New Computational Intelligence Approach; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Liu, T.; Wang, S.; Liu, H.; Fe, G. Engineering Perspective on Bird Flight: Scaling, Geometry, Kinematics, and Aerodynamics. Prog. Aerosp. Sci. 2023, 142, 100933. [Google Scholar] [CrossRef]
- Collins, C.M.; Safiuddin, M. Lotus-Leaf-Inspired Biomimetic Coatings: Different Types, Key Properties, and Applications in Infrastructures. Infrastructures 2022, 7, 46. [Google Scholar] [CrossRef]
- Vesela, R.; Harjuntausta, A.; Hakkarainen, A.; Rönnholm, P.; Pellikka, P.; Rikkinen, J. Termite Mound Architecture Regulates Nest Temperature and Correlates with Species Identities of Symbiotic Fungi. PeerJ 2019, 6, e6237. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. Comput. Aided Des. 2011, 41, 303–315. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Nayyef, H.M.; Ibrahim, A.A.; Zainuri, M.A.A.M.; Zulkifley, M.A.; Shareef, H. A Novel Hybrid Algorithm Based Jellyfish Search and Particle Swarm Optimization. Mathematics 2023, 11, 3210. [Google Scholar] [CrossRef]
- Coelho, L.; Mariani, V.C. Use of Chaotic Sequences in a Biologically Inspired Algorithm for Engineering Design Optimization. Expert Syst. Appl. 2008, 34, 1905–1913. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Liu, Y.; Li, C.; Zeng, S. Opposition-Based Particle Swarm Algorithm with Cauchy Mutation. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4750–4756. [Google Scholar]
- Azad, A.V.; Azad, N.V. Application of Nanofluids for the Optimal Design of Shell and Tube Heat Exchangers Using Genetic Algorithm. Case Stud. Therm. Eng. 2016, 8, 198–206. [Google Scholar] [CrossRef]
- Hajabdollahi, H. Economic Optimization of Shell and Tube Heat Exchanger Using Nanofluid. Int. J. Mech. Mechatron. Eng. 2017, 11, 1436–1440. [Google Scholar]
- Singh, S.; Sarkar, J. Energy, Exergy, and Economic Assessments of Shell and Tube Condenser Using Nanofluid as Coolant. Int. Commun. Heat Mass Transf. 2018, 98, 41–48. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Khodadadi, N.; Mirjalili, S. Mountain Gazelle Optimizer: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems. Adv. Eng. Softw. 2022, 174, 103282. [Google Scholar] [CrossRef]
- Abbasi, R.; Saidi, S.; Urooj, S.; Alhasnawi, B.N.; Alawad, M.A.; Premkumar, M. An Accurate Metaheuristic Mountain Gazelle Optimizer for Parameter Estimation of Single- and Double-Diode Photovoltaic Cell Models. Mathematics 2023, 11, 4565. [Google Scholar] [CrossRef]
- Zellagui, M.; Belbachir, N.; El-Sehiemy, R.A. Solving the Optimal Power Flow Problem in Power Systems Using the Mountain Gazelle Algorithm. Eng. Proc. 2023, 56, 176. [Google Scholar]
- Houssein, E.H.; Dirar, M.; Khalil, A.A.; Ali, A.A.; Mohamed, W.M. Optimized Deep Learning Architecture for Predicting Maximum Temperatures in Key Egyptian Regions Using Hybrid Genetic Algorithm and Mountain Gazelle Optimizer. Artif. Intell. Rev. 2025, 58, 258. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1978, 21, 239–245. [Google Scholar]
- Tizhoosh, H.R. Oppositional Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; pp. 275–281. [Google Scholar]
- Turgut, O.E.; Turgut, M.S. Quasi-Dynamic Oppositional Learning Enhanced Runge-Kutta Optimizer for Solving Complex Optimization Problems. Evol. Intell. 2024, 17, 2899–2962. [Google Scholar] [CrossRef]
- Tharwat, A.; Hassanian, A. Chaotic Antlion Algorithm for Parameter Optimization of Support Vector Machine. Appl. Intell. 2018, 48, 670–686. [Google Scholar] [CrossRef]
- Sayed, G.; Hassanien, A.; Azar, A. Feature Selection via a Novel Chaotic Crow Search Algorithm. Neural Comput. Appl. 2019, 31, 171–188. [Google Scholar] [CrossRef]
- Arnold, V.I.; Avez, A. Problèmes Ergodiques de la Mécanique Classique; Gauther–Villars: Paris, France, 1967. [Google Scholar]
- Gonzales, R.F.M.; Mendez, J.A.D.; Luenges, L.P.; Hernandez, J.L.; Median, R.V. A Steganographic Method Using Bernoulli’s Chaotic Map. Comput. Electr. Eng. 2016, 54, 435–449. [Google Scholar]
- Wang, X.; Zhao, J. An Improved Key Agreement Protocol Based on Chaos. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 4052–4057. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, D. Double Optical Image Encryption Using Discrete Chirikov Standard Map and Chaos-Based Fractional Random Transform. Opt. Lasers Eng. 2013, 51, 472–480. [Google Scholar] [CrossRef]
- Hilborn, R.C. Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers, 2nd ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Debaney, R.L. Fractal Patterns Arising in Chaotic Dynamical Systems. In The Science of Fractal Images; Peitgen, H.O., Saupe, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 137–168. [Google Scholar]
- Henon, M. A Two-Dimensional Mapping with a Strange Attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Ikeda, K. Multiple-Valued Stationary State and Instability of the Transmitted Light by a Ring Cavity System. Opt. Commun. 1979, 30, 257–261. [Google Scholar] [CrossRef]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Konno, H.; Kondo, T. Iterative Chaotic Map as Random Number Generator. Ann. Nucl. Energy 1997, 24, 1183–1188. [Google Scholar] [CrossRef]
- Chua, L.O.; Yao, Y. Generating Randomness from Chaos and Constructing Chaos with Desired Randomness. Int. J. Circuit Theory Appl. 1990, 18, 215–240. [Google Scholar] [CrossRef]
- May, R.M. Simple Mathematical Models with Very Complicated Dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Zheng, W.M. Symbolic Dynamics for the Lozi Map. Chaos Solitons Fractals 1991, 1, 243–248. [Google Scholar] [CrossRef]
- Wang, X.; Jin, C. Image Encryption Using Game of Life Permutation and PWLCM Chaotic System. Opt. Commun. 2012, 285, 412–417. [Google Scholar] [CrossRef]
- Dastgheib, M.A.; Farhang, M. A Digital Pseudo-Random Number Generator Based on Sawtooth Chaotic Map with a Guaranteed Enhanced Period. Nonlinear Dyn. 2017, 89, 2957–2966. [Google Scholar] [CrossRef]
- Skanderova, L.; Zelinka, I. Arnold Cat Map and Sinai as Chaotic Numbers Generators in Evolutionary Algorithms. In Recent Advances in Electrical Engineering and Related Sciences (AETA 2013); Springer: Berlin/Heidelberg, Germany, 2013; pp. 381–389. [Google Scholar]
- Mansouri, A.; Wang, X. A Novel One-Dimensional Sine Powered Chaotic Map and Its Application in a New Image Encryption Scheme. Inf. Sci. 2020, 520, 46–62. [Google Scholar] [CrossRef]
- Tubishat, M.; Ja’afar, S.; Idris, N.; Al-Betar, M.A.; Alswaitti, M.; Jarrah, H.; Ismail, M.A.; Omar, M.S. Improved Sine-Cosine Algorithm with Simulated Annealing and Singer Chaotic Map for Hadith Classification. Neural Comput. Appl. 2022, 34, 1385–1406. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Guo, Q. Modified Whale Optimization Algorithm Based on Tent Chaotic Mapping and Its Application in Structure Optimization. KSCE J. Civ. Eng. 2020, 24, 3703–3713. [Google Scholar] [CrossRef]
- Zaslavskii, G.M. The Simplest Case of a Strange Attractor. Phys. Lett. A 1978, 69, 145–147. [Google Scholar] [CrossRef]
- Yang, W.; Liu, J.; Tan, S.; Zhang, W.; Liu, Y. Evolutionary Dynamic Grouping Based Cooperative Co-Evolution Algorithm for Large-Scale Optimization. Appl. Intell. 2024, 54, 4585–4601. [Google Scholar] [CrossRef]
- Wu, C.; Teng, T. An Improved Differential Evolution with a Quasi-Oppositional Based Learning Strategy for Global Optimization Problems. Appl. Soft Comput. 2013, 13, 4581–4590. [Google Scholar]
- Xu, Y.; Yang, Z.; Li, X.; Kang, H.; Yang, X. Dynamic Opposite Learning Enhanced Teaching-Learning-Based Optimization. Knowl. Based Syst. 2020, 188, 104966. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta Ray Foraging Optimization: An Effective Bio-Inspired Optimizer for Engineering Applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the Metaphor: An Efficient Optimization Algorithm Based on Runge–Kutta Method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African Vultures Optimization Algorithm: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Pan, J.S.; Zhang, L.G.; Wang, R.B.; Snasel, V.; Chu, S.C. Gannet Optimization Algorithm: A New Metaheuristic Algorithm for Solving Engineering Optimization Problems. Math. Comput. Simul. 2022, 202, 343–373. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z.; Fan, H.; Zhang, J.; Mirjalili, S.; Khodadadi, N.; Cao, Q. Electric Eel Foraging Optimization: A New Bio-Inspired Optimizer for Engineering Applications. Expert Syst. Appl. 2024, 238, 122200. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Haddad, O.B.; Chu, X. Gradient-Based Optimizer: A New Metaheuristic Optimization Algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd-Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A Nature-Inspired Meta-Heuristic Optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovska, E.; Trojovsky, P. Coati Optimization Algorithm: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. Quasi-Oppositional Differential Evolution. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 2229–2236. [Google Scholar]
- Tizhoosh, H.R.; Ventresca, M.; Rahnamayan, S. Opposition-Based Computing. In Oppositional Concepts in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 11–28. [Google Scholar]
- Rahnamayan, S.; Jesuthasan, J.; Bourennani, F.; Salehinejad, H.; Natarer, G.F. Computing Opposition by Involving Entire Population. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1800–1807. [Google Scholar]
- Tang, J.; Zhao, X. On the Improvement of Opposition-Based Differential Evolution. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 4, pp. 2407–2411. [Google Scholar]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A Practical Tutorial on the Use of Nonparametric Statistical Tests as a Methodology for Comparing Evolutionary and Swarm Intelligence Algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A Nature-Inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A Nature-Inspired Metaheuristic Algorithm for Engineering Applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New Metaheuristic Algorithm for Solving Optimization Problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler Optimization Algorithm: A New Metaheuristic Algorithm Inspired by Kepler’s Laws of Planetary Motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Zidan, M.; Jameel, M.; Abouhawwash, M. Mantis Search Algorithm: A Novel Bio-Inspired Algorithm for Global Optimization and Engineering Design Problems. Comput. Methods Appl. Mech. Eng. 2023, 415, 116200. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime Mould Algorithm: A New Method for Stochastic Optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Han, M.; Du, Z.; Yuen, K.F.; Zhu, H.; Li, Y.; Yuan, Q. Walrus Optimizer: A Novel Nature-Inspired Metaheuristic Algorithm. Expert Syst. Appl. 2024, 239, 122413. [Google Scholar] [CrossRef]
- Incropera, F.; DeWitt, D.; Bergman, T.; Lavine, A. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Shah, R.K.; Sekulic, D.P. Fundamentals of Heat Exchanger Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Rosenhow, W.M.; Harnett, P.J. Handbook of Heat Transfer; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Kakac, S.; Liu, H.; Pramuanjaroenkij, A. Heat Exchangers: Selection, Rating, and Thermal Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Żyła, G.; Fal, J. Viscosity, Thermal and Electrical Conductivity of Silicon Dioxide–Ethylene Glycol Transparent Nanofluids: An Experimental Study. Thermochim. Acta 2017, 650, 106–113. [Google Scholar] [CrossRef]
- Anitha, S.; Thomas, T.; Parthiban, P.; Pichumani, M. What Dominates Heat Transfer Performance of Hybrid Nanofluid in Single Pass Shell and Tube Heat Exchanger? Adv. Powder Technol. 2019, 30, 3107–3117. [Google Scholar] [CrossRef]
- Taal, M.; Bulatov, I.; Klemes, J.; Stehlik, P. Cost Estimation and Energy Price Forecast for Economic Evaluation of Retrofit Projects. Appl. Therm. Eng. 2003, 23, 1819–1835. [Google Scholar] [CrossRef]
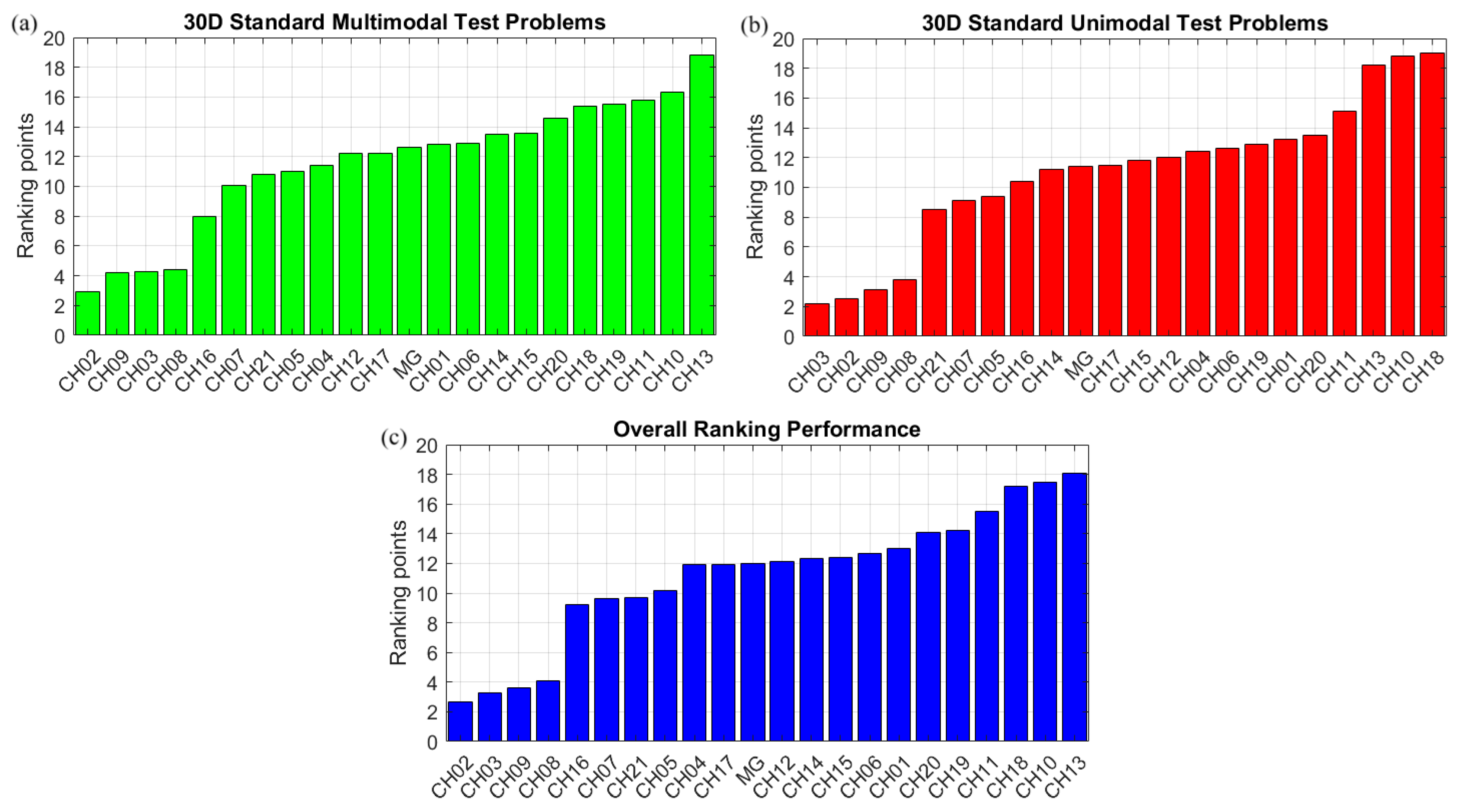
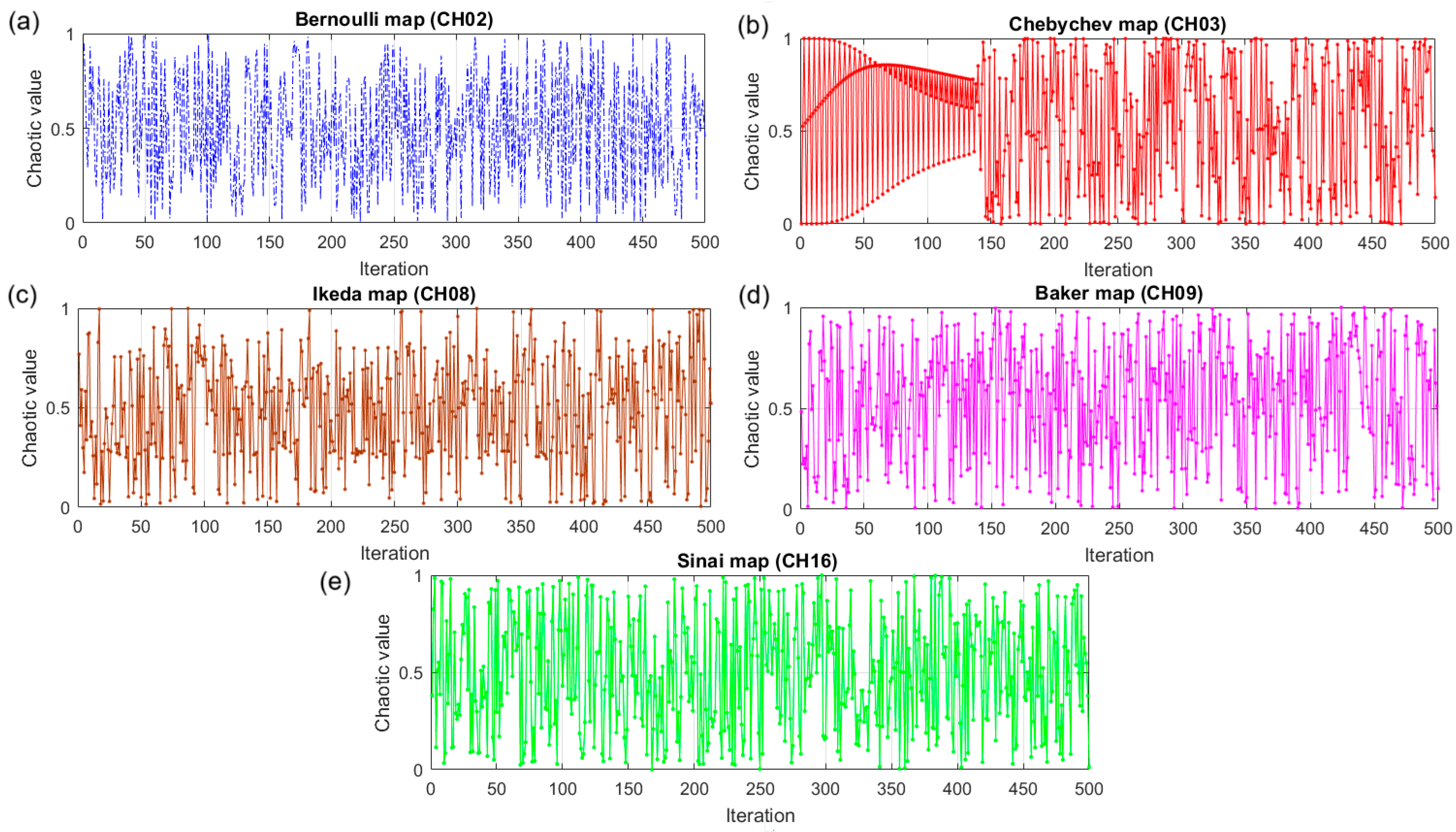

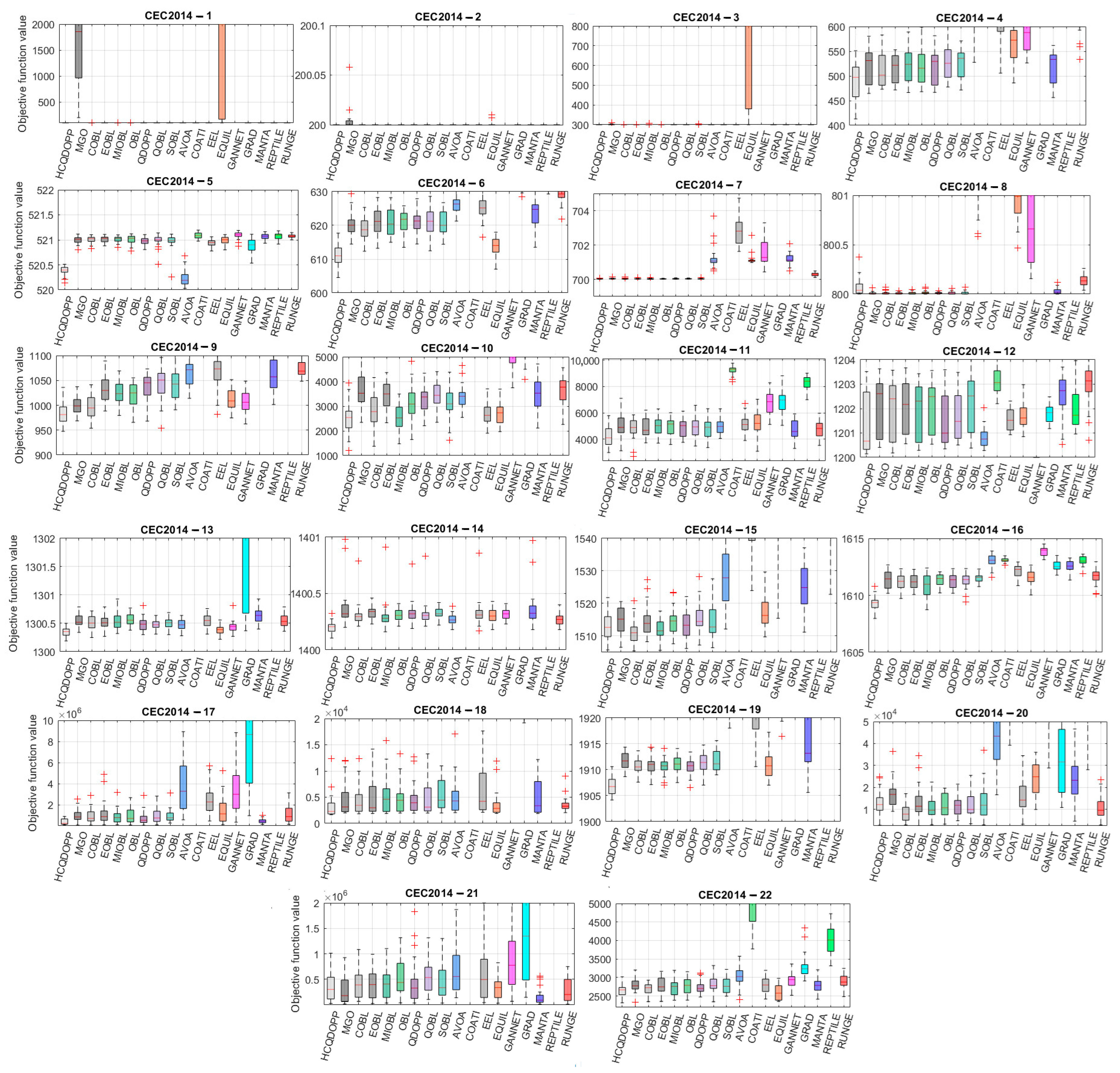
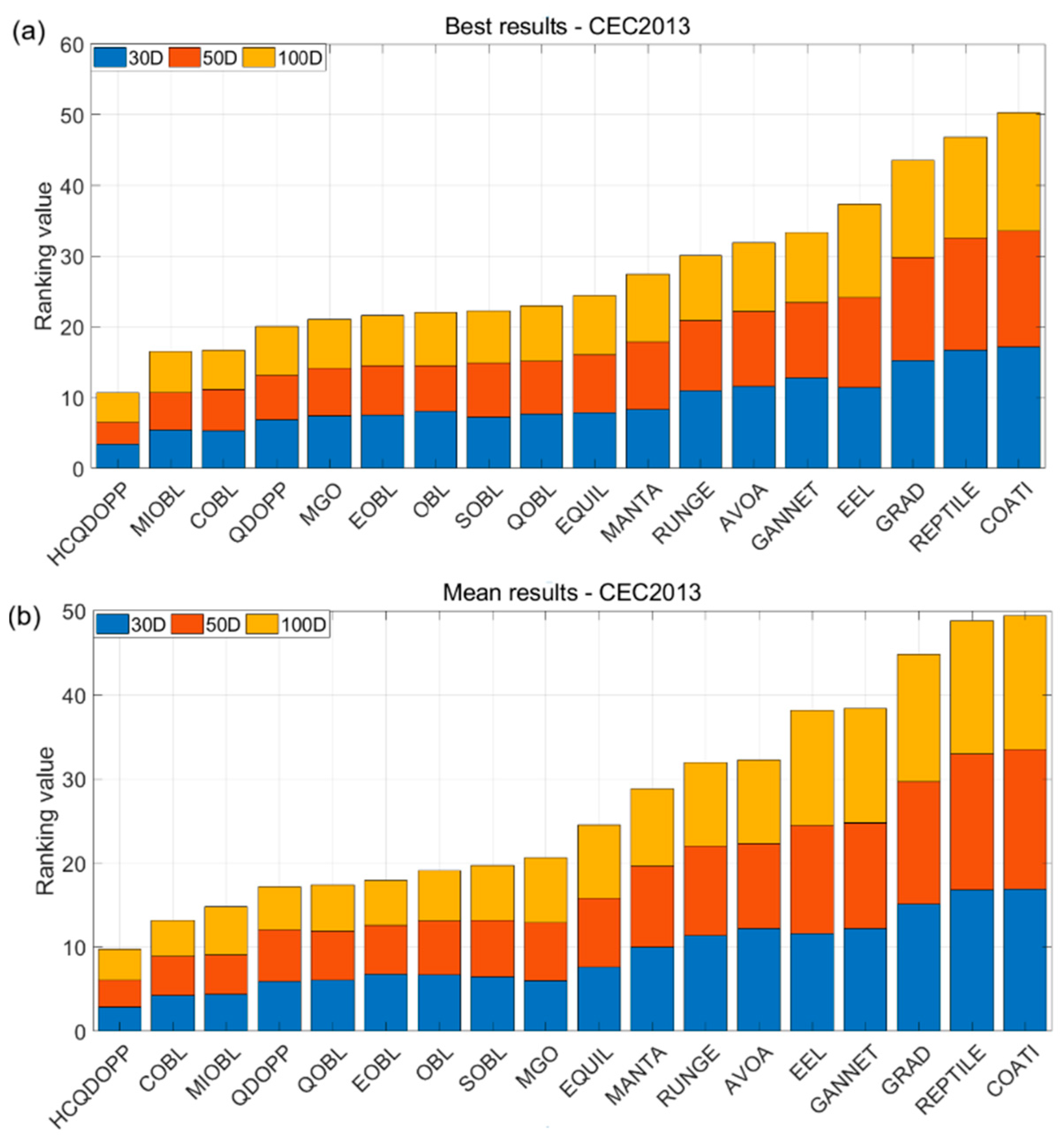


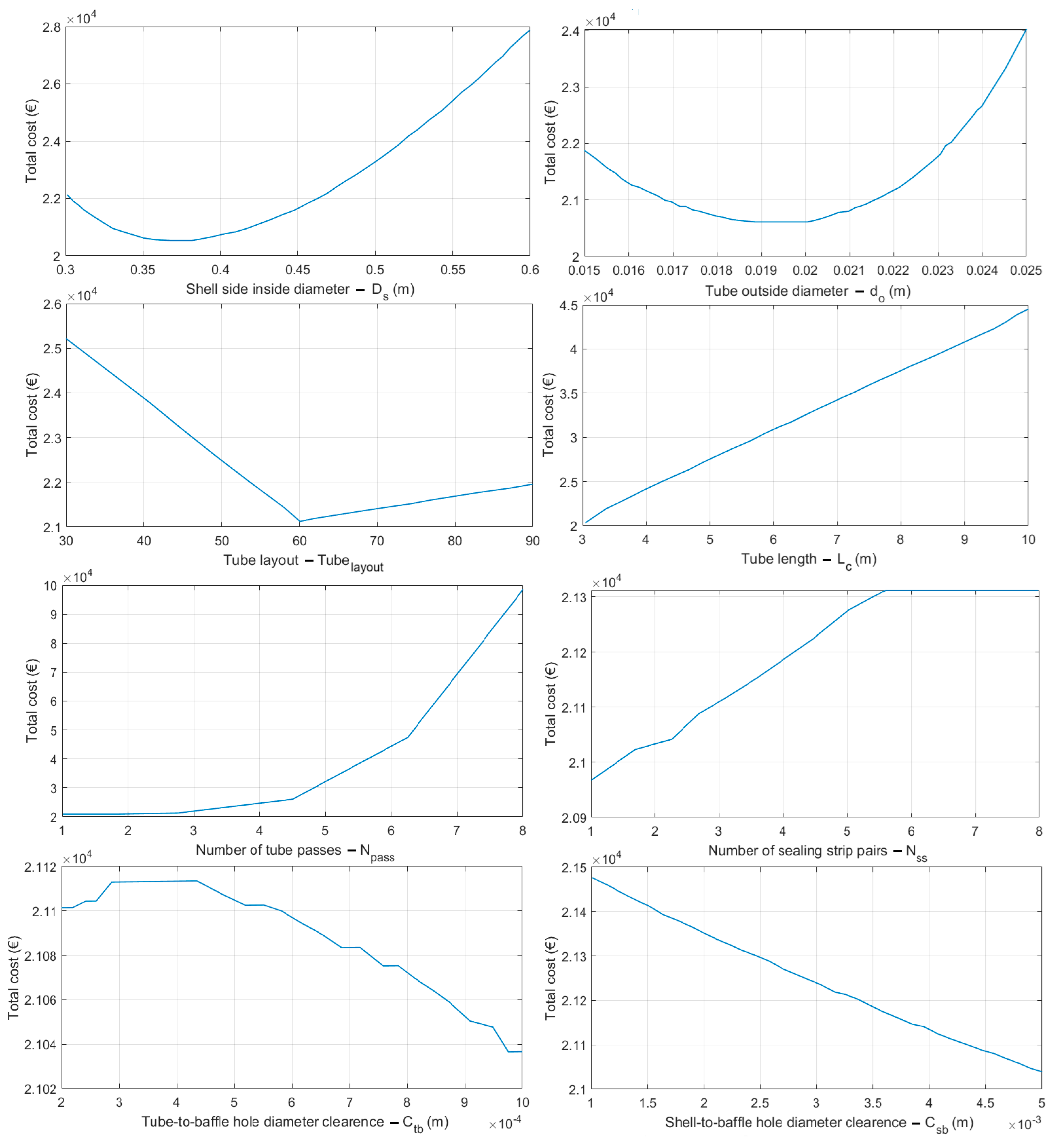
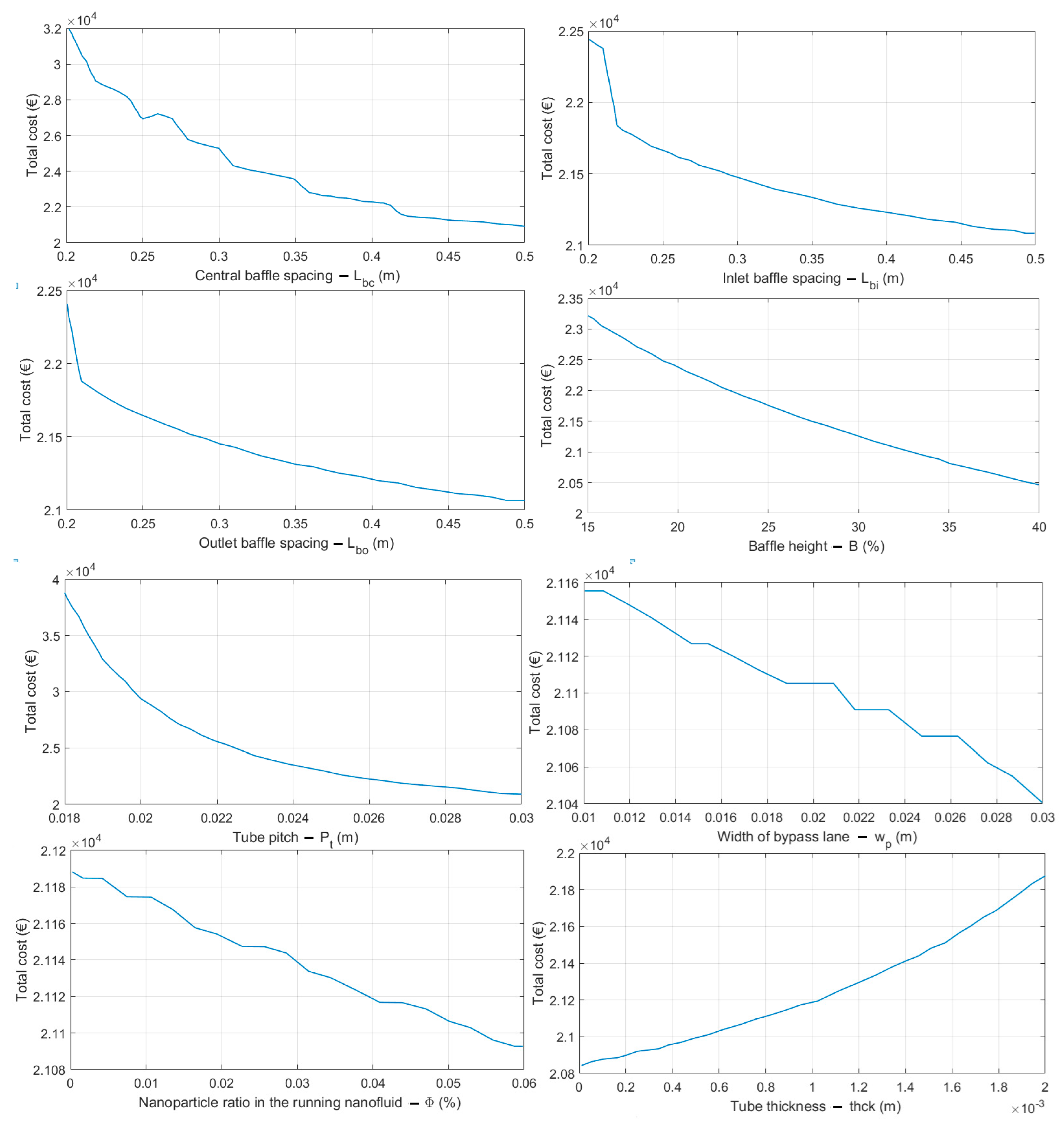
| Multimodal Function Name | Range | Unimodal Function Name | Range |
|---|---|---|---|
| F1—Ackley | [−32, 32] D | F25—Sphere | [−5.12, 5.12] D |
| F2—Griewank | [−600, 600] D | F26—Rosenbrock | [−30.0, 30.0] D |
| F3—Rastrigin | [−5.12, 5.12] D | F27—Brown | [−1.0, 4.0] D |
| F4—Zakharov | [−5.0, 10.0] D | F28—Stretched V Sine Wave | [−10.0, 10.0] D |
| F5—Alpine | [0, 10] D | F29—Powell | [0.0, 10.0] D |
| F6—Penalized1 | [−50.0, 50.0] D | F30—Sum of Different Powers | [−1.0, 1.0] D |
| F7—Csendes | [−5.0, 5.0] D | F31—Bent cigar | [−5.0, 5.0] D |
| F8—Schaffer | [−100.0, 100.0] | F32—Discus | [−100.0, 100.0] D |
| F9—Salomon | [−50.0, 50.0] D | F33—Schwefel 2.20 | [−100.0, 100.0] D |
| F10—Inverted cosine mixture | [−10.0, 10.0] D | F34—Schwefel 2.21 | [−100.0, 100.0] D |
| F11—Wavy | [−3.14, 3.14] D | F35—Schwefel 2.23 | [−10.0, 10.0] D |
| F12—Xin She Yang1 | [−5.0, 5.0] D | F36—Schwefel 2.25 | [0.0, 10.0] D |
| F13—Xin She Yang4 | [−6.28, 6.28] D | F37—Dropwave | [−5.12, 5.12] D |
| F14—Xin She Yang2 | [−10.0, 10.0] D | F38—Trid | [D2, D2] D |
| F15—Pathological | [−10.0, 10.0] D | F39—Generalized White & Holst | [−10.0, 10.0] D |
| F16—Quintic | [−10.0, 10.0] D | F40—BIGGSB1 | [−10, 10] D |
| F17—Levy | [−10.0, 10.0] D | F41—Anescu01 | [−2.0, 2.0] D |
| F18—Qing | [−500.0, 500.0] D | F42—Anescu02 | [1.39, 4.0] D |
| F19—Diagonal1 | [−10.0, 10.0] D | F43—Anescu03 | [−4.0, 1.39] D |
| F20—Hager | [−10.0, 10.0] D | F44—Anescu04 | [0.001, 2.0] D |
| F21—Diagonal4 | [−10.0, 10.0] D | F45—Anescu06 | [0.001, 2.0] D |
| F22—Perturbed Quadratic Diagonal | [−10.0, 10.0] D | F46—Anescu07 | [−2.0, 2.0] D |
| F23—SINE | [−10.0, 10.0] D | F47—Schumer-Steiglitz 3 | [−100.0, 100.0] D |
| F24—Diagonal9 | [−10.0, 10.0] D | F48—Schumer-Steiglitz 2 | [−100.0, 100.0] D |
| No | Functions | Global Optimum–f(x) | |
|---|---|---|---|
| 1 | Sphere function | −1400 | |
| Unimodal | 2 | Rotated High Conditioned Elliptic Function | −1300 |
| Functions | 3 | Rotated Bent Cigar Function | −1200 |
| 4 | Rotated Discus Function | −1100 | |
| 5 | Different Powers Function | −1000 | |
| 6 | Rotated Rosenbrock’s Function | −900 | |
| 7 | Rotated Schaffers F7 Function | −800 | |
| 8 | Rotated Ackley’s Function | −700 | |
| 9 | Rotated Weierstrass Function | −600 | |
| 10 | Rotated Griewank’s Function | −500 | |
| Basic | 11 | Rastrigin’s Function | −400 |
| Multimodal | 12 | Rotated Rastrigin’s Function | −300 |
| Functions | 13 | Non-Continuous Rotated Rastrigin’s Function | −200 |
| 14 | Schwefel’s Function | −100 | |
| 15 | Rotated Schwefel’s Function | 100 | |
| 16 | Rotated Katsuura Function | 200 | |
| 17 | Lunacek–Bi-Rastrigin Function | 300 | |
| 18 | Rotated Lunacek–Bi-Rastrigin Function | 400 | |
| 19 | Expanded Griewank’s plus Rosenbrock’s Function | 500 | |
| 20 | Expanded Scaffer’s F6 Function | 600 | |
| 21 | Composition Function 1 (n = 5, Rotated) | 700 | |
| 22 | Composition Function 2 (n = 3, Unrotated) | 800 | |
| Composite | 23 | Composition Function 3 (n = 3, Rotated) | 900 |
| Functions | 24 | Composition Function 4 (n = 3, Rotated) | 1000 |
| 25 | Composition Function 5 (n = 3, Rotated) | 1100 | |
| 26 | Composition Function 6 (n = 5, Rotated) | 1200 | |
| 27 | Composition Function 7 (n = 5, Rotated) | 1300 | |
| 28 | Composition Function 8 (n = 5, Rotated) | 1400 |
| No | Functions | Global Optimum–f(x) | |
|---|---|---|---|
| 1 | Rotated High Conditioned Elliptic Function | 100 | |
| Unimodal | 2 | Rotated Bent Cigar Function | 200 |
| Functions | 3 | Rotated Discus Function | 300 |
| 4 | Shifted and Rotated Rosenbrock’s Function | 400 | |
| 5 | Shifted and Rotated Ackley’s Function | 500 | |
| 6 | Shifted and Rotated Weierstrass Function | 600 | |
| 7 | Shifted and Rotated Griewank’s Function | 700 | |
| 8 | Shifted Rastrigin’s Function | 800 | |
| 9 | Shifted and Rotated Rastrigin’s Function | 900 | |
| 10 | Shifted Schwefel’s Function | 1000 | |
| Basic | 11 | Shifted and Rotated Schwefel’s Function | 1100 |
| Multimodal | 12 | Shifted and Rotated Katsuura Function | 1200 |
| Functions | 13 | Shifted and Rotated HappyCat Function | 1300 |
| 14 | Shifted and Rotated HGBat Function | 1400 | |
| 15 | Shifted and Rotated Expanded Griewank’s plus Rosenbrock’s Function | 1500 | |
| 16 | Shifted and Rotated Expanded Scaffer’s F6 Function | 1600 | |
| 17 | Hybrid Function 1 (n = 3) | 1700 | |
| 18 | Hybrid Function 2 (n = 3) | 1800 | |
| Hybrid | 19 | Hybrid Function 3 (n = 4) | 1900 |
| Functions | 20 | Hybrid Function 4 (n = 4) | 2000 |
| 21 | Hybrid Function 5 (n = 5) | 2100 | |
| 22 | Hybrid Function 6 (n = 5) | 2200 |
| Algorithms | Parameters |
|---|---|
| AVOA | p1 = 0.6, p2 = 0.4, p3 = 0.6, α = 0.8, β = 0.2, γ = 2.5 |
| GANNET | M = 2.5, Velocity = 1.5 |
| REPTILE | α = 0.1, β = 0.1 |
| EQUIL | a1 = 2.0, a2 = 1.0, GP = 0.5 |
| COATI | No tunable algorithm parameters |
| EEL | No tunable algorithm parameters |
| GRAD | No tunable algorithm parameters |
| MANTA | No tunable algorithm parameters |
| RUNGE | No tunable algorithm parameters |
| MGO | No tunable algorithm parameters |
| HCQDOPP vs. | Wilcoxon Signed-Rank Test | |||||
|---|---|---|---|---|---|---|
| + | − | = | p-Value | α = 0.05 | α = 0.1 | |
| COATI | 141 | 6 | 3 | <0.05 | Yes | Yes |
| REPTILE | 140 | 5 | 5 | <0.05 | Yes | Yes |
| GANNET | 139 | 7 | 4 | <0.05 | Yes | Yes |
| GRAD | 141 | 6 | 3 | <0.05 | Yes | Yes |
| AVOA | 136 | 8 | 6 | <0.05 | Yes | Yes |
| EEL | 134 | 7 | 9 | <0.05 | Yes | Yes |
| MANTA | 137 | 7 | 6 | <0.05 | Yes | Yes |
| EQUIL | 132 | 10 | 8 | <0.05 | Yes | Yes |
| MGO | 134 | 10 | 6 | <0.05 | Yes | Yes |
| OBL | 133 | 9 | 8 | <0.05 | Yes | Yes |
| SOBL | 135 | 9 | 6 | <0.05 | Yes | Yes |
| QOBL | 131 | 10 | 9 | <0.05 | Yes | Yes |
| EOBL | 127 | 13 | 10 | <0.05 | Yes | Yes |
| QDOPP | 129 | 11 | 10 | <0.05 | Yes | Yes |
| MIOBL | 130 | 10 | 10 | <0.05 | Yes | Yes |
| COBL | 125 | 15 | 10 | <0.05 | Yes | Yes |
| Type | D | LI | NI | LE | NE | fopt (x) | |
|---|---|---|---|---|---|---|---|
| G01 | Quadratic | 13 | 9 | 0 | 0 | 0 | −15.000000 |
| G02 | Nonlinear | 20 | 0 | 2 | 0 | 0 | −0.8036191 |
| G03 | Polynomial | 10 | 0 | 0 | 0 | 1 | −1.0005001 |
| G04 | Quadratic | 5 | 0 | 6 | 0 | 0 | −30,665.538 |
| G06 | Cubic | 2 | 0 | 2 | 0 | 0 | −6961.8138 |
| G07 | Quadratic | 10 | 3 | 5 | 0 | 0 | 24.306209 |
| G09 | Polynomial | 7 | 0 | 4 | 0 | 0 | 680.63005 |
| G10 | Linear | 8 | 3 | 3 | 0 | 0 | 7048.24802 |
| G13 | Nonlinear | 5 | 0 | 0 | 0 | 3 | 0.05394151 |
| G14 | Nonlinear | 10 | 0 | 0 | 3 | 0 | −47.764888 |
| G18 | Quadratic | 9 | 0 | 13 | 0 | 0 | −0.8660254 |
| G19 | Nonlinear | 15 | 0 | 5 | 0 | 0 | 32.6555929 |
| HCQDOPP | MANTA | MARINE | MGO | AVOA | DANDEL | EQUIL | HBADGER | KEPLER | MANTIS | RUNGE | SLIME | WALRUS | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G01 | Best | −1.500 × 101 | −1.499 × 101 | −1.499 × 101 | −1.500 × 101 | −1.275 × 101 | −1.299 × 101 | −1.483 × 101 | −1.425 × 101 | −1.492 × 101 | −1.497 × 101 | −1.446 × 101 | −1.499 × 101 | −1.483 × 101 |
| Mean | −1.500 × 101 | −1.033 × 101 | −1.496 × 101 | −1.500 × 101 | −9.764 × 100 | −8.686 × 100 | −1.402 × 101 | −1.151 × 101 | −1.243 × 101 | −1.492 × 101 | −1.252 × 101 | −1.153 × 101 | −9.454 × 100 | |
| Std | 4.632 × 10−5 | 3.039 × 100 | 3.752 × 10−2 | 0 | 1.462 × 100 | 1.585 × 100 | 8.060 × 10−1 | 1.173 × 100 | 2.444 × 100 | 4.832 × 10−2 | 9.763 × 10−1 | 2.026 × 100 | 2.264 × 100 | |
| rank | 2 | 10 | 3 | 1 | 11 | 13 | 5 | 9 | 7 | 4 | 6 | 8 | 12 | |
| G02 | Best | −7.842 × 10−1 | −7.682 × 10−1 | −7.878 × 10−1 | −7.241 × 10−1 | −7.818 × 10−1 | −7.508 × 10−1 | −7.977 × 10−1 | −7.807 × 10−1 | −7.444 × 10−1 | −7.906 × 10−1 | −7.741 × 10−1 | −6.698 × 10−1 | −6.502 × 10−1 |
| Mean | −7.312 × 10−1 | −6.645 × 10−1 | −7.354 × 10−1 | −5.521 × 10−1 | −6.456 × 10−1 | −5.971 × 10−1 | −7.473 × 10−1 | −6.836 × 10−1 | −6.204 × 10−1 | −7.261 × 10−1 | −6.823 × 10−1 | −5.632 × 10−1 | −4.851 × 10−1 | |
| Std | 3.097 × 10−2 | 8.249 × 10−2 | 3.505 × 10−2 | 8.650 × 10−2 | 8.144 × 10−2 | 6.564 × 10−2 | 3.525 × 10−2 | 4.411 × 10−2 | 6.350 × 10−2 | 4.941 × 10−2 | 5.737 × 10−2 | 3.911 × 10−2 | 4.286 × 10−2 | |
| Rank | 3 | 7 | 2 | 12 | 8 | 10 | 1 | 5 | 9 | 4 | 6 | 11 | 13 | |
| G03 | Best | −9.058 × 10−1 | −7.680 × 10−1 | −1.908 × 10−1 | N/A | −1.462 × 10−1 | −8.390 × 10−2 | −2.971 × 10−1 | −1.440 × 10−1 | N/A | −5.955 × 10−1 | −3.105 × 10−1 | −1.000 × 100 | N/A |
| Mean | −2.878 × 10−1 | −9.094 × 10−2 | −3.652 × 10−2 | N/A | −1.405 × 10−2 | −3.818 × 10−3 | −5.114 × 10−2 | −2.046 × 10−2 | N/A | −7.851 × 10−2 | −5.196 × 10−2 | −1.000 × 100 | N/A | |
| Std | 2.393 × 10−1 | 1.310 × 10−1 | 5.024 × 10−2 | N/A | 3.257 × 10−2 | 1.449 × 10−2 | 6.136 × 10−2 | 3.444 × 10−2 | N/A | 1.121 × 10−1 | 7.927 × 10−2 | 0 | N/A | |
| rank | 2 | 3 | 7 | 13 | 9 | 10 | 6 | 8 | 13 | 4 | 5 | 1 | 13 | |
| G04 | Best | −3.066 × 104 | −3.066 × 104 | −3.066 × 104 | −3.066 × 104 | −3.062 × 104 | −3.066 × 104 | −3.066 × 104 | −3.065 × 104 | −3.066 × 104 | −3.066 × 104 | −3.066 × 104 | −3.066 × 104 | −3.066 × 104 |
| Mean | −3.066 × 104 | −3.066 × 104 | −3.066 × 104 | −3.065 × 104 | −3.035 × 104 | −3.065 × 104 | −3.066 × 104 | −3.058 × 104 | −3.066 × 104 | −3.066 × 104 | −3.059 × 104 | −3.066 × 104 | −3.065 × 104 | |
| Std | 5.825 × 10−3 | 1.360 × 100 | 1.732 × 10−1 | 3.078 × 101 | 2.175 × 102 | 4.046 × 101 | 4.193 × 101 | 4.560 × 101 | 1.143 × 10−1 | 5.724 × 10−1 | 5.833 × 101 | 1.589 × 100 | 4.858 × 101 | |
| rank | 1 | 5 | 3 | 8 | 13 | 7 | 10 | 12 | 4 | 2 | 11 | 6 | 9 | |
| G06 | Best | −6.961 × 103 | −6.961 × 103 | −6.961 × 103 | −6.961 × 103 | −6.955 × 103 | −6.960 × 103 | −6.961 × 103 | −6.961 × 103 | −6.961 × 103 | −6.961 × 103 | −6.961 × 103 | −6.961 × 103 | −6.953 × 103 |
| Mean | −6.961 × 103 | −6.942 × 103 | −6.961 × 103 | −6.961 × 103 | −6.771 × 103 | −6.951 × 103 | −6.943 × 103 | −6.956 × 103 | −6.903 × 103 | −6.961 × 103 | −6.960 × 103 | −6.957 × 103 | −6.877 × 103 | |
| Std | 7.055 × 10−3 | 9.623 × 100 | 2.407 × 10−1 | 9.400 × 10−7 | 7.553 × 102 | 6.473 × 100 | 1.349 × 101 | 3.912 × 100 | 2.768 × 102 | 1.206 × 10−2 | 1.391 × 100 | 4.309 × 100 | 6.939 × 101 | |
| rank | 3 | 9 | 4 | 2 | 13 | 8 | 10 | 7 | 11 | 1 | 5 | 6 | 12 | |
| G07 | Best | 2.445 × 101 | 2.437 × 101 | 2.435 × 101 | 2.443 × 101 | 2.595 × 101 | 2.512 × 101 | 2.462 × 101 | 2.638 × 101 | 2.452 × 101 | 2.441 × 101 | 2.550 × 101 | 2.530 × 101 | 2.625 × 101 |
| Mean | 2.475 × 101 | 2.612 × 101 | 2.469 × 101 | 2.712 × 101 | 4.238 × 101 | 2.827 × 101 | 2.716 × 101 | 3.488 × 101 | 2.501 × 101 | 2.499 × 101 | 3.236 × 101 | 2.801 × 101 | 3.133 × 101 | |
| Std | 1.984 × 10−1 | 1.540 × 100 | 2.216 × 10−1 | 2.048 × 100 | 3.044 × 101 | 3.011 × 100 | 3.549 × 100 | 8.601 × 100 | 3.970 × 10−1 | 4.310 × 10−1 | 8.339 × 100 | 2.519 × 100 | 3.945 × 100 | |
| rank | 2 | 5 | 1 | 6 | 13 | 9 | 7 | 12 | 4 | 3 | 11 | 8 | 10 | |
| G09 | Best | 6.806 × 102 | 6.806 × 102 | 6.806 × 102 | 6.808 × 102 | 6.819 × 102 | 6.806 × 102 | 6.806 × 102 | 6.808 × 102 | 6.806 × 102 | 6.806 × 102 | 6.806 × 102 | 6.814 × 102 | 6.813 × 102 |
| Mean | 6.806 × 102 | 6.807 × 102 | 6.806 × 102 | 6.827 × 102 | 6.899 × 102 | 6.814 × 102 | 6.808 × 102 | 6.838 × 102 | 6.806 × 102 | 6.806 × 102 | 6.834 × 102 | 6.852 × 102 | 6.844 × 102 | |
| Std | 4.337 × 10−3 | 6.221 × 10−2 | 2.991 × 10−2 | 1.519 × 100 | 9.938 × 100 | 5.173 × 10−1 | 1.765 × 10−1 | 4.592 × 100 | 2.086 × 10−2 | 2.182 × 10−2 | 1.688 × 100 | 4.879 × 100 | 2.155 × 100 | |
| rank | 1 | 5 | 3 | 8 | 13 | 7 | 6 | 10 | 4 | 2 | 9 | 12 | 11 | |
| G10 | Best | 7.105 × 103 | 7.145 × 103 | 7.066 × 103 | 7.261 × 103 | 7.619 × 103 | 7.503 × 103 | 7.257 × 103 | 7.535 × 103 | 7.178 × 103 | 7.096 × 103 | 7.557 × 103 | 7.676 × 103 | 7.648 × 103 |
| Mean | 7.211 × 103 | 7.907 × 103 | 7.341 × 103 | 8.137 × 103 | 9.327 × 103 | 8.786 × 103 | 7.901 × 103 | 8.290 × 103 | 7.468 × 103 | 7.389 × 103 | 8.359 × 103 | 8.933 × 103 | 8.838 × 103 | |
| Std | 8.199 × 101 | 6.408 × 102 | 1.976 × 102 | 5.553 × 102 | 1.191 × 103 | 1.106 × 103 | 3.619 × 102 | 7.257 × 102 | 2.188 × 102 | 1.509 × 102 | 5.715 × 102 | 6.497 × 102 | 7.369 × 102 | |
| rank | 1 | 6 | 2 | 7 | 13 | 10 | 5 | 8 | 4 | 3 | 9 | 12 | 11 | |
| G13 | Best | 1.297 × 10−1 | 7.531 × 10−2 | 6.086 × 10−2 | 7.356 × 10−2 | 4.242 × 10−1 | 1.826 × 10−1 | 8.835 × 10−2 | 1.652 × 10−1 | N/A | 5.446 × 10−2 | 7.527 × 10−2 | 7.556 × 10−1 | 4.431 × 10−1 |
| Mean | 3.414 × 10−1 | 5.663 × 10−1 | 2.786 × 10−1 | 8.042 × 10−1 | 7.657 × 10−1 | 8.090 × 10−1 | 7.819 × 10−1 | 7.304 × 10−1 | N/A | 2.497 × 10−1 | 6.734 × 10−1 | 9.619 × 10−1 | 8.094 × 10−1 | |
| Std | 1.833 × 10−1 | 2.847 × 10−1 | 1.581 × 10−1 | 2.621 × 10−1 | 2.081 × 10−1 | 2.554 × 10−1 | 2.616 × 10−1 | 2.867 × 10−1 | N/A | 1.766 × 10−1 | 2.939 × 10−1 | 8.488 × 10−2 | 2.038 × 10−1 | |
| rank | 1 | 4 | 2 | 9 | 7 | 10 | 8 | 6 | 13 | 1 | 5 | 12 | 11 | |
| G14 | Best | −4.763 × 101 | −4.728 × 101 | −4.709 × 101 | −4.608 × 101 | −4.686 × 101 | −4.707 × 101 | −4.703 × 101 | −4.673 × 101 | −4.727 × 101 | −4.752 × 101 | −4.759 × 101 | N/A | −4.653 × 101 |
| Mean | −4.697 × 101 | −4.576 × 101 | −4.630 × 101 | −4.482 × 101 | −4.486 × 101 | −4.365 × 101 | −4.511 × 101 | −4.462 × 101 | −4.666 × 101 | −4.676 × 101 | −4.424 × 101 | N/A | −4.438 × 101 | |
| Std | 7.152 × 10−1 | 8.714 × 10−1 | 4.795 × 10−1 | 7.260 × 10−1 | 1.008 × 100 | 1.758 × 100 | 1.148 × 100 | 1.147 × 100 | 5.842 × 10−1 | 5.433 × 10−1 | 1.441 × 100 | N/A | 1.122 × 100 | |
| rank | 1 | 5 | 4 | 8 | 7 | 12 | 6 | 9 | 3 | 2 | 11 | 13 | 10 | |
| G18 | Best | −8.626 × 10−1 | −8.660 × 10−1 | −8.660 × 10−1 | −8.656 × 10−1 | −8.617 × 10−1 | N/A | −8.657 × 10−1 | −7.704 × 10−1 | −8.637 × 10−1 | −8.657 × 10−1 | −8.610 × 10−1 | −8.642 × 10−1 | −8.526 × 10−1 |
| Mean | −8.389 × 10−1 | −7.115 × 10−1 | −8.590 × 10−1 | −8.107 × 10−1 | −5.609 × 10−1 | N/A | −7.020 × 10−1 | −5.391 × 10−1 | −7.964 × 10−1 | −8.308 × 10−1 | −6.052 × 10−1 | −8.208 × 10−1 | −6.413 × 10−1 | |
| Std | 2.238 × 10−2 | 1.427 × 10−1 | 8.768 × 10−3 | 8.711 × 10−2 | 1.199 × 10−1 | N/A | 1.419 × 10−1 | 1.099 × 10−1 | 9.135 × 10−2 | 6.708 × 10−2 | 1.232 × 10−1 | 8.417 × 10−2 | 1.606 × 10−1 | |
| rank | 2 | 7 | 1 | 5 | 11 | 13 | 8 | 12 | 6 | 3 | 10 | 4 | 9 | |
| G19 | Best | 3.640 × 101 | 3.973 × 101 | 4.031 × 101 | 3.684 × 101 | 4.595 × 101 | N/A | 4.833 × 101 | 3.963 × 101 | 3.730 × 101 | 4.166 × 101 | 4.414 × 101 | 3.521 × 101 | 3.989 × 101 |
| Mean | 4.166 × 101 | 5.776 × 101 | 4.793 × 101 | 5.816 × 101 | 1.064 × 102 | N/A | 6.579 × 101 | 5.079 × 101 | 4.626 × 101 | 5.384 × 101 | 7.811 × 101 | 5.397 × 101 | 7.276 × 101 | |
| Std | 4.308 × 100 | 1.112 × 101 | 4.350 × 100 | 1.629 × 101 | 5.790 × 101 | N/A | 1.203 × 101 | 9.063 × 100 | 5.127 × 100 | 7.024 × 100 | 1.819 × 101 | 1.350 × 101 | 2.083 × 101 | |
| rank | 1 | 7 | 3 | 8 | 12 | 13 | 9 | 4 | 2 | 5 | 11 | 6 | 10 | |
| Aver.rank | 1.666 | 6.083 | 2.916 | 7.250 | 10.833 | 10.167 | 6.750 | 8.500 | 6.666 | 2.833 | 8.25 | 8.25 | 10.971 | |
| Rankings | 1 | 4 | 3 | 7 | 12 | 11 | 6 | 10 | 5 | 2 | 8 | 9 | 13 |
| Base Fluid | Nanoparticles | ||||||
|---|---|---|---|---|---|---|---|
| Components | Water | Al2O3 | CuO | TiO2 | Cu | SiO2 | Boehmite |
| ρ (kg/m3) | 995 | 3970 | 6000 | 4250 | 8933 | 2220 | 3050 |
| Cp (J/kg.K) | 4178 | 765 | 551 | 686 | 385 | 745 | 618.8 |
| k (W/mK) | 0.619 | 40 | 33 | 8.9 | 400 | 1.4 | 30 |
| Formula | Parameters Employed in the Equation |
|---|---|
| The value of Fc can be found in Shah and Sekulic [74]. | |
Here, Ao,sb, Ao,tb, Ao,cr are given in Shah and Sekulic [74]. | |
|
,
, Explicit formulations of Nss and Nr,cc are given in Shah and Sekulic [74] | |
|
,
, Lbi, Lbo, and Lbc are, respectively, baffle spacing at the inlet, outlet, and center | |
| , where Nr,cc and Nr,cw are calculated by the formulations given in Shah and Sekulic [74]. |
| Shell Side | Tube Side | ||||||
|---|---|---|---|---|---|---|---|
| Process Fluids | Oil | Al2O3 + H2O | CuO + H2O | TiO2 + H2O | Cu + H2O | SiO2 + H2O | Boehmite + H2O |
| Flow rate (kg/s) | 36.3 | 5.1 | 5.1 | 5.1 | 5.1 | 5.1 | 5.1 |
| Inlet Temp. (°C) | 65.6 | 32.2 | 32.2 | 32.2 | 32.2 | 32.2 | 32.2 |
| Outlet Temp. (°C) | 60.4 | 52.5 | 52.3 | 53.2 | 53.7 | 52.3 | 50.8 |
| Density (kg/m3) | 849 | 1080.88 | 1076.56 | 1114.83 | 1151.12 | 1052.49 | 997.34 |
| Heat Capacity (J/kg.K) | 2094 | 3816.14 | 3848.59 | 3687.92 | 3599.11 | 3838.18 | 4165.62 |
| Viscosity (Pa.s) | 0.0646 | 0.00081 | 0.00079 | 0.000829 | 0.000796 | 0.000848 | 0.000761 |
| Thermal Conductivity (W/m.K) | 0.14 | 0.67164 | 0.648068 | 0.676573 | 0.656078 | 0.645164 | 0.620988 |
| Parameter | Lower Bound | Upper Bound |
|---|---|---|
| Shell-side inside diameter—Ds (m) | 0.3 | 0.6 |
| Tube-side outside diameter—do (m) | 0.012 | 0.025 |
| Tube length—L (m) | 3 | 10 |
| Tube pitch—pt (m) | 0.015 | 0.03 |
| Central baffle spacing—Lbc (m) | 0.2 | 0.5 |
| Inlet baffle spacing—Lbi (m) | 0.2 | 0.5 |
| Outlet baffle spacing—Lbo (m) | 0.2 | 0.5 |
| Baffle spacing (%) | 15 | 40 |
| Width of bypass lane—wp (m) | 0.01 | 0.03 |
| Tube-to-baffle hole diametral clearance—δtb (m) | 0.0001 | 0.001 |
| Shell-to-baffle diametral clearance—δsb (m) | 0.001 | 0.005 |
| Tube thickness—thck (m) | 0.0002 | 0.002 |
| The nanoparticle ratio—φv (%) | 0 | 0.6 |
| Number of tube passes—Npass | 1 2 4 6 8 | |
| Number of sealing strip pairs—Nss | 1 2 4 8 | |
| Tube layout—Tlayout (°) | 30 45 90 | |
| Water | Al2O3 | CuO | TiO2 | Cu | SiO2 | Boehmite | |
|---|---|---|---|---|---|---|---|
| Optimization Variables | |||||||
| Shell-side inside diameter—Ds (m) | 0.458 | 0.456 | 0.451 | 0.495 | 0.433 | 0.429 | 0.457 |
| Tube-side outside diameter—do (mm) | 22.9 | 17.5 | 16.8 | 20.4 | 17.2 | 16.3 | 22.3 |
| Tube layout—Tlayout (°) | 45 | 45 | 45 | 45 | 45 | 45 | 45 |
| Number of tube passes—Npass | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Tube length—L (m) | 4.59 | 3.12 | 3.22 | 3.01 | 3.52 | 3.24 | 4.41 |
| Tube pitch—pt (mm) | 28.7 | 29.7 | 29.3 | 29.7 | 27.8 | 29.1 | 28.8 |
| Central baffle spacing—Lbc (m) | 0.493 | 0.448 | 0.484 | 0.459 | 0.427 | 0.469 | 0.491 |
| Inlet baffle spacing—Lbi (m) | 0.398 | 0.335 | 0.469 | 0.425 | 0.446 | 0.463 | 0.399 |
| Outlet baffle spacing—Lbo (m) | 0.387 | 0.438 | 0.497 | 0.491 | 0.361 | 0.459 | 0.392 |
| Baffle spacing (%) | 41.242 | 30.932 | 33.372 | 26.832 | 39.324 | 31.632 | 39.873 |
| Width of bypass lane—wp (mm) | 14.9 | 23.8 | 13.7 | 19.3 | 27.6 | 17.4 | 15.2 |
| Tube-to-baffle hole diametral clearance—δtb (mm) | 0.354 | 0.65 | 0.527 | 0.421 | 0.419 | 0.422 | 0.367 |
| Shell-to-baffle diametral clearance—δsb (mm) | 3.562 | 3.762 | 3.289 | 3.361 | 2.772 | 4.183 | 3.601 |
| Number of sealing strip pairs—Nss | 8 | 2 | 1 | 2 | 8 | 2 | 8 |
| Tube thickness—thck (mm) | 1.2 | 1.2 | 1.6 | 1 | 0.7 | 1 | 1.2 |
| The nanoparticle ratio—φv (%) | 0.111 | 2.975 | 1.62 | 3.665 | 1.983 | 4.693 | 0.121 |
| Model parameters | |||||||
| Transverse tube pitch—Xt (mm) | 40.3 | 42.1 | 41.8 | 42.4 | 39.3 | 40.9 | 40.6 |
| Longitudinal tube pitch—Xl (mm) | 20.3 | 21.5 | 20.7 | 21.3 | 19.7 | 20.5 | 20.4 |
| Total number of tubes—N | 149 | 277 | 297 | 246 | 256 | 271 | 151 |
| Tube clearance—Cl (mm) | 6.4 | 12.3 | 12.6 | 9.8 | 10.7 | 12.5 | 6.7 |
| Shell side mass velocity—Gs (kg/m2 s) | 523.482 | 309.642 | 282.694 | 347.893 | 382.134 | 305.045 | 506.132 |
| Shell side Reynolds number—Res | 278.333 | 117.932 | 101.987 | 153.245 | 142.832 | 107.99 | 249.783 |
| Shell side heat transfer coefficient—hs (W/m2K) | 531.892 | 519.983 | 481.563 | 542.981 | 512.782 | 531.697 | 526.891 |
| Pressure drops in the central section—Δpcr (Pa) | 3601.374 | 2306.482 | 1824.698 | 3179.421 | 2581.232 | 2232.91 | 3533.792 |
| Pressure drops in the window area—Δpw (Pa) | 10,193.742 | 5453.392 | 5192.784 | 5767.911 | 8041.273 | 5979.75 | 10,053.56 |
| Pressure drops in inlet and outlet section—Δpi-o (Pa) | 9856.392 | 4471.744 | 3163.942 | 4796.472 | 5198.481 | 3748.34 | 9457.232 |
| Total shell side pressure drop—Δpshell (Pa) | 24,083.974 | 12,231.42 | 10,181.84 | 13,740.14 | 15,817.8 | 11,961.0 | 23,042.74 |
| Total number of baffles—Nb | 8 | 6 | 6 | 6 | 6 | 6 | 8 |
| Tube-side Reynolds number—Ret | 23,331.635 | 14,177.4 | 15,825.72 | 13,259.13 | 15,261.32 | 13,823.25 | 22,106.07 |
| Tube-side heat transfer coefficient—hi (W/m2 K) | 4421.732 | 4039.831 | 4960.753 | 3224.129 | 4009.93 | 4186.97 | 4384.231 |
| Overall heat transfer coefficient—Uo (W/m2 K) | 409.572 | 400.535 | 379.753 | 405.223 | 398.184 | 410.464 | 408.932 |
| Total heat transfer area—Ao (m2) | 45.113 | 46.484 | 48.421 | 46.78 | 47.532 | 45.127 | 45.001 |
| Effectiveness (ε) | 0.2675 | 0.2696 | 0.2641 | 0.2847 | 0.2905 | 0.2626 | 0.2441 |
| Tube-side pressure drop—Δpt (Pa) | 5783.321 | 3899.932 | 6898.933 | 2181.42 | 4119.134 | 5522.524 | 5637.842 |
| Annual operating cost—Co (€/year) | 1423.848 | 760.231 | 713.123 | 806.071 | 958.283 | 783.63 | 1406.124 |
| Total discounted operating cost—CoD (€) | 8932.982 | 4672.832 | 4379.592 | 4947.941 | 5885.133 | 4815.06 | 8638.201 |
| Capital investment cost—Ci (€) | 16,298.733 | 16,525.932 | 16,946.78 | 16,488.13 | 16,615.212 | 16,301.7 | 16,277.391 |
| Total cost of heat exchanger—Ctot (€) | 25,231.71 | 21,198.76 | 21,326.37 | 21,436.07 | 22,500.345 | 21,116.13 | 24,915.591 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turgut, O.E.; Asker, M.; Yesiloz, H.B.; Genceli, H.; AL-Rawi, M. Chaotic Mountain Gazelle Optimizer Improved by Multiple Oppositional-Based Learning Variants for Theoretical Thermal Design Optimization of Heat Exchangers Using Nanofluids. Biomimetics 2025, 10, 454. https://doi.org/10.3390/biomimetics10070454
Turgut OE, Asker M, Yesiloz HB, Genceli H, AL-Rawi M. Chaotic Mountain Gazelle Optimizer Improved by Multiple Oppositional-Based Learning Variants for Theoretical Thermal Design Optimization of Heat Exchangers Using Nanofluids. Biomimetics. 2025; 10(7):454. https://doi.org/10.3390/biomimetics10070454
Chicago/Turabian StyleTurgut, Oguz Emrah, Mustafa Asker, Hayrullah Bilgeran Yesiloz, Hadi Genceli, and Mohammad AL-Rawi. 2025. "Chaotic Mountain Gazelle Optimizer Improved by Multiple Oppositional-Based Learning Variants for Theoretical Thermal Design Optimization of Heat Exchangers Using Nanofluids" Biomimetics 10, no. 7: 454. https://doi.org/10.3390/biomimetics10070454
APA StyleTurgut, O. E., Asker, M., Yesiloz, H. B., Genceli, H., & AL-Rawi, M. (2025). Chaotic Mountain Gazelle Optimizer Improved by Multiple Oppositional-Based Learning Variants for Theoretical Thermal Design Optimization of Heat Exchangers Using Nanofluids. Biomimetics, 10(7), 454. https://doi.org/10.3390/biomimetics10070454









