Multi-Agent Reinforcement Learning in Games: Research and Applications
Abstract
1. Introduction
2. Theoretical Foundation of MARL
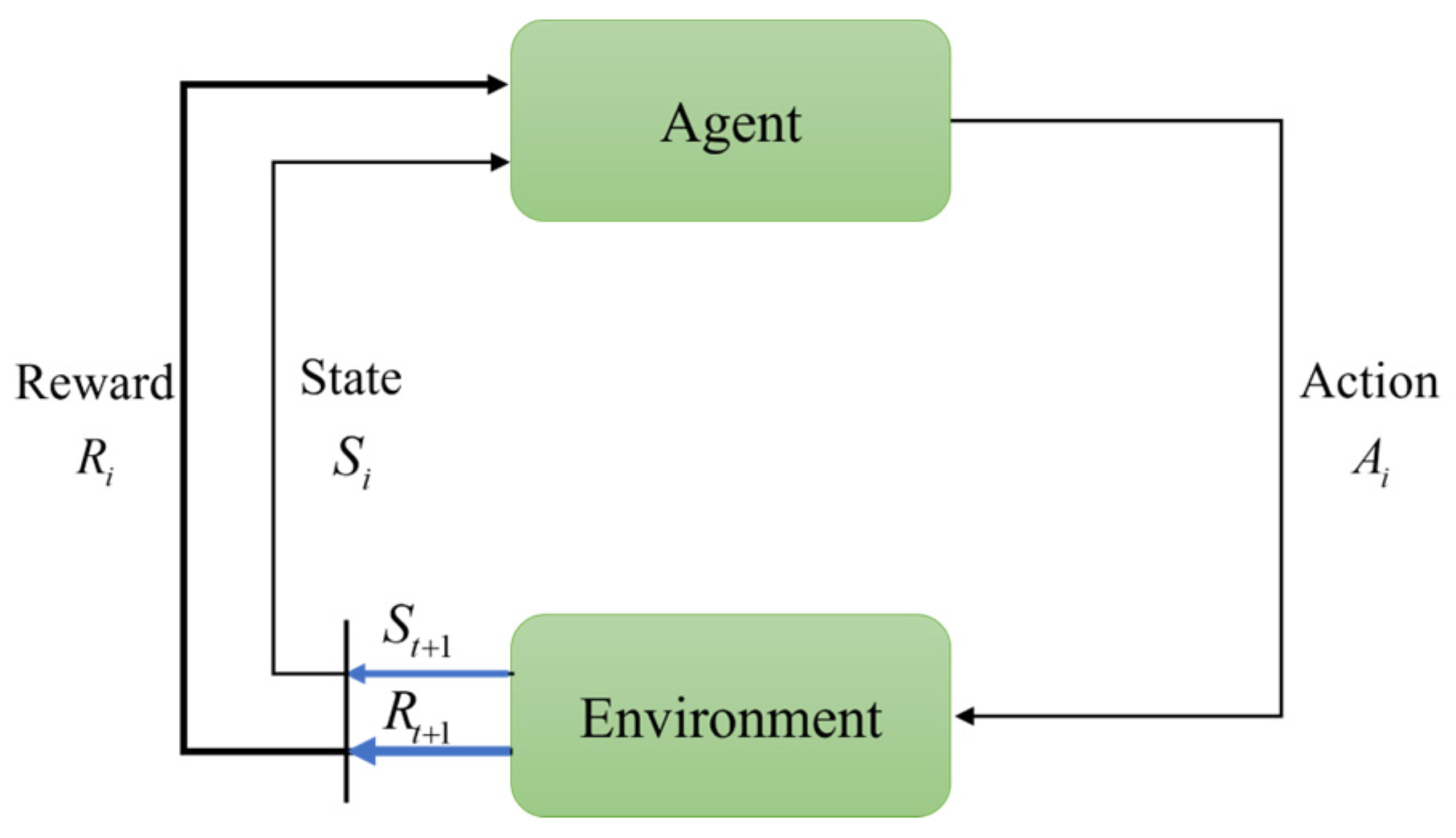
2.1. Single-Agent Reinforcement Learning
- S: The state space encompassing all possible environmental configurations;
- A: The action space containing all executable agent behaviors;
- : The state transition function , specifying the probability of transitioning to state when executing action in state ;
- : The reward function , representing the expected immediate return obtained when transitioning to state through action in state .
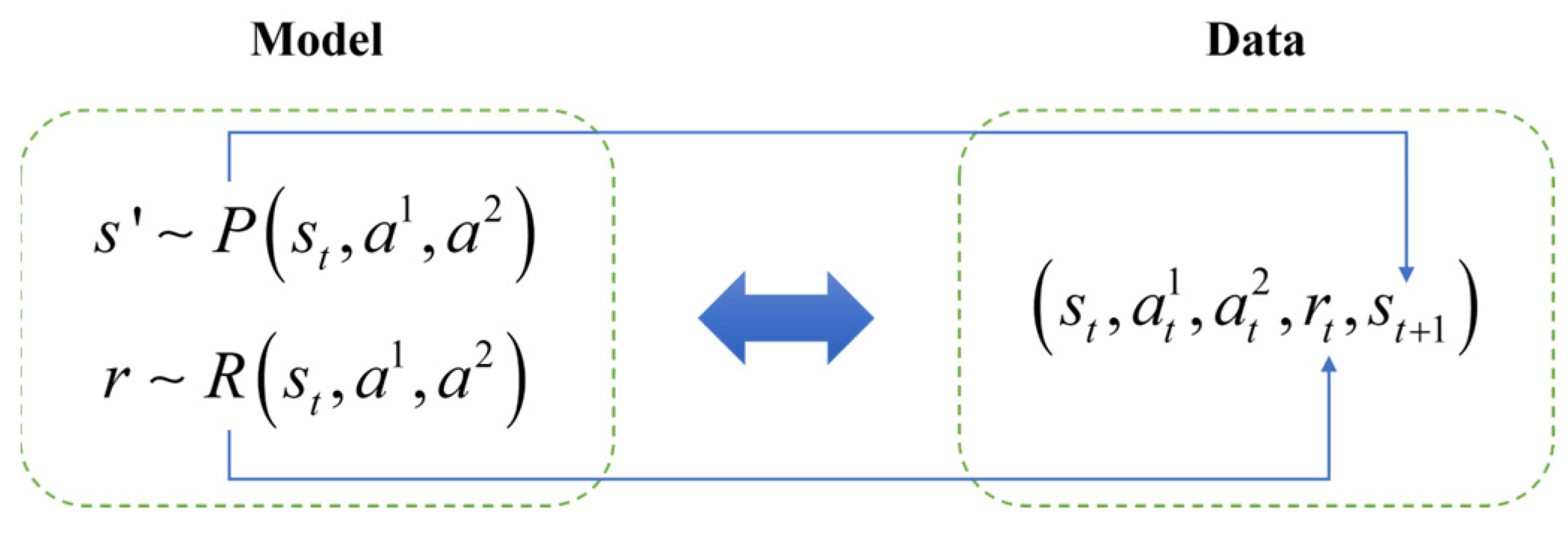
2.2. Multi-Agent Game Modeling
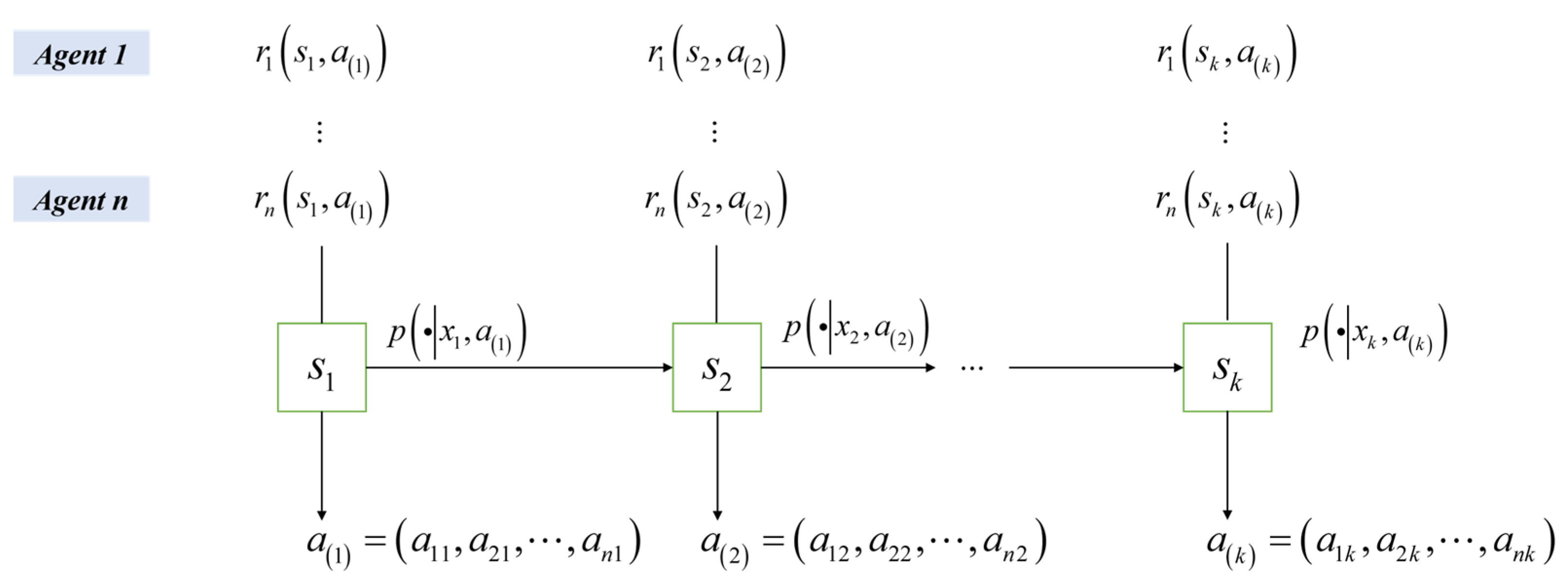
2.2.1. Stochastic Games
- S: The set of state spaces;
- N: Cardinality of autonomous agents, ;
- : The action space of agent , with joint action space ;
- : The state transfer probability function ;
- : The reward function ;
- : Temporal discount factor .
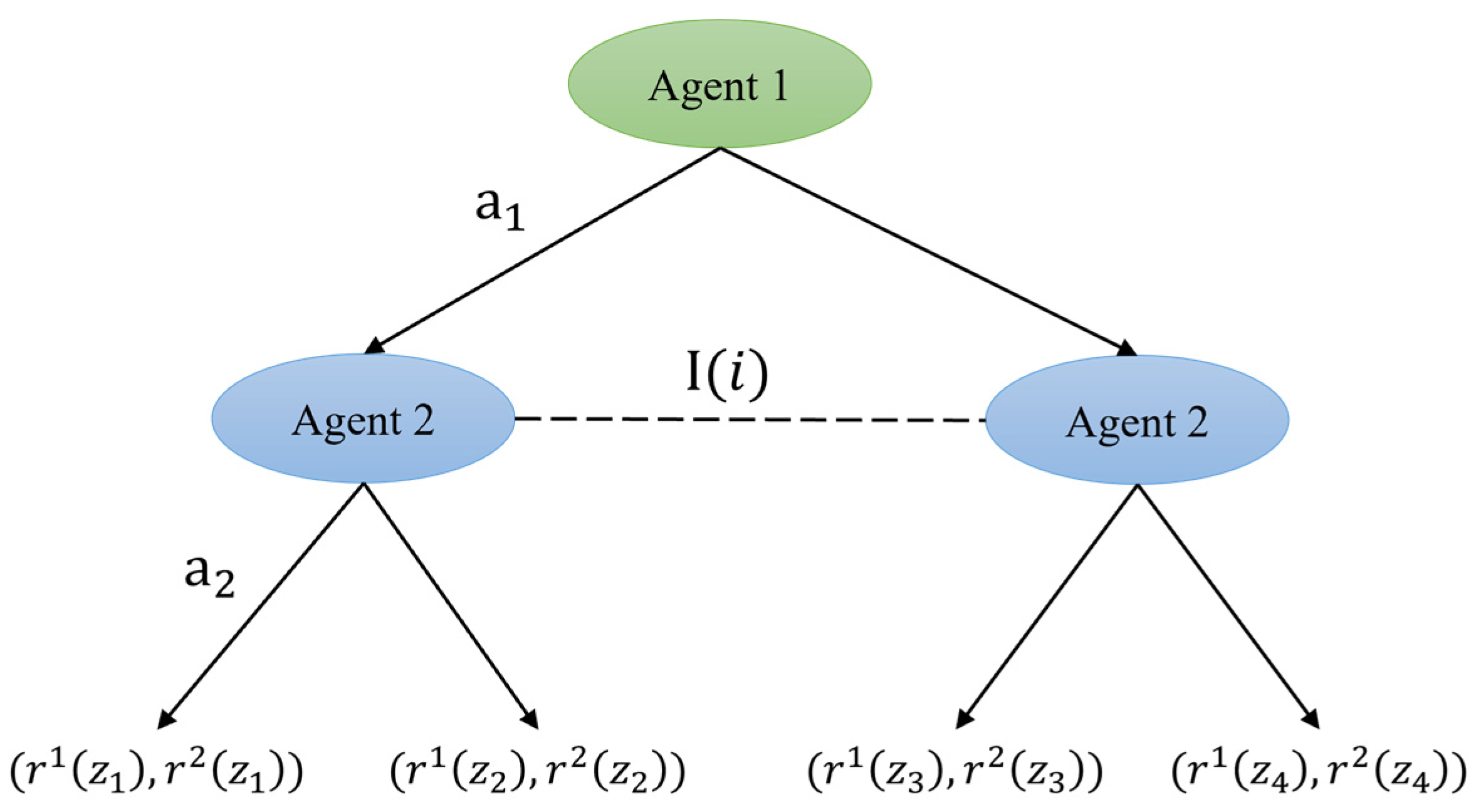
2.2.2. Extensive-Form Games
- (a)
- The normal form representation, specifically designed for modeling simultaneous-move decision processes, serves as the standard paradigm for strategic interactions with parallel action selection [23].
- (b)
- The sequence form representation, engineered to capture multi-stage behavioral strategies, provides an optimal mathematical framework for sequential decision-making scenarios involving intertemporal strategy commitments [24].
3. MARL Solution Method
3.1. Value-Based RL
3.1.1. Bellman Equation and Nash Equilibrium
3.1.2. Dynamic Programming Algorithm
3.1.3. Sample-Based Approach to RL
3.2. Policy-Based RL
3.2.1. Independent Reinforcement Learning
3.2.2. Strategic Game and Coordination Mechanism Enhancement
3.2.3. Evolutionary Reinforcement Learning Methods
3.2.4. Optimization in Continuous Action Spaces
3.3. Search-Based RL
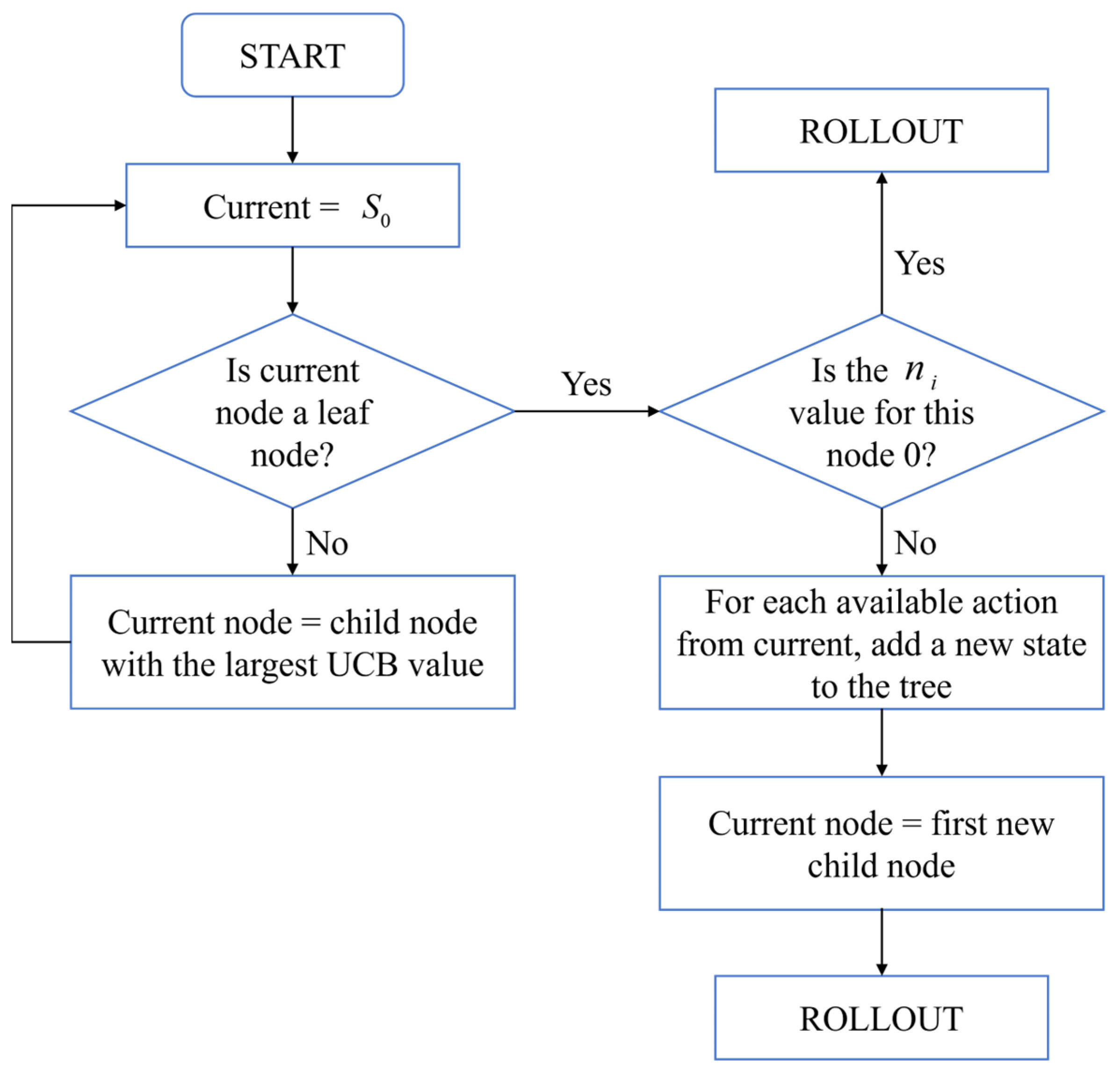
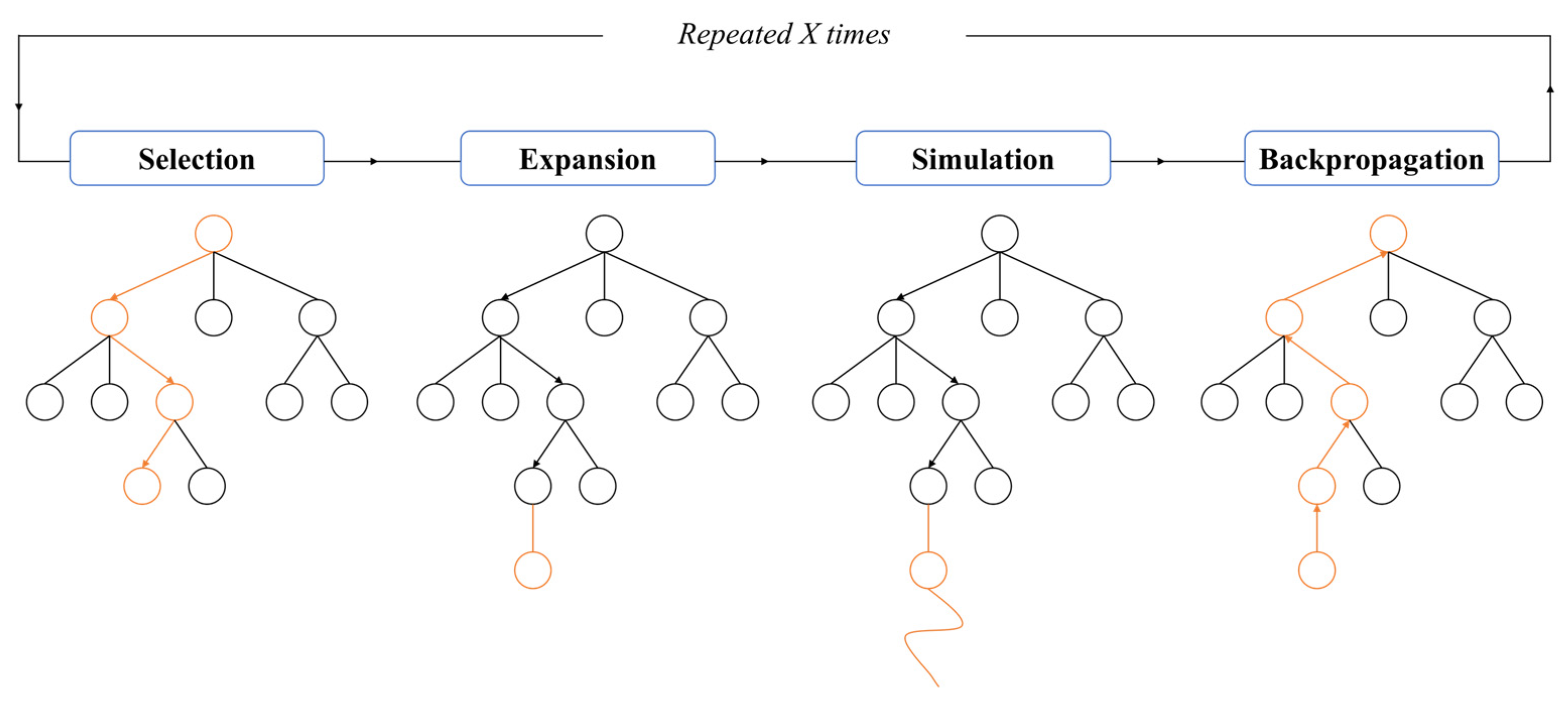
3.3.1. Monte Carlo Tree Search
- Universality: The tree-search framework is universally applicable to any finite state space game problem.
- Adaptability: Real-time updates of node statistics enable dynamic optimization of search paths.
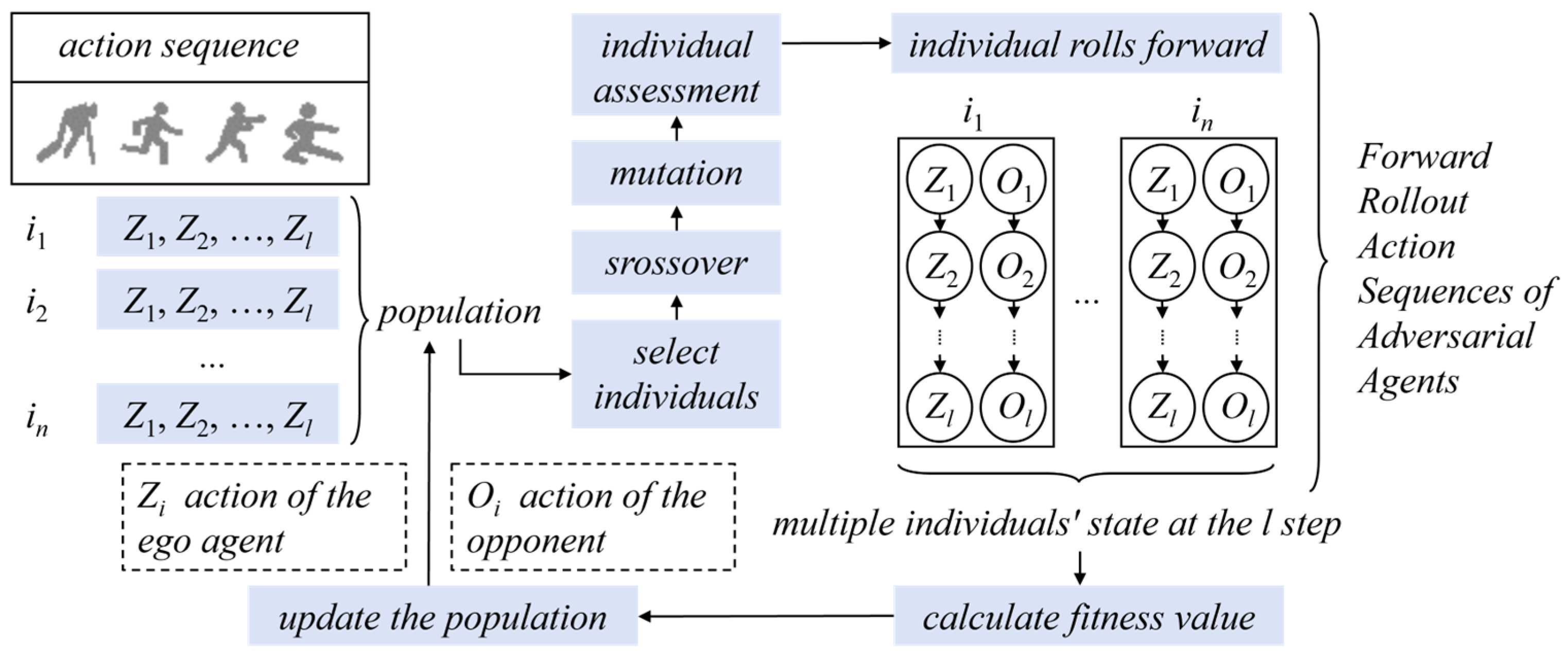
3.3.2. Rolling Horizon Evolution Algorithm
4. Applications and Challenges of MARL
5. Conclusions and Future Directions
- Dynamic Environment Adaptation Mechanisms
- 2.
- Imperfect-Information Game Reasoning Paradigms
- 3.
- Ultra-Large-Scale Game Computing Architecture
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Che, A.; Wang, Z.; Zhou, C. Multi-Agent Deep Reinforcement Learning for Recharging-Considered Vehicle Scheduling Problem in Container Terminals. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16855–16868. [Google Scholar] [CrossRef]
- Wang, K.; Shen, Z.; Lei, Z.; Liu, X.; Zhang, T. Towards Multi-agent Reinforcement Learning based Traffic Signal Control through Spatio-temporal Hypergraphs. In IEEE Transactions on Mobile Computing; IEEE: Piscataway, NJ, USA, 2024; pp. 1–14. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, C.; Yan, Y.; Hu, Y. Distributed real-time scheduling in cloud manufacturing by deep reinforcement learning. IEEE Trans. Ind. Inform. 2022, 18, 8999–9007. [Google Scholar] [CrossRef]
- Xiong, K.; Wei, Q.; Liu, Y. Community Microgrid Energy Co-Scheduling Based on Deep Reinforcement Learning and Contribution Mechanisms. IEEE Trans. Smart Grid 2025, 16, 1051–1061. [Google Scholar] [CrossRef]
- Xiong, W.; Guo, L.; Jiao, T. A multi-agent path planning algorithm based on game theory and reinforcement learning. Shenzhen Daxue Xuebao (Ligong Ban)/J. Shenzhen Univ. Sci. Eng. 2024, 41, 274–282. [Google Scholar] [CrossRef]
- Gu, H.; Wang, S.; Ma, X.; Jia, D.; Mao, G.; Lim, E.G.; Wong, C.P.R. Large-Scale Traffic Signal Control Using Constrained Network Partition and Adaptive Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2024, 7, 7619–7632. [Google Scholar] [CrossRef]
- Qian, T.; Yang, C. Large-scale deep reinforcement learning method for energy management of power supply units considering regulation mileage payment. Front. Energy Res. 2024, 11, 1333827. [Google Scholar] [CrossRef]
- Hu, J.; Wellman, M.P. Nash Q-Learning for General-Sum Stochastic Games. J. Mach. Learn. Res. 2003, 4, 1039–1069. [Google Scholar] [CrossRef]
- Croitoru, F.A.; Ristea, N.C.; Ionescu, R.T.; Sebe, N. Learning Rate Curriculum. Int. J. Comput. Vis. 2025, 133, 291–314. [Google Scholar] [CrossRef]
- Li, K.; Xu, H.; Fu, H.; Fu, Q.; Xing, J. Automatically designing counterfactual regret minimization algorithms for solving imperfect information games. Artif. Intell. 2024, 337, 104232. [Google Scholar] [CrossRef]
- Yao, L.; Liu, P.-Y.; Teo, J.C. Hierarchical multi-agent deep reinforcement learning with adjustable hierarchy for home energy management systems. Energy Build. 2025, 331, 115391. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Tian, F.; Ma, J.; Jin, Q. Intelligent games meeting with multi-agent deep reinforcement learning: A comprehensive review. Artif. Intell. Rev. 2025, 58, 165. [Google Scholar] [CrossRef]
- Deng, X.; Li, N.; Mguni, D.; Wang, J.; Yang, Y. Corrigendum to on the complexity of computing Markov perfect equilibrium in general-sum stochastic games. Natl. Sci. Rev. 2023, 10, nwad024. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Y.; Dang, C. A Variant of the Logistic Quantal Response Equilibrium to Select a Perfect Equilibrium. J. Optim. Theory Appl. 2024, 201, 1026–1062. [Google Scholar] [CrossRef]
- Korivand, S.; Galvani, G.; Ajoudani, A.; Gong, J.; Jalili, N. Optimizing Human-Robot Teaming Performance through Q-Learning-Based Task Load Adjustment and Physiological Data Analysis. Sensors 2024, 24, 2817. [Google Scholar] [CrossRef]
- Lin, S.-W.; Chu, C.-C. Distributed Q-Learning-Based Voltage Restoration Algorithm in Isolated AC Microgrids Subject to Input Saturation. IEEE Trans. Ind. Appl. 2024, 60, 5447–5459. [Google Scholar] [CrossRef]
- Shankar, S.; Young, R.A.; Young, M.E. Action-Project Method: An approach to describing and studying goal-oriented joint actions. Med. Educ. 2023, 57, 131–141. [Google Scholar] [CrossRef]
- Park, Y.-J.; Kim, J.-E.; Lee, S.-H.; Cho, K.-H. An Effective Design Formula for Single-Layer Printed Spiral Coils with the Maximum Quality Factor (Q-Factor) in the Megahertz Frequency Range. Sensors 2022, 22, 7761. [Google Scholar] [CrossRef]
- Li, X.; Xi, L.; Zha, W.; Peng, Z. Minimax Q-learning design for H ∞ control of linear discrete-time systems. Front. Inf. Technol. Electron. Eng. 2022, 23, 438–451. [Google Scholar] [CrossRef]
- Liu, X. A large-scale equilibrium model of energy emergency production: Embedding social choice rules into Nash Q-learning automatically achieving consensus of urgent recovery behaviors. Energy 2022, 259, 125023. [Google Scholar]
- Zhao, X.; Hu, H.; Sun, D. Cooperation with Humans of Unknown Intentions in Confined Spaces Using the Stackelberg Friend-or-Foe Game. In IEEE Transactions on Aerospace and Electronic Systems; IEEE: Piscataway, NJ, USA, 2024; pp. 1–13. [Google Scholar]
- Xi, L.; Yu, T.; Yang, B.; Zhang, X. A novel multi-agent decentralized win or learn fast policy hill-climbing with eligibility trace algorithm for smart generation control of interconnected complex power grids. Energy Convers. Manag. 2015, 103, 82–93. [Google Scholar] [CrossRef]
- Bajaj, S.; Das, P.; Vorobeychik, Y.; Gupta, V. Rationality of Learning Algorithms in Repeated Normal-Form Games. IEEE Control Syst. Lett. 2024, 8, 2409–2414. [Google Scholar] [CrossRef]
- Leal, D.; Nguyen, N.H.; Skvortsov, A.; Arulampalam, S.; Piraveenan, M. A Sequential Game Framework for Target Tracking. IEEE Access 2024, 12, 189122–189135. [Google Scholar] [CrossRef]
- Xiao, Y.; Liang, J. Optimal resource allocation in hierarchical organizations under uncertainty: An interval-valued n-person cooperative game approach. J. Intell. Fuzzy Syst. 2024, 46, 9987–9998. [Google Scholar] [CrossRef]
- Hu, G.; Zhu, Y.; Li, H.; Zhao, D. FM3Q: Factorized Multi-Agent MiniMax Q-Learning for Two-Team Zero-Sum Markov Game. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 4033–4045. [Google Scholar] [CrossRef]
- Diddigi, R.B.; Kamanchi, C.; Bhatnagar, S. A Generalized Minimax Q-learning Algorithm for Two-Player Zero-Sum Stochastic Games. IEEE Trans. Autom. Control 2022, 67, 4816–4823. [Google Scholar] [CrossRef]
- Morita, K.; Morishima, M.; Sakai, K.; Kawaguchi, Y. Reinforcement Learning: Computing the Temporal Difference of Values via Distinct Corticostriatal Pathways: (Trends in Neurosciences 35, 457–467; 2012). Trends Neurosci. 2017, 40, 453. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI 2016), Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Wang, L.; Wang, Y.; Zheng, B. Dynamic Power Control Method Based on Stacked SRU Network Combined with NoisyNet DQN for CRN. In Proceedings of the 2023 19th International Conference on Mobility, Sensing and Networking (MSN), Nanjing, China, 14–16 December 2023; pp. 105–112. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, W.; Li, Q.; Chen, S. Dual-Correction–Adaptation Network for Noisy Knowledge Transfer. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 1081–1091. [Google Scholar] [CrossRef]
- Tadele, S.B.; Kar, B.; Wakgra, F.G.; Khan, A.U. Optimization of End-to-End AoI in Edge-Enabled Vehicular Fog Systems: A Dueling-DQN Approach. IEEE Internet Things J. 2025, 12, 843–853. [Google Scholar] [CrossRef]
- Deguale, D.A.; Yu, L.; Sinishaw, M.L.; Li, K. Enhancing Stability and Performance in Mobile Robot Path Planning with PMR-Dueling DQN Algorithm. Sensors 2024, 24, 1523. [Google Scholar] [CrossRef]
- Kamran, D.; Engelgeh, T.; Busch, M.; Fischer, J.; Stiller, C. Minimizing Safety Interference for Safe and Comfortable Automated Driving with Distributional Reinforcement Learning. arXiv 2021, arXiv:2107.07316. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Y.; Chen, Y.; Liu, J.; Zhou, X.; Peng, Y.; Xie, S. Path planning of the unmanned surface vehicle in island and reef environments with time-varying vortices. Ocean Eng. 2025, 320, 120231. [Google Scholar] [CrossRef]
- Liu, J.; Yin, J.; Jiang, Z.; Liang, Q.; Li, H. Attention-Based Distributional Reinforcement Learning for Safe and Efficient Autonomous Driving. IEEE Robot. Autom. Lett. 2024, 9, 7477–7484. [Google Scholar] [CrossRef]
- Nachum, O.; Norouzi, M.; Xu, K.; Schuurmans, D. Bridging the Gap Between Value and Policy Based Reinforcement Learning. arXiv 2017, arXiv:1702.08892. [Google Scholar] [CrossRef]
- Chrustowski, K.; Duch, P. Policy-Based Reinforcement Learning Approach in Imperfect Information Card Game. Appl. Sci. 2025, 15, 2121. [Google Scholar] [CrossRef]
- Lee, K.M.; Subramanian, S.G.; Crowley, M. Investigation of independent reinforcement learning algorithms in multi-agent environments. Front. Artif. Intell. 2022, 5, 805823. [Google Scholar] [CrossRef]
- Vijayakumar, P.; Rajkumar, S.C. Deep Reinforcement Learning-Based Pedestrian and Independent Vehicle Safety Fortification Using Intelligent Perception. Int. J. Softw. Sci. Comput. Intell. 2022, 14, 1–33. [Google Scholar] [CrossRef]
- Zhou, S.; Ren, W.; Ren, X.; Wang, Y.; Yi, X. Independent Deep Deterministic Policy Gradient Reinforcement Learning in Cooperative Multiagent Pursuit Games. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2021; Volume 12894, pp. 625–637. [Google Scholar]
- Tesauro, G. Programming backgammon using self-teaching neural nets. Artif. Intell. 2002, 134, 181–199. [Google Scholar] [CrossRef]
- Tandon, A.; Karlapalem, K. Medusa: Towards Simulating a Multi-Agent Hide-and-Seek Game. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018. [Google Scholar] [CrossRef]
- Wang, K.; Tang, Z.; Mu, C. Dynamic Event-Triggered Model-Free Reinforcement Learning for Cooperative Control of Multiagent Systems. In IEEE Transactions on Reliability; IEEE: Piscataway, NJ, USA, 2024; pp. 1–14. [Google Scholar]
- Zhou, R.; Zhang, H. Self-play training for general impulsive orbital game. J. Phys. Conf. Ser. 2025, 2977, 012106. [Google Scholar] [CrossRef]
- Li, K.; Jiu, B.; Pu, W.; Liu, H.; Peng, X. Neural Fictitious Self-Play for Radar Anti-Jamming Dynamic Game with Imperfect In-formation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5533–5547. [Google Scholar] [CrossRef]
- Heinrich, J.; Silver, D. Deep Reinforcement Learning from Self-Play in Imperfect-Information Games. arXiv 2016, arXiv:1603.01121. [Google Scholar] [CrossRef]
- Liu, T.; Li, L.; Shao, G.; Wu, X.; Huang, M. A novel policy gradient algorithm with PSO-based parameter exploration for continuous control. Eng. Appl. Artif. Intell. 2020, 90, 103525. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, J.; Tan, K.C.; Xu, Z. Learning Adaptive Differential Evolution by Natural Evolution Strategies. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 872–886. [Google Scholar] [CrossRef]
- Huang, Y.; Lai, L.; Wu, H. Neighbourhood-based small-world network differential evolution with novelty search strategy. Int. J. Bio-Inspired Comput. 2023, 22, 65–76. [Google Scholar] [CrossRef]
- Japa, L.; Serqueira, M.; Mendonça, I.; Aritsugi, M.; Bezerra, E.; González, P.H. A Population-based Hybrid Approach for Hyperparameter Optimization of Neural Networks. IEEE Access 2023, 11, 50752–50768. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, G.; Zhang, M.; Xue, B. Proximal evolutionary strategy: Improving deep reinforcement learning through evolutionary policy optimization. Memetic Comput. 2024, 16, 445–466. [Google Scholar] [CrossRef]
- Jaderberg, M.; Dalibard, V.; Osindero, S.; Czarnecki, W.M.; Donahue, J.; Razavi, A.; Vinyals, O.; Green, T.; Dunning, I.; Simonyan, K.; et al. Population based training of neural networks. arXiv 2017, arXiv:1711.09846. [Google Scholar] [CrossRef]
- Bai, H.; Cheng, R. Generalized Population-Based Training for Hyperparameter Optimization in Reinforcement Learning. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 3450–3462. [Google Scholar] [CrossRef]
- Zhou, M.; Wan, Z.; Wang, H.; Wen, M.; Wu, R.; Wen, Y.; Yang, Y.; Yu, Y.; Wang, J.; Zhang, W. MALib: A parallel framework for population-based multi-agent reinforcement learning. J. Mach. Learn. Res. (JMLR) 2023, 24, 150. [Google Scholar]
- Chai, J.; Chen, W.; Zhu, Y.; Yao, Z.-X.; Zhao, D. A Hierarchical Deep Reinforcement Learning Framework for 6-DOF UCAV Air-to-Air Combat. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 5417–5429. [Google Scholar] [CrossRef]
- Wang, X.; Yang, C.; Zhao, J.; Wu, T. Energy management of solar spectral beam-splitting integrated energy systems using Soft Actor-Critic Method. Appl. Therm. Eng. 2025, 269, 125966. [Google Scholar] [CrossRef]
- Yu, Z.; Zheng, W.; Zeng, K.; Zhao, R.; Zhang, Y.; Zeng, M. Energy optimization management of microgrid using improved soft actor-critic algorithm. Int. J. Renew. Energy Dev. 2024, 13, 329–339. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, W.; Zou, Y.; Zhang, X. Energy management in HDHEV with dual APUs: Enhancing soft actor-critic using clustered experience replay and multi-dimensional priority sampling. Energy 2025, 319, 134926. [Google Scholar] [CrossRef]
- Li, W.; Wu, H.; Zhao, Y.; Jiang, C.; Zhang, J. Study on indoor temperature optimal control of air-conditioning based on Twin Delayed Deep Deterministic policy gradient algorithm. Energy Build. 2024, 317, 114420. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Shuai, H.; Li, F.; She, B.; Wang, X.; Zhao, J. Post-storm repair crew dispatch for distribution grid restoration using stochastic Monte Carlo tree search and deep neural networks. Int. J. Electr. Power Energy Syst. 2023, 144, 108477. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Jiang, Y.; Duan, R. Adaptive Hierarchical Text Classification Using ERNIE and Dynamic Threshold Pruning. IEEE Access 2024, 12, 193641–193652. [Google Scholar] [CrossRef]
- Kang, J.H.; Kim, H.J. Dynamic UCB Adaptation Strategy for MCTS based GVGAI. Int. J. Eng. Res. Technol. 2019, 12, 2769–2774. [Google Scholar]
- Perez, D.; Samothrakis, S.; Lucas, S.; Rohlfshagen, P. Rolling Horizon Evolution versus Tree Search for Navigation in Single-Player Real-Time Games. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation (GECCO’13), New York, NY, USA, 6–10 July 2013; pp. 351–358. [Google Scholar]
- Tang, Z.; Zhu, Y.; Zhao, D.; Lucas, S.M. Enhanced Rolling Horizon Evolution Algorithm with Opponent Model Learning: Results for the Fighting Game AI Competition. IEEE Trans. Games 2023, 15, 5–15. [Google Scholar] [CrossRef]
- Zhao, H.; Dong, C.; Cao, J.; Chen, Q. A survey on deep reinforcement learning approaches for traffic signal control. Eng. Appl. Artif. Intell. 2024, 133, 108100. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of MAPPO in Cooperative, Multi-Agent Games. arXiv 2021, arXiv:2103.01955. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Song, B. HORSE-CFR: Hierarchical opponent reasoning for safe exploitation counter-factual regret minimization. Expert Syst. Appl. 2025, 263, 125697. [Google Scholar] [CrossRef]
- Li, L.; Zhao, W.; Wang, C.; Luan, Z. POMDP Motion Planning Algorithm Based on Multi-Modal Driving Intention. IEEE Trans. Intell. Veh. 2023, 8, 1777–1786. [Google Scholar] [CrossRef]
- Jain, A.; Khetarpal, K.; Precup, D. Safe option-critic: Learning safety in the option-critic architecture. Knowl. Eng. Rev. 2021, 36, e4. [Google Scholar] [CrossRef]
- Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Dębiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C.; et al. Dota 2 with Large Scale Deep Reinforcement Learning. arXiv 2019, arXiv:1912.06680. [Google Scholar] [CrossRef]
- Espeholt, L.; Marinier, R.; Stanczyk, P.; Wang, K.; Michalski, M. SEED RL: Scalable and Efficient Deep-RL with Accelerated Central Inference. arXiv 2019, arXiv:1910.06591. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, Y.; Zhang, W.; Wang, C.; Yu, Q.; Wang, X. Crop Land Change Detection with MC&N-PSPNet. Appl. Sci. 2024, 14, 5429. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 2. [Google Scholar]
- Christodoulou, P. Soft Actor-Critic for Discrete Action Settings. arXiv 2019, arXiv:1910.07207. [Google Scholar] [CrossRef]
- Halpern, J.Y. Beyond Nash Equilibrium: Solution Concepts for the 21st Century. Comput. Sci. 2008, 7037, 1–10. [Google Scholar] [CrossRef]
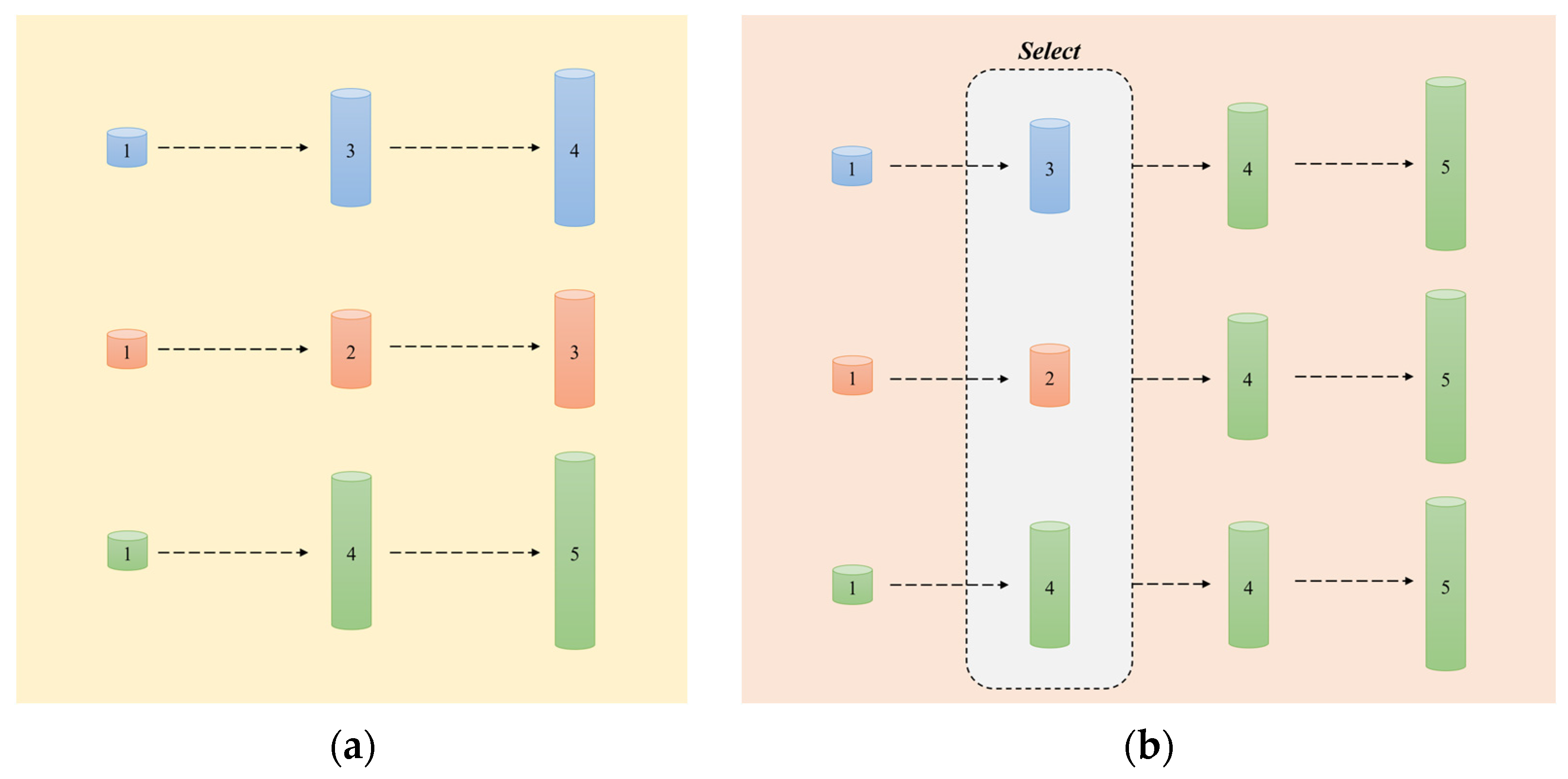
| Game Type | Methodology | Applicable Scenario and Performance |
|---|---|---|
| Cooperative Game | Team-Q [15] | Suitable for fully collaborative scenarios requiring global state sharing; high communication costs; poor scalability in large-scale systems. |
| Distributed-Q [16] | Distributed collaboration with partial observations; may fall into local optima, requiring additional coordination mechanisms. | |
| Joint Action Learner [17] | Distributed collaboration with partial observations; may fall into local optima, requiring additional coordination mechanisms. | |
| Frequency Maximum Q [18] | Effective in dynamic environments via frequency–domain exploration balancing; exhibits slow convergence speed. | |
| Competitive Game | Minimax-Q [19] | Zero-sum games with strong robustness; requires known opponent strategies; and poorly adapts to imperfect-information games. |
| Mixed Cooperative–Competitive Game | Nash-Q [20] | Multi-agent competitive scenarios, supports Nash equilibrium solutions; low computational efficiency in high-dimensional policy spaces. |
| Friend-or-Foe-Q [21] | Multi-team adversarial environments; high strategic flexibility; relies on accurate prior friend/foe knowledge; prone to policy oscillation in heterogeneous strategy spaces. | |
| Win or Learn Fast [22] | Non-stationary competitive environments; short-term strategies converge quickly, but may overfit local game models in the long run. |
| Categorization | Representative Algorithm | Characteristic |
|---|---|---|
| Parameter Distribution Search | PEPG | Parameter perturbation combined with gradient update |
| NES | Natural gradient and covariance adaptation | |
| CEM | Elite sample-driven distribution update | |
| Policy Gradient Approximation | OpenAI-ES | Evolution strategy for gradient-free optimization |
| NS-ES | Novelty-driven behavior exploration | |
| NSR-ES | Quality–diversity Pareto optimization | |
| Policy Population Search | PBT | Dynamic hyperparameter adjustment |
| PB2 | Bayesian optimization-enhanced PBT | |
| DERL | Morphological evolution for diverse agent generation | |
| Evolution-Guided DRL | ERL | Parallel evolution and DRL with policy sharing |
| CEM-RL | CEM-TD3 hybrid with population evaluation | |
| PDERL | Backpropagation-constrained mutation | |
| QD-RL | Archive policy Pareto selection |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Yang, P.; Liu, W.; Yan, S.; Zhang, X.; Zhu, D. Multi-Agent Reinforcement Learning in Games: Research and Applications. Biomimetics 2025, 10, 375. https://doi.org/10.3390/biomimetics10060375
Li H, Yang P, Liu W, Yan S, Zhang X, Zhu D. Multi-Agent Reinforcement Learning in Games: Research and Applications. Biomimetics. 2025; 10(6):375. https://doi.org/10.3390/biomimetics10060375
Chicago/Turabian StyleLi, Haiyang, Ping Yang, Weidong Liu, Shaoqiang Yan, Xinyi Zhang, and Donglin Zhu. 2025. "Multi-Agent Reinforcement Learning in Games: Research and Applications" Biomimetics 10, no. 6: 375. https://doi.org/10.3390/biomimetics10060375
APA StyleLi, H., Yang, P., Liu, W., Yan, S., Zhang, X., & Zhu, D. (2025). Multi-Agent Reinforcement Learning in Games: Research and Applications. Biomimetics, 10(6), 375. https://doi.org/10.3390/biomimetics10060375







