1. Introduction
Balance dysfunction is a key factor that restricts movement and activities of daily living in patients during the post-stroke recovery phase [
1,
2]. In various balance and mobility scales [
3,
4], dynamic balance is a high-scoring evaluation item and also an important goal in later-stage walking training. Currently, existing commercial products, such as ReWalk [
5], WalkON Suit [
6], and HAL [
7], assist patients with basic gait rehabilitation training. However, these devices rely on external rigid supports to maintain balance, leading to low patient initiative. In contrast, utilizing a floating-based lower-limb exoskeleton rehabilitation robot for ground walking training, modeled after the assistance techniques used by physical therapists, should offer a more beneficial training approach [
8].
Predefined trajectory tracking control is a commonly used control method, which fits human gait data and generates motion trajectories tailored to the patient by considering trunk movement and center of mass changes [
9]. Ma, Y. et al. [
10] proposed a gait planning method that considers the process of center of mass (COM) shifting. This method uses a finite state machine (FSM) model to switch gait trajectories based on the wearer’s body parameters and posture. Park, K.W. et al. [
11] developed an adaptive gait mode adjustment approach that iteratively determines the optimal trunk tilt angle by analyzing ground contact time and subsequently adjusts the joint reference trajectories. Wu, X. et al. [
12] introduced a Gaussian process regression-based methodology to generate appropriate gait trajectories according to the patient’s physiological parameters. While these methods enable realistic leg movements and effectively guide the patient’s gait, they constrain human balance responses, thus making them more appropriate for early-stage rehabilitation training using fixed-base exoskeleton robots.
To provide flexible assistance to patients without enforcing step length and step frequency, control methods have been developed to reduce human-robot interaction forces and align with human intent. Caulcrick, C. et al. [
13] proposed a model predictive control (MPC) framework that estimates the human-exoskeleton interaction model. This framework utilizes reference angular velocities and joint torques estimated from electromyography (EMG) signals to track human intent. To adjust the human-robot interaction torque, Küçüktabak, E.B. et al. [
14] introduced an exoskeleton closed-loop compensation method. This method calculates the interaction torques during the gait cycle by utilizing the measured torques at the exoskeleton’s hip and knee joints, in conjunction with the whole-body dynamics of the exoskeleton.
To further clarify patients’ motor intentions, some researchers have employed fractal dimension methods to quantify gait complexity for assessing patient status and detecting early abnormalities. Dierick et al. [
15] applied nonlinear analysis techniques to gait time series, using complexity measures to enhance gait classification accuracy. Chakraborty et al. [
16] attempted to differentiate Parkinson’s patients from healthy individuals using fractal dimension, aiming to explore the relationship between the central nervous system and motor function; however, the results were suboptimal, with limited accuracy. In clinical studies, Dehghan et al. [
17] found significantly reduced fractal dimensions in several cortical regions of patients with the postural instability and gait difficulty (PIGD) subtype, indicating the potential value of this method in disease identification. Nonetheless, current research remains in the exploratory stage, requiring further validation and standardization.
Some studies have attempted to introduce impedance control to model and predict human motion trajectories. Zhu, A. et al. [
18] proposed an impedance control strategy for lower-limb exoskeleton rehabilitation robots based on adaptive force control. This strategy takes the gait of healthy individuals as a reference and implements position control on the exoskeleton, adjusting the gait trajectory according to the patient’s own leg strength. Huang, R. et al. [
19] introduced a novel coupled cooperative primitives (CCP) strategy, where a human-robot interaction model, represented using an impedance model, serves as a modulation term. The impedance coefficient of this modulation term is adjusted online to ensure the stability of the human-exoskeleton system. Zhang, T. et al. [
20] proposed a hip joint controller based on the extrapolated center of mass. This controller responds to balance disturbances through a combination of a series elastic actuator (SEA) and active compliance control based on adaptive admittance control. By adjusting the hip joint angle, the controller generates compliant guiding forces, ensuring that the zero-moment point (ZMP) remains within the support domain, thereby maintaining the balance of the exoskeleton. Soliman, A.F. et al. [
21] proposed a stack-of-tasks approach, in which a priority-based ordering is applied to the task variables of the CoM, left foot, and right foot. A motion controller incorporating ZMP impedance feedback ensures that the ZMP remains within the support domain, thereby maintaining system balance. These methods exhibit rapid responsiveness to changes in interaction forces but still depend on trajectory error correction. Additionally, achieving full compliance may pose a risk of instability and potential falling [
22].
To enhance wearer comfort, Martínez, A. et al. [
23] proposed a method that allows the user to control the exoskeleton’s step length and timing during the swing phase, avoiding interference with the body’s balance response. Leestma, J.K. et al. [
24] designed a hip exoskeleton with both frontal and sagittal plane drives. The exoskeleton’s balance capability is enhanced during steady-state and perturbation walking by adjusting step length and width. Tian, D. et al. [
25] introduced a CoM modification controller based on center of mass dynamics. Designed according to human body structure, this controller eliminates axial errors and enhances the exoskeleton’s center of mass stability, achieving self-balancing during walking.
Beck, O.N. et al. conducted an analysis of physiological data, including soleus muscle length, surface electromyography (sEMG) signals, and joint reaction torques, when the human body is subjected to external disturbances. The experimental findings demonstrated that when the exoskeleton provides assistive torque aligned with human intent, applying assistance within the first 50–70 ms before the body’s initial balance correction response increases human-exoskeleton interaction forces but contributes to reducing CoM disturbance and maintaining balance. Conversely, delaying assistance by 50–70 ms reduces interaction forces yet fails to effectively support balance maintenance [
26]. Thus, achieving effective coordination with the body’s balance correction response remains a critical challenge for floating-base lower-limb rehabilitation exoskeletons in assisting overground gait training.
Based on the above analysis, an optimal gait controller is designed using deep reinforcement learning to explore how the exoskeleton robot can provide physiologically plausible guidance and compliant assistance in coordination with the human balance correction response.
The main contributions of this study are as follows:
- (1)
A BDMG based on a confidence domain strategy optimization algorithm is designed, incorporating physiological gait trajectories, system balance states, and compliance states into the reward function. To improve the model’s convergence speed, a staged training method is proposed, controlling the model’s training direction and exploration difficulty by adjusting the reward function.
- (2)
Based on the training and evaluation data of the BDMG model, an abnormal command recognizer is designed and trained to identify abnormal commands after the user–exoskeleton system performs actions. To correct these abnormal commands from the BDMG, an abnormal command corrector is designed. The closest point on the physiological gait trajectory to the current joint position is considered the physiological trajectory’s extreme point. The optimal action combination is explored within the closed space formed by the abnormal commands and the physiological trajectory’s extreme point.
- (3)
Based on the optimal action combination data, a supervised learning algorithm is used to train the abnormal command corrector. An overall control framework, consisting of the abnormal command corrector, abnormal command recognizer, and BDMG, is then designed to form the optimal gait controller, achieving end-to-end balance and compliance control for the lower-limb exoskeleton robot.
The structure of this paper is as follows:
Section 2 provides a detailed description of the design process of the BDMG to obtain the optimal motion strategy.
Section 3 addresses the issue of policy drift and introduces the abnormal command recognizer to identify erroneous commands.
Section 4 further designs the abnormal command corrector to correct the abnormal commands. These three components together form the optimal gait controller. In
Section 5, the performance of the optimal gait controller in terms of balance and compliance is verified through simulations.
Section 6 presents related experiments, comparing the optimal gait controller’s performance with traditional position control and impedance control, thereby validating its superiority in performance. Finally,
Section 7 concludes the paper.
2. Design of the BDMG
The BDMG constitutes a vital element of the optimal gait controller, playing a pivotal role in shaping the overall system performance. Its design is critical for ensuring balanced and coordinated movement, providing a foundational basis for the development of an effective gait control strategy.
Figure 1 illustrates the overall architecture of the optimal gait controller, highlighting the integrated interactions among its key components.
Physiological trajectory is derived from the joint angle data of 14 full-body joints during normal human walking. The specific design is outlined as follows.
2.1. Action Space and State Space Design
The expression of the action space is as follows:
where,
and
represent the position and velocity values, respectively, of each joint degree of freedom in the human body at time
, where
. Among these, the action space formed by the knees and hips of both legs constitutes the physically actuated action space, whereas the remaining elements form the virtual action space.
The expression of the action space is as follows:
where,
represents the physiological trajectory information, which is the current full-body coordinated optimal value determined based on the action from the physiological trajectory cluster;
represents the angle of the
-th degree of freedom at time
;
represents the actual joint position information of the lower-limb exoskeleton human-machine system, referred to as real-time state information.
represents the real-time position of the
-th joint of the human body;
represents the real-time velocity of the
-th joint of the human body;
,
and
represent the position, velocity, and angular velocity at the pelvis of the exoskeleton, respectively;
represents the ZMP position coordinates of the exoskeleton;
represents the center coordinates of the support domain at the sole of the exoskeleton; and
is a Boolean value that represents the relationship between the ZMP and the support domain. When the ZMP is within the support domain,
; otherwise,
.
represents the scalar value of the human-machine interaction force;
represents the right thigh;
represents the left thigh;
represents the right lower leg; and
represents the left lower leg.
2.2. Reward Function Design
The reward function comprises four key components: physiological reward, forward progress reward, balance reward, and compliance reward. These components collectively characterize the maximum reward attainable when the exoskeleton’s physiological guidance, compliance assistance, and human balance correction responses are effectively coordinated.
The physiological reward is designed to enable the human-machine system to converge toward the human physiological trajectory with the greatest possible efficiency. It is defined as follows:
The forward progress reward is designed to incentivize the human-machine system to advance. It is defined as follows:
where
represents the x-direction coordinate value of the human pelvis position at time
.
The balance reward aims to improve the balance ability of the human-machine system. It is defined as follows:
where
, and simulation results confirm that the model exhibits stable and satisfactory performance. This threshold is critical for preventing the lower-limb exoskeleton rehabilitation robot from experiencing balance-related stagnation before acquiring sufficient locomotor capability.
The compliance reward is designed to ensure that the exoskeleton joints move in alignment with the user’s intent, thereby minimizing the interaction force and enhancing the compliance capability of the human-machine system. It is defined as follows:
where,
represents the maximum interaction force that human joints can withstand, with 300 N set for the hip joint and 65 N for the knee joint;
is uniformly set to 10 N.
2.3. Network Structure and Parameter Design
In the trust region policy optimization (TRPO) algorithm [
27], both the value network and the policy network utilize state space values as inputs. The value network generates the corresponding state function values, whereas the policy network produces the probability distribution over actions. The parameter configurations for both the policy network and the value network are presented in
Table 1.
The output of the policy network consists of 60 neurons, corresponding to the target positions and velocities of the 30 actuated joints in the human-machine system, while the output of the value network is a single neuron, representing the cumulative expected reward of the current input state.
2.4. Stepwise Training Method
Due to the high dimensionality of the state and action spaces in the BDMG, the training process presents considerable challenges and may lead to the agent becoming trapped in a local optimum. Therefore, the stepwise training method is employed to systematically escalate the training difficulty. The training process of the BDMG model is structured into four sequential phases, where the training of each subsequent phase commences upon the convergence of the preceding model. The final reward function is presented in
Table 2.
During the training process, the reward function evolves through four stages to gradually enhance the performance of the human-machine system, avoid model overfitting and undergeneralization, and improve training efficiency.
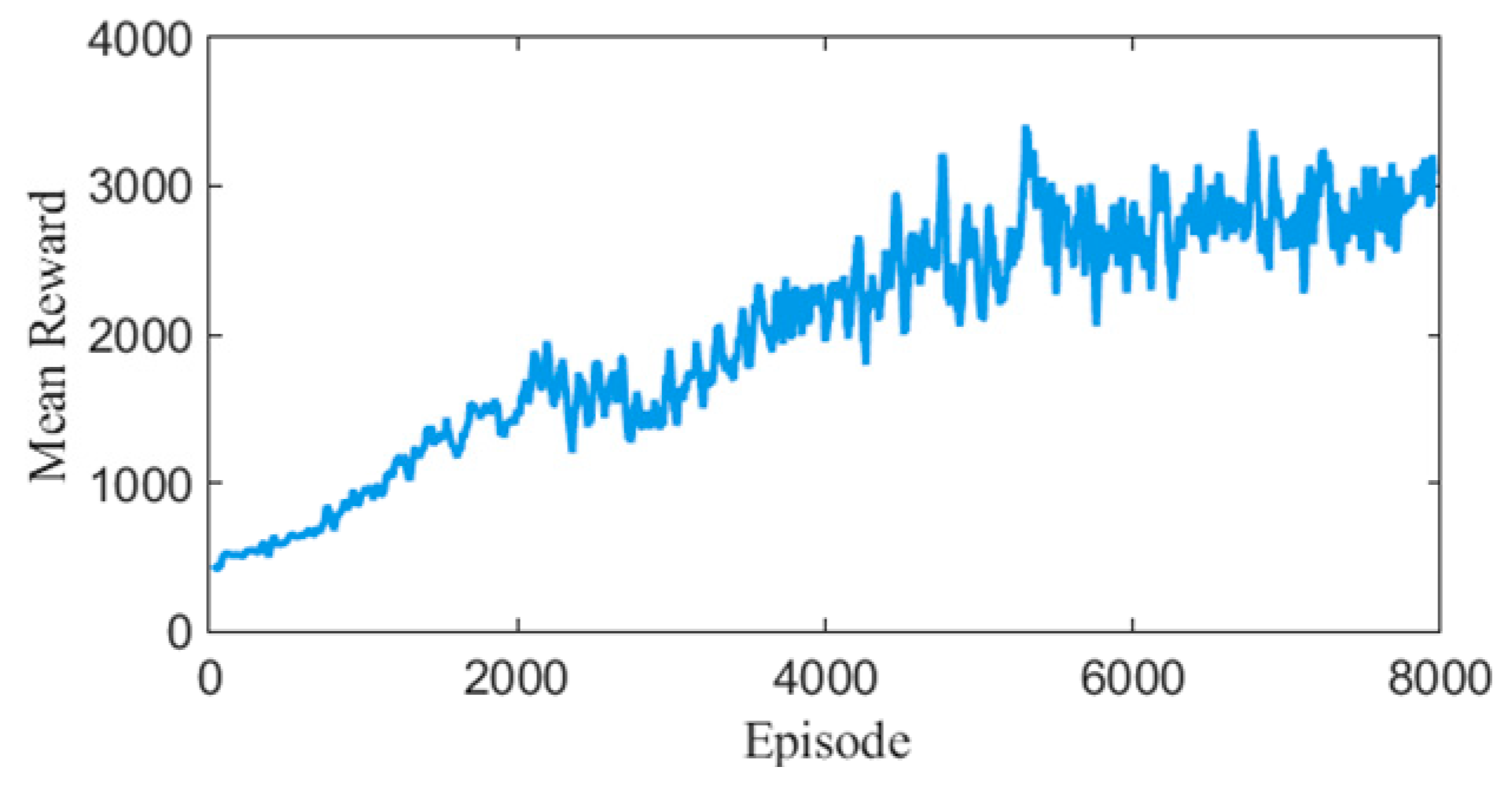
Training 1: The reward function includes two components—forward reward and physiological reward. The goal is to enable the system to achieve physiologically reasonable walking on a smooth surface with a ground friction coefficient of 1. The model converged after 2000 episodes.
Training 2: Based on the previous stage, a balance reward is introduced to enhance system stability while maintaining natural gait characteristics. The model converged after 4800 episodes.
Training 3: Building on the previous stage, the ground friction coefficient is increased to 1.7 to allow the model to adapt to surfaces that more closely resemble real-world walking conditions, thereby improving robustness. The model converged after 1500 episodes.
Training 4: On top of the prior training structure, a compliance reward is added, and the weight of the physiological reward is reduced. This encourages the model to improve compliance during rehabilitation training while maintaining gait balance and physiological plausibility. The final model converged after 4500 episodes.
4. Abnormal Command Corrector
In the optimization of abnormal commands, the PSO algorithm was selected. As a swarm intelligence algorithm, PSO can efficiently explore complex solution spaces without the need for gradient information, making it particularly suitable for the sparse and non-differentiable reward environment in this study. Based on this, a sample generation optimizer is developed using PSO to identify the optimal combination of action samples within the closed space defined by abnormal commands and the extremum points of physiological trajectories. Furthermore, a supervised learning approach is employed to train an abnormal command corrector, which adjusts the transient abnormal commands generated by the BDMG.
4.1. Objective Function and Parameter Design of PSO Algorithm
Solution space is defined as
and consists of the hip and knee joint position commands of both legs, represented as
, along with the corresponding hip and knee joint position commands and the polar distance point of the physiological trajectory in the BDMG at the same time step, denoted as
. Where
represents the polar distance point of the physiological trajectory, which is the point on the physiological trajectory that is closest (in terms of L2 norm) to the current joint positions of the knee and hip joints of both legs in the sagittal plane degrees of freedom of the human-machine system. The mathematical formulation is given as:
where
,
;
denotes the search particles in the PSO algorithm.
In this implementation of the PSO algorithm, each particle updates its velocity and position during the optimization process based on the following formulas:
is the inertia weight, which controls the influence of a particle’s previous velocity on its current velocity, helping balance global and local search capabilities. represents the velocity of particle at time . and are acceleration coefficients that represent the cognitive (individual) and social (global) learning components, respectively. and are random numbers uniformly distributed in the range [0, 1], introduced to increase the randomness of the search process. denotes the best position found so far by particle at time , is the current position of particle at time , and is the global best position found by the entire swarm up to time .
Considering that the objective function in the PSO algorithm should be capable of evaluating the impact of predicted correction commands on the model’s balance and compliance, the prediction network trained in the previous section is adopted as the objective function in PSO to maximize the model’s stability and compliance performance. The objective function
is defined as follows:
where
and
denote the objective terms for balance and compliance, respectively. The weighting factors
and
are both set to 0.5. The fitness function
is defined as the negative of the objective function, as follows:
The hyperparameters of the PSO algorithm are set as shown in
Table 6.
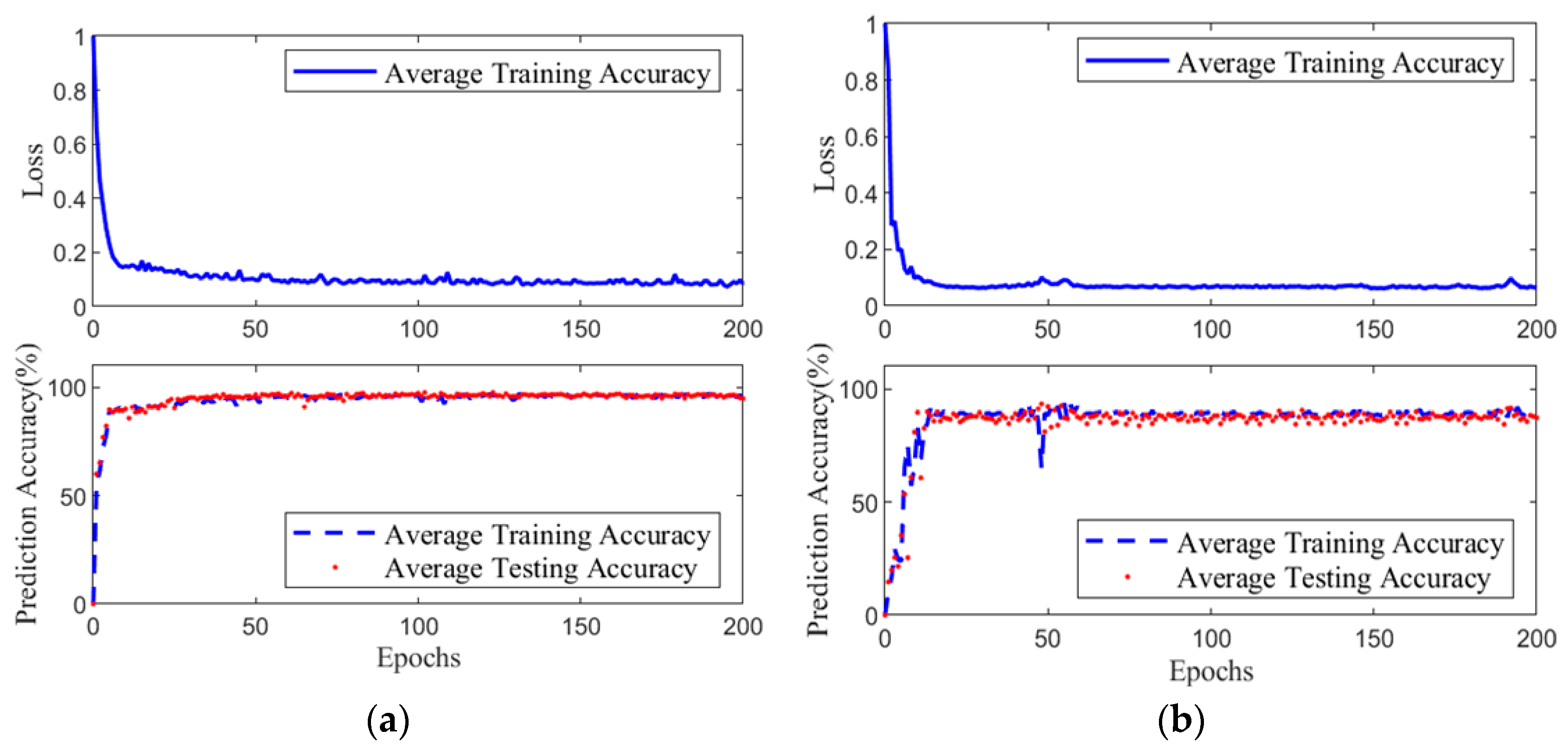
4.2. Abnormal Command Corrector Training
One hundred thousand samples of balance-related state information , compliance-related state information , and BDMG commands were collected at the moment immediately preceding the abnormal command. For each abnormal data sample, the corresponding physiological trajectory polar distance point was computed and stored in the abnormal state dataset. The PSO algorithm was then applied to each abnormal data sample in this dataset to optimize the action selection, and the optimized results were stored in the optimal action combination sample set.
After the correction sample dataset has been generated, the abnormal command corrector was trained via a supervised learning algorithm. Specifically, balance-related state information
, compliance-related state information
, BDMG command values
, and physiological trajectory polar distance points
extracted from the correction sample dataset were utilized as input features for the supervised learning algorithm. Meanwhile, the corrected command values acted as the supervision labels. The hyperparameters employed during the training process are summarized in
Table 7.
The loss function is defined as:
where
represents the
-th element in the
-th set of corrected position command values within the batch, while
refers to the corresponding instruction used for training evaluation.
6. Experiment
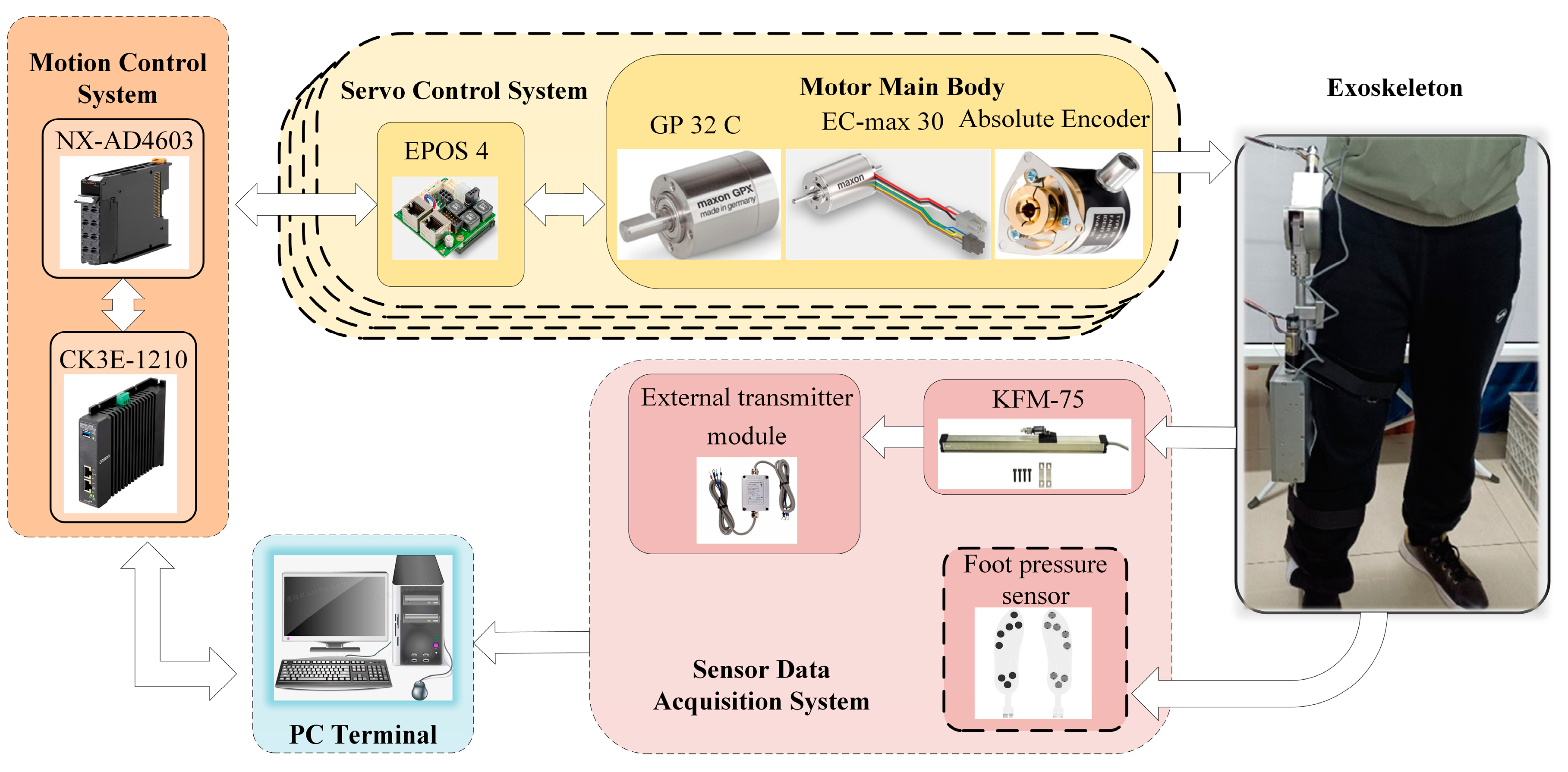
The overall structure of the lower-limb exoskeleton hardware platform is illustrated in
Figure 8. It primarily consists of a computer terminal, motion control system, motor servo system, sensor data acquisition system, and the exoskeleton itself. The lower-limb exoskeleton robot is equipped with four sets of motor servo systems, which are responsible for actuating the exoskeleton joints. Control strategies are generated by the computer terminal and transmitted to the control system to assist the patient’s movement via joint actuators. During exoskeleton operation, joint states and sensor data are collected in real time and fed back to the terminal for processing.
All participants in this study were healthy adult males, with a height range of (170 ± 2) cm and a weight range of (70 ± 4) kg. The experimental protocol involving human subjects was reviewed and approved by the Ethics Committee of the First Hospital of Qinhuangdao, China.
6.1. Abnormal Command Corrector: Effectiveness Analysis
Verification of the corrective effect of the abnormal command corrector on the BDMG was conducted through two experiments. For consistency, the joint position data for the BDMG in both experiments were derived from the optimal gait control strategy and were not processed by the abnormal command corrector. The human-machine interaction force data for the BDMG were computed based on the joint position data and the thigh center coordinates of the user’s load-bearing leg. The balance state of the BDMG was predicted using the balance prediction network.
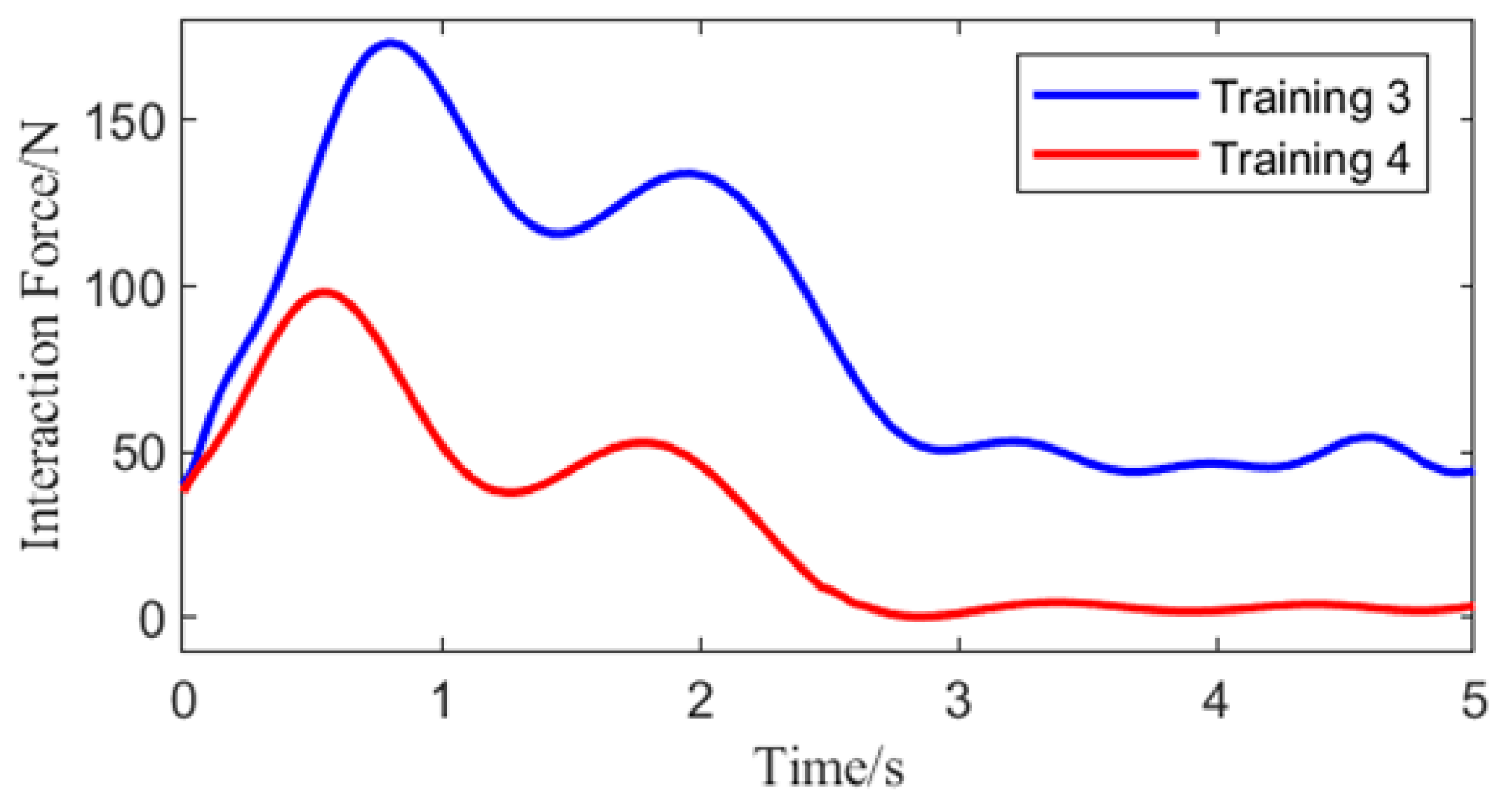
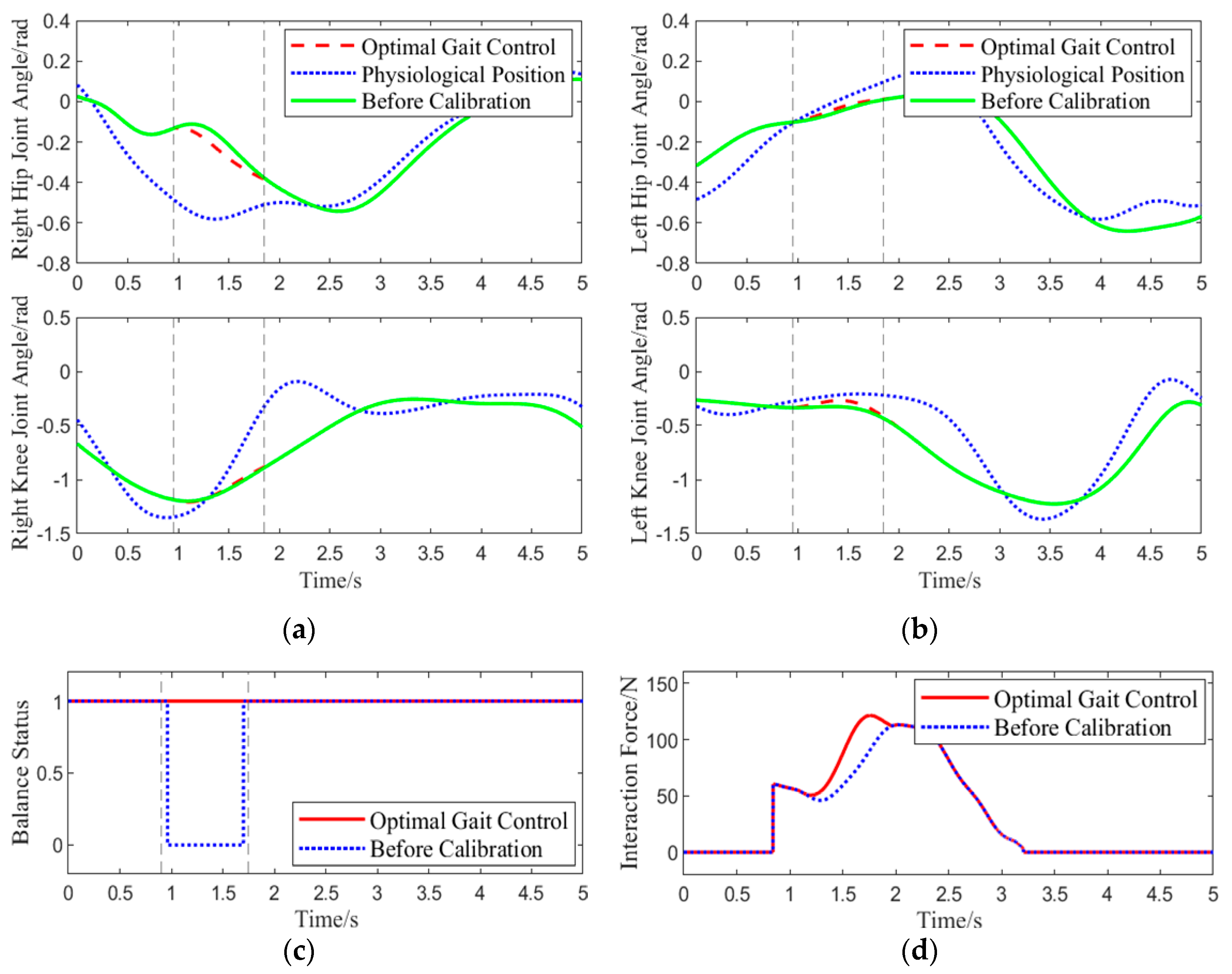
Experiment 1: The participants wore the lower-limb exoskeleton rehabilitation robot, using the optimal gait control strategy as the control strategy for the robot. The participants walked along a pre-arranged path, and during one gait cycle, when the right leg was lifted approximately 0.15 rad, an interaction force of approximately 60 N was applied downward at the center of the right thigh of the exoskeleton. The angles of four joint motors were collected, real-time human-machine interaction force was calculated, and the system’s balance status was assessed using data from a pressure insole. This experiment aimed to simulate the situation where the BDMG caused an imbalance in the lower-limb exoskeleton rehabilitation robot system, specifically as a result of actions taken to enhance compliance, thereby verifying the correction effect of the Abnormal Command Corrector. The results of the experiment are shown in
Figure 9.
As shown in
Figure 9, at 0.9 s, the center of the subject’s right hip joint experiences a downward interaction force of 60 N. When using the BDMG, the controller prioritizes overall compliance, which compromises balance and results in a loss of stability. At the same moment, the abnormal command corrector detects and improves the abnormal command. The dashed line from 0.9 s to 1.75 s indicates the active period of the abnormal command corrector, during which it acts to reduce the interaction force while maintaining the subject’s balance. Although the interaction force generated by the corrected command is slightly higher than that from the BDMG alone, it effectively maintains balance during movement. After 1.75 s, no further abnormal commands are generated, and a significant deviation is observed between the motion generator’s command and the actual joint angles, requiring some time for convergence. Overall, the abnormal command corrector demonstrates a clear corrective effect on the output of the BDMG.
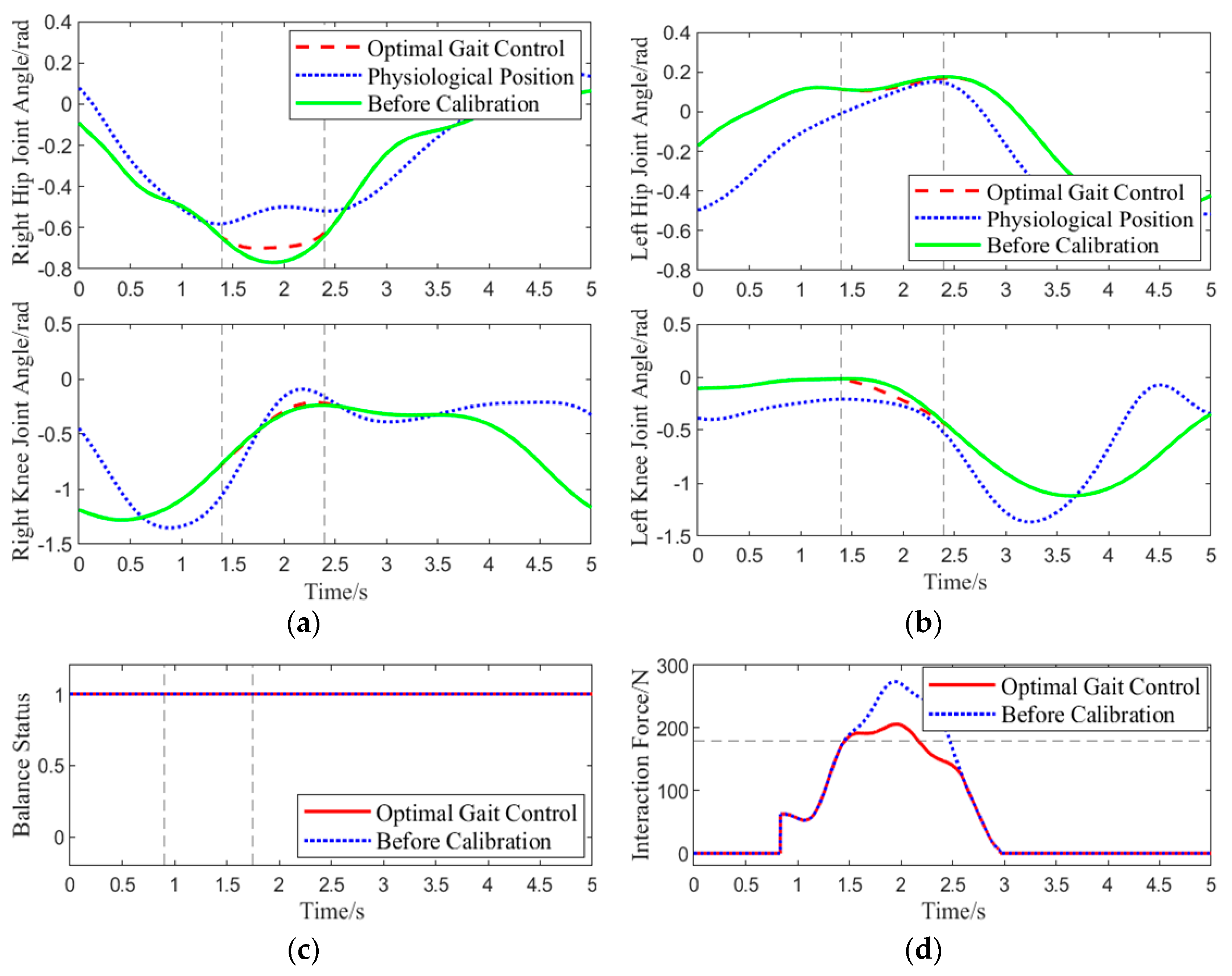
Experiment 2: The same experimental procedure as in Experiment 1 was followed. When the subject, wearing the lower-limb exoskeleton rehabilitation robot, lifted the right leg to about 0.45 rad, an approximately 60 N downward human-machine interaction force was applied at the center of the right thigh, and sensor data were collected. This experiment aimed to verify the correction effect of the abnormal command corrector when the BDMG exceeded the human safety threshold of 180 N. The results of the experiment are shown in
Figure 10.
Unlike in Experiment 1, at 1.4 s in this gait cycle, the BDMG prioritized overall balance at the expense of compliance, resulting in an interaction force exceeding the predefined threshold of 180 N. At the same moment, the abnormal command corrector received and improved the abnormal command. As shown by the blue dashed line in the human–robot interaction force plot, the corrected command reduced the rate of increase in the interaction force, thereby improving system compliance. After 2.8 s, the interaction force decreased to its minimum level, and no further abnormal commands were generated. Throughout the correction process, the interaction force between the subject and the exoskeleton remained within 205 N, effectively mitigating the abnormal command generated by the BDMG and enhancing compliance without compromising overall balance.
6.2. Optimal Gait Control Strategy Performance Verification
Two comparative tests were conducted to verify the performance of the optimal gait control strategy in terms of physiological response, balance maintenance, and compliance.
Test 1: The subject wore the exoskeleton rehabilitation robot and walked while being controlled by three control strategies: traditional position control [
28], admittance control [
29], and optimal gait control. When the left thigh reached a certain angle, a downward interaction force of approximately 30 N was applied at the center of the left thigh. The purpose of this test was to evaluate how the three control methods handle interaction forces, assessing the performance of the optimal gait control strategy when faced with short-term imbalance or lack of compliance.
Test 2: The subject wore the lower-limb exoskeleton rehabilitation robot and walked for 10 gait cycles at a speed of approximately 0.4 m/s on a pre-arranged track. A human-machine interaction force ranging from 30 to 60 N was randomly applied five times at the centers of the upper and lower leg. The exoskeleton was controlled using traditional position control, admittance control, and optimal gait control strategies. Each control method was tested three times, ensuring that the average initial interaction force applied in each test was approximately 45 N.
In the test, the trajectory for position control was based on the physiological gait trajectory obtained when training the BDMG. Since admittance control requires a high level of autonomous control from the human body to avoid injury to the subject, admittance control was applied only to the joints of the load-bearing leg. Position control was used for the other joints, including the hip and knee joints.
6.2.1. Physiological Performance Evaluation
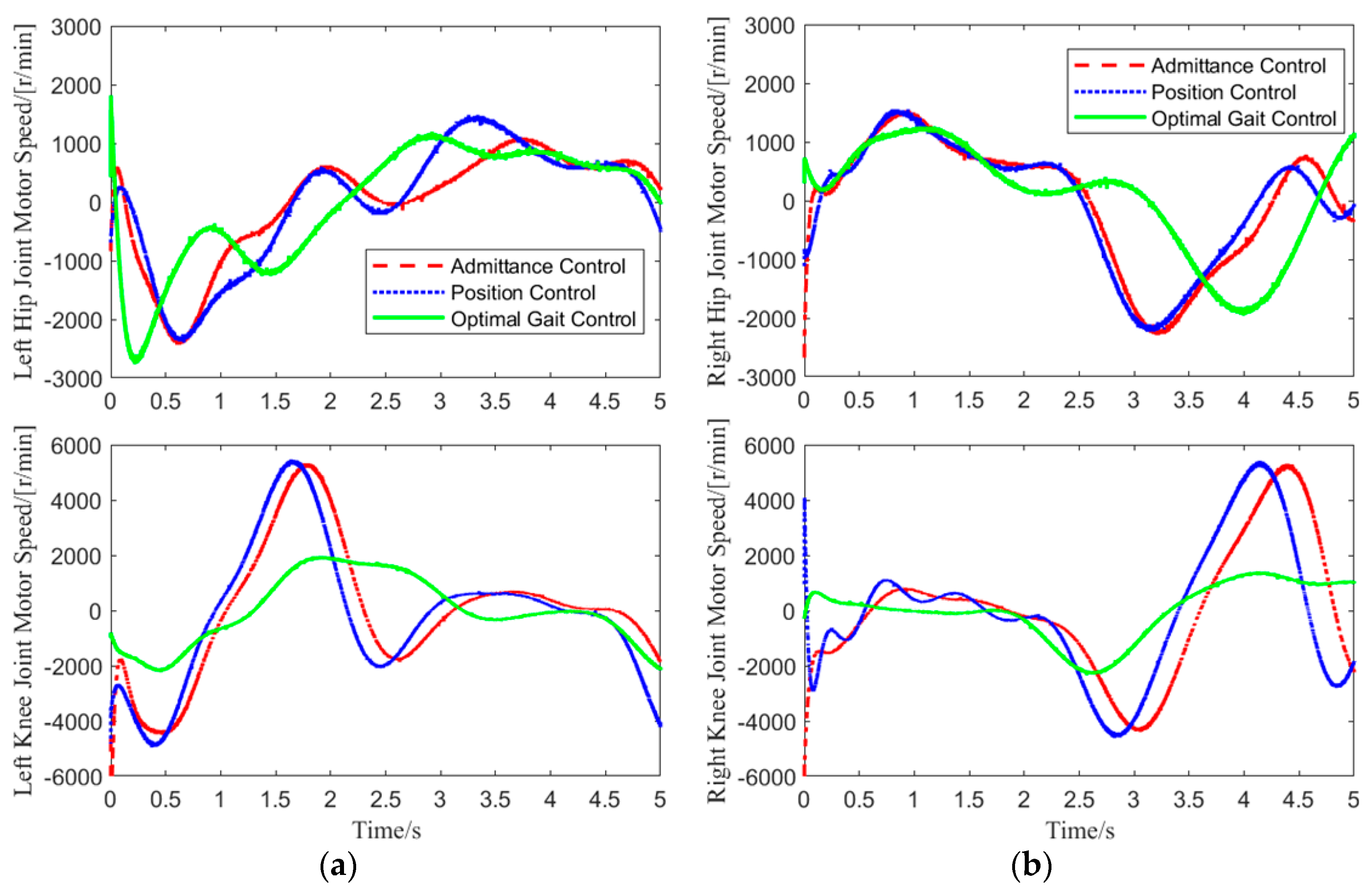
In Test 1, data for the hip and knee joint angles of both legs, as well as the motor speeds, were collected over one gait cycle. The motor speed variation curves for the hip and knee joints of both legs are shown in
Figure 11.
As shown in
Figure 11, in the experiment, admittance control was applied only to the joints of the loaded leg, while the hip and knee joints of the other leg were controlled using position control. Therefore, the motor speed variations for the left knee joint, right hip joint, and right knee joint under admittance and position control were identical. Under this motor speed control, the joint angle variations are shown in
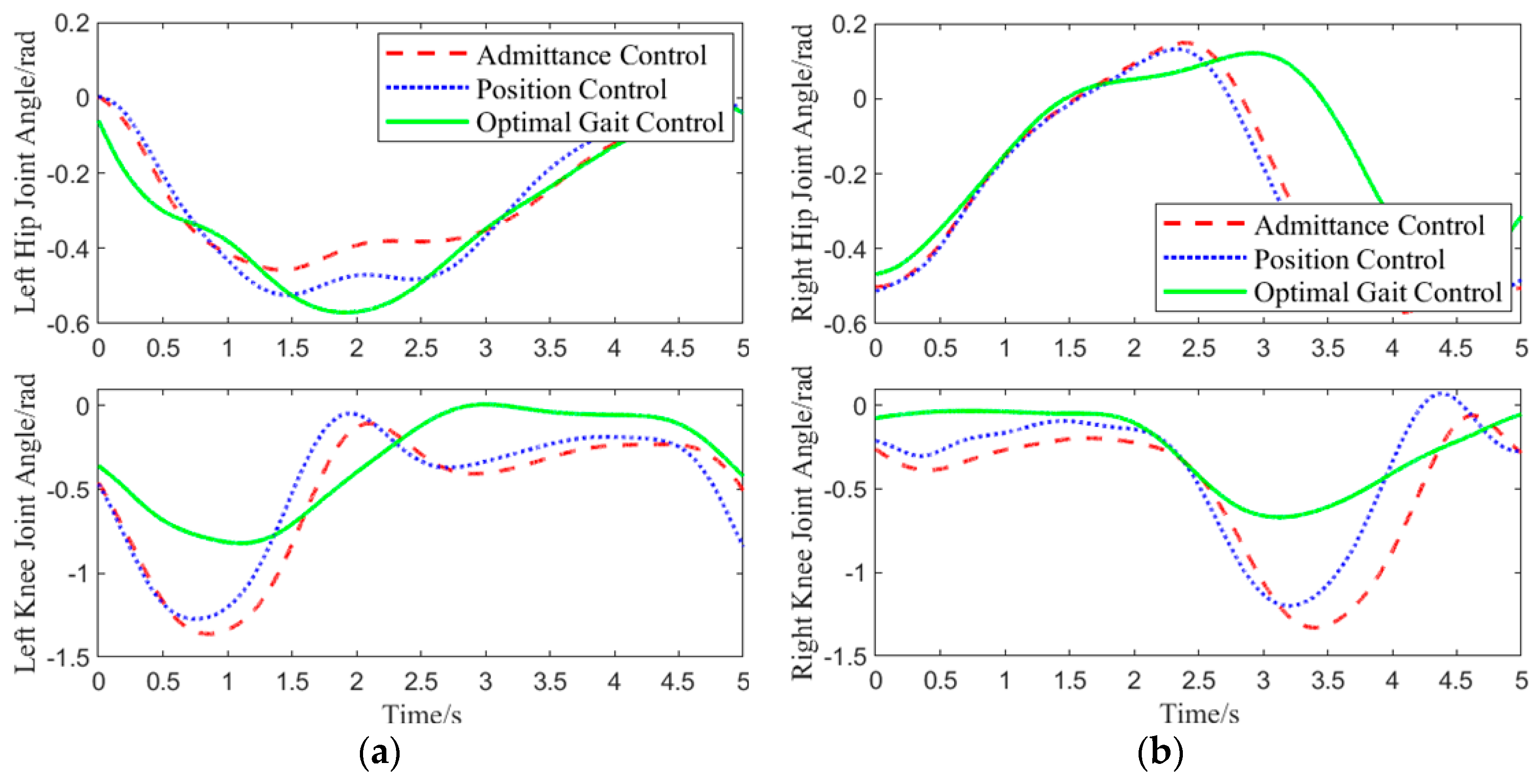
Figure 12.
As shown in
Figure 12, when the left hip joint was raised by approximately 0.32 rad, an interaction force was applied to the center of the left thigh. Upon receiving the interaction force, the optimal gait control strategy reduced the angle of the left hip joint’s upward movement to lower the interaction force. When the left hip joint was raised to 0.45 rad, the hip joint deviated too much from the physiological trajectory. To counteract the imbalance, the optimal gait control strategy increased the hip joint’s upward angle. Under admittance control, with increasing interaction force, the left hip joint’s angle changed significantly, and the interaction force continued to grow as the hip joint rotated downward, eventually reducing the interaction force to 0 N. Position control, on the other hand, did not consider human-machine interaction force throughout the entire gait cycle and forced the human body to walk according to the predetermined trajectory.
For a more accurate evaluation of the physiological performance of the three control methods in response to interaction forces, dynamic time warping (DTW) was applied to compare the left hip joint curve under each control method and the physiological joint trajectory from 0.6 to 3.5 s [
30]. A smaller distance between the two curves indicates a higher similarity. Calculation results show that the joint curve under position control had the smallest distance to the physiological joint trajectory, with a value of 0.6148. The optimal gait control strategy followed with a distance of 3.26895. Admittance control had the largest distance of 6.197, indicating the lowest physiological performance.
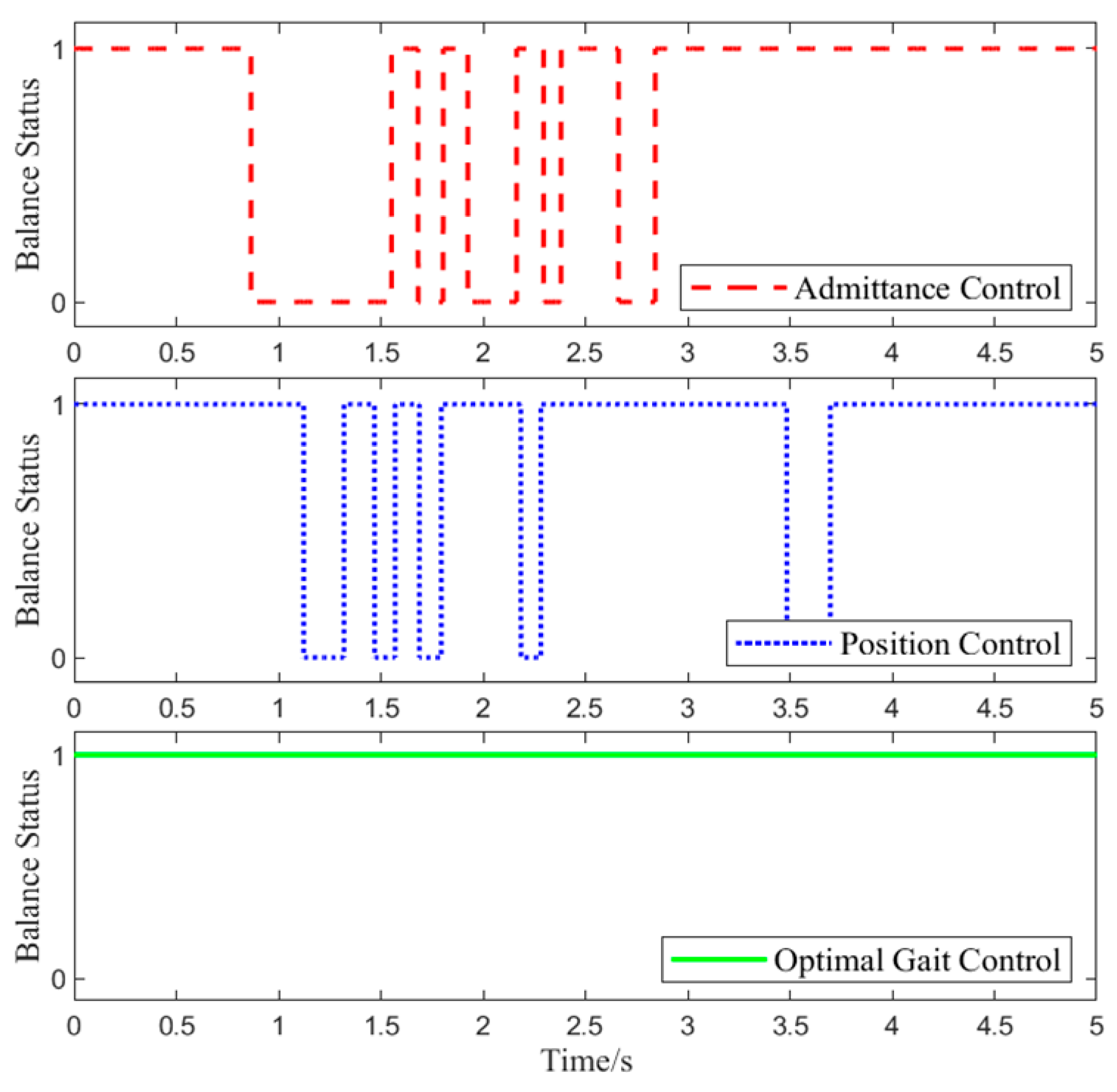
6.2.2. Balance Performance Evaluation
Foot pressure data were collected during Experiment 1 to assess the balance state of the lower-limb exoskeleton rehabilitation robot system. The specific changes are shown in
Figure 13.
In Test 1, at 0.6 s, the interaction force was applied. As shown in
Figure 13, with position control, the lower-limb exoskeleton rehabilitation robot system experiences alternating states of balance and imbalance throughout the gait cycle. This is because the target position of position control does not change in response to the interaction force, leading to a conflict between the human joint target position and the exoskeleton joint target position, which causes system imbalance.
Foot pressure data from all time points in Experiment 2 were collected to determine the balance state of the lower-limb exoskeleton rehabilitation robot. The closer the ZMP is to the center of the support polygon, the better the balance performance. For the three different control methods, the proportion of the ZMP falling within 20%, 40%, 60%, 80%, and 100% of the region around the support polygon center is statistically calculated, as shown in
Table 11.
From
Table 11, it can be seen that the optimal gait control strategy ensures the highest system balance with a maximum of 96.8%, where the proportion of the ZMP in the 20–40% support domain is the largest at 32.8%. Under position control, the maximum proportion of the ZMP in the 40% support domain is 62.2%. Throughout the entire process, admittance control consistently shows the lowest balance gait proportion among the three control methods. Therefore, the optimal gait control strategy has the best balance performance, with 96.7% in the 100% support domain range, followed by position control at 89.2%, while admittance control exhibits the worst balance performance.
6.2.3. Compliance Performance Evaluation
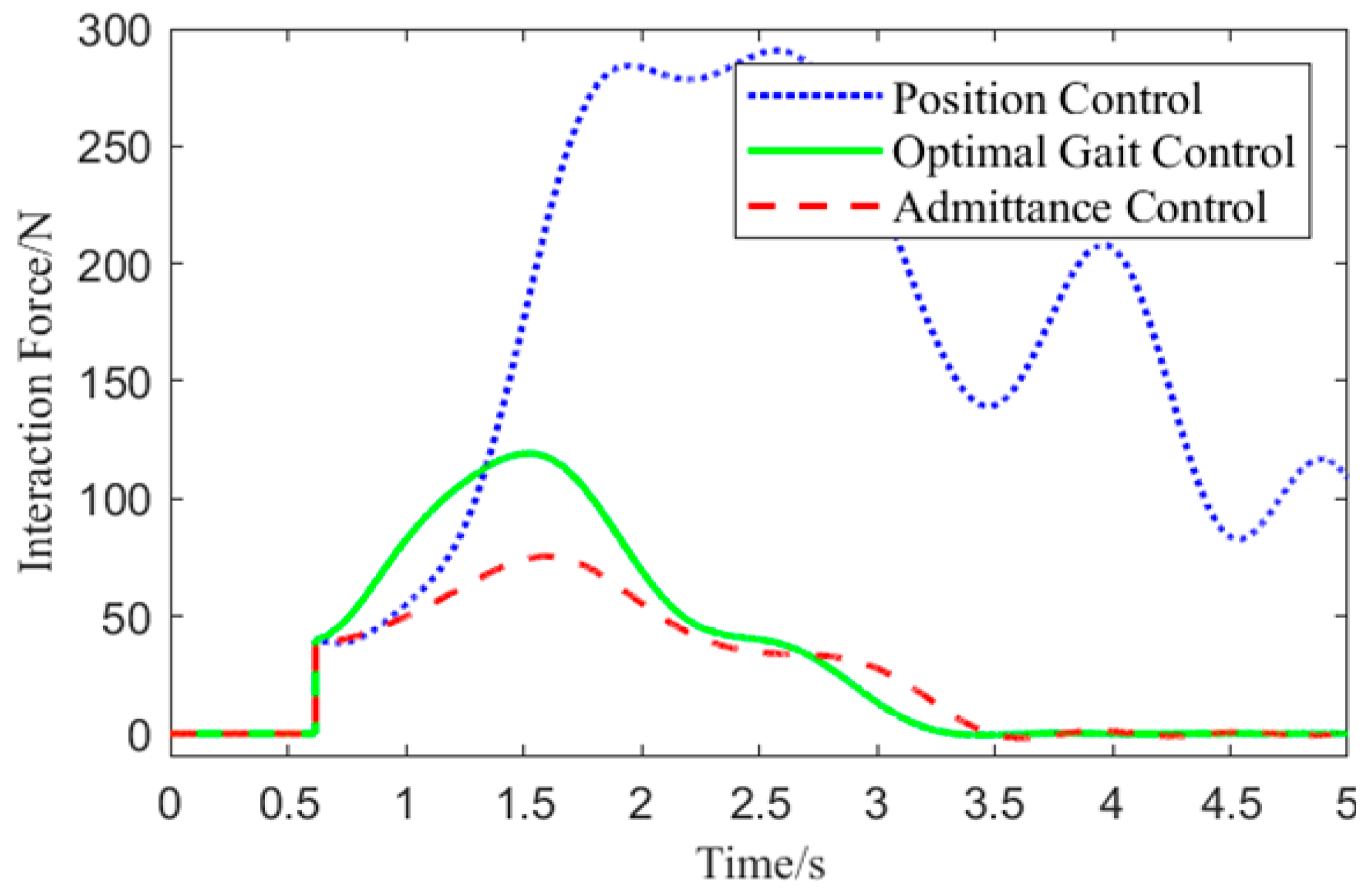
Experiment One involved collecting the motor angle of the exoskeleton’s left hip joint and the position coordinates of the human left thigh center in the local coordinate system. Based on these data, the interaction force was calculated, and the interaction force variation curve is shown in
Figure 14.
From
Figure 14, it can be observed that at 0.65 s, the interaction force is applied. Since the direction of the interaction force opposes the movement direction of the left hip joint, the interaction force increases under all three control methods. Due to the need to balance compliance and stability, the optimal gait control strategy responds more slowly to the initial interaction force compared to admittance control. However, compared to position control, it significantly reduces the interaction force. Among the three control methods, the optimal gait control strategy has the shortest response time in handling interaction forces, effectively reducing the interaction force to 10 N in a shorter time, demonstrating superior compliance performance.