Obstacle Feature Information-Based Motion Decision-Making Method for Obstacle-Crossing Motions in Lower Limb Exoskeleton Robots
Abstract
1. Introduction
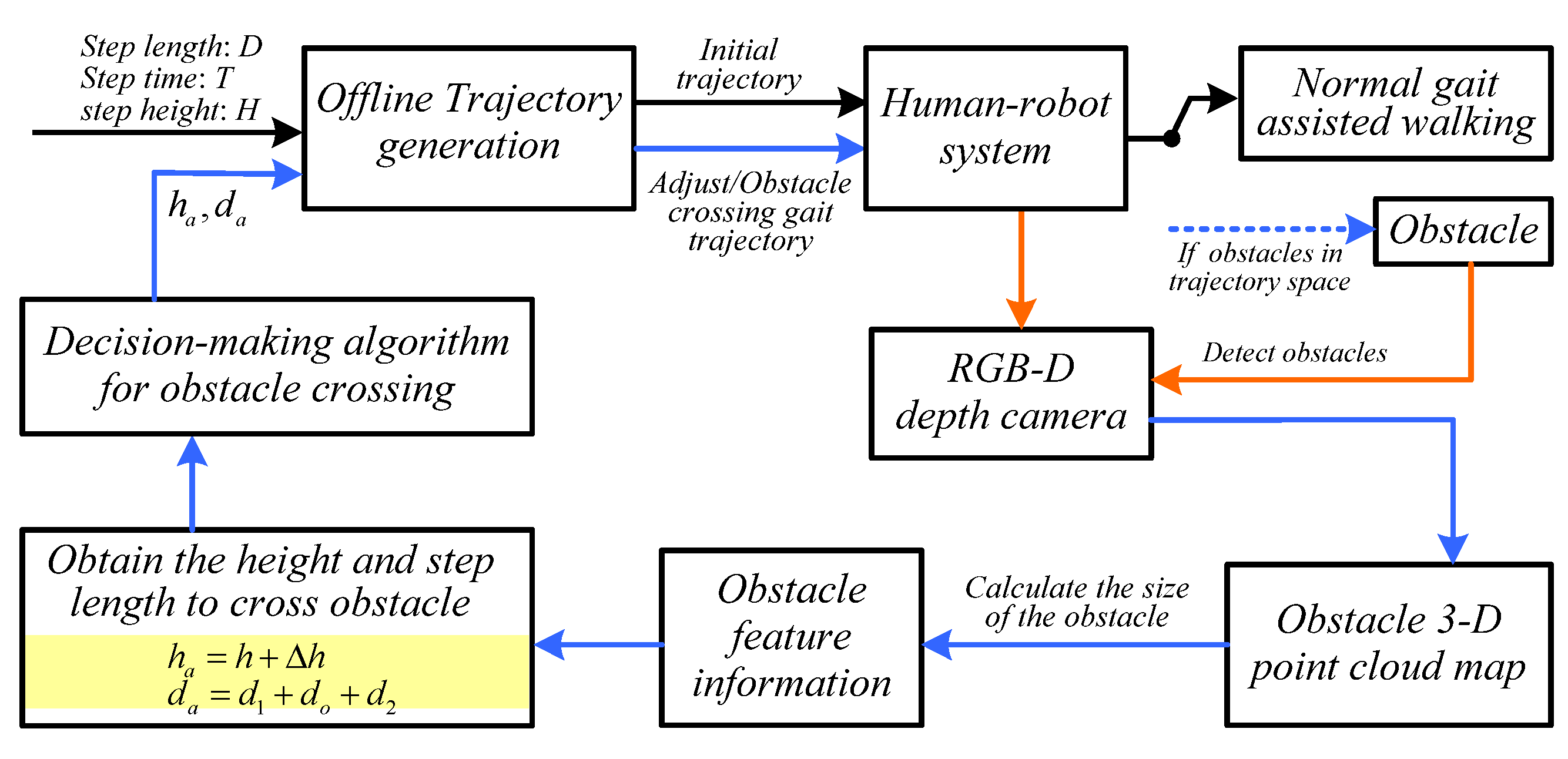
2. Method of Obstacle-Crossing Motions
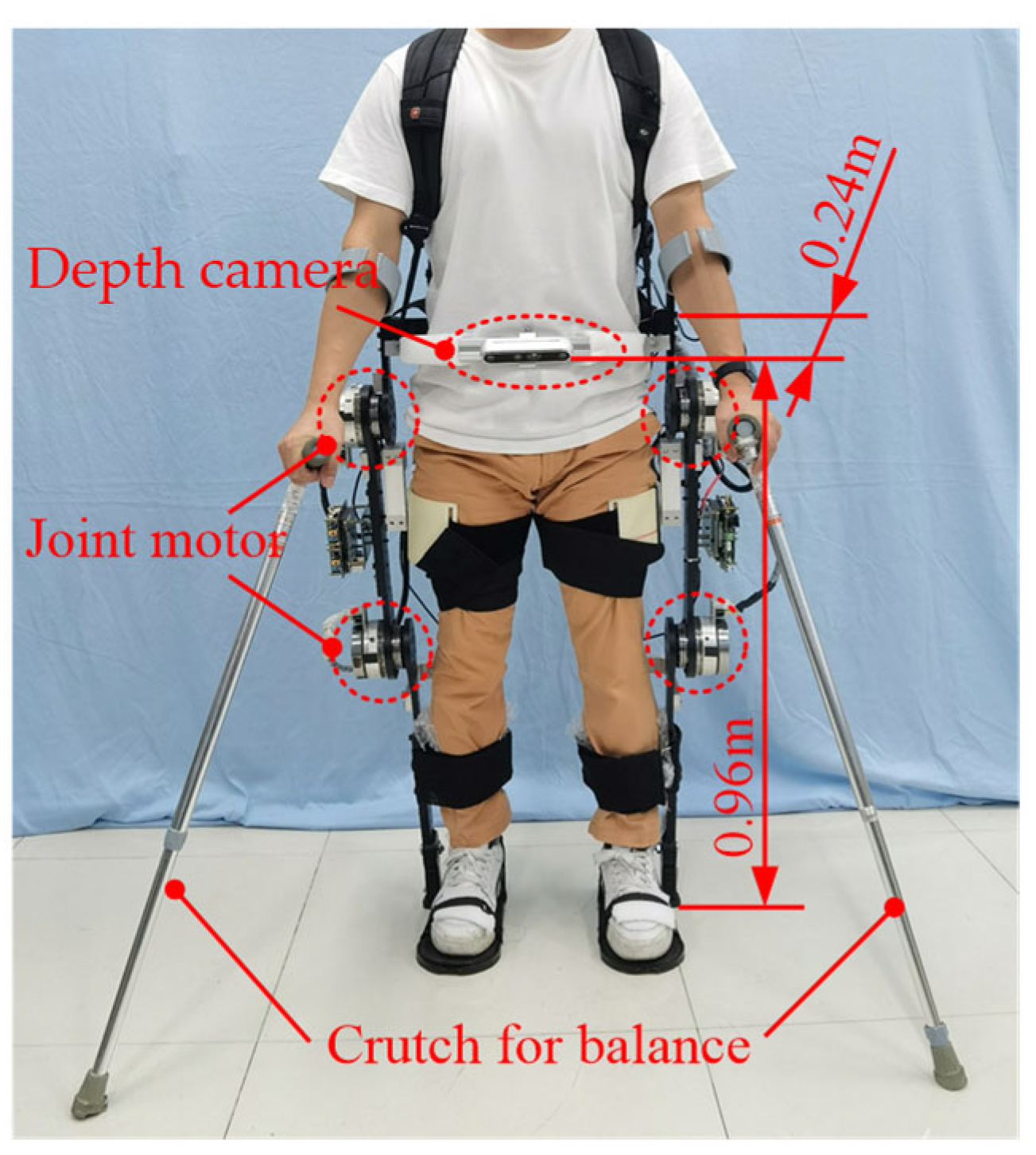
2.1. Acquisition of Obstacle Feature Information
2.2. Gait Parameters Based on Obstacle Feature Information
2.3. Gait Trajectory Planning Based on Obstacle Feature Information
- Description of gait trajectory planning problem
- Offline gait trajectory planning
- (1)
- Adjusted gait trajectory: when the distance between the lower limb exoskeleton robot and the obstacle cannot achieve safe crossing within one gait cycle, the step length needs to be adjusted appropriately when approaching the obstacle.
- (2)
- Obstacle-crossing gait trajectory: when the lower limb exoskeleton robot reaches a safe crossing position after adjusting its gait trajectory, it selects an appropriate obstacle-crossing gait trajectory from the trajectory library based on the detected obstacle information.
2.4. Obstacle-Crossing Motion Decision-Making Algorithm Based on Obstacle Feature Information
| Algorithm 1. Decision-making algorithm for obstacle-crossing motions of lower limb exoskeleton robot |
|
- (1)
- Normal motions: the lower limb exoskeleton robot maintains a fixed step length and leg lift height in its motion trajectory.
- (2)
- Transition motions: the gait distance is adjusted based on the distance information between the detected lower limb exoskeleton robot and obstacles, so that the lower limb exoskeleton robot moves to the appropriate position, ensuring the safety of obstacle-crossing motions.
- (3)
- Obstacles-crossing motions: the lower limb exoskeleton robot detects obstacle feature information through a depth camera, adjusts the distance through transition motions, selects appropriate crossing motion trajectory, and safely crosses obstacles.
3. Experimental Section
3.1. Experimental Design for Different Obstacle Distances
- (1)
- To ensure that the obstacle feature information detected by the depth camera was the same, the lower limb exoskeleton robot was set to cross the same obstacles.
- (2)
- The motion step length of the lower limb exoskeleton robot was 0.28 m, and the initial distance between the obstacle and the lower limb exoskeleton robot must have been greater than two step lengths. In the experiment, we set the step time to 1.6 s.
- (3)
- Due to measurement errors between obstacles and robots, the measured distance was rounded to two decimal places. The distance between the obstacle and the robot was set to 1.26 m, 1.14 m, and 1.21 m, respectively.
- (4)
- To ensure that there was no sudden change in position during movements, the starting state of each gait trajectory was consistent with the ending state of the previous trajectory. In two types of offline trajectory library generations, this situation was considered.
3.2. Experimental Design of Different Obstacle Feature Information
4. Results and Discussion
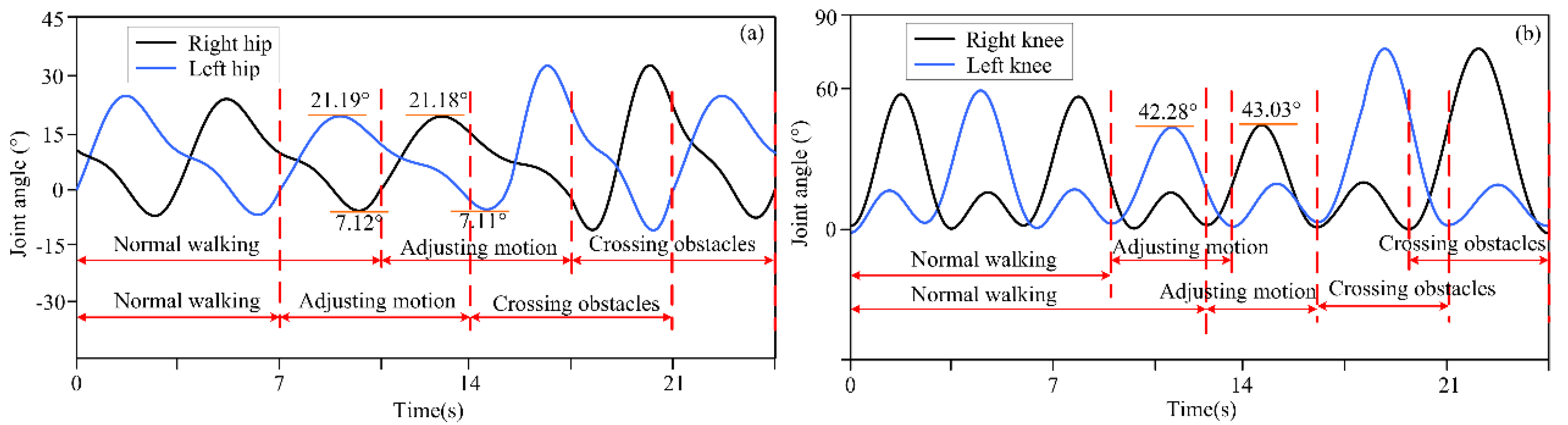
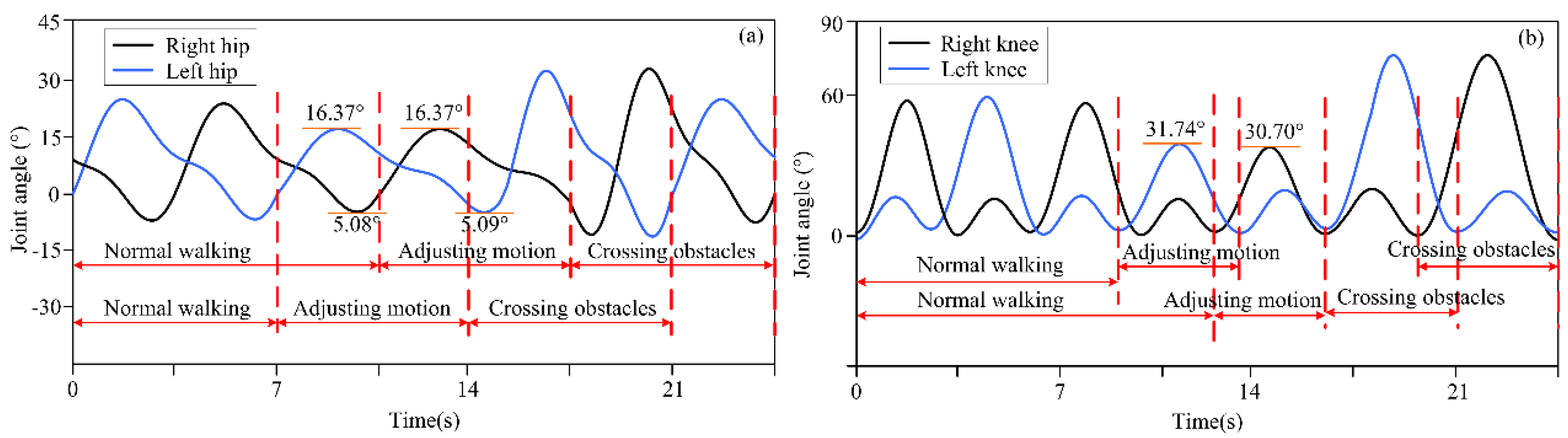
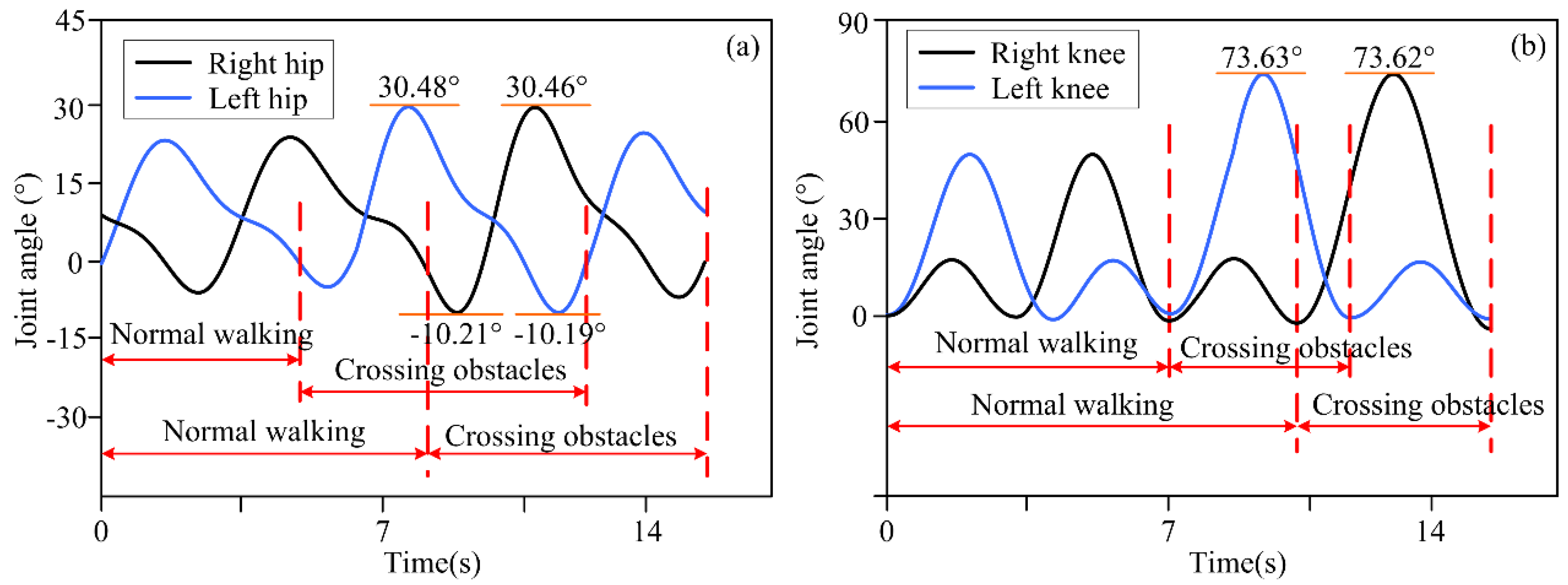
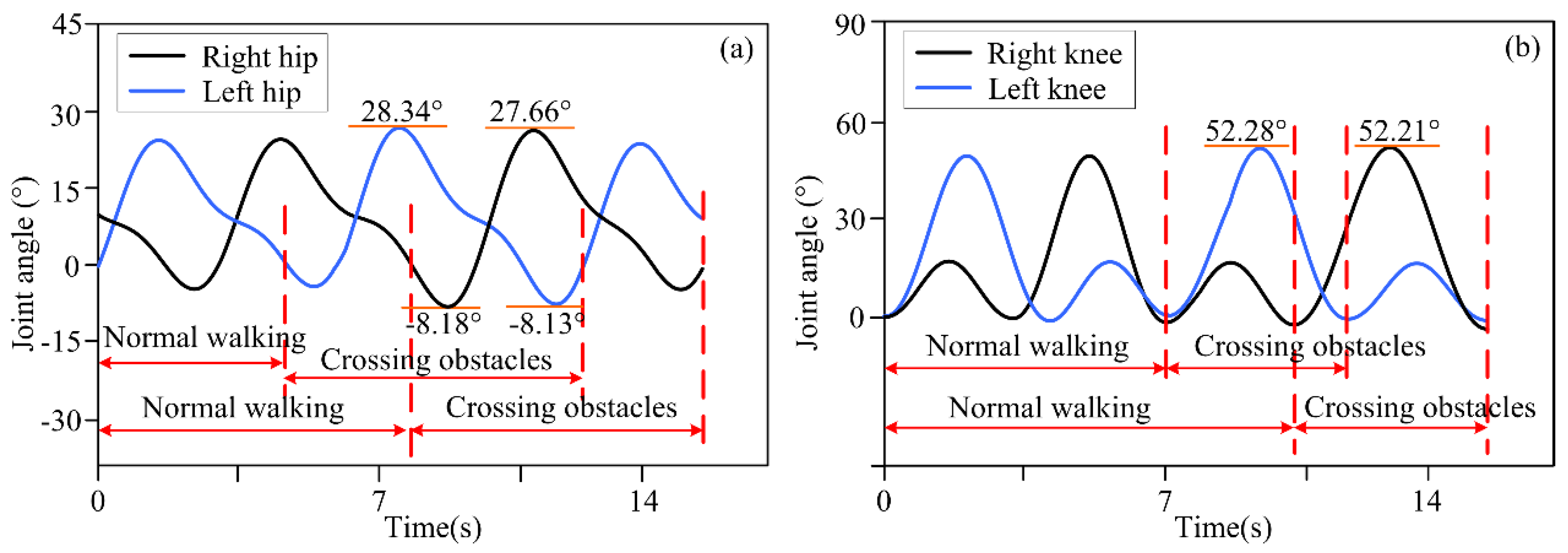
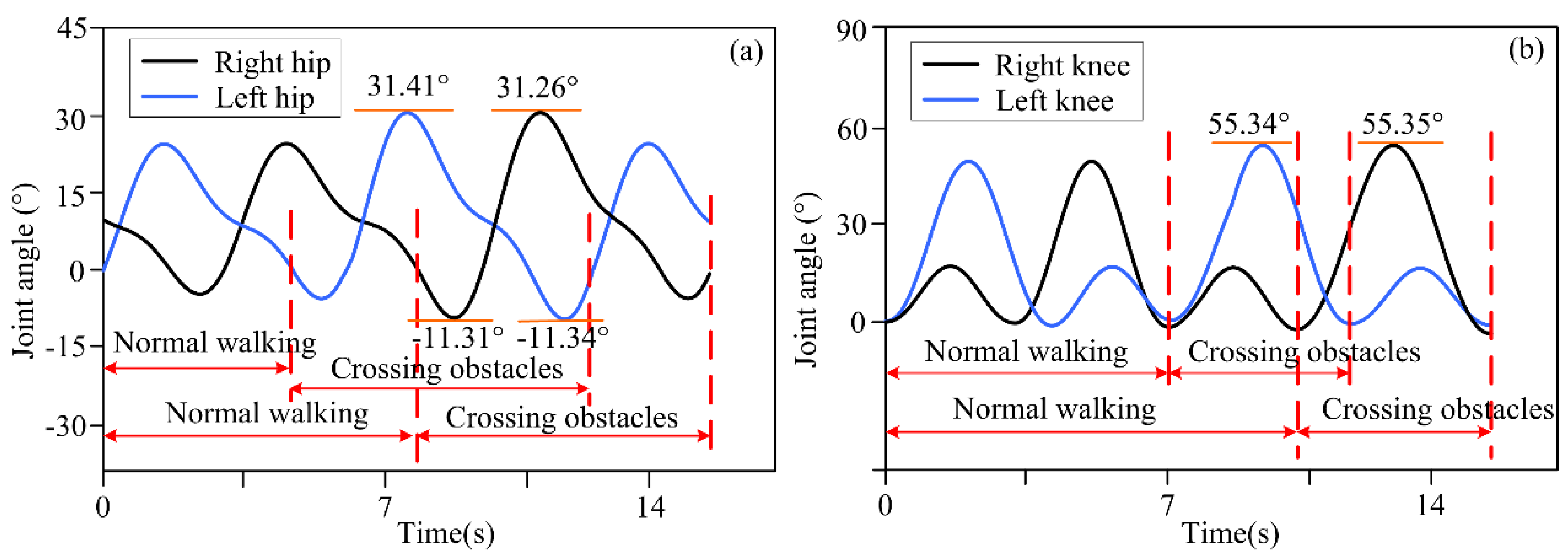
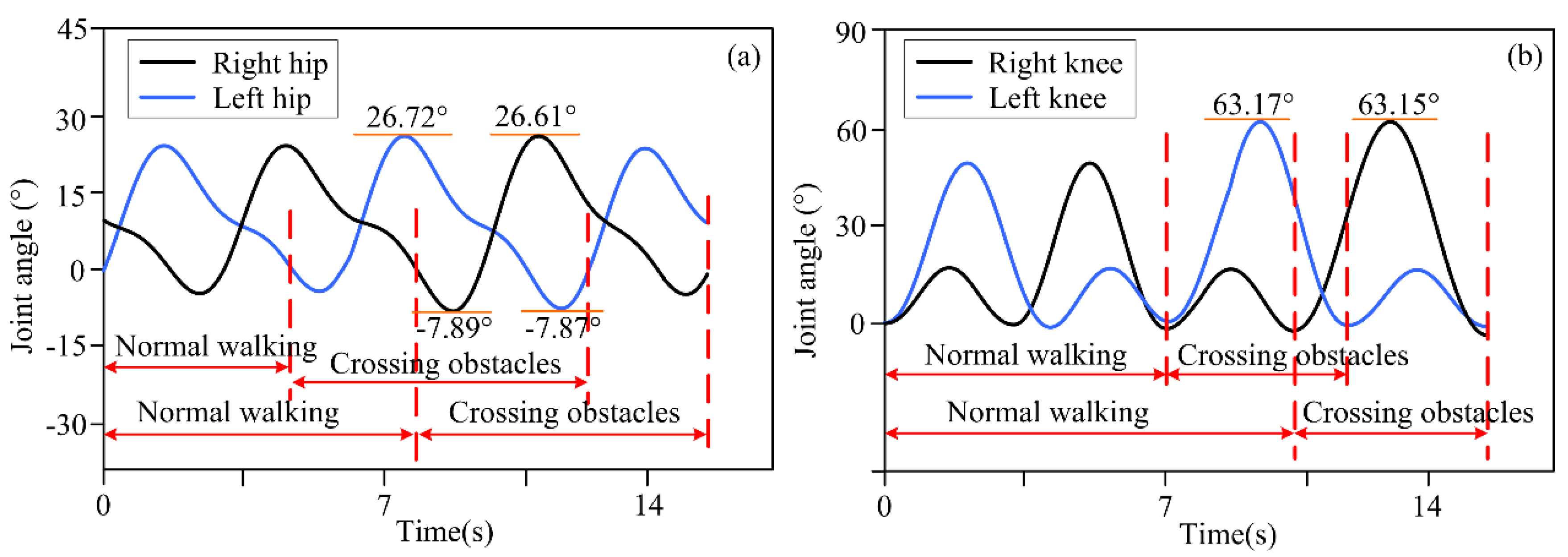
4.1. Experimental Results for Motion Decision-Making for Different Obstacle Distances
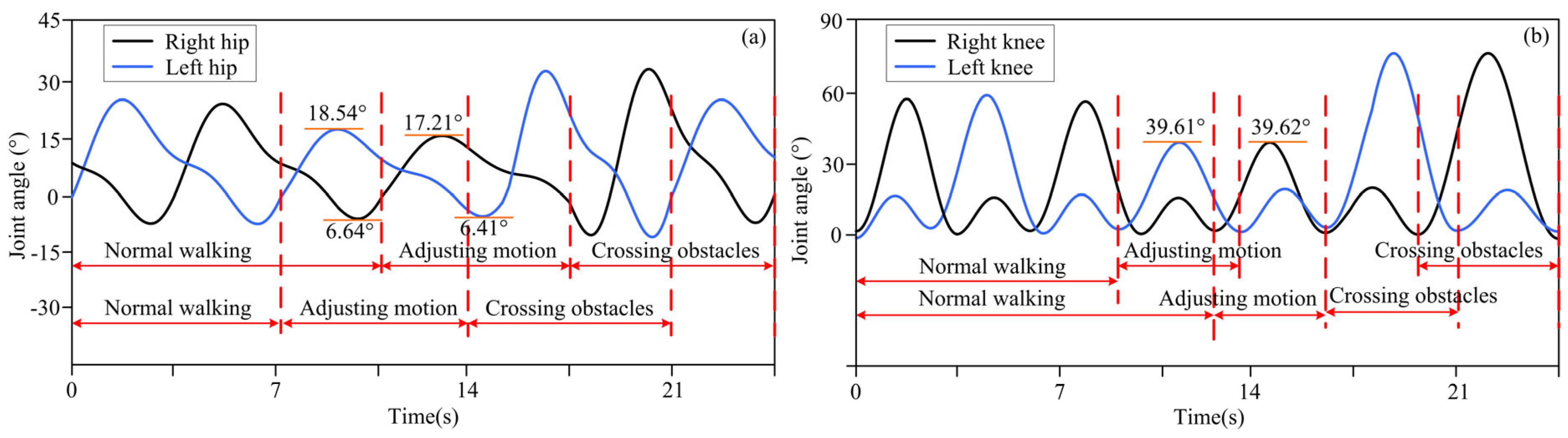
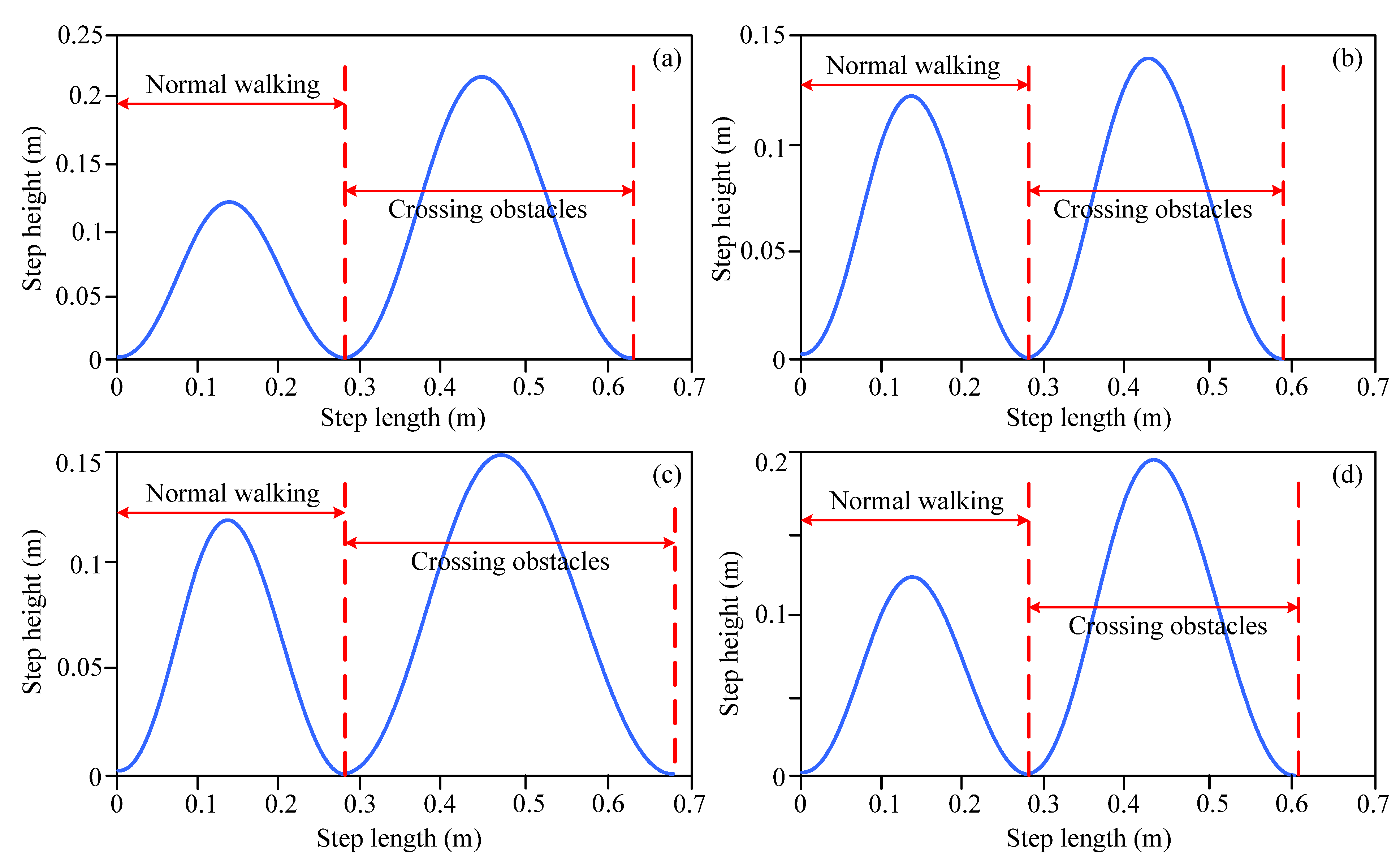
4.2. Obstacle-Crossing Experiment with Different Obstacle Feature Information
4.3. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gallivan, J.P.; Chapman, C.S.; Wolpert, D.M.; Flanagan, J.R. Decision-Making in Sensorimotor Control. Nat. Rev. Neurosci. 2018, 19, 519–534. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Xu, Z.; Occhipinti, E.; Yi, W.; Xu, M.; Kumar, S.; Virk, G.S.; Gao, S.; Occhipinti, L.G. From Brain to Movement: Wearables-Based Motion Intention Prediction across the Human Nervous System. Nano Energy 2023, 115, 108712. [Google Scholar] [CrossRef]
- Plaza, A.; Hernandez, M.; Puyuelo, G.; Garces, E.; Garcia, E. Lower-Limb Medical and Rehabilitation Exoskeletons: A Review of the Current Designs. IEEE Rev. Biomed. Eng. 2023, 16, 278–291. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Cao, G.Z.; Li, L.L.; Diao, D.F. Interactive Control of Lower Limb Exoskeleton Robots: A Review. IEEE Sens. J. 2024, 24, 5759–5784. [Google Scholar] [CrossRef]
- Asanza, V.; Peláez, E.; Loayza, F.; Lorente-Leyva, L.L.; Peluffo-Ordóñez, D.H. Identification of Lower-Limb Motor Tasks via Brain–Computer Interfaces: A Topical Overview. Sensors 2022, 22, 2028. [Google Scholar] [CrossRef]
- Ferrero, L.; Soriano-Segura, P.; Navarro, J.; Jones, O.; Ortiz, M.; Iáñez, E.; Azorín, J.M.; Contreras-Vidal, J.L. Brain–Machine Interface Based on Deep Learning to Control Asynchronously a Lower-Limb Robotic Exoskeleton: A Case-of-Study. J. Neuroeng. Rehabil. 2024, 21, 48. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.J.; Sie, T.Y. Integration of Virtual Reality-Enhanced Motor Imagery and Brain-Computer Interface for a Lower-Limb Rehabilitation Exoskeleton Robot. Actuators 2024, 13, 244. [Google Scholar] [CrossRef]
- Ortiz, M.; Iáñez, E.; Contreras-Vidal, J.L.; Azorín, J.M. Analysis of the EEG Rhythms Based on the Empirical Mode Decomposition During Motor Imagery When Using a Lower-Limb Exoskeleton. A Case Study. Front. Neurorobot. 2020, 14, 48. [Google Scholar] [CrossRef]
- Huang, X.; Xu, Y.; Hua, J.; Yi, W.; Yin, H.; Hu, R.; Wang, S. A Review on Signal Processing Approaches to Reduce Calibration Time in EEG-Based Brain–Computer Interface. Front. Neurosci. 2021, 15, 733546. [Google Scholar] [CrossRef]
- Gu, X.; Cao, Z.; Jolfaei, A.; Xu, P.; Wu, D.; Jung, T.P.; Lin, C.T. EEG-Based Brain-Computer Interfaces (BCIs): A Survey of Recent Studies on Signal Sensing Technologies and Computational Intelligence Approaches and Their Applications. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 1645–1666. [Google Scholar] [CrossRef]
- Mridha, M.F.; Das, S.C.; Kabir, M.M.; Lima, A.A.; Islam, M.R.; Watanobe, Y. Brain-Computer Interface: Advancement and Challenges. Sensors 2021, 21, 5746. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Pei, Z.; Fan, Y.; Qiu, S.; Tang, Z. Review of Vision-Based Environmental Perception for Lower-Limb Exoskeleton Robots. Biomimetics 2024, 9, 254. [Google Scholar] [CrossRef] [PubMed]
- Khalili, M.; Ozgoli, S. Environment Recognition for Controlling Lower-Limb Exoskeletons, by Computer Vision and Deep Learning Algorithm. In Proceedings of the 2022 8th International Conference on Control, Instrumentation and Automation (ICCIA 2022), Tehran, Iran, 2–3 March 2022; pp. 1–5. [Google Scholar]
- Laschowski, B.; McNally, W.; Wong, A.; McPhee, J. Computer Vision and Deep Learning for Environment-Adaptive Control of Robotic Lower-Limb Exoskeletons. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Guadalajara, Mexico, 1–5 November 2021; pp. 4631–4635. [Google Scholar]
- Ren, B.; Luo, X.; Wang, Y.; Chen, J. A Gait Trajectory Control Scheme through Successive Approximation Based on Radial Basis Function Neural Networks for the Lower Limb Exoskeleton Robot. J. Comput. Inf. Sci. Eng. 2020, 20, 31008. [Google Scholar] [CrossRef]
- Bao, W.; Villarreal, D.; Chiao, J.C. Vision-Based Autonomous Walking in a Lower-Limb Powered Exoskeleton. In Proceedings of the IEEE 20th International Conference on Bioinformatics and Bioengineering (BIBE 2020), Cincinnati, OH, USA, 26–28 October 2020; pp. 830–834. [Google Scholar]
- Liu, D.X.; Xu, J.; Chen, C.; Long, X.; Tao, D.; Wu, X. Vision-Assisted Autonomous Lower-Limb Exoskeleton Robot. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3759–3770. [Google Scholar] [CrossRef]
- Hua, Y.; Zhang, H.; Li, Y.; Zhao, J.; Zhu, Y. Vision Assisted Control of Lower Extremity Exoskeleton for Obstacle Avoidance With Dynamic Constraint Based Piecewise Nonlinear MPC. IEEE Robot. Autom. Lett. 2022, 7, 12267–12274. [Google Scholar] [CrossRef]
- Sharifi, M.; Mehr, J.K.; Mushahwar, V.K.; Tavakoli, M. Autonomous Locomotion Trajectory Shaping and Nonlinear Control for Lower Limb Exoskeletons. IEEE/ASME Trans. Mechatron. 2022, 27, 645–655. [Google Scholar] [CrossRef]
- Karacan, K.; Meyer, J.T.; Bozma, H.I.; Gassert, R.; Samur, E. An Environment Recognition and Parameterization System for Shared-Control of a Powered Lower-Limb Exoskeleton. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 623–628. [Google Scholar]
- Luo, J.; Zhou, X.; Zeng, C.; Jiang, Y.; Qi, W.; Xiang, K.; Pang, M.; Tang, B. Robotics Perception and Control: Key Technologies and Applications. Micromachines 2024, 15, 531. [Google Scholar] [CrossRef]
- Mohamad, H.; Ozgoli, S. Online Gait Generator for Lower Limb Exoskeleton Robots: Suitable for Level Ground, Slopes, Stairs, and Obstacle Avoidance. Robot. Auton. Syst. 2023, 160, 104319. [Google Scholar] [CrossRef]
- Ramanathan, M.; Luo, L.; Er, J.K.; Foo, M.J.; Chiam, C.H.; Li, L.; Yau, W.Y.; Ang, W.T. Visual Environment Perception for Obstacle Detection and Crossing of Lower-Limb Exoskeletons. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems; IEEE, Kyoto, Japan, 23–27 October 2022; pp. 12267–12274. [Google Scholar]
- Trombin, E.; Tortora, S.; Menegatti, E.; Tonin, L. Environment-Adaptive Gait Planning for Obstacle Avoidance in Lower-Limb Robotic Exoskeletons. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 13640–13647. [Google Scholar]
- Wang, J.; Mattamala, M.; Kassab, C.; Zhang, L.; Fallon, M. Exosense: A Vision-Centric Scene Understanding System For Safe Exoskeleton Navigation. IEEE Robot. Autom. Lett. 2025, 10, 3510–3517. [Google Scholar] [CrossRef]
- Wu, X.; Li, J.; Liu, L.; Tao, D. The Visual Footsteps Planning System for Exoskeleton Robots Under Complex Terrain. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 5149–5160. [Google Scholar] [CrossRef]
- Tricomi, E.; Mossini, M.; Missiroli, F.; Lotti, N.; Zhang, X.; Xiloyannis, M.; Roveda, L.; Masia, L. Environment-Based Assistance Modulation for a Hip Exosuit via Computer Vision. IEEE Robot. Autom. Lett. 2023, 8, 2550–2557. [Google Scholar] [CrossRef]
- Kao, Y.H.; Chen, C.K.; Chen, C.C.; Lan, C.Y. Object Pose Estimation and Feature Extraction Based on PVNet. IEEE Access 2022, 10, 122387–122398. [Google Scholar] [CrossRef]
- Li, L.L.; Zhang, Y.P.; Cao, G.Z.; Li, W.Z. Human-in-the-Loop Trajectory Optimization Based on SEMG Biofeedback for Lower-Limb Exoskeleton. Sensors 2024, 24, 5684. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chen, X.; Dong, C.; Yu, Z.; Huang, Q. Online Running Pattern Generation for Humanoid Robot with Direct Collocation of Reference-Tracking Dynamics. IEEE/ASME Trans. Mechatron. 2024, 29, 2091–2102. [Google Scholar] [CrossRef]
- Bordalba, R.; Schoels, T.; Ros, L.; Porta, J.M.; Diehl, M. Direct Collocation Methods for Trajectory Optimization in Constrained Robotic Systems. IEEE Trans. Robot. 2023, 39, 183–202. [Google Scholar] [CrossRef]
| Parameter Symbols | Parameter Meaning | Values |
|---|---|---|
| Backward inclination angle of the torso | ||
| Forward inclination angle of the torso | ||
| Protective margin for excessive extension of the knee joint | ||
| Step length when crossing obstacles | Calculated from the length of obstacles | |
| Step height when crossing obstacles | Calculated from the height of obstacles | |
| Ground clearance constraint for swinging legs | ||
| Safety margin for crossing obstacles | Customized according to experimental constraints | |
| Step time | Set up from the experiment | |
| One step length of normal trajectory | From the normal trajectory measurement of the experiment | |
| Step height of normal trajectory | From the normal trajectory measurement of the experiment | |
| Threshold for trajectory selection in motion decision-making algorithm for obstacle crossing | Customized from experimental constraints | |
| Actual horizontal distance between the support foot and the obstacle | Obtained from depth camera detection | |
| Horizontal distance between the support foot and the obstacle | Customized from experimental constraints | |
| Horizontal distance between the swinging foot and the obstacle after landing | Customized from experimental constraints | |
| Horizontal distance extending from the toe to the end of the swinging leg | Customized from experimental constraints |
| Real Images | Size | Length (m) | Width (m) | Height (m) |
|---|---|---|---|---|
 | Actual size | 0.125 | 0.019 | 0.08 |
| Measure size | 0.1284 | 0.19702 | 0.0921 | |
 | Actual size | 0.11 | 0.20 | 0.03 |
| Measure size | 0.1307 | 0.2063 | 0.0386 | |
 | Actual size | 0.185 | 0.26 | 0.03 |
| Measure size | 0.1901 | 0.2704 | 0.4011 | |
 | Actual size | 0.09 | 0.165 | 0.053 |
| Measure size | 0.1012 | 0.1723 | 0.6029 |
| Distances | Joint Angles (°) | |||
|---|---|---|---|---|
| Left Hip | Left Knee | Right Hip | Right Knee | |
| Distance 1: 1.26 m | 21.19 | 42.28 | 21.18 | 43.03 |
| 7.12 | 7.11 | |||
| Distance 2: 1.14 m | 16.37 | 31.74 | 16.37 | 30.70 |
| 5.08 | 5.09 | |||
| Distance 3: 1.21 m | 18.54 | 39.61 | 17.21 | 39.62 |
| 6.64 | 6.41 | |||
| Objects | Specific Values | |
|---|---|---|
| Step Height (m) | Step Length (m) | |
| Obstacle 1 | 0.22 | 0.34 |
| Obstacle 2 | 0.14 | 0.31 |
| Obstacle 3 | 0.15 | 0.40 |
| Obstacle 4 | 0.19 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Cao, G.; Wu, J.; Gao, B.; Xia, L.; Lu, C.; Wang, H. Obstacle Feature Information-Based Motion Decision-Making Method for Obstacle-Crossing Motions in Lower Limb Exoskeleton Robots. Biomimetics 2025, 10, 311. https://doi.org/10.3390/biomimetics10050311
Zhang Y, Cao G, Wu J, Gao B, Xia L, Lu C, Wang H. Obstacle Feature Information-Based Motion Decision-Making Method for Obstacle-Crossing Motions in Lower Limb Exoskeleton Robots. Biomimetics. 2025; 10(5):311. https://doi.org/10.3390/biomimetics10050311
Chicago/Turabian StyleZhang, Yuepeng, Guangzhong Cao, Jun Wu, Bo Gao, Linzhong Xia, Chen Lu, and Hui Wang. 2025. "Obstacle Feature Information-Based Motion Decision-Making Method for Obstacle-Crossing Motions in Lower Limb Exoskeleton Robots" Biomimetics 10, no. 5: 311. https://doi.org/10.3390/biomimetics10050311
APA StyleZhang, Y., Cao, G., Wu, J., Gao, B., Xia, L., Lu, C., & Wang, H. (2025). Obstacle Feature Information-Based Motion Decision-Making Method for Obstacle-Crossing Motions in Lower Limb Exoskeleton Robots. Biomimetics, 10(5), 311. https://doi.org/10.3390/biomimetics10050311








