Materials and Structures Inspired by Human Heel Pads for Advanced Biomechanical Function
Abstract
1. Introduction
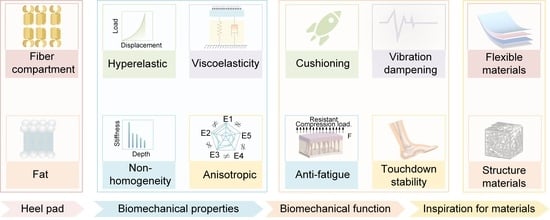
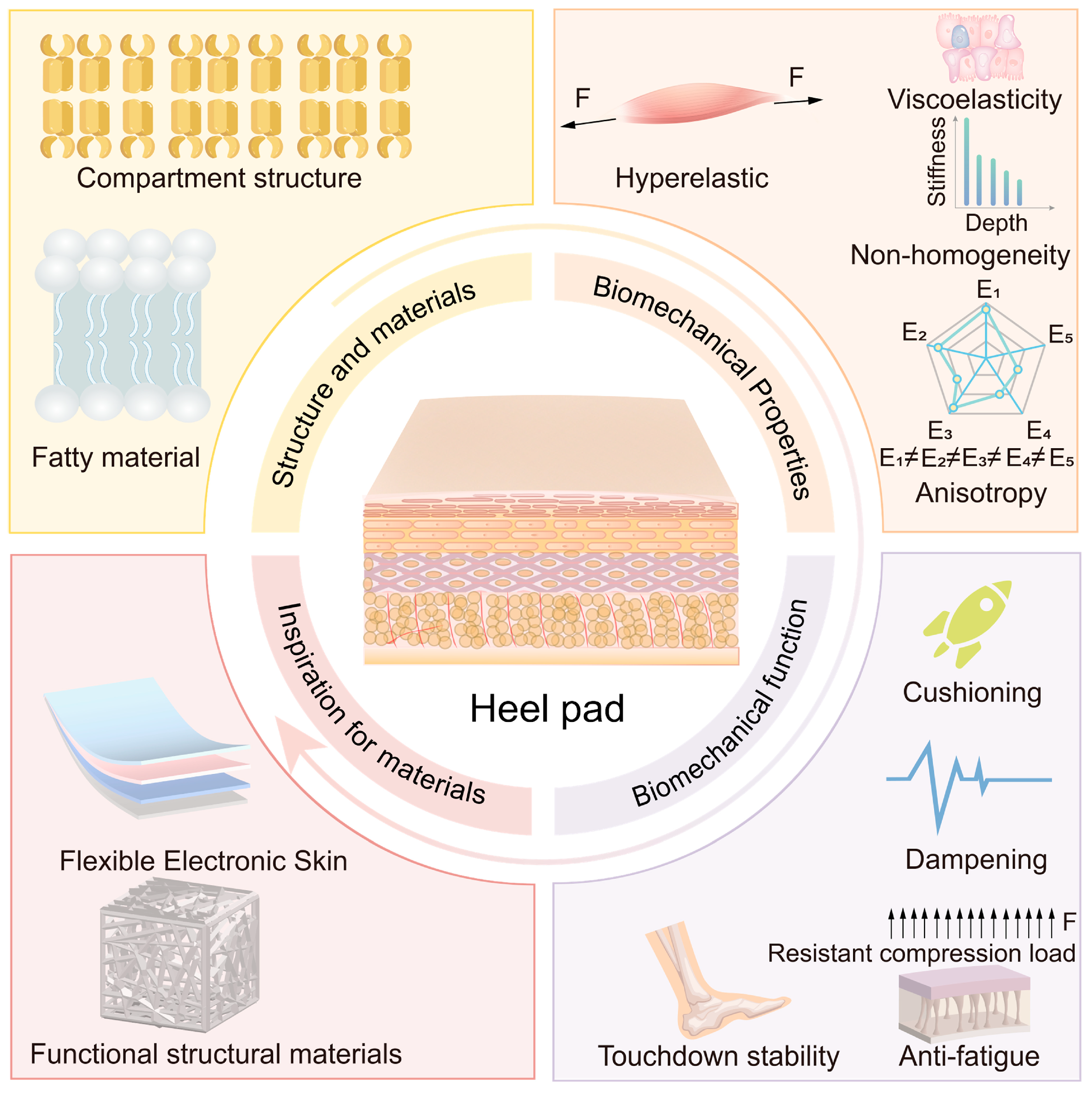
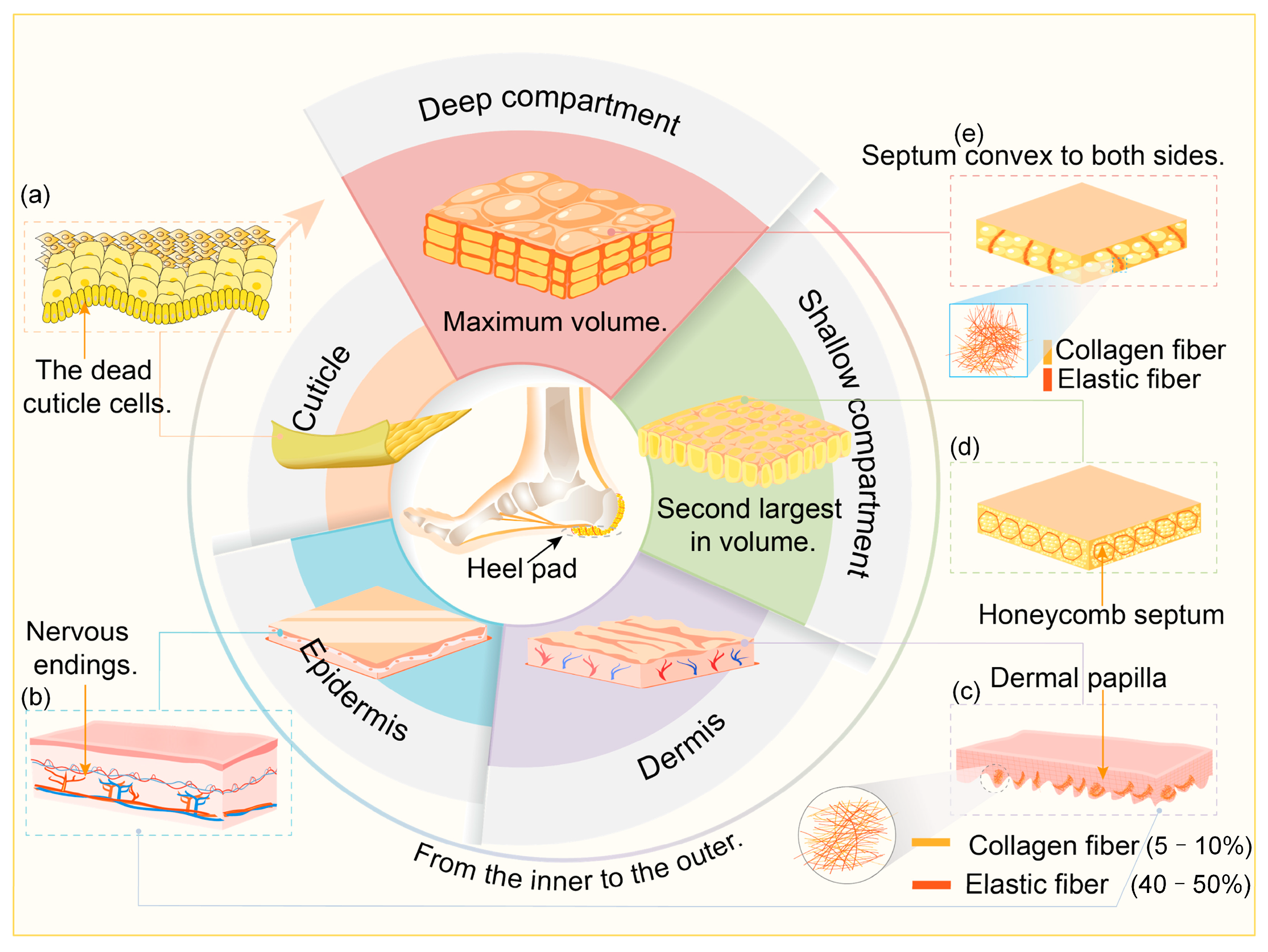
2. Structure and Materials of Heel Pad
Structure of the Heel Pad
3. Biomechanical Properties of Heel Pad
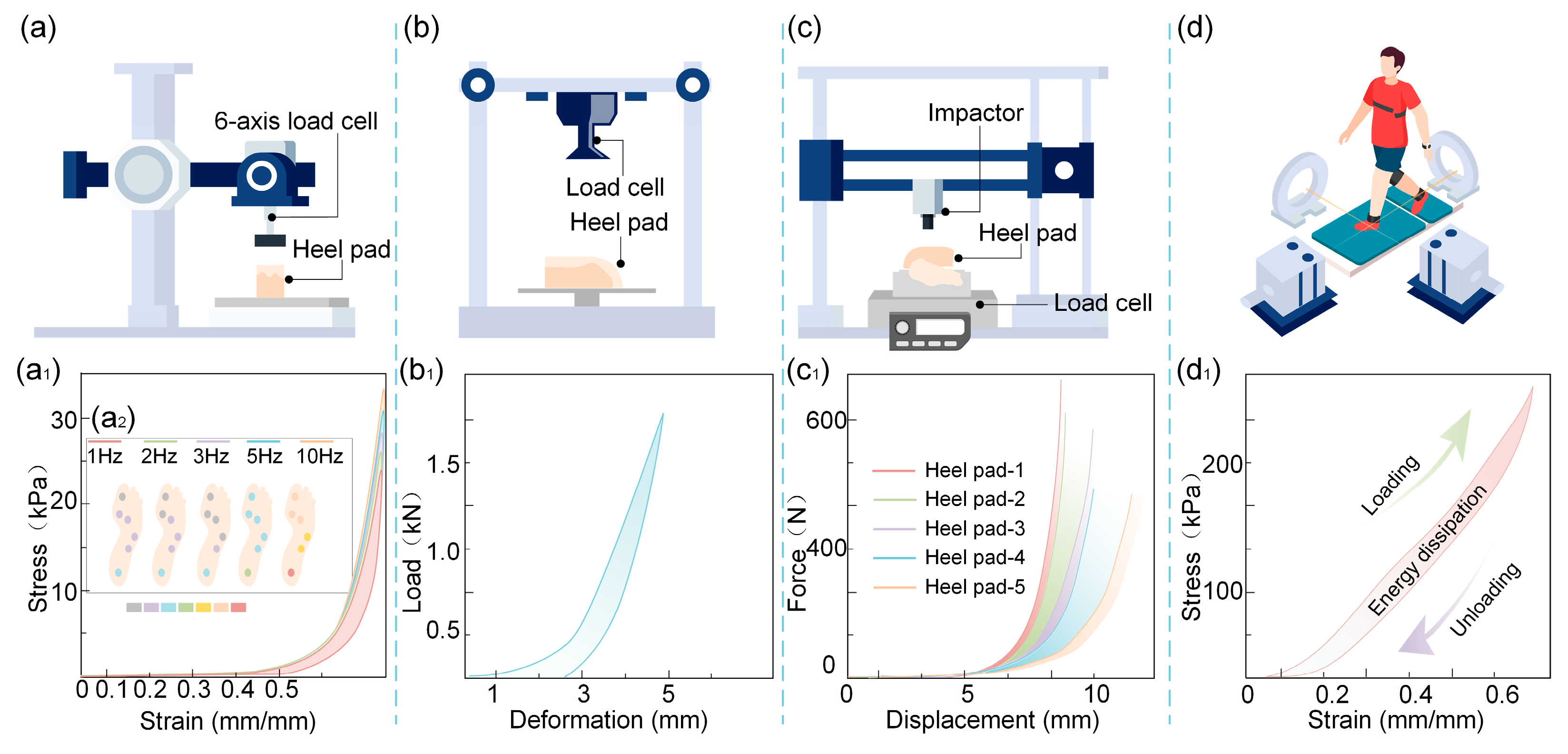
3.1. Nonlinear Stiffness (Hyperelasticity)
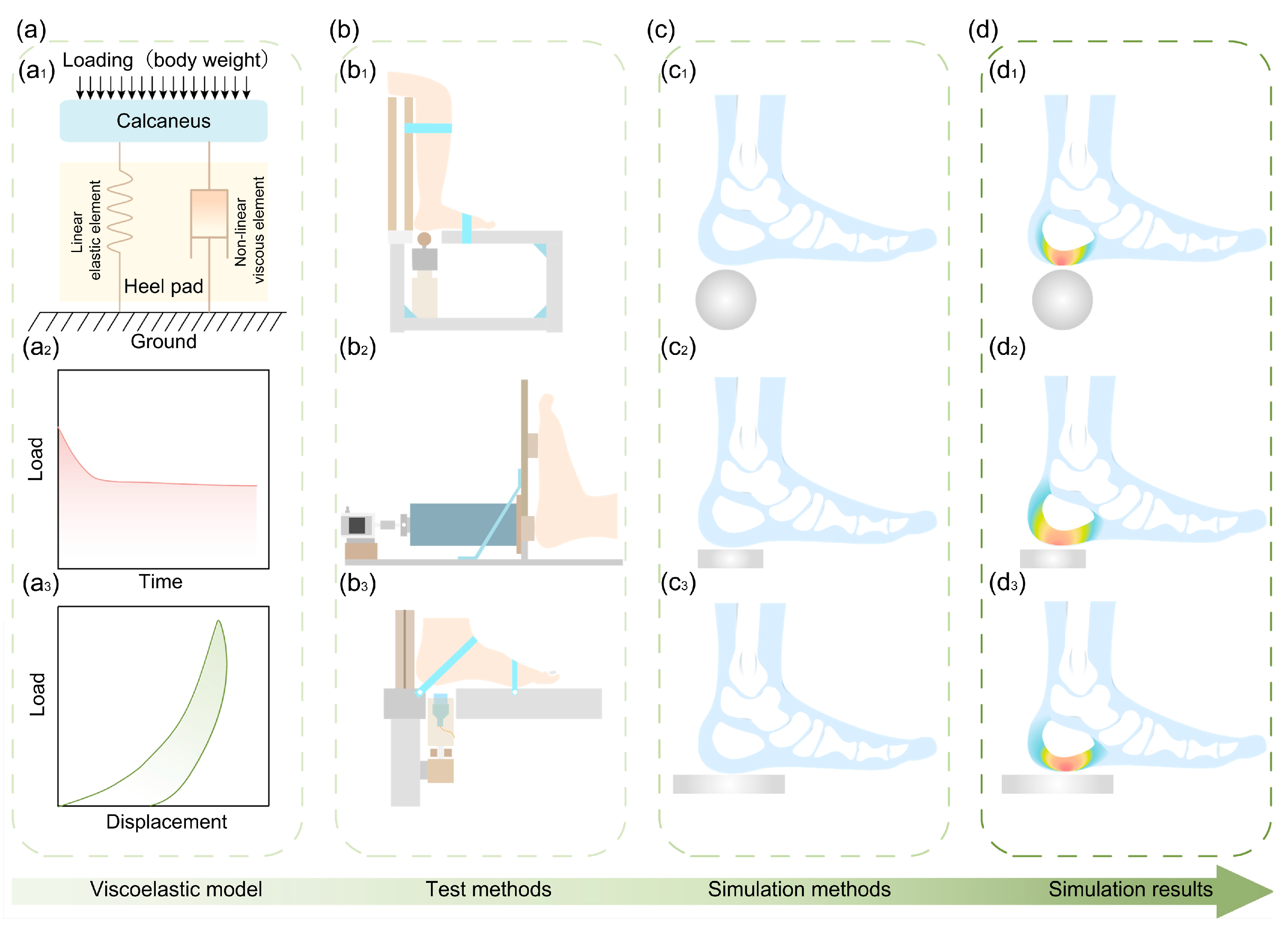
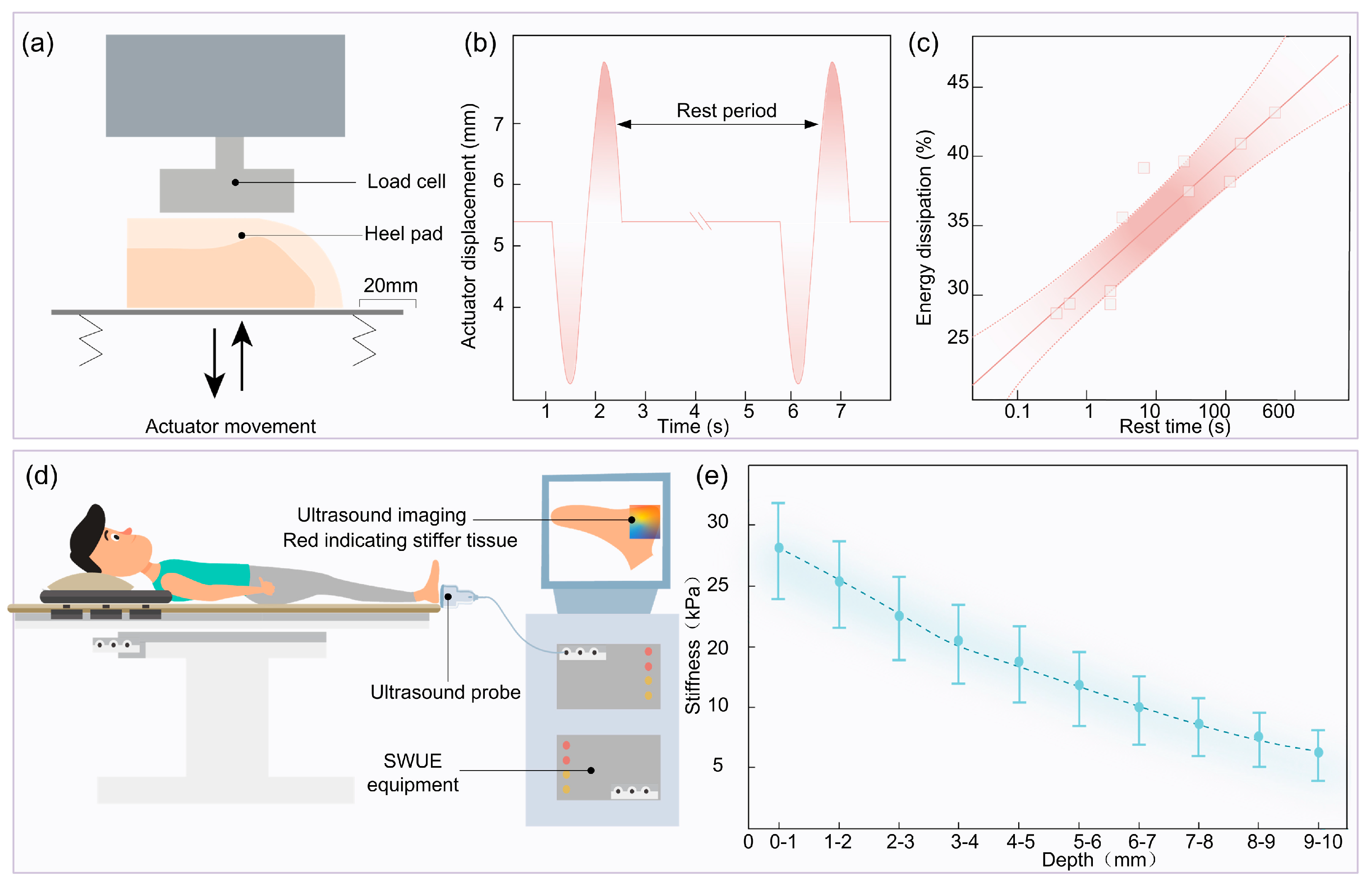
3.2. Viscoelasticity
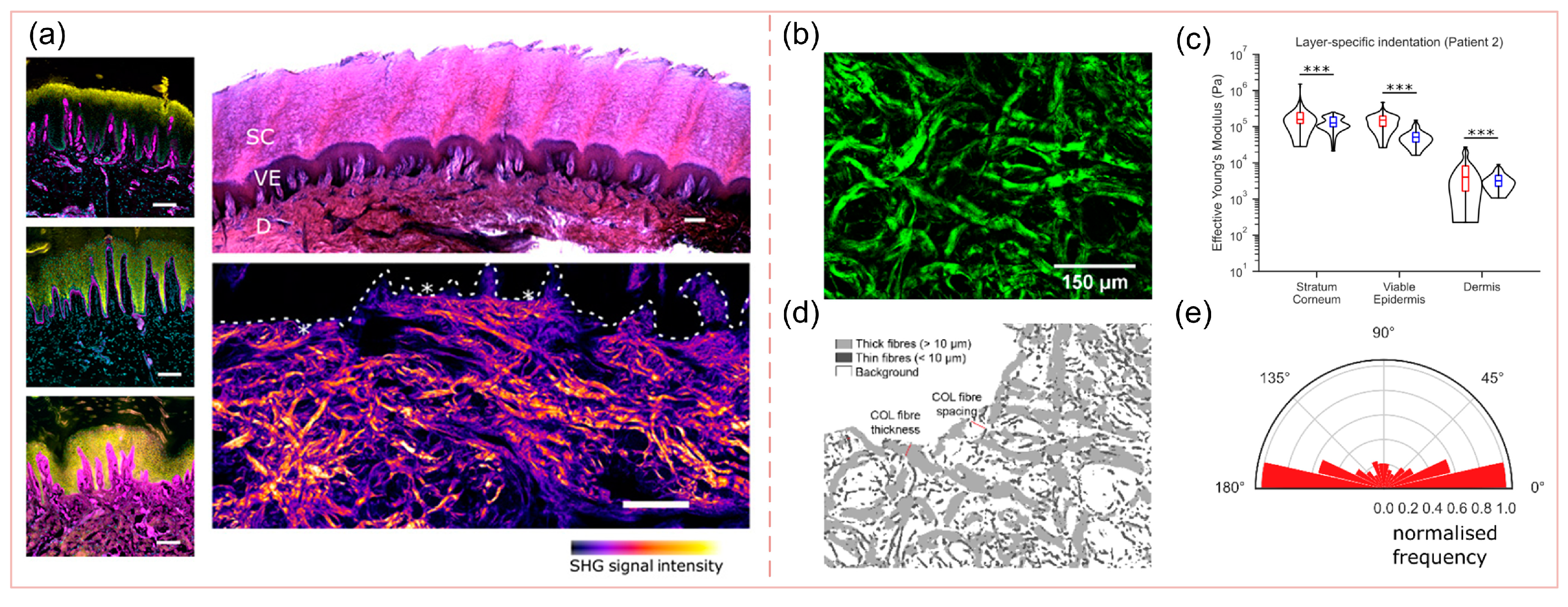
3.3. Non-Homogeneity
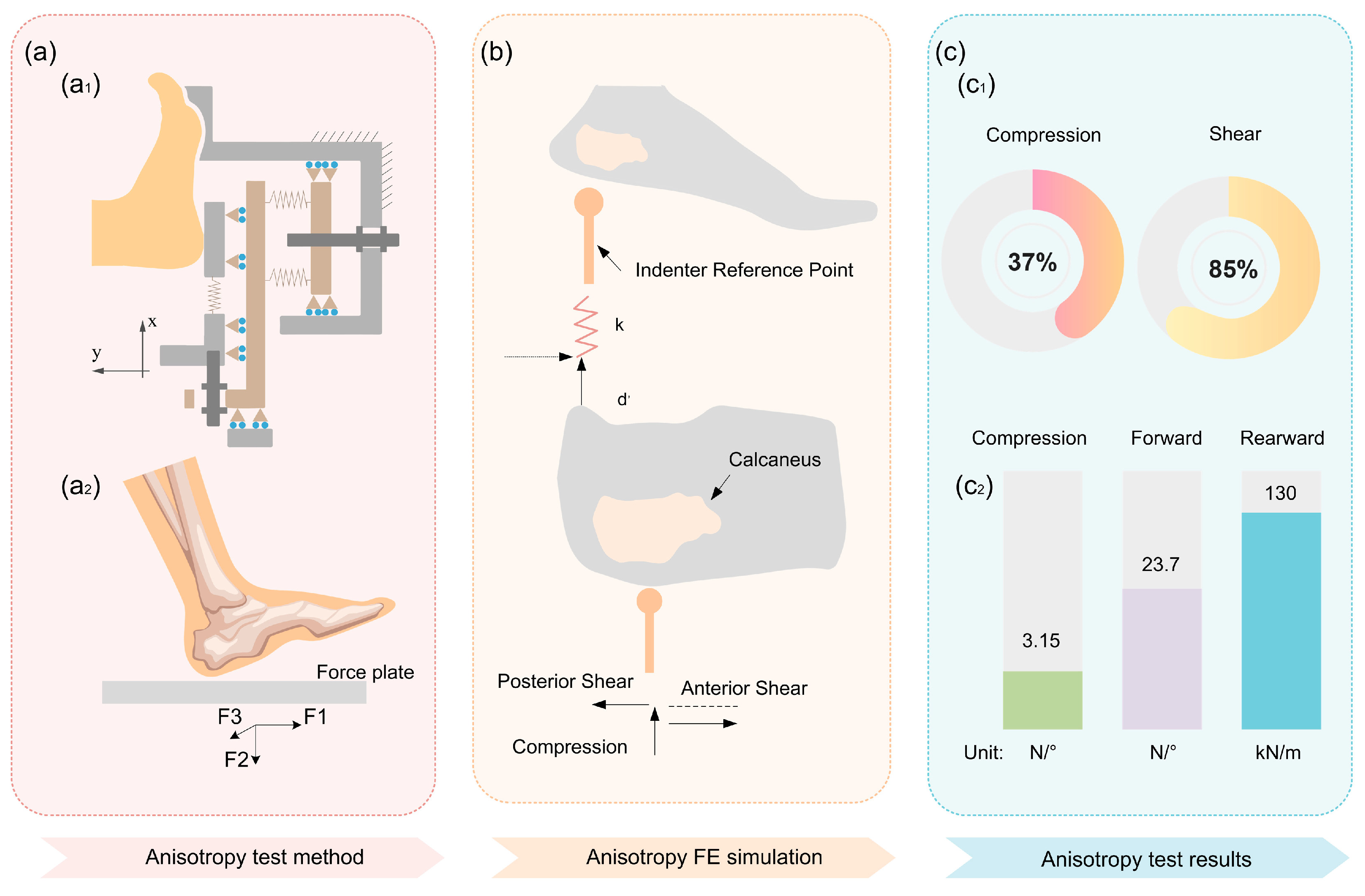
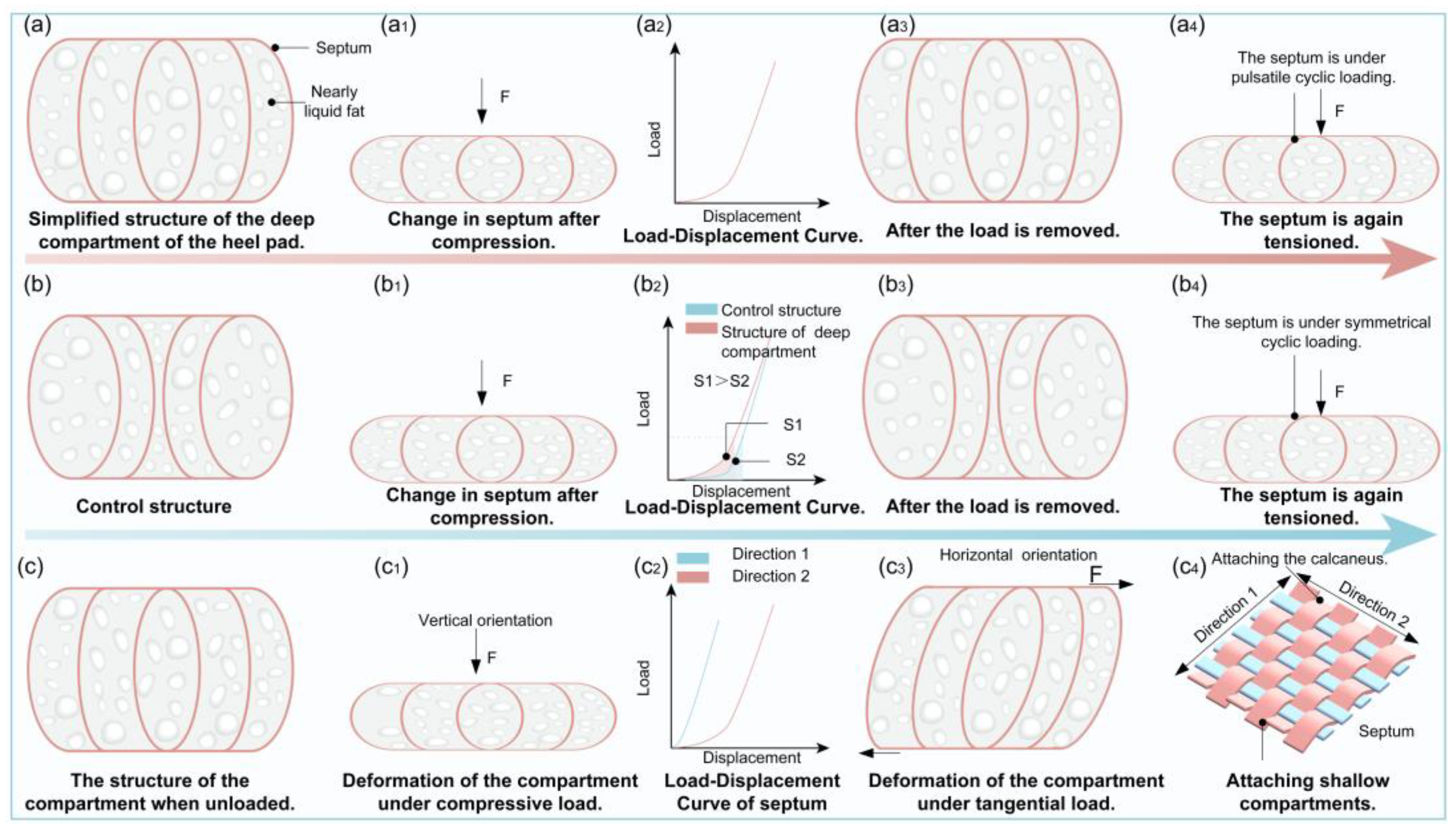
3.4. Mechanical Anisotropy
4. Biomechanical Function of Heel Pad
4.1. Cushioning
4.2. Vibration Damping
4.3. Anti-Fatigue
4.4. Touchdown Stability
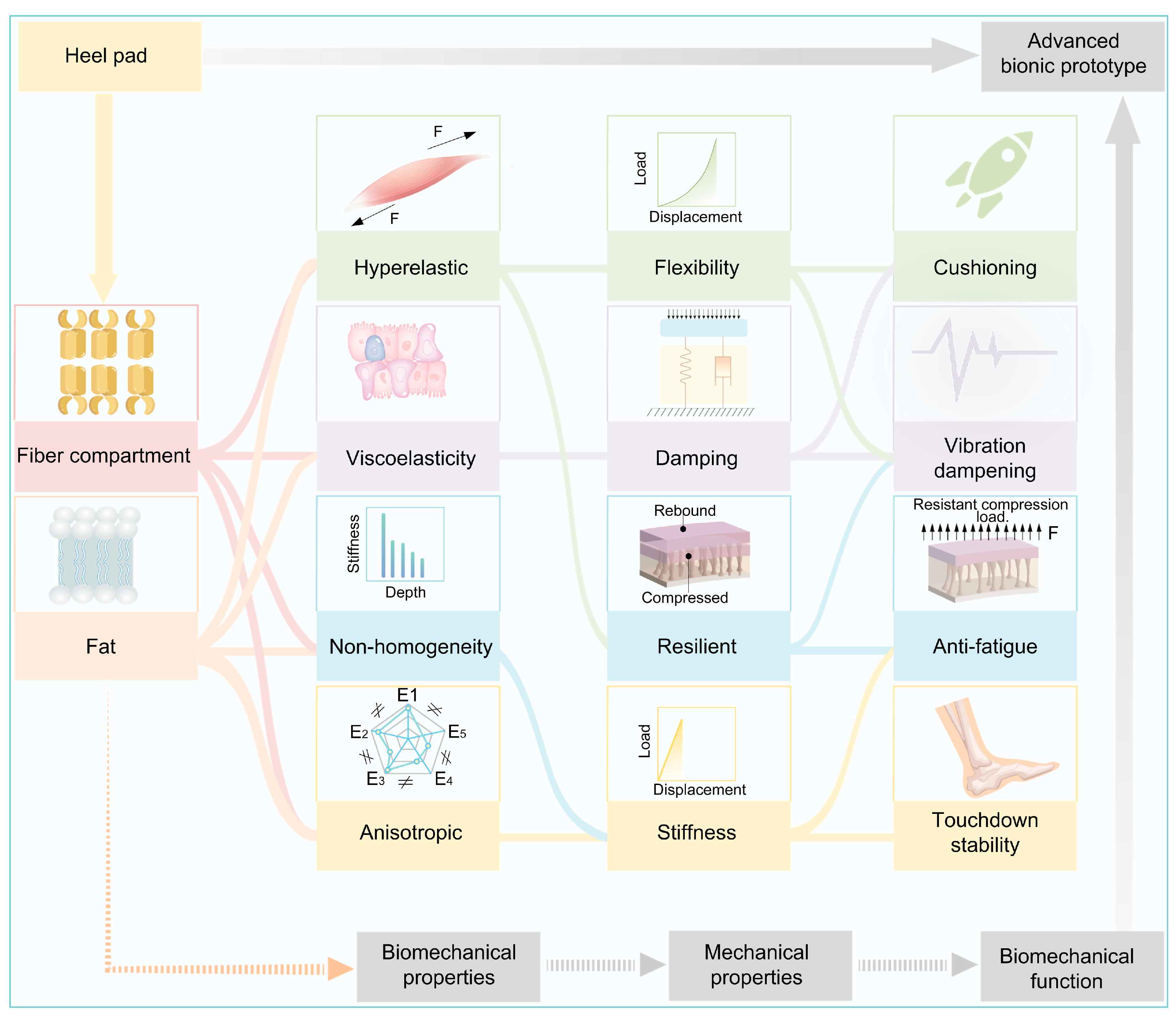
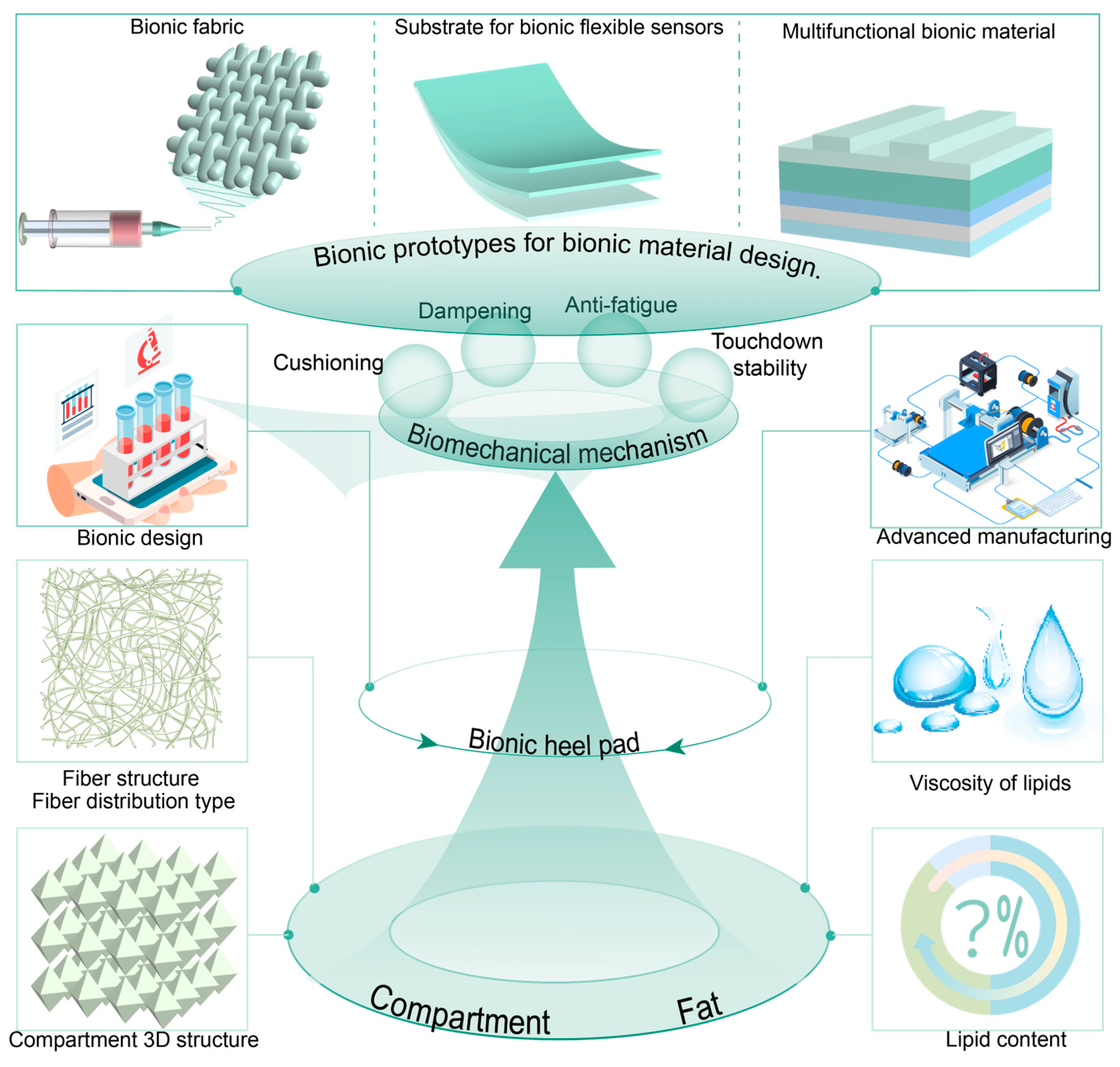
5. Relationship Between Heel Pad Structure and Materials, Biomechanical Properties, and Their Biomechanical Functions
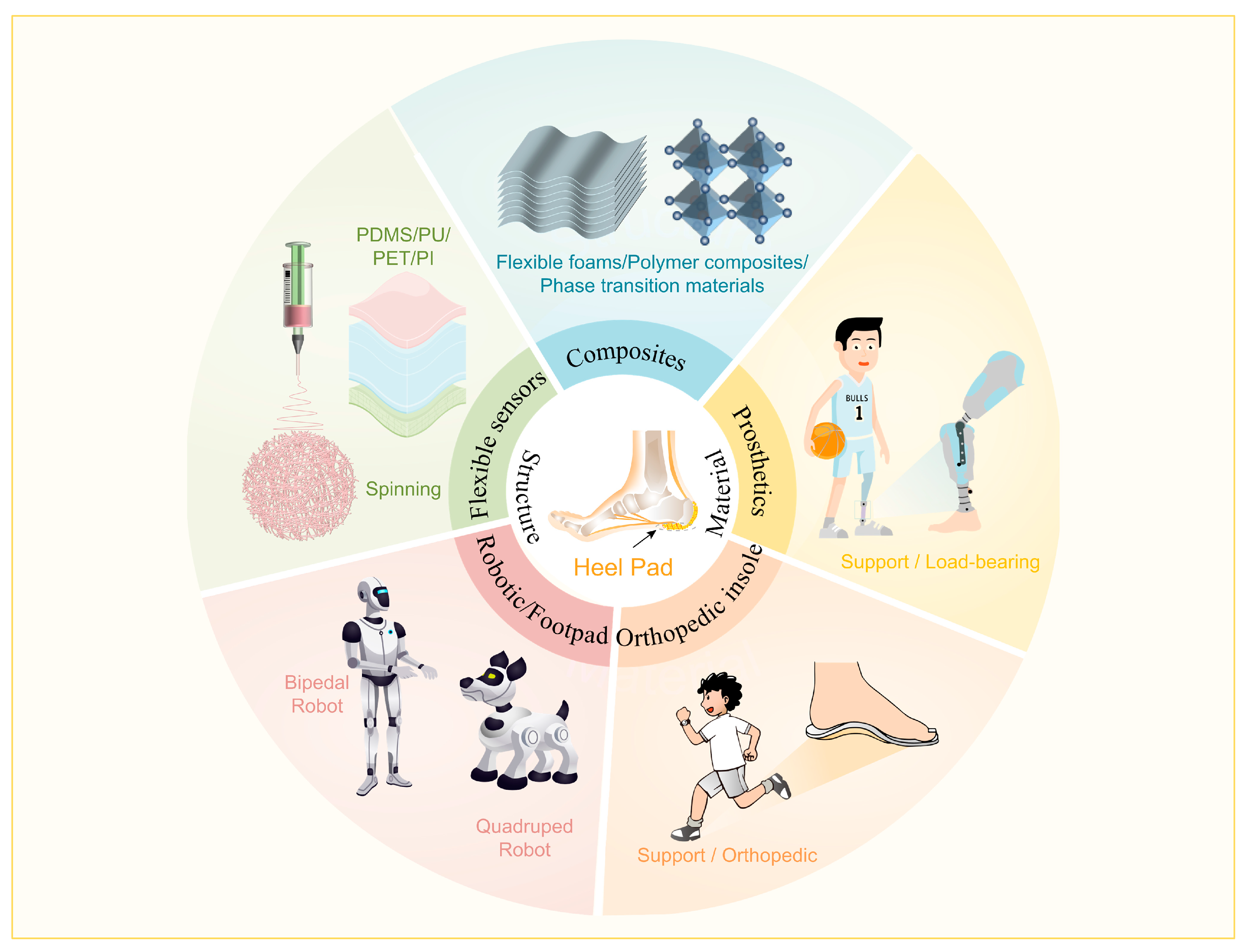
6. Perspective of Advanced Materials Based on Heel Pad as Bionic Prototype
7. Conclusions and Prospects for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lieberman, D.E.; Venkadesan, M.; Werbel, W.A.; Daoud, A.I.; Dandrea, S.; Davis, I.S.; Mangeni, R.O.; Pitsiladis, Y. Foot strike patterns and collision forces in habitually barefoot versus shod runners. Nature 2010, 463, 531–535. [Google Scholar] [CrossRef] [PubMed]
- Griffin, N.L.; Richmond, B.G. Joint orientation and function in great ape and human proximal pedal phalanges. Am. J. Phys. Anthropol. 2010, 141, 116–123. [Google Scholar] [CrossRef]
- Rolian, C.; Lieberman, D.E.; Hamill, J.; Scott, J.W.; Werbel, W. Walking, running and the evolution of short toes in humans. J. Exp. Biol. 2009, 212, 713–721. [Google Scholar] [CrossRef]
- Alexander, R.M.; Bennett, M.B.; Ker, R.F. Mechanical properties and function of the paw pads of some mammals. J. Zool. 1986, 209, 405–419. [Google Scholar] [CrossRef]
- Bojsen-Moller, F.I.N.N.; Flagstad, K.E. Plantar aponeurosis and internal architecture of the ball of the foot. J. Anat. 1976, 121, 599–611. [Google Scholar] [PubMed]
- Jahss, M.H.; Michelson, J.D.; Desai, P.; Kaye, R.; Kummer, F.; Buschman, W.; Watkins, F.; Reich, S. Investigations into the fat pads of the sole of the foot: Anatomy and Histology. Foot Ankle 1992, 13, 233–242. [Google Scholar] [CrossRef]
- Tietze, A. Concerning the architectural structure of the connective tissue in the human sole. Foot Ankle 1982, 2, 252–259. [Google Scholar] [CrossRef]
- Noe, D.; Voto, S.J.; Hoffmann, M.; Askew, M.J.; Gradisar, I. Papers role of the calcaneal heel pad and polymeric shock absorbers in attenuation of heel strike impact. J. Biomed. Eng. 1993, 15, 23–26. [Google Scholar] [CrossRef]
- Tudor-Locke, C.; Craig, C.L.; Aoyagi, Y.; Bell, R.C.; Croteau, K.A.; De Bourdeaudhuij, I.; Ewald, B.; Gardner, A.W.; Hatano, Y.; Lutes, L.D.; et al. How many steps/day are enough? For older adults and special populations. Int. J. Behav. Nutr. Phys. Act. 2011, 8, 80. [Google Scholar] [CrossRef]
- Wang, C.L.; Cheng, C.K.; Tsuang, Y.H.; Hang, Y.S.; Liu, T.K. Cushioning effect of heel cups. Clin. Biomech. 1994, 9, 297–302. [Google Scholar] [CrossRef]
- Smeathers, J.E. Transient vibrations caused by heel strike. J. Eng. Med. 1989, 203, 181–186. [Google Scholar] [CrossRef] [PubMed]
- Qian, Z.; Zhuang, Z.; Liu, X.; Bai, H.; Ren, L.; Ren, L. Effects of extreme cyclic loading on the cushioning performance of human heel pads under engineering test condition. Front. Bioeng. Biotechnol. 2023, 11, 1229976. [Google Scholar] [CrossRef]
- Ou, H.; Zhan, P.; Kang, L.; Su, J.; Hu, X.; Johnson, S. Region-specific constitutive modeling of the plantar soft tissue. Biomech. Model. Mechanobiol. 2018, 17, 1373–1388. [Google Scholar] [CrossRef]
- Hsu, C.C.; Tsai, W.C.; Wang, C.L.; Pao, S.H.; Shau, Y.W.; Chuan, Y.S. Microchambers and macrochambers in heel pads: Are they functionally different? J. Appl. Physiol. 2007, 102, 2227–2231. [Google Scholar] [CrossRef] [PubMed]
- Blechschmidt, E. The structure of the calcaneal padding. Foot Ankle 1982, 2, 260–283. [Google Scholar] [CrossRef]
- Bojsen-Møller, F. Anatomy of the forefoot, normal and pathologic. Clin. Orthop. Relat. Res. 1979, 142, 10–18. [Google Scholar]
- Bustamante, J.; Panzarino, J.F.; Rupert, T.J.; Loudon, C. Forces to pierce cuticle of tarsi and material properties determined by nanoindentation: The Achilles’ heel of bed bugs. Biol. Open 2017, 6, 1541–1551. [Google Scholar] [CrossRef] [PubMed]
- Robbins, S.; Gouw, G.J.; Mcclaran, J.; Waked, E. Protective sensation of the plantar aspect of the foot. Foot Ankle 1993, 14, 347–352. [Google Scholar] [CrossRef]
- Cichowitz, A.; Pan, W.R.; Ashton, M. The heel: Anatomy, blood supply, and the pathophysiology of pressure ulcers. Ann. Plast. Surg. 2009, 62, 423–429. [Google Scholar] [CrossRef]
- Buschmann, W.R.; Jahss, M.H.; Kummer, F.; Desai, P.; Gee, R.O.; Ricci, J.L. Histology and Histomorphometric Analysis of the Normal and Atrophic Heel Fat Pad. Foot Ankle Int. 1995, 16, 254–258. [Google Scholar] [CrossRef]
- Boyle, C.J.; Plotczyk, M.; Villalta, S.F.; Patel, S.; Hettiaratchy, S.; Masouros, S.D.; Masen, M.A.; Higgins, C.A. Morphology and composition play distinct and complementary roles in the tolerance of plantar skin to mechanical load. Sci. Adv. 2019, 5, e0244. [Google Scholar] [CrossRef] [PubMed]
- Ricci, V.; Abdulsalam, A.; Özçakar, L. From Plantar Fasciitis to Heel Fat Pad Syndrome: Sonographic Kaleidoscope for Heel Pain. Am. J. Phys. Med. Rehabil. 2024, 103, e172–e173. [Google Scholar] [CrossRef] [PubMed]
- Rome, K. Mechanical properties of the heel pad: Current theory and review of the literature. Foot 1998, 8, 179–185. [Google Scholar] [CrossRef]
- Winter, W.G.; Reiss, O.K. The Anatomy and Physiology of the Foot. Postgrad. Med. J. 1943, 19, 225–230. [Google Scholar] [CrossRef]
- Björntorp, P.; Hood, B.; Martinsson, A.; Persson, B. The composition of human subcutaneous adipose tissue in obesity. Acta Med. Scand. 1966, 180, 117–122. [Google Scholar] [CrossRef] [PubMed]
- Comley, K.; Fleck, N.A. A micromechanical model for the young’s modulus of adipose tissue. Int. J. Solids Struct. 2010, 47, 2982–2990. [Google Scholar] [CrossRef]
- Ker, R.F. Tendon, articular cartilage and the heel pad. J. Exp. Biol. 1999, 202, 3315–3324. [Google Scholar] [CrossRef]
- Pai, S.; Ledoux, W.R. The compressive mechanical properties of diabetic and non-diabetic plantar soft tissue. J. Biomech. 2010, 43, 1754–1760. [Google Scholar] [CrossRef]
- Ledoux, W.R.; Blevins, J.J. The compressive material properties of the plantar soft tissue. J. Biomech. 2007, 40, 2975–2981. [Google Scholar] [CrossRef]
- Bennettt, M.B.; Ker, R.F. The mechanical properties of the human subcalcaneal fat pad in compression. J. Anat. 1990, 131, 131–138. [Google Scholar] [CrossRef]
- Miller-Young, J.E.; Duncan, N.A.; Baroud, G. Material properties of the human calcaneal fat pad in compression: Experiment and theory. J. Biomech. 2002, 35, 1523–1531. [Google Scholar] [CrossRef]
- Teng, Z.; Yang, X.; Gang, X.; Gu, Y.; Huang, R.; Chen, W.; Wang, C.; Chen, L.; Zhang, C.; Helili, M.; et al. Effect of loading history on material properties of human heel pad: An in-vivo pilot investigation during gait. BMC Musculoskelet. Disord. 2022, 23, 254. [Google Scholar] [CrossRef] [PubMed]
- Xiang, P.; Yan, L.; Ge, L.; He, X.; Du, N.; Liu, X. Development of a Radial-Flux Machine With Multi-Shaped Magnet Rotor and Non-Ferromagnetic Yoke for Low Torque Ripple and Rotor Mass. IEEE Trans. Ind. Appl. 2025, 61, 2897–2910. [Google Scholar] [CrossRef]
- De Clercq, D.; Aerts, P.; Kunnen, M. The mechanical characteristics of the human heel pad during foot strike in running: An in vivo cineradiographic study. J. Biomech. 1994, 27, 1213–1222. [Google Scholar] [CrossRef] [PubMed]
- Hsu, T.-C.; Wang, C.-L.; Tsai, W.-C.; Kuo, J.-K.; Tang, F.-T. Comparison of the mechanical properties of the heel pad between young and elderly adults. Arch. Phys. Med. Rehabil. 1998, 79, 1101–1104. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, H.; Francis, P.R.; Murase, T.; Kawai, S.; Ogawa, T. The mechanical properties of the heel pad in elderly adults. Eur. J. Appl. Physiol. Occup. Physiol. 1996, 73, 404–409. [Google Scholar] [CrossRef]
- Hsu, C.C.; Tsai, W.C.; Hsiao, T.Y.; Tseng, F.Y.; Shau, Y.W.; Wang, C.L.; Lin, S.C. Diabetic effects on microchambers and macrochambers tissue properties in human heel pads. Clin. Biomech. 2009, 24, 682–686. [Google Scholar] [CrossRef]
- Kao, P.F.; Davis, B.L.; Hardy, P.A. Characterization of the calcaneal fat pad in diabetic and non-diabetic patients using magnetic resonance imaging. Magn. Reson. Imaging 1999, 17, 851–858. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. Hyperelastic structures: A review on the mechanics and biomechanics. Int. J. Non-Linear Mech. 2023, 148, 104275. [Google Scholar] [CrossRef]
- Isvilanonda, V.; Li, E.Y.; Williams, E.D.; Cavanagh, P.R.; Haynor, D.R.; Chu, B.; Ledoux, W.R. Subject-specific material properties of the heel pad: An inverse finite element analysis. J. Biomech. 2024, 165, 112016. [Google Scholar] [CrossRef]
- Lemmon, D.; Shiang, T.Y.; Hashmi, A.; Ulbrecht, J.S.; Cavanagh, P.R. The effect of insoles in therapeutic footwear—A finite element approach. J. Biomech. 1997, 30, 615–620. [Google Scholar] [CrossRef] [PubMed]
- Chokhandre, S.; Halloran, J.P.; Van Den Bogert, A.J.; Erdemir, A. A three-dimensional inverse finite element analysis of the heel pad. J. Biomech. Eng. 2012, 134, 031002. [Google Scholar] [CrossRef] [PubMed]
- Naemi, R.; Chatzistergos, P.E.; Chockalingam, N. A mathematical method for quantifying in vivo mechanical behaviour of heel pad under dynamic load. Med. Biol. Eng. Comput. 2016, 54, 341–350. [Google Scholar] [CrossRef]
- Natali, A.N.; Fontanella, C.G.; Carniel, E.L. Constitutive formulation and numerical analysis of the heel pad region. Comput. Methods Biomech. Biomed. Engin. 2012, 15, 401–409. [Google Scholar] [CrossRef]
- Suzuki, R.; Ito, K.; Lee, T.; Ogihara, N. Parameter identification of hyperelastic material properties of the heel pad based on an analytical contact mechanics model of a spherical indentation. J. Mech. Behav. Biomed. Mater. 2017, 65, 753–760. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.Y.; Chuang, H.J.; Cortes, D.H. Investigation of the optimum heel pad stiffness: A modeling study. Australas. Phys. Eng. Sci. Med. 2017, 40, 585–593. [Google Scholar] [CrossRef]
- Natali, A.N.; Fontanella, C.G.; Carniel, E.L.; Young, J.M. Biomechanical behaviour of heel pad tissue: Experimental testing, constitutive formulation, and numerical modelling. Proc. Inst. Mech. Eng. Part. H J. Eng. Med. 2011, 225, 449–459. [Google Scholar] [CrossRef]
- Mo, F.; Li, J.; Yang, Z.; Zhou, S.; Behr, M. In vivo measurement of plantar tissue characteristics and its indication for foot modeling. Ann. Biomed. Eng. 2019, 47, 2356–2371. [Google Scholar] [CrossRef]
- Grytz, R.; Meschke, G. Constitutive modeling of crimped collagen fibrils in soft tissues. J. Mech. Behav. Biomed. Mater. 2009, 2, 522–533. [Google Scholar] [CrossRef]
- Xiang, P.; Yan, L.; Liu, X.; He, X.; Du, N.; Wang, H. Structural Topology Design for Electromagnetic Performance Enhancement of Permanent-Magnet Machines. Chin. J. Mech. Eng. 2025, 38, 26. [Google Scholar] [CrossRef]
- Fontanella, C.G.; Nalesso, F.; Carniel, E.L.; Natali, A.N. Biomechanical behavior of plantar fat pad in healthy and degenerative foot conditions. Med. Biol. Eng. Comput. 2016, 54, 653–661. [Google Scholar] [CrossRef] [PubMed]
- Natali, A.N.; Fontanella, C.G.; Carniel, E.L. Constitutive formulation and analysis of heel pad tissues mechanics. Med. Eng. Phys. 2010, 32, 516–522. [Google Scholar] [CrossRef] [PubMed]
- Kardeh, M.; Vogl, T.J.; Huebner, F.; Nelson, K.; Stief, F.; Silber, G. Dynamic material characterization of the human heel pad based on in vivo experimental tests and numerical analysis. Med. Eng. Phys. 2016, 38, 940–945. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.M.; Lee, P.V.S. Explicit finite element modelling of heel pad mechanics in running: Inclusion of body dynamics and application of physiological impact loads. Comput. Methods Biomech. Biomed. Engin. 2015, 18, 1582–1595. [Google Scholar] [CrossRef]
- Williams, E.D.; Stebbins, M.J.; Cavanagh, P.R.; Haynor, D.R.; Chu, B.; Fassbind, M.J.; Isvilanonda, V.; Ledoux, W.R. The design and validation of a magnetic resonance imaging-compatible device for obtaining mechanical properties of plantar soft tissue via gated acquisition. Proc. Inst. Mech. Eng. H 2015, 229, 732–742. [Google Scholar] [CrossRef]
- Tecse, A.; Romero, S.E.; Naemi, R.; Castaneda, B. Characterisation of the soft tissue viscous and elastic properties using ultrasound elastography and rheological models: Validation and applications in plantar soft tissue assessment. Phys. Med. Biol. 2023, 68, 105005. [Google Scholar] [CrossRef]
- Marchionatti, E.; Desrochers, A.; Wenzlow, N.; Villemure, I.; Theoret, C.L. In vitro biomechanical properties of sole tissues: Comparison between healthy and ulcerated bovine claws. J. Dairy. Sci. 2020, 103, 6412–6421. [Google Scholar] [CrossRef]
- DeBerardinis, J.; Dufek, J.S.; Trabia, M.B. A viscoelastic ellipsoidal model of the mechanics of plantar tissues. J. Biomech. 2019, 92, 137–145. [Google Scholar] [CrossRef]
- Cenk Guïer, H.; Berme, N.; Simon, S.R. A viscoelastic sphere model for the representation of plantar soft tissue during simulations. J. Biomech. 1998, 31, 847–853. [Google Scholar] [CrossRef]
- Mauri, A.; Ehret, A.E.; De Focatiis, D.S.A.; Mazza, E. A model for the compressible, viscoelastic behavior of human amnion addressing tissue variability through a single parameter. Biomech. Model. Mechanobiol. 2016, 15, 1005–1017. [Google Scholar] [CrossRef][Green Version]
- Erdemir, A.; Viveiros, M.L.; Ulbrecht, J.S.; Cavanagh, P.R. An inverse finite-element model of heel-pad indentation. J. Biomech. 2006, 39, 1279–1286. [Google Scholar] [CrossRef]
- Natali, A.N.; Fontanella, C.G.; Carniel, E.L. A numerical model for investigating the mechanics of calcaneal fat pad region. J. Mech. Behav. Biomed. Mater. 2012, 5, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, R.; Ito, K.; Lee, T.; Ogihara, N. In-vivo viscous properties of the heel pad by stress-relaxation experiment based on a spherical indentation. Med. Eng. Phys. 2017, 50, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Negishi, T.; Ito, K.; Kamono, A.; Lee, T.; Ogihara, N. Strain-rate dependence of viscous properties of the plantar soft tissue identified by a spherical indentation test. J. Mech. Behav. Biomed. Mater. 2020, 102, 103470. [Google Scholar] [CrossRef]
- Matteoli, S.; Fontanella, C.G.; Carniel, E.L.; Wilhjelm, J.E.; Virga, A.; Corbin, N.; Corvi, A.; Natali, A.N. Investigations on the viscoelastic behaviour of a human healthy heel pad: In vivo compression tests and numerical analysis. Proc. Inst. Mech. Eng. H 2013, 227, 334–342. [Google Scholar] [CrossRef]
- Grigoriadis, G.; Newell, N.; Carpanen, D.; Christou, A.; Bull, A.M.J.; Masouros, S.D. Material properties of the heel fat pad across strain rates. J. Mech. Behav. Biomed. Mater. 2017, 65, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Fontanella, C.G.; Forestiero, A.; Carniel, E.L.; Natali, A.N. Analysis of heel pad tissues mechanics at the heel strike in bare and shod conditions. Med. Eng. Phys. 2013, 35, 441–447. [Google Scholar] [CrossRef]
- Yang, L.; Ye, M.; Huang, Y.; Dong, J. Study on mechanical properties of displacement-amplified mild steel bar joint damper. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 2177–2190. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, Z.; Zhang, N.; Li, J.; Zhou, P.; Hu, F.; Rong, Y.; Lu, B.; Gu, G. High-stretchability, ultralow-hysteresis conductingpolymer hydrogel strain sensors for soft machines. Adv. Mater. 2022, 34, 2203650. [Google Scholar] [CrossRef]
- Jplrgensen, U.; Larsen, E.; Varmarken, J.E. The HPC-Device: A method to quantify the heel pad shock absorbency. Foot Ankle 1989, 10, 93–98. [Google Scholar] [CrossRef]
- Fontanella, C.G.; Matteoli, S.; Carniel, E.L.; Wilhjelm, J.E.; Virga, A.; Corvi, A.; Natali, A.N. Investigation on the load-displacement curves of a human healthy heel pad: In vivo compression data compared to numerical results. Med. Eng. Phys. 2012, 34, 1253–1259. [Google Scholar] [CrossRef] [PubMed]
- Ahanchian, N.; Nester, C.J.; Howard, D.; Ren, L.; Parker, D. Estimating the material properties of heel pad sub-layers using inverse finite element analysis. Med. Eng. Phys. 2017, 40, 11–19. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, J.; Ren, Y.; Liang, C.; Liao, Y. Study on very long-term creep tests and nonlinear creep-damage constitutive model of salt rock. Int. J. Rock. Mech. Min. Sci. 2021, 146, 104873. [Google Scholar] [CrossRef]
- Wu, F.; Gao, R.; Liu, J.; Li, C. New fractional variable-order creep model with short memory. Appl. Math. Comput. 2020, 380, 125278. [Google Scholar] [CrossRef]
- Purslow, P.P.; Wess, T.J.; Hukins, D.W. Collagen orientation and molecular spacing during creep and stress-relaxation in soft connective tissues. J. Exp. Biol. 1998, 201, 135–142. [Google Scholar] [CrossRef]
- Minns, R.J.; Soden, P.D.; Jackson, D.S. The role of the fibrous components and ground substance in the mechanical properties of biological tissues: A preliminary investigation. J. Biomech. 1973, 6, 153–165. [Google Scholar] [CrossRef]
- Lanir, Y. Fibrous tissues growth and remodeling: Evolutionary micro-mechanical theory. J. Mech. Phys. Solids. 2017, 107, 115–144. [Google Scholar] [CrossRef]
- Thornton, G.M.; Frank, C.B.; Shrive, N.G. Ligament creep behavior can be predicted from stress relaxation by incorporating fiber recruitment. J. Rheol. 2001, 45, 493–507. [Google Scholar] [CrossRef]
- Krasteva, V.T.; Papazov, S.P.; Daskalov, I.K. Peripheral nerve magnetic stimulation: Influence of tissue non-homogeneity. Biomed. Eng. Online 2003, 23, 19. [Google Scholar] [CrossRef]
- Latif, M.A.; Sanei, S.; Chambers, J.; Spyrou, L. Partially constrained blind source separation for localization of unknown sources exploiting non-homogeneity of the head tissues. J. VLSI Signal Process Syst. Signal Image Video Technol. 2007, 49, 217–232. [Google Scholar] [CrossRef]
- Rachev, A.; Gleason, R.L. Theoretical study on the effects of pressure-induced remodeling on geometry and mechanical non-homogeneity of conduit arteries. Biomech. Model. Mechanobiol. 2011, 10, 79–93. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.Y.; Chen, P.Y.; Shau, Y.W.; Tai, H.C.; Wang, C.L. Spatial-dependent mechanical properties of the heel pad by shear wave elastography. J. Biomech. 2017, 53, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.H.; Lin, C.Y.; Hsiao, M.Y.; Cheng, Y.H.; Chen, W.S.; Wang, T.G. Altered stiffness of microchamber and macrochamber layers in the aged heel pad: Shear wave ultrasound elastography evaluation. J. Formos. Med. Assoc. 2018, 117, 434–439. [Google Scholar] [CrossRef]
- Han, S.-M.; Rho, J.-Y. Dependence of broadband ultrasound attenuation on the elastic anisotropy of trabecular bone. Proc. Inst. Mech. Eng. H 1998, 212, 223–227. [Google Scholar] [CrossRef]
- Topol, H.; Gou, K.; Demirkoparan, H.; Pence, T.J. Hyperelastic modeling of the combined effects of tissue swelling and deformation-related collagen renewal in fibrous soft tissue. Biomech. Model. Mechanobiol. 2018, 17, 1543–1567. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Auricchio, F.; Morganti, S.; Lu, J. Uniaxial properties of ascending aortic aneurysms in light of effective stretch. Acta Biomater. 2021, 136, 306–313. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Sun, G.; Shi, L. Shear-induced anisotropy analysis of rock masses containing non-coplanar intermittent joints. Arch. Appl. Mech. 2024, 94, 841–864. [Google Scholar] [CrossRef]
- Thomopoulos, S.; Fomovsky, G.M.; Holmes, J.W. The development of structural and mechanical anisotropy in fibroblast populated collagen gels. J. Biomech. Eng. 2005, 127, 742–750. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, Y.; Kawazoe, N.; Yang, Y.; Chen, G. Influences of viscosity on the osteogenic and adipogenic differentiation of mesenchymal stem cells with controlled morphology. J. Mater. Chem. B 2022, 10, 3989–4001. [Google Scholar] [CrossRef]
- Ghosh, S.; Mutalib, H.A.; Kaur, S.; Ghoshal, R.; Retnasabapathy, S. Corneal cell morphology in keratoconus: A confocal microscopic observation. Malays. J. Med. Sci. 2017, 24, 44–54. [Google Scholar] [CrossRef]
- Saccomandi, P.; Vogel, V.; Bazrafshan, B.; Maurer, J.; Schena, E.; Vogl, T.J.; Silvestri, S.; Mäntele, W. Estimation of anisotropy coefficient of swine pancreas, liver and muscle at 1064 nm based on goniometric technique. J. Biophotonics 2015, 8, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, R.M.; Stanisz, G.J.; Kim, J.K.; Bronskill, M.J. Anisotropy of nmr properties of tissues. Magn. Reson. Med. 1994, 32, 592–601. [Google Scholar] [CrossRef] [PubMed]
- Trebbi, A.; Perrier, A.; Bailet, M.; Payan, Y. MR-compatible loading device for assessment of heel pad internal tissue displacements under shearing load. Med. Eng. Phys. 2021, 98, 125–132. [Google Scholar] [CrossRef]
- Chi, K.-J.; Roth, V.L. Functional Morphology and Biomechanics of Mammalian Footpads. Ph.D. Thesis, Duke University, Durham, NC, USA, 2006. [Google Scholar]
- Okita, M.; Yoshimura, T.; Nakano, J.; Motomura, M.; Eguchi, K. Effects of reduced joint mobility on sarcomere length, collagen fibril arrangement in the endomysium, and hyaluronan in rat soleus muscle. J. Muscle Res. Cell Motil. 2004, 25, 159–166. [Google Scholar] [CrossRef]
- Jsrgensen, U.; Bojsen-Mdler, F. Shock absorbency of factors in the shoe/heel interaction-with special focus on role of the heel pad. Foot Ankle 1989, 9, 294–299. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, H.; Ogawa, T.; Kuzuhara, K.; Ikuta, K. In vivo examination of the dynamic properties of the human heel pad. Int. J. Sports Med. 1993, 14, 312–319. [Google Scholar] [CrossRef]
- Quagliato, L.; Kim, S.; Hassan, O.R.; Lee, T. Heel pad’s hyperelastic properties and gait parameters reciprocal modelling by a Gaussian Mixture Model and Extreme Gradient Boosting framework. Biomed. Signal Process. Control. 2025, 107, 107818. [Google Scholar] [CrossRef]
- Belhan, O.; Kaya, M.; Gurger, M. The thickness of heel fat-pad in patients with plantar fasciitis. Acta Orthop. Traumatol. Turc. 2019, 53, 463–467. [Google Scholar] [CrossRef]
- Maemichi, T.; Tsutsui, T.; Matsumoto, M.; Iizuka, S.; Torii, S.; Kumai, T. The relationship of heel fat pad thickness with age and physiques in Japanese. Clin. Biomech. 2020, 80, 105110. [Google Scholar] [CrossRef]
- Kwak, Y.; Kim, J.; Lee, K.M.; Koo, S. Increase of stiffness in plantar fat tissue in diabetic patients. J. Biomech. 2020, 107, 109857. [Google Scholar] [CrossRef]
- Fernando, I.; Fei, J.; Stanley, R.; Enshaei, H. Measurement and evaluation of the effect of vibration on fruits in transit—Review. Packag. Technol. Sci. 2018, 31, 723–738. [Google Scholar] [CrossRef]
- Pain, M.T.G.; Challis, J.H. The role of the heel pad and shank soft tissue during impacts: A further resolution of a paradox. J. Biomech. 2001, 34, 327–333. [Google Scholar] [CrossRef]
- Preserve, L.; Wee, H.B. The Dynamic Model of the Foot and Ankle System. Dissertations Thesis, Lehigh University, Bethlehem, PA, USA, 2012. [Google Scholar]
- Aerts, P.; Ker, R.F.; De Clercq, D.; Ilsleyg, D.W.; McN Alexander, R. The mechanical properties of the human heel pad: A paradox resolved. J. Biomech. 1995, 11, 1299–1308. [Google Scholar] [CrossRef] [PubMed]
- Qian, Z.; Ren, L.; Ren, L. A coupling analysis of the biomechanical functions of human foot complex during locomotion. J. Bionic Eng. 2010, 7, s150–s157. [Google Scholar] [CrossRef]
- Zimmerman, B.K.; Maas, S.A.; Weiss, J.A.; Ateshian, G.A. Modeling fatigue failure of cartilage and fibrous biological tissues using constrained reactive mixture theory. J. Biomech. Eng. 2024, 146, 121001. [Google Scholar] [CrossRef]
- Dong, H.; Liu, M.; Martin, C.; Sun, W. A residual stiffness-based model for the fatigue damage of biological soft tissues. J. Mech. Phys. Solids 2020, 143, 104074. [Google Scholar] [CrossRef]
- Roth, D.; Şahin, A.T.; Ling, F.; Tepho, N.; Senger, C.N.; Quiroz, E.J.; Calvert, B.A.; van der Does, A.M.; Güney, T.G.; Glasl, S.; et al. Structure and function relationships of mucociliary clearance in human and rat airways. Nat. Commun. 2025, 16, 2446. [Google Scholar] [CrossRef]
- Place, N.; Yamada, T.; Bruton, J.D.; Westerblad, H. Muscle fatigue: From observations in humans to underlying mechanisms studied in intact single muscle fibres. Eur. J. Appl. Physiol. 2010, 110, 1–15. [Google Scholar] [CrossRef]
- Lee, S.C.K.; Braim, A.; Becker, C.N.; Prosser, L.A.; Tokay, A.M.; Binder-Macleod, S.A. Diminished fatigue at reduced muscle length in human skeletal muscle. Muscle Nerve 2007, 36, 789–797. [Google Scholar] [CrossRef]
- Borotikar, B.S.; Newcomer, R.; Koppes, R.; McLean, S.G. Combined effects of fatigue and decision making on female lower limb landing postures: Central and peripheral contributions to ACL injury risk. Clin. Biomech. 2008, 23, 81–92. [Google Scholar] [CrossRef]
- Almonroeder, T.G.; Tighe, S.M.; Miller, T.M.; Lanning, C.R. The influence of fatigue on decision-making in athletes: A systematic review. Sports Biomech. 2020, 19, 76–89. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, J.H.; Screen, H.R.C. Fatigue loading of tendon. Int. J. Exp. Pathol. 2013, 94, 260–270. [Google Scholar] [CrossRef]
- Nan, J.; Zhang, G.; Zhu, T.; Wang, Z.; Wang, L.; Wang, H.; Chu, F.; Wang, C.; Tang, C. A highly elastic and fatigue-resistant natural protein-reinforced hydrogel electrolyte for reversible-compressible quasi-solid-state supercapacitors. Adv. Sci. 2020, 7, 2000587. [Google Scholar] [CrossRef]
- Xiang, P.; Yan, L.; Guo, Y.; He, X.; Gerada, C.; Chen, I. A concentrated-Flux-Type PM Machine With Irregular Magnets and Iron Poles. IEEE/ASME Trans. Mechatron. 2024, 29, 691–702. [Google Scholar] [CrossRef]
- Papachatzis, N.; Slivka, D.R.; Pipinos, I.I.; Schmid, K.K.; Takahashi, K.Z. Does the heel’s dissipative energetic behavior affect its thermodynamic responses during walking? Front. Bioeng. Biotechnol. 2022, 10, 908725. [Google Scholar] [CrossRef]
- Yang, X.G.; Teng, Z.L.; Zhang, Z.M.; Wang, K.; Huang, R.; Chen, W.M.; Wang, C.; Chen, L.; Zhang, C.; Huang, J.Z.; et al. Comparison of material properties of heel pad between adults with and without type 2 diabetes history: An in-vivo investigation during gait. Front. Endocrinol 2022, 13, 894383. [Google Scholar] [CrossRef] [PubMed]
- Simpkins, C.; Ahn, J.; Yang, F. Effects of anteriorly-loaded treadmill walking on dynamic gait stability in young adults. Gait Posture 2022, 94, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.W.; Liu, W.; Yang, F. Influence of multiple sclerosis on dynamic gait stability. J. Biomech. 2020, 106, 109827. [Google Scholar] [CrossRef] [PubMed]
- Ba, K.; Liu, G.; Ma, G.; Chen, C.; Pu, L.; He, X.; Chen, X.; Wang, Y.; Zhu, Q.; Wang, D.; et al. Bionic perception and transmission neural device based on a self-powered concept. Cell Rep. Phys. Sci. 2024, 5, 102048. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, M.; Gao, F.; Wang, Y.; Pu, L.; Song, Y.; She, J.; Wang, D.; Yu, B.; Ba, K.; et al. Bioinspired fiber-based flexible self-powered sensor for wearable applications. Device 2024, 2, 100508. [Google Scholar] [CrossRef]
- Wang, D.; Ma, G.; Zhang, X.; Zheng, K.; Zhang, J.; Ma, Z.; Han, Z.; Ren, L. Flexible pressure sensor composed of multi-layer textile materials for Human-Machine Interaction applications. ACS Sens. 2025, 10, 350–359. [Google Scholar] [CrossRef] [PubMed]
- Ba, K.; Chen, C.; Ma, G.; Song, Y.; Wang, Y.; Yu, B.; Kong, X. A compensation strategy of end-effector pose precision based on the virtual constraints for serial robots with RDOFs. Fundam. Res. 2024. Early view. [Google Scholar] [CrossRef]
- Yu, B.; Li, H.; Ma, G.; Liu, X.; Chen, C.; Zheng, B.; Ba, K.; Kong, X. Design and matching control strategy of electro-hydraulic load-Sensitive hydraulic power unit for legged robots. Energy 2024, 313, 133730. [Google Scholar] [CrossRef]
- Ba, K.; Song, Y.; Yu, B.; Wang, C.; Zhang, J.; Ma, G. Kinematics correction algorithm for the LHDS of a legged robot with semi-cylindrical foot end based on V-DOF. Mech. Syst. Signal Process. 2021, 167, 108566. [Google Scholar] [CrossRef]
- Yu, B.; Li, H.; Gu, C.; Shen, A.; Zhang, S.; Liu, X.; Li, J.; Ba, K.; Ma, G.; Kong, X. Design of lightweight hydraulic power unit for legged robots based on the sobol sensitivity analysis. Energy Convers. Manag. 2025, 328, 119620. [Google Scholar] [CrossRef]
- Yang, H.; Li, S.; Wu, Y.; Bao, X.; Xiang, Z.; Xie, Y.; Pan, L.; Chen, J.; Liu, Y.; Li, R.W. Advances in flexible magnetosensitive materials and devices for wearable electronics. Adv. Mater. 2024, 36, 2311996. [Google Scholar] [CrossRef]
- Park, H.; Kim, S.; Lee, J.; Lee, I.; Bontapalle, S.; Na, Y.; Sim, K. Organic flexible electronics with closed-loop recycling for sustainable wearable technology. Nat. Electron. 2024, 7, 39–50. [Google Scholar] [CrossRef]
- Keum, K.; Kim, J.W.; Hong, S.Y.; Son, J.G.; Lee, S.S.; Ha, J.S. Flexible/Stretchable supercapacitors with novel functionality for wearable electronics. Adv Mater. 2020, 32, 2002180. [Google Scholar] [CrossRef]
- Gao, J.; Shang, K.; Ding, Y.; Wen, Z. Material and configuration design strategies towards flexible and wearable power supply devices: A review. J. Mater. Chem. A 2021, 9, 8950–8965. [Google Scholar] [CrossRef]
- Xiang, X.; He, Q.; Xia, S.; Deng, Z.; Zhang, H.; Li, H. Study of capacitance type flexible electronic devices based on polyacrylamide and reduced graphene oxide composite hydrogel. Eur. Polym. J. 2022, 171, 111200. [Google Scholar] [CrossRef]
- Qu, Y.; Li, X.; Wang, X.; Dai, H. Multifunctional AgNWs@MXene/AgNFs electromagnetic shielding composites for flexible and highly integrated advanced electronics. Compos. Sci. Technol. 2022, 230, 109753. [Google Scholar] [CrossRef]
- Tee, B.C.K.; Ouyang, J. Soft electronically functional polymeric composite materials for a flexible and stretchable digital future. Adv. Mater. 2018, 30, 1802560. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Wang, Y.; Cheng, L.; Guo, S.; Liu, T.; Hu, Z.; Yu, H.; Chen, D.; Li, Y.; Yuan, H. Structure design and assembly mode of carbon nanotube-based flexible electrode materials and flexible supercapacitors. J. Energy Storage 2023, 73, 109179. [Google Scholar] [CrossRef]
- Liu, X.; Guan, C.; Hu, Y.; Zhang, L.; Elshahawy, A.M.; Wang, J. 2D Metal–Organic Frameworks derived nanocarbon arrays for substrate enhancement in flexible supercapacitors. Small 2018, 14, 1702641. [Google Scholar] [CrossRef]
- Balogun, M.S.; Yang, H.; Luo, Y.; Qiu, W.; Huang, Y.; Liu, Z.Q.; Tong, Y. Achieving high gravimetric energy density for flexible lithium-ion batteries facilitated by core-double-shell electrodes. Energy Environ. Sci. 2018, 11, 1859–1869. [Google Scholar] [CrossRef]
- Yin, T.; Cheng, Y.; Hou, Y.; Sun, L.; Ma, Y.; Su, J.; Zhang, Z.; Liu, N.; Li, L.; Gao, Y. 3D porous structure in mxene/pani foam for a high-performance flexible pressure sensor. Small 2022, 18, 2204806. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, B.; Tian, X.; Liu, S.; Xu, Z.; Sun, G.; Qin, G.; Chen, Q. Self-powered wearable sensing devices based on a flexible ammonium-ion battery with fatigue resistance and frost resistance based on a strong and tough hydrogel. J. Mater. Chem. C Mater. 2022, 10, 17675–17683. [Google Scholar] [CrossRef]
- Vonsul, M.I.; Dhandapani, R.; Webster, D.C. Unlocking the potential of functionalized cottonseed oil for the production of biobased epoxy foams. Ind. Crops Prod. 2024, 222, 119735. [Google Scholar] [CrossRef]
- Shen, C.; Shao, R.; Wang, W.; Wu, X.; Zhou, B.; Zhao, L.; Siddique, A.; Xu, Z. Progress of flame retardant research on flexible polyurethane foam. Eur. Polym. J. 2024, 220, 113478. [Google Scholar] [CrossRef]
- Li, T.T.; Zang, K.; Liu, P.; Wang, Y.T.; Hu, X.; Wang, X.; Lou, C.W.; Lin, J.H. Construction of soft polyurethane cushioning composites based on integral fabric air layer: Reaching new levels in compression and cushioning behaviors. Polym. Compos. 2022, 43, 8250–8258. [Google Scholar] [CrossRef]
- Li, W.; Qian, X.; Li, J. Phase transitions in 2D materials. Nat. Rev. Mater. 2021, 6, 829–846. [Google Scholar] [CrossRef]
- Jiang, W.; Gong, X.; Wang, S.; Chen, Q.; Zhou, H.; Jiang, W.; Xuan, S. Strain rate-induced phase transitions in an impact-hardening polymer composite. Appl. Phys. Lett. 2014, 104, 121915. [Google Scholar] [CrossRef]
- Jitkokkruad, K.; Jarukumjorn, K.; Raksakulpiwat, C.; Chaiwong, S.; Rattanakaran, J.; Trongsatitkul, T. Effects of bamboo leaf fiber content on cushion performance and biodegradability of natural rubber latex foam composites. Polymers 2023, 15, 654. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhong, W.; Li, J.; Luo, J. Mechanical properties and cushioning effectiveness of fpuf-eps Combination Materials. Materials 2023, 16, 6886. [Google Scholar] [CrossRef]
- Liu, B.; Huang, X.; Wang, S.; Wang, D.; Guo, H. Performance of polyvinyl alcohol/bagasse fibre foamed composites as cushion packaging materials. Coatings 2021, 11, 1094. [Google Scholar] [CrossRef]
- Foster, M.M.; Morrison, D.C.; Landauer, A.K.; Herynk, M.D.; Lamberson, L.E. Assessment of frequency and amplitude dependence on the cyclic degradation of polyurethane foams. J. Appl. Polym. Sci. 2024, 141, e55846. [Google Scholar] [CrossRef]
- Demirel, S.; Ergun Tuna, B. Evaluation of the cyclic fatigue performance of polyurethane foam in different density and category. Polym. Test. 2019, 76, 146–153. [Google Scholar] [CrossRef]
- Sharma, S.C.; Krishna, M.; Narasimha Murthy, H.N.; Sathyamoorthy, M.; Bhattacharya, D. Fatigue studies of polyurethane sandwich structures. J. Mater. Eng. Perform. 2004, 13, 637–641. [Google Scholar] [CrossRef]
- Jiang, S.; Ding, M.; Chen, W.; Wang, J. Preparation and properties of flexible cushioning composites based on silicone rubber and Warp—Knitted spacer fabric. Silicon 2023, 15, 3323–3338. [Google Scholar] [CrossRef]
- Yu, A.; Sukigara, S.; Shirakihara, M. Effect of silicone inlaid materials on reinforcing compressive strength of weft-knitted spacer fabric for cushioning applications. Polymers 2021, 13, 3645. [Google Scholar] [CrossRef]
- Grella, R.; Nicoletti, G.; D’Ari, A.; Romanucci, V.; Santoro, M.; D’Andrea, F. A useful method to overcome the difficulties of applying silicone gel sheet on irregular surfaces. Int. Wound J. 2015, 12, 185–188. [Google Scholar] [CrossRef] [PubMed]
- Cooper, S.; Hanning, J.; Hegarty, C.; Generalis, C.; Smith, A.; Hall, T.; Starbuck, C.; Kaux, J.F.; Schwartz, C.; Buckley, C. Effects of a range of 6 prefabricated orthotic insole designs on plantar pressure in a healthy population: A randomized, open-label crossover investigation. Prosthet. Orthot. Int. 2024, 48, 474–480. [Google Scholar] [CrossRef]
- Anderson, A.J.; Hudak, Y.F.; Muir, B.C.; Aubin, P.M. Design, control, and evaluation of a robotic ankle-foot prosthesis emulator. IEEE Trans. Med. Robot. Bionics. 2023, 5, 741–752. [Google Scholar] [CrossRef]
- Herrin, K.; Geil, M. A comparison of orthoses in the treatment of idiopathic toe walking: A randomized controlled trial. Prosthet. Orthot. Int. 2016, 40, 262–269. [Google Scholar] [CrossRef] [PubMed]
- Queen, R.M.; Abbey, A.N.; Verma, R.; Butler, R.J.; Nunley, J.A. Plantar loading during cutting while wearing a rigid carbon fiber insert. J. Athl. Train. 2014, 49, 297–303. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Li, B.; Niu, S.; Zhang, J.; Wang, D.; Wang, Z.; Zhou, L.; Liu, Q.; Liu, L.; Wang, J.; et al. A bioinspired triboelectric nanogenerator for all state energy harvester and self-powered rotating monitor. Nano Energy 2022, 91, 106637. [Google Scholar] [CrossRef]
- Ma, G.; Wang, D.; Wang, J.; Li, J.; Wang, Z.; Li, B.; Mu, Z.; Niu, S.; Zhang, J.; Ba, K.; et al. A durable triboelectric nanogenerator with a coaxial counter-rotating design for efficient harvesting of random mechanical energy. Nano Energy 2023, 105, 108006. [Google Scholar] [CrossRef]
- Ma, G.; Gao, F.; Zhang, M.; Wang, Y.; Gu, C.; Meng, F.; She, J.; Song, Y.; He, X.; Wang, D.; et al. An endurable triboelectric nanogenerator for wind energy harvesting based on centrifugal force induced automatic switching between sliding and rolling modes. ACS Sustain. Chem. Eng. 2024, 12, 12956–12965. [Google Scholar] [CrossRef]
- Gu, C.; Ma, G.; Zhang, M.; Shen, H.; Pu, L.; Song, Y.; Yan, S.; Wang, D.; Ba, K.; Yu, B.; et al. A Neural Device Inspired by Neuronal Oscillatory Activity with Intrinsic Perception and Decision-Making. Adv. Sci. 2025, 12, e2414173. [Google Scholar] [CrossRef]
- Ma, G.; Pu, L.; Gu, C.; Shen, H.; Meng, F.; Ma, K.; Wang, D.; Liu, L.; Wang, C.; Ba, K.; et al. Body-coupled multifunctional Human-machine interfaces with double spiral electrode structure. Adv. Funct. Mater. 2025, Early view, 2424979. [Google Scholar] [CrossRef]
- Zhang, B.; Han, Q.; Zhang, J.; Han, Z.; Niu, S.; Ren, L. Advanced bio-inspired structural materials: Local properties determine overall performance. Mater. Today 2020, 41, 177–199. [Google Scholar] [CrossRef]
| Mathematical Model of Viscoelasticity | Parameters |
|---|---|
| QLV [66] |
|
| Helmholtz free energy function [67] | |
| Mooney-Rivlin [31] | |
| Maxwell’s model of fifth order [64] | (s) |
| Generalized Rivlin [62] |
|
| Ogden [63] |
|
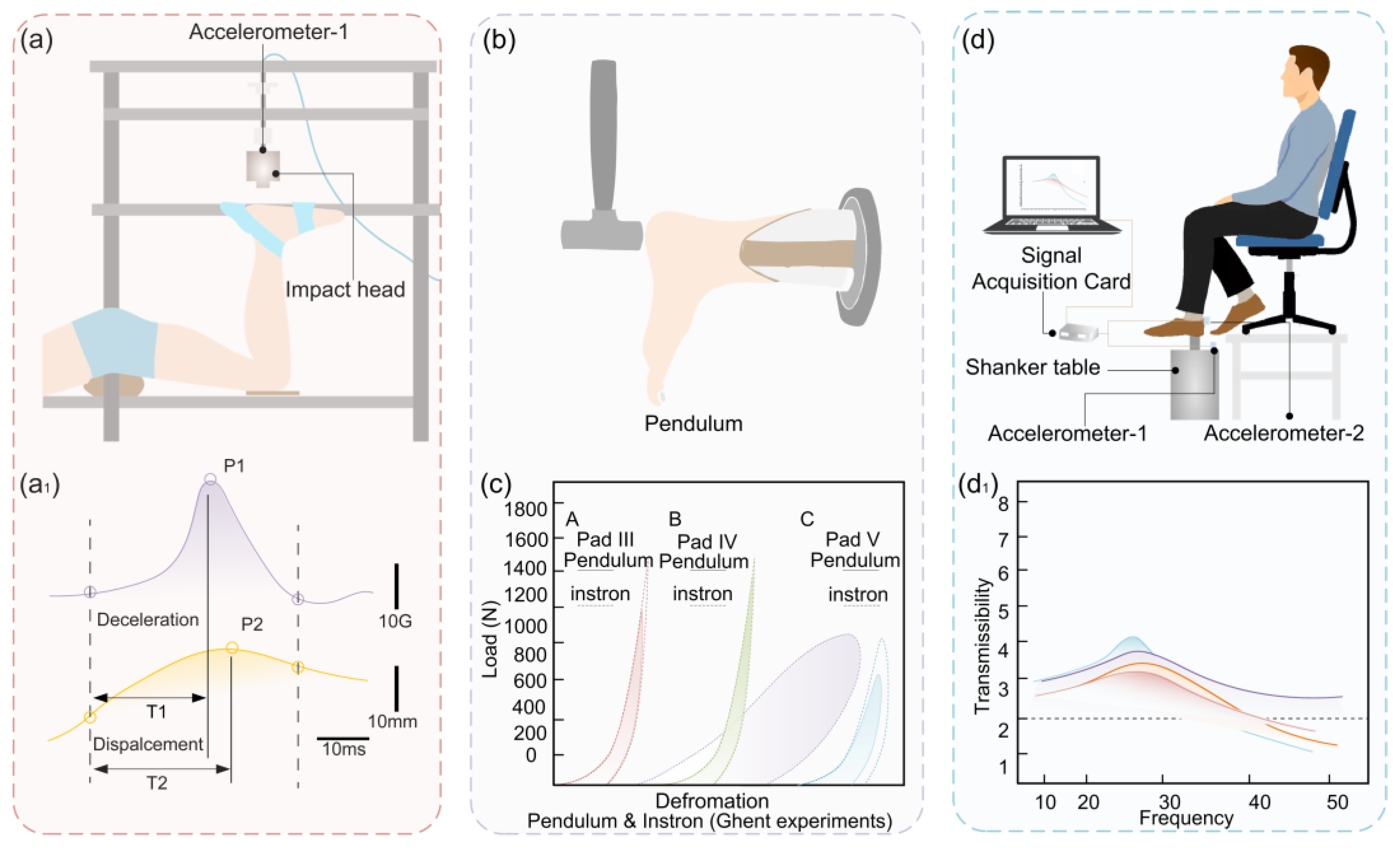
| In vivo impact test [36] | Instrument | Speed /Frequency | Energy loss EDR/% | |
| Impact tester | 0.72 m/s | 77.4 | ||
| 0.93 m/s | 78.8 | |||
| 0.57 m/s | 73.8 | |||
| 0.94 m/s | 73.6 | |||
| In vitro test [4] | Instron | 2.2 Hz | 28.6 ± 6.9 (with calcaneus) | 32.3 ± 5.4 (without calcaneus) |
| Comparison test [105] | Instron | 50.4 | ||
| Pendulum | 65.5 | |||
| Category | Subcategory/ Research Focus | Author/ Citation | Research Objective | Key Conclusions/Findings |
|---|---|---|---|---|
| Structure & Material Properties | Anatomical Structure and Composition | Ker [29] | Effects of cyclic loading on compartments | Shorter intervals and higher frequencies increase stiffness |
| Age and Pathological Effects | Hsu, T. [35,36] | Impact of aging on collagen/elastic fibers | Elderly heel pads show higher stiffness due to collagen loss and fibrosis | |
| Hsu, C.C [37,38] | Pathological changes in compartment structure | Thickened/hardened septa reduce cushioning performance | ||
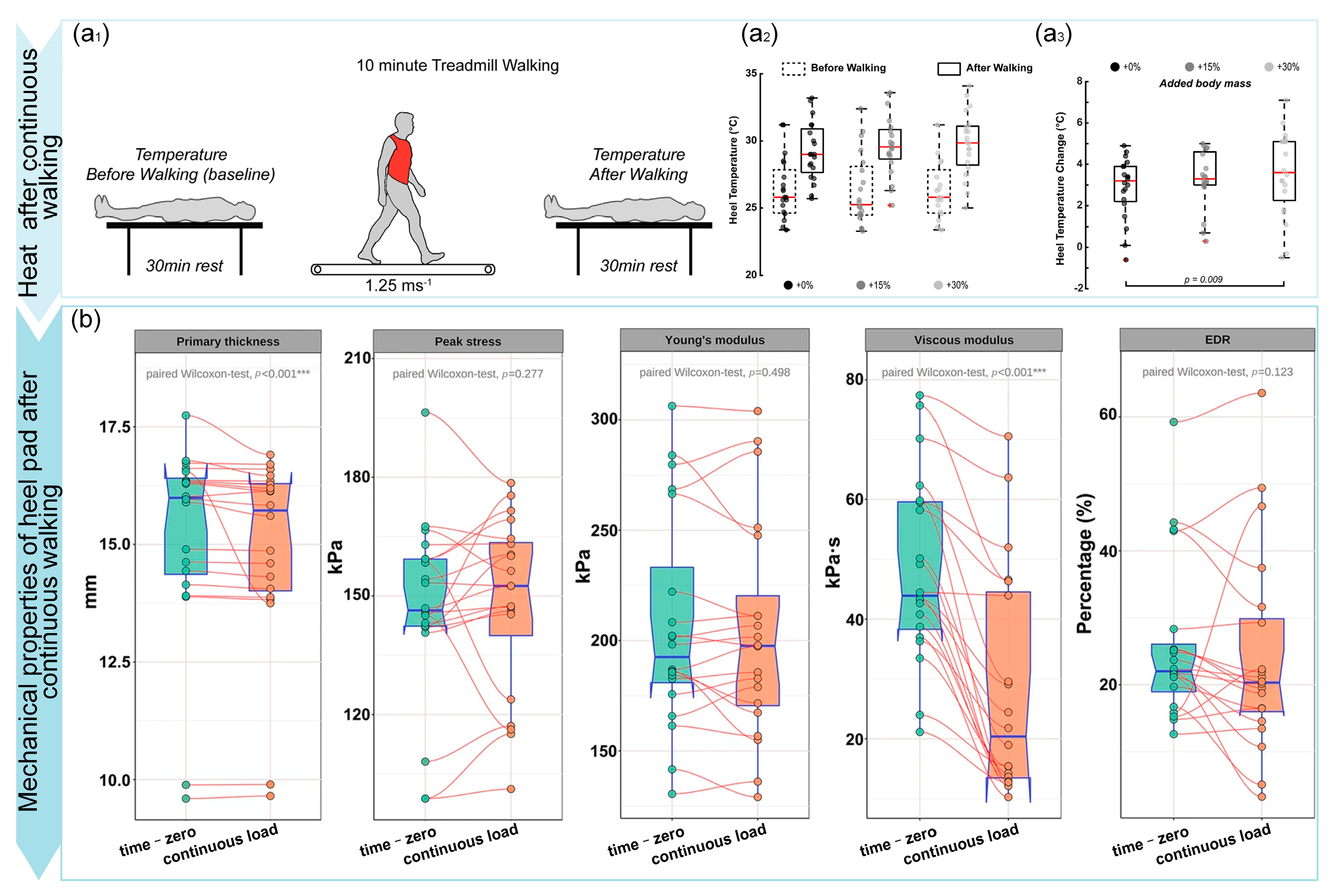
| Thermodynamic Response | Tudor-Locke [9] | Temperature changes during continuous walking | Increased body weight elevates temperature, indicating energy dissipation | |
| Biomechanical Properties | 2.1 Nonlinear Stiffness | Miller-Young [31] | Elastic modulus under varying compression speeds | Cutting samples disrupts compartments, lowering modulus (18.4 kPa vs. 2 MPa) |
| Ker [29,30] | Differences in in vivo vs. in vitro stiffness | Higher in vivo stiffness due to energy absorption by adjacent tissues | ||
| 2.2 Viscoelasticity | Takuo Negishi [64] | Stress relaxation under indentation | Fifth-order Maxwell model fits relaxation curves | |
| A. N. Natali [52] | Development of visco-hyperelastic constitutive model | Model integrates nonlinearity and time dependence, validated for stress relaxation | ||
| C.G. Fontanella [71] | Quantification of hysteresis | Nonlinear viscoelastic model quantifies energy loss rates | ||
| Robert. Ker [30] | Effect of time intervals on hysteresis | 3.7% increase in energy loss rate per 10× interval time increase | ||
| Biomechanical Functions | 3.1 Cushioning | Kinoshita, H [97] | Age-related cushioning performance | Reduced deformation capacity in elderly leads to higher peak accelerations |
| 3.2 Vibration Damping | Bennett A N [4] | Energy dissipation in vitro | 28.6–32.3% energy loss linked to compartment structure and fat fluidity | |
| Aerts, P. [105] | Vibration attenuation at resonance | Heel pad absorbs 75–80% energy in 20–35 Hz range, outperforming ankle joints | ||
| 3.3 Anti-Fatigue | Qian, Z [12] | Fatigue resistance | Reduced viscous modulus in diabetics increases ulceration risk | |
| 3.4 Touchdown Stability | Chi, K.-J. [94] | Role of mechanical anisotropy | Vertical cushioning + horizontal slip resistance enhance stability |
| Inadequacies of Research | Research Methods in the Future | ||
|---|---|---|---|
| Structure | Lack of 3D modeling of deep large compartments. The arrangement of collagen and elastic fibers in the septum remains to be revealed. | The in vitro heel pad is scanned by micro-CT or micro-MR and modeled by software such as Mimics. The septum obtained by dissecting the heel pad is scanned using electron microscopy to observe the structure and distribution pattern of collagen and elastic fibers. | |
| Materials | Lack of quantification of fat content and septum content. Mechanical properties of fiber septum need to be characterized. | The volume calculation of the modeled deep compartment is done by SolidWorks software 2023. Mechanical properties of the fiber septum obtained by dissection are tested using a universal testing machine. | |
| Biomechanical properties | Hyperelasticity | Since the hyperelasticity of heel pad depends on the deep compartment, hyperelasticity studies of the deep compartment are lacking. | Compression tests are performed on the deep compartment to study its hyperelasticity. |
| Viscoelasticity | Lack of research on creep properties of heel pad. | In vitro heel pad tested in combination with testing machine to characterize its creep properties. | |
| Non-homogeneity | Lack of research on the mechanical properties of heel pad in different positions. | Tests are performed on horizontal section of the heel pad using an ultrasound equipment. | |
| Anisotropy | Lack of testing of heel pad load–displacement in different directions during human walking. | Combining biplane X-ray transmission system and force plate equipment to test the heel pad in human walking. | |
| Biomechanical function | Cushioning | Lack of cushioning performance testing of in vitro heel pad. | Cushioning performance of in vitro heel pads is tested by an impact tester. |
| Vibration damping | Lack of research on the vibration damping properties of in vitro heel pad. | A vibration damping tester need to be constructed using shakers, signal generators, and power amplifiers to test the vibration transfer characteristics of in vitro heel pad. | |
| Anti-fatigue | The anti-fatigue properties of in vitro heel pad need to be characterized in depth. | The S-N fatigue curves are obtained to characterize the fatigue properties of the in vitro heel pad by applying cyclic loads to it with fatigue testing machine. | |
| Touchdown stability | Quantification of the relationship between mechanical anisotropy and touchdown stability of heel pad is lacking. | By preparing bionic materials with mechanical properties comparable to heel pad, the experimental study of mechanical anisotropy on touchdown stability is carried out by adjusting the mechanical anisotropy of the bionic materials. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Z.; Gu, C.; Li, S.; Shen, H.; Liu, N.; Li, Z.; Wang, D.; Wang, C.; Liu, L.; Ba, K.; et al. Materials and Structures Inspired by Human Heel Pads for Advanced Biomechanical Function. Biomimetics 2025, 10, 267. https://doi.org/10.3390/biomimetics10050267
Zhuang Z, Gu C, Li S, Shen H, Liu N, Li Z, Wang D, Wang C, Liu L, Ba K, et al. Materials and Structures Inspired by Human Heel Pads for Advanced Biomechanical Function. Biomimetics. 2025; 10(5):267. https://doi.org/10.3390/biomimetics10050267
Chicago/Turabian StyleZhuang, Zhiqiang, Congtian Gu, Shunlin Li, Hu Shen, Ning Liu, Ziwei Li, Dakai Wang, Cong Wang, Linpeng Liu, Kaixian Ba, and et al. 2025. "Materials and Structures Inspired by Human Heel Pads for Advanced Biomechanical Function" Biomimetics 10, no. 5: 267. https://doi.org/10.3390/biomimetics10050267
APA StyleZhuang, Z., Gu, C., Li, S., Shen, H., Liu, N., Li, Z., Wang, D., Wang, C., Liu, L., Ba, K., Yu, B., & Ma, G. (2025). Materials and Structures Inspired by Human Heel Pads for Advanced Biomechanical Function. Biomimetics, 10(5), 267. https://doi.org/10.3390/biomimetics10050267