IA-DTPSO: A Multi-Strategy Integrated Particle Swarm Optimization for Predicting the Total Urban Water Resources in China
Abstract
1. Introduction
- It is an approximate method that is not specific to a particular problem.
- It is a process of continuously learning towards the optimal solution through trial and error.
- Demonstrates significant multi-functionality and robustness.
- It is an optimization logic used to determine approximate solutions to complex global optimization problems.
- (i)
- Swarm-behavior inspired: Swarm-behavior-inspired algorithms are techniques that mimic collaborative behavior in biological social systems to solve problems. They organize a large number of simple individual units (such as ants, bees, bird swarm agents) together, allowing them to interact and learn in complex environments, and jointly search for optimal solutions. In recent years, newly proposed population-based algorithms include: Whale Optimization Algorithm (WOA) [18], Northern Goshawk Optimization (NGO) [19], Bottlenose Dolphin Optimizer (BDO) [20], Nutcracker Optimization Algorithm (NOA) [21], Mantis Search Algorithm (MSA) [22], Genghis Khan Shark Optimizer (GKSO) [23], Black-winged kite algorithm (BKA) [24], Secretary Bird Optimization Algorithm (SBOA) [25], and Horned Lizard Optimization Algorithm (HLOA) [26].
- (ii)
- Human-behavior inspired: Human-behavior-inspired algorithms typically draw inspiration from human creativity, artistic thinking, and problem-solving approaches, simulating the process of humans making a series of decisions through team collaboration. In recent years, this type of algorithm includes: Enterprise Development Optimizer (EDO) [27], Hiking Optimization Algorithm (HOA) [28], Great Wall Construction Algorithm (GWCA) [29], Football Team Training Algorithm (FTTA) [30], Alpine Skiing Optimization (ASO) [31], Information Acquisition Optimizer (IAO) [32], Adolescent Identity Search Algorithm (AISA) [33], and Information Decision Search Algorithm (IDSE) [34].
- (iii)
- Evolution-phenomena inspired: Evolution-phenomena-inspired algorithms are mainly a type of computational technology that draw inspiration from biological evolution theory. These mainly include Genetic Algorithm (GA) [35], Genetic Programming (GP) [36], Evolutionary Programming (EP) [37], Evolutionary Strategy (ES) [38], Differential Evolution (DE) algorithm [39], Biogeography-based optimization (BBO) [40], Clonal Selection Algorithm (CSA) [41], and Alpha Evolution (AE) [42].
- (iv)
- Nature-science-phenomena inspired: Nature-science-phenomena-inspired algorithms based on natural science phenomena mainly come from observations of natural phenomena and scientific laws in various fields. The latest achievements in this research direction mainly include: Tangent Search Algorithm (TSA) [43], Kepler Optimization Algorithm (KOA) [44], Exponential- Trigonometric Optimization (ETO) algorithm [45], Artemisinin Optimization (AO) algorithm [46], Weighted Average Algorithm (WAA) [5], Newton-Raphson-based Optimizer (NRBO) [47], Polar Lights Optimization (PLO) [48], and FATA morgana algorithm (FATA) [49].
- Difficulty in achieving the optimal balance of ENE, resulting in MAs to local optimum.
- Multiple operators are typically used to approximate the optimum, complicating the search scenario.
- Performance degradation in high-dimensional search space.
- (i)
- A multi-strategy PSO with information acquisition, referred to as IA-DTPSO, is proposed and the entire optimization process is modeled.
- (ii)
- The good ENE ability of IA-DTPSO is validated on CEC2022.
- (iii)
- IA-DTPSO is compared with 11 other algorithms on different dimensions of CEC2022, verifying the superiority of IA-DTPSO.
- (iv)
- IA-DTPSO and seven other algorithms are employed to optimize parameters of TDGM (1,1,r,ξ,Csz) and applied to predict TUWRs in China. In addition, the IA-DTPSO optimized model is compared with three existing models, and the results indicate that the model optimized by IA-DTPSO achieves the minimum error among the four error evaluation metrics in both comparisons.
2. The Classic PSO
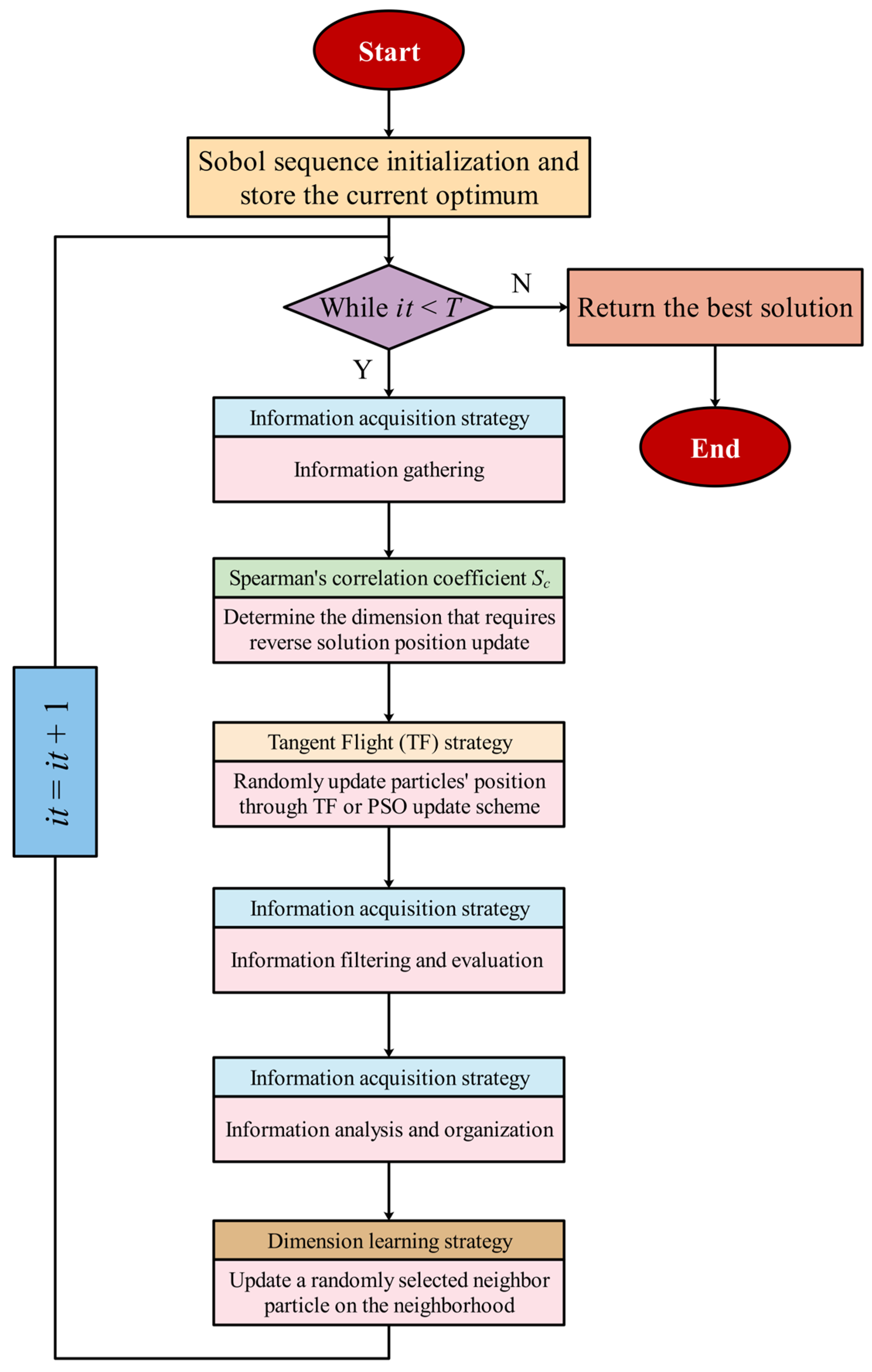
3. The Proposed IA-DTPSO
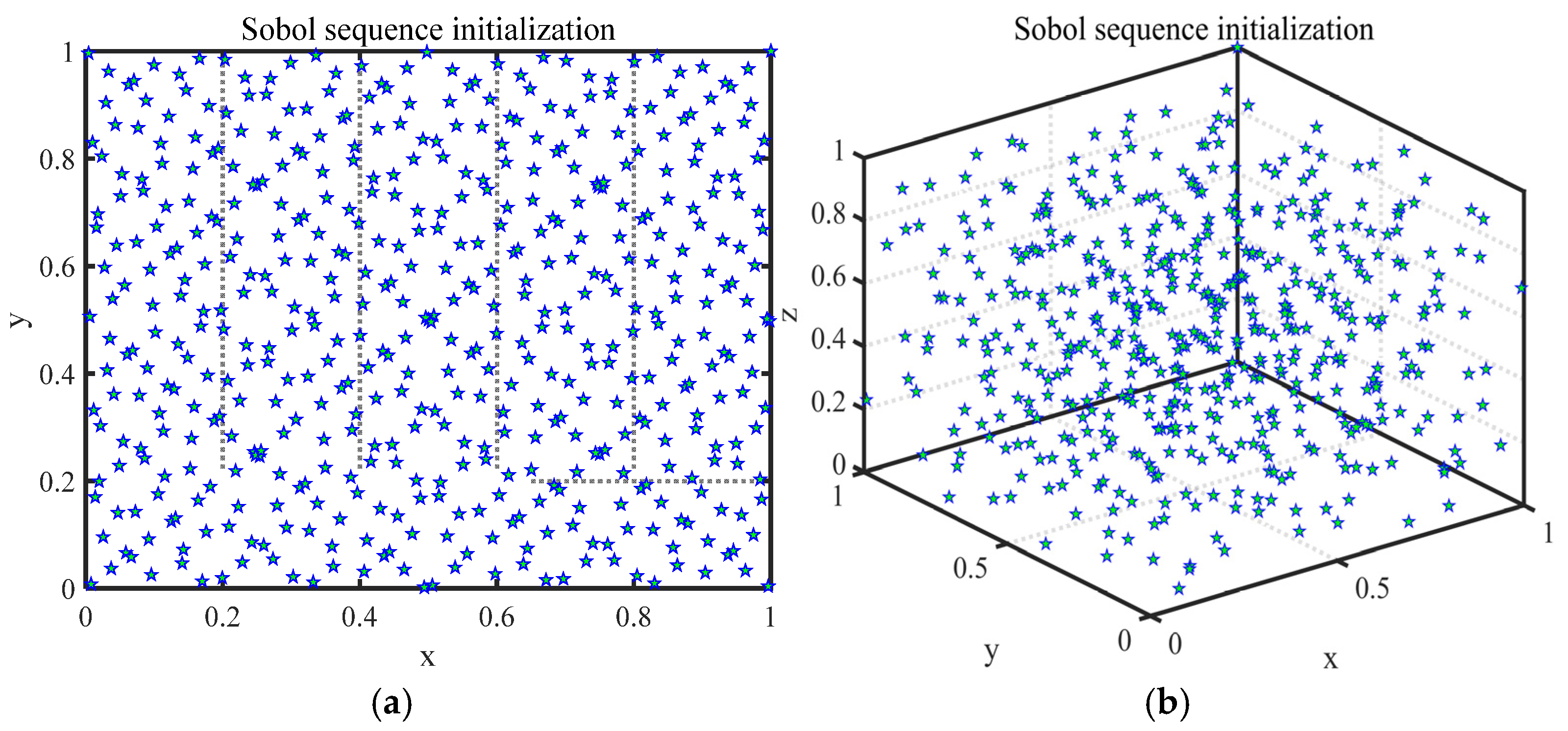
3.1. Sobol Sequence Initialization
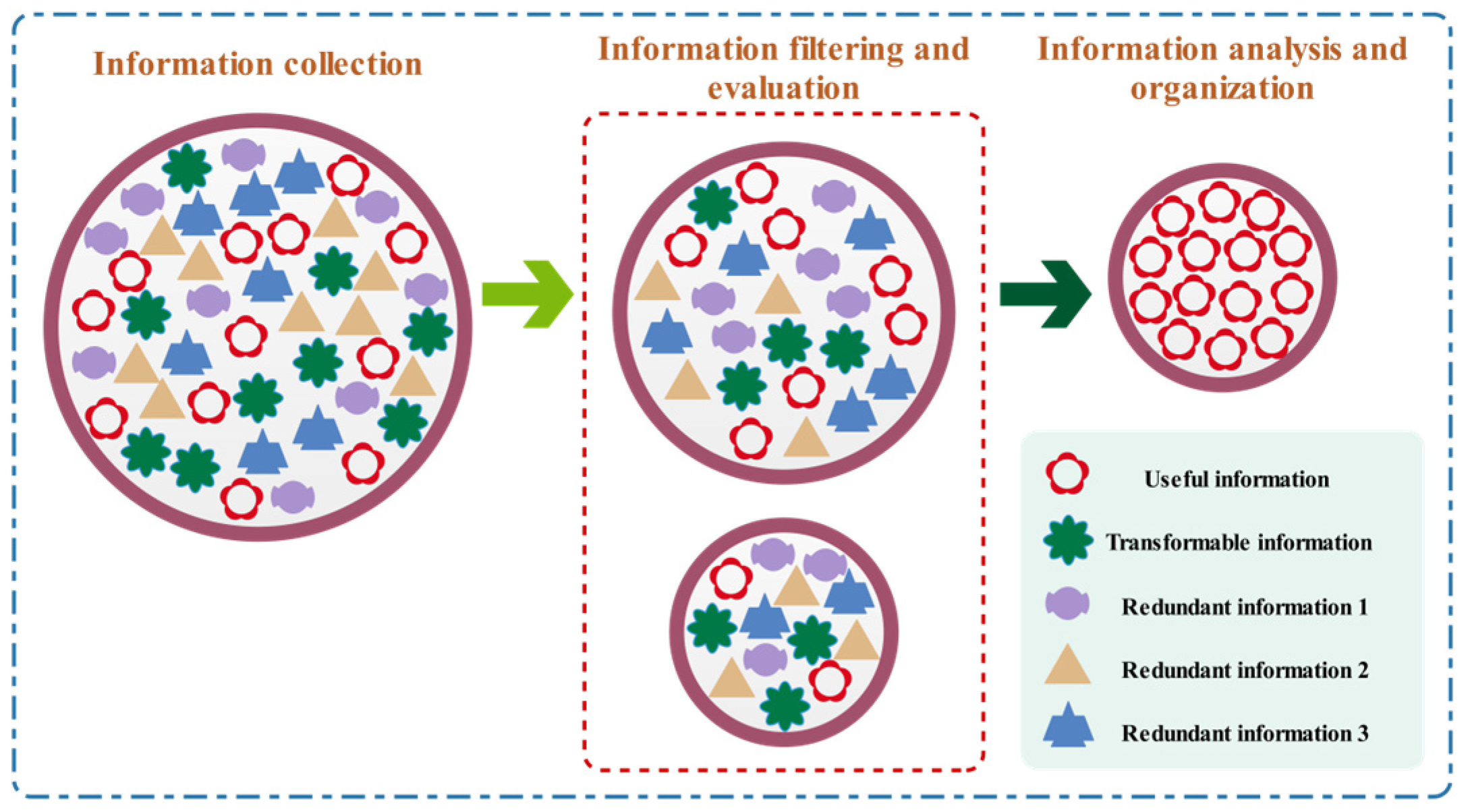
3.2. Information Acquisition Strategy
3.2.1. Information Gathering
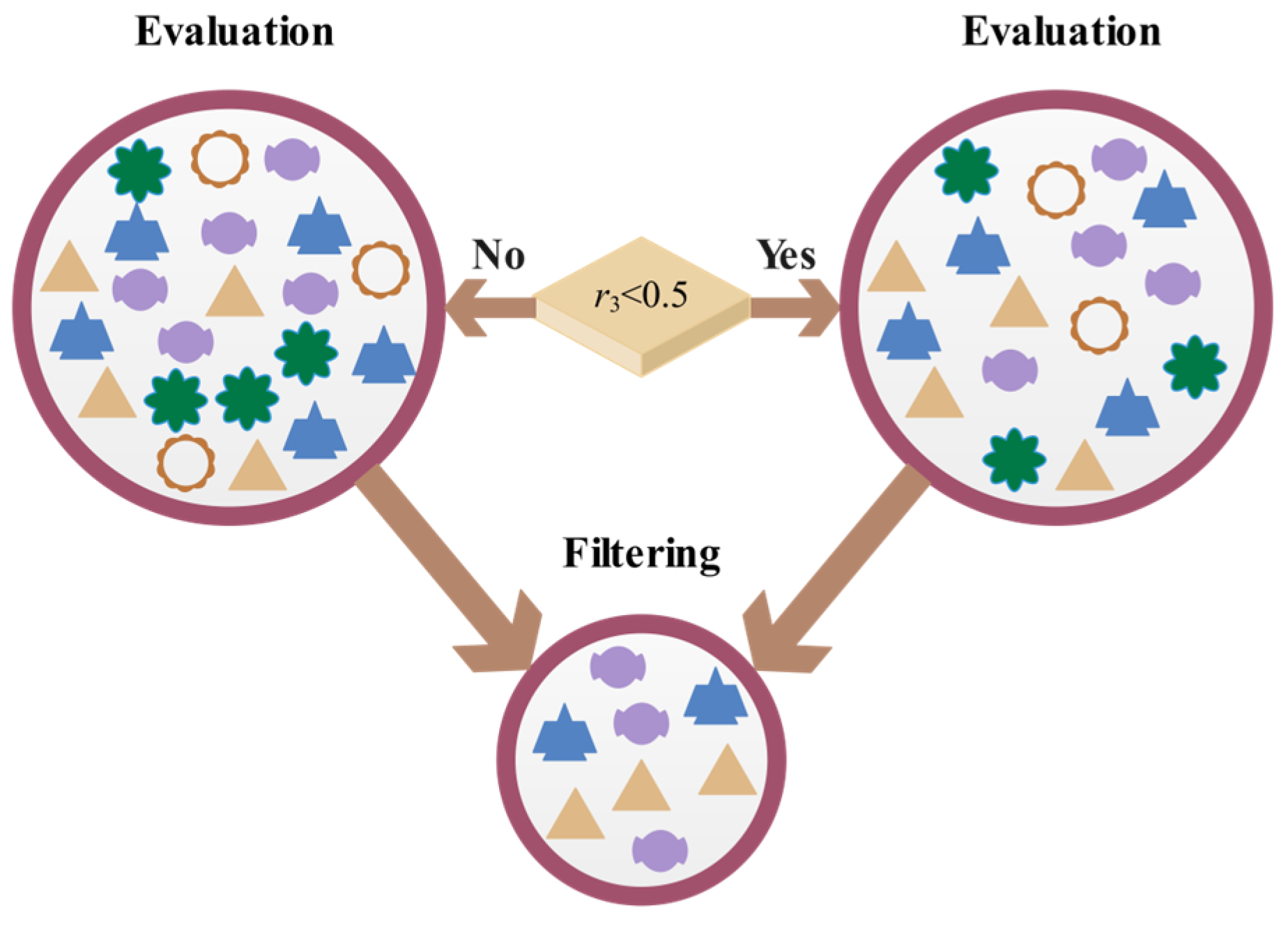
3.2.2. Information Filtering and Evaluation
3.2.3. Information Analysis and Organization
3.3. SCC Method
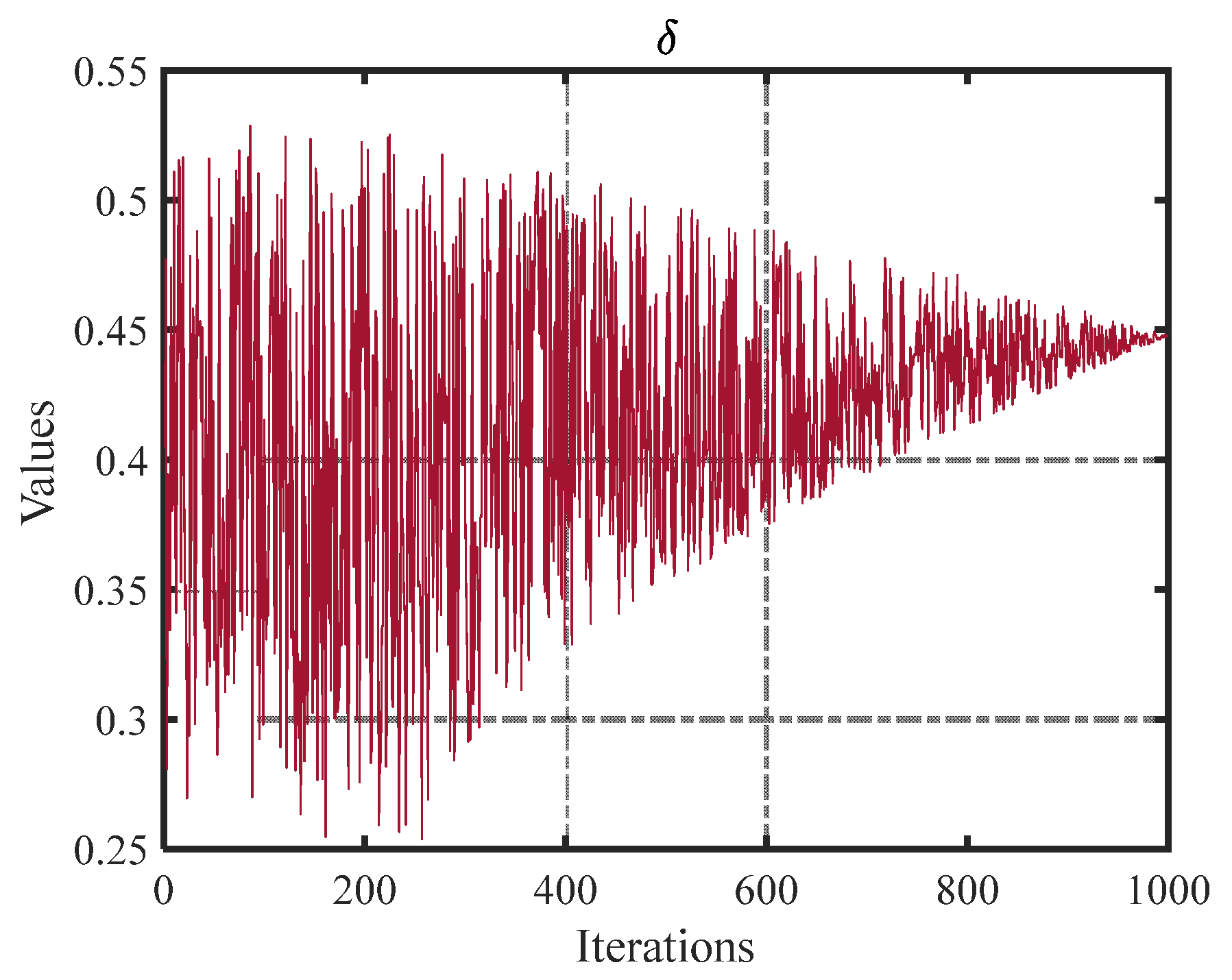
3.4. Tangent Flight Strategy
3.5. Dimension Learning Strategy
| Algorithm 1: IA-DTPSO’s pseudo-code |
| Start IA-DTPSO Input: Particles’ number (N) and iterations (T) Output: The optimum 1: Use Equation (3) for Sobol sequence initialization and store the current optimum |
| 2: While (it < T) Do 3: For i = 1 to N Do 4: Use Equation (4) to form the initial information system 5: End For 6: Update the parameter a using Equation (15) 7: Calculate the Spearman’s correlation coefficient Sc using Equations (12) and (14) 8: For i = 1 to N Do 9: For j = 1 to D Do 10: If Sc <= 0 11: For 12: Use Equation (13) to determine the dimension that requires reverse solution position update 13: End For 14: End If 15: End For 16: End For 17: For i = 1 to N Do 18: Calculate the movement size step using Equation (15) 19: Use Equation (16) for the tangent flight or PSO update scheme to randomly update particles’ position 20: End For 21: For i = 1 to N Do 22: Exploration 23: Update relevant parameters using Equations (6)–(9) 24: Use Equation (5) for information filtering and evaluation process 25: End 26: Exploitation 27: Update parameter using Equation (11) 28: Use Equation (10) for information analysis and organization 29: End 30: End For 31: For i = 1 to N Do 32: Update radius using Equation (18) 33: Construct the neighborhood using Equation (19) 34: For j = 1 to D Do 35: Update a randomly selected neighbor particle on the neighborhood using Equation (20) 36: End For 37: End For 38: Compute fitness values and store the current optimum 39: it = it + 1 40: End While 41: Output the optimum |
| End IA-DTPSO |
3.6. Time Complexity Analysis of IA-DTPSO
4. Experimental Results and Discussion
4.1. Experimental Design and Parameter Setting
- (1)
- (2)
- PSO [17] and its various improved versions: Elite Archives-driven PSO (EAPSO) [60], Gaussian Quantum-behaved PSO (G-QPSO) [61], Hybrid algorithm based on Jellyfish Search PSO (HJSPSO) [62], single-objective variant PSO (PSO-sono) [63], and Multi-strategy PSO incorporating Snow Ablation Optimizer (SAO-MPSO) [64].
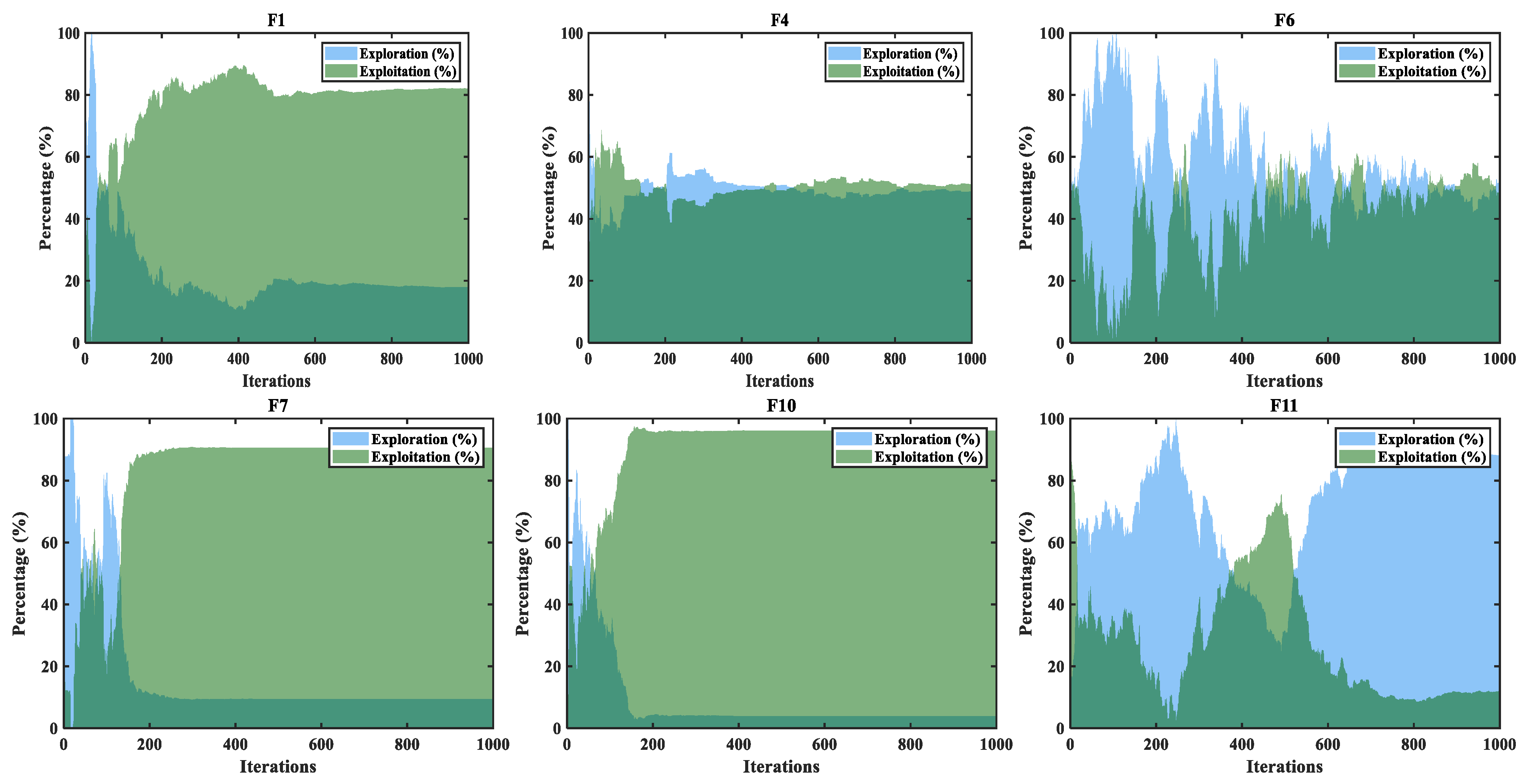
4.2. ENE Behavior Analysis
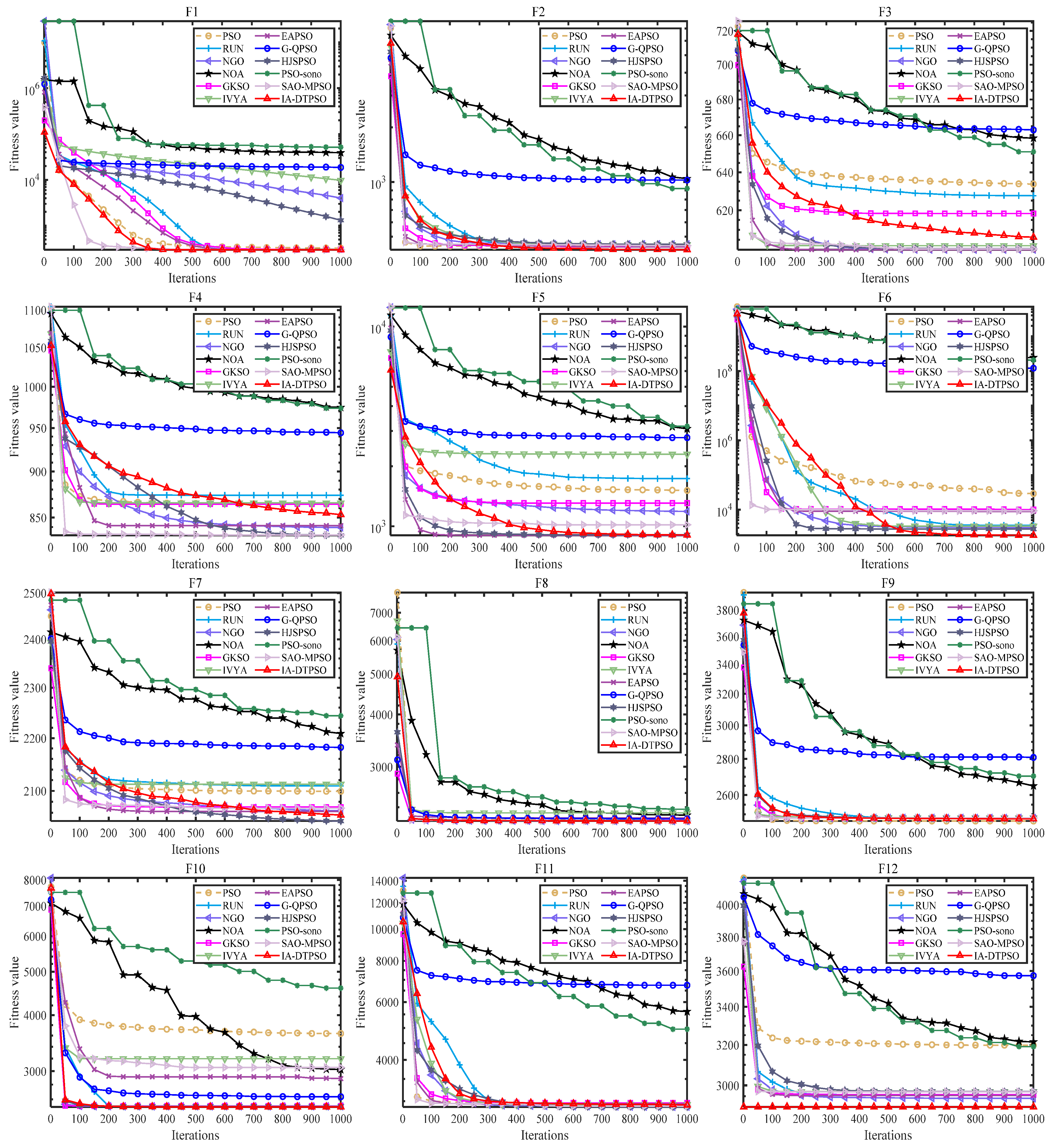
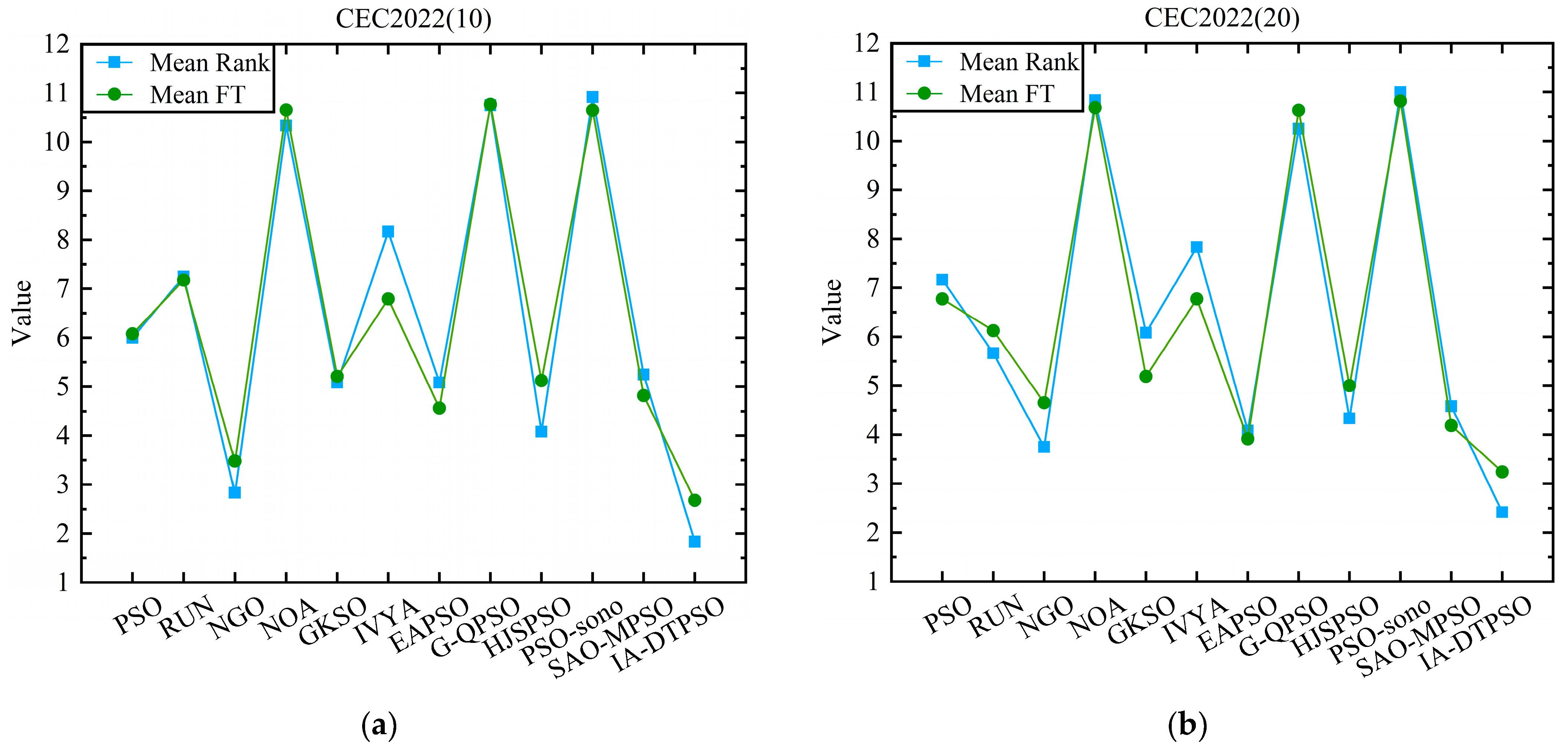
4.3. Experimental Results and Analysis
5. Simulation and Prediction of TUWRs in China Based on IA-DTPSO and TDGM(1,1,r,ξ,Csz)
5.1. TDGM(1,1,r,ξ,Csz)
5.2. Investigation Data Analysis
5.3. Model Evaluation Criteria
5.4. IA-DTPSO and Other Algorithms for Parameter Optimization and Prediction of TDGM (1,1,r,ξ,Csz)
5.5. Four Models for Simulating and Predicting TUWRs in China
6. Conclusions and Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Wang, Y.; Yang, Y.; Ma, Y.; Dai, Z. Fault diagnosis and intelligent maintenance of industry 4.0 power system based on internet of things technology and thermal energy optimization. Therm. Sci. Eng. Prog. 2024, 55, 102902. [Google Scholar]
- Li, Z.; Song, P.; Li, G.; Han, Y.; Ren, X.; Bai, L.; Su, J. AI energized hydrogel design, optimization and application in biomedicine. Mater. Today Bio 2024, 25, 101014. [Google Scholar]
- Yaiprasert, C.; Hidayanto, A.N. AI-powered ensemble machine learning to optimize cost strategies in logistics business. Int. J. Inf. Manag. Data Insights 2024, 4, 100209. [Google Scholar]
- Hong, Q.; Jun, M.; Bo, W.; Sichao, T.; Jiayi, Z.; Biao, L.; Tong, L.; Ruifeng, T. Application of Data-Driven technology in nuclear Engineering: Prediction, classification and design optimization. Ann. Nucl. Energy 2023, 194, 110089. [Google Scholar]
- Cheng, J.; De Waele, W. Weighted average algorithm: A novel meta-heuristic optimization algorithm based on the weighted average position concept. Knowl. -Based Syst. 2024, 305, 112564. [Google Scholar]
- Huang, L.; Wang, Y.; Guo, Y.; Hu, G. An Improved Reptile Search Algorithm Based on Lévy Flight and Interactive Crossover Strategy to Engineering Application. Mathematics 2022, 10, 2329. [Google Scholar] [CrossRef]
- Gobashy, M.; Abdelazeem, M. Metaheuristics Inversion of Self-Potential Anomalies. In Self-Potential Method: Theoretical Modeling and Applications in Geosciences; Biswas, A., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 35–103. [Google Scholar]
- Peng, L.; Cai, Z.; Heidari, A.A.; Zhang, L.; Chen, H. Hierarchical Harris hawks optimizer for feature selection. J. Adv. Res. 2023, 53, 261–278. [Google Scholar]
- Zamani, H.; Nadimi-Shahraki, M.H.; Mirjalili, S.; Gharehchopogh, F.S.; Oliva, D. A Critical Review of Moth-Flame Optimization Algorithm and Its Variants: Structural Reviewing, Performance Evaluation, and Statistical Analysis. Arch. Comput. Methods Eng. 2024, 31, 2177–2225. [Google Scholar]
- Sahoo, S.K.; Houssein, E.H.; Premkumar, M.; Saha, A.K.; Emam, M.M. Self-adaptive moth flame optimizer combined with crossover operator and Fibonacci search strategy for COVID-19 CT image segmentation. Expert Syst. Appl. 2023, 227, 120367. [Google Scholar]
- Li, X.; Lin, Z.; Lv, H.; Yu, L.; Heidari, A.A.; Zhang, Y.; Chen, H.; Liang, G. Advanced slime mould algorithm incorporating differential evolution and Powell mechanism for engineering design. iScience 2023, 26, 107736. [Google Scholar]
- Minh, H.-L.; Sang-To, T.; Wahab, M.A.; Cuong-Le, T. A new metaheuristic optimization based on K-means clustering algorithm and its application to structural damage identification. Knowl. -Based Syst. 2022, 251, 109189. [Google Scholar]
- Salcedo-Sanz, S. Modern meta-heuristics based on nonlinear physics processes: A review of models and design procedures. Phys. Rep. 2016, 655, 1–70. [Google Scholar]
- Abualigah, L.; Diabat, A.; Geem, Z.W. A Comprehensive Survey of the Harmony Search Algorithm in Clustering Applications. Appl. Sci. 2020, 10, 3827. [Google Scholar] [CrossRef]
- Hu, G.; Guo, Y.; Sheng, G. Salp Swarm Incorporated Adaptive Dwarf Mongoose Optimizer with Lévy Flight and Gbest-Guided Strategy. J. Bionic Eng. 2024, 21, 2110–2144. [Google Scholar]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2020, 11, 1501–1529. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proc. ICNN’95—Int. Conf. Neural Netw. 1995, 1944, 1942–1948. [Google Scholar]
- Mahmood, S.; Bawany, N.Z.; Tanweer, M.R. A comprehensive survey of whale optimization algorithm: Modifications and classification. Indones. J. Electr. Eng. Comput. Sci. 2023, 29, 899–910. [Google Scholar]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar]
- Srivastava, A.; Das, D.K. A bottlenose dolphin optimizer: An application to solve dynamic emission economic dispatch problem in the microgrid. Knowl. -Based Syst. 2022, 243, 108455. [Google Scholar]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl. -Based Syst. 2023, 262, 110248. [Google Scholar]
- Abdel-Basset, M.; Mohamed, R.; Zidan, M.; Jameel, M.; Abouhawwash, M. Mantis Search Algorithm: A novel bio-inspired algorithm for global optimization and engineering design problems. Comput. Methods Appl. Mech. Eng. 2023, 415, 116200. [Google Scholar]
- Hu, G.; Guo, Y.; Wei, G.; Abualigah, L. Genghis Khan shark optimizer: A novel nature-inspired algorithm for engineering optimization. Adv. Eng. Inform. 2023, 58, 102210. [Google Scholar]
- Wang, J.; Wang, W.-C.; Hu, X.-X.; Qiu, L.; Zang, H.-F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar]
- Peraza-Vázquez, H.; Peña-Delgado, A.; Merino-Treviño, M.; Morales-Cepeda, A.B.; Sinha, N. A novel metaheuristic inspired by horned lizard defense tactics. Artif. Intell. Rev. 2024, 57, 59. [Google Scholar]
- Truong, D.-N.; Chou, J.-S. Metaheuristic algorithm inspired by enterprise development for global optimization and structural engineering problems with frequency constraints. Eng. Struct. 2024, 318, 118679. [Google Scholar]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl. -Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Guan, Z.; Ren, C.; Niu, J.; Wang, P.; Shang, Y. Great Wall Construction Algorithm: A novel meta-heuristic algorithm for engineer problems. Expert Syst. Appl. 2023, 233, 120905. [Google Scholar]
- Tian, Z.; Gai, M. Football team training algorithm: A novel sport-inspired meta-heuristic optimization algorithm for global optimization. Expert Syst. Appl. 2024, 245, 123088. [Google Scholar]
- Yuan, Y.; Ren, J.; Wang, S.; Wang, Z.; Mu, X.; Zhao, W. Alpine skiing optimization: A new bio-inspired optimization algorithm. Adv. Eng. Softw. 2022, 170, 103158. [Google Scholar] [CrossRef]
- Wu, X.; Li, S.; Jiang, X.; Zhou, Y. Information acquisition optimizer: A new efficient algorithm for solving numerical and constrained engineering optimization problems. J. Supercomput. 2024, 80, 25736–25791. [Google Scholar] [CrossRef]
- Bogar, E.; Beyhan, S. Adolescent Identity Search Algorithm (AISA): A novel metaheuristic approach for solving optimization problems. Appl. Soft Comput. 2020, 95, 106503. [Google Scholar] [CrossRef]
- Wang, K.; Guo, M.; Dai, C.; Li, Z. Information-decision searching algorithm: Theory and applications for solving engineering optimization problems. Inf. Sci. 2022, 607, 1465–1531. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Banzhaf, W.; Koza, J.R.; Ryan, C.; Spector, L.; Jacob, C. Genetic programming. IEEE Intell. Syst. Their Appl. 2000, 15, 74–84. [Google Scholar] [CrossRef]
- Sinha, N.; Chakrabarti, R.; Chattopadhyay, P.K. Evolutionary programming techniques for economic load dispatch. IEEE Trans. Evol. Comput. 2003, 7, 83–94. [Google Scholar] [CrossRef]
- Bäck, T. Evolution strategies: An alternative evolutionary algorithm. In Artificial Evolution; Alliot, J.-M., Lutton, E., Ronald, E., Schoenauer, M., Snyers, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 1–20. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution–A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- De Castro, L.N.; Von Zuben, F.J. The clonal selection algorithm with engineering applications. In Proceedings of the GECCO, Las Vegas, NV, USA, 8–12 July 2000; pp. 36–39. [Google Scholar]
- Gao, H.; Zhang, Q. Alpha evolution: An efficient evolutionary algorithm with evolution path adaptation and matrix generation. Eng. Appl. Artif. Intell. 2024, 137, 109202. [Google Scholar] [CrossRef]
- Layeb, A. Tangent search algorithm for solving optimization problems. Neural Comput. Appl. 2022, 34, 8853–8884. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl. -Based Syst. 2023, 268, 110454. [Google Scholar]
- Luan, T.M.; Khatir, S.; Tran, M.T.; De Baets, B.; Cuong-Le, T. Exponential-trigonometric optimization algorithm for solving complicated engineering problems. Comput. Methods Appl. Mech. Eng. 2024, 432, 117411. [Google Scholar]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Wu, Z.; Chen, H. Artemisinin optimization based on malaria therapy: Algorithm and applications to medical image segmentation. Displays 2024, 84, 102740. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-based optimizer: A new population-based metaheuristic algorithm for continuous optimization problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar]
- Qi, A.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. FATA: An efficient optimization method based on geophysics. Neurocomputing 2024, 607, 128289. [Google Scholar] [CrossRef]
- Yan, J.; Hu, G.; Shu, B. MGCHMO: A dynamic differential human memory optimization with Cauchy and Gauss mutation for solving engineering problems. Adv. Eng. Softw. 2024, 198, 103793. [Google Scholar]
- Hu, G.; Gong, C.; Shu, B.; Xu, Z.; Wei, G. DHRDE: Dual-population hybrid update and RPR mechanism based differential evolutionary algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2024, 431, 117251. [Google Scholar]
- Li, Y.; Su, S.; Hu, F.; He, X.; Su, J.; Zhang, J.; Li, B.; Liu, S.; Man, W. A novel fault location method for distribution networks with distributed generators based on improved seagull optimization algorithm. Energy Rep. 2025, 13, 3237–3245. [Google Scholar]
- Jamal, R.; Khan, N.H.; Ebeed, M.; Zeinoddini-Meymand, H.; Shahnia, F. An improved pelican optimization algorithm for solving stochastic optimal power flow problem of power systems considering uncertainty of renewable energy resources. Results Eng. 2025, 26, 104553. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Sirsant, S.; Reddy, M.J. Improved MOSADE algorithm incorporating Sobol sequences for multi-objective design of Water Distribution Networks. Appl. Soft Comput. 2022, 120, 108682. [Google Scholar]
- Dhargupta, S.; Ghosh, M.; Mirjalili, S.; Sarkar, R. Selective Opposition based Grey Wolf Optimization. Expert Syst. Appl. 2020, 151, 113389. [Google Scholar]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl. -Based Syst. 2024, 295, 111850. [Google Scholar]
- Zhang, Y. Elite archives-driven particle swarm optimization for large scale numerical optimization and its engineering applications. Swarm Evol. Comput. 2023, 76, 101212. [Google Scholar]
- Coelho, L.D.S. Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems. Expert Syst. Appl. 2010, 37, 1676–1683. [Google Scholar]
- Nayyef, H.M.; Ibrahim, A.A.; Zainuri, M.A.A.; Zulkifley, M.A.; Shareef, H. A Novel Hybrid Algorithm Based on Jellyfish Search and Particle Swarm Optimization. Mathematics 2023, 11, 3210. [Google Scholar] [CrossRef]
- Meng, Z.; Zhong, Y.; Mao, G.; Liang, Y. PSO-sono: A novel PSO variant for single-objective numerical optimization. Inf. Sci. 2022, 586, 176–191. [Google Scholar]
- Hu, G.; Guo, Y.; Zhao, W.; Houssein, E.H. An adaptive snow ablation-inspired particle swarm optimization with its application in geometric optimization. Artif. Intell. Rev. 2024, 57, 332. [Google Scholar] [CrossRef]
- Zeng, B.; He, C.; Mao, C.; Wu, Y. Forecasting China’s hydropower generation capacity using a novel grey combination optimization model. Energy 2023, 262, 125341. [Google Scholar] [CrossRef]
- Guan, Y.; Xiao, Y.; Niu, R.; Zhang, N.; Shao, C. Characterizing the water resource-environment-ecology system harmony in Chinese cities using integrated datasets: A Beautiful China perspective assessment. Sci. Total Environ. 2024, 921, 171094. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wang, W.; Wu, Y.; Li, W. Assessment of water retention dynamic in water resource formation area: A case study of the northern slope of the Qinling Mountains in China. J. Hydrol. Reg. Stud. 2024, 56, 102063. [Google Scholar] [CrossRef]
- Hu, G.; Song, K.; Abdel-salam, M. Sub-population evolutionary particle swarm optimization with dynamic fitness-distance balance and elite reverse learning for engineering design problems. Adv. Eng. Softw. 2025, 202, 103866. [Google Scholar] [CrossRef]
- Yuan, C.Q.; Liu, S.F.; Fang, Z.G. Comparison of China’s primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM(1,1) model. Energy 2016, 100, 384–390. [Google Scholar] [CrossRef]
- Ye, J.; Dang, Y.; Ding, S.; Yang, Y. A novel energy consumption forecasting model combining an optimized DGM (1, 1) model with interval grey numbers. J. Clean. Prod. 2019, 229, 256–267. [Google Scholar] [CrossRef]
- Wang, Z.X.; Hipel, K.W.; Wang, Q.; He, S.W. An optimized NGBM(1,1) model for forecasting the qualified discharge rate of industrial wastewater in China. Appl. Math. Model. 2011, 35, 5524–5532. [Google Scholar] [CrossRef]
- Hu, G.; Guo, Y.; Zhong, J.; Wei, G. IYDSE: Ameliorated Young’s double-slit experiment optimizer for applied mechanics and engineering. Comput. Methods Appl. Mech. Eng. 2023, 412, 116062. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Alzahrani, A.I.; Alblehai, F.; Zitar, R.A.; Abualigah, L. An improved Genghis Khan optimizer based on enhanced solution quality strategy for global optimization and feature selection problems. Knowl. -Based Syst. 2024, 302, 112347. [Google Scholar] [CrossRef]
- Hu, G.; Huang, F.; Seyyedabbasi, A.; Wei, G. Enhanced multi-strategy bottlenose dolphin optimizer for UAVs path planning. Appl. Math. Model. 2024, 130, 243–271. [Google Scholar] [CrossRef]





| Algorithms | Proposed Year | Parameter | Value |
|---|---|---|---|
| PSO | 1995 | ω, c1, c2 | 0.8, 2, 2 |
| RUN | 2021 | a, b | 20, 12 |
| NGO | 2021 | - | - |
| NOA | 2023 | Prp, Pa2, N, | 0.2, 0.4, 25, 0.05 |
| GKSO | 2023 | m | 1.5 |
| IVYA | 2024 | - | - |
| EAPSO | 2023 | - | - |
| G-QPSO | 2010 | ω1, ω2, c1, c2 | 0.6, 0.8, 2, 2 |
| HJSPSO | 2023 | cmin, cmax, ωmin, ωmax, β, γ, c0 | 0.5, 2.5, 0.4, 0.9, 0.1, 0.1, 0.5 |
| PSO-sono | 2022 | ωmin, ωmax, iw, r | 0.6, 0.8, [0.4, 0.9], 0.5 |
| SAO-MPSO | 2024 | m, fads, Jump | 1.5, 2, [0, 1] |
| IA-DTPSO | 2025 | θ, a, ω, c1, c2 | [−1, 1], [0, 2], 0.8, 2, 2 |
| Settings | Specifications |
|---|---|
| OS | Windows 11 Version 23H2 22631.4317 |
| CPU | 11th Gen Intel (R) Core (TM) i7-11700 @ 2.50 GHz |
| RAM | 8 GB |
| Language (version) | Matlab (R2024a) |
| F | Index | Algorithms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSO | RUN | NGO | NOA | GKSO | IVYA | EAPSO | G-QPSO | HJSPSO | PSO-Sono | SAO-MPSO | IA-DTPSO | ||
| F1 | Best | 3.001 × 102 | TO | TO | 2.628 × 103 | TO | TO | TO | 1.891 × 103 | TO | 3.875 × 103 | TO | TO |
| Worst | 3.009 × 102 | TO | TO | 1.997 × 104 | TO | 3.075 × 102 | TO | 3.548 × 103 | TO | 2.374 × 104 | TO | TO | |
| Mean | 3.004 × 102 | TO | TO | 8.435 × 103 | TO | 3.011 × 102 | TO | 2.679 × 103 | TO | 1.147 × 104 | TO | TO | |
| WRST | 8.007 × 10−9/- | 8.007 × 10−9/- | 7.992 × 10−9/- | 8.007 × 10−9/- | 6.054 × 10−9/- | 8.007 × 10−9/- | 3.338 × 10−4/- | 8.007 × 10−9/- | 8.007 × 10−9/- | 8.007 × 10−9/- | 1.427 × 10−6/- | - | |
| FT | 8.800 | 7.100 | 5.300 | 11.300 | 3.675 | 8.100 | 2.275 | 10.000 | 5.700 | 11.700 | 2.675 | 1.375 | |
| Rank | 8 | 7 | 5 | 11 | 4 | 9 | 3 | 10 | 6 | 12 | 2 | 1 | |
| F2 | Best | TO | TO | TO | 4.562 × 102 | TO | TO | TO | 5.000 × 102 | TO | 4.576 × 102 | TO | TO |
| Worst | 4.073 × 102 | 4.089 × 102 | 4.071 × 102 | 6.144 × 102 | 4.089 × 102 | 4.742 × 102 | 4.089 × 102 | 6.265 × 102 | 4.041 × 102 | 6.218 × 102 | 4.089 × 102 | 4.001 × 102 | |
| Mean | 4.025 × 102 | 4.036 × 102 | 4.024 × 102 | 5.194 × 102 | 4.055 × 102 | 4.101 × 102 | 4.050 × 102 | 5.678 × 102 | 4.007 × 102 | 5.004 × 102 | 4.049 × 102 | TO | |
| WRST | 4.388 × 10−2/- | 6.949 × 10−1/= | 5.310 × 10−2/= | △/- | 1.604 × 10−4/- | 6.220 × 10−4/- | 1.135 × 10−2/- | △/- | 1.264 × 10−1/= | △/- | 5.842 × 10−7/- | - | |
| FT | 5.300 | 4.400 | 4.750 | 10.900 | 5.750 | 6.350 | 5.475 | 11.800 | 3.850 | 10.250 | 6.125 | 3.050 | |
| Rank | 4 | 5 | 3 | 11 | 8 | 9 | 7 | 12 | 2 | 10 | 6 | 1 | |
| F3 | Best | 6.001 × 102 | 6.002 × 102 | TO | 6.111 × 102 | TO | TO | TO | 6.246 × 102 | TO | 6.184 × 102 | TO | TO |
| Worst | 6.103 × 102 | 6.209 × 102 | TO | 6.414 × 102 | 6.100 × 102 | 6.005 × 102 | TO | 6.437 × 102 | TO | 6.387 × 102 | 6.004 × 102 | 6.002 × 102 | |
| Mean | 6.034 × 102 | 6.097 × 102 | TO | 6.278 × 102 | 6.018 × 102 | TO | TO | 6.365 × 102 | TO | 6.260 × 102 | TO | TO | |
| WRST | 1.065 × 10−7/- | △/- | 2.946 × 10−8/+ | △/- | 2.062 × 10−6/- | 4.355 × 10−7/- | 2.439 × 10−8/+ | △/- | 6.810 × 10−7/+ | △/- | 6.092 × 10−7/- | - | |
| FT | 8.000 | 8.700 | 3.200 | 10.800 | 7.250 | 1.475 | 2.825 | 11.800 | 4.625 | 10.350 | 3.075 | 5.900 | |
| Rank | 8 | 9 | 2 | 11 | 7 | 6 | 1 | 12 | 3 | 10 | 5 | 4 | |
| F4 | Best | 8.080 × 102 | 8.109 × 102 | 8.030 × 102 | 8.369 × 102 | 8.090 × 102 | 8.090 × 102 | 8.040 × 102 | 8.304 × 102 | 8.030 × 102 | 8.397 × 102 | 8.060 × 102 | 8.025 × 102 |
| Worst | 8.448 × 102 | 8.338 × 102 | 8.107 × 102 | 8.640 × 102 | 8.328 × 102 | 8.348 × 102 | 8.318 × 102 | 8.432 × 102 | 8.090 × 102 | 8.691 × 102 | 8.259 × 102 | 8.149 × 102 | |
| Mean | 8.194 × 102 | 8.205 × 102 | 8.069 × 102 | 8.512 × 102 | 8.176 × 102 | 8.186 × 102 | 8.174 × 102 | 8.374 × 102 | 8.064 × 102 | 8.540 × 102 | 8.133 × 102 | 8.083 × 102 | |
| WRST | 3.293 × 10−5/- | 1.431 × 10−7/- | 4.388 × 10−2/+ | △/- | 1.198 × 10−6/- | 1.200 × 10−6/- | 1.103 × 10−5/- | △/- | 7.114 × 10−3/+ | △/- | 5.111 × 10−3/- | - | |
| FT | 6.700 | 7.400 | 2.100 | 11.350 | 6.250 | 6.900 | 6.350 | 10.000 | 1.950 | 11.500 | 4.550 | 2.950 | |
| Rank | 8 | 9 | 2 | 11 | 6 | 7 | 5 | 10 | 1 | 12 | 4 | 3 | |
| F5 | Best | TO | 9.023 × 102 | TO | 9.975 × 102 | TO | 1.007 × 103 | TO | 1.079 × 103 | TO | 1.001 × 103 | TO | TO |
| Worst | 9.001 × 102 | 1.021 × 103 | 9.001 × 102 | 1.381 × 103 | 9.017 × 102 | 1.710 × 103 | 9.005 × 102 | 1.182 × 103 | 9.005 × 102 | 1.366 × 103 | 9.005 × 102 | 9.006 × 102 | |
| Mean | TO | 9.714 × 102 | TO | 1.199 × 103 | 9.003 × 102 | 1.243 × 103 | TO | 1.110 × 103 | TO | 1.161 × 103 | 9.001 × 102 | TO | |
| WRST | 2.745 × 10−4/+ | △/- | 9.996 × 10−7/+ | △/- | 4.088 × 10−1/= | △/- | 6.326 × 10−6/- | △/- | 4.703 × 10−3/+ | △/- | 2.033 × 10−2/- | - | |
| FT | 5.650 | 8.000 | 2.875 | 11.000 | 4.900 | 10.900 | 1.600 | 9.750 | 4.550 | 10.350 | 3.375 | 5.050 | |
| Rank | 2 | 8 | 1 | 11 | 7 | 12 | 5 | 9 | 3 | 10 | 6 | 4 | |
| F6 | Best | 1.866 × 103 | 1.903 × 103 | 1.828 × 103 | 8.824 × 105 | 1.826 × 103 | 1.857 × 103 | 1.942 × 103 | 3.479 × 105 | 1.843 × 103 | 4.901 × 105 | 1.902 × 103 | TO |
| Worst | 6.960 × 103 | 4.950 × 103 | 1.943 × 103 | 3.144 × 107 | 5.528 × 103 | 8.090 × 103 | 7.181 × 103 | 4.242 × 106 | 3.069 × 103 | 2.214 × 107 | 7.657 × 103 | 1.803 × 103 | |
| Mean | 3.069 × 103 | 3.096 × 103 | 1.882 × 103 | 8.279 × 106 | 2.236 × 103 | 4.031 × 103 | 4.335 × 103 | 2.007 × 106 | 2.109 × 103 | 6.362 × 106 | 4.436 × 103 | 1.801 × 103 | |
| WRST | △/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | - | |
| FT | 5.700 | 6.450 | 2.750 | 11.350 | 3.950 | 6.850 | 7.150 | 10.500 | 4.150 | 11.150 | 7.000 | 1.000 | |
| Rank | 5 | 6 | 2 | 12 | 4 | 7 | 8 | 10 | 3 | 11 | 9 | 1 | |
| F7 | Best | 2.002 × 103 | 2.017 × 103 | 2.001 × 103 | 2.046 × 103 | 2.002 × 103 | 2.001 × 103 | TO | 2.070 × 103 | 2.001 × 103 | 2.051 × 103 | 2.001 × 103 | 2.001 × 103 |
| Worst | 2.045 × 103 | 2.058 × 103 | 2.011 × 103 | 2.096 × 103 | 2.026 × 103 | 2.084 × 103 | 2.054 × 103 | 2.105 × 103 | 2.025 × 103 | 2.121 × 103 | 2.025 × 103 | 2.022 × 103 | |
| Mean | 2.028 × 103 | 2.036 × 103 | 2.004 × 103 | 2.072 × 103 | 2.020 × 103 | 2.021 × 103 | 2.017 × 103 | 2.088 × 103 | 2.010 × 103 | 2.085 × 103 | 2.012 × 103 | 2.009 × 103 | |
| WRST | 2.062 × 10−6/- | 1.431 × 10−7/- | 1.782 × 10−3/+ | △/- | 1.610 × 10−4/- | 1.143 × 10−2/- | 1.404 × 10−1/= | △/- | 8.392 × 10−1/= | △/- | 8.392 × 10−1/= | - | |
| FT | 7.500 | 8.000 | 2.050 | 10.300 | 5.700 | 5.700 | 4.650 | 11.400 | 4.100 | 11.200 | 3.800 | 3.600 | |
| Rank | 8 | 9 | 1 | 10 | 6 | 7 | 5 | 12 | 3 | 11 | 4 | 2 | |
| F8 | Best | 2.202 × 103 | 2.204 × 103 | 2.208 × 103 | 2.228 × 103 | TO | 2.201 × 103 | TO | 2.224 × 103 | 2.210 × 103 | 2.221 × 103 | TO | 2.207 × 103 |
| Worst | 2.228 × 103 | 2.226 × 103 | 2.223 × 103 | 2.245 × 103 | 2.221 × 103 | 2.224 × 103 | 2.222 × 103 | 2.235 × 103 | 2.227 × 103 | 2.312 × 103 | 2.221 × 103 | 2.215 × 103 | |
| Mean | 2.223 × 103 | 2.222 × 103 | 2.218 × 103 | 2.237 × 103 | 2.216 × 103 | 2.219 × 103 | 2.220 × 103 | 2.232 × 103 | 2.223 × 103 | 2.246 × 103 | 2.216 × 103 | 2.210 × 103 | |
| WRST | 1.201 × 10−6/- | 1.201 × 10−6/- | 3.705 × 10−5/- | △/- | 7.114 × 10−3/- | 1.807 × 10−5/- | 1.201 × 10−6/- | △/- | 4.539 × 10−7/- | △/- | 7.114 × 10−3/- | - | |
| FT | 7.250 | 7.100 | 4.800 | 11.150 | 3.400 | 5.200 | 4.500 | 10.100 | 7.550 | 11.500 | 3.450 | 2.000 | |
| Rank | 8 | 7 | 4 | 11 | 3 | 5 | 6 | 10 | 8 | 12 | 2 | 1 | |
| F9 | Best | 2.486 × 103 | 2.529 × 103 | 2.529 × 103 | 2.570 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.643 × 103 | 2.529 × 103 | 2.586 × 103 | 2.529 × 103 | 2.486 × 103 |
| Worst | 2.486 × 103 | 2.529 × 103 | 2.529 × 103 | 2.710 × 103 | 2.529 × 103 | 2.676 × 103 | 2.529 × 103 | 2.669 × 103 | 2.529 × 103 | 2.683 × 103 | 2.529 × 103 | 2.490 × 103 | |
| Mean | 2.486 × 103 | 2.529 × 103 | 2.529 × 103 | 2.620 × 103 | 2.529 × 103 | 2.537 × 103 | 2.529 × 103 | 2.659 × 103 | 2.529 × 103 | 2.640 × 103 | 2.529 × 103 | 2.488 × 103 | |
| WRST | △/+ | △/- | 1.127 × 10−8/- | △/- | 6.777 × 10−8/- | 5.366 × 10−8/- | 8.007 × 10−9/- | △/- | 6.644 × 10−8/- | △/- | 1.945 × 10−8/- | - | |
| FT | 1.000 | 8.850 | 4.250 | 10.400 | 7.525 | 6.375 | 4.175 | 11.550 | 6.550 | 10.900 | 4.425 | 2.000 | |
| Rank | 1 | 8 | 4 | 10 | 7 | 9 | 3 | 12 | 6 | 11 | 5 | 2 | |
| F10 | Best | TO | TO | TO | 2.503 × 103 | TO | TO | TO | 2.508 × 103 | TO | 2.502 × 103 | TO | TO |
| Worst | 2.633 × 103 | 2.619 × 103 | TO | 2.676 × 103 | TO | 2.638 × 103 | 2.618 × 103 | 2.651 × 103 | TO | 2.684 × 103 | TO | TO | |
| Mean | 2.555 × 103 | 2.534 × 103 | TO | 2.533 × 103 | TO | 2.541 × 103 | 2.512 × 103 | 2.539 × 103 | TO | 2.547 × 103 | TO | TO | |
| WRST | △/- | 6.674 × 10−6/- | 8.604 × 10−1/= | △/- | 6.868 × 10−4/- | 4.540 × 10−6/- | 1.105 × 10−5/- | △/- | 3.048 × 10−4/- | △/- | 6.750 × 10−1/= | - | |
| FT | 6.750 | 8.100 | 4.000 | 9.950 | 3.550 | 7.950 | 6.550 | 10.400 | 5.650 | 9.600 | 3.650 | 1.850 | |
| Rank | 12 | 8 | 5 | 7 | 2 | 10 | 6 | 9 | 3 | 11 | 4 | 1 | |
| F11 | Best | 2.601 × 103 | TO | TO | 2.762 × 103 | TO | TO | TO | 2.822 × 103 | TO | 2.769 × 103 | TO | TO |
| Worst | 3.001 × 103 | 3.184 × 103 | TO | 2.871 × 103 | 3.000 × 103 | 3.000 × 103 | 3.000 × 103 | 2.899 × 103 | TO | 3.429 × 103 | 3.184 × 103 | TO | |
| Mean | 2.672 × 103 | 2.659 × 103 | TO | 2.815 × 103 | 2.640 × 103 | 2.768 × 103 | 2.673 × 103 | 2.865 × 103 | TO | 2.835 × 103 | 2.964 × 103 | TO | |
| WRST | 3.473 × 10−8/- | 3.473 × 10−8/- | 2.512 × 10−1/= | 3.473 × 10−8/- | 1.889 × 10−4/- | 6.682 × 10−5/- | 5.164 × 10−2/= | 3.473 × 10−8/- | 1.512 × 10−5/- | 3.473 × 10−8/- | 8.221 × 10−6/- | - | |
| FT | 7.750 | 6.750 | 2.400 | 8.900 | 4.675 | 7.100 | 4.075 | 10.050 | 5.200 | 8.900 | 9.900 | 2.300 | |
| Rank | 6 | 5 | 2 | 9 | 4 | 8 | 7 | 11 | 3 | 10 | 12 | 1 | |
| F12 | Best | 2.801 × 103 | 2.862 × 103 | 2.859 × 103 | 2.872 × 103 | 2.863 × 103 | 2.864 × 103 | 2.863 × 103 | 2.931 × 103 | 2.865 × 103 | 2.875 × 103 | 2.862 × 103 | 2.846 × 103 |
| Worst | 2.926 × 103 | 2.867 × 103 | 2.864 × 103 | 2.967 × 103 | 2.868 × 103 | 2.920 × 103 | 2.866 × 103 | 2.966 × 103 | 2.871 × 103 | 3.000 × 103 | 2.866 × 103 | 2.849 × 103 | |
| Mean | 2.857 × 103 | 2.864 × 103 | 2.862 × 103 | 2.891 × 103 | 2.865 × 103 | 2.871 × 103 | 2.864 × 103 | 2.948 × 103 | 2.866 × 103 | 2.898 × 103 | 2.864 × 103 | 2.847 × 103 | |
| WRST | 1.803 × 10−6/- | △/- | △/- | △/- | 6.786 × 10−8/- | 6.757 × 10−8/- | 6.786 × 10−8/- | △/- | △/- | △/- | 6.786 × 10−8/- | - | |
| FT | 2.550 | 5.300 | 3.300 | 10.450 | 5.900 | 8.600 | 5.150 | 11.850 | 7.600 | 10.400 | 5.800 | 1.100 | |
| Rank | 2 | 6 | 3 | 10 | 7 | 9 | 5 | 12 | 8 | 11 | 4 | 1 | |
| Mean Rank | 6.000 | 7.250 | 2.833 | 10.333 | 5.083 | 8.167 | 5.083 | 10.750 | 4.083 | 10.917 | 5.250 | 1.833 | |
| Final Ranking | 7 | 8 | 2 | 10 | 4 | 9 | 4 | 11 | 3 | 12 | 6 | 1 | |
| Mean FT | 6.079 | 7.179 | 3.481 | 10.654 | 5.210 | 6.792 | 4.565 | 10.767 | 5.123 | 10.650 | 4.819 | 2.681 | |
| Final FT | 7 | 9 | 2 | 11 | 6 | 8 | 3 | 12 | 5 | 10 | 4 | 1 | |
| +/=/− | 2/0/10 | 0/1/11 | 4/3/5 | 0/0/12 | 0/1/11 | 0/0/12 | 1/2/9 | 0/0/12 | 3/2/7 | 0/0/12 | 0/2/10 | -/-/- | |
| F | Index | Algorithms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSO | RUN | NGO | NOA | GKSO | IVYA | EAPSO | G-QPSO | HJSPSO | PSO-Sono | SAO-MPSO | IA-DTPSO | ||
| F1 | Std | 2.461 × 10−1 | 1.625 × 10−5 | 5.384 × 10−10 | 4.211 × 103 | 1.258 × 10−13 | 2.249 | 4.124 × 10−14 | 4.362 × 102 | 3.157 × 10−9 | 5.113 × 103 | 2.916 × 10−14 | 0.000 |
| RMSE | 2.994 × 102 | 2.990 × 102 | 2.990 × 102 | 9.379 × 103 | 2.990 × 102 | 3.001 × 102 | 2.990 × 102 | 2.711 × 103 | 2.990 × 102 | 1.251 × 104 | 2.990 × 102 | 2.990 × 102 | |
| δ | 2.991 × 102 | 2.990 × 102 | 2.990 × 102 | 2.627 × 103 | 2.990 × 102 | 2.990 × 102 | 2.990 × 102 | 1.890 × 103 | 2.990 × 102 | 3.874 × 103 | 2.990 × 102 | 2.990 × 102 | |
| F2 | Std | 2.265 | 4.481 | 2.538 | 3.991 × 101 | 3.834 | 2.175 × 101 | 3.660 | 3.138 × 101 | 1.458 | 3.467 × 101 | 4.042 | 3.083 × 10−2 |
| RMSE | 4.015 × 102 | 4.026 × 102 | 3.990 × 102 | 5.198 × 102 | 4.045 × 102 | 4.096 × 102 | 4.040 × 102 | 5.676 × 102 | 3.997 × 102 | 5.005 × 102 | 4.039 × 102 | 4.014 × 102 | |
| δ | 3.990 × 102 | 3.990 × 102 | 3.990 × 102 | 4.552 × 102 | 3.990 × 102 | 3.990 × 102 | 3.990 × 102 | 4.990 × 102 | 3.990 × 102 | 4.566 × 102 | 3.990 × 102 | 3.990 × 102 | |
| F3 | Std | 2.602 | 7.359 | 1.744 × 10−6 | 7.342 | 2.593 | 1.228 × 10−1 | 6.901 × 10−14 | 3.930 | 4.006 × 10−3 | 4.209 | 9.164 × 10−2 | 4.160 × 10−2 |
| RMSE | 6.024 × 102 | 6.087 × 102 | 5.990 × 102 | 6.268 × 102 | 6.008 × 102 | 5.990 × 102 | 5.990 × 102 | 6.355 × 102 | 5.990 × 102 | 6.250 × 102 | 5.990 × 102 | 5.990 × 102 | |
| δ | 5.991 × 102 | 5.992 × 102 | 5.990 × 102 | 6.101 × 102 | 5.990 × 102 | 5.990 × 102 | 5.990 × 102 | 6.236 × 102 | 5.990 × 102 | 6.174 × 102 | 5.990 × 102 | 5.990 × 102 | |
| F4 | Std | 9.612 | 5.622 | 2.012 | 7.638 | 6.515 | 6.833 | 6.587 | 3.618 | 1.618 | 8.390 | 6.020 | 2.867 |
| RMSE | 8.185 × 102 | 8.196 × 102 | 8.059 × 102 | 8.503 × 102 | 8.166 × 102 | 8.176 × 102 | 8.165 × 102 | 8.364 × 102 | 8.054 × 102 | 8.531 × 102 | 8.124 × 102 | 8.073 × 102 | |
| δ | 8.070 × 102 | 8.099 × 102 | 8.020 × 102 | 8.359 × 102 | 8.080 × 102 | 8.080 × 102 | 8.030 × 102 | 8.294 × 102 | 8.020 × 102 | 8.387 × 102 | 8.050 × 102 | 8.015 × 102 | |
| F5 | Std | 3.486 × 10−2 | 3.548 × 101 | 2.002 × 10−2 | 1.137 × 102 | 4.573 × 10−1 | 1.707 × 102 | 1.543 × 10−1 | 2.964 × 101 | 1.139 × 10−1 | 8.556 × 101 | 1.385 × 10−1 | 1.334 × 10−1 |
| RMSE | 8.990 × 102 | 9.710 × 102 | 8.990 × 102 | 1.203 × 103 | 8.993 × 102 | 1.254 × 103 | 8.990 × 102 | 1.109 × 103 | 8.990 × 102 | 1.163 × 103 | 8.991 × 102 | 8.990 × 102 | |
| δ | 8.990 × 102 | 9.013 × 102 | 8.990 × 102 | 9.965 × 102 | 8.990 × 102 | 1.006 × 103 | 8.990 × 102 | 1.078 × 103 | 8.990 × 102 | 9.998 × 102 | 8.990 × 102 | 8.990 × 102 | |
| F6 | Std | 1.600 × 103 | 1.128 × 103 | 3.221 × 101 | 9.251 × 106 | 8.287 × 102 | 2.139 × 103 | 2.003 × 103 | 1.298 × 106 | 3.062 × 102 | 5.700 × 106 | 2.261 × 103 | 9.067 × 10−1 |
| RMSE | 3.442 × 103 | 3.284 × 103 | 1.881 × 103 | 1.224 × 107 | 2.376 × 103 | 4.537 × 103 | 4.753 × 103 | 2.372 × 106 | 2.129 × 103 | 8.446 × 106 | 4.952 × 103 | TO | |
| δ | 1.865 × 103 | 1.902 × 103 | 1.827 × 103 | 8.824 × 105 | 1.825 × 103 | 1.856 × 103 | 1.941 × 103 | 3.479 × 105 | 1.842 × 103 | 4.901 × 105 | 1.901 × 103 | 1.799 × 103 | |
| F7 | Std | 9.656 | 1.171 × 101 | 3.449 | 1.378 × 101 | 6.571 | 1.823 × 101 | 1.383 × 101 | 9.648 | 9.078 | 1.718 × 101 | 9.943 | 5.864 |
| RMSE | 2.027 × 103 | 2.035 × 103 | 2.003 × 103 | 2.071 × 103 | 2.019 × 103 | 2.020 × 103 | 2.016 × 103 | 2.087 × 103 | 2.009 × 103 | 2.084 × 103 | 2.011 × 103 | 2.008 × 103 | |
| δ | 2.001 × 103 | 2.016 × 103 | TO | 2.045 × 103 | 2.001 × 103 | TO | 1.999 × 103 | 2.069 × 103 | TO | 2.050 × 103 | TO | TO | |
| F8 | Std | 5.340 | 4.507 | 5.146 | 4.450 | 8.882 | 5.876 | 4.653 | 2.753 | 4.466 | 1.754 × 101 | 8.845 | 2.329 |
| RMSE | 2.222 × 103 | 2.221 × 103 | 2.217 × 103 | 2.236 × 103 | 2.215 × 103 | 2.218 × 103 | 2.219 × 103 | 2.231 × 103 | 2.222 × 103 | 2.246 × 103 | 2.215 × 103 | 2.209 × 103 | |
| δ | 2.201 × 103 | 2.203 × 103 | 2.207 × 103 | 2.227 × 103 | 2.199 × 103 | TO | 2.199 × 103 | 2.223 × 103 | 2.209 × 103 | 2.220 × 103 | 2.199 × 103 | 2.206 × 103 | |
| F9 | Std | 1.141 × 10−3 | 3.325 × 10−5 | 1.043 × 10−13 | 3.961 × 101 | 4.092 × 10−9 | 3.286 × 101 | 0.000 | 8.315 | 5.291 × 10−12 | 2.874 × 101 | 1.807 × 10−13 | 1.108 |
| RMSE | 2.485 × 103 | 2.528 × 103 | 2.528 × 103 | 2.619 × 103 | 2.528 × 103 | 2.536 × 103 | 2.528 × 103 | 2.659 × 103 | 2.528 × 103 | 2.639 × 103 | 2.528 × 103 | 2.487 × 103 | |
| δ | 2.485 × 103 | 2.528 × 103 | 2.528 × 103 | 2.569 × 103 | 2.528 × 103 | 2.528 × 103 | 2.528 × 103 | 2.642 × 103 | 2.528 × 103 | 2.585 × 103 | 2.528 × 103 | 2.485 × 103 | |
| F10 | Std | 6.277 × 101 | 5.267 × 101 | 8.037 × 10−2 | 5.130 × 101 | 5.454 × 10−2 | 5.760 × 101 | 3.488 × 101 | 4.883 × 101 | 7.003 × 10−2 | 7.598 × 101 | 7.548 × 10−2 | 5.131 × 10−2 |
| RMSE | 2.555 × 103 | 2.534 × 103 | 2.499 × 103 | 2.532 × 103 | 2.499 × 103 | 2.541 × 103 | 2.511 × 103 | 2.538 × 103 | 2.499 × 103 | 2.547 × 103 | 2.499 × 103 | 2.499 × 103 | |
| δ | 2.499 × 103 | 2.499 × 103 | 2.499 × 103 | 2.502 × 103 | 2.499 × 103 | 2.499 × 103 | 2.499 × 103 | 2.507 × 103 | 2.499 × 103 | 2.501 × 103 | 2.499 × 103 | 2.499 × 103 | |
| F11 | Std | 1.455 × 102 | 1.378 × 102 | 6.211 × 10−10 | 3.421 × 101 | 1.231 × 102 | 1.808 × 102 | 1.352 × 102 | 2.235 × 101 | 2.612 × 10−9 | 1.603 × 102 | 1.852 × 102 | 3.460 × 10−13 |
| RMSE | 2.674 × 103 | 2.662 × 103 | 2.599 × 103 | 2.815 × 103 | 2.642 × 103 | 2.772 × 103 | 2.675 × 103 | 2.864 × 103 | 2.599 × 103 | 2.839 × 103 | 2.969 × 103 | 2.599 × 103 | |
| δ | TO | 2.599 × 103 | 2.599 × 103 | 2.761 × 103 | 2.599 × 103 | 2.599 × 103 | 2.599 × 103 | 2.821 × 103 | 2.599 × 103 | 2.768 × 103 | 2.599 × 103 | 2.599 × 103 | |
| F12 | Std | 2.080 × 101 | 1.145 | 1.688 | 2.276 × 101 | 1.362 | 1.232 × 101 | 1.064 | 9.563 | 1.749 | 3.320 × 101 | 9.740 × 10−1 | 7.480 × 10−1 |
| RMSE | 2.856 × 103 | 2.863 × 103 | 2.861 × 103 | 2.890 × 103 | 2.864 × 103 | 2.870 × 103 | 2.863 × 103 | 2.947 × 103 | 2.865 × 103 | 2.897 × 103 | 2.863 × 103 | 2.846 × 103 | |
| δ | 2.800 × 103 | 2.861 × 103 | 2.858 × 103 | 2.871 × 103 | 2.862 × 103 | 2.863 × 103 | 2.862 × 103 | 2.930 × 103 | 2.864 × 103 | 2.874 × 103 | 2.861 × 103 | 2.845 × 103 | |
| F | Index | Algorithms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSO | RUN | NGO | NOA | GKSO | IVYA | EAPSO | G-QPSO | HJSPSO | PSO-Sono | SAO-MPSO | IA-DTPSO | ||
| F1 | Best | 3.153 × 102 | TO | 2.016 × 103 | 2.665 × 104 | TO | 5.133 × 103 | TO | 1.452 × 104 | 6.166 × 102 | 2.779 × 104 | TO | TO |
| Worst | 3.434 × 102 | TO | 6.215 × 103 | 6.186 × 104 | TO | 1.751 × 104 | TO | 2.237 × 104 | 2.105 × 103 | 9.624 × 104 | TO | TO | |
| Mean | 3.247 × 102 | TO | 4.014 × 103 | 3.917 × 104 | TO | 9.801 × 103 | TO | 1.873 × 104 | 1.314 × 103 | 5.183 × 104 | TO | TO | |
| WRST | △/- | △/- | △/- | △/- | △/- | △/- | 5.075 × 10−1/= | △/- | △/- | △/- | 6.653 × 10−8/+ | - | |
| FT | 6.000 | 4.000 | 8.000 | 11.200 | 5.000 | 9.000 | 2.750 | 10.000 | 7.000 | 11.800 | 1.000 | 2.250 | |
| Rank | 6 | 4 | 8 | 11 | 5 | 9 | 3 | 10 | 7 | 12 | 1 | 2 | |
| F2 | Best | 4.154 × 102 | TO | 4.002 × 102 | 8.056 × 102 | TO | 4.289 × 102 | TO | 9.092 × 102 | 4.449 × 102 | 7.176 × 102 | 4.026 × 102 | 4.105 × 102 |
| Worst | 4.753 × 102 | 4.491 × 102 | 4.747 × 102 | 1.499 × 103 | 4.685 × 102 | 4.723 × 102 | 4.491 × 102 | 1.118 × 103 | 4.755 × 102 | 1.157 × 103 | 4.686 × 102 | 4.316 × 102 | |
| Mean | 4.429 × 102 | 4.417 × 102 | 4.536 × 102 | 1.045 × 103 | 4.402 × 102 | 4.522 × 102 | 4.388 × 102 | 1.025 × 103 | 4.546 × 102 | 9.211 × 102 | 4.462 × 102 | 4.238 × 102 | |
| WRST | 8.182 × 10−1/= | 1.610 × 10−4/- | 1.201 × 10−6/- | △/- | 1.481 × 10−3/- | 7.898 × 10−8/- | 1.217 × 10−3/- | △/- | △/- | △/- | 1.587 × 10−5/- | - | |
| FT | 4.900 | 4.650 | 7.050 | 11.300 | 4.500 | 6.650 | 3.050 | 11.350 | 7.600 | 10.350 | 4.300 | 2.300 | |
| Rank | 5 | 4 | 8 | 12 | 3 | 7 | 2 | 11 | 9 | 10 | 6 | 1 | |
| F3 | Best | 6.154 × 102 | 6.164 × 102 | TO | 6.294 × 102 | 6.087 × 102 | TO | TO | 6.518 × 102 | TO | 6.291 × 102 | TO | 6.026 × 102 |
| Worst | 6.459 × 102 | 6.431 × 102 | 6.002 × 102 | 6.817 × 102 | 6.324 × 102 | 6.223 × 102 | TO | 6.686 × 102 | 6.033 × 102 | 6.675 × 102 | 6.030 × 102 | 6.181 × 102 | |
| Mean | 6.337 × 102 | 6.277 × 102 | TO | 6.585 × 102 | 6.184 × 102 | 6.020 × 102 | TO | 6.630 × 102 | 6.006 × 102 | 6.511 × 102 | 6.004 × 102 | 6.063 × 102 | |
| WRST | 1.235 × 10−7/- | 2.218 × 10−7/- | △/+ | △/- | 2.690 × 10−6/- | 1.251 × 10−5/+ | △/+ | △/- | 7.898 × 10−8/+ | △/- | 7.898 × 10−8/+ | - | |
| FT | 8.700 | 8.000 | 3.000 | 10.950 | 7.200 | 2.500 | 1.550 | 11.550 | 4.350 | 10.400 | 3.800 | 6.000 | |
| Rank | 9 | 8 | 2 | 11 | 7 | 5 | 1 | 12 | 4 | 10 | 3 | 6 | |
| F4 | Best | 8.399 × 102 | 8.438 × 102 | 8.247 × 102 | 9.495 × 102 | 8.328 × 102 | 8.428 × 102 | 8.199 × 102 | 9.244 × 102 | 8.195 × 102 | 9.414 × 102 | 8.139 × 102 | 8.319 × 102 |
| Worst | 8.897 × 102 | 8.955 × 102 | 8.515 × 102 | 9.987 × 102 | 9.025 × 102 | 8.866 × 102 | 8.955 × 102 | 9.565 × 102 | 8.468 × 102 | 1.008 × 103 | 8.557 × 102 | 8.762 × 102 | |
| Mean | 8.642 × 102 | 8.739 × 102 | 8.396 × 102 | 9.745 × 102 | 8.643 × 102 | 8.655 × 102 | 8.414 × 102 | 9.444 × 102 | 8.315 × 102 | 9.737 × 102 | 8.318 × 102 | 8.531 × 102 | |
| WRST | 2.074 × 10−2/- | 4.680 × 10−5/- | 3.382 × 10−4/+ | △/- | 6.557 × 10−3/- | 4.320 × 10−3/- | 8.355 × 10−3/+ | △/- | 7.948 × 10−7/+ | △/- | 9.278 × 10−5/+ | - | |
| FT | 6.650 | 7.950 | 3.400 | 11.300 | 6.800 | 6.950 | 3.550 | 10.150 | 2.000 | 11.550 | 2.500 | 5.200 | |
| Rank | 6 | 9 | 3 | 12 | 7 | 8 | 4 | 10 | 1 | 11 | 2 | 5 | |
| F5 | Best | 9.019 × 102 | 1.341 × 103 | 9.081 × 102 | 2.247 × 103 | 9.091 × 102 | 1.940 × 103 | TO | 2.579 × 103 | 9.001 × 102 | 2.379 × 103 | 9.002 × 102 | 9.006 × 102 |
| Worst | 2.213 × 103 | 2.316 × 103 | 1.514 × 103 | 4.371 × 103 | 2.304 × 103 | 2.498 × 103 | 9.258 × 102 | 3.076 × 103 | 9.551 × 102 | 5.071 × 103 | 1.590 × 103 | 9.079 × 102 | |
| Mean | 1.511 × 103 | 1.732 × 103 | 1.186 × 103 | 3.080 × 103 | 1.306 × 103 | 2.295 × 103 | 9.015 × 102 | 2.780 × 103 | 9.061 × 102 | 3.171 × 103 | 1.017 × 103 | 9.042 × 102 | |
| WRST | 4.680 × 10−5/- | △/- | △/- | △/- | △/- | △/- | 1.306 × 10−6/+ | △/- | 1.404 × 10−1/= | △/- | 4.903 × 10−1/= | - | |
| FT | 6.700 | 7.400 | 5.300 | 11.100 | 5.950 | 8.950 | 1.250 | 10.550 | 3.200 | 11.250 | 3.750 | 2.600 | |
| Rank | 7 | 8 | 5 | 11 | 6 | 9 | 1 | 10 | 3 | 12 | 4 | 2 | |
| F6 | Best | 5.703 × 103 | 1.923 × 103 | 2.288 × 103 | 7.281 × 107 | 1.864 × 103 | 1.926 × 103 | 1.930 × 103 | 3.348 × 107 | 1.842 × 103 | 9.198 × 107 | 1.947 × 103 | 1.815 × 103 |
| Worst | 7.610 × 104 | 4.447 × 103 | 4.619 × 103 | 5.995 × 108 | 2.266 × 104 | 5.921 × 103 | 2.277 × 104 | 1.987 × 108 | 4.698 × 103 | 3.962 × 108 | 2.505 × 104 | 1.919 × 103 | |
| Mean | 2.908 × 104 | 3.547 × 103 | 3.083 × 103 | 2.420 × 108 | 1.002 × 104 | 3.351 × 103 | 8.944 × 103 | 1.201 × 108 | 2.769 × 103 | 2.049 × 108 | 9.325 × 103 | 1.833 × 103 | |
| WRST | △/- | △/- | △/- | △/- | 9.173 × 10−8/- | △/- | △/- | △/- | 1.431 × 10−7/- | △/- | △/- | - | |
| FT | 8.750 | 5.000 | 4.400 | 11.400 | 6.250 | 4.300 | 5.900 | 10.350 | 3.400 | 11.250 | 5.900 | 1.100 | |
| Rank | 9 | 5 | 3 | 12 | 8 | 4 | 6 | 10 | 2 | 11 | 7 | 1 | |
| F7 | Best | 2.048 × 103 | 2.045 × 103 | 2.045 × 103 | 2.143 × 103 | 2.027 × 103 | 2.067 × 103 | 2.021 × 103 | 2.163 × 103 | 2.029 × 103 | 2.168 × 103 | 2.021 × 103 | 2.045 × 103 |
| Worst | 2.167 × 103 | 2.142 × 103 | 2.085 × 103 | 2.318 × 103 | 2.142 × 103 | 2.155 × 103 | 2.172 × 103 | 2.195 × 103 | 2.059 × 103 | 2.352 × 103 | 2.181 × 103 | 2.072 × 103 | |
| Mean | 2.099 × 103 | 2.109 × 103 | 2.064 × 103 | 2.209 × 103 | 2.070 × 103 | 2.112 × 103 | 2.062 × 103 | 2.182 × 103 | 2.045 × 103 | 2.244 × 103 | 2.068 × 103 | 2.056 × 103 | |
| WRST | 1.600 × 10−5/- | 1.803 × 10−6/- | 4.679 × 10−2/- | △/- | 1.332 × 10−2/- | 1.235 × 10−7/- | 5.979 × 10−1/= | △/- | 1.481 × 10−3/+ | △/- | 9.892 × 10−1/= | - | |
| FT | 6.550 | 7.650 | 4.500 | 10.950 | 5.100 | 7.850 | 3.750 | 10.300 | 2.200 | 11.600 | 3.850 | 3.700 | |
| Rank | 7 | 8 | 4 | 11 | 6 | 9 | 3 | 10 | 1 | 12 | 5 | 2 | |
| F8 | Best | 2.225 × 103 | 2.223 × 103 | 2.223 × 103 | 2.250 × 103 | 2.221 × 103 | 2.221 × 103 | 2.221 × 103 | 2.238 × 103 | 2.225 × 103 | 2.239 × 103 | 2.221 × 103 | 2.216 × 103 |
| Worst | 2.363 × 103 | 2.243 × 103 | 2.229 × 103 | 2.424 × 103 | 2.341 × 103 | 2.576 × 103 | 2.358 × 103 | 2.263 × 103 | 2.236 × 103 | 2.532 × 103 | 2.240 × 103 | 2.231 × 103 | |
| Mean | 2.243 × 103 | 2.227 × 103 | 2.227 × 103 | TO | 2.232 × 103 | 2.329 × 103 | 2.264 × 103 | 2.253 × 103 | 2.230 × 103 | 2.376 × 103 | 2.227 × 103 | 2.226 × 103 | |
| WRST | 1.116 × 10−3/- | 5.250 × 10−1/= | 9.031 × 10−1/= | △/- | 6.787 × 10−2/= | 8.292 × 10−5/- | 5.979 × 10−1/= | △/- | 1.159 × 10−4/- | △/- | 1.636 × 10−1/= | - | |
| FT | 6.550 | 4.350 | 4.500 | 10.300 | 3.550 | 9.200 | 5.500 | 8.950 | 6.150 | 11.250 | 4.300 | 3.400 | |
| Rank | 7 | 3 | 2 | 10 | 6 | 11 | 9 | 8 | 5 | 12 | 4 | 1 | |
| F9 | Best | 2.465 × 103 | 2.481 × 103 | 2.481 × 103 | 2.565 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.712 × 103 | 2.481 × 103 | 2.579 × 103 | 2.481 × 103 | 2.472 × 103 |
| Worst | 2.465 × 103 | 2.481 × 103 | 2.481 × 103 | 2.775 × 103 | 2.481 × 103 | 2.482 × 103 | 2.481 × 103 | 2.916 × 103 | 2.481 × 103 | 2.816 × 103 | 2.481 × 103 | 2.481 × 103 | |
| Mean | 2.465 × 103 | 2.481 × 103 | 2.481 × 103 | 2.650 × 103 | 2.481 × 103 | 2.481 × 103 | 2.481 × 103 | 2.809 × 103 | 2.481 × 103 | 2.703 × 103 | 2.481 × 103 | 2.476 × 103 | |
| WRST | △/+ | △/- | △/- | △/- | △/- | △/- | 5.903 × 10−8/- | △/- | △/- | △/- | 6.541 × 10−8/- | - | |
| FT | 1.000 | 7.550 | 5.300 | 10.200 | 5.600 | 9.000 | 3.200 | 11.850 | 7.450 | 10.950 | 3.900 | 2.000 | |
| Rank | 1 | 8 | 4 | 10 | 6 | 9 | 3 | 12 | 7 | 11 | 5 | 2 | |
| F10 | Best | TO | 2.501 × 103 | TO | 2.538 × 103 | TO | TO | 2.501 × 103 | 2.601 × 103 | 2.501 × 103 | 2.522 × 103 | TO | TO |
| Worst | 4.867 × 103 | 2.627 × 103 | 2.625 × 103 | 6.769 × 103 | 2.711 × 103 | 5.023 × 103 | 3.985 × 103 | 2.674 × 103 | 2.637 × 103 | 7.760 × 103 | 4.510 × 103 | 2.501 × 103 | |
| Mean | 3.639 × 103 | 2.507 × 103 | 2.507 × 103 | 3.024 × 103 | 2.511 × 103 | 3.197 × 103 | 2.886 × 103 | 2.634 × 103 | 2.508 × 103 | 4.594 × 103 | 3.056 × 103 | 2.501 × 103 | |
| WRST | 1.227 × 10−3/- | 2.218 × 10−7/- | 7.205 × 10−2/= | △/- | 2.561 × 10−3/- | 1.929 × 10−2/- | 4.540 × 10−6/- | △/- | 1.794 × 10−4/- | △/- | 5.874 × 10−6/- | - | |
| FT | 8.900 | 5.950 | 3.650 | 8.350 | 2.050 | 6.600 | 7.750 | 8.600 | 4.750 | 9.500 | 9.050 | 2.850 | |
| Rank | 11 | 3 | 2 | 8 | 5 | 10 | 7 | 6 | 4 | 12 | 9 | 1 | |
| F11 | Best | 2.651 × 103 | 2.900 × 103 | TO | 4.176 × 103 | 2.900 × 103 | 2.900 × 103 | 2.900 × 103 | 6.225 × 103 | TO | 3.676 × 103 | 2.900 × 103 | TO |
| Worst | 3.008 × 103 | 3.000 × 103 | 3.000 × 103 | 7.276 × 103 | 3.360 × 103 | 3.000 × 103 | 3.000 × 103 | 7.128 × 103 | 3.000 × 103 | 5.998 × 103 | 2.900 × 103 | 3.038 × 103 | |
| Mean | 2.950 × 103 | 2.910 × 103 | 2.888 × 103 | 5.612 × 103 | 2.963 × 103 | 2.930 × 103 | 2.945 × 103 | 6.742 × 103 | 2.885 × 103 | 4.959 × 103 | 2.900 × 103 | 2.922 × 103 | |
| WRST | 3.852 × 10−2/- | 7.557 × 10−1/= | 3.382 × 10−4/+ | △/- | 8.103 × 10−2/= | 3.639 × 10−3/- | 5.231 × 10−2/= | △/- | 2.561 × 10−3/+ | △/- | 7.656 × 10−7/+ | - | |
| FT | 7.050 | 6.250 | 4.500 | 10.850 | 5.500 | 4.400 | 4.350 | 11.950 | 5.150 | 10.200 | 1.350 | 6.450 | |
| Rank | 8 | 4 | 2 | 11 | 9 | 6 | 7 | 12 | 1 | 10 | 3 | 5 | |
| F12 | Best | 2.896 × 103 | 2.941 × 103 | 2.935 × 103 | 3.113 × 103 | 2.944 × 103 | 2.947 × 103 | 2.934 × 103 | 3.469 × 103 | 2.954 × 103 | 3.059 × 103 | 2.945 × 103 | 2.900 × 103 |
| Worst | 3.394 × 103 | 2.984 × 103 | 2.947 × 103 | 3.371 × 103 | 2.981 × 103 | 3.060 × 103 | 2.999 × 103 | 3.668 × 103 | 2.998 × 103 | 3.596 × 103 | 3.016 × 103 | 2.900 × 103 | |
| Mean | 3.198 × 103 | 2.954 × 103 | 2.939 × 103 | 3.215 × 103 | 2.957 × 103 | 2.971 × 103 | 2.953 × 103 | 3.574 × 103 | 2.972 × 103 | 3.191 × 103 | 2.970 × 103 | 2.900 × 103 | |
| WRST | 1.201 × 10−6/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | △/- | - | |
| FT | 9.550 | 4.750 | 2.250 | 10.300 | 4.800 | 5.900 | 4.400 | 11.950 | 6.800 | 9.700 | 6.550 | 1.050 | |
| Rank | 10 | 4 | 2 | 11 | 5 | 7 | 3 | 12 | 8 | 9 | 6 | 1 | |
| Mean Rank | 7.167 | 5.667 | 3.750 | 10.833 | 6.083 | 7.833 | 4.083 | 10.250 | 4.333 | 11.000 | 4.583 | 2.417 | |
| Final Ranking | 8 | 6 | 2 | 11 | 7 | 9 | 3 | 10 | 4 | 12 | 5 | 1 | |
| Mean FT | 6.775 | 6.125 | 4.654 | 10.683 | 5.192 | 6.775 | 3.917 | 10.629 | 5.004 | 10.817 | 4.188 | 3.242 | |
| Final FT | 8 | 7 | 4 | 11 | 6 | 8 | 2 | 10 | 5 | 12 | 3 | 1 | |
| +/=/− | 1/1/10 | 0/2/10 | 3/2/7 | 0/0/12 | 0/2/10 | 1/0/11 | 3/4/5 | 0/0/12 | 4/1/7 | 0/0/12 | 4/3/5 | -/-/- | |
| F | Index | Algorithms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSO | RUN | NGO | NOA | GKSO | IVYA | EAPSO | G-QPSO | HJSPSO | PSO-Sono | SAO-MPSO | IA-DTPSO | ||
| F1 | Std | 6.898 | 7.562 × 10−4 | 1.241 × 103 | 8.173 × 103 | 8.985 × 10−4 | 3.391 × 103 | 8.880 × 10−6 | 1.993 × 103 | 3.761 × 102 | 1.630 × 104 | 4.304 × 10−13 | 5.222 × 10−7 |
| RMSE | 3.238 × 102 | 2.990 × 102 | 4.192 × 103 | 3.998 × 104 | 2.995 × 102 | 1.034 × 104 | 2.990 × 102 | 1.883 × 104 | 1.363 × 103 | 5.420 × 104 | 2.990 × 102 | 2.990 × 102 | |
| δ | 3.143 × 102 | 2.990 × 102 | 2.015 × 103 | 2.665 × 104 | 2.990 × 102 | 5.132 × 103 | 2.990 × 102 | 1.452 × 104 | 6.156 × 102 | 2.779 × 104 | 2.990 × 102 | 2.990 × 102 | |
| F2 | Std | 2.793 × 101 | 1.797 × 101 | 1.656 × 101 | 1.700 × 102 | 2.180 × 101 | 1.055 × 101 | 1.948 × 101 | 5.161 × 101 | 1.057 × 101 | 1.316 × 102 | 1.585 × 101 | 3.711 |
| RMSE | 4.427 × 102 | 4.411 × 102 | 4.529 × 102 | 1.057 × 103 | 4.397 × 102 | 4.513 × 102 | 4.383 × 102 | 1.025 × 103 | 4.537 × 102 | 9.290 × 102 | 4.455 × 102 | 4.228 × 102 | |
| δ | 4.144 × 102 | 3.990 × 102 | 3.992 × 102 | 8.046 × 102 | 3.990 × 102 | 4.279 × 102 | 3.990 × 102 | 9.082 × 102 | 4.439 × 102 | 7.166 × 102 | 4.016 × 102 | 4.095 × 102 | |
| F3 | Std | 9.017 | 8.651 | 7.371 × 10−2 | 1.211 × 101 | 7.627 | 6.064 | 9.377 × 10−4 | 3.797 | 8.564 × 10−1 | 9.456 | 7.621 × 10−1 | 4.275 |
| RMSE | 6.328 × 102 | 6.267 × 102 | 5.990 × 102 | 6.576 × 102 | 6.174 × 102 | 6.011 × 102 | 5.990 × 102 | 6.620 × 102 | 5.996 × 102 | 6.501 × 102 | 5.994 × 102 | 6.053 × 102 | |
| δ | 6.144 × 102 | 6.154 × 102 | 5.990 × 102 | 6.284 × 102 | 6.077 × 102 | 5.990 × 102 | 5.990 × 102 | 6.508 × 102 | 5.990 × 102 | 6.281 × 102 | 5.990 × 102 | 6.016 × 102 | |
| F4 | Std | 1.502 × 101 | 1.415 × 101 | 6.527 | 1.365 × 101 | 1.409 × 101 | 1.287 × 101 | 1.670 × 101 | 8.125 | 7.039 | 1.627 × 101 | 1.267 × 101 | 1.231 × 101 |
| RMSE | 8.633 × 102 | 8.730 × 102 | 8.386 × 102 | 9.736 × 102 | 8.634 × 102 | 8.646 × 102 | 8.406 × 102 | 9.434 × 102 | 8.305 × 102 | 9.729 × 102 | 8.309 × 102 | 8.522 × 102 | |
| δ | 8.389 × 102 | 8.428 × 102 | 8.237 × 102 | 9.485 × 102 | 8.318 × 102 | 8.418 × 102 | 8.189 × 102 | 9.234 × 102 | 8.185 × 102 | 9.404 × 102 | 8.129 × 102 | 8.309 × 102 | |
| F5 | Std | 3.758 × 102 | 2.793 × 102 | 2.020 × 102 | 5.955 × 102 | 3.863 × 102 | 1.738 × 102 | 5.727 | 1.492 × 102 | 1.234 × 101 | 6.723 × 102 | 1.766 × 102 | 2.139 |
| RMSE | 1.554 × 103 | 1.752 × 103 | 1.202 × 103 | 3.133 × 103 | 1.358 × 103 | 2.301 × 103 | 9.005 × 102 | 2.782 × 103 | 9.052 × 102 | 3.237 × 103 | 1.030 × 103 | 9.032 × 102 | |
| δ | 9.009 × 102 | 1.340 × 103 | 9.071 × 102 | 2.246 × 103 | 9.081 × 102 | 1.939 × 103 | 8.990 × 102 | 2.578 × 103 | 8.991 × 102 | 2.378 × 103 | 8.992 × 102 | 8.996 × 102 | |
| F6 | Std | 2.008 × 104 | 7.669 × 102 | 6.916 × 102 | 1.425 × 108 | 7.584 × 103 | 1.261 × 103 | 7.327 × 103 | 3.893 × 107 | 8.278 × 102 | 9.403 × 107 | 7.738 × 103 | 2.375 × 101 |
| RMSE | 3.505 × 104 | 3.624 × 103 | 3.155 × 103 | 2.790 × 108 | 1.245 × 104 | 3.568 × 103 | 1.144 × 104 | 1.259 × 108 | 2.883 × 103 | 2.244 × 108 | 1.199 × 104 | 1.832 × 103 | |
| δ | 5.702 × 103 | 1.922 × 103 | 2.287 × 103 | 7.281 × 107 | 1.863 × 103 | 1.925 × 103 | 1.929 × 103 | 3.348 × 107 | 1.841 × 103 | 9.198 × 107 | 1.946 × 103 | 1.814 × 103 | |
| F7 | Std | 3.216 × 101 | 2.292 × 101 | 1.181 × 101 | 4.638 × 101 | 2.474 × 101 | 2.839 × 101 | 3.994 × 101 | 9.078 | 9.092 | 5.094 × 101 | 4.697 × 101 | 8.845 |
| RMSE | 2.099 × 103 | 2.108 × 103 | 2.063 × 103 | 2.208 × 103 | 2.070 × 103 | 2.112 × 103 | 2.062 × 103 | 2.181 × 103 | 2.044 × 103 | 2.243 × 103 | 2.068 × 103 | 2.055 × 103 | |
| δ | 2.047 × 103 | 2.044 × 103 | 2.044 × 103 | 2.142 × 103 | 2.026 × 103 | 2.066 × 103 | 2.020 × 103 | 2.162 × 103 | 2.028 × 103 | 2.167 × 103 | 2.020 × 103 | 2.044 × 103 | |
| F8 | Std | 3.882 × 101 | 4.257 | 1.411 | 4.428 × 101 | 2.676 × 101 | 9.088 × 101 | 5.559 × 101 | 6.503 | 2.490 | 7.743 × 101 | 8.026 | 3.748 |
| RMSE | 2.242 × 103 | 2.226 × 103 | 2.226 × 103 | 2.299 × 103 | 2.231 × 103 | 2.329 × 103 | 2.263 × 103 | 2.252 × 103 | 2.229 × 103 | 2.376 × 103 | 2.226 × 103 | 2.225 × 103 | |
| δ | 2.224 × 103 | 2.222 × 103 | 2.222 × 103 | 2.249 × 103 | 2.220 × 103 | 2.220 × 103 | 2.220 × 103 | 2.237 × 103 | 2.224 × 103 | 2.238 × 103 | 2.220 × 103 | 2.215 × 103 | |
| F9 | Std | 1.829 × 10−2 | 3.946 × 10−3 | 1.702 × 10−6 | 5.092 × 101 | 9.247 × 10−5 | 2.422 × 10−1 | 1.368 × 10−12 | 5.391 × 101 | 1.078 × 10−3 | 6.991 × 101 | 3.306 × 10−5 | 2.286 |
| RMSE | 2.464 × 103 | 2.480 × 103 | 2.480 × 103 | 2.649 × 103 | 2.480 × 103 | 2.480 × 103 | 2.480 × 103 | 2.808 × 103 | 2.480 × 103 | 2.703 × 103 | 2.480 × 103 | 2.476 × 103 | |
| δ | 2.464 × 103 | 2.480 × 103 | 2.480 × 103 | 2.564 × 103 | 2.480 × 103 | 2.480 × 103 | 2.480 × 103 | 2.711 × 103 | 2.480 × 103 | 2.578 × 103 | 2.480 × 103 | 2.471 × 103 | |
| F10 | Std | 8.723 × 102 | 2.812 × 101 | 2.785 × 101 | 1.170 × 103 | 4.710 × 101 | 8.874 × 102 | 4.374 × 102 | 1.884 × 101 | 3.044 × 101 | 2.323 × 103 | 4.664 × 102 | 1.253 × 10−1 |
| RMSE | 3.736 × 103 | 2.506 × 103 | 2.506 × 103 | 3.231 × 103 | 2.510 × 103 | 3.311 × 103 | 2.917 × 103 | 2.633 × 103 | 2.507 × 103 | 5.120 × 103 | 3.088 × 103 | TO | |
| δ | 2.499 × 103 | TO | 2.499 × 103 | 2.537 × 103 | 2.499 × 103 | 2.499 × 103 | TO | TO | TO | 2.521 × 103 | 2.499 × 103 | 2.499 × 103 | |
| F11 | Std | 7.486 × 101 | 3.072 × 101 | 9.754 × 101 | 8.589 × 102 | 1.058 × 102 | 4.702 × 101 | 5.104 × 101 | 2.046 × 102 | 1.187 × 102 | 6.222 × 102 | 7.807 × 10−13 | 9.178 × 101 |
| RMSE | 2.950 × 103 | 2.909 × 103 | 2.888 × 103 | 5.673 × 103 | 2.964 × 103 | 2.929 × 103 | 2.944 × 103 | 6.744 × 103 | 2.886 × 103 | 4.995 × 103 | 2.899 × 103 | 2.923 × 103 | |
| δ | 2.650 × 103 | 2.899 × 103 | 2.599 × 103 | 4.175 × 103 | 2.899 × 103 | 2.899 × 103 | 2.899 × 103 | 6.224 × 103 | 2.599 × 103 | 3.675 × 103 | 2.899 × 103 | 2.599 × 103 | |
| F12 | Std | 1.481 × 102 | 1.042 × 101 | 3.139 | 7.512 × 101 | 1.007 × 101 | 2.848 × 101 | 1.459 × 101 | 5.104 × 101 | 1.208 × 101 | 1.195 × 102 | 1.768 × 101 | 1.037 × 10−4 |
| RMSE | 3.200 × 103 | 2.953 × 103 | 2.938 × 103 | 3.215 × 103 | 2.956 × 103 | 2.970 × 103 | 2.952 × 103 | 3.573 × 103 | 2.971 × 103 | 3.192 × 103 | 2.969 × 103 | 2.899 × 103 | |
| δ | 2.895 × 103 | 2.940 × 103 | 2.934 × 103 | 3.112 × 103 | 2.943 × 103 | 2.946 × 103 | 2.933 × 103 | 3.468 × 103 | 2.953 × 103 | 3.058 × 103 | 2.944 × 103 | 2.899 × 103 | |
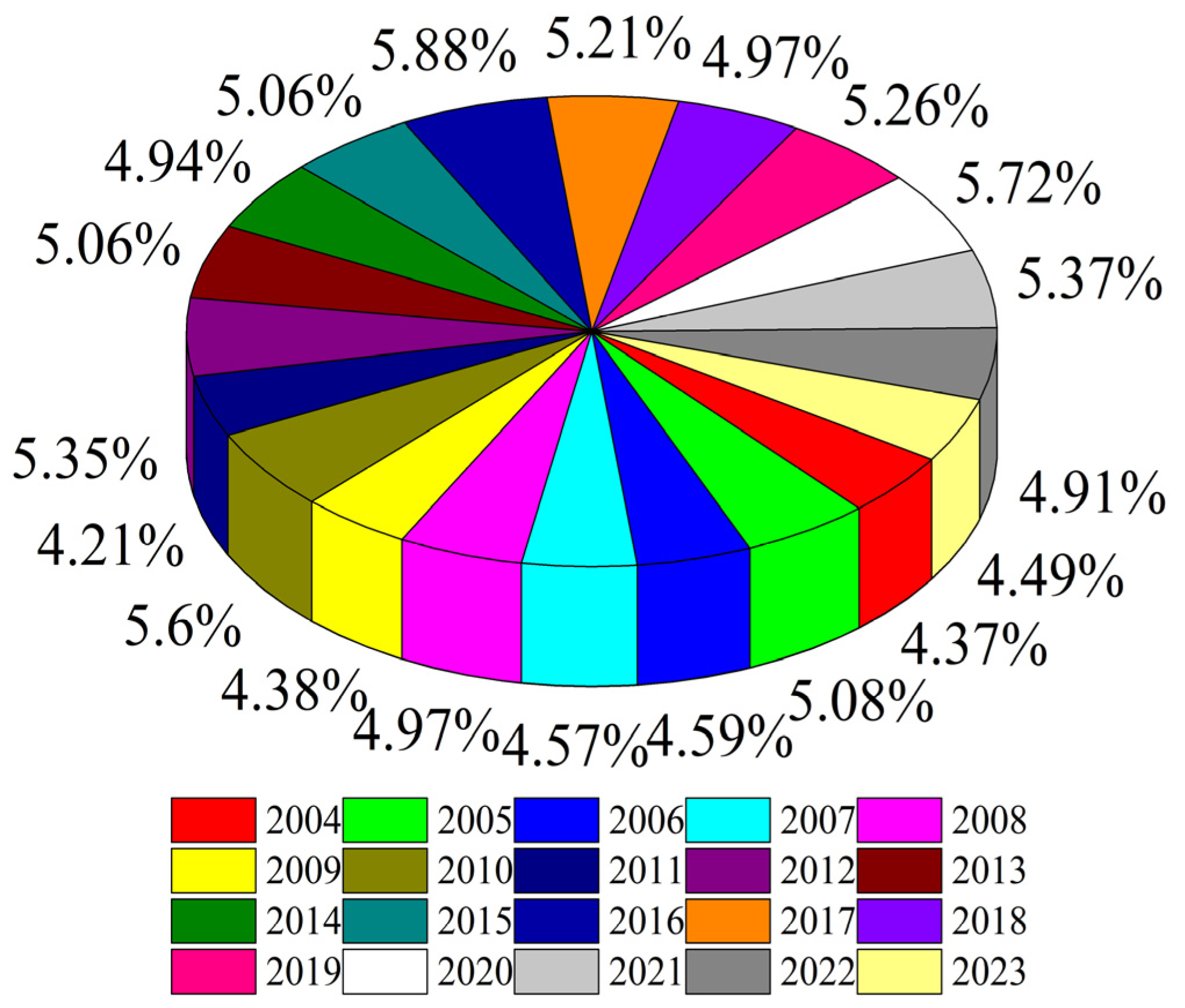
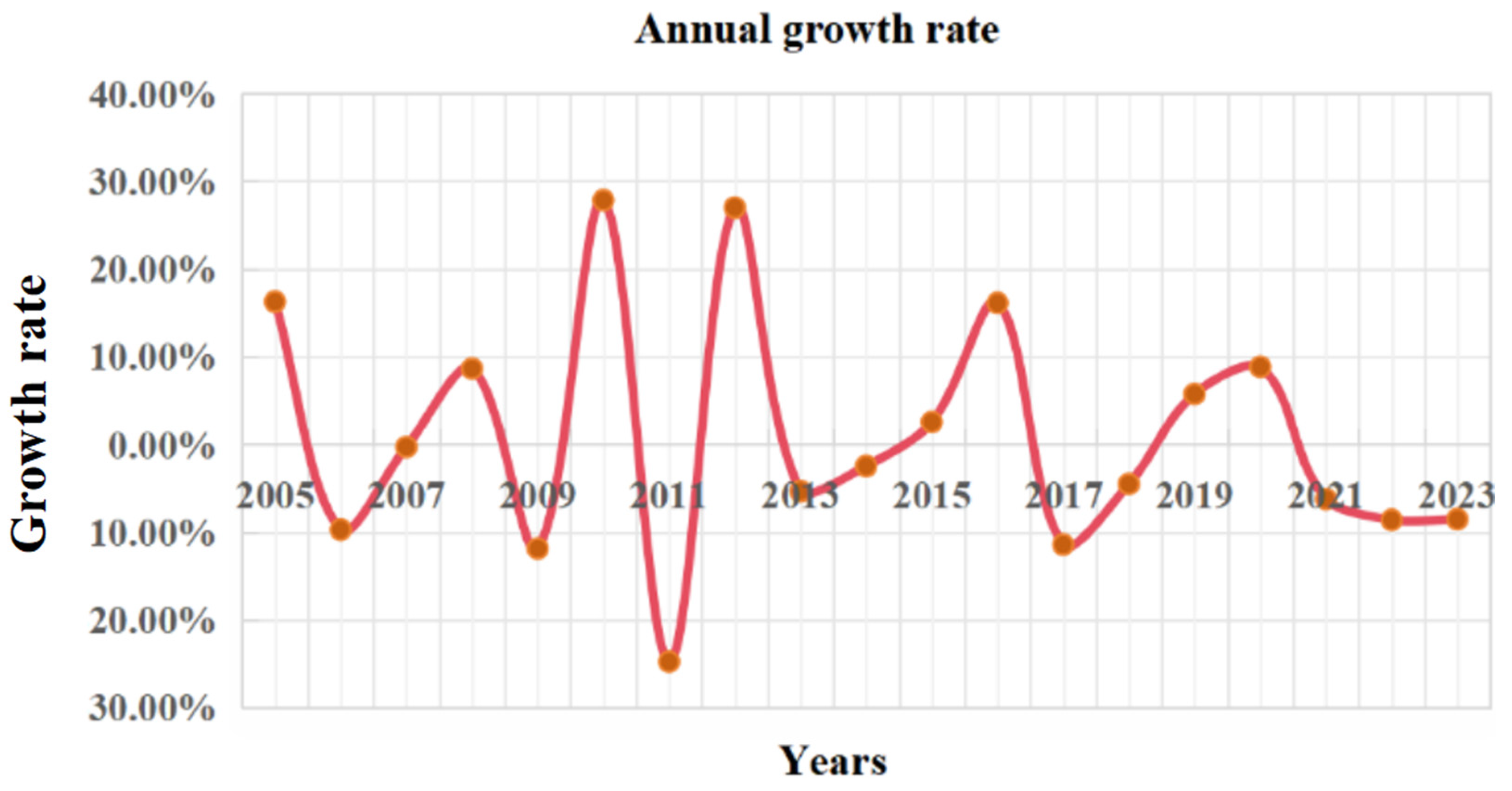
| Years | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|---|---|---|---|---|
| TUWRs | 24,129.6 | 28,053.1 | 25,330.1 | 25,255.2 | 27,434.3 | 24,180.2 | 30,906.4 | 23,256.7 | 29,528.8 | 27,957.9 |
| Years | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| TUWRs | 27,266.9 | 27,962.6 | 32,466.4 | 28,761.2 | 27,462.5 | 29,041.0 | 31,605.2 | 29,638.2 | 27,088.1 | 24,780.0 |
| Years | Real Value | IA-DTPSO | PSO | GKSO | IVYA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SimD | ResE | APE (%) | SimD | ResE | APE (%) | SimD | ResE | APE (%) | SimD | ResE | APE (%) | ||
| 2005 | 28,053.1 | 27,916.57 | −136.53 | 0.49 | 24,398.68 | −3654.42 | 13.03 | 26,529.37 | −1523.73 | 5.43 | 25,472.86 | −2580.23 | 9.19 |
| 2006 | 25,330.1 | 25,594.21 | 264.11 | 1.04 | 25,454.02 | 123.92 | 0.49 | 26,220.56 | 890.46 | 3.52 | 25,966.25 | 636.15 | 2.51 |
| 2007 | 25,255.2 | 25,617.06 | 361.86 | 1.43 | 26,417.97 | 1162.77 | 4.60 | 26,288.93 | 1033.73 | 4.09 | 26,595.10 | 1339.90 | 5.30 |
| 2008 | 27,434.3 | 26,010.91 | −1423.39 | 5.19 | 27,180.11 | −254.19 | 0.93 | 26,494.88 | −939.41 | 3.42 | 27,052.92 | −381.37 | 1.39 |
| 2009 | 24,180.2 | 26,496.10 | 2315.90 | 9.58 | 27,742.49 | 3562.29 | 14.73 | 26,770.27 | 2590.07 | 10.71 | 27,386.22 | 3206.02 | 13.25 |
| 2010 | 30,906.4 | 26,978.82 | −3927.58 | 12.71 | 28,130.40 | −2776.00 | 8.98 | 27,071.13 | −3835.27 | 12.41 | 27,628.87 | −3277.52 | 10.60 |
| 2011 | 23,256.7 | 27,423.85 | 4167.15 | 17.92 | 28,372.31 | 5115.61 | 22.00 | 27,373.44 | 4116.74 | 17.70 | 27,805.52 | 4548.82 | 19.55 |
| 2012 | 29,528.8 | 27,818.17 | −1710.63 | 5.79 | 28,494.53 | −1034.27 | 3.50 | 27,665.48 | −1863.32 | 6.31 | 27,934.13 | −1594.66 | 5.40 |
| 2013 | 27,957.9 | 28,158.21 | 200.31 | 0.72 | 28,519.84 | 561.94 | 2.01 | 27,942.35 | −15.55 | 0.06 | 28,027.75 | 69.85 | 0.24 |
| 2014 | 27,266.9 | 28,444.74 | 1177.84 | 4.32 | 28,467.42 | 1200.52 | 4.40 | 28,202.71 | 935.81 | 3.43 | 28,095.92 | 829.02 | 3.04 |
| 2015 | 27,962.6 | 28,680.48 | 717.88 | 2.57 | 28,353.20 | 390.60 | 1.40 | 28,446.89 | 484.29 | 1.73 | 28,145.54 | 182.94 | 0.65 |
| 2016 | 32,466.4 | 28,869.04 | −3597.36 | 11.08 | 28,190.29 | −4276.11 | 13.17 | 28,675.96 | −3790.44 | 11.67 | 28,181.67 | −4284.72 | 13.19 |
| 2017 | 28,761.2 | 29,014.29 | 253.09 | 0.88 | 27,989.42 | −771.78 | 2.68 | 28,891.27 | 130.07 | 0.45 | 28,207.97 | −553.22 | 1.92 |
| 2018 | 27,462.5 | 29,120.10 | 1657.60 | 6.04 | 27,759.33 | 296.83 | 1.08 | 29,094.15 | 1631.65 | 5.94 | 28,227.12 | 764.62 | 2.78 |
| MAPEsimulation (%) | 5.6366 | 6.6432 | 6.2061 | 6.3627 | |||||||||
| 2019 | 29,041 | 29,106.99 | 65.99 | 0.23 | 28,640.37 | −400.63 | 1.3795 | 29,285.85 | 244.85 | 0.84 | 28,241.06 | −799.93 | 2.75 |
| 2020 | 31,605.2 | 29,112.08 | −2493.12 | 7.89 | 28,817.00 | −2788.20 | 8.8220 | 29,467.49 | −2137.70 | 6.76 | 28,251.21 | −3353.98 | 10.61 |
| 2021 | 29,638.2 | 29,086.75 | −551.45 | 1.86 | 29,009.75 | −628.45 | 2.1204 | 29,640.08 | 1.88 | 0.01 | 28,258.59 | −1379.60 | 4.65 |
| 2022 | 27,088.1 | 29,034.33 | 1946.23 | 7.18 | 29,216.74 | 2128.64 | 7.8582 | 29,804.48 | 2716.37 | 10.02 | 28,263.97 | 1175.87 | 4.34 |
| 2023 | 24,780 | 28,957.86 | 4177.86 | 16.86 | 29,436.13 | 4656.13 | 18.7899 | 29,961.43 | 5181.43 | 20.90 | 28,267.89 | 3487.89 | 14.07 |
| MAPEprediction (%) | 6.8041 | 7.2254 | 7.7102 | 7.2876 | |||||||||
| MAPE (%) | 5.9439 | 6.7964 | 6.6019 | 6.6061 | |||||||||
| Years | Real Value | EAPSO | HJSPSO | PSO-sono | SAO-MPSO | ||||||||
| SimD | ResE | APE (%) | SimD | ResE | APE (%) | SimD | ResE | APE (%) | SimD | ResE | APE (%) | ||
| 2005 | 28,053.1 | 28,036.28 | −16.81 | 0.06 | 27,865.98 | −187.11 | 0.66 | 27,772.07 | −281.02 | 1.00 | 27,744.11 | −308.98 | 1.10 |
| 2006 | 25,330.1 | 24,823.89 | −506.20 | 1.99 | 26,510.91 | 1180.81 | 4.66 | 26,521.71 | 1191.61 | 4.70 | 25,728.56 | 398.46 | 1.57 |
| 2007 | 25,255.2 | 25,798.03 | 542.83 | 2.14 | 25,896.87 | 641.67 | 2.54 | 25,936.51 | 681.31 | 2.69 | 26,184.17 | 928.97 | 3.67 |
| 2008 | 27,434.3 | 26,288.65 | −1145.64 | 4.17 | 25,813.99 | −1620.30 | 5.90 | 25,854.32 | −1579.97 | 5.75 | 26,590.81 | −843.48 | 3.07 |
| 2009 | 24,180.2 | 26,745.13 | 2564.93 | 10.60 | 26,043.52 | 1863.32 | 7.70 | 26,074.90 | 1894.70 | 7.83 | 26,952.85 | 2772.65 | 11.46 |
| 2010 | 30,906.4 | 27,137.43 | −3768.96 | 12.19 | 26,433.89 | −4472.50 | 14.47 | 26,454.43 | −4451.96 | 14.40 | 27,270.65 | −3635.74 | 11.76 |
| 2011 | 23,256.7 | 27,484.06 | 4227.36 | 18.17 | 26,897.13 | 3640.43 | 15.65 | 26,907.61 | 3650.91 | 15.69 | 27,546.62 | 4289.92 | 18.44 |
| 2012 | 29,528.8 | 27,794.22 | −1734.57 | 5.87 | 27,385.82 | −2142.97 | 7.25 | 27,387.58 | −2141.21 | 7.25 | 27,784.27 | −1744.52 | 5.90 |
| 2013 | 27,957.9 | 28,075.01 | 117.11 | 0.41 | 27,875.64 | −82.25 | 0.29 | 27,869.90 | −87.99 | 0.31 | 27,987.46 | 29.56 | 0.10 |
| 2014 | 27,266.9 | 28,331.62 | 1064.72 | 3.90 | 28,354.76 | 1087.86 | 3.98 | 28,342.48 | 1075.58 | 3.94 | 28,159.99 | 893.09 | 3.27 |
| 2015 | 27,962.6 | 28,568.01 | 605.40 | 2.16 | 28,817.97 | 855.37 | 3.05 | 28,799.80 | 837.20 | 2.99 | 28,305.45 | 342.85 | 1.22 |
| 2016 | 32,466.4 | 28,787.22 | −3679.17 | 11.33 | 29,263.39 | −3203.00 | 9.86 | 29,239.83 | −3226.56 | 9.93 | 28,427.14 | −4039.25 | 12.44 |
| 2017 | 28,761.2 | 28,991.69 | 230.49 | 0.80 | 29,690.86 | 929.66 | 3.23 | 29,662.25 | 901.05 | 3.13 | 28,528.04 | −233.15 | 0.81 |
| 2018 | 27,462.5 | 29,183.33 | 1720.83 | 6.26 | 30,100.99 | 2638.49 | 9.60 | 30,067.59 | 2605.09 | 9.48 | 28,610.82 | 1148.32 | 4.18 |
| MAPEsimulation (%) | 5.7233 | 6.3508 | 6.3688 | 5.6466 | |||||||||
| 2019 | 29,041 | 29,363.72 | 322.72 | 1.11 | 30,494.74 | 1453.74 | 5.00 | 30,456.75 | 1415.75 | 4.87 | 28,677.83 | −363.16 | 1.25 |
| 2020 | 31,605.2 | 29,534.15 | −2071.04 | 6.55 | 30,873.19 | −732.01 | 2.31 | 30,830.78 | −774.41 | 2.45 | 28,731.17 | −2874.02 | 9.09 |
| 2021 | 29,638.2 | 29,695.73 | 57.53 | 0.19 | 31,237.40 | 1599.20 | 5.39 | 31,190.71 | 1552.51 | 5.23 | 28,772.67 | −865.52 | 2.92 |
| 2022 | 27,088.1 | 29,849.35 | 2761.25 | 10.19 | 31,588.41 | 4500.31 | 16.61 | 31,537.54 | 4449.44 | 16.42 | 28,803.96 | 1715.86 | 6.33 |
| 2023 | 24,780 | 29,995.80 | 5215.80 | 21.04 | 31,927.15 | 7147.15 | 28.84 | 31,872.23 | 7092.23 | 28.62 | 28,826.43 | 4046.43 | 16.32 |
| MAPEprediction (%) | 7.8201 | 11.6347 | 11.522 | 7.1856 | |||||||||
| MAPE (%) | 6.2751 | 7.7413 | 7.7249 | 6.0516 | |||||||||
| Parameters | IA-DTPSO | PSO | GKSO | IVYA | EAPSO | HJSPSO | PSO-Sono | SAO-MPSO |
|---|---|---|---|---|---|---|---|---|
| Csz | 24,123.6 | 24,160.2 | 24,385.5 | 24,346.2 | 24,488.9 | 24,146.9 | 24,500 | 24,245.4 |
| ξ | 0.080129 | 0.560555 | 0.377924 | 0.439050 | 0.198431 | 0.029187 | 0.345376 | 0.067554 |
| r | 1.453199 | 0.360578 | 0.927702 | 0.899874 | 0.905127 | 0.937307 | 1 | 0.925674 |
| a | 0.058716 | 0.17176 | 0.64349 | 0.27198 | 1.4176 | 0.64964 | 0.64406 | 0.12418 |
| b | 6780.2789 | −39.7023 | 13,448.3342 | 7691.1691 | 30,532.6828 | 9443.9293 | 9426.1429 | 4152.6776 |
| c | 23,519.5322 | 8199.7156 | 20,248.424 | 16,383.655 | 6180.5493 | 24,060.5466 | 24,153.8696 | 21,550.6303 |
| Years | 2024 | 2025 | 2026 | 2027 | 2028 |
|---|---|---|---|---|---|
| TUWRs | 26,376.97 | 26,028.78 | 24,960.55 | 28,731.54 | 33,688.46 |
| Years | Real Value | ID_T | GM(1,1) | DGM(1,1) | NGBM(1,1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SimD | ResE | APE (%) | SimD | ResE | APE (%) | SimD | ResE | APE (%) | SimD | ResE | APE (%) | ||
| 2005 | 28,053.1 | 27,916.57 | −136.53 | 0.49 | 25,987.99 | −2065.11 | 7.36 | 26,023.11 | −2029.99 | 7.24 | 25,987.99 | −2065.11 | 7.36 |
| 2006 | 25,330.1 | 25,594.21 | 264.11 | 1.04 | 26,221.03 | 890.93 | 3.52 | 26,251.27 | 921.17 | 3.64 | 26,221.03 | 890.93 | 3.52 |
| 2007 | 25,255.2 | 25,617.06 | 361.86 | 1.43 | 26,456.15 | 1200.95 | 4.76 | 26,481.43 | 1226.23 | 4.86 | 26,456.15 | 1200.95 | 4.76 |
| 2008 | 27,434.3 | 26,010.91 | −1423.39 | 5.19 | 26,693.38 | −740.92 | 2.70 | 26,713.60 | −720.70 | 2.63 | 26,693.38 | −740.92 | 2.70 |
| 2009 | 24,180.2 | 26,496.10 | 2315.90 | 9.58 | 26,932.74 | 2752.54 | 11.38 | 26,947.82 | 2767.62 | 11.45 | 26,932.74 | 2752.54 | 11.38 |
| 2010 | 30,906.4 | 26,978.82 | −3927.58 | 12.71 | 27,174.25 | −3732.15 | 12.08 | 27,184.08 | −3722.32 | 12.04 | 27,174.25 | −3732.15 | 12.08 |
| 2011 | 23,256.7 | 27,423.85 | 4167.15 | 17.92 | 27,417.92 | 4161.22 | 17.89 | 27,422.42 | 4165.72 | 17.91 | 27,417.92 | 4161.22 | 17.89 |
| 2012 | 29,528.8 | 27,818.17 | −1710.63 | 5.79 | 27,663.78 | −1865.02 | 6.32 | 27,662.85 | −1865.95 | 6.32 | 27,663.78 | −1865.02 | 6.32 |
| 2013 | 27,957.9 | 28,158.21 | 200.31 | 0.72 | 27,911.84 | −46.06 | 0.16 | 27,905.39 | −52.51 | 0.19 | 27,911.84 | −46.06 | 0.16 |
| 2014 | 27,266.9 | 28,444.74 | 1177.84 | 4.32 | 28,162.12 | 895.22 | 3.28 | 28,150.05 | 883.15 | 3.24 | 28,162.12 | 895.22 | 3.28 |
| 2015 | 27,962.6 | 28,680.48 | 717.88 | 2.57 | 28,414.65 | 452.05 | 1.62 | 28,396.85 | 434.25 | 1.55 | 28,414.65 | 452.05 | 1.62 |
| 2016 | 32,466.4 | 28,869.04 | −3597.36 | 11.08 | 28,669.45 | −3796.95 | 11.70 | 28,645.83 | −3820.57 | 11.77 | 28,669.45 | −3796.95 | 11.70 |
| 2017 | 28,761.2 | 29,014.29 | 253.09 | 0.88 | 28,926.52 | 165.32 | 0.57 | 28,896.98 | 135.78 | 0.47 | 28,926.52 | 165.32 | 0.57 |
| 2018 | 27,462.5 | 29,120.10 | 1657.60 | 6.04 | 29,185.91 | 1723.41 | 6.28 | 29,150.34 | 1687.84 | 6.15 | 29,185.91 | 1723.41 | 6.28 |
| MAPEsimulation (%) | 5.6366 | 6.4009 | 6.3887 | 6.4005 | |||||||||
| 2019 | 29,041 | 29,106.99 | 65.99 | 0.23 | 29,447.62 | 406.62 | 1.40 | 29,405.91 | 364.91 | 1.26 | 29,447.62 | 406.62 | 1.40 |
| 2020 | 31,605.2 | 29,112.08 | −2493.12 | 7.89 | 29,711.67 | −1893.53 | 5.99 | 29,663.73 | −1941.47 | 6.14 | 29,711.67 | −1893.53 | 5.99 |
| 2021 | 29,638.2 | 29,086.75 | −551.45 | 1.86 | 29,978.10 | 339.90 | 1.15 | 29,923.81 | 285.61 | 0.96 | 29,978.10 | 339.90 | 1.15 |
| 2022 | 27,088.1 | 29,034.33 | 1946.23 | 7.18 | 30,246.91 | 3158.81 | 11.66 | 30,186.17 | 3098.07 | 11.44 | 30,246.91 | 3158.81 | 11.66 |
| 2023 | 24,780 | 28,957.86 | 4177.86 | 16.86 | 30,518.14 | 5738.14 | 23.16 | 30,450.83 | 5670.83 | 22.88 | 30,518.14 | 5738.14 | 23.16 |
| MAPEprediction (%) | 6.8041 | 8.6711 | 8.5370 | 8.5839 | |||||||||
| MAPE (%) | 5.9439 | 6.9983 | 6.9540 | 6.9751 | |||||||||
| Years | 2024 | 2025 | 2026 | 2027 | 2028 |
|---|---|---|---|---|---|
| ID_T | 26,376.97 | 26,028.78 | 24,960.55 | 28,731.54 | 33,688.46 |
| GM(1,1) | 30,791.79 | 31,067.90 | 31,346.48 | 31,627.57 | 31,911.17 |
| DGM(1,1) | 30,717.80 | 30,987.12 | 31,258.80 | 31,532.87 | 31,809.33 |
| NGBM(1,1) | 29,691.42 | 29,811.48 | 29,928.85 | 30,043.79 | 30,156.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Wang, J.; Yu, K. IA-DTPSO: A Multi-Strategy Integrated Particle Swarm Optimization for Predicting the Total Urban Water Resources in China. Biomimetics 2025, 10, 233. https://doi.org/10.3390/biomimetics10040233
Zhu Z, Wang J, Yu K. IA-DTPSO: A Multi-Strategy Integrated Particle Swarm Optimization for Predicting the Total Urban Water Resources in China. Biomimetics. 2025; 10(4):233. https://doi.org/10.3390/biomimetics10040233
Chicago/Turabian StyleZhu, Zheyu, Jiawei Wang, and Kanhua Yu. 2025. "IA-DTPSO: A Multi-Strategy Integrated Particle Swarm Optimization for Predicting the Total Urban Water Resources in China" Biomimetics 10, no. 4: 233. https://doi.org/10.3390/biomimetics10040233
APA StyleZhu, Z., Wang, J., & Yu, K. (2025). IA-DTPSO: A Multi-Strategy Integrated Particle Swarm Optimization for Predicting the Total Urban Water Resources in China. Biomimetics, 10(4), 233. https://doi.org/10.3390/biomimetics10040233






