3D-Printed Soft Bionic Inchworm Robot Powered by Magnetic Force
Abstract
1. Introduction
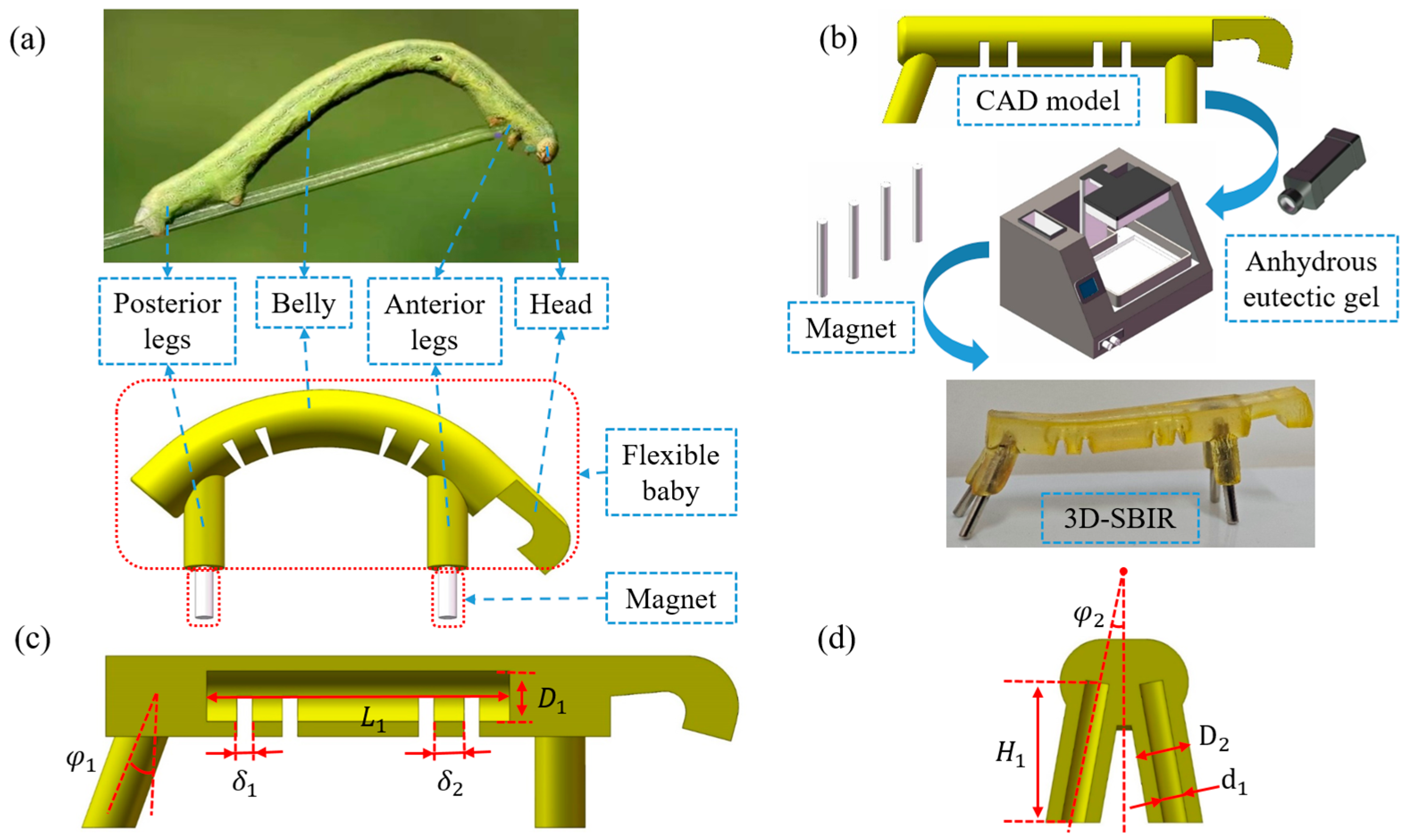
2. The Design and Production Process of the 3D-SBIR
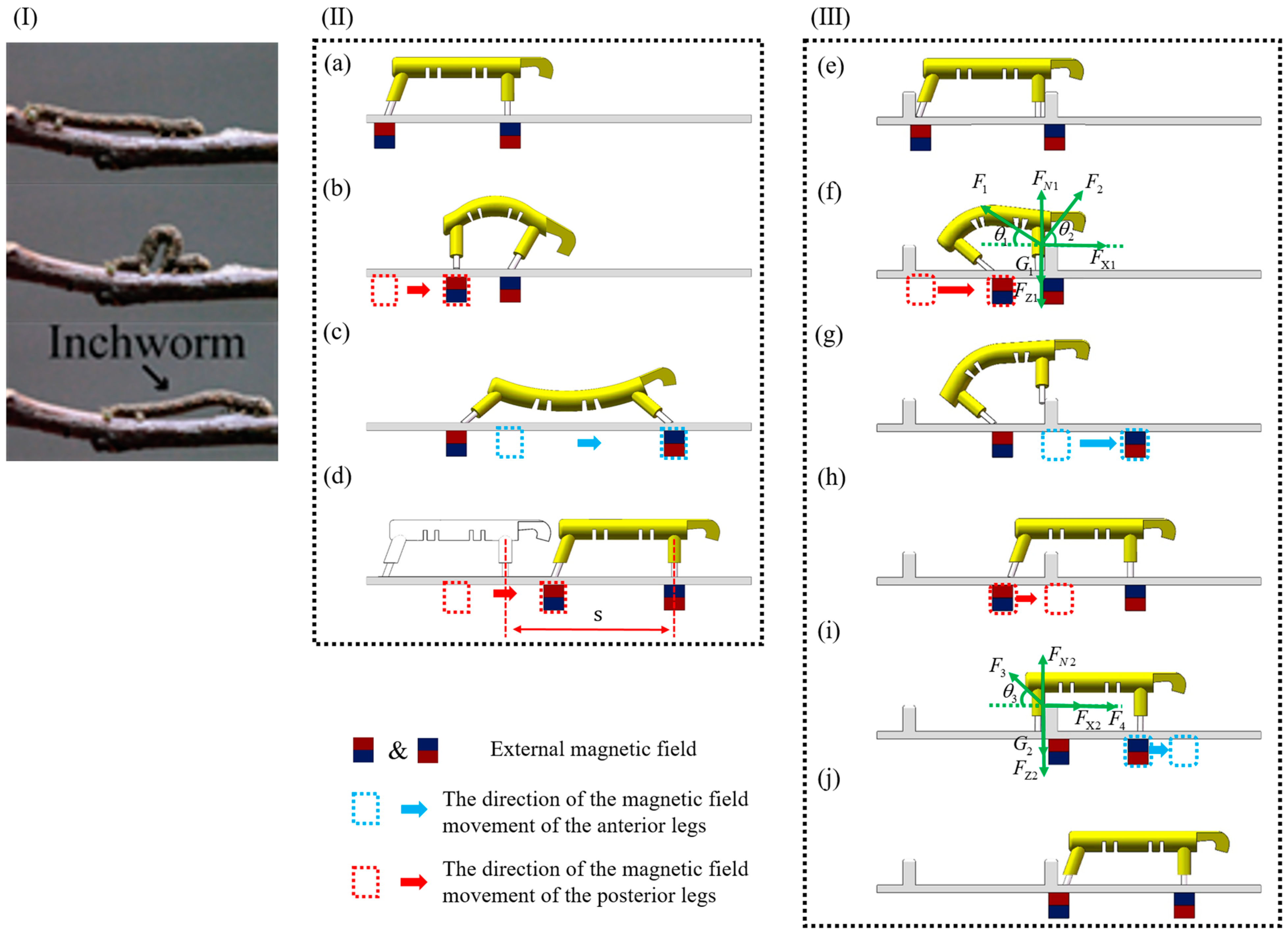
3. The Motion Gait Analysis of the 3D-SBIR
3.1. Gait Analysis of Motion on a Horizontal Plane
3.2. Gait Analysis of Climbing Obstacles
4. Model Construction and Simulation Analysis
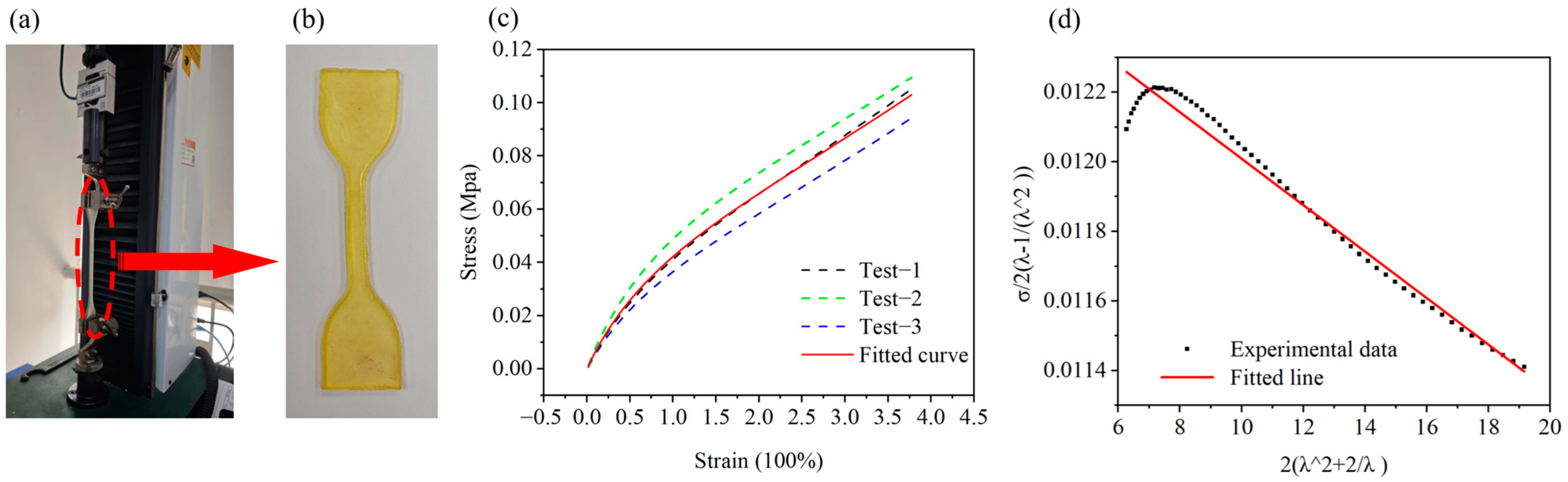
4.1. Constitutive Model of the Materials
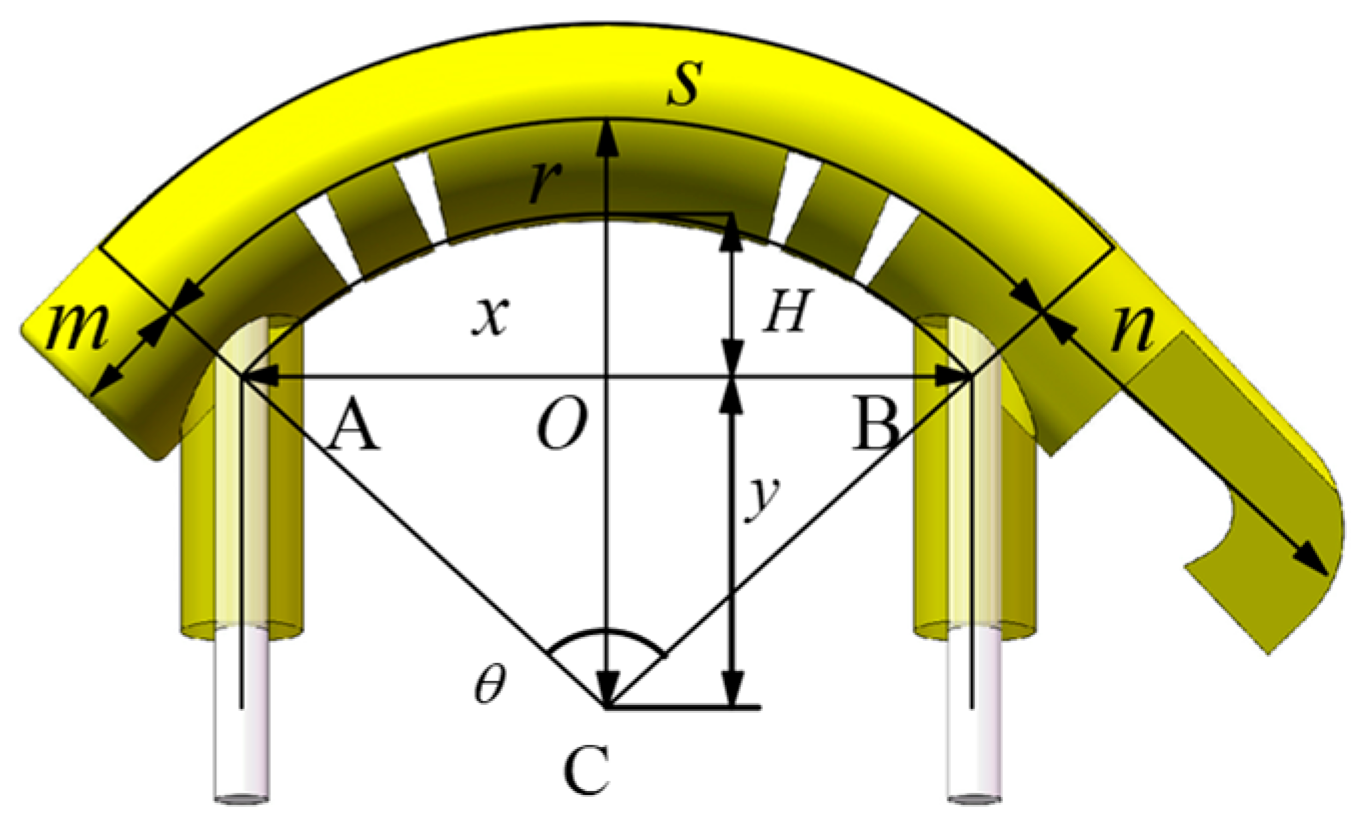
4.2. The Bending Deformation Model of the 3D-SBIR
4.3. Simulation and Experimentation of the Bending Deformation
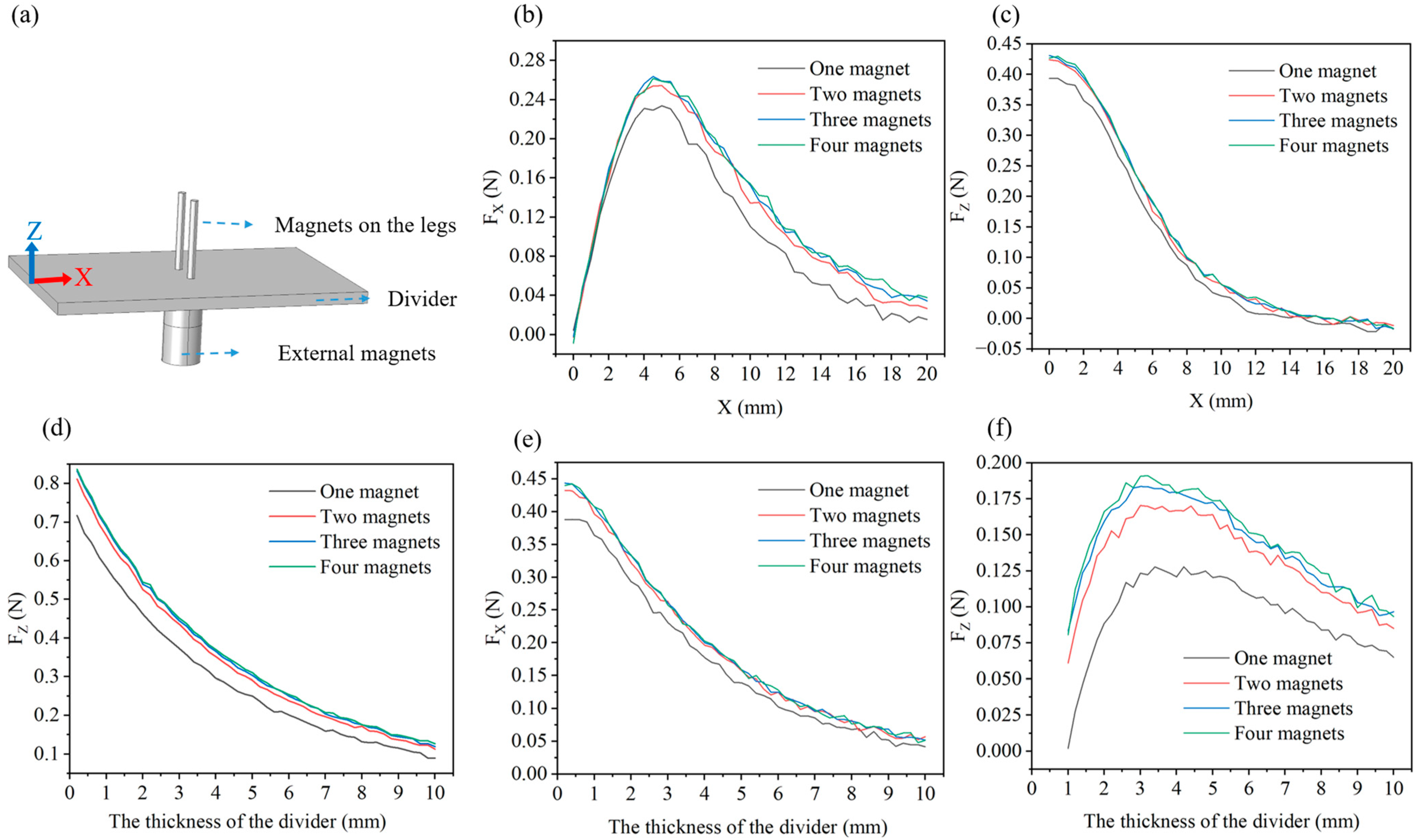
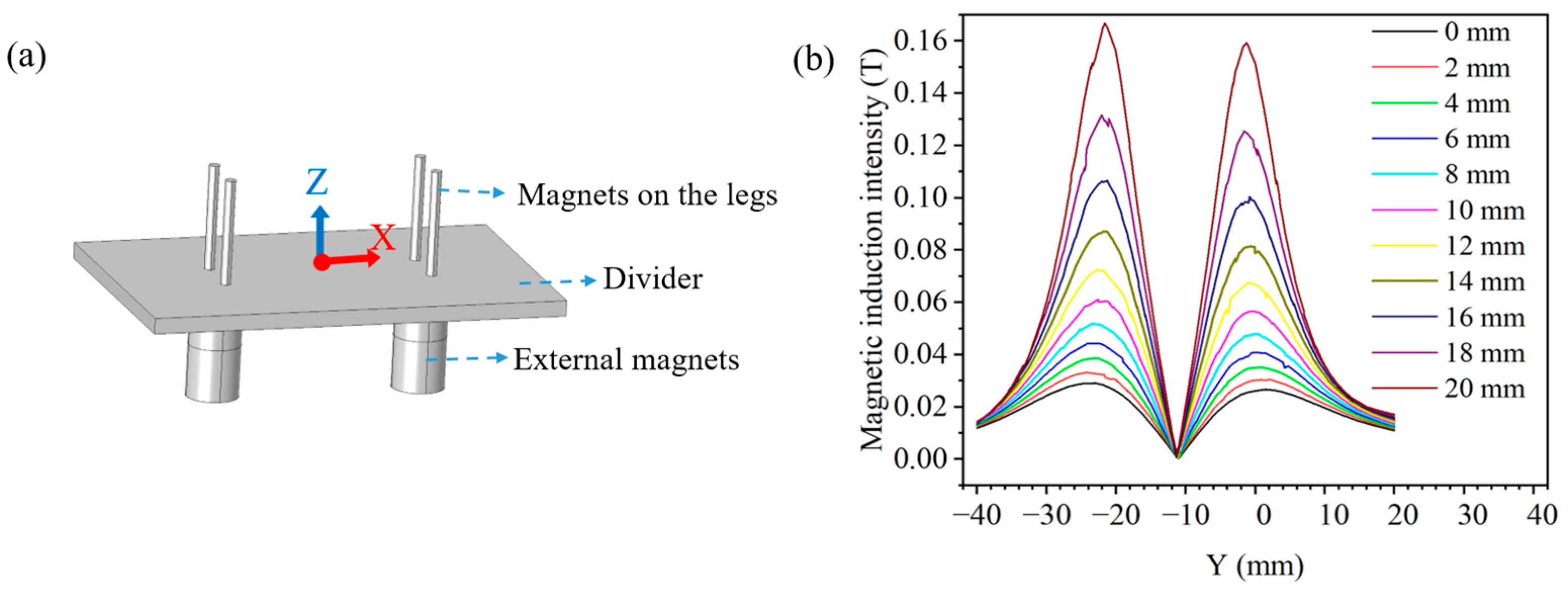
4.4. Magnetic Simulation and Analysis
5. Test Experiments on Movement Ability of the 3D-SBIR
5.1. Test of the 3D-SBIR Movement on a Horizontal Plane
5.2. Test of Climbing Obstacles for the 3D-SBIR
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Niu, H.; Feng, R.; Xie, Y.; Jiang, B.; Sheng, Y.; Yu, Y.; Baoyin, H.; Zeng, X. MagWorm: A Biomimetic Magnet Embedded Worm-Like Soft Robot. Soft Robot. 2021, 8, 507–518. [Google Scholar] [CrossRef] [PubMed]
- Romano, D.; Giovanni, A.; Stefanini, C. Assessing black solider fly pupation and survival in lunar regolith simulant: Implications for sustainable controlled habitats on the Moon. Acta Astronaucica 2024, 223, 505–511. [Google Scholar]
- Kandhari, A.; Wang, Y.; Chiel, H.J.; Quinn, R.D.; Daltorio, K.A. An analysis of peristaltic locomotion for maximizing velocity or minimizing cost of transport of earchworm-like robots. Soft Robot. 2021, 8, 458–505. [Google Scholar]
- Li, R.; Liu, Y.; Guo, A.; Shou, M.; Zhao, M.; Zhu, D.; Yang, P.-A.; Lee, C.-H. An Inchworm-Like Climbing Robot Based on Cable-Driven Grippers. IEEE/ASME Trans. Mechatron. 2024, 29, 1591–1600. [Google Scholar]
- Liu, J.R.; Liu, L.W.; Liu, Y.J.; Leng, J.S. Dielectric Elastomer Spring-Roll Bending Actuators: Applications in Soft Robotics and Design. Soft Robot. 2019, 6, 69–81. [Google Scholar]
- Xu, Z.F.; Hu, L.K.; Xiao, L.Y.; Jiang, H.J.; Zhou, Y.T. Modular Soft Robotic Crawlers Based on Fluidic Prestressed Composite Actuators. J. Bionic Eng. 2024, 21, 694–706. [Google Scholar]
- Jiao, P.C.; Hao, Z.; Hong, L.Q.; Yang, Y.; Li, W.T. Piezo-Wormbots for Continuous Crawling. Soft Robot. 2024, 11, 260–269. [Google Scholar]
- Cao, J.; Qin, L.; Liu, J.; Ren, Q.; Foo, C.C.; Wang, H.; Lee, H.P.; Zhu, J. Untethered soft robot capable of stable locomotion using soft electrostatic actuators. Extrem. Mech. Lett. 2018, 21, 9–16. [Google Scholar]
- Gu, G.; Zou, J.; Zhao, R.; Zhao, X.; Zhu, X. Soft wall-climbing robots. Sci. Robot. 2018, 3, 2874. [Google Scholar]
- Ding, J.; Su, H.; Nong, W.; Huang, C. An inchworm-inspired soft robot with combined functions of omni-directional steering and obstacle surmounting. Ind. Robot. Int. J. Robot. Res. Appl. 2023, 50, 456–466. [Google Scholar]
- Zhang, Y.; Huang, P.; Li, D.; Zhou, J.; Li, Y.; You, B.; Zhu, Y. Multi-modal Bionic Motion Analysis of A Cpg-controlled Pneumatic Soft Robot. J. Bionic Eng. 2024, 21, 2247–2257. [Google Scholar] [CrossRef]
- Huang, H.; Xie, J.; Huang, C.; Wu, D.; Ouyang, J.; Pang, C.; Zheng, L. Soft robot based on dual-mode deformation driving variable configuration. J. Shenzheng Univ. Sci. Eng. 2024, 41, 602–611. [Google Scholar] [CrossRef]
- Lara-Ortiz, V.; Guarneros, A.; Llorente-Vidrio, D.; Cruz-Ortiz, D.; Salgado, I.; Chairez, I. Active Disturbance Rejection Controller for a Flexible Walking Bioinspired Inchworm Mobile Robot Actuated with Shape Memory Alloy Devices. IEEE Trans. Control. Syst. Technol. 2022, 30, 1790–1797. [Google Scholar] [CrossRef]
- Hu, W.Q.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Shen, H.; Cai, S.; Wang, Z.; Yuan, Z.; Yu, H.; Yang, W. A Programmable Inchworm-Inspired Soft Robot Powered by a Rotating Magnetic Field. J. Bionic Eng. 2023, 20, 506–514. [Google Scholar] [CrossRef]
- Steiner, J.A.; Pham, L.N.; Abbott, J.J.; Leang, K.K. Modeling and Analysis of a Soft Endoluminal Inchworm Robot Propelled by a Rotating Magnetic Dipole Field. J. Mech. Robot. 2022, 14, 051002. [Google Scholar] [CrossRef]
- Steiner, J.A.; Nagel, W.S.; Leang, K.K. Magnetically-Actuated Endoluminal Soft Robot with Electroactive Polymer Actuation for Enhanced Gait Performance. J. Mech. Robot. 2024, 16, 104503. [Google Scholar] [CrossRef]
- Xu, R.; Xu, Q. Design of Bio-Inspired Untethered Soft Octopodal Robot Driven by Magnetic Field. Biomimetics 2023, 8, 269. [Google Scholar] [CrossRef]
- Xie, D.S.; Liu, J.B.; Kang, R.J.; Zuo, S.Y. Fully 3D-Printed Modular Pipe-Climbing Robot. IEEE Robot. Autom. Lett. 2021, 6, 462–469. [Google Scholar] [CrossRef]
- Sun, B.; Jia, R.; Yang, H.; Chen, X.; Tan, K.; Deng, Q.; Tang, J. Magnetic Arthropod Millirobots Fabricated by 3D-Printed Hydrogels. Adv. Intell. Syst. 2022, 4, 2100139. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, N.; Chen, Z.; He, H.; Wang, Z.; Gu, Z.; Chen, Y.; Mao, J.; Luo, Y.; He, Y. 3D-Printed High-Frequency Dielectric Elastomer Actuator toward Insect-Scale Ultrafast Soft Robot. ACS Mater. Lett. 2023, 5, 704–714. [Google Scholar]
- Joyee, E.; Pan, Y. A Fully Three-Dimensional Printed Inchworm-Inspired Soft Robot with Magnetic Actuation. Soft Robot. 2019, 6, 333–345. [Google Scholar] [PubMed]
- Li, X.B.; Wei, Y.T. An Improved Yeoh Constitutive Model for Hyperelastic Material. Eng. Mech. 2016, 33, 38–43. [Google Scholar]
- Fei, Y.Q.; Peng, W.; Yu, W.B. Movement of Air-driven Soft Robot. J. Mech. Eng. 2017, 53, 14–18. [Google Scholar]
- Li, X.; Liu, S.; Xu, Q.Y.; Zhang, Y.; Huo, Q.; Zhang, Y. Research on Prediction Method of Bending of Imitation Manta Soft Body Driver. Chin. Hydraul. Pneum. 2023, 47, 63–69. [Google Scholar]





| Ref | Actuation | Cable-Free | Product Process | Movement Capability |
|---|---|---|---|---|
| [4] | Voltage actuation | No | Complex | Climbing pipes |
| [5] | Voltage actuation | No | Complex | Moving on a horizontal surface |
| [6] | Pneumatic actuation | No | Complex | Climbing pipes and slopes |
| [11] | Pneumatic actuation | No | Simple | Moving in two-dimensional space |
| [15] | Magnetic actuation | Yes | Simple | Moving on a horizontal surface |
| [16] | Magnetic actuation | Yes | Simple | Moving inside the pipeline |
| [17] | Magnetic actuation | Yes | Simple | Moving inside the pipeline |
| [22] | Magnetic actuation | Yes | Simple | Moving on a horizontal surface |
| This work | Magnetic actuation | Yes | Simple | Moving on a horizontal surface, climbing obstacles, steps and transitions from horizontal to vertical surfaces |
| Part | Parameter Name | Symbol | Value |
|---|---|---|---|
| Belly | Cavity diameter | 5.0 mm | |
| Cavity length | 30.0 mm | ||
| Gap size | 1.5 mm | ||
| Gap distance | 3.0 mm | ||
| Legs | Backward tilt angle | 20° | |
| Outward tilt angle | 10° | ||
| Outside diameter | 5.0 mm | ||
| Inside diameter | 2.2 mm | ||
| Height | 10.0 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, D.; Zhang, L.; Nong, W.; Duan, Q.; Ding, J. 3D-Printed Soft Bionic Inchworm Robot Powered by Magnetic Force. Biomimetics 2025, 10, 202. https://doi.org/10.3390/biomimetics10040202
Xia D, Zhang L, Nong W, Duan Q, Ding J. 3D-Printed Soft Bionic Inchworm Robot Powered by Magnetic Force. Biomimetics. 2025; 10(4):202. https://doi.org/10.3390/biomimetics10040202
Chicago/Turabian StyleXia, Deli, Luying Zhang, Weihang Nong, Qingshan Duan, and Jiang Ding. 2025. "3D-Printed Soft Bionic Inchworm Robot Powered by Magnetic Force" Biomimetics 10, no. 4: 202. https://doi.org/10.3390/biomimetics10040202
APA StyleXia, D., Zhang, L., Nong, W., Duan, Q., & Ding, J. (2025). 3D-Printed Soft Bionic Inchworm Robot Powered by Magnetic Force. Biomimetics, 10(4), 202. https://doi.org/10.3390/biomimetics10040202







