GOHBA: Improved Honey Badger Algorithm for Global Optimization
Abstract
:1. Introduction
- (1)
- The introduction of the Tent Chaos algorithm for initialization improves the diversity of the population and the quality of the initial population to achieve better optimization results.
- (2)
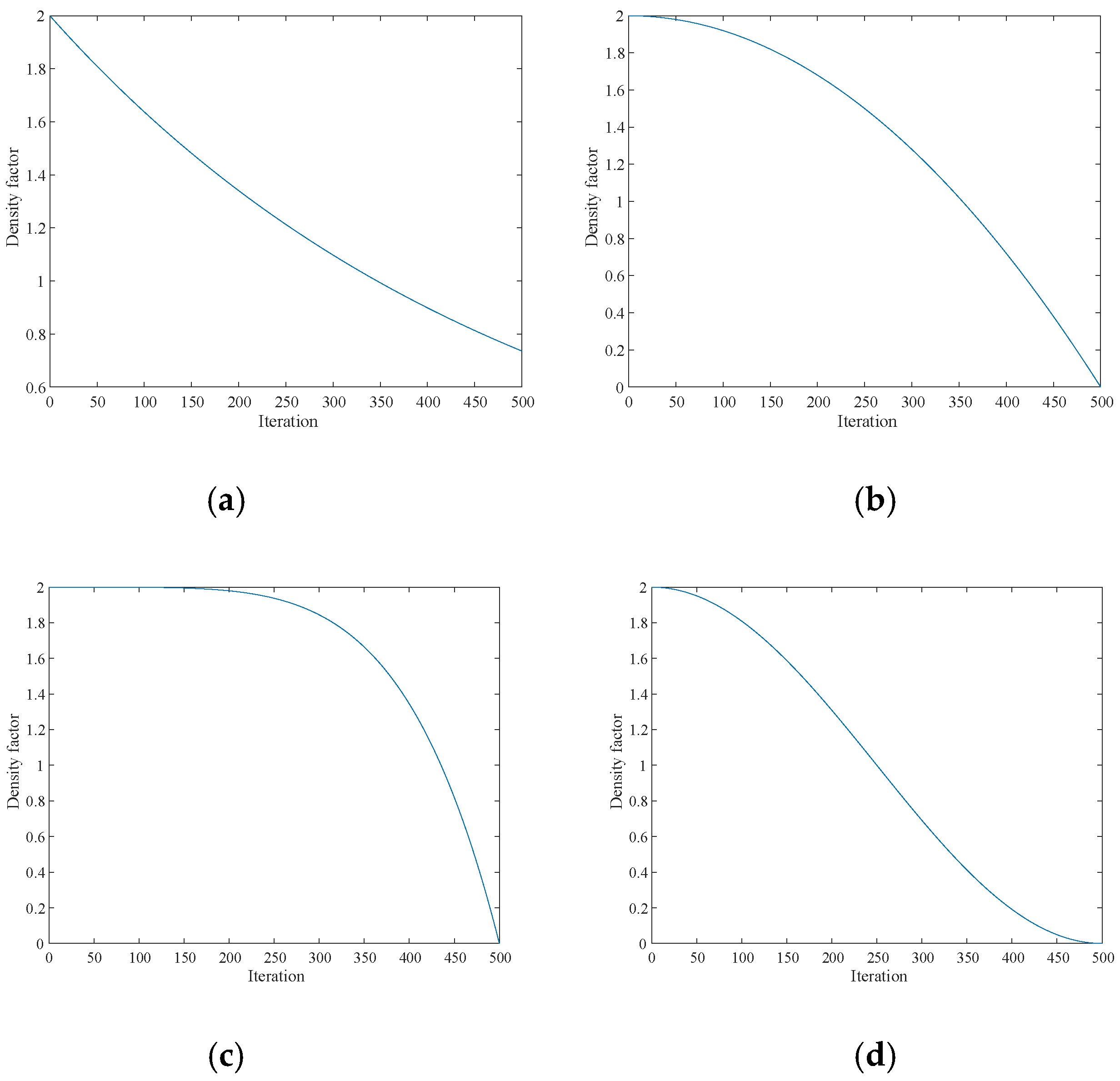
- The use of a new density factor helps the algorithm to explore more extensively in the whole solution space, especially in the early stage of the algorithm, which can effectively avoid premature convergence to a local optimal solution.
- (3)
- The golden sine strategy is introduced to improve the global search capability, accelerate the convergence speed, and help avoid falling into local optimal solutions.
- (4)
- Test the GOHBA on 23 test functions. Successfully solve two examples of engineering optimization problems as well as a quadruped robot path planning problem.
- Section 2: introduces the honey badger algorithm and proposes an improved GOHBA.
- Section 3: Compares the GOHBA with seven algorithms using 23 test functions. Analyzes performance via statistical tests and convergence analysis.
- Section 4: demonstrates the GOHBA’s application in engineering optimization and quadruped robot path planning.
- Section 5: summarizes experimental results, discusses limitations, and explores future development directions, such as integrating the GOHBA with other techniques.
2. Algorithm Analysis
2.1. The Honey Badger Algorithm
2.2. The Proposed Algorithm
2.2.1. Tent Sequence Initialization Population
2.2.2. Introduction of New Density Factors
2.2.3. Gold Sine Strategy
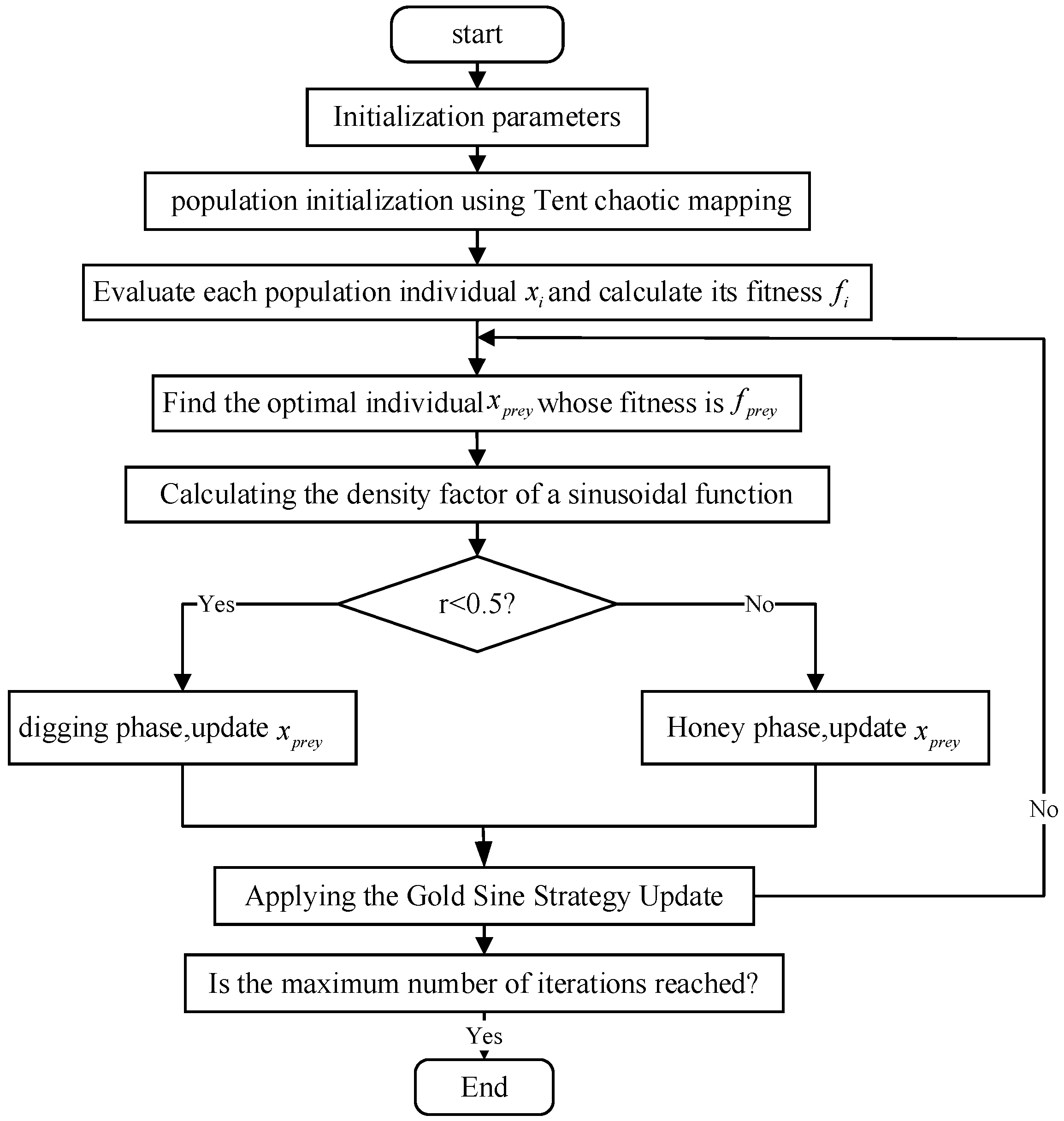
2.2.4. Algorithm Flow
2.3. Complexity Analysis
2.3.1. Computational Complexity
2.3.2. Space Complexity
2.4. The Path Planning Optimization Problem
3. Experiments
3.1. Experimental Setup and Assessment Criteria
3.2. Test Functions
3.3. Sensitivity Analysis
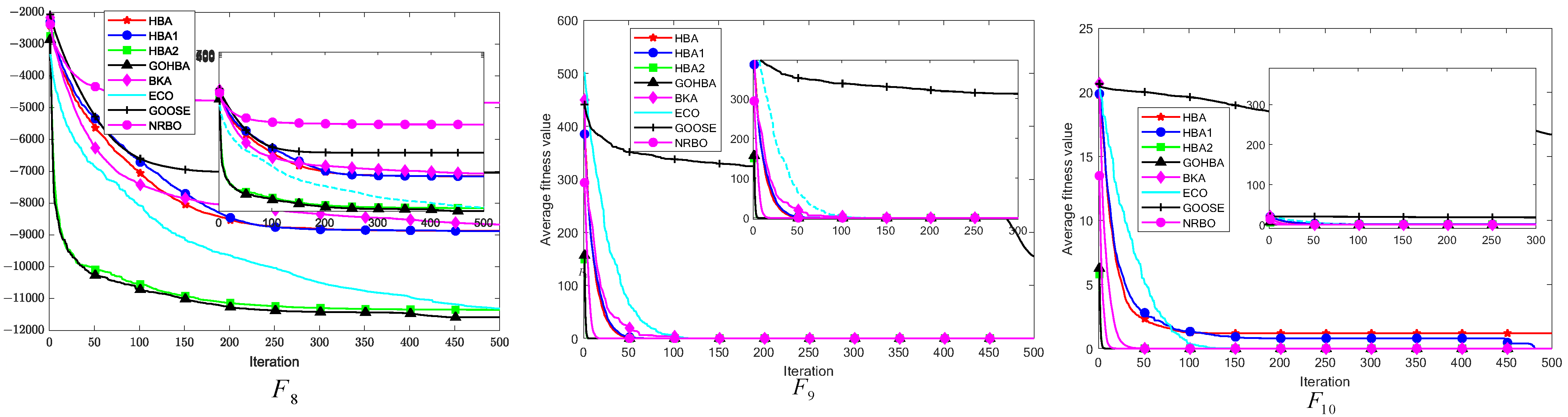
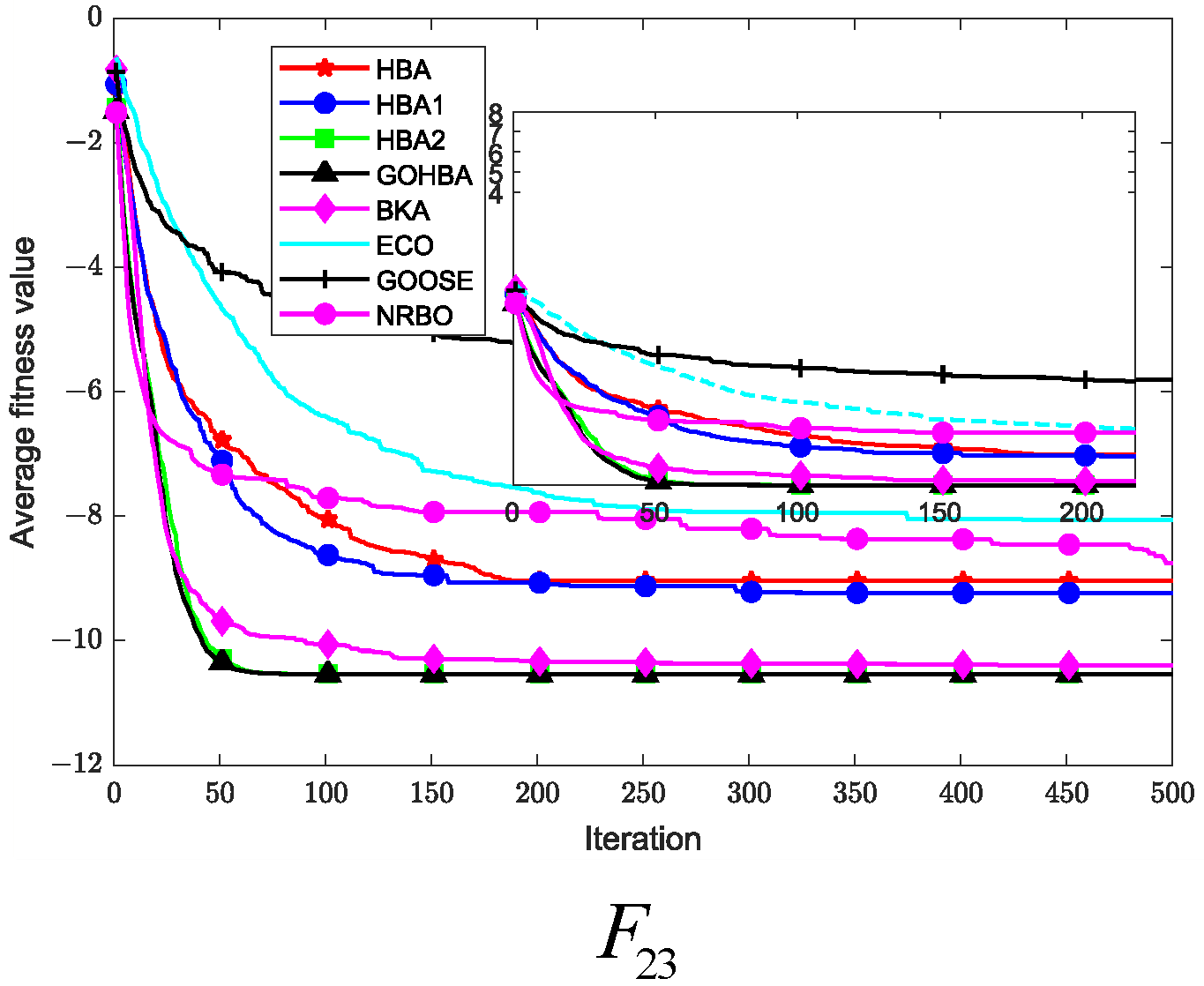
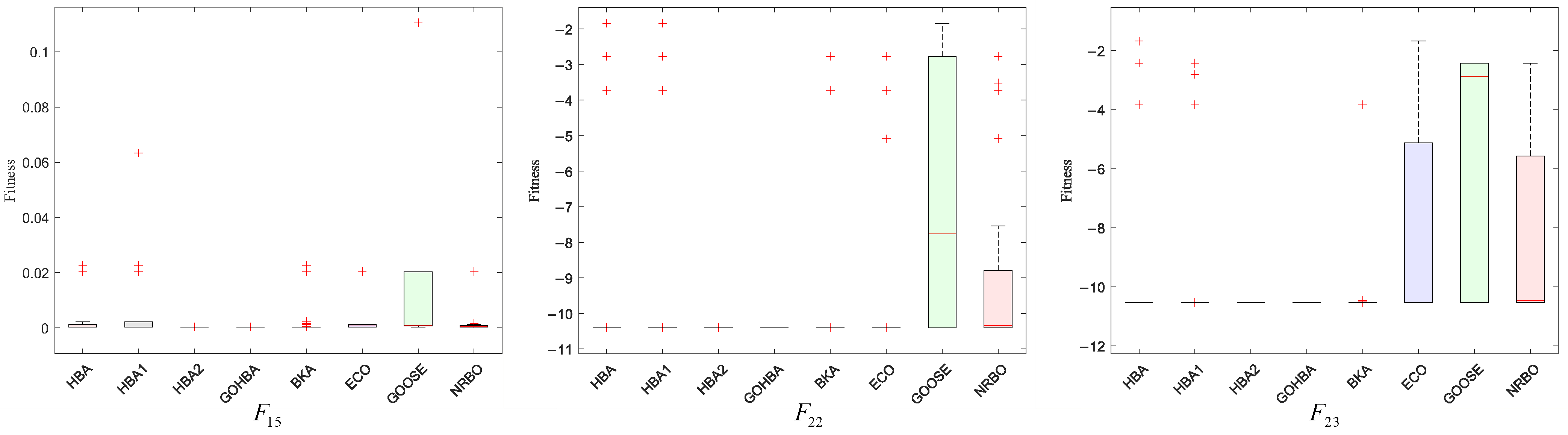
3.4. Experimental Results
3.5. Friedman Calibration
3.6. Wilcoxon Symbolic Rank Calibration
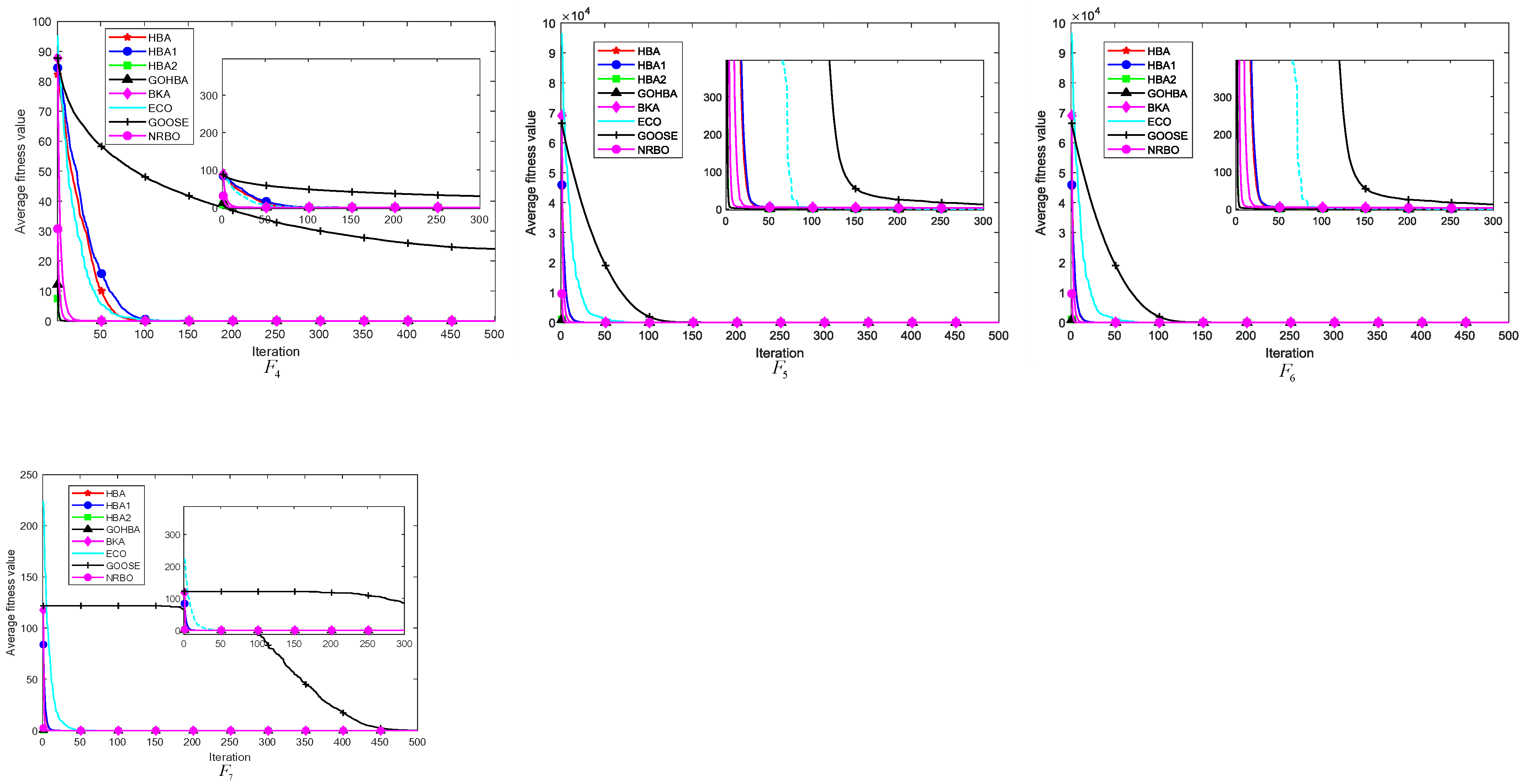
3.7. Convergence Analysis
3.8. Stability Analysis
4. GOHBA Application
4.1. Application to Engineering Design Problems
4.1.1. Robot Gripper Design Problem
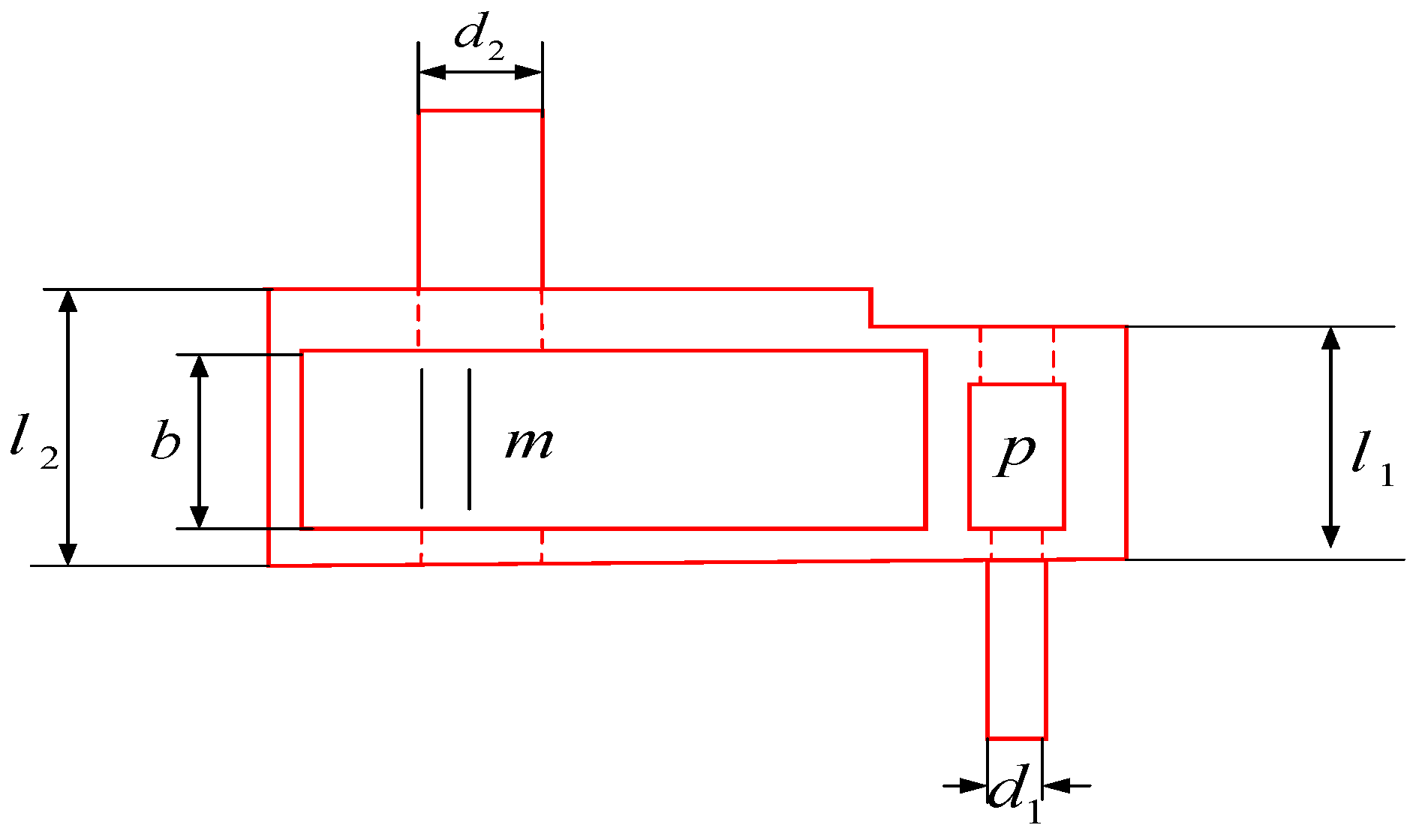
4.1.2. Speed Reducer Design Problem
4.2. Robot Path Planning with GOHBA
Simulation of Robot Path Planning
4.3. GOHBA Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.; Fang, C.; Lin, Z. Accelerated first-order optimization algorithms for machine learning. Proc. IEEE 2020, 108, 2067–2082. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, L.; Yu, F.; Heidari, A.A.; Wang, M.; Oliva, D.; Muhammad, K.; Chen, H. Ant colony optimization with horizontal and vertical crossover search: Fundamental visions for multi-threshold image segmentation. Expert Syst. Appl. 2021, 167, 114122. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Zidan, M.; Jameel, M.; Abouhawwash, M. Mantis Search Algorithm: A novel bio-inspired algorithm for global optimization and engineering design problems. Comput. Methods Appl. Mech. Eng. 2023, 415, 116200. [Google Scholar] [CrossRef]
- Barzilai, J.; Borwein, J.M. Two-point step size gradient methods. IMA J. Numer. Anal. 1988, 8, 141–148. [Google Scholar] [CrossRef]
- Borgwardt, K.H. The average number of pivot steps required by the simplex method is polynomial. Math. Program. 1982, 24, 141–158. [Google Scholar] [CrossRef]
- Agrawal, P.; Abutarboush, H.F.; Ganesh, T.; Mohamed, A.W. Metaheuristic algorithms on feature selection: A survey of one decade of research (2009–2019). IEEE Access 2021, 9, 26766–26791. [Google Scholar] [CrossRef]
- Akinola, O.O.; Ezugwu, A.E.; Agushaka, J.O.; Abu Zitar, R.; Abualigah, L. Multiclass feature selection with metaheuristic optimization algorithms: A review. Neural Comput. Appl. 2022, 34, 19751–19790. [Google Scholar] [CrossRef]
- Ahmed, I.; Alvi, U.-E.; Basit, A.; Rehan, M.; Hong, K.-S. Multi-objective whale optimization approach for cost and emissions scheduling of thermal plants in energy hubs. Energy Rep. 2022, 8, 9158–9174. [Google Scholar] [CrossRef]
- Kiani, F.; Nematzadeh, S.; Anka, F.A.; Findikli, M.A. Chaotic sand cat swarm optimization. Mathematics 2023, 11, 2340. [Google Scholar] [CrossRef]
- Wu, J.; Su, Z. Flavoring search algorithm with applications to engineering optimization problems and robot path planning. Appl. Math. Model. 2024, 135, 396–437. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, C.; Farhad, S.G.; Mirjalili, S. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems. Expert Syst. Appl. 2023, 215, 119269. [Google Scholar] [CrossRef]
- Amiri, M.H.; Hashjin, N.M.; Montazeri, M.; Mirjalili, S.; Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef] [PubMed]
- Peraza-Vázquez, H.; Peña-Delgado, A.; Merino-Treviño, M.; Morales-Cepeda, A.B.; Sinha, N. A novel metaheuristic inspired by horned lizard defense tactics. Artif. Intell. Rev. 2024, 57, 59. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Xu, Y.; Zhong, R.; Cao, Y.; Zhang, C.; Yu, J. Symbiotic mechanism-based honey badger algorithm for continuous optimization. Clust. Comput. 2025, 28, 133. [Google Scholar] [CrossRef]
- Majumdar, P.; Mitra, S. Enhanced honey badger algorithm based on nonlinear adaptive weight and golden sine operator. Neural Comput. Appl. 2024, 37, 367–386. [Google Scholar] [CrossRef]
- Sun, J.; Wang, L.; Razmjooy, N. Anterior cruciate ligament tear detection based on deep belief networks and improved honey badger algorithm. Biomed. Signal Process. Control. 2023, 84, 105019. [Google Scholar] [CrossRef]
- Jose, R.A.; Paulraj, E.D.; Rajesh, P. Enhancing Steady-State power flow optimization in smart grids with a hybrid converter using GBDT-HBA technique. Expert Syst. Appl. 2024, 258, 125047. [Google Scholar] [CrossRef]
- Guo, L.; Xu, C.; Yu, T.; Wumaier, T.; Han, X. Ultra-short-term wind power forecasting based on long short-term memory network with modified honey badger algorithm. Energy Rep. 2024, 12, 3548–3565. [Google Scholar] [CrossRef]
- Düzenli, T.; Onay, F.K.; Aydemi, S.B. Improved honey badger algorithms for parameter extraction in photovoltaic models. Optik 2022, 268, 169731. [Google Scholar] [CrossRef]
- Ye, Z.; Zhao, T.; Liu, C.; Zhang, D.; Bai, W. An Improved Honey Badger Algorithm through Fusing Multi-Strategies. Comput. Mater. Contin. 2023, 76, 1479–1495. [Google Scholar] [CrossRef]
- Yang, B.; Zhou, Y.; Liu, B.; Li, M.; Duan, J.; Cao, P.; Zheng, C.; Jiang, L.; Sang, Y. Optimal array layout design of wave energy converter via honey badger algorithm. Renew. Energy 2024, 234, 121182. [Google Scholar] [CrossRef]
- Bansal, A.K.; Sangtani, V.S.; Bhukya, M.N. Optimal configuration and sensitivity analysis of hybrid nanogrid for futuristic residential application using honey badger algorithm. Energy Convers. Manag. 2024, 315, 118784. [Google Scholar] [CrossRef]
- Huang, P.; Zhou, Y.; Deng, W.; Zhao, H.; Luo, Q.; Wei, Y. Orthogonal opposition-based learning honey badger algorithm with differential evolution for global optimization and engineering design problems. Alex. Eng. J. 2024, 91, 343–367. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Feda, A.K.; Ishaya, M.M.; Agyekum, E.B.; Kim, K.-C.; Mbasso, W.F.; Kamel, S. Antenna S-parameter optimization based on golden sine mechanism based honey badger algorithm with tent chaos. Heliyon 2024, 9, e21296. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Fu, S.; Chen, J.; He, L. Enhanced Aquila optimizer based on tent chaotic mapping and new rules. Sci. Rep. 2024, 14, 3013. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Q.; Song, H.; Han, T.; Li, T. CMGWO: Grey wolf optimizer for fusion cell-like P systems. Heliyon 2024, 10, e34496. [Google Scholar] [CrossRef]
- Duan, Y.; Yu, X. A collaboration-based hybrid GWO-SCA optimizer for engineering optimization problems. Expert Syst. Appl. 2023, 213, 119017. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden Sine Algorithm: A Novel Math-Inspired Algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Bae, S. Big-O Notation. In JavaScript Data Structures and Algorithms; Apress: Berkeley, CA, USA, 2019. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Röhmel, J. The permutation distribution of the Friedman test. Comput. Stat. Data Anal. 1997, 26, 83–99. [Google Scholar] [CrossRef]
- Dewan, I.; Rao, B.P. Wilcoxon-signed rank test for associated sequences. Stat. Probab. Lett. 2005, 71, 131–142. [Google Scholar] [CrossRef]
- Antczak, T. Exactness of penalization for exact minimax penalty function method in nonconvex programming. Appl. Math. Mech. 2015, 36, 541–556. [Google Scholar] [CrossRef]
- Wang, K.; Guo, M.; Dai, C.; Li, Z. Information-decision searching algorithm: Theory and applications for solving engineering optimization problems. Inf. Sci. 2022, 607, 1465–1531. [Google Scholar] [CrossRef]
- Zhao, W.G.; Zhang, Z.X.; Wang, L.Y. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Guan, Z.; Ren, C.; Niu, J.; Wang, P.; Shang, Y. Great Wall construction algorithm: A novel meta-heuristic algorithm for engineer problems. Expert Syst. Appl. 2023, 233, 120905. [Google Scholar] [CrossRef]








| Function | D | R | f (x*) |
|---|---|---|---|
| 30 | [−100,100] | 0 | |
| 30 | [−10,10] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−30,30] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−1.28,1.28] | 0 | |
| 30 | [−500,500] | −12569.4 | |
| 30 | [−5.12,5.12] | 0 | |
| 30 | [−32,32] | 0 | |
| 30 | [−600,600] | 0 | |
| 30 | [−50,50] | 0 | |
| 30 | [−50,50] | 0 | |
| 2 | [−65,65] | 1 | |
| 4 | [−5,5] | 0.00003075 | |
| 2 | [−5,5] | −1.0316285 | |
| 2 | [−5,5] | 0.398 | |
| 2 | [−2,2] | 3 | |
| 3 | [0,1] | −3.86 | |
| 6 | [0,1] | −3.32 | |
| 4 | [0,10] | −10 | |
| 4 | [0.10] | −10 | |
| 4 | [0,10] | −10 |
| Function | Criterion | p/t 60/250 | p/t 30/500 | p/t 15/1000 |
|---|---|---|---|---|
| F1 | Mean Std Rank | 1.7142 × 10−283 0 2 | 0 0 2 | 0 0 2 |
| F2 | Mean Std Rank | 1.5485 × 10−145 8.7921 × 10−145 3 | 1.2544 × 10−273 0 1.5 | 0 0 1.5 |
| F3 | Mean Std Rank | 2.5563E−273 0 2 | 0 0 2 | 0 0 2 |
| F4 | Mean Std Rank | 2.2952 × 10−143 9.0280 × 10−143 3 | 1.0078 × 10−268 0 1.5 | 0 0 1.5 |
| F5 | Mean Std Rank | 2.5151 × 101 4.6295 × 10−1 2 | 2.4791 × 101 5.2181 × 10-1 3 | 2.4916 × 101 3.6635 × 10−1 1 |
| F6 | Mean Std Rank | 1.0971 × 10−3 6.6149 × 10−4 3 | 2.3806 × 10−04 1.7511 × 10−04 2 | 9.5836 × 10−5 7.7331 × 10−5 1 |
| F7 | Mean | 1.5468 × 10−4 | 1.3085 × 10−4 | 1.6314 × 10−4 |
| Std | 1.3565 × 10−4 | 9.6256 × 10−5 | 1.5177 × 10−4 | |
| Rank | 2 | 1 | 3 | |
| F8 | Mean Std Rank | −1.1565 × 104 8.7136 × 102 3 | −1.1419 × 104 7.5399 × 102 1 | −1.1425 × 104 8.7099 × 102 2 |
| F9 | Mean Std Rank | 0 0 2 | 0 0 2 | 0 0 2 |
| F10 | Mean Std Rank | 4.4409 × 10−16 0 2 | 4.4409 × 10−16 0 2 | 4.4409 × 10−16 0 2 |
| F11 | Mean Std Rank | 0 0 2 | 0 0 2 | 0 0 2 |
| F12 | Mean Std Rank | 1.3269 × 10−4 7.5080 × 10−5 3 | 3.1881E × 10−5 2.6201 × 10−5 1 | 1.9846 × 10−5 3.1180 × 10−5 2 |
| F13 | Mean Std Rank | 5.7978 × 10−3 6.7686 × 10−3 1 | 9.7015 × 10−3 2.0111 × 10−2 2 | 1.5350 × 10−2 2.1065 × 10−2 3 |
| F14 | Mean Std Rank | 2.3088 3.1913 1 | 2.9375 3.5261 2 | 4.0693 4.2901 3 |
| F15 | Mean Std Rank | 3.0756 × 10−4 1.3235 × 10−7 1 | 3.0780 × 10−4 8.7970 × 10−7 2 | 4.6868 × 10−4 1.1350 × 10−3 3 |
| F16 | Mean Std Rank | −1.0316 3.7532 × 10−16 3 | −1.0316 3.5037 × 10−16 2 | −1.0316 3.4164 × 10−16 1 |
| F17 | Mean Std Rank | 3.9789 × 10−1 0 2 | 3.9789 × 10−1 0 2 | 3.9789 × 10−1 0 2 |
| F18 | Mean Std Rank | 3.0000 2.6773 × 10−15 1 | 3.5400 3.8184 2 | 6.7800 13.373 3 |
| F19 | Mean Std Rank | −3.8622 2.1599 × 10−3 2 | −3.8626 1.1146 × 10−03 1 | −3.8620 2.3885 × 10−03 3 |
| F20 | Mean Std Rank | −3.2282 6.3648 × 10−02 1 | −3.2142 8.4419 × 10−2 2 | −3.2353 8.9149 × 10−2 3 |
| F21 | Mean Std Rank | −10.153 2.3119 × 10−15 3 | −10.153 1.1061 × 10−15 1 | −10.153 1.6833 × 10−15 2 |
| F22 | Mean Std Rank | −10.403 1.4355 × 10−15 1 | −10.403 2.1682 × 10−15 2 | −10.250 1.0800 3 |
| F23 | Mean | −10.536 | −10.536 | −10.536 |
| Std | 2.2697 × 10−15 | 2.2555 × 10−15 | 2.4864 × 10−15 | |
| Rank | 2 | 1 | 3 | |
| Rank-Count Ave-Rank Overall-Rank | 47.00 2.04 2 | 40.00 1.74 1 | 51.00 2.22 3 |
| Function | Algorithm | Mean | Std | Function | Algorithm | Mean | Std |
|---|---|---|---|---|---|---|---|
| F1 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 9.5334 × 10−136 1.8327 × 10−147 0 0 1.7665 × 10−73 4.7616 × 10−43 6.6684 × 10−2 4.8704 × 10−280 | 3.1770 × 10−135 8.6713 × 10−147 0 0 1.2490 × 10−72 3.2749 × 10−42 2.2264 × 10−02 0 | F13 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 0.50283 0.54545 6.3470 × 10−3 1.0836 × 10−2 1.8507 0.29398 4.9868 × 10−2 2.4079 | 0.35069 0.33952 1.0825 × 10-2 2.3800 × 10-2 0.48175 0.81989 2.7722 × 10-2 0.42596 |
| F2 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 1.1649 × 10−72 3.1952 × 10−77 5.1704 × 10−242 7.3796 × 10−275 1.5914 × 10−36 1.0658 × 10−25 2.9972 × 103 2.3919 × 10−141 | 2.5286 × 10−72 1.0432 × 10−76 0 0 1.1253 × 10−35 5.3651 × 10−25 1.9594 × 1004 1.2551 × 10−140 | F14 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 1.9601 1.4506 3.7002 3.3275 1.0179 1.3150 10.788 3.6973 | 2.4640 1.6106 3.9934 3.8655 0.14058 0.88036 5.9670 4.1621 |
| F3 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 1.8839 × 10−95 1.1811 × 10E−121 0 0 6.2076 × 10−82 5.0568 × 10−52 1.0715 × 102 1.7675 × 10−262 | 9.4665 × 10−95 6.3943 × 10−121 0 0 3.1551 × 10−81 2.4078 × 10−51 67.106 0 | F15 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 4.9888 × 10−3 5.8892 × 10−3 3.0749 × 10−4 3.0782 × 10−4 2.0645 × 10−3 1.4895E × 10−3 7.6863 × 10−3 4.0657 × 10−3 | 8.6964 × 10-3 1.1639 × 10-2 1.0135 × 10-10 1.3621 × 10-6 5.6323 × 10-3 3.9106 × 10-3 1.7056 × 10-2 7.7180 × 10-3 |
| F4 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 1.3975 × 10−57 1.5153 × 10−65 5.6896 × 10−239 3.7000 × 10−268 1.9947 × 10−44 7.0883 × 1024 24.065 1.1857 × 10−138 | 3.5954E−57 3.5655E−65 0 0 1.0643 × 10−43 4.5737 × 10−23 6.4515 7.2777 × 10−138 | F16 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 | 3.0917 × 10-16 3.2349 × 10-16 3.2812 × 10-16 3.5888 × 10-16 3.7532 × 10-16 3.5110 × 10-10 2.7862 × 10-7 3.9746 × 10-16 |
| F5 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 24.006 25.336 23.477 24.851 27.655 27.430 338.14 27.824 | 0.71976 0.70241 0.47340 0.53801 0.94309 0.47233 5.5200 × 102 0.75809 | F17 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 0.39789 0.39789 0.39789 0.39789 0.39789 0.39789 0.39789 0.39789 | 3.0917 × 10-16 3.2349 × 10-16 3.2812 × 10-16 3.5888 × 10-16 3.7532 × 10-16 3.5110 × 10-10 2.7862 × 10-7 3.9746 × 10-16 |
| F6 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 2.4071 × 10−2 0.11606 5.4509 × 10−6 2.4749 × 10−4 2.2955 5.9312 × 10−3 5.8685 × 10−2 2.9545 | 7.2801 × 10−2 0.15916 7.5596 × 10−6 1.3729 × 10−4 1.5747 6.8283 × 10−3 2.1420 × 10−2 0.43331 | F18 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 3.0000 5.7000 3.0000 4.6200 3.0000 3.0000 4.6200 3.0000 | 1.8485 × 10-15 12.499 1.7690 × 10-15 6.4772 1.8485 × 10-15 7.5191 × 10-14 11.455 3.3020 × 10-15 |
| F7 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 3.4028 × 10−4 3.8793 × 10−4 1.4679 × 10−4 1.2001 × 10−4 3.6102 × 10−4 2.6341 × 10-4 0.28906 2.9395 × 10−4 | 2.6880 × 10−4 2.7480 × 10−4 1.0950 × 10−4 1.1524 × 10−4 3.0664 × 10−4 2.2036 × 10−4 0.12683 2.5676 × 10−04 | F19 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | −3.8618 −3.8612 −3.8623 −3.8623 −3.8628 −3.8628 −3.8627 −3.8628 | 2.5872 × 10-3 3.1846 × 10-3 1.8908 × 10-03 1.8908 × 10-03 1.0031 × 10-15 2.7858 × 10-12 4.2399 × 10-05 1.0327 × 10-15 |
| F8 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | −8.8728 × 103 −8.8750 × 103 −1.1355 × 104 −1.1591 × 104 −8.6730 × 103 −1.1312 × 104 −7.0389 × 103 −4.8415 × 103 | 9.6921 × 102 9.2706 × 102 9.7941 × 102 7.0580 × 102 1.7590 × 103 7.9397 × 102 5.8050 × 102 7.0982 × 102 | F20 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | −3.2660 −3.2475 −3.2341 −3.2325 −3.2951 −3.2483 −3.1988 −3.2342 | 7.4959 × 10-2 0.10054 7.7610 × 10-2 7.8819 × 10-2 5.3324 × 10-2 5.8297 × 10-2 3.3200 × 10-2 8.3160 × 10-2 |
| F9 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 0 0 0 0 0 0 1.5466 × 102 0 | 0 0 0 0 0 0 37.430 0 | F21 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | −8.8796 −9.3659 −10.153 −10.1531 −10.003 −9.4977 −4.9875 −8.7948 | 2.9636 2.3962 3.5436 × 10-15 3.7725 × 10-15 1.0639 2.0217 2.9565 2.2724 |
| F10 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 1.1944 1.0086 × 10−10 4.4409 × 10−16 0 4.4409 × 10−16 4.4409 × 10−16 16.703 4.4409 × 10−16 | 4.7756 6.2654 × 10−10 0 0 0 0 5.8009 0 | F22 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | −9.6398 −9.2391 −10.403 −10.403 −10.117 −9.3778 −6.9863 −9.1301 | 2.3204 2.7069 2.0142 × 10-15 1.1349 × 10-15 1.4202 2.4018 3.5595 2.1995 |
| F1 F11 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 0 0 0 0 0 0 2.0920 × 102 0 | 0 0 0 0 0 0 37.885 0 | F23 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | −9.0399 −9.2326 −10.536 −10.536 −10.400 −8.0526 −5.8102 −8.7555 | 3.0454 2.8235 2.4074 × 10-15 2.6250 × 10-15 0.94744 3.5864 3.7933 2.6778 |
| F12 | HBA HBA1 HBA2 GOHBA BKA ECO GOOSE NRBO | 1.4532 × 10−4 4.5309 × 10−3 1.0044 × 10−6 3.0860 × 10−5 0.13958 2.7357 × 10−4 5.5369 0.26140 | 9.4521 × 10−4 1.5462 × 10-2 1.0240 × 10−6 2.1128 × 10−5 0.21776 7.7691 × 10−4 1.9790 8.2184 × 10−2 |
| Functions | HBA | HBA1 | HBA2 | GOHBA | |
|---|---|---|---|---|---|
| F3 | Mean Std Rank | 1.1649 × 10−72 2.5286 × 10−72 5 | 3.1952 × 10−77 1.0423 × 10−76 4 | 5.1704 × 10−242 0 2 | 7.3796 × 10−275 0 1 |
| F4 | Mean Std Rank | 1.3975 × 10−57 3.5954 × 10−57 5 | 1.5153 × 10−65 3.5655 × 10−65 4 | 5.6896 × 10−239 0 2 | 3.7007 × 10−268 0 1 |
| F7 | Mean Std Rank | 3.4028 × 10−4 2.6880 × 10−4 5 | 3.8793 × 10−4 2.7480 × 10−4 7 | 1.4679 × 10−4 1.0950 × 10−4 2 | 1.2001 × 10−4 1.1524 × 10−4 1 |
| F10 | Mean Std Rank | 1.1944 4.77567 7 | 1.0086 × 10−10 6.2654 × 10−10 6 | 4.4409 × 10−16 0 3 | 4.4409 × 10−16 0 3 |
| F11 | Mean Std Rank | 0 0 4 | 0 0 4 | 0 0 4 | 0 0 4 |
| F13 | Mean Std Rank | 0.50283 0.35069 5 | 0.54545 0.33952 6 | 6.3470 × 10−3 1.0825 × 10−2 1 | 1.0836 × 10−2 2.3835 × 10−2 2 |
| F17 | Mean Std Rank | 0.39789 0 3 | 0.39789 0 3 | 0.39789 0 3 | 0.39789 0 3 |
| F21 | Mean Std Rank | −8.8796 2.9636 6 | −9.3659 2.3962 5 | −10.153 3.5436 × 10−15 1 | −10.153 3.7725 × 10−15 2 |
| F22 | Mean Std Rank | −9.6398 2.3204 4 | −9.2391 2.7069 6 | −10.403 2.0142 × 10−15 2 | −10.403 1.1349 × 10−15 1 |
| F23 | Mean Std Rank | −9.0399 3.0454 5 | −9.2326 2.8235 4 | −10.536 2.4074 × 10−15 1 | −10.536 2.6250 × 10−15 2 |
| Rank-Count | 49 | 49 | 21 | 20 | |
| Ave-Rank | 4.9 | 4.9 | 2.1 | 2.0 | |
| Overall-Rank | 5.5 | 5.5 | 2 | 1 | |
| Functions | BKA | ECO | GOOSE | NRBO | |
| F2 | Mean Std Rank | 1.5914 × 10−36 1.1253 × 10−35 6 | 1.0658 × 10−25 5.3651 × 10−25 7 | 2.9972 × 103 1.9594 × 104 8 | 2.3919 × 10−141 1.2551 × 10−140 3 |
| F4 | Mean Std Rank | 1.9947 × 10−44 1.0643 × 10−43 6 | 7.0883 × 10−24 4.5737 × 10−23 7 | 24.065 6.4515 8 | 1.1857 × 10−138 7.2777 × 10−138 3 |
| F7 | Mean Std Rank | 3.6102 × 10−4 3.0664 × 10−4 6 | 2.6341 × 10−4 2.2036 × 10−4 3 | 0.28906 0.12683 8 | 2.9395 × 10−4 2.5676 × 10−4 4 |
| F10 | Mean Std Rank | 4.4409 × 10−16 0 3 | 4.4409 × 10−16 0 3 | 16.703 5.8009 × 100 8 | 4.4409 × 10⁻¹⁶ 0.0000 × 10⁰ 3 |
| F11 | Mean Std Rank | 0 0 4 | 0 0 4 | 2.0920 × 102 37.885 8 | 0 0 4 |
| F13 | Mean Std Rank | 1.8507 0.48175 7 | 0.29398 0.81989 4 | 4.9868 × 10−2 2.7722 × 10−2 3 | 2.4079 0.42596 8 |
| F17 | Mean Std Rank | 3.6102 × 10−4 3.0664 × 10−4 6 | 0.39789 1.8099 × 10−7 8 | 0.39789 9.2929 × 10−8 7 | 0.39789 0 3 |
| F21 | Mean Std Rank | −10.003 1.0639 3 | −9.4977 2.0217 4 | −4.9875 2.9565 8 | −8.7948 2.2724 7 |
| F22 | Mean Std Rank | −10.117 1.4202 3 | −9.3778 2.40180 5 | −6.9863 3.5595 8 | −9.1301 2.1995 7 |
| F23 | Mean Std Rank | −10.400 0.94744 3 | −8.0526 3.5864 7 | −5.8102 3.7933 8 | −8.7555 2.6778 6 |
| Rank-Count | 47 | 52 | 74 | 48 | |
| Ave-Rank | 4.7 | 5.2 | 7.4 | 4.8 | |
| Overall-Rank | 3 | 7 | 8 | 4 |
| Functions | HBA vs. GOHBA | HBA1 vs. GOHBA | HBA2 vs. GOHBA | BKA vs. GOHBA | ||||
|---|---|---|---|---|---|---|---|---|
| p | h | p | h | p | h | p | h | |
| F1 | 3.3110 × 10−20 | 1 | 3.3110 × 10−20 | 1 | NaN | 0 | 3.3110 × 10−20 | 1 |
| F2 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 |
| F3 | 3.3110 × 10−20 | 1 | 3.3110 × 10−20 | 1 | NaN | 0 | 3.3110 × 10−20 | 1 |
| F4 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 |
| F5 | 3.1180 × 10−9 | 1 | 4.0380 × 10−5 | 1 | 9.5300 × 10−17 | 1 | 1.9520 × 10−17 | 1 |
| F6 | 5.2790 × 10−6 | 1 | 9.5400 × 10−18 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 |
| F7 | 1.5240 × 10−7 | 1 | 4.5400 × 10−9 | 1 | 0.10900 | 0 | 3.6920 × 10−7 | 1 |
| F8 | 4.2060 × 10−17 | 1 | 1.5390 × 10−17 | 1 | 0.31580 | 0 | 8.8640 × 10−16 | 1 |
| F9 | NaN | 0 | NaN | 0 | NaN | 0 | NaN | 0 |
| F10 | 8.2230 × 10−2 | 0 | 0.15940 | 0 | NaN | 0 | NaN | 0 |
| F11 | NaN | 0 | NaN | 0 | NaN | 0 | NaN | 0 |
| F12 | 3.2870 × 10−8 | 1 | 2.7840 × 10−17 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 |
| F13 | 5.0380 × 10−16 | 1 | 9.5400 × 10−18 | 1 | 2.4160 × 10−5 | 1 | 7.0660 × 10−18 | 1 |
| F14 | 0.14290 | 0 | 1.2920 × 10−2 | 1 | 0.51920 | 0 | 6.3950 × 10−4 | 1 |
| F15 | 0.49270 | 0 | 1.8870 × 10−5 | 1 | 1.5440 × 10−10 | 1 | 0.45030 | 0 |
| F16 | 2.6330 × 10−2 | 1 | 0.10970 | 0 | 0..6270 | 0 | 0.42500 | 0 |
| F17 | NaN | 0 | NaN | 0 | NaN | 0 | 0.15940 | 0 |
| F18 | 0.64770 | 0 | 0.98320 | 0 | 0.76590 | 0 | 0.26960 | 0 |
| F19 | 0.71350 | 0 | 3.1040 × 10−2 | 1 | 0.94920 | 0 | 2.6060 × 10−3 | 1 |
| F20 | 1.3870 × 10−2 | 1 | 0.30880 | 0 | 0.34250 | 0 | 0.47070 | 0 |
| F21 | 1.8480 × 10−2 | 1 | 7.0320 × 10−7 | 1 | 0.91390 | 0 | 3.8370 × 10−18 | 1 |
| F22 | 9.2660 × 10−2 | 0 | 2.9130 × 10−5 | 1 | 7.0470 × 10−2 | 0 | 1.5940 × 10−18 | 1 |
| F23 | 2.0950 × 10−6 | 1 | 5.3930 × 10−8 | 1 | 0.36810 | 0 | 3.6880 × 10−18 | 1 |
| Functions | ECO vs. GOHBA | GOOSE vs. GOHBA | NRBO vs. GOHBA | |||||
| p | h | p | h | p | h | |||
| F1 | 3.3110 × 10−20 | 1 | 3.3110 × 10−20 | 1 | 3.3110 × 10-20 | 1 | ||
| F2 | 7.0660 × 10-18 | 1 | 7.0660 × 10-18 | 1 | 7.0660 × 10-18 | 1 | ||
| F3 | 3.3110 × 10-20 | 1 | 3.3110 × 10-20 | 0 | 3.3110 × 10-20 | 1 | ||
| F4 | 7.0660 × 10-18 | 1 | 7.0660 × 10-18 | 1 | 7.0660 × 10-18 | 1 | ||
| F5 | 1.0750 × 10-17 | 1 | 7.0660 × 10−18 | 1 | 8.4620 × 10−18 | 1 | ||
| F6 | 6.3190 × 10−16 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | ||
| F7 | 1.4760 × 10−4 | 1 | 7.0660 × 10−18 | 1 | 3.2740 × 10−5 | 1 | ||
| F8 | 0.11360 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | ||
| F9 | NaN | 0 | 3.3110 × 10−20 | 1 | NaN | 0 | ||
| F10 | NaN | 0 | 3.3110 × 10−20 | 1 | NaN | 0 | ||
| F11 | NaN | 0 | 3.3110 × 10−20 | 1 | NaN | 0 | ||
| F12 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | 7.0660 × 10−18 | 1 | ||
| F13 | 7.0660 × 10−18 | 1 | 2.7980 × 10−14 | 1 | 7.0660 × 10−18 | 1 | ||
| F14 | 6.3950 × 10−4 | 0 | 1.6950 × 10−11 | 1 | 0.11500 | 0 | ||
| F15 | 0.45030 | 1 | 7.0660 × 10−18 | 1 | 2.7920 × 10−11 | 1 | ||
| F16 | 0.42500 | 1 | 2.0940 × 10−18 | 1 | 8.6570 × 10−2 | 0 | ||
| F17 | 0.15940 | 1 | 3.3110 × 10−20 | 1 | NaN | 0 | ||
| F18 | 0.26960 | 1 | 2.6330 × 10−14 | 1 | 3.4860 × 10−2 | 1 | ||
| F19 | 2.6060 × 10−3 | 1 | 1.3570 × 10−14 | 1 | 1.0770 × 10−2 | 1 | ||
| F20 | 0.47070 | 0 | 6.4630 × 10−6 | 1 | 6.3850 × 10−2 | 0 | ||
| F21 | 3.8370 × 10−18 | 1 | 2.7650 × 10−18 | 1 | 2.7650 × 10−18 | 1 | ||
| F22 | 1.5940 × 10−18 | 1 | 1.5940 × 10−18 | 1 | 1.6440 × 10−18 | 1 | ||
| F23 | 3.6880 × 10−18 | 1 | 3.0830 × 10−18 | 1 | 3.0830 × 10−18 | 1 | ||
| Algorithm | Best-Pos | Best-Score | ||||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | e | f | l | δ | ||
| HBA | 1.5000 × 102 | 1.5000 × 102 | 2.0000 × 102 | 0 | 10.000 | 1.0000 × 102 | 1.5978 | 4.2893 |
| HBA1 | 1.5000 × 102 | 95.763 | 2.0000 × 102 | 50.000 | 1.5000 × 102 | 1.5059 × 102 | 3.1399 | 4.1529 |
| HBA2 | 1.0238 × 102 | 10.000 | 1.7590 × 102 | 0 | 10.000 | 1.0000 × 102 | 1.0000 | 7.4389 × 10−16 |
| GOHBA | 1.0000 × 102 | 38.197 | 2.0000 × 102 | 0 | 10.000 | 1.0000 × 102 | 1.5610 | 7.2741 × 10−17 |
| BKA | 99.870 | 38.066 | 1.7466 × 102 | 0 | 32.737 | 1.0000 × 102 | 1.5215 | 8.4241 × 10−17 |
| ECO | 1.5000 × 102 | 1.0825 × 102 | 1.5296 × 102 | 34.726 | 1.3030 × 102 | 1.6653 × 102 | 3.1400 | 5.4861 |
| GOOSE | 1.2231 × 102 | 1.1863 × 102 | 1.9356 × 102 | 16.159 | 58.996 | 1.7274 × 102 | 2.4542 | 80.715 |
| NRBO | 1.4884 × 102 | 1.4454 × 102 | 1.8424 × 102 | 0.56062 | 12.874 | 1.6113 × 102 | 1.7935 | 3.8083 |
| Algorithm | Best-Pos | Best-Score | ||||||
|---|---|---|---|---|---|---|---|---|
| b | m | p | l1 | l2 | d1 | d2 | ||
| HBA | 3.50000 | 0.70000 | 17.000 | 7.3000 | 7.7153 | 3.3502 | 5.2867 | 2.9945 × 103 |
| HBA1 | 3.5047 | 0.70000 | 17.000 | 7.3000 | 7.7153 | 3.3502 | 5.2867 | 2.9963 × 103 |
| HBA2 | 3.5000 | 0.70000 | 17.000 | 7.3000 | 7.7155 | 3.3502 | 5.2867 | 2.9945 × 103 |
| GOHBA | 3.5000 | 0.70000 | 17.000 | 7.3000 | 7.7154 | 3.3502 | 5.2867 | 2.9945 × 103 |
| BKA | 3.5000 | 0.70000 | 17.000 | 7.9660 | 7.9278 | 3.3515 | 5.2868 | 3.0054 × 103 |
| ECO | 3.5026 | 0.70000 | 17.000 | 8.1823 | 7.7605 | 3.3549 | 5.2867 | 3.0059 × 103 |
| GOOSE | 3.5030 | 0.70000 | 17.000 | 7.4587 | 8.3000 | 3.3553 | 5.2874 | 3.0117 × 103 |
| NRBO | 3.5000 | 0.70000 | 17.000 | 7.3000 | 8.2906 | 3.3502 | 5.4968 | 3.1419 × 103 |
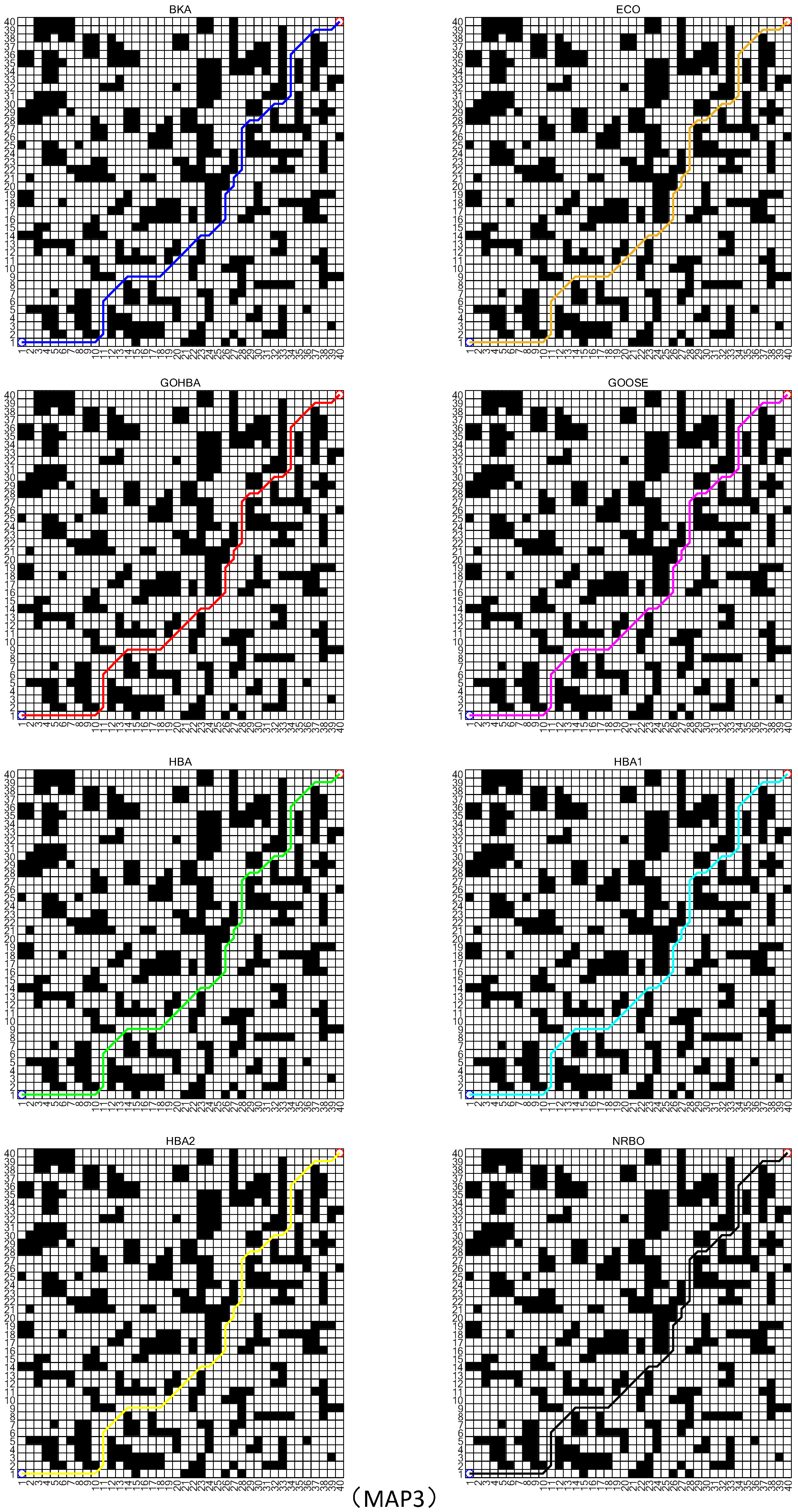
| Algorithm | Map | |||
|---|---|---|---|---|
| MAP1 | MAP2 | MAP3 | ||
| BKA | Mean | 32.142 | 47.456 | 65.6981 |
| Std | 7.2900 × 10−15 | 2.1870 × 10−14 | 0 | |
| ECO | Mean | 32.084 | 47.456 | 65.698 |
| Std | 0.26197 | 2.1870 × 10−14 | 0 | |
| GOHBA | Mean | 32.025 | 47.456 | 65.698 |
| Std | 0.30645 | 2.1870 × 10−14 | 0 | |
| GOOSE | Mean | 32.084 | 47.56 | 65.6981 |
| Std | 0.18030 | 2.1870 × 10−14 | 0 | |
| HBA | Mean | 32.142 | 47.456 | 65.698 |
| Std | 7.2900 × 10−15 | 2.1870 × 10−14 | 0 | |
| HBA1 | Mean | 32.054 | 47.456 | 65.698 |
| Std | 0.28666 | 2.1870 × 10−14 | 0 | |
| HBA2 | Mean | 32.084 | 47.456 | 65.6981 |
| Std | 0.18030 | 2.1870 × 10−14 | 0 | |
| NRBO | Mean | 32.142 | 47.456 | 65.698 |
| Std | 7.2900 × 10−15 | 2.1870 × 10−14 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Lu, S.; Liu, Q.; Han, T.; Li, T. GOHBA: Improved Honey Badger Algorithm for Global Optimization. Biomimetics 2025, 10, 92. https://doi.org/10.3390/biomimetics10020092
Huang Y, Lu S, Liu Q, Han T, Li T. GOHBA: Improved Honey Badger Algorithm for Global Optimization. Biomimetics. 2025; 10(2):92. https://doi.org/10.3390/biomimetics10020092
Chicago/Turabian StyleHuang, Yourui, Sen Lu, Quanzeng Liu, Tao Han, and Tingting Li. 2025. "GOHBA: Improved Honey Badger Algorithm for Global Optimization" Biomimetics 10, no. 2: 92. https://doi.org/10.3390/biomimetics10020092
APA StyleHuang, Y., Lu, S., Liu, Q., Han, T., & Li, T. (2025). GOHBA: Improved Honey Badger Algorithm for Global Optimization. Biomimetics, 10(2), 92. https://doi.org/10.3390/biomimetics10020092







