Water Body Identification from Satellite Images Using a Hybrid Evolutionary Algorithm-Optimized U-Net Framework
Abstract
1. Introduction
- (1)
- An evolutionary-hybrid neural framework for automated optimization of water body segmentation models. We develop a novel approach that integrates a multi-algorithm evolutionary optimization system (combining GA, ACO, PSO, and AE) with deep neural networks to automate hyperparameter configuration for water body identification. This framework effectively addresses the critical challenge of manual parameter tuning in deep learning-based water segmentation methods by dynamically optimizing the learning rate, batch size, and momentum, thereby significantly enhancing model performance and training efficiency while reducing human intervention.
- (2)
- Adopting a learnable multi-loss function fusion strategy with adaptive weighting, a linearly weighted loss function fusion strategy is proposed to collaboratively optimize classification confidence and geometric consistency. Through adaptive adjustments during training, the contributions of different loss terms to model optimization are balanced, addressing the class imbalance problem in water segmentation. Weights are automatically adjusted during training using an evolutionary algorithm to ensure an optimal balance between the various loss function objectives throughout the learning process.
- (3)
- The method was verified on two public remote sensing datasets. It significantly outperformed the baseline model in multiple quantitative indicators (such as mIoU and F1_Score), especially when dealing with complex remote sensing scenes such as urban areas (building shadow interference), cloud cover (noise interference), and multi-scale water bodies (from small rivers to large lakes). It demonstrated stronger generalization ability and boundary segmentation accuracy, providing a better automated solution for the automated high-precision extraction of remote sensing water bodies.
2. Related Work
2.1. Water Body Interpretation Method Based on Deep Learning Model
2.2. Deep Model Parameter Optimization
3. Proposed Methods
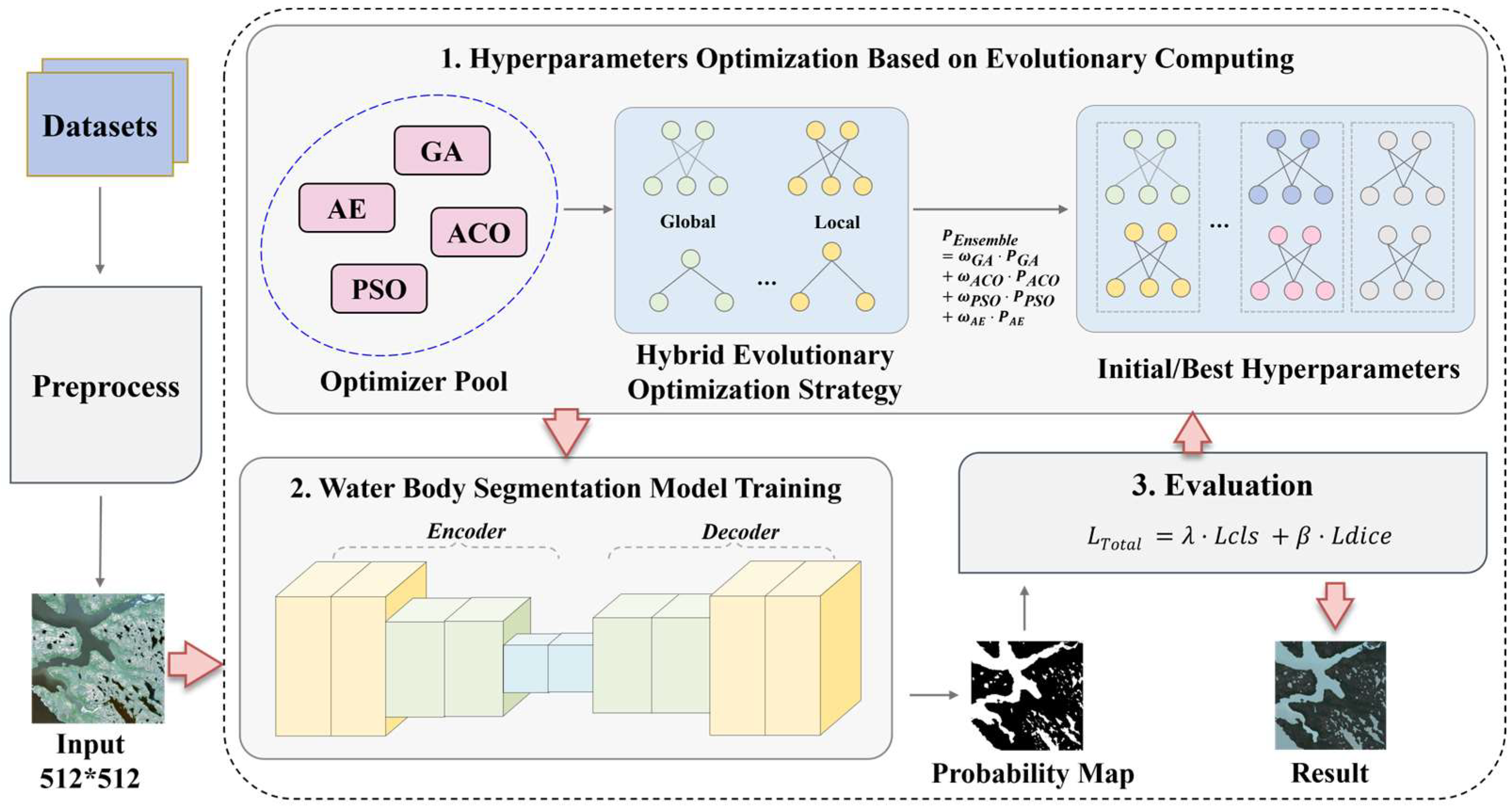
3.1. Overall Framework
3.2. Backbone
3.2.1. Network Model Selection
3.2.2. The Network Structure
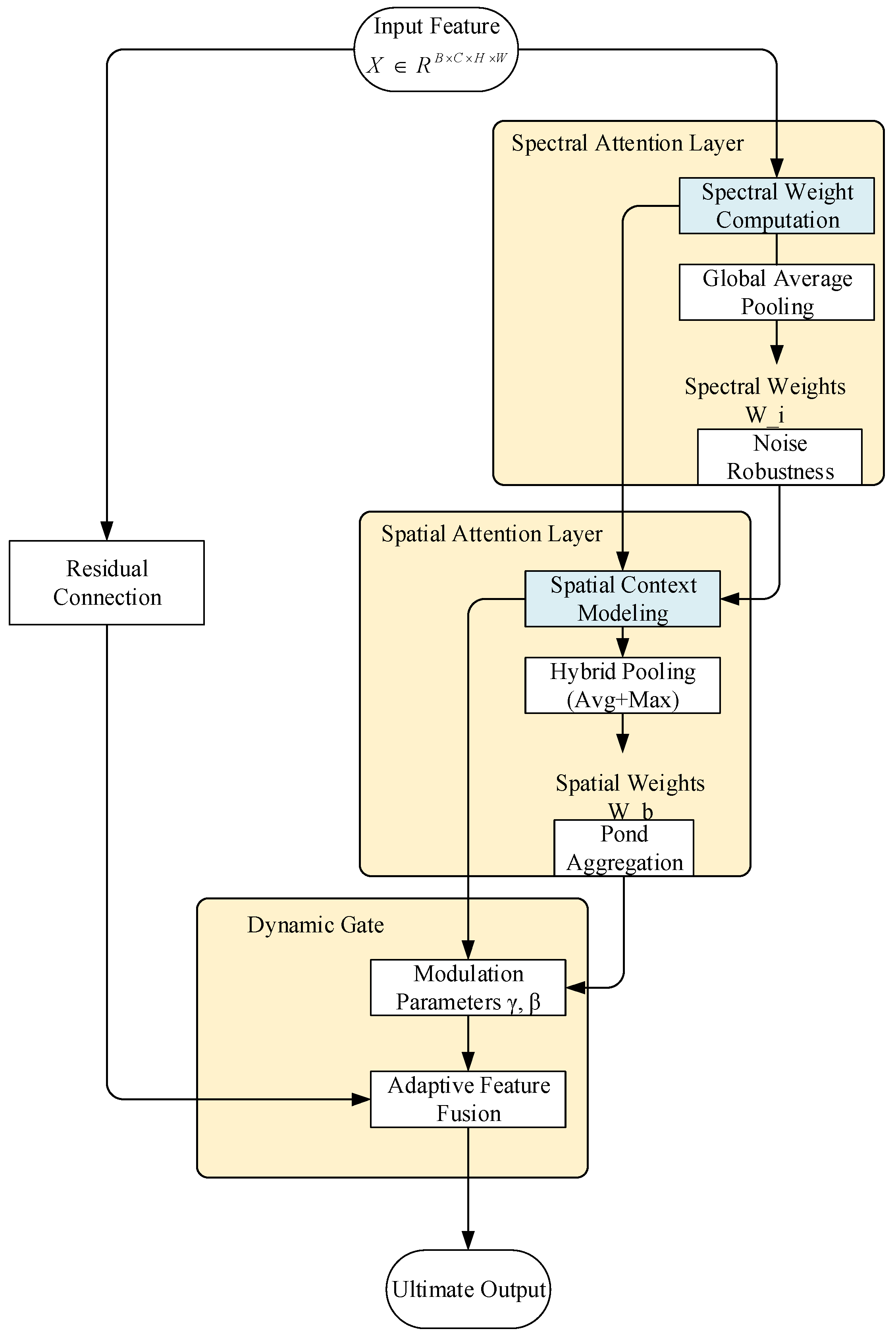
3.2.3. Dynamic Parameter Adjustment
- Spectral Attention Layer: Uses multi-scale one-dimensional convolution to capture cross-channel spectral dependency.
- Spatial Attention Layer: Based on direction-aware convolution to extract spatial contextual feature.
- Dynamic Gating Layer: Generates spatially adaptive attention intensity and feature retention coefficients.
3.3. Hyperparameter Tuning Combined with Multiple Evolutionary Algorithms
3.3.1. Hyperparameter Optimization
3.3.2. Weight Adaptive Optimization Based on Multi-Algorithm Fusion
3.4. Loss Function
4. Experiments and Results
4.1. Datasets
4.2. Evaluation Metrics
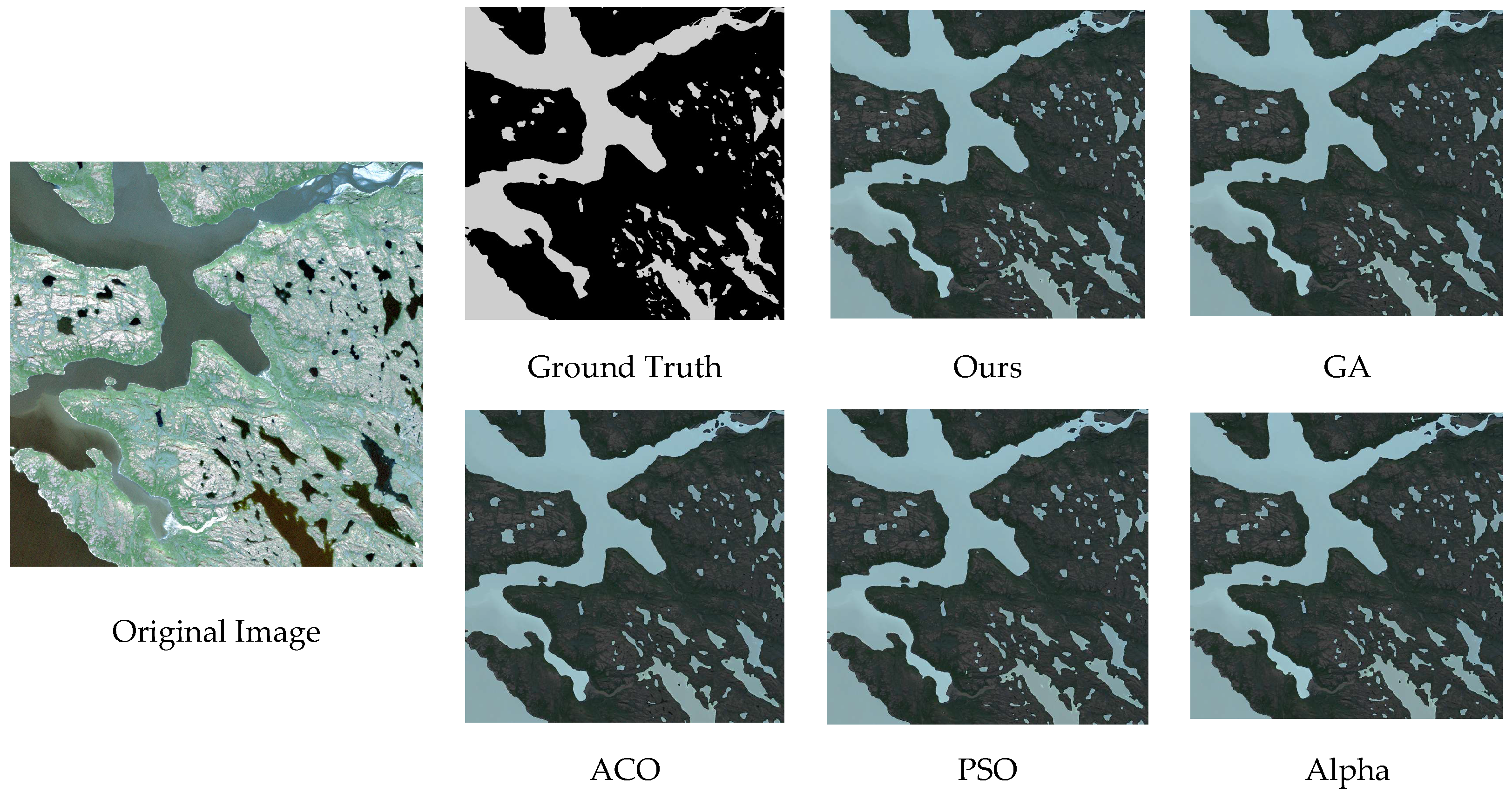
4.3. Results and Analysis
4.4. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, A.; Jiao, L.; Zhu, H.; Li, L.; Liu, F. Multitask Semantic Boundary Awareness Network for Remote Sensing Image Segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5400314. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, G.; Amankwah, S.O.Y.; Wei, X.; Hu, Y.; Feng, A. Monitoring the Summer Flooding in the Poyang Lake Area of China in 2020 Based on Sentinel-1 Data and Multiple Convolutional Neural Networks. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102400. [Google Scholar] [CrossRef]
- Wambugu, N.; Chen, Y.; Xiao, Z.; Wei, M.; Bello, S.A.; Junior, J.M.; Li, J. A Hybrid Deep Convolutional Neural Network for Accurate Land Cover Classification. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102515. [Google Scholar] [CrossRef]
- He, C.; Sadeghpour, H.; Shi, Y.; Mishra, B.; Roshankhah, S. Mapping Distribution of Fractures and Minerals in Rock Samples Using Res-VGG-UNet and Threshold Segmentation Methods. Comput. Geotech. 2024, 175, 106675. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A New Technique for Surface Water Mapping Using Landsat Imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Maksimovic, V.; Jaksic, B.; Milosevic, M.; Todorovic, J.; Mosurovic, L. Comparative Analysis of Edge Detection Operators Using a Threshold Estimation Approach on Medical Noisy Images with Different Complexities. Sensors 2024, 25, 87. [Google Scholar] [CrossRef] [PubMed]
- Kılıç, Z.A.; Kaya, K.; Yener, A.K. A Data Mining-Based Daylighting Design Decision Support Model for Achieving Visual Comfort Conditions in the Multi-Functional Residential Space. J. Build. Eng. 2025, 103, 112141. [Google Scholar] [CrossRef]
- Zhang, Y.; Ming, D.; Dong, D.; Xu, L. Object-Oriented U-GCN for Open-Pit Mining Extraction from High Spatial Resolution Remote-Sensing Images of Complex Scenes. Int. J. Remote Sens. 2024, 45, 8313–8333. [Google Scholar] [CrossRef]
- Isaksson, J.; Arvidsson, I.; Åaström, K.; Heyden, A. Semantic Segmentation of Microscopic Images of H&E Stained Prostatic Tissue Using CNN. In Proceedings of the International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; pp. 1252–1256. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wang, G.; Wu, M.; Wei, X.; Song, H. Water Identification from High-Resolution Remote Sensing Images Based on Multidimensional Densely Connected Convolutional Neural Networks. Remote Sens. 2020, 12, 794. [Google Scholar] [CrossRef]
- Wagner, F.; Eltner, A.; Maas, H.-G. River Water Segmentation in Surveillance Camera Images: A Comparative Study of Offline and Online Augmentation Using 32 CNNs. Int. J. Appl. Earth Obs. Geoinf. 2023, 119, 103305. [Google Scholar] [CrossRef]
- Rasley, J.; Rajbhandari, S.; Ruwase, O.; He, Y. DeepSpeed: System Optimizations Enable Training Deep Learning Models with Over 100 Billion Parameters. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 3505–3506. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zhang, L.; Li, Y.; Hou, Z.; Li, X.; Geng, H.; Wang, Y.; Li, J.; Zhu, P.; Mei, J.; Jiang, Y.; et al. Deep Learning and Remote Sensing Data Analysis. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 1857–1864. [Google Scholar] [CrossRef]
- Sun, D.; Gao, G.; Huang, L.; Liu, Y.; Liu, D. Extraction of water bodies from high-resolution remote sensing imagery based on a deep semantic segmentation network. Sci. Rep. 2024, 14, 14604. [Google Scholar] [CrossRef]
- Feng, S.; Yang, Q.; Jia, W.; Wang, M.; Liu, L. Information Extraction of Inland Surface Water Bodies Based on Optical Remote Sensing: A Review. Remote Sens. Nat. Resour. 2024, 36, 41–56. [Google Scholar] [CrossRef]
- Wen, Q.; Li, L.; Xiong, L.; Du, L.; Liu, Q.; Wen, Q. A Review of Water Body Extraction from Remote Sensing Images Based on Deep Learning. Remote Sens. Nat. Resour. 2024, 36, 57–71. [Google Scholar] [CrossRef]
- Tomczyk, M.K.; Kadziński, M. Decomposition-Based Interactive Evolutionary Algorithm for Multiple Objective Optimization. IEEE Trans. Evol. Comput. 2020, 24, 320–334. [Google Scholar] [CrossRef]
- Ye, T.; Zhang, X.; Wang, C.; Jin, Y. An Evolutionary Algorithm for Large-Scale Sparse Multiobjective Optimization Problems. IEEE Trans. Evol. Comput. 2020, 24, 380–393. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant System: Optimization by a Colony of Cooperating Agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Li, B.; Wei, Z.; Wu, J.; Yu, S.; Zhang, T.; Zhu, C.; Zheng, D.; Guo, W.; Zhao, C.; Zhang, J. Machine Learning-Enabled Globally Guaranteed Evolutionary Computation. Nat. Mach. Intell. 2023, 5, 123–134. [Google Scholar] [CrossRef]
- Liang, J.; Zhu, K.; Li, Y.; Li, Y.; Gong, Y. Multi-Objective Evolutionary Neural Architecture Search with Weight-Sharing Supernet. Appl. Sci. 2024, 14, 6143. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, Y.; Zhao, J.; Zhou, Y. Co-Evolution-Based Parameter Learning for Remote Sensing Scene Classification. Remote Sens. 2021, 13, 4125. [Google Scholar] [CrossRef]
- Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-Scale Evolution of Image Classifiers. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2902–2911. [Google Scholar]
- Lakhan, A.; Grønli, T.M.; Muhammad, G.; Tiwari, P. EDCNNS: Federated Learning Enabled Evolutionary Deep Convolutional Neural Network for Alzheimer Disease Detection. Appl. Soft Comput. 2023, 147, 110804. [Google Scholar] [CrossRef]
- Xiang, D.; Zhang, X.; Wu, W.; Liu, H. DensePPMUNet-a: A robust deep learning network for segmenting water bodies from aerial images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4202611. [Google Scholar] [CrossRef]
- Liu, W.; Chen, X.; Ran, J.; Liu, L.; Wang, Q.; Xin, L.; Li, G. LaeNet: A Novel Lightweight Multitask CNN for Automatically Extracting Lake Area and Shoreline from Remote Sensing Images. Remote Sens. 2021, 13, 56. [Google Scholar] [CrossRef]
- Luo, X.; Hu, Z.; Liu, L. Investigating the seasonal dynamics of surface water over the Qinghai–Tibet Plateau using Sentinel-1 imagery and a novel gated multiscale ConvNet. Int. J. Digit. Earth 2023, 16, 1372–1394. [Google Scholar] [CrossRef]
- Li, M.; Wu, P.; Wang, B.; Park, H.; Yang, H.; Wu, Y. A Deep Learning Method of Water Body Extraction From High Resolution Remote Sensing Images With Multisensors. IEEE J-STARS 2021, 14, 3120–3132. [Google Scholar] [CrossRef]
- Dai, X.; Xia, M.; Weng, L.; Hu, K.; Lin, H.; Qian, M. Multiscale Location Attention Network for Building and Water Segmentation of Remote Sensing Image. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5609519. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q. Alpha evolution: An efficient evolutionary algorithm with evolution path adaptation and matrix generation. Eng. Appl. Artif. Intell. 2024, 137, 109202. [Google Scholar] [CrossRef]

| Algorithm | Parameter and Task | Initial Value |
|---|---|---|
| GA | Population Size: Determines the diversity of potential hyperparameter sets in the gene pool. | 20 |
| Crossover Rate: Controls the probability of combining genetic material from two parents to produce offspring. | 0.7 | |
| Mutation Rate: Introduces random changes to offspring, maintaining population diversity and preventing premature convergence to local optima. | 0.1 | |
| Selection Method: Governs which individuals are chosen for reproduction. Tournament selection provides good selective pressure. | Tournament (size = 3) | |
| ACO | Number of Ants: Analogous to population size. Each ant constructs a solution (a path representing a hyperparameter set). | 20 |
| Pheromone Influence (α): Determines the weight of pheromone trails in path selection. Higher values increase exploitation of known good paths. | 1.0 | |
| Heuristic Influence (β): Determines the weight of heuristic information in path selection. Higher values favor exploration. | 2.0 | |
| Pheromone Evaporation Rate (ρ): Simulates the evaporation of pheromones over time, preventing unlimited accumulation and allowing the colony to forget poorer paths, facilitating exploration. | 0.5 | |
| PSO | Number of Particles Similarly to population size. Each particle represents a potential hyperparameter set flying through the search space. | 20 |
| Inertia Weight (w): Balances exploration (high w) and exploitation (low w). It controls the particle’s momentum based on its previous velocity. | 0.5 | |
| Cognitive Coefficient (c1): Attracts the particle towards its personal best position (pbest), encouraging exploitation of personally found good solutions. | 1.5 | |
| Social Coefficient (c2): Attracts the particle towards the swarm’s global best position (gbest), encouraging convergence towards the best-known solution. | 2.0 | |
| AE | Population Size: Determines the number of candidate solutions maintained per iteration. | 20 |
| Decay Coefficient of Disturbance: Controls the decaying speed of the disturbance intensity (alpha) during the algorithm’s iterative process | 0.9 | |
| Evaporation Rate: Simulates the pheromone evaporation mechanism like Ant Colony Optimization | 0.2 |
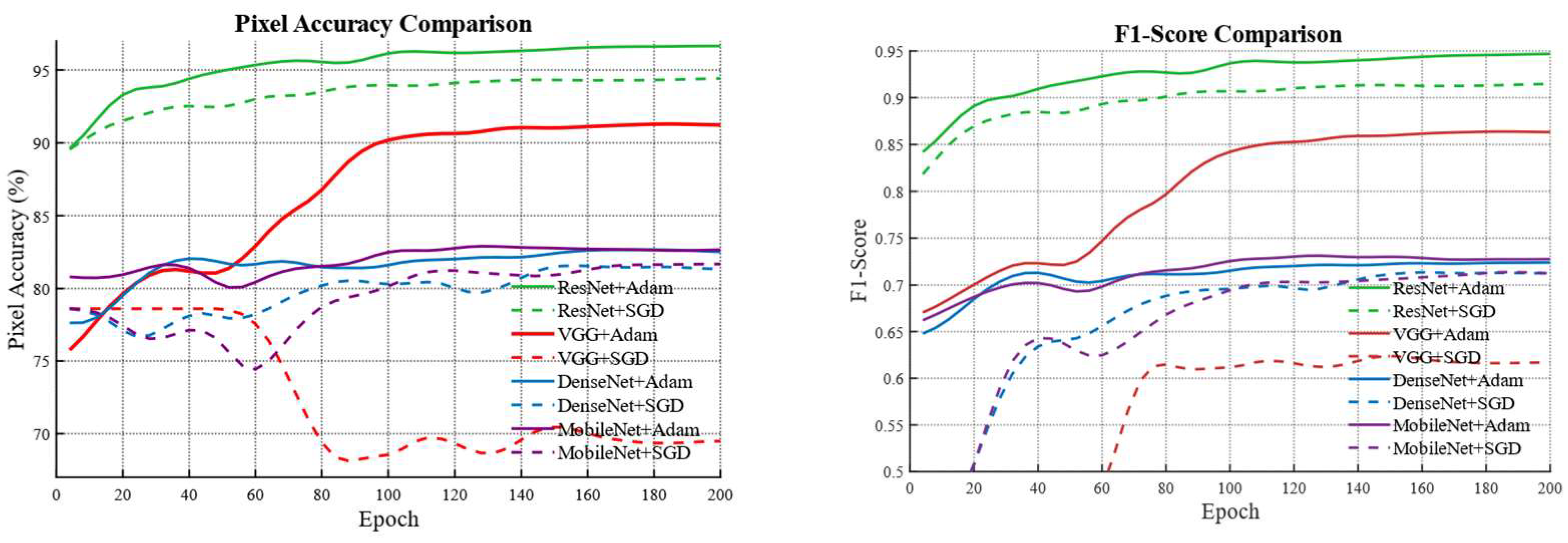
| Backbone + Optimizer | Best PA(%) | Best F1_Score(%) |
|---|---|---|
| ResNet50 + Adam | 96.7897 | 94.75 |
| ResNet50 + SGD | 94.4729 | 91.59 |
| VGG16 + Adam | 81.2445 | 69.24 |
| VGG16 + SGD | 78.6100 | 65.83 |
| DenseNet + Adam | 82.8770 | 72.59 |
| DenseNet + SGD | 81.8651 | 71.67 |
| MobileNet + Adam | 83.3628 | 73.45 |
| MobileNet + SGD | 81.9363 | 71.78 |
| Methods | PA(%) | F1_Score(%) | mIoU(%) | mPA(%) | mPrecision(%) |
|---|---|---|---|---|---|
| U-Net | 96.28 | 93.90 | 88.87 | 93.84 | 94.66 |
| U-Net +CELoss | 96.67 | 94.50 | 89.67 | 93.85 | 95.49 |
| U-Net +FocalLoss | 96.70 | 94.50 | 89.91 | 93.90 | 95.46 |
| U-Net +FocalLoss + Dice Loss + CBAM | 96.93 | 94.90 | 90.61 | 94.62 | 95.57 |
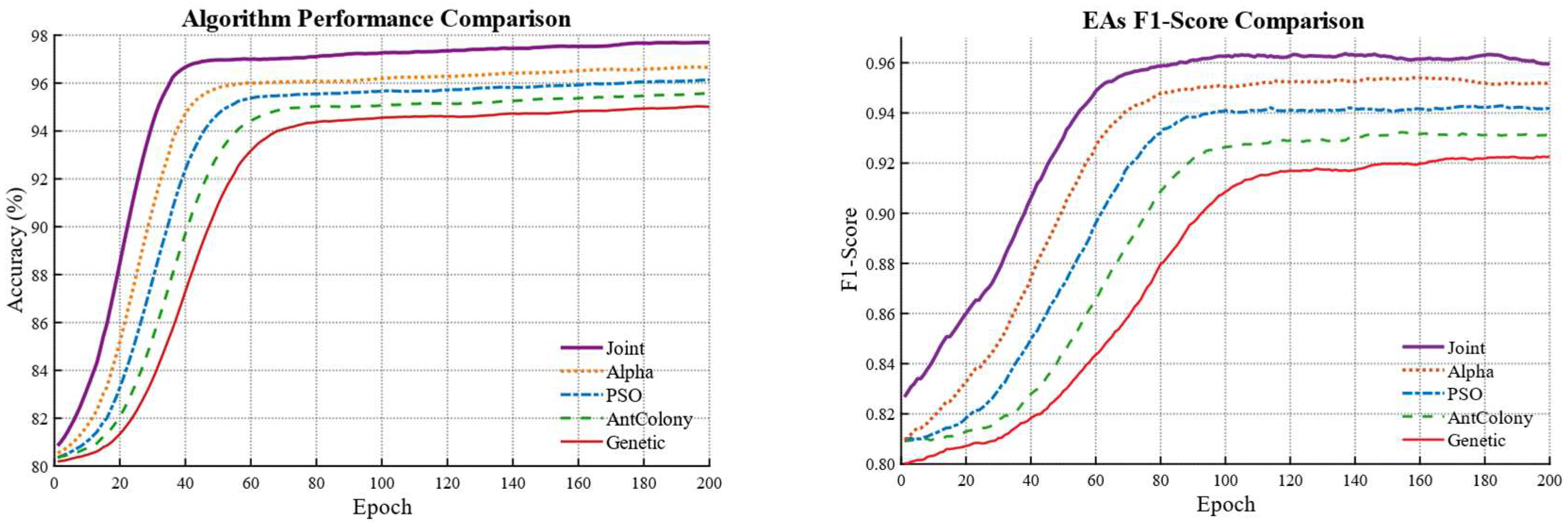
| Algorithm | Best PA(%) | Best F1Score(%) |
|---|---|---|
| Genetic Algorithm (GA) | 95.58 | 92.21 |
| Ant Colony Optimization (ACO) | 95.79 | 93.15 |
| Particle Swarm Optimization (PSO) | 96.11 | 94.31 |
| Alpha Evolutionary (AE) | 96.53 | 95.57 |
| The Joint: GA + ACO + PSO + AE | 97.69 | 96.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Wei, P.; Qi, Z.; Deng, X.; Zhang, J.; Gan, J.; Chen, T.; Li, Z. Water Body Identification from Satellite Images Using a Hybrid Evolutionary Algorithm-Optimized U-Net Framework. Biomimetics 2025, 10, 732. https://doi.org/10.3390/biomimetics10110732
Yuan Y, Wei P, Qi Z, Deng X, Zhang J, Gan J, Chen T, Li Z. Water Body Identification from Satellite Images Using a Hybrid Evolutionary Algorithm-Optimized U-Net Framework. Biomimetics. 2025; 10(11):732. https://doi.org/10.3390/biomimetics10110732
Chicago/Turabian StyleYuan, Yue, Peiyang Wei, Zhixiang Qi, Xun Deng, Ji Zhang, Jianhong Gan, Tinghui Chen, and Zhibin Li. 2025. "Water Body Identification from Satellite Images Using a Hybrid Evolutionary Algorithm-Optimized U-Net Framework" Biomimetics 10, no. 11: 732. https://doi.org/10.3390/biomimetics10110732
APA StyleYuan, Y., Wei, P., Qi, Z., Deng, X., Zhang, J., Gan, J., Chen, T., & Li, Z. (2025). Water Body Identification from Satellite Images Using a Hybrid Evolutionary Algorithm-Optimized U-Net Framework. Biomimetics, 10(11), 732. https://doi.org/10.3390/biomimetics10110732






