Enhancing Gait Symmetry via Intact Limb Kinematic Mapping Control of a Hip Disarticulation Prosthesis
Abstract
1. Introduction
2. Materials and Methods
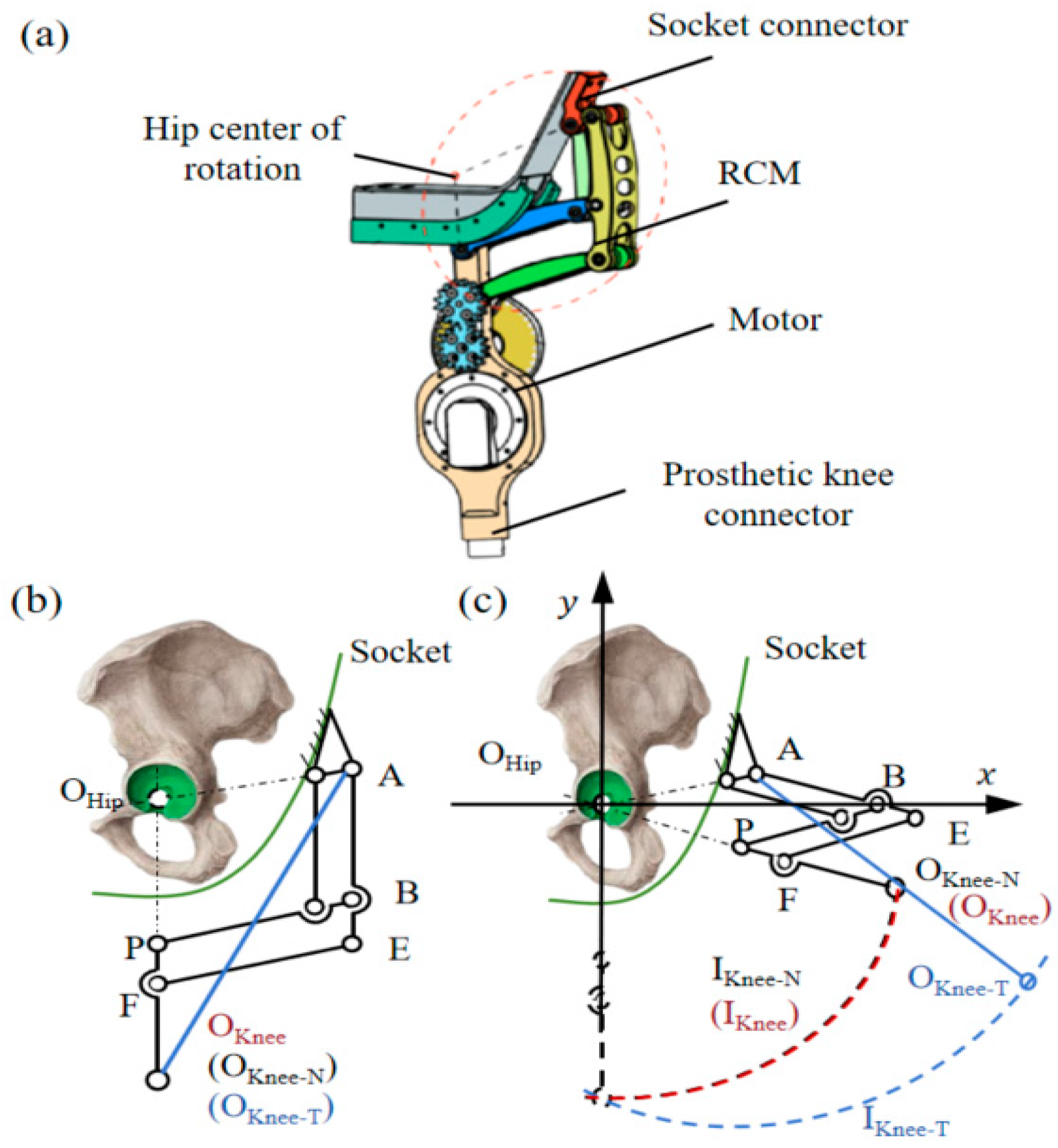
2.1. Bionic Power Hip Disarticulation Prosthesis
2.2. Control System for the Hip Disarticulation Prosthesis
2.3. Kinematic Mapping Model of the Healthy Side-Prosthetic Side
2.3.1. Quaternion Based Hip Joint Angle Solving
2.3.2. Kinematic Mapping Model Based on GRU Network
3. Experiments and Results
3.1. Participants
3.2. Kinematic Mapping Model Prediction Experiment
3.3. Experiment on Amputee Wear
4. Discussion
4.1. Advantages of the Powered Prosthesis
4.2. Future Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saif, A.; Francis, R.; Sullivan, J.; Sedki, I. Factors Affecting Successful Prosthetic Use after Hemipelvectomy and Hip Disarticulation Amputations: Five-Year Experience from a Tertiary Prosthetic Rehabilitation Center. Prosthet. Orthot. Int. 2024, 48, 20–24. [Google Scholar] [CrossRef]
- Kralovec, M.E.; Houdek, M.T.; Andrews, K.L.; Shives, T.C.; Rose, P.S.; Sim, F.H. Prosthetic Rehabilitation After Hip Disarticulation or Hemipelvectomy. Am. J. Phys. Med. Rehabil. 2015, 94, 1035–1040. [Google Scholar] [CrossRef]
- De Marchis, C.; Ranaldi, S.; Varrecchia, T.; Serrao, M.; Castiglia, S.F.; Tatarelli, A.; Ranavolo, A.; Draicchio, F.; Lacquaniti, F.; Conforto, S. Characterizing the Gait of People With Different Types of Amputation and Prosthetic Components Through Multimodal Measurements: A Methodological Perspective. Front. Rehabil. Sci. 2022, 3, 804746. [Google Scholar] [CrossRef]
- Sivapuratharasu, B.; Bull, A.M.J.; McGregor, A.H. Understanding Low Back Pain in Traumatic Lower Limb Amputees: A Systematic Review. Arch. Rehabil. Res. Clin. Transl. 2019, 1, 100007. [Google Scholar] [CrossRef] [PubMed]
- Golshan, F.; Baddour, N.; Gholizadeh, H.; Lemaire, E.D. A Pelvic Kinematic Approach for Calculating Hip Angles for Active Hip Disarticulation Prosthesis Control. J. Neuroeng. Rehabil. 2023, 20, 152. [Google Scholar] [CrossRef]
- Luo, S.; Shu, X.; Zhu, H.; Yu, H. Design and Optimization of a New Integrated Hip and Knee Prosthesis Structure. Artif. Organs 2024, 48, 50–60. [Google Scholar] [CrossRef]
- Gailledrat, E.; Moineau, B.; Seetha, V.; DeAngelis, M.P.; Saurel, B.; Chabloz, P.; Nougier, V.; Pérennou, D. Does the New Helix 3D Hip Joint Improve Walking of Hip Disarticulated Amputees? Ann. Phys. Rehabil. Med. 2013, 56, 411–418. [Google Scholar] [CrossRef]
- Ludwigs, E.; Bellmann, M.; Schmalz, T.; Blumentritt, S. Biomechanical Differences between Two Exoprosthetic Hip Joint Systems during Level Walking. Prosthet. Orthot. Int. 2010, 34, 449–460. [Google Scholar] [CrossRef] [PubMed]
- Ueyama, Y.; Kubo, T.; Shibata, M. Robotic Hip-Disarticulation Prosthesis: Evaluation of Prosthetic Gaits in a Non-Amputee Individual. Adv. Robot. 2020, 34, 37–44. [Google Scholar] [CrossRef]
- Bader, Y.; Langlois, D.; Baddour, N.; Lemaire, E.D. Development of an Integrated Powered Hip and Microprocessor-Controlled Knee for a Hip–Knee–Ankle–Foot Prosthesis. Bioengineering 2023, 10, 614. [Google Scholar] [CrossRef] [PubMed]
- Elery, T.; Rezazadeh, S.; Nesler, C.; Gregg, R.D. Design and Validation of a Powered Knee–Ankle Prosthesis With High-Torque, Low-Impedance Actuators. IEEE Trans. Robot. 2020, 36, 1649–1668. [Google Scholar] [CrossRef]
- Azocar, A.F.; Mooney, L.M.; Duval, J.-F.; Simon, A.M.; Hargrove, L.J.; Rouse, E.J. Design and Clinical Implementation of an Open-Source Bionic Leg. Nat. Biomed. Eng. 2020, 4, 941–953. [Google Scholar] [CrossRef]
- Vaskov, A.K.; Vu, P.P.; North, N.; Davis, A.J.; Kung, T.A.; Gates, D.H.; Cederna, P.S.; Chestek, C.A. Surgically Implanted Electrodes Enable Real-Time Finger and Grasp Pattern Recognition for Prosthetic Hands. IEEE Trans. Robot. 2022, 38, 2841–2857. [Google Scholar] [CrossRef] [PubMed]
- Fleming, A.; Stafford, N.; Huang, S.; Hu, X.; Ferris, D.P.; Huang, H. (Helen) Myoelectric Control of Robotic Lower Limb Prostheses: A Review of Electromyography Interfaces, Control Paradigms, Challenges and Future Directions. J. Neural Eng. 2021, 18, 041004. [Google Scholar] [CrossRef]
- Hunt, G.R.; Hood, S.; Lenzi, T. Stand-Up, Squat, Lunge, and Walk With a Robotic Knee and Ankle Prosthesis Under Shared Neural Control. IEEE Open J. Eng. Med. Biol. 2021, 2, 267–277. [Google Scholar] [CrossRef]
- Hood, S.; Gabert, L.; Lenzi, T. Powered Knee and Ankle Prosthesis With Adaptive Control Enables Climbing Stairs With Different Stair Heights, Cadences, and Gait Patterns. IEEE Trans. Robot. 2022, 38, 1430–1441. [Google Scholar] [CrossRef]
- Luo, S.; Shu, X.; Zhu, H.; Yu, H. Early Prediction of Lower Limb Prostheses Locomotion Mode Transition Based on Terrain Recognition. IEEE Sens. J. 2023, 23, 27941–27948. [Google Scholar] [CrossRef]
- Eslamy, M.; Schilling, A.F. Estimation of Knee and Ankle Angles during Walking Using Thigh and Shank Angles. Bioinspir. Biomim. 2021, 16, 066012. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; She, H.; Lu, H.; Fukuda, T.; Shen, Y. State of the Art: Bipedal Robots for Lower Limb Rehabilitation. Appl. Sci. 2017, 7, 1182. [Google Scholar] [CrossRef]
- Kim, M.-J.; Han, J.-H.; Shin, W.-C.; Hong, Y.-S. Gait Pattern Identification Using Gait Features. Electronics 2024, 13, 1956. [Google Scholar] [CrossRef]
- Bian, Y.; Zhao, J.; Li, J.; Wei, G.; Li, J. A Class of Spatial Remote Center-of-Motion Mechanisms and Its Forward Kinematics. Robotica 2022, 41, 885–899. [Google Scholar] [CrossRef]
- Li, X.; Deng, Z.; Meng, Q.; Bai, S.; Chen, W.; Yu, H. Design and Optimization of a Hip Disarticulation Prosthesis Using the Remote Center of Motion Mechanism. Technol. Health Care 2021, 29, 269–281. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Yu, H. A Microprocessor-Controlled Prosthetic Knee and Its Gait Symmetry Assessment. Chin. J. Rehabil. Theory Pract. 2023, 4, 402–407. [Google Scholar]
- Lu, C.; Xu, X.; Liu, Y.; Li, D.; Wang, Y.; Xian, W.; Chen, C.; Wei, B.; Tian, J. An Embedded Electromyogram Signal Acquisition Device. Sensors 2024, 24, 4106. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, S.; Yu, T.; Zhang, Y.; Ye, G.; Cui, H.; He, C.; Jiang, W.; Zhai, Y.; Lu, C.; et al. Ultra-Conformal Skin Electrodes with Synergistically Enhanced Conductivity for Long-Time and Low-Motion Artifact Epidermal Electrophysiology. Nat. Commun. 2021, 12, 4880. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Zhang, S.; Yang, Y.; Liu, X.; Li, J.; Bao, B.; Liu, C.; Yang, H.; Guo, K.; Cheng, H. Conformal, Stretchable, Breathable, Wireless Epidermal Surface Electromyography Sensor System for Hand Gesture Recognition and Rehabilitation of Stroke Hand Function. Mater. Des. 2024, 243, 113029. [Google Scholar] [CrossRef]





| Prosthesis Type | Features | Advantages | Limitations | |
|---|---|---|---|---|
| Passive Prosthesis | [7,8] | Purely mechanical structure | Lightweight with excellent support | No power, No intelligent control, Difficult to operate |
| Intelligent Prosthesis | [9] | Powered Prosthesis | Provides leg-lifting power | Excessive weight, restricted mobility |
| [10] | Powered Prosthesis | Provides leg-lifting power | Low biomimetic fidelity, limited durability | |
| Gait Parameters | Conventional Prosthesis | New Prosthesis | ||||
|---|---|---|---|---|---|---|
| Step length | 31.33% | 1.37 | 27.08% | 8.12% | 1.08 | 7.80% |
| Step frequency | −22.62% | 0.80 | −20.33% | −17.65% | 0.84 | −16.22% |
| Hip trajectory | −75.65% | 0.45 | −54.89% | −7.58% | 0.93 | −7.30% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Shu, X.; Du, J.; Li, H.; Yu, H. Enhancing Gait Symmetry via Intact Limb Kinematic Mapping Control of a Hip Disarticulation Prosthesis. Biomimetics 2025, 10, 714. https://doi.org/10.3390/biomimetics10100714
Luo S, Shu X, Du J, Li H, Yu H. Enhancing Gait Symmetry via Intact Limb Kinematic Mapping Control of a Hip Disarticulation Prosthesis. Biomimetics. 2025; 10(10):714. https://doi.org/10.3390/biomimetics10100714
Chicago/Turabian StyleLuo, Shengli, Xiaolong Shu, Jiahao Du, Hui Li, and Hongliu Yu. 2025. "Enhancing Gait Symmetry via Intact Limb Kinematic Mapping Control of a Hip Disarticulation Prosthesis" Biomimetics 10, no. 10: 714. https://doi.org/10.3390/biomimetics10100714
APA StyleLuo, S., Shu, X., Du, J., Li, H., & Yu, H. (2025). Enhancing Gait Symmetry via Intact Limb Kinematic Mapping Control of a Hip Disarticulation Prosthesis. Biomimetics, 10(10), 714. https://doi.org/10.3390/biomimetics10100714





