TBC-HRL: A Bio-Inspired Framework for Stable and Interpretable Hierarchical Reinforcement Learning
Abstract
1. Introduction
- We introduce TBC-HRL, a hierarchical reinforcement learning framework that integrates timed subgoal scheduling with a biologically inspired neural circuit model (NDBCNet), addressing core challenges of unstable coordination, delayed response, and limited interpretability in HRL.
- We evaluate TBC-HRL across six simulated robot tasks with sparse rewards and long horizons, demonstrating consistent improvements in sample efficiency, subgoal stability, and policy generalization compared to standard HRL methods.
- We analyze NDBCNet in detail and show how structural sparsity, temporal dynamics, and adaptive responses contribute to robust and interpretable low-level control in complex environments.
2. Related Work
2.1. Limitations of Hierarchical Reinforcement Learning in Real-World Tasks
2.2. Subgoal Scheduling and Temporal Abstraction Mechanisms
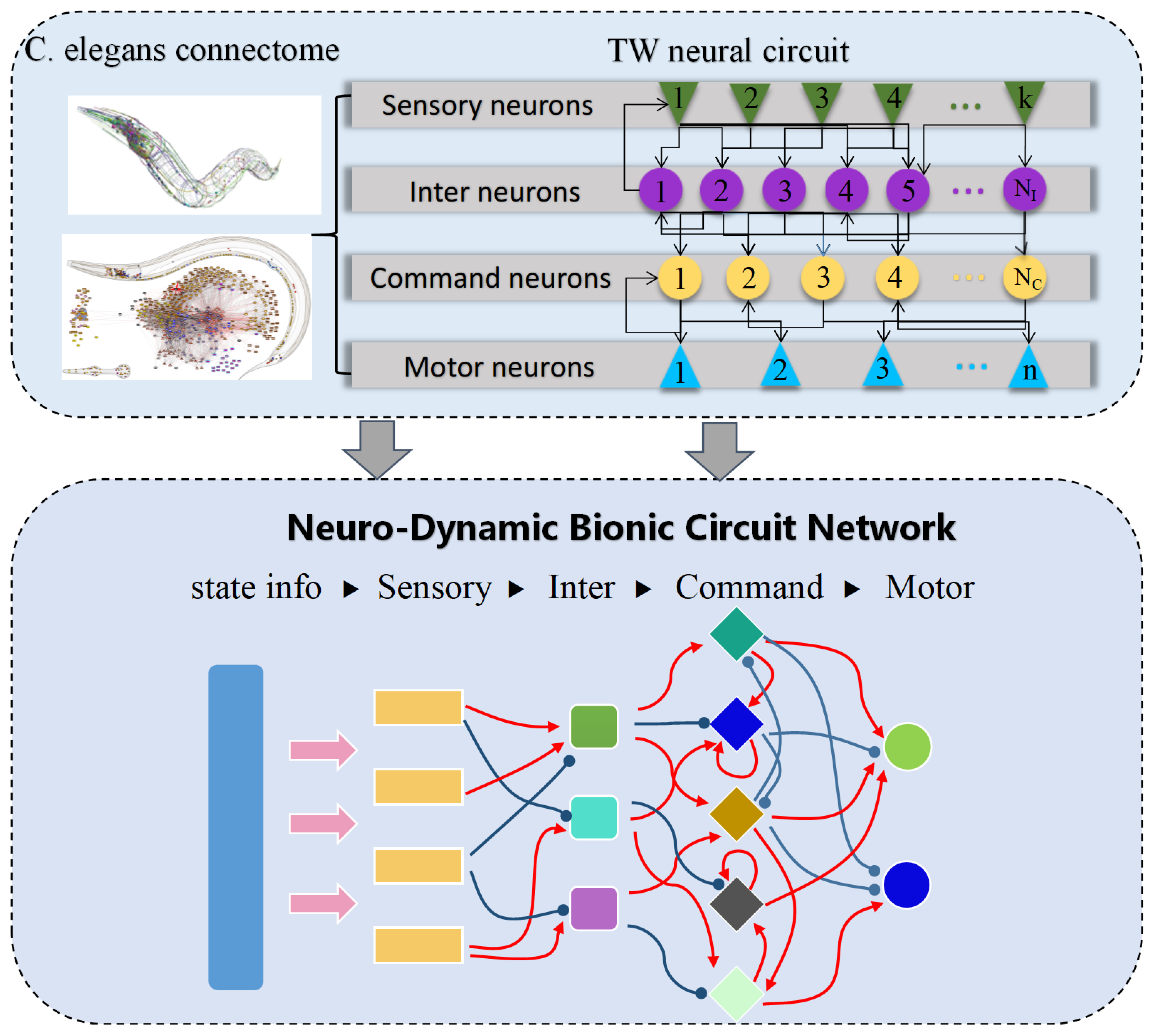
2.3. Applications of Bio-Inspired Neural Network Structures in Intelligent Control
3. Background
3.1. MDP and SMDP
3.2. Subgoal-Based HRL
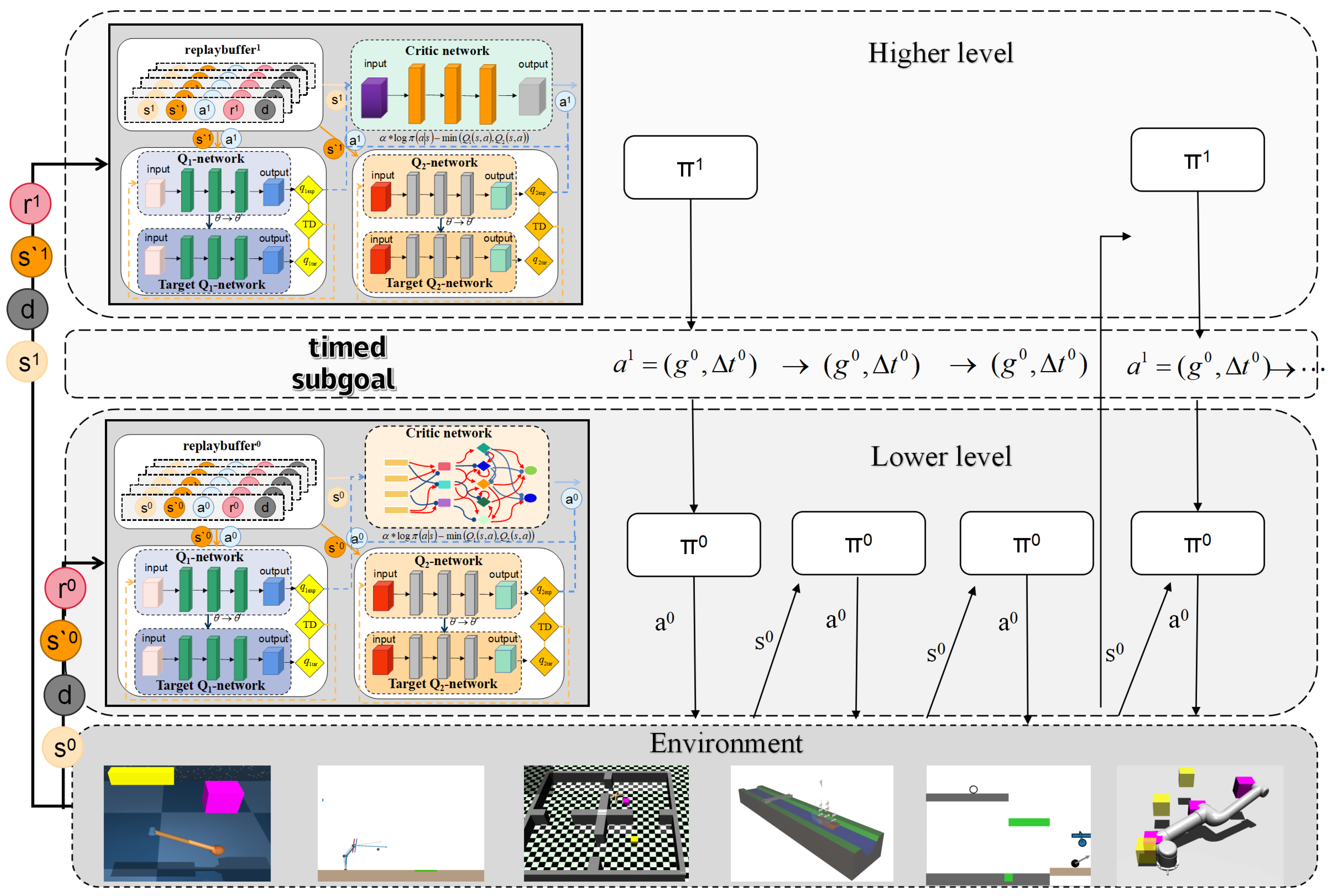
4. Method
4.1. Overall Architecture: TBC-HRL
4.2. High-Level Policy Generation
4.3. Neuro-Dynamic Bionic Control Network
4.4. Low-Level Policy Generation and Optimization
4.5. Strategy Optimization and Training Procedure
| Algorithm 1 TBC-HRL: Strategy Optimization and Training Procedure |
|
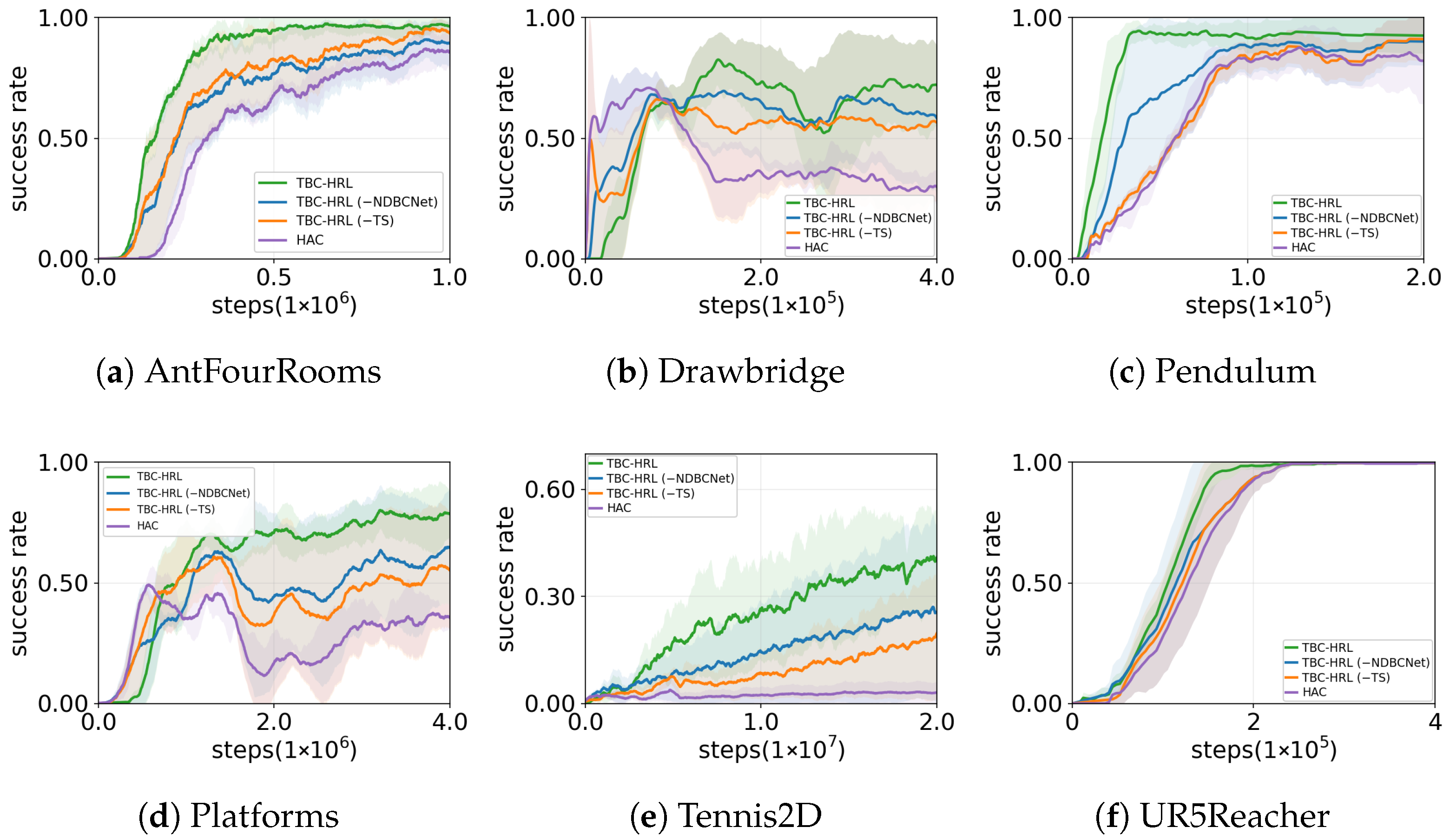
5. Experiments
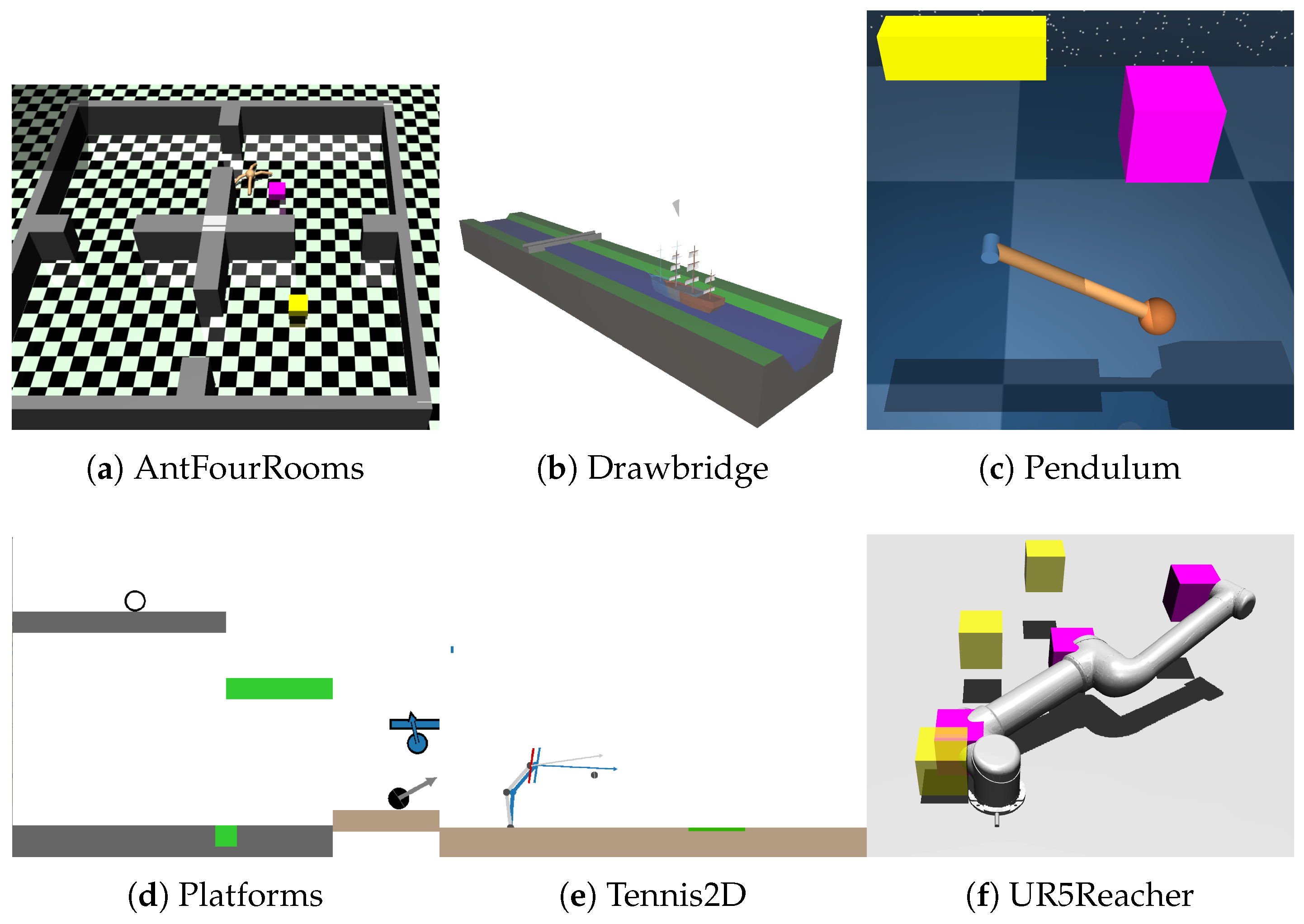
5.1. Experimental Environments
- AntFourRooms:A quadrupedal robot navigates through a four-room maze from a start point to a designated goal room. The environment contains narrow passages and obstacles, emphasizing long-horizon planning and obstacle avoidance.
- Drawbridge: A timing-control scenario where the agent must operate a drawbridge to allow ships to pass safely. The task highlights temporal coordination and proactive anticipation in dynamic environments.
- Pendulum: A classic control problem requiring the pendulum to be swung upright and stabilized at the top. Its nonlinear dynamics and continuous action space demand precise force application and balance maintenance.
- Platforms: A side-scrolling style task where the agent must trigger moving platforms at the correct moment to reach the target. Delayed action effects and sparse rewards make it a benchmark for temporal reasoning and credit assignment.
- Tennis2D: A robotic arm must strike a ball so that it lands in a target zone. Success requires accurate timing under high stochasticity and frequent contacts, with minimal latency in control.
- UR5Reacher: An industrial robotic arm control task involving reaching multiple targets while avoiding collisions. It evaluates accuracy, path efficiency, and energy minimization in high-degree-of-freedom systems.
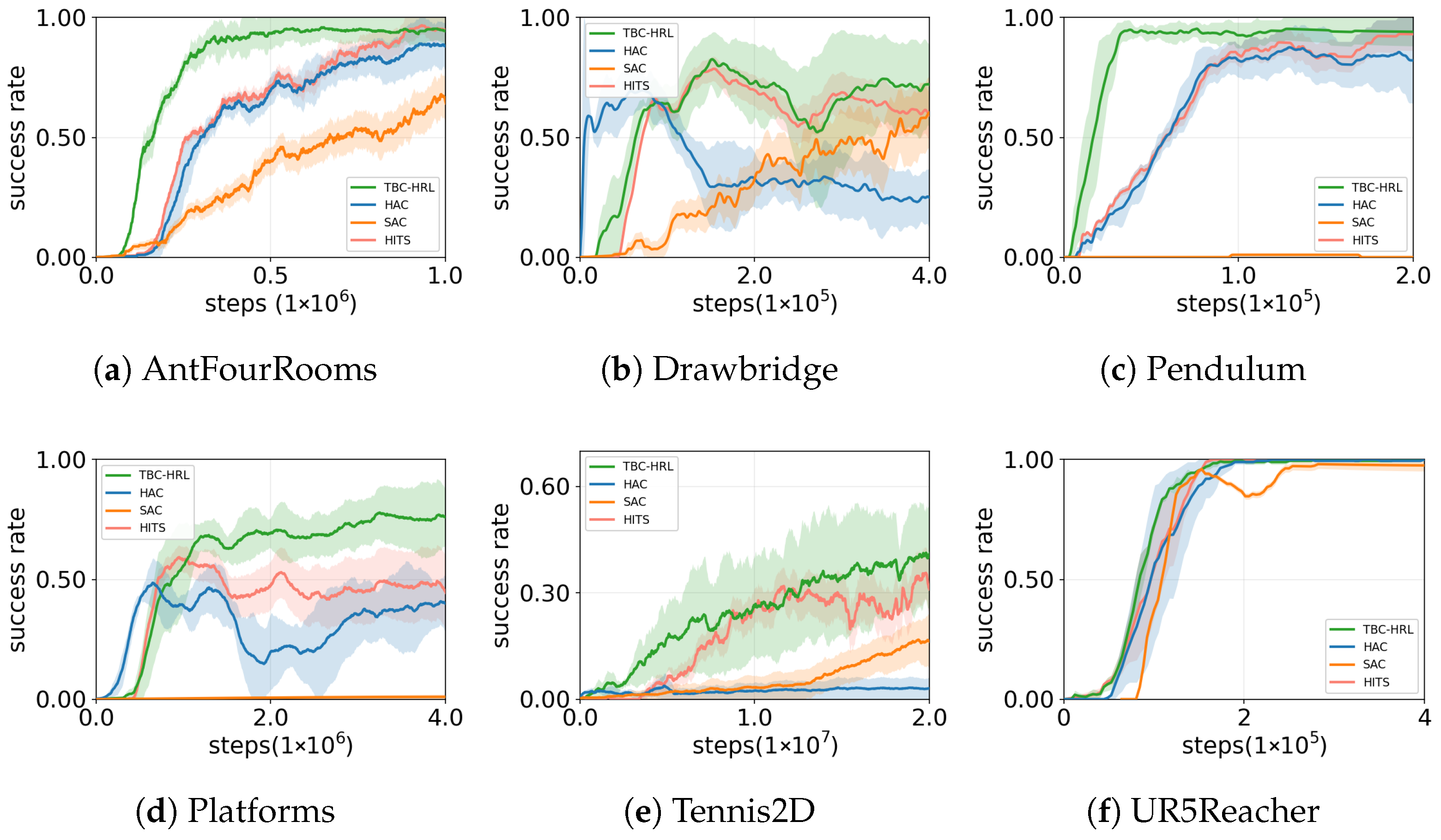
5.2. Experimental Results
5.3. Ablation Study
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Environment | Inter Neurons | Command Neurons | Motor Neurons | Sensory Fanout | Inter Fanout | Recurrent Command Synapses | Motor Fanin |
|---|---|---|---|---|---|---|---|
| AntFourRooms | 12 | 10 | 8 | 5 | 8 | 2 | 6 |
| UR5Reacher | 6 | 4 | 3 | 4 | 5 | 2 | 5 |
| Drawbridge | 6 | 6 | 1 | 3 | 4 | 3 | 4 |
| Tennis2D | 8 | 6 | 3 | 4 | 6 | 4 | 6 |
| Pendulum | 6 | 6 | 1 | 3 | 4 | 1 | 4 |
| Platforms | 6 | 6 | 1 | 4 | 5 | 3 | 5 |
| Algorithm | Env | LR | Batch | Alpha (L0/L1) | Polyak | Hindsight | Max n Actions (HL2) | ( Scaling) | |
|---|---|---|---|---|---|---|---|---|---|
| SAC | AntFourRooms | 2.404 × 10−3 | 1024 | target/— | 3.290 × 10−3 | 3 | — | — | — |
| Drawbridge | 9.602 × 10−3 | 256 | 0.6836/— | 9.823 × 10−3 | 3 | — | — | — | |
| Pendulum | 8.955 × 10−4 | 256 | target/— | 2.650 × 10−4 | 3 | — | — | — | |
| Platforms | 3.752 × 10−4 | 1024 | 0.00208/— | 0.00780 | 3 | — | — | — | |
| Tennis2D | 6.355 × 10−4 | 1024 | target/— | 1.056 × 10−4 | 1 | — | — | — | |
| UR5Reacher | 2.167 × 10−3 | 1024 | 0.005156/— | 0.06666 | 3 | — | — | — | |
| HiTS | AntFourRooms | 9.289 × 10−4 | 1024 | 0.00261/1.1267 | 1.086 × 10−3 | 3 | −1 | 22 | — |
| Drawbridge | 7.228 × 10−5 | 256 | 0.05413/0.02071 | 0.3144 | 3 | −1 | 5 | — | |
| Pendulum | 6.441 × 10−3 | 256 | target/2.5253 | 0.01259 | 3 | −1 | 22 | — | |
| Platforms | 1.940 × 10−4 | 512 | 0.00419/1.1173 | 0.02142 | 3 | −1 | 10 | — | |
| Tennis2D | 5.680 × 10−4 | 1024 | 0.03605/target | 8.910 × 10−5 | 3 | −1 | 8 | — | |
| UR5Reacher | 4.968 × 10−4 | 1024 | 0.000532/target | 0.02726 | 3 | −1 | 24 | — | |
| TBC–HRL | AntFourRooms | 9.753 × 10−4 | 1024 | 0.00261/1.1267 | 1.200 × 10−3 | 3 | −1 | 22 | 0.95 |
| Drawbridge | 7.589 × 10−5 | 256 | 0.05413/0.02071 | 0.3460 | 3 | 5 | 0.85 | ||
| Pendulum | 6.763 × 10−3 | 256 | target/2.5253 | 0.01390 | 3 | 22 | 1.10 | ||
| Platforms | 2.037 × 10−4 | 512 | 0.00419/1.1173 | 0.02360 | 3 | 10 | 1.00 | ||
| Tennis2D | 5.964 × 10−4 | 1024 | 0.03605/target | 9.900 × 10−5 | 3 | 8 | 0.90 | ||
| UR5Reacher | 5.216 × 10−4 | 1024 | 0.000532/target | 0.03000 | 3 | 24 | 1.05 | ||
| HAC | AntFourRooms | 1.652 × 10−3 | 1024 | 0.04873/target | 1.710 × 10−3 | 3 | — | 17 | — |
| Drawbridge | 2.147 × 10−4 | 1024 | 0.001009/target | 0.2031 | 3 | — | 5 | — | |
| Pendulum | 1.707 × 10−3 | 256 | 9.593 × 10−5/0.3715 | 0.01698 | 3 | — | 27 | — | |
| Platforms | 1.436 × 10−4 | 1024 | 0.00460/1.6896 | 0.01244 | 3 | — | 10 | — | |
| Tennis2D | 6.913 × 10−5 | 1024 | 2.905 × 10−4/target | 6.278 × 10−4 | 3 | — | 8 | — | |
| UR5Reacher | 4.332 × 10−3 | 1024 | 0.02822/0.4880 | 0.01199 | 3 | — | 24 | — |
References
- Zhu, K.; Zhang, T. Deep reinforcement learning based mobile robot navigation: A review. Tsinghua Sci. Technol. 2021, 26, 674–691. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, S.; Xie, Y.; Zheng, S.; Shi, P.; Rudas, I.; Cheng, X. Deep reinforcement learning-based mapless navigation for mobile robot in unknown environment with local optima. IEEE Robot. Autom. Lett. 2025, 10, 628–635. [Google Scholar] [CrossRef]
- Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F. Voronoi-based multi-robot autonomous exploration in unknown environments via deep reinforcement learning. IEEE Trans. Veh. Technol. 2020, 69, 14413–14423. [Google Scholar] [CrossRef]
- Ibarz, J.; Tan, J.; Finn, C.; Kalakrishnan, M.; Pastor, P.; Levine, S. How to train your robot with deep reinforcement learning: Lessons we have learned. Int. J. Robot. Res. 2021, 40, 698–721. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep reinforcement learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5064–5078. [Google Scholar] [CrossRef]
- Pateria, S.; Subagdja, B.; Tan, A.H.; Quek, C. Hierarchical reinforcement learning: A comprehensive survey. ACM Comput. Surv. 2021, 54, 3453160. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, F.; Liu, Q.; Fu, Y. Hierarchical reinforcement learning with automatic sub-goal identification. IEEE-CAA J. Autom. Sin. 2021, 8, 1686–1696. [Google Scholar] [CrossRef]
- Yu, L.S.; Marin, A.; Hong, F.; Lin, J. Studies on hierarchical reinforcement learning in multi-agent environment. In Proceedings of the 2008 IEEE International Conference on Networking, Sensing and Control, Sanya, China, 6–8 April 2008; pp. 1714–1720. [Google Scholar]
- Chai, R.; Niu, H.; Carrasco, J.; Arvin, F.; Yin, H.; Lennox, B. Design and experimental validation of deep reinforcement learning-based fast trajectory planning and control for mobile robot in unknown environment. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5778–5792. [Google Scholar] [CrossRef]
- Aradi, S. Survey of deep reinforcement learning for motion planning of autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 740–759. [Google Scholar] [CrossRef]
- Teng, S.; Chen, L.; Ai, Y.; Zhou, Y.; Xuanyuan, Z.; Hu, X. Hierarchical interpretable imitation learning for end-to-end autonomous driving. IEEE Trans. Intell. Veh. 2023, 8, 673–683. [Google Scholar] [CrossRef]
- Lei, K.; Guo, P.; Wang, Y.; Zhang, J.; Meng, X.; Qian, L. Large-scale dynamic scheduling for flexible job-shop with random arrivals of new jobs by hierarchical reinforcement learning. IEEE Trans. Ind. Inf. 2024, 20, 1007–1018. [Google Scholar] [CrossRef]
- Wang, X.; Garg, S.; Lin, H.; Hu, J.; Kaddoum, G.; Piran, M.J.; Hossain, M.S. Toward accurate anomaly detection in industrial Internet of Things using hierarchical federated learning. IEEE Internet Things J. 2022, 9, 7110–7119. [Google Scholar] [CrossRef]
- Liang, H.; Zhu, L.; Yu, F.R. Collaborative edge intelligence service provision in blockchain empowered urban rail transit systems. IEEE Internet Things J. 2024, 11, 2211–2223. [Google Scholar] [CrossRef]
- Wei, T.; Webb, B. A bio-inspired reinforcement learning rule to optimise dynamical neural networks for robot control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Xu, K.; Li, Y.; Sun, J.; Du, S.; Di, X.; Yang, Y.; Li, B. Targets capture by distributed active swarms via bio-inspired reinforcement learning. Sci. China Phys. Mech. Astron. 2025, 68, 218711. [Google Scholar] [CrossRef]
- Gruber, R.; Schiestl, M.; Boeckle, M.; Frohnwieser, A.; Miller, R.; Gray, R.D.; Clayton, N.S.; Taylor, A.H. New Caledonian crows use mental representations to solve metatool problems. Curr. Biol. 2019, 29, 686–692. [Google Scholar] [CrossRef]
- Lechner, M.; Hasani, R.; Amini, A.; Henzinger, T.A.; Rus, D.; Grosu, R. Neural circuit policies enabling auditable autonomy. Nat. Mach. Intell. 2020, 2, 642–649. [Google Scholar] [CrossRef]
- Ocana, F.M.; Suryanarayana, S.M.; Saitoh, K.; Kardamakis, A.A.; Capantini, L.; Robertson, B.; Grillner, S. The lamprey pallium provides a blueprint of the mammalian motor projections from cortex. Curr. Biol. 2015, 25, 413–423. [Google Scholar] [CrossRef] [PubMed]
- Bacon, P.-L.; Harb, J.; Precup, D. The Option-Critic Architecture. In Proceedings of the 31st AAAI Conference on Artificial Intelligence (AAAI), San Francisco, CA, USA, 4–9 February 2017; pp. 1726–1734. [Google Scholar]
- Vezhnevets, A.S.; Osindero, S.; Schaul, T.; Heess, N.; Jaderberg, M.; Silver, D.; Kavukcuoglu, K. FeUdal Networks for Hierarchical Reinforcement Learning. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 3540–3549. [Google Scholar]
- Nachum, O.; Gu, S.; Lee, H.; Levine, S. Data-Efficient Hierarchical Reinforcement Learning. In Advances in Neural Information Processing Systems (NeurIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2018; pp. 3303–3313. [Google Scholar]
- Gürtler, N.; Büchler, D.; Martius, G. Hierarchical Reinforcement Learning with Timed Subgoals. In Advances in Neural Information Processing Systems (NeurIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2021; pp. 2113–2125. [Google Scholar]
- Florensa, C.; Duan, Y.; Abbeel, P. Stochastic Neural Networks for Hierarchical Reinforcement Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Wang, R.; Li, Y.; Jin, Y. Spiking Neural Networks: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 60738–60764. [Google Scholar]
- Hasani, R.; Lechner, M.; Amini, A.; Liebenwein, L.; Ray, A.; Tschaikowski, M.; Teschl, G.; Rus, D. Closed-form continuous-time neural networks. Nat. Mach. Intell. 2022, 4, 992–1003. [Google Scholar]
- Tylkin, P.; Harakeh, A.; Hasani, R.; Allen, R.; Siu, H.C.; Wrafter, D.; Seyde, T.; Amini, A.; Rus, D. Interpretable autonomous flight via compact visualizable neural circuit policies. IEEE Robot. Autom. Lett. 2022, 7, 3265–3272. [Google Scholar] [CrossRef]
- Chahine, M.; Hasani, R.; Kao, P.; Ray, A.; Shubert, R.; Lechner, M.; Amini, A.; Rus, D. Robust flight navigation out of distribution with liquid neural networks. Sci. Robot. 2023, 8, eadc8892. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Bai, Y.; Li, Y.; Geng, J.; Huang, Y.; Chen, H. Evolutionary end-to-end autonomous driving model with continuous-time neural networks. IEEE/ASME Trans. Mechatron. 2024, 29, 2983–2990. [Google Scholar] [CrossRef]
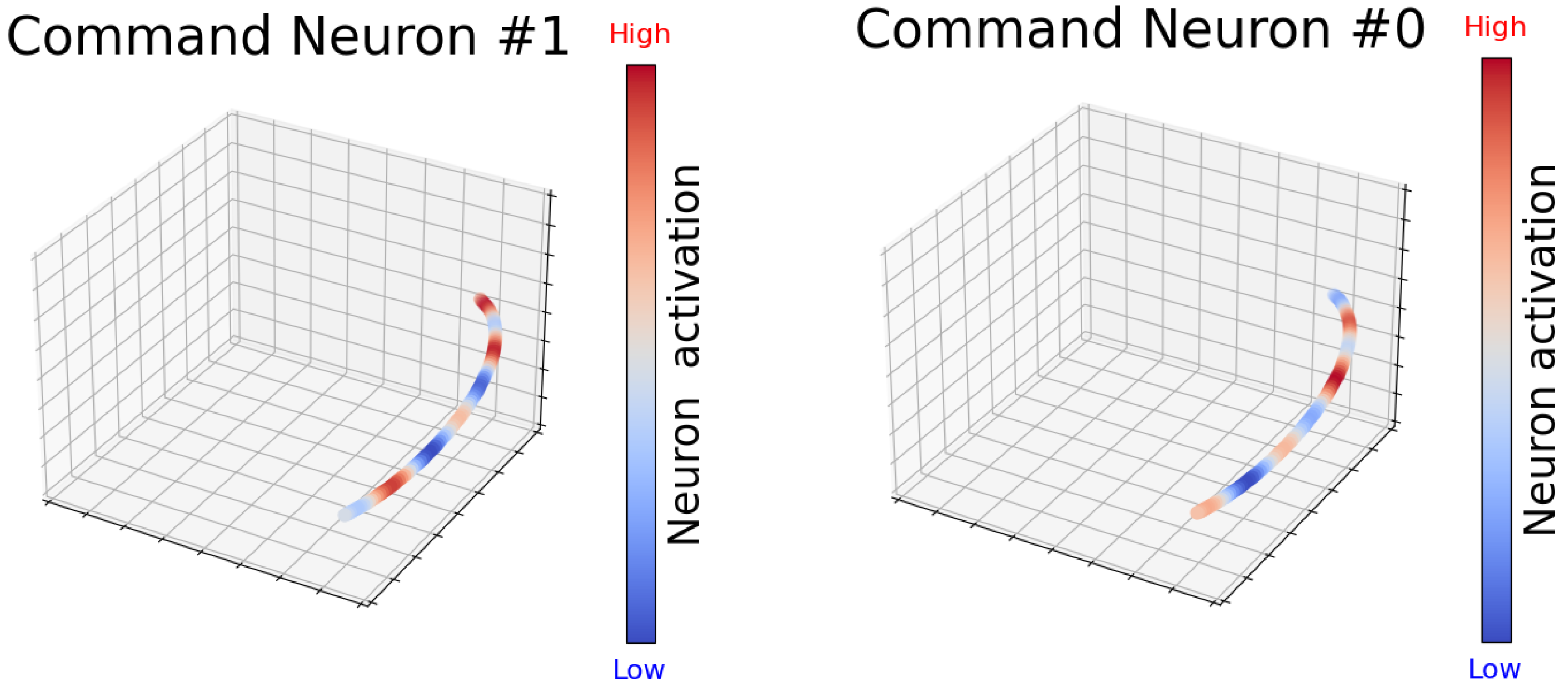
| Environment | Training Steps | State/Action Dim. | Key Characteristics |
|---|---|---|---|
| AntFourRooms | 1.0 M | , | Four-room maze, sparse rewards, long-horizon planning |
| Drawbridge | 0.4 M | , | Dynamic obstacle, timing-critical actions |
| Pendulum | 0.2 M | , | Classic control, simple dynamics |
| Platforms | 4.0 M | , | Multi-stage navigation, sparse rewards |
| Tennis2D | 20 M | , | High stochasticity, frequent contacts |
| UR5Reacher | 0.4 M | , | Robotic arm reaching, high precision |
| Environment | SAC Success (%) | HAC Success (%) | HITS Success (%) | TBC-HRL Success (%) | Convergence Gain (M Env Steps; vs. Best Baseline) |
|---|---|---|---|---|---|
| AntFourRooms | * | M | |||
| Drawbridge | * | M | |||
| Pendulum | * | M | |||
| Platforms | * | M | |||
| Tennis2D | * | N/A † | |||
| UR5Reacher | * | M |
| Environment | HAC | TBC-HRL (-NDBCNet) | TBC-HRL (-TS) | TBC-HRL |
|---|---|---|---|---|
| AntFourRooms | ||||
| Drawbridge | ||||
| Pendulum | ||||
| Platforms | ||||
| Tennis2D | ||||
| UR5Reacher |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Shan, Y.; Mo, H. TBC-HRL: A Bio-Inspired Framework for Stable and Interpretable Hierarchical Reinforcement Learning. Biomimetics 2025, 10, 715. https://doi.org/10.3390/biomimetics10110715
Li Z, Shan Y, Mo H. TBC-HRL: A Bio-Inspired Framework for Stable and Interpretable Hierarchical Reinforcement Learning. Biomimetics. 2025; 10(11):715. https://doi.org/10.3390/biomimetics10110715
Chicago/Turabian StyleLi, Zepei, Yuhan Shan, and Hongwei Mo. 2025. "TBC-HRL: A Bio-Inspired Framework for Stable and Interpretable Hierarchical Reinforcement Learning" Biomimetics 10, no. 11: 715. https://doi.org/10.3390/biomimetics10110715
APA StyleLi, Z., Shan, Y., & Mo, H. (2025). TBC-HRL: A Bio-Inspired Framework for Stable and Interpretable Hierarchical Reinforcement Learning. Biomimetics, 10(11), 715. https://doi.org/10.3390/biomimetics10110715






