Modeling the Impact of Driving Styles on Crash Severity Level Using SHRP 2 Naturalistic Driving Data
Abstract
1. Introduction
2. Literature Review
2.1. Identifying Driving Styles
2.2. Relationship between Driving Styles and Crash Severity
3. Rationale and Objective
4. Materials and Methods
4.1. SHRP 2 Database
4.2. Independent Variables
4.2.1. Driving Styles
4.2.2. Other Driver Characteristics
4.3. Dependent Variables
4.4. Model Selection—Diagonal Inflated Bivariate Poisson Regression
5. Model Estimation Results
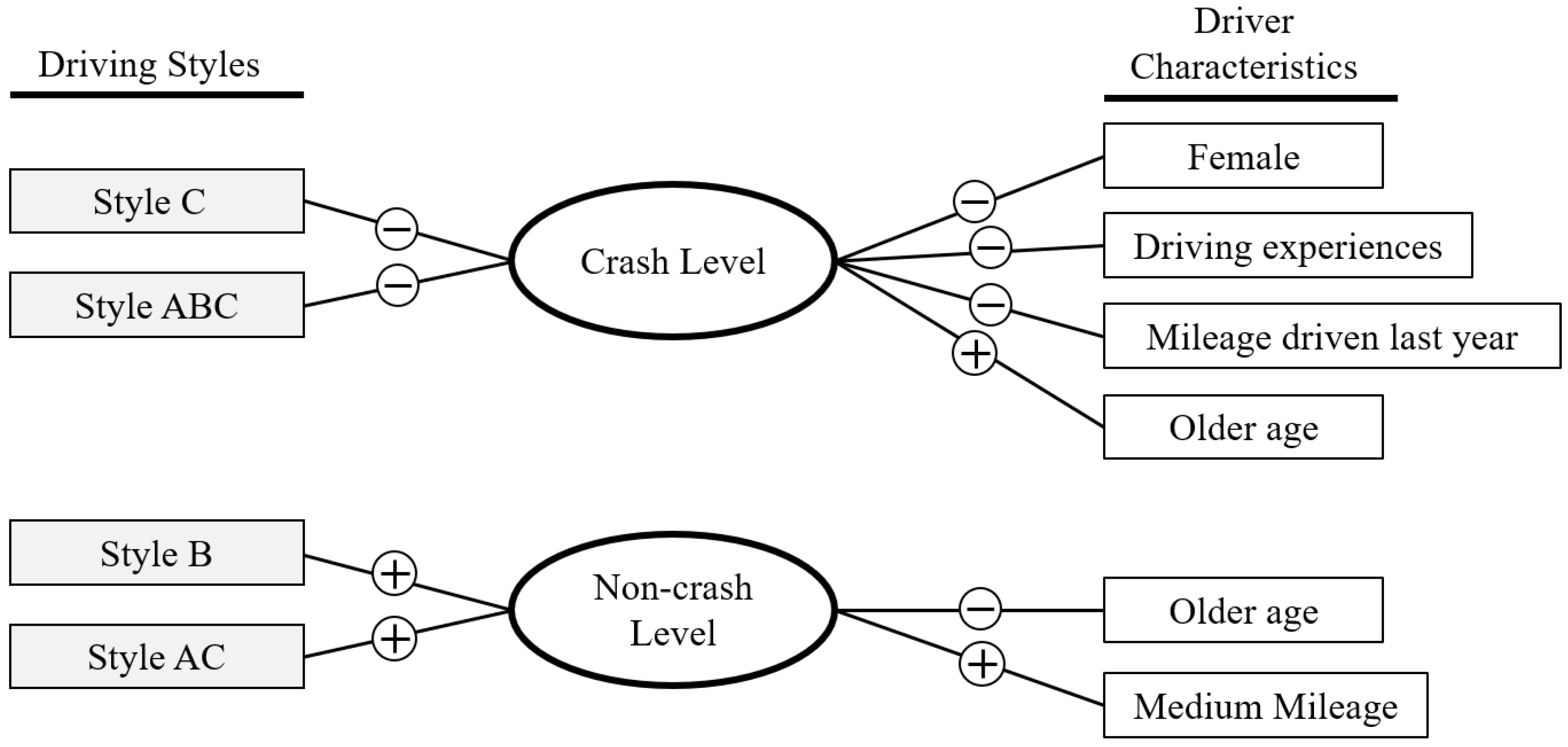
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mckenna, F.P. Accident Proneness: A Conceptual Analysis. Accid. Anal. Prev. 1983, 15, 65–71. [Google Scholar] [CrossRef]
- Elander, J.; West, R.; French, D. Behavioral Correlates of Individual Differences in Road-Traffic Crash Risk: An Examination of Methods and Findings. Psychol. Bull. 1993, 113, 279–294. [Google Scholar] [CrossRef]
- French, D.J.; West, R.J.; Elander, J.; Wilding, J.M. Decision-Making Style, Driving Style, and Self-Reported Involvement in Road Traffic Accidents. Ergonomics 1993, 36, 627–644. [Google Scholar] [CrossRef] [PubMed]
- Shinar, D. Traffic Safety and Human Behavior, 1st ed.; Emerald Publishing Limited: Bradford, UK, 2007; ISBN 0080450296. [Google Scholar]
- Jovanis, P.; Aguero-Valverde, J.; Wu, K.-F.; Shankar, V. Analysis of Naturalistic Driving Event Data. Transp. Res. Rec. J. Transp. Res. Board 2011, 2236, 49–57. [Google Scholar]
- Wu, K.F.; Aguero-Valverde, J.; Jovanis, P.P. Using Naturalistic Driving Data to Explore the Association between Traffic Safety-Related Events and Crash Risk at Driver Level. Accid. Anal. Prev. 2014, 72, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Milton, J.C.; Shankar, V.N.; Mannering, F.L. Highway Accident Severities and the Mixed Logit Model: An Exploratory Empirical Analysis. Accid. Anal. Prev. 2008, 40, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Haleem, K.; Alluri, P.; Gan, A. Analyzing Pedestrian Crash Injury Severity at Signalized and Non-Signalized Locations. Accid. Anal. Prev. 2015, 81, 14–23. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, G.; Tarefder, R.; Ma, J.; Wei, H.; Guan, H. A Multinomial Logit Model-Bayesian Network Hybrid Approach for Driver Injury Severity Analyses in Rear-End Crashes. Accid. Anal. Prev. 2015, 80, 76–88. [Google Scholar] [CrossRef]
- Behnood, A.; Roshandeh, A.M.; Mannering, F.L. Latent Class Analysis of the Effects of Age, Gender, and Alcohol Consumption on Driver-Injury Severities. Anal. Methods Accid. Res. 2014, 3–4, 56–91. [Google Scholar] [CrossRef]
- Yasmin, S.; Eluru, N.; Bhat, C.R.; Tay, R. A Latent Segmentation Based Generalized Ordered Logit Model to Examine Factors Influencing Driver Injury Severity. Anal. Methods Accid. Res. 2014, 1, 23–38. [Google Scholar] [CrossRef]
- Paleti, R.; Eluru, N.; Bhat, C.R. Examining the Influence of Aggressive Driving Behavior on Driver Injury Severity in Traffic Crashes. Accid. Anal. Prev. 2010, 42, 1839–1854. [Google Scholar] [CrossRef] [PubMed]
- Sagberg, F.; Selpi; Bianchi Piccinini, G.F.; Engström, J. A Review of Research on Driving Styles and Road Safety. Hum. Factors: J. Hum. Factors Ergon. Soc. 2015, 57, 1248–1275. [Google Scholar] [CrossRef] [PubMed]
- Reason, J.; Manstead, A.; Stephen, S.; Baxter, J.; Campbell, K. Errors and Violations on the Roads: A Real Distinction? Ergonomics 1990, 33, 1315–1332. [Google Scholar] [CrossRef] [PubMed]
- Taubman-Ben-Ari, O.; Mikulincer, M.; Gillath, O. The Multidimensional Driving Style Inventory—Scale Construct and Validation. Accid. Anal. Prev. 2004, 36, 323–332. [Google Scholar] [CrossRef]
- Chen, S.W.; Fang, C.Y.; Tien, C.T. Driving Behaviour Modelling System Based on Graph Construction. Transp. Res. Part C Emerg. Technol. 2013, 26, 314–330. [Google Scholar] [CrossRef]
- Kalsoom, R.; Halim, Z. Clustering the Driving Features Based on Data Streams. In Proceedings of the International Multi Topic Conference (INMIC), Lahore, Pakistan, 19–20 December 2013; IEEE: New York, NY, USA, 2013; pp. 89–94. [Google Scholar]
- Desai, A.V.; Haque, M.A. Vigilance Monitoring for Operator Safety: A Simulation Study on Highway Driving. J. Saf. Res. 2006, 37, 139–147. [Google Scholar] [CrossRef]
- Mantouka, E.G.; Barmpounakis, E.N.; Vlahogianni, E.I. Identifying Driving Safety Profiles from Smartphone Data Using Unsupervised Learning. Saf. Sci. 2019, 119, 84–90. [Google Scholar] [CrossRef]
- Johnson, D.A.; Trivedi, M.M. Driving Style Recognition Using a Smartphone as a Sensor Platform. In Proceedings of the 14th International Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; IEEE: New York, NY, USA, 2011; pp. 1609–1615. [Google Scholar]
- Hong, J.-H.H.; Margines, B.; Dey, A.K. A Smartphone-Based Sensing Platform to Model Aggressive Driving Behaviors. In Proceedings of the 32nd Annual Conference on Human Factors in Computing Systems—CHI ’14, Toronto, ONT, Canada, 26 April–1 May 2014; ACM Press: New York, NY, USA, 2014; pp. 4047–4056. [Google Scholar]
- Chen, K.-T.; Chen, H.-Y.W. Driving Style Clustering Using Naturalistic Driving Data. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 176–188. [Google Scholar] [CrossRef]
- Constantinescu, Z.; Marinoiu, C.; Vladoiu, M. Driving Style Analysis Using Data Mining Techniques. Int. J. Comput. Commun. Control. 2010, 5, 654. [Google Scholar] [CrossRef]
- Eboli, L.; Mazzulla, G.; Pungillo, G. How to Define the Accident Risk Level of Car Drivers by Combining Objective and Subjective Measures of Driving Style. Transp. Res. Part F Traffic Psychol. Behav. 2017, 49, 29–38. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Z.; Zhang, Y.; Qu, X.; Zhang, M.; Wu, C. Driving Style Recognition under Connected Circumstance Using a Supervised Hierarchical Bayesian Model. J. Adv. Transp. 2021, 2021, 6687378. [Google Scholar] [CrossRef]
- Li, G.; Li, S.E.; Cheng, B.; Green, P. Estimation of Driving Style in Naturalistic Highway Traffic Using Maneuver Transition Probabilities. Transp. Res. Part C: Emerg. Technol. 2017, 74, 113–125. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, M. Maneuver-Based Driving Behavior Classification Based on Random Forest. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Häkkinen, S. Traffic Accidents and Driver Characteristics: A Statistical and Psychological Study. Ph.D. Thesis, Institute of Technology Otaniemi, Helsinki, Finland, 1958. [Google Scholar]
- Sabbour, S.M.; Ibrahim, J.M. Driving Behaviour, Driver Style and Road Traffic Accidents among Young Medical Group. Inj. Prev. 2010, 16, A33. [Google Scholar] [CrossRef]
- Useche, S.A.; Cendales, B.; Alonso, F.; Orozco-Fontalvo, M. A Matter of Style? Testing the Moderating Effect of Driving Styles on the Relationship between Job Strain and Work-Related Crashes of Professional Drivers. Transp. Res. Part F Traffic Psychol. Behav. 2020, 72, 307–317. [Google Scholar] [CrossRef]
- Eluru, N.; Bhat, C.R. A Joint Econometric Analysis of Seat Belt Use and Crash-Related Injury Severity. Accid. Anal. Prev. 2007, 39, 1037–1049. [Google Scholar] [CrossRef]
- Lajunen, T.; Corry, A.; Summala, H.; Hartley, L. Impression Management and Self-Deception in Traffic Behaviour Inventories. Personal. Individ. Differ. 1997, 22, 341–353. [Google Scholar] [CrossRef]
- Arthur, W.; Graziano, W.G. The Five-Factor Model, Conscientiousness, and Driving Accident Involvement. J. Personal. 1996, 64, 593–618. [Google Scholar] [CrossRef]
- Transportation Research Board of the National Academies of Science. The 2nd Strategic Highway Research Program Naturalistic Driving Study Dataset. 2013. Available online: https://insight.shrp2nds.us (accessed on 27 January 2018).
- Hankey, J.M.; Perez, M.A.; McClafferty, J.A. Description of the SHRP 2 Nauralistic Database and the Crash, Near-Crash, and Baseline Data Set. Task Report; Virginia Tech Transportation Institute: Blacksburg, VA, USA, 2016. [Google Scholar]
- Virginia Tech Transportation Institute. Event Detail Table Data Dictionary. 2015. Available online: https://insight.shrp2nds.us/ (accessed on 12 December 2017).
- Virginia Tech Transportation Institute. SHPR 2 Researcher Dictionary for Video Reduction Data. 2015. Available online: https://insight.SHRP2nds.us/ (accessed on 30 September 2018).
- Savolainen, P.T.; Mannering, F.L.; Lord, D.; Quddus, M.A. The Statistical Analysis of Highway Crash-Injury Severities: A Review and Assessment of Methodological Alternatives. Accid. Anal. Prev. 2011, 43, 1666–1676. [Google Scholar] [CrossRef]
- Ma, J.; Kockelman, K.M. Bayesian Multivariate Poisson Regression for Models of Injury Count, by Severity. Transp. Res. Rec. J. Transp. Res. Board 2006, 1950, 24–34. [Google Scholar] [CrossRef]
- Ma, J.; Kockelman, K.M.; Damien, P. A Multivariate Poisson-Lognormal Regression Model for Prediction of Crash Counts by Severity, Using Bayesian Methods. Accid. Anal. Prev. 2008, 40, 964–975. [Google Scholar] [CrossRef] [PubMed]
- Park, E.S.; Lord, D. Multivariate Poisson-Lognormal Models for Jointly Modeling Crash Frequency by Severity. Transp. Res. Rec. 2007, 2019, 1–6. [Google Scholar] [CrossRef]
- El-Basyouny, K.; Sayed, T. Collision Prediction Models Using Multivariate Poisson-Lognormal Regression. Accid. Anal. Prev. 2009, 41, 820–828. [Google Scholar] [CrossRef] [PubMed]
- Aguero-Valverde, J.; Jovanis, P.P. Bayesian Multivariate Poisson Lognormal Models for Crash Severity Modeling and Site Ranking. Transp. Res. Rec. 2009, 2136, 82–91. [Google Scholar] [CrossRef]
- Wang, K.; Ivan, J.N.; Ravishanker, N.; Jackson, E. Multivariate Poisson Lognormal Modeling of Crashes by Type and Severity on Rural Two Lane Highways. Accid. Anal. Prev. 2017, 99, 6–19. [Google Scholar] [CrossRef]
- Bermúdez i Morata, L. A Priori Ratemaking Using Bivariate Poisson Regression Models. Insur. Math. Econ. 2009, 44, 135–141. [Google Scholar] [CrossRef]
- Karlis, D.; Ntzoufras, I. Bivariate Poisson and Diagonal Inflated Bivariate Poisson Regression Models in R. J. Stat. Softw. 2005, 14, 1–36. [Google Scholar] [CrossRef]
- Ver Hoef, J.M.; Boveng, P.L. Quasi-Poisson vs. Negative Binomial Regression: How Should We Model Overdispersed Count Data? Ecology 2007, 88, 2766–2772. [Google Scholar] [CrossRef]
- Oh, J.; Washington, S.P.; Nam, D. Accident Prediction Model for Railway-Highway Interfaces. Accid. Anal. Prev. 2006, 38, 346–356. [Google Scholar] [CrossRef]
- Lao, Y.; Wu, Y.J.; Corey, J.; Wang, Y. Modeling Animal-Vehicle Collisions Using Diagonal Inflated Bivariate Poisson Regression. Accid. Anal. Prev. 2011, 43, 220–227. [Google Scholar] [CrossRef]
- Karlis, D.; Ntzoufras, L. Analysis of Sports Data by Using Bivariate Poisson Models. J. R. Stat. Soc. Ser. D Stat. 2003, 52, 381–393. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Krishnan, T. The EM Algorithm and Extensions, 2nd ed.; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; ISBN 9780470191613. [Google Scholar]
- Zhou, H.; Zhao, J.; Pour-Rouholamin, M.; Tobias, P.A. Statistical Characteristics of Wrong-Way Driving Crashes on Illinois Freeways. Traffic Inj. Prev. 2015, 16, 760–767. [Google Scholar] [CrossRef] [PubMed]
- Regev, S.; Rolison, J.J.; Moutari, S. Crash Risk by Driver Age, Gender, and Time of Day Using a New Exposure Methodology. J. Saf. Res. 2018, 66, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Arun, A.; Haque, M.M.; Bhaskar, A.; Washington, S.; Sayed, T. A Systematic Mapping Review of Surrogate Safety Assessment Using Traffic Conflict Techniques. Accid. Anal. Prev. 2021, 153, 106016. [Google Scholar] [CrossRef]
- Fu, C.; Sayed, T. A Multivariate Method for Evaluating Safety from Conflict Extremes in Real Time. Anal. Methods Accid. Res. 2022, 36, 100244. [Google Scholar] [CrossRef]
| Variable | Selection Criteria |
|---|---|
| Event Severity 1 | (1) Balanced-Sample Baseline; (2) Additional Baseline. (3) Crash. (4) Near Crash. |
| Alignment | Straight Alignment. |
| Traffic Density | (1) LOS A1; (2) LOS A2; (3) LOS B; (4) LOS C. |
| Locality | (1) Interstate or Bypass or Divided highway with no traffic signals; (2) Bypass or Divided Highway with traffic signals. |
| Vehicle Kinematic Parameters | Variables |
|---|---|
| Speed | Mean Speed Standard Deviation of Speed Maximum Speed Minimum Speed |
| Lateral Acceleration | Mean Positive Acceleration Mean Negative Acceleration Standard Deviation of Acceleration Maximum Acceleration to the right Maximum Acceleration to the left |
| Longitudinal Acceleration | Mean Positive Acceleration Mean Negative Acceleration Standard Deviation of Acceleration Maximum Acceleration Minimum Acceleration |
| Factors | Cluster A | Cluster B | Cluster C |
|---|---|---|---|
| Speed maintenance | Medium to high speed | Medium to high speed | Low to medium speed |
| Lateral acceleration maneuver | Low lateral maneuver variability | Low lateral maneuver variability | High lateral maneuver variability |
| Braking Maneuver | Mild braking maneuver | Moderate braking | Harder braking maneuver |
| Longitudinal acceleration Maneuvering | Mild variability in acceleration maneuvering | Moderate variability in acceleration maneuvering | High variability in acceleration maneuvering |
| Explanatory Variable | Description |
|---|---|
| Gender | Female (n = 235) |
| Male (n = 256) | |
| Miles Driven Last Year/1000 | The approximation of miles participant drove last year divided by 1000. (Mean = 21.8, Std. = 16.5, n = 491) |
| Years of Driving | The number of years the participant has been driving. (Mean = 18.71, Std. = 18.67, n = 491) |
| Age Group | Young age group (Age 16–29, n = 283) |
| Middle age group (Age 30–59, n = 136) | |
| Old age group (Age over 60, n = 72) | |
| Annual Mileage | Low mileage (<10,000 miles, n = 110) |
| Medium mileage (10,000–20,000 miles, n = 130) | |
| High mileage (over 20,000 miles, n = 251) | |
| Identified Driving Style | Style A (n = 129) |
| Style B (n = 91) | |
| Style C (n = 85) | |
| Style AB (n = 58) | |
| Style AC (n = 52) | |
| Style BC (n = 40) | |
| Style ABC (n = 36) |
| Level | Description | Frequency |
|---|---|---|
| I. Most Severe | Any crash that includes an airbag deployment; any injury of driver, pedal cyclist or pedestrian; a vehicle roll over; a high Delta V (speed change of the subject vehicle during impact greater than 20 mph); or that requires vehicle towing. Injury if present should be sufficient to require a doctor’s visit. | 10 |
| II. Police Reportable Crash | Severity that does not meet level 1 requirement. Includes sufficient property damage that is police-reportable. Includes crashes that reach an acceleration on any axis greater than +/− 1.3 g (excluding curb strikes) as well. | 9 |
| III. Minor Crash | Crashes not included in above levels. Includes physical contact with another object but with minimal damage. Includes most road departures, small animal strikes, all curbs and tires strikes potentially in conflict with oncoming traffic and other curb strikes with an increased risk element. | 32 |
| IV. Low-Risk Tire Strike | Tire Strike, Low Risk. Tire strike only with little/no risk element. | 5 |
| V. Not a crash | Includes all event severity levels except for crash. (Baseline excluded in the analysis) | 850 |
| Count of Crash | Count of Non-Crash | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | >6 | |
| 0 | 0 | 278 | 80 | 40 | 18 | 11 | 3 | 10 |
| 1 | 21 | 15 | 7 | 3 | 0 | 0 | 0 | 0 |
| 2 | 3 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| Variable | Crash | Non-Crash | Covariance | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λ1 = 0.155 | λ2 = 1.690 | λ3 = 0.000 | |||||||
| Coef. | Std. err. | |t-Stat| | Coef. | Std. err. | |t-Stat| | Coef. | Std. err. | |t-Stat| | |
| Constant | 0.291 ** | 0.006 | 3.210 | 0.291 ** | 0.006 | 3.210 | −14.790 * | 0.621 | 1.685 |
| Gender (Female = 1, Male = 0) | −1.082 ** | 0.020 | 3.896 | 0.072 | 0.005 | 1.083 | |||
| Miles Driven Last Year (divided by 1000) | −0.035 ** | 0.000 | 3.649 | −0.001 | 0.000 | 0.508 | |||
| Years of Driving | −0.055 ** | 0.001 | 4.012 | 0.004 | 0.000 | 0.981 | |||
| Age Group (Middle age group = 1, otherwise = 0) | −0.117 | 0.131 | 0.063 | 0.054 | 0.008 | 0.465 | |||
| Age Group (Old age group = 1, otherwise = 0) | 2.123 ** | 0.046 | 3.254 | −0.509 ** | 0.016 | 2.236 | |||
| Annual Mileage (Low mile = 1, otherwise = 0) | −0.124 | 0.025 | 0.352 | 0.013 | 0.006 | 0.015 | |||
| Annual Mileage (Medium mile = 1, otherwise = 0) | −0.145 | 0.022 | 0.477 | 0.166 * | 0.007 | 1.653 | |||
| Driving Style (Style B = 1, otherwise = 0) | −1.725 | 0.131 | 0.929 | 0.247 ** | 0.007 | 2.362 | |||
| Driving Style (Style C = 1, otherwise = 0) | −0.687 * | 0.026 | 1.889 | 0.128 | 0.007 | 1.173 | |||
| Driving Style (Style AB = 1, otherwise = 0) | −1.214 | 0.130 | 0.660 | 0.178 | 0.009 | 1.330 | |||
| Driving Style (Style AC = 1, otherwise = 0) | −1.220 | 0.131 | 0.656 | 0.372 ** | 0.009 | 2.953 | |||
| Driving Style (Style BC = 1, otherwise = 0) | −1.17 | 0.141 | 0.588 | 0.115 | 0.010 | 0.839 | |||
| Driving Style (Style ABC = 1, otherwise = 0) | −15.674 ** | 0.02 | 54.426 | 0.133 | 0.011 | 0.893 | |||
| Pm = 0.0105 † | |||||||||
| θ1, θ2, θ3 = 1, 0, 0 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.-T.; Chen, H.-Y.W. Modeling the Impact of Driving Styles on Crash Severity Level Using SHRP 2 Naturalistic Driving Data. Safety 2022, 8, 74. https://doi.org/10.3390/safety8040074
Chen K-T, Chen H-YW. Modeling the Impact of Driving Styles on Crash Severity Level Using SHRP 2 Naturalistic Driving Data. Safety. 2022; 8(4):74. https://doi.org/10.3390/safety8040074
Chicago/Turabian StyleChen, Kuan-Ting, and Huei-Yen Winnie Chen. 2022. "Modeling the Impact of Driving Styles on Crash Severity Level Using SHRP 2 Naturalistic Driving Data" Safety 8, no. 4: 74. https://doi.org/10.3390/safety8040074
APA StyleChen, K.-T., & Chen, H.-Y. W. (2022). Modeling the Impact of Driving Styles on Crash Severity Level Using SHRP 2 Naturalistic Driving Data. Safety, 8(4), 74. https://doi.org/10.3390/safety8040074





