Using Tolerance Bounds for Estimation of Characteristic Fatigue Curves for Composites with Confidence
Abstract
:1. Introduction
2. Theoretical Methods
2.1. Theory of Tolerance Bounds for Random Variables
2.1.1. Independent Variables
2.1.2. Dependent Variables
2.2. Tolerance Bounds for Dependent Variables
2.2.1. Theory
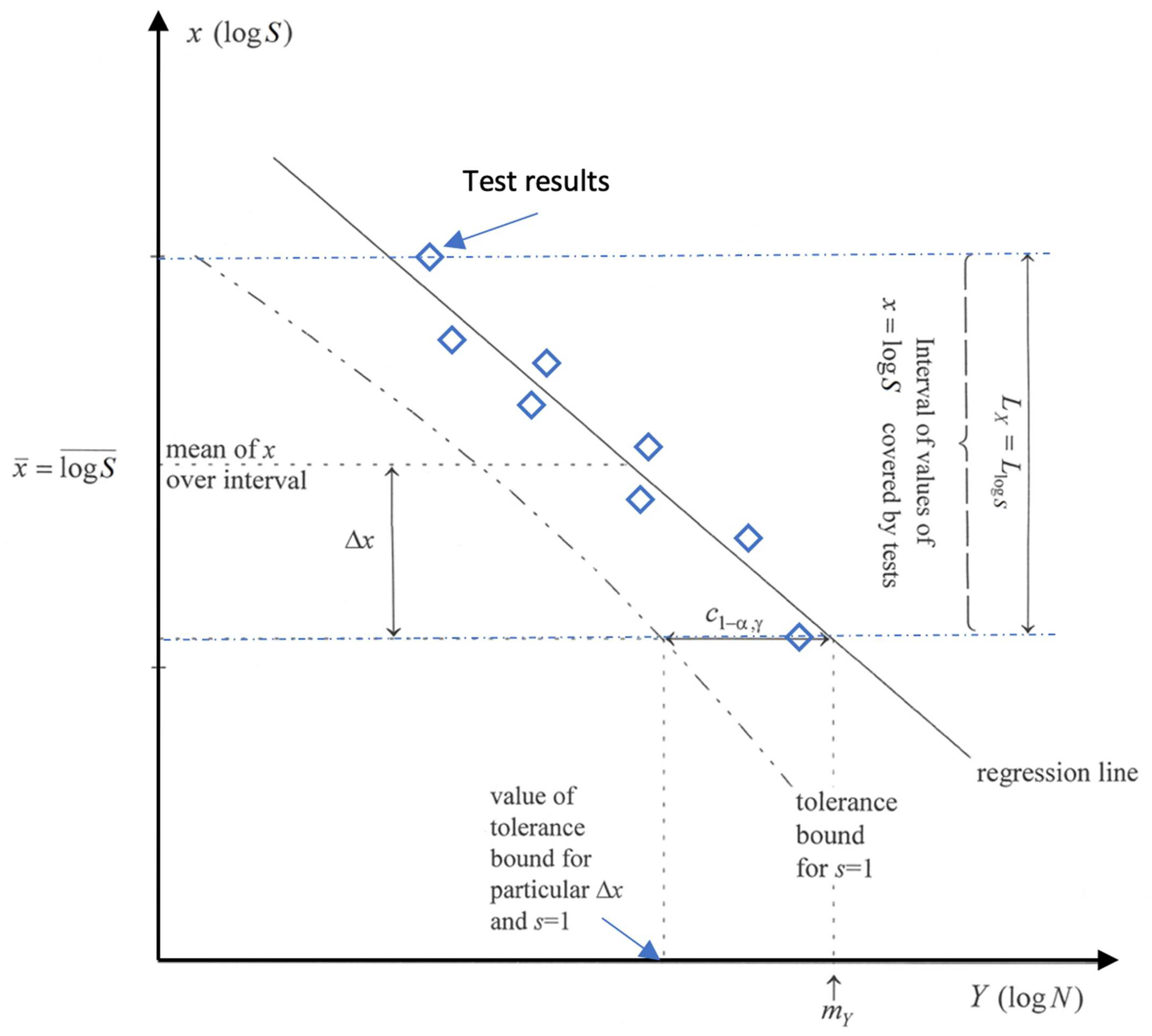
2.2.2. Graphical Representation of the Quantile
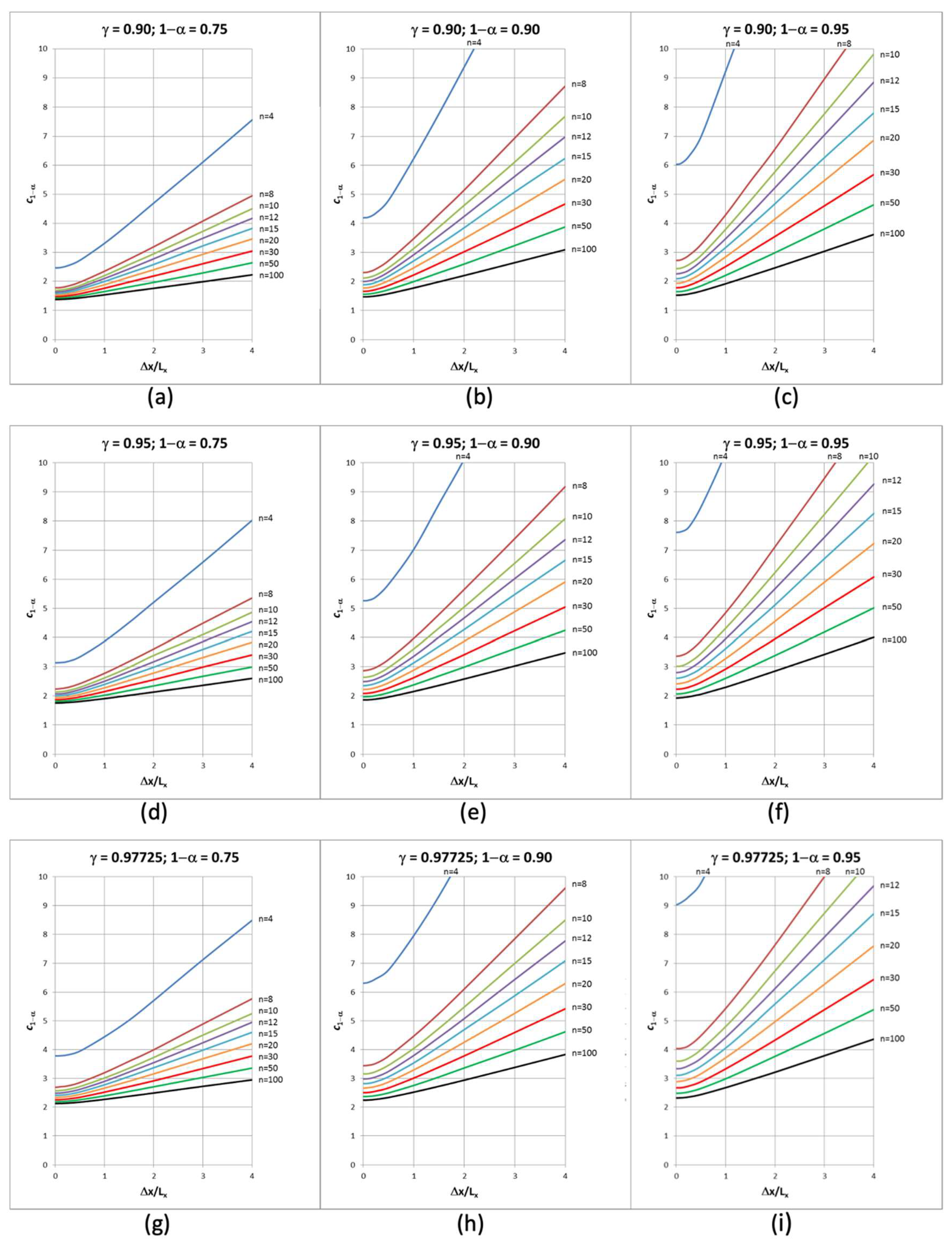
2.2.3. Mathematical Representation of the Quantile c1−α
3. Results
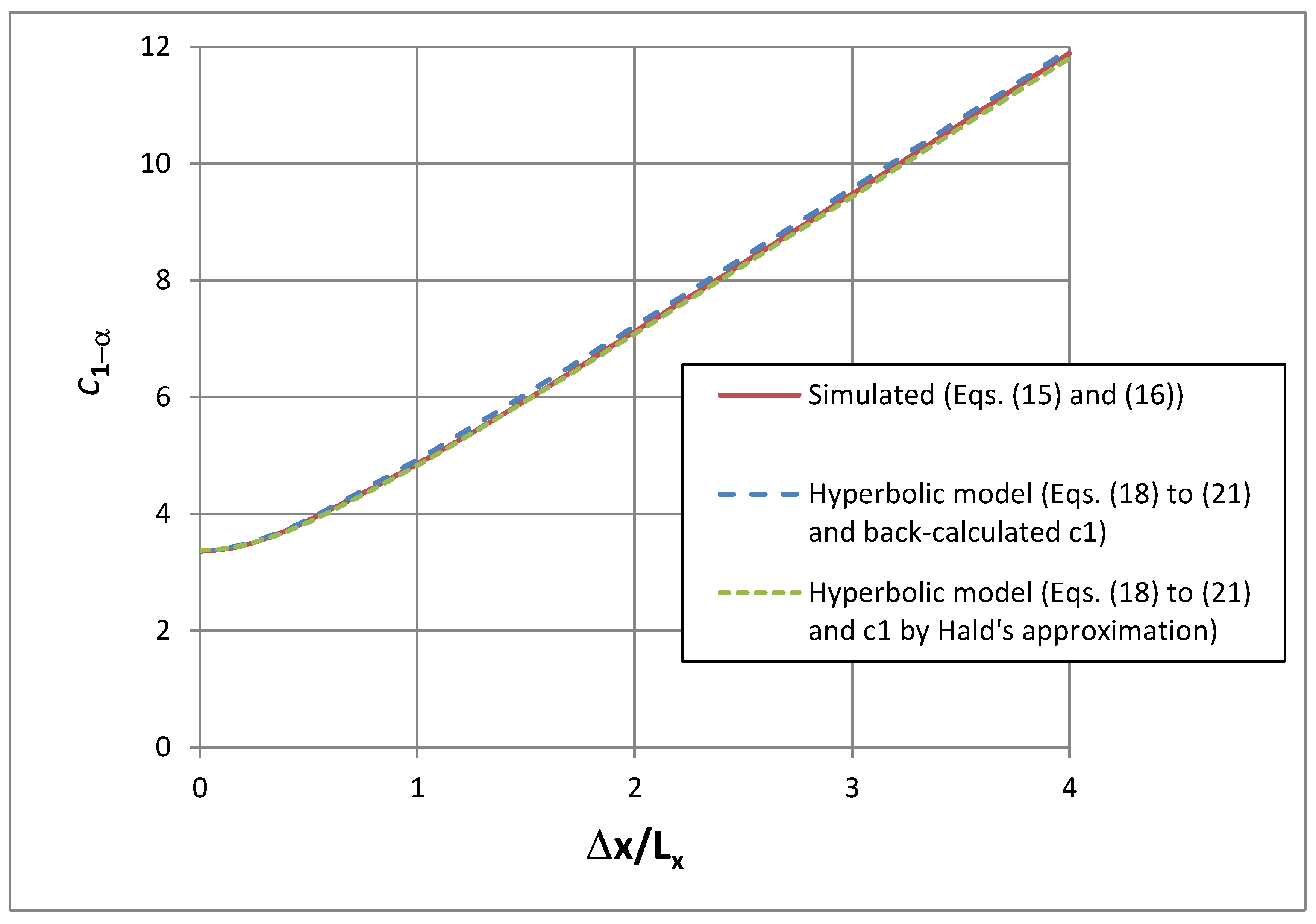
3.1. Verification
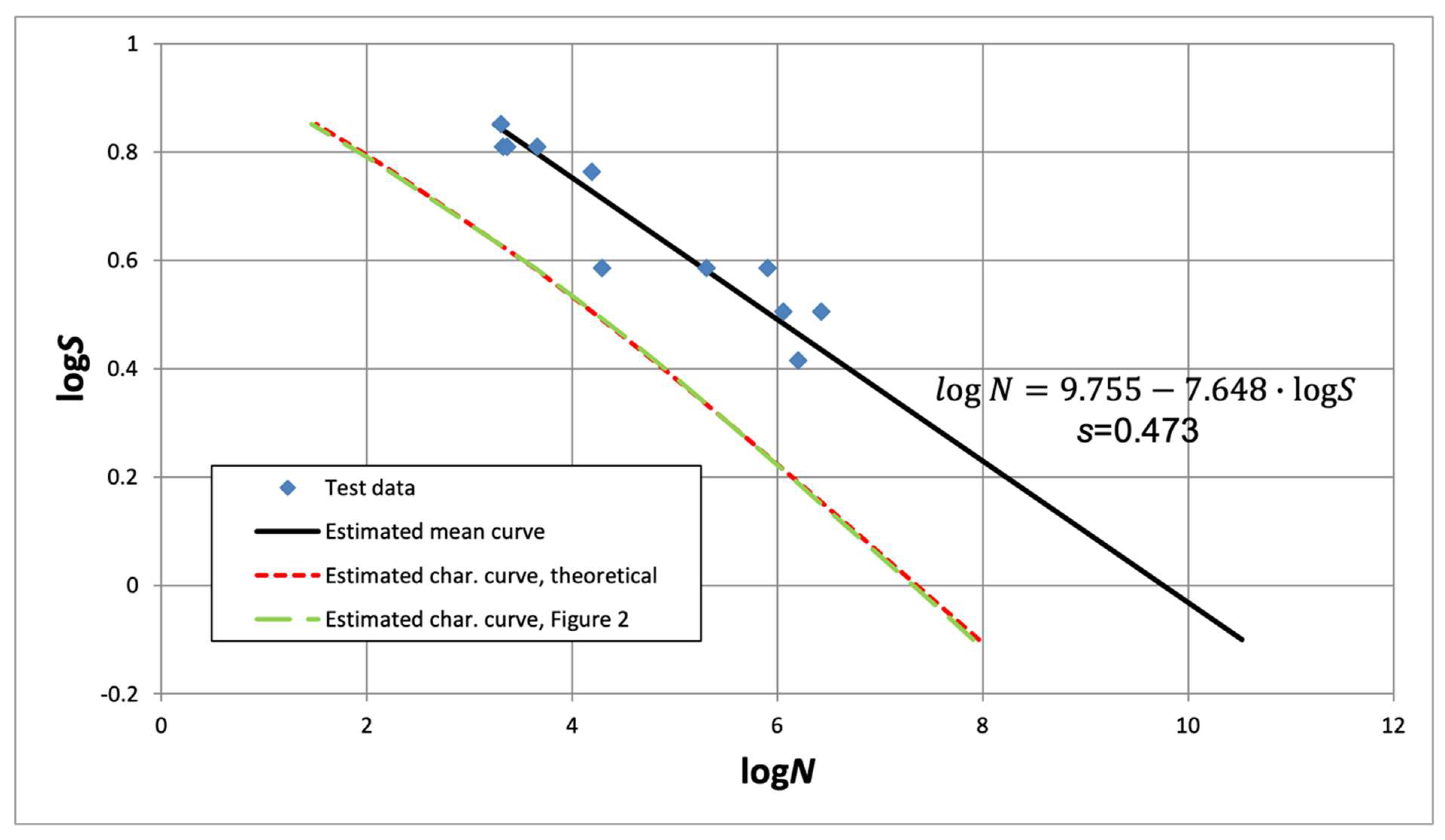
3.2. Numerical Example
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DNV Standard. Submarine Pipeline Systems; DNV-OS-F101; DNV Offshore Standard: Høvik, Norway, 2015. [Google Scholar]
- DNV Standard. Composite Components; DNVGL-OS-C501; DNV Offshore Standard: Høvik, Norway, 2013. [Google Scholar]
- DNV Standard. Thermoplastic Composite Pipes; DNVGL-ST-F119; DNV Standard: Høvik, Norway, 2018. [Google Scholar]
- Madsen, H.O.; Krenk, S.; Lind, N.C. Methods of Structural Safety; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Metallic Materials and Elements for Aerospace Vehicle Structures. In Military Standardization Handbook; MIL-HDBK-5B; Department of Defense: Washington, DC, USA, 1971.
- Jones, D.R.; Ashby, M.F. Engineering Materials 1: An Introduction to Properties, Applications and Design; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Callister, W.D., Jr.; Rethwisch, D.G. Fundamentals of Materials Science and Engineering: An Integrated Approach; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tsai, S.W. Theory of Composites Design; Think Composites: Dayton, OH, USA, 1992. [Google Scholar]
- Carlsson, L.A.; Gillespie, J.W.; Zweben, C.H. Delaware Composites Design Encyclopedia: Mechanical Behavior and Properties of Composite Materials; CRC: Boca Raton, FL, USA, 1989. [Google Scholar]
- Mayer, R.M. (Ed.) Design of Composite Structures against Fatigue: Applications to Wind Turbine Blades; Mechanical Engineering Publications: Bury St Edmunds, UK, 1996. [Google Scholar]
- Nijssen, R.P.L. Fatigue Life Prediction and Strength Degradation of Wind Turbine Rotor Blade Composites; Sandia Report, SAND2006-7810P; Sandia National Laboratories: Albuquerque, NM, USA, 2007.
- Bond, I.P. Fatigue life prediction of GRP subject to variable amplitude loading. Compos. Part A 1999, 30, 961–970. [Google Scholar] [CrossRef]
- Westphal, T.; Nijssen, R.P.L. Fatigue life prediction of rotor blade composites: Validation of constant amplitude formulations with variable amplitude experiments. J. Phys. Conf. Ser. 2014, 555, 012107. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, H.; Sankararaman, S.; Escobet, T.; Puig, V.; Frost, S.; Goebel, K. Analysis of two modeling approaches for fatigue estimation and remaining useful life predictions of wind turbine blades. In Proceedings of the Third European PHM, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Passipoularidis, V.A.; Brønsted, P. Fatigue Evaluation Algorithms: Review; Risø-R-Report-1740 (EN); NLSE: Risø, Denmark, 2009. [Google Scholar]
- API; Recommended Practice. Design of Risers for Floating Production Systems (FPS) and Tension-Leg Platforms (TLPs); American Petroleum Institute: Washington, DC, USA, 1998. [Google Scholar]
- Lotsberg, I. Fatigue Design of Marine Structures; Cambridge University Press: New York, NY, USA, 2016. [Google Scholar]
- Post, N.L. Reliability Based Design Methodology Incorporating Residual Strength Prediction of Structural Fiber Reinforced Polymer Composites under Stochastic Variable Amplitude Fatigue Loading. Ph.D. Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2008. [Google Scholar]
- Castro, O.; Branner, K.; Dimitrov, N. Assessment and propagation of mechanical property uncertainties in fatigue life predictions of composite laminates. J. Compos. Mater. 2018, 52, 3381–3398. [Google Scholar] [CrossRef]
- Nishijima, S. Statistical Fatigue Properties of Some Heat-Treated Steeis for Macliine Structural Use. In Statistical Analysis of Fatigue Data; ASTM STP 744; Little, R.E., Ekvall, J.C., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1981; pp. 75–88. [Google Scholar]
- Sudret, B.; Hornet, P.; Stephan, J.M.; Guede, Z.; Lemaire, M. Probabilistic assessment of fatigue life including statistical uncertainties in the S-N curve. In Proceedings of the 17th International Conference on Paper # M03-4 Structural Mechanics in Reactor Technology (SMiRT 17), Prague, Czech Republic, 17–22 August 2003. [Google Scholar]
- Schneider, C.R.A.; Maddox, S.J. Best Practice Guide on Statistical Analysis of Fatigue Data; TWI: Cambridge, UK, February 2003. [Google Scholar]
- Owen, D.B. Tables of Factors of One-Sided Tolerance Limits for a Normal Distribution; SCR-13; Sandia Corporation Monograph: Washington, DC, USA, 1958. [Google Scholar]
- Wirsching, P.H. Statistical Summaries of Fatigue Data for Design Purposes; NASA Contractor Report 3697; NASA: Washington, DC, USA, 1983.
- Wei, Z.; Dogan, B.; Luo, L.; Lin, B.; Konson, D. Design Curve Construction Based on Tolerance Limit Concept. In Proceedings of the ASME 2012 Pressure Vessels & Piping Conference (PVP 2012), Toronto, ON, Canada, 15–19 July 2012. [Google Scholar]
- Ronold, K.O.; Echtermeyer, A.T. Estimation of fatigue curves for design of composite laminates. J. Compos. Part A 1996, 27A, 485–491. [Google Scholar] [CrossRef]
- Echtermeyer, A.T. Integrating Durability in Marine Composite Certification. In Durability of Composites in a Marine Environment; Solid Mechanics and Its Applications 208; Springer Science + Business Media: Dordrecht, The Netherlands, 2014; pp. 179–194. ISBN 978-94-007-7416-2. [Google Scholar]
- DIN. Statistische Auswertung von Daten, Bestimmung Eines Statistischen Anteilsbereichs (Statistical Interpretation of Data; Determination of a Statistical Tolerance Interval); DIN55303, Part 5; Deutsches Institut für Normung E.V. (DIN): Berlin, Germany, 1987. (In Germany) [Google Scholar]
- ASTM. Standard Practice for Obtaining Hydrostatic or Pressure Design Basis for “Fiberglass (Glass-Fiber-Reinforced Thermosetting-Resin) Pipe and Fittings; ASTM Standard D2992-12; American Society for Testing Materials: Philadelphia, PA, USA, 2012. [Google Scholar] [CrossRef]
- Mandell, J.F.; Samborsky, D.D.; Wahl, N.K.; Sutherland, H.J. Testing and Analysis of Low Cost Composite Materials Under Spectrum Loading and High Cycle Fatigue Condition. Conference Paper, ICCM14, Paper # 1811; SME/ASC. 2003. Available online: https://www.semanticscholar.org/paper/Testing-and-Analysis-of-Low-Cost-Composite-Under-Mandell-Samborsky/8cef98d9ccec02d1e54489c597c0eb536de26bdb (accessed on 12 November 2021).
- Echtermeyer, A.T.; Engh, B.; Buene, L. Influence of matrix and fabric. In Design of Composite Structures Against Fatigue: Applications to Wind Turbine Blades; Mayer, R.M., Ed.; Mechanical Engineering Publications Ltd.: Suffolk, UK, 1996; pp. 33–49. [Google Scholar]
- Echtermeyer, A.T.; Kensche, C.; Bach, P.; Poppen, M.; Lilholt, L.; Andersen, S.I.; Brønsted, P. Method to Predict Fatigue Lifetimes of GRP Wind Turbine Blades and Comparison with Experiments. In Proceedings of the 1996 European Union Wind Energy Conference and Exhibition, Gothenburg, Sweden, 20–24 May 1996; H.P. Stephens & Associates: Bedford, UK, 1996; pp. 907–913. [Google Scholar]
- Ronold, K.O.; Lotsberg, I. On the estimation of characteristic S–N curves with confidence. J. Mar. Struct. 2012, 27, 29–44. [Google Scholar] [CrossRef]
- Resnikoff, G.J.; Lieberman, G.J. Tables of the Noncentral t-Distribution; Stanford University Press: Stanford, CA, USA, 1957. [Google Scholar]
- Pearson, E.S.; Hartley, H.O. Biometrika Tables for Statisticians, 3rd ed.; Biometrika Trust: London, UK, 1976. [Google Scholar]
- Hald, A. Statistical Theory with Engineering Applications; John Wiley: Hoboken, NJ, USA, 1952. [Google Scholar]
- Guttman, I. Statistical Tolerance Regions: Classical and Bayesian; Griffin: London, UK, 1970. [Google Scholar]
- Zacks, S. The Theory of Statistical Inference; John Wiley and Sons, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Little, R.E. Review of statistical analysis of fatigue life data using one-sided lower statistical tolerance limits. In Statistical Analysis of Fatigue Data; ASTM STP 744; Little, R.E., Ekvall, J.C., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1981; pp. 3–23. [Google Scholar]
- Beaumont, P.W.R.; Schultz, J.M. Statistical Aspects of Fracture. In Failure Analysis of Composite Materials; Chapter 4.6; Beaumont, P.W.R., Schultz, J.M., Friedrich, K., Eds.; Technomic Publishing Co., Inc.: Lancaster, PA, USA, 1990; Volume 4. [Google Scholar]
- Ang, A.H.-S.; Tang, W.H. Probability Concepts in Engineering Planning and Design, Vol. I, Basic Principles; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Pascual, F.G. Planning Fatigue Experiments and Analyzing Fatigue Data with the Random Fatigue-Limit Model and Modified Sudden Death Tests. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1997. [Google Scholar]
- Tvedt, L. Proban—Probabilistic Analysis. Struct. Saf. 2006, 28, 150–163. [Google Scholar] [CrossRef]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods; Iowa State University Press: Ames, IA, USA, 1989. [Google Scholar]
- Veritas, D.N. Statistical Representation of Soil Data; DNV-RP-C207; Recommended Practice: Høvik, Norway, 2012. [Google Scholar]
- Echtermeyer, A.T.; Ekeberg, T.S.; Sund, O.E. Long-Term Testing of Composite Through-Thickness Properties; Research Report 131; Health & Safety Executive, HSE: Norwich, UK, 2004. [Google Scholar]
- American Society for Testing and Materials. Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data; ASTM E739–91; American Society for Testing and Materials: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Little, R.E.; Jebe, E.H. Statistical Design of Fatigue Experiments; Applied Science Publishers Ltd.: London, UK, 1975. [Google Scholar]
- Bowden, D.C. Query 26: Tolerance Interval in Regression. Technometrics 1968, 10, 207–209. [Google Scholar] [CrossRef]
| Symbol | |
|---|---|
| α | probability complement of confidence level |
| 1 − α | statistical confidence level |
| Γ | gamma function |
| ε | strain |
| Φ | standard Gaussian cumulative distribution function |
| σ | standard deviation |
| Δx | increment of x |
| Lx | length of finite interval of x = logS |
| hn | function of n |
| m | material property of fiber strength |
| n | number of fatigue tests |
| W | chi-square distributed variable with specific number of degrees of freedom |
| C | non-central t-distributed variable |
| S | stress range |
| s | estimate of standard deviation σ |
| S | stochastic standard deviation |
| N | number of stress cycles to failure at stress range S |
| mean fibre strength | |
| σf | fibre bundle strength |
| # Test Data | tn−2(1 − α) | ||
|---|---|---|---|
| n | 1 − α = 0.75 | 1 − α = 0.90 | 1 − α = 0.95 |
| 4 | 0.816 | 1.886 | 2.920 |
| 8 | 0.718 | 1.440 | 1.943 |
| 10 | 0.706 | 1.397 | 1.860 |
| 12 | 0.700 | 1.372 | 1.812 |
| 15 | 0.694 | 1.350 | 1.771 |
| 20 | 0.688 | 1.333 | 1.734 |
| 30 | 0.683 | 1.313 | 1.701 |
| 50 | 0.679 | 1.300 | 1.676 |
| 100 | 0.677 | 1.290 | 1.660 |
| ∞ | 0.674 | 1.282 | 1.645 |
| Survival Probability (Tolerance) γ | γ Quantile of Standard Normal Variate Φ−1 (γ) |
|---|---|
| 0.50 | 0.000 |
| 0.75 | 0.674 |
| 0.90 | 1.282 |
| 0.95 | 1.645 |
| 0.97725 | 2.000 |
| 0.99 | 2.326 |
| No. of Observations, n | Auxiliary Proportion k = 0.90 | Auxiliary Proportion k = 0.95 | Auxiliary Proportion k = 0.99 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 − α = 0.75 | 1 − α = 0.90 | 1 − α = 0.95 | 1 − α = 0.75 | 1 − α = 0.90 | 1 − α = 0.95 | 1 − α = 0.75 | 1 − α = 0.90 | 1 − α = 0.95 | |
| 4 | 2.501 | 4.258 | 6.158 | 3.152 | 5.312 | 7.657 | 4.396 | 7.340 | 10.552 |
| 8 | 1.791 | 2.333 | 2.755 | 2.251 | 2.904 | 3.404 | 3.126 | 3.972 | 4.641 |
| 10 | 1.702 | 2.133 | 2.454 | 2.147 | 2.660 | 3.038 | 2.977 | 3.641 | 4.143 |
| 12 | 1.646 | 2.012 | 2.275 | 2.078 | 2.511 | 2.825 | 2.885 | 3.444 | 3.852 |
| 15 | 1.591 | 1.895 | 2.108 | 2.012 | 2.366 | 2.621 | 2.796 | 3.257 | 3.585 |
| 20 | 1.536 | 1.781 | 1.949 | 1.947 | 2.237 | 2.429 | 2.710 | 3.078 | 3.331 |
| 30 | 1.479 | 1.664 | 1.788 | 1.877 | 2.094 | 2.233 | 2.619 | 2.895 | 3.079 |
| 50 | 1.428 | 1.563 | 1.651 | 1.817 | 1.976 | 2.075 | 2.540 | 2.740 | 2.870 |
| 100 | 1.380 | 1.471 | 1.528 | 1.758 | 1.862 | 1.929 | 2.470 | 2.601 | 2.683 |
| ∞ | 1.282 | 1.282 | 1.282 | 1.645 | 1.645 | 1.645 | 2.326 | 2.326 | 2.326 |
| Stress Amplitude S (MPa) | Number of Cycles to Failure N | logS | logN |
|---|---|---|---|
| 2.60 | 1,591,872 | 0.415 | 6.202 |
| 3.20 | 1,140,319 | 0.505 | 6.057 |
| 3.20 | 2,680,000 | 0.505 | 6.428 |
| 3.85 | 19,550 | 0.585 | 4.291 |
| 3.85 | 802,398 | 0.585 | 5.904 |
| 3.85 | 204,100 | 0.585 | 5.310 |
| 5.80 | 15,639 | 0.763 | 4.194 |
| 6.45 | 4595 | 0.810 | 3.662 |
| 6.45 | 2137 | 0.810 | 3.330 |
| 6.45 | 2330 | 0.810 | 3.367 |
| 7.10 | 2034 | 0.851 | 3.308 |
| Stress Amplitude S (MPa) | logS Covered by Tests | By Theory (Simulation by Equation (13)) | By Figure 2 | |
|---|---|---|---|---|
| 2.60 | 0.415 | 3.79 | 0.455 | 3.75 |
| 3.20 | 0.505 | 3.59 | 0.267 | 3.57 |
| 3.85 | 0.585 | 3.48 | 0.099 | 3.46 |
| 5.80 | 0.763 | 3.52 | 0.272 | 3.57 |
| 6.45 | 0.810 | 3.59 | 0.368 | 3.66 |
| 7.10 | 0.851 | 3.67 | 0.455 | 3.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ronold, K.O.; Echtermeyer, A.T. Using Tolerance Bounds for Estimation of Characteristic Fatigue Curves for Composites with Confidence. Safety 2022, 8, 1. https://doi.org/10.3390/safety8010001
Ronold KO, Echtermeyer AT. Using Tolerance Bounds for Estimation of Characteristic Fatigue Curves for Composites with Confidence. Safety. 2022; 8(1):1. https://doi.org/10.3390/safety8010001
Chicago/Turabian StyleRonold, Knut O., and Andreas T. Echtermeyer. 2022. "Using Tolerance Bounds for Estimation of Characteristic Fatigue Curves for Composites with Confidence" Safety 8, no. 1: 1. https://doi.org/10.3390/safety8010001
APA StyleRonold, K. O., & Echtermeyer, A. T. (2022). Using Tolerance Bounds for Estimation of Characteristic Fatigue Curves for Composites with Confidence. Safety, 8(1), 1. https://doi.org/10.3390/safety8010001






