Mathematical Modeling of Heat Transfer in an Element of Combustible Plant Material When Exposed to Radiation from a Forest Fire
Abstract
1. Introduction
2. Background
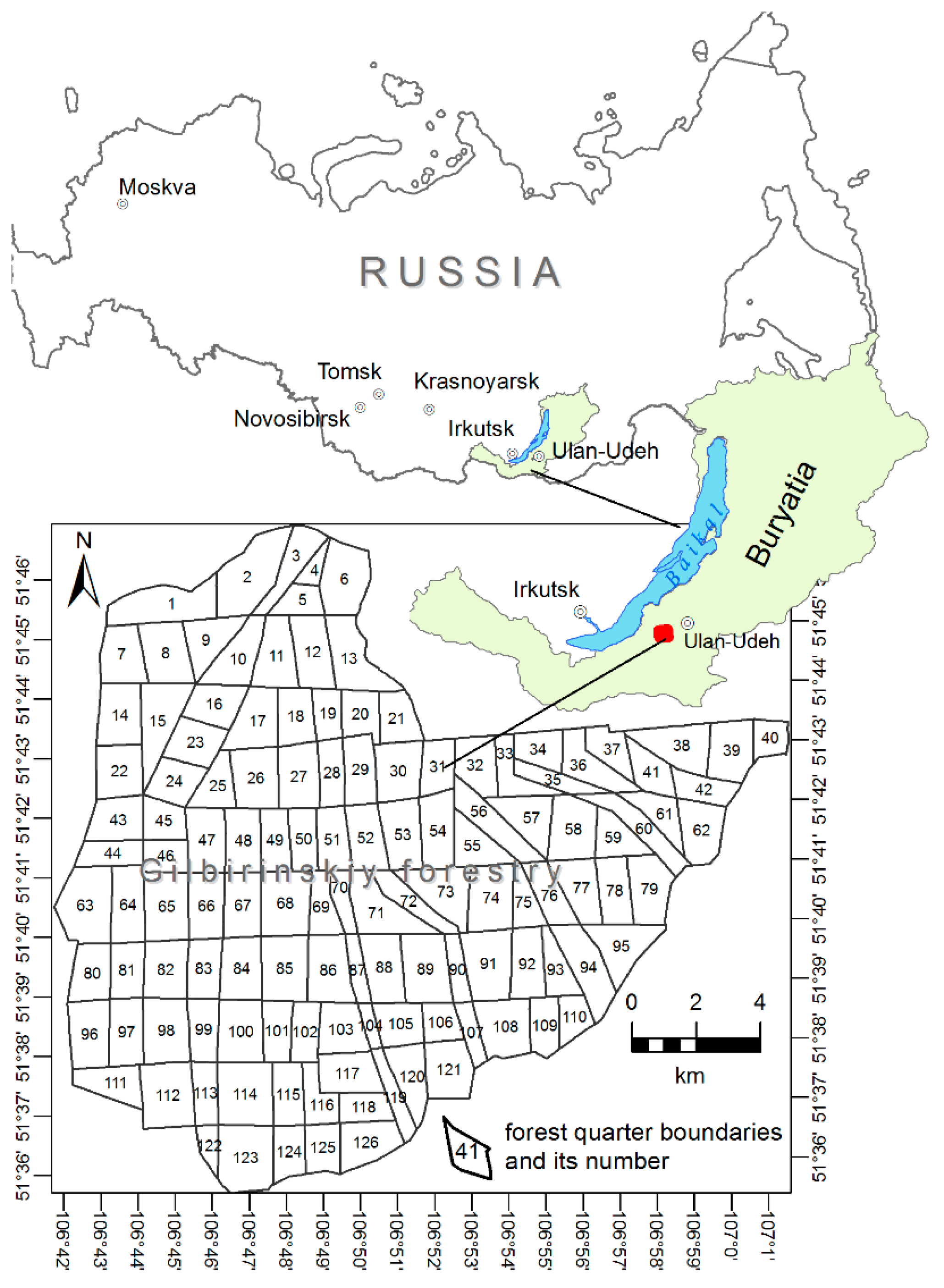
3. Study Area and Object
4. Physical Model
- (1)
- The spring season of the fire season is considered and the grass is dried.
- (2)
- The catastrophic scenario of forest fire danger is considered when moisture in the forest fuel material is absent.
- (3)
- The evaporation of moisture is neglected.
- (4)
- The thermophysical characteristics do not depend on temperature.
- (5)
- The pyrolysis of dry organic matter is considered as a one-step process with known thermokinetic constants.
- (6)
- The two-dimensional formulation of the problem is considered.
- (7)
- The process of heat transfer in the element of combustible plant material occurs due to thermal conductivity.
- (8)
- The main damaging factor of a forest fire is radiant heat flux, and other types of heat transfer are neglected.
- (9)
- The layered and structurally inhomogeneous composition of the combustible plant material is considered.
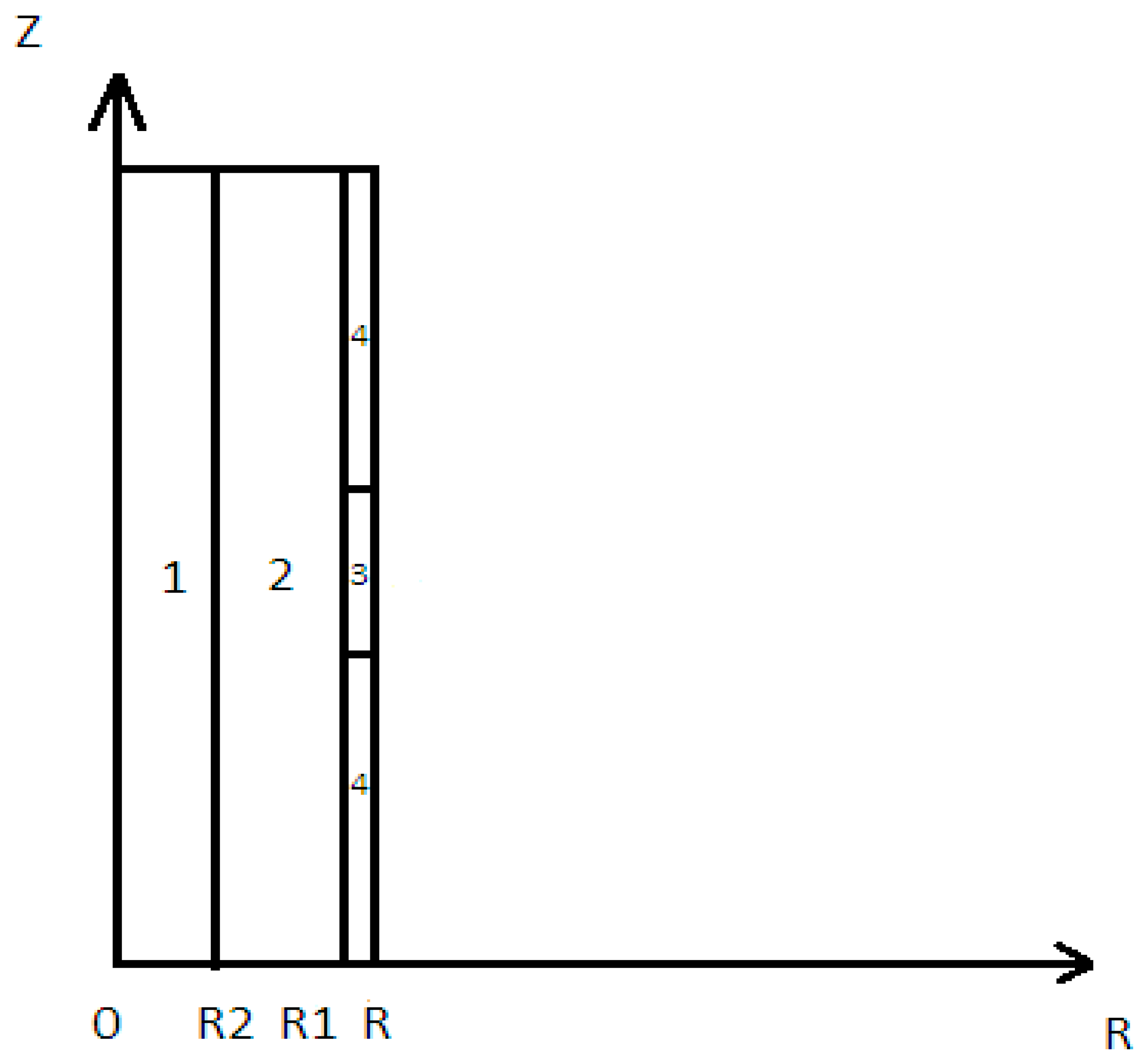
5. Mathematical Models
5.1. Simplified Mathematical Model of Heat Transfer in the Stem
5.2. Mathematical Model of Heat Transfer with the Joint
6. Results and Discussion
- short exposure time (up to 3 s at q < 3 kW/m2),
- a large distance from the fire line (from 3 to 10 m depending on fire intensity),
- low fire intensity (surface fires with a height of 0.5 m).
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Scenario | Joint | d, mm | tff, s | q, kW/m2 | c, J/(kg K) | ρ, kg/m3 | λ, W/(m K) |
|---|---|---|---|---|---|---|---|
| 1 | No | 2 | 0.5 | 0.5 | 1400 | 500 | 0.16 |
| 2 | No | 2 | 2 | 0.5 | 1400 | 500 | 0.16 |
| 3 | No | 2 | 3 | 0.5 | 1400 | 500 | 0.16 |
| 4 | No | 2 | 6 | 0.5 | 1400 | 500 | 0.16 |
| 5 | No | 2 | 0.5 | 3 | 1400 | 500 | 0.16 |
| 6 | No | 2 | 2 | 3 | 1400 | 500 | 0.16 |
| 7 | No | 2 | 3 | 3 | 1400 | 500 | 0.16 |
| 8 | No | 2 | 6 | 3 | 1400 | 500 | 0.16 |
| 9 | No | 2 | 0.5 | 15 | 1400 | 500 | 0.16 |
| 10 | No | 2 | 2 | 15 | 1400 | 500 | 0.16 |
| 11 | No | 2 | 3 | 15 | 1400 | 500 | 0.16 |
| 12 | No | 2 | 6 | 15 | 1400 | 500 | 0.16 |
| 13 | No | 2 | 0.5 | 30 | 1400 | 500 | 0.16 |
| 14 | No | 2 | 2 | 30 | 1400 | 500 | 0.16 |
| 15 | No | 2 | 3 | 30 | 1400 | 500 | 0.16 |
| 16 | No | 2 | 6 | 30 | 1400 | 500 | 0.16 |
| Scenario | Joint | d, mm | tff, s | q, kW/m2 | c, J/(kg K) | ρ, kg/m3 | λ, W/(m K) |
|---|---|---|---|---|---|---|---|
| 17 | No | 2.5 | 0.5 | 0.5 | 1400 | 500 | 0.16 |
| 18 | No | 2.5 | 2 | 0.5 | 1400 | 500 | 0.16 |
| 19 | No | 2.5 | 3 | 0.5 | 1400 | 500 | 0.16 |
| 20 | No | 2.5 | 6 | 0.5 | 1400 | 500 | 0.16 |
| 21 | No | 2.5 | 0.5 | 3 | 1400 | 500 | 0.16 |
| 22 | No | 2.5 | 2 | 3 | 1400 | 500 | 0.16 |
| 23 | No | 2.5 | 3 | 3 | 1400 | 500 | 0.16 |
| 24 | No | 2.5 | 6 | 3 | 1400 | 500 | 0.16 |
| 25 | No | 2.5 | 0.5 | 15 | 1400 | 500 | 0.16 |
| 26 | No | 2.5 | 2 | 15 | 1400 | 500 | 0.16 |
| 27 | No | 2.5 | 3 | 15 | 1400 | 500 | 0.16 |
| 28 | No | 2.5 | 6 | 15 | 1400 | 500 | 0.16 |
| 29 | No | 2.5 | 0.5 | 30 | 1400 | 500 | 0.16 |
| 30 | No | 2.5 | 2 | 30 | 1400 | 500 | 0.16 |
| 31 | No | 2.5 | 3 | 30 | 1400 | 500 | 0.16 |
| 32 | No | 2.5 | 6 | 30 | 1400 | 500 | 0.16 |
| Scenario | Joint | d, mm | tff, s | q, kW/m2 | c, J/(kg K) | ρ, kg/m3 | λ, W/(m K) |
|---|---|---|---|---|---|---|---|
| 33 | No | 3 | 0.5 | 0.5 | 1400 | 500 | 0.16 |
| 34 | No | 3 | 2 | 0.5 | 1400 | 500 | 0.16 |
| 35 | No | 3 | 3 | 0.5 | 1400 | 500 | 0.16 |
| 36 | No | 3 | 6 | 0.5 | 1400 | 500 | 0.16 |
| 37 | No | 3 | 0.5 | 3 | 1400 | 500 | 0.16 |
| 38 | No | 3 | 2 | 3 | 1400 | 500 | 0.16 |
| 39 | No | 3 | 3 | 3 | 1400 | 500 | 0.16 |
| 40 | No | 3 | 6 | 3 | 1400 | 500 | 0.16 |
| 41 | No | 3 | 0.5 | 15 | 1400 | 500 | 0.16 |
| 42 | No | 3 | 2 | 15 | 1400 | 500 | 0.16 |
| 43 | No | 3 | 3 | 15 | 1400 | 500 | 0.16 |
| 44 | No | 3 | 6 | 15 | 1400 | 500 | 0.16 |
| 45 | No | 3 | 0.5 | 30 | 1400 | 500 | 0.16 |
| 46 | No | 3 | 2 | 30 | 1400 | 500 | 0.16 |
| 47 | No | 3 | 3 | 30 | 1400 | 500 | 0.16 |
| 48 | No | 3 | 6 | 30 | 1400 | 500 | 0.16 |
| Scenario | Joint | d, mm | tff, s | q, kW/m2 | c, J/(kg K) | ρ, kg/m3 | λ, W/(m K) |
|---|---|---|---|---|---|---|---|
| 1 | Yes | 2 | 0.5 | 0.5 | 1400 | 500 | 0.16 |
| 2 | Yes | 2 | 2 | 0.5 | 1400 | 500 | 0.16 |
| 3 | Yes | 2 | 3 | 0.5 | 1400 | 500 | 0.16 |
| 4 | Yes | 2 | 6 | 0.5 | 1400 | 500 | 0.16 |
| 5 | Yes | 2 | 0.5 | 3 | 1400 | 500 | 0.16 |
| 6 | Yes | 2 | 2 | 3 | 1400 | 500 | 0.16 |
| 7 | Yes | 2 | 3 | 3 | 1400 | 500 | 0.16 |
| 8 | Yes | 2 | 6 | 3 | 1400 | 500 | 0.16 |
| 9 | Yes | 2 | 0.5 | 15 | 1400 | 500 | 0.16 |
| 10 | Yes | 2 | 2 | 15 | 1400 | 500 | 0.16 |
| 11 | Yes | 2 | 3 | 15 | 1400 | 500 | 0.16 |
| 12 | Yes | 2 | 6 | 15 | 1400 | 500 | 0.16 |
| 13 | Yes | 2 | 0.5 | 30 | 1400 | 500 | 0.16 |
| 14 | Yes | 2 | 2 | 30 | 1400 | 500 | 0.16 |
| 15 | Yes | 2 | 3 | 30 | 1400 | 500 | 0.16 |
| 16 | Yes | 2 | 6 | 30 | 1400 | 500 | 0.16 |
| Scenario | Joint | d, mm | tff, s | q, kW/m2 | c, J/(kg K) | ρ, kg/m3 | λ, W/(m K) |
|---|---|---|---|---|---|---|---|
| 17 | Yes | 2.5 | 0.5 | 0.5 | 1400 | 500 | 0.16 |
| 18 | Yes | 2.5 | 2 | 0.5 | 1400 | 500 | 0.16 |
| 19 | Yes | 2.5 | 3 | 0.5 | 1400 | 500 | 0.16 |
| 20 | Yes | 2.5 | 6 | 0.5 | 1400 | 500 | 0.16 |
| 21 | Yes | 2.5 | 0.5 | 3 | 1400 | 500 | 0.16 |
| 22 | Yes | 2.5 | 2 | 3 | 1400 | 500 | 0.16 |
| 23 | Yes | 2.5 | 3 | 3 | 1400 | 500 | 0.16 |
| 24 | Yes | 2.5 | 6 | 3 | 1400 | 500 | 0.16 |
| 25 | Yes | 2.5 | 0.5 | 15 | 1400 | 500 | 0.16 |
| 26 | Yes | 2.5 | 2 | 15 | 1400 | 500 | 0.16 |
| 27 | Yes | 2.5 | 3 | 15 | 1400 | 500 | 0.16 |
| 28 | Yes | 2.5 | 6 | 15 | 1400 | 500 | 0.16 |
| 29 | Yes | 2.5 | 0.5 | 30 | 1400 | 500 | 0.16 |
| 30 | Yes | 2.5 | 2 | 30 | 1400 | 500 | 0.16 |
| 31 | Yes | 2.5 | 3 | 30 | 1400 | 500 | 0.16 |
| 32 | Yes | 2.5 | 6 | 30 | 1400 | 500 | 0.16 |
| Scenario | Joint | d, mm | tff, s | q, kW/m2 | c, J/(kg K) | ρ, kg/m3 | λ, W/(m K) |
|---|---|---|---|---|---|---|---|
| 33 | Yes | 3 | 0.5 | 0.5 | 1400 | 500 | 0.16 |
| 34 | Yes | 3 | 2 | 0.5 | 1400 | 500 | 0.16 |
| 35 | Yes | 3 | 3 | 0.5 | 1400 | 500 | 0.16 |
| 36 | Yes | 3 | 6 | 0.5 | 1400 | 500 | 0.16 |
| 37 | Yes | 3 | 0.5 | 3 | 1400 | 500 | 0.16 |
| 38 | Yes | 3 | 2 | 3 | 1400 | 500 | 0.16 |
| 39 | Yes | 3 | 3 | 3 | 1400 | 500 | 0.16 |
| 40 | Yes | 3 | 6 | 3 | 1400 | 500 | 0.16 |
| 41 | Yes | 3 | 0.5 | 15 | 1400 | 500 | 0.16 |
| 42 | Yes | 3 | 2 | 15 | 1400 | 500 | 0.16 |
| 43 | Yes | 3 | 3 | 15 | 1400 | 500 | 0.16 |
| 44 | Yes | 3 | 6 | 15 | 1400 | 500 | 0.16 |
| 45 | Yes | 3 | 0.5 | 30 | 1400 | 500 | 0.16 |
| 46 | Yes | 3 | 2 | 30 | 1400 | 500 | 0.16 |
| 47 | Yes | 3 | 3 | 30 | 1400 | 500 | 0.16 |
| 48 | Yes | 3 | 6 | 30 | 1400 | 500 | 0.16 |
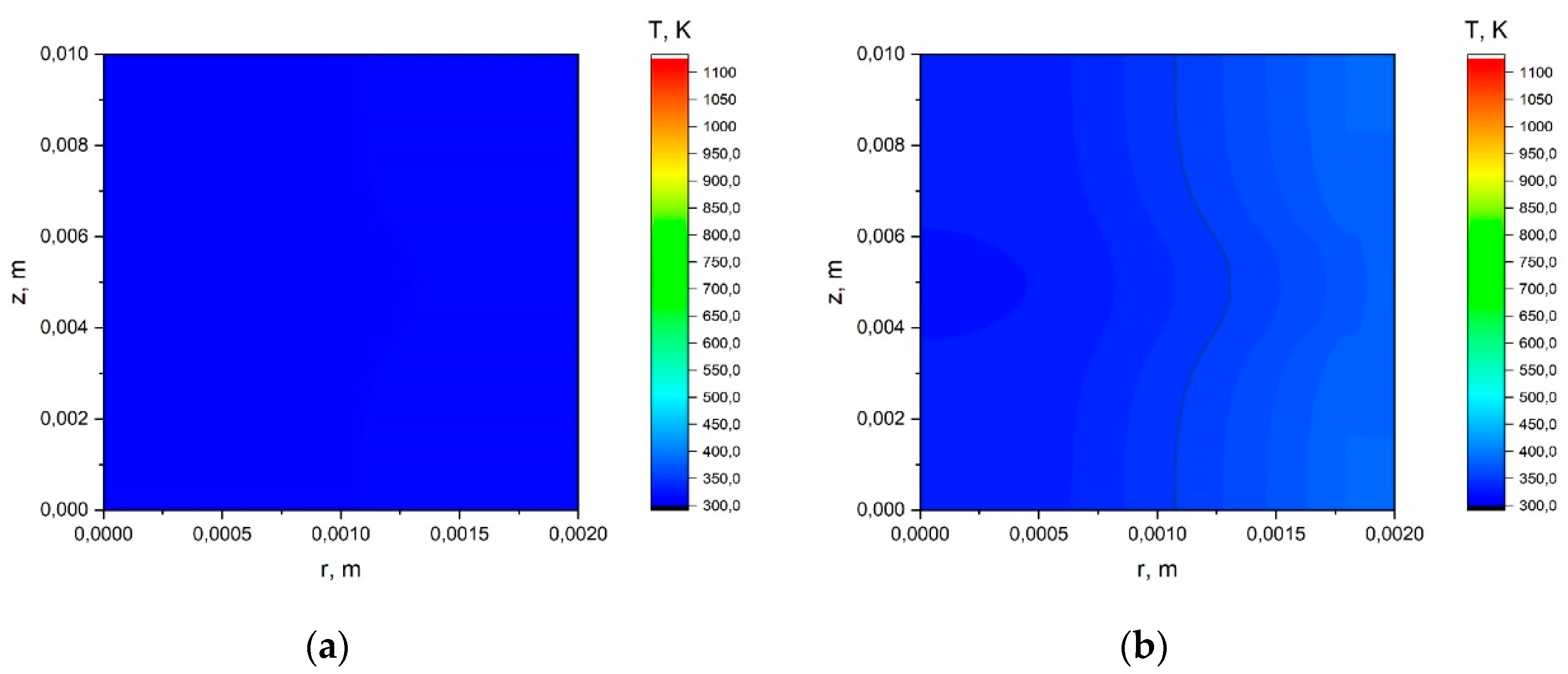
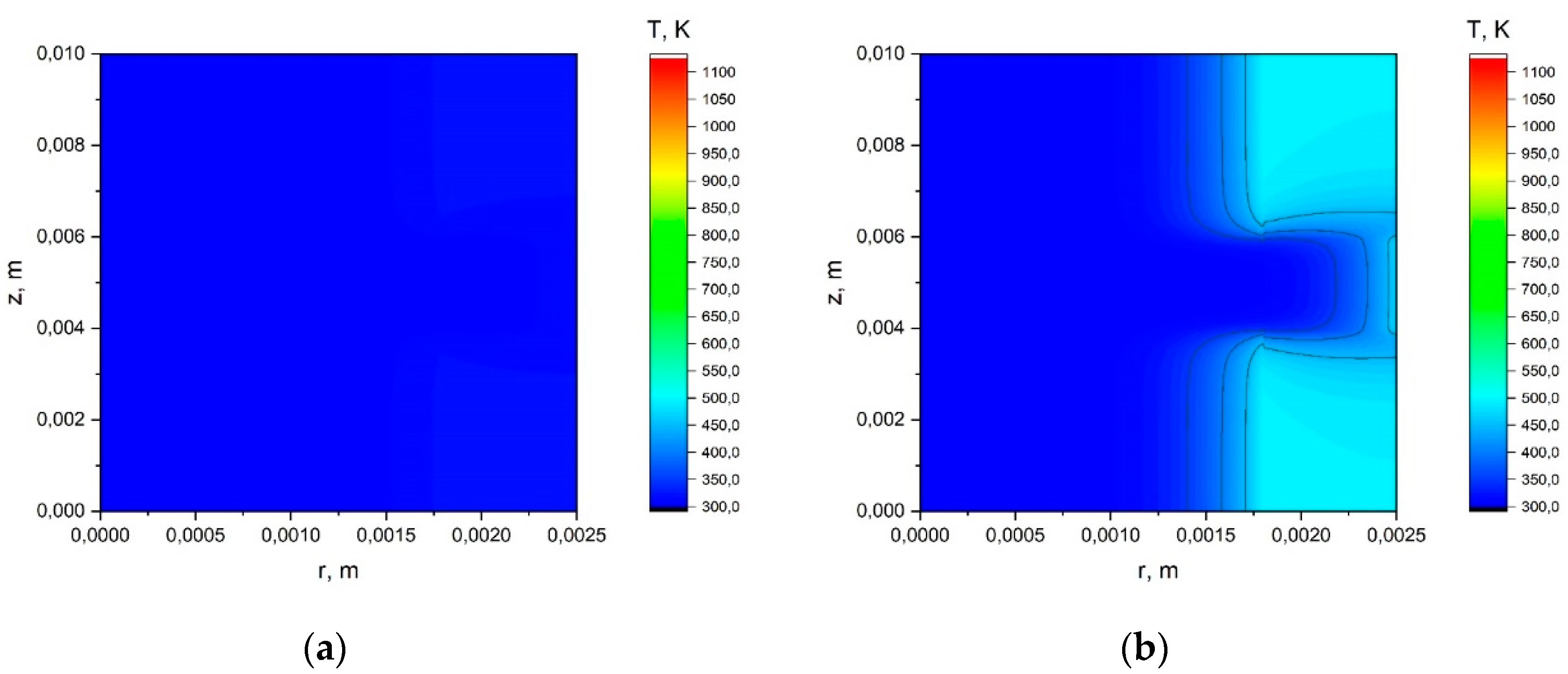
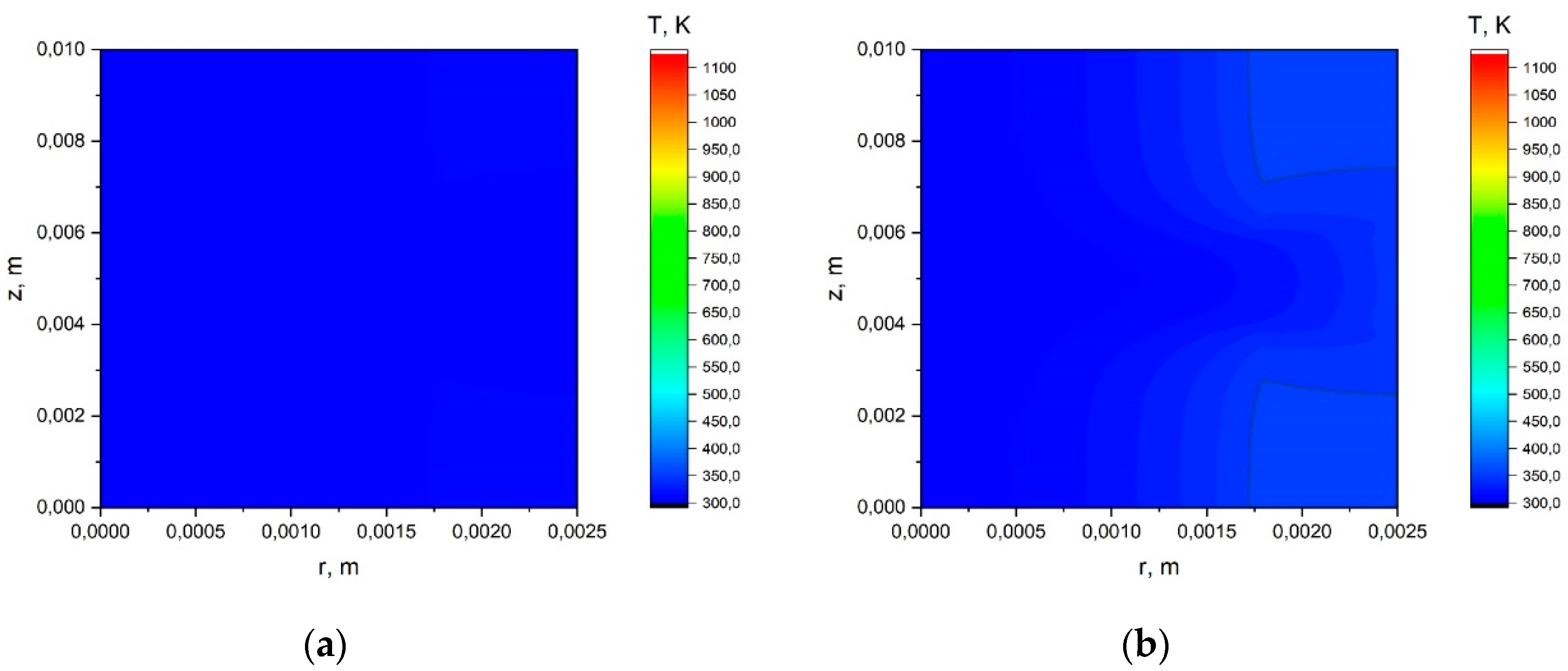
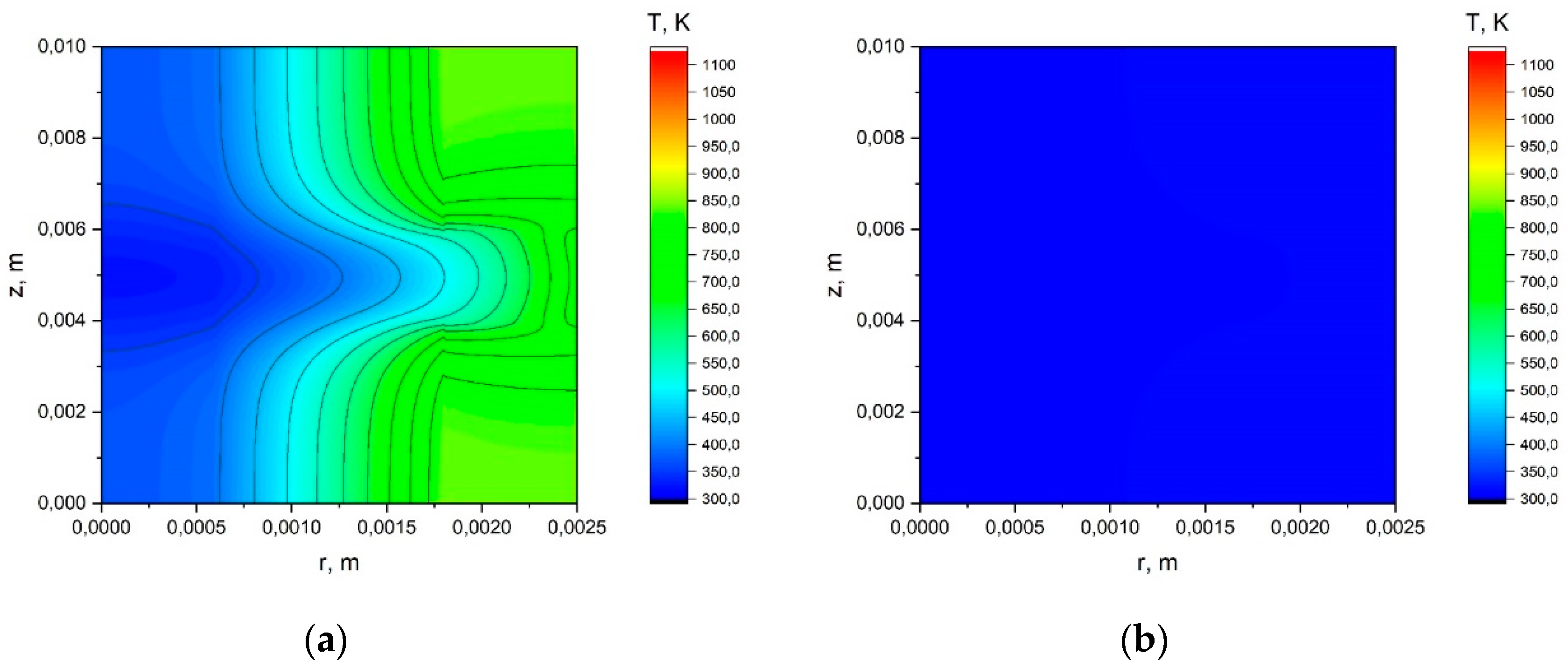
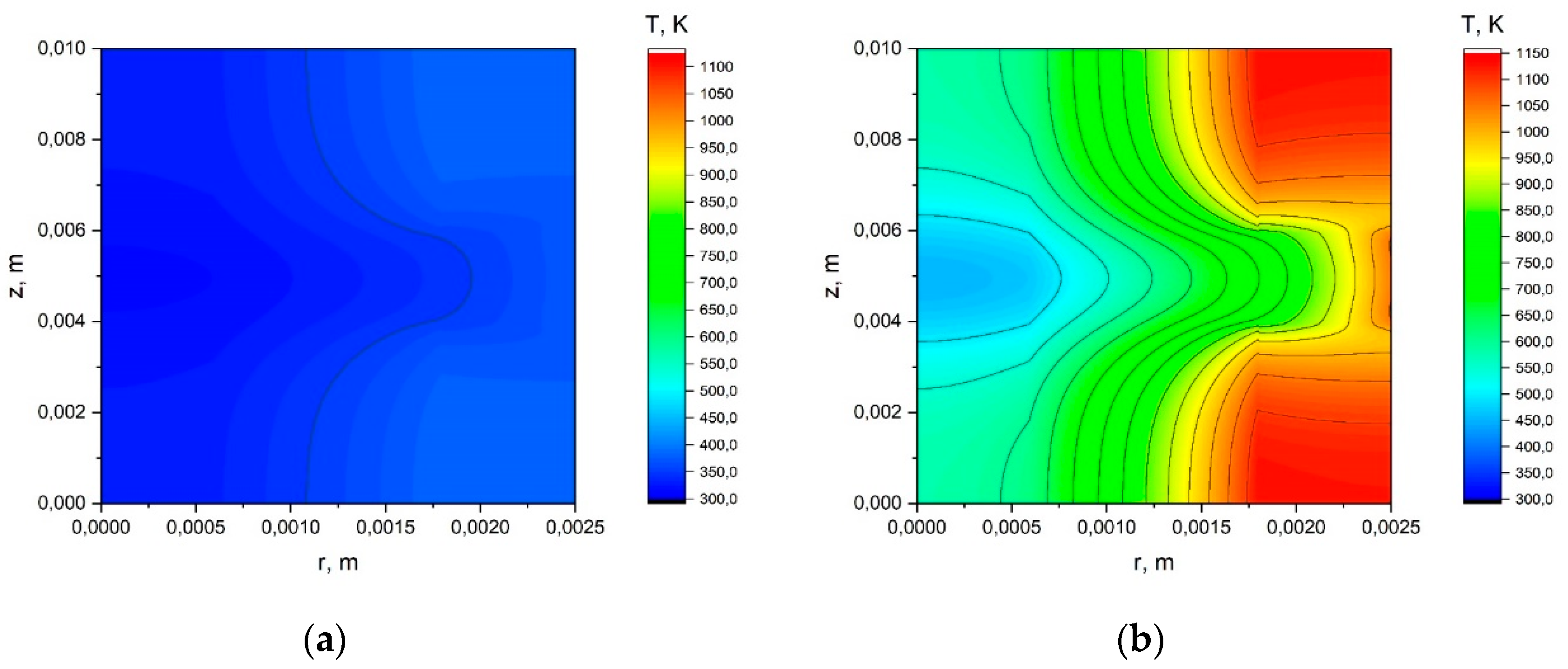
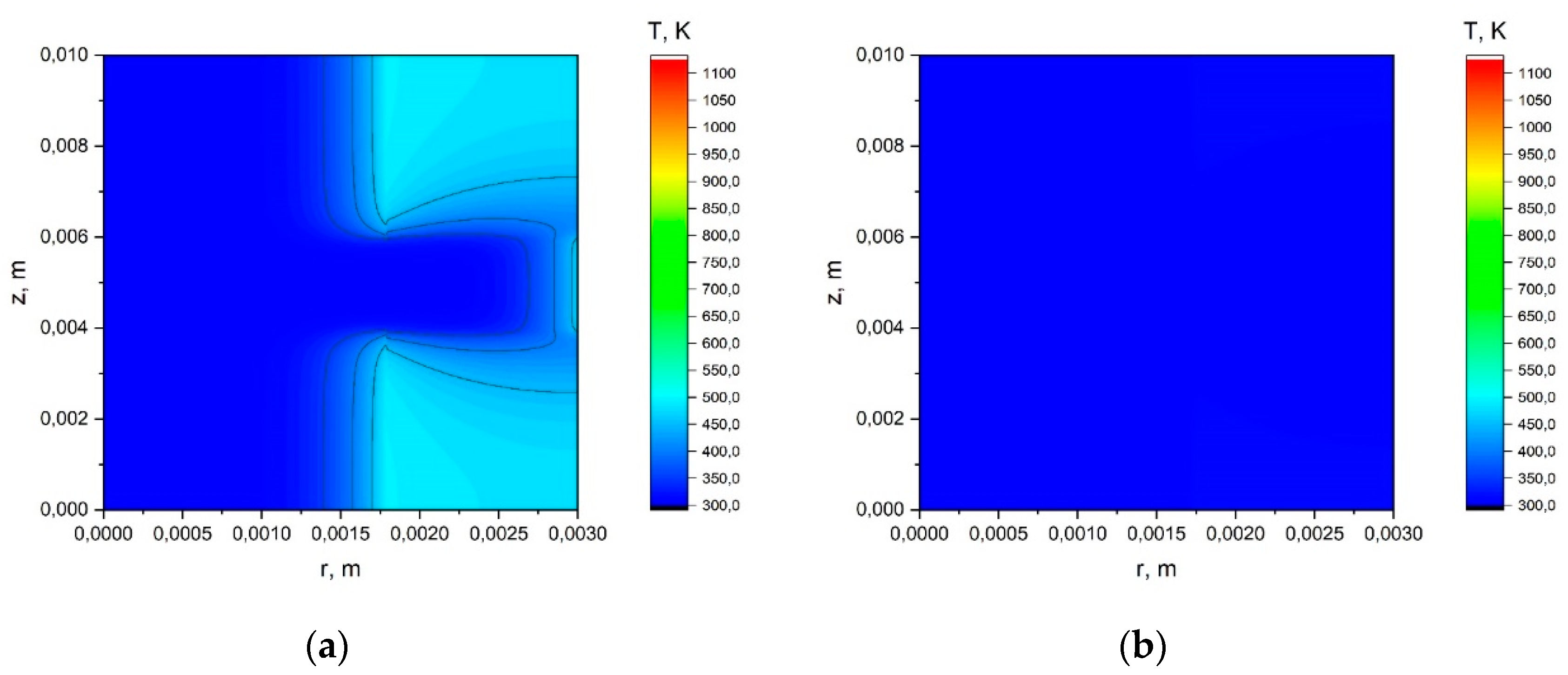
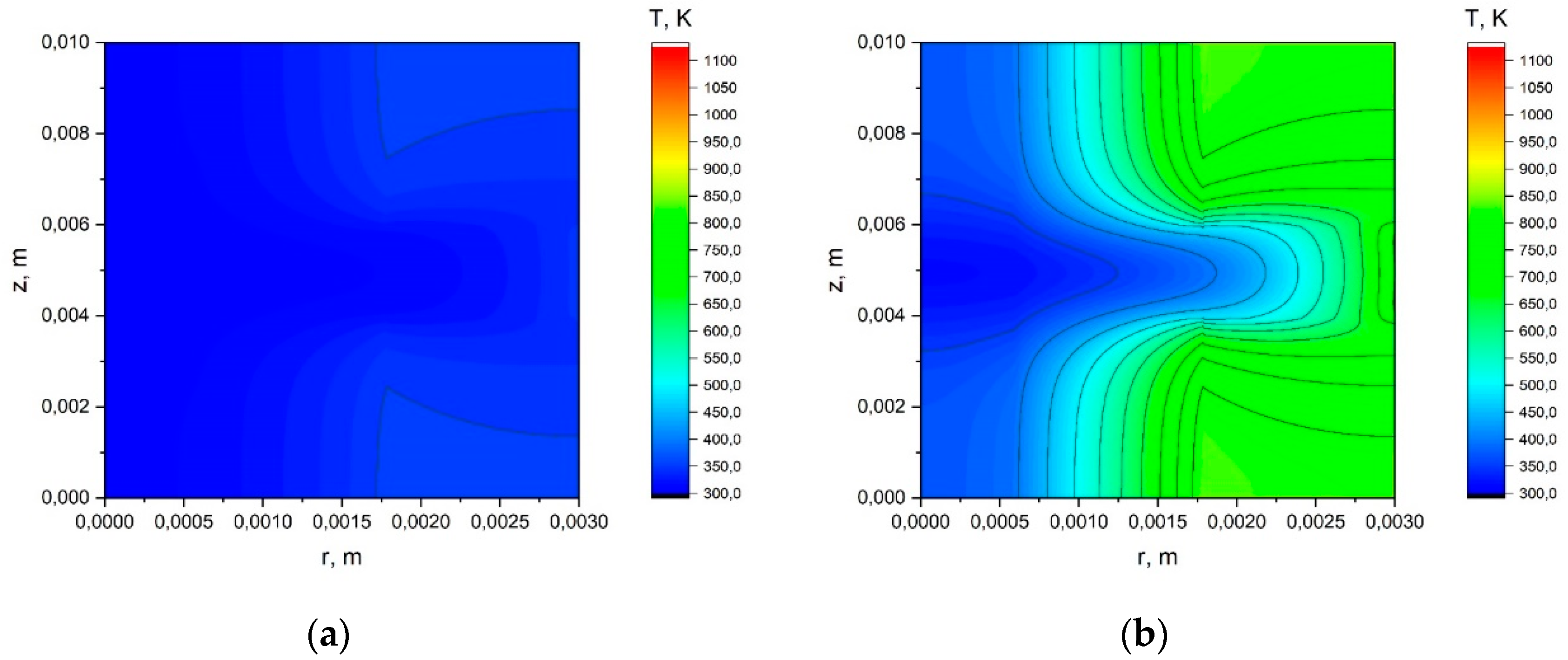
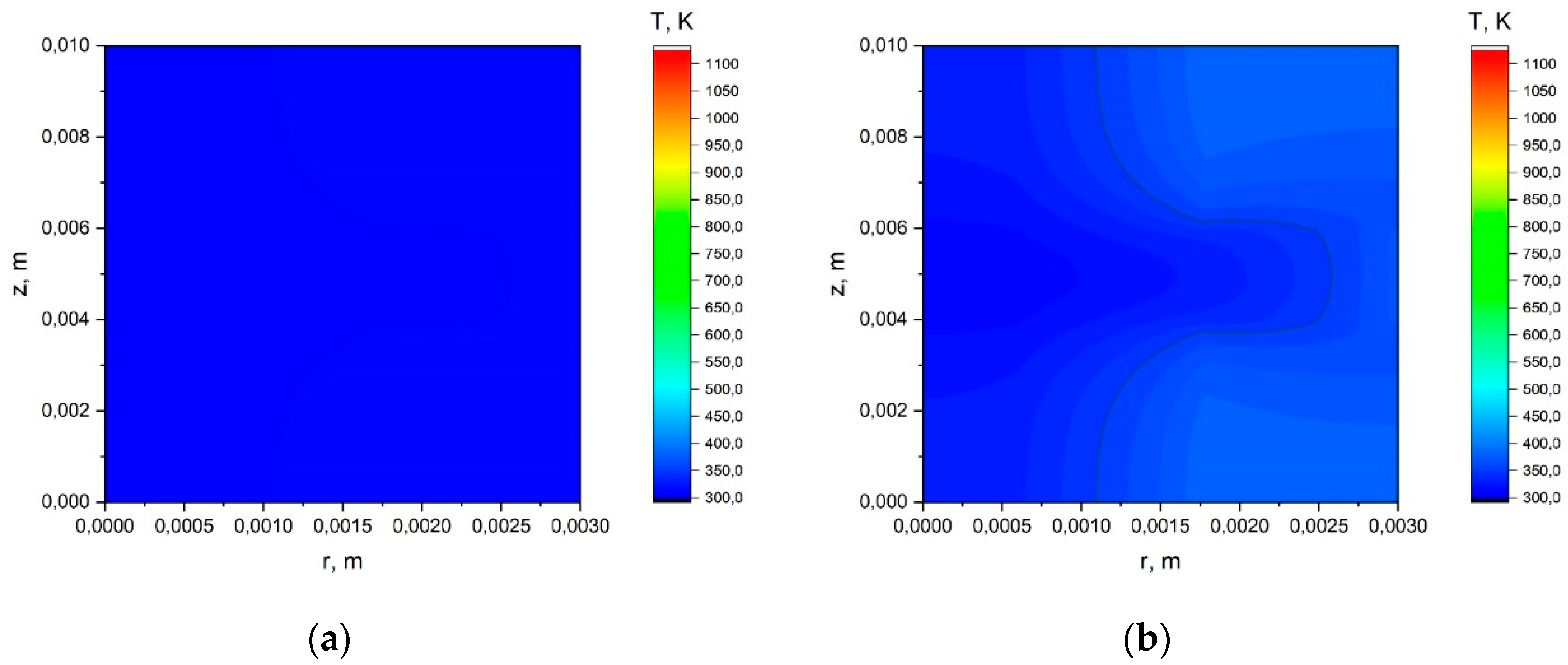
Appendix A.1. The Results of the Calculation Using the Simplified Model.
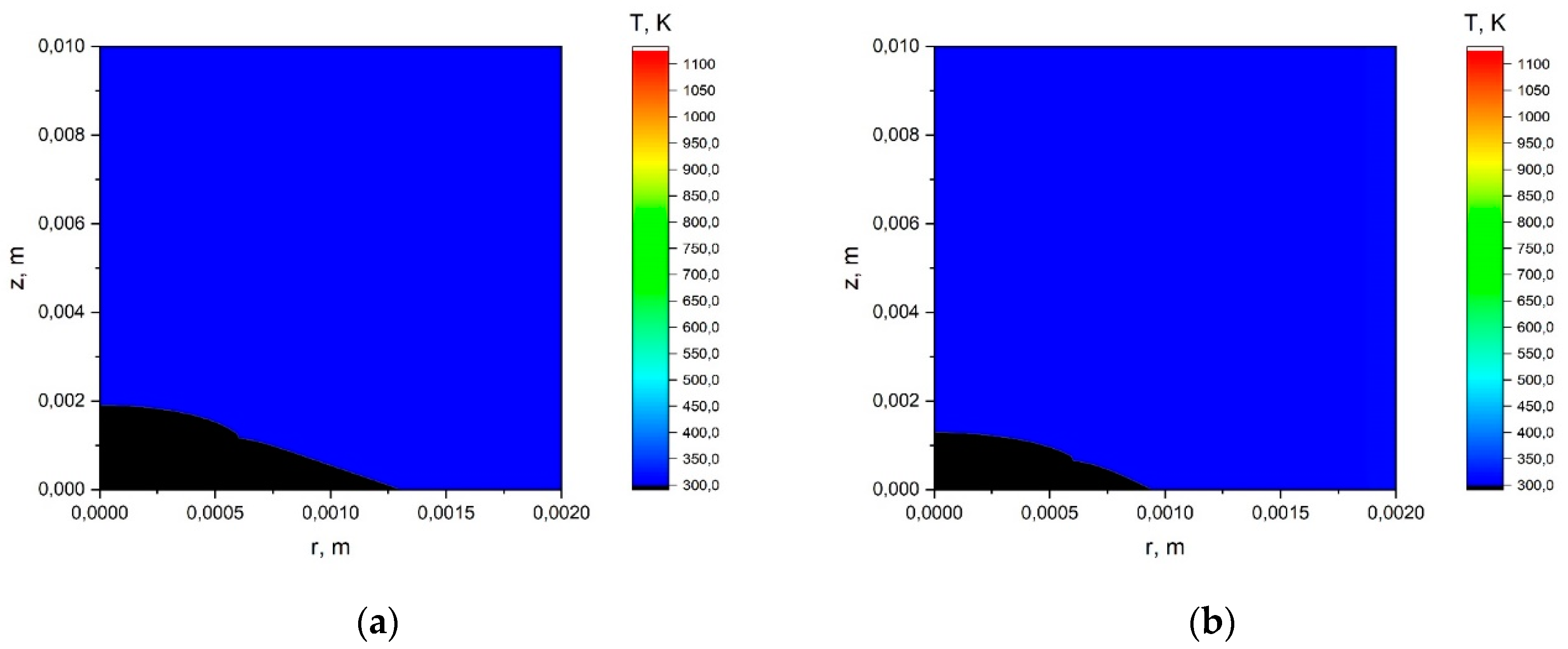

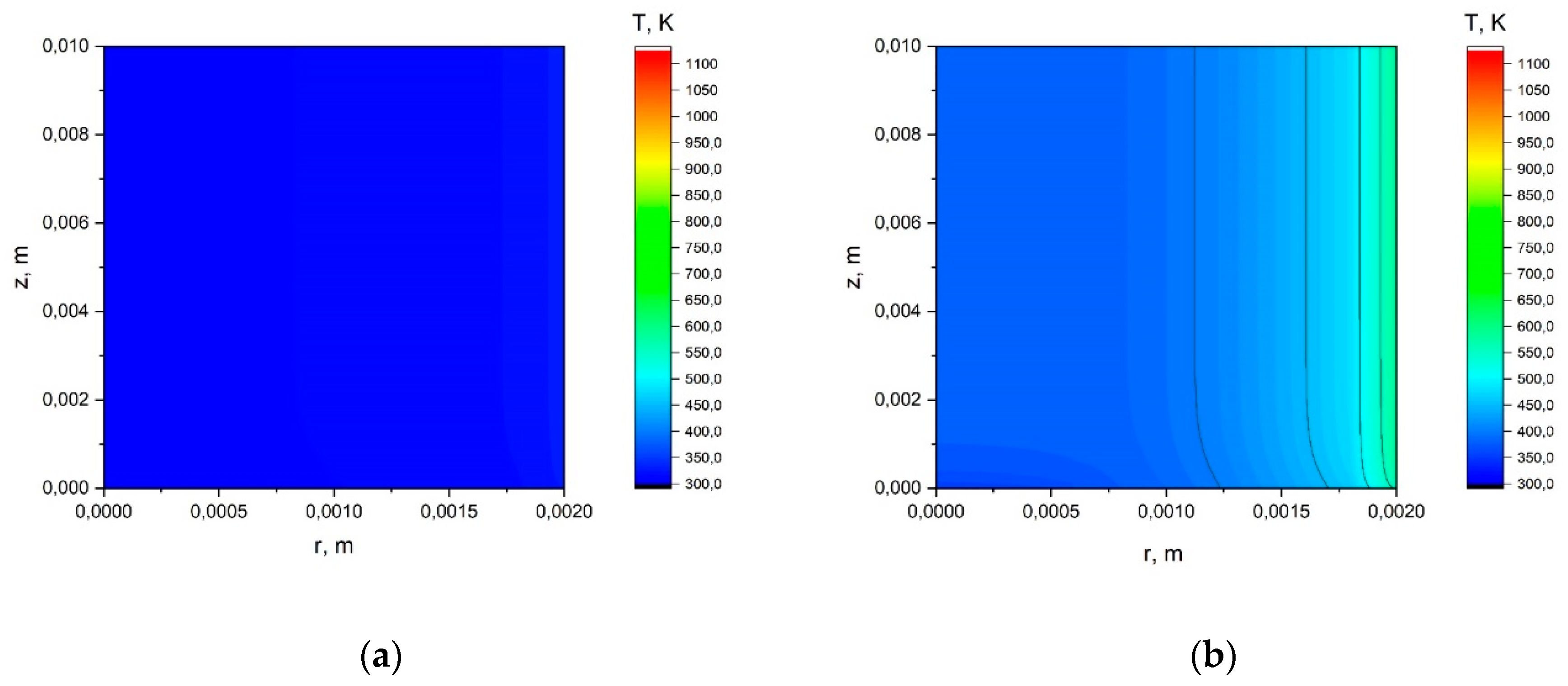
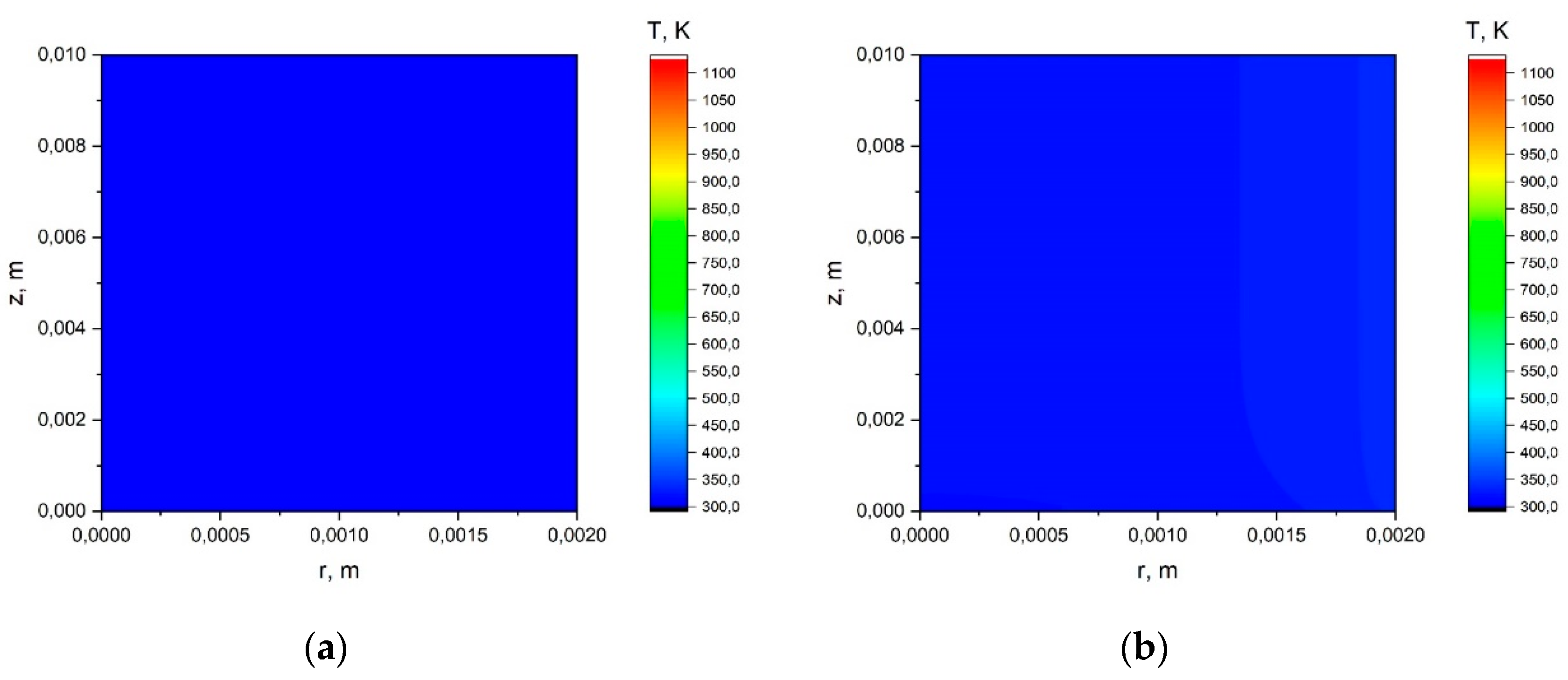
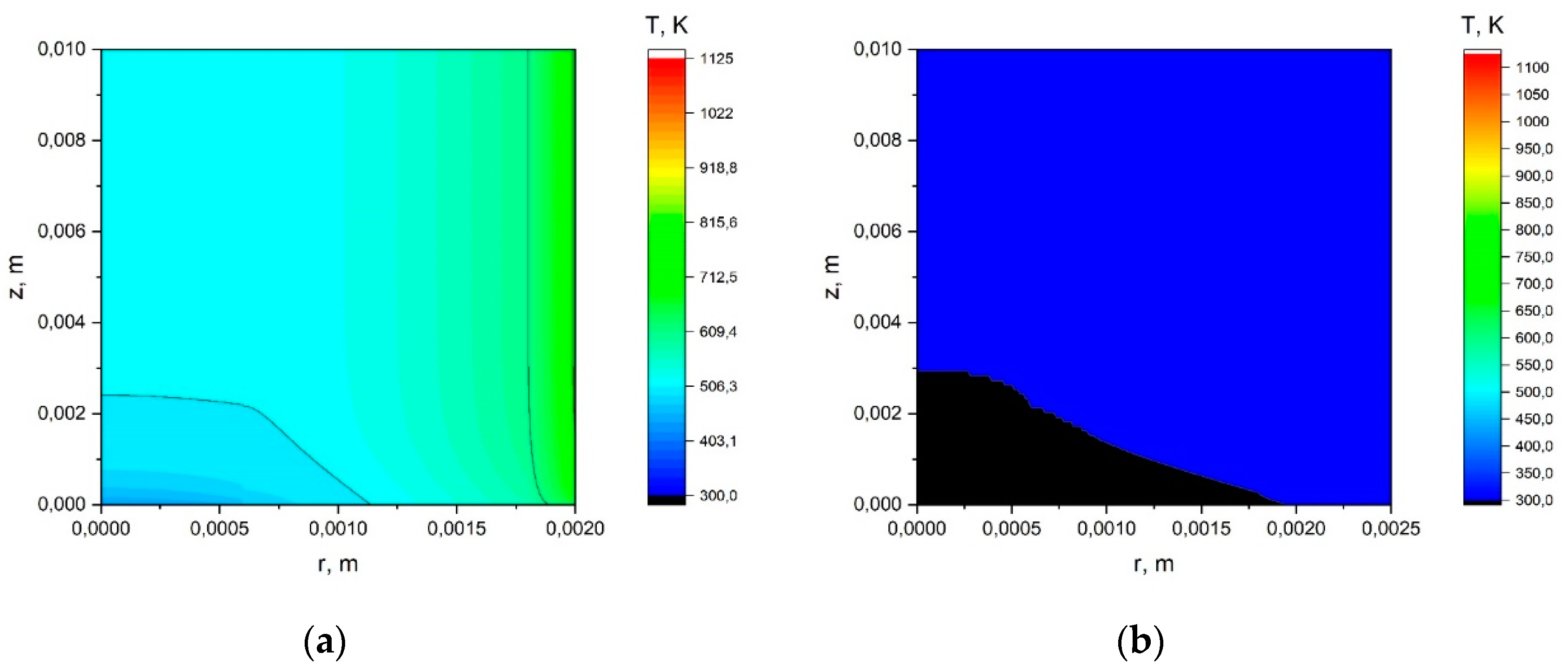
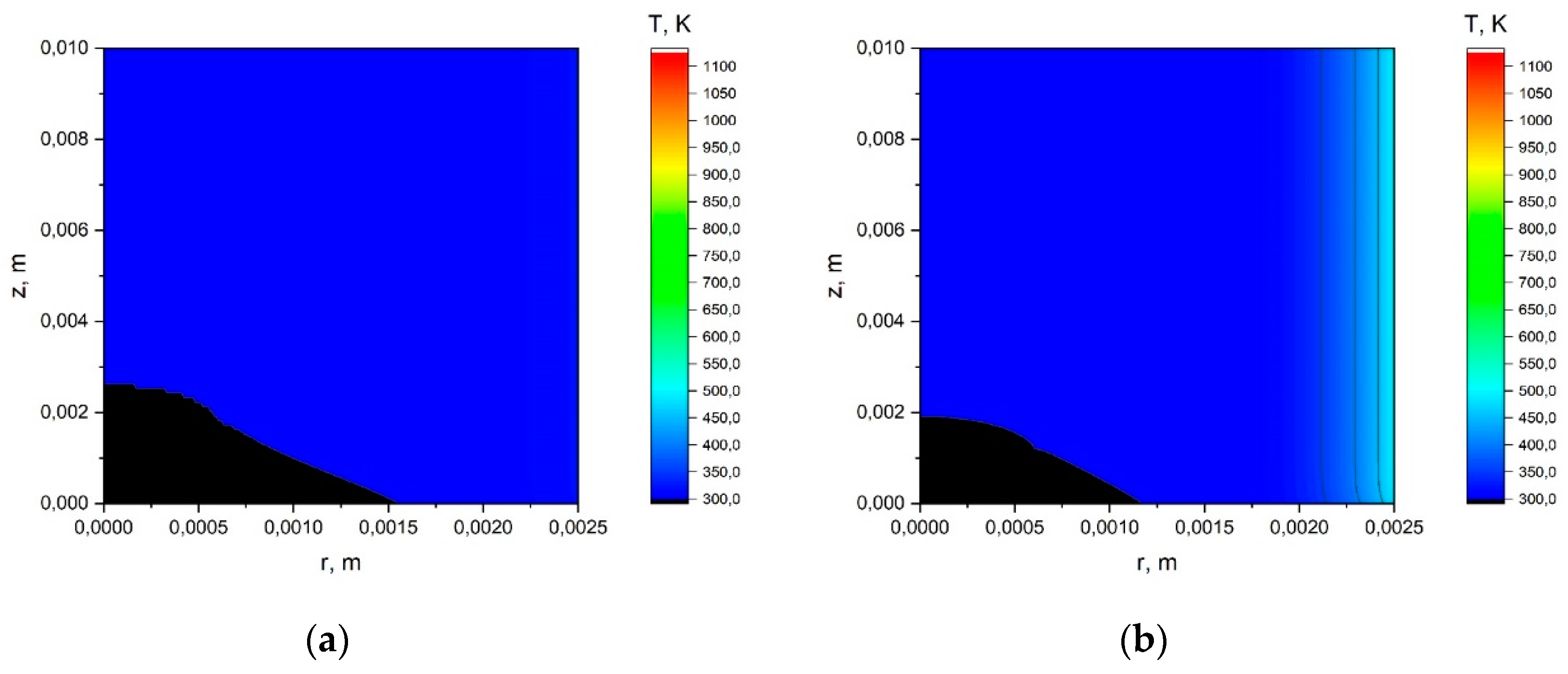
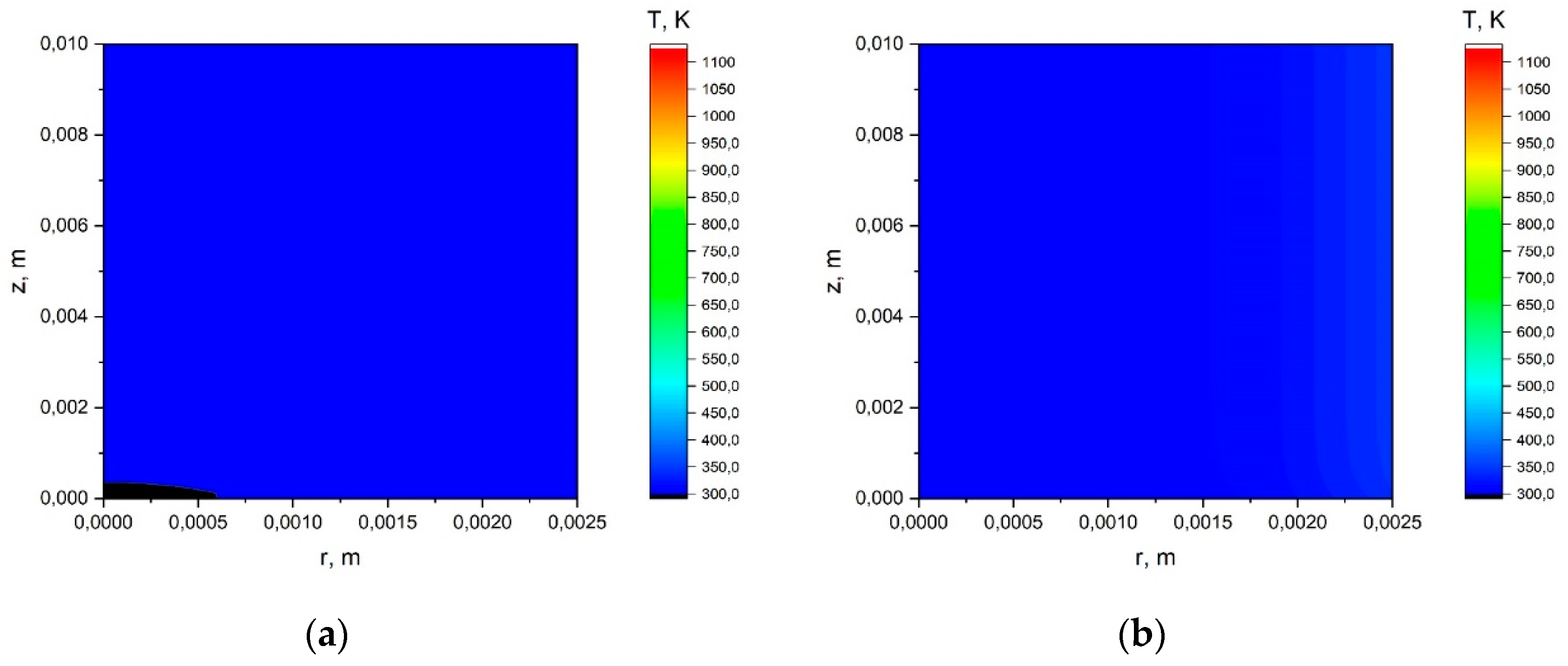
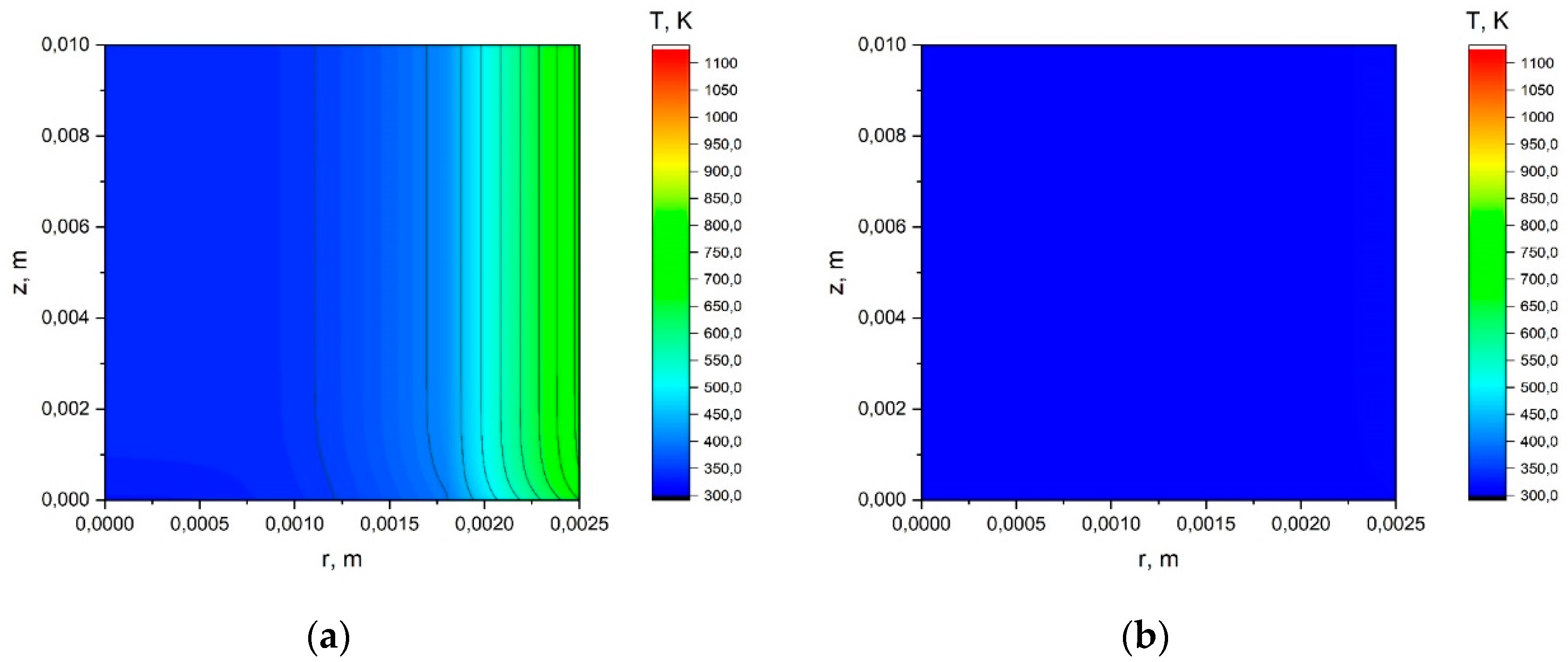
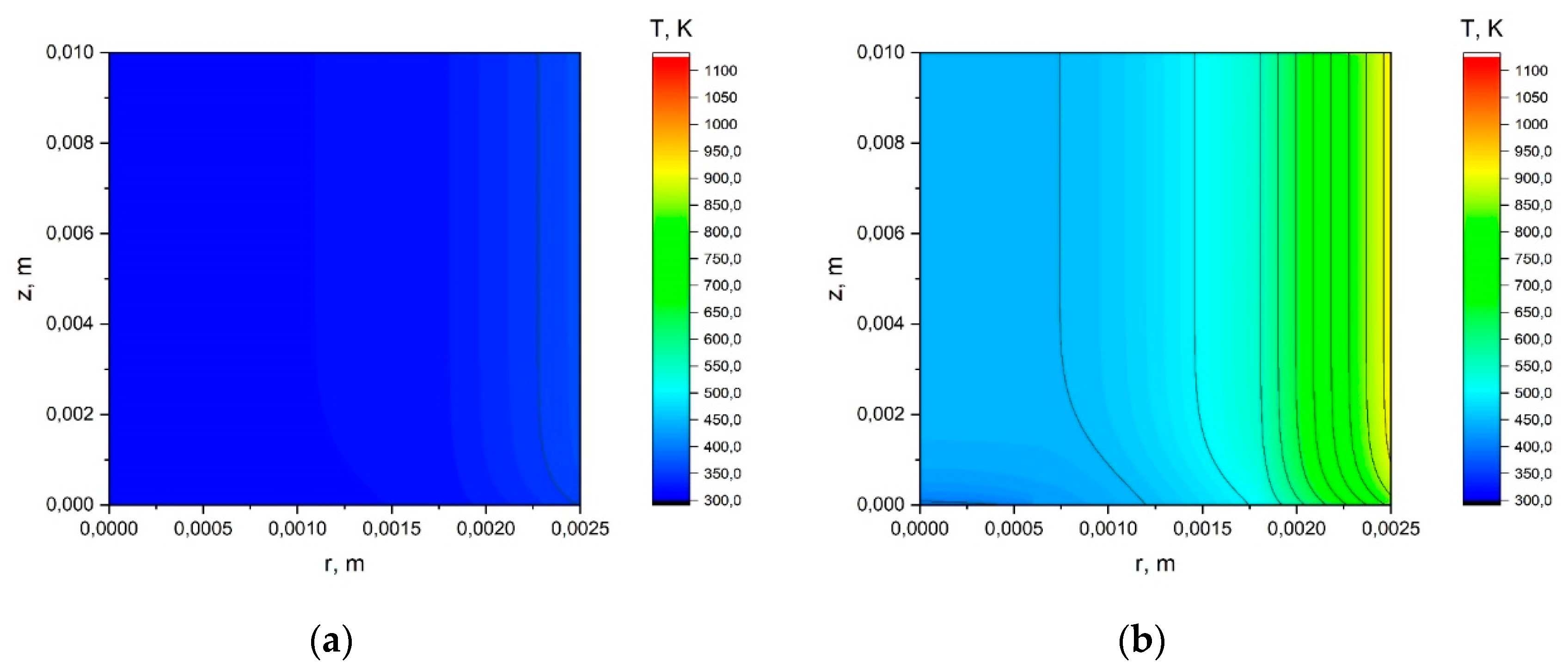
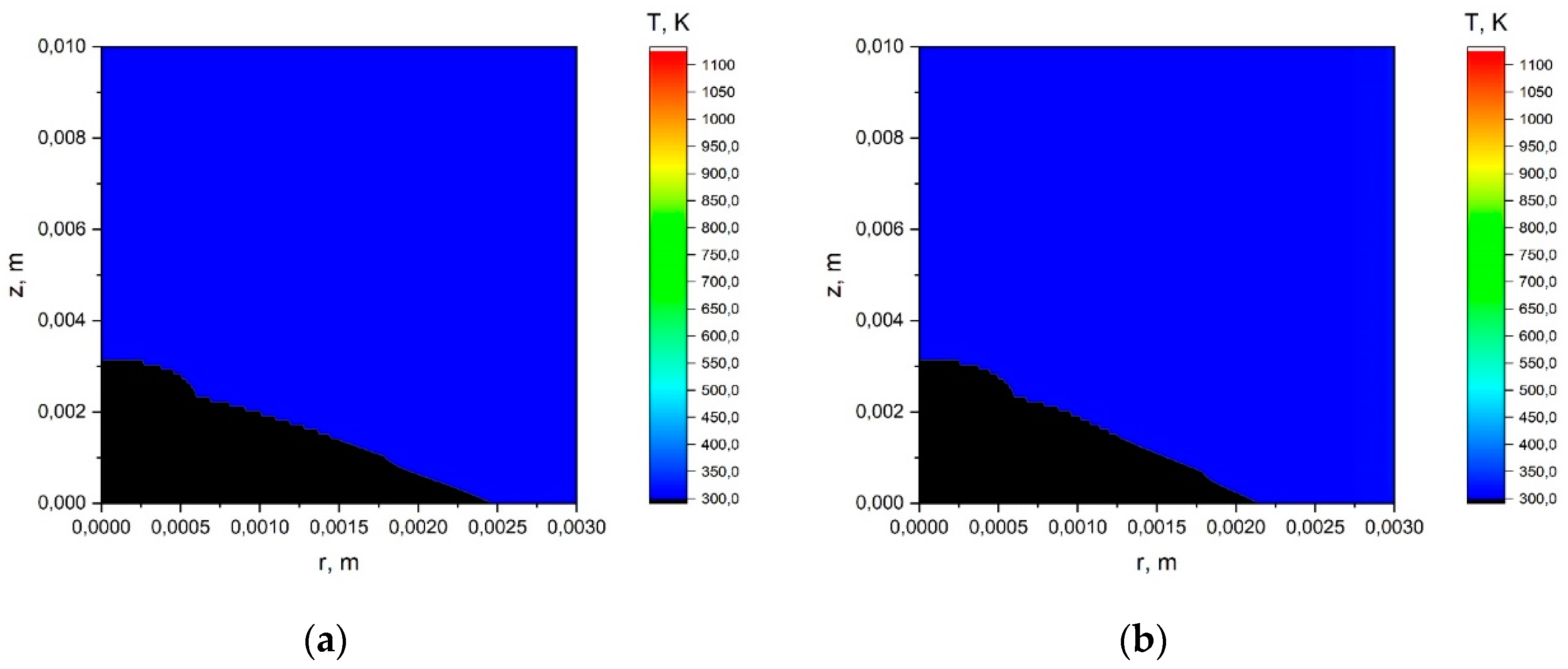

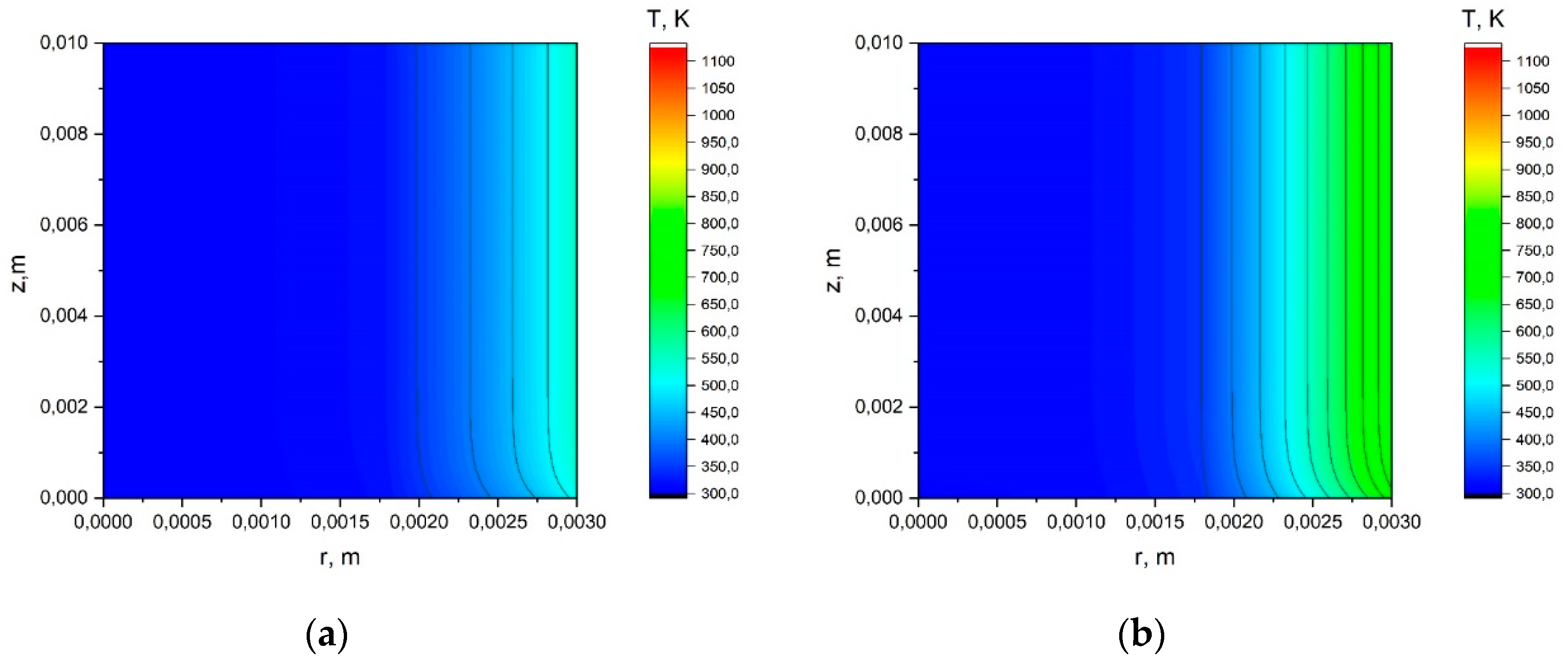


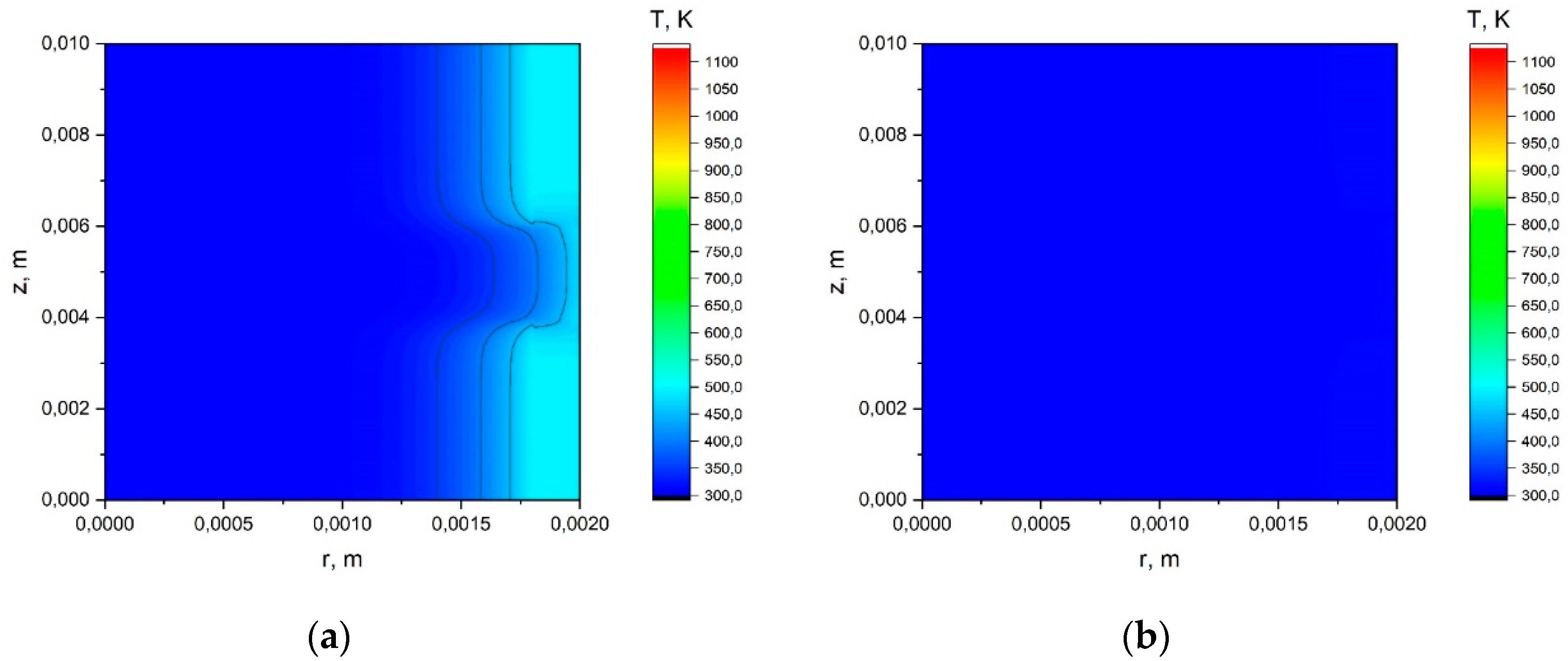
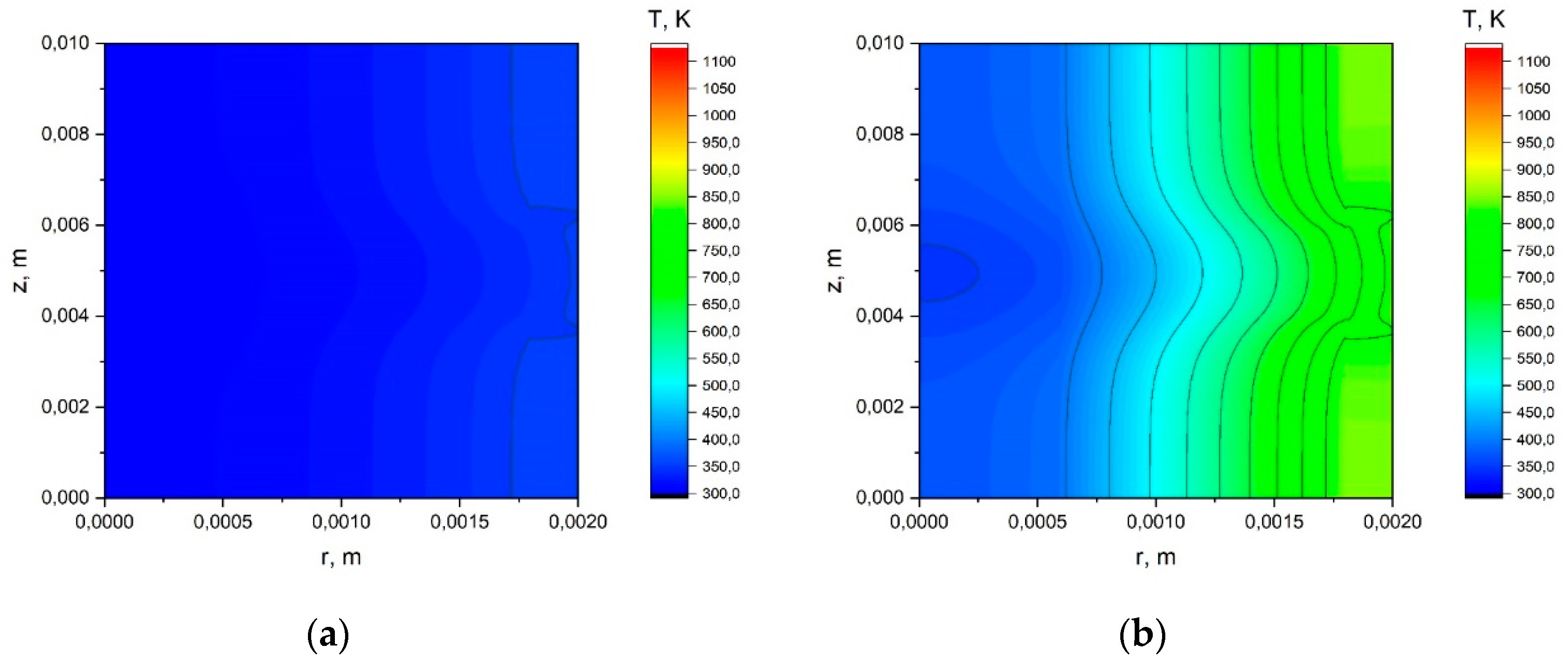
Appendix A.2. The Results of the Calculation Using the Model with a Joint




References
- Volokitina, A.V.; Sofronov, M.A. Classification and Mapping of Plant Combustible Materials; Publishing House of the Siberian Branch of the Russian Academy of Sciences: Novosibirsk, Russia, 2002; p. 314. [Google Scholar]
- Baranovskiy, N.V.; Demikhova, A.N. Mathematical Model of Heat Transfer in Morphological Part of Vegetation at Influence by Thermal Radiation from Surface Forest Fire Front. MATEC Web Conf. 2016, 72, 01025. [Google Scholar] [CrossRef]
- Esau, K. Anatomy of Seed Plants, 2nd ed.; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Grishin, A.M. Mathematical Modeling of Forest Fire and New Methods of Fighting Them; Publishing House of the Tomsk State University: Tomsk, Russia, 1997; p. 390. [Google Scholar]
- Perminov, V.; Soprunenko, E. Numerical solution of crown forest fire initiation and spread problem. In Proceedings of the 2016 11th International Forum on Strategic Technology, IFOST, Novosibirsk, Russia, 1–3 June 2016; pp. 400–404. [Google Scholar] [CrossRef]
- Valette, J.-C.; Gomendy, V.; Houssard, C.; Gillon, D. Heat transfer in the soil during very low-intensity experimantal fires—The role of duff and soil-moisture content. Int. J. Wildland Fire 1994, 4, 225. [Google Scholar] [CrossRef]
- Scotter, D.R. Soil temperature under grass fires. Aust. J. Soil Res. 1970, 8, 273–279. [Google Scholar] [CrossRef]
- Stoof, C.R. Soil heating. In Fire Effects on Soil Properties; CSIRO Publishing: Clayton South, Australia, 2019; pp. 229–240. [Google Scholar]
- Pereira, P.; Úbeda, X.; Francos, M. Laboratory fire simulations: Plant litter and soils. In Fire Effects on Soil Properties; CSIRO Publishing: Clayton South, Australia, 2019; pp. 15–38. [Google Scholar]
- Redmann, R.E. Nitrogen losses to the atmosphere from grassland fires in Saskatchewan, Canada. Int. J. Wildland Fire 1991, 1, 239–244. [Google Scholar] [CrossRef]
- Strand, T.; Gullett, B.; Urbanski, S.; O’Neil, S.; Potter, B.; Aurell, J.; Holder, A.; Larkin, N.; Moore, M.; Rorig, M. Grassland and forest understorey biomass emissions from prescribed fires in the southeastern United States—RxCADRE 2012. Int. J. Wildland Fire 2016, 25, 102–113. [Google Scholar] [CrossRef]
- Wang, S.; Ali Baig, M.H.; Liu, S.; Wan, H.; Wu, T.; Yang, Y. Estimating the area burned by agricultural fires from Landsat 8 data using the Vegetation Difference Index and Burn Scar Index. Int. J. Wildland Fire 2018, 27, 217–227. [Google Scholar] [CrossRef]
- Kurbatsky, N.P. Terminology of forest pyrology. In Questions of forest pyrology; ILID SB AS USSR: Krasnoyarsk, Russia, 1972; pp. 171–231. [Google Scholar]
- Baranovskiy, N.V.; Kuznetsov, G.V. Forest Fire Occurrences and Ecological Impact Prediction: Monograph; Publishing House of the Siberian Branch of the Russian Academy of Science: Novosibirsk, Russia, 2017. [Google Scholar]
- Kipfmueller, K.; Elizabeth, A.; Schneider, S.A.; Weyenberg, L.B.; Johnson, G. Historical drivers of the frequent fire regime in the red pine forests of Voyageurs National Park, MN, USA. For. Ecol. Manag. 2017, 405, 31–43. [Google Scholar] [CrossRef]
- Baranovskiy, N.V.; Kuznetsov, G.V. Coniferous tree ignition by cloud-to-ground lightning discharge using approximation of “ideal” crack in bark. JP J. Heat Mass Transf. 2017, 14, 173–186. [Google Scholar] [CrossRef]
- Vorobiev, Y.L. Forest fires on the territory of Russia: Status and problems. Ecol. J. 2009, 3, 9–11. [Google Scholar]
- Amatulli, G.; Perez-Cabello, F.; Du la Riva, J. Mapping lightning/human-caused wildfires occurrence under ignition point location uncertainty. Ecol. Model. 2007, 200, 321–333. [Google Scholar] [CrossRef]
- Clarke, H.; Tran, B.; Boer, M.M.; Price, O.; Kenny, B.; Bradstock, R. Climate change effects on the frequency, seasonality and interannual variability of suitable prescribed burning weather conditions in south-eastern Australia. Agric. For. Meteorol. 2019, 271, 148–157. [Google Scholar] [CrossRef]
- Ilina, V.P. Pyrogenic effect on vegetation cover. Samara Luka: Problems of regional and global ecology. 2011, 20, 4–30. [Google Scholar]
- Bryukhanov, A.V. Environmental assessment of the state of forests in Siberia. Sustain. For. Manag. 2009, 2, 21–31. [Google Scholar]
- Staggs, J.E.J. A simple model of polymer pyrolysis including transport of volatiles. Fire Saf. J. 2000, 34, 69–80. [Google Scholar] [CrossRef]
- Di Blasi, C. Modelling and simulation of combustion processes of charring and non-charring solid fuels. Prog. Energy Combust. Sci. 1993, 19, 71–104. [Google Scholar] [CrossRef]
- Carlslaw, S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1984; p. 510. [Google Scholar]
- Landau, G. Heat conduction in a melting solid. Q. J. Appl. Math. 1950, 8, 81–94. [Google Scholar] [CrossRef]
- Billings, M.J.; Warren, L.; Wilkins, R. Thermal erosion of electrical insulating materials. IEEE Trans. Electr. Insulation 1971, 6, 82–90. [Google Scholar] [CrossRef]
- Whiting, P.; Dowden, J.M.; Kapadia, P.D.; Davis, M.P. A one-dimensional mathematical model of laser induced thermal ablation of biological tissue. Lasers Med. Sci. 1992, 7, 357–368. [Google Scholar] [CrossRef]
- Kindelan, M.; Williams, F.A. Theory for endothermic gasification of a solid by a constant energy flux. Combust. Sci. Technol. 1975, 10, 1–9. [Google Scholar] [CrossRef]
- Wichman, I.S. A model describing the steady-state gasification of bubble-forming thermoplastics in response to an incident heat flux. Combust. Flame 1986, 63, 217–229. [Google Scholar] [CrossRef]
- Spearpoint, M.J.; Quintiere, J.G. Predicting the piloted ignition of wood in the cone calorimeter using an integral model—Effect of species, grain orientation and heat flux. Fire Saf. J. 2001, 36, 391–415. [Google Scholar] [CrossRef]
- Mackay, G.D.M. Mechanism of Thermal Degradation of Cellulose: A Review of the Literature; Forestry Branch Departmental Publication no 1201; Canada Department of Forestry and Rural Development: Petawawa, ON, Canada, 1967; p. 2. [Google Scholar]
- Moghtaderi, B. The state-of-the-art in pyrolysis modeling of lignocellulosic solid fuels. Fire Mater. 2006, 30, 1–34. [Google Scholar] [CrossRef]
- Galgano, A.; Di Blasi, C. Modeling the propagation of drying and decomposition fronts in wood. Combust. Flame 2004, 139, 16–27. [Google Scholar] [CrossRef]
- Shen, D.K.; Fang, M.X.; Luo, Z.Y.; Cen, K.F. Modeling pyrolysis of wet wood under external heat flux. Fire Saf. J. 2007, 42, 210–217. [Google Scholar] [CrossRef]
- Cruz, M.G.; Sullivan, A.L.; Gould, J.S.; Hurley, R.J.; Plucinski, M.P. Got to burn to learn: The effect of fuel load on grassland fire behavior and its management implications. Int. J. Wildland Fire 2018, 27, 727–741. [Google Scholar] [CrossRef]
- Deeming, J.E.; Burgan, R.E.; Cohen, J.D. The National Fire Danger Rating System—1978; General Technical Report INT—39; USDA Forest Service, Intermountain Forest and Range Experimental Station: Odgen, UT, USA, 1977. [Google Scholar]
- Alexander, M.E. Proposed Revision of Fire Danger Class Criteria for Forest and Rural Areas in New Zeland; National Rural Fire Authority: Wellington, New Zeland, 2008. [Google Scholar]
- Byram, G.M. Combustion of Forest Fuels//In Forest Fire: Control and Use; Davis, K.P., Ed.; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Research Paper INT-115; USDA Forest Service, Intermountain Forest and Range Experimental Station: Odgen, UT, USA, 1972. [Google Scholar]
- Luke, R.H.; McArthur, A.G. Bushfires in Australia; Australian Government Publishing Service: Canberra, Australia, 1978. [Google Scholar]
- Fernandes, P.M.; Botelho, H.S. A review of prescribed burning effectiveness in fire hazard reduction. Int. J. Wildland Fire 2003, 12, 117–128. [Google Scholar] [CrossRef]
- Fernandes, P.M. Empirical support for the use of prescribed burning as a fuel treatment. Curr. For. Rep. 2015, 1, 118–127. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Feng, Z.; Li, X.; Bi, Y.; Shi, D.; Zhou, D.; Wang, Y.; Duwala; Zhao, J. A method for estimating the amount of dead grass fuel based on spectral reflectance characteristics. Int. J. Wildland Fire 2015, 24, 940–948. [Google Scholar] [CrossRef]
- Lu, B.; He, Y.; Tong, A. Evaluation of spectral indices for estimating burn severity in semiarid grasslands. Int. J. Wildland Fire 2016, 25, 147–157. [Google Scholar] [CrossRef]
- Martin, D.; Chen, T.; Nichols, D.; Bessell, R.; Kidnie, S.; Alexander, J. Integrating ground and satellite-based observations to determine the degree of grassland curing. Int. J. Wildland Fire 2015, 24, 329–339. [Google Scholar] [CrossRef]
- Dimitrakopoulos, A.P.; Mitsopoulos, I.D.; Gatoulas, K. Assessing ignition probability and moisture of extinction in a Mediterranean grass fuel. Int. J. Wildland Fire 2010, 19, 29–34. [Google Scholar] [CrossRef]
- Nelson, R.M., Jr. Water relations of forest fuels. In Forest Fires: Behavior and Ecological Effects; Johnson, E.A., Miyanishi, K., Eds.; Academic Press: Cambridge, CA, USA, 2001; pp. 79–150. [Google Scholar]
- Drysdale, D. An Introduction to Fire Dynamics; Wiley: Chichester, UK, 1998. [Google Scholar]
- Cheney, N.P.; Gould, J.S.; Catchpole, W.R. Prediction of fire spread in grasslands. Int. J. Wildland Fire 1998, 8, 1–13. [Google Scholar] [CrossRef]
- Mell, W.; Jenkins, M.A.; Gould, J.; Cheney, P. A physics-based approach to modeling grassland fires. Int. J. Wildland Fire 2007, 16, 1–22. [Google Scholar] [CrossRef]
- Cruz, M.G. Monte Carlo-based ensemble method for prediction of grassland fire spread. Int. J. Wildland Fire 2010, 19, 521–530. [Google Scholar] [CrossRef]
- Clements, C.B. Thermodynamic structure of a grass fire plume. Int. J. Wildland Fire 2010, 19, 895–902. [Google Scholar] [CrossRef]
- GEOPORTAL FGBU «ROSLESINFORG». Available online: http://geoportal.roslesinforg.ru:8080/ (accessed on 8 July 2019).
- Lesohozyaystvennyie Reglamentyi. Available online: http://egov-buryatia.ru/ralh/activities/documents/lesokhozyaystvennye-reglamenty/ (accessed on 8 July 2019).
- Official Site MO “Ivolginskiy Rayon”. Available online: http://egov-buryatia.ru/ivolga/o-munitsipalnom-obrazovanii/ob-organizatsii/ (accessed on 8 July 2019).
- Forest Resources. Available online: http://egov-buryatia.ru/about_republic/nature-resources/lesnye-resursy-/ (accessed on 9 July 2019).
- Yankovich, K.S.; Yankovich, E.P.; Baranovskiy, N.V. Classification of Vegetation to Estimate Forest Fire Danger Using Landsat 8 Images: Case Study. Math. Probl. Eng. 2019, 2019, 6296417. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Vabishchevich, P.N. Computational Heat Transfer, Volume 1, Mathematical Modelling; Wiley: Chichester, UK, 1995. [Google Scholar]
- Samarskii, A.A.; Vabishchevich, P.N. Computational Heat Transfer, Volume 2, The Finite Difference Method; Wiley: Chichester, UK, 1995. [Google Scholar]
- Von Arx, G.; Crivellaro, A.; Prendin, A.L.; Čufar, K.; Carrer, M. Quantitative wood anatomy-practical guidelines. Front. Plant Sci. 2016, 7, 781. [Google Scholar] [CrossRef] [PubMed]
- Ward, D. Combustion chemistry and smoke. In Forest Fires: Behavior and Ecological Effects; Johnson, E.A., Miyanishi, K., Eds.; Academic Press: Cambridge, CA, USA, 2001; pp. 55–77. [Google Scholar]
- Grishin, A.M.; Golovanov, A.N.; Kataeva, L.Y.; Loboda, E.L. Problem of drying of a layer of combustible forest materials. Inzhenerno-Fizicheskii Zhurnal 2001, 74, 58–64. [Google Scholar]
- Grishin, A.M.; Golovanov, A.N.; Kataeva, L.Y.; Loboda, E.L. Formulation and solution of the problem of drying of a layer of combustible forest materials. Combust. Explos. Shock Waves 2001, 37, 57–66. [Google Scholar] [CrossRef]
- Cawson, J.G.; Duff, T.J. Forest fuel bed ignitability under marginal fire weather conditions in Eucalyptus forests. Int. J. Wildland Fire 2019, 28, 198–204. [Google Scholar] [CrossRef]
- Grishin, A.M.; Filkov, A.I. A deterministic-probabilistic system for predicting forest fire hazard. Fire Saf. J. 2011, 46, 56–62. [Google Scholar] [CrossRef]
- Grishin, A.M.; Sinitsyn, S.P.; Akimova, I.V. Comparative analysis of the thermokinetic constants for drying and pyrolyzing forest fuels. Combust. Explos. Shock Waves 1991, 27, 663–669. [Google Scholar] [CrossRef]
- Naresh, K.; Kumar, A.; Korobeinichev, O.; Shmakov, A.; Osipova, K. Downward flame spread along a single pine needle: Numerical modeling. Combust. Flame 2018, 197, 161–181. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Paletsky, A.A.; Gonchikzhapov, M.B.; Shundrina, I.K.; Chen, H.; Liu, N. Combustion chemistry and decomposition kinetics of forest fuels. Procedia Eng. 2013, 62, 182–193. [Google Scholar] [CrossRef]
- Bhattarai, C.; Samburova, V.; Sengupta, D.; Iaukea-Lum, M.; Watts, A.C.; Moosmüller, H.; Khlystov, A.Y. Physical and chemical characterization of aerosol in fresh and aged emissions from open combustion of biomass fuels. Aerosol Sci. Technol. 2018, 52, 1266–1282. [Google Scholar] [CrossRef]
- Morvan, D.; Accary, G.; Meradji, S.; Frangieh, N.; Bessonov, O. A 3D physical model to study the behavior of vegetation fires at laboratory scale. Fire Saf. J. 2018, 101, 39–52. [Google Scholar] [CrossRef]
- Bandowe, B.A.M.; Leimer, S.; Meusel, H.; Velescu, A.; Dassen, S.; Eisenhauer, N.; Hoffmann, T.; Oelmann, Y.; Wilcke, W. Plant diversity enhances the natural attenuation of polycyclic aromatic compounds (PAHs and oxygenated PAHs) in grassland soils. Soil Biol. Biochem. 2019, 129, 60–70. [Google Scholar] [CrossRef]
- Hu, T.; Hu, H.; Li, F.; Zhao, B.; Wu, S.; Zhu, G.; Sun, L. Long-term effects of post-fire restoration types on nitrogen mineralisation in a Dahurian larch (Larix gmelinii)forest in boreal China. Sci. Total Environ. 2019, 679, 237–247. [Google Scholar] [CrossRef]
- Rovira, P.; Romanyà, J.; Duguy, B. Long-term effects of wildfires on the biochemical quality of soil organic matter: A study on Mediterranean shrublands. Geoderma 2012, 179–180, 9–19. [Google Scholar] [CrossRef]
- Majlingová, A.; Sedliak, M.; Smreček, R. Spatial distribution of surface forest fuel in the Slovak Republic. J. Maps 2018, 14, 368–372. [Google Scholar] [CrossRef]
- Eskandari, S. A new approach for forest fire risk modeling using fuzzy AHP and GIS in Hyrcanian forests of Iran. Arabian J. Geosci. 2017, 10, 190. [Google Scholar] [CrossRef]
- Qiao, C.; Wu, L.; Chen, T.; Huang, Q.; Li, Z. Study on Forest Fire Spreading Model Based on Remote Sensing and GIS. IOP Conf. Ser. Earth Environ. Sci. 2018, 199, 022017. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Mura, M.; Zolli, C.; Maselli, F.; Chiesi, M.; Bottai, L.; Chirici, G. The potential of multifrequency SAR images for estimating forest biomass in Mediterranean areas. Remote Sens. Environ. 2017, 200, 63–73. [Google Scholar] [CrossRef]
- Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Hermosilla, T.; White, J.C. Analyzing spatial and temporal variability in short-term rates of post-fire vegetation return from Landsat time series. Remote Sens Environ. 2018, 205, 32–45. [Google Scholar] [CrossRef]
- GRASS GIS Manual: I.atcorr. Available online: https://grass.osgeo.org/grass76/manuals/i.atcorr.html (accessed on 5 December 2018).
- Matlab Official Web-site. Available online: https://matlab.ru/products/matlab (accessed on 25 May 2019).
- RAD Studio. Available online: https://www.embarcadero.com/ru/products/rad-studio (accessed on 25 May 2019).
- Origin Lab Official Web-site. Available online: https://www.originlab.com/ (accessed on 25 May 2019).
- Di Bona, G.; Duraccio, V.; Silvestri, A.; Forcina, A. Validation and application of a safety allocation technique (integrated hazard method) to an aerospace prototype. In Proceedings of the IASTED International Conference on Model Identification and Control, Innsbruck, Austria, 17–19 February 2014; pp. 284–290. [Google Scholar]
- Di Bona, G.; Silvestri, A.; Forcina, A.; Petrillo, A. Total efficient risk priority number (TERPN): A new method fo risk assessment. J. Risk Res. 2018, 21, 1384–1408. [Google Scholar] [CrossRef]
- Moinuddin, K.A.M.; Sutherland, D.; Mell, W. Simulation study of grass fire using a physics-based model: Striving towards numerical rigour and the effect of grass height on the rate of spread. Int. J. Wildland Fire 2018, 27, 800–814. [Google Scholar] [CrossRef]
- Keane, R.E.; Burgan, R.; van Wagtendonk, J. Mapping wildland fuels for fire management across multiple scales: Integrating remote sensing, GIS, and biophysical modeling. Int. J. Wildland Fire 2001, 10, 301–319. [Google Scholar] [CrossRef]
- Oddi, F.J.; Ghermandi, L. Fire regime from 1973 to 2011 in north-western Patagonian grasslands. Int. J. Wildland Fire 2016, 25, 922–932. [Google Scholar] [CrossRef]
- Fosberg, M.A.; Cramer, W.; Brovkin, V.; Fleming, R.; Gardner, R.; Gill, A.M.; Goldammer, J.G.; Keane, R.; Koehler, P.; Lenihan, J.; et al. Strategy for a fire module in Dynamic Global Vegetation Models. Int. J. Wildland Fire 1999, 9, 79–84. [Google Scholar] [CrossRef]
- Boyd, C.S.; Davies, K.W.; Hulet, A. Predicting fire-based perennial bunchgrass mortality in big sagebrush plant communities. Int. J. Wildland Fire 2015, 24, 527–533. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baranovskiy, N.; Demikhova, A. Mathematical Modeling of Heat Transfer in an Element of Combustible Plant Material When Exposed to Radiation from a Forest Fire. Safety 2019, 5, 56. https://doi.org/10.3390/safety5030056
Baranovskiy N, Demikhova A. Mathematical Modeling of Heat Transfer in an Element of Combustible Plant Material When Exposed to Radiation from a Forest Fire. Safety. 2019; 5(3):56. https://doi.org/10.3390/safety5030056
Chicago/Turabian StyleBaranovskiy, Nikolay, and Alena Demikhova. 2019. "Mathematical Modeling of Heat Transfer in an Element of Combustible Plant Material When Exposed to Radiation from a Forest Fire" Safety 5, no. 3: 56. https://doi.org/10.3390/safety5030056
APA StyleBaranovskiy, N., & Demikhova, A. (2019). Mathematical Modeling of Heat Transfer in an Element of Combustible Plant Material When Exposed to Radiation from a Forest Fire. Safety, 5(3), 56. https://doi.org/10.3390/safety5030056





