ATC Separation Assurance for RPASs and Conventional Aircraft in En-Route Airspace

Abstract

Remotely-piloted aircraft systems (RPASs) present interesting and complex challenges for air traffic management. One of the most critical aspects of the integration of RPASs in non-segregated airspace is safety assessments. This paper lays out a methodology for estimating the minimum protection distance (MPD) that is required to avoid potential conflicts between RPASs and conventional aircraft. The MPD determines the final moment that air traffic control may instruct a RPAS to start climbing with a fixed rate of climb (ROC) to avoid separation minima infringement. The methodology sets out a conflict-resolution algorithm to estimate the MPD. It also models the impact of communication, navigation, and surveillance requirements on the MPD. The main difference between RPASs and conventional aircraft is that the former needs additional communication between the RPAS and pilot in the form of a required Comand and Control link performance (RLP). Finally, the authors carried out Monte Carlo simulations to estimate the value of the MPD only for the head-on encounter, which is the worst scenario. The results showed that the main factors affecting the MPD were RLP and ROC. By increasing RLP and decreasing ROC it was possible to reduce the MPD from 28 to 17 nautical miles; however, the variation in the MPD was not linear.

1. Introduction

In the near future, remotely-piloted aircraft systems (RPASs) and conventional aircraft will share the skies; consequently, one of the major challenges that the civil aviation faces is the systematic integration of RPASs in non-segregated airspace. Many organisations, administrations, and regulators are increasingly demanding this integration [1,2,3,4]. However, there needs to be consolidated regulations and a single standard, which is currently lacking [5,6,7,8]. Clothier et al. [9] dealt with the basic requirements of the regulatory framework for RPASs in non-segregated airspace. They concluded that there is an absence of agreement between the different stakeholders. The systematic integration of RPASs is a complex issue [10]. In Europe, the European Union Aviation Safety Agency (EASA) [11,12] set out detailed regulations governing airworthiness, certification, and operations; however, these in no way resolve the issue of RPAS integration.

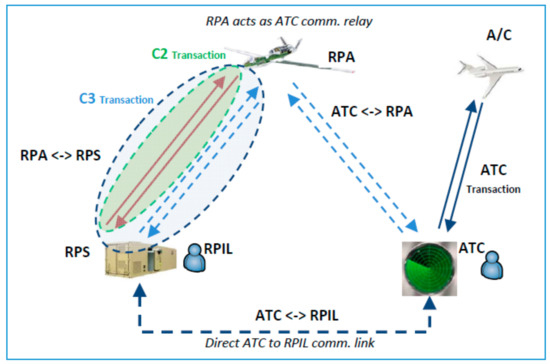
Up till now, the basic underlying principle of air traffic management (ATM) is that air traffic control (ATC) is responsible for ensuring separation in controlled airspace. The integration of RPASs must take the operational environment into consideration. Therefore, one of the main tasks is to analyse the impact of the introduction of RPASs into non-segregated airspace. Roman et al. [13,14] described the concept of operation for the safe operation of a RPAS in non-segregated airspace. The biggest difference between RPASs and conventional aircraft is that, in the case of the former, the RPAS station (RPS) is on the ground when the RPAS aircraft (RPA) is airborne. Bueno et al. [15] performed real RPAS flights under ATC control and supervision. The exercise highlighted a problem with the new required C2 link performance (RLP) between RPA and RPS, namely, that ATC did not receive any information about the behaviour of the RPAS via RLP and did not know how ATC tactical intervention was affected. Therefore, it is vital that RLP is studied in depth to learn how it affects the capacity of ATC to intervene, and to ascertain which RLP value (s) is acceptable to regulators.

The introduction of RPASs in an airspace with conventional aircraft will imply the appearance of potential conflicts. There are three possible manoeuvres to avoid a conflict—vertical, horizontal, and change in speed [16]. Speed change and horizontal manoeuvres are only valid for the medium and long-term horizon (up to 20 min before a conflict), while the vertical manoeuvre is adequate for the short-term horizon (up to 5 min before a conflict). Typically, ATC prefers to avoid any potential conflict by using vertical manoeuvres because they are the fastest manoeuvres [17]. On the other hand, airlines prefer a horizontal manoeuvre because they can reduce the impact and may achieve a benefit. For instance, an aircraft may be able to shorten the trajectory by using vectoring [16].

The first conflict-resolution algorithms for RPASs were developed some years ago. assessed the resolution of potential conflicts between RPAS and conventional aircraft in en-route airspace is expressed in [18,19,20]. The resolutions sought to apply different conflict-avoidance manoeuvres based on a set of horizontal techniques performed by the RPASs. Allignol et al. [21] evaluated horizontal manoeuvres to prevent conflicts among conventional aircraft and RPASs. Although some mathematical complex analyses were carried out [22,23,24], most of them focused on resolving potential conflicts by using horizontal manoeuvres instead of vertical manoeuvres. Their main argument for doing this was that most of the current RPAS fleets had poorer flight-performances, with respect to climb and descent, than commercial aircraft. However, most modern RPASs are capable of achieving practically the same rate of climb (ROC) as conventional aircraft [25,26]. Therefore, if the aviation community wishes to integrate RPASs, it will be necessary to define ROC requirements for RPASs at different flight levels (FLs). Finally, conflict-resolution algorithms rarely assess the impact of communication, navigation, and surveillance (CNS), which are key to modelling separation minima [27]. The complexities due to CNS requirements must be borne in mind when assessing real operations.

The situation we analyse in this paper is when the trajectories of a RPAS and a conventional aircraft coincide at a point, meaning that there is a potential conflict. The question is, “When does ATC have to start a resolution manoeuvre?” Therefore, the purpose of this research is to model the CNS requirements for RPASs and conventional aircraft and estimate the value of the minimum protection distance (MPD). To facilitate the work of ATC, the MPD is a single value which can be used to resolve all conflicts between RPASs and conventional aircraft. The main aim of the study is to fully understand how to use separation assurance to integrate RPASs in non-segregated airspace. Section 2 introduces the operational concept, assumptions, and the conflict-resolution algorithms of our model. In Section 3, the CNS requirements for RPASs and conventional aircraft are defined and modelled. Section 4 describes the Monte Carlo simulations, and Section 5 presents and discusses the results.

2. Methodology

This section sets out the operational concept for a shared operation involving a RPAS and a conventional aircraft and presents an algorithm for conflict-resolution.

2.1. Operational Concept

The presence of a RPAS in non-segregated airspace creates potential problems for other aircraft. The prohibition forbidding both types of aircraft from operating in the same airspace will disappear in the forthcoming years. Therefore, the integration of RPASs is fundamental for operators, regulators, and airlines. In this paper, the authors attempt to answer the following question, “When must a RPAS start climbing to avoid a conflict?” The answer is not trivial and requires in-depth analysis of the factors that influence separation assurance.

The description of the problem is as follows: A RPAS and a conventional aircraft fly in opposite directions along the same route. They are going to experience a conflict if ATC does not intervene. The goal is to calculate the minimum separation between both aircraft, at which ATC must instruct the RPAS to start climbing. We refer to this minimum separation as the MPD. In a previous study [28], the authors assessed the impact of variations in conflict-geometry on the MPD where the conflict-geometry depended on the angle of intersection of the approaching paths. The study concluded that the worst scenario was when both aircraft coincided on the same route flying in opposite directions. The relationship was clear: The greater the crossing angle (0º for aircraft flying in opposite directions), the less the separation required.

We oblige the RPASs to perform a vertical manoeuvre to avoid causing detriment to conventional aircraft, with respect to time, distance, or fuel consumption (Persiani and Bagassi, 2013). Furthermore, vertical manoeuvres require shorter reaction times to resolve potential conflicts, although this imposes certain operational demands [29]. The MPD depends on operational factors pertaining to both aircraft, such as speed and FL, and environmental factors, such as the wind. The situation is depicted in Figure 1.

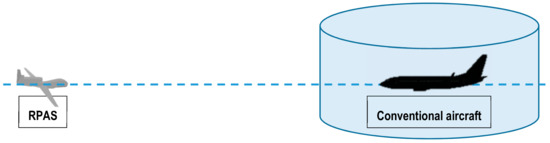
Figure 1. Conflict-geometry for a remotely-piloted aircraft system (RPAS) and a conventional aircraft flying in opposite directions. The cylinder represents the safety volume of the conventional aircraft.

The first step is to define the conflict-resolution algorithms, bearing in mind that when the aircraft cross they must both satisfy the longitudinal ($L_{min}$) and vertical ($H_{min}$) separation minima. The conflict-resolution algorithms are designed to model the case of a RPAS and a conventional aircraft; however, they work equally well with two aircraft of the same type. The key factors are the relative speed of the two aircraft, regardless of aircraft type, and the manoeuvring capabilities. When dealing with vertical manoeuvring, the main manoeuvring capability is the ROC achievable. The integration of RPASs in a non-segregated airspace must also respond to the new functionalities of a RPAS. A key feature of a RPAS is that the pilot is not located in the aircraft. This necessarily requires crucial modifications to the CNS parameters. These modifications are detailed in Section 3.

Lastly, the assumptions are as follows:

• Both aircraft fly at constant (cst) speed ($\mathrm{Mach} = \mathrm{cst}$);
• The model focusses on the en-route airspace;
• It is the RPAS which performs a vertical manoeuvre to avoid the conventional aircraft. The RPAS performs the vertical manoeuvre at constant ROC. This assumption is in line with current ATC techniques for vertical manoeuvres: Typically, ATC resolves a tactical conflict by indicating an ROC and a change of FL;
• The vertical manoeuvre must ensure safe crossing between the RPAS and conventional aircraft (separation assurance), i.e., it must respect both the vertical separation ($H_{min}$) and the longitudinal separation ($L_{min}$) minima. According to the current regulation, the separation minima in the upper airspace are $H_{min}=1000$ ft. (feet) vertical and $L_{min}=5$ nautical miles (NM) longitudinal [30]. As such, the safety volume is a cylinder of radio $L_{min}$ and height $2H_{min}$;
• The RPAS must satisfy the CNS requirements expected of en-route airspace.

2.2. Conflict-Resolution Algorithms

The goal of the conflict-resolution algorithms is to calculate the MPD, which is the final moment in which ATC should act to avoid a potential conflict. The kinematic movements of a RPAS ($x_{RPAS}, y_{RPAS}, z_{RPAS}$) and a conventional aircraft ($x_{CONV}, y_{CONV}, z_{CONV}$) are modelled by the following equations:

$$\begin{gathered} \dot{x}=V_x \\ \dot{y}=V_y \\ \dot{z}=V_z \end{gathered}$$

(1)

where $x$ is the longitudinal, $y$ the lateral, $z$ the vertical position, $t$ the time, and $V_x, V_y$, and $V_z$ the speed for each variable. Each variable acquires different values depending on the kinematic motion of the RPAS or the conventional aircraft. The lateral movement is considered null ($V_y=0$) because both aircraft are flying the same route and cross-track errors are discarded. As the conflict-resolution algorithms are based on en-route airspace, RPAS and conventional aircraft trajectories respond to the following equations:

$$\begin{gathered} V_{z CONV}=0 \\ {V}_{z RPAS}=0, \mathrm{Stretch} 1 (\mathrm{horizontal} \mathrm{stretch}) \\ {V}_{z RPAS}=ROC, \mathrm{Stretch} 2 (\mathrm{climbing} \mathrm{stretch}) \end{gathered}$$

(2)

In Stretch 1, both the conventional aircraft and the RPAS are on the same FL. In Stretch 2, the RPAS climbs at a constant ROC, while the conventional aircraft continues flying at the same FL. The RPAS manoeuvre consists of climbing in advance so as not to infringe the separation minima. The vertical separation must be $H_{min}$ when the RPAS has a horizontal separation of $L_{min}$, with respect to the conventional aircraft. Therefore, the RPAS must know in advance when it should start climbing. We call this instant the latest point of resolution (LPR), when both aircraft are separated by the MPD. The MPD is given by the following equations:

$$\begin{gathered} MPD=∆x_{RPAS}+∆x_{CONV}+L_{min}; \\ ∆x_{RPAS}=V_{x RPAS}{t}_{asc}; \\ ∆x_{CONV}=V_{x CONV}{t}_{asc}; \\ {t}_{asc}=\frac{H_{min}}{ROC}; \end{gathered}$$

(3)

where $t_{asc}$ is the time required for the RPAS to climb $H_{min}$, and $∆x_{RPAS}$ and $∆x_{CONV}$ are the horizontal distances flown by the RPAS and conventional aircraft, respectively, in the time period $t_{asc}$. Both $∆x_{RPAS}$ and $∆x_{CONV}$ (Equation (3)) are dependent on the ROC of the RPAS. Using Equations (1–3), we calculate the location of the RPAS at the moment it starts climbing to ensure the separation minima with the conventional aircraft ($t_{LPR}$). Figure 2 gives a schematic diagram of the conflict-resolution algorithm in en-route airspace.

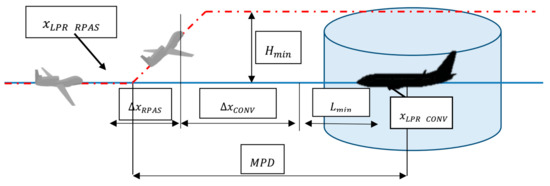
Figure 2. Schematic diagram of the conflict-resolution algorithm in en-route airspace.

Using Equation (3), the value of the MPD can be obtained by itemising $∆x_{RPAS}$ and $∆x_{CONV}$ as functions of the initial conditions ($x_{0 RPAS}, x_{0 CONV}, t_0$) and the kinematic variables of Stretch 1. The positions of the RPAS and the conventional aircraft at the LPR ($x_{LPR RPAS}, x_{LPR CONV}$) are:

$$\begin{gathered} x_{LPR RPAS}= x_{0 RPAS}+V_{x RPAS stretch 1}(t_{LPR}-t_0) \\ {x}_{LPR CONV}= x_{0 CONV}-V_{x CONV}(t_{LPR}-t_0) \\ {t}_{LPR }=t_0+\frac{\left(x_{LPR RPAS}-x_{0 RPAS}\right)-\left(x_{LPR CONV}-x_{0 CONV}\right)}{\left(V_{x RPAS stretch1}-V_{x CONV}\right)} \end{gathered}$$

(4)

3. Communication, Navigation, and Surveillance

The model set out in Section 2.2 calculates the MPD in a hypothetical scenario. This scenario is not realistic because it does not take factors that affect the behaviour of the aircraft movement or the intervention capacity of ATC into consideration. The International Civil Aviation Organization (ICAO) [31] stated that the time required to efficiently resolve a route deviation or conflict depends on three parameters:

• Navigation performance;
• Communication performance;
• Surveillance performance.

These CNS parameters have a significant influence on separation assurance because they take different errors that condition the operation. These parameters are grouped under three headings: Capacity of navigation, capacity of intervention, and risk exposure. The capacity of navigation is the accuracy with which the aircraft can fly a predefined trajectory. The capacity of intervention is the potential of the system to act appropriately in the event of potential risk and depends on surveillance, communication and ATC systems. Risk exposure is intimately bound up with the complexity of the airspace and air traffic flows. Airspace design [32,33] models risk exposure as a combination of route configuration, operational error, and traffic density:

• Route configuration involves assessing the crossing angle and the number of airways that coincide in an intersection;
• Operational error is the probability of pilot error, e.g., a pilot selecting a wrong route;
• Traffic density is the number of aircraft that operate on each airway.

As such, risk exposure lies outside the scope of this paper:

• We only consider one pairwise route configuration (although the results can be applied to different crossing angles);
• We do not take pilot errors into consideration (although they can be modelled using a failure probability [34,35]);
• We are evaluating the pairwise movement of a RPAS and a conventional aircraft.

Further work will focus on conflict risk assessment with the implementation of this new MPD in en-route airspace.

3.1. CNS Requirements

The authors carried out a literature review to ascertain the values that the CNS parameters should have to ensure that the model reflects a real operational situation. Although the parameters can be modified depending on the operational environment, if a RPAS is introduced in an airspace then the RPAS navigation systems should satisfy the CNS requirements set out by the air safety regulator.

3.1.1. Communications

The communications parameters for a RPAS are different to those of a conventional aircraft. As previously mentioned, the RPAS is not managed by a pilot on board, but rather is operated by a ground-based controller [5]. Therefore, an additional communication system is required to connect the RPS with the RPA, as can be seen in Figure 3.

Figure 3. Schematic diagram of communications between a RPAS (RPA to RPS), a conventional aircraft, and ATC [36].

The communication system comprises two channels:

• Command and control data-link (C2 data-link) between RPA and RPS;
• Communication data-link between ATC and RPS, by communication via RPA or direct to RPS.

ATC–RPS Communications:

The requirements for communication between ATC and RPAS are the same as those for communication with conventional aircraft. There are two types of communications between ATC and RPAS: Via the RPA or direct to the RPS. The authors chose to use direct communication with the RPS. The reason for this is that in the ICAO concept of operation, an intermediate communication provider communicates to the RPA via the RPS [5]. Therefore, the communication between the ATC-RPS is the same as the current communications between the ATC-conventional aircraft. The current architecture for communications between ATC and conventional aircraft is as per the required communication performance (RCP) concept. The RCP sets out the communication requirements, as regards separation assurance and flight information, without focusing on the specific technology [37]. The RCP type depends on the transaction time. The transaction time is the length of time between the start of the communication, i.e., when the pilot or controller initiates the communication, until the reply of the receptor is received. Table 1 shows the different RCP types proposed by ICAO.

Table 1. Required communication performance (RCP) requirements [37].

RCP	Transaction Time (s)	Continuity (Prob./FH)	Availability (Prob./FH)	Integrity (Acceptance Rate/FH)
RCP 10	10	0.995	0.99998	10−5
RCP 60	60	0.99	0.9995	10−5
RCP 120	120	0.99	0.9995	10−5
RCP 240	240	0.99	0.9995	10−5
RCP 400	400	0.99	0.999	10−5

The RCP type used in this study is RCP 10. The transaction time is defined as the time at which 95% ($2\sigma$) of all transactions that are initiated are, in fact, completed. This RCP is typical for environments where the longitudinal separation minimum is 5 NM.

RPS–RPA Communications:

Communications between the RPA and the RPS are key to the introduction of RPASs in non-segregated airspace. This requirement is based on the RLP (required end to end C2 link performance) concept [38] and is similar to the RCP requirement. Therefore, RLP determines the values of the communications requirements for the command and control (C2) data-link of a RPAS. Similar to RCP, each RLP type depends on the transaction time, continuity, availability, and integrity. A different RLP type may be used depending on the level of safety required in the airspace or operation. Table 2 gives the different RLP types that RPAS regulators typically use:

Table 2. Required C2 link performance (RLP) requirements [38].

RLP	Transaction Time (s)	Continuity (Probability)	Availability (Probability)	Integrity (Acceptable Rate)
RLP A	3	0.999	0.9999	10−5
RLP B	5	0.999	0.999	10−4
RLP C	15	0.999	0.999	10−4

Each of these RLPs specifies the RPA-RPS communications requirements for the RPAS operation. The relationship between RLP and transaction time is similar to that of the RCP and transaction time. The transaction time is the length of time between the start of the communication, i.e., when the pilot or the C2 system starts the transaction, until the answer is received by the receptor and the transaction has been completed. Therefore, the RLP is the maximum nominal time, within which 95% ($2\sigma$) of the operational communication transactions must be completed. The authors did not select any RLPs because there are currently no regulations specifying which RLP should be used. The RLP was considered to be a variable and, in the study, we assessed how the MPD varied as a function of the RLP.

3.1.2. Navigation

When characterising navigation performance, the assumption is that aircraft operate in a specific airspace. European en-route airspace is currently being developed for area navigation 5 (RNAV 5) [33]. RNAV 5 is a specification of area navigation that requires a determined accuracy value for across-track positioning (which must be satisfied 95% ($2\sigma$) of the time) but not for along-track. Moreover, Global Positioning System’s (GPS) positioning errors can be discarded by comparison with communication and surveillance errors. Therefore, the navigation error is not considered in this work.

3.1.3. Surveillance

The aviation surveillance system is based on the radar system in use in Europe and the USA. The surveillance system provides ATC with a view of the air traffic situation. Although there are other surveillance systems, in this work the authors did not consider them. Eurocontrol [39] specified the operational requirement for a secondary radar (SSR) to support the ATC system. The main surveillance requirement for this study is the en-route positioning error $N\left(0;0.27\right)$ NM.

3.2. CNS Modelling

The last step is to model the CNS requirements and to introduce them into the conflict-resolution algorithms. As previously mentioned, the CNS requirements are considered to be errors of position or time. If these errors are not taken into consideration when estimating the MPD, the result is not reliable because it does not take the possibility of the systems failing into account. Consequently, the value of MPD in Section 2 is less than the real value. See Figure 4.

Figure 4. Schematic diagram of conflict-resolution between a RPAS and a conventional aircraft.

In the situation shown in Figure 4, the conflict-resolution algorithms assess the situation of a RPAS and a conventional aircraft flying along the same route in opposite directions. As per the assumptions set out in Section 2.1, across-track errors (XTT) were discarded, i.e., the XTT navigation error was not considered. Table 3 summarises the operational requirements that affect the calculation of the MPD.

Table 3. Summary of communication, navigation, and surveillance (CNS) operational requirements.

CNS Operational Requirements
Communication	RPA–RPS Communications: 3, 5, or, 15 s (RLP A, B, or C)
	RPS–ATC Communication: 10 s (RCP 10)
Navigation	No error is considered
Surveillance	Route error: 0.27 NM

The estimation of the real MPD depends on the errors associated with the CNS parameters. The authors used the root mean square of the CNS errors applied to the MPD. This hypothesis is widely used with CNS errors and is based on the independency of the errors by independent variables [40,41]. Thus, Equation 5 gives the final value of the MPD:

$$\begin{gathered} MPD=x_A-x_B \\ {x}_A=x_{LPR CONV}+\sqrt{x_{CO{M}_{CONV}}^2+x_{SUR}^2} \\ {x}_B=x_{LPR RPAS}-\sqrt{x_{CO{M}_{RPAS}}^2+x_{SUR}^2} \end{gathered}$$

(5)

where $x_{COM}=V_x\left(t_{RCP}+t_{RLP}\right)$ is the communication error that depends on the RCP/RLP time and the speed of the conventional aircraft or RPAS. $x_{SUR}$ is the communication, navigation, and surveillance error. Therefore, the MPD is obtained based on the resolution manoeuvre and the CNS-error buffer.

4. Monte Carlo Simulations

The Monte Carlo (MC) method is a technique used to resolve mathematical problems via the simulation of random variables [40]. This method can solve a large variety of determinist or stochastic mathematical problems by combining statistical concepts with the generation of pseudo-random numbers. MC simulations are useful in situations where it is not possible to obtain information about the true state, or when experimentation is not possible.

MC method is the most suitable technique for calculating a global MPD to facilitate the work of ATC in resolving conflicts with RPASs. MC simulations analyse a large number of potential situations between a RPAS and a conventional aircraft, taking the statistical relationships between the variables into account. However, there are different optimisation methods that could provide the optimal solution for a specific air traffic scenario [42,43,44,45]. Optimisation techniques may be used in future studies to optimise ATC interventions to improve the integration of RPASs in non-segregated airspace.

Monte Carlo Modelling

This section explains how the different variables that the authors selected for the Monte Carlo simulations are modelled. The main aim is to ascertain how variations in the operational variables affect the MPD. Monte Carlo simulations are defined based on different types of variables:

• Boundary conditions are those variables that are fixed. These variables do not change and cannot be considered independent variables. If the boundary conditions change, the results of the Monte Carlo simulations may differ. For instance, in this study the authors set specific values for FL and the Mach of the RPAS;
• Independent variables have a statistical distribution. These variables typically have normal distributions, though some may have uniform distributions;
• Dependent variables are the unknowns whose values we wish to estimate.

Table 4 gives the boundary conditions and independent and dependent variables.

Table 4. Boundary conditions, independent and dependent variables for the Monte Carlo simulations.

Boundary Conditions
Mach RPAS (VRPAS)	0.5
ROC RPAS (ROC)	1000–2000 ft/min (minute)
Flight Level (FL)	FL 250–350
RLP Communications	Lognormal (A, B, and C)
RCP Communications	Lognormal (RCP 10)
Independent Variables
Mach Conventional Aircraft (VCONV)	$U\left(0.76;0.8\right)$
Wind (W)	$N\left(15.2;20.3\right)$ (m) meter/s
Speed Error (ϵV)	$N\left(0;5\right)$ knots
Vertical Error (ϵZ)	$N\left(0;50\right)$ ft
ROC Error (ϵROC)	$N\left(0;25\right)$ ft/min
Surveillance Error (xSUR)	$N\left(0; 0.27\right)$ NM
Dependent Variables
MPD	(NM)

Table 4 shows the variations that affect the variables referred to in the equations in Section 2 and Section 3. The variables were treated as follows:

• The RPAS Mach did not vary because there was no available data on the speed at which the RPAS could operate. In other words, the RPAS Mach was considered to be a boundary condition. However, this could be treated as an independent variable in future studies;
• The ROC varied from 1000–2000 ft/min in increments of 100 ft/min, although smaller increments could also be used. The ROC error (${ϵ}_{ROC}$) was assumed to have normal distribution [46];
• RLP communications were calculated for the three cases (A, B, and C). Although MC simulations were performed considering each RLP, the transaction time associated was modelled as a lognormal distribution. Lognormal distribution was selected because the transactions time must be strictly positive;
• The RCP communications were fixed as a technical requirement for ATC purposes in 10 s. However, due to the stochastic behaviour of the communication transaction time, it was modelled as a lognormal distribution, similar to RLP;
• The vertical positioning error (${ϵ}_z$) was considered to be an independent variable. Unlike along-track or across-track navigation, there is no vertical navigation requirement for en-route flights. We, therefore, modelled the vertical positioning error as a normal distribution $N(0;50$) ft [47], as per GPS standard requirements;
• The authors chose to carry out the simulations at FL 270. This FL was selected because it ensured that all flights were above a terminal manoeuvring area (TMA) and took place in the upper airspace (>FL 245). Nonetheless, a sensitivity analysis was carried out for the airspace between FL 250 and 350;
• Variations in Mach number ($V_{CONV}$) affect the MPD because the faster the conventional aircraft, the larger the MPD. The authors studied the variation in speed of conventional aircraft in Spanish en-route airspace. The study concluded that the variation in speed of the conventional aircraft followed a typical statistical distribution. To overcome this uncertainty, we chose to model the most typical Mach values, i.e., those in the range 0.76–0.8, using a uniform distribution;
• Aircraft in en-route airspace must satisfy a speed requirement, namely, that the speed error (${ϵ}_V$. ) be $\pm 5$ knots [46]. The same speed error was used for the RPAS Mach;
• The wind was modelled as a normal distribution using real data, obtained at FL 270 in Madrid (Spain). Wind affects the speed of RPASs and conventional aircraft, according to the following equation:

  $$\dot{x}=V_x+W+{ϵ}_V$$

  (6)

5. Results and Discussion

This section presents the results of the Monte Carlo simulations to estimate the MPD and discusses their implications with respect to ATC. At total of 10⁵ simulations were carried out to ensure that the value obtained was statistically significant. The two main variables of this study (boundary conditions) are the ROC and the RLP. Both variables are crucial because they can impose limitations on RPAS operations. Figure 5 gives the results of the Monte Carlo simulations for a ROC of 2000 ft/min and varying RLP. The results show that as the RLP time increases, so too does the average value of the MPD, although it keeps the shape of a normal distribution. Furthermore, the results of the simulations followed a normal distribution. Although the plots show a light deviation from the typical normal distributions, the Kolmogorov–Smirnov test confirmed the adequacy of the results to a normal distribution, with a coefficient of 5%.

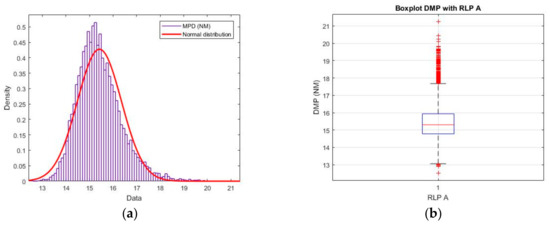
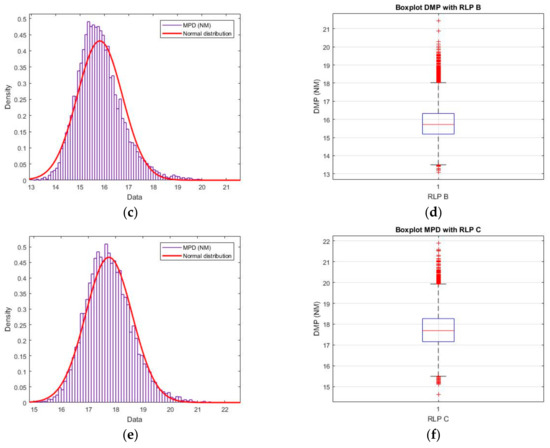
Figure 5. Results of Monte Carlo simulation for a ROC of 2000 ft/min and varying RLP. The charts on the left-hand side (a,c,e) show the normal distributions for each experiment. The charts on the right-hand side (b,d,f) give the corresponding boxplots.

Figure 6 shows the 95% statistical value of the MPD for different values of RLP (RLP A, B, and C) and ROC (increments of 100 ft/min).

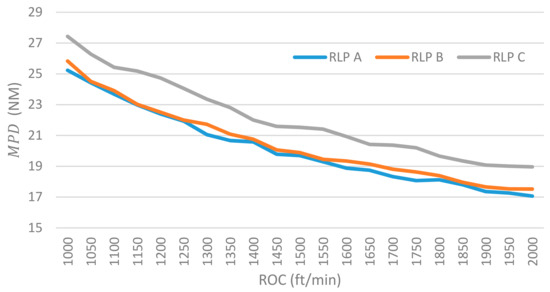
Figure 6. Variation of the minimum protection distance $\left(\mathrm{MPD}\right)$ as a function of RLP and rate of climb (ROC).

Figure 6 shows how the MPD decreases as the ROC increases and the RLP decreases. This result was expected because, by increasing the vertical airspeed and reducing the communication time, it is only logical that the MPD will become shorter. However, if we look at the shape of the MPD curves, we see that the relationship is not linear. Therefore, an increase in ROC does not imply a proportional decrease in MPD. This result is significant because it could impose specific ROC values when operating in non-segregated airspace. The reduction in the MPD obtained by increasing the ROC from 1000 ft/min to1500 ft/min is double that obtained by increasing the ROC from 1500 ft/min to 2000 ft/min. The investment in RPAS navigation systems may vary significantly depending on whether a fixed ROC of 1500 ft/min or 2000 ft/min is used. The extra investment required for a ROC of 2000 ft/min may not be justifiable when the reduction in MPD is minimal. The consequences of this finding for ATC will be studied in conjunction with the aviation authority in future works.

Table 5 summarises the statistical values of the Monte Carlo simulations, specifically for ROC = 1000, 1500 and 2000 ft/min. These results confirm that the average value of the MPD increases when the RLP is degraded, but the standard deviation does not increase in the same proportion, although it is reduced with ROC increments. Moreover, if we attend the ROC variation, the MPD increases when the ROC decreases. Both results were expected because they respond to the natural behaviour of aircraft performances.

Table 5. Statistical values of $\mathrm{MPD}$ estimated using the Monte Carlo simulations.

Boundary Conditions	$MPD$ $\mathit{N}\mathbf{\left(}\mathit{\mu },\mathit{\sigma }\mathbf{\right)}$ NM	$\mathbf{95}\mathbf{\%} \mathbf{\left(}\mathbf{2}\mathit{\sigma }\mathbf{\right)} MPD$
ROC = 1000 ft/min
RLP A	$N\left(22.58; 1.75\right)$	26.08 NM
RLP B	$N\left(22.82; 1.71\right)$	26.24 NM
RLP C	$N\left(24.90; 1.72\right)$	28.34 NM
ROC = 1500 ft/min
RLP A	$N\left(17.88; 1.10\right)$.	20.08 NM
RLP B	$N\left(18.29; 1.05\right)$	20.39 NM
RLP C	$N\left(20.16; 1.01\right)$	22.18 NM
ROC = 2000 ft/min
RLP A	$N\left(15.63; 0.88\right)$	17.39 NM
RLP B	$N\left(15.96; 0.83\right)$	17.62 NM
RLP C	$N\left(17.96; 0.81\right)$	19.58 NM

The results of the Monte Carlo simulations are as follows:

• An increase in the RLP (the communication time between the RPS and RPA) leads to an increase in the MPD. With a ROC of 2000 ft/min, going from the RLP A to RLP B, the increase in the MPD is about 1.5%. Going from the RLP A to the RLP C, the increase is up to 10%. The relationship between a variation in the RLP and the corresponding variation in the MPD is not linear;
• An increase in the ROC leads to a decrease in the MPD; however, the relationship is not linear. For example, if we examine the decrease in the MPD with the RLP A, we see that, by increasing the ROC from 1000 ft/min to 1500 ft/min, we get a reduction in the MPD of almost 6 NM. However, if we increase the ROC from 1500 ft/min to 2000 ft/min, the corresponding reduction is roughly 2.6 NM. This result is significant because it could limit the ROC values that can be used;
• The standard deviations for all the experiments are less than 2 NM. Variations in the RLP barely affect the standard deviation. However, by increasing the ROC to 2000 ft/min, we can reduce the standard deviations by more than 1 NM;
• The MPD varies from 17 NM to 26 NM. The minimum MPD value (17.33 NM) is obtained for RLP A (3 s) and the maximum ROC (2000 ft/min). If the regulators set a fixed MPD of 20 NM, then several combinations of RLP and ROC are possible. For example, with a ROC of 2000 ft/min, all values of the RLP give a MPD of less than 20 NM. With a ROC of 1500 ft/min, both the RLP A and RLP B give a MPD of less than 20 NM. These combinations can be key for the future integration of RPASs in non-segregated airspace because they will have a significant impact on ATC and RPAS manufacturers;
• The results are for FL 270. However, a sensitivity analysis of the FLs from FL 250 to 350 leads to a variation in the MPD of less than 1NM. These results show that the impact of FLs on the MPD is not significant and may be discounted.

This study concludes that the main operational variables affecting the MPD are the ROC and RLP. The range of values that these variables are allowed to have may limit the potential for integrating RPASs. Therefore, a RPAS may be required to have a specific ROC for every FL. If ATC specifies an operational limit for the value of the MPD and the regulator specifies a RLP, the RPAS manufacturer may be required to ensure a specific ROC for each FL. If the RPAS manufacturer is unable to guarantee the required ROC, then it may be necessary to prohibit the RPAS from operating at that FL. This restriction could have regulatory and practical consequences that may require further research.

6. Conclusions

This paper studied the definition, development, and estimation of the minimum protection distance (MPD) required to avoid a potential conflict between a RPAS and a conventional aircraft. The MPD is the distance at which ATC has the final opportunity to instruct a RPAS to start climbing to avoid a separation minima infringement. This study only presents the results for a head-on encounter between a RPAS and conventional aircraft because it is the worst scenario. The main contribution of this paper to the literature on RPAS separation assurance is that it quantifies the MPD. To the best of the authors’ knowledge, no previous study has attempted to do this. Furthermore, the study introduces two fundamental concepts: The use of vertical manoeuvres for RPASs and the impact of CNS requirements on the MPD. The CNS requirements for RPASs are the same as those currently in force for conventional aircraft, except for the fact that, in the case of RPASs, an additional communications link, RLP, will be required. The most significant finding of this research was that the main contributors to the value of the MPD were the ROC and the RLP. Going from RLP A to RLP B, the increase in the MPD was about 1.5%. Going from RLP A to RLP C, the increase was up to 10%. Conversely, an increase in the ROC led to a decrease in the MPD. However, the relationships between the impact of variations in the RLP and ROC on variations in the MPD were not linear. This fact could be crucial for the future integration of RPASs, because the extra investment required to increase the ROC may not be justifiable when compared to the improvement in the MPD and, consequently, the ability of ATC to intervene. Further research is required to study the impact of specific RLP and ROC values on ATC.