Bayesian Network-Based Failure Risk Assessment and Inference Modeling for Biomethane Supply Chain

Abstract

To identify and evaluate the failure issues in the livestock manure-to-biomethane supply chain, this study employs a Bayesian network approach with three inference analysis methods: diagnostic analysis, sensitivity analysis, and maximum causal chain inference. First, the main hazard categories affecting the failure of the supply chain are identified, establishing risk indicators for feedstock collection, pretreatment, anaerobic digestion, purification and upgrading, transportation, and biomethane end-use. Then, the half-interval method and possibility superiority comparison are used to calculate and rank the severity of related accidents, obtaining the severity ranking of secondary indicators as well as the severity ranking of work items and risk items. Finally, Bayesian forward inference is applied to investigate the failure probability of the supply chain, combined with backward inference to identify the risk factors most likely to cause supply chain failures and trace the formation of failure hazards. The Bayesian sensitivity analysis method is ultimately applied to determine the key hazards affecting supply chain failures and the correlations between accident hazards, followed by validation. The results show that the failure probability of the supply chain through causal inference is approximately 54.76%, indicating relatively high failure risk. The three factors with the highest posterior probabilities are mechanical stirring failure C₃ (88.11%), corrosion-induced ammonia leakage poisoning D6, and equipment explosion caused by excessive pressure due to overheating during dehumidification heating D₉, which are the hazards most likely to cause failures in the supply chain. Improper operations and the toxicity of related chemicals are key hazards leading to supply chain failures, with the correlation between accident hazards presented as a hazard chain by integrating severity and accident probability, and the key risk points in the supply chain are identified.

1. Introduction

In the face of intensifying global climate change, the pursuit of carbon neutrality has become a critical worldwide strategic objective [1]. Achieving this, particularly within the “dual carbon” framework, accords significant strategic value to processes like anaerobic digestion, which converts waste into renewable biomethane [2]. The agricultural sector, a major contributor accounting for approximately 10–12% of global anthropogenic greenhouse gas emissions, presents a key mitigation opportunity [3]. Implementing effective manure management is therefore imperative, offering substantial potential to reduce emissions and curb global warming [4]. Internationally, biomethane is gaining prominence, as evidenced by its inclusion in the EU’s Green Deal renewable energy targets. Germany, a leader in this field, hosts over 9000 biogas plants and its installed capacity represents nearly half of Europe’s total [5,6]. Similarly, China is vigorously promoting the biogas industry through national policy. The National Development and Reform Commission (NDRC) has set a goal to exceed a 75% comprehensive utilization rate for livestock and poultry manure by 2025 [7]. To this end, China has already constructed and operationalized approximately 7400 large-scale biogas projects, the majority of which include power generation capabilities [8,9,10,11].

However, ensuring the safe operation of these biogas projects is a critical concern. In Germany and the EU, industry statistics report an accident rate for biogas facilities ranging from 0.1% to 0.3%. Globally, this frequency may be higher due to disparities in regulatory standards and management practices. In China, the rapid scaling of biogas infrastructure has intensified pressure on safety management systems, with incident reports in recent years highlighting the urgent need for enhanced risk control measures [12]. Despite these challenges, the resource utilization of livestock manure delivers a dual benefit: it effectively addresses agricultural pollution while contributing significantly to the energy supply. Thus, advancing this practice remains an imperative strategy.

Livestock manure holds distinct potential for energy conversion. Through anaerobic digestion, it can be transformed into biogas, which is subsequently purified to produce high-value biomethane—a resource pivotal for climate mitigation and efficient resource cycling [13]. Nevertheless, the supply chain for converting manure to biomethane is notably complex, involving multiple interconnected stages and critical components. Optimizing this chain faces several significant hurdles, including the integration of multi-source, heterogeneous data [14]; navigating complex uncertainty factors [15]; and meeting multi-dimensional decision-making requirements [16]. While existing research has largely focused on trade-offs among economic, environmental, and social objectives [17], studies dedicated to supply chain risk management within this context are scarce. The conventional, experience-driven management paradigm is insufficient for achieving precise, whole-chain oversight, underscoring an urgent need for a decision-support risk management system that integrates mathematical modeling with intelligent algorithms.

The increasing frequency of accidents at biogas projects worldwide has revealed significant technical and managerial deficiencies in the sector. While biogas is poised to expand its share in the global renewable energy mix, the lack of comprehensive safety standards remains a major barrier to its widespread adoption. Operational risks are further amplified by inherent challenges such as the high moisture content and corrosive nature of manure feedstocks, coupled with the intrinsic complexity of anaerobic digestion processes. If unaddressed, these safety concerns risk not only impeding technological adoption but also causing secondary pollution, thereby contradicting the fundamental goal of sustainable development.

Effective risk determination for the Livestock Manure-to-Biomethane (LMtB) process requires the calculation of both consequence severity and probability of occurrence. Current risk management research reflects this dual focus, with one stream dedicated to assessing severity levels at risk points and another to quantifying their likelihood, both representing methodological advances through mathematical modeling.

Risk identification forms the critical foundation for ensuring the safe and stable operation of hazardous materials logistics supply chains. Established methods such as Fault Tree Analysis (FTA), Event Tree Analysis (ETA), and Hazard and Operability Analysis (HAZOP) are commonly employed for this purpose [18,19,20,21,22]. While effective for analyzing equipment failures or simple system accidents, these traditional approaches primarily model linear event chains. Consequently, they exhibit considerable limitations when applied to complex, highly coupled systems like logistics supply chains, particularly in analyzing the interrelationships within risk networks and depicting their dynamic propagation [23,24,25,26,27]. For example, while the WBS-RBS method facilitates systematic risk identification through structural decomposition [24,25,26,27,28,29,30,31], it offers limited capability for quantitatively analyzing interactions and probability propagation among risk factors. Similarly, multi-attribute decision-making methods based on interval number ordering [32,33,34,35,36] can handle evaluative uncertainty but often depend on static weightings, making it difficult to capture the dynamic accumulation and diffusion of risks throughout a supply chain network.

In the realm of quantitative risk assessment and inference, scholars have increasingly turned to probabilistic models like Bayesian Networks (BN). For example, Jiang et al. [37] integrated Fault Tree Analysis (FTA) with fuzzy BN to assess electric vehicle fire risks, while Wang et al. [38] applied grounded theory and BN to analyze causal factors in hazardous chemical accidents. Others, such as Wang et al. [39], used Bow-tie diagrams for qualitative inference to map accident evolution in dangerous goods transport, and Lu et al. [40] employed BN to examine interactions among emergency factors. Zhang et al. [41] further demonstrated their utility in dynamic risk inference. Collectively, these studies validate BN’s effectiveness in modeling causal risk mechanisms and managing uncertainty [39,40,41,42,43,44,45,46,47].

However, existing applications largely concentrate on isolated stages or post-accident analysis, lacking an integrated, systematic framework for “end-to-end, multi-node” risk identification and dynamic assessment across the entire hazardous materials logistics supply chain. A significant methodological gap remains in effectively translating structured identification outputs—such as those from WBS-RBS—into BN topologies. Furthermore, integrating fuzzy theory to address uncertainties in expert judgment, thereby establishing a seamless chain from risk factor enumeration to probabilistic inference, is an area ripe for further exploration.

The LMtB supply chain, with its complex, multi-stage nature, presents distinct risk management challenges. Current research and practice reveal three core limitations: (1) risk identification tends to be fragmented rather than holistic, (2) quantification methods often fail to precisely capture interconnected risks, and (3) a disconnect persists between structural analysis (e.g., WBS-RBS) and predictive mathematical modeling. These shortcomings contribute to operational disruptions and inefficiencies. To address these gaps, this study proposes an integrated methodology combining WBS-RBS with Bayesian Networks. This approach offers: (1) a systematic framework for comprehensive risk identification, (2) quantitative evaluation of risk interactions via probabilistic modeling, and (3) dynamic assessment capabilities that account for complex supply chain interdependencies. Building on established BN applications for risk probability calculation, the methodology innovatively adapts WBS-RBS structuring to the bioenergy context, enabling the simultaneous evaluation of both risk severity and occurrence probability—a critical need unmet by current methods.

Accordingly, this study first employs WBS-RBS to identify risk sub-indicators within defined system boundaries. It then utilizes the half-interval method and a possibility superiority comparison matrix to calculate and rank the severity of potential accidents, thereby deriving corresponding risk consequence severity values.

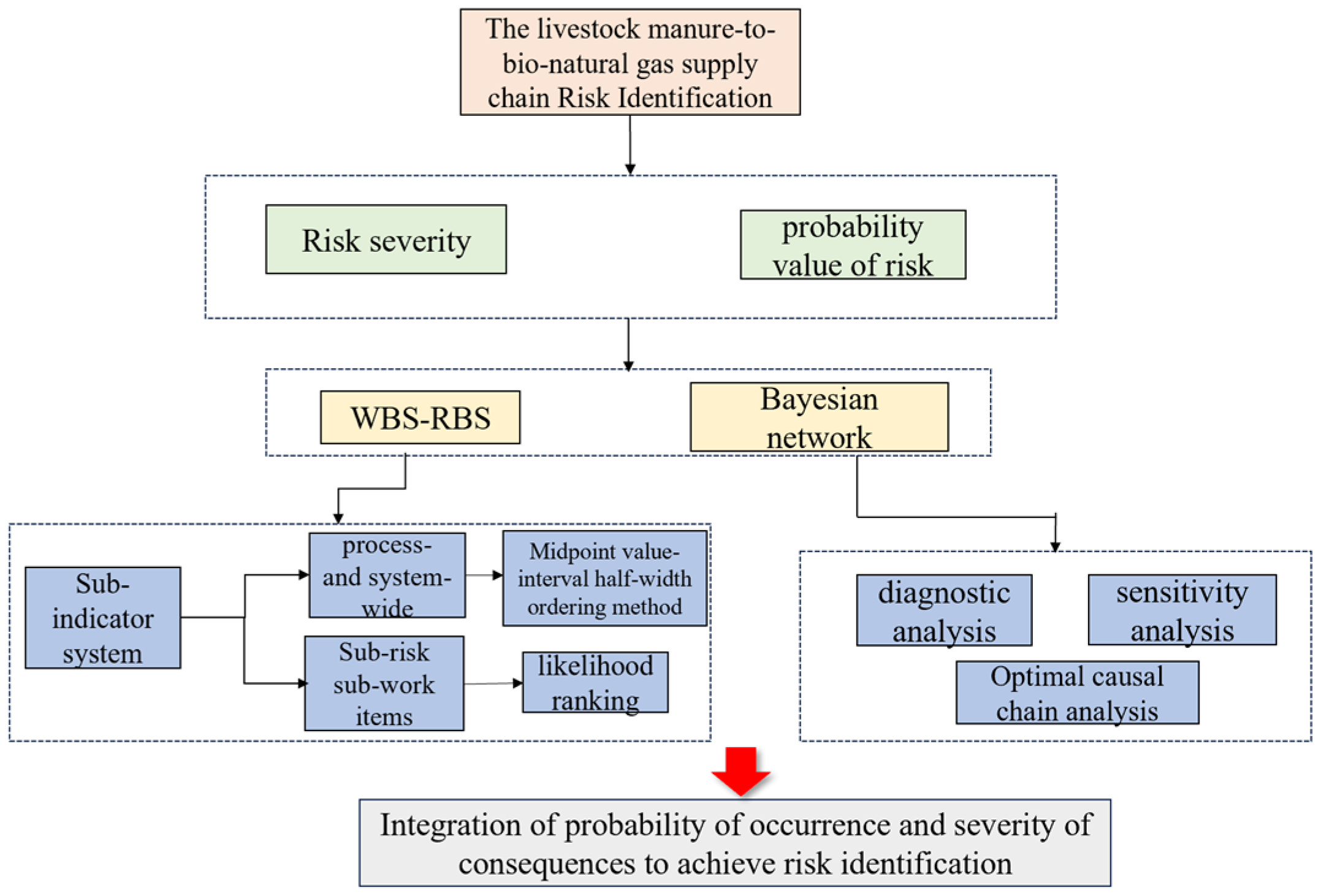
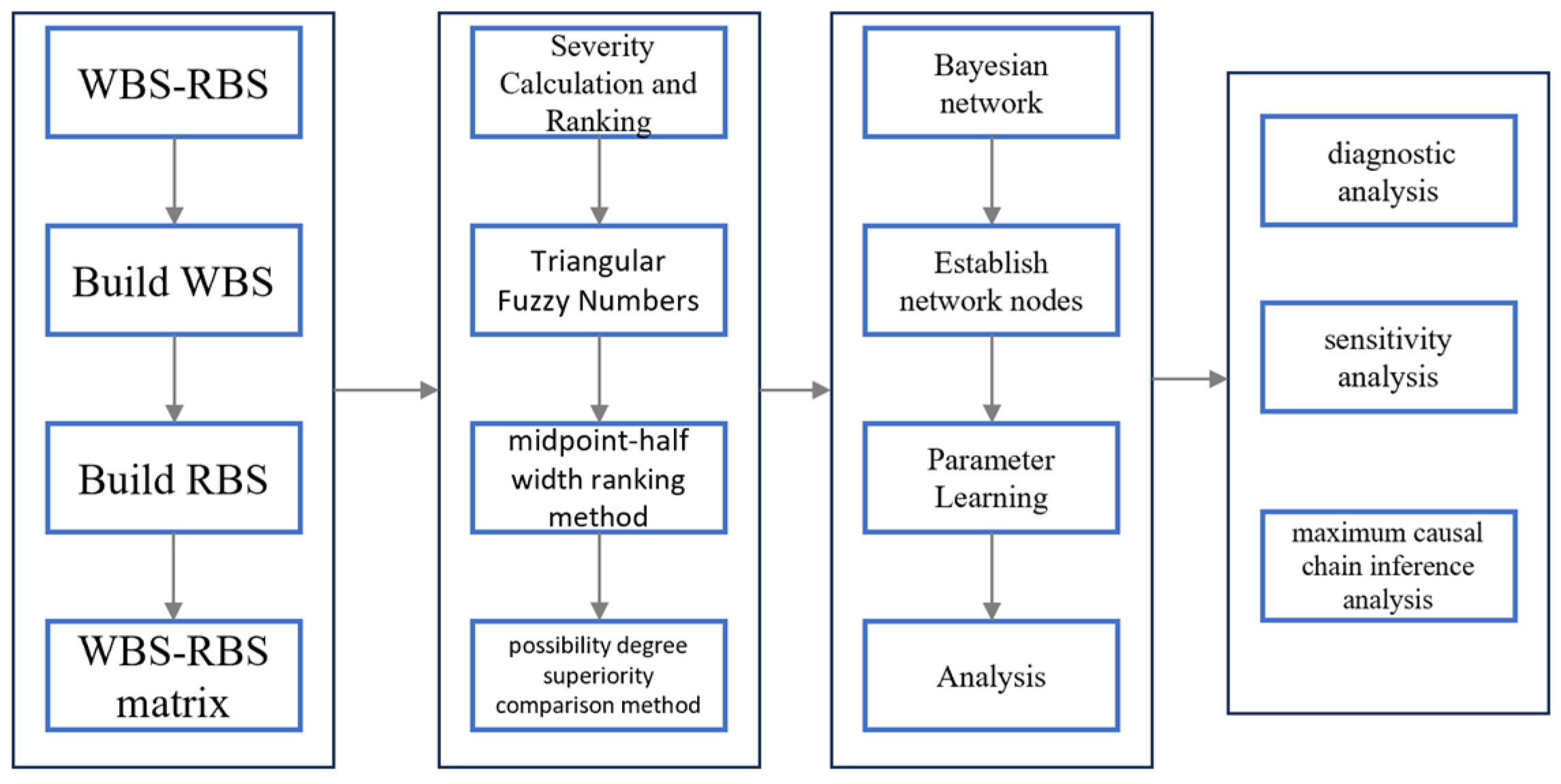
2. Materials and Methods

This study employs the Work Breakdown Structure–Risk Breakdown Structure (WBS-RBS) coupling method to systematically identify risk factors across the LMtB supply chain, defining key sub-indicators within its system boundaries. Based on this structured identification, we apply the Interval Number-Half Width Method and Possibility Degree Dominance Matrix to quantify, rank, and assign comprehensive consequence values to risk events according to their severity.

Leveraging the identified risk factors, we then construct a multi-level network model to analyze their causal interdependencies. This model is mapped into a BN to establish a probabilistic dependency structure. During the parameter learning phase, we integrate expert assessment data—expressed as qualitative interval judgments—and utilize GeNIE 4.0 software for machine learning to optimize prior probability distributions and enhance model accuracy. The resulting probability analysis enables us to propose targeted risk prevention and control strategies aimed at reducing failure risks within the LMtB supply chain, thereby providing data-driven support and a decision-making basis for industrial safety management. The overall research framework of this methodology is illustrated in Figure 1, ensuring a systematic, quantifiable, and actionable approach to risk analysis.

A distinctive feature of this study lies in its data processing methodology. The core input consists of qualitative expert judgments expressed as interval numbers. These data are utilized in two complementary ways: first, as direct input for the interval-halfwidth method to compute severity rankings; second, they are converted into constraints and observational inputs to inform BN parameter learning. For example, for root nodes, the interval midpoint is adopted as the initial prior probability, while the interval range serves as a boundary for sensitivity analysis. For causally linked nodes, interval relationships guide the initial construction of conditional probability tables, ensuring that expert uncertainty is systematically incorporated into the model’s quantitative foundation.

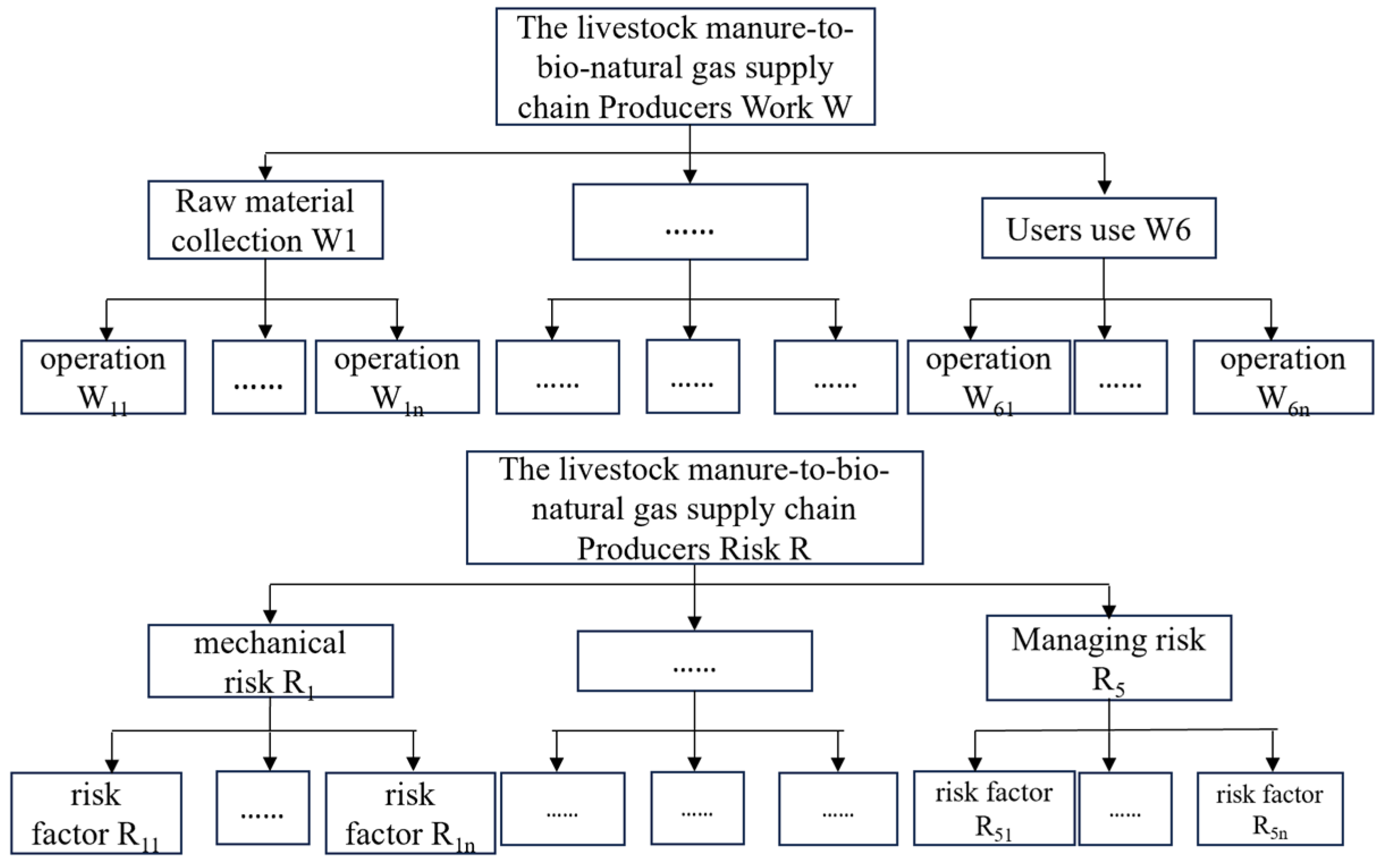
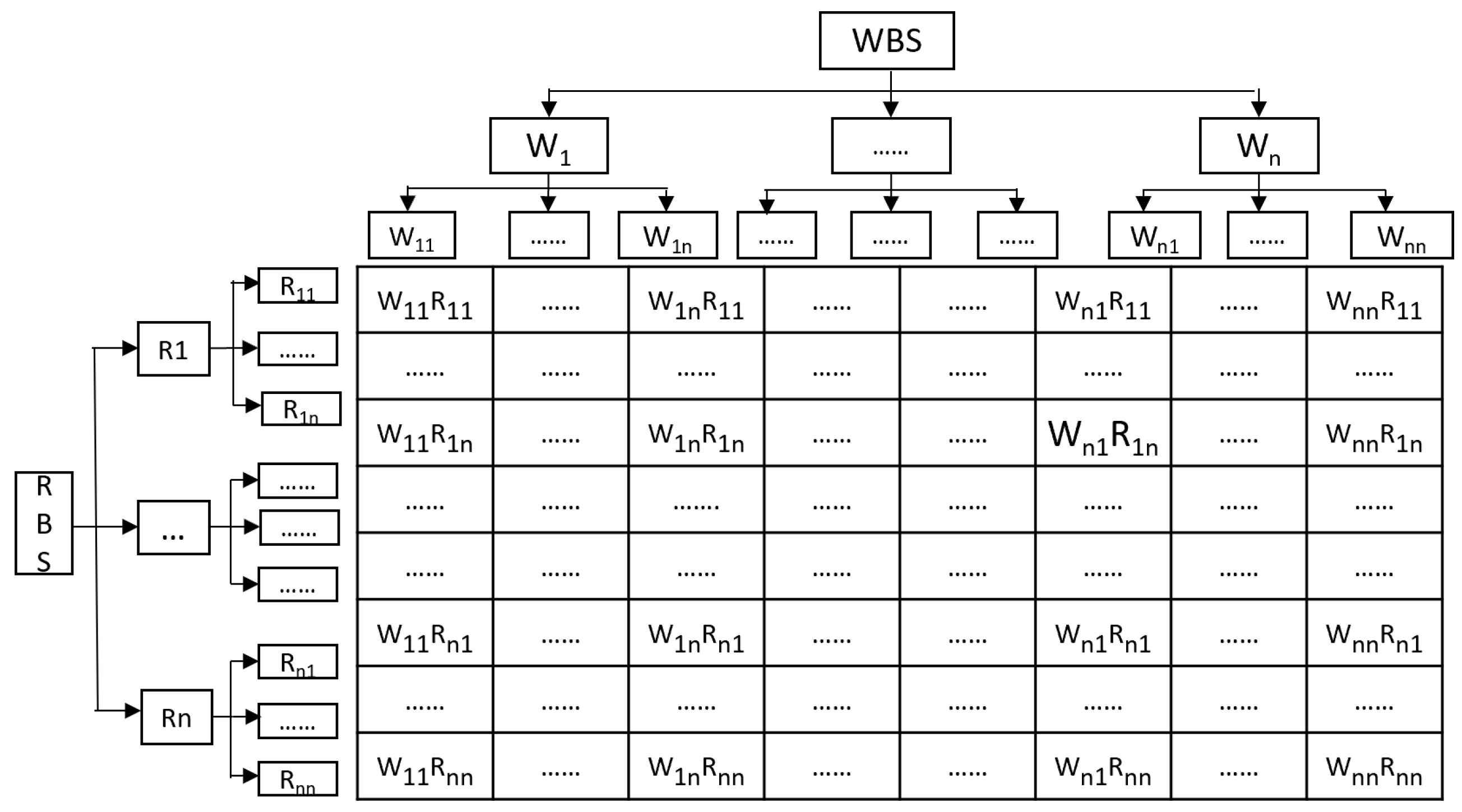
2.1. Establishment of the Indicator System

The LMtB supply chain operates as a continuous process, guided by the core principles of safety first, human-centricity, and preventive management. Structurally, the chain is divided into six distinct modules: raw material collection, raw material pretreatment, anaerobic fermentation, purification and refining, transportation, and end-use.

Given that risks within the LMtB system are dynamic and vary across production stages, a systematic analytical approach is required. The WBS-RBS method is particularly suited for this purpose, as it aligns with the sequential gas production process, enabling refined decomposition and subsequent quantitative risk analysis. Accordingly, this paper applies a WBS decomposition to the LMtB supply chain system and an RBS decomposition to transportation system risks. These are then integrated via a 0–1 coupling matrix to establish a comprehensive WBS-RBS risk matrix.

The underlying principle of this method is to deconstruct the LMtB system into its minimal working units. By analyzing the risks associated with these fundamental units, the overall system safety risks can be systematically deduced. Specifically, the WBS breaks down the production process into discrete activity units, while the RBS concurrently decomposes potential risks. The resulting WBS-RBS matrix clarifies the relationships and interdependencies among various production stages. A detailed breakdown of work items and corresponding risk items is provided in Figure 2. The analysis steps of the WBS-RBS method are shown in Figure 3.

Through WBS and RBS analysis of operational systems, a WBS-RBS matrix can be formed. By judging the risks of matrix elements, risks can be identified systematically and comprehensively. The analysis steps of the WBS-RBS method are as follows: construct WBS → construct RBS → construct WBS-RBS matrix, with the simplest operations of WBS as matrix columns and the lowest risks of RBS as matrix rows. Among them, the intersection of rows and columns represents potential risks during the operation process.

2.2. Severity Calculation and Ranking

This study applies the interval number midpoint-half width ranking method to perform system-wide risk identification and ranking for the WBS-RBS intervals across the entire LMtB supply chain. The resulting severity ranking vector is then used for segmented and categorized risk analysis.

The ranking process involves calculating a comparative value for each interval number [44]. Expert judgments are collected for scenarios where precise quantification is difficult. To standardize these qualitative inputs, linguistic variables based on a seven-level scale—from Very Low (VL) to Very High (VH) [48,49]—are used. Each linguistic term corresponds to a defined fuzzy number with associated α-cut sets. Risk levels are divided into seven grades: VL, L, FL, M, H, FH, and VH, as shown in

Table 1. Triangular Fuzzy Numbers.

Fuzzy Set	Cut Set
fVL = (0, 0, 0.1, 0.2)	fλVL = [0.1λ + 0, −0.1λ + 0.2]
fL = (0.1, 0.2, 0.3)	fλL = [0.1λ + 0.1, −0.1λ + 0.2]
fFL = (0.2, 0.3, 0.4, 0.5)	fλFL = [0.1λ + 0.2, −0.1λ + 0.5]
fM = (0.4, 0.5, 0.6)	fλM = [0.1λ + 0.4, −0.1λ + 0.6]
fFH = (0.5, 0.6, 0.7, 0.8)	fλFH = [0.1λ + 0.5, −0.1λ + 0.8]
fH = (0.7, 0.8, 0.9)	fλH = [0.1λ + 0.7, −0.1λ + 0.9]
fVH = (0.8, 0.9, 1.0)	fλVH = [0.1λ + 0.8, −0.1λ + 1.0]

. The integrated value method is employed to defuzzify these evaluations, as it offers computational simplicity and practicality. This process converts expert assessments into baseline severity values for each risk factor, utilizing the principle of fuzzy sets where membership is expressed on a continuum between 0 and 1. Specifically, triangular fuzzy numbers are applied in this analysis, with their membership function defined as shown in Equation (1).

$$F(x)=\left\{\begin{array}{ll}0\hfill & x<u\hfill \\ {\displaystyle \frac{x-u}{m-u}}& u\le x<m\hfill \\ {\displaystyle \frac{x-m}{m-d}}& m\le x\le d\hfill \\ 0& x>d\hfill \end{array}\right.$$

(1)

According to the interval number arithmetic rules as shown in Equations (2) and (3).

$${\left(u_{ij}^{kl}\right)}^{-}={\displaystyle \frac{1}{X}}{{\displaystyle \sum _x\left(u_{ij}^{kjx}\right)}}^{-}$$

(2)

$$\begin{gathered} {\left(u_{ij}^{kl}\right)}^{-}={\displaystyle \frac{1}{X}}{{\displaystyle \sum _x\left(u_{ij}^{kjx}\right)}}^{+} \\ 0\le {\left(u_{ij}^{kl}\right)}^{-}\le {\left(u_{ij}^{kl}\right)}^{+}\le 1 \end{gathered}$$

(3)

The midpoint value ${\displaystyle \frac{1}{2}}\left[{\left(u_{ij}^{kl}\right)}^{-}+{\left(u_{ij}^{kl}\right)}^{+}\right]$ e of an interval number $\left(u_{ij}^{kl}\right)$ reflects its magnitude, while the half-width ${\displaystyle \frac{1}{2}}\left[{\left(u_{ij}^{kl}\right)}^{-}-{\left(u_{ij}^{kl}\right)}^{+}\right]$ reflects the uncertainty degree of the information carried by the interval number.

The whole-process, system-wide risk identification and ranking using the interval number midpoint-half width ranking method requires calculating the ranking value of each interval number, which is then compared with the ranking values of other interval numbers. Chen and Chen [46] introduced a decision-maker penalty factor ε and proposed a relatively reasonable calculation method for interval number ranking values as Equation (4) shows:

$$\begin{gathered} f\left(a\right)={\displaystyle \frac{\left(a^{+}+a^{-}\right)}{2}}-{\displaystyle \frac{\epsilon \left(a^{+}-a^{-}\right)}{\left(a^{+}+a^{-}\right)}} \\ \epsilon >0 \end{gathered}$$

(4)

The penalty factor ε > 0 varies among different decision-makers, where more cautious individuals tend to have larger penalty factors [50].

For segmented-process and categorized-risk-factor identification and ranking, unlike the interval number midpoint-half width ranking method, the severity degree ranking method requires pairwise comparison of the obtained interval numbers, calculation of their possibility degrees, and construction of a matrix. Finally, the ranking of each risk factor is computed, thereby identifying various risks in the transportation process.

Let $a=\left[a^L,a^R\right]$, $b=\left[b^L,b^R\right]$ M_r be the maximum interval number among intervals a and b. The relative dominance degree of a over b is defined as shown in Equation (5).

$$P\left(a>b\right)={\displaystyle \frac{d\left(b,M_r\right)}{d\left(a,M_r\right)+d\left(b,M_r\right)}}$$

(5)

Assume we need to sort n interval numbers $A_i=\left[a_i^L,a_i^R\right]$ (i = 1, 2, …, n). According to the definition of relative dominance degree, pairwise comparisons are performed on the interval numbers, resulting in a dominance degree matrix as shown in Matrix (6).

$$P=\left[\begin{array}{cccc}0.5& p_{12}& \dots & p_{1n}\\ p_{21}& 0.5& \dots & p_{2n}\\ \dots & \dots & \dots & \dots \\ p_{n1}& p_{n2}& \dots & 0.5\end{array}\right]$$

(6)

Interval Number Ranking Method Steps:

Step 1: Determine the maximum interval number M_r from the given interval numbers $A_i=\left[a_i^l,a_i^R\right]$ based on the definition.

Step 2: Perform pairwise comparisons of all interval numbers to construct a dominance degree matrix $p={\left(p_{ij}\right)}_{n\times n}$.

Step 3: Calculate the ranking vector of the multiplicative consistent matrix

Assuming $w=\left(w_1,w_2,\dots ,w_n\right)$ is the ranking vector of the multiplicative consistent matrix (7)

$$w_i={\displaystyle \frac{1}{{\displaystyle \sum _{ij}^n\left(\frac{1}{a_{ij}}\right)-n}}}$$

(7)

Sort the interval numbers A₁, A₂, A₃, …, A_n in descending order based on the magnitude of $V_i\left(i=1,2,\dots ,n\right)$.

This study applies the midpoint-half width ranking method to perform a system-wide, comparative risk assessment across the LMtB supply chain using WBS-RBS interval data. This approach establishes an ordered prioritization of all sub-risk points, clarifying their relative significance. Concurrently, the possibility degree superiority comparison method enables a segmented analysis by work items and risk categories. This identifies the specific activities and factors most likely to cause severe failures, providing critical guidance for targeted risk management interventions.

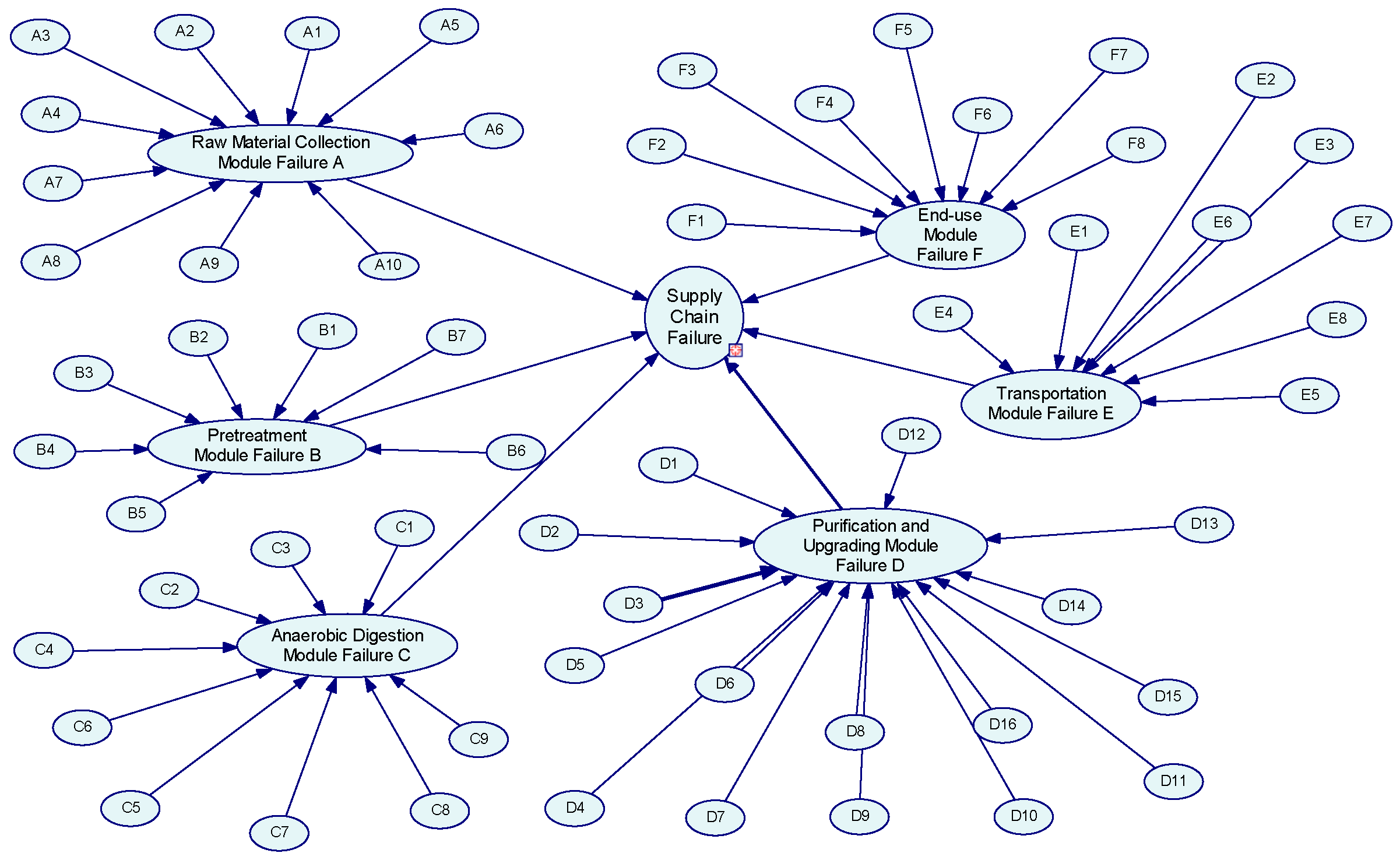
2.3. Bayesian Network (BN)

BN combines Bayesian probability reasoning with graph theory and is primarily used for decision-making under uncertainty or incomplete information [51]. Similarly to neural networks, it is a directed acyclic graph (DAG) composed of node circles and directed edges, where new information propagates between nodes. The node circles and directed edges represent variables and causal relationships between variables, respectively. As a theoretical model for uncertainty reasoning, BN can fully utilize prior information and expert knowledge to intuitively express causal relationships between random variables in graphical form and perform probabilistic inference calculations. Therefore, it is suitable for describing the relationship between failures and potential risks in the LMtB supply chain, and has significant advantages in inferring and calculating the probability of risk occurrences.

A BN is a probabilistic graphical model that integrates Bayesian probability theory with graph theory, primarily employed for decision-making under conditions of uncertainty or incomplete information [51]. It is structured as a directed acyclic graph (DAG), comprising nodes (representing variables) and directed edges (representing causal relationships), which together allow for the propagation of information throughout the network. As a formal model for uncertain reasoning, BN effectively incorporates prior information and expert knowledge to visually represent causal dependencies among variables and to perform probabilistic inference. Consequently, BN is well-suited for modeling the relationships between failures and risks within the LMtB supply chain, offering distinct advantages in inferring and quantifying the probability of risk events.

For a set of influencing events (A₁, A₂, …, A_n), Bayes’ theorem is applied to update belief in the occurrence of event B, as shown in Equation (8).

$$p\left(A_i|B\right)={\displaystyle \frac{p\left(B|A_i\right)p\left(A_i\right)}{{\displaystyle \sum _{i=1}^{n}P\left(B|A_i\right)p\left(A_i\right)}}}$$

(8)

where P(A_i) is the prior probability of event A_i; P(B|A_i) is the conditional probability of event B occurring given that A_i has occurred; P(A_i|B) is the posterior probability; i = 1, 2, …, n.

The joint probability distribution P(A) of its nodes is given by Equation (9).

$$p(A)={\displaystyle \prod _{i=1}^{n}p\left(A_i|p_a\left(A_i\right)\right)}$$

(9)

where A represents each node variable in the network; Pa(A_i) denotes all parent nodes of node A_i.

In BN analysis, three primary inference methods are utilized:

Diagnostic Analysis: This method reasons from observed effects (e.g., a system failure) back to probable causes. By setting the state of a target risk node and observing shifts in the conditional probabilities of other nodes, key risk factors can be identified. A larger change in probability indicates a stronger causal relationship with the target risk.

Sensitivity Analysis: This technique identifies the model parameters to which the output is most sensitive. A parameter is considered a sensitive factor if a small adjustment leads to a significant change in the posterior probability of a target node, indicating a high potential influence on overall system risk.

Maximum Causal Chain Analysis: This approach traces the most probable pathways of risk propagation. Beginning from a root node, it sequentially identifies the parent nodes with the highest posterior probabilities, mapping out critical risk factor chains. Visually, thicker connecting lines in the network denote stronger causal importance, highlighting key control points within the project.

Parameter learning in a BN involves estimating the conditional probability distributions that define dependencies between nodes. Common algorithms include Maximum Likelihood Estimation (MLE), Bayesian estimation, and the Expectation-Maximization (EM) algorithm. The EM algorithm is particularly valuable for handling incomplete data, as it iteratively performs maximum likelihood estimation through two steps: the Expectation (E) step, which computes expected values, and the Maximization (M) step, which updates parameters to maximize the log-likelihood function. Iteration continues until improvements in the log-likelihood fall below a predetermined threshold (e.g., ${10}^{-8}$), indicating convergence.

These learned parameters populate the network’s conditional probability tables, which form the basis for all probabilistic inferences. In this study, parameter learning and network analysis are conducted using GeNIE 4.0 software to facilitate data-driven risk management of key indicators within the LMtB supply chain.

3. Results and Discussion

Based on the integrated methodology, a network of risk factor nodes was constructed to model their logical interrelationships, which was then mapped into a BN framework. The BN inference analysis not only quantifies the relative importance of each risk factor but also delineates the potential evolution pathways of risk events. By analyzing these prior probabilities, targeted safety prevention and control measures were formulated to effectively mitigate accident likelihood, thereby providing a data-driven foundation for decision-making in LMtB supply chain management.

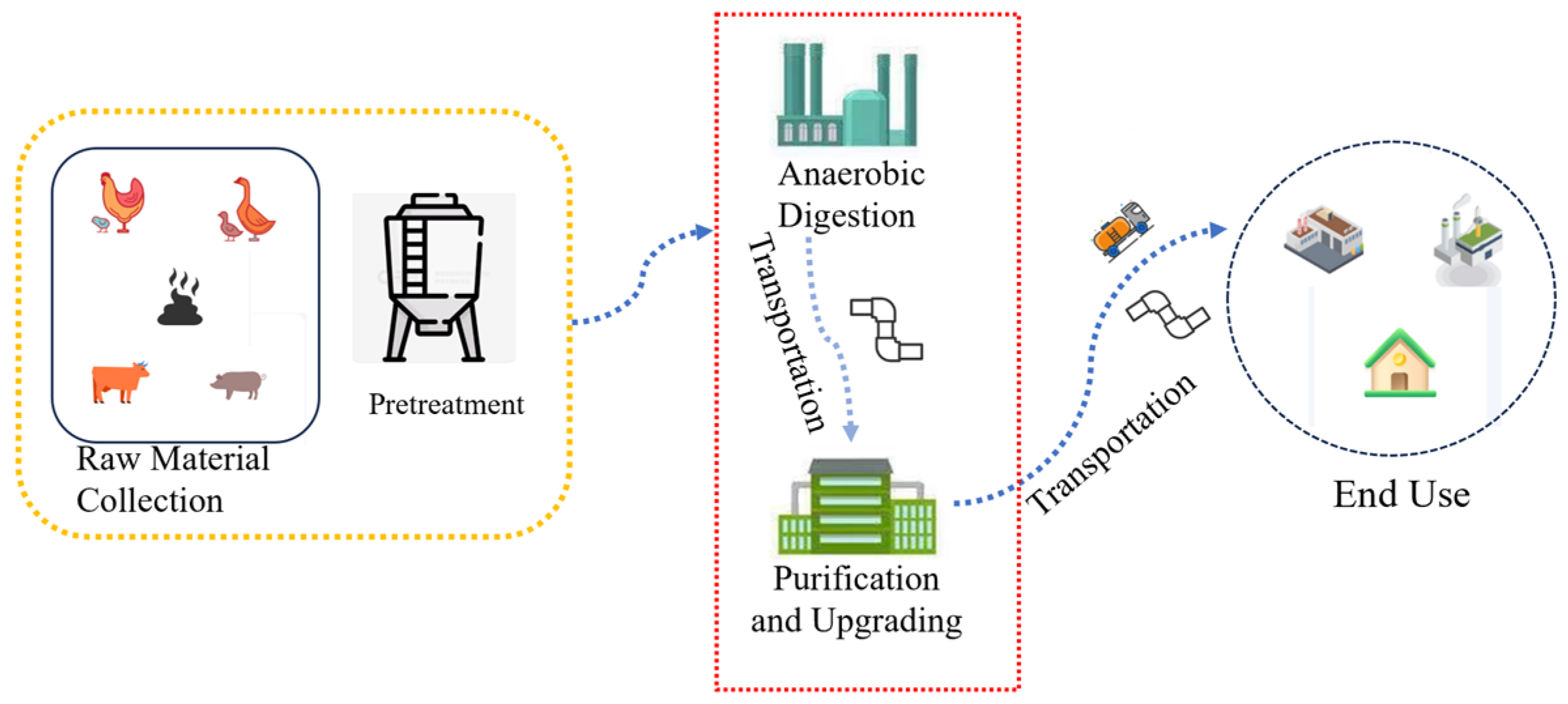
3.1. Case Study: Data and Process

This study centers on a livestock manure biogas project with a processing capacity of 100,000 kg/h as its core case study. This selection is based on its representative scale, technological typicality, data sufficiency, and policy relevance. As a mainstream medium-sized facility, its technical configuration and operational experience offer a direct reference for similar projects. Using livestock manure as feedstock, the case encompasses the complete process chain—from pretreatment and anaerobic digestion to biogas purification and digestate treatment, as shown in Figure 4. This integrated scope enables a systematic examination of core challenges in technology integration while providing a reliable data foundation for model validation and performance assessment.

The livestock manure-to-biomethane (LMtB) supply chain aims to convert agricultural waste into renewable energy, encompassing stages from raw material collection and storage to pretreatment, transportation, biomethane delivery, and end-use. However, its development is often constrained by insufficient economies of scale, unstable supply, and process integration uncertainties, leaving it reliant on policy and market support. Systematic modeling and optimization of this supply chain are therefore critical for enhancing evidence-based decision-making in agricultural waste valorization.

Using this project as a case study, the research applies the WBS-RBS method to decompose the supply chain into six sub-modules and 58 secondary risk indicators. A questionnaire was distributed to biogas field experts, yielding 64 valid responses (approximately 21.33% response rate). Respondents spanned environmental engineering, safety assessment, and manure treatment disciplines, ensuring professional breadth and structural balance. Module scores were analyzed for validity and reliability using SPSS 27.0.1 to confirm result robustness (see Tables S1–S3 in the Supplementary Materials).

The implementation process follows four main steps, illustrated in Figure 5.

Sub-indicator System Establishment: Work items and risk items were decomposed separately via WBS and RBS, then coupled using a matrix to establish sub-indicator systems for the six modules: raw material collection, pretreatment, anaerobic fermentation, purification and refinement, transportation, and end-use.

Severity Calculation: Experts evaluated sub-indicators using a seven-level linguistic scale (VL to VH). Scores were processed using triangular fuzzy numbers, validated via SPSS, and analyzed using the midpoint-halfwidth method and possibility degree comparison to derive severity values.

BN Probability Calculation: Expert scores were imported into GeNIE 4.0 for parameter learning. The BN was then analyzed to identify the most probable causal indicators, the most sensitive risk factors, and key causal chains, as outlined in Section 2.

Method Integration: Risks within the supply chain were comprehensively assessed by integrating severity rankings with probabilistic inferences, enabling prioritized and targeted risk management.

3.2. WBS-RBS Sub-Indicator Identification

According to the WBS-RBS coupling matrix, different modules of the LMtB supply chain have different risk factors. Risk Matrix Example 1 is included in Table S4 in the Supplementary Materials. The matrix of each risk factor has been studied as follows.

(1)

From the perspective of the raw material collection module, the risk factors that may cause supply chain failure in the raw material collection module are mainly divided into mechanical injury, fire risk, biological hazard, environmental risk and management risk. Mainly including: Mechanical injury in solid–liquid separation A₁ (W₁₁₁ coupled with R₁₅); Biological hazard of livestock manure to human body A₂ (W₁₁₁ coupled with R₃₁); Improper sewage collection and disposal A₃ (W₁₂₁ coupled with R₃₁, R₃₂); Improper treatment of harmful gases during incineration A₄ (W₁₃₁ coupled with R₂₁); Improper preservation during transportation of dead livestock manure A₅ (W₁₃₁ coupled with R₂₂); Improper handling by personnel leading to contact with viruses/bacteria A₆ (W₁₃₁ coupled with R₃₁, R₃₃); Unreasonable deep burial design A₇ (W₁₃₂ coupled with R₃₁); Deep burial leakage caused by natural disasters A₈ (W₁₃₂ coupled with R₄₁); Improper harmless treatment operation A₉ (W₁₃₃ coupled with R₂₃); Handling pollution and human harm caused by various heavy metals A₁₀ (W₁₄ with R₃₂).

(2)

From the perspective of the pretreatment module, the factors causing module failure include: Mechanical injury caused by improper operation during solid–liquid separation process B₁ (W₂₁₁ coupled with R₁₅); Corrosiveness caused by pH adjustment process B₂ (W₂₁₂ coupled with R₃₆); Operator poisoning caused by odor overflow B₃ (W₂₁₄ coupled with R₃₃); Mechanical injury to operators caused by improper crushing operation B₄ (W₂₁₅ coupled with R₁₁, R₁₃, R₁₅); Incomplete disinfection leading to virus/bacteria transmission and personnel injury B₅ (W₂₁₆ coupled with R₂₂); Mechanical failure injury in feed buffer system B₆ (W₂₂₁ coupled with R₁₁, R₁₃, R₁₅₎; Mechanical injury to personnel caused by pump delivery failure or improper operation B₇ (W₂₂₂ coupled with R₁₁, R₁₄, R₁₅).

(3)

Anaerobic Digestion Module. Risk factors causing module failure include: Mechanical agitator operation failure injury C₁ (W₃₁ coupled with R₁₁, R₁₄, R₁₅); Fire risk during anaerobic digestion C₂ (W₃₁ coupled with R₂₁); Mechanical agitator failure due to poor management/organization C₃ (W₃₁ coupled with R₅₁, R₅₂); Chemical toxicity from sulfide leakage during pre-desulfurization C₄ (W₃₂ coupled with R₂₂, R₃₃, R₃₅, R₃₆); Operator burns from improper coil contact C₅ (W₃₂ coupled with R₂₂, R₃₃, R₃₅, R₃₆); Burns due to inadequate heating coil supervision C₆ (W₃₃ coupled with R₁₂, R₂₂); Mechanical failure in feed buffer system C₇ (W₃₄ coupled with R₁₁, R₁₃, R₁₅, R₂₁); Operational impacts from poor supervision C₈ (W₃₄ coupled with R₅₁); Poor equipment pipeline design C₉ (W₃₄ coupled with R₅₂).

(4)

Purification and Upgrading Module. Risk factors include: Chemical toxicity from leaks D₁ (W₄₁ coupled with R₂₃); Oxygen deficiency from sulfur compound leaks D₂ (W₄₁ coupled with R₃₄, R₃₅); Equipment corrosion from improper desulfurization D₃ (W₄₁ coupled with R₃₆); Combustion from ignition sources D₄ (W₄₁ coupled with R₂₁); Oxygen deficiency from nitrogen compound leaks D₅ (W₄₂ coupled with R₂₃); Ammonia poisoning from corrosion leaks D₆ (W₄₂ coupled with R₃₄, R₃₅); Operator burns from improper dehumidifier contact D₇ (W₄₃ coupled with R₁₂); Physical injuries from operational errors D₈ (W₄₃ coupled with R₁₃); Equipment explosion from overheating D₉ (W₄₃ coupled with R₂₂); Leakage incidents D₁₀ (W₄₃ coupled with R₂₃, R₃₄); Other solid handling operations Mechanical failure injury D₁₁ (W₄₄ coupled with R₁₅); Solid treatment failures from poor management D₁₂ (W₄₄ coupled with R₅₁, R₅₂); Explosions from improper flare operation D₁₃ (W₄₅ coupled with R₂₁, R₂₂); Harmful gas leaks D₁₄ (W₄₅ coupled with R₂₃); Oxygen deficiency D₁₅ (W₄₅ coupled with R₃₄); Accidents from pipeline design flaws D₁₆ (W₄₅ coupled with R₄₂).

(5)

Transportation Module. Risk factors include: Leaks from operational errors E₁ (W₅₁ coupled with R₂₂, R₂₃); Explosions when leaks meet ignition sources E₂ (R₅₁ coupled with R₂₁); Operator frostbite from leaks E₃ (W₅₁ coupled with R₂₂); Insufficient safety training/supervision E₄ (W₅₁ coupled with R₅₂); Pipeline explosions from leaks/ignition E₅ (W₅₂ coupled with R₂₁, R₂₂, R₂₃, R42, R₅₂); Poor pipeline network design E₆ (W₅₂ coupled with R₄₂); Management deficiencies E₇ (W₅₂ coupled with R₅₂); Natural disaster damage E₈ (R₄₁).

(6)

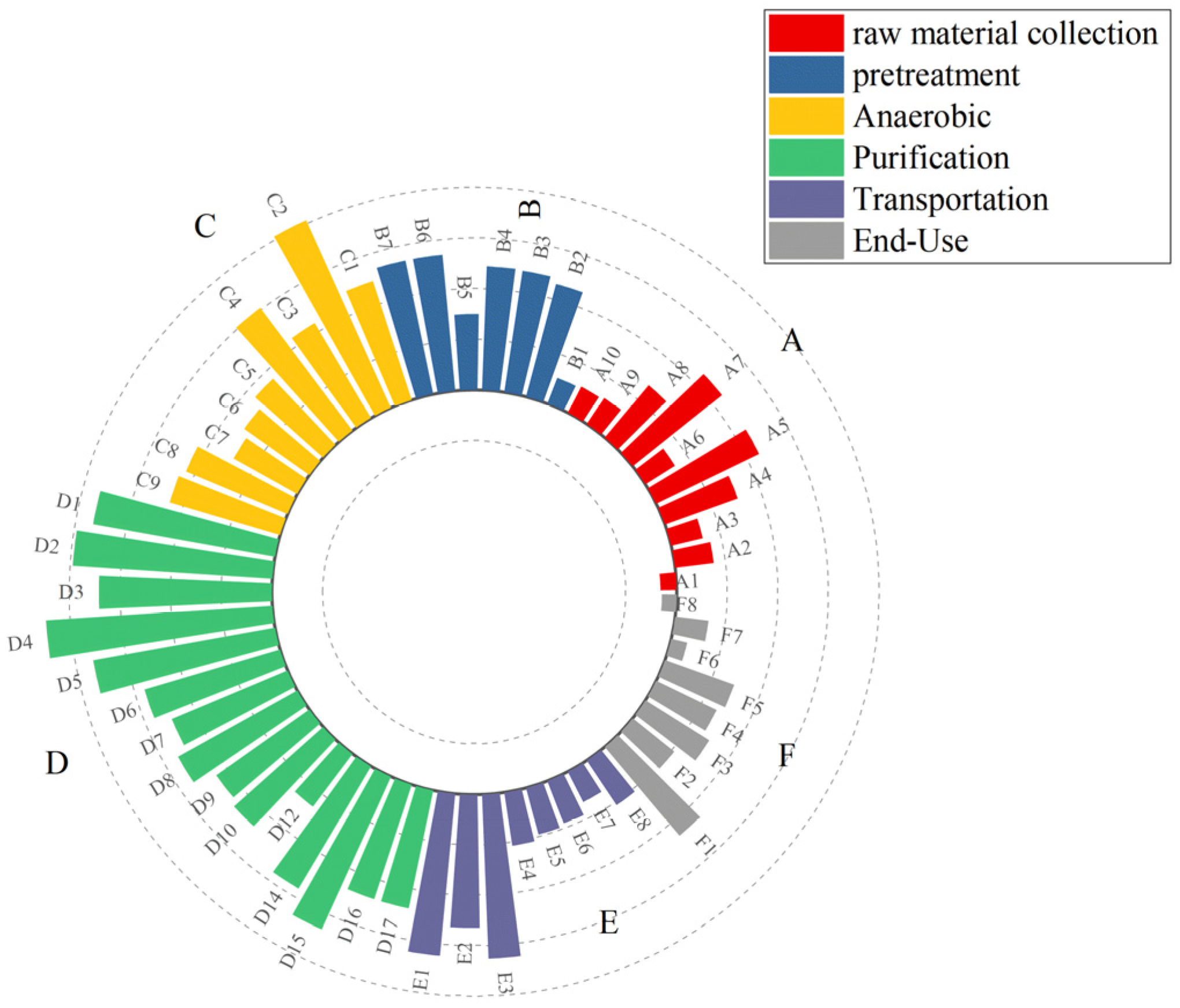
End-Use Module Risk factors include: Fuel supply explosions F₁ (W₆₁ coupled with R₂₁); Consequences of poor pipeline design F₂ (W₆₁ coupled with R₄₂); Insufficient safety awareness F₃ (W₆₁ coupled with R₅₂); Inadequate supervision F₄ (W₆₁ coupled with R₅₃); Burns from circulating water pipes F₅ (W₆₂ coupled with R₂₁); Mechanical explosions from overpressure F₆ (W₆₂ coupled with R₄₂); Chain explosions from poor heating pipe management F₇ (W₆₂ coupled with R₅₂); Combustion explosions during pipeline injection F₈ (W₆₃ coupled with R₂₁); The complete indicator system and full process risk values are shown in Figure 6. The detailed indicators are listed in Table S1 in the Supplementary Materials.

3.3. The Whole-Process, System-Wide Risk Identification

The midpoint-radius interval ranking method requires calculating the ranking values of interval numbers throughout the Biomethane supply chain process from livestock and poultry manure, then comparing them with other interval ranking values. Risk levels are categorized into seven grades: VL, L, FL, M, H, FH, and VH, with fuzzy processing applied as shown in Table 1. We calculated the relevant severity using Equations (1)–(7). The results indicate that risks are concentrated in the purification and upgrading module, where both the highest risk value and sub-risk points occur within this module, as shown in Figure 7.

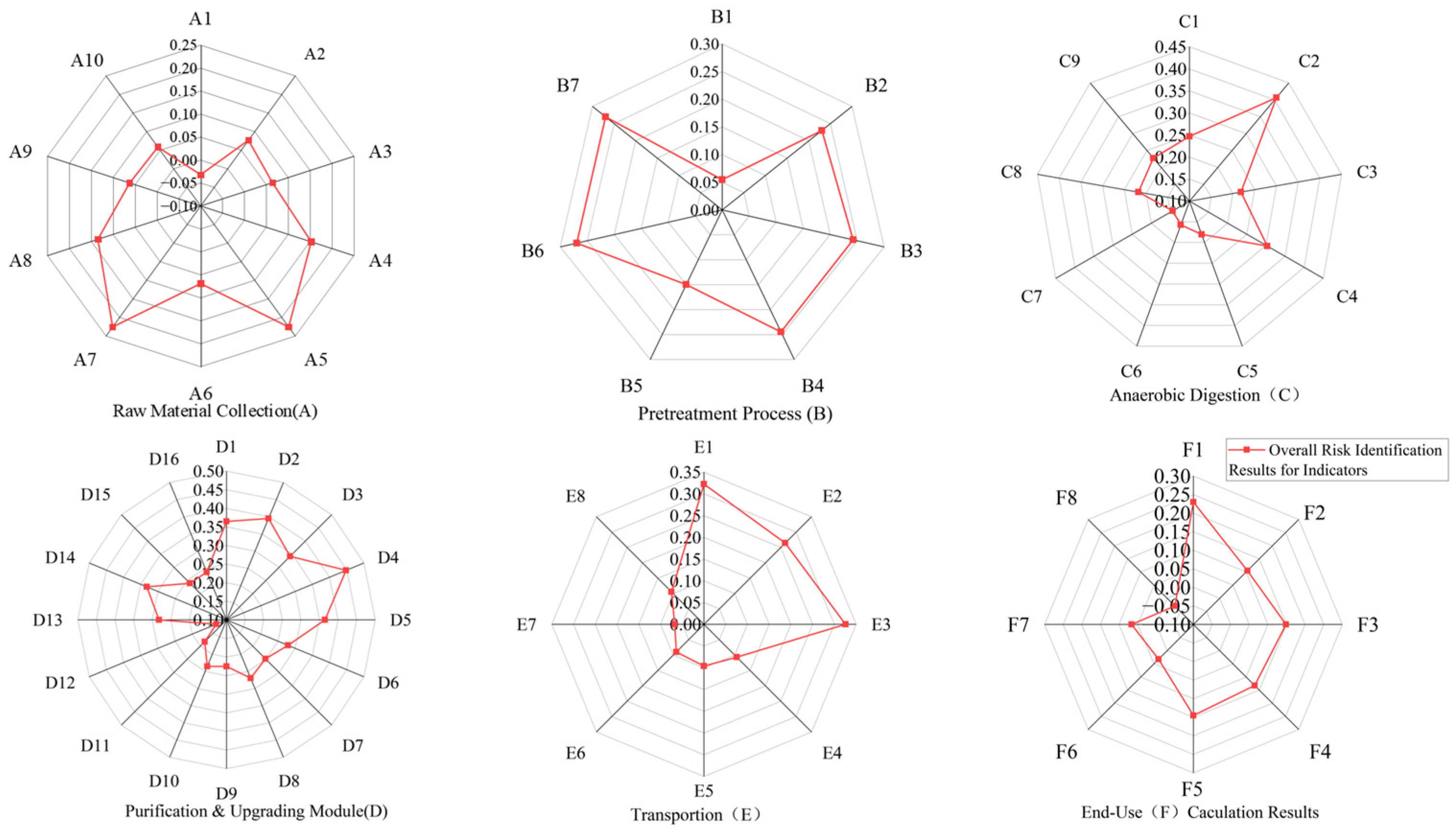
(1)

Overall, the top three highest risks are: D2—hypoxia caused by sulfur compound leakage (0.395), C2—fire caused by anaerobic fermentation process (0.406), and D4—combustible gas burning due to ignition sources (0.448).

(2)

From the perspective of work breakdown items, W₄₁ (desulfurization operation) has the most risks and the highest risk values, followed by W₃₁ (mechanical stirring), while W₁₁ (manure collection) presents the lowest risk.

(3)

From the perspective of risk factor breakdown, R₅₁ (unreasonable management organization) has the most risks and the highest risk values, followed by R₂₁ (ignition sources). The lowest risks are R₁₃ (struck by objects), R₁₄ (falls and puncture wounds), R₁₆ (frostbite), R₃₂ (heavy metals), and R₃₅ (presence of chemical toxicity).

(4)

From a comprehensive module perspective, both the anaerobic fermentation and purification and upgrading modules contain the most sub-risk items and have the highest risk values, warranting special attention.

When the interval number degenerates to 0, it indicates that the WBS-RBS pair carries no risk. The negative values in the figure are related to the decision-maker’s penalty factor ε, which is set to 1 in this case (ε = 1).

As can be seen from Figure 8a, the possibility analysis from the perspective of work item factors reveals:

(1)

In the entire W₁ (raw material collection) process, overall, W₁₁₁, W₁₁₂, and W₁₁₃ each have one severe risk point, while W₁₃₁ has three risk points with relatively high risk values. This indicates that W₁₃₁ (incineration of dead livestock) presents relatively more serious risks during the entire raw material treatment process.

(2)

In the W₄ (purification and upgrading) process, there are the most risk factors, with 6 out of the top 10 risks belonging to W₄. The highest-ranked risk is D₄—combustion of flammable gas due to ignition sources (0.034), demonstrating that the purification and upgrading module contains the most risk points and has the highest risk values in the LMtB supply chain, requiring key supervision.

(3)

In the W₃ (anaerobic fermentation) process, C₂—fire caused by anaerobic fermentation process is the second highest risk point. W₃₃ and W₃₄ each have two types of highest-ranked risks.

(4)

Compressed gas tanker transportation (W₅₁) and pipeline transportation (W₅₂) each have one highest-ranked risk. The above processes require special attention from relevant departments.

As shown in Figure 8b, the possibility analysis of risk factors reveals:

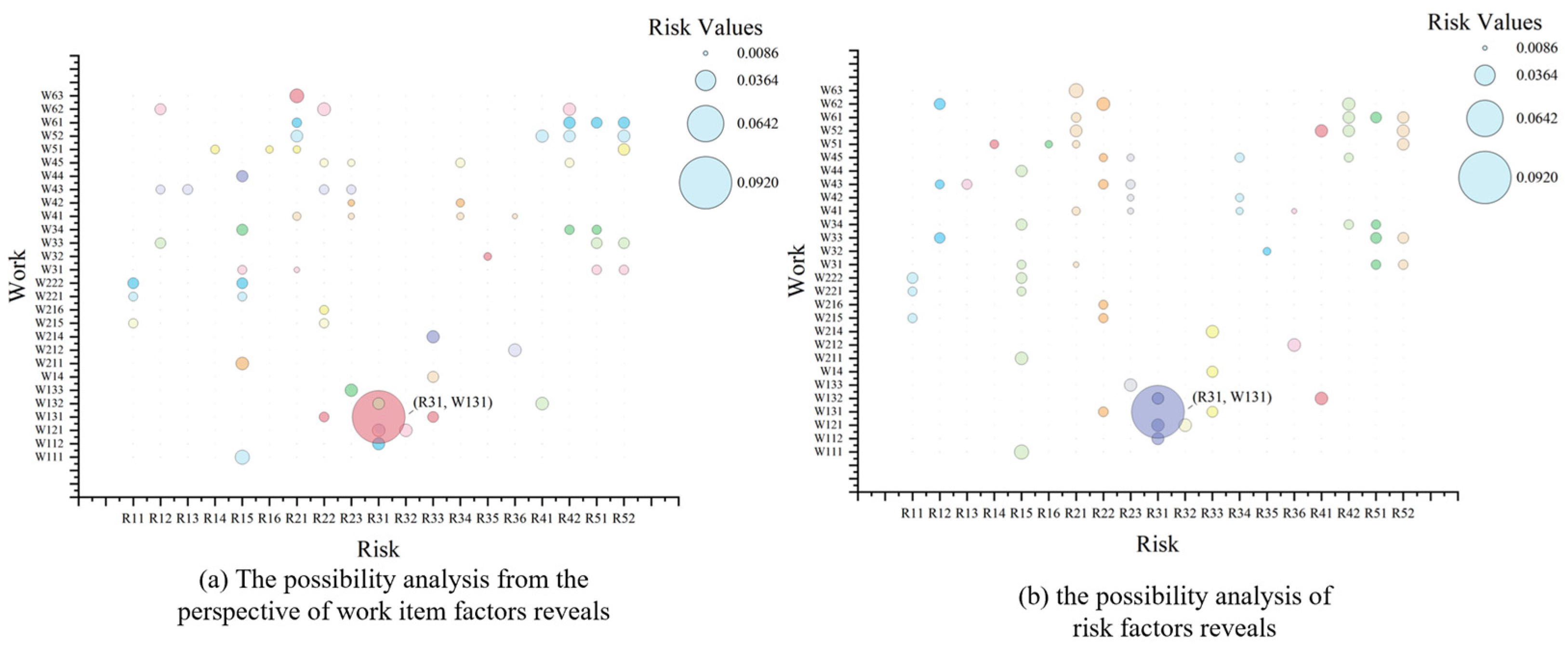
(1)

The two risk factors R₁₅ (unreasonable management organization) and R₂₁ (ignition sources) show the highest occurrence frequencies across all transportation processes, with 8 and 6 occurrences, respectively. This indicates that special attention should be paid to the rationality of management organization design, and strict monitoring should be implemented for ignition source control. These two risk factors require prioritized management by relevant departments.

(2)

The four risk factors R₂₂ (improper operation), R₂₃ (leakage), R₄₂ (pipeline risks), and R₅₂ (personnel management) demonstrate identical occurrence frequencies (5 times each), which are also relatively high. These risk categories warrant significant attention.

(3)

In conclusion, from the perspective of risk factor analysis, the following aspects require particular attention and control in the LMtB supply chain system: rational design of management organization, effective control of ignition sources, proper operational procedures, valve control to prevent leakage risks, safety-conscious pipeline design, and personnel management for operational supervision.

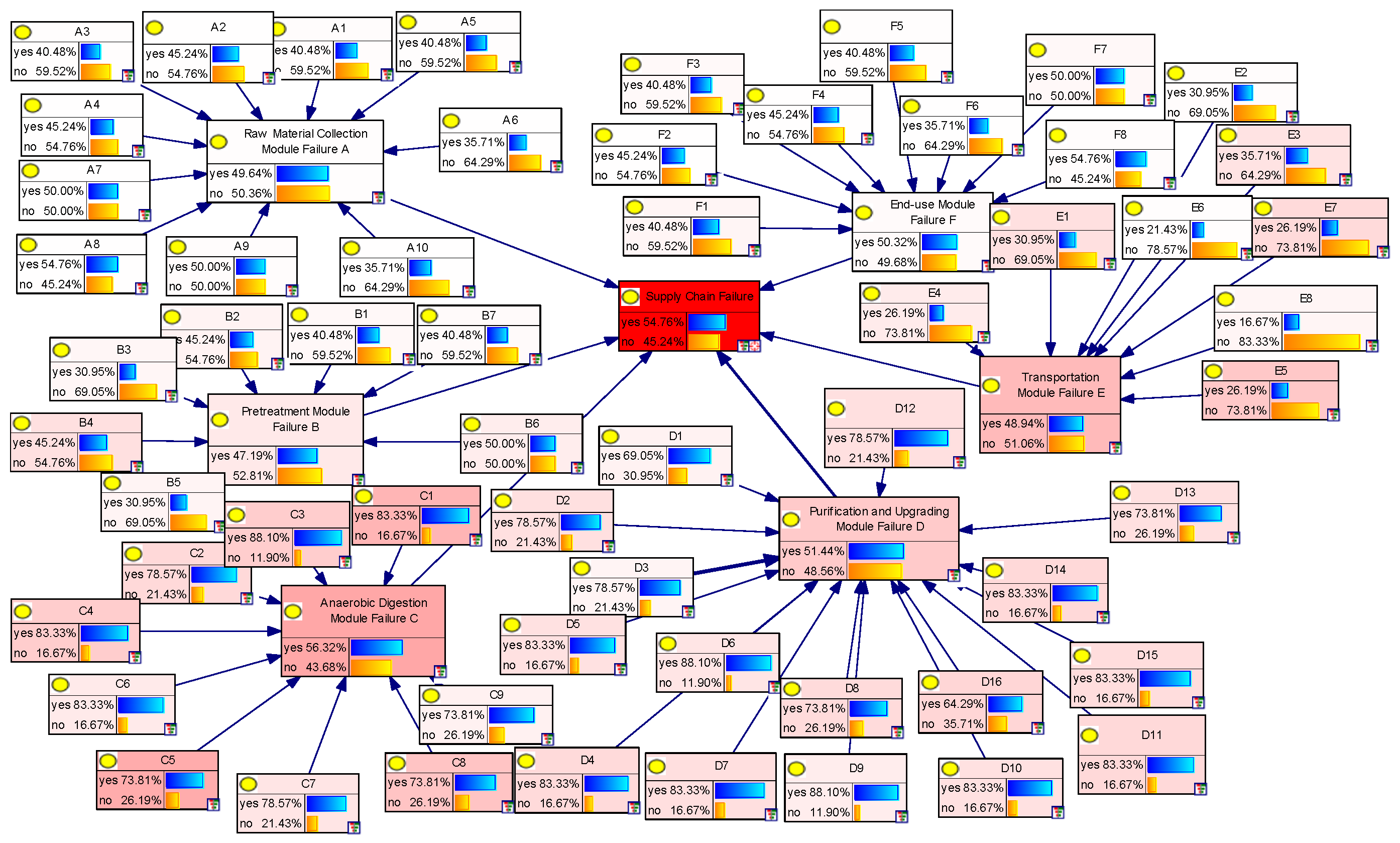
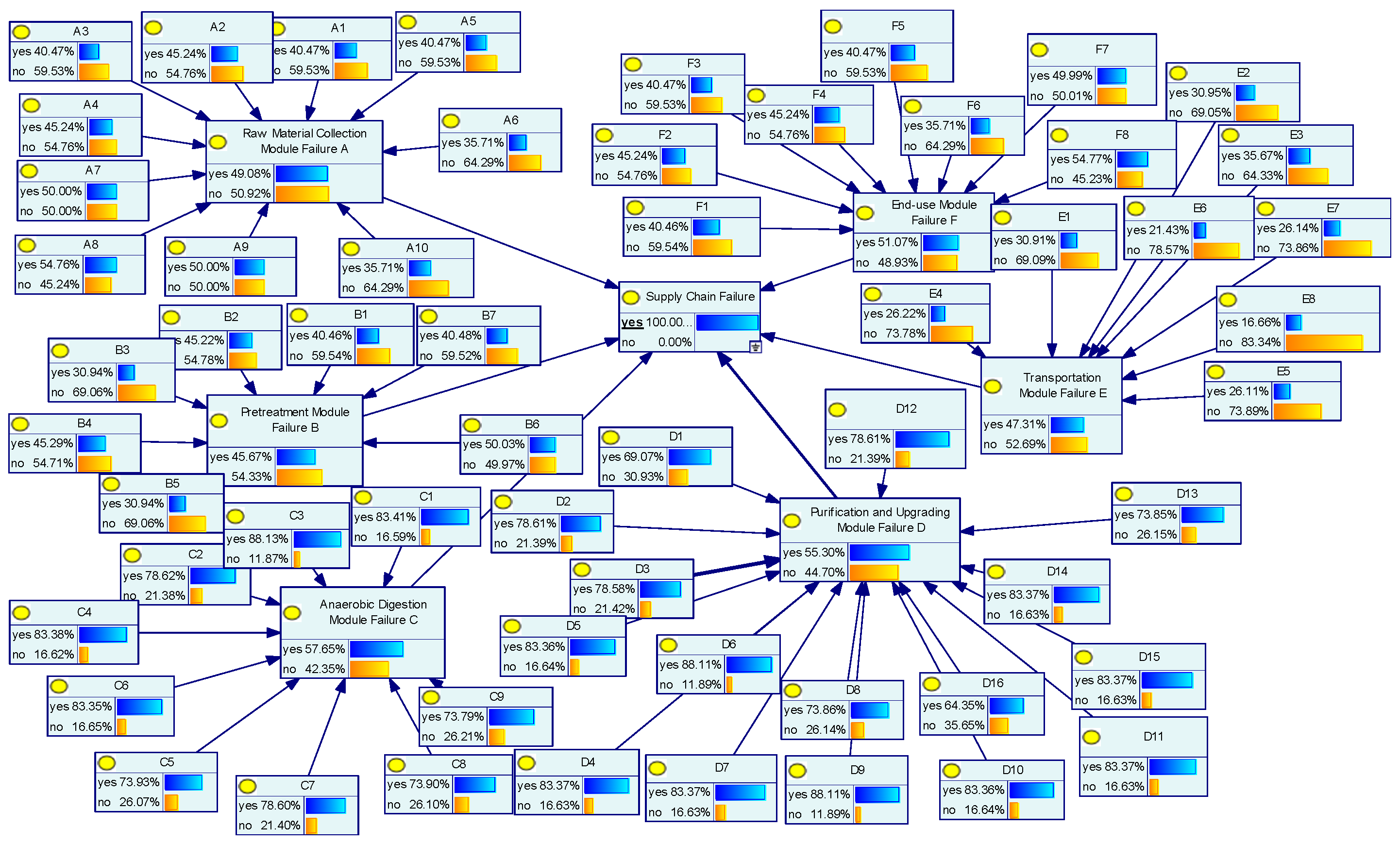
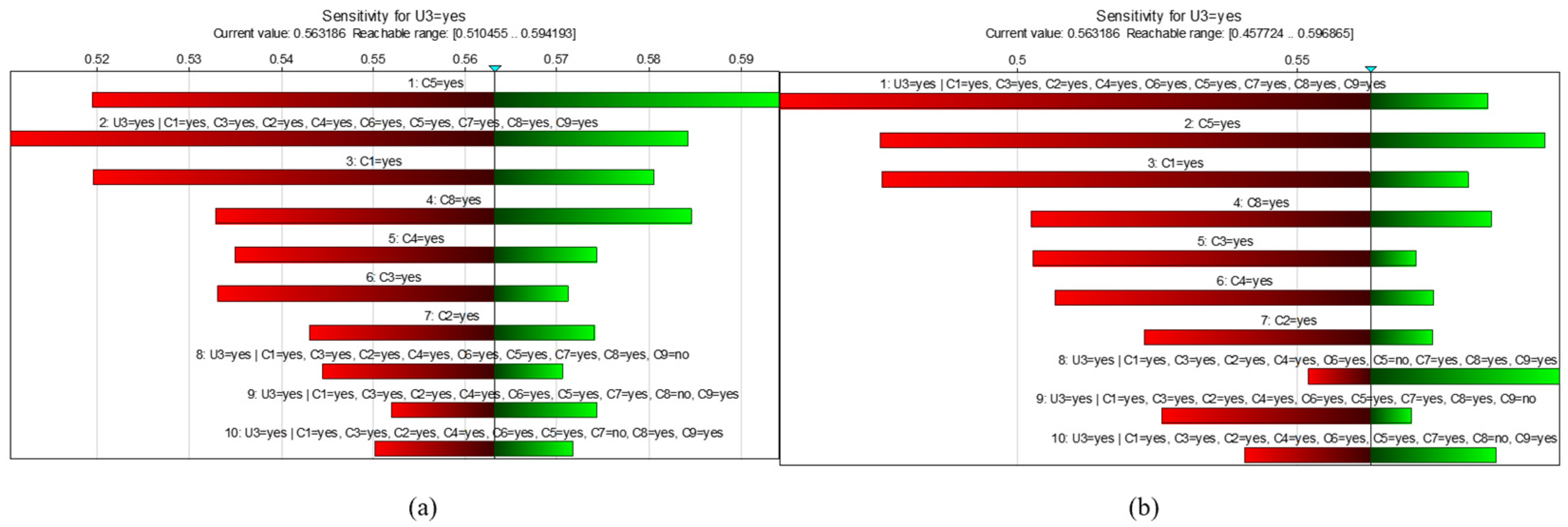
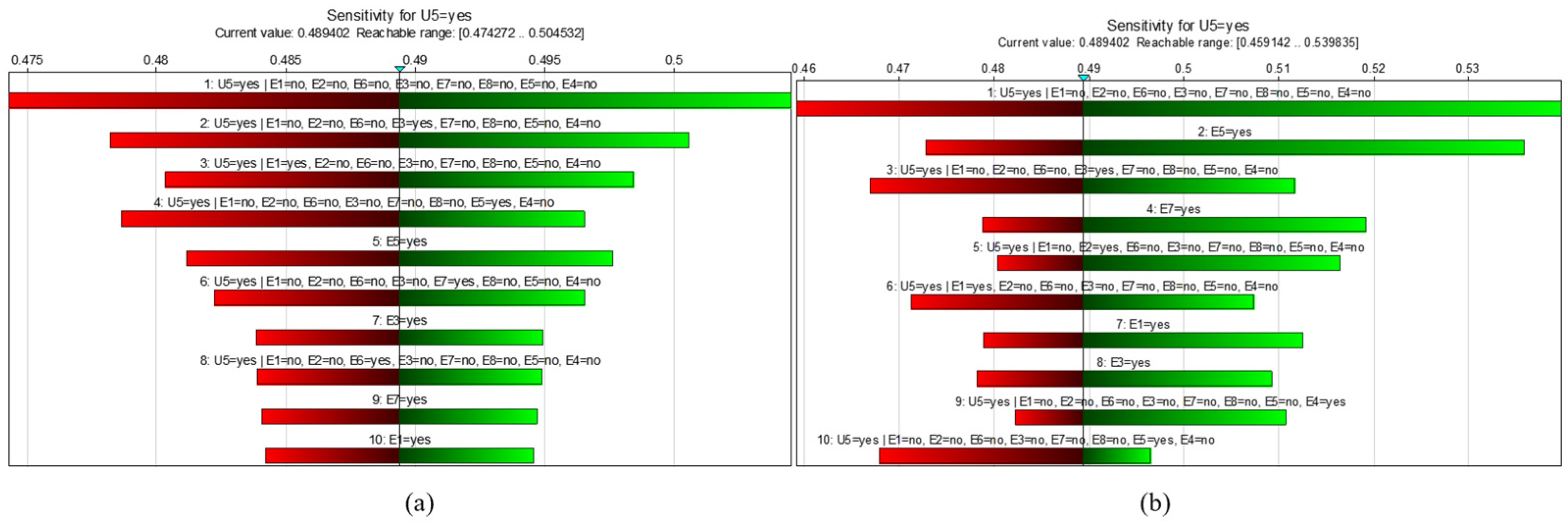
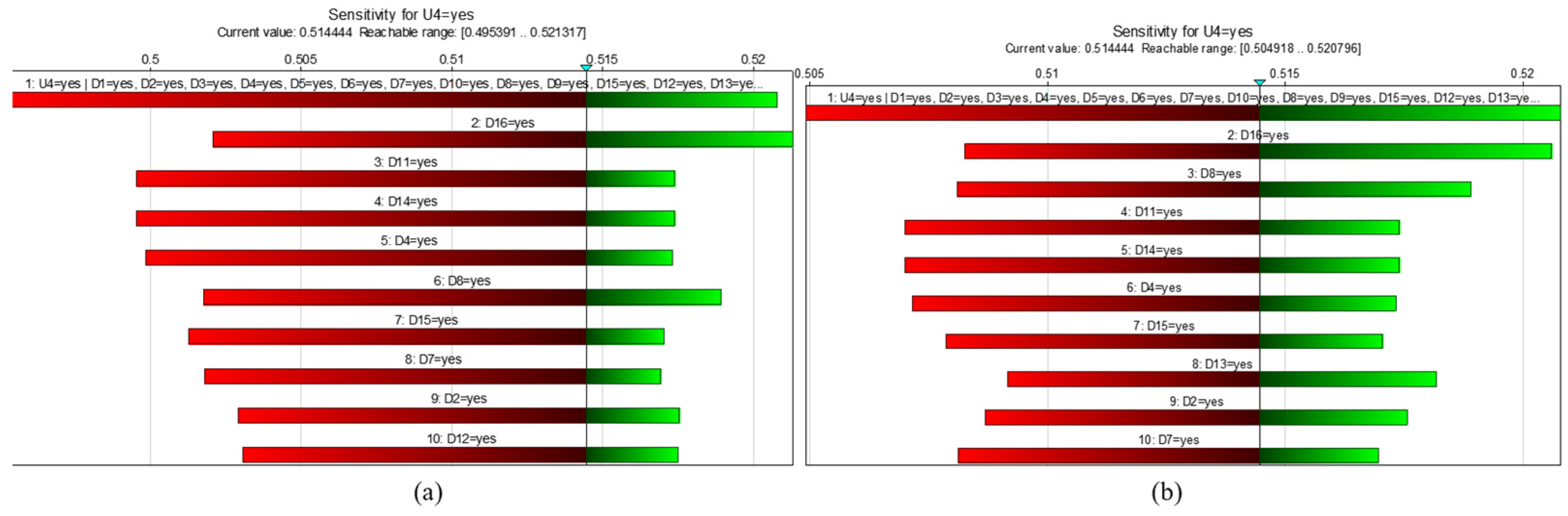
3.4. Bayesian Modeling Analysis

The processed structured data (Tables S5–S11 in the Supplementary Materials) was imported into the BN software GeNIE 4.0, and structural learning was performed using relevant expectation algorithms. The BN model was adjusted and refined by incorporating node correlation analysis results. In order to calculate the BN, experts in relevant fields were invited to conduct a linguistic assessment of the probability of these 58 risk factors according to the probability of occurrence of each risk factor. As shown in Figure 9, the BN model comprehensively reflects the causation of failure accidents in the LMtB supply chain and the causal relationships among various factors. By setting target nodes in the model, perform correlation analysis. The directional arrows between nodes represent cause–effect relationships between variables. The target node (Supply Chain Failure) serves as the study subject in the model, demonstrating significant inherent causal relationships with: A (Raw Material Collection Module Failure); B (Pretreatment Module Failure); C (Anaerobic Digestion Module Failure); D (Purification and Upgrading Module Failure); E (Transportation Module Failure); F (End-use Module Failure) Furthermore, close causal relationships exist among other nodes. Investigating these relationships enables in-depth analysis of the contributing factors to accidents in the biomethane supply chain from livestock manure, facilitating identification of the most critical influencing factors at their source.

The E-step and M-step are iterated repeatedly to obtain the optimal solution. The Bayesian conditional probability table serves as the link reflecting relationships between nodes and forms the foundation for BN inference. Through parameter learning, the conditional probabilities between nodes can be derived. This is achieved by using the “Learn Parameters” function in GeNIE software. For this purpose, the established node names and states are matched with the data, where “Yes” indicates the node state is “True (failure)” and “No” indicates the node state is “False (no failure)”. The values of the conditional probability in Tables S6–S11 in the Supplementary Materials are input into GeNIE 4.0 for parameter learning.

Equations (10) and (11) were used to solve the fuzzy number. When the optimistic coefficient α is 0.5, the representative value of blur value P_A1 is:

$$P_{A1}={\displaystyle \frac{f_{FL}+f_{FL}+\dots +f_{FL}}{64}}$$

(10)

$$\begin{array}{l}I=\alpha u_R\left(P\right)+\left(1-\alpha \right)u_L(P)\\ =0.5\times (0.1+0.30)+0.5\times (-0.1+0.50)\\ =0.40\end{array}$$

(11)

From the calculation results, we obtained P (X1 = Yes) = 0.40, P (X1 = No) = 0.60. Similarly, we obtained the prior probability of other nodes. These results can be batch-calculated using the parameter learning feature built into GeNIE 4.0.

Causal reasoning was performed using GeNIE 4.0 software according to the prior and conditional probabilities of nodes. Under normal operating conditions, the calculated probabilities are of supply chain failure: 54.76%; Probability of non-failure (safe operation): 45.24%. The established reasoning model is shown in Figure 10.

Assuming the livestock manure supply chain has already failed (P(Supply Chain Failure) = 1), the posterior probabilities of each node were calculated through deductive reasoning. By analyzing and comparing the magnitudes of these posterior probabilities, we identified the most likely hazard categories responsible for the supply chain failure accident.

As shown in Figure 11, under the condition that the entire LMtB supply chain has failed, the posterior probability analysis reveals that the anaerobic digestion module and purification and upgrading module exhibit the highest failure probabilities. Three failure points show the maximum occurrence probability of 88.11%: mechanical stirring failure (C₃), corrosion-induced ammonia leakage poisoning (D₆), and equipment explosion caused by excessive pressure from overheating during dehumidification (D₉). When ranked by posterior probability in descending order, the failures are: mechanical stirring failure (C₃) caused by unreasonable management organization and insufficient supervision, ammonia poisoning (D₆), and pressure-induced equipment explosion (D₉). This indicates these three secondary risk factors are the primary causes of supply chain failures.

The root causes are analyzed as follows: Mechanical stirring failure (C₃) results from poorly designed management systems and inadequate supervision implementation. Ammonia poisoning (D₆) likely occurs due to improper operation during nitrogen removal in purification processes, leading to ammonia leakage and operator exposure. The pressure-induced explosion (D₉) may be caused by incorrect dehumidification/heating operations coupled with malfunctioning pressure relief valves.

Therefore, during supply chain risk identification, particular attention must be paid to: examining the rationality of management systems and supervision effectiveness, ensuring proper execution of nitrogen removal operations according to guidelines, and verifying correct operation of pressure valves and dehumidification processes. The translation maintains all technical terms consistently, including “anaerobic digestion module”, “purification and upgrading module”, “mechanical stirring failure”, and preserves the exact probability values (88.11%) and failure codes (C₃, D₆, D₉) from the original text.

Based on the constructed LMtB supply chain model, with supply chain failure selected as the target node, the sensitivity between nodes was calculated through reasoning using GeNIE software. The Sensitivity Analysis algorithm was applied to conduct sensitivity analysis on the root nodes of the supply chain, as shown in Figure 12. The quantitative analysis results from the sensitivity tornado diagram were transformed into an intuitive sensitivity analysis chart. In Figure 9, the darker the color of a root node, the greater its impact on the leaf node, indicating higher sensitivity. As illustrated, among anaerobic digestion failures, the three hazard categories with the highest sensitivity are C₁ (mechanical stirring operation failure causing harm), C₅ (improper operation by workers leading to sulfide overflow and chemical toxicity), and C₈ (inadequate supervision affecting subsequent operations). These are followed by E₅ (improper pipeline transportation operation causing leakage and severe explosion upon encountering ignition sources), E₇ (insufficient management awareness and inadequate supervision), and E₃ (leakage causing frostbite to operators) in the transportation module. Further down are D₁₆ (unreasonable pipeline design) and D₁₁ (mechanical failure in other solid treatment operations) in the purification and upgrading process. These results indicate that they are the key hazards leading to supply chain failures. The data obtained from the BN model of supply chain failure aligns well with actual failure impacts, demonstrating its reference value.

By conducting sensitivity analysis on the root nodes of the BN diagnostic model for the livestock manure-to-natural gas supply chain, the degree of influence of changes in root node network parameters on the output probability of leaf nodes was obtained. With T = yes (failure) set as the target for supply chain failure sensitivity analysis, parameter fluctuation ranges were set at 50% and 100% to most effectively and clearly reflect the differences in sensitivity of various root nodes to leaf nodes.

As shown in Figure 10 and Figure 12, among the top 10 influencing nodes, the individual root node C₅ (improper operation by workers leading to sulfide overflow and chemical toxicity) demonstrates the highest degree of impact on the leaf node T = yes (failure condition). Following closely in sensitivity are C₁ (mechanical stirring operation failure causing harm), C₈ (inadequate supervision and management resulting in scald injuries), and C₄ (improper operation during pre-desulfurization process causing sulfide overflow and chemical toxicity damage). The results clearly indicate that operational procedure failures and management supervision deficiencies constitute the most critical sensitivity factors affecting system failure in the anaerobic digestion module, with chemical toxicity risks showing particularly prominent sensitivity characteristics. This pattern remains consistent across both the sensitivity diagram and tornado chart analyses, confirming the reliability of these findings for risk management prioritization in the LMtB supply chain system.

As shown in Figure 10 and Figure 13, within the transportation module’s top 10 influential nodes, the individual root node E₅ (improper pipeline transportation operation causing leakage and severe explosion upon encountering ignition sources) demonstrates the greatest impact on the leaf node T = yes (failure state). Following closely in sensitivity are E₁ (leakage caused by operational errors), E₃ (leakage-induced frostbite to operators), and E₇ (insufficient safety awareness among management personnel and inadequate supervision). The results clearly indicate that pipeline operation risks and management oversight deficiencies constitute the most critical sensitivity factors affecting transportation failure, with operational procedure violations showing the most substantial impact on system reliability.

In the purification and upgrading module, with T = yes (failure) set as the target for supply chain sensitivity analysis, parameter fluctuation ranges of 50% and 100% were, respectively, established to most effectively and clearly demonstrate the sensitivity differences in various root nodes on the leaf node, as shown in Figure 14.

As can be seen from Figure 14, among the top 10 influential nodes, the single root node D₁₆ (unreasonable pipeline design leading to serious accidents) exhibits the greatest impact on the leaf node T = yes (failure state). This is followed by nodes with relatively high sensitivity: D₁₁ (mechanical failure in other solid treatment operations causing harm), D₁₄ (leakage of hazardous gases), and D₄ (presence of ignition sources causing combustible gas combustion). These results clearly indicate that equipment design flaws and mechanical operational failures constitute the most critical sensitivity factors affecting purification process failures, with pipeline design risks showing the most substantial impact on system reliability.

By identifying the maximum causation chains to locate critical risk factors, we highlight the key risk pathways (most probable accident causation chains) using bold arrows. With supply chain failure (T = yes) set as the target node, through variable sensitivity and maximum causation chain analysis, we determined that among all potential causation chains leading to failure in the LMtB supply chain, the most likely causation chain is as shown in Figure 9 and Figure 10: Improper desulfurization operation may cause equipment corrosion → Purification and upgrading failure → Entire supply chain failure.

4. Conclusions

This study comprehensively employs the WBS-RBS method and BN model to identify and assess risks within the LMtB supply chain. Severity analysis using mathematical methods indicates that risks are most concentrated in the anaerobic digestion and purification modules, where consequences are also most severe. Bayesian diagnosis further identified the three critical risk points with the highest occurrence probability: mechanical stirring failure C3 (88.11%), ammonia poisoning D6 (88.11%), and equipment explosion D9 (88.11%) caused by overheating and overpressure. Sensitivity analysis revealed the core risk transmission chain: Improper desulfurization → Equipment corrosion → System failure. In summary, the purification process warrants special attention in risk management due to its high probability and severity.

Based on this quantitative analysis, the critical risk points and their probability rankings provide clear priorities for management. It is recommended that the operator translate these findings into three concrete actions: implement preventive monitoring for high-probability risk points (e.g., mechanical agitation failure C3, 88.11%); install gas interlock alarm systems in purification processes to prevent ammonia poisoning (D6) and explosions (D9); and establish mandatory standard operating procedures and training targeting the root cause of desulfurization operations. This approach transforms theoretical models into targeted safety control measures. However, this study still has the following limitations: First, model construction relies on expert experience and historical experience, which may limit its applicability in scenarios with scarce data or emerging risks. Second, although the BN structure is determined based on WBS-RBS decomposition and causal logic, it still involves some subjective judgment. Future research could optimize this through data-driven methods (such as structure learning).